Abstract
The permeability of multicomponent phospholipid bilayers in the gel phase is investigated via molecular dynamics simulation. The physical role of the different molecules is probed by comparing multiple mixed-component bilayers containing distearylphosphatidylcholine (DSPC) with varying amounts of either the emollient isostearyl isostearate or long-chain alcohol (dodecanol, octadecanol, or tetracosanol) molecules. Permeability is found to depend on both the tail packing density and hydrogen bonding between lipid headgroups and water. Whereas the addition of emollient or alcohol molecules to a gel-phase DSPC bilayer can increase the tail packing density, it also disturbed the hydrogen-bonding network, which in turn can increase interfacial water dynamics. These phenomena have opposing effects on bilayer permeability, which is found to depend on the balance between enhanced tail packing and decreased hydrogen bonding.
Introduction
Permeation is essential to the regulating function of biological systems, such as the bilayers found in cell membranes,1 including the blood–brain barrier,2 and the lamellar lipid structures found in the skin.3,4 Whereas the permeability of fluidlike (i.e., liquid-crystalline) bilayers has been actively studied,5−8 little work has focused on dense gel-phase mixtures, for which the permeability is likely to be dictated by different mechanisms than for fluidlike bilayers. For example, it has been suggested that the barrier domain is located deeper in fluidlike phospholipid bilayers than in gel-phase bilayers.9 This is based upon the idea that for fluidlike bilayers the area occupied by the lipid tails exceeds the projected headgroup area and thus provides space for water molecules to be able to freely move between the lipid headgroups; in contrast, gel-phase systems tend to have densely packed headgroups, which limits the water mobility at the interface.10 It is also known that the diffusion coefficient of water in a fluidlike bilayer interior is similar to that of bulk water,11 whereas water diffusion in gel-phase bilayers is typically 2 orders of magnitude smaller than in bulk.12 As such, although partitioning has been suggested to be the rate-limiting step in the permeability of fluidlike bilayers,11 diffusion may play a more dominant role in gel-phase bilayers. Experimentally, it is not possible to determine direct cause-and-effect relationships because of the difficulty of inferring molecular-level details from experiments. For example, some researchers have ascribed a low permeability in gel-phase ceramide-based multicomponent bilayers to a hexagonal-to-orthorhombic transition in the lateral lipid packing, driven by the presence of long-chain free fatty acids,13 whereas others have attributed the low permeability to a long-periodicity lamellar phase.14 The permeability of ceramide-based bilayers has been reported to decrease further when emollient molecules (such as the ones considered in this study) are added.15 This decrease has again been associated with the long-periodicity phase by some,15 whereas others found little change in the lamellar phase and suggested that the formation of emollient domains decreased the permeability,16 with emollients serving as space-filler molecules.17
These questions surrounding the permeability mechanism of gel-phase systems clearly indicate that the process is not fully understood. Although various experimental methods are able to measure permeability, they are unable to elucidate local contributions to the membrane resistance or the pathway of the permeating molecules. Molecular dynamics (MD) simulations have played a key role in the study of bilayer permeability since the pivotal paper by Marrink and Berendsen in 1994,18 in which MD was used to investigate the permeation of water across a fluidlike dipalmitoylphosphatidylcholine (DPPC) bilayer. The authors derived the inhomogeneous solubility–diffusion equation, which relates the bilayer permeability to the one-dimensional excess free energy and transverse diffusion coefficient profiles across the bilayer. It thus relates a global property, which can be compared to experiments, to local information that is not accessible in experiments, but available in a simulation. The number of simulations reporting permeability has increased rapidly in recent years,7,19,20 with a particular focus on the permeation of small drug molecules across fluidlike bilayers.2,21−24 Simulations of gel-phase bilayer permeability are far less common because of the high computational cost of gel-phase bilayer simulations combined with the cost of permeability simulations. Some studies25,26 have mitigated these issues by calculating only free-energy profiles and not permeability; permeability also requires the determination of the diffusional contribution. Such an approach can give an indication of how different bilayers or permeants compare but is not sufficient to provide a detailed understanding of permeation mechanisms.
To the best of our knowledge, permeability coefficients for water in gel-phase bilayers have been calculated in silico by two groups;27−29 however, neither of which considered gel-phase phospholipid bilayers or the effect of long-chain alcohols/emollients on bilayer permeability. In one study, Das et al.27 calculated via MD simulations the permeation of water across ceramide-based lipid bilayers. The free-energy barrier was found to be twice that of a fluidlike phospholipid bilayer and was attributed to the denser tail packing in the gel phase. Furthermore, once water permeated past the lipid headgroups, it could diffuse easily through the tail region, such that the free energy of solvation was the main barrier to permeation. Others30 have compared the permeation of small hydrophobic drug molecules through a fluidlike dioleoylphosphatidylcholine (DOPC) bilayer and through a gel-phase ceramide bilayer. The penetration free energy barrier was found to be larger and closer to the surface for the gel-phase ceramide bilayer, owing to its dense tail packing. Another MD study28 focused on permeation of hydrophilic and hydrophobic molecules across gel-phase ceramide bilayers. Although the diffusion profiles obtained were qualitatively similar for each of the permeate molecules, the barrier domain was found to be located deeper into the bilayer interior for hydrophilic permeates than for hydrophobic ones. The same group subsequently studied the effect of ceramide tail length on the permeability of water and found that the permeability decreased with an increasing ceramide tail length.29
The aim of the present study is to explore the composition–structure–permeability relationships of gel-phase phospholipid-based bilayers. To this end, the permeability and structural properties of different pure and mixed-component bilayers are compared, with lipid molecules varying in tail length, headgroup chemistry, number of tails per molecule, and tail side branching. Specifically, we examine systems whose structural properties have been previously studied in detail,31,32 namely, pure distearylphosphatidylcholine (DSPC) bilayers and binary mixtures of DSPC with isostearyl isostearate (ISIS, an emollient molecule) and with alcohol molecules with acyl tail lengths of 12 (lauryl or dodecanol), 18 (stearyl or octadecanol), and 24 (lignoceryl or tetracosanol) carbon atoms (see Table 1). The lauryl, stearyl, and lignoceryl alcohols are henceforth referred to as C12, C18, and C24, respectively. The remainder of this article is organized as follows. First, details of the simulations and analysis are given, followed by a discussion of bilayer permeability theory. We then present and discuss our results and, finally, summarize our findings and draw conclusions.
Table 1. Overview of the Bilayers Simulated in This Studya.
| pure | 7:1 | 3:1 | 1:1 | 1:2 | |
|---|---|---|---|---|---|
| DSPC | √ | ||||
| DSPC–ISIS | √ | √ | |||
| DSPC–C12 | √ | √ | √ | √ | |
| DSPC–C18 | √ | ||||
| DSPC–C24 | √ |
Each system contains either pure DSPC or DSPC mixed with emollient (ISIS) or alcohol molecules with tail lengths of 12, 18, or 24 carbons in the compositions indicated.
Materials and Methods
Simulation System
The structural properties and permeability of a pure DSPC bilayer and eight two-component DSPC-based bilayers were investigated, as listed in Table 1. Compositions were varied from bilayers in which the phospholipid concentration dominates (7:1) to systems in which the alcohol molecules dominate (1:2).
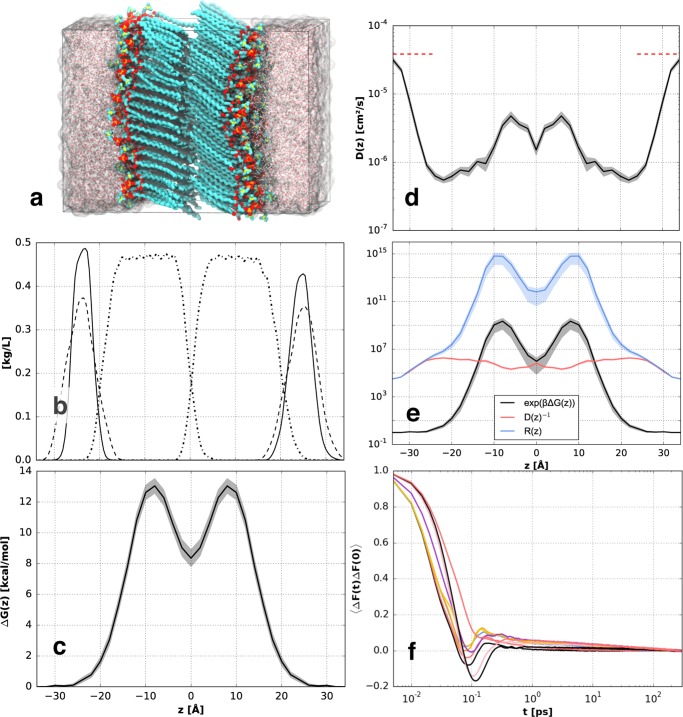
Bilayers were assembled by placing 2 leaflets, each with 64 lipids organized in a square lattice, in a bath of 2560 water molecules, where the initial lattice spacing was chosen to correspond to an area per lipid (APL) of approximately 20% larger than the estimated final APL, based on prior simulations.31,32 This larger initial APL enabled lipids to rearrange and reorient during the equilibration. The lipids were initially randomly rotated about their long axis and tilted 10° with respect to the bilayer normal. The lipids in the two-component bilayers were randomly distributed among the lattice sites to mimic a mixed system, with both leaflets having a different random arrangement with the same relative lipid concentration. The importance of random rotations about the long axis of molecules was recently demonstrated for a phosphatidylethanolamine bilayer in the gel phase;33 unrealistic tilt of the lipid tails has been observed if the lipid backbones (i.e., the part connecting the two tails of a molecule) are initially aligned in the bilayer plane. The headgroup of the alcohol or emollient molecules was placed at the same depth as the phosphate group of the phospholipids. Lipids were represented by the united atom GROMOS g53a6 forcefield34 with partial charges from Chiu et al.35 for the DSPC molecules, whereas the other molecules were created using Automated Topology Builder Version 2.1.36 Water was modeled with the simple point charge (SPC) model, with the rigid structure preserved using the SHAKE algorithm. MD simulations were performed using the LAMMPS simulation engine.37 Dispersion interactions were described by a Lennard-Jones potential, with a cutoff distance of 14 Å. The particle–particle particle–mesh method was used to calculate electrostatic interactions, with the real part truncated at 14 Å.38 The Nosé–Hoover thermostat and barostat were used to maintain a constant temperature of 305 K and a pressure of 1 atm, respectively. Following the protocols that were used and validated in prior work to equilibrate the systems studied,31 each bilayer was simulated for 160 ns, of which the last 60 ns was used for structural analysis. The final configuration of each simulation was then used as a starting configuration for the permeability simulations, as described below. Figure 1 provides the structures of the molecules studied and a representative simulation snapshot for a (1:1) DSPC–C12 alcohol bilayer immersed in water.
Figure 1.
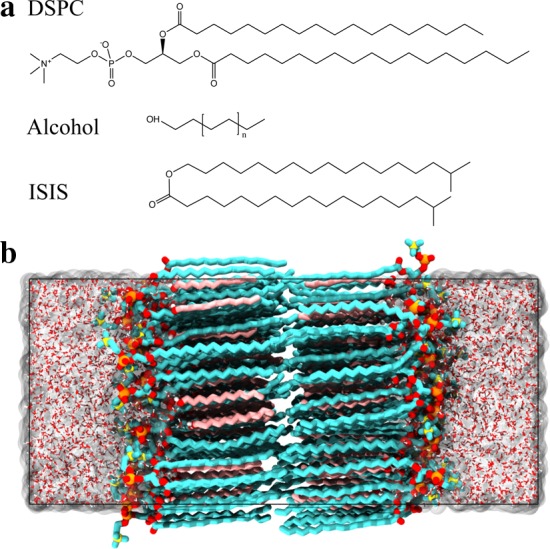
(a) Structure of the DSPC, alcohol, and ISIS molecules. (b) Snapshot of a typical bilayer configuration of an equimolar mixture of DSPC and C12 alcohol immersed in water. Hydrocarbons are shown in cyan (DSPC) and pink (alcohol), oxygen is shown in red, phosphorus is shown in orange, nitrogen is shown in yellow, and hydrogen is shown in white.
The atom positions and the size of the simulation box throughout the simulation were used to calculate the area per lipid (APL), the offset distance, the bilayer height, H, the average tail tilt angle, θ, and the area per tail (APT). The APL was calculated by dividing the cross-sectional area of the simulation box by the number of lipids in the leaflet. The offset distance was determined as the difference between the average depth (z-position) of the phosphate group of the DSPC molecules and the hydroxyl (alcohol) or ester (emollient) headgroup. The bilayer height was defined as the distance between the average z-position of the phosphates in both leaflets. The tilt of lipid tails was calculated from the average angle between the long axis of each tail and the transmembrane axis, where the long axis is the eigenvector corresponding to the minimum eigenvalue of the inertia tensor. Finally, the APT was calculated by dividing the APL by the average number of tails per molecule and multiplying this by the cosine of the average tilt angle, to project the area onto a plane perpendicular to the average chain direction. The APT can be considered as an inverse tail packing density, with the packing considered in the plane perpendicular to the orientation of the tails.
Permeability Calculations
The global permeability coefficient, P, can be calculated from the inhomogeneous solubility–diffusion equation18
| 1 |
where R is the resistance, β is the inverse of the thermal energy, ΔG(z) is the local excess free energy, and D(z) is the local diffusion coefficient. We note that eq 1 can be derived from the one-dimensional Nernst–Planck equation assuming that the system is at a steady state.7 Furthermore, the use of eq 1 is based on the assumption that the movement of a permeating molecule across the bilayer is the only relevant slow variable in the system.39 The diffusion coefficient and free energy were calculated via the z-constraint method,18 which has been widely adopted because it simultaneously provides access to the excess free energy and the transverse diffusion coefficient profiles, in contrast to other methods, which can be used only to calculate either the free energy24,40,41 or the diffusion coefficient profile.42−44 In the z-constraint method, the excess free energy and diffusion profiles are calculated from the forces in the z-direction acting on “tracer” water molecules constrained in z along the transmembrane axis as
| 2 |
| 3 |
where the angular brackets denote an ensemble average, Rg is the gas constant, T is the temperature, and ΔFz = Fz – ⟨Fz⟩t is the force fluctuation. Between 35 and 48 z-positions (depending on the bilayer height; see Table S1 in the Supporting Information) were defined, separated by 2 Å. A randomly selected water molecule was moved to one of the z-positions (“windows”) and then constrained in z (additional details provided in the Supporting Information). The simulation system was then equilibrated for an additional 500 ps beyond the initial 160 ns, followed by a 1.3 ns simulation during which the net z-force on the constrained water molecule was measured. These relaxation and sampling times, although short compared to the slow lipid dynamics, are a multiple of the slowest relaxation time of water molecules in the bilayer. Specifically, the force autocorrelation functions indicate a maximum relaxation time of 200–300 ps in the headgroup region, where water molecules form hydrogen bonds (HBs) with their environment. Shorter relaxation times were found in the tail region where water molecules were observed to move through the triangular voids between the hexagonally packed tails, thus requiring no lipid reorganization and no hydrogen bonds to be broken or formed. Furthermore, no unconstrained water molecules were found to partition into the lipid tail region along with the tracer molecule. To sample a water molecule at various locations in the bilayer and to reduce statistical uncertainty, between 35 and 75 simulations (“sweeps”) were performed for each window, with different random water molecules selected from the aqueous phase. Sampling multiple locations is particularly important to accurately represent the lateral heterogeneity of multicomponent bilayers. The computational efficiency was improved by simultaneously sampling multiple water molecules in different windows that were separated by at least 1 nm in the z-direction (see Figure S1 in the Supporting Information). Sweeps were performed until the relative uncertainty in the free-energy profile was less than 5%; bilayers with a large energy barrier typically required more sweeps than bilayers with a small barrier. The uncertainties in the calculated diffusion and excess free energy profiles both contribute to a greater uncertainty in the resistance profile, which propagates further by integrating over the profile, resulting in a final uncertainty in the permeability coefficients of approximately 20%. Even though these uncertainties are considerable, they do not affect the comparison between bilayers because the difference between the permeability coefficients is found to be much larger. Additional details on the sampling process are given in the Supporting Information.
Results and Discussion
Structural Properties
In previous work,31,32 the structure of a pure DSPC bilayer and equimolar mixtures of DSPC with alcohol or emollient molecules was investigated in detail. Although the systems in the present study are similar, smaller bilayers are considered (128 lipids instead of 200) to offset the large computational cost of permeability calculations. We first validated that the structural bilayer properties (listed in Table 2) are in good agreement with those calculated for the larger bilayer systems.31,32 Specifically, the APL and tilt angle of the pure DSPC bilayer studied here are 50.1 (0.3) and 36.5 (0.7)° Å2, respectively, compared to 49.7 (0.2) and 36.3 (0.4)° Å2 for the larger systems.31 Even closer agreement is found for each of the equimolar multicomponent bilayers, indicating that size effects are negligible for the systems considered. This is consistent with the findings of Tjörnhammar and Edholm,45 who simulated gel-phase phospholipid bilayers containing between 128 and 1296 lipids and found no significant system size dependence.
Table 2. Overview of Structural Properties (Area per Lipid, Area per Tail, Offset, Bilayer Height, and Tilt Angle) for the Bilayers Studieda.
| APL [Å2] | APT [Å2] | offset [Å] | H [Å] | θ [deg] | |
|---|---|---|---|---|---|
| DSPC | 50.1 (0.3) | 20.2 (0.2) | 48.2 (2.1) | 36.4 (0.7) | |
| (7:1) DSPC–ISIS | 44.3 (0.2) | 19.9 (0.1) | 8.0 (0.7) | 53.1 (2.1) | 25.9 (1.4) |
| (1:1) DSPC–ISIS | 42.5 (0.1) | 20.1 (0.1) | 6.6 (0.6) | 54.8 (1.7) | 18.8 (0.7) |
| (7:1) DSPC–C12 | 43.3 (0.1) | 20.0 (0.1) | 8.9 (0.6) | 50.8 (1.8) | 30.1 (0.2) |
| (3:1) DSPC–C12 | 37.5 (0.2) | 20.0 (0.1) | 8.6 (0.6) | 53.6 (1.8) | 21.1 (0.7) |
| (1:1) DSPC–C12 | 29.4 (0.1) | 19.4 (0.1) | 7.5 (1.0) | 54.1 (1.8) | 7.4 (0.4) |
| (1:2) DSPC–C12 | 26.1 (0.1) | 19.5 (0.1) | 6.9 (0.6) | 52.0 (1.8) | 6.1 (0.2) |
| (1:1) DSPC–C18 | 30.5 (0.1) | 19.8 (0.1) | 5.3 (0.5) | 56.4 (1.4) | 13.7 (0.4) |
| (1:1) DSPC–C24 | 30.0 (0.2) | 19.6 (0.1) | 5.8 (1.0) | 63.0 (1.6) | 10.8 (1.0) |
The numbers in parentheses are error estimates based on the standard deviation.
The headgroup size largely determines the APL of pure phospholipid bilayers in the gel phase because the projected headgroup area is larger than the combined cross-sectional area of the two acyl tails.9 This mismatch between cross sections is compensated for by a collective tilt of the lipid tails with respect to the transmembrane axis, thus increasing the packing density of the tails. The APT found for the pure DSPC bilayer is 20.2 Å2, in good agreement with the 19.8 Å2 found via X-ray diffraction.10 Combining the lipids with molecules that have a smaller headgroup has two major effects on the bilayer structure. First, the presence of other molecules increases the distances between phosphatidylcholine (PC) headgroups and thus mitigates the steric effects of the PC headgroups.31 Second, the difference between the molecular structures of the molecules facilitates a more efficient spatial packing and an offset forms between the headgroup depths in the bilayer.31 The effects of these mechanisms on the APT vary with the concentration of the added molecule type, with large alcohol concentrations resulting in an APT as low as 19.4 Å2. Although the offset between headgroup depths helps facilitate dense tail packing, the packing density does not always scale with the offset distance; increasing the alcohol or emollient concentration decreases the offset (owing to the decreased PC concentration), whereas it increases the packing density. Similar to the offset, the chain tilt is also closely related to the composition (i.e., the concentration of PC groups) because tilt is a consequence of the mismatch between the headgroup size and the cross section of the tails. The pure DSPC bilayer has the largest tilt (36.4°) of the bilayers considered, but the tilt drops to 25.9–30.1° when only 12.5 mol % of alcohol or emollient molecules is added to the bilayer (i.e., 7:1 mixtures), with the resulting tilt depending on the size and structure of the added molecule. The tilt angle of bilayers containing 50 mol % alcohol depends on the offset, which in turn depends on the relative tail lengths of the different molecules in the bilayer.32 Tail-length asymmetry tends to increase the offset and leads to a smaller APL, APT, and tilt than in mixtures with symmetric tail lengths (i.e., DSPC–C18). Shorter alcohol molecules (C12) can sink further into the bilayer than longer ones (C24), as shown by the location of the alcohols in the bilayer density profiles (Figure S2, Supporting Information). A large concentration of short alcohol molecules thus results in the smallest tilt, around 6–7°. Finally, the bilayer height does not follow a clear trend with the alcohol or emollient concentration.
Water–Lipid Hydrogen Bonds
It has been suggested that water partitioning into a bilayer depends on the affinity of lipid headgroups to form hydrogen bonds with water molecules.46 Although this affinity is typically seen as a property of the molecule, our recent study of multicomponent gel-phase bilayers showed that the number of hydrogen bonds and their residence times depended not only on the lipid headgroups but also on their environment and thus on the bilayer composition.31 The average number of hydrogen bonds per molecule and the hydrogen-bond residence times are calculated here (Table 3) to investigate the link among permeability, hydrogen bonding, and bilayer composition. The criterion used to determine the presence of a hydrogen bond was based on a combination of the O···H distance, rOH, being <2.35 Å and the Oj–Oi···Hi angle, ∠OOH, being <30°, where molecule i is the donor molecule and j is the acceptor.47
Table 3. Number of Hydrogen Bonds between Water and a DSPC or an Alcohol/ISIS (A, I) Molecule in the Bilayera.
| DSPC | A, I | HB/mol. | τDSPC [ps] | τA,I [ps] | |
|---|---|---|---|---|---|
| DSPC | 3.29 | 3.29 | 192.3 | ||
| (7:1) DSPC–ISIS | 3.58 | 0.40 | 3.19 | 119.1 | 145.0 |
| (1:1) DSPC–ISIS | 3.88 | 0.62 | 2.25 | 72.5 | 64.1 |
| (7:1) DSPC–C12 | 3.44 | 0.43 | 3.06 | 111.6 | 327.3 |
| (3:1) DSPC–C12 | 3.45 | 0.69 | 2.83 | 115.9 | 324.9 |
| (1:1) DSPC–C12 | 3.85 | 0.74 | 2.30 | 80.4 | 191.6 |
| (1:2) DSPC–C12 | 4.33 | 0.89 | 2.03 | 52.3 | 97.1 |
| (1:1) DSPC–C18 | 3.78 | 0.75 | 2.27 | 78.7 | 96.8 |
| (1:1) DSPC–C24 | 3.86 | 0.78 | 2.32 | 77.9 | 109.1 |
HB/mol. denotes the average number of water–lipid hydrogen bonds per molecule in the bilayer and τDSPC denotes the average residence time of the water–DSPC and τA,I denotes the water–alcohol/ISIS hydrogen bonds.
The data in Table 3 show that the number of hydrogen bonds per DSPC and per alcohol (or ISIS) molecule increases with the concentration of alcohol (or ISIS) in the bilayer. Nevertheless, the overall number of hydrogen bonds between water and the bilayer decreases with an increasing alcohol (or ISIS) concentration, caused by differences in headgroup hydration, as shown in Figure 2. The small distance between headgroups in a pure DSPC bilayer (Figure 2a) results in a partial hydration, such that the number of hydrogen bonds per PC headgroup is lower than that in a mixed-lipid bilayer, in which PC headgroups are further apart (Figure 2b–d). Similarly, an increase in the alcohol or ISIS concentration causes those headgroups to also become more accessible to water. Yet, the total number of hydrogen bonds per molecule decreases as more DSPC is replaced by alcohol or ISIS molecules because these molecules contain fewer potential hydrogen-bonding sites. Furthermore, the increased space between the headgroups gives rise to faster motion of the interfacial water, which results in shorter-lived hydrogen bonds compared to those seen in a pure DSPC bilayer. While the tail length of the alcohol molecules has a notable influence on the tail packing density and on the offset distance between headgroup depths, the tail length was found not to influence hydrogen bond numbers; however, the water–alcohol hydrogen-bond lifetime was found to increase with the depth of the alcohol headgroup in the bilayer.
Figure 2.
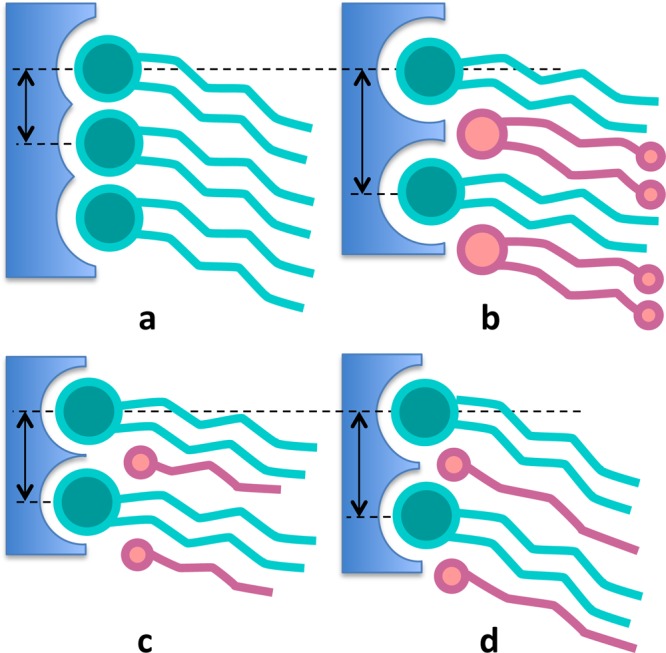
Schematic to illustrate how the amount of headgroup hydration (depicted in blue) and the space for water to move around the headgroups depends on the size and concentration of molecular species. Little space is available around headgroups in a pure DSPC bilayer (a), whereas space around the headgroups becomes accessible to water when ISIS molecules are present (b) or to a lesser extent when short (c) or long (d) alcohol molecules are added.
Permeability
Pure DSPC Bilayer
The permeability of the pure DSPC bilayer (shown in Figure 3a) is first investigated to provide a baseline before the permeability of multicomponent bilayers is studied. Figure 3b–e shows the density, excess free energy, diffusion coefficient, and resistance profile for the DSPC bilayer, respectively, whereas Figure 3f shows the force autocorrelation function corresponding to multiple windows ranging from the aqueous phase to the bilayer center. Time-averaged forces and force autocorrelation functions in each window were calculated for each sweep, after which the data were symmetrized about the middle of the bilayer and averaged over the sweeps to reduce the statistical uncertainty, depicted by the shaded areas in Figure 3c–e. The excess free energy (ΔG(z), Figure 3c) increases monotonically from 0, at the aqueous phase, toward its maximum of 13.1 kcal/mol, located in the dense tail region. The free-energy profile is comparable in shape and magnitude to the data presented by Das et al.27 for a ceramide gel-phase bilayer. The free energy denotes the energetic cost of moving water from the aqueous phase to a certain depth into the bilayer, which is partially determined by the hydration energy. One of the important contributions to this energy is the cost of breaking hydrogen bonds; for example, the hydrogen-bond strength in bulk water is approximately 2.4 kcal/mol,48 with each water molecule being involved in approximately 3.47 hydrogen bonds.47 Thus, the combined hydrogen-bond energy of water is approximately 8.3 kcal/mol. Another contribution to the partition free energy involves the cost of placing a water molecule in a dense, unfavorable (hydrophobic) environment. The free energy decreases again toward the middle of the bilayer, where water molecules can escape the dense tail packing. Interestingly, the excess free energy in the middle of the bilayer is approximately equal to the hydrogen-bond energy of bulk water, suggesting that there is no significant cost to perturbing the bilayer when water is located between the two leaflets.
Figure 3.
(a) Simulation snapshot of a DSPC bilayer, (b) mass density profile of choline (dashed lines), phosphate/glycerol (solid lines), and the lipid tails (dash-dotted lines), (c) the excess free energy profile, and (d) diffusion profile corresponding to water permeating a gel-phase DSPC bilayer, with the reference bulk SPC water diffusion at 298 K49 indicated by the red dashed lines, (e) resistance profile with the contributions due to free energy and diffusion, (f) z-force autocorrelation function for different windows ranging from the aqueous phase to the bilayer center. The shaded areas in (c)–(e) indicate the statistical uncertainty calculated from multiple sweeps.
The transverse diffusion coefficient profile (D(z), Figure 3d) decreases approximately 2 orders of magnitude from its bulk value, in the aqueous phase, toward a minimum value in the headgroup region, where water molecules are strongly confined and hydrogen-bonded to lipids and to other water molecules.31 The diffusion coefficient then increases by an order of magnitude toward the tail region. This might seem counterintuitive because diffusional freedom is often associated with available space. However, diffusion across the densely packed tail region in a gel-phase bilayer can more appropriately be seen as the movement of water toward a less unfavorable environment. Similarly, the diffusion coefficient in the middle of the bilayer is smaller, as it is unfavorable for water to diffuse from the middle into the denser tail region.
The resistance profile (R(z), Figure 3e) across the bilayer is calculated from the partition coefficient profile, K(z) = exp(βΔG(z)), and the inverse diffusion profile. The partition coefficient clearly dominates the shape of the resistance curve within the bilayer, whereas the resistance is diffusive outside of the bilayer. The local resistance varies over many orders of magnitude, such that the peak of the resistance profile predominantly determines the global resistance and permeability coefficient (calculated via eq 1). This demonstrates that the barrier domain is strongly heterogeneous, rendering, as expected, the classical “homogeneous” solubility–diffusion equation inadequate for bilayer permeability analysis.12Figure 3f shows the force autocorrelation function at various z-positions for the pure DSPC bilayer. Time integrals of these force autocorrelation functions are used to calculate the local diffusion coefficient. The correlation functions in the different windows show different decay behaviors depending on the local environments; the tail of the correlation function for the window in the aqueous phase is shorter than 4 ps, which is similar to the rotational correlation time of bulk water.50 Conversely, correlation times are 200–300 ps in the windows with the lowest diffusion coefficients (i.e., in the headgroup region), which are comparable to water–DSPC headgroups hydrogen-bonding lifetimes (192 ps, Table 3).
The simulated DSPC permeability is found to be P = 1.4 × 10–8 cm/s, which is lower than the value P = 8.1 × 10–7 cm/s measured via the H2O/D2O exchange method for DSPC at 293 K.46 A similar discrepancy was reported by Das et al.,27 who calculated the permeability of ceramide lipid membranes via MD simulations and found a value approximately 30 times smaller than that from the experiment. Conversely, Gupta et al.28 computed the permeability of multiple permeants across a ceramide lipid bilayer and found a permeability coefficient for water that exceeded experimental results by almost 2 orders of magnitude. Similar discrepancies between experimental and computational permeabilities were found for fluidlike bilayers,51 but trends in the permeation simulations of different bilayers are found to be self-consistent and the MD simulations thus able to provide microscopic understanding and valid comparison between bilayers.
We consider here some factors that can contribute to inaccuracies in the simulated permeabilities. First is the simulation forcefield, which is optimized to model structural features of fluidlike bilayers.34 Although the structural properties of gel-phase phospholipid bilayers are in good agreement with experiments, dynamics and interaction energies may be less accurate; this applies to the lipid forcefield as well as to water. The SPC model overestimates the experimental bulk diffusion coefficient of water at room temperature by 70%.49 A second possible cause for deviation from experimental permeability values is the fact that the simulated bilayers do not show large defects, domain edges, or transient pores, which might be present in macroscopically large samples. In fact, recent X-ray measurements on gel-phase phospholipid bilayers have indicated the presence of low-frequency transverse modes associated with the formation of transient pores and lipid clusters.52 Although the energetic cost of pore formation increases with the packing density of lipids,53 pores could form in gel-phase bilayers but are not likely to be observed on the time and length scales accessible to MD simulation. Finally, the inhomogeneous solubility–diffusion equation is a simplified one-dimensional model that assumes homogeneity in the bilayer plane and transbilayer permeation to be the only slow variable. Such assumptions, although likely appropriate for small permeate molecules, such as water, are less suitable when large permeates are considered. Cardenas et al.39 found, via MD simulation of tryptophan permeating a fluidlike DOPC bilayer, a permeability coefficient 32 times higher than in experiments when using the inhomogeneous solubility–diffusion equation and a rate twice the experimental value when using milestoning. The large discrepancy in the case of the inhomogeneous solubility–diffusion equation was due to deformation of the liquidlike bilayer caused by the large permeate molecules, whereas the milestoning approach was not affected by the deformation. We note that no bilayer deformation is observed in the present study, owing to the rigid gel-phase structure and the fact that the permeating water molecules are small.
In addition to the possibility of bilayer deformation, it was recently argued54 that rotational motion should be taken into account when calculating the permeation of large molecules across a fluidlike bilayer; the same argument could potentially apply to small molecules permeating a densely packed gel-phase bilayer. However, in the present study, the permeating water molecules rotate to their preferred orientation within picoseconds, much faster than their translational motion, after which they do not rotate much. Force autocorrelation functions (Figure 3f) indicate that it takes up to 200–300 ps for forces to become uncorrelated, compared with approximately 4 ps in bulk water. In comparison, Marrink and Berendsen estimated a correlation time of 30 ps in the dense part of a fluidlike DPPC bilayer.55 The fact that the correlation time is an order of magnitude longer in gel-phase bilayers than in fluidlike bilayers means that significantly more data are needed to obtain the same level of accuracy. Regardless, Das et al.27 calculated force autocorrelation functions only up to 10 ps for gel-phase ceramide bilayers, with the length of the correlation function based on an estimated decay time in the ballistic regime. Such short correlation functions especially affect the regions where correlation times are long but also the reported bulk water diffusion exceeded the diffusion coefficient associated with SPC water by 30%. Similar bulk diffusion values were found by Gupta et al., who did not report the length of the correlation functions.28 Integrating the correlation functions up to 10 ps would lead to an overestimation of the diffusion in the tail region by approximately a factor of 4–5 based on our data.
DSPC–ISIS Bilayers
Multiple experimental studies15,56 have associated the presence of ISIS in ceramide-based gel-phase bilayers with a low permeability; however, these studies have not been able to determine the cause of the lower permeability. Nor have they investigated the range of conditions under which a decrease in permeability occurred. The influence of bilayer composition is of particular interest, as this can strongly affect structural properties, as discussed above. The bilayer permeability of the 7:1 and 1:1 DSPC–ISIS bilayers are compared here to investigate if composition has a strong influence on bilayer permeability.
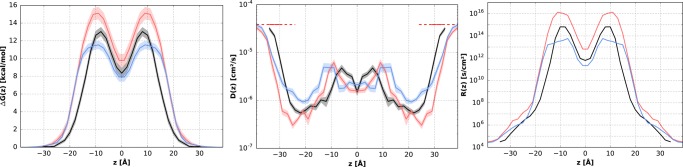
The maximum free energy of the (7:1) DSPC–ISIS bilayer is found to be 16% larger than that of the pure DSPC bilayer, whereas the equimolar DSPC–ISIS mixture has a maximum free energy that is 13% lower than that of a pure DSPC bilayer (see Figures 4 and 5; peak values are provided in Table S2 in the Supporting Information). The free-energy profiles in Figure 5 show that the equimolar DSPC–ISIS mixture exhibits less pronounced peaks in the tail region of the bilayer compared with those of the (7:1) DSPC–ISIS bilayer (mass density profiles corresponding to these bilayers are provided in Figure S2 in the Supporting Information). This is explained by the fact that the many side branches of the ISIS tails prevent dense packing (Table 2). The concentration of carbonyl groups, which are at the base of the DSPC tails, also decreases with an increasing ISIS concentration and in turn reduces hydrogen bonds between water and the carbonyl groups that decreases the diffusion coefficient in the tail region. Consequently, the diffusion in the equimolar mixture is larger than in the DSPC bilayer, whereas the diffusion coefficient in the (7:1) DSPC–ISIS bilayer is small due to the presence of many hydrogen bonds combined with a dense packing. The ISIS concentration clearly has a strong and nonmonotonic influence on the bilayer permeability. The lower permeability of the 7:1 mixture, compared to that of the pure DSPC bilayer and the equimolar DSPC–ISIS mixture, can be explained by its denser tail packing (Table 2), whereas the larger permeability of the equimolar DSPC–ISIS bilayer can be ascribed to differences between the headgroups of both molecule types. As shown in Table 3, the 1:1 DSPC–ISIS bilayer forms significantly fewer hydrogen bonds than the pure DSPC bilayer, and these hydrogen bonds are also shorter-lived, indicating faster water dynamics at the interface of the binary mixture. These few and short-lived hydrogen bonds, compared to those in the pure DSPC bilayer, lead to a relatively high probability of water partitioning into the bilayer and thus a larger bilayer permeability.
Figure 4.
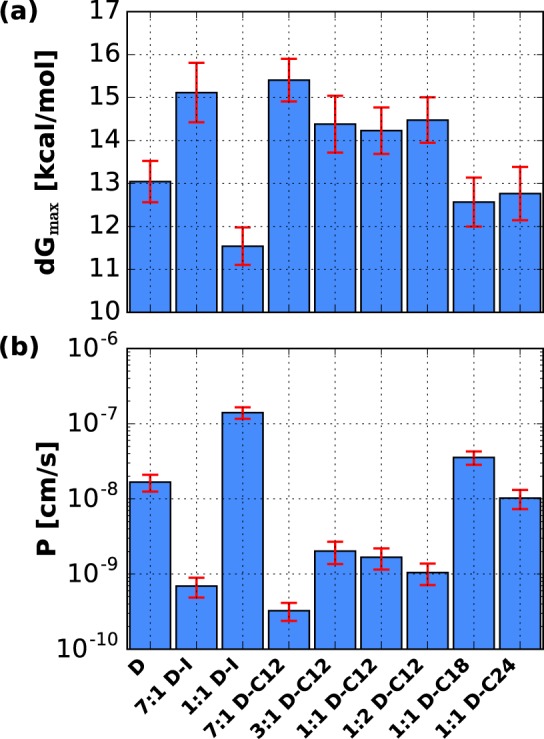
(a) Maximum free energy barriers and (b) permeability coefficient of the bilayers considered here. The uncertainty estimates are shown in red, with the uncertainty of the energy barrier calculated from the standard error of the sweeps and the permeability coefficients showing a propagated uncertainty.
Figure 5.
Nonmonotonic influence of the ISIS composition in a DSPC bilayer on the excess free energy profiles (left), diffusion profiles (center), and resistance profiles (right). The profiles correspond to DSPC (black), 7:1 DSPC–ISIS (red), and 1:1 DSPC–ISIS (blue). The shaded area indicates the statistical uncertainty, calculated from the multiple sweeps.
In summary, the 7:1 DSPC–ISIS bilayer exhibits low permeability because of the combination of dense tail packing, significant hydrogen bonding, and slow dynamics in the headgroup region. The 1:1 DSPC–ISIS mixture has a tail packing density comparable to that of the pure DSPC bilayer, but the fewer and shorter-lived hydrogen bonds lead to a larger permeability.
DSPC–Alcohol Bilayers
The DSPC–alcohol bilayers are less permeable than bilayers containing ISIS at the same concentration, which is again caused by the differences in headgroup and a different lipid packing (Figure 2). Bilayers with alcohol molecules and those with ISIS form a similar number of hydrogen bonds with water (Table 3), but hydrogen bonds between water and alcohol molecules are more stable than those between water and ISIS, as evidenced by their longer residence time. This can be caused by the difference between the hydroxyl and the ester headgroup but also by the different available space for water molecules to move around, as depicted in Figure 2. Because alcohol molecules have a single tail and no side branches on the tails, their projected area in the bilayer plane is smaller than that of the two-tailed ISIS molecules.
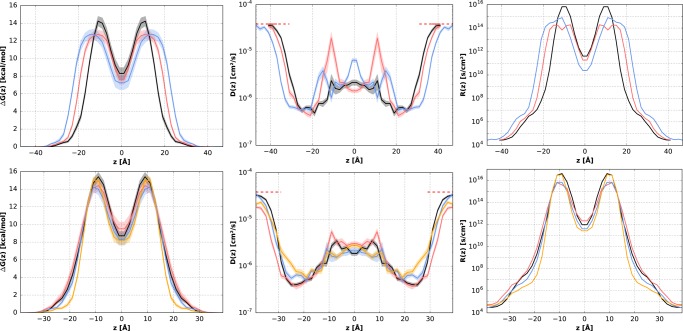
The DSPC–alcohol bilayers considered here show that the alcohol tail length affects the bilayer permeability, with the C12 mixtures having the smallest permeability coefficient, followed by the DSPC–C24 bilayer, whereas the DSPC–C18 bilayer is most permeable. This shows again that permeability does not scale with the bilayer height (i.e., tail length), as was suggested in the classical solubility–diffusion equation.12 Such a scaling would also not be expected based on the heterogeneous nature of the bilayers. The data in Figure 6 shows that the free-energy profiles of the C18 and C24 bilayer systems are very similar, whereas the free-energy profile of the C12 bilayer has a more pronounced peak in the tail region (the corresponding mass density profiles are provided in Figure S2 of the Supporting Information). The same characteristics can be found in the shape of the resistance profiles. The difference in permeability of the equimolar DSPC–alcohol bilayers is thus not caused by the difference in bilayer height, or by differences between headgroups, because these are the same, as are the hydrogen-bonding statistics corresponding to these bilayers. Therefore, the relative permeabilities of these bilayers depend predominantly on differences between their packing densities and interdigitation of lipid tails caused by the differences in tail lengths. DSPC/alcohol binary mixtures can form a densely packed bilayer when the tail lengths are asymmetric and especially when the alcohol tails are shorter than the DSPC tails, as explained in a previous study.32 Indeed, the permeability coefficients of the equimolar mixtures with alcohol molecules follow the same relative trend as the APTs of these bilayers.
Figure 6.
Excess free energy profiles (left), diffusion profile (center), and resistance profile (right) of various bilayers. Top: The influence of the alcohol tail length. The profiles correspond to 1:1 DSPC–C12 (black), 1:1 DSPC–C18 (red), and 1:1 DSPC–C24 (blue). Bottom: The influence of the C12 alcohol concentration, with profiles corresponding to 7:1 (black), 3:1 (red), 1:1 (blue), and 1:2 (yellow) DSPC–C12 bilayers. The shaded area denotes the statistical uncertainty as calculated from multiple sweeps.
The data in Figure 4 and in Table S2 show that the permeability of the DSPC–C12 bilayers is low for each of the compositions studied, but it is not directly obvious how the composition affects the permeability of these bilayers. The 7:1 DSPC–C12 bilayer has a similar APT as that of the pure DSPC bilayer, suggesting that the headgroup region may be responsible for the low permeability of the mixture. Because the alcohol molecules have only one tail, the space between protruding DSPC headgroups is smaller for the 7:1 DSPC–C12 bilayer than for the 7:1 DSPC–ISIS bilayer, as evinced by the smaller APL. The small space between the polar DSPC headgroups reduces the mobility of the interfacial water molecules, as shown by the long hydrogen-bond residence times and by the low diffusion coefficient in the headgroup region (Figure 6). Owing to the dense headgroup region combined with a low APT, the 7:1 DSPC–C12 bilayer has a large free-energy barrier and a permeability coefficient of P = 3.3 × 10–10 cm/s, 50 times smaller than that of a pure DSPC bilayer. As the alcohol concentration increases, more space is available for the water molecules to move around between the PC headgroups and the number of potential hydrogen-bonding sites decreases. The barrier of the headgroup region thus decreases with an increasing alcohol concentration, whereas the barrier of the tail region may increase if the tail packing density increases, making it harder for water molecules to partition into and through the tail region. This transition in the barrier domain is apparent from the shape of the resistance profile in Figure 6; the 7:1 DSPC–C12 bilayer has a larger resistance in the headgroup region than that for the 1:2 mixture, whereas both bilayers have a similar maximum resistance. The tail packing density of the 3:1 DSPC–C12 bilayer is similar to that of the 7:1 mixture but exhibits fewer hydrogen bonds with interfacial water molecules. Consequently, the permeability is larger than that for the 7:1 mixture but still smaller than that of a pure DSPC bilayer. The 1:1 and 1:2 DSPC–C12 bilayers exhibit fewer hydrogen bonds than the bilayers with less alcohol, and the residence times of the hydrogen bonds are shorter, especially for hydrogen bonds between water and alcohol molecules. The diffusion coefficient in the headgroup region of these bilayers is much larger than that for the 7:1 and 3:1 mixtures, as shown in Figure 6. Although the headgroup region of the 1:1 and 1:2 mixtures provides relatively little resistance, the tail packing density of these bilayers is very dense, resulting in a slightly lower permeability for these bilayers than for the 3:1 DSPC–C12 bilayer.
Conclusions
Passive permeation of water through phospholipid-based gel-phase bilayers has been investigated via MD simulation. The bilayers considered included distearylphosphatidylcholine (DSPC), either pure or combined with the emollient isostearyl isostearate (ISIS) or with long-chain (lauryl, palmityl, lignoceryl) alcohol molecules. These molecules are relevant to various biological systems as well as in healthcare applications. In addition to comparing different molecule types and tail lengths, different bilayer compositions were also considered to gain a comprehensive understanding of the role of molecular structure and chemistry in bilayer permeability. Differences in permeability of the bilayers studied are explained on the basis of the packing density, the number of water–lipid hydrogen bonds, and the hydrogen-bond residence times.
The permeability of the mixed-component bilayers was found to vary significantly between different compositions, even when tail packing densities were similar. Bilayer composition was shown to affect hydrogen bonding between interfacial water molecules and the bilayer because of the different headgroup chemistry of the lipids, alcohol molecules, and emollients. The number of hydrogen bonds formed affects the free energy of partitioning, whereas the hydrogen-bond lifetime is related to local diffusivity. The lowest permeability coefficients were found for bilayers in which a small amount of alcohol or emollient molecules was added to a DSPC bilayer. The permeation barrier of these bilayers profited from a reasonably dense tail packing combined with a dense hydrophilic headgroup region with little room for water to move around. The headgroups in these bilayers formed many long-lived hydrogen bonds with interfacial water molecules. Adding more additive molecules to the phospholipid bilayer resulted in a denser packing of the tails, whereas the headgroups formed fewer and less stable hydrogen bonds.
In summary, the headgroup region strongly affects the permeability of gel-phase bilayers, in contrast to fluidlike bilayers, for which the hydrophobic tails largely determine the bilayer permeability. Adding alcohol or emollient molecules to a gel-phase DSPC bilayer increases the space between protruding DSPC headgroups, which increases the interfacial water diffusion and diminishes the hydrogen bonding between lipids and interfacial water molecules. This, in turn, reduces the free-energy barrier of the headgroup region, whereas the free-energy barrier in the tail region may increase because of a denser tail packing. The global bilayer permeability results from a balance between these competing effects.
Acknowledgments
This research used resources of the Oak Ridge Leadership Computing Facility at the Oak Ridge National Laboratory, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC05-00OR22725. Additional computational resources were provided by the National Energy Research Scientific Computing Center, supported by the Office of Science of the Department of Energy under Contract No. DE-AC02-05CH11231.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpcb.8b00747.
Further details about the implementation of the permeability simulations including tabulated free-energy barriers and permeability coefficients and the mass density profile for each of the bilayers considered in this study (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Bemporad D.; Luttmann C.; Essex J. W. Behaviour of Small Solutes and Large Drugs in a Lipid Bilayer from Computer Simulations. Biochim. Biophys. Acta, Biomembr. 2005, 1718, 1–21. 10.1016/j.bbamem.2005.07.009. [DOI] [PubMed] [Google Scholar]
- Carpenter T. S.; Kirshner D. A.; Lau E. Y.; Wong S. E.; Nilmeier J. P.; Lightstone F. C. A Method to Predict Blood-Brain Barrier Permeability of Drug-Like Compounds Using Molecular Dynamics Simulations. Biophys. J. 2014, 107, 630–641. 10.1016/j.bpj.2014.06.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madison K. C. Barrier Function of the Skin: “‘La Raison d’Etre”’ of the Epidermis. J. Invest. Dermatol. 2003, 121, 231–241. 10.1046/j.1523-1747.2003.12359.x. [DOI] [PubMed] [Google Scholar]
- Hua S. Lipid-Based Nano-Delivery Systems for Skin Delivery of Drugs and Bioactives. Front. Pharmacol. 2015, 6, 219. 10.3389/fphar.2015.00219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Katz Y.; Diamond J. M. A Method for Measuring Nonelectrolyte Partition Coefficients between Liposomes and Water. J. Membr. Biol. 1974, 17, 69–86. 10.1007/BF01870173. [DOI] [PubMed] [Google Scholar]
- Marsh D. Polarity and Permeation Profiles in Lipid Membranes. Proc. Natl. Acad. Sci. U.S.A. 2001, 98, 7777–7782. 10.1073/pnas.131023798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Awoonor-Williams E.; Rowley C. N. Molecular Simulation of Nonfacilitated Membrane Permeation. Biochim. Biophys. Acta 2016, 1858, 1672–1687. 10.1016/j.bbamem.2015.12.014. [DOI] [PubMed] [Google Scholar]
- Lopez M.; Denver J.; Evangelista S. E.; Armetta A.; Di Domizio G.; Lee S. Effects of Acyl Chain Unsaturation on Activation Energy of Water Permeability across Droplet Bilayers of Homologous Monoglycerides: Role of Cholesterol. Langmuir 2018, 34, 2147–2157. 10.1021/acs.langmuir.7b03590. [DOI] [PubMed] [Google Scholar]
- Nitsche J. M.; Kasting G. B. A Universal Correlation Predicts Permeability Coefficients of Fluid- and Gel-Phase Phospholipid and Phospholipid-Cholesterol Bilayers for Arbitrary Solutes. J. Pharm. Sci. 2016, 105, 1762–1771. 10.1016/j.xphs.2016.02.012. [DOI] [PubMed] [Google Scholar]
- Sun W. J.; Tristram-Nagle S.; Suter R. M.; Nagle J. F. Structure of Gel Phase Saturated Lecithin Bilayers: Temperature and Chain Length Dependence. Biophys. J. 1996, 71, 885–891. 10.1016/S0006-3495(96)79290-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawaczeck R. On the Permeability of Water Molecules across Vesicular Lipid Bilayers. J. Membr. Biol. 1979, 51, 229–261. 10.1007/BF01869086. [DOI] [Google Scholar]
- Finkelstein A.; Cass A. Permeability and Electrical Properties of Thin Lipid Membranes. J. Gen. Physiol. 1968, 52, 145–173. 10.1085/jgp.52.1.145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pilgram G. S. K.; Vissers D. C. J.; Van Der Meulen H.; Pavel S.; Lavrijsen S. P. M.; Bouwstra J. A.; Koerten H. K. Aberrant Lipid Organization in Stratum Corneum of Patients with Atopic Dermatitis and Lamellar Ichthyosis. J. Invest. Dermatol. 2001, 117, 710–717. 10.1046/j.0022-202x.2001.01455.x. [DOI] [PubMed] [Google Scholar]
- De Jager M.; Groenink W.; Bielsa I Guivernau R.; Andersson E.; Angelova N.; Ponec M.; Bouwstra J. A. A Novel in Vitro Percutaneous Penetration Model: Evaluation of Barrier Properties with P-Aminobenzoic Acid and Two of Its Derivatives. Pharm. Res. 2006, 23, 951–960. 10.1007/s11095-006-9909-1. [DOI] [PubMed] [Google Scholar]
- Pennick G.; Harrison S.; Jones D.; Rawlings A. V. Superior Effect of Isostearyl Isostearate on Improvement in Stratum Corneum Water Permeability Barrier Function as Examined by the Plastic Occlusion Stress Test. Int. J. Cosmet. Sci. 2010, 32, 304–312. 10.1111/j.1468-2494.2010.00604.x. [DOI] [PubMed] [Google Scholar]
- Caussin J.; Gooris G. S.; Groenink H. W. W.; Wiechers J. W.; Bouwstra J. A. Interaction of Lipophilic Moisturizers on Stratum Corneum Lipid Domains in Vitro and in Vivo. Skin Pharmacol. Physiol. 2007, 20, 175–186. 10.1159/000101387. [DOI] [PubMed] [Google Scholar]
- Kim H.; Kim J. T.; Barua S.; Yoo S.-Y.; Hong S.-C.; Lee K. B.; Lee J. Seeking Better Topical Delivery Technologies of Moisturizing Agents for Enhanced Skin Moisturization. Expert Opin. Drug Delivery 2018, 15, 17–31. 10.1080/17425247.2017.1306054. [DOI] [PubMed] [Google Scholar]
- Marrink S.-J.; Berendsen H. J. C. Simulation of Water Transport through a Lipid Membrane. J. Phys. Chem. 1994, 98, 4155–4168. 10.1021/j100066a040. [DOI] [Google Scholar]
- Shinoda W. Permeability across Lipid Membranes. Biochim. Biophys. Acta 2016, 1858, 2254–2265. 10.1016/j.bbamem.2016.03.032. [DOI] [PubMed] [Google Scholar]
- Vermaas J. V.; Beckham G. T.; Crowley M. F. Membrane Permeability of Fatty Acyl Compounds Studied via Molecular Simulation. J. Phys. Chem. B 2017, 121, 11311–11324. 10.1021/acs.jpcb.7b08233. [DOI] [PubMed] [Google Scholar]
- Lee C. T.; Comer J.; Herndon C.; Leung N.; Pavlova A.; Swift R. V.; Tung C.; Rowley C. N.; Amaro R. E.; Chipot C. J.; et al. Simulation-Based Approaches for Determining Membrane Permeability of Small Compounds. J. Chem. Inf. Model. 2016, 56, 721–733. 10.1021/acs.jcim.6b00022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bemporad D.; Luttmann C.; Essex J. W. Computer Simulation of Small Molecule Permeation across a Lipid Bilayer: Dependence on Bilayer Properties and Solute Volume, Size, and Cross-Sectional Area. Biophys. J. 2004, 87, 1–13. 10.1529/biophysj.103.030601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orsi M.; Sanderson W. E.; Essex J. W. Permeability of Small Molecules through a Lipid Bilayer: A Multiscale Simulation Study. J. Phys. Chem. B 2009, 113, 12019–12029. 10.1021/jp903248s. [DOI] [PubMed] [Google Scholar]
- Sugii T.; Takagi S.; Matsumoto Y. A Molecular-Dynamics Study of Lipid Bilayers: Effects of the Hydrocarbon Chain Length on Permeability. J. Chem. Phys. 2005, 123, 184714 10.1063/1.2102900. [DOI] [PubMed] [Google Scholar]
- Qiao B.; Olvera de la Cruz M. Driving Force for Water Permeation across Lipid Membranes. J. Phys. Chem. Lett. 2013, 4, 3233–3237. 10.1021/jz401730s. [DOI] [Google Scholar]
- Redmill P. S.; McCabe C. Molecular Dynamics Study of the Behavior of Selected Nanoscale Building Blocks in a Gel-Phase Lipid Bilayer. J. Phys. Chem. B 2010, 114, 9165–9172. 10.1021/jp1039942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Das C.; Olmsted P. D.; Noro M. G. Water Permeation through Stratum Corneum Lipid Bilayers from Atomistic Simulations. Soft Matter 2009, 5, 4549–4555. 10.1039/b911257j. [DOI] [Google Scholar]
- Gupta R.; Sridhar D. B.; Rai B. Molecular Dynamics Simulation Study of Permeation of Molecules through Skin Lipid Bilayer. J. Phys. Chem. B 2016, 120, 8987–8996. 10.1021/acs.jpcb.6b05451. [DOI] [PubMed] [Google Scholar]
- Gupta R.; Dwadasi B. S.; Rai B. Molecular Dynamics Simulation of Skin Lipids: Effect of Ceramide Chain Lengths on Bilayer Properties. J. Phys. Chem. B 2016, 120, 12536–12546. 10.1021/acs.jpcb.6b08059. [DOI] [PubMed] [Google Scholar]
- Paloncýová M.; DeVane R. H.; Murch B. P.; Berka K.; Otyepka M. Rationalization of Reduced Penetration of Drugs through Ceramide Gel Phase Membrane. Langmuir 2014, 30, 13942–13948. 10.1021/la503289v. [DOI] [PubMed] [Google Scholar]
- Hartkamp R.; Moore T. C.; Iacovella C. R.; Thompson M.; Bulsara P. A.; Moore D. J.; McCabe C. Investigating the Structure of Multicomponent Gel Phase Lipid Bilayers. Biophys. J. 2016, 111, 813–823. 10.1016/j.bpj.2016.07.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartkamp R.; Moore T. C.; Iacovella C. R.; Thompson M. A.; Bulsara P. A.; Moore D. J.; McCabe C. Structural Properties of Phospholipid-Based Bilayers with Long-Chain Alcohol Molecules in the Gel Phase. J. Phys. Chem. B 2016, 120, 12863–12871. 10.1021/acs.jpcb.6b10192. [DOI] [PubMed] [Google Scholar]
- Uppulury K.; Coppock P. S.; Kindt J. T. Molecular Simulation of the DPPE Lipid Bilayer Gel Phase: Coupling Between Molecular Packing Order and Tail Tilt Angle. J. Phys. Chem. B 2015, 119, 8725–8733. 10.1021/acs.jpcb.5b05720. [DOI] [PubMed] [Google Scholar]
- Oostenbrink C.; Villa A.; Mark A. E.; Van Gunsteren W. F. A Biomolecular Force Field Based on the Free Enthalpy of Hydration and Solvation: The GROMOS Force-Field Parameter Sets 53A5 and 53A6. J. Comput. Chem. 2004, 25, 1656–1676. 10.1002/jcc.20090. [DOI] [PubMed] [Google Scholar]
- Chiu S. W.; Clark M.; Balaji V.; Subramaniam S.; Scott H. L.; Jakobsson E. Incorporation of Surface Tension into Molecular Dynamics Simulation of an Interface: A Fluid Phase Lipid Bilayer Membrane. Biophys. J. 1995, 69, 1230–1245. 10.1016/S0006-3495(95)80005-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malde A. K.; Zuo L.; Breeze M.; Stroet M.; Poger D.; Nair P. C.; Oostenbrink C.; Mark A. E. An Automated Force Field Topology Builder (ATB) and Repository: Version 1.0. J. Chem. Theory Comput. 2011, 7, 4026–4037. 10.1021/ct200196m. [DOI] [PubMed] [Google Scholar]
- Plimpton S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. 10.1006/jcph.1995.1039. [DOI] [Google Scholar]
- Hockney R. W.; Eastwood J. W.. Computer Simulation Using Particles; Taylor & Francis, Inc.: Bristol, PA, 1988. [Google Scholar]
- Cardenas A. E.; Jas G. S.; DeLeon K. Y.; Hegefeld W. A.; Kuczera K.; Elber R. Unassisted Transport of N-Acetyl-L-Tryptophanamide through Membrane: Experiment and Simulation of Kinetics. J. Phys. Chem. B 2012, 116, 2739–2750. 10.1021/jp2102447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neale C.; Madill C.; Rauscher S.; Pomès R. Accelerating Convergence in Molecular Dynamics Simulations of Solutes in Lipid Membranes by Conducting a Random Walk along the Bilayer Normal. J. Chem. Theory Comput. 2013, 9, 3686–3703. 10.1021/ct301005b. [DOI] [PubMed] [Google Scholar]
- Jämbeck J. P. M.; Lyubartsev A. P. Exploring the Free Energy Landscape of Solutes Embedded in Lipid Bilayers. J. Phys. Chem. Lett. 2013, 4, 1781–1787. 10.1021/jz4007993. [DOI] [PubMed] [Google Scholar]
- Hummer G. Position-Dependent Diffusion Coefficients and Free Energies from Bayesian Analysis of Equilibrium and Replica Molecular Dynamics Simulations. New J. Phys. 2005, 7, 34. 10.1088/1367-2630/7/1/034. [DOI] [Google Scholar]
- Comer J.; Chipot C. J.; Gonzalez-Nilo F. D. Calculating Position-Dependent Diffusivity in Biased Molecular Dynamics Simulations. J. Chem. Theory Comput. 2013, 9, 876–882. 10.1021/ct300867e. [DOI] [PubMed] [Google Scholar]
- Holland B. W.; Gray C. G.; Tomberli B. Calculating Diffusion and Permeability Coefficients with the Oscillating Forward-Reverse Method. Phys. Rev. E 2012, 86, 036707 10.1103/PhysRevE.86.036707. [DOI] [PubMed] [Google Scholar]
- Tjörnhammar R.; Edholm O. Reparameterized United Atom Model for Molecular Dynamics Simulations of Gel and Fluid Phosphatidylcholine Bilayers. J. Chem. Theory Comput. 2014, 10, 5706–5715. 10.1021/ct500589z. [DOI] [PubMed] [Google Scholar]
- Jansen M.; Blume A. A Comparative Study of Diffusive and Osmotic Water Permeation across Bilayers Composed of Phospholipids with Different Head Groups and Fatty Acyl Chains. Biophys. J. 1995, 68, 997–1008. 10.1016/S0006-3495(95)80275-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hartkamp R.; Coasne B. Structure and Transport of Aqueous Electrolytes: From Simple Halides to Radionuclide Ions. J. Chem. Phys. 2014, 141, 124508 10.1063/1.4896380. [DOI] [PubMed] [Google Scholar]
- Silverstein K. A. T.; Haymet A. D. J.; Dill K. A. The Strength of Hydrogen Bonds in Liquid Water and Around Nonpolar Solutes The Strength of Hydrogen Bonds in Liquid Water and Around Nonpolar Solutes. J. Am. Chem. Soc. 2000, 122, 8037–8041. 10.1021/ja000459t. [DOI] [Google Scholar]
- Raabe G.; Sadus R. J. Molecular Dynamics Simulation of the Effect of Bond Flexibility on the Transport Properties of Water. J. Chem. Phys. 2012, 137, 104512 10.1063/1.4749382. [DOI] [PubMed] [Google Scholar]
- Zhang Z.; Berkowitz M. L. Orientational Dynamics of Water in Phospholipid Bilayers with Different Hydration Levels. J. Phys. Chem. B 2009, 113, 7676–7680. 10.1021/jp900873d. [DOI] [PubMed] [Google Scholar]
- Saito H.; Shinoda W. Cholesterol Effect on Water Permeability through DPPC and PSM Lipid Bilayers: A Molecular Dynamics Study. J. Phys. Chem. B 2011, 115, 15241–15250. 10.1021/jp201611p. [DOI] [PubMed] [Google Scholar]
- Zhernenkov M.; Bolmatov D.; Soloviov D.; Zhernenkov K.; Toperverg B. P.; Cunsolo A.; Bosak A.; Cai Y. Q. Revealing the Mechanism of Passive Transport in Lipid Bilayers via Phonon-Mediated Nanometre-Scale Density Fluctuations. Nat. Commun. 2016, 7, 11575 10.1038/ncomms11575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zocher F.; Van Der Spoel D.; Pohl P.; Hub J. S. Local Partition Coefficients Govern Solute Permeability of Cholesterol-Containing Membranes. Biophys. J. 2013, 105, 2760–2770. 10.1016/j.bpj.2013.11.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parisio G.; Stocchero M.; Ferrarini A. Passive Membrane Permeability: Beyond the Standard Solubility-Diffusion Model. J. Chem. Theory Comput. 2013, 9, 5236–5246. 10.1021/ct400690t. [DOI] [PubMed] [Google Scholar]
- Marrink S.-J.; Berendsen H. J. C. Permeation Process of Small Molecules across Lipid Membranes Studied by Molecular Dynamics Simulations. J. Phys. Chem. 1996, 100, 16729–16738. 10.1021/jp952956f. [DOI] [Google Scholar]
- Caussin J.; Gooris G. S.; Bouwstra J. A. FTIR Studies Show Lipophilic Moisturizers to Interact with Stratum Corneum Lipids, Rendering the More Densely Packed. Biochim. Biophys. Acta 2008, 1778, 1517–1524. 10.1016/j.bbamem.2008.03.006. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.