The conductance of the strong inward rectifier K+ channel depends on the “square root” of the extracellular K+ concentration. The present study shows that this physiologically important phenomenon is caused by a channel blockade by extracellular Na+, which is competitive with extracellular K+.
Abstract
Strong inward rectifier K+ (sKir) channels determine the membrane potentials of many types of excitable and nonexcitable cells, most notably the resting potentials of cardiac myocytes. They show little outward current during membrane depolarization (i.e., strong inward rectification) because of the channel blockade by cytoplasmic polyamines, which depends on the deviation of the membrane potential from the K+ equilibrium potential (V – EK) when the extracellular K+ concentration ([K+]out) is changed. Because their open-channel conductance is apparently proportional to the “square root” of [K+]out, increases/decreases in [K+]out enhance/diminish outward currents through sKir channels at membrane potentials near their reversal potential, which also affects, for example, the repolarization and action-potential duration of cardiac myocytes. Despite its importance, however, the mechanism underlying the [K+]out dependence of the open sKir channel conductance has remained elusive. By studying Kir2.1, the canonical member of the sKir channel family, we first show that the outward currents of Kir2.1 are observed under the external K+-free condition when its inward rectification is reduced and that the complete inhibition of the currents at 0 [K+]out results solely from pore blockade caused by the polyamines. Moreover, the noted square-root proportionality of the open sKir channel conductance to [K+]out is mediated by the pore blockade by the external Na+, which is competitive with the external K+. Our results show that external K+ itself does not activate or facilitate K+ permeation through the open sKir channel to mediate the apparent external K+ dependence of its open channel conductance. The paradoxical increase/decrease in outward sKir channel currents during alternations in [K+]out, which is physiologically relevant, is caused by competition from impermeant extracellular Na+.
Introduction
Inward rectifier potassium (Kir) channels are distinct from voltage-gated K+ (KV) channels because they are constitutively open at membrane potentials around the K+ equilibrium potential (EK). Canonical inward rectifiers in their native tissues exhibit “strong” inward rectification, with little outward current during depolarization. This is because their conductance declines steeply with membrane depolarization or with increasing deviation of the membrane potential from EK (V − EK; Hille, 2001). This property of strong inward rectifier K+ (sKir) channels is crucial for background K+ conductance in excitable tissues, such as the myocardium, because it allows the K+ conductance to maintain a very negative resting potential, near EK, and enables prompt and long-lasting depolarization and, hence, rapid conduction of excitation and coordinated cardiac contraction (Nichols et al., 1996).
Structurally, Kir channels are two-transmembrane domain channels, which lack voltage sensors like those of six-transmembrane domain KV channels (Kubo et al., 1993; Tao et al., 2009). The strong inward rectification arises from voltage-dependent pore blockade by cytoplasmic cationic polyamines (Nichols et al., 1996). Using Kir2.1, a representative member of the Kir2 subfamily that recapitulates the properties of native sKir channels (Kubo et al., 1993), the molecular mechanisms underlying the sKir channel blockade by polyamines have been studied extensively (Taglialatela et al., 1995; Yang et al., 1995; Kubo and Murata, 2001; Guo and Lu, 2003; Guo et al., 2003; Xie et al., 2003; Ishihara and Ehara, 2004; Fujiwara and Kubo, 2006; Ishihara and Yan, 2007), although many aspects of those mechanisms remain obscure (Xu et al., 2009; Liu et al., 2012). Importantly, when the external K+ concentration ([K+]out) is varied, the voltage dependence of the inward rectification (i.e., polyamine block) shifts with changes in EK (Kubo et al., 1993; Lopatin and Nichols, 1996b; Ishihara and Yan, 2007), as has been reported for the native sKirs (Hagiwara and Takahashi, 1974; Hestrin, 1981). This implies that K+ ions are themselves involved in the channel blockade induced by polyamines (Lopatin and Nichols, 1996b; Shin and Lu, 2005), although the rectification and polyamine block are reportedly dependent on external K+ but not much on internal K+ (Hagiwara and Yoshii, 1979; Kubo, 1996; Lopatin and Nichols, 1996b).
sKir channels also exhibit another important external K+ dependence; that is, the open (polyamine-unblocked) channel conductance determined from macroscopic and single-channel currents is proportional to [K+]out with a power of 0.2–0.6 (Hagiwara and Takahashi, 1974; Ohmori, 1978; Sakmann and Trube, 1984; Matsuda, 1988; Kubo et al., 1993). Although this “square root” proportionality of the sKir conductance to [K+]out may not be qualitatively surprising for the inward K+ flux, it is also applicable to the outward K+ conductance (Hagiwara and Takahashi, 1974; Hille and Schwarz, 1978), which has a significant role in regulating the action-potential duration within the myocardium (Shimoni et al., 1992; Nichols et al., 1996; Matsuoka et al., 2003) and is a determinant of cardiac contractility (Bouchard et al., 2004) and arrhythmogenicity (Ishihara et al., 2009; Maruyama et al., 2011; Asakura et al., 2014). The involvement of external K+ in the mechanism underlying this property has remained uncertain; however, an interaction between K+ and the outer mouth of sKir channels may have a functional role in enhancing K+ permeation (Claydon et al., 2004; Chang et al., 2010). In fact, a similar function of external K+ is known to mediate C-type inactivation in the KV family channels (López-Barneo et al., 1993; Baukrowitz and Yellen, 1995; Hoshi and Armstrong, 2013).
Here, we studied the mechanisms governing the complete inhibition of sKir currents under the external K+-free condition and square-root proportionality of open (polyamine-unblocked) sKir channel conductance to [K+]out using Kir2.1. The phenomenon in which cardiac sKir currents are completely inhibited by extracellular K+-free solutions has been used to isolate sKir currents (Matsuda and Noma, 1984; Ishihara et al., 1989; Yan et al., 2005). Although the outward currents at 0 [K+]out may be inhibited by its strong inward rectification, which depends on V − EK, it was not known whether the currents can flow through the polyamine-unblocked sKir channels at 0 [K+]out. We show that outward currents concordant with K+ efflux were observed using external K+-free solution with Kir2.1 mutants (E224G and E299S) showing reduced sensitivity to polyamines and with WT channels when internal polyamine-free solution was used. Furthermore, those outward currents were completely blocked by cytoplasmic spermine at a concentration that restores the native degree of sKir rectification in the presence of external K+. The findings indicate that the shift in the voltage dependence of the polyamine block, in parallel with the negative shift in EK, produces complete inhibition of outward currents through Kir2.1 at 0 [K+]out and that the lack of external K+ does not inhibit the outward currents through Kir2.1. We further show that open conductance of Kir2.1 does not notably change over a [K+]out range between 10 and 150 mM in the absence of external Na+ but is competitively inhibited by external Na+ in a voltage-dependent manner—i.e., at a site within the pore. Our results reveal that pore blockade by impermeant cations mediate the apparent external K+ dependence of open sKir channel conductance and provide a simple, mechanistic explanation for the basic property of sKir channels, which is related to cardiac physiology and pathophysiology.
Materials and methods
Cell culture and transfection
Human embryonic kidney (HEK) 293T cells were cultured in Dulbecco’s modified Eagle’s medium and supplemented with 10% FBS, penicillin (100 U/ml), and streptomycin (100 µg/ml). HEK293T cells were cotransfected using Effectene (QIAGEN), with the cDNA encoding mouse Kir2.1 (Kubo et al., 1993), which was subcloned into the pCXN2 expression vector (Niwa et al., 1991; Ishihara et al., 1996) and that encoding enhanced GFP, enabling transient expression of the genes (Ishihara and Yan, 2007). Mouse L cells stably expressing the mouse Kir2.1 gene (Ishihara et al., 1996) were cultured in Dulbecco’s modified Eagle’s medium, supplemented with 5% FBS, penicillin (100 U/ml), streptomycin (100 µg/ml), and G418 (400 µg/ml). cDNAs for mouse Kir2.1 and its E224G and E299S mutants (Kubo and Murata, 2001) were provided by L.Y. Jan (University of California, San Francisco, CA) and Y. Kubo (National Institute for Physiological Sciences, Okazaki, Japan), respectively.
Patch-clamp recordings
Membrane currents were recorded using standard patch-clamp methods (Hamill et al., 1981) with an Axopatch 200B amplifier (Molecular Devices) in whole-cell mode, outside-out patch mode, inside-out patch mode, and cell-attached mode. In transient-expression experiments, cells exhibiting green fluorescence were used 16–96 h after transfection. For whole-cell current recordings, HEK293T cells transfected with cDNAs were treated with 0.25% trypsin–EDTA solution (Fujifilm Wako Pure Chemical) on the day of patch-clamp experiments, and dissociated, single, spherical cells were used. For outside-out/inside-out patch recordings, HEK293T cells seeded onto polylysine-coated glass coverslips (Iwaki) on the day of transfection were used. For cell-attached, single-channel recordings, L cells stably expressing Kir2.1 were treated with 0.05% trypsin–EDTA solution (Sigma) on the day of patch-clamp experiments, and dissociated cells were used for recordings. Membrane potentials of Kir2.1-expressing L cells were obtained by the β-escin perforation method (Fan and Palade, 1998).
The recording chamber (area, 5 × 20 mm; volume, ∼0.5 ml) was mounted on the stage of an inverted microscope (TE-2000U; Nikon) and continuously perfused with bath solution at a rate of ∼2 ml/min. Silicone-coated patch electrodes were made from borosilicate glass capillaries (for excised patch recordings, 1.65 mm OD, 0.165 mm wall thickness from Hilgenberg; for single channel recordings, G-1.5 from Narishige). In excised patch recordings, patch electrodes were fire polished before use (MF-830 microforge; Narishige). Patch pipettes typically had a resistance of 5, 2, and 8–10 MΩ, for whole-cell, excised patch, and single-channel recordings, respectively, when filled with pipette solution of physiological ionic strength. Bath solutions were grounded with an agar/Ag-AgCl bridge containing 3 M KCl. Voltage stimulation and data acquisition were performed with an analogue-to-digital converter (Digidata 1440A; Molecular Devices) using a personal computer and pCLAMP software (versions 9 and 10; Molecular Devices). Single-channel currents were obtained at a sampling rate of 10 kHz and low-pass filtered at 1 kHz. All experiments were conducted at room temperature (23–25°C).
Solution and liquid-junction potentials (Vj)
The recording solutions used in the experiments are listed in Table 1. The standard composition of the modified Tyrode’s solution was (in mM) 140 NaCl, 5.4 KCl, 1.8 CaCl2, 0.5 MgCl2, 0.33 NaH2PO4, and 5 HEPES (pH adjusted to 7.4 with NaOH); K+-free Tyrode’s solution was made by subtracting KCl. The intracellular solution for whole-cell recordings contained (in mM) 85 potassium aspartate, 30 KCl, 2 K2ATP, 2 K2EDTA, 10 KH2PO4, 5 MgCl2, 0.3 Na2–guanosine 5′-triphosphate sodium, and 5 HEPES (pH adjusted to 7.2 with KOH). 150 Na/1 Ca (HEPES) solution contained (in mM) 148 NaCl, 1 CaCl2, and 5 HEPES (pH adjusted to 7.4 with ∼2 mM of NaOH). The compositions of phosphate-buffered solutions are described in Table 2. For outside-out/inside-out patch recordings, the pH of the internal (cytoplasmic) solutions was adjusted using phosphate buffer to avoid HEPES-induced inward rectification (Guo and Lu, 2000), and those phosphate-buffered solutions were also used for external solutions. Assuming the amounts of Ca2+ and Mg2+ contained in the solution were ∼10 µM each, the free Mg2+ and Ca2+ concentrations in phosphate-buffered solutions were calculated to be at submicromolar levels (Fabiato and Fabiato, 1979). Solutions containing spermine were made by adding appropriate amounts of spermine–4HCl (Nacalai Tesque) as a 10-mM stock solution in distilled water which was stored in small aliquots at −20°C before use.
Table 1. Solutions used in experiments.
| Figure | Patch configuration | External | Internal (cytoplasmic) | Vj uncorrecteda |
|---|---|---|---|---|
| Fig. 1 A | Whole cell | B: modified Tyrode’s solution | P: intracellular solution | +13 mV |
| Fig. 1 B | Outside out | B: modified Tyrode’s solution | P: 150 K (phos) | +6 mV |
| Fig. 2 | Inside out | P: 150 Na/1 Ca (HEPES) | B: 150 K and 150 Na (phos) | −6 mV |
| Fig. 3 | Outside out | B: 150 K, 50 K, 20 K, 10 K, 50 K/100 Na, and 20 K/130 Na (phos) | P: 150 K (phos) | 0 |
| Fig. 4 | Cell attached | P: 150 K, 50 K, 20 K, 50 K/100 Na, and 20 K/130 Na (phos) | None | +6, +11, +13, +2, and +1 mV with 150 K, 50 K, 20 K, 50 K/100 Na, and 20 K/130 Na pipette solutions, respectively. |
| B: modified Tyrode’s solution | ||||
| Fig. 5 | Outside out | B: 150 K, 50 K, 20 K, 10 K, 50 K/100 Na, 20 K/100 Na, and 10 K/100 Na (phos) | P: 150 K (phos) | 0 |
B, bath solution; HEPES, HEPES-buffered solution; P, pipette solution; phos, phosphate-buffered solution.
Vj values (in the bath solution with respect to the pipette solution) were calculated using pCLAMP software (version 10).
Table 2. Compositions of phosphate-buffered solutions (in millimolars).
| Solution | 150 K | 50 K | 20 K | 20 K | 10 K | 50 K/100 Na | 50 K/100 Na | 20 K/130 Na | 20 K/100 Na | 10 K/100 Na | 150 Na |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Figuresa | Figs. 1 B, 2, 3, 4, and 5 | Figs. 3, 4, and 5 | Figs. 3 and 5 | Fig. 4 | Figs. 3 and 5 | Figs. 3 and 4 | Fig. 5 | Figs. 3 and 4 | Fig. 5 | Fig. 5 | Fig. 2 |
| KCl | 120 | 20 | 10 | 50 | 20 | 20 | |||||
| K2EDTAb | 4 | 4 | 2 | 1 | 1 | 4 | 2 | 1 | |||
| K2HPO4 | 7.2 | 7.2 | 7.2 | 3.6 | 3.6 | 7.2 | 7.2 | 3.6 | |||
| KH2PO4 | 2.8 | 2.8 | 2.8 | 1.4 | 1.4 | 2.8 | 2.8 | 1.4 | |||
| KOHc | ∼3.9 | ∼3.2 | ∼1.1 | ∼0.7 | ∼0.5 | ∼3.2 | ∼1.1 | ∼0.5 | |||
| NaCl | 70 | 100 | 100 | 100 | 100 | 120 | |||||
| Na2EDTA | 4 | 4 | 4 | ||||||||
| Na2HPO4 | 6.8 | 6.8 | 6.8 | ||||||||
| NaH2PO4 | 3.2 | 3.2 | 3.2 | ||||||||
| NaOHc | ∼3 | ∼3 | ∼2.6 | ||||||||
| Total [K+] | 149.1 | 48.4 | 22.3 | 21.3 | 11.1 | 50.0 | 48.4 | 20.0 | 22.3 | 11.1 | 0 |
| Ionic strength (M) | 0.168 | 0.067 | 0.036 | 0.028 | 0.018 | 0.167 | 0.167 | 0.167 | 0.136 | 0.118 | |
| Activity coefficient (dimensionless) | 0.75 | 0.80 | 0.84 | 0.85 | 0.88 | 0.75 | 0.75 | 0.75 | 0.76 | 0.77 | |
| [K+] activity | 112.5 | 38.9 | 18.7 | 17.8 | 9.7 | 37.7 | 36.5 | 15.1 | 17.0 | 8.6 |
Figures showing the experiment in which the solution was used.
For calculating ionic strength, fractions of HEDTA3− and H2EDTA2− at pH 7.2 were assumed to be 0.915 and 0.08 of the total EDTA, respectively.
pH was adjusted to 7.2 with KOH or NaOH.
Data analysis
Currents (I) and membrane potentials (V) were obtained from the digitalized data using pCLAMP software (versions 9 and 10). Membrane potentials were not corrected for the liquid-junction potentials (Vj) between the bath and pipette solutions used to offset electrode potentials at the beginning of individual experiments (Table 1 for the uncorrected Vj values). Chord conductances (G) of macroscopic currents were calculated as G = I/(V − Vrev), where Vrev is the reversal potential of the currents. Amplitudes of single-channel currents (i) were obtained as the difference between the peaks of Gaussian curves fitted to all-points histograms of the currents using pCLAMP (version 10). Fittings of data to theoretical lines were performed with Origin software (version 2016J; OriginLab).
Because the ionic strength varied among external solutions when the effects of different [K+]out were examined, the K+ concentration in the solutions was replaced with K+ activity in some figures. The K+ activity in solutions was calculated from the activity coefficient f obtained using the Davies equation (Davies, 1962; Stumm and Morgan, 1981), logf = −0.51 [I0.5/(1 + I0.5) − 0.3I], at the ionic strength (I) of the solution, determined as I = 0.5∑cizi2, where ci is the concentration of ion i in the solution, and zi is its charge. The values for ionic strength, activity coefficient, and K+ activity in solutions are described in Table 2.
Analysis of the inhibitory effects of Na+ on Kir2.1 conductance
The effects of 100 mM external Na+ on the polyamine-unblocked Kir2.1 conductance at different [K+]out were analyzed using the Lineweaver–Burk equation (double reciprocal form of the Michaelis-Menten equation):
where G(V) is the chord conductance at different membrane potentials, and Gmax(V) is its maximum value at [K+]out = infinity at each membrane potential. For G(V) values, those normalized to that at 150 mM [K+]out (0 Na+) in each experiment were used. Because the y-axis intercept of the straight lines fitted to the relations between 1/[K+]out and 1/G(V), which indicates the 1/Gmax(V) value, was found to be at a value near 1 at all membrane potentials examined, the apparent Km(V) values in the presence and absence of 100 mM Na+ were obtained from the respective slopes of the straight lines. Because the analysis showed that the effect of Na+ on the Kir2.1 conductance was competitive with external K+, the dissociation constant for Na+ (Ki(Na)) at each membrane potential was obtained from those Km(V) values using the following equation:
Reconstruction of the external Na+ effects on the [K+]out dependence of the sKir I–V relationship
The I–V relationships at different [K+]out levels (3.5, 10, and 40 mM) in the absence and presence of external Na+ (140 and 120 mM) were reconstructed using the EK value calculated using 150 mM internal K+ and the relative chord conductances calculated as follows:
where [Na+]out is the external Na+ concentration. The fractional currents in the presence of endogenous cytoplasmic polyamines were reconstructed using 10 µM spermine and the voltage-dependent dissociation constant for the low-affinity spermine block of Kir2.1, which regulates the amplitude of outward currents near EK (Ishihara and Ehara, 2004).
Statistical analysis
The error bars shown in the figures indicate SD with the number of data points (n) given in parentheses. Statistical analysis was undertaken using Origin software (version 2016J).
Online supplemental material
Fig. S1 shows the Lineweaver–Burk plots for the open (polyamine-unblocked) Kir2.1 channel conductance at various [K+]out levels obtained at different membrane potentials.
Results
Loss of phenomenal external K+-free inhibition in Kir2.1 with reduced inward rectification
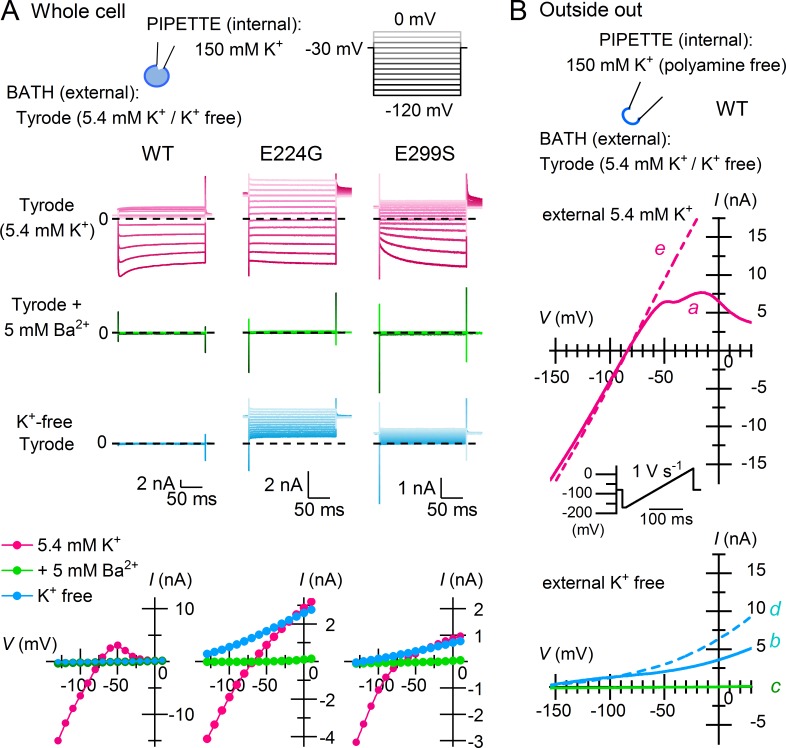
As was shown with native sKir channels, Kir2.1 was completely inhibited by removing K+ from the external solution, which appears similar to the complete blockade of the currents caused by 5 mM external Ba2+ (Fig. 1 A; WT; representative of 12 experiments). We then examined Kir2.1 with an E224G or E299S mutation, which shows significantly reduced inward rectification because of lowered sensitivities to blockade by cytoplasmic polyamines (Taglialatela et al., 1995; Yang et al., 1995; Kubo and Murata, 2001). The mutant channels showed prominent outward currents at 0 [K+]out throughout the entire voltage range examined, although their Ba2+ sensitivities were unaffected (Fig. 1 A; E224G and E299S; representative of five and eight experiments, respectively). These results suggested that the significantly reduced channel blockade by polyamines allowed outward sKir currents to flow at 0 [K+]out.
Figure 1.
Loss of phenomenal external K+-free inhibition in Kir2.1 with reduced inward rectification. (A) Whole-cell currents and I–V relationships obtained from the WT channel and point mutants (E224G and E299S) using 5.4 mM K+ Tyrode’s (top), Tyrode’s with 5 mM Ba2+ (middle), and K+-free Tyrode’s (bottom) external solutions. Test pulses were applied from a holding potential of −30 mV, and current amplitudes were measured at the end of the step pulses. Current traces are shown at test potentials between −120 and 0 mV in 10-mV steps. Cells contain endogenous cytoplasmic polyamines. Dashed lines superimposed on current traces indicate the zero-current level. (B) K+ efflux through Kir2.1 under the external K+-free condition was observed using a polyamine-free, 150-mM K+ internal solution. The external solution was switched between 5.4 mM K+ (top) and K+-free (bottom) Tyrode’s solutions; currents were recorded from an outside-out patch membrane in the sequence indicated alphabetically in the figure (a–e). A depolarizing ramp pulse (1 V s−1) was used to obtain I-V relationships.
We made outside-out patches with polyamine-free, 150 mM K+ internal solution, and the external solution was switched between 5.4 mM K+ and K+-free Tyrode’s solutions, just as in the whole-cell recordings (Fig. 1 B; representative of five independent experiments). The currents observed at 5.4 mM [K+]out showed a Vrev that was near EK (approximately −85 mV) and immediately exhibited weak inward rectification (Fig. 1 B, top, trace a). Upon making the external solution K+-free, outward currents flowed over the entire voltage range (Fig. 1 B, bottom, trace b) and could be completely and reversibly inhibited by 5 mM external Ba2+ (Fig. 1 B, bottom, traces c and d), as were the currents at 5.4 mM [K+]out (Fig. 1 A). The outward currents observed at 5.4 mM and 0 [K+]out both increased with time (Fig. 1 B, bottom, trace d and top, trace e), which is consistent with depletion of endogenous polyamines from the submembrane space.
Complete inhibition of sKir currents at 0 [K+]out is caused solely by the “polyamine block”
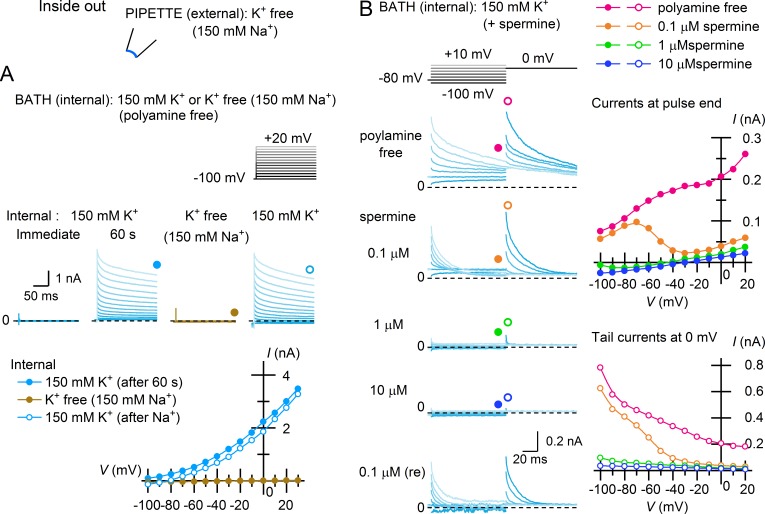
When inside-out patches made with a K+-free (150 mM Na+) external solution were bathed in internal (cytoplasmic) 150 mM K+ solution containing no polyamines, no currents were detected immediately after the patch excision, but outward currents soon emerged over the entire voltage range examined, which is consistent with K+ currents occurring with a very negative EK in 0 [K+]out solution (Fig. 2 A, immediate and 60 s). The outward currents showed a slow decay, which is commonly observed with Kir2 channels and reflects the difficulty of removing trace amounts of endogenous polyamines from the submembrane space of patch membranes (Lopatin et al., 1995). That the outward currents are mediated by K+ ions was confirmed by switching the internal solution to a K+-free one (150 mM Na+), which reversibly eliminated the currents (Fig. 2 A).
Figure 2.
Polyamine block completely inhibits the outward currents of Kir2.1 at 0 [K+]out. (A) Outward K+ currents and their I–V relationships obtained from an inside-out patch membrane using K+-free (150 mM Na+) external solution ∼60 s after excising the patch in polyamine-free, 150 mM K+ solution. Currents were not observed immediately after patch excision. Test pulses were applied from a holding potential of −100 mV. Subsequent disappearance of the outward currents with K+-free (150 mM Na+) internal solution and their recovery are also shown. (B) Inhibition of the outward currents observed under the external K+-free (150 mM Na+) condition with subsequent application of 0.1–10 µM cytoplasmic spermine. Currents were recorded from an inside-out patch membrane using test pulses applied from a holding potential of −80 mV and followed by a step pulse to 0 mV. Left: Selected current traces obtained at test potentials between −100 and 20 mV in 10-mV steps. Top right: I–V relationships obtained at the end of test pulses. Bottom right: Amplitudes of tail currents during the subsequent step to 0 mV, reflecting fractional openings of Kir2.1 at the end of the test pulses. Dashed lines superimposed on current traces indicate the zero-current level. Data are representative of eight independent experiments.
The outward currents observed using K+-free (150 mM Na+) external solution and polyamine-free internal solution were inhibited by 0.1–10 µM internal (cytoplasmic) spermine, like those observed in the presence of external K+ (Ishihara and Ehara, 2004; Ishihara and Yan, 2007; Fig. 2 B, left and top-right). The tail currents observed after the test pulses showed that the conductance was inhibited by spermine in a concentration- and voltage-dependent manner (Fig. 2 B, lower-right). Notably, 10 µM spermine, which has been shown to restore the native sKir rectification in Kir2.1 (Ishihara and Ehara, 2004; Ishihara and Yan, 2007), completely and reversibly suppressed the emergent outward currents. These findings indicate that inhibition of Kir2.1 as well as that of native sKir channels using external K+-free solutions results solely from channel blockade caused by intracellular polyamines, which is enhanced by an enlarged V − EK at 0 [K+]out.
External K+ dependence of the open (polyamine-unblocked) Kir2.1 conductance
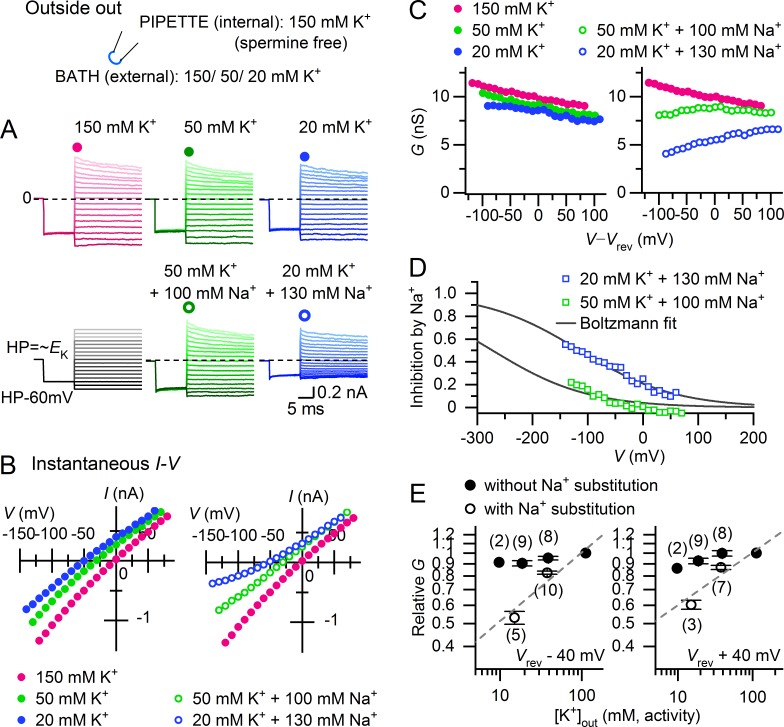
The results indicated that Kir2.1 is constitutively open in the absence of external K+. On the other hand, the open sKir channel conductance is reportedly proportional to the square root of [K+]out, which may reflect facilitation of K+ permeation by external K+. We therefore examined the [K+]out dependence of polyamine-unblocked macroscopic Kir2.1 conductance with a polyamine-free internal solution and a hyperpolarizing prepulse that ensured relief of the block by residual endogenous polyamines (Fig. 3, A and B). When [K+]out was reduced to <150 mM without cation substitution, current amplitude did not markedly decrease. The instantaneous I–V relationships reflecting the polyamine-unblocked conductance remained nearly ohmic (with slight inward rectification), even under asymmetric K+ conditions, as was previously shown (Matsuda, 1991; Lopatin and Nichols, 1996a). With Na+ substitution, however, the inward currents in particular decreased as [K+]out was lowered, exhibiting a weak outward rectification in the I–V relationships. In the absence of Na+, the chord conductance (G) of the polyamine-unblocked channels showed a similar monotonic decline as the voltage became more positive for all [K+]out, but it showed a marked [K+]out dependence with an inverse voltage dependence when Na+ was substituted (Fig. 3 C). The inhibitory effect of Na+ on the conductances exhibited a sigmoidal voltage dependence (Fig. 3 D). Fittings of the Boltzmann equation to the relations at 20 mM [K+]out indicated that Na+ blocks Kir2.1 channels at a site within the membrane electric field at an apparent electrical distance of 0.18 ± 0.1 (n = 3) from the outside.
Figure 3.
[K+]out dependence of the polyamine-unblocked Kir2.1 conductance. (A) Representative currents recorded from an outside-out patch membrane at different [K+]out levels (150, 50, and 20 mM) in the absence (top) and presence (bottom) of Na+ substitution ([K+]out + [Na+]out = 150 mM). Holding potentials were set near the theoretical EK value at each [K+]out, and a 10-ms hyperpolarizing prepulse (60 mV negative to HP) ensured relief of any polyamine block before applying test pulses. Traces are at potentials between −80 and 80 mV relative to the holding potentials. Dashed lines superimposed on current traces indicate the zero-current level. (B) Instantaneous I–V relationships at the onset of test pulses obtained from the currents shown in A. (C) Chord conductances (G) plotted against V–Vrev, obtained from the I–Vs shown in B. (D) Voltage dependence of Na+ inhibition. Fractional inhibition of conductances observed with Na+ substitution at 50 mM and 20 mM [K+]out was obtained from the data shown in C and was plotted against V. Lines are the fits to the Boltzmann equation: fractional inhibition = 1/{1 + exp[−(V − V1/2)]/s}, with s = 86 mV. In this experiment, the electrical distance (δ) of the Na+ blocking site is ∼0.3 from the outside. (E) [K+]out dependence of the polyamine-unblocked conductance with and without Na+ substitution. Relative G values (normalized to the value at 150 mM [K+]out (0 Na+) in each experiment) are plotted against external K+ activity on double-logarithmic coordinates (left: Vrev −40 mV; right: Vrev +40 mV). Error bars represent SD. The slopes of the dashed lines are 0.29 and 0.22 in the left and right panels, respectively.
With Na+ substitution, the relations between [K+]out and the chord conductances plotted on double logarithmic coordinates could be approximated by a linear slope with factors of 0.29 and 0.22 at 40 mV negative and positive to Vrev, respectively (Fig. 3 E). Because this "square root" of the [K+]out dependence of sKir conductance has been attributed to the properties of the single-channel conductance (Sakmann and Trube, 1984), we recorded single-channel currents with and without Na+ substitution in the cell-attached mode, as they were previously performed. When a portion of the K+ ions were substituted with Na+, the unitary current amplitudes were markedly reduced as [K+]out was lowered from 150 mM to 50 and 20 mM (Fig. 4 A). The i–V relationships under different external conditions were all nearly linear within the voltage range examined (Fig. 4 B). The slope conductance of the relationships obtained by fitting a straight line only marginally decreased as [K+]out was decreased in the absence of external Na+, whereas it noticeably decreased in the presence of Na+ substitution (Fig. 4 C). With Na+ substitution, the relationship between [K+]out and slope conductance plotted on double logarithmic coordinates could be approximated by a linear slope with a factor of 0.41. These findings indicated that the square-root of [K+]out dependence of Kir2.1 conductance is mediated by the effects of external Na+ on the single-channel conductance.
Figure 4.
Inhibition of single-channel conductance of Kir2.1 by external Na+. (A) Single-channel currents recorded at different [K+]out levels (150, 50, and 20 mM) in the absence and presence of Na+ substitution ([K+]out + [Na+]out = 150 mM). Currents were recorded in the cell-attached mode from L cells stably expressing Kir2.1. Shown on the top are typical whole-cell currents recorded from Kir2.1-expressing L cells immersed in Tyrode solution at membrane potentials between −130 and +40 mV. The membrane potentials (means ± SD) of the cells (Vcell) measured by escin perforation were −47 ± 3 mV (n = 5); patch membrane potentials (VP) indicated near the current traces were calculated by assuming the membrane potential of the cells was −50 mV. Dashed lines superimposed on current traces indicate the closed-state level. (B) i–VP relationships obtained from cell-attached patches at different [K+]out in the absence (left) and presence (right) of Na+ substitution. Relationships are fitted with straight lines. (C) [K+]out dependence of the single-channel conductance in the presence and absence of Na+ substitution shown on double-logarithmic coordinates. Error bars represent SD. The slope of the dashed line is 0.41.
External Na+ is a competitive inhibitor of the K+ conductance through Kir2.1
For both the polyamine-unblocked macroscopic conductance (Fig. 3) and single-channel conductance (Fig. 4), a relatively small increase in the Na+ concentration (100 and 130 mM) evoked a marked difference in its inhibitory effect on Kir2.1 conductance at 50 mM and 20 mM [K+]out, which suggests the effect of Na+ on K+ conductance may be competitive with external K+. We therefore analyzed the Lineweaver–Burk plots of the polyamine-unblocked macroscopic Kir2.1 conductance at various [K+]out levels (10, 20, and 50 mM) in the absence and presence of 100 mM external Na+ (Fig. 5 A). The relations between 1/[K+]out and 1/G(V) obtained in the presence and absence of Na+ crossed the y axis (i.e., 1/[K+]out = 0) at similar values (∼1) at all voltages (see also Fig. S1), indicating that inhibition of conductance by external Na+ is competitive with external K+ ions. Apparent Km values of [K+]out for the K+ conductance in the absence and presence of 100 mM Na+ (at different voltages) were obtained from the slope of the Lineweaver–Burk plots, and the dissociation constants for the inhibition (Ki) by Na+ (at different voltages) were determined from those values (Fig. 5 B). The Km values for the K+ conductance were less than a few millimolars at all voltages, which matches the apparent saturation of K+ permeation at >10 mM [K+]out (Fig. 3 E). The estimated Ki values for Na+ ranged between ∼20 mM at −90 mV and ∼70 mM at +50 mV. These parameters successfully reproduced the [K+]out and voltage dependences of the open (polyamine-unblocked) channel K+ conductance observed in the experiments (Fig. 5 C; compare with Fig. 3 C).
Figure 5.
External Na+ is a competitive inhibitor of K+ conductance through Kir2.1. (A) Lineweaver–Burk plot of the open (polyamine-unblocked) Kir2.1 conductance (G) at various [K+]out levels (50, 20, and 10 mM) in the presence and absence of 100 mM external Na+ (left: −100 mV; right: 0 mV). The relative G values are the chord conductances normalized to the value obtained at 150 mM [K+]out (0 Na+) in each experiment at each V. Error bars represent SD. (B) Apparent Km values for Kir2.1 conductance in the presence and absence of 100 mM Na+ obtained from the slopes of the Lineweaver–Burk plots (left) and Ki values for Na+ inhibition (right). Lines show Km (without Na)(V) = 2.2 ⋅ exp(V/601) and Ki(Na)(V) = 51 ⋅ exp(V/115). (C) Simulation of the inhibitory effects of external Na+ on polyamine-unblocked Kir2.1 conductance. G/Gmax(V) values at different external conditions were calculated using G(V) = {Gmax(V) ⋅ [K+]out}/{Km (without Na) ⋅ (1 + [Na+]out/Ki(Na)) + [K+]out}. See Materials and methods for the details of the analysis.
Discussion
The proportionality of the open sKir channel conductance to [K+]out (with a power of ∼0.5) suggests that interaction of external K+ with the channel may enhance its bidirectional permeation. In line with this notion, complete inhibition of sKir channel currents by external K+-free solution implies that the channels may be closed or K+ ions may not permeate the channels in the absence of external K+. The present study, however, revealed that the properties are mediated by the impermeant cations Na+ and polyamines. The complete disappearance of currents under the external K+-free condition was produced solely by a complete pore blockade caused by cytoplasmic polyamines, which occurs physiologically during membrane depolarization when there is an increased outward driving force for K+. The square-root proportionality of the open K+ conductance to [K+]out reflected a fast pore blockade by physiologic concentrations of external Na+, which is competitive with external K+ (Fig. 6). These results indicate that the two phenomena are not mediated by an interaction of K+ with sKir channels, which plays a functional role in activating or facilitating the K+ permeation.
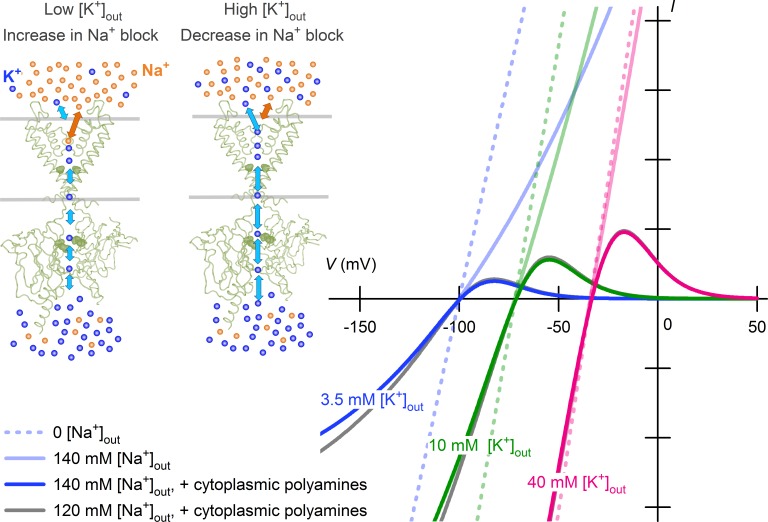
Figure 6.
[K+]out dependence of sKir currents reconstructed using Na+ block in competition with external K+. An increase in external K+ ions surmounts the fast-pore block of sKir channels by external Na+, thereby increasing both the inward and outward currents. The channel blockade by external Na+ shows a weak voltage dependence. Blockade of sKir channels by cytoplasmic polyamines (spermine), which causes their inward rectification, depends on V – EK when the [K+]out is changed. Shown are theoretical currents calculated at 3.5 mM (blue), 10 mM (green), and 40 mM (magenta) [K+]out levels in the absence of both external Na+ and cytoplasmic polyamines (dashed lines), in the presence of 140 mM external Na+ and no cytoplasmic polyamines (continuous lines with faint colors), and in the presence of 140 mM external Na+ and cytoplasmic polyamines (continuous lines with bold colors). Theoretical currents at 120 mM external Na+ (in the presence of polyamines) are also superimposed at each [K+]out (gray), but are only partly visible. Current amplitudes are given in arbitrary units. See Materials and methods for the details of calculations.
We first showed that the complete inhibition of Kir2.1 currents in external K+-free solution simply reflects the behavior of the polyamine blockade, which is apparently dependent on V – EK (Figs. 1 and 2). Conversely, the finding confirmed that cytoplasmic polyamines do not penetrate or enhance K+ efflux through sKir (Kir2) channels upon increasing V – EK (known as “punch-through” effect); that is, sKir channels do not exhibit N-shaped I–V relations by carrying outward currents during large depolarizations. In contrast, the effects of polyamines as a permeant blocker have been observed with other subtypes of Kir channels exhibiting weaker rectification (Makary et al., 2005; Kucheryavykh et al., 2007).
The present results showed that Kir2.1 is open in the absence of external K+ unless it is blocked by polyamines. However, we were unable to quantify the polyamine-unblocked conductance at 0 [K+]out because it is impossible to apply a prepulse to a voltage more negative than “EK” to relieve the block caused by residual endogenous polyamines stuck in the submembrane compartment. Instead, the finding led us to reexamine the effects of [K+]out on macroscopic Kir2.1 conductance in the absence of a polyamine block (Lopatin and Nichols, 1996a) over the [K+]out and voltage ranges commonly used in previous studies of native sKir channels (Fig. 3). The polyamine-unblocked conductances for macroscopic inward and outward currents nearly saturated at [K+]out at less than ∼10 mM. A concordant finding was obtained for the single channel conductance (Fig. 4). A low Km value for K+ permeation, comparable to the present study (Fig. 5 B), was also reported for Kir1.1 (Yang et al., 2012). The saturation of sKir channel conductance with Km values higher than we obtained was previously demonstrated using various methods and conditions (210 mM [Sakmann and Trube, 1984]; >150 mM [Lopatin and Nichols, 1996a]; and 40 mM [Stampe et al., 1998]). In some of those studies, however, K+ was substituted with Na+, which may have caused them to be biased to some extent by the effect of Na+, as we demonstrated (Fig. 5 B). In the present study, the [K+]out dependence of polyamine-unblocked conductances was obtained without compensating for the reduced K+, as was previously done (Matsuda, 1991; Lopatin and Nichols, 1996a; Ishihara and Yan, 2007; Chang et al., 2010), because a large variety of cation species, including Tris, choline, Li+, tetramethylammonium, and NMDG, are all known to interfere with sKir conductances (Biermans et al., 1987; Harvey and Ten Eick, 1989). Consequently, an increase in the negative surface charges caused by the use of low ionic strength (low [K+]out) solution could have biased our results by increasing the local K+ concentration near the outermost K+-selective site in the permeation pathway (MacKinnon et al., 1989; D’Avanzo et al., 2005). However, we suspect that this effect, which should be essentially voltage independent, contributed only to a limited extent over the [K+]out range examined in the present study, as conductances obtained in the absence and presence of Na+ substitution (keeping the ionic strength constant) did not significantly differ at large positive voltages (Fig. 3 D).
Linear relations between [K+]out and inward K+ conductances on double logarithmic coordinates (Fig. 3 E, left) have been observed with sKir channels (with slopes of ∼0.5 [Hagiwara and Takahashi, 1974], 0.62 [Sakmann and Trube, 1984], 0.21 [Matsuda, 1988], 0.29 [macroscopic current in this study] and 0.41 [unitary current in this study]) as well as in different subtypes of inward rectifiers, including cardiac ATP-sensitive K+ channels (Kir6.2; with a slope of 0.24 [Kakei et al., 1985]) and cardiac muscarinic K+ channels (Kir3.1/3.4; with a slope of 0.48 [Noma, 1987]). In each of these cases, Na+ was used to replace K+. Thus, a common mechanism may underlie the [K+]out dependence of the open conductance in the Kir family. The Goldman–Hodgkin–Katz constant field theory or the multi-ion, single-file pore model might explain the empirical property described above (Ciani et al., 1978; Hille and Schwarz, 1978; Lopatin and Nichols, 1996a), yet a mechanism whereby external K+ “activates” K+ permeation has also been proposed for Kir3.1/3.4 (Claydon et al., 2004). In a more recent study of Kir2.1 (Chang et al., 2010), it was shown that the peak amplitudes of outward currents obtained in the presence of an endogenous polyamine block exhibit a marked [K+]out dependence through the effects of external Na+ and Ca2+, which is consistent with the present results but differs in that it was attributed to the effects on the negative surface charges as well as the above “K+-activation mechanism.” Our results showed that the [K+]out dependence of the “open channel” conductance simply reflects a pore blockade induced by Na+ at ∼20% of the electrical distance from the extracellular surface. In single-channel recordings of cardiac sKir channels, the conductance obtained with asymmetrical K+ concentrations without cation substitution is fairly “ohmic” (Matsuda, 1988, 1991), as we and others have found with macroscopic Kir2.1 currents obtained in the absence of the polyamine block (Fig. 3 in this study and Lopatin and Nichols, 1996a). Moreover, the unitary current–voltage relationship exhibited an outward rectification with 25 mM K+ + 125 mM Na+ external solution (Matsuda, 1993), which is also consistent with the effects of Na+ on the polyamine-unblocked conductance shown in this study (Fig. 3 B). In the present study, external Na+ inhibited single-channel conductance of inward Kir2.1 currents (Fig. 4). It was also shown for Kir1.1 that a voltage-dependent pore blockade by Na+ is manifested as a reduction in unitary current amplitudes, which suggests the fast kinetics of the channel blockade are unresolved at the recoding bandwidth (Yang et al., 2012). These findings all support our conclusion. It should be noted that through pore blockade, external Na+ causes significant time- and voltage-dependent inactivation of inward currents through native sKirs during large hyperpolarizations (Ohmori, 1978; Standen and Stanfield, 1979; Biermans et al., 1987). In our experiments with Kir2.1, the time-dependent decay of inward currents was not evident in the macroscopic currents recorded in the presence of Na+ over the voltage range and the timescale of hyperpolarization used (Fig. 3 A).
Although sKir channels (the IK1 channel in the heart) carry much less current in the outward direction than the inward direction, the outward currents through the sKir channels show significant amplitudes compared with the other ionic currents in the human heart (Himeno et al., 2015), and it is the outward current that has a pivotal role in cardiac physiology and pathophysiology. In the case of increasing [K+]out, both a shift of the I–V relation in the depolarized direction and an increase in the open-channel conductance occur with sKir channels, and vice versa, and these two factors cause the shortening and prolongation of cardiac action potentials observed with hyperkalemia and hypokalemia, respectively (Matsuoka et al., 2003). The present study revealed that the paradoxical increase in K+ efflux through the open sKir channel with elevated [K+]out is a consequence of surmounting the competitive inhibition caused by Na+, which provides a mechanistic explanation for this important cardiac function. With the severe hyponatremia (<120 mM) observed under some pathologic conditions, the present mechanism may increase outward K+ efflux through sKir channels, although the effect appears to be insignificant by itself, as is predicted in Fig. 6.
Supplementary Material
Acknowledgments
I thank Sachiyo Igata, Makoto Takano, and Takayuki Tokimasa for help with preliminary experiments, and Yoshihiro Kubo, Shigetoshi Oiki, and Satoshi Matsuoka for valuable discussions. I also thank Natsu Mizumoto and Hiroko Fujiyoshi for technical assistance, and Hideko Yoshitake and Akemi Sakamoto for secretarial support.
This work was supported by Japan Society for the Promotion of Science KAKENHI grant JP16K08509 and a grant from the Ishibashi Foundation for the Promotion of Science.
The author declares no competing financial interests.
Author contributions: K. Ishihara designed the research, performed the experiments, analyzed the data, and wrote the manuscript.
Richard W. Aldrich served as editor.
References
- Asakura K., Cha C.Y., Yamaoka H., Horikawa Y., Memida H., Powell T., Amano A., and Noma A.. 2014. EAD and DAD mechanisms analyzed by developing a new human ventricular cell model. Prog. Biophys. Mol. Biol. 116:11–24. 10.1016/j.pbiomolbio.2014.08.008 [DOI] [PubMed] [Google Scholar]
- Baukrowitz T., and Yellen G.. 1995. Modulation of K+ current by frequency and external [K+]: A tale of two inactivation mechanisms. Neuron. 15:951–960. 10.1016/0896-6273(95)90185-X [DOI] [PubMed] [Google Scholar]
- Biermans G., Vereecke J., and Carmeliet E.. 1987. The mechanism of the inactivation of the inward-rectifying K current during hyperpolarizing steps in guinea-pig ventricular myocytes. Pflugers Arch. 410:604–613. 10.1007/BF00581320 [DOI] [PubMed] [Google Scholar]
- Bouchard R., Clark R.B., Juhasz A.E., and Giles W.R.. 2004. Changes in extracellular K+ concentration modulate contractility of rat and rabbit cardiac myocytes via the inward rectifier K+ current IK1. J. Physiol. 556:773–790. 10.1113/jphysiol.2003.058248 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang H.K., Lee J.R., Liu T.A., Suen C.S., Arreola J., and Shieh R.C.. 2010. The extracellular K+ concentration dependence of outward currents through Kir2.1 channels is regulated by extracellular Na+ and Ca2+. J. Biol. Chem. 285:23115–23125. 10.1074/jbc.M110.121186 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ciani S., Krasne S., Miyazaki S., and Hagiwara S.. 1978. A model for anomalous rectification: Electrochemical-potential-dependent gating of membrane channels. J. Membr. Biol. 44:103–134. 10.1007/BF01976035 [DOI] [PubMed] [Google Scholar]
- Claydon T.W., Makary S.Y., Dibb K.M., and Boyett M.R.. 2004. K+ activation of Kir3.1/Kir3.4 and Hv1.4 K+ channels is regulated by extracellular charges. Biophys. J. 87:2407–2418. 10.1529/biophysj.103.039073 [DOI] [PMC free article] [PubMed] [Google Scholar]
- D’Avanzo N., Cho H.C., Tolokh I., Pekhletski R., Tolokh I., Gray C., Goldman S., and Backx P.H.. 2005. Conduction through the inward rectifier potassium channel, Kir2.1, is increased by negatively charged extracellular residues. J. Gen. Physiol. 125:493–503. 10.1085/jgp.200409175 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davies C.W. 1962. Ion association. Butterworth, London: 190 pp. [Google Scholar]
- Fabiato A., and Fabiato F.. 1979. Calculator programs for computing the composition of the solutions containing multiple metals and ligands used for experiments in skinned muscle cells. J. Physiol. (Paris). 75:463–505. [PubMed] [Google Scholar]
- Fan J.S., and Palade P.. 1998. Perforated patch recording with β-escin. Pflugers Arch. 436:1021–1023. 10.1007/PL00008086 [DOI] [PubMed] [Google Scholar]
- Fujiwara Y., and Kubo Y.. 2006. Functional roles of charged amino acid residues on the wall of the cytoplasmic pore of Kir2.1. J. Gen. Physiol. 127:401–419. 10.1085/jgp.200509434 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo D., and Lu Z.. 2000. Pore block versus intrinsic gating in the mechanism of inward rectification in strongly rectifying IRK1 channels. J. Gen. Physiol. 116:561–568. 10.1085/jgp.116.4.561 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo D., and Lu Z.. 2003. Interaction mechanisms between polyamines and IRK1 inward rectifier K+ channels. J. Gen. Physiol. 122:485–500. 10.1085/jgp.200308890 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo D., Ramu Y., Klem A.M., and Lu Z.. 2003. Mechanism of rectification in inward-rectifier K+ channels. J. Gen. Physiol. 121:261–275. 10.1085/jgp.200208771 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagiwara S., and Takahashi K.. 1974. The anomalous rectification and cation selectivity of the membrane of a starfish egg cell. J. Membr. Biol. 18:61–80. 10.1007/BF01870103 [DOI] [PubMed] [Google Scholar]
- Hagiwara S., and Yoshii M.. 1979. Effects of internal potassium and sodium on the anomalous rectification of the starfish egg as examined by internal perfusion. J. Physiol. 292:251–265. 10.1113/jphysiol.1979.sp012849 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamill O.P., Marty A., Neher E., Sakmann B., and Sigworth F.J.. 1981. Improved patch-clamp techniques for high-resolution current recording from cells and cell-free membrane patches. Pflugers Arch. 391:85–100. 10.1007/BF00656997 [DOI] [PubMed] [Google Scholar]
- Harvey R.D., and Ten Eick R.E.. 1989. On the role of sodium ions in the regulation of the inward-rectifying potassium conductance in cat ventricular myocytes. J. Gen. Physiol. 94:329–348. 10.1085/jgp.94.2.329 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hestrin S. 1981. The interaction of potassium with the activation of anomalous rectification in frog muscle membrane. J. Physiol. 317:497–508. 10.1113/jphysiol.1981.sp013839 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hille B. 2001. Ion Channels of Excitable Membranes. 3rd ed Sinauer Associates, Sunderland, MA: 814 pp. [Google Scholar]
- Hille B., and Schwarz W.. 1978. Potassium channels as multi-ion single-file pores. J. Gen. Physiol. 72:409–442. 10.1085/jgp.72.4.409 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Himeno Y., Asakura K., Cha C.Y., Memida H., Powell T., Amano A., and Noma A.. 2015. A human ventricular myocyte model with a refined representation of excitation-contraction coupling. Biophys. J. 109:415–427. 10.1016/j.bpj.2015.06.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoshi T., and Armstrong C.M.. 2013. C-type inactivation of voltage-gated K+ channels: pore constriction or dilation? J. Gen. Physiol. 141:151–160. 10.1085/jgp.201210888 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishihara K., and Ehara T.. 2004. Two modes of polyamine block regulating the cardiac inward rectifier K+ current IK1 as revealed by a study of the Kir2.1 channel expressed in a human cell line. J. Physiol. 556:61–78. 10.1113/jphysiol.2003.055434 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishihara K., and Yan D.H.. 2007. Low-affinity spermine block mediating outward currents through Kir2.1 and Kir2.2 inward rectifier potassium channels. J. Physiol. 583:891–908. 10.1113/jphysiol.2007.136028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishihara K., Mitsuiye T., Noma A., and Takano M.. 1989. The Mg2+ block and intrinsic gating underlying inward rectification of the K+ current in guinea-pig cardiac myocytes. J. Physiol. 419:297–320. 10.1113/jphysiol.1989.sp017874 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishihara K., Hiraoka M., and Ochi R.. 1996. The tetravalent organic cation spermine causes the gating of the IRK1 channel expressed in murine fibroblast cells. J. Physiol. 491:367–381. 10.1113/jphysiol.1996.sp021222 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ishihara K., Sarai N., Asakura K., Noma A., and Matsuoka S.. 2009. Role of Mg2+ block of the inward rectifier K+ current in cardiac repolarization reserve: A quantitative simulation. J. Mol. Cell. Cardiol. 47:76–84. 10.1016/j.yjmcc.2009.03.008 [DOI] [PubMed] [Google Scholar]
- Kakei M., Noma A., and Shibasaki T.. 1985. Properties of adenosine-triphosphate-regulated potassium channels in guinea-pig ventricular cells. J. Physiol. 363:441–462. 10.1113/jphysiol.1985.sp015721 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kubo Y. 1996. Effects of extracellular cations and mutations in the pore region on the inward rectifier K+ channel IRK1. Receptors Channels. 4:73–83. [PubMed] [Google Scholar]
- Kubo Y., and Murata Y.. 2001. Control of rectification and permeation by two distinct sites after the second transmembrane region in Kir2.1 K+ channel. J. Physiol. 531:645–660. 10.1111/j.1469-7793.2001.0645h.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kubo Y., Baldwin T.J., Jan Y.N., and Jan L.Y.. 1993. Primary structure and functional expression of a mouse inward rectifier potassium channel. Nature. 362:127–133. 10.1038/362127a0 [DOI] [PubMed] [Google Scholar]
- Kucheryavykh Y.V., Pearson W.L., Kurata H.T., Eaton M.J., Skatchkov S.N., and Nichols C.G.. 2007. Polyamine permeation and rectification of Kir4.1 channels. Channels (Austin). 1:172–178. 10.4161/chan.4389 [DOI] [PubMed] [Google Scholar]
- Liu T.A., Chang H.K., and Shieh R.C.. 2012. Revisiting inward rectification: K ions permeate through Kir2.1 channels during high-affinity block by spermidine. J. Gen. Physiol. 139:245–259. 10.1085/jgp.201110736 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopatin A.N., and Nichols C.G.. 1996a [K+] dependence of open-channel conductance in cloned inward rectifier potassium channels (IRK1, Kir2.1). Biophys. J. 71:682–694. 10.1016/S0006-3495(96)79268-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopatin A.N., and Nichols C.G.. 1996b [K+] dependence of polyamine-induced rectification in inward rectifier potassium channels (IRK1, Kir2.1). J. Gen. Physiol. 108:105–113. 10.1085/jgp.108.2.105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lopatin A.N., Makhina E.N., and Nichols C.G.. 1995. The mechanism of inward rectification of potassium channels: “Long-pore plugging” by cytoplasmic polyamines. J. Gen. Physiol. 106:923–955. 10.1085/jgp.106.5.923 [DOI] [PMC free article] [PubMed] [Google Scholar]
- López-Barneo J., Hoshi T., Heinemann S.H., and Aldrich R.W.. 1993. Effects of external cations and mutations in the pore region on C-type inactivation of Shaker potassium channels. Receptors Channels. 1:61–71. [PubMed] [Google Scholar]
- MacKinnon R., Latorre R., and Miller C.. 1989. Role of surface electrostatics in the operation of a high-conductance Ca2+-activated K+ channel. Biochemistry. 28:8092–8099. 10.1021/bi00446a020 [DOI] [PubMed] [Google Scholar]
- Makary S.M., Claydon T.W., Enkvetchakul D., Nichols C.G., and Boyett M.R.. 2005. A difference in inward rectification and polyamine block and permeation between the Kir2.1 and Kir3.1/Kir3.4 K+ channels. J. Physiol. 568:749–766. 10.1113/jphysiol.2005.085746 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maruyama M., Lin S.-F., Xie Y., Chua S.-K., Joung B., Han S., Shinohara T., Shen M.J., Qu Z., Weiss J.N., and Chen P.-S.. 2011. Genesis of phase 3 early afterdepolarizations and triggered activity in acquired long-QT syndrome. Circ Arrhythm Electrophysiol. 4:103–111. 10.1161/CIRCEP.110.959064 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuda H. 1988. Open-state substructure of inwardly rectifying potassium channels revealed by magnesium block in guinea-pig heart cells. J. Physiol. 397:237–258. 10.1113/jphysiol.1988.sp016998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuda H. 1991. Effects of external and internal K+ ions on magnesium block of inwardly rectifying K+ channels in guinea-pig heart cells. J. Physiol. 435:83–99. 10.1113/jphysiol.1991.sp018499 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuda H. 1993. Effects of internal and external Na+ ions on inwardly rectifying K+ channels in guinea-pig ventricular cells. J. Physiol. 460:311–326. 10.1113/jphysiol.1993.sp019473 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuda H., and Noma A.. 1984. Isolation of calcium current and its sensitivity to monovalent cations in dialysed ventricular cells of guinea-pig. J. Physiol. 357:553–573. 10.1113/jphysiol.1984.sp015517 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuoka S., Sarai N., Kuratomi S., Ono K., and Noma A.. 2003. Role of individual ionic current systems in ventricular cells hypothesized by a model study. Jpn. J. Physiol. 53:105–123. 10.2170/jjphysiol.53.105 [DOI] [PubMed] [Google Scholar]
- Nichols C.G., Makhina E.N., Pearson W.L., Sha Q., and Lopatin A.N.. 1996. Inward rectification and implications for cardiac excitability. Circ. Res. 78:1–7. 10.1161/01.RES.78.1.1 [DOI] [PubMed] [Google Scholar]
- Niwa H., Yamamura K., and Miyazaki J.. 1991. Efficient selection for high-expression transfectants with a novel eukaryotic vector. Gene. 108:193–199. 10.1016/0378-1119(91)90434-D [DOI] [PubMed] [Google Scholar]
- Noma A. 1987. Chemical-receptor–dependent potassium channels in cardiac muscles. In Electrophysiology of Single Cardiac Cells. Noble D., and Powell T., editors. Academic Press, London: 223–246. [Google Scholar]
- Ohmori H. 1978. Inactivation kinetics and steady-state current noise in the anomalous rectifier of tunicate egg cell membranes. J. Physiol. 281:77–99. 10.1113/jphysiol.1978.sp012410 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakmann B., and Trube G.. 1984. Conductance properties of single inwardly rectifying potassium channels in ventricular cells from guinea-pig heart. J. Physiol. 347:641–657. 10.1113/jphysiol.1984.sp015088 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shimoni Y., Clark R.B., and Giles W.R.. 1992. Role of an inwardly rectifying potassium current in rabbit ventricular action potential. J. Physiol. 448:709–727. 10.1113/jphysiol.1992.sp019066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shin H.G., and Lu Z.. 2005. Mechanism of the voltage sensitivity of IRK1 inward-rectifier K+ channel block by the polyamine spermine. J. Gen. Physiol. 125:413–426. 10.1085/jgp.200409242 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stampe P., Arreola J., Pérez-Cornejo P., and Begenisich T.. 1998. Nonindependent K+ movement through the pore in IRK1 potassium channels. J. Gen. Physiol. 112:475–484. 10.1085/jgp.112.4.475 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Standen N.B., and Stanfield P.R.. 1979. Potassium depletion and sodium block of potassium currents under hyperpolarization in frog sartorius muscle. J. Physiol. 294:497–520. 10.1113/jphysiol.1979.sp012943 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stumm W., and Morgan J.J.. 1981. Aquatic Chemistry: An Introduction Emphasizing Chemical Equilibria in Natural Waters. John Wiley & Sons, New York: 135 pp. [Google Scholar]
- Taglialatela M., Ficker E., Wible B.A., and Brown A.M.. 1995. C-terminus determinants for Mg2+ and polyamine block of the inward rectifier K+ channel IRK1. EMBO J. 14:5532–5541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tao X., Avalos J.L., Chen J., and MacKinnon R.. 2009. Crystal structure of the eukaryotic strong inward-rectifier K+ channel Kir2.2 at 3.1 A resolution. Science. 326:1668–1674. 10.1126/science.1180310 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie L.H., John S.A., and Weiss J.N.. 2003. Inward rectification by polyamines in mouse Kir2.1 channels: synergy between blocking components. J. Physiol. 550:67–82. 10.1113/jphysiol.2003.043117 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Y., Shin H.G., Szép S., and Lu Z.. 2009. Physical determinants of strong voltage sensitivity of K+ channel block. Nat. Struct. Mol. Biol. 16:1252–1258. 10.1038/nsmb.1717 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan D.H., Nishimura K., Yoshida K., Nakahira K., Ehara T., Igarashi K., and Ishihara K.. 2005. Different intracellular polyamine concentrations underlie the difference in the inward rectifier K+ currents in atria and ventricles of the guinea-pig heart. J. Physiol. 563:713–724. 10.1113/jphysiol.2004.077677 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J., Jan Y.N., and Jan L.Y.. 1995. Control of rectification and permeation by residues in two distinct domains in an inward rectifier K+ channel. Neuron. 14:1047–1054. 10.1016/0896-6273(95)90343-7 [DOI] [PubMed] [Google Scholar]
- Yang L., Edvinsson J., Sackin H., and Palmer L.G.. 2012. Ion selectivity and current saturation in inward-rectifier K+ channels. J. Gen. Physiol. 139:145–157. 10.1085/jgp.201110727 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.