Molecular determination of claudin-15 organization and channel selectivity

Members of the claudin family form tight junctions between adjacent epithelial and endothelial cells. Samanta et al. build an atomic model of claudin-15 using molecular dynamics simulations and conclude that four claudin-15 molecules each contribute an aspartic acid residue to form a selectivity filter.

Abstract

Tight junctions are macromolecular structures that traverse the space between adjacent cells in epithelia and endothelia. Members of the claudin family are known to determine tight junction permeability in a charge- and size-selective manner. Here, we use molecular dynamics simulations to build and refine an atomic model of claudin-15 channels and study its transport properties. Our simulations indicate that claudin-15 forms well-defined channels for ions and molecules and otherwise “seals” the paracellular space through hydrophobic interactions. Ionic currents, calculated from simulation trajectories of wild-type as well as mutant channels, reflect in vitro measurements. The simulations suggest that the selectivity filter is formed by a cage of four aspartic acid residues (D55), contributed by four claudin-15 molecules, which creates a negative electrostatic potential to favor cation flux over anion flux. Charge reversal or charge ablation mutations of D55 significantly reduce cation permeability in silico and in vitro, whereas mutations of other negatively charged pore amino acid residues have a significantly smaller impact on channel permeability and selectivity. The simulations also indicate that water and small ions can pass through the channel, but larger cations, such as tetramethylammonium, do not traverse the pore. Thus, our model provides an atomic view of claudin channels, their transport function, and a potential three-dimensional organization of its selectivity filter.

Introduction

Tight junctions form a selective barrier limiting paracellular transport across epithelia and endothelia (Chalcroft and Bullivant, 1970; Tang and Goodenough, 2003; Anderson and Van Itallie, 2009; Furuse, 2010; Lingaraju et al., 2015; Zihni et al., 2016; Odenwald and Turner, 2017). Claudins are one of the major tight junction components and are thought to define paracellular permeability to small ions (Furuse et al., 1999; Morita et al., 1999; Colegio et al., 2003; González-Mariscal et al., 2003; Piontek et al., 2008; Gonçalves et al., 2013; Günzel and Yu, 2013) by sealing the paracellular space and by forming ion channels that provide a selective pathway for the passage of water and ions (Tang and Goodenough, 2003; Yu et al., 2009; Rosenthal et al., 2010; Weber et al., 2015). However, the molecular architecture of claudin channels and how it defines function remain poorly defined.

Each claudin monomer contains four transmembrane (TM) helices (TM1–TM4), two extracellular segments, and a short extracellular helix (ECH). The first extracellular segment (ECS1; ∼40 amino acids) contains the highly conserved signature sequence W-G/NLW-C-C and is thought to contain the residues that line the conduction pathway and determine the claudin pore charge selectivity (Colegio et al., 2002, 2003; Van Itallie et al., 2003; Van Itallie and Anderson, 2006; Anderson and Van Itallie, 2009; Yu et al., 2009; Günzel and Yu, 2013; Suzuki et al., 2014). The second extracellular segment (ECS2; ∼10 amino acids) contains residues thought to be involved in claudin–claudin interaction and mediate the assembly of claudins into tight junctions (Piontek et al., 2008, 2017; Anderson and Van Itallie, 2009; Piehl et al., 2010; Krause et al., 2015). The recently defined claudin-15 crystal structure provided additional insight (Suzuki et al., 2014). Part of ECS1 and ECS2 forms a unique “palm-like” β-sheet structure that is suggested to line the permeation pathway and define the pore surface (Angelow et al., 2008; Suzuki et al., 2014, 2015). However, the crystal structure does not contain portions of the extracellular loops and does not consider interactions of claudins between adjacent cells, making it impossible to define channel structure and function.

Suzuki et al. (2015) proposed an organization of multiple claudin monomers within adjacent lipid membranes. In this model, claudin pores are formed by association of two antiparallel double rows of claudins in the membranes of two adjacent cells. Claudin monomers in the two rows interact with each other through their β-sheet domains, forming an extended β-sheet structure that is maintained by hydrogen bonds. However, the proposed model does not provide any details on how the disordered regions in the ECSs, which were not fully resolved in the crystal structure, interact at a molecular level. In addition, it remains unclear how this claudin-15 model can define pore permeability.

To understand the molecular basis of how claudins form ion-selective paracellular channels and how these channels form selectively permeable pathways, we combined MD simulation with in vitro analyses of claudin-15 function in model epithelium. All-atom simulations allowed us to generate a functional model for claudin-15 conductance and selectivity. Simulations indicate that claudin-15 seals the paracellular space and forms well-defined pathways for transport of ions and water molecules. In addition, the pores are cation selective and sensitive to mutation of negatively charged residues lining the pore. The simulations have suggested D55 as the key residue defining channel cation permeability and demonstrate how it interacts with permeating cations. Mutational analysis in silico and in vitro further support our findings. Thus, our study provides novel insight into claudin-15 structure and function.

Materials and methods

Simulation details

All-atom MD simulations were performed using the program NAMD (Phillips et al., 2005) and the CHARMM36 force field for proteins (MacKerell et al., 1998; Mackerell et al., 2004; Best et al., 2012), ions (Jorgensen et al., 1983), and phospholipids (Klauda et al., 2010) with the TIP3P water model (Jorgensen et al., 1983). Assuming periodic boundary conditions, long-range electrostatic forces were calculated using the particle mesh Ewald method (Darden et al., 1993) with a grid spacing of at least 1 Å in each direction. The simulations used time steps of 1 fs, 2 fs, and 4 fs for bonded, nonbonded, and electrostatic calculations, respectively. Langevin dynamics with a friction coefficient of γ = 5 ps⁻¹ was used to keep the temperature constant at 333°K. The Langevin Nosé-Hoover method (Feller et al., 1995) was used to maintain the pressure at 1 atm in constant-pressure simulations. Additional restraints on the protein backbone were applied by enforcing a harmonic potential with a force constant of 3.0 kcal/mol/Ų unless otherwise stated.

System setup

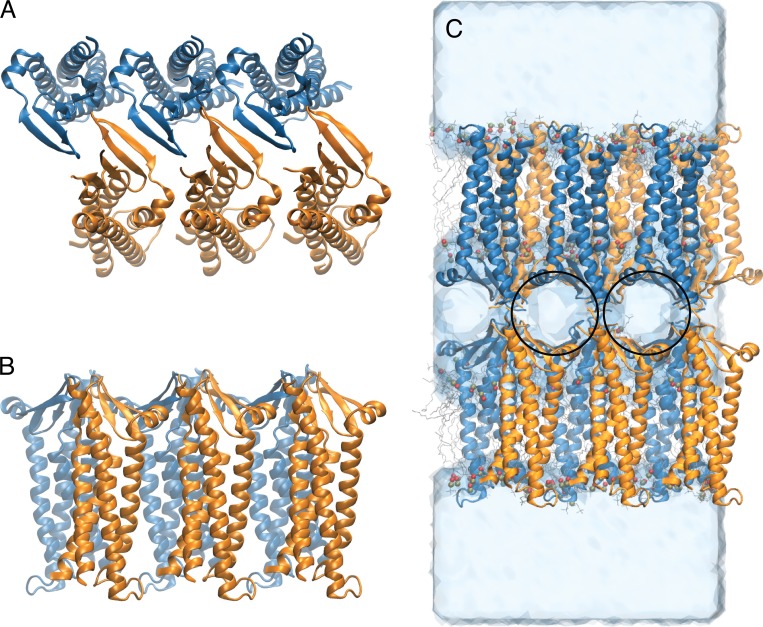
The crystal structure of mouse claudin-15 (Protein Data Bank accession no. 4P79; Suzuki et al., 2014) was used as the starting point for the simulations. To build a complete model of the claudin-15 monomer, the missing residues 34–41 on ECS1 were modeled using the program MODELLER (Sali and Blundell, 1993). The initial structure of claudin-15 channels was built based on the modeled structure of the monomer and the proposed architectural model (Suzuki et al., 2015). In this model, each membrane contains claudin monomers that are arranged in an antiparallel double row (Fig. 1, A and B). Claudin pores are formed by head-to-head interaction of the extracellular domains of claudins in two parallel membranes, mimicking the membranes of adjacent cells within the tight junction (Fig. 1 C).

Figure 1.

Claudin-15 monomers assemble into double-row strands and form paracellular channels. (A) Top view of the model of six claudin-15 molecules. The two rows are colored orange and blue. (B) Side view of the model. (C) Snapshot of the simulation system consisting of two parallel lipid membranes and claudin pores after equilibration. In this conformation, the claudins form paracellular channels shown with black circles.

To build an atomic model of claudin pores in their native environment, we built a system consisting of two parallel POPC lipid membranes, each including six claudin monomers. The resulting system contains 710 POPC lipid molecules, 70,899 water molecules, and 328 ions with a total of 341,609 atoms. The system was equilibrated in a multistep process (described in detail below), in which the claudin-15 pores were further refined through extensive MD simulations.

Initially, six monomers were arranged in an antiparallel double row in a single membrane of POPC surrounded by 150 mM NaCl in water. The size of the system was chosen such that the intermolecular contacts between claudin-15 monomers in each unit cell were identical to those between claudins at two neighboring cells, resulting in a continuous strand of claudin-15 in the membrane. The system was minimized for 5,000 steps followed by 100 ps of simulation in which the lipid tails were allowed to melt. The system was then equilibrated for 15 ns at constant pressure and temperature with the backbone of the protein constrained, allowing only the extracellular loops (residues 34–41, 149–154, and 56–58) to move. To improve the packing of the lipids between the two claudin rows, the protein backbone was released for a short period of time (1 ns), allowing further adjustment of the lipids without disruption of the interprotein contacts at the extracellular domains. The simulations were then continued for another 5 ns at constant volume with the protein backbone constrained to obtain a well-packed protein-membrane system in a single POPC bilayer. To ensure the stability of the protein structure, the protein backbone was released and the simulation was continued for another 10 ns, during which the RMSD of the protein backbone remained within 3.08 Å of the initial structure.

Next, to build the two-membrane system, the equilibrated protein structure was replicated based on the previously proposed architectural model (Suzuki et al., 2015), resulting in a system of three pores between two parallel rows of claudin-15. The modeled loop (residues 34–41) contained one of the two variable regions that are proposed to be responsible for head-to-head interaction of claudin-15 and formation of the channels (Suzuki et al., 2015). To further refine these loops, short MD simulations (100–500 ps) were performed in which the extracellular loops were allowed to move freely in the full channel structure while the backbone of the rest of the protein was constrained. To avoid any bias toward the initial conformations that might allow the loops to be entangled and confined to certain configurations, nonbonded interactions between mobile regions of claudin-15 pairs were turned off, allowing the loops to pass through each other and explore a wider collection of conformations. Such methods have been used to model overlapping loops in other membrane proteins (Sandtner et al., 2011; Shen et al., 2015). To facilitate the equilibration, steered MD (Lu and Schulten, 1999; Isralewitz et al., 2001) was performed on the modeled loops with a soft force constant of 2.2 kcal/mol/Ų and a pulling velocity of 0.01 Å/ps for durations of 50–100 ps to avoid possible entanglements.

The model of 12 claudin-15 monomers was then embedded in two parallel and identical layers of POPC lipid bilayers that were obtained in the first step of the refinement. The resulting system was solvated with an aqueous solution of ∼110 mM NaCl. To avoid electroporation in the double-membrane system, ion concentrations were chosen such that the net electrostatic charge between the two sides of each membrane was zero and the unit cell remained neutral. To achieve this, we added 52 Na⁺ and 28 Cl⁻ in the central compartment of the simulation system and 112 Na⁺ and 136 Cl⁻ in the outer compartments, resulting in a net electrostatic charge of zero across the two sides of each membrane. A snapshot of the simulated system is shown in Fig. 1 C.

To equilibrate the complete system, it was first minimized for 5,000 steps, followed by 8 ns of equilibration where the protein backbone was constrained at constant pressure and temperature, allowing the loops to relax. The constrained backbone was gradually released by reducing the force constant to 1.5, 0.75 to 0.3 kcal/mol in 6 ns under constant pressure. It was minimized for 5,000 steps and run for 6 ns of equilibration where everything was released, at constant pressure, followed by 25 ns of free equilibration at constant volume. To assess the stability of the model, the equilibration was continued for 250 ns. Structural properties and interaction surfaces of claudin monomers were characterized during this trajectory.

It has to be noted that it is imperative to use a system with claudin strands that continue periodically across the unit cell boundaries if the system is used to study ion permeation across claudin pores. A noncontinuous strand of claudins will result in leakage and nonuniform voltage drops across claudin pores. However, to assess the stability of the proposed double-row arrangement of claudins, we have repeated the simulations of six and twelve claudins in larger lipid membranes in a noncontinuous setup. These systems confer more flexibility to the protein systems and allow lateral diffusion of the claudins in the membrane or partial adjustment of the distance between claudins in two membranes (trans-interactions). Both of these systems proved to be stable after 50–100 ns of equilibration with mean RMSDs of 3.7–4.7 Å with respect to the initial setup.

Ion transport simulations

To simulate the passage of ions through claudin-15 pores and measure the ionic current of monovalent cations of different sizes, four additional systems were prepared in which the 110-mM NaCl solution was replaced with 110 mM methylammonium chloride, ethylammonium chloride, tetramethylammonium chloride, or tetraethylammonium chloride. Each system was equilibrated for 20 ns after ion replacement and subjected to potential biases of −1.2 V, −0.8 V, −0.4 V, 0.4 V, 0.8 V, or 1.2 V across the pores. The voltage bias was generated by application of a constant electric field parallel to the pores (Gumbart et al., 2012). During these simulations, the protein backbone of the TM region was constrained with a small force constant of 0.9 kcal/mol/Ų to avoid drift of the protein in the membrane in the presence of the applied voltage. The CHARMM36 general force field was used for the cation parameters (Vanommeslaeghe et al., 2010), and each simulation was run for 35 ns at constant volume (V) and temperature (T; NVT ensemble). The total ionic current was calculated from the displacement current corresponding to all partial charges of the system (Khalili-Araghi et al., 2013; Adelman and Grabe, 2015). Cation and anion currents in each system were also calculated from displacement currents of each ion throughout the simulations.

Analysis of claudin-15 mutants

To simulate the ionic currents passing through claudin-15 pores containing claudin-15 single mutations, multiple mutant systems (D55N, D55K, D64K, and E46K/D55K/D64K) were prepared using molecular visualization program VMD, starting from the equilibrated system of claudin-15 pores. Each mutant system was equilibrated for 12 ns at constant volume and temperature and subjected to external potential bias for 35 ns. Current–voltage relationships in these systems were calculated from the 35-ns trajectories using the same procedure as described above.

Concentration dependence studies

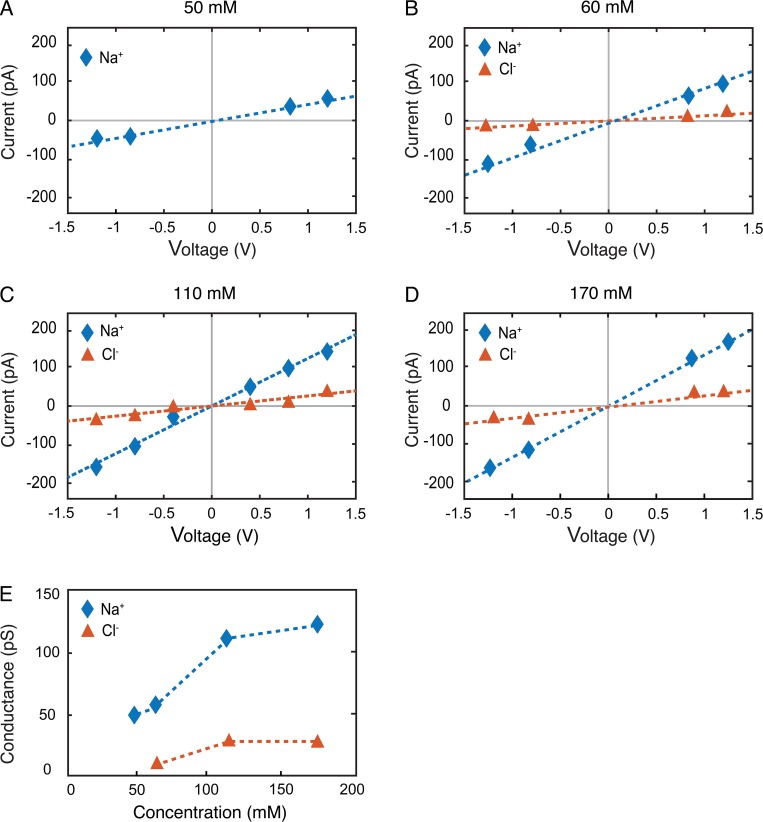
To accurately calculate the permeability of the claudin-15, it is essential that we study channel properties over a region of concentrations where the channel is saturated (Levitt, 1978; Nadler et al., 2004). To test this, the Na⁺ and Cl⁻ concentrations were varied from 50 to 170 mM, and in each case, ionic conductance was calculated from 35-ns simulation trajectories as described above (Fig. 2, A–D). In each system, the number of ions was chosen to ensure that (a) the unit cell was neutral and (b) the net charge across the membranes was zero. In addition to the systems containing NaCl, ionic currents were calculated in a system that was neutralized by 24 TEA⁺, a cation that is impermeable in the course of the simulation and was ionized with 60 mM NaCl (Fig. 2 B). These results demonstrate that at 110 mM, the calculated ionic conductance is relatively independent of ion concentrations (Fig. 2 E).

Figure 2.

Claudin-15 channel conductance is saturated within the physiological range of Na⁺ and Cl⁻. (A–D) I-V plots are calculated with 50 mM of Na⁺ and no Cl⁻ (A), neutralized with 24 TEA⁺ and 60 mM NaCl (B), 110 mM NaCl (C), or 170 mM NaCl (D). (E) Conductance of the Na⁺ ions for the WT channel for the four systems above.

Generation of enhanced GFP–claudin-15 coding plasmid

Full-length human claudin-15 was synthesized (Integrated DNA) and cloned into a single vector–based doxycycline-inducible EGFP-fusion protein expressing PiggyBac plasmid using the InFusion ligase-independent cloning system (Clontech). This plasmid also encodes the Tet3G transcription activator (Buschmann et al., 2013). Claudin-15 point mutants (E64K, D55N, and D55K) were generated using the QuickChange Lightning site-directed mutagenesis kit (Agilent). For claudin-15 E46K/D55K/E64K triple mutant, the full-length mutant human claudin-15 sequence was synthesized and cloned similar to WT claudin-15.

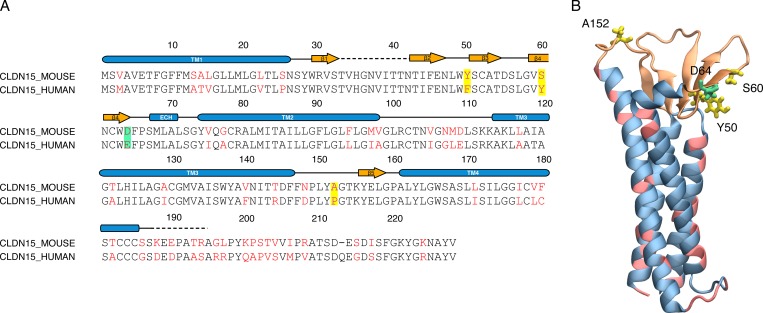
Because of the high sequence similarity between mouse claudin-15 and human claudin-15 (78% identity and 92% similarity; Fig. 3), no significant differences are expected between the mouse and human claudin-15 channels. The sequence alignment demonstrates only one amino acid difference within the pore lining residues (D64 vs. E64), which does not impart any significant difference.

Figure 3.

Human and mouse claudin-15 are similar. (A) Sequence alignment of mouse claudin-15 and human claudin-15. Identical residues are shown in black and nonidentical residues in red. The residues highlighted in the sequence lie in the extracellular region of claudin-15 monomer. (B) A snapshot of mouse claudin-15 monomer showing the nonidentical residues in the extracellular region (Y50, S60, and A152) in licorice and in the backbone of the helices in pink.

Cell culture and generation of stably transfected cell lines

High-resistance Madin–Darby canine kidney (MDCK) I cells (obtained from E. Rodringez-Boulan, Cornell University, Ithaca, NY) were cultured in Dulbecco's modified Eagle's media with 1g/liter glucose, 15 mM HEPES, pH 7.4, and 10% FBS. They were fed three times a week and subcultured every 3–4 d.

To generate stable cell lines, individual EGFP– and EGFP–claudin-15 encoding plasmids were double transfected with a PiggyBac transposase-encoding plasmid and transfected into MDCK I cells using Lipofectamine 2000 (Life Technology). Cells with PiggyBac transposase-mediated plasmid integration were selected by culturing transfected cells in complete medium supplemented with 300 µg/ml hygromycin until individual colonies had grown out. Pooled clones were maintained in complete medium supplemented with 150 µg/ml hygromycin.

For functional analysis, MDCK I cells were plated on 0.33-cm² polycarbonate semipermeable membranes with 0.4-µm pores (Corning Life Sciences) at confluent density. Cells were fed every day and were used 4 d after plating as described previously (Buschmann et al., 2013; Weber et al., 2015). To induce EGFP and EGF–claudin-15 expression, doxycycline (10–50 ng/ml, depending on the genes expressed, to ensure equal exogenous gene expression) was included in the complete culture medium 1 d after plating.

In vitro measurements of claudin-15 barrier function

MDCK I monolayers with doxycycline-induced EGFP, EGFP–claudin-15 expression, and their respective controls without doxycycline-induced exogenous gene expression grown on 0.33 cm² semipermeable supports (Transwells) were used. A current-clamp technique was used to measure barrier function as previously described (Yu et al., 2009; Weber et al., 2010, 2015; Buschmann et al., 2013). Voltage- and current-sensing electrodes consisted of two pairs of Hank’s balanced salt solution (HBSS)–containing agar bridges that bridge from the Transwells (located on a heating plate 37°C) to glass vials containing voltage- and current-sensing electrodes. Each pair consisted of one apical and one basolateral electrode. Voltage-sensing electrodes were Beckman Calomel-pHree electrodes in KCl, and current-sensing electrodes were Ag-AgCl wires in HBSS. Both pairs of electrodes connect to the voltage clamp amplifier via a preamplifier (University of Iowa Bioengineering).

Transwells with confluent monolayers were transferred to HBSS with 1 g/ml glucose and incubated at 37°C for 30 min before the experiment. After equilibration, transepithelial electrical resistance (TER) was calculated from Ohm’s law using 10-μA current clamp steps and measured voltage. TER values are corrected for the resistance of an empty insert and multiplied by insert size. P_Na⁺/P_Cl⁻ was measured as previously described (Weber et al., 2010, 2015) from NaCl dilution potentials by replacing the basal HBSS with HBSS containing half the apical NaCl concentration but osmotically balanced with mannitol. The Goldmann–Hodgkin–Katz equation (V_rev = −(RT/F)ln[(α + β)/(1 + αβ)]; β = P_Cl⁻/P_Na⁺, α = 1.9, RT/F = 26.6) was used to calculate the relative permeability of sodium to chloride (P_Na⁺/P_Cl⁻). V_rev was determined by current clamping at I = 0. To determine claudin-15 channel size selectivity to monovalent cations, bi-ionic potentials were measured by replacing Na⁺ in basal HBSS with the following larger-sized cations: methylammonium (MA⁺; radius 2.1 Å; Jishi, 2016), ethylammonium (EA⁺; radius 2.7 Å; Niga et al., 2010), tetramethylammonium (TMA⁺; radius 3.0 Å; McCleskey and Almers, 1985), and tetraethylammonium (TEA⁺; radius 3.5 Å; Ikuno et al., 2015). P_M⁺/P_Na⁺ was calculated from V_rev = (RT/F)ln[(γ + β)/(1 + β)], where γ = P_M⁺/P_Na⁺.

Results

Generation of the claudin-15 channel model

Based on the claudin-15 crystal structure, a model of claudin assembly was established (Suzuki et al., 2015). In this model, claudin-15 monomers assemble into linear strands consisting of an antiparallel double row of claudins in a single membrane. Claudin monomers interact with each other through their extracellular β-sheets, forming a half-pipe structure that is maintained by hydrogen bonds between the β-strands. The Suzuki et al. model is consistent with cysteine cross-linking experiments that show dimerization of claudins through extracellular β-sheets (Angelow and Yu, 2009; Li et al., 2013), as well as the strand dimensions observed in freeze-fracture electron microscopy images (Suzuki et al., 2015), and we used this model as the basis for understanding claudin-15 quaternary structure.

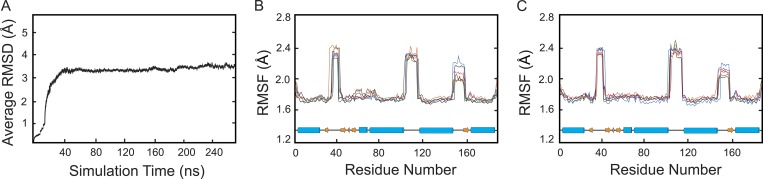
To build a complete structure of the pore, the claudin-15 extracellular loop domains (missing from the crystal structure) were restored using MODELLER software (Sali and Blundell, 1993). The protein was relaxed in a single lipid membrane containing six claudins. The claudins in the single membrane were arranged in an antiparallel double row (Fig. 1, A and B) that continued beyond the edges of the periodic box to form a continuous strand. The single membrane system was then replicated based on the proposed model (Suzuki et al., 2015) to build a system of claudin pores in two parallel POPC lipid membranes (Fig. 1 C). The continuous strand formation of pores was necessary to avoid ionic leakage and potential drops across claudin channels in the presence of an externally applied voltage gradient. The resulting model, containing three claudin pores, was then refined in a series of MD simulations until a stable conformation of the protein was reached. During the last 50 ns of the simulation, the mean root-mean-square fluctuation (RMSF) of the claudin-15 backbone was 1.95 Å, showing that stability was achieved. Our model had a mean backbone RMSD of 3.49 Å relative to the initial model of claudin pores in the membrane, indicating that the extracellular loop structure in our simulations does not destabilize the overall model. The mean RMSD of the protein backbone over 250 ns of simulation and the RMSF of the monomers over the last 50 ns of the equilibration are plotted in Fig. 4.

Figure 4.

Claudin-15 pore stability. (A) RMSD of the protein backbone with respect to the initial model of claudin pores in the membrane over the equilibration trajectory. Rigid body movement of the entire system is removed before calculating the RMSD at each frame. (B and C) RMSF of the protein residues over the last 50 ns of equilibrium trajectory for each claudin monomer. The RMSF values of six claudin monomers in each layer are shown separately in B and C.

Claudin-15 channel structure

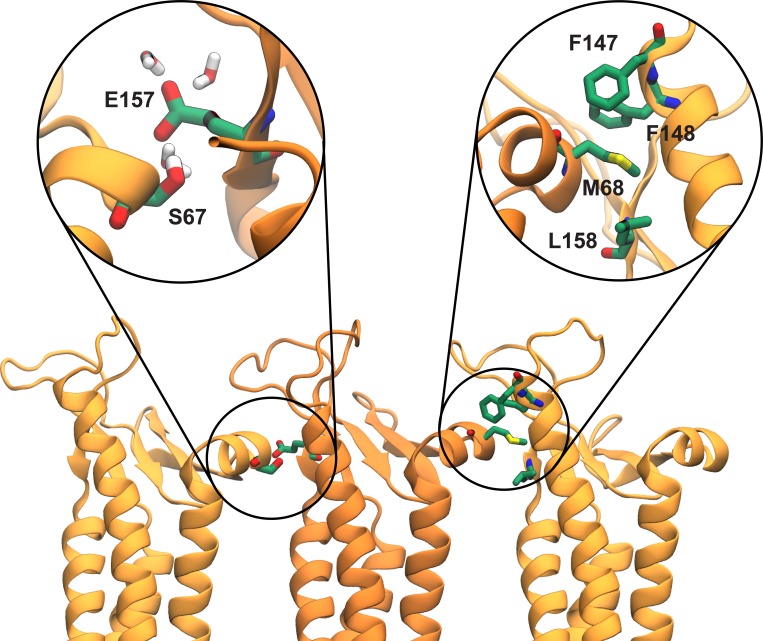
Once a stable model was generated (Fig. 1 C), we characterized the structure and stability of interactions between claudin monomers. The linear arrangement of claudin monomers, as observed in the crystal packing, remains stable throughout the simulation. Fig. 5 shows a snapshot of the interface formed between the ECH of one claudin and the conserved F-Y/F-(X)_9-10-E-L/I/M/F motif of a neighboring claudin after 135 ns of equilibration. Comparison of these residues with the crystallographic arrangement shows little deviation or disruption of the cis-interactions observed in the crystal packing, with a mean RMSD of 1.95 Å with respect to the crystal structure during the simulation. In addition, simulations show that E157, a highly conserved residue among channel- and barrier-forming claudins (Lim et al., 2008b; Piontek et al., 2008, 2017; Krause et al., 2015), forms a stable hydrogen bond with S67 of the ECH (Fig. 5).

Figure 5.

Cis-interactions between claudin monomers. Snapshot of three claudins monomers after 135 ns of equilibration in the double-bilayer system shows interactions between S67 of ECH and E157 of a neighboring claudin. E157 located at the interface of two monomers is hydrated and interacts with permeating cations. The cis-interactions observed in the crystal structure of claudin-15 (Suzuki et al., 2014) between M68 on ECH and the hydrophobic pocket of a neighboring claudin formed by F146, F147, and M158 of neighboring claudins are maintained throughout the simulation.

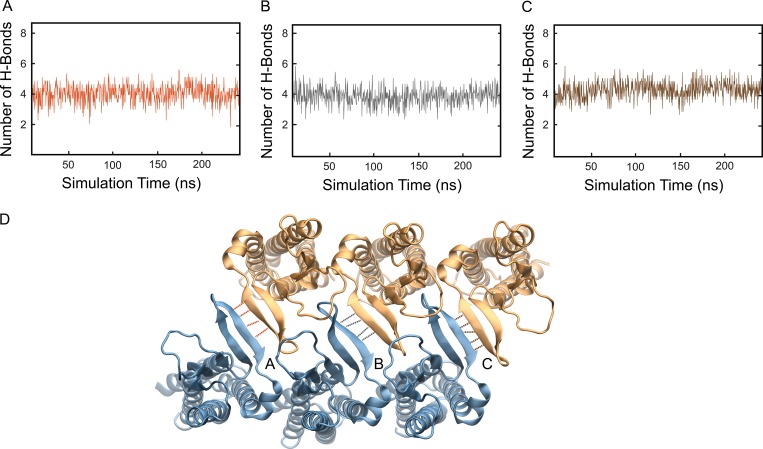
Consistent with the proposed model of Suzuki et al. (2015), simulations show that surface interactions between claudin-15 monomers in the double-row strands were maintained through hydrogen bonds between β-sheets of adjacent claudins. The number of hydrogen bonds remains stable over the course of the simulation across each interface, further supporting the stability of the double-row arrangement of claudins (Fig. 6).

Figure 6.

The double-row arrangement of claudins in the membrane remains stable through hydrogen bonds between β-sheets of adjacent claudins. (A–C) The number of hydrogen bonds between β-sheets of adjacent claudin-15 monomers in the lipid membrane remains stable over the course of the simulation. (D) Snapshot of the model showing the hydrogen bonds between β-sheets of adjacent claudin-15 monomers. Simulation unit cell contains six monomers in each membrane and three interfaces forming between claudin pairs marked with A, B, and C.

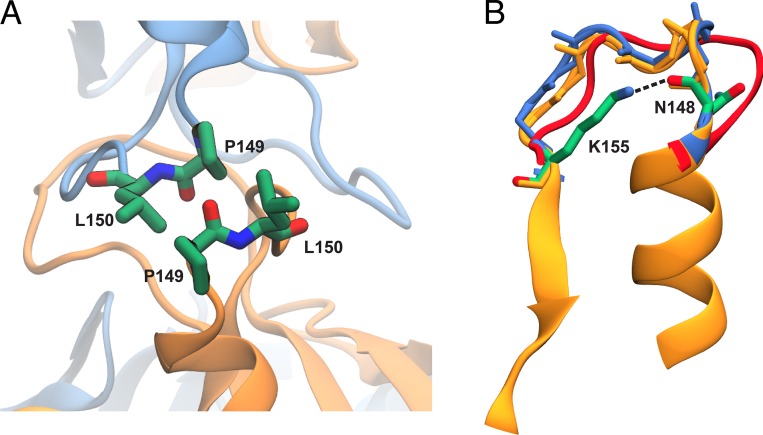
Claudin molecules possess two extracellular segments, ECS1 and ECS2, which are thought to mediate trans-interactions between claudins in two opposing membranes (Furuse et al., 1999; Lim et al., 2008a,b; Piontek et al., 2008, 2017; Piehl et al., 2010). Modeling in the presence of a second membrane allowed us to look more closely at these interactions. The second extracellular segment ECS2 containing residues 148–155 is suggested to associate with itself and participate in trans-interactions between claudins in two opposing membranes (Piontek et al., 2008, 2017; Piehl et al., 2010). This segment, which was partially omitted in the initial model of Suzuki et al., was included in the simulation and equilibrated in the presence of the second membrane. To improve sampling and avoid any clashes caused by the initial placement of the extracellular loops, we used a simulation protocol (Sandtner et al., 2011; Shen et al., 2015) in which the loops from opposing membranes were allowed to pass through each other without entanglement (see Materials and methods). Fig. 7 A shows a snapshot of two ECS2 loops after 135 ns of equilibration. Trans-interactions between claudins are partly maintained through pairwise interactions between P149 and L150 of ECS2 segments that form two complementary hydrophobic patches. The simulation shows that with little adjustment and partial tilting of TM helices, the conformation of the loops as observed in the crystal structure of claudin-15 can accommodate the trans-interactions observed here (Fig. 7 B). In addition, the salt bridge between the side chain of K155 and backbone of N148 in ECS2 is maintained throughout the simulation (∼60% of the time), conferring relative rigidity to the ECS2 loops.

Figure 7.

Trans-interactions between ECS2 loops. (A) Conformation of ECS2 loops after 135 ns of equilibration is shown for two claudin monomers. L150 and P149 of two opposing monomers interact with each other throughout the simulations. (B) Snapshots of the ECS2 before (red) and after (blue) equilibration are compared the crystal structure (orange). The initial model of Suzuki et al. (2015) did not include the ECS2 loop because of possible clashes between the two claudin rows. The conformation of ECS2 loop in red corresponds to our initial model of claudin pores, in which partial clashes or entanglement of the loops were removed through MD simulations. After removing the rigid body movement of TM3 and β5 (selection shown here), the equilibrated structure of ECS2 (blue) matches that of the crystal structure (orange), indicating that a tilting of TM helices in the claudin pore model will remove potential clashes in the initial model (Suzuki et al., 2015). The salt bridge between the side chain of K155 and backbone of N148 in ECS2 is maintained throughout the simulation (∼60% of the time), conferring relative rigidity to the ECS2 loops.

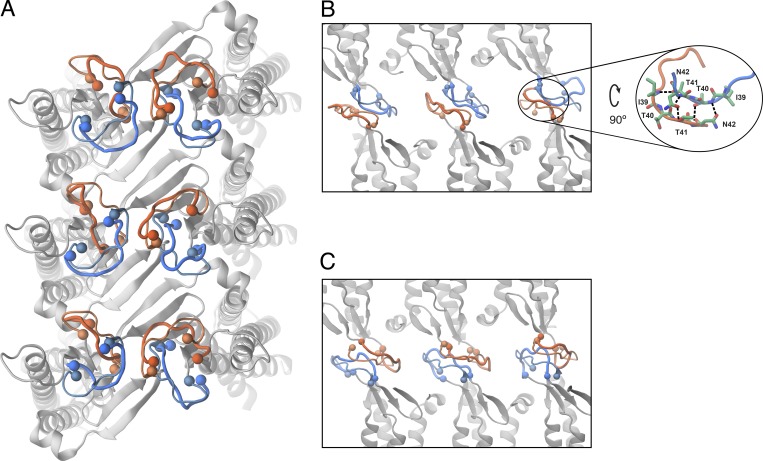
The sequence between β1 and β2 strands in ECS1 (residues 34–41) is highly variable among claudins and has been suggested to be involved in trans-interactions (Krause et al., 2008; Angelow and Yu, 2009). This variable region, which was not resolved in the crystal structure of claudin-15, was included in the atomic model of the pore and equilibrated in a manner similar to the smaller ECS2 loop. Fig. 8 shows snapshots of this loop before and after equilibration and its variation among 12 claudin monomers. Without any prior assumptions, pairwise interactions between residues 39 and 42 of two opposing loops establish strong hydrophobic interactions (Fig. 8, B and C). A snapshot of hydrogen bond networks between residues 39 and 42 of two opposing claudins is shown in Fig. 8 B.

Figure 8.

Snapshot of the ECS1 loop forming the trans-interactions between claudin rows. (A) The protein backbone of six monomers in one lipid bilayer is shown in gray. The initial and final conformations of the extracellular loop (residues 34–43) between β1 and β2 are shown with thin and thick lines, respectively. The loops are colored in the same manner as Fig. 1 for the top and bottom monomers. (B and C) Side view of the trans-interactions between the loops between two claudin rows. The inset shows hydrogen bonds between hydrophobic residues 39 and 42 of two opposing loops that seal the paracellular space to water molecules.

Thus, our simulations show that trans-interactions between extracellular segments are maintained predominantly through hydrophobic interactions. Similar interactions were also observed in a recent simulation study (Alberini et al., 2017). These interactions are crucial for sealing the paracellular space and guiding the flow of water and ions through claudin pores in a controlled fashion. As such, the hydrophobic nature of these interactions plays an important role in keeping the water away and creating a well-defined pore surface attracting the flow of water molecules and ions.

Claudin-15 forms water-filled paracellular pores

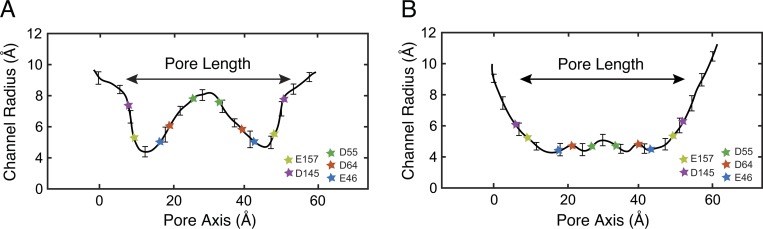
The atomic model of the pore gives us a unique opportunity to study the structural properties of the proposed model and their functional implications. The claudin-15 pore is formed by two hemichannels, each consisting of two adjacent claudin-15 monomers (one from each antiparallel row). Overall, the pore is 49 Å long, with a mean radius of 4.2 Å in the narrowest region and a mean radius of 8.1 Å in the widest region. This is best appreciated through examination of the pore’s radial profile (Fig. 9). The pore is wide enough to allow partially hydrated ions such as Na⁺ and Cl⁻ to go through while discriminating against larger ions.

Figure 9.

The claudin-15 selectivity filter is near the center of the pore, where the channel is widest. The mean pore radius (±SD) from 250-ns simulation is plotted in two different dimensions along the pore axis. (A) Radius along the x axis. (B) Radius along the z axis.

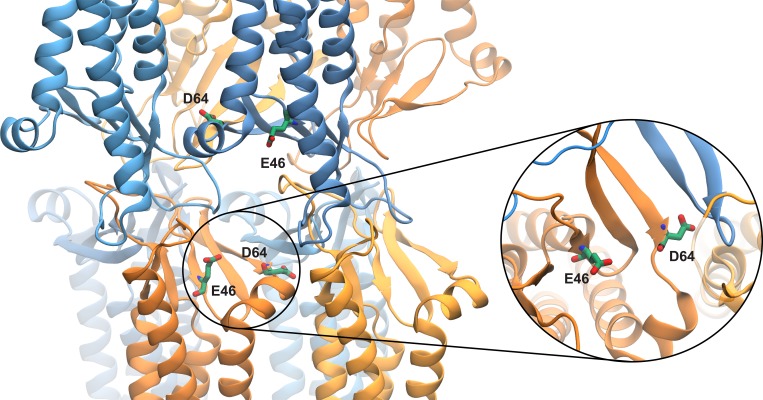
The permeation pathway is lined by β-sheets contributed by each monomer, forming a channel that is symmetric along the permeation pathway. The narrowest part of the channel is located near the entrance of the pore, with a wide cavity in the middle of the pore. Negatively charged residues, in particular D55, E46, and D64, line the permeation pathway, with D55 located in the widest region of the pore and E46 and D64 both located at the narrower region of the pore closer to the entrance. D145 and E157, two other conserved negatively charged residues (Piontek et al., 2008, 2017; Krause et al., 2015), are located near the mouth of the protein on either side. The position of these residues along the permeation pathway is shown in Fig. 9.

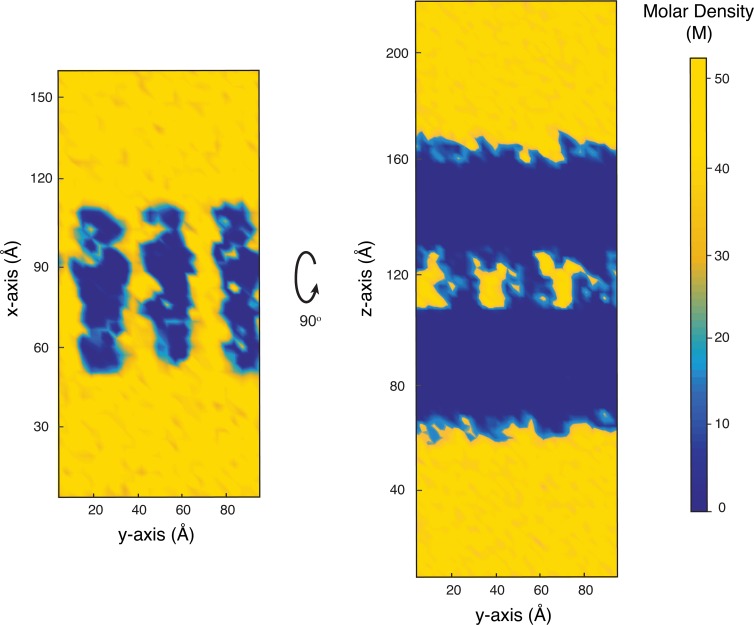
Simulations show that claudin pores occupy the paracellular space and provide well-defined pathways for ions and water molecules between the two membranes. Analysis of water density across the simulation box shows that water molecules are confined to the claudin pores with little or no access to the paracellular space within the claudin-15 strands (Fig. 10). Water molecules occupy the vestibules formed by claudin pores with a density very close to the bulk density of water. Thus, the model supports that cis- and trans-interactions between claudins provide a hydrophobic seal between monomers that is impermeable to water molecules as well as small ions within the paracellular space.

Figure 10.

Water density across paracellular space. The mean density of water molecules is calculated from the equilibration trajectories (∼250 ns) and is shown across two planes: a plane parallel to the two membranes crossing the pores in the middle (left) and a plane normal to the two membranes and crossing the pores in the middle (right). The plots show a complete seal of paracellular space to water molecules. Water molecules can only flow through the channels defined by claudin pores.

Claudin-15 charge and size selectivity

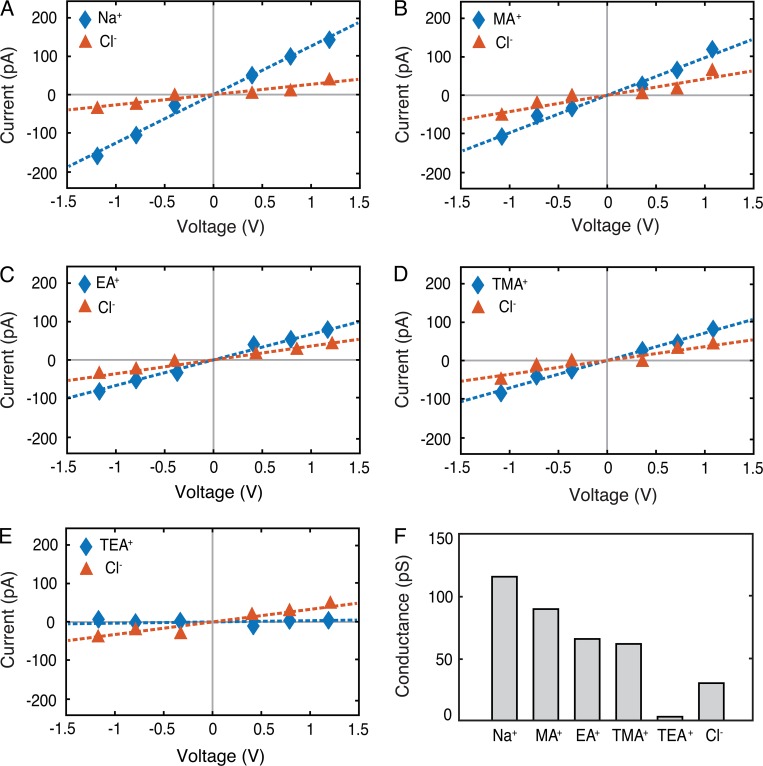
We used MD to simulate ionic currents passing through the pores in the presence of an external voltage gradient. Ionic current was calculated from the displacement current corresponding to partial charges of the ions. Because Na⁺ and Cl⁻ are the principle extracellular ions, we first measured their conductance in our model. The relationship between current and voltage was linear, consistent with a passive paracellular channel (Im and Roux, 2002; Yu et al., 2009; Jensen et al., 2010; Khalili-Araghi et al., 2013), and the slope was used to determine conductance. The channel showed a mean conductance of 150 pS, with Na⁺ conductance of 121 pS and Cl⁻ conductance of 29 pS (Fig. 11, A and F), demonstrating a relative selectivity of Na⁺/Cl⁻ of ∼4.2.

Figure 11.

MD simulations show the paracellular claudin-15 channels are cation and size selective. (A–E) I-V curves were calculated for systems containing 110 mM solutions of NaCl (A), methylammonium chloride (MACl; B), ethylammonium chloride (EACl; C), tetramethylammonium chloride (TMACl; D), and tetraethylammonium chloride (TEACl; E). Cationic and anionic currents are shown in blue and orange, respectively. (F) Conductance of the ions (Na⁺, MA⁺, TMA⁺, TEA⁺, and Cl⁻) for the WT channel. Error bars represent SEM.

Because claudin pores are known to be size selective (Anderson and Van Itallie, 2009; Yu et al., 2009; Weber et al., 2015), we simulated claudin-15 channel conductance to larger monovalent cations: methylammonium (MA⁺), ethylammonium (EA⁺), tetramethylammonium (TMA⁺), and TEA⁺ (Fig. 11, B–E). As with Na⁺ and Cl⁻, the slope of the current–voltage relationship was linear, and we used it to determine conductance. TEA⁺ conductance was significantly lower than the other cations tested. The very small currents reported here correspond to partial movement of TEA⁺ across the pore without permeation. These results show that the claudin-15 model presented here is cation and size selective. Conductance measurements for different sized cations showed a sharp cutoff between TMA⁺ (radius 3.0 Å) and TEA⁺ (radius 3.5 Å; Fig. 11 F). Cl⁻ permeability was consistent across all five of our simulations, demonstrating that our simulation durations were long enough to minimize random data variation.

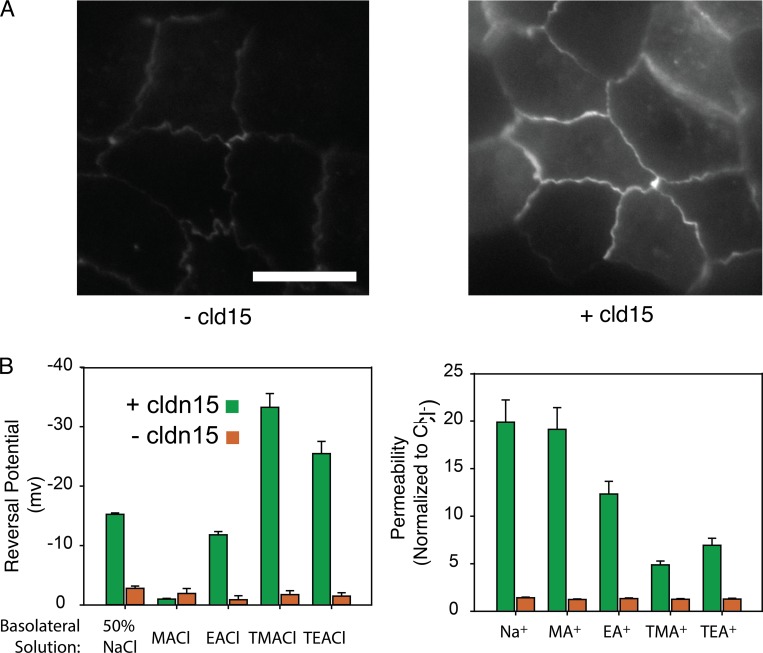
To validate our model, we compared modeling results with MDCK I monolayers expressing claudin-15. This model was chosen because parental MDCK I monolayers have very low claudin-2 and claudin-15 expression and very high transepithelial resistance (Weber et al., 2015). In this tetracycline-inducible expression system, the addition of doxycycline-induced claudin-15 expression, (Fig. 12 A) decreased TER from 1,342 ± 308 to 127 ± 25 Ωcm² and increased the relative permeability of Na⁺ to Cl⁻ (P_Na⁺/P_Cl⁻) from 1.4 ± 0.1 to 19.9 ± 2.4. It has to be noted that a ∼14-fold increase in P_Na⁺/P_Cl⁻ in vitro does not necessarily correspond to a relative permeability of ∼14 for claudin-15, but it is an indication that claudin-15 pores are highly cation selective, like in the model. To extract the relative permeability of Na⁺ to Cl⁻ for claudin-15, one has to know the absolute baseline permeabilities of Na⁺ and Cl⁻ in the parental lines and the contribution of claudin-15–independent permeabilities rather than their ratio. Thus, the magnitude of the values cannot be directly compared with the model, which lacks claudin-15–independent baseline tight-junction sodium permeability present in vitro.

Figure 12.

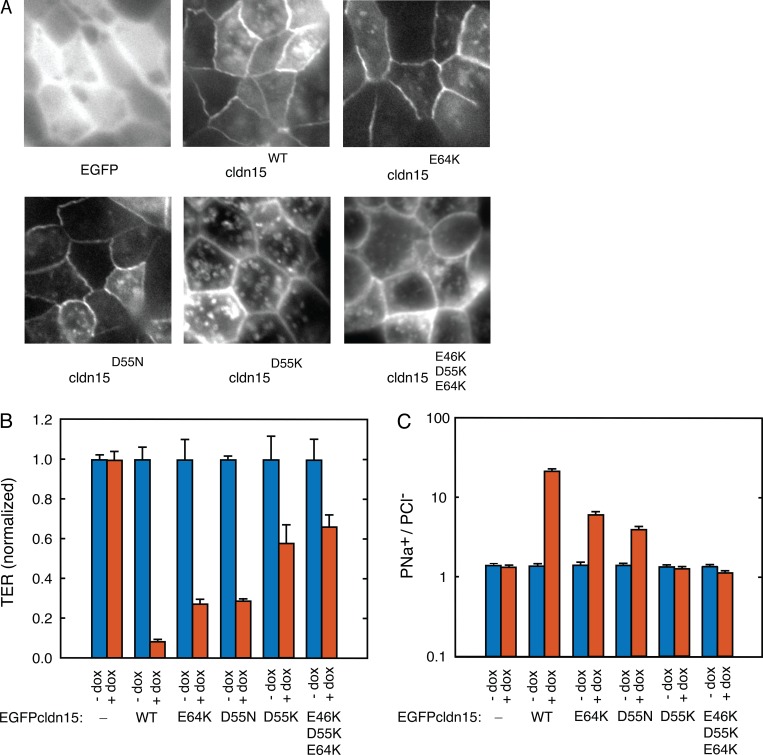
In vitro permeability measurements of WT claudin-15 demonstrate cation and size selectivity. (A) Doxycycline was used to express claudin-15 in MDCK I monolayers stably transfected with tetracycline-inducible EGFP-claudin-15 expression plasmid. Bar, 15 µm. (B) Permeability measurements demonstrate that induction of claudin-15 expression results in increased permeability to small monovalent cations. Error bars represent SEM.

To measure the in vitro size selectivity of claudin-15 pores, we measured equilibrium potentials after basolateral substitution of Na⁺ with the same monovalent cations studied in silico. We used the Goldmann–Hodgkin–Katz equation to calculate the relative permeability of these ions to Cl⁻ (Yu et al., 2009; Weber et al., 2015). The data show claudin-15 pores are cation selective and the permeability of monovalent cations decreases as their size increases, similar to the simulation results (Fig. 12 B vs. Fig. 11 F).

Molecular determinants of the selectivity filter

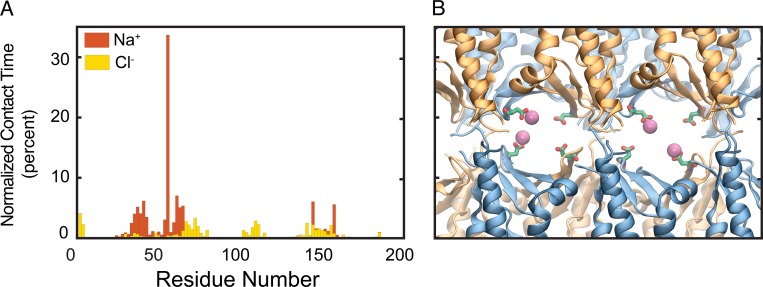
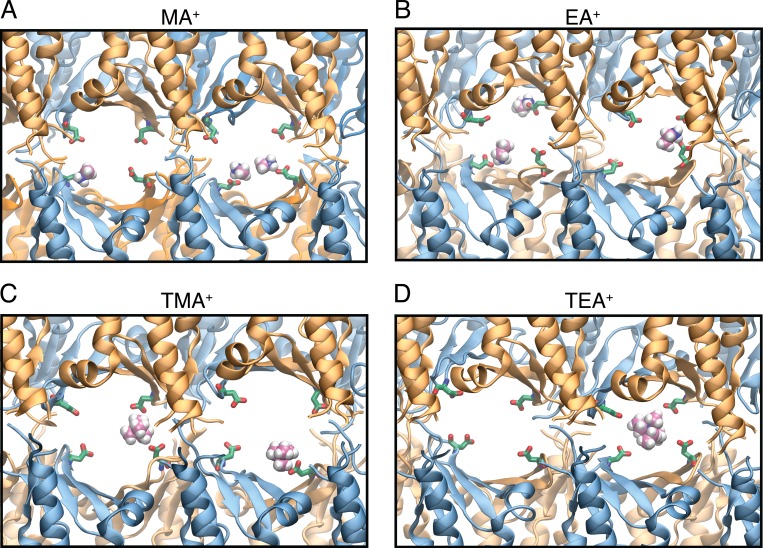
Because the simulations showed that claudin-15 pores are cation and size selective, we aimed to map the entire permeation pathway to the principal extracellular cation (Na⁺) and anion (Cl⁻). We mapped the interaction times between permeating Na⁺ and Cl⁻ and the amino acid residues lining the inner surface of the pore (Fig. 13 A). Although Na⁺ interacts with the pore-lining residues, Cl⁻ ions pass through the center of the pore with little interaction with the protein and remain hydrated throughout their passage. The peak interacting site for Na⁺ was at D55. In contrast, other negatively charged residues within the pore (E46 and D64) have much shorter interaction times with Na⁺. Although D55 is positioned in the middle of the pore, D64 and E46 are located closer to the entrance near the narrowest region of the pore (Figs. 9 and 14). D64 is located at the interface of two claudins, lines the surface of the pore, and interacts with permeating ions as they pass through. A snapshot of the pore at the level of D55 demonstrates a cage-like arrangement of these negatively charged residues pointing to the ion permeation pathway (Fig. 13 B). Simultaneous binding of more than one partially hydrated Na⁺ to these binding sites was observed at all voltages applied. Similar interactions were also observed for other permeating cations MA⁺, EA⁺, and TMA⁺ (Fig. 15). The large cation TEA⁺ interacts with all four D55 residues simultaneously (Fig. 15 D), effectively preventing its passage through the pore, explaining its very low conductance.

Figure 13.

Negatively charged residue D55 interacts strongly with Na⁺ ions. (A) Normalized contact time (percent) of the Na⁺ and Cl⁻ ions with claudin-15 amino acid residues obtained from simulation trajectories. The ions are assumed to be in contact with the protein if they are within 4 Å of the heavy atoms of the protein. The peak at D55 represents a strong binding site for Na⁺ ions inside the claudin-15 pore. (B) Representative snapshot of claudin-15 pores from permeation trajectories in which Na⁺ ions (magenta) interact with D55 residues (green and red) inside the pore.

Figure 14.

Snapshot of a claudin pore after 100 ns of equilibration showing the position of E46 and D64 near the entrance of the pore. The inset shows the top-view orientation of D64 at the interface of two claudins with its side chain parallel to the permeation pathway.

Figure 15.

Claudin-15 D55 amino acid residues interact with monovalent cations. (A–D) Representative snapshots of claudin-15 pores from permeation trajectories show interactions with MA⁺ (A), EA⁺ (B), TMA⁺ (C), and TEA⁺ (D); carbon atoms are shown in pink, nitrogen in blue, and hydrogen in white. D55 amino acid residues are shown in green and red.

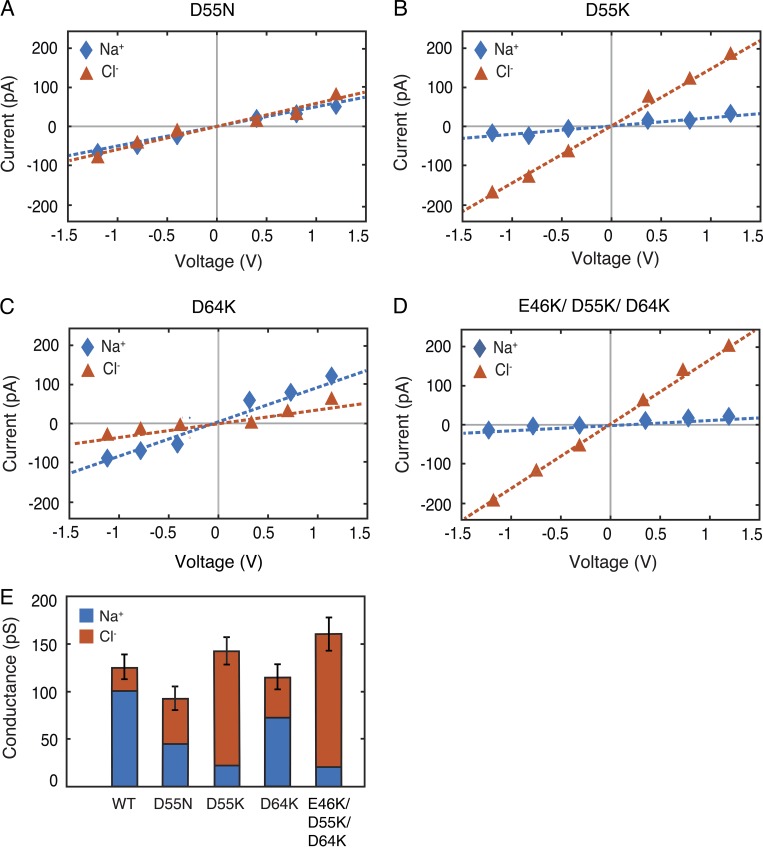
The above data support D55 as the key residue controlling the charge selectivity of claudin-15 in this model. To further define its role, we simulated conductance of several claudin-15 pore mutants. Mutation of D55 to a neutral amino acid asparagine (N) abolished claudin-15 charge selectivity and decreased total channel conductance. The permeability ratio of Na⁺ to Cl⁻ reduced from 4.2 in the WT channel to 0.95 in the D55N mutant (Fig. 16, A and E). Mutation of D55 to a positive amino acid lysine (K) reversed the charge selectivity of the channel and slightly increased the overall conductance (Fig. 16, B and E). Because D64 (E64 for humans) may impact ion permeation through the claudin-15 pores (Colegio et al., 2002; Krause et al., 2015), we mutated D64 (E64 for humans) to a positively charged K. This decreased channel cation selectivity without significantly altering overall channel conductance (Fig. 16, C and E). Finally, we simulated a triple mutation of E46K/D55K/D64K that, like D55K, reversed the charge selectivity of the pore, making the pore more conductive to Cl⁻, and resulted in increased conductance (Fig. 16, D and E). Thus, these data indicate a critical role for D55 and relatively minor roles for D64 and E46 in defining claudin-15 charge selectivity.

Figure 16.

D55 is a key amino residue that defines claudin-15 cation selectivity. (A–D) I-V curves were calculated for systems containing 110-mM NaCl solutions for D55N (A), D55K (B), D64K (C), and triple mutation of E46K/D55K/D64K (D). The cationic and anionic currents are shown in blue and red, respectively. (E) Conductance of claudin-15 pores for Na⁺ and Cl⁻ ions obtained from simulation trajectories of the mutants and WT demonstrates the importance of D55. Error bars for the total conductance represent the statistical error in estimating the total conductance from finite number of permeation events.

The simulated claudin-15 data agree with previously reported recordings of claudin-15 mutants (D55R, E64K, and E46K/D55R/E64K) in MDCK II monolayers (Colegio et al., 2002). However, MDCK II monolayers are known to express high levels of another paracellular cation channel, claudin-2. Thus, a more appropriate epithelial background on which to study the function of claudin-15 is high-resistance MDCK I monolayers, which have very low baseline paracellular cation conductance and low baseline expression of claudin-15 and claudin-2 (Günzel and Yu, 2013). We therefore studied the effect of the same mutations (E64K, D55N, D55K, and E46K/D55K/E64K) within claudin-15 expressed in MDCK I monolayers (Fig. 17 A). All mutants significantly increased TER and decreased P_Na⁺/P_Cl⁻ (Fig. 17, B and C). The most dramatic effects on pore permeability occurred with claudin-15 D55K mutant, which increased TER to 683 ± 11% of WT claudin-15–expressing monolayers and eliminated charge selectivity. Additional substitution of the other two negatively charged amino acid residues with positively charged amino acids (E46K/D55K/E64K) further induced the anion-selective shift in paracellular ion selectivity and increased channel resistance to 783 ± 71% of WT claudin-15–expressing monolayers. However, the effects of such additional mutations are relatively minor relative to changes caused by D55K alone. Thus, our in vitro recordings corroborate the importance of D55 in establishing the claudin-15 charge-selectivity filter, whereas other residues (E64 and E46) have smaller effects.

Figure 17.

D55 is a critical amino acid residue defining transepithelial resistance and ion selectivity for claudin-15 channels. (A) Doxycycline was used to express claudin-15 in MDCK I monolayers stably transfected with tetracycline-inducible EGFP-claudin-15 constructs with and without point mutations. Matched exposures are shown which reveal similar tight junction claudin-15 localization and expression. (B) TER expressed normalized to MDCK I monolayers that were not induced to express claudin-15. (C) Relative permeability of Na⁺ to Cl⁻ (P_Na⁺/P_Cl⁻) shows loss of cation selectivity with mutation of D55. Error bars represent SEM.

Claudin-15 permeability

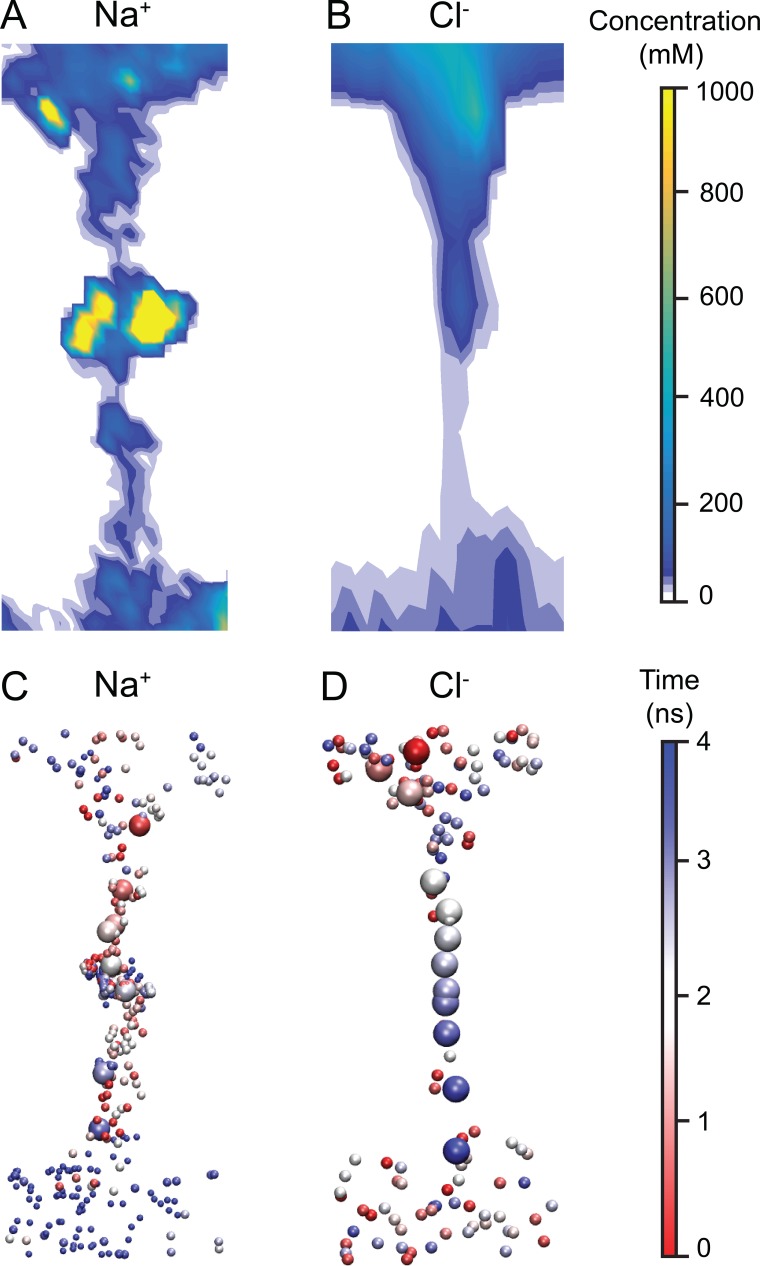
To better understand the entire claudin-15 permeation pathway, we evaluated the density profile of permeating ions inside the claudin-15 channel (Fig. 18). In the case of Na⁺, the high-density regions in the middle of the pore corresponds to the four distinct cation binding sites (Fig. 18 A). These binding sites are located in the widest region of the channel (Fig. 9) and correspond to the four D55 residues. During the simulation, binding sites were occupied 32% of the time (Fig. 13 A). The density profile of Cl⁻ ions shows negligible interaction between the permeating ions and the pore surface, resulting in a narrow ion-permeation pathway for anions localized at the center of the pore (Fig. 18, B and D). Incoming Na⁺ spends a significant amount of time at the binding sites and then diffuses through the pore quickly (Fig. 18 C). At the same time, two negatively charged residues (D145 and E157) facing the pore and located at the mouth facilitate the entrance of cations without slowing them down, as demonstrated by the sparse positioning of Na⁺ ions near the vestibule mouths. Their interaction with Na⁺ could also be seen from the contact map of the ions in Fig. 13 A. Cl⁻ ions, on the other hand, diffuse freely through the pore, with little or no interaction with the pore surface. The relatively uniform distribution of Cl⁻ ions inside the pore indicates free movement of the anions down the electrochemical gradient once they enter the channel (Fig. 18 D).

Figure 18.

The claudin-15 pore favors permeation of Na⁺, but not Cl⁻. (A and B) Density profile of Na⁺ and Cl⁻ ions along the permeation pathway of claudin-15 pore. (C and D) Permeation pathways of Na⁺ and Cl⁻ ions across the pore. The ions are shown in van der Waals representation and are colored by time step with red representing the beginning of their trajectory and blue representing the end. The trajectory of one Na⁺ and one Cl⁻ ion is highlighted (enlarged).

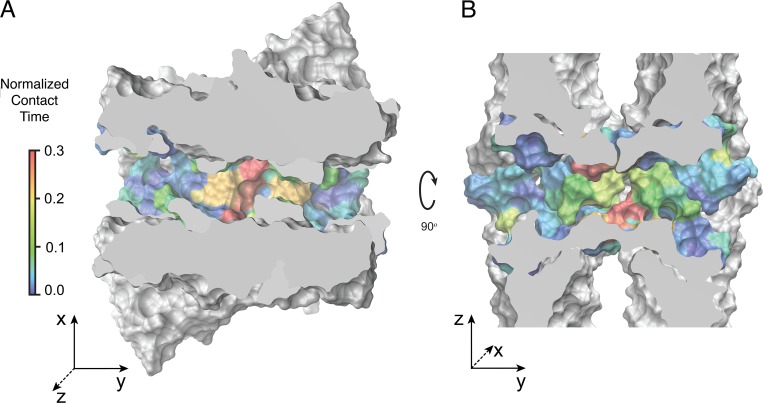
To better understand the factors defining ion conductance through the channel, we analyzed the surface of the pore and the residues lining the permeation pathway (Fig. 19). Cross sections of the pore along two orthogonal planes show an oval-shaped cavity that is wider at the center of the pore in the direction parallel to the membranes and wider near the entrance in the direction normal to the two parallel membranes. The residues interacting with permeating cations are highlighted in the figure. Two half-circles colored in red show the cation binding sites formed by D55 residues. The two half-circles, slightly displaced with respect to each other, form a negatively charged cage. Simulations show that smaller cations such as Na⁺, MA⁺, EA⁺, and TMA⁺ (Fig. 15) bind to one of the D55 side chains while passing through the pore. This results in an asymmetric path of cation permeation. In addition, simultaneous binding of more than one cation is frequently observed in the simulations. Larger cations, such as TEA⁺, interact with the binding sites differently; they enter the cage that is formed by four D55 residues and temporarily get trapped inside the pore.

Figure 19.

The selectivity filter, located near the center of the claudin-15 pore, has a high affinity for Na⁺ ions. (A and B) Cross sections of the claudin-15 pore across the planes parallel (A) or perpendicular (B) to the membrane. Protein surface is shown in van der Waals representation. The residues lining the pore are colored based on their contact time with permeating Na⁺ ions as shown in Fig. 13 A.

Discussion

Tight junctions limit paracellular flux in a size- and charge-selective manner. One of the earliest models to describe tight junction function was based on the number of tight junction strands and was modeled as simple resistors (Claude and Goodenough, 1973). Subsequent models by Claude (1978) predicted that tight-junction strands are populated by paracellular channels. In 1998, we came to know that these paracellular channels are established by claudins (Furuse et al., 1998), but until recently, there was no understanding of the molecular basis of this paracellular pathway (Furuse et al., 2001; Amasheh et al., 2002). During the past 20 yr, it has become possible to study the impact of the claudin sequence on barrier function.

In the study by Yu et al. (2009) detailing claudin-2 function, the critical amino acid residue in the claudin-2 charge-selectivity filter was identified. Mutation of one amino acid residue (i.e., D65N) exhibits threefold lower conductance and Na⁺ permeability, with no change in Cl⁻ permeability relative to WT claudin-2 (Yu et al., 2009). These data were used to establish a Brownian dynamics model of channel function (Yu et al., 2009), where the channels were modeled as simple cylindrical pores lined by fixed negatively charged spheres (attributed to D65) that defined the pore’s selectivity. The theoretical advancement of this model enabled prediction of ionic currents and water flux (Laghaei et al., 2016), but the model did not provide molecular level details of pore structure.

It was not until the determination of the crystal structure for claudin-15 that it became possible to start to understand the relationship between channel structure and function. The crystal structure defined the claudin monomers and atomic structure of critical components of the pore, but the crystal structure did not show the organization of claudin monomers into channels (Suzuki et al., 2014). However, based on the crystal structure and cysteine cross-linking experiments, Suzuki et al. (2015) suggested one potential model of claudin pores in which each pore was formed by four claudin monomers that make a β-barrel structure similar to other plasma membrane ion channels. Nevertheless, the critical extracellular loops, responsible for paracellular channel formation, were not part of this model, and it was not tested if such organization of claudin-15 could explain functional paracellular ion channels. Therefore, we turned to all-atom MD simulation.

Using MD simulations, we have developed an all-atom model of claudin-15 channels that is stable in relatively long MD simulations and represents a cation-selective ion channel. The pores are established at the interface between claudin strands, each comprised of two antiparallel rows of claudin monomers. This arrangement results in a β-barrel-like structure, as previously predicted (Suzuki et al., 2015). Cis-interactions identified in the crystal structure are preserved throughout the simulation. In addition to the hydrophobic interactions between F147, F148, and L158 of the ECS2 and M68 of ECH, the simulations show strong interactions between E157 and S67, both highly conserved residues in channel- or barrier-forming claudins (Piontek et al., 2008, 2017). In a very recent study by Alberini et al. (2017), similar interfaces between claudin monomers were identified. The proposed interfaces are consistent with multiple studies on channel- and barrier-forming claudins (Piontek et al., 2008; Angelow and Yu, 2009; Suzuki et al., 2014); however, this model of claudin-15 does not conclusively explain experimentally obtained results on all different types of claudins (Conrad et al., 2016; Milatz et al., 2017; Piontek et al., 2017). In particular, the proposed model does not predict specific interactions between TM helices, which has been suggested to play an important role in strand formation (Van Itallie et al., 2011; Rossa et al., 2014; Gong et al., 2015; Irudayanathan et al., 2016; Milatz et al., 2017). Such interactions between TM helices are also observed in coarse-grained MD simulations of claudin dimerization (Irudayanathan et al., 2016), and based on these interactions, alternative claudin pore models have been proposed (Conrad et al., 2016; Irudayanathan et al., 2017; Piontek et al., 2017). However, the stability of these models, their functional implications for ion permeation and selectivity, and whether the models can recapitulate in vitro function remains to be determined.

In our model, the pore is 49 Å long, with a mean radius of 4.2 Å in the narrowest region and 8.1 Å in the widest region. The centers of two adjacent pores are separated by ∼25 Å defining an upper limit of ∼300 pores per micron in tight-junction strands. Simulations show that claudin pores completely seal the paracellular space and limit the permeation of water and small molecules to the intermolecular space defined by the pore surface. Hydrophobic interactions between two layers of claudins (trans-interactions) limit the presence of water molecules in paracellular space and confine them to the channels formed by four claudin monomers.

Our model provides insight into a potential mechanism of claudin-15 ion selectivity. Each pore is lined by four claudin-15 monomers, and the pore’s selectivity filter is established by four critical D55 residues (one from each monomer), located ∼21 Å from the channel orifice. Our detailed analysis of the channel ionic conductance shows that small cations like Na⁺ are attracted to the pore’s negatively charged amino acid residues. The modeling predicts single channel conductance for NaCl to be ∼150 pS. Although such absolute measures of conductance are extremely sensitive to simulation force fields, it is remarkable that these values are close to what was previously predicted (Yu et al., 2009) and measured (Weber et al., 2015). The pore-lining residues provide four binding sites for small partially hydrated cations, whereas chloride is repelled. Water passes freely through the pore. Larger cations, such as TEA⁺, are attracted into the pore, but get trapped at the pore’s selectivity filter. The model also recapitulates in vitro channel function (size and charge selectivity). In addition, mutation of D55 resulted in altered channel selectivity in vitro, as predicted by the model and as previously shown in high conductance MDCK II monolayers expressing claudin-15 (Colegio et al., 2002). Notably, claudin-2 channels, which are similarly cation selective, have a critical residue at D65 rather than D55 (Yu et al., 2009; Li et al., 2014). This would suggest that the selectivity filter for claudin-2 may have different structure. Future modeling efforts to look at differences in the selectivity filters between different members of the claudin family will be needed to confirm that the present model is more broadly applicable. However, the present model is stable and largely consistent with experimentally determined claudin-15 function providing a key advancement over previous claudin modeling efforts.

Despite the strengths of our model in predicting structure–function relationships for claudin-15, elucidated above, the model presents some minor differences compared with in vitro measurements. One difference is that the model had a slightly higher size cutoff than was observed in vitro in MDCK I monolayers induced to express claudin-15. That is, we observed measureable conductance of TMA⁺ in silico but very low TMA⁺ permeability in vitro (Fig. 11, D and F, vs. Fig. 12 B). Although our model predicts that the magnitude of cationic permeability changes in all mutants studied, another difference is that the D55K mutant and the triple mutant both exhibited an increase in Cl⁻ permeability in the model, making the pore very anion selective. Our in vitro data also show a significant decrease in the relative permeability of cations to anions with this mutation. However, the effect is not as great as predicted by the simulation. This may be caused by the presence of other cation selective claudins that dominate in the setting of a defective claudin-15 sodium pore, but it may also relate to errors within the modeling (described below).

There are several possible sources of error to account for the discrepancies between in vitro and in silico data. First, there is inherent statistical error in calculating the frequency of rare stochastic events. The statistical error of the calculated conductance increases as $\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{n}$}\right.$, where n is the number of permeation events observed during the course of the simulation. This error results in a high uncertainty in the conductance of the low-permeating ions near the size cutoff and significantly affects the permeability ratios (P_cation/P_anion) reported here (with much larger errors in the denominator).

It is also possible that there are small inaccuracies in the atomic force fields in the model or undefined allosteric interactions with other tight-junction proteins that are missing from our model. Importantly, these sources of error may affect the calculated permeability of cations to anions and the exact size cutoff for permeation. However, these sources of error do not affect the overall conclusions regarding the effect of specific mutations on channel selectivity and the pore-lining residues identified here. Another source of error in determination of the exact size cutoff of the channel in the simulation (a difference of ∼0.5 Å with experiments) is the fact that the putative distance between the two membranes in this initial model (derived from Suzuki et al., 2015) is somewhat arbitrary. The model was created to be consistent with the structural features of claudin monomers observed in the crystal structure (Suzuki et al., 2014). By omitting the disordered extracellular loops, Suzuki et al. have achieved the closest distance possible between the two membranes while avoiding any clashes between β-sheets (and more rigid structural elements) of opposing claudins. During the simulations, an overall tilting of claudin monomers and small adjustments in the extracellular loops resulted in a stable pore model that correctly predicted the ion permeation surface. Comparison of the simulation results with experiments show that while the current structure is highly stable in relatively long MD simulations, small adjustments to make the pore smaller might improve certain features of the model (e.g., the relative displacement of claudins in the two membranes). Future in vitro experiments will be required to better define this distance and its implication on simulated pore size cutoffs and channel conductance. Despite these quantitative differences, our model builds on previous claudin modeling studies (Suzuki et al., 2015; Alberini et al., 2017) and is the first functional all-atom claudin model.

With this information in hand, we can now begin to understand how ions and molecules enter, interact, and traverse the pore under physiological conditions, and we may begin to consider approaches to develop selective pore-blocking agents. In addition, there are many questions that remain unanswered about claudin function that we can now start to address. For example, we do not understand the structure–function relationship of other members of the claudin family, nor do we understand how different claudin family members can interact with one another at the tight junction to define barrier function. Also, it remains unclear how claudins exhibit gated channel openings and closings (Weber et al., 2015). It will also be important to define the molecular interactions of claudins with other tight junction proteins such as ZO-1. The modeling efforts will help us to start answering many of these questions as computing power improves and we attain more in vitro data.