Deep imaging in highly scattering media by combining reflection matrix measurement with Bessel-like beam based optical coherence tomography

Abstract

Multiple scattering in biomedical tissue limits the imaging depth within a range of 1–2 mm for conventional optical imaging techniques. To extend the imaging depth into the scattering medium, a computational method based on the reflection matrix measurement has been developed to retrieve the singly back-scattered signal light from the dominant detrimental multiple-scattered background. After applying singular value decomposition on the measured matrix in the post-process, the target image underneath the turbid media is clearly recovered. To increase the depth of focus of the incident light by elongating the focal spot along the optical axis, a digital grating pattern is specially designed and displayed on a phase-only spatial light modulator to generate the Bessel-like beam for lateral point scanning. According to the results, the depth of focus is increased up to 2.4 mm which is much longer than the value of ∼50 μm obtained by using the conventional focused Gaussian beam, leading to a deeper penetration depth due to the self-healing feature of the Bessel-like beam. In addition, generation of the Bessel-like beam simplifies the axial scanning process by getting rid of the need to mechanically translate the focal zone along the optical axis of an objective with a high numerical aperture. By combining this method with an optical coherence tomography system with a low coherence light source, a depth-resolved optical image is obtained underneath a highly turbid medium.

Optical imaging in deep tissue without ionizing radiation has undergone rapid development over the past years. Among all the imaging modalities, the systems with a scanned focused beam (generally characterized by point-by-point or line-by-line scanning) chiefly collect the singly back-scattered ballistic light instead of multi-scattered diffuse light to form images with a relatively high spatial resolution.¹ When the focused light is back-scattered by the targets toward the detector, the significant multiple scattered light bounced from different layers makes it difficult to form sharp images in deep tissue. To retrieve depth-resolved images from the multi-scattering dominated background in the backward process, different techniques have been developed to minimize the detrimental effects of multiple scattering. These techniques include placing a pinhole spatial filter as in confocal microscopy, using a nonlinear excitation and longer wavelength detection as in two-photon microscopy, or adopting coherence gating as in optical coherence tomography (OCT).² Among these techniques, OCT can work in depths where multiple scattering events occur since it primarily detects the singly back-scattered light from the target layer^3–6 while most of the multi-scattered light is temporally rejected by the coherence gating and spatially removed by the confocal pinhole aperture of the fiber-tip. Although OCT has found widespread applications,^7–9 the penetration depth of conventional OCT is limited to a range of ∼1–2 mm inside human tissue due to the increased multiple scattering of photons when probed deeper.

An en-face (transversely scanning) time domain OCT system was proposed to investigate the reflection matrix in the focal plane on a point-to-point basis.¹⁰ Compared with conventional OCT systems (specifically, the fiber-coupled cross sectional OCT systems) in which the photons back-scattered from the peripheral outside area of each focal spot (in the lateral focal plane) are mostly rejected by the fiber-tip pinhole, these photons were selectively recorded on a two-dimensional (2D) camera detector in the en-face OCT system by using a digital pinhole filter with a relatively enlarged aperture. Hundreds of frames of pinhole filtered back-scattered 2D complex amplitudes, each of which corresponding to one focal spot, were then combined altogether to form the reflection matrix. This matrix, having complex amplitude components,^11,12 contains abundant information including the position and reflectivity of the targets located in the focal plane. The singly back-scattered components, the main carrier of the target information, were then separated (retrieved) during the post-process of the matrix analysis. Although this measuring and analyzing process of reflection matrix enhances the utilization efficiency of singly back-scattered light (due to the wide field detection and the noise removal ability in the post-process of matrix analysis) and thus leads to an increased imaging penetration depth, it relies on forming a focal spot at each scanning position on the target layer. Thus, the reported system using Gaussian beam illumination can only obtain one en-face image at the focal plane of the objective (considering a high NA objective is usually used in the en-face time domain OCT system),¹⁰ unless the sample stage is mechanically translated stepwise along the optical axis. In addition, the focusing of the Gaussian beam will gradually decay and finally lose focus when probing deeper inside tissue due to scattering,¹⁰ limiting the penetration depth of the focused beam. Recently, Bessel beam illumination experienced a growing interest as it offers an elongated illumination in the axial direction while maintaining a good lateral resolution.¹³ Here, a Bessel-like beam illumination is generated in our system through a designed phase grating pattern displayed on the spatial light modulator (SLM), to increase the depth of focus (DOF) of the sample beam by elongating the focal spot along the optical axis. The designed pattern consists of a digital annular aperture formed by two phase gratings with different spatial frequencies, resulting in an output diffracted field after the SLM. After the diffracted light is transmitted through the objective, a Bessel-like beam with an increased DOF up to 2.4 mm (compared with the original value of ∼50 μm using the same objective) is formed near the focal plane of the objective lens, leading to deeper penetration depth up to 3.28 times the reduced scattering mean free path, as well as reduced system complexity of depth scanning if 3D volumetric scanning is needed.

The Bessel beam can be generated by a physical annular aperture placed in the back focal plane of a lens. In our scheme, the actual physical annular aperture is replaced by the digital phase-only grating pattern displayed on the SLM, as shown in Fig. 1.¹⁰ This designed phase-only grating pattern with two different spatial frequencies is similar to the function of binary amplitude mask. Specifically, the series of gratings displayed inside the annular aperture function as a Galvo mirror to scan the incident beam at different lateral positions.

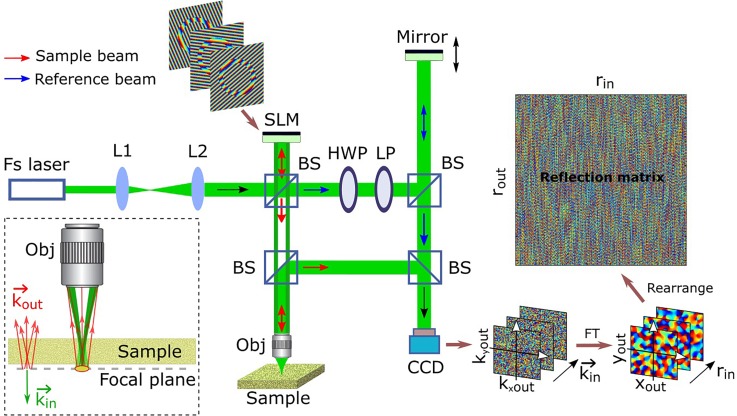
FIG. 1.

Schematic of the experimental setup. The target particle is placed in the focal plane of the incident beam underneath a scattering sample layer. Fs laser, femtosecond pulse laser; L, lens; BS, beam splitter; HWP, half-wave plate; LP, linear polarizer; Obj, objective; SLM, phase-only spatial light modulator (reflection type); CCD, charge-coupled device; FT, Fourier transform; $k_{\mathit{\text{xout}}}$ and $k_{\mathit{\text{yout}}}$ represent the coordinate values of Fourier spatial frequency of the target area in the focal plane; ${\overrightarrow{k}}_{in}$ is the wave vector related to the incident angle of the collimated beam; $x_{out}$ and $y_{out}$ are the coordinate integer numbers indicating different lateral positions (scanning points) in the focal plane; and $r_{in}$ and $r_{out}$ represent the coordinates in the reflection matrix. Only the phase components are displayed in the measured images and the matrix on the right side.

A femtosecond laser output a collimated beam at a center wavelength of λ = 793 nm with a bandwidth of ∼100 nm. This beam was expanded and collimated by two lens, L1 and L2, and split into a sample beam (red color) and a reference beam (blue color) by a beam splitter. The sample beam was modulated by a phase-only SLM which displayed a designed grating pattern with a wrapped phase ramp to deflect (or tilt) the incident beam to different angles determined by the slope and orientation of the phase ramp. The deflected sample beam retained its collimated feature while transmitting through a beam splitter and focused by an objective lens (10× Olympus Plan Achromat Objective, 0.25 NA, 10.6 mm WD) onto different scanning positions in the sample. The back-scattered light transmitted through the same objective and was received by the CCD after being reflected by two beam splitters. Specifically, the light singly back-scattered by the targets was drawn in the inset with red color. The reference beam's optical path was modulated by a mirror attached to a piezo-electric transducer which stepwise translated its position along the direction of incident light with a high displacement resolution at the nanoscale. The four-step phase-shifting method was then adopted¹⁴ to calculate the phase and the amplitude of the sample beam by stepwise shifting the axial position of PZT. The half-wave plate and linear polarizer were combined together to continuously adjust the incident power of the reference beam. Since each wave vector ${\overrightarrow{k}}_{in}$ is solely related to a focused beam passing through the objective lens, the vector ${\overrightarrow{k}}_{in}$ was replaced by its corresponding focal position $r_{in}$ after carrying out FT. The digital SLM was used to deflect the incident beam to simplify the system's scanning setting (by replacing the conventional Galvo mirror). A digital size-enlarged pinhole was adopted in the post-process of matrix filtering to obtain the wide-field images which were then combined all together and assembled to form the reflection matrix. More details can be found in the supplementary material.

By using the designed grating pattern with two spatial frequencies to replace the previously used normal uniform grating pattern,¹⁰ the incident light was divided into two individual parts (with different diffraction angles) which were then both focused in the focal plane by the objective lens. The beam diffracted by the inner and outside grating patterns (with a high spatial frequency) had a relatively large diffraction angle, making its focal spot area (not drawn in Fig. 1 for simplicity) far away from the center of the scanning area. In the ideal case, this part of unwanted beam would be totally driven outside of the objective entrance pupil and not illuminate the sample. The other beam which was diffracted by the annular ring grating had a smaller diffraction angle for lateral scanning, similar to putting an annular apodized aperture in the path of the incident scanning sample beam. After passing through the objective, a Bessel-like beam was generated with increased DOF along the optical axis near the focal plane.

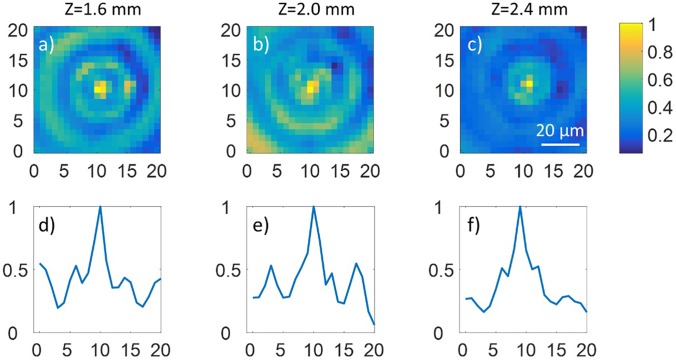
The DOF of a focused beam can be defined as the confocal parameter and expressed as $4\lambda /(\pi N{A}^2)$, where $\lambda$ represents the center wavelength of light and $NA$ represents the numerical aperture of the objective.¹⁷ According to this definition, the DOF for a normal Gaussian beam is calculated as ∼50 μm for NA = 0.14 (considering the incident beam has a diameter of ∼5 mm and the effective focal length of the objective is 18 mm). In contrast, the experimental DOF of the Bessel beam is found to increase up to ∼2.4 mm. The lateral spot size remains almost constant along the optical axis (z axis) within a range of long distance as shown in Fig. 2.

FIG. 2.

Experiment demonstration of the increased depth of focus by using the designed grating pattern consisting of two different spatial frequencies compared with the result by using the normal grating pattern. (a)–(c) The measured 2D intensity profile (perpendicular to the optical axis) of the focused beam showing that the Bessel-like beam with increased DOF is generated near the focal plane of the objective along the beam path (Z axis). Z = 0 represents the focal plane. (d)–(f) The normalized intensity curves corresponding to the center lines of (a)–(c), respectively. The coordinate values correspond to the pixel numbers of the CCD camera with the pixel size of 3.6 μm.

The Bessel-like beam illumination was adopted in the following imaging experiments. A white paper sheet cropped from standard A4 printing paper (Amazon Basics 92 Bright Multipurpose Copy Paper) was used in our experiment as the scattering tissue. The white paper is a strong scattering sample with relatively low absorption, and the scattering mean free path $l_s$ is measured as 5.92 μm for our paper tissue sample by measuring the ratio of power between the output ballistic light and the input laser beam according to Beer's law.¹⁰ That is to say, for every transport distance of 5.92 μm, the transmitted photons will on an average undergo one scattering event. For paper sample with a measured thickness $L$ of 97 μm, the total scattering events the photons will experience would be $L/l_s\approx$ 16.39. This value indicates that the targets put underneath the paper are at a depth where multiple scattering photons dominate, ∼2 times of the penetration depth at which conventional OCT can probe.^10,15,16 If considering the paper's scattering anisotropy g = 0.8 as reported in the literature,¹⁸ the number of the reduced scattering mean free path is calculated as ∼3.28, higher than the previously reported number of 2.45 which used a conventional focused Gaussian beam for illumination.¹⁰ The original image and the reconstructed images after carrying out the matrix analysis are displayed in Fig. 3.

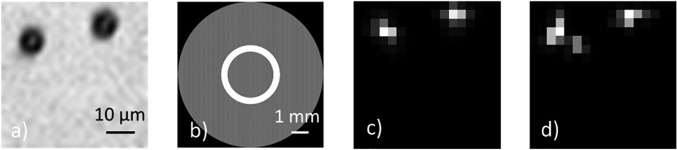
FIG. 3.

The original image and reconstructed image according to the calculated singular vectors of the reflection matrix. (a) The original microscopic image of two microspheres (with 8 μm diameter) put on the cover glass. (b) The pattern displayed on the SLM while scanning at the central point of the image field, functioning as the annular apodized aperture to generate the Bessel-like beam. The high spatial frequency (31 lines/mm) of the outside and inside gratings makes the outside ring difficult to observe by the human eye. (c) and (d) The recovered image of the microsphere targets under the Bessel-like beam illumination without (c) and with (d) the scattering layer placed ∼1 mm above, respectively.

Figure 3(a) is obtained by putting a LED white light source between the top left beam splitter and the half-wave plate in the reference arm while an imaging lens is temporarily embedded right before the CCD. After that, the LED light and the imaging lens are removed, and the home-developed application program is run to automatically scan the sample to obtain the reflection matrix (which is then filtered by the digital pinhole). By carrying out singular value decomposition (SVD) to the matrix, the singular vectors are retrieved while the corresponding singular values are obtained in an order arranged from large to small real positive numbers. The two pairs of singular vectors ($U_1$, $V_1$) and ($U_2$, $V_2$) which correspond to the two biggest singular values (${\sigma }_1$ and ${\sigma }_2$) are picked out, and the images of two microspheres are reconstructed by $|{\overline{U}}_1+{\overline{V}}_1|\cdot {\sigma }_1+|{\overline{U}}_2+{\overline{V}}_2|\cdot {\sigma }_2$ as displayed in Figs. 3(c) and 3(d). Here, $| |$ denotes the normalized complex modulus of the Hadamard product between the two reshaped matrixes ${\overline{U}}_i$ and ${\overline{V}}_i$. According to the results shown in Fig. 3, the SVD process applied on the measured reflection matrix can retrieve the primary components which are helpful to reconstruct the target image hidden underneath a strong scattering tissue by Bessel-like beam illumination.

The matrix method used in the article is based on the pulse-echo scheme adopted first in ultrasound imaging,¹⁹ in which each element of the ultrasonic array is the pulse emitter and the whole array receives the wide-field back-scattered echo. When transplanting this method to the OCT system with a low coherence light source, there are two basic requirements. First, a tight focal spot (functioning as the optical pulse at the target layer) is always needed in the lateral direction for the lateral scanning purpose. For the Gaussian beam illumination with a limited depth of focus, however, the beam diameter will be notably increased and gradually lose the tight focus when moving away from the focal plane. In this case, to acquire an en-face image in other layers, the holder of the sample has to be moved mechanically along the beam path so that the tight focal spot of the incident Gaussian beam is always located in the target layer to be imaged. Second, the mirror (mounted on a PZT) in the reference arm needs to be translated along the axial direction to ensure the position of the coherence gate to be right at the new target layer by compensating the change of the optical path length in the sample arm (when the focal spot is at different layers inside the sample). The mechanical movement in both the sample arm (sample holder) and the reference arm (mirror) as described above would lower the acquisition speed of volumetric imaging and increase the system complexity. In contrast, if using the Bessel-like beam for illumination, only the mirror (mounted on a PZT) in the reference arm needs to be moved for axial scanning while getting rid of the need to translate the sample holder in the sample arm, since the extended focusing range is provided by the Bessel-like beam within the sample. This would speed up the volume scanning process.

Compared with conventional time-domain full-field OCT in which the en-face image is obtained by wide-field temporal coherence gating,²⁰ this method based on matrix measurement is able to retrieve the singly back-scattered signal light from a background of residual multiple scattering components which still exist even after temporal coherence gating. Compared with spatial and frequency compounding methods,²¹ which utilize multiple uncorrelated OCT measurements to suppress the background speckle noise but do not significantly increase the depth of penetration, our method not only notably increases the penetration depth of OCT but can also locate the targets in a descending order which is consistent with their different scattering/reflection ratios.

In this article, a flying-spot (point scanning) en-face OCT system with an elongated Bessel-like beam was developed for deep tissue imaging. The imaging system based on matrix measurement captures a wide-field image at each focal spot and then reassembles all the images into one matrix. By applying SVD on the matrix, the singly back-scattered signal light related to the targets is retrieved as the principal components while the unwanted noise components (introduced by the size-enlarged digital pinhole) corresponding to the unfiltered residual multiple scattered light are effectively removed, resulting in a penetration depth enhancement of ∼2 times compared to conventional OCT. To increase the DOF of the incident sample beam, a phase pattern including two different spatial frequencies was designed to generate the Bessel-like beam. We demonstrate that the Bessel-like beam illumination can significantly increase the penetration depth of the focused beam so that the image depth of the system is increased due to the self-healing property of the Bessel-like beam.^23,24 The measured number of the reduced scattering mean free path of our tissue sample is 3.28, higher than the previously reported number of 2.45.¹⁰ In addition, the system complexity is simplified by getting rid of the need for translating the sample for axial scanning. The time-consuming process of the current system sets a limitation for imaging living tissue such as the human eye if considering the motion sensitivity of the interference detection.²² To address this issue, a high-speed camera combined with a fast wavefront measurement is being developed for extending this method to future applications of in vivo biomedical imaging. This matrix-based imaging approach with Bessel-like beam illumination could be well suited for tracking functional micro-particles at deep penetration depths in complex scattering samples, such as biomedical tissues, membranes, and live embryos. Specifically, it is also useful to locate the position of microbeads having a refractive index different from the background base placed underneath a scattering layer, since both amplitude and phase profile are measured in the wide field detection scheme.

See supplementary material for more technical details and discussions, including the scanning and recording settings of the imaging system, the simulated Bessel-like beam profile, the method of dispersion compensation and position control, and the effect of angular dispersion on the SLM.