Abstract
We report the first detailed characterization of the sheet third-harmonic optical susceptibility, χ(3)s, of tungsten diselenide (WSe2). With a home-built multiphoton microscope setup developed to study harmonics generation, we map the second and third-harmonic intensities as a function of position in the sample, pump power and polarization angle, for single- and few-layers flakes of WSe2. We register a value of |χ(3)s| ≈ 0.9 × 10−28 m3 V−2 at a fundamental excitation frequency of ℏω = 0.8 eV, which is comparable in magnitude to the third-harmonic susceptibility of other group-VI transition metal dichalcogenides. The simultaneously recorded sheet second-harmonic susceptibility is found to be |χ(2)s| ≈ 0.7 × 10−19 m2 V−1 in very good agreement on the order of magnitude with recent reports for WSe2, which asserts the robustness of our values for |χ(3)s|.
Introduction
Atomically thin two-dimensional crystals of semiconducting transition-metal dichalcogenides (TMD) are currently a subject of intense research. The most prominent members of this family have been molybdenum disulfide (MoS2) and diselenide (MoSe2), as well as tungsten disulfide (WS2) and diselenide (WSe2). Their unique electronic, optical and structural characteristics are under active scrutiny for applications in photonics, optoelectronics and electronic devices. In addition to the ability of tuning their carrier densities on demand by field-effect, such properties include high charge-carrier mobility1,2, a direct band gap in monolayer crystals that evolves to indirect with additional layers3, photoluminescent emission in the visible-NIR spectral range4–6, high nonlinear optical susceptibilities7,8, strong spin-orbit coupling9,10 and spin-valley locking and novel valleytronics phenomena11.
Owing to their semiconducting character and favorable band gaps for conventional optoelectronics12, the pressing need for detailed characterization of their intrinsic optical response has stimulated a steady and broad array of experimental results12,13. In particular, nonlinear optical applications hinge upon the nature of the second and third-order optical susceptibilities (χ(2) and χ(3), respectively), which are conventionally obtained from harmonic generation experiments. Whereas second-harmonic generation (SHG) in the most prominent TMD had been studied in a number of recent experiments7,8,14–16, reports on third-harmonic generation (THG) among this family have been scarce17,18. Remarkably, THG in either single or few-layer selenide-TMD remains unexplored. These results on harmonic generation in TMD and in other 2D layered materials have been summarized in a recent review by Autere et al.19,20.
In this context, we have used multiphoton spectroscopy to simultaneously measure SHG and THG intensities of exfoliated single- and few-layers WSe2. By studying the harmonics generation as a function of pump power, layer-dependence and spatial position, and correlating the data with atomic force microscopy, we are able to report a robust characterization of third-harmonic χ(3). We demonstrate that THG is independent on the polarization angle and is proportional to the square of the number of layers. We further show that the magnitude of WSe2 χ(3) is comparable to that of sulfides of the same TMD family. Even though this type of experiment has been broadly applied to determine χ(2) and χ(3) in several two-dimensional materials14,18,21, the characterization of THG and a quantitative measurement of χ(3) in WSe2 had remained unknown.
Results and Discussion
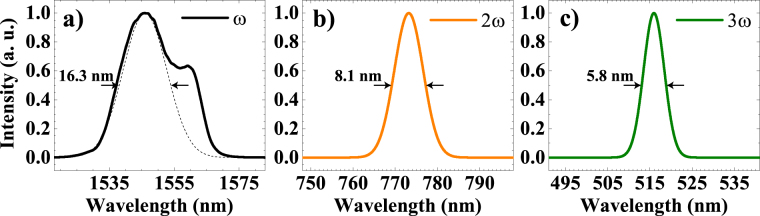
We investigated the nonlinear optical properties of mechanically exfoliated atomically thin 2H-WSe2 (2H polytype) with a home-built multiphoton microscope specifically designed for harmonics generation. Before nonlinear optical experiments, the sample was extensively characterized by photoluminescence and Raman spectroscopy, as well as by atomic force microscopy (for details on the sample preparation, characterization and experimental setup, see materials and methods section and supporting information). The pump wavelength for the harmonic experiments is 1546 nm, therefore SHG emission is centered at 773 nm and THG emission at 516 nm, as shown in Fig. 1.
Figure 1.
Spectra for (a) 1550 nm pump, (b) SHG at λcentral = 773 nm and (c) THG at λcentral = 516 nm. The pump beam full-width at half-maximum (FWHM) bandwidth is 25.1 nm, but only the peak centered at 1546 nm contributes for the harmonic generation (dotted line, FWHM bandwidth ~ 16.3 nm). The FWHM bandwidth and central wavelength for SHG are 8.1 nm and 773 nm, and for THG are 5.8 nm and 516 nm, respectively.
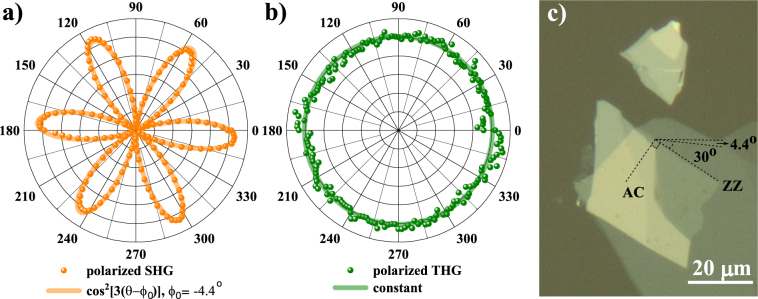
The absolute orientation of the WSe2 crystal, relatively to the laboratory frame, was determined by polarized second-harmonic generation (pSHG), where the incident pump linear polarization and a parallel polarizer were rotated simultaneously by the same angle θ while recording the spectrum. Since 2H-WSe2 belongs to the D3h point group22, as expected from the threefold rotational symmetry along the c crystallographic axis and demonstrated for a number of odd-layered TMD of this family, the pSHG intensity is proportional to cos2[3(θ-ϕ0)], where ϕ0 is the angle of the armchair direction of the flake in the laboratory frame. The result of our pSHG is shown in Fig. 2a. This strong polarization dependence makes pSHG a preferred tool for fast crystallographic alignment of these materials7,8,14,23. In contrast, the THG is polarization independent, as can be seen from Fig. 2b, as expected for all other crystals belonging to the D3h group18. Figure 2c shows an optical image of the sample with the identification of armchair (AC) and zig-zag (ZZ) directions of the flakes8.
Figure 2.
Polarized harmonic generation in WSe2: (a) SHG, ϕ0 = −4.4° and (b) THG, constant intensity with θ; (c) optical image of the sample with armchair (AC) and zig-zag (ZZ) directions.
We hence determined the AC direction to lie at ϕ0 = − 4.4° + m × 60°, m∈Z, and set the pump polarization parallel to this direction of maximum response for our subsequent SHG and THG experiments.
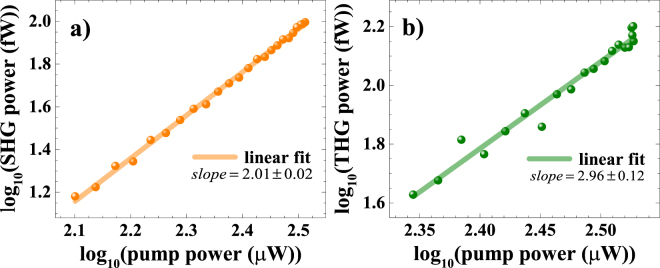
To assert the second and third-harmonic nature of the signals discussed so far, we measured their dependence on the pump power via Malus’ law experiment, by inserting a fixed polarizer before the sample in the experimental setup used for pSHG measurements (for more details on the experimental setup, see supporting information). Additionally, we carried out a calibration leading to actual average power readings from spectrometer counts in order to extract the magnitude of the susceptibilities (for more details on calibration factors, see supporting information). Figure 3 shows power-dependent double logarithmic plots of SHG and THG actual average power. The power scaling of the SHG and THG intensities is shown to follow very well the respectively expected quadratic and cubic dependences.
Figure 3.
Double logarithmic plots of the power-dependent nonlinear signals for (a) the SHG of single-layer and (b) the THG of 9-layers WSe2.
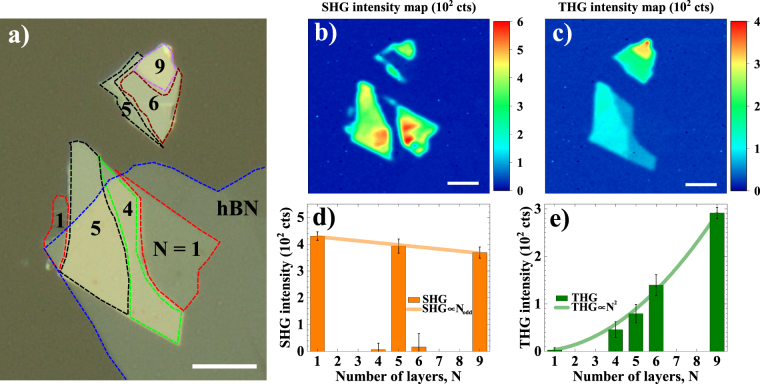
To acquire spatial maps, the sample was raster scanned across the pump beam in 0.5 µm steps, while SHG and THG intensities were recorded simultaneously. The results are shown in Fig. 4. An image of the sample with the number of layers (N) labeled in each region, is shown in Fig. 4a. The thickness assignment was performed by correlating atomic force microscopy data with the SHG contrast. The image also shows the presence of a thin film of hexagonal boron nitride (hBN) partially covering the WSe2 multilayer, which was used to prevent environmental degradation (for more details on sample fabrication, see supporting information).
Figure 4.
(a) Optical image of the sample with labeled number of layers (N); (b) Spatial SHG and (c) THG intensity mappings across the WSe2 sample; (d) Spatial average SHG and (e) THG intensities as a function of N. The values and error bars indicated for the SHG and THG correspond to the mean ± 3 × (standard deviation). Scale bars = 10 µm.
Figure 4b shows the sharp SHG contrast between regions of odd- and even-N, as SHG in these TMD is expected for odd-N flakes24,25, with a decreasing intensity for increasing number of layers10,26. Yet, even though SHG is expected to be strictly zero for even-N, a residual non-zero intensity is recorded for 4- and 6-layers regions, as shown in Fig. 4d. This effect might be attributed to incomplete destructive interference between SHG from adjacent layers, as discussed previously by Li et al.25, although its fundamental cause remains unexplored. Moreover, this effect might be responsible for a small negative slope for the SHG intensity as a function of the odd-N. Extrapolating the linearly decreasing trend inferred from Fig. 4d, significant SHG intensity in WSe2 should be observed for samples with up to ~50 layers. However, the challenges in unambiguously determining N for samples with more than 10 layers make this observation difficult.
Figure 4c shows the THG map of the sample. In addition to the signal now arising from all regions of the sample, the key observation is that the intensity clearly scales up with the number of layers. To be more specific and quantitative, we compiled the average intensity over regions with same N in Fig. 4c. The THG intensity is proportional to N2, as shown in Fig. 4e. This quadratic scaling with thickness is a direct evidence that we can consider each layer as contributing independently to the overall THG, since the linear relation of the third-harmonic susceptibility indeed implies in .
No border effect for enhancement of SHG or THG was observed. In fact, DFT calculations for chemical vapour deposited (CVD) WS2 showed that at the borders the bandgap becomes indirect27,28, which actually contributes to quenching of SHG and, probably, THG at the edges.
A direct comparison between Fig. 4a and c indicates that regions with same N have slightly weaker harmonic intensities when covered by hBN, which the most notable case being the 5-layers region. This can be explained by the Fresnel reflection/transmission coefficients, since the total transmittance depends on the layer stacking, total sample thickness and refractive index mismatch. We observed that, by recording the transmitted power at the fundamental frequency with a reference photodetector, regions without hBN may have up to 4% higher pump transmittance than covered regions (for more details on reference transmittance mapping, see supporting information). This difference in pump power leads to SHG and THG intensities of, respectively, 8% and 12% higher in non-covered regions. The analysis presented in Fig. 4d and e already corrects the intensities by the pump power in each region. The contribution to SHG and THG from hBN solely is negligible, as we have confirmed by pumping hBN regions of the sample (Fig. 4b and c). This agrees with previous report by Li et al.25, where the authors show that hBN |χ(2)s| is 2 orders of magnitude lower than that of TMD.
Taking advantage of the spatial resolution and well defined layer assignment in our experiment, the magnitude of the nonlinear susceptibilities χ(2) and χ(3) for WSe2 were extracted from the harmonic mapping by using the model deducted by Woodward et al.18. Simple modifications were implemented in the model, accounting for harmonic generation in transmittance, with fundamental beam pumping the sample from the substrate-sample interface, as shown in Equation (1) and (2):
| 1 |
| 2 |
where P(2ω) and P(3ω) are second-harmonic and third-harmonic average powers, respectively, and P(ω) is the fundamental average power. c is the speed of light in vacuum, ε0 is the vacuum electric permittivity. RR is the repetition rate (80 MHz), A is the minimum spot area (2.0 ± 0.3 μm2, obtained from the half-width at 1/e2 beam radius of 0.8 ± 0.1 µm), Δτ is the full-width at half maximum pulse duration at the sample spot (200 ± 10 fs) and λ is the wavelength (1545 nm) for the fundamental beam. Finally, n is the substrate refractive index at the fundamental wavelength (1.47 at 1545 nm) and S = 0.94 is a shape factor assuming Gaussian pulses. The average power of the fundamental beam was kept constant at 0.65 mW, and the calibration factors to obtain harmonic average powers from counts, as in Fig. 4, are 0.275 fW counts−1 and 0.512 fW counts−1, respectively, for SHG and THG. |χ(2)| and |χ(3)| results are summarized in Table 1.
Table 1.
Harmonic susceptibilities of WSe2 as a function of number of layers N.
| Number of layers (N) | |χ(2)N| (10−19 m2 V−1) | |χ(3)N| (10−28 m3 V−2) |
|---|---|---|
| 1 | 0.70 ± 0.09 | 0.9 ± 0.2 |
| 4 | 0.08 ± 0.08 | 3.4 ± 0.5 |
| 5 | 0.67 ± 0.09 | 4.5 ± 0.6 |
| 6 | 0.2 ± 0.1 | 6.0 ± 0.8 |
| 9 | 0.65 ± 0.08 | 8.6 ± 0.9 |
| Average/sheet (per layer) | — | 0.91 ± 0.07 |
| |χ(2)b| (10−10 m V−1) | |χ(3)b| (10−19 m2 V−2) | |
| Bulk susceptibility | 0.9 ± 0.1 | 1.16 ± 0.09 |
As only odd-N regions contribute with appreciable SHG, the second-order susceptibility is expressed in terms of an effective value |χ(2)N|, which was directly obtained from each region on the WSe2 sample. The third-order susceptibility is expressed in terms of both an effective value, |χ(3)N|, and the average per layer, |χ(3)s|. The bulk-like values are obtained from the expression |χb| = |χs|/δ, where δ is the inter-layer distance of the flake (for our WSe2 flake, δ = 0.79 ± 0.02 nm – for more details on the thickness characterization, see supporting information).
The values obtained for sheet and bulk second-order susceptibility agree with those previously reported7,29 within the order of magnitude, and the sheet and bulk values of third-harmonic susceptibility are reported here for the first time. The χ(3) magnitude is comparable to other TMD18,30 and is larger than that reported for graphene18,31. Although the presented results have small errors inherent from the model and parameters we used (~13% for SHG at odd-N, ~13% for THG – except N = 1 with 20% error), those should only be taken as a good estimative for the order of magnitude of such susceptibilities, since their determination relies on the precise measurement of many important parameters (which can vary upon definitions and measurement techniques). The measurement of harmonic susceptibilities of two-dimensional layered materials is known to be sensitive to the fabrication process (Woodward et al.18 reported 26% variation between exfoliated and CVD MoS2), stacking order, and surrounding environment (substrate and superstrate)19.
Excitons are strongly present in semiconductor TMD, excitonic effects may also play role by enhancing nonlinear optical transitions, as reported previously for MoS28 and for WSe232,33: when the harmonic photon energies are in resonances to excitonic or single-particle energy levels from the material, harmonic signals up to 1 order of magnitude higher might be observed. Since in our experiment WSe2 is pumped by photons of 0.8 eV, no resonant enhancement effect is expected to take place, because both SHG (1.6 eV) and THG (2.4 eV) are off-resonance with energy levels of the material34. Nevertheless, our SHG results agrees to those off-resonance published results. Although no resonance has been observed, the presented characterization provides important parameters to support the realization of 2D-materials-based devices for applications in telecommunication systems and silicon photonics.
Benefiting from the small sample thickness and THG efficiency, multi-layer WSe2 appears to be a potential material for nonlinear optical applications as, for example, on-chip optical frequency conversion35, silicon photonics36,37, or other third-order related phenomena like all-optical switching38,39, which depends on a different χ(3).
Conclusion
By extensively characterizing single- and few-layers flakes of 2H-WSe2 with photoluminescence, Raman spectroscopy and atomic force microscopy, we obtained the precise number of layers of each regions of the flake. We mapped the spatial emission of the second- and third-harmonic signals to study the layer dependence of the nonlinear response and quantified the corresponding susceptibilities. We obtained the values |χ(3)s| = (0.91 ± 0.07) × 10−28 m3 V−2 and |χ(3)b| = (1.16 ± 0.09) × 10−19 m2 V−2, which are comparable to the third-harmonic susceptibility of related semiconducting TMD and provide one step forward towards the complete characterization of the nonlinear optical properties of this family (MX2; M = W, Mo; X = S, Se). The reliability of these values is supported by the good agreement of our values for |χ(2)|, extracted from the simultaneously recorded second-harmonic signal, with previous reports for the same material. The strong nonlinear response of WSe2 in the infrared makes it a material suitable for applications in silicon photonics, all-optical switching and optical frequency conversion.
Materials and Methods
Sample fabrication and characterization
Flakes of WSe2 were obtained via micromechanical exfoliation from a single bulk crystal and transferred onto a fused silica substrate. To prevent degradation, the sample was partially covered with multi-layer hBN. The sample’s properties were characterized by photoluminescence, Raman spectroscopy and atomic force microscopy (for more details sample fabrication and characterization, see supporting information).
Experimental setup
Nonlinear optical properties of WSe2 were investigated in a home-built multiphoton microscope setup. We used a half-waveplate to control the input linear polarization and a polarizer to analyze the harmonic signals. The pump laser was a 1545 nm, 200 fs, 80 MHz mode-locked fiber. A 100x objective lens focused the pump beam down to a spot size of 2 μm2. The step used in the sample displacement during spatial mapping was 0.5 µm (for more details on the experimental setup, see supporting information).
Data availability
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Electronic supplementary material
Acknowledgements
Y.W.H. acknowledges scholarship support from NGS. G.E. acknowledges financial support from National Research Foundation of Singapore (NRF Research Fellowship NRF-NRFF2011-02 and medium-sized centre programme) and Ministry of Education of Singapore (AcRF Tier 2 MOE2015-T2-2-123). V. M. P. acknowledges financial support from Ministry of Education of Singapore (FRC AcRF Tier 1 R-144-000-386-114). J.C.V.G. acknowledges financial support from CA2DM through National Research Foundation of Singapore (NRF-CRP Grant No. R-144-000-295-281).
Author Contributions
H.G.R. and Y. W. H. performed sample characterization, nonlinear optical experiments and analyzed the data. I.V. fabricated the hBN/WSe2 sample. M.J.F.L.R. set up the multiphoton microscope system. T.T. and K.W. provided the hexagonal boron nitride flake. G.E., V.M.P. and J.C.V.G. supervised the work and revised the manuscript. All authors discussed and interpreted the results and contributed to the writing of the manuscript.
Competing Interests
The authors declare no competing interests.
Footnotes
Henrique G. Rosa and Yi Wei Ho contributed equally to this work.
Electronic supplementary material
Supplementary information accompanies this paper at 10.1038/s41598-018-28374-1.
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Contributor Information
Vitor M. Pereira, Email: vpereira@nus.edu.sg
José C. V. Gomes, Email: phyvjc@nus.edu.sg
References
- 1.Podzorov V, Gershenson ME, Kloc C, Zeis R, Bucher E. High-mobility field-effect transistors based on transition metal dichalcogenides. Appl. Phys. Lett. 2004;84:3301–3303. doi: 10.1063/1.1723695. [DOI] [Google Scholar]
- 2.Yu Z, et al. Analyzing the Carrier Mobility in Transition-Metal Dichalcogenide MoS2 Field-Effect Transistors. Adv. Funct. Mater. 2017;27:1604093. doi: 10.1002/adfm.201604093. [DOI] [Google Scholar]
- 3.Mak KF, Lee C, Hone J, Shan J, Heinz TF. Atomically Thin MoS2: A New Direct-Gap Semiconductor. Phys. Rev. Lett. 2010;105:136805. doi: 10.1103/PhysRevLett.105.136805. [DOI] [PubMed] [Google Scholar]
- 4.Gutiérrez HR, et al. Extraordinary Room-Temperature Photoluminescence in Triangular WS2 Monolayers. Nano Lett. 2013;13:3447–3454. doi: 10.1021/nl3026357. [DOI] [PubMed] [Google Scholar]
- 5.Tonndorf P, et al. Photoluminescence emission and Raman response of monolayer MoS2, MoSe2, and WSe2. Opt. Express. 2013;21:4908–4916. doi: 10.1364/OE.21.004908. [DOI] [PubMed] [Google Scholar]
- 6.Splendiani A, et al. Emerging Photoluminescence in Monolayer MoS2. Nano Lett. 2010;10:1271–1275. doi: 10.1021/nl903868w. [DOI] [PubMed] [Google Scholar]
- 7.Ribeiro-Soares J, et al. Second Harmonic Generation in WSe2. 2D Mater. 2015;2:45015. doi: 10.1088/2053-1583/2/4/045015. [DOI] [Google Scholar]
- 8.Malard LM, et al. Observation of intense second harmonic generation from MoS2 atomic crystals. Phys. Rev. B. 2013;87:201401(R). doi: 10.1103/PhysRevB.87.201401. [DOI] [Google Scholar]
- 9.Reyes-Retana JA, Cervantes-Sodi F. Spin-orbital effects in metal-dichalcogenide semiconducting monolayers. Sci. Rep. 2016;6:24093. doi: 10.1038/srep24093. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Zeng H, et al. Optical signature of symmetry variations and spin-valley coupling in atomically thin tungsten dichalcogenides. Sci. Rep. 2013;3:1608. doi: 10.1038/srep01608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Xu X, Yao W, Xiao D, Heinz TF. Spin and pseudospins in layered transition metal dichalcogenides. Nat. Phys. 2014;10:343–350. doi: 10.1038/nphys2942. [DOI] [Google Scholar]
- 12.Mak KF, Shan J. Photonics and optoelectronics of 2D semiconductor transition metal dichalcogenides. Nat. Photonics. 2016;10:216–226. doi: 10.1038/nphoton.2015.282. [DOI] [Google Scholar]
- 13.Wang G, et al. Colloquium: Excitons in atomically thin transition metal dichalcogenides. Rev. Mod. Phys. 2018;90:21001. doi: 10.1103/RevModPhys.90.021001. [DOI] [Google Scholar]
- 14.Janisch C, et al. Extraordinary second harmonic generation in Tungsten Disulfide monolayers. Sci. Rep. 2014;4:5530. doi: 10.1038/srep05530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Le CT, et al. Nonlinear optical characteristics of monolayer MoSe2. Ann. Phys. 2016;528:551–559. doi: 10.1002/andp.201600006. [DOI] [Google Scholar]
- 16.Kumar N, et al. Second harmonic microscopy of monolayer MoS2. Phys. Rev. B. 2013;87:161403. doi: 10.1103/PhysRevB.87.161403. [DOI] [Google Scholar]
- 17.Torres-Torres C, et al. Third order nonlinear optical response exhibited by mono- and few-layers of WS2. 2D Mater. 2016;3:21005. doi: 10.1088/2053-1583/3/2/021005. [DOI] [Google Scholar]
- 18.Woodward RI, et al. Characterization of the second- and third-order nonlinear optical susceptibilities of monolayer MoS2 using multiphoton microscopy. 2D Mater. 2016;4:11006. doi: 10.1088/2053-1583/4/1/011006. [DOI] [Google Scholar]
- 19.Autere, A. et al. Nonlinear Optics with 2D Layered Materials. Adv. Mater. 1705963 (2018). [DOI] [PubMed]
- 20.In the review paper published by Autere and collaborators (Adv. Mater. 1705963 (2018)), authors show values for third-harmonic susceptibilities of WSe2 and MoSe2, however such values are based on internal/unpublished data.
- 21.Karvonen L, et al. Investigation of second- and third-harmonic generation in few-layer gallium selenide by multiphoton microscopy. Sci. Rep. 2015;5:10334. doi: 10.1038/srep10334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Boyd, R. W. The Nonlinear Optical Susceptibility. Nonlinear Optics - Chapter 1 (Academic Press, 2008).
- 23.Kim DH, Lim D. Optical second-harmonic generation in few-layer MoSe2. J. Korean Phys. Soc. 2015;66:816–820. doi: 10.3938/jkps.66.816. [DOI] [Google Scholar]
- 24.Hsu W-T, et al. Second Harmonic Generation from Artificially Stacked Transition Metal Dichalcogenide Twisted Bilayers. 2014;8:2951–2958. doi: 10.1021/nn500228r. [DOI] [PubMed] [Google Scholar]
- 25.Li Y, et al. Probing symmetry properties of few-layer MoS2 and h-BN by optical second-harmonic generation. Nano Lett. 2013;13:3329–3333. doi: 10.1021/nl401561r. [DOI] [PubMed] [Google Scholar]
- 26.Li D, et al. Multimodal Nonlinear Optical Imaging of MoS2 and MoS2-Based van der Waals Heterostructures. ACS Nano. 2016;10:3766–3775. doi: 10.1021/acsnano.6b00371. [DOI] [PubMed] [Google Scholar]
- 27.Rosa, H. G. et al. Second-Harmonic Spectroscopy for Defects Engineering Monitoring in Transition Metal Dichalcogenides. Adv. Opt. Mater. 10.1002/adom.201701327 (2018).
- 28.Liu H, et al. Fluorescence Concentric Triangles: A Case of Chemical Heterogeneity in WS2 Atomic Monolayer. Nano Lett. 2016;16:5559–5567. doi: 10.1021/acs.nanolett.6b02111. [DOI] [PubMed] [Google Scholar]
- 29.Yu H, Talukdar D, Xu W, Khurgin JB, Xiong Q. Charge-Induced Second-Harmonic Generation in Bilayer WSe2. Nano Lett. 2015;15:5653–5657. doi: 10.1021/acs.nanolett.5b02547. [DOI] [PubMed] [Google Scholar]
- 30.Wang R, et al. Third-harmonic generation in ultrathin films of MoS2. ACS Appl. Mater. Interfaces. 2014;6:314–318. doi: 10.1021/am4042542. [DOI] [PubMed] [Google Scholar]
- 31.Rodrigues MJLF, et al. Resonantly Increased Optical Frequency Conversion in Atomically Thin Black Phosphorus. Adv. Mater. 2016;28:10693–10700. doi: 10.1002/adma.201603119. [DOI] [PubMed] [Google Scholar]
- 32.Seyler KL, et al. Electrical control of second-harmonic generation in a WSe2 monolayer transistor. Nat. Nanotechnol. 2015;10:407–411. doi: 10.1038/nnano.2015.73. [DOI] [PubMed] [Google Scholar]
- 33.Wang G, et al. Giant Enhancement of the Optical Second-Harmonic Emission of WSe2 Monolayers by Laser Excitation at Exciton Resonances. Phys. Rev. Lett. 2015;114:97403. doi: 10.1103/PhysRevLett.114.097403. [DOI] [PubMed] [Google Scholar]
- 34.Li Y, et al. Measurement of the optical dielectric function of monolayer transition-metal dichalcogenides: MoS2, MoSe2, WS2, and WSe2. Phys. Rev. B. 2014;90:205422. doi: 10.1103/PhysRevB.90.205422. [DOI] [Google Scholar]
- 35.Fryett TK, et al. Silicon photonic crystal cavity enhanced second-harmonic generation from monolayer WSe2. 2D Mater. 2016;4:15031. doi: 10.1088/2053-1583/4/1/015031. [DOI] [Google Scholar]
- 36.Liu L, et al. Enhanced optical Kerr nonlinearity of MoS2 on silicon waveguides. Photonics Res. 2015;3:206. doi: 10.1364/PRJ.3.000206. [DOI] [Google Scholar]
- 37.Youngblood N, Li M. Integration of 2D materials on a silicon photonics platform for optoelectronics applications. Nanophotonics. 2017;6:1205–1218. [Google Scholar]
- 38.Wu K, et al. All-optical phase shifter and switch near 1550 nm using tungsten disulfide (WS2) deposited tapered fiber. Opt. Express. 2017;25:17639–17649. doi: 10.1364/OE.25.017639. [DOI] [PubMed] [Google Scholar]
- 39.Srivastava YK, et al. MoS2 for Ultrafast All-Optical Switching and Modulation of THz Fano Metaphotonic Devices. Adv. Opt. Mater. 2017;5:1700762. doi: 10.1002/adom.201700762. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.