Abstract
Andreev bound states are an expression of quantum coherence between particles and holes in hybrid structures composed of superconducting and non-superconducting metallic parts. Their spectrum carries important information on the nature of the pairing, and determines the current in Josephson devices. Here, I focus on Andreev bound states in systems involving superconductors and ferromagnets with strong spin-polarization. I provide a general framework for non-local Andreev phenomena in such structures in terms of coherence functions, and show how the latter link wave function and Green-function based theories.
This article is part of the theme issue ‘Andreev bound states’.
Keywords: Andreev bound states, superconductivity and magnetism, superconducting proximity effect
1. Andreev reflection phenomena
In an isotropic non-magnetic superconductor, the normal-state single-particle excitation spectrum εk is modified in the superconducting state to Ek=[(εk−μ)2+Δ2]1/2, acquiring a gap Δ around the electrochemical potential μ, and the density of states is characterized by a coherence peak just above the gap, accounting for the missing sub-gap states. This spectral signature, predicted by Bardeen–Cooper–Schrieffer (BCS) theory [1,2] has been first observed by infrared absorption spectroscopy [3,4] and by tunnelling spectroscopy [5].
The spectral features above the gap may show information about electron–phonon interaction (or about interaction with some low-energy bosonic modes, e.g. spin-fluctuations [6]), or may exhibit geometric interference patterns. Features due to electron–phonon interaction, predicted by Migdal–Eliashberg theory [7–10] and studied in detail by Scalapino et al. [11], were measured early in tunnelling experiments by Giaever et al. [12]. They are a consequence of electronic particle-hole coherence in a superconductor and build the basis for the McMillan–Rowell inversion procedure for determining the Eliashberg effective interaction spectrum α2F(ω) [13]. Geometric interference effects include oscillations in the density of states, such as Tomasch oscillations in N-I-S and N-I-S-N’ tunnel structures with a superconductor of thickness dS (and with transverse Fermi velocity vF,S), giving rise to voltage peaks at 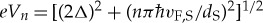 (n integer) [14–16]; and Rowell–McMillan oscillations in N-I-N’-S tunnel structures with a normal metal N’ of thickness dN′ (transverse Fermi velocity vF,N′), giving rise to voltage peaks at
(n integer) [14–16]; and Rowell–McMillan oscillations in N-I-N’-S tunnel structures with a normal metal N’ of thickness dN′ (transverse Fermi velocity vF,N′), giving rise to voltage peaks at 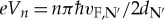 [17]. Possible offsets due to spatial variation of the gap Δ may occur [18].
[17]. Possible offsets due to spatial variation of the gap Δ may occur [18].
Inhomogeneous superconducting states also exhibit features at energies inside the gap. Surface bound states in a normal metal overlayer on a superconductor were predicted first by de Gennes & Saint-James [19,20] and measured by Rowell [21] and Bellanger et al. [22]. These de Gennes–Saint-James bound states have a natural explanation in terms of the so-called Andreev reflection process, an extremely fruitful physical picture suggested in 1964 by Andreev [23,24]. For example, geometric resonances above the gap appear due to Andreev reflection at N-S interfaces, which describe (for normal impact) scattering of a particle at wavevector  into a hole at wavevector
into a hole at wavevector  or vice versa. Below the gap Andreev reflections lead to subharmonic gap structure due to multiple Andreev reflections at voltages V
n=2Δ/en (n integer) in SIS junctions [25] (for a general treatment in diffusive systems, see [26]), and control electrical and thermal resistance of a superconductor/normal-metal interface and the Josephson current in a superconductor/normal-metal/superconductor junction. The Andreev mechanism also gives rise to bound states in various other systems with inhomogeneous superconducting order parameter, which are named in the general case Andreev bound states.
or vice versa. Below the gap Andreev reflections lead to subharmonic gap structure due to multiple Andreev reflections at voltages V
n=2Δ/en (n integer) in SIS junctions [25] (for a general treatment in diffusive systems, see [26]), and control electrical and thermal resistance of a superconductor/normal-metal interface and the Josephson current in a superconductor/normal-metal/superconductor junction. The Andreev mechanism also gives rise to bound states in various other systems with inhomogeneous superconducting order parameter, which are named in the general case Andreev bound states.
Transport trough an N-S contact is strongly influenced by Andreev scattering, and is described in the single-channel case by the theory of Blonder et al. [27], generalized to the multi-channel case by Beenakker [28]. Andreev scattering at N-S interfaces is the cause of the superconducting proximity effect [29,30]. Interference effects in transport appear also as the result of impurity disorder. In contrast to unconventional superconductors, where normal impurities are pair breaking, isotropic s-wave superconductors are insensitive to scattering from normal impurities for not too high impurity concentration, which is the content of a theorem by Abrikosov & Gor’kov [31–34], and by Anderson [35]. In strongly disordered superconductors (weak localization regime), the superconducting transition temperature Tc is reduced [36,37], accompanied by localized tail states (similar to Lifshitz tail states in semiconductors [38–40]) just below the gap edge [41–43]. An interference effect is the so-called reflectionless tunnelling [28,44–49], which leads to a zero-bias conductance peak in a diffusive N-I-S structure. It results from multiple scattering of Andreev-reflected coherent particle-hole pairs at impurities, and from the resulting backscattering to the interface barrier, making the barrier effectively transparent near the electrochemical potential for a pair current even in the tunnelling regime.
In 1960 Abrikosov and Gor’kov developed a theory for pair-breaking by paramagnetic impurities, showing that at a critical value for the impurity concentration superconductivity is destroyed, and that gapless superconductivity can exist in a narrow region below this critical value [50,51]. Yu [52], Shiba [53] and Rusinov [54,55] (who happened to work isolated from each other in China, Japan and Russia) independently discovered within the framework of a full t-matrix treatment of the problem that local Andreev bound states (now called the Yu–Shiba–Rusinov states) are present within the BCS energy gap due to multiple scattering between conduction electrons and paramagnetic impurities. Andreev bound states also exist in the cores of vortices in type II superconductors. These are called Caroli–de Gennes–Matricon bound states [56], and carry current in the core region of a vortex [57]. Their dynamics plays a crucial role in the absorption of electromagnetic waves [58–61].
In an S-N-I or S-N-S junction, Andreev bound states appear in the normal metal region at energies below the gaps of the superconductors. The number and distribution of these bound states depend on details such as interface transmission, mean free path and length of the normal metal dN. In general, there is a characteristic energy, the Thouless energy [62] (related to the dwell time between Andreev reflections), given by  for the clean limit, and by
for the clean limit, and by  for the diffusive limit, with Fermi velocity vF,N and diffusion constant DN of the normal metal. In the diffusive limit, the Andreev states build a quasi-continuum below the superconducting gap, whereas in the case of ballistic junctions bands of Andreev bound states arise. For the case that no superconducting phase gradient (and no paramagnetic pair breaking) is present in the system; however, a low-energy gap always arises in the spectrum of Andreev states in the normal metal. This so-called minigap scales for sufficiently thick normal metal layers approximately with its Thouless energy and with the transmission probability (possibly further reduced by inelastic scattering processes). It was found first by McMillan [63] and can be probed by scanning tunnelling microscopy [64]. In chaotic Andreev billiards [65], where disorder is restricted to boundaries, a second time scale, the Ehrenfest time, competes with the dwell time to set the minigap [66].
for the diffusive limit, with Fermi velocity vF,N and diffusion constant DN of the normal metal. In the diffusive limit, the Andreev states build a quasi-continuum below the superconducting gap, whereas in the case of ballistic junctions bands of Andreev bound states arise. For the case that no superconducting phase gradient (and no paramagnetic pair breaking) is present in the system; however, a low-energy gap always arises in the spectrum of Andreev states in the normal metal. This so-called minigap scales for sufficiently thick normal metal layers approximately with its Thouless energy and with the transmission probability (possibly further reduced by inelastic scattering processes). It was found first by McMillan [63] and can be probed by scanning tunnelling microscopy [64]. In chaotic Andreev billiards [65], where disorder is restricted to boundaries, a second time scale, the Ehrenfest time, competes with the dwell time to set the minigap [66].
The importance of Andreev bound states in S-N-S Josephson junctions for current transport was first discussed by Kulik [67,68]. Andreev bound states form in a sufficiently long normal region, which are doubly degenerate (carrying current in opposite direction) for zero phase difference between the superconducting banks. For a finite phase difference, this degeneracy is lifted. The gap or minigap in a Josephson structure is reduced and eventually closes when a supercurrent flows across the junction. This is a result of a ‘dispersion’ of the energy Eb.s. of the Andreev bound states as function of phase difference Δχ between the superconducting banks [67–70]. The contribution of the bound states to the supercurrent is given by  , with e<0 the electron charge. Apart from the current carried by the Andreev bound states, there is also a contribution from continuum states above the gap [67,68]. For a single-channel weak link between two superconductors with normal-state transmission probability τ2, there is one pair of Andreev bound states with dispersion
, with e<0 the electron charge. Apart from the current carried by the Andreev bound states, there is also a contribution from continuum states above the gap [67,68]. For a single-channel weak link between two superconductors with normal-state transmission probability τ2, there is one pair of Andreev bound states with dispersion 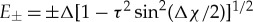 .
.
The large size of a Cooper pair in conventional superconductors leads to a pronounced non-locality of Andreev reflection processes. This allows for interference effects due to crossed Andreev reflection, in which the particle and hole involved in the process enter different normal-state (typically spin-polarized) terminals, which are both simultaneously accessible to one Cooper pair [71,72]. This effect has been first experimentally observed by Beckmann et al. [73].
Finally, an important role is played by Andreev zero modes as topological surface states. Examples are zero-bias states at the surface of a d-wave superconductor [74,75], and Majorana zero modes in topological superconductors [76,77] and superfluids [78].
2. Andreev bound states at magnetically active interfaces
(a). Spin-dependent interface scattering phase shifts
The importance of spin-dependent interface scattering phase shifts for superconducting phenomena has been pioneered in the work of Tokuyasu, Sauls and Rainer in 1988 [79]. Consider an interface between a normal metal (N) at x<0 and a ferromagnetic insulator (FI) or a half-metallic ferromagnet (HM) at x>0. For simplicity, let us model the FI (or HM) by a single electronic band with energy gap V
↓ for spin-down particles and an energy gap V
↑=V
↓−2J for spin-up particles, where J>0 denotes an effective exchange field. The exchange field can be related to an effective magnetic field via μBeff=J (for free electrons the magnetic moment is μ=μe<0). Let us assume an incoming Bloch electron with energy 0<E<V
↑ and spin σ∈{↑,↓}, reflected back from the interface with amplitude rσ. It is described by a wave function  at x<0 and
at x<0 and  at x>0. For the normal metal
at x>0. For the normal metal  . For the FI
. For the FI  . The reflection scattering matrix is
. The reflection scattering matrix is
 |
2.1 |
In the range V
↑<E<V
↓ the spin-up electron can be transmitted for sufficiently small k∥ with amplitude 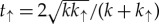 , where
, where  . In this case, the reflection amplitude is also real, and equal to rσ=(k−k↑)/(k+k↑). The reflection phase is −π for k<k↑ and zero for k>k↑. In figure 1, V
↓=3EF is fixed and V
↑ varied from −EF to 3EF, k∥=0. A phase shift for reflected waves between the two spin projections appears.
. In this case, the reflection amplitude is also real, and equal to rσ=(k−k↑)/(k+k↑). The reflection phase is −π for k<k↑ and zero for k>k↑. In figure 1, V
↓=3EF is fixed and V
↑ varied from −EF to 3EF, k∥=0. A phase shift for reflected waves between the two spin projections appears.
Figure 1.

Spin-dependent scattering phase shifts for Bloch waves with energy EF reflected from an N-FI or N-HM interface (at x=0). Here V ↓=3EF is fixed and V ↑ varied from −EF to 3EF (i.e. the parameter (V ↑−EF)/EF is varied from −2 to 2), k∥=0. For V ↑>EF, this describes an FI, for V ↑<EF a HM. For V ↑<0 the Fermi surface of the spin-up band in the HM becomes larger than in N. Shown are for x<0 the (normalized) reflected wave, quantified by −Im(rσ e−ikx)/|rσ|, and for x>0 the transmitted wave, quantified by −Im(tσ e−κσx) (for real κσ) or −Im(t↑ eik↑x) (for real k↑, i.e. V ↑<EF). The spin-up wave is shown in orange, the spin-down wave in blue.
It results from the well-known effect that reflection from an insulating region results in a phase-delay of the reflected wave with respect to the case of an infinite interface potential. This phase delay appears due to the quantum mechanical penetration of the wave function into the classically forbidden region. The range V
↑−EF>0 in figure 1 corresponds to an N-FI interface, where both spin-projections are evanescent in FI. Here, the reflected spin-up wave trails that of the spin-down wave, and the effect increases when V
↑−EF approaches zero. The phase ϑ=ϑ↑−ϑ↓ of the parameter  is called spin-mixing angle [79], or spin-dependent scattering phase shift [80]. It is an important parameter for superconducting spintronics. For the N-FI model interface, it is given by
is called spin-mixing angle [79], or spin-dependent scattering phase shift [80]. It is an important parameter for superconducting spintronics. For the N-FI model interface, it is given by
| 2.2 |
which is positive due to κ↓>κ↑. The range V ↑−EF<0 corresponds to an N-HM interface, with the spin-up band itinerant in HM. Here, as long as the spin-up Fermi wavevector in the HM is smaller than that in N (for −1<(V ↑−EF)/EF<0), the reflection phase in r↑ is zero, and
| 2.3 |
which can acquire large values. Finally, in the range (V ↑−EF)/EF<−1 the Fermi wavevector in the HM is larger than in N, which leads to a reflection phase of π for spin-up particles, and
| 2.4 |
which now is negative.
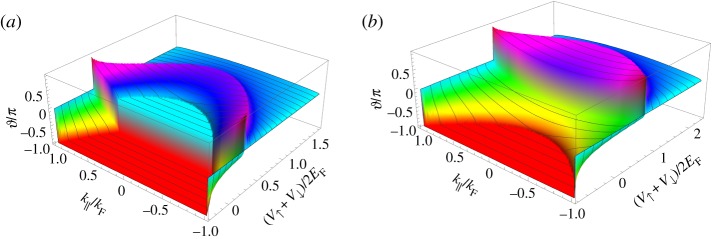
In ballistic structures, the spin-mixing angle depends on the momentum  parallel to the interface, as illustrated in figure 2 for varying Fermi surface geometry in the ferromagnet, here parametrized by varying (V
↑+V
↓)/2 keeping J fixed. If both spin-bands are itinerant in the ferromagnet (F), then the spin-mixing angle is either zero (if k>k↑,k↓ or k<k↑,k↓, cyan area in figure 2a) or −π (if k↑>k>k↓, red areas in figure 2), unless an interface potential exists, rendering the reflection amplitudes complex valued. In general, the spin-mixing angle should be considered as material parameter, which in addition depends on the impact angle of the incoming electron or on transport channel indices.
parallel to the interface, as illustrated in figure 2 for varying Fermi surface geometry in the ferromagnet, here parametrized by varying (V
↑+V
↓)/2 keeping J fixed. If both spin-bands are itinerant in the ferromagnet (F), then the spin-mixing angle is either zero (if k>k↑,k↓ or k<k↑,k↓, cyan area in figure 2a) or −π (if k↑>k>k↓, red areas in figure 2), unless an interface potential exists, rendering the reflection amplitudes complex valued. In general, the spin-mixing angle should be considered as material parameter, which in addition depends on the impact angle of the incoming electron or on transport channel indices.
Figure 2.
Spin mixing angle ϑ as function of parallel momentum k∥/kF and ν=(V ↑+V ↓)/2; (a) for effective exchange field J=0.3EF (FI for ν>1.3, HM for ν>0.7) and (b) for J=0.8EF (FI for ν>1.8, HM for ν>0.2).
Note that the parameter  has become well known in the spintronics community, as it governs the spin mixing conductance [81] in spintronics devices.
has become well known in the spintronics community, as it governs the spin mixing conductance [81] in spintronics devices.
It is also instructive to study an incoming Bloch-electron polarized in a direction different from the magnetization direction in the ferromagnet. Let us consider the case of an FI. For a Bloch electron polarized in a direction n(α,ϕ), parametrized by polar and azimuthal angles, α and ϕ,
| 2.5 |
the reflected wave will have the form
 |
2.6 |
with  . Similarly, ↓α,ϕ scatters into
. Similarly, ↓α,ϕ scatters into  . This means that scattering leads, apart from an unimportant spin-independent phase factor
. This means that scattering leads, apart from an unimportant spin-independent phase factor 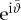 , to a precession of the spin around the magnetization axis [79]. The direction of precession depends on the Fermi surface geometries, and is determined by the sign of the spin-mixing angle ϑ.
, to a precession of the spin around the magnetization axis [79]. The direction of precession depends on the Fermi surface geometries, and is determined by the sign of the spin-mixing angle ϑ.
The discussion above is generic and is easily generalized to anisotropic Fermi surfaces, Fermi velocities and effective exchange fields. The central quantity of the theory is the scattering matrix S, the eigenvalues of which are given for conserved k∥ by eiϑ↑(k∥) and eiϑ↓(k∥), and the eigenvectors of which determine for each k∥ the quantization axis along which the scattering matrix is diagonal, and around which the spin precession takes place.
(b). Andreev reflection in an S-N-FI structure
An important consequence of spin-mixing phases is the appearance of Andreev bound states at magnetically active interfaces, predicted theoretically [82–88] and verified experimentally [89].
Consider a superconductor near an interface with a ferromagnetic insulator. Let us assume that the superconducting order parameter is suppressed to zero in a layer of thickness d next to the FI interface, such that the structure can be described as an S-N-FI junction with identical normal state parameters in S and N. For simplicity, I consider here a spatially constant order parameter in S (extending to the half space x<0). The FI (x>d) will be parametrized by reflection phases ϑ↑ and ϑ↓, with spin-mixing angle ϑ=ϑ↑−ϑ↓. Solving the corresponding Bogoliubov–de Gennes equations in the superconductor (σi are spin Pauli matrices, σ0 a 2×2 unit spin matrix)
 |
2.7 |
with spinors u and v, the (still unnormalized) eigenvectors for given energy ε and k∥=0 are
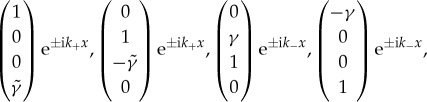 |
2.8 |
where to first order in |Δ|/EF the wavevectors are  and
and
| 2.9 |
For |ϵ|>|Δ|, the expression 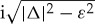 is replaced by
is replaced by  (which corresponds to ε→ε+i0+ with infinitesimally small positive 0+). In the N layer the solutions are obtained by setting Δ=0. In the FI, only evanescent solutions of the form e−κ↑x and e−κ↓x are allowed. The reflection coefficients connect incoming (eik+x, e−ik−x) solutions with outgoing (e−ik+x, eik−x) solutions. For scattering from electron-like to electron-like Bogoliubov quasi-particles and for electron-like to hole-like Bogoliubov quasi-particles in leading order in |Δ|/EF they are
(which corresponds to ε→ε+i0+ with infinitesimally small positive 0+). In the N layer the solutions are obtained by setting Δ=0. In the FI, only evanescent solutions of the form e−κ↑x and e−κ↓x are allowed. The reflection coefficients connect incoming (eik+x, e−ik−x) solutions with outgoing (e−ik+x, eik−x) solutions. For scattering from electron-like to electron-like Bogoliubov quasi-particles and for electron-like to hole-like Bogoliubov quasi-particles in leading order in |Δ|/EF they are
| 2.10 |
and
| 2.11 |
and similar relations hold for  and simultaneously ϑ→−ϑ, γ→−γ,
and simultaneously ϑ→−ϑ, γ→−γ, 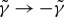 . These relations have a simple interpretation. The coherence functions
γ and
. These relations have a simple interpretation. The coherence functions
γ and  represent probability amplitudes for hole-to-particle conversion (−γ) or particle-to-hole conversion (
represent probability amplitudes for hole-to-particle conversion (−γ) or particle-to-hole conversion ( ), whereas the factors
), whereas the factors  represent the electron-hole dephasing when crossing the N layer. Thus, the factors
represent the electron-hole dephasing when crossing the N layer. Thus, the factors  represent a Rowell–McMillan process of four times crossing N with two reflections from FI (once as particle and once as hole, contributing eiϑ↑ and e−iϑ↓), and two Andreev conversions. When this factor equals −1, which happens for energies below the gap, a bound state appears in N due to constructive interference between particles and holes. Note that for |ε|≤|Δ| the coherence functions have unit modulus:
represent a Rowell–McMillan process of four times crossing N with two reflections from FI (once as particle and once as hole, contributing eiϑ↑ and e−iϑ↓), and two Andreev conversions. When this factor equals −1, which happens for energies below the gap, a bound state appears in N due to constructive interference between particles and holes. Note that for |ε|≤|Δ| the coherence functions have unit modulus:  , such that with Δ=|Δ|eiχ one can write γ=i eiΨ(ε) eiχ and
, such that with Δ=|Δ|eiχ one can write γ=i eiΨ(ε) eiχ and 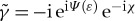 , with
, with 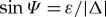 ,
,  . For |ε|<|Δ|, only outgoing wavevectors −k+ and k− lead to normalizable solutions in the superconductor, which are restricted to the bound state energies, given by the solution of
. For |ε|<|Δ|, only outgoing wavevectors −k+ and k− lead to normalizable solutions in the superconductor, which are restricted to the bound state energies, given by the solution of  .
.
In figure 3, results for the quantity Im(re↑→h↓) for normal impact are shown. For energies above the gap, the typical Rowell–McMillan oscillations are visible. Below the gap sharp bound states exist, the energies of which depend on both ϑ and d. In (a–c) the influence of varying d is illustrated. The special case ϑ=0, shown in (figure 3a), corresponds to the classical Rowell–McMillan S-N-I structure. For ϑ=π, shown in (figure 3c), a midgap bound state exists for all d. For 0<ϑ<π particle-hole symmetry is broken, as shown in figure 3b,d–f. A corresponding bound state at negative energy exists for re↓→h↑. The two corresponding bound states in the density of states have opposite spin polarization. With increasing d more and more bound states enter the sub-gap region, emerging from the continuum Rowell–McMillan resonances. For d=0, a bound state exists for any non-zero ϑ, as shown in (figure 3d), and as discussed in [82]. The influence of ϑ is shown for various d in (d–f). These results can be interpreted as one spin-polarized chiral branch crossing the gap region with increasing ϑ. For d=0, this happens when varying ϑ from zero to 2π. For d≠0, one needs a variation exceeding 2π (up to multiple times) until the branch crosses the entire gap. The figure shows results for normal impact, k∥=0. In general, an integration over k∥ will lead to Andreev bands instead of sharp bound states, similar as in the case of de Gennes–Saint-James bound states in S-N-I structures.
Figure 3.
Imaginary part of Andreev reflection amplitudes for spin-up Bogoliubov quasi-particle to spin-down Bogoliubov quasihole, Im(re↑→h↓), at normal impact, for an S-N-FI structure with a normal region of thickness d, as function of energy ε, and of d (in units of  with vF,z the projection of the Fermi velocity on the surface normal). The reflection amplitude at the N-FI interface is for spin-up eiϑ↑ and for spin-down eiϑ↓. The spin-mixing angle is defined as ϑ=ϑ↑−ϑ↓. It has the values (a) ϑ=0, (b) ϑ=π/2, (c) ϑ=π. In (d–f), the thickness of the normal layer is fixed to (d) d=0, (e) d=ξ0, (f) d=2ξ0, and the spin-mixing angle ϑ varied. The negative reflection amplitude for spin-down quasi-particle to spin-up quasi-hole, −Im(re↓→h↑), is obtained by inverting the energy axis,
with vF,z the projection of the Fermi velocity on the surface normal). The reflection amplitude at the N-FI interface is for spin-up eiϑ↑ and for spin-down eiϑ↓. The spin-mixing angle is defined as ϑ=ϑ↑−ϑ↓. It has the values (a) ϑ=0, (b) ϑ=π/2, (c) ϑ=π. In (d–f), the thickness of the normal layer is fixed to (d) d=0, (e) d=ξ0, (f) d=2ξ0, and the spin-mixing angle ϑ varied. The negative reflection amplitude for spin-down quasi-particle to spin-up quasi-hole, −Im(re↓→h↑), is obtained by inverting the energy axis,  . (Online version in colour.)
. (Online version in colour.)
Finally, note that with the reflection matrix (2.1) the resulting coherence function develops a spin-triplet component from a singlet component γin=γ0iσ2:
 |
2.12 |
which implies that a singlet pair is scattered into a superposition of a singlet and a triplet pair:
| 2.13 |
(c). Andreev bound states in an S-FI-N structure
As the next example, I summarize some results from Linder et al. [90,91] and section IV of Eschrig [92] for an S-FI-N junction, consisting of a bulk superconductor coupled via a thin ferromagnetic insulator (such as EuO) of thickness dI to a normal layer of thickness dN. I assume here the ballistic case, and refer for the diffusive case to references [90,91,93]. The interface is characterized by potentials V
↑ and V
↓=V
↑+2J, such that the energy dispersion in the superconductor is  , in the normal metal
, in the normal metal  and in the barrier
and in the barrier  , σ∈{↑,↓}. The parameter V
N is used to vary the Fermi surface mismatch. We note here in passing that having different effective masses on the two sides of the interface does not introduce new physics: any kinetic energy term of the form
, σ∈{↑,↓}. The parameter V
N is used to vary the Fermi surface mismatch. We note here in passing that having different effective masses on the two sides of the interface does not introduce new physics: any kinetic energy term of the form  with spatially varying m≡m(x) and with a+b+c=1 transforms with the substitution
with spatially varying m≡m(x) and with a+b+c=1 transforms with the substitution  into a potential energy term of the form
into a potential energy term of the form  . Thus, the effect on the scattering problem is essentially to renormalize the interface potential and to introduce a Fermi surface mismatch. The Fermi wave vectors and Fermi velocities in S and N are denoted kF,S, vF,S and kF,N, vF,N, respectively. The Fermi energy is
. Thus, the effect on the scattering problem is essentially to renormalize the interface potential and to introduce a Fermi surface mismatch. The Fermi wave vectors and Fermi velocities in S and N are denoted kF,S, vF,S and kF,N, vF,N, respectively. The Fermi energy is  . For shorter notation, let us introduce a directional vector for electrons moving in positive x-direction,
. For shorter notation, let us introduce a directional vector for electrons moving in positive x-direction,  (i.e.
(i.e.  ), and the corresponding x-component of the Fermi velocity, vF,N,x≡vx≥0, in the normal metal (situated at 0≤x≤dN). It is convenient to define coherence functions γ and
), and the corresponding x-component of the Fermi velocity, vF,N,x≡vx≥0, in the normal metal (situated at 0≤x≤dN). It is convenient to define coherence functions γ and  as 2×2 spin matrices. The coherence functions in the superconductor are given by γ=γ0iσ2 and
as 2×2 spin matrices. The coherence functions in the superconductor are given by γ=γ0iσ2 and 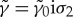 , where γ0 and
, where γ0 and  are given by the expressions in (2.9). The solutions in the normal metal are (for simplicity of notation, I also suppress the arguments k∥ and ε in γ and
are given by the expressions in (2.9). The solutions in the normal metal are (for simplicity of notation, I also suppress the arguments k∥ and ε in γ and  )
)
| 2.14 |
and
| 2.15 |
At x=dN, one obtains  and
and 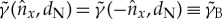 , with
, with
 |
2.16 |
The scattering parameters are the modulus of the transmission amplitudes, t↑ and t↓, the modulus of the reflection amplitudes  and
and  (equal on both sides of the FI), as well as the phase factors of the scattering parameters (all these parameters depend on k∥). The relevant energy scale in the normal metal for given direction
(equal on both sides of the FI), as well as the phase factors of the scattering parameters (all these parameters depend on k∥). The relevant energy scale in the normal metal for given direction  is
is
| 2.17 |
with the Thouless energy εTh. Matching the wavefunctions at x=0 to the thin FI layer and the superconductor, leads to  and
and  , as well as [90,91]
, as well as [90,91]
| 2.18 |
where σ∈{+,−}, and the function νσ(ε) is defined as
| 2.19 |
with  , where ϑN and ϑS are the spin-mixing angles for reflection at the FI-N interface and the S-FI interface, respectively, and the variable σ is to be understood as a factor ±1 for σ=±. Note that (2.18) has the same form as (2.9) with the role of Δ and ε taken over by δ and νσ, respectively. Note also that |γσ|=1 for νσ<δ, even in the tunnelling limit. This is an example of reflectionless tunnelling at low energies and results from multiple reflections within the normal layer. Quasi-particles in the normal layer stay fully coherent in this energy range.
, where ϑN and ϑS are the spin-mixing angles for reflection at the FI-N interface and the S-FI interface, respectively, and the variable σ is to be understood as a factor ±1 for σ=±. Note that (2.18) has the same form as (2.9) with the role of Δ and ε taken over by δ and νσ, respectively. Note also that |γσ|=1 for νσ<δ, even in the tunnelling limit. This is an example of reflectionless tunnelling at low energies and results from multiple reflections within the normal layer. Quasi-particles in the normal layer stay fully coherent in this energy range.
The density of states at the outer surface of the N layer is obtained as
 |
2.20 |
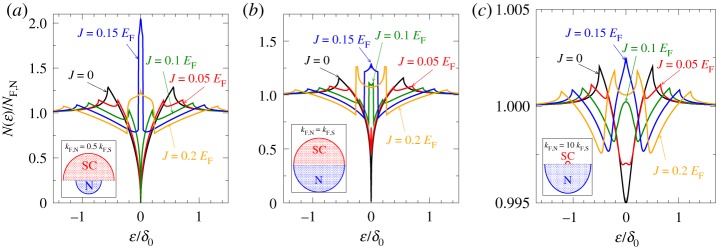
where 〈…〉 denotes Fermi surface averaging, and NF,N is the density of states at the Fermi level of the bulk normal metal. Results for this density of states are shown in figure 4. The various panels (a)–(c) show examples for various Fermi surface mismatches. In (c), there are non-transmissive channels present in the normal layer (|k∥|>kF,S), leading to a large constant background density of states. In each panel, the curve for J=0 corresponds to the case of an non-spin-polarized SIN junction. There is a critical value Jcrit (independent of the Fermi surface mismatch and equal to ≈0.15EF in the figure) above which the system is in a state where no singlet correlations are present in the normal metal at the chemical potential (ε=0), and pure odd-frequency spin-triplet correlations remain. In this range, the density of states is enhanced above its bulk normal state value [91]. On either side of this critical value, the density of states decreases as function of J, however, stays always above NF,N for J>Jcrit. In the diffusive limit, a similar scenario arises, with a peak centred at zero energy in the density of states [90,91]. A zero-energy peak in the density of states has been suggested as a signature of odd-frequency spin-triplet pairing also in hybrid structures with an itinerant ferromagnet or a half-metallic ferromagnet coupled to a superconductor [94–96].
Figure 4.
Energy-resolved DOS in the normal metal for different values of the interface exchange field J. The energy scale is δ0=(t↑t↓εTh)k∥=0, with the Thouless energy  . The interlayer thickness is dI=2/kF,S and the interface potentials are V
↑=1.2EF, V
↓=V
↑+2J. The width of the normal layer is
. The interlayer thickness is dI=2/kF,S and the interface potentials are V
↑=1.2EF, V
↓=V
↑+2J. The width of the normal layer is  . The inset in the lower left corner of each panel illustrates the Fermi-surface mismatch: in (a) kF,N= 0.5kF,S, in (b) kF,N=kF,S and in (c) kF,N=10kF,S. Adapted from [91]. Copyright © 2010 American Physical Society. (Online version in colour.)
. The inset in the lower left corner of each panel illustrates the Fermi-surface mismatch: in (a) kF,N= 0.5kF,S, in (b) kF,N=kF,S and in (c) kF,N=10kF,S. Adapted from [91]. Copyright © 2010 American Physical Society. (Online version in colour.)
It is interesting to study the tunnelling limit, t↑≪1, t↓≪1, for small excitation energies ε≪min(εTh,Δ) and small spin-mixing angles ϑN, ϑS. Then  , i.e. νσ depends only on the spin mixing angle at the FI-N interface, which acts in this case as an (anisotropic) effective exchange field
, i.e. νσ depends only on the spin mixing angle at the FI-N interface, which acts in this case as an (anisotropic) effective exchange field  on the quasi-particles. For diffusive structures, a similar connection between an effective exchange field and the spin-mixing angle has been made [97]. The parameter
on the quasi-particles. For diffusive structures, a similar connection between an effective exchange field and the spin-mixing angle has been made [97]. The parameter 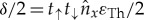 on the other hand acts as effective (anisotropic) gap function. For each direction
on the other hand acts as effective (anisotropic) gap function. For each direction 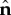 , the gap closes at a critical value of effective exchange field, b=δ/2, which happens for ϑN=t↑t↓.
, the gap closes at a critical value of effective exchange field, b=δ/2, which happens for ϑN=t↑t↓.
3. Andreev bound states in Josephson junctions with strongly spin-polarized ferromagnets
(a). Triplet rotation
Interfaces with strongly spin-polarized ferromagnets polarize the superconductor in proximity with it, as shown in the previous section. However, in order for superconducting correlations to penetrate the ferromagnet, it is necessary to turn the triplet correlations of the form ↑↓+↓↑ into equal spin pair correlations of the form ↑↑ and ↓↓. The reason is that correlations involving spin-up and spin-down electrons involve a phase factor kF↑−kF↓, which in strongly spin-polarized ferromagnets oscillates on a short length scale. This leads to destructive interference and allows to neglect such pair correlations on the superconducting coherence length scale [98].
The way to achieve this is to allow for a non-trivial magnetization profile at the interface between the ferromagnet and the superconductor. This can include, for example, strong spin-orbit coupling, or a misaligned (with respect to the bulk magnetization) magnetic moment in the interface region. For strongly spin-polarized ferromagnets, this has been suggested in [83,99–101]. For weakly spin-polarized ferromagnets, a theory was developed in 2001 involving a spiral inhomogeneity on the scale of the superconducting coherence length [102,103]. A multilayer arrangement was subsequently also suggested [104,105]. For various reviews of this field, see [98,106–118].
The idea is to rotate the triplet component, once created by spin-mixing phases in the S-F interfaces, into equal-spin triplet amplitudes with respect to the bulk magnetization of the ferromagnet [115]. This is achieved by writing a triplet component with respect to a new axis
| 3.1 |
where α and ϕ are polar and azimuthal angles of the new quantization axis, respectively. Then, if a thin FI layer oriented along the (α,ϕ) direction is inserted between the superconductor and the strongly spin-polarized ferromagnet with magnetization in z-direction, equal spin-correlations can penetrate with amplitudes  and
and 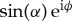 , respectively. These correlations are long-range and not affected by dephasing on the short length scale associated with kF↑−kF↓.
, respectively. These correlations are long-range and not affected by dephasing on the short length scale associated with kF↑−kF↓.
(b). Pair amplitudes at an S-FI-F interface
It is instructive to consider the scattering matrix of an S-FI-F interface between a superconductor and an itinerant ferromagnet, with a thin FI interlayer of width d, in the tunnelling limit. In this case, one can achieve an intuitive understanding of the various spin-mixing phases involved in the reflection and transmission processes. Denoting wavevector components perpendicular to the interface as k in the superconductor, q↑ and q↓ in the ferromagnet (I assume k∥ such that both spin directions are itinerant), and imaginary wavevectors iκ↑ and iκ↓ in the FI, the FI magnetic moment aligned in direction  , and a F magnetization aligned with the z-direction in spin space (α=0), matching of wave functions leads to a scattering matrix
, and a F magnetization aligned with the z-direction in spin space (α=0), matching of wave functions leads to a scattering matrix
 |
3.2 |
where ΦS,F are phase matrices which include the spin-mixing phase factors,  , Dα, Dβ are spin-rotation matrices, νS,F carry information about S-FI and FI-F wavevector mismatch, and
, Dα, Dβ are spin-rotation matrices, νS,F carry information about S-FI and FI-F wavevector mismatch, and  contains the tunnelling amplitudes including wavevector mismatch between S and F. In particular, if one denotes diagonal matrices with diagonal elements a, b by diag(a,b), then K=diag(κ↑/k,κ↓/k), Q=diag(q↑/k,q↓/k), the spin-rotation matrices
contains the tunnelling amplitudes including wavevector mismatch between S and F. In particular, if one denotes diagonal matrices with diagonal elements a, b by diag(a,b), then K=diag(κ↑/k,κ↓/k), Q=diag(q↑/k,q↓/k), the spin-rotation matrices  , Dα between the quantization axis in the FI and the z-axis, and the phase matrices ΦS,F are
, Dα between the quantization axis in the FI and the z-axis, and the phase matrices ΦS,F are
 |
3.3 |
and the spin-rotation matrix Dβ at the FI-F interface results from  with Z=diag(ζ↑,ζ↓). The angle β vanishes for α=0, and ζ↑ varies from κ↑/q↑ at α=0 to κ↓/q↑ at α=π, correspondingly ζ↓ varies from κ↓/q↓ to κ↑/q↓. Also, ΦS=(σ0−iK)/(σ0+iK), ΦF=(σ0−iZ)/(σ0+iZ),
with Z=diag(ζ↑,ζ↓). The angle β vanishes for α=0, and ζ↑ varies from κ↑/q↑ at α=0 to κ↓/q↑ at α=π, correspondingly ζ↓ varies from κ↓/q↓ to κ↑/q↓. Also, ΦS=(σ0−iK)/(σ0+iK), ΦF=(σ0−iZ)/(σ0+iZ),  ,
, 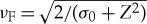 , and the tunnelling amplitude is
, and the tunnelling amplitude is  with V =diag(e−κ↑d,e−κ↓d) and the real-valued mismatch matrix
with V =diag(e−κ↑d,e−κ↓d) and the real-valued mismatch matrix  , of which the off-diagonal elements appear for α≠0,π only.
, of which the off-diagonal elements appear for α≠0,π only.
One can see from equation (3.2) that the spin-mixing phases, which appear in the reflection amplitudes, also enter the transmission amplitudes; in the tunnelling limit they contribute from each side of the interface one half [83]. Furthermore, one should notice that the interface is described by two spin-rotation matrices: one given by the misalignment of the FI magnetic moment with the z-axis in spin space, and one which is combined from the magnetization in F and the magnetic moment in FI. The latter appears because the wave function at the FI-F interface is delocalized over the FI-F interface region on the scale of the Fermi wavelength and experiences an averaged effective exchange field, which lies in the plane spanned by the z-axis and the direction of the FI magnetic moment (same  in equation (3.2)).
in equation (3.2)).
Pair correlation functions f are related to coherence functions by  , with f, γ and
, with f, γ and  2×2 matrices in spin space [119]. When both are small (near Tc or induced from a reservoir by tunnelling through a barrier), f and γ are proportional. Assuming an incoming singlet coherence function γ0 in S, the coherence functions reflected back into S and the ones transmitted to F can be calculated to linear order in the pair tunnelling amplitude according to
2×2 matrices in spin space [119]. When both are small (near Tc or induced from a reservoir by tunnelling through a barrier), f and γ are proportional. Assuming an incoming singlet coherence function γ0 in S, the coherence functions reflected back into S and the ones transmitted to F can be calculated to linear order in the pair tunnelling amplitude according to
 |
3.4 |
For the reflected amplitude in S, one obtains ( )
)
 |
3.5 |
which is just equation (2.12) rotated in spin-space by the spherical angles α and φ. For the equal-spin coherence functions (or pair amplitudes) in F follows up to leading order in the misalignment angles α, β (denoting  )
)
 |
3.6 |
and
 |
3.7 |
with C=4 e−(κ↑+κ↓)d(νS↑νS↓νF↑νF↓)κ↑κ↓/[k(q↑q↓)1/2]. The transmitted ↑↓ and ↓↑ coherence functions γ(F)out↑↓≈Cγ0e(i/2)(ϑS+ϑF) and γ(F)out↓↑≈−Cγ0 e−(i/2)(ϑS+ϑF) spatially oscillate with a wavevector eik∥r∥ e±i(q↑−q↓)x in F, and are suppressed (except in ballistic one-dimensional channels) due to dephasing after a short distance 1/|q↑−q↓| away from the interface. Importantly, from (3.6) and (3.7), it is visible that the equal-spin amplitudes acquire phases ±φ from the azimuthal angle in spin space, which play an important role in Josephson structures with half-metallic ferromagnets [98,100,101] and with strongly spin-polarized ferromagnets when two interfaces with different azimuthal angles φ1 and φ2 are involved [120,121].
The misalignment of FI with F also induces a spin-flip term during reflection on the ferromagnetic side of the interface, which creates in F for an incoming amplitude γ↑↑ a reflected amplitude  , and for an incoming amplitude γ↓↓ a reflected amplitude
, and for an incoming amplitude γ↓↓ a reflected amplitude 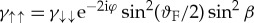 . In this case, twice the azimuthal angle ±φ enters.
. In this case, twice the azimuthal angle ±φ enters.
(c). Andreev bound states in S-FI-HM-FI’-S junctions
For an S-FI-HM interface with a half-metallic ferromagnet (HM) in which one spin-band (e.g. spin-down) is insulating and the other itinerant, equation (3.6) is modified to [100,101]
 |
3.8 |
The same equation also holds at an S-FI-F interface when the conserved wavevector k∥ is such that only one spin-projection on the magnetization axis is itinerant in F. For strongly spin-polarized F, this is an appreciable contribution to the transmitted pair correlations.
In order to describe Josephson structures, it is necessary to handle the spatial variation (and possibly phase dynamics) of both coherence amplitudes and superconducting order parameter (which are coupled to each other). For this, a powerful generalization of the 2×2 spin-matrix coherence functions has been introduced [92,119], based on previous work for spin-scalar functions in equilibrium [122,123] and non-equilibrium [58]. The generalized coherence functions γ(pF,R,ε,t) and  fulfill transport equations
fulfill transport equations
| 3.9 |
and
| 3.10 |
with pF a Fermi momentum vector, Σ and Δ include particle-hole diagonal and off-diagonal self-energies and mean fields (e.g. for impurity scattering; Δ includes the superconducting order parameter), and external potentials. The time-dependent case is included by the convolution over the internal energy-time variables in Wigner coordinate representation,
| 3.11 |
In the time-independent case, it reduces to a simple spin-matrix product. Furthermore, the particle-hole conjugation operation is defined by  . Particle-hole diagonal [
. Particle-hole diagonal [ and
and  ] and off-diagonal [
] and off-diagonal [ and
and  ] pair correlation functions (quasi-classical propagators) are obtained in terms of these coherence functions by solving the following algebraic (or in the time-dependent case, differential) equations
] pair correlation functions (quasi-classical propagators) are obtained in terms of these coherence functions by solving the following algebraic (or in the time-dependent case, differential) equations
| 3.12 |
The Fermi-momentum-resolved density of states is  , with NF the density of states in the normal state. A Fermi surface average yields the local density of states.
, with NF the density of states in the normal state. A Fermi surface average yields the local density of states.
In figure 5, an example for a fully self-consistent calculation of the spectrum of subgap Andreev states in an S-FI-HM-FI’-S junction is shown, obtained by solving equations (3.9) and (3.10) as well as the self-consistency equation for the superconducting order parameter in S. For details of the calculation and parameters, see [83,110]. The ferromagnetic insulating barriers FI and FI’ are taken identical in this calculation, and the spectra are shown at the half-metallic side of the S-FI-HM interface. The most prominent feature in these spectra is an Andreev quasi-particle band centred at zero energy [83,92,124]. Further bands at higher excitation energies are separated by gaps. The zero-energy band is a characteristic feature of the nature of superconducting correlations in the half metal: they are spin-triplet with a phase shift of ±π/2 with respect to the singlet correlations they are created from. The dispersion of the Andreev states with applied phase difference between the two S banks determine the direction of current carried by these states. This direction is indicated in the figure by + and − signs. In figure 5b,d for a selected phase difference, the Fermi-momentum-resolved spectra for positive and negative propagation direction are shown. These spectra, multiplied with the equilibrium distribution function (Fermi function) determine the positive and negative contributions of the Andreev bound states to the Josephson current in the system. Spectra in figure 5b,d are shown for normal impact direction (k∥=0). An integration over k∥ gives the local density of states.
Figure 5.
Density of Andreev states (DOS) at the HM side of the S-FI-HM interface in an S-FI-HM-FI’-S Josephson structure, as function of phase difference Δχ over the junction, for quasi-particles with normal impact (k∥=0), at T=0.05Tc. All states are fully spin-polarized. (a,c) Dispersion of the maxima of the DOS as function of phase difference. Regions with low DOS are white, regions of high DOS (bands of Andreev bound states) are shaded. The signs indicate the direction of the current carried by the Andreev states. (b,d) Spectra for a fixed phase difference, both for positive (full lines) and negative (dashed lines) propagation direction. In (a,b) is for a large misalignment between FI and HM, and (c,d) for a small misalignment. (b,d) Adapted from [83]. Copyright © 2003 by the American Physical Society. (Online version in colour.)
For the case that one can neglect the variation of the order parameter Δ in S, one can derive quite a number of analytical expressions [92,98,125]. Examples for integrated spectra are shown in figure 6, taken from Eschrig [92]. In figure 6a, the well-known spectrum of de Gennes–Saint-James bound states is seen for an S-N-S junction [126], showing a dispersion with phase bias Δχ between the two superconductors. At Δχ=π, a zero energy bound state is present, which is a topological feature of the particular Andreev differential equations describing this system, for real-valued order parameters that change sign when going from the left S reservoir to the right S reservoir. The origin is the same as for the midgap state in polyacetylene [127], which is governed by similar differential equations. Such midgap states have been studied in more general context by Jackiw & Rebbi [128] and ultimately have their deep mathematical foundation in the Atiyah–Patodi–Singer index theorem [129]. For the S-FI-HM-FI-S junction, shown in figure 6b–d, the prominent feature for all values of Δχ is the band of Andreev states centred around zero energy. The width W of this low-energy Andreev band depends on the parameter 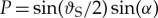 and can be calculated for the limit of short junctions (L→0) for t=1 as [92]
and can be calculated for the limit of short junctions (L→0) for t=1 as [92]
| 3.13 |
In the limit P→0, this gives W(Δχ=0)=2|Δ| and  . Note that compared to the S-N-S junction, the low-energy features disperse in opposite direction when increasing Δχ for the S-FI-HM-FI-S junction. This means that the current flows in opposite direction, and typically a π-junction is realized for identical interfaces. If the azimuthal interface misalignment angles φ differ by π in FI and FI’, then this phase would add to Δχ according to equation (3.8) and a zero-junction would be realized. In the general case, a ϕ-junction appears, both for ballistic and diffusive structures [98,100,101,130].
. Note that compared to the S-N-S junction, the low-energy features disperse in opposite direction when increasing Δχ for the S-FI-HM-FI-S junction. This means that the current flows in opposite direction, and typically a π-junction is realized for identical interfaces. If the azimuthal interface misalignment angles φ differ by π in FI and FI’, then this phase would add to Δχ according to equation (3.8) and a zero-junction would be realized. In the general case, a ϕ-junction appears, both for ballistic and diffusive structures [98,100,101,130].
Figure 6.
Local density of states in the centre of a current biased high-transmissive symmetric Josephson junction for (a) an S-N-S junction and (b–d) an S-FI-HM-FI-S junction. In (a,b) the phase difference Δχ over the junction is varied from 0 to π. In (c,d) the length of the junction is varied for a zero-junction and a π-junction. The temperature is T=0.1Tc, the coherence length of the half metal 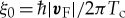 . The FI misalignment angle is α=π/2. The transmission parameter t and spin-mixing angle ϑS depend on the impact angle Ψn measured from the surface normal; this is modelled here by
. The FI misalignment angle is α=π/2. The transmission parameter t and spin-mixing angle ϑS depend on the impact angle Ψn measured from the surface normal; this is modelled here by  and
and  . Adapted from [92]. Copyright © 2009 American Physical Society. (Online version in colour.)
. Adapted from [92]. Copyright © 2009 American Physical Society. (Online version in colour.)
(d). Spin torque in S-FI-N-FI’-S’ structures
Andreev states play also an important role in the non-equilibrium spin torque and in the spin-transfer torque in S-F structures [131–134]. Zhao and Sauls found that in the ballistic limit the equilibrium torque is related to the spectrum of spin-polarized Andreev bound states, while the AC component, for small bias voltages, is determined by the nearly adiabatic dynamics of the Andreev bound states [135,136]. The equilibrium spin-transfer torque τeq in an S-FI-N-FI’-S’ structure is related to the Josephson current Ie, the phase difference between S and S’, Δχ, and the angle Δα between FI and FI’, by [137]
| 3.14 |
Similarly, as the dispersion of the Andreev bound states with superconducting phase difference Δχ yields the contribution of the bound state to the Josephson current, the dispersion of the Andreev states with Δα yields the contribution of this state to the spin current for spin polarization in direction of the spin torque. The DC spin current shows subharmonic gap structure due to multiple Andreev reflections (MAR), similar as for the charge current in voltage biased Josephson junctions [138,139]. For high transmission junctions, the main contribution to the DC spin current comes from consecutive spin rotations according to equation (2.6) when electrons and holes undergo MAR [136] (figure 7a).
Figure 7.
(a) Subgap excitation undergo multiple Andreev reflections (MAR), thus gaining multiples of the voltage eV. Whereas charge is transferred to Cooper pairs during each Andreev reflection, spin can only escape the N region at energies above the gap. During each reflection particles and holes experience, a spin rotation due to spin-dependent phase shifts. (b) Time evolution of the spin-transfer torque on FI′ in the adiabatic limit, for α=π/2 and two values of spin-dependent phase shifts, at zero temperature. Adapted from [136]. Copyright © 2008 American Physical Society. (Online version in colour.)
Turning to AC effects, for a voltage eV ≪Δ the time evolution of spin-transfer torque is governed by the nearly adiabatic dynamics of the Andreev bound states. However, the dynamics of the bound state spectrum leads to non-equilibrium population of the Andreev bound states, for which reason the spin-transfer torque does not assume its instantaneous equilibrium value [136]. For the occupation to change, the bound state energy must evolve in time to the continuum gap edges, where it can rapidly equilibrate with the quasi-particles, similar as in the adiabatic limit of AC Josephson junctions [140]. An example of the adiabatic time evolution of the spin torque is shown in figure 7b.
The effect of rough interfaces and of spin-flip scattering on spin-transfer torque in the presence of Andreev reflections has been discussed by Wang et al. [141]. For diffusive structures, see [142]. Magnetization dynamics has been also addressed recently [143–145].
Andreev sidebands in a system with two superconducting leads coupled by a precessing spin proved important to study spin-transfer torques acting on the precessing spin [146]. Spin-polarized Shapiro steps were studied in [147].
4. Andreev spectroscopy in F-S and F-S-F′ structures
Andreev point contact spectra in S-F structures are modified with respect to those in S-N structures due to spin-filtering effects and the spin-sensitivity of Andreev scattering [99,148–154]. Spin-dependent phase shifts also crucially affect Andreev point contact spectra [87,155–160]. Point contacts have lateral dimensions much smaller than the superconducting coherence lengths of the materials on either side of the contact. Typically, a voltage will be applied over the contact, which makes it necessary to study in addition to the coherence amplitudes γ and  also distribution functions. I follow the definition in [58,119], where 2×2 distribution function spin-matrices x and
also distribution functions. I follow the definition in [58,119], where 2×2 distribution function spin-matrices x and  for particles and holes are introduced which obey a transport equation
for particles and holes are introduced which obey a transport equation
| 4.1 |
and
| 4.2 |
The distribution functions matrices are hermitian, x=x† and  , and depend on the arguments pF,R,ε,t. The right-hand sides of equation (4.1) and (4.2) contain collision terms (see [119] for details), which vanish in ballistic structures. In general, these distribution functions can be related to quasi-classical Keldysh propagators
, and depend on the arguments pF,R,ε,t. The right-hand sides of equation (4.1) and (4.2) contain collision terms (see [119] for details), which vanish in ballistic structures. In general, these distribution functions can be related to quasi-classical Keldysh propagators  and
and  . The Fermi distribution functions for particles, fp, and holes, fh, are related to x,
. The Fermi distribution functions for particles, fp, and holes, fh, are related to x,  in the normal state by fp=(σ0−x)/2 and
in the normal state by fp=(σ0−x)/2 and  .
.
(a). Andreev processes in point contact geometry
In this section, I consider point contacts of dimensions large compared with the Fermi wavelength and small compared with the superconducting coherence lengths. In this case, the wavevector k∥ parallel to the contact interface is approximately conserved. The current on the ferromagnetic side of a point contact, being directed along the interface normal, can be decomposed into
| 4.3 |
where the various terms are the incoming current, II, the normally reflected part, IR and the Andreev reflected part, IAR. The sign convention here is such that a positive current denotes a current into the superconductor. Thus, in the normal state the current I is positive when the voltage in the ferromagnet is positive. The various currents can be expressed as
 |
4.4 |
where e=−|e| is the charge of the electron,  is the contact area and
is the contact area and 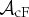 is the projection of the Fermi surfaces in the ferromagnet on the contact plane. For each value k∥, there will be a number of (spin-polarized) Fermi surface sheets involved in the interface scattering (in the simplest case spin-up and spin-down, or only spin-up), and the dimension and structure of the scattering matrix will depend on how many Fermi surface sheets are involved. The sum over α and β runs over those Fermi surface sheets 1,…,ν for each given value of k∥. In the superconductor, I assume for simplicity that only one Fermi surface sheet is involved for each k∥. The reflection and transmission amplitudes for each k∥ are related to the scattering matrix as
is the projection of the Fermi surfaces in the ferromagnet on the contact plane. For each value k∥, there will be a number of (spin-polarized) Fermi surface sheets involved in the interface scattering (in the simplest case spin-up and spin-down, or only spin-up), and the dimension and structure of the scattering matrix will depend on how many Fermi surface sheets are involved. The sum over α and β runs over those Fermi surface sheets 1,…,ν for each given value of k∥. In the superconductor, I assume for simplicity that only one Fermi surface sheet is involved for each k∥. The reflection and transmission amplitudes for each k∥ are related to the scattering matrix as
 |
4.5 |
where directions 1 and 2 refer to the superconductor, and 3 and 4 to the ferromagnet. R12 is a 2×2 spin matrix, R34 is a ν×ν matrix with elements Rαβ, T14 is a 2×ν matrix with elements T1β, and T32 is a ν×2 matrix with elements Tα2. Note that the theory presented here does not rely on any modelling of interface potentials or exchange fields, nor does it employ any free-electron dispersions in the conducting leads. It rather works with the fully renormalized interface scattering matrix (4.5) as well as with the fully renormalized Fermi surface data. The spectral current densities jX are given by (I restrict formulae here and below to stationary situations)
| 4.6 |
and
| 4.7 |
where δxβ and  are the differences between the distribution functions in the ferromagnet and in the superconductor, respectively. If there is no spin-accumulation present, they are independent of the index β and given by
are the differences between the distribution functions in the ferromagnet and in the superconductor, respectively. If there is no spin-accumulation present, they are independent of the index β and given by
| 4.8 |
with TS the temperature in the superconductor. Equations (4.6) and (4.7) are valid for general normal-state scattering matrices S, and can be applied to non-collinear magnetic structures. For the case that all reflection and transmission amplitudes are spin-diagonal, considering an isotropic singlet superconductor with order parameter Δ=Δ0iσ2, and assuming on the superconducting side of the interface a spin-mixing angle ϑ, these expressions are explicitly given by
| 4.9 |
and
| 4.10 |
with γ0=−|Δ0|/(ε+iΩ), 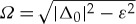 ,
,  , and the energy ε is assumed to have an infinitesimally small positive imaginary part. Andreev resonances arise for energies fulfilling 1=γ0(ε)2r↑r↓ e±iϑ (in agreement with the discussion in §2b for d=0).
, and the energy ε is assumed to have an infinitesimally small positive imaginary part. Andreev resonances arise for energies fulfilling 1=γ0(ε)2r↑r↓ e±iϑ (in agreement with the discussion in §2b for d=0).
On the other hand, for half-metallic ferromagnets the Andreev reflection contribution is zero in collinear magnetic structures. In non-collinear structures, however, the process of spin-flip Andreev reflection takes place, introduced in [155], and illustrated there in figure 11. Spin-flip Andreev reflection is the only process providing particle-hole coherence in a half-metallic ferromagnet. Such structures are described by the theory developed in appendix C of Eschrig [92]. Application of this theory to experiment on CrO2 is provided in [87,159]. A generalization to strongly spin-polarized ferromagnets with two itinerant bands is given in [155] with application to experiment in [156].
Figure 11.
Andreev bound states in an F-S-F structure of the type shown in figure 9. (a) ΔN≡(N↑−N↓) as function of ε and ϑR at a position in S midway between the contacts, for L=2ξ0 (with the coherence length of the superconductor  ) and ϑL=0.7π. An avoided crossing appears for equally spin-polarized Andreev states, which is absent for opposite polarization. (b) Dependence on L/ξ0 for fixed ϑR=ϑL=0.7π. (c–f): ΔN as function of ε and x for L=2ξ0 and ϑL=0.7π, and (c) ϑR=0.7π (d) ϑR=0.5π (e) ϑR=−0.6π (f) ϑR=−0.7π. At the avoided crossing, all bound states have equal weight at both interfaces. In all other cases, the bound states for fixed spin projection are localized at one interface only. In all panels, (r↑r↓)L=(r↑r↓)R=0.95. (Online version in colour.)
) and ϑL=0.7π. An avoided crossing appears for equally spin-polarized Andreev states, which is absent for opposite polarization. (b) Dependence on L/ξ0 for fixed ϑR=ϑL=0.7π. (c–f): ΔN as function of ε and x for L=2ξ0 and ϑL=0.7π, and (c) ϑR=0.7π (d) ϑR=0.5π (e) ϑR=−0.6π (f) ϑR=−0.7π. At the avoided crossing, all bound states have equal weight at both interfaces. In all other cases, the bound states for fixed spin projection are localized at one interface only. In all panels, (r↑r↓)L=(r↑r↓)R=0.95. (Online version in colour.)
In figure 8, selected results are shown. In figure 8a,b, it is demonstrated that the spin-mixing angle can acquire large values if a smooth spatial interface profile is used instead of an atomically clean interface. Correspondingly, in figure 8c Andreev resonances are more pronounced for smoother interfaces. In figure 8d,e, a comparison of the model by Mazin et al. [152] for various spin polarizations P with the spin-mixing model for P=100% and various spin-mixing angles ϑ shows that the two can be experimentally differentiated by studying the low-temperature behaviour [87].
Figure 8.
(a) Shape function of the (spin-averaged) interface barrier potential. A shape parameter σ=0…0.7 λF increases for increasing smoothness. (b) Spin-mixing angle ϑS as a function of |k∥| for the shape functions in (a). ϑS increases with increasing σ. (c) The differential conductance of an F-FI-S structure with various degrees of smoothness if the FI barrier, at T=0; σ increases from back to front in steps of 0.1 λF. (d,e) Temperature dependence of the zero-voltage conductance of an HM-FI-S point contact as predicted by (d) the modified BTK model [152] and (e) the spin-active interface model [92,155]. Adapted from [155,87]. Copyright © 2010 American Physical Society. (Online version in colour.)
In an experiment by Visani et al. [161] geometric resonances (Tomasch resonances and Rowell–McMillan resonances) in the conductance across a La0.7Ca0.3Mn3O/YBa2Cu3O7 interface were studied, demonstrating long-range propagation of superconducting correlations across the half metal La0.7Ca0.3Mn3O. The effect is interpreted in terms of spin-flip Andreev reflection (or, as named by the authors of [161], ‘equal-spin Andreev reflection’).
Spin-dependent scattering phases qualitatively affect the zero- and finite-frequency current noise in S-F point contacts [162,163]. It was found that for weak transparency noise steps appear at frequencies or voltages determined directly by the spin dependence of scattering phase shifts.
(b). Andreev bound states in non-local geometry
A particular interesting case is that of two F-S point contacts separated by a distance L of the order of the superconducting coherence length. This is effectively an F-S-F’ system, or if barriers are included, an F-FI-S-FI′-F′ system. In this case, for a ballistic superconductor, one must consider separately trajectories connecting the two contacts [164]. Along these trajectories the distribution function is out of equilibrium, and equations (4.1) and (4.2) must be solved. In addition, the coherence functions at these trajectories experience both ferromagnetic contacts, and are consequently different from the homogeneous solutions γ0,  of all other quasi-particle trajectories.
of all other quasi-particle trajectories.
The current on the ferromagnetic side of one particular interface (positive in direction of the superconductor), can be decomposed in an exact way,
| 4.11 |
where the various terms are the incoming current, II, the normally reflected part, IR, the Andreev reflected part, IAR and the two non-local contributions due to elastic co-tunnelling, IEC and crossed Andreev reflection, ICAR.
There will be contributions from trajectories in the superconductor which do not connect the two contacts. These will be described by equations (4.6) and (4.7) above. Here, I will concentrate on the non-local contributions, which arise from the particular trajectories connecting the two contacts. Assuming the area of each contact much smaller than the superconducting coherence length (however, larger than the Fermi wavelength, such that the momentum component parallel to the contact interfaces are approximately conserved), one can identify all trajectories connecting the two contacts, treating only one and scaling the result with the contact area. The solid angle from a point at the first contact to the area  of the second contact is given by
of the second contact is given by  , where
, where  is the projection of the area of the second contact to the plane perpendicular to the line 2,2′ which connects the contacts (see figure 9 for the notation).
is the projection of the area of the second contact to the plane perpendicular to the line 2,2′ which connects the contacts (see figure 9 for the notation).
Figure 9.
Illustration of notation used in text. For brevity of notation, I sometimes omit labels 3 and 4, implying that α then means 3α and β means 4β. For example, in (b), the ferromagnet has two-spin Fermi surfaces (red and blue), labelled by α∈{3↑,3↓} and β∈{4↑,4↓}. The superconductor’s Fermi surface is drawn in green.
Using the conservation of k∥, and that consequently  (where
(where  is the contact surface normal), one can express the currents as
is the contact surface normal), one can express the currents as
 |
4.12 |
where pF2 is the particular Fermi momentum in the superconductor corresponding to a Fermi velocity in direction of the line 2,2′ (I assume for simplicity that only one such Fermi momentum exists), and d2S/dΩ is the differential fraction of the Fermi surface of the superconductor per solid angle Ω in direction of the Fermi velocity vF2 that connects the two contacts. Note that d2S/dΩ is the same at both contacts for superconductors with inversion symmetry, as then this quantity is equal at pF2 and −pF2. Reversed directions are denoted by an overline:  , etc. Let us introduce scattering matrices S(12;34) as well as
, etc. Let us introduce scattering matrices S(12;34) as well as  at the left interface, the latter being equal to S(12;34) for materials with centrosymmetric symmetry groups, which I consider here. Analogously, for the right interface let us introduce the scattering matrices
at the left interface, the latter being equal to S(12;34) for materials with centrosymmetric symmetry groups, which I consider here. Analogously, for the right interface let us introduce the scattering matrices  . The scattering matrices for holes are related to the scattering matrices for particles by
. The scattering matrices for holes are related to the scattering matrices for particles by 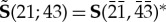 etc. One obtains for this case
etc. One obtains for this case
| 4.13 |
| 4.14 |
 |
4.15 |
| 4.16 |
| 4.17 |
where the vertex corrections due to multiple Andreev processes are 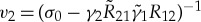 and
and  . For unitary order parameters (
. For unitary order parameters (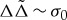 ), let us define
), let us define 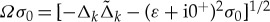 as well as γ=−Δ/(ε+iΩ),
as well as γ=−Δ/(ε+iΩ),  . Using the amplitudes
. Using the amplitudes
| 4.18 |
and denoting with L the distance between 2 and 2′,
 |
4.19 |
and
 |
4.20 |
with 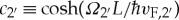 and
and 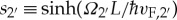 . For the distribution functions, one obtains for the two leads
. For the distribution functions, one obtains for the two leads
| 4.21 |
and
| 4.22 |
Here, TS is the temperature in the superconductor, T and V are temperature and voltage in the left lead, and T′ and V ′ are temperature and voltage in the right lead. The voltages are measured with respect to the superconductor. The expressions appearing in equations (4.13)–(4.17) have an intuitive interpretation, and selected processes are illustrated in figure 10. These terms involve propagation of particles or holes, represented as full lines and dashed lines in the figure. Certain processes involve conversions between particles and holes, accompanied by the creation or destruction of a Cooper pair (loops in the figure), and correspond to the factors  , γ1′,
, γ1′,  and
and  in (4.14)–(4.17). Propagation of particles or holes between the left and right interface is represented in these equations by the factors u22′ and
in (4.14)–(4.17). Propagation of particles or holes between the left and right interface is represented in these equations by the factors u22′ and  . Vertex corrections v2 and
. Vertex corrections v2 and  correspond to multiple Andreev reflections at either interface. The factors γ2 and
correspond to multiple Andreev reflections at either interface. The factors γ2 and  combine propagation between the two interfaces with Andreev reflections at the other interface.
combine propagation between the two interfaces with Andreev reflections at the other interface.
Figure 10.
Illustration of selected processes contributing to expressions (4.13)–(4.17). Andreev reflections are denoted as loops, turning particles (p, full lines) into holes (h, dashed lines) or vice versa. (a,b) Contributions to the reflection components, equation (4.14); (c,d) Contributions to the Andreev reflection components, equation (4.15); (e,f) contributions to the coherent electron transfer components, equation (4.16); (g,h) contributions to the crossed Andreev reflection components, equation (4.17). (Online version in colour.)
As an example, for an isotropic singlet superconductor and collinear arrangement of the magnetization directions, one obtains
| 4.23 |
| 4.24 |
| 4.25 |
| 4.26 |
where I defined (with s≡s2′ and c≡c2′)
| 4.27 |
and
 |
4.28 |
Early studies of non-local transport in F-S-F structures include the study of Mélin & Feinberg [165]. In [88], the non-local conductance was explained in terms of the processes discussed above for an F-S-F structure with strong spin-polarization. Andreev bound states appear on both ferromagnet–superconductor interfaces, which decay trough the superconductor towards the opposite contact. Parallel and antiparallel alignment of the magnetizations lead to qualitatively different Andreev spectra. The non-local processes have a natural explanation in terms of overlapping spin-polarized Andreev states. The density of states for the trajectory connecting the two contacts is obtained from
| 4.29 |
and for N↓ the same expression holds with + and − interchanged. In figure 11, I show an example of such a set-up. As can be seen, avoided crossings of Andreev bound states with equal spin polarization play an important role in such systems. At the avoided crossing, the bound states have equal weight at both interfaces. This contrasts the case when bound states have opposite spin polarization, where no avoided crossings appear, and the case when the two S-F interfaces have markedly different spin-dependent phase shifts, in which case bound states do not overlap and stay localized at one of the two interfaces only. The spin-polarization and weight of the bound states at energies εb and −εb determine the magnitude of the non-local currents due to crossed Andreev reflection and elastic co-tunnelling. A detailed discussion of how the weights, transmission probabilities, and bound-state geometries influence CAR and EC processes is given in [88]. In diffusive S-F systems, a theory for non-local transport was developed in [166].
Equations (4.23)–(4.26) have been applied to the study of thermoelectric effects in non-local set-ups [167,168]. The contributions to the energy current are obtained as
| 4.30 |
where the respective contributions are given by analogous equations as in equations (4.12)–(4.17), however, with replacing the charge e by energy ε. Spin-dependent interface scattering phases in combination with spin filtering leads to giant thermoelectric effects in F-S-F devices [167,169].
There have been a number of experimental studies of non-local transport in S-F hybrid structures (e.g. [73,170–172]). Colci et al. investigate S-FF-S junctions with two parallel running wires [173]. Recent experiments show a non-local inverse proximity effect in an (F-N-F’)-S-N structure [174]. The inverse proximity effect transfers magnetization from the ferromagnet into the superconductor or across a superconductor. For strongly spin-polarized systems, this occurs as a result of spin-mixing phases [100,101,121]. A giant thermoelectric effect was experimentally observed by Kolenda et al. [175]. A combination of non-local effects in S-F structures with non-equilibrium Andreev interferometer geometries, in analogy to experiments in S-N structures [176,177], seems to be another exciting avenue for future applications [178].
5. Generalized Andreev equations
In this section, I discuss the physical interpretation of the coherence functions. To this end, I present a generalized set of Andreev equations which is equivalent to equations (3.9) and (3.10). Let us define for each pair of Fermi momenta pF, −pF and corresponding Fermi velocities vF(pF), vF(−pF)=−vF(pF) a pair of mutually conjugated trajectories
| 5.1 |
Using  , let us define the following differential operators:
, let us define the following differential operators:
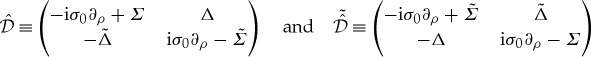 |
5.2 |
which fulfil  (and σ0 is the unit spin matrix). Let us also define the adjoint operator
(and σ0 is the unit spin matrix). Let us also define the adjoint operator  . For a fixed conjugated trajectory pair, the set of generalized Andreev equations (retarded and advanced) is,
. For a fixed conjugated trajectory pair, the set of generalized Andreev equations (retarded and advanced) is,
 |
5.3 |
and
 |
5.4 |
where the boundary conditions at ρ=ρ0 and ρ=ρ1 for the solutions fulfill the restrictions shown on the right-hand side of the equations. Then the relation between the Andreev amplitudes u, v,  and
and  and the coherence amplitudes γ and
and the coherence amplitudes γ and  is given along the entire trajectories by [119]
is given along the entire trajectories by [119]
| 5.5 |
with γR≡γ,  ,
,  ,
,  . It is easy to show that the following conservation law along the trajectory holds
. It is easy to show that the following conservation law along the trajectory holds
 |
5.6 |
Thus, the matrix inside the curly brackets is given by its value at one point on the trajectory. The off-diagonal elements are zero due to the conditions in equation (5.3) for ρ0 and ρ1, leading to  and
and  along the entire trajectory. The diagonal components ∂ρ[(uA)†° uR−(vA)†° vR]=0 and
along the entire trajectory. The diagonal components ∂ρ[(uA)†° uR−(vA)†° vR]=0 and  translate into
translate into  and
and  . In particular, if at one point
. In particular, if at one point  or
or 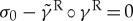 (signifying Andreev bound states), then this property is conserved along the entire trajectory.
(signifying Andreev bound states), then this property is conserved along the entire trajectory.
If one writes equation (5.3) formally as  , then the conjugated equation
, then the conjugated equation  holds with
holds with  , which leads, however, to a system identical to equation (5.3). The adjoint equation
, which leads, however, to a system identical to equation (5.3). The adjoint equation  defines adjoined Andreev amplitudes (left eigenvectors)
defines adjoined Andreev amplitudes (left eigenvectors)  ,
, 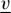 ,
, 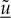 and
and  . These are, however, equivalent to the advanced eigenvectors in equation (5.4).
. These are, however, equivalent to the advanced eigenvectors in equation (5.4).
6. Conclusion
I have presented theoretical tools for studying Andreev reflection phenomena and Andreev bound states in superconductor–ferromagnet hybrid structures. Concentrating on ballistic heterostructures with strong spin-polarization, I have formulated theories for point contact spectroscopy and for non-local transport, as well as for Andreev states in Josephson structures in terms of coherence functions and distribution functions. The connection to coherence amplitudes appearing in the solutions of Andreev equations has been made explicit. The formulae for non-local transport have been given in a general form, allowing for non-collinear geometries, and using the normal-state scattering matrix as input.
Acknowledgements
I acknowledge the hospitality and the financial support from the Lars Onsager Award committee during my stay at the Norwegian University of Science and Technology, as well as stimulating discussions within the Hubbard Theory Consortium.
Data accessibility
All data can be obtained from the author.
Competing interests
I declare I have no competing interests.
Funding
This work is supported by the Engineering and Physical Science Research Council (EPSRC grant no. EP/J010618/1).
References
- 1.Cooper LN. 1956. Bound electron pairs in a degenerate Fermi gas. Phys. Rev. 104, 1189–1190. ( 10.1103/PhysRev.104.1189) [DOI] [Google Scholar]
- 2.Bardeen J, Cooper LN, Schrieffer JR. 1957. Theory of superconductivity. Phys. Rev. 108, 1175–1204. ( 10.1103/PhysRev.108.1175) [DOI] [Google Scholar]
- 3.Glover RE III, Tinkham M. 1956. Transmission of superconducting films at millimeter-microwave and far infrared frequencies. Phys. Rev. 104, 844–845. ( 10.1103/PhysRev.104.844) [DOI] [Google Scholar]
- 4.Tinkham M. 1956. Energy gap interpretation of experiments on infrared transmission through superconducting films. Phys. Rev. 104, 845–846. ( 10.1103/PhysRev.104.845) [DOI] [Google Scholar]
- 5.Giaever I. 1960. Energy gap in superconductors measured by electron tunneling. Phys. Rev. Lett. 5, 147–148. ( 10.1103/PhysRevLett.5.147) [DOI] [Google Scholar]
- 6.Eschrig M. 2006. The effect of collective spin-1 excitations on electronic spectra in high-Tc superconductors. Adv. Phys. 55, 47–183. ( 10.1080/00018730600645636) [DOI] [Google Scholar]
-
7.Migdal AB.
1958.
 . Zh. Eksp. Teor. Fiz.
34, 1438–1446. [In Russian.] [Google Scholar]
. Zh. Eksp. Teor. Fiz.
34, 1438–1446. [In Russian.] [Google Scholar] - 8.Migdal AB. 1958. Interaction between electrons and lattice vibrations in a normal metal. Sov. Phys. JETP 7, 996–1001. [English transl.] [Google Scholar]
-
9.Eliashberg G.
1960.
 . Zh. Eksp. Teor. Fiz.
38, 966–974. [In Russian.] [Google Scholar]
. Zh. Eksp. Teor. Fiz.
38, 966–974. [In Russian.] [Google Scholar] - 10.Eliashberg G. 1960. Interactions between electrons and lattice vibrations in a superconductor. Sov. Phys. JETP 11, 696–702. [English transl.] [Google Scholar]
- 11.Scalapino DJ, Schrieffer JR, Wilkins JW. 1966. Strong-coupling superconductivity. I. Phys. Rev. 148, 263–279. ( 10.1103/PhysRev.148.263) [DOI] [Google Scholar]
- 12.Giaever I Jr., Hart HR, Megerle K. 1962. Tunneling into superconductors at temperatures below 1°K. Phys. Rev. 126, 941–948. ( 10.1103/PhysRev.126.941) [DOI] [Google Scholar]
- 13.McMillan WL, Rowell JM. 1965. Lead phonon spectrum calculated from superconducting density of states. Phys. Rev. Lett. 14, 108–112. ( 10.1103/PhysRevLett.14.108) [DOI] [Google Scholar]
- 14.Tomasch WJ. 1965. Geometrical resonance in the tunneling characteristics of superconducting Pb. Phys. Rev. Lett. 15, 672–675. ( 10.1103/PhysRevLett.15.672) [DOI] [Google Scholar]
- 15.McMillan WL, Anderson PW. 1966. Theory of geometrical resonances in the tunneling characteristics of thick films of superconductors. Phys. Rev. Lett. 16, 85–87. ( 10.1103/PhysRevLett.16.85) [DOI] [Google Scholar]
- 16.Wolfram T. 1968. Tomasch oscillations in the density of states of superconducting films. Phys. Rev. 170, 481–490. ( 10.1103/PhysRev.170.481) [DOI] [Google Scholar]
- 17.Rowell JM, McMillan WL. 1966. Electron interference in a normal metal induced by superconducting contracts. Phys. Rev. Lett. 16, 453–456. ( 10.1103/PhysRevLett.16.453) [DOI] [Google Scholar]
- 18.Nédellec P, Guyon E. 1971. Effect of the detailed variation of pair potential on the ‘Tomasch’ effect. Solid State Comm. 9, 113–116. ( 10.1016/0038-1098(71)90267-5) [DOI] [Google Scholar]
- 19.de Gennes PG, Saint-James D. 1963. Elementary excitations in the vicinity of a normal metal-superconducting metal contact. Phys. Lett. 4, 151–152. ( 10.1016/0031-9163(63)90148-3) [DOI] [Google Scholar]
- 20.Saint-James D. 1964. Excitations élémentaires au voisinage de la surface de séparation d’un métal normal et d’un métal supraconducteur (Elementary excitations in the vicinity of the surface separating a normal metal and a superconducting metal). J. Phys. (Paris) 25, 899–905. [In French.] See https://hal.archives-ouvertes.fr/jpa-00205891. [Google Scholar]
- 21.Rowell JM. 1973. Tunneling observation of bound states in a normal metal-superconductor sandwich. Phys. Rev. Lett. 30, 167–170. ( 10.1103/PhysRevLett.30.167) [DOI] [Google Scholar]
- 22.Bellanger D, Klein J, Léger A, Belin M, Defourneau D. 1973. Tunneling measurements of electron interference effects in Cu-Pb sandwiches. Phys. Lett. A 42, 459–460. ( 10.1016/0375-9601(73)90753-6) [DOI] [Google Scholar]
-
23.Andreev AF.
1964.
 . Zh. Eksp. Teor. Fiz.
46, 1823–1828. [In Russian.] [Google Scholar]
. Zh. Eksp. Teor. Fiz.
46, 1823–1828. [In Russian.] [Google Scholar] - 24.Andreev AF. 1964. Thermal conductivity of the intermediate state of superconductors. Sov. Phys. JETP 19, 1228–1231.[English transl.] [Google Scholar]
- 25.Klapwijk TM, Blonder GE, Tinkham M. 1982. Explanation of subharmonic energy gap structure in superconducting contacts. Phys. B C 109, 1657–1664. ( 10.1016/0378-4363(82)90528-9) [DOI] [Google Scholar]
- 26.Cuevas JC, Hammer J, Kopu J, Viljas JK, Eschrig M. 2006. Proximity effect and multiple Andreev reflections in diffusive superconductor-normal-metal-superconductor junctions. Phys. Rev. B 73, 184505 (1–6) ( 10.1103/PhysRevB.73.184505) [DOI] [Google Scholar]
- 27.Blonder GE, Tinkham M, Klapwijk TM. 1982. Transition from metallic to tunneling regimes in superconducting microconstrictions: excess current, charge imbalance, and supercurrent conversion. Phys. Rev. B 25, 4515–4532. ( 10.1103/PhysRevB.25.4515) [DOI] [Google Scholar]
- 28.Beenakker CWJ. 1992. Quantum transport in semiconductor-superconductor microjunctions. Phys. Rev. B 46, 12 841–12 844 (R). ( 10.1103/PhysRevB.46.12841) [DOI] [PubMed] [Google Scholar]
- 29.de Gennes PG, Guyon E. 1963. Superconductivity in ‘normal’ metals. Phys. Lett. 3, 168–169. ( 10.1016/0031-9163(63)90401-3) [DOI] [Google Scholar]
- 30.Werthamer NR. 1963. Theory of the superconducting transition temperature and energy gap function of superposed metal films. Phys. Rev. 132, 2440–2445. ( 10.1103/PhysRev.132.2440) [DOI] [Google Scholar]
-
31.Abrikosov AA, Gor’kov LP.
1958.
K
 . Zh. Eksp. Teor. Fiz.
35, 1558–1571. [In Russian.] [Google Scholar]
. Zh. Eksp. Teor. Fiz.
35, 1558–1571. [In Russian.] [Google Scholar] - 32.Abrikosov AA, Gor’kov LP. 1959. On the theory of superconducting alloys, I. The electrodynamics of alloys at absolute zero. Sov. Phys. JETP 8, 1090–1098. [English transl.] [Google Scholar]
-
33.Abrikosov AA, Gor’kov LP.
1959.
 . Zh. Eksp. Teor. Fiz.
36, 319–320. [In Russian.] [Google Scholar]
. Zh. Eksp. Teor. Fiz.
36, 319–320. [In Russian.] [Google Scholar] - 34.Abrikosov AA, Gor’kov LP. 1959. Superconducting alloys at finite temperatures. Sov. Phys. JETP 9, 220–221. [English transl.] [Google Scholar]
- 35.Anderson PW. 1959. Theory of dirty superconductors. J. Phys. Chem. Solids 11, 26–30. ( 10.1016/0022-3697(59)90036-8) [DOI] [Google Scholar]
-
36.Finkel’shtein AM.
1987.
 . Pis’ma Zh. Eksp. Teor. Fiz.
45, 37–40. [In Russian.] [Google Scholar]
. Pis’ma Zh. Eksp. Teor. Fiz.
45, 37–40. [In Russian.] [Google Scholar] - 37.Finkel’shtein AM. 1987. Superconducting transition temperature in amorphous films. JETP Lett. 45, 46–49. [English transl.] [Google Scholar]
-
38.Lifshitz IM.
1964.

 . Uspekhi Fiz. Nauk
83, 617–663. [In Russian.] ( 10.3367/UFNr.0083.196408c.0617) [DOI] [Google Scholar]
. Uspekhi Fiz. Nauk
83, 617–663. [In Russian.] ( 10.3367/UFNr.0083.196408c.0617) [DOI] [Google Scholar] - 39.Lifshitz IM. 1965. Energy spectrum structure and quantum states of disordered condensed systems. Soviet Physics Uspekhi 7, 549–573. [English transl.] ( 10.1070/PU1965v007n04ABEH003634) [DOI] [Google Scholar]
- 40.Lifshitz IM. 1964. The energy spectrum of disordered systems. Adv. Phys. 13, 483–536. ( 10.1080/00018736400101061) [DOI] [Google Scholar]
-
41.Larkin AI, Ovchinnikov YuN.
1971.

 . Zh. Eksp. Teor. Fiz.
61, 2147–2159. [In Russian.] [Google Scholar]
. Zh. Eksp. Teor. Fiz.
61, 2147–2159. [In Russian.] [Google Scholar] - 42.Larkin AI, Ovchinnikov YuN. 1972. Density of states in inhomogeneous superconductors. Sov. Phys. JETP 34, 1144–1150. [English transl.] [Google Scholar]
- 43.Balatsky AV, Trugman SA. 1997. Lifshitz tail in the density of states of a superconductor with magnetic impurities. Phys. Rev. Lett. 79, 3767–3770. ( 10.1103/PhysRevLett.79.3767) [DOI] [Google Scholar]
- 44.Kastalsky A, Kleinsasser AW, Greene LH, Bhat R, Milliken FP, Harbison JP. 1991. Observation of pair currents in superconductor-semiconductor contacts. Phys. Rev. Lett. 67, 3026–3029. ( 10.1103/PhysRevLett.67.3026) [DOI] [PubMed] [Google Scholar]
- 45.van Wees BJ, de Vries P, Magnée P, Klapwijk TM. 1992. Excess conductance of superconductor-semiconductor interfaces due to phase conjugation between electrons and holes. Phys. Rev. Lett. 69, 510–513. ( 10.1103/PhysRevLett.69.510) [DOI] [PubMed] [Google Scholar]
-
46.Zaĭtsev FV.
1990.
 . Pis’ma Zh. Eksp. Teor. Fiz.
51, 35–39. [In Russian.] [Google Scholar]
. Pis’ma Zh. Eksp. Teor. Fiz.
51, 35–39. [In Russian.] [Google Scholar] - 47.Zaĭtsev FV. 1990. Properties of ‘dirty’ S-S∗-N and S-S∗-S structures with potential barriers at the metal boundaries. JETP Lett. 51, 41–46. [English transl.] [Google Scholar]
-
48.Volkov AF.
1992.

 . Pis’ma Zh. Eksp. Teor. Fiz.
55, 713–716. [In Russian.] [Google Scholar]
. Pis’ma Zh. Eksp. Teor. Fiz.
55, 713–716. [In Russian.] [Google Scholar] - 49.Volkov AF. 1992. Conductance anomaly at superconductor-semiconductor contacts. JETP Lett. 55, 746–749. [English transl.] [Google Scholar]
-
50.Abrikosov AA, Gor’kov LP.
1960.

 . Zh. Exp. Teor. Fiz.
39, 1781–1796. [In Russian.] [Google Scholar]
. Zh. Exp. Teor. Fiz.
39, 1781–1796. [In Russian.] [Google Scholar] - 51.Abrikosov AA, Gor’kov LP. 1961. Contribution to the theory of superconducting alloys with paramagnetic impurities. Sov. Phys. JETP 12, 1243–1253. [English transl.] [Google Scholar]
- 52.Yu Luh. 1965. Bound state in superconductors with paramagnetic impurities. Acta Phys. Sinica 21, 75–91. See http://wulixb.iphy.ac.cn/EN/Y1965/V21/I1/075 [in Chinese, Engl. abstract]. [Google Scholar]
- 53.Shiba H. 1968. Classical spins in superconductors. Prog. Theor. Phys. 40, 435–451. ( 10.1143/PTP.40.435) [DOI] [Google Scholar]
-
54.Rusinov AI.
1969.
 . Pis’ma Zh. Eksp. Teor. Fiz.
9, 146–149. [In Russian.] [Google Scholar]
. Pis’ma Zh. Eksp. Teor. Fiz.
9, 146–149. [In Russian.] [Google Scholar] - 55.Rusinov AI. 1969. Superconductivity near a paramagnetic impurity. JETP Lett. 9, 85–87. [English transl.] [Google Scholar]
- 56.Caroli C, de Gennes PG, Matricon J. 1964. Bound Fermion states on a vortex line in a type II superconductor. Phys. Lett. 9, 307–309. ( 10.1016/0031-9163(64)90375-0) [DOI] [Google Scholar]
- 57.Rainer D, Sauls JA, Waxman D. 1996. Current carried by bound states of a superconducting vortex. Phys. Rev. B 54, 10 094–10 106. ( 10.1103/PhysRevB.54.10094) [DOI] [PubMed] [Google Scholar]
- 58.Eschrig M, Sauls JA, Rainer D. 1999. Electromagnetic response of a vortex in layered superconductors. Phys. Rev. B 60, 10 447–10 454. ( 10.1103/PhysRevB.60.10447) [DOI] [Google Scholar]
- 59.Eschrig M, Rainer D, Sauls JA. 2002. Vortex core structure and dynamics in layered superconductors. In Vortices in unconventional superconductors and superfluids (eds RP Huebener, N Schopohl, GE Volovik), pp. 175–202. Berlin, Germany: Springer.
- 60.Sauls JA, Eschrig M. 2009. Vortices in chiral, spin-triplet superconductors and superfluids. New J. Phys. 11, 075008 (1–26) ( 10.1088/1367-2630/11/7/075008) [DOI] [Google Scholar]
- 61.Eschrig M, Sauls JA. 2009. Charge dynamics of vortex cores in layered chiral triplet superconductors. New J. Phys. 11, 075009 (1–21) ( 10.1088/1367-2630/11/7/075009) [DOI] [Google Scholar]
- 62.Edwards JT, Thouless DJ. 1972. Numerical studies of localization in disordered systems. J. Phys. C: Solid State Phys. 5, 807–820. ( 10.1088/0022-3719/5/8/007) [DOI] [Google Scholar]
- 63.McMillan WL. 1968. Tunneling model of the superconducting proximity effect. Phys. Rev. 175, 537–542. ( 10.1103/PhysRev.175.537) [DOI] [Google Scholar]
- 64.Guéron S, Pothier H, Birge NO, Esteve D, Devoret MH. 1996. Superconducting proximity effect probed on a mesoscopic length scale. Phys. Rev. Lett. 77, 3025–3028. ( 10.1103/PhysRevLett.77.3025) [DOI] [PubMed] [Google Scholar]
- 65.Kosztin I, Maslov DL, Goldbart PM. 1995. Chaos in Andreev Billiards. Phys. Rev. Lett. 75, 1735–1738. ( 10.1103/PhysRevLett.75.1735) [DOI] [PubMed] [Google Scholar]
- 66.Lodder A, Nazarov YuV. 1998. Density of states and the energy gap in Andreev billiards. Phys. Rev. B 58, 5783–5788. ( 10.1103/PhysRevB.58.5783) [DOI] [Google Scholar]
-
67.Kulik IO.
1969.
 . Zh. Eksp. Teor. Fiz.
57, 1745–1759. [In Russian.] [Google Scholar]
. Zh. Eksp. Teor. Fiz.
57, 1745–1759. [In Russian.] [Google Scholar] - 68.Kulik IO. 1970. Macroscopic quantization and the proximity effect in S-N-S junctions. Soviet Physics JETP 30, 944–950. [English transl.] [Google Scholar]
- 69.Zhou F, Charlat P, Spivak B, Pannetier B. 1998. Density of states in superconductor-normal metal-superconductor junctions. J. Low Temp. Phys. 110, 841–850. ( 10.1023/A:1022628927203) [DOI] [Google Scholar]
- 70.le Sueur H, Joyez P, Pothier H, Urbina C, Esteve D. 2008. Phase controlled superconducting proximity effect probed by tunneling spectroscopy. Phys. Rev. Lett. 100, 197002 (1–4) ( 10.1103/PhysRevLett.100.197002) [DOI] [PubMed] [Google Scholar]
- 71.Byers C, Flatte T. 1995. Probing spatial correlations with nanoscale two-contact tunneling. Phys. Rev. Lett. 74, 306–309. ( 10.1103/PhysRevLett.74.306) [DOI] [PubMed] [Google Scholar]
- 72.Deutscher G, Feinberg D. 2002. Coupling superconducting-ferromagnetic point contacts by Andreev reflections. Appl. Phys. Lett. 76, 487–489. ( 10.1063/1.125796) [DOI] [Google Scholar]
- 73.Beckmann D, Weber HB, von Löhneysen H. 2004. Evidence for crossed Andreev reflection in superconductor-ferromagnet hybrid structures. Phys. Rev. Lett. 93, 197003 (1–4) ( 10.1103/PhysRevLett.93.197003) [DOI] [PubMed] [Google Scholar]
- 74.Hu C-R. 1994. Midgap surface states as a novel signature for dx2a−x2b-wave superconductivity. Phys. Rev. Lett. 72, 1526–1529. ( 10.1103/PhysRevLett.72.1526) [DOI] [PubMed] [Google Scholar]
- 75.Tanaka Y, Kashiwaya S. 1995. Theory of tunneling spectroscopy of d-wave superconductors. Phys. Rev. Lett. 74, 3451–3454. ( 10.1103/PhysRevLett.74.3451) [DOI] [PubMed] [Google Scholar]
- 76.Volovik GE. 1999. Fermion zero modes on vortices in chiral superconductors. Pis’ma Zh. Eksp. Teor. Fiz. 70, 601–606. JETP Lett.70 609–614 (Reprinted) ( 10.1134/1.568223) [DOI] [Google Scholar]
- 77.Kitaev AYu. 2001. Unpaired Majorana fermions in quantum wires. Uspekhi Fiz. Nauk 171, 131–136. (Phys. Usp.44) (suppl.) ( 10.1070/1063-7869/44/10S/S29) [DOI] [Google Scholar]
- 78.Volovik GE. 2003. The universe in a helium droplet. Clarendon, UK: Clarendon Press. [Google Scholar]
- 79.Tokuyasu T, Sauls JA, Rainer D. 1988. Proximity effect of a ferromagnetic insulator in contact with a superconductor. Phys. Rev. B 38, 8823–8833. ( 10.1103/PhysRevB.38.8823) [DOI] [PubMed] [Google Scholar]
- 80.Cottet A, Belzig W. 2005. Superconducting proximity effect in a diffusive ferromagnet with spin-active interfaces. Phys. Rev. B 72, 180503(R) (1–4) ( 10.1103/PhysRevB.72.180503) [DOI] [Google Scholar]
- 81.Brataas A, Nazarov YuV, Bauer GEW. 2000. Finite-element theory of transport in ferromagnet-normal metal systems. Phys. Rev. Lett. 11, 2481–2484. ( 10.1103/PhysRevLett.84.2481) [DOI] [PubMed] [Google Scholar]
- 82.Fogelström M. 2000. Josephson currents through spin-active interfaces. Phys. Rev. B 62, 11 812–11 819. ( 10.1103/PhysRevB.62.11812) [DOI] [Google Scholar]
- 83.Eschrig M, Kopu J, Cuevas JC, Schön G. 2003. Theory of half-metal/superconductor heterostructures. Phys. Rev. Lett. 90, 137003 (1–4) ( 10.1103/PhysRevLett.90.137003) [DOI] [PubMed] [Google Scholar]
- 84.Krawiec M, Györffy BL, Annett JF. 2004. Current-carrying Andreev bound states in a superconductor-ferromagnet proximity system. Phys. Rev. B 70, 134519 (1–5) ( 10.1103/PhysRevB.70.134519) [DOI] [Google Scholar]
- 85.Zhao E, Löfwander T, Sauls JA. 2004. Nonequilibrium superconductivity near spin-active interfaces. Phys. Rev. B 70, 134510 (1–12) ( 10.1103/PhysRevB.70.134510) [DOI] [Google Scholar]
- 86.Annett JF, Krawiec M, Györffy BL. 2006. Origin of spontaneous currents in a superconductor-ferromagnetic proximity system. Phys. C: Supercond. 437–438, 7–10. ( 10.1016/j.physc.2005.12.009) [DOI] [Google Scholar]
- 87.Löfwander T, Grein R, Eschrig M. 2010. Is CrO2 fully spin polarized? Analysis of Andreev spectra and excess current. Phys. Rev. Lett. 105, 207001 (1–4) ( 10.1103/PhysRevLett.105.207001) [DOI] [PubMed] [Google Scholar]
- 88.Metalidis G, Eschrig M, Grein R, Schön G. 2010. Nonlocal conductance via overlapping Andreev bound states in ferromagnet-superconductor heterostructures. Phys. Rev. B 82, 180503(R) (1–4) ( 10.1103/PhysRevB.82.180503) [DOI] [Google Scholar]
- 89.Hübler F, Wolf MJ, Scherer T, Wang D, Beckmann D, von Löhneysen H. 2012. Observation of Andreev bound states at spin-active interfaces. Phys. Rev. Lett. 109, 087004 (1–5) ( 10.1103/PhysRevLett.109.087004) [DOI] [PubMed] [Google Scholar]
- 90.Linder J, Yokoyama T, Sudbø A, Eschrig M. 2009. Pairing symmetry conversion by spin-active interfaces in magnetic normal-metal-superconductor junctions. Phys. Rev. Lett. 102, 107008 (1–4) ( 10.1103/PhysRevLett.102.107008) [DOI] [PubMed] [Google Scholar]
- 91.Linder J, Yokoyama T, Sudbø A, Eschrig M. 2010. Signature of odd-frequency pairing correlations induced by a magnetic interface. Phys. Rev. B 81, 214504 (1–13) ( 10.1103/PhysRevB.81.214504) [DOI] [Google Scholar]
- 92.Eschrig M. 2009. Scattering problem in nonequilibrium quasiclassical theory of metals and superconductors: general boundary conditions and applications. Phys. Rev. B 80, 134511 (1–22) ( 10.1103/PhysRevB.80.134511) [DOI] [Google Scholar]
- 93.Cottet A. 2011. Inducing odd-frequency triplet superconducting correlations in a normal metal. Phys. Rev. Lett. 107, 177001 (1–5) ( 10.1103/PhysRevLett.107.177001) [DOI] [PubMed] [Google Scholar]
- 94.Yokoyama T, Tanaka Y, Golubov AA. 2007. Manifestation of the odd-frequency spin-triplet pairing state in diffusive ferromagnet/superconductor junctions. Phys. Rev. B 75, 134510 (1–8) ( 10.1103/PhysRevB.75.134510) [DOI] [Google Scholar]
- 95.Asano Y, Tanaka Y, Golubov AA. 2007. Josephson effect due to odd-frequency pairs in diffusive half metals. Phys. Rev. Lett. 98, 107002 (1–4) ( 10.1103/PhysRevLett.98.107002) [DOI] [PubMed] [Google Scholar]
- 96.Braude V, Nazarov YuV. 2007. Fully developed triplet proximity effect. Phys. Rev. Lett. 98, 077003 (1–4) ( 10.1103/PhysRevLett.98.077003) [DOI] [PubMed] [Google Scholar]
- 97.Huertas-Hernando D, Nazarov YuV, Belzig W. 2002. Absolute spin-valve effect with superconducting proximity structures. Phys. Rev. Lett. 88, 047003 (1–4) ( 10.1103/PhysRevLett.88.047003) [DOI] [PubMed] [Google Scholar]
- 98.Eschrig M, Löfwander T, Champel T, Cuevas JC, Kopu J, Schön G. 2007. Symmetries of pairing correlations in superconductor-ferromagnet nanostructures. J. Low Temp. Phys. 147, 457–476. ( 10.1007/s10909-007-9329-6) [DOI] [Google Scholar]
- 99.Kopu J, Eschrig M, Cuevas JC, Fogelström M. 2004. Transfer-matrix description of heterostructures involving superconductors and ferromagnets. Phys. Rev. B 69, 094501 (1–9) ( 10.1103/PhysRevB.69.094501) [DOI] [Google Scholar]
- 100.Eschrig M, Löfwander T. 2008. Triplet supercurrents in clean and disordered half-metallic ferromagnets. Nat. Phys. 4, 138–143. ( 10.1038/nphys831) [DOI] [Google Scholar]
- 101.Eschrig M, Löfwander T.2006. Triplet supercurrents in clean and disordered half-metallic ferromagnets. (http://arxiv.org/abs/cond-mat/0612533. )
- 102.Bergeret FS, Volkov AF, Evetov KB. 2001. Long-range proximity effects in superconductor-ferromagnet structures. Phys. Rev. Lett. 86, 4096–4099. ( 10.1103/PhysRevLett.86.4096) [DOI] [PubMed] [Google Scholar]
- 103.Kadigrobov A, Shekhter RI, Jonson M. 2001. Quantum spin fluctuations as a source of long-range proximity effects in diffusive ferromagnet-super conductor structures. Europhys. Lett. 54, 394–400. ( 10.1209/epl/i2001-00107-2) [DOI] [Google Scholar]
- 104.Volkov AF, Bergeret FS, Efetov KB. 2003. Odd triplet superconductivity in superconductor-ferromagnet multilayered structures. Phys. Rev. Lett. 90, 117006 (1–4) ( 10.1103/PhysRevLett.90.117006) [DOI] [PubMed] [Google Scholar]
- 105.Houzet M, Buzdin AI. 2007. Long range triplet Josephson effect through a ferromagnetic trilayer. Phys. Rev. B 76, 060504(R) (1–4) ( 10.1103/PhysRevB.76.060504) [DOI] [Google Scholar]
-
106.Izyumov YuA, Proshin YuN, Khusainov MG.
2002.
 . Usp. Fiz. Nauk
172, 113–154. [In Russian.] ( 10.3367/UFNr.0172.200202a.0113) [DOI] [Google Scholar]
. Usp. Fiz. Nauk
172, 113–154. [In Russian.] ( 10.3367/UFNr.0172.200202a.0113) [DOI] [Google Scholar] - 107.Izyumov YuA, Proshin YuN, Khusainov MG. 2002. Competition between superconductivity and magnetism in ferromagnet/superconductor heterostructures. Phys. Usp. 45, 109–148. [English transl.] ( 10.1070/PU2002v045n02ABEH001025) [DOI] [Google Scholar]
-
108.Fominov YaV, Kupriyanov MYu, Feigel’man MV.
2003.


 . Usp. Fiz. Nauk
173, 113–115. [In Russian.] ( 10.3367/UFNr.0173.200301l.0113) [DOI] [Google Scholar]
. Usp. Fiz. Nauk
173, 113–115. [In Russian.] ( 10.3367/UFNr.0173.200301l.0113) [DOI] [Google Scholar] - 109.Fominov YaV, Kupriyanov MYu, Feigel’man MV. 2003. A comment on the paper ‘Competition between superconductivity and magnetism in ferromagnet/superconductor heterostructures’ by YuA Izyumov, YuN Proshin, and MG Khusainov. Phys. Usp. 46, 105–107. (Engl. ransl.)) ( 10.1070/PU2003v046n01ABEH001390) [DOI] [Google Scholar]
- 110.Eschrig M, Kopu J, Konstandin A, Cuevas JC, Fogelström M, Schön G. 2004. Singlet-triplet mixing in superconductor-ferromagnet hybrid devices. Adv. Solid State Phys. 44, 533–545. ( 10.1007/978-3-540-39970-4_41) [DOI] [Google Scholar]
- 111.Golubov AA, Kupriyanov MYu, Il’ichev E. 2004. The current-phase relation in Josephson junctions. Rev. Mod. Phys. 76, 411–469. ( 10.1103/RevModPhys.76.411) [DOI] [Google Scholar]
- 112.Buzdin AI. 2005. Proximity effects in superconductor-ferromagnet heterostructures. Rev. Mod. Phys. 77, 935–976. ( 10.1103/RevModPhys.77.935) [DOI] [Google Scholar]
- 113.Bergeret FS, Volkov AF, Evetov KB. 2005. Odd triplet superconductivity and related phenomena in superconductor-ferromagnet structures. Rev. Mod. Phys. 77, 1321–1373. ( 10.1103/RevModPhys.77.1321) [DOI] [PubMed] [Google Scholar]
- 114.Lyuksyutov IF, Pokrovsky VL. 2007. Ferromagnet-superconductor hybrids. Adv. Phys. 54, 67–136. ( 10.1080/00018730500057536) [DOI] [Google Scholar]
- 115.Eschrig M. 2011. Spin-polarized supercurrents for spintronics. Phys. Today 64, 43–49. ( 10.1063/1.3541944) [DOI] [PubMed] [Google Scholar]
- 116.Blamire MG, Robinson JWA. 2014. The interface between superconductivity and magnetism: understanding and device prospects. J. Phys. Condens. Matter 26, 453201 (1–13) ( 10.1088/0953-8984/26/45/453201) [DOI] [PubMed] [Google Scholar]
- 117.Linder J, Robinson JWA. 2015. Superconducting spintronics. Nat. Phys. 11, 307–315. ( 10.1038/nphys3242) [DOI] [Google Scholar]
- 118.Eschrig M. 2015. Spin-polarized supercurrents for spintronics: a review of current progress. Rep. Prog. Phys. 78, 104501 (1–50) ( 10.1088/0034-4885/78/10/104501) [DOI] [PubMed] [Google Scholar]
- 119.Eschrig M. 2000. Distribution functions in nonequilibrium theory of superconductivity and Andreev spectroscopy in unconventional superconductors. Phys. Rev. B 61, 9061–9076. ( 10.1103/PhysRevB.61.9061) [DOI] [Google Scholar]
- 120.Grein R, Eschrig M, Metalidis G, Schön G. 2009. Spin-dependent cooper pair phase and pure spin supercurrents in strongly polarized ferromagnets. Phys. Rev. Lett. 102, 226005 (1–4) ( 10.1103/PhysRevLett.102.227005) [DOI] [PubMed] [Google Scholar]
- 121.Grein R, Löfwander T, Eschrig M. 2013. Inverse proximity effect and influence of disorder on triplet supercurrents in strongly spin-polarized ferromagnets. Phys. Rev. B 88, 054502 (1–11) ( 10.1103/PhysRevB.88.054502) [DOI] [Google Scholar]
- 122.Nagato Y, Nagai K, Hara J. 1993. Theory of the Andreev reflection and the density of states in proximity contact normal-superconducting infinite double-layer. J. Low Temp. Phys. 93, 33–56. ( 10.1007/BF00682280) [DOI] [Google Scholar]
- 123.Schopohl N, Maki K. 1995. Quasiparticle spectrum around a vortex line in a d-wave superconductor. Phys. Rev. B 52, 490–493. ( 10.1103/PhysRevB.52.490) [DOI] [PubMed] [Google Scholar]
- 124.Halterman K, Valls OT. 2009. Emergence of triplet correlations in superconductor/half-metallic nanojunctions with spin-active interfaces. Phys. Rev. B 80, 104502 (1–13) ( 10.1103/PhysRevB.80.104502) [DOI] [Google Scholar]
- 125.Galaktionov AV, Kalenkov MS, Zaikin AD. 2008. Josephson current and Andreev states in superconductor-half metal-superconductor heterostructures. Phys. Rev. B 77, 094520 (1–11) ( 10.1103/PhysRevB.77.094520) [DOI] [Google Scholar]
- 126.Deutscher G. 2005. Andreev-Saint-James reflections: a probe of cuprate superconductors. Rev. Mod. Phys. 77, 109–135. ( 10.1103/RevModPhys.77.109) [DOI] [Google Scholar]
- 127.Heeger AJ, Kivelson S, Schrieffer JR, Su W-P. 1988. Solitons in conducting polymers. Rev. Mod. Phys. 60, 781–850. ( 10.1103/RevModPhys.60.781) [DOI] [Google Scholar]
- 128.Jackiw R, Rebbi C. 1976. Solitons with fermion number 1_ 2. Phys. Rev. D 13, 3398–3409. ( 10.1103/PhysRevD.13.3398) [DOI] [Google Scholar]
- 129.Atiyah MF, Patodi VK, Singer IM. 1975. Spectral asymmetry and Riemannian geometry. I. Math. Proc. Cambridge Philos. Soc. 77, 43–69. ( 10.1017/S0305004100049410) [DOI] [Google Scholar]
- 130.Eschrig M, Cottet A, Belzig W, Linder J. 2015. General boundary conditions for quasiclassical theory of superconductivity in the diffusive limit: application to strongly spin-polarized systems. New. J. Phys. 17, 083037 (1–21) ( 10.1088/1367-2630/17/8/083037) [DOI] [Google Scholar]
- 131.Slonczewski JC. 1996. Current-driven excitation of magnetic multilayers. J. Magn. Magn. Mater. 159, L1–L7. ( 10.1016/0304-8853(96)00062-5) [DOI] [Google Scholar]
- 132.Ralph DC, Stiles MD. 2008. Spin transfer torques. J. Magn. Magn. Mater. 320, 1190–1216. ( 10.1016/j.jmmm.2007.12.019) [DOI] [Google Scholar]
- 133.Brataas A, Kent AD, Ohno H. 2012. Current-induced torques in magnetic materials. Nat. Mater. 11, 372–381. ( 10.1038/nmat3311) [DOI] [PubMed] [Google Scholar]
- 134.Locatelli N, Cros V, Grollier J. 2014. Spin-torque building blocks. Nat. Mater. 13, 11–20. ( 10.1038/nmat3823) [DOI] [PubMed] [Google Scholar]
- 135.Zhao E, Sauls JA. 2007. Dynamics of spin transport in voltage-biased Josephson junctions. Phys. Rev. Lett. 98, 206601 (1–4) ( 10.1103/PhysRevLett.98.206601) [DOI] [PubMed] [Google Scholar]
- 136.Zhao E, Sauls JA. 2008. Theory of nonequilibrium spin transport and spin-transfer torque in superconducting-ferromagnetic nanostructures. Phys. Rev. B 78, 174511 (1–15) ( 10.1103/PhysRevB.78.174511) [DOI] [Google Scholar]
- 137.Waintal X, Brouwer PW. 2002. Magnetic exchange interaction induced by a Josephson current. Phys. Rev. B 65, 054407 (1–11) ( 10.1103/PhysRevB.65.054407) [DOI] [Google Scholar]
- 138.Kümmel R, Senftinger W. 1985. Andreev-reflected wave packets in voltage-biased superconducting quantum wells. Z. Phys. B Condens. Matter 59, 275–281. ( 10.1007/BF01307432) [DOI] [Google Scholar]
- 139.Arnold GB. 1987. Superconducting tunneling without the tunneling Hamiltonian. II. Subgap harmonic structure. J. Low Temp. Phys. 68, 1–27. ( 10.1007/BF00682620) [DOI] [Google Scholar]
- 140.Averin DV, Bardas A. 1995. ac Josephson effect in a single quantum channel. Phys. Rev. Lett. 75, 1831–1834. ( 10.1103/PhysRevLett.75.1831) [DOI] [PubMed] [Google Scholar]
- 141.Wang S, Tang L, Xia K. 2010. Spin transfer torque in the presence of Andreev reflections. Phys. Rev. B 81, 094404 (1–7) ( 10.1103/PhysRevB.81.094404) [DOI] [Google Scholar]
- 142.Shomali Z, Zareyan M, Belzig W. 2011. Spin supercurrent in Josephson contacts with noncollinear ferromagnets. New. J. Phys. 13, 083033 (1–14) ( 10.1088/1367-2630/13/8/083033) [DOI] [Google Scholar]
- 143.Linder J, Yokoyama T. 2011. Supercurrent-induced magnetization dynamics in a Josephson junction with two misaligned ferromagnetic layers. Phys. Rev. B 83, 012501 (1–4) ( 10.1103/PhysRevB.83.012501) [DOI] [Google Scholar]
- 144.Mai S, Kandelaki E, Volkov AF, Efetov KB. 2011. Interaction of Josephson and magnetic oscillations in Josephson tunnel junctions with a ferromagnetic layer. Phys. Rev. B 84, 144519 (1–12) ( 10.1103/PhysRevB.84.144519) [DOI] [Google Scholar]
- 145.Kulagina I, Linder J. 2014. Spin supercurrent, magnetization dynamics, and ϕ-state in spin-textured Josephson junctions. Phys. Rev. B 90, 054504 (1–14) ( 10.1103/PhysRevB.90.054504) [DOI] [Google Scholar]
- 146.Holmqvist C, Teber S, Fogelström M. 2011. Nonequilibrium effects in a Josephson junction coupled to a precessing spin. Phys. Rev. B 83, 104521 (1–18) ( 10.1103/PhysRevB.83.104521) [DOI] [Google Scholar]
- 147.Holmqvist C, Fogelström M, Belzig W. 2014. Spin-polarized Shapiro steps and spin-precession-assisted multiple Andreev reflection. Phys. Rev. B 90, 014516 (1–9) ( 10.1103/PhysRevB.90.014516) [DOI] [Google Scholar]
- 148.de Jong MJM, Beenakker CWJ. 1995. Andreev reflection in ferromagnet-superconductor junctions. Phys. Rev. Lett. 74, 1657–1660. ( 10.1103/PhysRevLett.74.1657) [DOI] [PubMed] [Google Scholar]
- 149.Kashiwaya S, Tanaka Y, Yoshida N, Beasley MR. 1999. Spin current in ferromagnet-insulator-superconductor junctions. Phys. Rev. B 60, 3572–3580. ( 10.1103/PhysRevB.60.3572) [DOI] [Google Scholar]
- 150.Žutić I, Valls OT. 2000. Tunneling spectroscopy for ferromagnet/superconductor junctions. Phys. Rev. B 61, 1555–1566. ( 10.1103/PhysRevB.61.1555) [DOI] [Google Scholar]
- 151.Žutić I, Valls OT. 2000. Tunneling spectroscopy for ferromagnet/superconductor junctions. Phys. Rev. B 61, 14 845 ( 10.1103/PhysRevB.61.14845.2) [DOI] [Google Scholar]
- 152.Mazin II, Golubov AA, Nadgorny B. 2001. Probing spin polarization with Andreev reflection: a theoretical basis. J. Appl. Phys. 89, 7576–7578. ( 10.1063/1.1357127) [DOI] [Google Scholar]
- 153.Pérez-Willard F, Cuevas JC, Sürgers C, Pfundstein P, Kopu J, Eschrig M, von Löhneysen H. 2004. Determining the current polarization in Al/Co nanostructured point contacts. Phys. Rev. B 69, 140502 (1–4) ( 10.1103/PhysRevB.69.140502) [DOI] [Google Scholar]
- 154.Eschrig M, Golubov AA, Mazin II, Nadgorny B, Tanaka Y, Valls OT, Žutić I. 2013. Comment on ‘Unified formalism of Andreev reflection at a ferromagnet/superconductor interface’. Phys. Rev. Lett. 111, 139703 (1–2) ( 10.1103/PhysRevLett.111.139703) [DOI] [PubMed] [Google Scholar]
- 155.Grein R, Löfwander T, Metalidis G, Eschrig M. 2010. Theory of superconductor-ferromagnet point-contact spectra: the case of strong spin polarization. Phys. Rev. B 81, 094508 (1–17) ( 10.1103/PhysRevB.81.094508) [DOI] [Google Scholar]
- 156.Piano S, Grein R, Mellor CJ, Výborný K, Campion R, Wang M, Eschrig M, Gallagher BL. 2011. Spin polarization of (Ga,Mn)As measured by Andreev spectroscopy: the role of spin-active scattering. Phys. Rev. B 83, 081305(R) (1–4) ( 10.1103/PhysRevB.83.081305) [DOI] [Google Scholar]
- 157.Kupferschmidt JN, Brouwer PW. 2011. Andreev reflection at half-metal/superconductor interfaces with nonuniform magnetization. Phys. Rev. B 83, 014512 (1–14) ( 10.1103/PhysRevB.83.014512) [DOI] [Google Scholar]
- 158.Wilken FB, Brouwer PW. 2012. Impurity-assisted Andreev reflection at a spin-active half metal-superconductor interface. Phys. Rev. B 85, 134531 (1–10) ( 10.1103/PhysRevB.85.134531) [DOI] [Google Scholar]
- 159.Yates KA, Anwar MS, Aarts J, Conde O, Eschrig M, Löfwander T, Cohen LF. 2013. Andreev spectroscopy of CrO2 thin films on TiO2 and Al2O3. Europhys. Lett. 103, 67005 (1–5) ( 10.1209/0295-5075/103/67005) [DOI] [Google Scholar]
- 160.Kuei S, Shah N. 2015. General framework for transport in spin-orbit-coupled superconducting heterostructures: nonuniform spin-orbit coupling and spin-orbit-active interfaces. Phys. Rev. B 91, 144508 (1–8) ( 10.1103/PhysRevB.91.144508) [DOI] [Google Scholar]
- 161.Visani C, Sefrioui Z, Tornos J, Leon C, Briatico J, Bibes M, Barthélémy A, Santamaría J, Villegas JE. 2012. Equal-spin Andreev reflection and long-range coherent transport in high-temperature superconductor/half-metallic ferromagnet junctions. Nat. Phys. 8, 539–543. ( 10.1038/NPHYS2318) [DOI] [Google Scholar]
- 162.Cottet A, Belzig W. 2008. Conductance and current noise of a superconductor/ferro- magnet quantum point contact. Phys. Rev. B 77, 064517 (1–8) ( 10.1103/PhysRevB.77.064517) [DOI] [PubMed] [Google Scholar]
- 163.Cottet A, Douçot B, Belzig W. 2008. Finite frequency noise of a superconductor-ferromagnet quantum point contact. Phys. Rev. Lett. 101, 257001 (1–4) ( 10.1103/PhysRevLett.101.257001) [DOI] [PubMed] [Google Scholar]
- 164.Kalenkov M, Zaikin AD. 2007. Nonlocal Andreev reflection at high transmissions. Phys. Rev. B 75, 172503 (1–4) ( 10.1103/PhysRevB.75.172503) [DOI] [Google Scholar]
- 165.Mélin R, Feinberg D. 2004. Sign of the crossed conductances at a ferromagnet/ superconductor/ferromagnet double interface. Phys. Rev. B 70, 174509 (1–9) ( 10.1103/PhysRevB.70.174509) [DOI] [Google Scholar]
- 166.Kalenkov MS, Zaikin AD. 2010. Nonlocal spin-sensitive electron transport in diffusive proximity heterostructures. Phys. Rev. B 82, 024522 (1–8) ( 10.1103/PhysRevB.82.024522) [DOI] [Google Scholar]
- 167.Machon P, Eschrig M, Belzig W. 2013. Nonlocal thermoelectric effects and nonlocal onsager relations in a three-terminal proximity-coupled superconductor-ferromagnet device. Phys. Rev. Lett. 110, 047002 (1–5) ( 10.1103/PhysRevLett.110.047002) [DOI] [PubMed] [Google Scholar]
- 168.Machon P, Eschrig M, Belzig W. 2014. Giant thermoelectric effects in a proximity-coupled superconductor-ferromagnet device. New. J. Phys. 16, 073002 (1–19) ( 10.1088/1367-2630/16/7/073002) [DOI] [PubMed] [Google Scholar]
- 169.Ozaeta A, Virtanen P, Bergeret FS, Heikkilä TT. 2014. Predicted very large thermoelectric effect in ferromagnet-superconductor junctions in the presence of a spin-splitting magnetic field. Phys. Rev. Lett. 112, 057001 (1–5) ( 10.1103/PhysRevLett.112.057001) [DOI] [PubMed] [Google Scholar]
- 170.Cadden-Zimansky P, Jiang Z, Chandrasekhar V. 2007. Charge imbalance, crossed Andreev reflection and elastic co-tunnelling in ferromagnet/superconductor/normal-metal structures. New. J. Phys. 9, 116 (1–25) ( 10.1088/1367-2630/9/5/116) [DOI] [Google Scholar]
- 171.Brauer J, Hübler F, Smetanin M, Beckmann D, von Löhneysen H. 2010. Nonlocal transport in normal-metal/superconductor hybrid structures: role of interference and interaction. Phys. Rev. B 81, 024515 (1–7) ( 10.1103/PhysRevB.81.024515) [DOI] [Google Scholar]
- 172.Wolf MJ, Sürgers C, Fischer G, Beckmann D. 2014. Spin-polarized quasiparticle transport in exchange-split superconducting aluminum on europium sulfide. Phys. Rev. B 90, 144509 (1–5) ( 10.1103/PhysRevB.90.144509) [DOI] [Google Scholar]
- 173.Colci M, Kuei Sun, Shah N, Vishveshwara S, Van Harlingen DJ. 2012. Anomalous polarization-dependent transport in nanoscale double-barrier superconductor/ ferromagnet/superconductor junctions. Phys. Rev. B 85, 180512 (1–5) ( 10.1103/PhysRevB.85.180512) [DOI] [Google Scholar]
- 174.Flokstra MG. et al. 2016. Remotely induced magnetism in a normal metal using a superconducting spin-valve. Nat. Phys. 12, 57–61. ( 10.1038/nphys3486) [DOI] [Google Scholar]
- 175.Kolenda S, Wolf MJ, Beckmann D. 2016. Observation of thermoelectric currents in high-field superconductor-ferromagnet tunnel junctions. Phys. Rev. Lett. 116, 097001 (1–5) ( 10.1103/PhysRevLett.116.097001) [DOI] [PubMed] [Google Scholar]
- 176.Cadden-Zimansky P, Wei J, Chandrasekhar V. 2009. Cooper-pair-mediated coherence between two normal metals. Nat. Phys. 5, 393–397. ( 10.1038/nphys1252) [DOI] [Google Scholar]
- 177.Eschrig M. 2009. Superconductor-metal heterostructures: coherent conductors at a distance. Nat. Phys. 5, 384–385. ( 10.1038/nphys1293) [DOI] [Google Scholar]
- 178.Noh T, Houzet M, Meyer JS, Chandrasekhar V. 2013. Nonlocal spin correlations mediated by a superconductor. Phys. Rev. B 87, 220502(R) (1–4) ( 10.1103/PhysRevB.87.220502) [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All data can be obtained from the author.