Multifaceted properties of Andreev bound states: interplay of symmetry and topology

Abstract

Andreev bound states (ABSs) ubiquitously emerge as a consequence of non-trivial topological structures of the order parameter of superfluids and superconductors and significantly contribute to thermodynamics and low-energy quantum transport phenomena. We here share the current status of our knowledge on their multifaceted properties such as Majorana fermions and odd-frequency pairing. A unified concept behind ABSs originates from a soliton state in the one-dimensional Dirac equation with mass domain wall and interplay of ABSs with symmetry and topology enrich their physical characteristics. We make an overview of ABSs with a special focus on superfluid ³He. The quantum liquid confined to restricted geometries serves as a rich repository of noteworthy quantum phenomena, such as the mass acquisition of Majorana fermions driven by spontaneous symmetry breaking, topological quantum criticality, Weyl superfluidity and the anomalous magnetic response. The marriage of the superfluid ³He and nano-fabrication techniques will take one to a new horizon of topological quantum phenomena associated with ABSs.

This article is part of the theme issue ‘Andreev bound states’.

1. Introduction

Andreev bound states (ABSs) mirror the complexity of the topological structure of order parameter manifold in superconductors (SCs) and superfluids (SFs) [1–3]. They ubiquitously emerge in topological defects, such as vortices, surfaces, interfaces and domain walls. The simplest example is an SC/normal/SC (SNS) junction, where low-lying quasi-particles that are bound to the interface manifest the relative phase difference between two superconducting domains. It is widely recognized that low-lying ABSs play fundamental roles in thermodynamics and quantum transport phenomena in low temperatures. In Pauli-limited SCs, furthermore, ABSs provide a key to capture the essence of the thermodynamic stability of the Fulde–Ferrell–Larkin–Ovchinnikov (FFLO) state [4–6], a self-organized periodic structure of the superconducting gap. Indeed, surface and vortex ABSs have been directly observed in various kinds of SCs and SFs, including ³He [7–10], high-T_c cuprates [11–13] and type-II SCs under a magnetic field [14]. Recently, it has been recognized that the marriage of ABSs with symmetry and topology gives rise to a diversity of their characteristics and sheds light on new facets of ABSs, Majorana fermions and odd-frequency pair correlations.

Majorana fermions are defined as self-conjugate Dirac fermions in quantum field theory [15]. They are represented by the quantized fermionic field Ψ that satisfies the constraint of the self-charge-conjugation

1.1

where denotes the charge-conjugation operator or particle-hole operator in the context of condensed matter physics. Self-charge-conjugated Majorana fermions exist in topological and Weyl SCs/SFs as topologically protected gapless ABSs [2,7,8,16]. It has recently been found that extra discrete symmetries adds a diversity of characteristics to such exotic quasi-particle, such as non-Abelian anyons subject to mirror reflection symmetry [17,18] and time-reversal symmetry [19], Majorana Ising spins in time-reversal-invariant SCs/SFs with magnetic point group symmetry [20–25]. The mirror-protected non-Abelian Majorana fermions are realized in ³He-A thin film, while the typical example of the latter is the SF ³He-B confined to a restricted geometry.

Another remarkable facet of ABSs is odd-frequency Cooper pair correlations [2,7,26]. Anomalous charge and spin transport, electromagnetic responses and proximity effects via ABSs have been clarified in light of odd-frequency Cooper pairing. The odd-frequency pairing expands the classification of possible Cooper pairs. In accordance with the Fermi–Dirac statistics, the pairing symmetries of Cooper pair wave functions in a single-band superconductor can be classified into the four-fold way when the inversion symmetry is preserved [27–29]. Two of them are even-frequency spin-singlet even-parity (ESE) and even-frequency spin-triplet odd-parity (ETO) pairings, which do not change the sign of Cooper pair wave function by the exchange of times of paired fermions. There still remain two possibilities, odd-frequency spin-singlet odd-parity (OSO) and spin-triplet even-parity (OTE) pairs. Although there is no conclusive evidence on bulk odd-frequency SCs [30–33], odd-frequency pair correlations ubiquitously appear in the topological defects of SCs and SFs as fluctuations of the condensate generated by pair-breaking and ABS formation.

This article gives us a review of recent progress on the interplay of symmetry and topology in ABSs with a special focus on SF ³He. In §2, we start with a soliton state in the one-dimensional Dirac equation with a mass domain wall which offers a minimal model to capture an essence of gapless ABSs in SCs and SFs. The central part of this article is devoted to giving a unified description on the emergence of gapless ABSs on the basis of the soliton state and to clarify their connection with topology. We discuss the fundamental roles of ABSs in spontaneous translational symmetry breaking in Pauli-limited SCs. In addition, the topological aspects of surface and vortex ABSs in Weyl SCs are uncovered, where the surface and vortex Fermi arc are topologically protected by the pairwise Weyl points. In §3, after briefly introducing Majorana fermions, we show the current status of our knowledge on topological quantum phenomena woven by the intertwining of Majorana fermions with symmetry and topology. We here focus on the SF ³He as a rich repository of such topological phenomena. This includes the quantum mass acquisition of Majorana fermions driven by spontaneous symmetry breaking and topological quantum criticality. In addition, we clarify another facet of ABSs that the diagonal component of the Green’s function constructed from ABSs is equivalent to the anomalous Green’s function associated with odd frequency Cooper pair correlations. This clarifies that the formation of the ABS in SF ³He leads to the anomalous enhancement of surface spin susceptibilities [34]. In §4, we give some prospects on searching exotic quasi-particles associated with the interplay of symmetry and topology in SFs and SCs.

Throughout this paper, we set and the repeated Greek (Roman) indices imply the sum over x,y,z (spins ↑ and ↓). The Pauli matrices in spin and particle-hole (Nambu) spaces are denoted by σ_μ and τ_μ, respectively.

2. A unified concept for Andreev bound states

Let us start to give an overview on the topologically non-trivial structure of the one-dimensional Dirac equation with a spatially inhomogeneous mass m(y),

2.1

The above equation enables one to capture the essence of the Gross–Neveu model [35] or Nambu–Jona–Lasinio model in 1+1 dimensions [36] which is the central part of a renormalizable quantum field theory for interacting fermions with N flavours. Although the model holds the discrete or continuous chiral symmetry, spontaneous chiral symmetry breaking in the vacuum gives rise to dynamical mass acquisition of fermions, m≠0, which is characterized by the auxiliary fields composed of pairwise fermions. For spatially uniform m, the fermion has a finite energy gap .

Jackiw & Rebbi [37] clarified that for the boundary condition , the eigenfunction of the zero-energy state is obtained by integrating equation (2.1) with E=0 as

2.2

where N is a normalization constant. As the mass m(y) approaches a uniform value in the limit of , the zero-energy solution is normalizable only when the mass term satisfies the condition

2.3

where . This indicates that, in addition to the continuum state with , there exits at least one zero-energy solution when the mass term m(y) changes its sign at , whose wave function is tightly bound to the mass domain wall. The stability of the zero-energy state is independent of the detailed structure of m(y).

Recently, general solutions of equation (2.1) have been found by using a technique of the Ablowitz–Kaup–Newell–Segur hierarchy well known in integrable systems [38]. These include a single-kink state of the mass m(y) [39–41], multiple kinks (kink–anti-kink and kink–polaron states) [42–45], and complex kinks and their crystalline states [46–49] as well as a single-kink solution. These non-trivial kink and crystalline structures are accompanied by low-lying solitonic fermions and band structures formed by the soliton lattice.

In superconducting states, electronic states are determined by the Bogoliubov–de Gennes (BdG) Hamiltonian, which is given in the basis of the Nambu spinor as

2.4

The matrix ε(r) describes the single-particle Hamiltonian in the normal state and the 2×2 gap function Δ(k,r) satisfies Δ(k,r)=−Δ(−k,r)^t. The BdG Hamiltonian is diagonalized in terms of the energy eigenstates as

2.5

where η_E and denote the annihilation and creation operators of quasi-particles with E, respectively. The particle-hole operator is given as with the complex conjugation operator K. The BdG Hamiltonian maintains the particle-hole symmetry, . The energy eigenstates in superconducting states are obtained by solving the BdG equation, . By employing the Andreev approximation where Δ is much smaller than the Fermi energy E_F, the normal state dispersion is reduced to (v_F denotes the Fermi velocity) and φ is decomposed to the slowly varying part and the rapid oscillation part with the Fermi wavelength . The slowly varying function is governed by the Andreev equation

2.6

We will see below that the Andreev equation for unconventional SCs and SFs can be mapped onto the one-dimensional Dirac equation (2.1) with an effective mass m, which gives a unified description for low-lying quasi-particle states bound to defects, including surface and vortex ABSs. We also emphasize the non-trivial topological aspect of such bound states.

(a). Fulde–Ferrell–Larkin–Ovchinnikov states

In the context of condensed matter physics, equation (2.1) serves as a unified description for low-lying electronic states in various ordered systems with self-organized periodic structure. This includes the one-dimensional Peierls system [50–52], spin density waves [53], the spin-Peierls system [54], the stripes in high-T_c cuprates [55], superconducting junction systems [1] and FFLO states [56,57]. We discuss here the fundamental roles of ABSs on the thermodynamic stability of the FFLO state in a spin-singlet Pauli-limited superconductor.

For one-dimensional spin-singlet s-wave SCs, Δ(k,r)=Δ(y)iσ_y, Andreev equation (2.6) is reduced to Dirac equation (2.1) with an appropriate unitary transformation of the spin Pauli matrices σ_μ, where fermions acquire an effective mass associated with the superconducting gap. Condition (2.3) indicates that a zero-energy solitonic state exists when two asymptotic superconducting gaps have the π-phase shift, 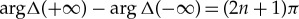. In other words, ABSs emerge in the interface of an SNS junction, whose energy is characterized by with an arbitrary phase shift φ [1]. The zero-energy solitonic state is, therefore, regarded as a special kind (φ=π) of ABSs in SNS junctions.

As the superconducting gap is constructed from pairwise quasi-particles, the BdG or Andreev equation is supplemented by the gap equation, which gives a closed set for describing self-consistent quasi-particle structures in spatially inhomogeneous SCs/SFs. The simplest form that satisfies condition (2.3) is a single-kink solution

2.7

where ξ=v_F/Δ₀ is the superconducting coherence length. The generic solution of the self-consistent equations is obtained in terms of Jacobi elliptic functions [56], which contains equation (2.7) as an exact solution.

The single-kink solution describes the domain wall of two degenerate vacua ±Δ₀ and condition (2.3) ensures the existence of the zero-energy state localized at the domain wall. The kink-shaped superconducting gap also generates phase shifts of continuum states. Owing to the presence of a soliton and phase shifts, the creation of the single-kink costs the energy E[Δ(y)]−E[Δ₀]=(2/π)Δ₀ [58] and thus the kink state cannot be thermodynamically stable at zero fields. The energy cost is, however, compensated by the Pauli paramagnetic energy, μ_BH, as the splitting of Fermi surfaces generated by a magnetic field accommodate an excess spin into the solitonic E=0 state. The kink structure is therefore stabilized in the high field regime, H>H_LO≡(2/πμ_B)Δ₀, which is lower than the Pauli limiting field . The field, H_LO, is known as the lower critical field to stabilize the FFLO state in Pauli-limited SCs. As the magnetic field increases, the superconducting gap Δ(y) forms self-organized periodic structure of multiple kink–anti-kink pairs and the quasi-particle spectrum possesses the zero-energy flat band which accommodate excess spins [56,59], as displayed in figure 1a. In the high field regime, the order parameter profile is transformed to a sinusoidal shape with a single modulation vector Q∼μ_BH/v_F. In this regime, the zero-energy solitonic states bound to each nodal point of interfere with their neighbours and the zero-energy flat band turns to the dispersive band structure due to the formation of a soliton lattice within the energy scale ∼e^−L/2ξ, where L=2π/Q is a period of the FFLO modulation, Δ(x+L)=Δ(x). The formation of the self-organized periodic structure in the FFLO state is a direct consequence of the synergistic effect between spin paramagnetism and superconductivity with the spontaneous breaking of the translational symmetry, and the solitonic state provides a key concept to capture the essence. Although the ABSs in FFLO SCs are not topologically protected, they possess the characteristics of odd-frequency spin-singlet odd-parity Cooper pair correlations due to the spontaneous breaking of the translational symmetry [60,61]. It has been discussed that ABSs play a key role on the observability of a signature of the FFLO modulation through the local density of states and modulated magnetization density [62–65]. In unconventional SCs, such as a twodimensional d-wave SC, the interplay of ABSs with the nodal pairing leads to the reorientation of the Q-vector from the nodal direction to anti-nodal direction in a high field [63].

Figure 1.

(a) Quasi-particle spectra in the reduced Brillouin zone (i) and self-consistent superconducting gap Δ(x) (ii) in a single-band FFLO state for various modulation periods L=4, 6 and 40ξ₀, where μ_↑,↓ denote the Fermi surface of spin ↑,↓ electrons. As L/ξ₀ decreases, the zero-energy ABSs become dispersive and we set k₀≡π/L. (b) Quasi-particle spectra for the minority band (i) and Δ_1,2(x) (ii) in the different subphases of two-band FFLO states. The gap |Δ₁| in the majority ‘1’ band is larger than |Δ₂|, and we set the ratio of the Fermi velocity as v_F,1/v_F,2>1. The spatial modulation of Δ_1,2(x) in L=9.6ξ₀ can be characterized by a single modulation vector Q, while a multiple-Q modulation structure emerges in L=24ξ₀. (Online version in colour.)

For Pauli-limited two-band SCs, as a result of the competing effect between two bands, the FFLO phase is divided by successive first-order transitions into an infinite family of FFLO subphases with rational modulation vectors [66,67]. When the electron bands have different superconducting gap |Δ₁|≠|Δ₂| and Fermi velocity v_F,1≠v_F,2, each band has its own favourite FFLO modulation vector Q₁≠Q₂. In figure 1b, we display the different FFLO subphases in two-band SCs, where |Δ₁|>|Δ₂| and v_F,1>v_F,2. The set of parameters indicates that in the vicinity of the FFLO lower critical field, the FFLO modulation period in the minority ‘2’ band, , is comparable to the coherence length and . These two modulation periods start to compete with each other, when the Cooper pair tunnelling between two bands is switched on. It was recently found in [66] that as a consequence of the competition, the overall modulation of the superconducting gap is characterized by a rational modulation vector of Q₂, such as Q=Q₂/(2n+1) (). The FFLO modulation is then expanded in terms of the higher harmonics (2m+1)Q as , which contains the favourable modulation vector Q₂ in addition to the long wavelength Q₂/(2n+1)∼Q₁. Hence, the resultant phase diagram realized in two-band Pauli-limited SCs may have FFLO subphases characterized by the series of the rational number Q₂/(2n+1). Figure 1b with L=24ξ₀ shows the typical subphase with n=3. The original band in the FFLO subphase with Q=Q₂/(2n+1) is folded back into a small reduced Brillouin zone by the mixed component with the larger modulation vector (2n+1)Q=Q₂. Then, the folding back generates new electron bands below the threshold energy of the continuum |E|<Δ₀ as displayed in the quasi-particle spectrum of figure 1b (green). The multiple-Q modulation structure in the FFLO subphases can be clearly reflected by the field dependences of the modulation vector and paramagnetic moment, which are found to form a devil’s staircase structure [66]. These features inherent to multiband SCs are distinct from those in single-band systems where the FFLO state emerges via the second-order transition and no subphases exist.

(b). Surface Andreev bound states in Weyl superconductors

Let us now apply the index theorem to surface ABSs emergent in unconventional SCs. As a pedagogical model, we here consider a chiral ℓ-wave pairing state, where ℓ=1, 2 and 3 correspond to chiral p-, d- and f-waves, respectively. We also do not take account of spin degrees of freedom and spatial uniformity of Δ is assumed. The superconducting gap is then given by

2.8

where . Owing to the spontaneous breaking of the time-reversal symmetry, the chiral state (ℓ≥1) in three dimensions is always accompanied by Fermi points at which the bulk quasi-particle excitation is gapless. The particle-hole symmetry of the BdG Hamiltonian guarantees the presence of pairwise Fermi points at k=k₀ and k=−k₀.

Volovik [10] found that in chiral pairing states, the Fermi points are protected by the non-trivial first Chern number defined on a two-dimensional plane embracing the Fermi points. The pairwise Fermi points thus cannot be removed by any perturbations, which are called the Weyl point. The effective Hamiltonian around the Weyl points is mapped onto the Weyl Hamiltonian, , and low-lying quasi-particles bound to the Fermi points behave as chiral Weyl fermions. Weyl fermions are massless fermions expressed by a two-dimensional spinor with a well-defined notion of the left- or right-handed coordinate, i.e. chirality. Owing to the particle-hole symmetry, the Weyl fermions residing on the pairwise Weyl points have opposite chirality. In the context of the Berry phase, the Weyl points are regarded as ‘magnetic monopoles’ in momentum space and the pairwise Weyl points are connected by a Dirac string which is accompanied by the Berry phase change γ(C)=2ℓπ along a closed loop ‘C’ embracing the string (figure 2a). Hence, three-dimensional SCs concomitant with Weyl points can be regarded as a layered structure of topological SCs with non-trivial first Chern number Ch₁ defined in each sliced two-dimensional momentum plane, where Ch₁(k_z)=ℓ, for |k_z|<k_F, and otherwise it is trivial. The bulk-edge correspondence guarantees the existence of the zero-energy states in each momentum plane. They form the zero-energy flat band structure along the k-direction connecting two Weyl points. Hence, the Fermi points of Weyl SCs correspond to the endpoint of the zero-energy flat band, leading to the ‘Fermi arc’ protected by pairwise Weyl points [8,68]. The presence of the topologically protected Fermi arc is responsible for a pronounced zero-bias conductance peak in tunnelling spectroscopy and may significantly affect quantum transport phenomena.

Figure 2.

(a) The topological structure of chiral p-wave pairing: pairwise Weyl points, Berry phase γ(C) around the Dirac string, and the first Chern number Ch₁ on each sliced momentum plane. The thick arrows denote the unit vector . Superconducting gap and surface Fermi arcs in the E_2u state (b) and E_1u state (c) as possible candidates for the B-phase of UPt₃. (Online version in colour.)

When the chemical potential is negative, the quasi-particle spectrum in the chiral state (2.8) is fully gapped and surface Fermi arcs disappear. In this situation, Ch₁ that protects the pairwise Fermi points becomes trivial and thus the Weyl points vanish. There exists the topological phase transition at μ=0, where the bulk excitation becomes gapless [69,70].

The chiral pairing state in equation (2.8) can be a prototype of Weyl SCs, superconducting analogue to Weyl semimetals [71–75]. The concrete example is the superfluid ³He-A confined to a thin film. The superfluid is known as the Anderson–Brinkman–Morel (ABM) state [76,77] which is the chiral p-wave pairing state with the orbital angular momentum L_z=1 and spin S_z=0 of the Cooper pair. In a thin film with a thickness much shorter than the dipole coherence length of around 10 μm, strong pair-breaking effect on surface restricts the orbital motion of chiral Cooper pairs into a two-dimensional plane, where the topological Fermi arc appears at the edge of the system [68,75,78,79]. Recently, Ikegami et al. [80,81] directly observed the chirality of the Cooper pairs through intrinsic Magnus force [82,83] acting on injected electrons in the surface of ³He-A. The definite chirality of the Cooper pairs generates the skew scattering of quasi-particles at injected electrons. The other candidates of Weyl SCs are the uranium compounds URu₂Si₂ [84,85] and UPt₃ [86], UCoGe [87], U_1-xTh_xBe₁₃ [88–90]. In URu₂Si₂, Yamashita et al. [84] observed the giant Nernst effect which is associated with the skew scattering of electrons due to the chirality of superconducting gap 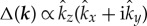[91]. The latter compound has facilitated many physicists since the first discovery of superconductivity, because it possesses similar properties with ³He as a spin-triplet superconductor. Among many proposed scenarios, the E_2u and E_1u states are most promising and competing scenarios [92–95]. The time-reversal broken E_2u states, , which assume a strong spin–orbit coupling, may possess two separated Fermi arcs terminated to Weyl points on a surface parallel to the c-axis [8,96]. Both the time-reversal broken and invariant pairings are possible in the E_1u scenario, where surface Fermi arc in the time-reversal-invariant E_1u state, or , is protected by an order-two magnetic point group symmetry [34,97]. Although both the pairing states have surface Fermi arcs as shown in figure 2b,c, only the time-reversal invariant E_1u state has anisotropic magnetic response associated with Majorana Ising spins [8,34,97].

Let us now revisit low-lying surface bound states of Weyl SCs from the viewpoint of the Jackiw–Rebbi’s index theorem in the Andreev equation. Consider a specular reflection on the xz-surface which is parallel to the nodal direction of the pairing in equation (2.8), and take the coordinate along the quasi-classical trajectory ρ≡y/v_y for incoming quasi-particle and ρ≡−y/v_y for outgoing one, where v_y denotes the Fermi velocity projected onto the y axis. The Andreev equation (2.6) with the superconducting gap (2.8) is then mapped onto the one-dimensional Dirac equation (2.1) along the trajectory ρ, where the effective mass is expressed as m(ρ)=Δ₀ e^{−iτ_zϑ(ρ)} [7]. The phase ϑ(ρ) is given as ϑ(ρ)=ℓϕ_k for ρ>0 and ϑ(ρ)=−ℓϕ_k for ρ<0. This is equivalent to a superconducting junction system with the relative phase difference 2ℓϕ_k∈[0,2π], and thus the ABSs come along the energy dispersion which is dispersive on k_x but flat band along the nodal direction k_z. According to the condition in equation (2.3), the chiral ℓ-wave pairing state has ℓ gapless points at [7]

2.9

which is insensitive to the detailed spatial profile of Δ₀ around the surface. For a specular surface perpendicular to the y axis, the ℓ Fermi arcs appear in the momentum space (k_x,k_z) projected onto the surface, which are terminated at the projection of pairwise Weyl points at (k_x,k_z)=(0,+k_F) and (0,−k_F). Owing to the spontaneous breaking of the time-reversal symmetry, the dispersion of surface ABSs must be asymmetric in k_x, i.e. E(k_x,k_z)=−E(−k_x,k_z), which is called the chiral edge state.

As the negative energy part of the branch is occupied in the ground state, the surface ABSs carry the spontaneous mass current in equilibrium [8,98–102]. In the case of the chiral p-wave pairing (ℓ=1), chiral edge ABSs along the wall of a cylindrical container carry the total angular momentum, , where N denotes the number of electrons. However, the emergence of the low-lying ABSs deviates the continuum states with |E|>Δ₀ from those in the bulk without surfaces. In other words, the existence of the mass domain wall in equation (2.1) gives rise to the phase shift of the continuum states with , in addition to the emergence of low-lying bound states. The significant contribution of the continuum state to the net edge mass current was first pointed out by Stone & Roy [98]. The modified continuum states are found to carry the net angular momentum and the total angular momentum in the chiral p-wave pairing is 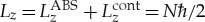. Hence, the emergence of surface ABSs in unconventional SFs/SCs simultaneously generates the ‘backaction’ in the vacuum state.

(c). Vortex Andreev bound states

The condition in equation (2.3) can also be applied to zero energy states bound to a vortex core of SCs/SFs. The chiral ℓ-wave superconducting gap having a single vortex is given as

2.10

where we introduce the cylindrical coordinate, . Here, we consider a straight and axisymmetric vortex line along the z-axis and denotes the vorticity. The superconducting gap vanishes at the vortex centre, where the phase is not well defined, and recovers to the bulk value within the length scale of ξ. As the phase continuously changes from 0 to 2κπ along the circumference enclosing the core, quasi-particles travelling along a trajectory across the vortex centre experience the phase shift of κπ. Hence, the low-energy effective theory can be mapped onto the Andreev equation in an SNS junction or the one-dimensional Dirac equation with a mass domain wall. Thus, singular vortices in SCs/SFs are accompanied by low-lying quasi-particles states, i.e. vortex ABSs.

Let us introduce a quasi-classical trajectory along parametrized as with an impact parameter b and the ‘coordinate’ [103]. The unit vector denotes the orientation of the Fermi velocity projected onto the xy-plane, . The parameters (b,s) are associated with the angles ϕ and α as and . The azimuthal angle ϕ is parametrized as , which changes from to . For a single vortex state with equation (2.10), then, the Andreev equation (2.6) is recast into the one-dimensional Dirac equation, , by employing the gauge transformation of the quasi-particle wave function (). The effective mass is expressed in terms of the vortex phase winding κϕ(s) as

2.11

As the phase factor of m(s) is reduced to sgn(s) at b=0, quasi-particles across the vortex centre with odd κ experience the mass domain wall, m(s)=−m(−s), which satisfies the condition (2.3). The correction of a small impact parameter b≪ξ twists the relative phase between s<0 and s>0 domains and deviates the relative phase from π. This indicates that the vortex bound states have dispersion with respect to the impact parameter b as E(b,k_z)∝−b, where k_z denotes the axial momentum along the vortex line. The wave function of the vortex bound states is well localized in the region of ρ∼b and has the azimuthal momentum k_F for small k_z. From the quasi-classical viewpoint; therefore, the impact parameter is associated with the angular momentum of the vortex bound states as L=b×k_F. As a result, the quasi-classical dispersion is linear on L and dispersionless on k_z as E(L,k_z)≈−ω₀L, where ω₀ denotes the energy scale of the vortex bound states and is determined by the detailed structure of Δ(ρ). However, the quantum correction discretizes L which may lift the zero-energy solution. As L is the canonically conjugate variable of α, the effective Hamiltonian for the vortex bound states is given as the one-dimensional chiral Hamiltonian . Volovik [10] found that owing to the single valuedness of the wave function, the discretized level of the vortex bound states remains as zero-energy when the net parity of the vorticity κ and chirality ℓ is even,

2.12

This includes chiral p-wave SCs with odd vorticity. For net odd parity, (−1)^κ+ℓ=−1, the quantum correction prohibits the presence of zero-energy vortex bound states. Tewari et al. [104] directly demonstrated that for chiral p-wave pairing, the Hamiltonian in the sector of the zero-energy state is mapped onto the Majorana (or Dirac) Hamiltonian with an effective mass that satisfies the condition (2.3), when the vorticity is odd. The index theorem can be extended to the vortex state of non-centrosymmetric SCs that may possess the mixing of spin-triplet and spin-singlet pairings [105].

In s-wave SCs (ℓ=0), the direct calculation of the BdG equation within k_Fξ≫1 shows (), where the zero-energy state is always absent. The discretized core levels, which are called the Caroli–de Gennes–Matricon (CdGM) state [106], were clearly observed in the spin-singlet SC YNi₂B₂C by using scanning tunnelling spectroscopy [107]. As the quantum regime () is approached, the level spacing becomes large, leading to the quantum depletion of the particle density around the core [108,109]. Pronounced depletions in the particle density were experimentally observed in rotating Fermi gases with an s-wave resonance [110] as a hallmark of superfluidity in the BCS-BEC crossover regime. The depletion also indicates the absence of vortex ABSs in the core.

Similarly with solitonic states in FFLO SCs, the CdGM states can accumulate Pauli paramagnetic moments in the vortex core when magnetic Zeeman field or population imbalance of two spin states is present [111,112]. A strong Pauli-paramagnetic effect in spin-singlet SCs drastically changes thermodynamics and transport properties in low temperatures from those in orbital-effect-dominant SCs [112]. For instance, the field dependence of low-temperature heat capacity shows a concave curve C(H)∝(H/H_c2)ⁿ (n>1) when the Pauli paramagnetic effect is dominant over the orbital depairing effect. The concave curves have been observed in heavy fermion SCs CeCoIn₅ [113], UBe₁₃ [114,115] and CeCu₂Si₂ [116]. The similar field dependence was also observed in Sr₂RuO₄ [117]. It is also worth mentioning that, if vortices and FFLO nodal planes coexist, the non-trivial topological structure of superconducting gap gives rise to the absence of low-lying ABSs at the crossing point [118]. This is attributed to the cancellation of the π-phase shift on a vortex line by an FFLO nodal plane. At this crossing point, the absence of low-lying ABSs results in the depletion of the local magnetization density. We also note that in the quantum limit with Δ²/E_F∼O(Δ), the spatial oscillation of the magnetization density inside the core manifests the energy level and vorticity of the superconducting gap and thus can be used for a fingerprint of core-level spectroscopy [111,119]. Furthermore, Eschrig et al. found that vortex core dynamics in unconventional SCs closely reflects features of the vortex ABSs [120,121].

The discretized energy levels of vortex ABSs in the chiral p-wave pairing (ℓ=1) is obtained as [102]

2.13

when the chemical potential is positive (μ>0). In contrast to the s-wave case, the zero energy state always exists when the condition of the net parity in equation (2.12) is satisfied. The zero-energy state realized in this system is protected by the topological invariant, ν, which is the parity of the second Chern number Ch₂=κℓ [122]. The zero-energy vortex ABS exists if the number is ν=(−1)^Ch₂=−1, which is consistent with (2.12). The number indicates that the zero-energy state is fragile against the quasi-particle tunnelling to the neighbouring vortex. Indeed, the intervortex tunnelling splits the zero-energy states to [123,124]. The sinusoidal and exponential factors represent the quantum oscillation of the zero-energy wave functions and localization at the vortex core, respectively. This is contrast to vortices realized in the (2+1)-dimensional Dirac equation, where the number of zero-energy states is guaranteed by the topological number [125,126]. The zero-energy states protected by the number can be realized in the interface of three-dimensional topological insulator (AII) and conventional superconductor with a fine-tuned chemical potential [127,128]. When the chemical potential becomes negative, however, the zero-energy vortex ABS disappears and the topological number is trivial, regardless of the vorticity and chirality. Hence, similarly with surface ABSs, the topological phase transition occurs at μ=0, where the bulk excitation becomes gapless.

3. Andreev bound states meet symmetry

In the previous section, we have shown a unified description for surface and vortex ABSs and non-trivial topological properties behind them. To extract multifaceted properties of ABSs and capture the essential roles of discrete symmetries, we here focus on the superfluid ³He, where various non-trivial phenomena associated with the interplay of topology and symmetry can be realized [8]. We start to introduce Majorana fermions that can be regarded as a special kind of ABSs, where we mention non-Abelian anyonic behaviours of mirror-symmetry-protected Majorana fermions in spinful odd parity SCs/SFs, such as ³He-A [17,18]. Then, we give an overview on symmetry-protected topological superfluidity realized in ³He-B confined to a slab geometry. This offers a unique platform to study the intertwining of quantum mass acquisition of surface ABSs and spontaneous symmetry breaking that protects the non-trivial topology of the bulk, resulting in the emergence of ‘topological quantum criticality’ [8,23]. We also clarify anomalous magnetic response of surface ABSs in the vicinity of the topological quantum criticality on the basis of odd-frequency pairing which is another facet of ABSs.

(a). Andreev bound states as Majorana fermions

In relativistic field theory, self-conjugate Dirac fermions are called Majorana fermions. They are represented by the quantized field Ψ that satisfies the constraint of the self-charge-conjugation in equation (1.1). The constraint is satisfied only when the antiunitary particle-hole (or charge conjugation) operator obeys , corresponding to odd parity SCs/SFs. In even parity SCs/SFs, however, the pair potential Δ(k) is always invariant under the spin rotation, and the particle-hole operator is given by 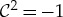. ABSs emergent to even parity SCs/SFs cannot satisfy equation (1.1) and thus cannot be Majorana fermions. The presence of a strong spin–orbit interaction may mix the spin-singlet and triplet pairings, which enables even spin singlet SCs to host Majorana fermions [105,129–131].

The fermionic field Ψ is, in general, expanded in terms of energy eigenstates as in equation (2.5). If there exist n zero-energy states (a=1,…,n), one can rewrite Ψ as

3.1

where we have used γ^(a), instead of η_E=0, in order to distinguish these zero modes. As explicitly shown in equation (2.2), the zero-energy states are composed of equal contributions from the particle-like and hole-like components of quasi-particles. This is the rigorous result guaranteed by the particle-hole symmetry of the zero energy state, , where the BdG Hamiltonian in equation (2.4) holds . The self-conjugate constraint in equation (1.1) imposes the following relations:

3.2

The zero modes satisfy the self-conjugate constraint, which are called as Majorana zero modes. As surface and zero-energy vortex ABSs in spin-triplet SCs always satisfy the self-conjugate condition, Majorana fermions can be regarded as a special facet of ABSs. When there is only a single zero mode (n=1), the local density operator defined in the particle-hole space is identically zero,

3.3

This indicates that an isolated Majorana zero mode cannot be coupled to the local density fluctuation and thus is very robust against non-magnetic impurities.

The relation in equation (3.2) also gives rise to a significant feature inherent to Majorana field. For instance, in the case of n=2, the minimal representation of the algebra in equation (3.2) is two-dimensional, which is built up by defining complex fermion operators c and c^† as

3.4

These operators obey anti-commutation relations, {c,c^†}=1 and {c,c}={c^†,c^†}=0. The two degenerate vacua |±〉 are defined as the eigenstate of the fermion parity, where |+〉 (|−〉) has the even (odd) fermion parity. The eigenstate of γ^(a) is a superposed state of opposite fermion parities, while the complex fermion preserves the fermion parity and thus can be a physical state [132]. Equations (3.2) and (3.4) bring two novel quantum phenomena: (i) non-local correlation [132] and (ii) non-Abelian statistics [133]. These two phenomena require Majorana zero modes to be spatially separated and well isolated from other quasi-particle states with higher energies. As mentioned in the previous section, a quantum vortex with a singular core in chiral p-wave SCs/SFs can host topologically protected Majorana zero modes. Ivanov [133] clarified that the low-energy physics on half-quantum vortices in spinful chiral p-wave SCs/SFs, e.g. ³He-A, is describable with singular vortices in a spin-polarized system, and the Majorana zero modes concomitant with vortices behave as non-Abelian anyons. For spinless chiral p-wave SCs/SFs with 2N vortices, N complex fermions constructed from the 2N Majorana zero modes give rise to 2^N−1-fold degeneracy of ground states with preserving fermion parity. The representations of the braiding operation of vortices are obtained as a discrete set of the unitary group which manipulates the occupation of complex fermions. As Majorana zero modes are topologically protected against quantum decoherence, they offer a promising platform to realize topological quantum computation [133,134].

Although spin-polarized Majorana zero modes behave as non-Abelian anyons, the realization of half-quantum vortices remains as an experimentally challenging task in both SF ³He-A thin film and spin-triplet SCs such as Sr₂RuO₄ [135–142]. The key to implement non-Abelian statistics of braiding vortices is a non-local pair of Majorana zero modes that form the complex fermion (3.4). Spinful Majorana zero modes can form the complex fermion as a local pair, c=(γ^(↑)+iγ^(↓)). However, it is recently recognized that mirror reflection symmetry may assist non-Abelian statistics of spinful Majorana zero modes realized in integer vortices of spin-triplet chiral p-wave SFs/SCs [17,18,143,144].

Let us assume that the normal state holds the mirror symmetry with respect to the xy plane, , where M_xy=iσ_z flips the spin σ and momentum k to (−σ_x,−σ_y,σ_z) and (k_x,k_y,−k_z). When Δ(k) has a definite parity under M_xy as [17,18]

3.5

the BdG Hamiltonian at k_z=0 is invariant under the mirror reflection, , where . Therefore, in the mirror invariant plane, k=(k_x,k_y,0), spinful quasi-particles are separated into the subsectors constructed from the eigenstates of the mirror operator. In each mirror subsector, there exists a single zero mode bound to the core of an integer vortex in chiral p-wave SFs/SCs, which is protected by the topological number. The properties of zero modes are, however, categorized into two classes, depending on the parity in equation (3.5). When the mirror operator satisfies the condition,

3.6

the particle-hole symmetry exists in each mirror subsector and the existence of the Majorana fermion is ensured by the mirror reflection symmetry. In spin-triplet SCs/SFs, the physical meaning of the condition (3.6) is associated with the orientation of the d-vector. Even though integer quantum vortices are accompanied by spinful Majorana fermions, the mirror symmetry protects multiple Majorana fermions as non-Abelian anyons unless a perturbation that breaks mirror reflection symmetry is present.

If the mirror operator violates the condition in equation (3.6), the particle-hole exchange maps a quasi-particle state to that in the different mirror subsector. This implies the absence of the particle-hole symmetry in each mirror subsector. The topological properties and nature of the zero-energy vortex ABS are categorized into class A in the Altland–Zirnbauer symmetry classes, where the zero-energy states behave as Dirac fermions [17,18].

(b). Helical Majorana fermions: surface Andreev bound states in ³He-B

Although the Weyl points are protected by the first Chern number and are responsible for the existence of the Fermi arc, it is known that the topological stability of point nodes is subject to discrete symmetries, such as the time-reversal symmetry. In particular, point nodes in time-reversal invariant SFs and SCs are no longer protected by the topological invariant when additional discrete symmetries are absent. We here discuss surface ABSs in the B and planar phases of the SF ³He, as a paradigm to capture an essence of additional discrete symmetries. The additional discrete symmetries, such as magnetic point group symmetry, enrich the characteristics of ABSs, including Majorana Ising spins [7,8,23].

The ³He atom is a neutral atom with nuclear spin and zero electron spin, and the system remains liquid phase down to zero temperatures. The quantum liquid is well describable with the strongly correlated Fermi liquid theory which holds the huge symmetry group, G=SO(3)_L×SO(3)_S×U(1)_ϕ×T. This contains three-dimensional rotations in coordinate and spin spaces (SO(3)_L and SO(3)_S), the global phase transformation group (U(1)_ϕ), and the time-reversal symmetry (T). Among possible broken symmetries of G, the phase which holds the maximal symmetry group, H_B=SO(3)_L+S×T, is known as the B-phase or the Balian–Werthamer (BW) phase. The BW state is the spontaneous breaking phase of the spin–orbit symmetry which is characterized by the broken symmetry group , where SO(3)_L−S is the relative rotation of the spin and orbital spaces. The generic form of the BW state that characterizes the order parameter manifold is obtained as

3.7

where d_μ(k)=tr[−iσ_yσ_μΔ(k)]/2. The rotation matrix R_μν is associated with SO(3)_L−S and we omit the U(1) phase. In the bulk BW state without a magnetic field, the angle φ is fixed to the so-called Leggett angl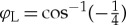e, . The -vector is affected by confinement and magnetic field. The bulk BW state has a fully gapped quasi-particle spectrum as .

(i). Surface Andreev bound states and its helicity

Let us now derive gapless states bound to the surface of the BW state, by mapping the Andreev equation (2.6) to equation (2.1). Here, we set a specular surface to be normal to the -axis and the region z>0 is occupied by the ³He-B. The unitary matrix with ϑ=ϕ_k/2−π/4 maps the Andreev equation (2.6) with equation (3.7) onto the time-reversal-symmetric pair of chiral p-wave SFs [3,7,24]

3.8

where is the SU(2) spin rotation associated with R_μν and we set . Hence, the general concept based on equation (2.1) can be extended to surface ABSs of ³He-B, which ensures the existence of the zero-energy ABSs on the surface of ³He-B. The bound state solution with |E(k_∥)|≤Δ_B has the gapless dispersion as

3.9

where k_∥=(k_x,k_y) denotes the momentum parallel to the surface. The wave function for the positive energy branch of the surface ABS in equation (3.9) is given as

3.10

where N is the normalization constant. The function with ξ_B=v_F/mξ_B denotes the spatial form of the surface ABSs. The spinors Φ₊≡(1,0,0,i)^t and Φ₋≡(0,i,1,0)^t are the eigenstates of the spin operator in the Nambu space, .

We emphasize that the spin structure of the surface ABS reflects the emergence of the spin–orbit coupling through the spontaneous spin–orbit symmetry breaking in the vacuum. The bulk quasi-particle states in the BW state are doubly degenerate as the φ_E(k) and , where and denote the operators of the time-reversal symmetry and inversion symmetry, respectively. They are also the simultaneous eigenstates of the helicity operator in the Nambu space

3.11

As the operation flips the helicity, the doubly degenerate quasi-particle states in the bulk BW state can be labelled by the eigenvalue of the helicity, h=±1. The helicity is cancelled out by two bands and the spin current is absent in the bulk. In contrast to the bulk BW state, the whole branch of the surface ABS in equation (3.10) has a well-defined helicity h_∥=+1 or h_∥=−1, where h_∥ denotes the helicity operator projected on the surface. Hence, the surface ABS in ³He-B has only a half degrees of freedom in comparison with the bulk quasi-particle states. The well-defined helicity in the whole branch of the surface ABS implies the generation of spontaneous spin current, J_μν, which denotes the spin ν flowing along the μ-direction on the surface. The orientations of the spin and flow depend on the order parameter structure and the non-zero components are given as [7,101]

3.12

where n denotes the particle density and we set . We note that similarly with the mass current in Weyl SCs/SFs (see §2b), the spin current is carried by both the ABS with |E|<Δ_B and continuum state with |E|>Δ_B, i.e. . However, the spin current J^spin_ABS carried by the surface ABS flows in the opposite direction of that carried by continuum states. This indicates that the emergence of ABSs in unconventional SCs/SFs generates the ‘backaction’ to the vacuum state. The temperature dependence of J^spin shows the T³-power behaviour in low temperatures. The power law behaviour is attributed to thermal excitations in the positive energy branch of surface ABSs and thus different from the exponential behaviour of the continuum state [7,101,145].

(ii). Topology and Majorana Ising spins

The existence of gapless surface ABSs reflects the non-trivial topological structure of the momentum space subject to the time-reversal symmetry. A generic form of a 4×4 hermitian matrix subject to time-reversal, particle-hole and inversion symmetries is expanded in terms of the four Dirac γ-matrix as , where we choose (γ₁,γ₂,γ₃,γ₄)=(−σ_zτ_x,−τ_y,σ_xτ_x,τ_z). As a result, the Hamiltonian is generally parametrized with the four-dimensional vector [m₁(k),m₂(k),m₃(k),m₄(k)]. In the above representation of γ matrices, the chiral operator Γ is written as Γ=γ₅≡γ₁γ₂γ₃γ₄. Flattening the Hamiltonian to Q(k), where Q²(k)=+1, we introduce the four-dimensional spinor that contains all the informations on , so it defines a three-dimensional sphere S³ with unit radius. The spinor defines the images of the three-dimensional k-space compactified on S³ onto the target space S³ that characterizes the Hamiltonian . The non-trivial mapping is represented by the homotopy group π₃(S³) and the winding number is given as

3.13

This indicates that w_3d counts how many the spinor warps the three dimensional sphere when one sweeps the whole momentum space. For ³He-B with equation (3.7), the winding number is evaluated as w_3d=1, which protects the existence of the gapless surface ABS with a well-defined helicity. The non-trivial topology of the BW state was pointed out by Schnyder et al. [146], Roy [147], Qi et al. [148], Volovik [149] and Sato [150].

Let us now clarify the Majorana nature of topologically protected ABSs and discuss their physical consequences, where the role of additional discrete symmetries is emphasized. Within the Andreev approximation (Δ_B≪E_F), as in equation (3.10), the whole branch of the surface ABS has equal contributions from the particle and hole components of quasi-particles. The fermionic field operator constructed from the helical ABS obeys the self-charge conjugation relation

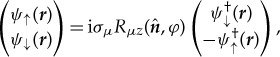3.14

which is called the helical Majorana fermion. This leads to the relation mentioned in equation (3.3) that the local density operator constructed from the surface ABSs are identically zero. Hence, it is expected that the surface ABS is robust against non-magnetic impurities. In addition, it turns out that the anomalous spin structure associated with the definite helicity generates the characteristic orientation of the local spin density operator as

3.15

where S^M_z is the logical spin operator constructed from the surface ABS for and φ=0. Equation (3.15) indicates that the surface helical ABS represented in equation (3.10) has a characteristic uniaxial orientation for the magnetic response, which is called the Majorana Ising spin [20–24]. The uniaxial orientation is determined by the order parameter of the BW state, , and thus the surface helical ABS can be coupled to an external magnetic field only when the order parameter satisfies the condition

3.16

where denotes the orientation of the applied magnetic field. In other words, the surface ABS in ³He-B remains gapless even in the presence of a magnetic field unless the condition (3.16) is satisfied.

Equation (3.16) thus indicates that the mass acquisition of surface Majorana fermions in ³He-B is associated with the configuration of the order parameter and orientation of an applied magnetic field. The effective Hamiltonian for the surface ABS is indeed mapped to the Hamiltonian for helical Majorana fermions as [7,8]

3.17

where c=Δ_B/k_F. The Majorana field ψ_M is associated with the original quantized field for surface states, ψ, as , which obeys {ψ_a,ψ_b}=δ_ab. The mass of helical Majorana fermions is parametrized by as

3.18

where γ is the gyromagnetic ratio of ³He nuclei. By replacing k_∥ to (−i∂_x,−i∂_y), one can derive the equation of motion for helical Majorana fermions from the effective Hamiltonian as

3.19

which reduces to the 2+1-dimensional Majorana equation. Without loss of generality, we set . The γ-matrices are introduced as (γ⁰,γ¹,γ²)=(σ_z,iσ_x,iσ_y), which satisfies {γ^μ,γ^ν}=2g^μν with the metric g^μν=g_μν=diag(+1,−1,−1) (μ,ν=0,1,2). The manifestation of the helical Majorana fermions is the coupling to the gravitational field through the gravitational instanton term [151,152], which is responsible for the quantization of thermal Hall conductivity. It is also predicted that the coupling of the Majorana fermions to the gravitational field gives rise to cross-correlated responses [153].

(iii). Topological origin of the mass acquisition

Equation (3.18) indicates that as long as 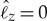is satisfied, the surface helical Majorana fermions remain gapless even in the presence of a magnetic field. We note that although the massless Majorana fermion under no magnetic field is a consequence of the non-trivial topological invariant w_3d=1 of the bulk BW state, the topological invariant in equation (3.13) is not well defined in the presence of a time-reversal breaking field. It, therefore, appears that the existence of the massless Majorana fermion under a magnetic field is not a consequence of the non-trivial topology and merely accidental. Contrary to the naive expectation, it is uncovered in [23] that the massless Majorana fermion under a magnetic field and its mass acquisition is a consequence of the intertwining effect of the hidden symmetry and topology behind the bulk BW state. The key observations are following two-fold: (i) the parameter or equivalently the mass in equation (3.18) is identified as the order parameter of an order-two magnetic point group symmetry which is referred to as the P₃ symmetry. The Ising order stays zero as long as the P₃ symmetry is preserved, but the symmetry breaking generates the non-zero Ising order . (ii) A topological invariant can be well defined if the P₃ symmetry is held. The topological invariant not only protects the existence of massless Majorana fermions but also guarantees that helical Majorana fermions possess the Ising-like spin anisotropy in equation (3.15).

To clarify the key observations, let us consider ³He-B confined in a slab geometry, where ³He is sandwiched by two parallel surfaces and is normal to the two parallel surfaces. The group symmetry subject to the confined ³He under a magnetic field is given by

3.20

The P₃ (P₂) symmetry is an order-two magnetic point group symmetry constructed by the combination of the time-reversal operation and joint π-rotation in spin and orbital spaces (mirror reflection), where the rotation about the surface normal 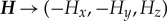(the mirror reflection in the xz plane ) is compensated by when H_z=0 (H_y=0). The combined discrete symmetries can be maintained even if each symmetry is explicitly broken. The operator of the P₃ symmetry can be constructed with the π spin rotation as with , where the joint π-rotation is expressed in terms of the SU(2) matrix as . The operator transforms the BdG Hamiltonian for the BW state as

3.21

where we introduce . Hence, can be regarded as the breaking field of the P₃ symmetry. This indicates that there are two possible subphases of G_slab, P₃ preserving phase (B_I) and breaking phase (B_II). The B_I phase maintains , while B_II has two degenerate ground states characterized by and . The quantity mentioned above is transformed non-trivially as

3.22

by the P₃ operator. Therefore, can be interpreted as an order parameter of the order-two magnetic point group P₃ symmetry, i.e. the Ising order [7,8,23].

By self-consistent calculation based on the microscopic quasi-classical theory, it is demonstrated in [23] that in ³He-B confined to a slab geometry there exists a critical field H* beyond which the P₃ symmetry is spontaneously broken by increasing a magnetic field parallel to the surface. In figure 3a, we display the phase diagram of ³He-B confined to a slab geometry in the presence of a P₃ preserving magnetic field H_∥ (parallel to the surface) and breaking field H_⊥ (perpendicular to the surface). The phase realized in H<H* and H_⊥=0 is identified as the P₃ symmetric B_I phase with , while the higher field phase in H>H* and H_⊥=0 (the thick line in figure 3a) is the B_II phase characterized by a finite Ising order . The B_II phase possesses the two degenerate Ising order and which are linked to each other by the P₃ symmetry operation as in equation (3.22). Within the Ginzburg–Landau theory, 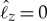for the P₃ symmetric B_I phase is favoured by the magnetic dipole interaction acting on nuclear magnetic moment of ³He atoms, while the magnetic Zeeman field stabilizes the symmetry broken B_II phase [7]. Hence, the critical field is estimated as H*≈50G associated with the dipolar field. In addition to the spontaneous symmetry breaking, as shown in figure 3a, the surface Majorana fermion in the B_II phase acquires the mass in equation (3.18).

Figure 3.

(a) Phase diagram of ³He-B in a slab geometry under magnetic fields, where H_∥ (H_⊥) denotes the magnetic field parallel (perpendicular) to the surface and preserves (explicitly breaks) the P₃ symmetry. The thin line corresponds to the symmetry protected topological phase, while the thick line is the non-topological phase with spontaneously breaking the P₃ symmetry. The momentum-resolved surface density of states in the corresponding phases is displayed in (b), which shows the dispersion of surface ABSs. (Online version in colour.)

When H_⊥ is applied, the P₃ symmetry is explicitly broken and the ground state is characterized by a definite orientation of the Ising order, or , depending on the orientation of H_⊥. The resultant phase diagram in figure 3a has the similar structure with that of the standard Ising model, where the symmetry preserving (breaking) field is replaced by the temperature T (magnetic field H). The B_II phase realized on the thick line of figure 3a is regarded as the first-order phase transition line between the phase for H_⊥>0 and for H_⊥<0. The first-order line is terminated at the quantum critical point, which is the critical field H*.

We, however, emphasize that the critical field H* is also the endpoint of the topological B_I phase protected by the P₃ symmetry. The key to understand the topological aspect of the B_I phase is the P₃ symmetry in equation (3.21) with and the particle-hole symmetry. Combining these two discrete symmetries, the BdG Hamiltonian of the B_I phase holds the chiral symmetry,

3.23

where k_⊥=(0,0,k_z) denotes the momentum along the surface normal direction and the chiral operator is defined as . As mentioned above, the non-trivial topological aspect of BdG Hamiltonian for the bulk BW state is understandable as the mapping of the base space k∈S³ onto the target space spanned by the four-dimensional unit vector , when the time-reversal symmetry is preserved. It turns out that the chiral symmetry in equation (3.23) imposes a constraint on both the base and target spaces. The symmetry reduces to the chiral symmetric momentum path k_⊥∈S¹ and . Hence, the topological invariant relevant to the non-trivial mapping is given by the one-dimensional winding number [7,23,154]

3.24

which is evaluated as w_1d=2 for the B_I phase. The chiral symmetry is preserved unless the P₃ symmetry is explicitly or spontaneously broken. The bulk-edge correspondence implies the topological protection of the massless nature of surface Majorana fermions in the case of zero Ising order . We also note that the relations on the surface spin in equations (3.15) and (3.16) are a direct consequence of the topological invariant associated with the P₃ symmetry, and thus the Majorana Ising spin, 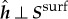, is a hallmark of the P₃ symmetric topological B_I phase [23].

The mass acquisition of Majorana fermions in equation (3.18) is directly linked to the topological phase transition concomitant with the spontaneous symmetry breaking of the vacuum. The topological origin of the mass acquisition indicates that the phase diagram around the critical field H* essentially differs from that of the standard Ising model. The ℓ_z>0 and ℓ_z<0 cannot be smoothly connected to each other along the path ‘B’ in figure 3a, but the topological phase transition occurs along the path across . The critical field H* is therefore regarded as the end point of both the first-order phase transition line and topological phase [8]. Grover et al. [155] recently predicted the emergence of the supersymmetry at the quantum critical point H*, which indicates the symmetry under the exchange of fermions (surface Majorana fermions) and bosons (Ising order).

Wu & Sauls [145] demonstrated that the P₃ symmetry is also maintained by the ³He-B in the presence of a superfluid flow, where the flow is parallel to the surface. Similarly with the B_I phase, the topological aspect of ³He-B under the superfluid flow is characterized by the non-trivial w_1d, which guarantees the existence of gapless Majorana fermions. They proposed that the power-law depletion of the superfluid current is attributed to the thermal excitations of gapless Majorana fermions.

In addition to the P₃ symmetry, there is another order-two magnetic point group symmetry that protects the non-trivial topological properties of ³He. This is referred to as the P₂ symmetry, where the operator is constructed from the combination of the mirror reflection and time-reversal operation (see equation (3.20)). The P₂ symmetry is a key to understand the topological aspect of the planar phase whose order parameter is given by . It is remarkable that although the planar phase is accompanied by pairwise point nodes, they cannot be protected by the first Chern number in contrast to Weyl SCs/SFs such as ³He-A. In [8,34,97], however, it is found that in the planar phase the zero-energy flat band terminated by the pairwise point nodes is protected by the P₂ symmetry. This is attributed to the fact that the BdG Hamiltonian having the P₂ symmetry preserves the chiral symmetry in equation (3.23) and thus the one-dimensional winding number is well defined in each one-dimensional momentum path which is perpendicular to the nodal direction (). This is another mechanism on the stability of the surface Fermi arc which essentially differs from that of Weyl SCs/SFs. We also note that the concept of the P₂ symmetry protected Fermi arc is extended to various superconducting materials, including the time-reversal-invariant E_1u scenario of the heavy-fermion UPt₃ [97] and the E_u state of superconducting topological insulator Cu_xBi₂Se₃ [156]. As the Majorana Ising spin is a generic consequence of the chiral symmetry in equation (3.23), the surface Fermi arc protected by the P₂ symmetry possesses the Ising-like magnetic anisotropy. The Fermi arc is gapped out by only a magnetic field perpendicular to the mirror plane.

(c). Andreev bound states as odd-frequency pairing

We here give an overview on another facet of ABSs in SCs/SFs, that is odd-frequency Cooper pair correlations. In SCs/SFs, the Cooper pair correlation function is defined with the anomalous part of the Matsubara Green’s function as . This denotes the Cooper pair correlation between the spin a particle at the coordinate r₁ and time −iτ and spin b particle at r₂ and 0. To classify the possible Cooper pairs, we introduce the following order-two operators, , and , which exchange the time, spin and coordinate of the paired particles as

3.25

3.26

3.27

We note that the order-two operators show , , and , and the Fermi–Dirac statistics requires . In the case of single-band SCs/SFs, therefore, exit the 2×2×2/2=4 classes of the possible Cooper pair correlations in terms of the parity of the coordinate, time and spin exchanges: ESE (), ETO (), OSO () and OTE () pairings.

In the case of spin-triplet SCs/SFs, such as ³He, only ETO pairing exists in the bulk. A time-reversal breaking perturbation can induce the mixing of spin-single pairing. As the spin-singlet pairing must have an odd parity unless the translational symmetry is broken, OSO pairing is emergent in bulk ETO SCs/SFs and ESE pairing is prohibited by the symmetry. Once a translational symmetry is broken by the existence of an interface, surface and vortices, the symmetry breaking induces OTE pairs in ETO SCs/SFs. All four pairings can emerge when both time-reversal symmetry and translational symmetry are broken. The concept of odd-frequency pairing has succeeded in extracting the fundamental roles of ABSs in anomalous spin and charge transport, electromagnetic responses, proximity effects [2,26]. In particular, odd-frequency pairing emergent in SCs/SFs is found to yield anomalous paramagnetic responses and negative superfluid density [61,157].

Using the quasi-classical approximation reliable for T_c/T_F≪1, Higashitani et al. [158] and Tsutsumi & Machida [159] demonstrated that in ³He-B, the momentum-resolved surface density of states, , is identical to the OTE pair amplitude as

3.28

for |E|<Δ_B. The OTE pairing amplitude, f^OF_z, is defined by the quasi-classical approximation of the anomalous Green’s function, , as . Hence, the surface ABS has multifaceted properties as odd-frequency pairing and Majorana fermions. The remarkable consequence of the identity between the odd-frequency pairing amplitude and surface ABSs in ³He-B is the anomalous enhancement of surface spin susceptibility χ_surf around the topological quantum critical point H* in figure 3a. For time-reversal-invariant spin-triplet (ETO) SCs/SFs, in general, the surface spin susceptibility is composed of the contributions of odd-parity (ETO/OSO) pair amplitudes, χ^OP_surf, and even-parity (OTE/ESE) pair amplitudes, χ^EP_surf, as . Mizushima [34] found that the emergent Cooper pair amplitudes and surface spin susceptibility are subject to the discrete symmetries that the superfluid/superconducting phases hold. In the ³He-B under a magnetic field, the surface spin susceptibility is expressed in terms of the Ising order as

3.29

where is the spin susceptibility of the BW state with the simplest form of the order parameter, and φ=0. The contribution of odd-parity pairings, χ^OP_surf, is understandable with the orientation of the d-vector relative to the applied field : χ^OP=0 for and χ^OP≤0 for . As the order parameter of the BW state has three d-vectors, the odd parity contribution always suppresses the spin susceptibility χ^OP<0. The even-parity contribution is estimated within the Ginzburg–Landau regime as [7,34], where ζ(3) is the Riemann zeta function and F^a₀≈−0.7 denotes Landau’s Fermi liquid parameter. Hence, equation (3.29) clearly shows that only the even-parity (OTE/ESE) pairs contribute to the surface spin susceptibility when (the P₃ symmetric topological B_I phase), while χ for (the non-topological B_II phase) is composed of only the odd-parity (ETO/OSO) Cooper pairs,

3.30

The symmetry consideration described above implies that although the OTE pair amplitudes always exist in the surface of ³He-B, they do not couple to the applied magnetic field when . This is consistent with the Majorana Ising spin of massless Majorana fermions realized in the P₃ symmetric topological B_I phase. In the B_II phase for H_∥>H*, owing to , the even-parity contribution χ^EP abruptly increases and χ^OP disappears. The paramagnetic response of the OTE pair amplitudes gives rise to the anomalous enhancement of the surface spin susceptibility that exceeds that of the normal state, χ_surf>χ_N. Since the H_∥-dependence of the surface susceptibility in ³He-B follows that of the Ising order , the measurement of the spin susceptibility in NMR experiments may detect the field-dependence of the quantum mass acquisition and topological phase transition associated with the spontaneous symmetry breaking.

4. Conclusion

We have reviewed surface and vortex ABSs in unconventional SCs and SFs and their multifaceted properties as Majorana fermions and odd-frequency pairing from the viewpoint of symmetry and topology. The unified description on the basis of the one-dimensional Dirac equation uncovers the fundamental roles of low-lying ABSs on the thermodynamic stability of FFLO SCs. In addition, the physical origin of the anomalous band structures of ABSs in Pauli-limited two-band SCs has been clarified in §2a.

The main part of the current review is devoted to giving an overview of the physics of ABSs woven by the intertwining of topology and symmetry. The special focus has been placed on the superfluid ³He as a prototype of Weyl SCs and symmetry-protected topological phases. In particular, it is recognized that the ³He-B confined in a slab geometry can serve as a unique platform to realize the topological quantum criticality as displayed in figure 3a, which may contain new quantum phenomena such as the spontaneous-symmetry-breaking-driven mass acquisition of ABSs, Majorana Ising spins, and emergent supersymmetry.

In ³He, the existence of gapless surface bound states was first pointed out by Buchholtz & Zwicknagl [160]. They uncovered the novel quasi-particle states by numerically solving the quasi-classical self-consistent theory with or without surface roughness. After the pioneering work, the efforts to detect ABSs in ³He have been made by numerous experimental groups. The manifestations of surface ABSs have been captured by several experimental groups through the heat capacity measurement [161,162], anomalous attenuation of transverse sound waves [163], and transverse acoustic impedance [9,164–168]. Among them, Murakawa et al. succeeded in the measurement of the transverse acoustic impedance with a controllable surface condition, which serves as a high-resolution spectroscopy of surface ABSs. Indeed, they observed the transformation of the characteristic shape of surface density of states by changing the surface condition from the diffusive to the specular limit. Hence, a pressing issue shared by extensive field of condensed matter physics is to capture a hallmark of Majorana nature of surface ABSs such as the Majorana Ising spins, spontaneous-symmetry-breaking-driven mass acquisition, and topological quantum criticality as discussed in §3.

Data accessibility

This article has no additional data.

Authors' contributions

Both authors contributed equally to this work.

Competing interests

The authors declare that they have no competing interests.

Funding

This work was supported by JSPS (nos. 25800199, 25287085, 25103716, 26400360, JP16K05448 and 17K05553) and ‘Topological Quantum Phenomena’ (no. 22103005) and ‘Topological Materials Science’ (no. 15H05855) KAKENHI on innovation areas from MEXT.