Spin-triplet supercurrents in Josephson junctions containing strong ferromagnetic materials

Abstract

The proximity effect between a superconducting material and a non-superconducting normal metal can extend over distances of the order of micrometres at sufficiently low temperatures. If the normal metal is replaced by a ferromagnetic material, the spatial extent of the proximity effect drops precipitously due to the exchange splitting between the majority and minority spin bands in the ferromagnet. In 2001, several theorists predicted that spin-triplet pair correlations could be induced in proximity systems involving multiple ferromagnetic materials (or multiple domains in one material) with non-collinear magnetizations. Such spin-triplet pair correlations should extend deep into the ferromagnet, producing a long-range proximity effect. In this paper, we review our experimental work in this area, which has focused primarily on Josephson junctions containing strong ferromagnetic materials. We show that Josephson junctions containing particular combinations of strong ferromagnetic materials can carry spin-triplet supercurrent over distances of at least several tens of nanometres, whereas spin-singlet supercurrent in similar samples decays over a length scale of about 1 nm. We also mention important work by other groups; however, this article is not intended to be a review of the whole field.

This article is part of the theme issue ‘Andreev bound states’.

1. Introduction

(a). The proximity effect in superconducting/ferromagnetic systems

When a superconducting (S) material is placed in contact with a non-superconducting or normal (N) metal, the properties of both materials are modified near their interface. This ‘superconducting proximity effect’ was studied extensively in the 1960s [1], and then revisited in the 1990s [2,3]. The proximity effect arises due to the process of Andreev reflection, whereby an electron incident from the N side is reflected as a hole, while a Cooper pair enters S [4]. (In the inverse process, a hole is reflected as an electron, so that a pair leaves S.) Alternatively, one can speak of Cooper pairs ‘leaking out’ of S into N, thereby endowing N with some S-like properties near the interface. (In this article, we will use the latter language, simply because it avoids awkward statements about phase coherence between an incident electron and a reflected hole.) The characteristic length scale governing the proximity effect on the N side of the interface is ξ_N, which is equal to ħv_F/2πk_BT in the ballistic limit or (ħD/2πk_BT)^1/2 in the diffusive limit, where v_F and D are the Fermi velocity and diffusion constant in N, respectively [2,3]. In the noble metal thin films used extensively in proximity effect experiments, ξ_N reaches several hundred nanometres or even 1 µm at temperatures well below 1 K.

Around 1980, theorists in the Soviet Union started addressing the issue of the proximity effect in ferromagnetic (F) materials [5]. Here, the situation is quite different from that in the S/N situation. In all but a handful of exotic S materials, the Cooper pairs consist of electrons taken from opposite sides of the Fermi surface and with opposite spins—i.e. in a spin-singlet state. In the ferromagnetic material, electrons with different spins are carried in distinct bands, which are offset in energy by twice the exchange energy, E_ex. If a spin-singlet Cooper pair ‘leaks out’ into F, then the two electrons placed at opposite sides of the Fermi surface cannot have equal and opposite momenta. Instead, the pair acquires a finite momentum ±ħQ = ħ(k_F^↑ − k_F^↓) perpendicular to the interface [6]. Alternatively, one can say that the pair correlation function acquires an oscillatory component with wavevector Q. In a three-dimensional system, the oscillations in the pair correlation function decay inversely with distance from the S/F interface, due to averaging over the angles of the possible electron pair trajectories. In a diffusive system, they decay exponentially. In an over-simplified parabolic band model for F, one can express Q as Q = 2E_ex/ħv_F, where E_ex is assumed to be sufficiently small such that one can ignore the difference in v_F between the majority and minority spin bands of F. In that case, the length scale governing the oscillations in the pair correlation function, called ξ_F, can be written as Q⁻¹ = ħv_F/2E_ex in the ballistic limit, or (ħD/E_ex)^1/2 in the diffusive limit. In the diffusive limit, both the oscillatory and exponentially decaying aspects of the correlation function are governed by the same length scale. In strong elemental ferromagnetic materials such as Ni, Fe or Co, the exchange energy is as large as an electronvolt, hence ξ_F is typically very short—of the order of a nanometre or less.

In the 1990s experimentalists made a concerted effort to observe the physical consequences of the oscillatory proximity effect predicted to occur in S/F systems, but the experiments were hampered by the very short values of ξ_F found in common F materials. For example, in thin S/F bilayers, the critical temperature T_c was predicted to oscillate as a function of F-layer thickness. Such oscillations were indeed observed in Nb/Gd multilayers [7], but those results were questioned by some workers because ferromagnetic films often have ‘magnetically dead layers' at interfaces with non-magnetic materials [8]. It is difficult to separate the effects of such dead layers from the interesting oscillatory behaviour predicted for T_c(d_F) in systems with sub-nanometre values of ξ_F. A major breakthrough occurred in 2001 when two groups carried out S/F proximity effect experiments using two different dilute ferromagnetic alloy systems. Their idea was to reduce E_ex in the F material and thereby increase ξ_F to a value more conducive to experimental control. Using tunnelling spectroscopy, Kontos et al. [9] studied the proximity effect in Nb/Pd_1−xNi_x bilayers with x = 0.12. They observed that the characteristic peaks and dips in the density of states (DOS) as a function of energy changed sign when the PdNi thickness exceeded a certain value—a clear signature of the oscillatory nature of the S/F proximity effect. Ryazanov et al. [10] studied the Josephson effect in Nb/Cu_1−xNi_x/Nb junctions with x = 0.45, and found that the critical supercurrent I_c had an oscillatory temperature dependence for certain CuNi layer thicknesses. That anomalous temperature dependence occurs in S/F/S Josephson junctions containing an F material, where E_ex is not too much larger than the critical temperature of the superconductor. Soon after, oscillations in I_c of S/F/S Josephson junctions as a function of F-layer thickness were reported by Kontos et al. [11], and thereafter by several groups in rapid succession [12–17].

(b). Prediction of long-range spin-triplet proximity effect in S/F systems

During the exciting times of 2001 described above, a few workers in the field of S/F systems were trying to understand some very puzzling experimental results that had appeared a couple of years earlier. Three groups had claimed to observe evidence for ‘long-ranged’ proximity effects in S/F systems [18–20]. The experimental evidence came in the form of resistance measurements of an F wire attached to a large S electrode. As the temperature was lowered below T_c, the resistance of the wires dropped substantially—by amounts reminiscent of what one would expect to see in an N metal with very long ξ_N, but orders of magnitude larger than what one should expect to see in an F metal with very short ξ_F. There was some concern that the experimental results could arise from a changing resistance right at the S/F interface, rather than deep into the F wire [21,22]. Nevertheless, the results could not be entirely explained away.

In 2001, two theoretical groups predicted that spin-triplet pair correlations could be created in S/F systems in the presence of certain types of magnetic inhomogeneities involving non-collinear magnetizations in different parts of the structure [23,24]. Spin-triplet pairs with full spin projection onto the quantization axis—called ‘equal-spin’ triplets by some—are not subject to the exchange energy in F, because both electrons are in the same spin band. Hence such equal-spin triplets should persist over long distances in F, giving rise to a long-range proximity effect. It was suggested by both Bergeret et al. [23] and by Kadigrobov et al. [24] that the presence of spin-triplet pair correlations might explain the anomalous resistance decrease observed in S/F systems and mentioned above. Several more theoretical works in 2003 extended the initial results to a variety of physical situations [25–27].

Confirmation of this theoretical suggestion by the experimental community took several years. While measuring the electrical resistance of a ferromagnetic wire connected to a superconductor might appear to be the simplest and most direct measure of the proximity effect, the interpretation of such measurements is not always straightforward. Several important parameters are not easily controlled in such experiments, including the resistance of the interface, the presence of stray magnetic fields from the F wire, the domain structure of the F wire, etc. Without control of those parameters, interpretation of the experimental results is open to debate. Two experimental breakthroughs came in 2006. Keizer et al. [28] observed supercurrent through Josephson junctions fabricated on the surface of CrO₂ with a superconducting electrode separation of about 300 nm. CrO₂ is a so-called ‘half-metallic’ ferromagnet, i.e. the DOS at the Fermi energy is completely spin polarized. Assuming that the surface of the CrO₂ maintains the half-metallic character of the bulk, it is simply not possible for a spin-singlet pair of electrons to propagate through the CrO₂. At about the same time, Sosnin et al. [29] observed a modulation of the resistance of Ho wires up to 150 nm in length, connected to superconducting electrodes at both ends, as a function of the superconducting condensate phase difference between the two electrodes. Both of these experiments defied explanation by the conventional S/F proximity effect, and were interpreted by their authors as evidence for the long-range spin-triplet correlations predicted in 2001.

In spite of those experimental breakthroughs, scepticism in the experimental community remained high. In neither experiment were the experimenters able to control the magnetic inhomogeneity that supposedly gave rise to the long-range proximity effect. And in the experiment by Keizer et al., the magnitude of the supercurrent varied by two orders of magnitude in different samples.

2. Observation of spin-triplet supercurrents

The breakthroughs by Keizer et al. [28] and Sosnin et al. [29] inspired the experimental community to search for spin-triplet pair correlations in better-controlled experiments. Several groups started attacking the problem using Josephson junctions containing strong ferromagnetic materials. In the absence of spin-triplet correlations, the critical current, I_c, of such junctions is expected to drop very rapidly with F-layer thickness, over a length scale ξ_F. There was a general realization by experimentalists that, to provide convincing evidence for spin-triplet supercurrents, one would have to systematically measure the dependence of I_c on the length or thickness of the ferromagnetic material, to distinguish the rapidly decaying spin-singlet supercurrent from the long-range spin-triplet supercurrent. The question that remained unanswered, however, was how to produce such spin-triplet supercurrents efficiently and reliably? In one of their early papers, Bergeret and co-workers had suggested making Josephson junctions of the form F′/S/F/S/F^″, where the adjacent pairs of ferromagnetic layers—F′ and F, and F and F^″—have non-collinear magnetizations, in order to produce spin-triplet correlations in the corresponding sandwiched S layers [27]. One difficulty with this proposal is that the S layers must have thicknesses d_S comparable to the superconducting coherence length ξ_S = (ħD/Δ)^1/2, where Δ is the superconducting gap in S. If d_S < ξ_S, then superconductivity is completely suppressed in S, whereas if , then the Cooper pairs in S hardly note the relative orientation of the magnetizations of the F layers on either side of S. In fact, there have been many experiments on trilayer samples of the form F′/S/F in which T_c of the trilayer varies with the relative orientation of the magnetizations of F′ and F (some of these will be mentioned later in this article), so the experimental difficulty of finding a suitable value of d_S is not insurmountable. A second objection to the F′/S/F/S/F^″ geometry is that it is difficult in a sandwich-style structure to attach leads to the two buried S layers. For whatever reasons, no successful experiments measuring supercurrent have been performed with samples of this geometry.

In 2007, Houzet & Buzdin [30] suggested an alternative Josephson junction geometry of the form S/F′/F/F^″/S. This geometry has two immediate advantages over the F′/S/F/S/F^″ geometry. First, there is no limit on the thickness of the S electrodes, and second, because those electrodes are on the outside of the structure, they are easy to contact. It is not clear how much immediate impact the proposal by Houzet & Buzdin had on the experimental community. Experimentalists have their own motivations for trying out specific materials combinations or sample geometries. What is clear several years later is that essentially every successful experimental realization of spin-triplet Josephson junctions can be viewed as some variant of the Houzet–Buzdin design.

Experimental success was still not immediate, however, and it was not until 2010 that five different groups, working independently, published results that convinced the majority of the community that spin triplets were for real. Our group studied Josephson junctions of the form S/F′/N/SAF/N/F^″/S, functionally identical to the proposal by Houzet & Buzdin [30], but with the addition of crucial non-magnetic buffer layers (N) to suppress exchange coupling between adjacent ferromagnetic layers, and with the central F layer replaced by a synthetic antiferromagnet (SAF) consisting of a Co/Ru/Co trilayer [31]. The SAF has the desirable property that the magnetizations of the two Co layers are coupled antiparallel to each other, so that the SAF introduces almost no net magnetic flux into the junction [32]. Figure 1 shows a schematic drawing of our sample structure. In our original samples, F′ and F^″ were thin layers of a weak ferromagnet alloy (PdNi or CuNi); such weak ferromagnetic alloys also do not inject much magnetic flux into the junction [34,35]. (We discovered later that thin layers of pure Ni worked just as well or better at generating spin-triplet supercurrent [36].) As we systematically varied the thickness of the SAF, we found that the critical current, I_c, of such junctions hardly decayed for SAF thicknesses up to 24 nm, as shown in figure 2. By contrast, I_c decayed very rapidly with SAF thickness in similar junctions without the two outer ferromagnetic layers. For a fixed SAF thickness, figure 3 shows that the magnitude of I_c varies non-monotonically with the thicknesses of the F′ and F^″ layers, first increasing rapidly at small thickness, reaching a maximum, and then decreasing more slowly. These results were consistent with the theoretical picture provided by Houzet & Buzdin, and they provided strong evidence that the supercurrent flowing through the samples containing the F′ and F^″ layers was spin-triplet in character.

Figure 1.

Schematic diagram (not to scale) of the Josephson junctions fabricated by our group. All of the layers through the Au layer are sputtered in a single run without breaking vacuum. The top Nb wiring layer is deposited after the junctions are patterned. The depth of the ion mill that defines the junction area can be adjusted as desired. Figure adapted from Klose et al. [33]. (Online version in colour.)

Figure 2.

Critical current I_c times normal-state resistance R_N versus total Co thickness D_Co for S/SAF/S junctions (black squares) and S/F′/SAF/F^″/S junctions (red circles). The SAF is Co/Ru/Co, and both F′ and F^″ layers are PdNi alloy of thickness 4 nm. The value of I_cR_N for the S/SAF/S junctions drops rapidly with D_Co, whereas it is nearly independent of D_Co for the S/F′/SAF/F^″/S junctions. Figure taken from Khaire et al. [31]. (Online version in colour.)

Figure 3.

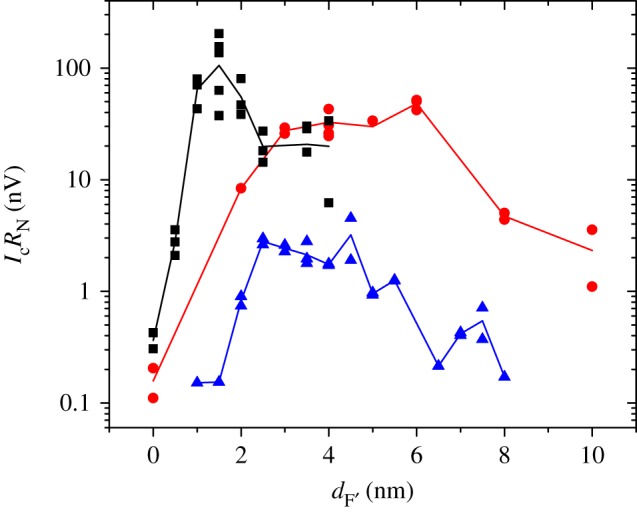
The I_cR_N product versus thickness of F′ and F^″ layers for three different sets of Josephson junctions. The F′ and F^″ layers are identical in each set, and are Ni (black squares), PdNi alloy (red circles) or CuNi alloy (blue triangles). The solid lines are guides to the eye. Figure taken from [36]. (Online version in colour.)

Results from four other groups appeared in rapid succession. Robinson, Witt & Blamire at Cambridge University had opted for a different materials approach, using the spiral magnetization structure of elemental Ho to generate non-collinear magnetizations in the samples [37]. Their sample structure was S/Ho/F/Ho/S, with Co as the F-layer material. Robinson et al. found that the supercurrent in their samples hardly decayed with Co thickness, whereas the supercurrent decayed very quickly with Co thickness in samples that did not contain the crucial Ho layers. In addition, the ability of the Ho layers to generate spin-triplet supercurrents varied non-monotonically with Ho thickness in a manner suggesting that the total angle through which the Ho magnetization rotates from one side of the layer to the other plays a crucial role. Later that summer Sprungmann et al. [38] showed intriguing results from Josephson junctions containing the ferromagnetic Heusler alloy Cu₂MnAl. As a function of F-layer thickness, the I_c of the junctions first dropped, then reached a plateau for 7 nm < d_F < 10 nm, then dropped precipitously for d_F > 10.3 nm. The authors postulated that the plateau in I_c was caused by spin-triplet pairs that were generated by regions of non-collinear magnetization at the interfaces between the CuMnAl and its neighbours. When d_F exceeds 10.3 nm, the magnetism in the bulk CuMnAl becomes sufficiently strong so as to fully align the magnetizations in the interface regions, thereby eliminating the source of non-collinear magnetization and killing the enhancement of I_c. Wang et al. fabricated Josephson junctions containing single-crystal Co wires, contacted by tungsten electrodes in a lateral geometry [39]. They observed supercurrent in wires as long as 0.6 µm, but only in samples with electrodes fabricated by focused-ion-beam (FIB) deposition. The authors' interpretation was that the FIB fabrication process induces magnetic disorder, hence regions of non-collinear magnetization, at the interface between the electrodes and the wire. (A very different interpretation of this experimental result also exists, relying on the ballistic nature of the electron transport in the wires [40].) Finally, Anwar et al. [41] revisited the earlier work by Keizer et al. [28] on Josephson junctions made from depositing a superconducting MoGe alloy on top of CrO₂ films. They found supercurrents in samples with a MoGe electrode spacing of 700 nm—surely of spin-triplet character. Anwar et al. emphasized that the growth morphology of CrO₂ is quite different when grown on different substrates. They observed supercurrents in a few samples grown on Al₂O₃, but none in samples grown on TiO₂ (Keizer et al., by contrast, did observe supercurrent in a few samples grown on TiO₂), but noted that their samples did not contain the biaxial magnetocrystalline anisotropy present in the samples of Keizer et al. A year later, Anwar et al. found that inserting thin layers of Ni between the CrO₂ and the MoGe electrodes enhanced the generation of spin-triplet supercurrent, and they observed supercurrents in several CrO₂ samples grown on TiO₂, with critical currents 100 times larger than in their previous CrO₂ samples grown on Al₂O₃ [42]. This was another triumph for the S/F′/F/F^″/S geometry suggested by Houzet & Buzdin [30].

3. Conceptual picture of spin-triplet supercurrent generation

The original theoretical predictions of spin-triplet correlations in S/F systems were the result of calculations using Green's function methods based on the Eilenberger or Usadel equations, for the ballistic or diffusive limits, respectively. For many experimentalists (including this author), the fundamental physical principles behind such calculations are not transparent. Fortunately, in 2010 Eschrig introduced a simple conceptual picture that explains how spin-singlet Cooper pairs in a conventional superconductor are converted into spin-triplet pairs in an S/F proximity system in the ballistic limit [43]. This picture should not be confused with a real theoretical calculation, but we include it here because of its immediate appeal to experimentalists, and because we believe that having such a picture is likely to foster new insights by both experimentalists and theorists. The starting point is the spin-singlet state of a single Cooper pair in S: |0, 0〉 = (1/√2) (|↑ ↓〉 − |↓ ↑〉), where we have omitted the spatial part of the wave function showing that a Cooper pair consists of a superposition of pairs of states at opposite sides of the Fermi surface. Next we consider what happens in a simple S/F bilayer. According to the picture described in the second paragraph of this article, if the up-spin electron goes into the majority spin band with wavevector +k_F^↑, then the down-spin electron must go into the minority band with wavevector −k_F^↓. The pair wave function thereby picks up an oscillatory component exp(iQX), where Q = k_F^↑ − k_F^↓ and X is the centre-of-mass coordinate of the pair along the direction perpendicular to the S/F interface. Alternatively, if the down-spin electron goes to the positive k side of the Fermi surface, then the pair will pick up the factor exp(−iQX). We write the resulting state as:

3.1

where we used the Euler formula to get the second line, and |1, 0〉 = (1/√2)(|↑↓〉 + |↓↑〉) is the m_s = 0 component of the spin-triplet state. Equation (3.1) shows that the |1, 0〉 component appears automatically in any S/F system due to the different phase shifts acquired by the up- and down-spin electrons as they propagate in F. Note that the m_s = 0 component of the spin-triplet state has all the same properties as the spin-singlet state, in that it oscillates and decays over a very short length scale in F. (The fact that the m_s = 0 triplet component is generated in any S/F proximity system was missed in some early theory papers. It has become commonplace to refer to short-ranged proximity effects as simply ‘spin-singlet’ when in fact one should say ‘spin-singlet plus m_s = 0 component of spin-triplet’, but the latter is too burdensome to write every time.) To get the long-range spin-triplet components, |1, 1〉 = |↑↑〉 or |1, −1〉 = |↓↓〉, we simply need to add a second ferromagnetic layer whose magnetization axis is non-collinear with that of the first ferromagnetic layer. So imagine now the system S/F′/N/F, where F′ is magnetized along the z-axis, and F is magnetized along an axis in the x–z plane at an angle θ with respect to the z-axis. Let the thickness of F′ be d_F′. Ignoring any phase shifts in N, we can write the state |χ〉 at the N/F interface from equation (3.1) in the rotated basis of F:

3.2

If we make F much thicker than the ferromagnetic coherence length ξ_F discussed in the Introduction, then the |0, 0〉 and |1, 0〉 components of |χ〉 will die out. The other two components, |1, 1〉_θ and |1, −1〉_θ, are long-ranged in F. Equation (3.2) also shows that the optimal thickness of F′ for generating spin-triplet correlations is of order Q⁻¹ ≈ ξ_F.

In a real system, there will be finite probabilities of reflection at each interface, and those reflection probabilities will be different for electrons entering or leaving the majority or minority bands of the ferromagnetic layers. None of those effects are taken into account in this simple picture, but they could be easily added, and would lead to different coefficients in front of the |1, 1〉_θ and |1, −1〉_θ components in (3.2). We are still not finished, however. To make a Josephson junction, we cannot simply slap the final S electrode onto our S/F′/N/F system, because the condensate in S will not recognize the spin-triplet components. So we have to reverse the process by adding a third ferromagnetic layer, which should also have thickness d_F^″ ≈ ξ_F. We finally arrive at the structure S/F′/N/F/N/F^″/S, which is the one proposed by Houzet & Buzdin [30] in 2007.

Equation (3.2) explains the data shown in figure 3, which show how the magnitude of the spin-triplet supercurrent varies with the thicknesses of the F′ and F^″ layers. The pure ferromagnet Ni generates spin-triplet components more quickly than the dilute ferromagnets Pd_1−xNi_x or Cu_1−xNi_x, because the former has larger E_ex hence smaller ξ_F. After reaching a maximum at a thickness d_F′ = d_F^″ ≈ ξ_F, the decrease in triplet supercurrent with further increase in d_F′ and d_F^″ reflects the exponential decay of the singlet and m_s = 0 component of the triplet in the diffusive limit.

4. Towards control of spin-triplet supercurrents

As the excitement of the 2010 discoveries subsided, it was clear that there was still a lot of work to be done. The properties of the Josephson junctions reported in 2010 were not entirely under the control of the experimentalists who had fabricated them. In particular, one could not vary the properties of the samples in situ, i.e. after fabrication. Rather, one had to fabricate a whole series of samples while systematically varying the thickness of some layer—e.g. the PdNi layers in the Michigan State junctions or the Ho layers in the Cambridge junctions—to ‘control’ the magnitude of the spin-triplet supercurrent. Theory predicted that the spin-triplet supercurrent should depend on the relative orientations of adjacent F-layer magnetizations. Taking the standard S/F′/F/F^″/S geometry for concreteness, the spin-triplet component of I_c should be zero if the magnetizations of either F′ and F or F and F^″ are collinear. An even more intriguing possibility arises in situations where the magnetizations are non-collinear so that the spin-triplet supercurrent is dominant. Theory predicts that the junctions should be standard or ‘0-junctions’ if the sense of magnetization rotation from F to F^″ is the same as from F′ to F, while they should be ‘π-junctions’ if the sense of rotation reverses. To be more specific, take the simplest case where all three magnetizations lie in the x–z layer plane, and with the magnetization of F′ along z and the magnetization of F along x. Then the junction will be a 0-junction if the magnetization of F^″ is along –z (antiparallel to the magnetization of F′), or a π-junction if the magnetization of F^″ is along +z (parallel to the magnetization of F′).

A second issue that was not fully addressed in the 2010 experiments was the true extent of the ‘long-range’ spin-triplet supercurrents. Experiments demonstrated clearly that the spin-triplet supercurrents persisted over length scales much longer than spin-singlet supercurrents, but the results from Michigan State, Cambridge and Bochum showed only that such supercurrents persisted over lengths of tens of nanometres at most. Only the results from Leiden on CrO₂ and from Penn State on single-crystal Co nanowires showed supercurrent persisting over hundreds of nanometres, but there was not yet a systematic attempt by any of the groups to determine the triplet decay length. Finally, the Josephson effect is not the only way to detect spin-triplet correlations. Other approaches, including tunnelling spectroscopy or measuring T_c of S/F/F′ trilayers, will be discussed briefly in the following section.

A first step towards control of spin-triplet supercurrents occurred in our laboratory. While writing her Ph.D. thesis, Trupti Khaire magnetized one of her S/F′/N/SAF/N/F^″/S samples. The expectation was that I_c would drop due to the alignment of the magnetizations. Instead, she found that I_c increases by a factor of 20. We immediately realized that this dramatic enhancement of I_c was caused by a peculiar property of the SAF, namely that it undergoes a ‘spin-flop’ transition when subjected to an in-plane magnetic field. While the two Co magnetizations in the SAF are trying to remain antiparallel due to the antiferromagnetic coupling mediated by the Ru, the external field is trying to align them. The result is that the magnetizations ‘scissor’ towards the direction of the external field. When the field is turned off, the magnetizations are left pointing perpendicular to the direction of the field. In the meantime, the outer F′ and F^″ layers have been magnetized in the direction of the field; hence adjacent layer magnetizations in the sample are now orthogonal, maximizing the generation of spin-triplet supercurrent. To verify this scenario, we sent samples to NIST in Gaithersburg, Maryland, for further magnetic analysis. There Julie Borchers and her team performed polarized neutron reflectivity (PNR) measurements on the samples in both the as-grown states and after being magnetized. John Unguris and his post-doc, Ben McMorran, performed scanning electron microscopy with polarization analysis (SEMPA) measurements on the samples. SEMPA is performed in slices, by ion milling the sample in situ in the electron microscope and taking pictures as they go with polarization information. Both the PNR and SEMPA results supported the spin-flop picture. In the meantime, Carolin Klose in our laboratory was replicating and extending Trupti Khaire's results, using Ni instead of PdNi as the F′ and F^″ material. As she varied the Ni thickness, d_Ni, she found the largest enhancement of I_c with d_Ni = 1.0 nm. Figure 4 shows I_c versus the external field H_applied used to magnetize the sample for a sample with d_Ni = 1.0 nm [33]. The large increase in I_c occurs when H_applied reaches the coercive field of the thin Ni film.

Figure 4.

The I_cR_N product measured at zero field, as a function of magnetizing field H_applied, for S/F′/SAF/F^″/S Josephson junctions containing 1.0 nm of Ni for the F′ and F^″ layers, and with a total SAF thickness of 20 nm. A large enhancement in I_cR_N occurs when the two Ni layers are magnetized and the SAF has undergone a spin-flop transition. Figure taken from Klose et al. [33].

The explanation given above for the enhancement of I_c is only half the story. The Josephson junctions we studied in our early work had diameters of 10 µm or more, hence the magnetic layers were multi-domain. If the domain structure in the as-grown state is truly random, then one would expect to create an ensemble of 0-coupled and π-coupled regions, with equal probabilities, across a typical junction area. One would expect the critical supercurrent, I_c, of such a junction to be smaller than in a similar junction with uniform coupling across its area. A sample with the F′ and F^″ layers magnetized in the same direction should have uniform π-coupling across the whole junction area, providing a second mechanism of I_c enhancement. Unfortunately, the experimental data do not provide any way to assess the relative importance of the two mechanisms; all we can say is that magnetizing our samples with the optimum d_Ni = 1.0 nm produces a factor of 20 increase in I_c.

The next major step forward in control of spin-triplet supercurrents was achieved by Banerjee et al. [44]. Those authors fabricated junctions with structure S/F′/N/F/N/F′/S, with F′ = Permalloy(1.5) and F = Co(5.5), with thicknesses in parentheses in nanometres. This structure is a straight realization of the Houzet & Buzdin [30] proposal. The reason that these authors could use such a thick Co layer without having to use a SAF to cancel the magnetic flux is that their junctions were extremely small—with lateral dimensions of 500 × 600 nm. The small sample size limits the magnetic flux contributed by the magnetic materials in the junction. Additionally, in the magnetically saturated state, the three ferromagnetic layers in such small junctions are single-domain, while during the switching process from one saturated state to the other, the magnetization configuration can be approximately deduced from micromagnetics simulations. Banerjee et al. found that the magnitude of I_c varied substantially as a function of applied field as the field was swept through zero to switch the magnetizations. The highest I_c occurred at applied fields of about ±10 Oe. Simulations showed that the Permalloy magnetization tended to switch at a lower field than the Co magnetization, as expected due to its low magnetocrystalline anisotropy. The maximum value of I_c occurred when the Permalloy magnetization had nearly completed its switching, whereas the Co magnetization was still in the middle of the switching process. As a result, there were substantial regions of the sample where the Permalloy and Co magnetizations were non-collinear, giving rise to large spin-triplet supercurrent.

The results of Banerjee et al. [44] were the best attempt at the time towards reproducible control of spin-triplet supercurrent. But they suffer from the fact that the magnetic configuration where the largest I_c is observed is not stable to small changes in the applied field. One would like to have a situation where a sample is put into a certain configuration by applying a field, the applied field is then removed, and the sample stays in the same configuration. Two ongoing experiments in our laboratory have this goal. The first experiment is similar in philosophy to the Banerjee experiment, with two major differences. First, we use a SAF rather than a single ferromagnet for the F layer. Our hope, confirmed by measurements of the anisotropic magnetoresistance, is that a Co/Ru/Co SAF is magnetically stiff enough not to change its magnetization in sufficiently small applied fields, of the order of 100–200 Oe. In addition, use of the SAF should minimize stray fields that could influence the magnetization of the soft ferromagnetic layer above it. The second difference is that the shape of one or more of the ferromagnetic layers is round rather than rectangular. (Since the shape of the junctions is determined by ion milling, we have the option of patterning only the top S electrode, or continuing the mill to pattern any number of the three ferromagnetic layers. If we pattern only the top F^″ layer while leaving both the SAF and the bottom F′ layer unpatterned, then we minimize stray field from them.) William Martinez in our group has observed promising behaviour in samples with the structure S/F′/N/SAF/N/F^″/S with F′ = Ni(1.2), SAF = Co(4.0)/Ru(0.75)/Co(4.0) and F^″ = Permalloy(1.0). The thin Ni F′ layer has a very high coercive field, so its magnetization hardly changes after it is magnetized. As long as the SAF magnetization is stationary, then we are able to rotate the Permalloy magnetization freely, using rather small fields, to turn the spin-triplet supercurrent on and off. Most importantly, the Permalloy magnetization stays put when the field is turned off. These results have since been published [45].

The second supercurrent control experiment we are working on is to control the phase shift across the junction, rather than the magnitude of I_c. We are also attempting this experiment using junctions of the structure S/F′/N/SAF/N/F^″/S. As explained earlier, if the magnetizations of the F′ and SAF are kept fixed, then one should be able to change the junction from a 0-junction to a π-junction by reversing the magnetization direction of the F^″ layer. So again we use Ni(1.2) for F′ because of its large coercive field, whereas we have used either Pd_1−xFe_x (with x = 1.5%) or Permalloy for F^″ because of their low coercive fields. Compared to the experiment described in the previous paragraph, this experiment has the advantage that the sample shape can be elliptical rather than circular, thereby contributing to the stability of the two magnetic states of the soft F^″ layer. The difficulty is in the measurement, because measuring a phase shift requires performing an interference experiment. Ideally one would like to fabricate a superconducting quantum interference device (SQUID) where one junction is a standard 0-junction (S/I/S or S/N/S), while the other junction is the switchable S/F′/N/SAF/N/F^″/S junction. Unfortunately, fabrication of a SQUID with two very different types of junctions is difficult. It is much easier to fabricate a SQUID with two similar junctions, but with different shapes so as to have different switching fields for the soft F^″ layers. Eric Gingrich has made such samples and performed the measurements. He observed 0–ϕ switching in several samples, but we have not yet published those results because we were not sufficiently convinced that we had full control over the magnetic configuration of all the ferromagnetic layers in the samples [46]. (See Note added in proof.)

5. Other advances using spin-triplet supercurrents

Using the spin-flop transition of a SAF is not the only way to ensure that the F-layer magnetization is perpendicular to the F′ and F^″ layer magnetizations. An alternative is to use a magnetic material with perpendicular magnetic anisotropy (PMA) for either the F layer or for both the F′ and F^″ layers. We followed the former approach, using a [Ni/Co] multilayer in place of the SAF for the F layer. Figure 5 shows our results for junctions containing a [Ni/Co] multilayer as the central F ferromagnet, both with and without the essential F′ and F^″ layers. We found that the maximum supercurrents in samples of this structure were slightly larger than in samples using the SAF [47]. These promising results lead us naturally to the question: Which is the better way to generate non-collinear magnetizations: using the SAF or the PMA material for F? Subsequent work in our group on controlling the spin-triplet supercurrent is favouring the SAF. Even though the PMA samples show slightly larger values of I_c, we believe that the stray fields above and below the PMA material adversely affect the magnetic properties of the F′ and F^″ layers just below and above.

Figure 5.

The I_cR_N product versus thickness of central Co/Ni multilayer for two sets of Josephson junctions. Black inverted triangles and green triangles correspond to S/F/S junctions where F is a Co/Ni multilayer with perpendicular magnetic anisotropy (PMA). Red circles correspond to S/F′/F/F^″/S junctions with the same F multilayer, but with 1.0 nm Ni added as F′ and F^″ layers. Figure taken from Gingrich et al. [47]. (Online version in colour.)

This section would not be complete without mentioning work by others on oxide materials. As early as 2003, Santamaria's group in Madrid fabricated and studied the transport properties of epitaxial superlattices of the half-metallic ferromagnet LaCaMnO and the high-T_c superconductor YBaCuO [48]. They observed signs of a long-range proximity effect, which they attributed to spin-triplet correlations [49]. Subsequent work on oxide heterostructures has been performed by groups in Poland [50], Canada [51], Israel [52] and Russia [53], among others. The interpretation of the experimental data in oxide materials has been controversial; a review of this area is beyond the scope of this article. We refer the interested reader to two recent papers in the field [53,54].

6. Evidence for spin-triplet correlations in other experiments

Measuring supercurrent is not the only way to detect the presence of spin-triplet pair correlations. Two other experimental approaches that have been followed by several groups are measuring the superconducting transition temperature T_c of F/S/F′ or S/F′/F trilayers, and using tunnelling spectroscopy to measure the DOS in S/F′/F systems.

As noted in the Introduction, several studies of the T_c of S/F bilayers as a function of F-layer thickness were carried out in the mid-1990s. More interesting, however, is the study of T_c of F/S/F′ or S/F′/F trilayers as a function of the relative direction of the magnetizations of the two ferromagnetic layers. This idea dates back to a suggestion by de Gennes in 1966 [55], followed by an experiment by Deutscher & Meunier in 1969 [56]. The idea then lay dormant for nearly three decades until Oh et al. [57], Tagirov [58] and Buzdin et al. [59] independently discovered different versions of the idea in the late 1990s and Tagirov named it a ‘spin switch’. In 2002, the idea was realized experimentally by Gu et al. [60], who measured the T_c of a thin Nb film sandwiched between two CuNi films, and found a slight difference in T_c between the configurations when the two magnetizations were parallel or antiparallel. We followed that up by replacing CuNi with pure Ni, and found a somewhat larger, but still rather small, T_c difference [61]. Since then, many groups have contributed to this area, using both F/S/F′ and S/F′/F configurations. There was some controversy over the fact that either the parallel or antiparallel configuration can have a larger T_c, which depends partly on the relative importance of exchange physics and stray field effects. We will not discuss here the many papers addressing that topic. The culmination of this work is the observation of complete switching between the normal-state resistance and zero resistance by changing from the parallel to the antiparallel magnetization state, which has been achieved in an S/F′/F system by a Russian–German collaboration [62], and in a FI/S/FI system (where FI = ferromagnetic insulator) by Moodera's group at MIT [63].

Keeping the two magnetizations in an F/S/F′ or S/F′/F structure either parallel or antiparallel limits the proximity effect to the short-range components only, i.e. the spin singlet and m_s = 0 spin triplet. If the two magnetizations are non-collinear, however, then spin-triplet components should be generated. It was predicted theoretically that, in that case, one should observe a T_c that is lower in the non-collinear configuration than in either the parallel or antiparallel configurations [64,65]. Several groups have now confirmed that prediction, first with rather small T_c shifts [66–69], and more recently in work by the Aarts group at Leiden on CrO₂, with a much larger T_c shift [70]. In our opinion, these experiments represent the first truly successful control of the spin-triplet proximity effect, even if shifting T_c may seem less spectacular than creating a supercurrent where none was possible without spin-triplet generation.

Tunnelling spectroscopy has played an important role in our understanding of superconductivity since the first tunnelling measurements on a Pb film by Giaever in 1962 [71]. As we mentioned in the Introduction, the tunnelling measurements of Kontos et al. [9] in 2001 on a Nb/Pd_1−xNi_x bilayer represented a major breakthrough in our understanding of the short-range proximity effect S/F systems. The sign change in the DOS anomaly they observed reflected only the singlet and m_s = 0 triplet components of the pair correlations. Many years later we repeated that experiment, replacing PdNi by pure Ni, and observed multiple oscillations in the sign of the DOS anomaly as a function of increasing Ni thickness [72]. Although we did not report it at the time, we also searched for signatures of the long-range spin-triplet proximity effect, by adding a second F′ layer into our samples. Theorists had predicted that the presence of the long-range triplet component should produce a peak in the DOS at the Fermi energy, which should persist to large distances in F, and should not oscillate in sign with F-layer thickness [73–75]. Alas, by the time the F-layer thickness was large enough to fully suppress the singlet component, the deviations in the DOS were too small for us to detect any possible triplet signature.

Even before our measurements, Char's group in Seoul in collaboration with Beasley's group at Stanford had also carried out tunnelling measurements on S/F systems containing strong ferromagnetic materials [76,77]. Tunnelling into the F side of a Nb/CoFe bilayer, they observed one sign inversion of the DOS anomaly with increasing CoFe thickness before the DOS anomaly became too small to measure [76]. In a Nb/Ni bilayer, they observed a ‘double-gap’ structure, which they later interpreted in terms of a p-wave spin-triplet component of the pair correlations [77,78]. We did not observe such a double-gap structure in our Nb/Cu/Ni trilayer samples, but our measurements were performed at much higher temperature (2.1 K rather than 0.28 K), so narrow features in the DOS may have been smeared out in our experiment. Suffice it to say, nobody had observed any signatures of a long-range spin-triplet proximity effect in tunnelling measurements before this year.

Very recently, the Cambridge group, working in collaboration with Scheer's group in Konstanz, tried a new approach [79]. Rather than tunnel into the F side of an S/F bilayer or S/F′/F trilayer, they decided to tunnel into the S side. One might think (as we did) that any induced spin-triplet component of the order parameter would be swamped by the much larger spin-singlet component. That may be true, but this approach has the advantage that any observable signal has zero background, due to the hard gap in the DOS of a conventional s-wave, spin-singlet superconductor. This strategy has paid off. The Cambridge–Konstanz group used their favourite ferromagnetic material, Ho, in a Nb/Ho bilayer to create a magnetic texture with non-collinear magnetization. Using scanning tunnelling microscopy, they observe a peak in the DOS at zero energy at some locations on the sample. The peak is sensitive to applied magnetic field in a manner consistent with their understanding of the evolution of the magnetic non-collinearity in the Ho. These exciting results certainly deserve further study.

7. Summary and outlook

This article has focused on our work studying spin-triplet supercurrents in Josephson junctions. While we have mentioned a few selected works by other groups, this article is not intended to be a review. We have not even discussed all of our own work, and we have ignored many promising predictions regarding spin–orbit scattering, interplay between triplet supercurrents and magnetization dynamics, as well as many other topics. Most egregiously, we have neglected hundreds of theoretical papers on the topic. That is ironic, given that theory has led experiment for most of the way in this field. Nevertheless, the experimental breakthroughs are what excite this author. Two reviews of the field have appeared recently, and we refer the interested reader to them [80,81]. For those interested in the historical development or theoretical underpinnings of the subject, we refer the reader to some older and more comprehensive reviews, which are still highly pertinent today [82–85].

Where does the field go from here? Clearly, there is much more work that needs to be done in designing systems where the spin-triplet proximity effect can be generated efficiently and controlled at will. Beyond that, however, the popular literature in the field refers to the promise of ‘superconducting spintronics’. That area, if indeed it exists, is certainly in its infancy. One area of application that is currently being pursued by industry is the application of ferromagnetic Josephson junctions to superconducting memory [86]. It is still too early to tell if spin-triplet effects will play a role in that development; nevertheless, it is promising to see that the field has moved beyond the confines of academia.

Note added in proof

This article was written in 2015. Since that time, there have been many exciting developments in the field achieved by many groups. We mention here only one of our own: the successful demonstration of controllable 0–π switching in a spin-triplet Josephson junction [87].

Data accessibility

All data can be obtained from the author.

Competing interests

We have no competing interests.

Funding

The work reported here was funded by the US Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering, under Award DEFG02-06ER46341, and was performed in part in the Keck Microfabrication Facility at Michigan State University. Work on switching a spin-triplet junction between its 0 and π states was supported in part by IARPA under SPAWAR contract N66001-12-C-2017. S. Diesch was also supported in part by the German–Israeli Project (DIP) from the Deutsche Forschungsgemeinschaft.