Abstract
Computational methods for identification of cell populations from polychromatic flow cytometry data are changing the paradigm of cytometry bioinformatics. Data clustering is the most common computational approach to unsupervised identification of cell populations from multidimensional cytometry data. However, interpretation of the identified data clusters is labor-intensive. Certain types of user-defined cell populations are also difficult to identify by fully automated data clustering analysis. Both are roadblocks before a cytometry lab can adopt the data clustering approach for cell population identification in routine use. We found that combining recursive data filtering and clustering with constraints converted from the user manual gating strategy can effectively address these two issues. We named this new approach DAFi: Directed Automated Filtering and Identification of cell populations. Design of DAFi preserves the data-driven characteristics of unsupervised clustering for identifying novel cell subsets, but also makes the results interpretable to experimental scientists through mapping and merging the multidimensional data clusters into the user-defined two-dimensional gating hierarchy. The recursive data filtering process in DAFi helped identify small data clusters which are otherwise difficult to resolve by a single run of the data clustering method due to the statistical interference of the irrelevant major clusters. Our experiment results showed that the proportions of the cell populations identified by DAFi, while being consistent with those by expert centralized manual gating, have smaller technical variances across samples than those from individual manual gating analysis and the nonrecursive data clustering analysis. Compared with manual gating segregation, DAFi-identified cell populations avoided the abrupt cut-offs on the boundaries. DAFi has been implemented to be used with multiple data clustering methods including K-means, FLOCK, FlowSOM, and the ClusterR package. For cell population identification, DAFi supports multiple options including clustering, bisecting, slope-based gating, and reversed filtering to meet various autogating needs from different scientific use cases.
Keywords: autogating, data prefiltering, recursive clustering, cell population identification, constrained clustering
The success of flow cytometry (FCM) is dependent on being able to accurately identify discriminant cell populations. Currently, the most common existing approach is still manual gating analysis, which is subjective, time-consuming, and difficult to reproduce. Technical variance is usually found in independent manual gating analysis conducted across experiments, studies, and labs (1,2). During the last decade, many computational methods have been developed for the identification of cell populations from polychromatic FCM data. State-of-the-art computational approaches are shown to be superior to manual gating analysis in terms of efficiency, reproducibility and reduction of human bias (3–16). Based on whether user inputs are required, these approaches can be broadly categorized into unsupervised (11,15–27) and supervised/semisupervised (28–31) approaches. The adoption of the unsupervised population identification methods in the routine use by research labs is still challenging. Two limitations that are known in the existing data clustering methods are: (a) interpretation of the identified data clusters and (b) identification of the “difficult-to-resolve” cell populations defined by the user. Addressing these two issues will help remove the roadblock for the adoption of the existing unsupervised clustering-based autogating approaches by the experimental scientists. In this article, we propose a constraint-based recursive filtering and clustering approach—DAFi (directed automated filtering and identification of cell populations)—to address these two issues. Our goal is not to propose a new data clustering or classification method. Instead, we aimed to develop a computational approach utilizing the existing data clustering methods for effectively and reliably accomplishing the task of autogating for identifying both user-defined and novel cell populations from multidimensional FCM data in both data-driven and interpretable way.
Figure 1 illustrates the design of DAFi. The input data will first be clustered by a data clustering method (Step 1 in Fig. 1A). Manual gating boundaries used to define the first cell population formed a hyper-polygon, which is used to identify whether a data cluster belongs to the user-defined cell population based on the position of the cluster centroid (Step 2 in Fig. 1A). The clusters with centroids within the hyperpolygon (the magenta cluster and the blue cluster) are merged in Step 3, before the merged data (colored in red, Fig. 1A) is output to the next run of clustering analysis in Step 4. The procedure repeats until all user-defined cell populations are identified. Both predefined and novel cell populations are organized within an easily interpreted gating hierarchy (Fig. 1B). We refer to this type of approach as directed unsupervised clustering. Figure 1C and 1D illustrates the challenge of identifying the difficult-to-resolve CD4+CD25+ regulatory T cells (Tregs) using either manual gating analysis or the existing data clustering methods in a single run. While DAFi using K-means clustering yielded cell populations with natural distributions (Fig. 1C), manual gating analysis using polygon partitions did not capture natural boundaries of cell populations (i.e., an abrupt lower boundary in the CD25 dimension); K-means clustering failed to identify the rare Treg cell population at all, even with K = 500. Cluster centroids (highlighted in red crosses) identified by FlowSOM (26) with K = 100 were shown in Figure 1D, none of which was in the CD4+ CD25+ region specified by the user-defined red rectangle. To provide more examples, Figure 1E shows DAFi-identified major (CD4+ T and CD8+ T cells) and rare (CD3+CD56+ T and CD3hiCD56+ T cells) cell populations. The CD3+CD56+ T and CD3hiCD56+ T cell populations are difficult to separate by manual gating analysis because the two clusters are both relatively rare and close to each other in CD3 expression distributions. However, they were well segregated with natural boundaries (unimodal distribution on each dimension) using DAFi, which applied recursive clustering with manual gating polygons as constraints rather than absolute boundaries.
Figure 1.
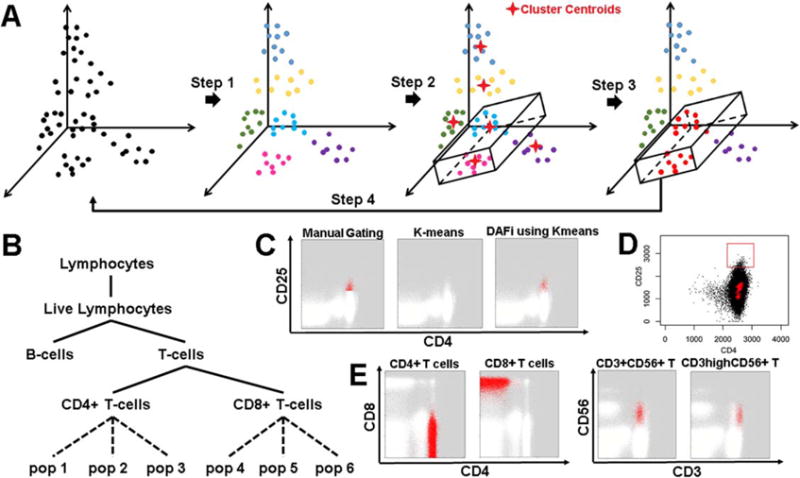
Design features of DAFi. (A) Steps in the DAFi workflow. In Step 1, putative cell populations are identified by data clustering in multidimensional space, with cell events colored by population membership. In Step 2, a hyper-polygon is provided from combining 2D manual gating boundaries to identify the dataspace region of interest. Cell clusters are selected if their centroids are located within the hyper-polygon (two clusters shown, in light blue and magenta). In Step 3, all cell events associated with the centroids are selected and retained as the filtered population (in red), which is used as the input to the next iteration in Step 4. (B) An example gating hierarchy in which the DAFi framework can be used to identify both predefined (solid lines) and novel (dotted lines) cell populations, and organize them within a user-provided gating hierarchy for simplified annotation and interpretation. (C) Comparison of different ways for identification of the putative CD4+CD25+ regulatory T cells (Tregs): manual gating analysis with abrupt cut-off; single run of K-means clustering (K = 500) applied to whole sample, and DAFi using the K-means for recursive filtering and clustering. The identified Treg cells are colored in red and the remaining cells colored in white. (D) Challenge in identification of user-defined (red rectangle showing gating boundary) CD4+CD25+ regulatory T cells (Tregs) using a single run of data clustering analysis. Centroids of data clusters identified by applying Flow-SOM clustering method (K = 100) to the whole sample are highlighted in red crosses, none of which is in the CD4+CD25+ region. E) DAFi (K-means clustering used) identification of CD4+ T, CD8+ T, CD3+CD56+ T and CD3hiCD56+ T cells. CD4+ T and CD8+ T cells are shown on CD4 vs. CD8 dot plots, while CD3+CD56+ T and CD3hiCD56+ T cells are on CD3 vs. CD56 plots. Cell populations identified by DAFi are colored in red. [Color figure can be viewed at wileyonlinelibrary.com]
Results
Evaluation of DAFi is focused on whether it can improve the capability of the existing data clustering methods for robust identification of various types of cell populations in an interpretable way. FCM data used in this study were from our HIPC studies (Human Immunology Project consortium, https://www.immuneprofiling.org) as well as the public Imm-Port database (Immunology Database and Analysis Portal, http://www.immport.org). Results of DAFi were assessed both quantitatively and by visual examination of the identified cell populations on dot plots. For the quantitative assessment, instead of using the “bulk assessment” such as the sample-level F-measure which is dominated by contributions from the abundant cell populations, we focus on cell type specific statistics for individual cell populations.
Cell Type Specific Assessment in Comparison with Individual and Centralized Manual Gating Analysis
The first assessment was focused on the identification of different T cell subsets using a representative 10-color reagent panel on multiple repeat runs of cryopreserved PBMC (peripheral blood mononuclear cells) from one sample donation of a healthy donor (1). Repeated FCM experiments were performed on various days throughout a 7-month period by three different operators on four different cytometers. This allows us to minimize the biological difference but measure the technical variance across the samples in the FCM experiment. Technical variability associated with each cell population across the 24 runs can be estimated and compared between the results of DAFi and those from the manual gating analysis.
Two manual gating analysis results were available for comparison—individual manual gating analysis (INDI) performed by different operators when the FCM data were acquired, and centralized manual gating analysis (CENT) performed by one analyst after data from all 24 samples had been acquired. The variety of cell subsets and their relationship specified by INDI in a predefined hierarchy are shown for a representative sample in Figure 2A. Among the 22 cell populations identified by manual gating analysis, 17 of them are of special user interest (Supporting Information File S1). They were divided into two categories based on the technical variance—“clearly defined” and “poorly resolved”—defined by coefficient of variation (CV) in cell population proportions across the 24 samples from individual manual gating analysis (1):
Clearly defined (low CV): 5: Monocytes; 7: B-cells; 8: NK cells; 11: T-cells; 12: CD4+ T cells; 13: CD8+ T cells; 15: Naïve CD4+ T cells; 19: Naïve CD8+ T cells.
Poorly resolved (high CV): 9: CD3+CD56+ T cells; 10: CD3hiCD56+ T cells; 14: Tregs (regulatory CD4+ T cells); 16: Tcm CD4+ T cells (central memory CD4+ T cells); 17: Tem CD4+ T cells (effector memory CD4+ T cells); 18: Temra CD4+ T cells (effector memory CD4+ T cells that express CD45RA); 20: Tcm CD8+ T cells; 21: Tem CD8+ T cells; 22: Temra CD8+ T cells.
Figure 2.
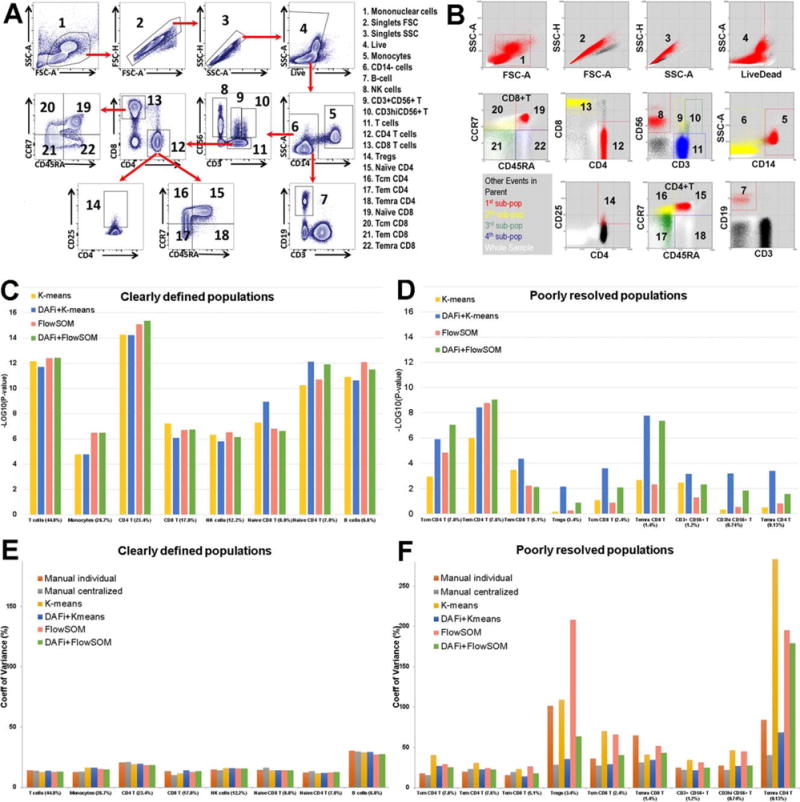
Results of DAFi using K-means and FlowSOM in comparison with individual and centralized manual gating analysis. (A) Illustration of the manual gating hierarchy for identifying the 22 predefined cell populations from the 10-color T cell panel, with gating boundaries shown on each 2D dot plot. Along the direction of the red arrows is the sequence of the gates with their parent populations. The cell populations are numbered. Names of the cell types are listed to the right. (B) Results of DAFi using K-means for identifying the corresponding 22 predefined cell populations. Events from the whole sample are colored in white. The black colored dots are events of the parent population, with events identified by DAFi highlighted in red, yellow, green, and blue. (C) Linear regression analysis of percentages of clearly defined cell populations identified by the K-means and the FlowSOM data clustering methods with and without DAFi compared with centralized manual gating. X axis: cell populations sorted based on their average percentage, from the largest to the smallest. Y axis: P values (–log10 transformed) of x-variable in linear regression analysis between percentages of the cell populations identified by four computational methods and the centralized manual gating analysis. (D) Linear regression analysis of percentages of poorly resolved cell populations identified by the K-means and the FlowSOM data clustering methods with and without DAFi compared with centralized manual gating. (E) CV of population percentages across the 24 samples for clearly defined cell populations by six different approaches. (F) CV of population percentages across the 24 samples for poorly resolved cell populations by the six different approaches. [Color figure can be viewed at wileyonlinelibrary.com]
Previously (1), we found that both INDI and CENT could achieve a high degree of concordance for identifying clearly defined cell populations; but for the poorly resolved ones, CENT significantly outperformed INDI.
We have implemented DAFi in a way so that different data clustering methods can be used to generate the filtered data and identify the cell populations. Here we reported the results from the K-means and the FlowSOM (26). The former is a classic unsupervised method while the latter one of the most recent methods representing the state-of-the-art approaches (32). Results of DAFi using the K-means (DAFi + K-means) were plotted in Figure 2B. Visual examination shows the main difference between DAFi + K-means and the manual gating analysis is that DAFi + K-means identified cell populations with natural boundaries, while manual gating analysis resulted in abrupt bisecting on some of the two-dimensional (2D) plots. Based on the dot plots, the three most difficult-to-resolve gating boundaries seem to be: (a) between CD3+CD56+ T (Pop#9) and CD3hiCD56+ T cells (Pop#10); (b) among Naïve CD4+ T and three memory CD4+ T cells; (c) between Tregs (Pop#14) and CD4+ helper T cells. Dot plots of these cell populations across all 24 samples can be found in Supporting Information File S2a and b. Visual examination showed that DAFi using K-means successfully identified natural boundaries of these difficult-to-resolve cell populations.
Linear regression analysis (Figs. 2C and 2D) was used to measure the consistency on the percentages of the identified cell populations between the results of CENT and those of four different computational approaches: K-means results mapped to user gating strategy (K-means), results of DAFi using K-means mapped to user gating strategy (DAFi + K-means), FlowSOM results mapped to user gating strategy (FlowSOM), and results of DAFi using FlowSOM mapped to user gating strategy (DAFi + FlowSOM). Number of clusters (K) was set to 500 for all four methods. The identified data clusters were mapped to user gating strategy based on the positions of the cluster centroids. We can see the cell population percentages identified by both the K-means and the Flow-SOM, with or without the recursive data filtering of DAFi, are highly consistent with those by CENT for clearly defined cell populations (Fig. 2C: all P values smaller than 0.0001, ranged from 1024 to 10214). The use of DAFi, however, clearly improved the identification of the poorly resolved populations. Both single-run K-means and FlowSOM failed to identify many of the poorly resolved populations in a consistent way with CENT (Fig. 2D), including Tregs, Tcm CD8+ T cells, CD3hiCD56+ T cells, and Temra CD4+ T cells. In contrast, the degree of concordance with the CENT result increases when the recursive DAFi filtering was used (Fig. 2D). Supporting Information File S3 shows the Pearson’s r (R2) and the linear equations identified in the linear regression analysis for each individual cell population, from both the DAFi + K-means and the DAFi + FlowSOM methods.
Figures 2E and 2F compare CV of population percentages across the 24 samples identified by six different approaches: INDI, CENT, K-means, DAFi + K-means, FlowSOM, and DAFi + FlowSOM. For clearly defined populations (Fig. 2E), the six approaches generated highly consistent CV values. For poorly resolved populations, K-means, FlowSOM and INDI generated relatively larger CV values than the other three approaches (Fig. 2F), especially for rare cell populations (e.g., Tregs and Temra CD4+ T cells). Supporting Information Files S4 and S5 include the results of using different values of K in FlowSOM and DAFi + FlowSOM for the correlation with the CENT result and the CV comparison, showing the identification of the poorly resolved cell populations could be further improved when a larger number of data clusters were identified.
Correlation Analysis between Cell Population Proportions with Subject Age and Gender
Results in the previous section showed the improvement that DAFi brought to the clustering-based identification of cell populations. While the results have shown that DAFi can effectively identify all 22 user-defined cell populations in a consistent way with the centralized manual gating analysis (CENT), we were interested in assessing whether the DAFi analysis can identify the same biologically meaningful findings as the CENT can do. In this section, we extended the single-donor analysis in the previous section to assess PBMC samples from 132 human subject participants, which were stained with the same 10-color panel used in the previous section. Details about the FCM experiment can be found in the published study (1). The goal of our assessment was twofold: (a) to determine if T cell population frequency determined by DAFi correlated with subject demographics, including age and gender, and (b) whether the correlation identified by DAFi is consistent with findings by CENT of the 132 samples and previous knowledge.
Before identifying whether there is correlation between proportions of cell populations and subject age and gender, we tested whether age and gender are confounders to each other. Figure 3A shows the distribution of the ages (Y axis) of the two gender groups. P values from the nonparametric Wilcoxon rank sum test between the two gender groups (Female vs. Male) showed the age difference is insignificant between genders. Therefore, we were able to mix the subjects from both genders to increase the statistical power for the age-based correlation analysis. Our analysis was focused on 12 predefined T-cell populations to compare with the results reported in (7): 11: T-cells; 12: CD4+ T cells; 13: CD8+ T cells; 14: Tregs; 15: Naïve CD4+ T cells; 16: Tcm CD4+ T cells; 17: Tem CD4+ T cells; 18: Temra CD4+ T cells; 19: Naïve CD8+ T cells; 20: Tcm CD8+ T cells; 21: Tem CD8+ T cells; 22: Temra CD8+ T cells. Percentages of these T cell populations were identified by DAFi using K-means (K = 500) across the 132 samples. Consistently with our previous analysis using CENT (1), we found that the proportion of Naïve CD4+ T and Naïve CD8+ T cells decreased with subject age (Figure 3B, linear regression P values after Bonferroni correction are 3.740 E 206 and 9.678 E 211, respectively). Figure 3C shows the Pearson correlation scores and the corrected linear regression P values between the results of DAFi and CENT, across all 12 cell populations. Again, the result of DAFi is highly consistent with that of CENT.
Figure 3.
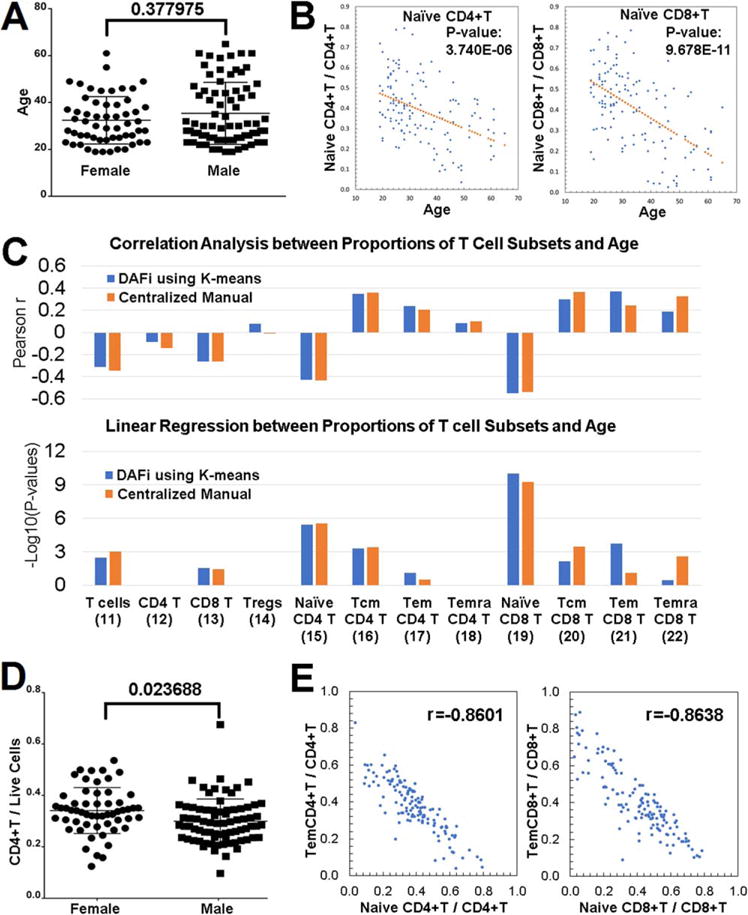
Correlation analysis of DAFi-defined cell population proportions with subject age and gender. (A) Age distribution of participants separated by gender. (B) Proportions of Naïve CD4+ T and Naïve CD8+ T cells (with CD4+ and CD8+ T cells as parents, respectively) versus age with linear regression P values reported. (C) Pearson correlation and linear regression analysis of proportions of T cell subsets with subject age. Parent population definitions of the T-cell subsets can be found in Figure 2A. P values of x-variable in linear regression analysis were –log10 transformed and multiple comparison corrected by Bonferroni correction. (D) Proportion of CD4+ T cells in female and male participants. (E) Correlation between the proportions of effector memory T cells versus Naïve T cells. [Color figure can be viewed at wileyonlinelibrary.com]
In the gender-based correlation analysis, DAFi identified that the proportion of the CD4+ T cell population seems to be significantly different between the female and male (Bonferroni-corrected P values 0.023688 using Wilcoxon rank sum test, Fig. 3D). In our previous analysis (1), we were not able to identify this correlation with a significant P values using CENT, although we previously found the average CD4+ T cell proportion was higher in the female group than the male group. We checked literature and found a number of previous studies have reported significant increases in CD4+ T cells in females (33–41). Most recently, the 10k Immunomes Project based on a meta-analysis of 578 subjects in the ImmPort Database reported the percentages of CD4+ T cells are significantly elevated in women as compared to men (42).
The DAFi analysis also disclosed there exists correlation in population proportions between different T cell subsets. Figure 3E shows the distributions of the population proportion values (Yaxis) from the two most significant Pearson correlation scores. One is between Naïve CD4+ T cells and Tem CD4+ T cells (r = 20.8601) and the other between Naïve CD8+ T cells and Tem CD8+ T cells (r = 20.8638). Both are negatively correlated. This finding is consistent with the age-based analytics, which showed the number of memory T cells increasing with age while the number of Naïve T cells decreasing with age. Compared with the result of CENT, DAFi identified a stronger association of the proportion increases with age for both Tem CD4+ and Tem CD8+ T cell populations (Fig. 3C).
Quantification of Human Immune Response to Influenza and Pneumococcal Vaccination
Results in the two previous sections were focused on population identification from the same T cell panel. In this section, we applied DAFi to identify plasmablasts/plasma cells, whose frequency is a commonly used measure of human immune responses to vaccination. The FCM dataset used, SDY180 (43), was downloaded from the ImmPort database (www.immport.org). 36 human subjects were enrolled into three immunization arms for FCM experiments: Fluzone (2009–2010 seasonal influenza vaccine, N = 12), Pneumovax23 (23-valent pneumococcal vaccine, N = 12), and Saline (N = 12). PBMC samples were collected at 10 different time points: Day-7, 0 (vaccination day), 0.5, 1, 3, 7, 10, 14, 21, and 28. FCM data files used in our data analysis (306 FCS files in total) were acquired using an 8-color reagent panel focused on identification of the plasmablasts/plasma cells and other types of B cells: FSC-A, SSC-A, FITC-A_IgD, Pacific-Orange-A_CD45, APC-A_CD138, APC-Cy7-A_CD27, PE-A_CD24, PE-Texas-Red-A_CD19, PE-Cy5-A_CD20, and PE-Cy7-A_CD38. Manual gating analysis was used to identify the cellular composition at the 10 different time points before and after vaccination, which revealed a peak in plasmablast frequencies at Day 7 post vaccination for both vaccines (43).
We reanalyzed the B-cell phenotyping FCM data of SDY180 using DAFi (K-means clustering used with K = 500). Dot plots of CD19+ B cells (Fig. 4A, blue) and Plasmablasts (Fig. 4B, magenta) identified by DAFi are shown with their defining rectangle boundaries. Note that events outside the 2D rectangles may still belong to the cell population as long as the centroid of their data cluster is within the hyper-rectangle. Similarly, an event inside the 2D rectangle may not be assigned to the cell population if its cluster centroid is outside the hyper-rectangle. In Day 7 samples only, the IgD−CD27hi plasmablasts can be clearly seen. The clear peaks on Day 7 post both Fluzone and Pneumovax23 vaccinations (Fig. 4C) confirmed the finding reported previously (43). We applied 0–1 min-max normalization to both results (medians of the population percentages across different samples on the same day were used) so that the time-series patterns identified by both approaches could be compared. The time-series pattern identified by DAFi is a close match with that by manual gating analysis (Fig. 4D), with a peak on Day 7 for both Fluzone and Pneumovax 23 groups. The second peak post vaccination in the Fluzone group is on Day 14, which also seems a close match between the two approaches. The baseline identified by DAFi seems smoother than that of manual gating analysis in all three groups. 11-fold and 47-fold increase were reported in the previous publication in the absolute numbers of plasma-blasts following vaccinations of Fluzone and Pneumovax23, respectively (43). When comparing the median percentage values of DAFi-identified plasmablasts on Day 7 with the baseline (Day 7), we achieved 16-fold and 43-fold increase post Fluzone and Pneumovax23 vaccinations, respectively, a close match to the manual gating analysis result reported previously.
Figure 4.
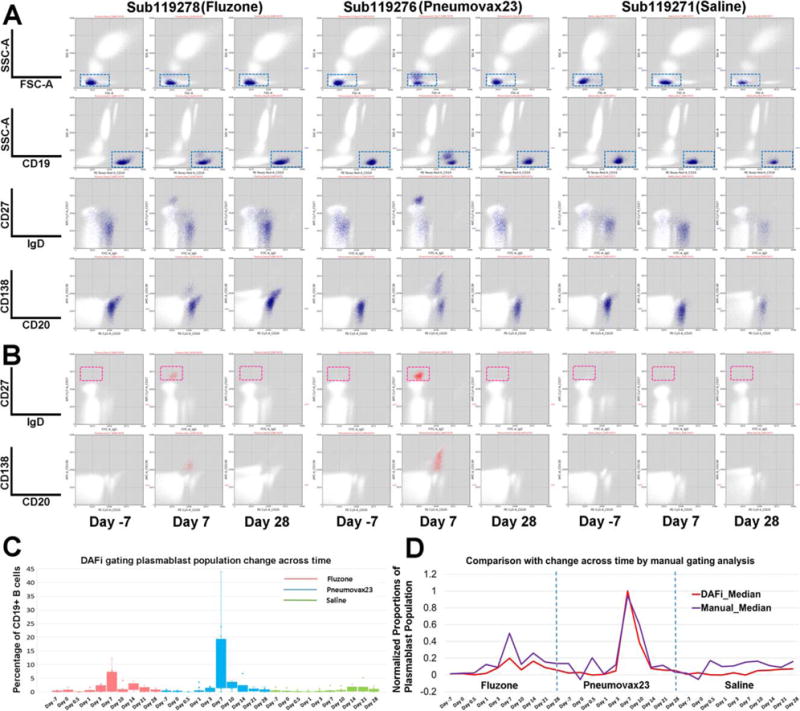
Quantification of human immune response to influenza and pneumococcal vaccination using DAFi. From left to right under each vaccine/saline treatment are three selected time points from one individual in each treatment group: 7 days before the treatment (Day 7), and Day 7 and Day 28 after treatment. (A) CD19+ B cells were identified by DAFi using the 2D rectangular gates in FSC/SSC-A and CD19/SSC-A plots illustrated in the first two rows. The two following rows show the B cell events (colored in blue) on IgD versus CD27 and CD20 versus CD138 dot pots. (B) Plasmablast cells identified by DAFi from the CD19+ B cell population. The plasmablasts, defined as IgD−CD27hi, are shown in the red box. (C) Percentage of plasmablast cells (with CD19+ B cell as parent) identified across times and treatment groups by DAFi in box plots. (D) Normalized proportions of the plasmablast population (with CD19+ B cell as parent) identified by DAFi and manual gating analysis across times and treatment groups. [Color figure can be viewed at wileyonlinelibrary.com]
Identification of Known and Novel Cell-Based Biomarkers for Latent Tuberculosis Infection
In previous sections, we showed how DAFi can improve the identification of user-defined cell populations. In this section, we assessed whether DAFi can be used to improve the identification of cell populations that have not been defined in a manual gating strategy. The dataset consists of 12 PBMC samples from 6 latently tuberculosis infected (LTBI) human subjects and 6 Mycobacterium tuberculosis (Mtb) uninfected control (healthy control; HC) subjects used in a previous study (44). Samples were stained with a 10-color panel with markers CXCR3, CD3, CD4, CD45RA, DUMP (CD8, CD14, CD19, and Live), CCR7, Tetramer, CCR4, CD25, and CCR6. The manual gating strategy aimed to identify the CD4+CD25−CCR6+CCR4−CXCR3+ memory T cells associated with subject phenotypes (Figs. 5A and 5B).
Figure 5.
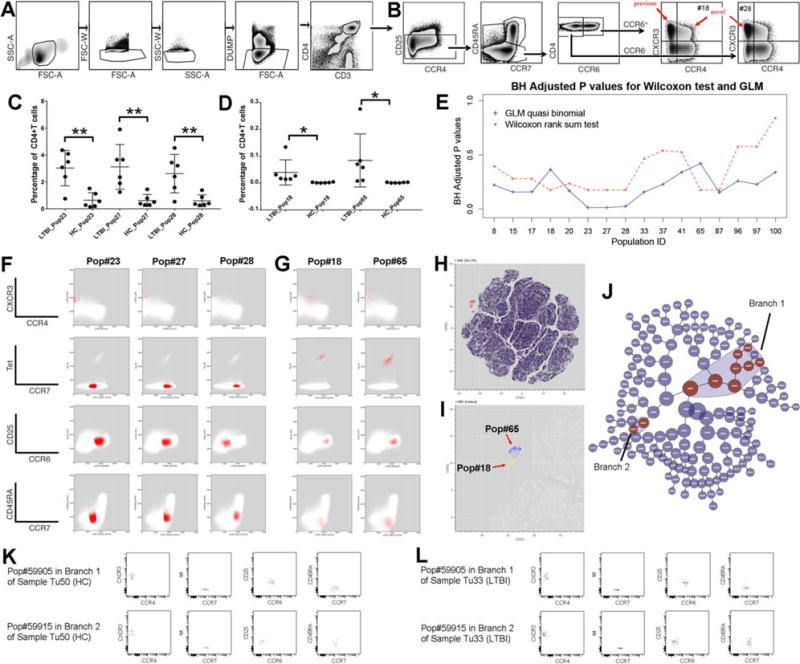
Identification of known and novel cell-based biomarkers for LTBI using constrained FLOCK clustering of DAFi filtered populations. (A) Manual gating strategy for identifying CD4+ T cells. The gating path sequentially identifies lymphocytes (FSC-A vs. SSC-A), singlet lymphocytes based on FSC-A/W, singlet lymphocytes based on SSC-A/W, live CD8− T lymphocytes (the DUMP channel includes CD8/CD14/CD19/LiveDead), and CD3+CD4+ T lymphocytes. (B) Manual gating strategy for identifying subset populations from the CD4+ T cells, based on CD25, CCR7, CD45RA, CCR4, CCR6, and CXCR3 expression. (C) Percentages of the three cell subsets (CD4+ T cell population as parent) that have P values < 0.05 (annotated with **) after BH correction identified by the GLM with quasi binomial distribution, between LTBI and HC. (D) Percentages of the two Tetramer+ cell populations which should only be found in the samples of LTBI. (E) Two types of statistical tests were applied to identify which CD4+ T cell subsets are significantly different in abundance between LTBI and HC. The X axis shows the IDs of the cell populations with P values < 0.05 by either statistical test before BH correction. The Y axis shows the P values after BH correction. (F) 2D dot plots of the three CD4+ T cell subsets (percentages shown in part C of this Figure) that differ between LTBI and HC. (G) The two Tetramer+ cell subsets (percentages shown in part D of this Figure) with their events highlighted in red on 2D plots of different markers. Both are very rare (average < 0.1% of CD4+ T cells). (H) t-SNE map of the filtered data. CD4+ T cells are color-coded based on expression level of tetramer to highlight the tetramer+ population in the mid-upper left region. (I) Zoomed-in tSNE map shows that the “island” of the tetramer+ population consists of two separated regions, corresponding to the Pop#18 (highlighted in yellow) and the Pop#65 (highlighted in blue). (J) The hierarchy of cell populations identified by the Citrus method. Cell populations that are significantly different between the LTBI and the HC groups are highlighted in red, which belong to two branches: Branch 1 (8 cell populations) and Branch 2 (2 cell populations). (K) One example sample in the HC group showing the two cell populations with the best P values generated by the Citrus method from Branch 1 and Branch 2, respectively. (L) One example sample in the LTBI group showing the two cell populations with the best P values generated by the Citrus method from Branch 1 and Branch 2, respectively. [Color figure can be viewed at wileyonlinelibrary.com]
We noticed that the manual gating strategy (Figs. 5A and 5B) after the CD4+ T cells gate was focused on cell populations with relatively arbitrary gating boundaries on CD25, CCR6, CXCR3, and CCR4, which may be better handled by a data clustering approach that can utilize multiple data dimensions simultaneously. Therefor we divided the DAFi analysis into two separate tasks: prefiltering to identify the CD4+ T cell population that has been defined in Figure 5A, and data clustering to identify unknown cell subsets within the CD4+ T cell population (Fig. 5B). The FLOCK clustering method (25) was used in both tasks to filter and identify the cell populations. For the first task, complete set of dot plots for data prefiltering by DAFi using FLOCK across all the 12 samples can be found in Supporting Information File S6.
For the second task, DAFi using FLOCK identified 101 cell populations from the 12 samples. The population percentages were then associated with the subject phenotype using two statistical tests: nonparametric Wilcoxon rank sum test, and the generalized linear model (GLM) with quasi binomial distributions following a similar approach as used in (45); both with a null hypothesis that there is no difference between the LTBI and the HC groups. The GLM model identified three cell populations: Pop#23, 27, and 28 with P values smaller than 0.05 after the Benjamini-Hochberg (BH) correction, as shown in Figure 5C. The Wilcoxon rank sum test did not identify any cell population with P values smaller than 0.05 after the BH correction. This was due to the limited number of samples in our study. The best possible P values in the Wilcoxon rank sum test for comparing two groups with 6 samples in each is 0.003948 before correction when there is no overlapping between the two groups in the ranks of their data objects, which became insignificant after the BH correction.
Figure 5E shows that Pop#18, 23, 27, 28, 65, and 87 were identified by the Wilcoxon rank sum test as the most different cell populations between the LTBI and the HC groups in population proportions (with CD4+ T cells as the parent). Among these 6 cell populations, Pop#87 is CD25+ while the other 5 are all CD25−, which are cells of interest in the original study design for identifying candidate cell-based biomarkers for LTBI. We plotted the percentage values of these 5 cell populations in Figures 5C and 5D with their 2D dot plots in Figures 5F and 5G. Pop#23, 27, and 28 are Tetramer− while Pop#18 and 65 are rare and Tetramer+. Because the peptide-MHC tetramer staining is supposed to bind to Mtb-specific cells only, it is known that the Tetramer+ Pop#18 and 65 are significantly different between the LTBI and the HC groups. As shown in Figure 5D, samples in the HC group do not have these two cell populations. Based on this result, the Wilcoxon rank sum test was more robust than the GLM quasi binomial model in identifying the difference when the cell populations are rare, while the GLM model addressed the statistical power better than the nonparametric Wilcoxon test when the number of samples is small, which was also useful in our case.
In the previous publication (44), a single cell population was identified by manual gating analysis in the CD25−CCR6+CCR4−CXCR3+ region that significantly differed between LTBI and HC in frequency [red arrow “previous” on CCR4 vs. CXCR3 plot in Figure 5B, corrected P values < 0.01 (44)]. In contrast, DAFi using FLOCK not only identified this known cell-based biomarker but also elucidated the composition of the CD25−CCR6+CCR4−CXCR3+ cell population, which includes Pop#23, 27, and 65. Further, DAFi using FLOCK identified two novel cell populations #18 and #28 that are also associated with the subject phenotype. Pop#18 is CD25−CCR6+CCR4loCXCR3+ and Pop#28 is CD25−CCR6-CCR4−CXCR3+. Their corresponding positions in the predefined cell type hierarchy are indicated with the red arrows “novel” in Figure 5B.
We conducted two experiments to verify the finding, using tSNE map (46) and the Citrus tool (18) at Cytobank [https://www.cytobank.org, (47)]. Figure 5H shows a tSNE map of the CD4+ T cells of the LTBI sample used in Figures 5F and 5G, color-coded based on the tetramer staining levels of the CD4+ T cells. Separation of the tetramer+ cells from the other cells on the tSNE map indicates that two very rare Pops 18 and 65 are indeed distinct (Fig. 5I). Results of Citrus highlighted two hierarchical branches including 10 cell populations identified as being significantly different in abundance between the LTBI and the HC groups (Fig. 5J). Branch 1 is CD25−CCR6+CCR4−CXCR3+ (upper rows of Figs. 5K and 5L; the most significant cell population in the branch shown) corresponding to the finding in the previous publication, while Branch 2 is CD25−CCR6−CCR4−CXCR3 (bottom rows of Figs. 5K and 5L; the most significant cell population in the branch shown), which matched to Pop#28 in our results. Boxplots of the 10 Citrus-identified clusters can be found in Supporting Information File S7. The tSNE visualization and the Citrus results confirmed the existence of the cell populations identified by the DAFi + FLOCK approach. Compared with Citrus and the manual gating analysis, the DAFi + FLOCK approach is the only approach that can elucidate the 5 rare and distinct cell subsets in both data-driven (based on FLOCK-identified data clusters) but also interpretable way.
Methods
Constrained clustering, in which user-provided constraints about cluster membership of data objects are involved, has proven highly effective for solving domain-specific problems (48). While DAFi does not require membership information of data objects, it utilizes the user manual gating strategy to filter and label the data clusters from polychromatic flow cytometry data in a recursive way. Our experimental results demonstrated the role of DAFi for improving the clustering-based identification of both user-defined and novel cell populations. The overall process of running an unsupervised data clustering method with DAFi can be regarded as a special class of the constrained clustering analysis.
Identification of User-Defined Cell Populations
When identifying user-defined cell populations, the manual gating boundary constraints were used to merge the data clusters whose centroids are within the same gated region. In traditional manual gating analysis, the basic unit for segregation is cellular events. The gating boundary directly decides which cell belongs to which cell population, which is precise but sensitive to minor data shifts and difficult to apply across different samples. The design of DAFi improved this situation by identifying data clusters as the basic unit of segregation. The segregation of cellular events based on data clusters is still data-driven but more robust to the data shift across samples. Unless most of a data cluster (represented by its centroid) has shifted out of the gating boundary, there is no need to change the gating boundaries used in the DAFi analysis for individual samples. Usually, only one set of gating boundaries is required for each batch of experiment samples. In Section Cell Type Specific Assessment in Comparison with Individual and Centralized Manual Gating Analysis, four sets of gating boundaries were created due to the use of four different cytometers. For Sections Correlation Analysis between Cell Population Proportions with Subject Age and Gender, Quantification of Human Immune Response to Influenza and Pneumococcal Vaccination, and Identification of Known and Novel Cell-Based Biomarkers for Latent Tuberculosis Infection, only one set of gating boundaries was used to process all the FCS files.
Table 1 illustrates an example set of gating boundaries used in DAFi as a configuration file for the recursive filtering and clustering analysis. Each row corresponds to a cell population defined by the user with Population ID (PopID) and Population Name (PopName). The two markers used to define the gate are Xname and Yname. Different data ranges across instruments and experiments are 0–1 min-max normalized into 0–200. Due to the use of cluster centroids as a robust way for segregation of cellular events, in the configuration file we simplify the shape of the gate into rectangles only, defined by four coordinate values: Xmin, Xmax, Ymin, and Ymax. The parent of each cell population is specified by the ID of its parent population (ParentID), with the Mode specifying the way of identifying the cell population from its parent (cluster, slope, bisecting, and reversed). RecursiveParent specifies whether this cell population will be used in downstream recursive filtering and clustering. By default, a cell population will be identified from its direct parent in clustering mode, while it can also be identified from a cell population at a higher level of the hierarchy based on the parent population ID specified by the user. The five major steps in the overall DAFi procedure for identifying user-defined cell populations are:
Step 1 Generation of DAFi configuration file (e.g., Table 1) based on user gating strategy.
Step 2 Apply a data clustering method to identify data clusters in each input file.
Step 3 Merge data clusters whose centroids are within the hyper-rectangle formed by gating boundaries; output the merged data as the input file for next-run clustering analysis.
Step 4 Repeat Steps 2 and 3 until all predefined cell populations of interest in the user-defined hierarchy are identified.
Step 5 Output the 2D dot plots and statistics of the identified cell populations together with their names and phenotypes as defined in the user gating strategy.
Table 1.
An example configuration table used in DAFi to specify gating boundary coordinates and hierarchical relationships among cell populations
| POPID | POPNAME | XNAME | YNAME | XMIN | XMAX | YMIN | YMAX | PARENTID | MODE | RECURSIVEPARENT |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Lymphocyte | FSC-A | SSC-A | 30 | 100 | 5 | 70 | 0 | Cluster | Yes |
| 2 | Singlet Lymphocytes | FSC-A | FSC-H | 200 | 200 | 100 | 200 | 1 | Slope | Yes |
| 3 | Singlet Lymphocytes | SSC-A | SSC-H | 200 | 200 | 110 | 200 | 2 | Slope | Yes |
| 4 | Live CD3T | CD3 | LiveDead | 100 | 200 | 0 | 100 | 3 | Cluster | Yes |
| 5 | CD4T | CD4 | CD8 | 100 | 200 | 0 | 90 | 4 | Cluster | No |
| 6 | CD8T | CD4 | CD8 | 0 | 80 | 120 | 200 | 4 | Cluster | No |
Identification of Cell Populations Undefined in Manual Gating Strategy
When the cell populations of interest are at even lower level than the available user gating hierarchy can define, DAFi uses the gating boundary constraints to annotate the identified data clusters for cell phenotype interpretation, instead of merging the data clusters as in the identification of the user-defined cell populations. To map the cell populations across different samples, the remaining events after DAFi filtering were first normalized across the samples and then merged together for the FLOCK analysis. The cross-sample normalization (a.k.a., sample alignment) was done using the Gaussian-Norm approach (49). Supporting Information File S8 illustrates the application of the GaussianNorm method to normalize the individual data dimensions CCR6 and CD45RA. Only data dimensions needed in the unsupervised FLOCK analysis are kept, resulting in a seven-dimensional data matrix (CD25, CXCR3, CCR4, CCR6, CCR7, CD45RA, and Tetramer), from which FLOCK was applied to identify the 101 cell subsets (number of bins = 12 and density threshold = 3). The population membership of the events in the merged file is then mapped back to the individual samples for cross-sample statistics and comparisons. For phenotyping the novel cell populations in Section Novel Cell-Based Biomarkers for Latent Tuberculosis Infection, a set of gating boundary coordinates based on user gating strategy in Figure 5B were input to the FLOCK algorithm as thresholds to define the phenotype of each FLOCK-identified cluster (input data ranged from 0 to 4095): CXCR3: 1700; CD45RA: 1500; CCR7: 1400; Tetramer: 1400; CCR4: 1000; CD25: 1800; CCR6: 1500. When the coordinate of a cluster centroid is smaller than the threshold on the data dimension/marker, it is a negative phenotype; otherwise it is positive. Multiple thresholds can be defined when there are more than two phenotypes on each dimension. For comparing the population proportions between two cohorts to identify the significantly different cell population in Section Novel Cell-Based Bio-markers for Latent Tuberculosis Infection, we evaluated the statistical methods in (18,45,50,51) besides the use of the nonparametric Wilcoxon rank sum test. Based on the input data type (number of events vs. percentages of cell populations), random factors in sample selection, number of samples, and frequency of the cells of interest (abundant vs. rare), we chose to perform GLM with quasi binomial using the glm function in R (stats package) and used glht function (multcomp package) for general linear hypothesis testing to test the hypothesis. We tested for the null hypothesis that there is no significant difference between the two groups, LTBI and HC samples. Each cell population was tested, resulting in 101 tests. Benjamini-Hochberg adjustment method was applied to control the false discovery rate.
The four major steps in the overall DAFi procedure for identifying undefined cell populations in an interpretable way are:
Step 1 Identify a predefined cell population (base cell population) that needs to be explored for undefined cell subsets, and prepare gating boundary constraints based on user gating strategy.
Step 2 Normalize the base cell population across samples and merge the normalized events across samples into a single data file.
Step 3 Apply a data clustering method to the data file to identify data clusters in a fully unsupervised way, and map the clustering results back to individual samples.
Step 4 Phenotype each identified cluster using gating boundary constraints in Step 1, and output the 2D dot plots and statistics of the identified cell populations for cross-sample comparisons.
Implementation of DAFi and Software Availability
The implementation of DAFi supports four different gating options/modes to identify the individual cell populations through specifying in the DAFi configuration file: clustering (default mode), bisecting, slope-based bisecting (e.g., identification of singlets based on FSC-A vs. FSC-H), and reversed filtering (e.g., in Fig. 5B, the identification of memory T cells based on CCR7 vs. CD45RA can be achieved by drawing a reversed gate around the Naïve T cells in the double positive region). We implemented DAFi in both C and R languages, supporting the use of different data clustering algorithms within DAFi, including K-means, FLOCK, FlowSOM, and those in the ClusterR package (Gaussian Mixture Model, K-means++ (52), etc.). Bioinformaticians and data analysts who have different preferred data clustering methods are welcome to implement their own clustering methods in the same way and update the GitHub repository. Source code of DAFi (in both R and C languages) and executables with readme files have been uploaded to the GitHub repository (https://github.com/JCVenterInstitute/DAFi-gating). We provided precompiled C executables for direct execution on both MS Windows and Mac OS platforms. In addition, for computing platforms with containerization support, we provided the Docker images on the GitHub for easy installation of the whole DAFi running environment without requiring system configuration. By default, FCSTrans (53) was used to convert and transform [logicle transformation (54), parameters as described in (53)] the binary FCS files for DAFi analysis. For R/Bioconductor users, other data transformation methods available in the flowCore package can also be used with the R version of DAFi. We benchmarked the performance of DAFi on the Comet cluster at the San Diego Supercomputer Center. The runtime was reduced using a specific intel compiler on the Comet cluster as well as multiple CPU cores, focused on data-parallel runs both within and across data files. The benchmarking showed that DAFi processing and analysis of the 306 files in the ImmPort SDY 180 (Section Quantification of Human Immune Response to Influenza and Pneumococcal Vaccination) was completed in about 30 min using a single compute node with 24 CPU cores, which was about 18 times faster than using a single CPU core. DAFi is also being integrated into the FlowGate cyberinfrastructure (55) we are developing to support interactive analytics of FCM data.
Discussions
The most significant contribution of DAFi is that it improves the interpretability of the data clusters identified from polychromatic FCM data by linking them to user-defined cell types and phenotypes. Consistent numbers and types of cell populations across samples with user-familiar phenotype definitions become feasible and available. Using DAFi the experimental scientists can avoid the abrupt cut-offs in the manual gating analysis but preserve the flexibility and interpretability of the manual gating analysis without a need to frequently customize the gates for each individual sample. Although the manual gating strategy is used, the results of DAFi are data-driven based on the results by unsupervised clustering methods. Both the predefined and novel cell populations identified by DAFi are managed under the same cell type hierarchy for knowledge integration. For bioinformaticians, an important take-home message is that recursive filtering and clustering can improve the capability of clustering-based identification of poorly resolved cell populations. DAFi can work with different data clustering methods and will help accelerate the adoption of these computational methods by experimental scientists.
The idea of incorporating user inputs into FCM data analysis is not new. Existing approaches such as SPADE (56) and SWIFT (23) require manual operation at the end of the data clustering to group or partition the data clusters into cell populations. Approaches like viSNE (46) and SPADE plot the single cell data in a graph or a transformed space for providing a 2D overview of the high-dimensional data, which can be difficult to interpret or operate on (e.g., grouping the nodes in a SPADE tree into a cell population can be error-prone without checking the events of the nodes on the original 2D plots; a viSNE map is on the tSNE-transformed data space whose dimensions have no biological meaning). In contrast, results of DAFi based on manual gating strategy are easier to validate and interpret.
Though DAFi was shown to be able to address the existing challenges faced by computational methods, there continue to be improvements needed in the future including eliminating the requirement for a user-provided gating example, which in some cases may be unavailable. For example, one idea is to use flowDensity (31) with DAFi to estimate the boundary coordinates based on 2D data distributions instead of relying on predefined gating boundaries. There are also computational methods being developed to identify the optimal gating path from a given set of cell population phenotypes, which can be used to configure DAFi. For result interpretation, the Cell Ontology (CL) (57) provides a standardized cell type hierarchy to support meta-analysis across different FCM experiments [e.g., FlowCL (58)]. Development of a graphical user interface for allowing the data analyst to create different gating sequences, connect with FlowJo workspace files, compare result statistics, and integrate with other data filtering and clustering methods will help improve the usability of DAFi.
Sample quality control (QC) and cross-sample normalization are important components in FCM data analysis. When a data cluster is slightly shifted outside the gating boundaries, its centroid remains within and its events outside of the boundaries will not be lost. However, if there is huge cross-sample variance, currently we need to manually adjust the gates used in DAFi. One solution is to integrate DAFi into a pipeline with components of QC and cross-sample normalization.
DAFi does not solve the problem of identifying the best number of clusters. The user will still face the challenge for setting the value of K, if the number of clusters is an input parameter of the clustering method. However, by merging the clusters within the user-defined gating region, the common problem of over-partitioning by data clustering analysis is partially solved by DAFi, when the goal is to identify user-defined cell populations. Even for the identification of novel cell populations, the cell type labels/phenotypes identified by DAFi based on user-provided constraints also help identify the cell populations with the same phenotype for further examination, saving manual efforts for checking each individual data cluster. We have experimented DAFi using K-means with different values of K from 100–600 using the LTBI dataset in Section Identification of Known and Novel Cell-Based Biomarkers for Latent Tuberculosis Infection. Supporting Information File S9 shows the F-measure values for each of the 5 cell populations comparing between the bisecting (i.e., manual gating analysis) and the clustering mode of DAFi. The box plot shows that the average F1 scores across the 12 samples are larger than 0.95 for all of K = 100–600. The variation of the F1 scores across samples is also small. The larger number of K, the closer the result is to the bisecting (the F1 scores seems the largest for K = 600). By setting the K, the user controls the sensitivity of the DAFi filtering to the data shift across samples.
We used the same LTBI dataset in Section Identification of Known and Novel Cell-Based Biomarkers for Latent Tuberculosis Infection and tested three sizes of gating boundaries for identifying the 5 cell populations across the 12 samples: (a) normal: the same size as the bisecting boundaries; (b) small: 10% smaller on each dimension than the bisecting boundaries, and (c) large: 10% larger on each dimension than the bisecting boundaries. We calculated the precision, recall, and F1 scores of comparing results of DAFi-filtering using these three sets of rectangles against the bisecting results (Supporting Information File S10). All the F1 scores as well as precisions and recalls are very high, while using a small rectangle seems increasing the precision but reducing the recall, compared with using a large rectangle. The variation of the F1 scores across the 12 samples is also small, without being affected much by the changing size of the rectangle gate.
Conclusions
How to integrate human intelligence on pattern recognition with the power of computation to identify cell populations robustly and interpretably across heterogeneous FCM samples is a challenge that has not been sufficiently addressed. In this article, we propose a recursive filtering and clustering computational approach and framework to improve the performance of data clustering identification of cell populations from polychromatic FCM data – DAFi. The characteristics of DAFi, demonstrated by our extensive experiments across multiple studies, include:
Generation of consistent cell type specific statistical measurements with expert centralized manual gating analysis;
Identification of natural shapes of both major and rare cell populations;
Identification of both clearly defined and poorly resolved cell populations, and
Easy interpretation and management of the identified cell populations using user-defined manual gating strategy.
We are integrating DAFi into a computational pipeline that has both QC and sample normalization functions for processing heterogeneous FCM samples. More experiments will be conducted to assess whether the DAFi-based pipeline can be made more automated without losing the robustness and flexibility of the current implementation for cell population identification.
Supplementary Material
Acknowledgments
La Jolla Institute for Allergy and Immunology: Veronique Schulten, Jason Greenbaum; Human Longevity: Rick Stanton; University of Rochester: David Topham, David Roumanes, Edward Walsh, Gloria Pryhuber, Nathan Laniewski, Kristin Scheible, Jeanne Holden-Wiltse; FlowJo LLC.: Josef Spidlen; San Diego Supercomputer Center: Robert Sinkovits.
Grant sponsor: NIH/NIAID, Grant number: U19AI118626 (HIPC) and R24AI108564
Grant sponsor: NIH/NCATS, Grant number: U01TR001801 (FlowGate)
Grant sponsor: NSF XSEDE allocation, Grant number: MCB170008
Funding provider: NIH/NIAID, Contract number: HHSN272201200005C (RPRC)
Footnotes
Additional supporting information may be found in the online version of this article.
Conflict Of Interest
The authors have no conflict of interest to declare.
Author Contributions
DAFi method design: YQ and RHS; DAFi method implementation: YQ, IC, and AJL; Computational processing and analysis of FCM data: AJL, IC, YQ, AM, and JB; Flow cytometry data acquisition and manual gating analysis: JB, CLA, and DW; Immunology use cases and result interpretation: RHS, BP, and AS; Manuscript preparation: YQ, AJL, and RHS. All authors helped with revision of the manuscript. All authors read and approved the final manuscript.
Availability of Data and Software
Source code of DAFi can be found at: https://github.com/JCVenterInstitute/DAFi-gating.(/p)(p)The FCM datasets used in this manuscript are publicly accessible at FlowRepository under accessions:
FR-FCM-ZYBS, FR-FCM-ZYBT, FR-FCM-ZYBU (https://flowrepository.org)
The HIPC study data used in this manuscript is also publicly available at the ImmPort database (SDY820); the ImmPort SDY 180 dataset is publicly accessible at ImmPort (https://www.immport.org) and can be downloaded at: https://aspera-immport.niaid.nih.gov:9443/browser?path=SDY180
LITERATURE CITED
- 1.Burel JG, Qian Y, Lindestam Arlehamn C, Weiskopf D, Zapardiel-Gonzalo J, Taplitz R, Gilman RH, Saito M, de Silva AD, Vijayanand P, et al. An integrated workflow to assess technical and biological variability of cell population frequencies in human peripheral blood by flow cytometry. J Immunol. 2017;198:1748–1758. doi: 10.4049/jimmunol.1601750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Pedersen NW, Chandran PA, Qian Y, Rebhahn J, Petersen NV, Hoff MD, White S, Lee AJ, Stanton R, Halgreen C, et al. Automated analysis of flow cytometry data to reduce inter-lab variation in the detection of major histocompatibility complex multimer-binding T cells. Front Immunol. 2017;8:858. doi: 10.3389/fimmu.2017.00858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Aghaeepour N, Finak G, FlowCAP Consortium; DREAM Consortium. Hoos H, Mosmann TR, Brinkman R, Gottardo R, Scheuermann RH. Critical assessment of automated flow cytometry data analysis techniques. Nat Methods. 2013;10:228–238. doi: 10.1038/nmeth.2365. Erratum: Nat Methods. 2013;10(5):445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Aghaeepour N, Chattopadhyay P, Chikina M, Dhaene T, Gassen SV, Kursa M, Lambrecht BN, Malek M, Qian Y, Qiu P, et al. A benchmark for evaluation of algorithms for identification of cellular correlates of clinical outcomes. Cytometry Part A. 2016;89A:16–21. doi: 10.1002/cyto.a.22732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bashashati A, Brinkman RR. A survey of flow cytometry data analysis methods. Adv Bioinf. 2009;2009:1. doi: 10.1155/2009/584603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Brinkman RR, Aghaeepour N, Finak G, Gottardo R, Mosmann T, Scheuermann RH. State-of-the-art in the computational analysis of cytometry data. Cytometry Part A. 2015;87A:591. doi: 10.1002/cyto.a.22707. [DOI] [PubMed] [Google Scholar]
- 7.Brinkman RR, Aghaeepour N, Finak G, Gottardo R, Mosmann T, Scheuermann RH. Automated analysis of flow cytometry data comes of age. Cytometry Part A. 2016;89A:13–15. doi: 10.1002/cyto.a.22810. [DOI] [PubMed] [Google Scholar]
- 8.Chester C, Maecker HT. Algorithmic tools for mining high-dimensional cytometry data. J Immunol. 2015;195:773–779. doi: 10.4049/jimmunol.1500633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kidd BA, Peters LA, Schadt EE, Dudley JT. Unifying immunology with informatics and multiscale biology. Nat Immunol. 2014;15:118–127. doi: 10.1038/ni.2787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kvistborg P, Gouttefangeas C, Aghaeepour N, Cazaly A, Chattopadhyay PK, Chan C, Eckl J, Finak G, Hadrup SR, Maecker HT, et al. Thinking outside the gate: single-cell assessments in multiple dimensions. Immunity. 2015;42:591–592. doi: 10.1016/j.immuni.2015.04.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Levine JH, Simonds EF, Bendall SC, Davis KL, Amir ED, Tadmor MD, Litvin O, Fienberg HG, Jager A, Zunder ER, et al. Data-driven phenotypic dissection of aml reveals progenitor-like cells that correlate with prognosis. Cell. 2015;162:184–197. doi: 10.1016/j.cell.2015.05.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Lugli E, Roederer M, Cossarizza A. Data analysis in flow cytometry: The future just started. Cytometry Part A. 2010;77A:705–713. doi: 10.1002/cyto.a.20901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Mair F, Hartmann FJ, Mrdjen D, Tosevski V, Krieg C, Becher B. The end of gating? An introduction to automated analysis of high dimensional cytometry data. Eur J Immunol. 2016;46:34–43. doi: 10.1002/eji.201545774. [DOI] [PubMed] [Google Scholar]
- 14.Saeys Y, Gassen SV, Lambrecht BN. Computational flow cytometry: helping to make sense of high-dimensional immunology data. Nat Rev Immunol. 2016;16:449–462. doi: 10.1038/nri.2016.56. [DOI] [PubMed] [Google Scholar]
- 15.Samusik N, Good Z, Spitzer MH, Davis KL, Nolan GP. Automated mapping of phenotype space with single-cell data. Nat Methods. 2016;13:493–496. doi: 10.1038/nmeth.3863. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Shekhar K, Brodin P, Davis MM, Chakraborty AK. Automatic Classification of Cellular Expression by Nonlinear Stochastic Embedding (ACCENSE) Proc Natl Acad Sci U S A. 2014;111:202–207. doi: 10.1073/pnas.1321405111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Aghaeepour N, Nikolic R, Hoos HH, Brinkman RR. Rapid cell population identification in flow cytometry data. Cytometry A. 2011;79A:6–13. doi: 10.1002/cyto.a.21007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bruggner RV, Bodenmiller B, Dill DL, Tibshirani RJ, Nolan GP. Automated identification of stratifying signatures in cellular subpopulations. Proc Natl Acad Sci U S A. 2014;111:E2770–E2777. doi: 10.1073/pnas.1408792111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Cron A, Gouttefangeas C, Frelinger J, Lin L, Singh SK, Britten CM, Welters MJP, van der Burg SH, West M, Chan C. Hierarchical modeling for rare event detection and cell subset alignment across flow cytometry samples. PLoS Comput Biol. 2013;9:e1003130. doi: 10.1371/journal.pcbi.1003130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Finak G, Bashashati A, Brinkman R, Gottardo R. Merging mixture components for cell population identification in flow cytometry. Adv Bioinformatics. 2009;2009:1. doi: 10.1155/2009/247646. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ge Y, Sealfon SC. flowPeaks: A fast unsupervised clustering for flow cytometry data via K-means and density peak finding. Bioinformatics. 2012;28:2052–2058. doi: 10.1093/bioinformatics/bts300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Lo K, Hahne F, Brinkman RR, Gottardo R. flowClust: A bioconductor package for automated gating of flow cytometry data. BMC Bioinf. 2009;10:145. doi: 10.1186/1471-2105-10-145. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Naim I, Datta S, Rebhahn J, Cavenaugh JS, Mosmann TR, Sharma G. SWIFT-scalable clustering for automated identification of rare cell populations in large, high-dimensional flow cytometry datasets, part 1: Algorithm design. Cytometry A. 2014;85A:408–421. doi: 10.1002/cyto.a.22446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Pyne S, Hu X, Wang K, Rossin E, Lin T, Maier LM, Baecher-Allan C, McLachlan GJ, Tamayo P, Hafler DA, et al. Automated high-dimensional flow cytometric data analysis. Proc Natl Acad Sci U S A. 2009;106:8519–8524. doi: 10.1073/pnas.0903028106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Qian Y, Wei C, Eun-Hyung Lee F, Campbell J, Halliley J, Lee JA, Cai J, Kong YM, Sadat E, Thomson E, et al. Elucidation of seventeen human peripheral blood B-cell subsets and quantification of the tetanus response using a density-based method for the automated identification of cell populations in multidimensional flow cytometry data. Cytometry B Clin Cytom. 2010;78B(Suppl 1):S69–S82. doi: 10.1002/cyto.b.20554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Van Gassen S, Callebaut B, Van Helden MJ, Lambrecht BN, Demeester P, Dhaene T, Saeys Y. FlowSOM: Using self-organizing maps for visualization and interpretation of cytometry data. Cytometry A. 2015;87A:636–645. doi: 10.1002/cyto.a.22625. [DOI] [PubMed] [Google Scholar]
- 27.Zare H, Shooshtari P, Gupta A, Brinkman RR. Data reduction for spectral clustering to analyze high throughput flow cytometry data. BMC Bioinformatics. 2010;11:403. doi: 10.1186/1471-2105-11-403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Arvaniti E, Claassen M. Sensitive detection of rare disease-associated cell subsets via representation learning. Nat Commun. 2017;8:14825. doi: 10.1038/ncomms14825. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Finak G, Frelinger J, Jiang W, Newell EW, Ramey J, Davis MM, Kalams SA, De Rosa SC, Gottardo R. OpenCyto: An open source infrastructure for scalable, robust, reproducible, and automated, end-to-end flow cytometry data analysis. PLoS Comput Biol. 2014;10:e1003806. doi: 10.1371/journal.pcbi.1003806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Lee H-C, Kosoy R, Becker CE, Dudley JT, Kidd BA. Automated cell type discovery and classification through knowledge transfer. Bioinformatics. 2017;33:1689–1695. doi: 10.1093/bioinformatics/btx054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Malek M, Taghiyar MJ, Chong L, Finak G, Gottardo R, Brinkman RR. flowDensity: Reproducing manual gating of flow cytometry data by automated density-based cell population identification. Bioinformatics. 2015;31:606–607. doi: 10.1093/bioinformatics/btu677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Weber LM, Robinson MD. Comparison of clustering methods for high-dimensional single-cell flow and mass cytometry data. Cytometry A. 2016;89A:1084–1096. doi: 10.1002/cyto.a.23030. [DOI] [PubMed] [Google Scholar]
- 33.Aina O, Dadik J, Charurat M, Amangaman P, Gurumdi S, Mang E, Guyit R, Lar N, Datong P, Daniyam C, Institute of Human Virology/Plateau State Specialist Hospital AIDS Prevention in Nigeria Study Team et al. Reference values of CD4 T lymphocytes in human immunodeficiency virus-negative adult Nigerians. Clin Diagn Lab Immunol. 2005;12:525–530. doi: 10.1128/CDLI.12.4.525-530.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.García-Dabrio MC, Pujol-Moix N, Martinez-Perez A, Fontcuberta J, Souto JC, Soria JM, Nomded eu JF. Influence of age, gender and lifestyle in lymphocyte subsets: Report from the Spanish Gait-2 Study. Acta Haematol. 2012;127:244–249. doi: 10.1159/000337051. [DOI] [PubMed] [Google Scholar]
- 35.Kam KM, Leung WL, Kwok MY, Hung MY, Lee SS, Mak WP. Lymphocyte subpopulation reference ranges for monitoring human immunodeficiency virus-infected Chinese adults. Clin Diagn Lab Immunol. 1996;3:326. doi: 10.1128/cdli.3.3.326-330.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Rudy BJ, Wilson CM, Durako S, Moscicki A-B, Muenz L, Douglas SD. Peripheral blood lymphocyte subsets in adolescents: a longitudinal analysis from the REACH project. Clin Diagn Lab Immunol. 2002;9:959–965. doi: 10.1128/CDLI.9.5.959-965.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Thakar MR, Abraham PR, Arora S, Balakrishnan P, Bandyopadhyay B, Joshi AA, Devi R, Vasanthapuram R, Vajpayee M, Desai A, et al. Establishment of reference CD4+ T cell values for adult Indian population. AIDS Res Ther. 2011;8:35. doi: 10.1186/1742-6405-8-35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Tollerud DJ, Clark JW, Brown LM, Neuland CY, Pankiw-Trost LK, Blattner WA, Hoover RN. The influence of age, race, and gender on peripheral blood mononuclear-cell subsets in healthy nonsmokers. J Clin Immunol. 1989;9:214–222. doi: 10.1007/BF00916817. [DOI] [PubMed] [Google Scholar]
- 39.Tollerud DJ, Ildstad ST, Brown LM, Clark JW, Blattner WA, Mann DL, Neuland CY, Pankiw-Trost L, Hoover RN. T-cell subsets in healthy teenagers: Transition to the adult phenotype. Clin Immunol Immunopathol. 1990;56:88–96. doi: 10.1016/0090-1229(90)90172-m. [DOI] [PubMed] [Google Scholar]
- 40.Tugume SB, Piwowar EM, Lutalo T, Mugyenyi PN, Grant RM, Mangeni FW, Pattishall K, Katongole-Mbidde E. Hematological reference ranges among healthy Ugandans. Clin Diagn Lab Immunol. 1995;2:233–235. doi: 10.1128/cdli.2.2.233-235.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Uppal SS, Verma S, Dhot PS. Normal values of CD4 and CD8 lymphocyte subsets in healthy Indian adults and the effects of sex, age, ethnicity and smoking. Cytometry B Clin Cytom. 2003;52B:32–36. doi: 10.1002/cyto.b.10011. [DOI] [PubMed] [Google Scholar]
- 42.Kan MJ, Zalocusky KA, Hu Z, Dunn P, Thomson E, Wiser J, Bhattacharya S, Butte AJ. The 10000 immunomes project: a resource for human immunology. Journal of Allergy and Clinical Immunology. 2018;141(2, Supplement):AB269. [Google Scholar]
- 43.Obermoser G, Presnell S, Domico K, Xu H, Wang Y, Anguiano E, Thompson-Snipes L, Ranganathan R, Zeitner B, Bjork A, et al. Systems scale interactive exploration reveals quantitative and qualitative differences in response to influenza and pneumococcal vaccines. Immunity. 2013;38:831–844. doi: 10.1016/j.immuni.2012.12.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Arlehamn CL, Seumois G, Gerasimova A, Huang C, Fu Z, Yue X, Sette A, Vijayanand P, Peters B. Transcriptional profile of tuberculosis antigen-specific T cells reveals novel multifunctional features. J Immunol. 2014;193:2931–2940. doi: 10.4049/jimmunol.1401151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Nowicka M, Krieg C, Weber LM, Hartmann FJ, Guglietta S, Becher B, Levesque MP, Robinson MD. CyTOF workflow: differential discovery in high-throughput high-dimensional cytometry datasets. F1000Res. 2017;6:748. doi: 10.12688/f1000research.11622.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Amir el-AD, Davis KL, Tadmor MD, Simonds EF, Levine JH, Bendall SC, Shenfeld DK, Krishnaswamy S, Nolan GP, Pe’er D. viSNE enables visualization of high dimensional single-cell data and reveals phenotypic heterogeneity of leukemia. Nat Biotechnol. 2013;31:545–552. doi: 10.1038/nbt.2594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Kotecha N, Krutzik PO, Irish JM. Web-based analysis and publication of flow cytometry experiments. Curr Protocols Cytometry. 2010 doi: 10.1002/0471142956.cy1017s53. Chapter 10:Unit10.17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Wagstaff K, Cardie C, Rogers S, Schrödl S. Constrained K-means clustering with background knowledge. Proceedings of the Eighteenth International Conference on Machine Learning; San Francisco, CA. June 28– July 01, 2001; Morgan Kaufmann; pp. 577–584. [Google Scholar]
- 49.Hahne F, Khodabakhshi AH, Bashashati A, Wong C-J, Gascoyne RD, Weng AP, Seyfert-Margolis V, Bourcier K, Asare A, Lumley T, et al. Per-channel basis normalization methods for flow cytometry data. Cytometry Part A. 2010;77A:121–131. doi: 10.1002/cyto.a.20823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Fonseka CY, Rao DA, Teslovich NC, Hannes SK, Slowikowski K, Gurish MF, Donlin LT, Weinblatt ME, Massarotti EM, Coblyn JS, et al. Mixed effects association of single cells identifies an expanded Th1-skewed cytotoxic effector CD4+ T cell subset in rheumatoid arthritis. bioRxiv. 2018:172403. doi: 10.1126/scitranslmed.aaq0305. doi: https://doi.org/10.1101/172403. [DOI] [PMC free article] [PubMed]
- 51.Lun ATL, Richard AC, Marioni JC. Testing for differential abundance in mass cytometry data. Nat Methods. 2017;14:707–709. doi: 10.1038/nmeth.4295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Arthur D, Vassilvitskii S. Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms SODA’07. Philadelphia, PA: Society for Industrial and Applied Mathematics; 2007. K-means++: The advantages of careful seeding; pp. 1027–1035. [Google Scholar]
- 53.Qian Y, Liu Y, Campbell J, Thomson E, Kong YM, Scheuermann RH. FCSTrans: An open source software system for FCS file conversion and data transformation. Cytometry A. 2012;81A:353–356. doi: 10.1002/cyto.a.22037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Parks DR, Roederer M, Moore WA. A new “Logicle” display method avoids deceptive effects of logarithmic scaling for low signals and compensated data. Cytometry A. 2006;69A:541–551. doi: 10.1002/cyto.a.20258. [DOI] [PubMed] [Google Scholar]
- 55.Qian Y, Kim H, Purawat S, Wang J, Stanton R, Lee A, Xu W, Altintas I, Sinkovits R, Scheuermann RH. Proceedings of the 4th annual XSEDE (Extreme Science and Engineering Discovery Environment) Conference. St. Louis, MO: ACM Press; 2015. FlowGate: Towards extensible and scalable web-based flow cytometry data analysis. [Google Scholar]
- 56.Qiu P, Simonds EF, Bendall SC, Gibbs KD, Jr, Bruggner RV, Linderman MD, Sachs K, Nolan GP, Plevritis SK. Extracting a cellular hierarchy from high-dimensional cytometry data with SPADE. Nat Biotechnol. 2011;29:886–891. doi: 10.1038/nbt.1991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Bard J, Rhee SY, Ashburner M. An ontology for cell types. Genome Biol. 2005;6:R21. doi: 10.1186/gb-2005-6-2-r21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Courtot M, Meskas J, Diehl AD, Droumeva R, Gottardo R, Jalali A, Taghiyar MJ, Maecker HT, McCoy JP, Ruttenberg A, et al. flowCL: Ontology-based cell population labelling in flow cytometry. Bioinformatics. 2015;31:1337–1339. doi: 10.1093/bioinformatics/btu807. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


