MIMoSA: An Automated Method for Inter-Modal Segmentation Analysis of Multiple Sclerosis Brain Lesions

Abstract

Background and Purpose

Magnetic resonance imaging (MRI) is crucial for in vivo detection and characterization of white matter lesions (WML) in multiple sclerosis. While WML have been studied for over two decades using MRI, automated segmentation remains challenging. Although the majority of statistical techniques for the automated segmentation of WML are based on single imaging modalities, recent advances have used multimodal techniques for identifying WML. Complementary modalities emphasize different tissue properties, which help identify interrelated features of lesions.

Methods

MIMoSA, a fully automatic lesion segmentation algorithm which utilizes novel covariance features from inter-modal coupling regression in addition to mean structure to model the probability lesion is contained in each voxel, is proposed. MIMoSA was validated by comparison with both expert manual and other automated segmentation methods in two datasets. The first included 98 subjects imaged at Johns Hopkins Hospital in which bootstrap cross-validation was used to compare the performance of MIMoSA against OASIS and LesionTOADS, two popular automatic segmentation approaches. For a secondary validation, a publicly available data from a segmentation challenge was used for performance benchmarking.

Results

In the Johns Hopkins study, MIMoSA yielded average Sørensen-Dice coefficient (DSC) of 0.57 and partial AUC of 0.68 calculated with false positive rates up to 1%. This was superior to performance using OASIS and LesionTOADS. The proposed method also performed competitively in the segmentation challenge dataset.

Conclusion

MIMoSA resulted in statistically significant improvements in lesion segmentation performance compared with LesionTOADS and OASIS, and performed competitively in an additional validation study.

Introduction

Multiple Sclerosis and MRI

Multiple sclerosis (MS) is an autoimmune disease of the central nervous system (CNS) that is characterized by pathologic changes in the brain and spinal cord. These pathologic changes include axonal injury and gliosis as well as demyelination, which is most prominent in focal white matter lesions (WML), although is also present in grey matter structures. It is well established that the accumulation of these WML is associated with disability and cognitive decline.¹ The in vivo assessment of lesion volume is primarily based on magnetic resonance imaging (MRI), as demyelination and other pathological changes cause tissue to have different water content compared to normal-appearing white matter (NAWM).² The number and volume of lesions are essential metrics for monitoring disease progression in clinical settings, and are also used for evaluating the efficacy of disease-modifying therapies in clinical trials and in clinical practice.³

The use of multiple MRI sequences can add significant value in identifying abnormalities in the brain. In MS, the most common MRI modalities acquired include; T2-weighted Fluid-Attenuated Inversion Recovery (FLAIR), T2-weighted (T2), Proton Density-weighted (PD), and T1-weighted (T1) images. WML appear as hyperintensities on the FLAIR, T2, and PD images while WML appear as isointense or hypointensities on the T1. The differing contrasts allow the viewer to detect different features of WML or NAWM in order to delineate WML. For example, the FLAIR, unlike T2 and PD, easily distinguishes WML from cerebrospinal fluid (CSF) and thus is useful when evaluating lesions near CSF.⁴ To gather as much information as possible about the demyelination occurring in the brain, it is now common to utilize the complementary information provided by different imaging sequences.

Lesion Segmentation

Segmentation of WML involves extracting locations in an image that contain intensity abnormalities. Currently, manual segmentation is the gold standard approach. Radiologists or other imaging scientists visually assess scans and manually delineate lesions in order to report the total number and volume of WML. Not only is this costly and time-consuming, but it is prone to large inter- and intra- observer variability due to the challenge of incorporating 3D information from several MRI modalities.^5,6 However, these WML metrics are vital in clinical trials where lesion metrics are important outcomes for assessing disease-related changes and treatment effects.⁷ In clinical trials, a consistent method for quick and accurate delineation of WML is necessary. Though manual lesion segmentation is flawed, it has retained its primacy due to artifacts and errors that occur with automated and semi-automated methods.

Automated methods eliminate the need for manual input, thus cutting cost and reducing implementation time even further. Automated methods additionally introduce stability and consistency into lesion segmentation as they eliminate human bias and error. Though many automated approaches and methods exist, no currently available algorithm is able to outperform manual lesion segmentation in terms of sensitivity and specificity across subjects, scanning protocol, and scanning centers.⁸ Thus, accurate automated detection and delineation of WML remains a challenging unmet need in the field.

Most automated WML segmentation methods consist of two components: feature extraction and a classification algorithm. Classification algorithms range from sophisticated machine learning methods to simpler algorithms such as voxel-wise logistic regression, linear discriminant analysis, and quadratic discriminant analysis.^8,9 Feature selection can also vary from simple raw intensities to complex functions of images. Deep learning algorithms which attempt to estimate the best features for classification and jointly optimize feature selection and classification methods are also gaining popularity in the segmentation literature.¹⁰ Unfortunately, deep learning methods require large and diverse datasets for training generalizable classifiers.¹¹ Additionally, deep learning approaches are opaque in their interpretability, and their external validity and generalizability are unknown; furthermore, as these models increase in complexity so does their interpretation.¹² In the past, studies have compared classification methods and shown that simple methods often yield performance equivalent to more sophisticated methods.¹³ Such studies have emphasized the importance of biologically relevant feature selection.⁸ This motivates the development of interpretable and discriminative features as key components for generalizable and accurate WML segmentation methods.

MIMoSA and IMCo Regression

We propose a fully automated segmentation algorithm that we refer to as A Method for Inter-Modal Segmentation Analysis (MIMoSA). As feature extraction is known to be pivotal for a segmentation algorithm’s accuracy and generalizability, we focus on the development of novel features. The majority of statistical techniques for the segmentation of WML are based on modeling intensity patterns for each imaging modality separately. However, recent advances in neuroimaging analysis have emphasized multimodal techniques in order to include covariance modeling across modalities.^14,15 This relationship, which we refer to as inter-modal coupling (IMCo), is known to differ across tissue types.^16,17 However, it is unknown whether IMCo is disrupted in pathological conditions such as MS. We propose to leverage IMCo information as features for lesion segmentation in order to quantify the coherent changes as tissue damage and repair occur across imaging modalities. We introduce MIMoSA, a segmentation algorithm which utilizes IMCo to incorporate information about covariance structures of different images at a given anatomic location.¹⁴ MIMoSA is a local-level logistic regression that accounts for mean structure as well as local covariance structure across imaging modalities. Additionally, we fully automate the model with a novel thresholding algorithm that detects the ideal threshold for probability maps in order to maximize similarity with manual segmentations. As described below, this approach is successful in detecting WML with increased accuracy relative to state-of-the-art methods.

Methods

In this section we introduce MIMoSA, an automatic lesion segmentation approach that uses a logistic regression as a classifier as well as features that model the mean and covariance within and across images. In the MIMoSA Procedure sections, we first present the steps associated with the MIMoSA algorithm. We evaluate the performance of MIMoSA on two datasets. The first consists of MRI volumes of the brain using a dataset collected at the Johns Hopkins Hospital consisting of 98 subjects with relapsing-remitting MS. These data were used to create the MIMoSA algorithm and then we assess performance using a bootstrapped cross-validation comparing MIMoSA with OASIS and LesionTOADS, two other competitive automatic approaches. We describe this data, preprocessing pipeline, and performance assessment in the Johns Hopkins Study section. We additionally apply the method to publically available data from the 2015 Longitudinal Multiple Sclerosis Lesion Segmentation Challenge in order to compare MIMoSA with a variety of automatic approaches.

MIMoSA Procedure

In this section, we describe the fully automated MIMoSA algorithm step by step including feature generation, modelling, and thresholding of probability maps to generate segmentations.

Statistical Modeling and Spatial Smoothing

We performed all statistical modeling in the R environment (version 3.1.0, R Foundation for Statistical Computing, Vienna, Austria) utilizing the packages oasis,¹⁸ ROCR,¹⁹ data.table,²⁰ brainR,²¹ oro.nifti,²² and fslr.²³

Brain Tissue Mask

The MIMoSA algorithm utilizes two masks for identifying tissue that may contain lesions: the brain tissue mask and the candidate mask.²⁴ We first identify voxels containing cerebral tissue but exclude cerebrospinal fluid (CSF). Because CSF appears hypointense on FLAIR, we exclude voxels with intensities below the 15th percentile after skull-stripping. We refer to this mask as the brain tissue mask. Since voxels within lesions appear as hyperintensities in the FLAIR volume, we restrict our classifier to exclude any voxels whose FLAIR intensities are not consistent with lesions: we select the 85^th percentile and above voxels in the brain tissue mask as candidate voxels. This step reduces computation time and restricts the modeling space, which we have found empirically to reduce false positives.

Intensity Normalized Features

As conventional MRI volumes are acquired in arbitrary units, we use a statistical intensity normalization in order to model intensities across subjects. We assess the method using both z-score and WhiteStripe normalization techniques.²⁵ In the z-score normalization, we calculate the mean and standard deviation for all voxels in the tissue mask, which excludes CSF. The WhiteStripe method is a fully-automated linear intensity normalization technique that is robust to pathology and heterogeneity in brain structure, which we use in studies where z-score normalization is found to fail based on visual inspection of normalized histograms. Figure 1 shows an example of normalized volumes for illustration.

Figure 1.

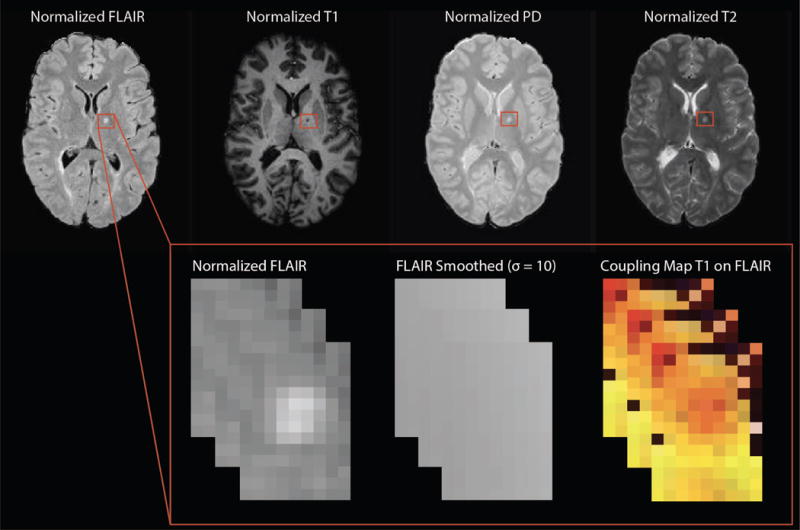
Features for MIMoSA including normalized images as well as an example of the T2-weighted Fluid-Attenuated Inversion Recovery (FLAIR) smoothed volumes (Gaussian smoother using $\mathrm{\sigma }=10\text{mm},20\text{mm}$) and a map for T1-weighted (T1) on FLAIR inter-modal coupling regression slopes.

Smoothed Features

To reduce noise and measure gross spatial context surrounding each voxel, we use Gaussian smoothers with kernel parameters $\mathrm{\sigma }=10$ and $\mathrm{\sigma }=20$ mm as features. Though these kernel sequences are large, they have been shown to aid in classification in previous work involving similar local image regression modeling.^8,24 These features have also been noted to mitigate missegmentation artifacts that are due to residual image inhomogeneities after N3 correction.²⁴ Figure 1 shows an example of a smoothed volume for illustration.

Inter-Modal Coupling Regression Features

In order to help distinguish the lesional tissue from NAWM, we utilize features we estimate from IMCo regression. These measures are intended to capture the local covariance structure across modalities as it varies across the brain. For example, as inflammation and demyelination occur in WML, not only do T1-weighted intensities decrease and FLAIR intensities increase; rather, voxels with more pathology tend to experience these changes concurrently to a greater extent. To quantify this, we perform a weighted local regression in a neighborhood around each voxel (see Figure 2), where the weight is proportional to a Gaussian kernel that is a function of the distance to the center voxel with fixed full-width half-max parameter (3mm).¹⁴ We record two coupling measures for each pair of imaging modalities at all voxels in the candidate mask: the locally estimated slope parameter as well as the intercept parameter estimate. An example is shown in Figure 1.

Figure 2.

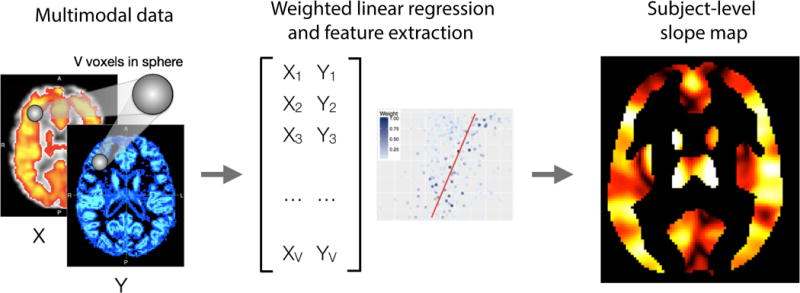
The inter-modal coupling (IMCo) pipeline is shown below. Both X, Y, and the subject-level map are for illustrative purposes only and do not depict data collected. We create IMCo for each pair of imaging modalities allowing each modality in the pair to be Y on X and X on Y. The MIMoSA model utilized the intercepts and slopes generated as features therefore we calculate 2 subject-level maps. While the subject-level map is for illustrative purposes, the coloring represents spatial variability where some regions have higher versus lower slopes or intercepts within subject.

We implement IMCo regression on 12 pairs of inter-modal contrasts. That is, we exhaust all possible combinations (6) of the 4 scanning contrasts: T1 and PD, T1 and FLAIR, T1 and T2, PD and FLAIR, PD and T2, and FLAIR and T2. As IMCo is a regression, we must assign one modality to be the outcome and the other to be the predictor variable. Since there is no natural choice for predictor or outcome variables, for each pair we include both regressions which result in complementary information. For example, one combination of volumes is T1 and FLAIR, so we perform IMCo regression using T1 as the predictor variable and FLAIR as the outcome variable. We then repeat the IMCo regression with FLAIR as the predictor variable and T1 is the outcome variable. This leaves us with 12 unique pairs for estimating IMCo for which we obtain slope and intercept parameter estimates.

MIMoSA Model

MIMoSA uses logistic regression to model the probability that a voxel contains lesional tissue. We choose logistic regression for two main reasons: first, it is straightforward to interpret and implement. Second, a previous automated segmentation model showed promising results with a logistic regression compared with more advanced machine learning classifiers⁸ but left significant room for improvement on the inclusion of intermodal features. We model the probability of lesion at the voxel level using FLAIR, PD, T2, and T1 normalized intensities as well as the intensities from smoothed volumes of each modality. Using these features alone captures the mean structure within modalities. For improved sensitivity and specificity to lesional tissue, we capture this covariance structure across scanning modalities using coupling measures for each pair of modalities, as described in the previous section, and we include these features in the model. Like all supervised lesion segmentation methods, we train MIMoSA on manually segmented images (see Figure 3 in section 3.1.3).

Figure 3.

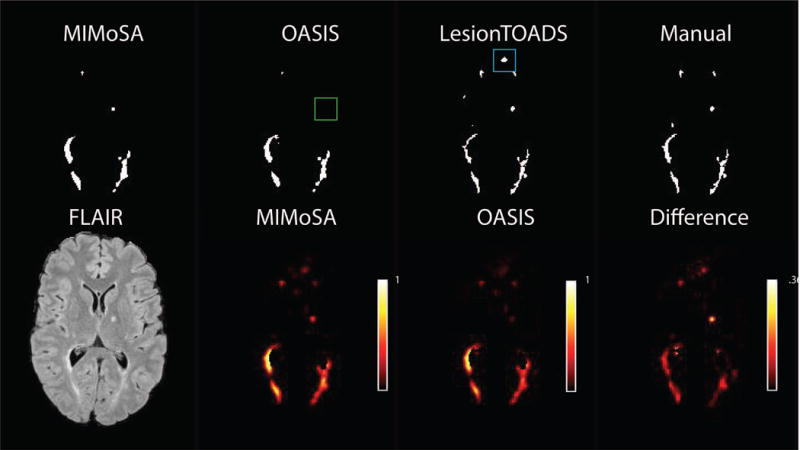
Probability maps for MIMoSA and OASIS as well as the difference (MIMoSA-OASIS) are shown in the second row. Using the thresholding algorithm, lesion segmentations for respective models are also shown in row 1 along with LesionTOADS hard segmentations. LesionTOADS and manual segmentations are also shown. The green box indicates a false negative result for OASIS and the blue box indicates a false positive result for LesionTOADS.

The next step in the MIMoSA procedure is to fit a voxel-level logistic regression model over the candidate voxels. $\mathrm{P}\left\{{\mathrm{L}}_{\mathrm{i}}\left(\mathrm{v}\right)=1\right\}$ represents the probability that a voxel is part of a lesion where ${\mathrm{L}}_{\mathrm{i}}\left(\mathrm{v}\right)$ is a random variable denoting voxel-level lesion presence. If there is a lesion in voxel $\mathrm{v}$ for subject $\mathrm{i}$, then ${\mathrm{L}}_{\mathrm{i}}\left(\mathrm{v}\right)$=1, otherwise ${\mathrm{L}}_{\mathrm{i}}\left(\mathrm{v}\right)=0$. We model the probability that a voxel $\mathrm{v}$ contains lesion with the following logistic regression model:

$$\text{logit}\left[\mathrm{P}\left\{{\mathrm{L}}_{\mathrm{i}}\left(\mathrm{v}\right)=1\right\}\right]= {\beta }_0+{\mathrm{X}}_{\mathrm{i}}^{\mathrm{T}}\left(\mathrm{v}\right)\mathrm{\beta }+\mathfrak{G}{\mathrm{X}}_{\mathrm{i}}^{\mathrm{T}}\left(\mathrm{v},10\right)\left\{{\beta }_{10}+{\mathrm{X}}_{\mathrm{i}}\left(\mathrm{v}\right)\otimes {\beta }_{10}^{\ast }\right\}+\mathfrak{G}{\mathrm{X}}_{\mathrm{i}}^{\mathrm{T}}\left(\mathrm{v},20\right)\left\{{\beta }_{20}+{\mathrm{X}}_{\mathrm{i}}\left(\mathrm{v}\right)\otimes {\beta }_{20}^{\ast }\right\}+\mathcal{C}{\mathrm{X}}_{\text{i,I}}^{\mathrm{T}}\left(\mathrm{v}\right){\beta }_{\mathrm{I}}+\mathcal{C}{\mathrm{X}}_{\text{i,S}}^{\mathrm{T}}\left(\mathrm{v}\right){\beta }_{\mathrm{S}},$$

where we denote the normalized images ${\mathrm{X}}_{\mathrm{i}}\left(\mathrm{v}\right)={\left[{\mathrm{T}}_{1,\mathrm{i}}\left(\mathrm{v}\right),{\text{FLAIR}}_{\mathrm{i}}\left(\mathrm{v}\right),{\mathrm{T}}_{2,\mathrm{i}}\left(\mathrm{v}\right),{\text{PD}}_{\mathrm{i}}\left(\mathrm{v}\right)\right]}^{\mathrm{T}}$and express the smoothed images in vector form by $\mathfrak{G}{\mathrm{X}}_{\mathrm{i}}\left(\mathrm{v},\mathrm{\delta }\right)={\left[\mathfrak{G}\left({\mathrm{T}}_{1,\mathrm{i}}\left(\mathrm{v}\right);\mathrm{N}\left(\mathrm{v},\mathrm{\delta }\right)\right),\dots .,\mathfrak{G}\left({\text{PD}}_{\mathrm{i}}\left(\mathrm{v}\right);\mathrm{N}\left(\mathrm{v},\mathrm{\delta }\right)\right)\right]}^{\mathrm{T}},$where $\mathfrak{G}$ denotes the image smoothing operator with parameter $\mathrm{\delta }\in \left\{10\text{mm},20\text{mm}\right\}$. We denote all combinations of intercept and slope IMCo parameters respectively by $\mathcal{C}{\mathrm{X}}_{\mathrm{i},\mathrm{I}}^{\mathrm{T}}\left(\mathrm{v}\right)$ and $\mathcal{C}{\mathrm{X}}_{\mathrm{i},\mathrm{S}}^{\mathrm{T}}\left(\mathrm{v}\right)$. We use ⊗ to represent the Hadamard product. The interaction terms between the normalized volumes and the smoothed volumes, denoted by ${\mathrm{\beta }}_{\mathrm{j}0}^{\ast }$, contribute to the model by capturing differences between voxel intensities and their local mean intensities. These aid in mitigating artifacts due to residual field inhomogeneity in some cases and generally improve lesion detection performance.

After training, the result of our model is a collection of coefficients that can be used to determine the probability that each voxel is part of a lesion in a new set of images. MIMoSA obtains the estimated probability of each voxel being lesion by including the 12 imaging features (the four imaging modalities and the 2 smoothed volumes for each modality) and capturing the covariance across the 12 pairs of IMCo parameters. One can then apply a threshold to the probability maps to create binary lesion segmentation masks, which are typically preferred in clinical applications.

Probability Map and Binary Segmentation

To determine where lesions are present, we estimate a probability map using the estimated regression coefficients for each voxel in the candidate mask. We use a Gaussian smoother with sigma parameter of 1.25mm on this probability map to reduce noise. To create a binary segmentation map from this smoothed probability map, we apply thresholding. Note that the threshold we use does not differ across subjects, but rather is a single parameter we apply to all subjects’ probability maps. Figure 3 shows a slice of a probability map and a binary segmentation after thresholding for a subject in a test set.

Optimal Thresholding Algorithm

After the MIMoSA model is trained, it can be applied to generate probability maps, which are thresholded to create binary lesion segmentations. In comparable methods, this threshold is determined manually post hoc. To fully automate the thresholding process and select a threshold that maximizes similarity to manual segmentations, we introduce an optimal thresholding algorithm. The MIMoSA model is fit using the training set of data with manual segmentations. After the model is fit, we generate probability maps on these training set subjects. The optimal thresholding algorithm allows for the specification of a grid of thresholds. For each threshold we create binary lesion masks, which we compare to the manual lesion segmentations by calculating Sørensen-Dice coefficient (DSC).²⁶ We select the threshold that produces the highest average DSC across the selected grid in the training set as the optimal threshold for application in the test set. This process yields an optimal threshold for the training set which empirically performs well in the test set.

Johns Hopkins Study

In this section we first describe the study population and imaging protocol for the data acquired at the Johns Hopkins Hospital. We then describe image preprocessing and our approach to implementing MIMoSA, OASIS, and LesionTOADS. These data are used in order to compare MIMoSA with OASIS and LesionTOADS on a large cohort of subjects with varying degrees of disease severity.

Study Population

We considered MRI studies from 98 subjects with MS. The median age of the MS subjects was 44 years (Q1, Q3) (33, 54), 72 were female, and the median Expanded Disability Status Score (EDSS) was 3.5 (2, 6). Due to poor image quality, we excluded 4 subjects, which resulted in a total of 94 subjects. The average total cerebral lesion volume for the 94 subjects was 11.5 mL.

Experimental Methods

Local institutional review boards approved the imaging protocol and data analysis. 3D T1-MPRAGE (T1w) images (repetition time (TR) = 10 ms; echo time (TE) = 6 ms; flip angle (FA) α = 8°; inversion time (TI) = 835 ms, resolution = .828 mm × .828 mm × 1.1 mm), 2D T2-weighted FLAIR images (TR = 11,000 ms; TE = 68 ms; TI = 2800 ms; in-plane resolution = 0.83 mm × 0.83 mm; slice thickness = 2.2 mm), and T2-weighted (T2w) and PD (PDw) images (TR = 4200 ms; TE = 12/80 ms; resolution = 0.83 mm × 0.83 mm × 2.2 mm) were acquired on a 3T MRI scanner (Philips Medical Systems, Best, The Netherlands). Manual segmentations were acquired by an imaging technologist with more than 10 years of experience in delineating lesions and neuroanatomy.

Image Preprocessing

All images were preprocessed using the Medical Image Processing Analysis and Visualization (MIPAV),²⁷ TOADS-CRUISE,²⁸ and Java Image Science Toolkit (JIST) software packages.²⁹ We first rigidly aligned the T1-weighted image of each subject into the Montreal Neurological Institute (MNI) template space at 1 mm isotropic resolution. We used the normalized mutual information cost function for co-registration and windowed sinc for interpolation. We then registered the FLAIR, PD, and T2-weighted images of each subject to these aligned T1-weighted images. We also applied the N3 inhomogeneity correction algorithm³⁰ to all images and removed extracerebral voxels using Simple Paradigm For Extra-Cerebral Tissue Removal: Algorithm And Analysis (SPECTRE).³¹ For normalization, we use a linear z-scoring method^25,32 with the brain tissue mask, making the units of each modality easily interpreted as standard deviations of the variability across the brain.

Bootstrap Cross-Validation

In this dataset, we conducted training and testing for proposed MIMoSA methods and OASIS using bootstrapped cross-validation. In order to fit the models and measure performance, we randomly allocated 42 subjects to the training set and 42 subjects to the test set. We then trained both the OASIS and MIMoSA models using only subjects in the training set. After we fit the models, we applied the estimated coefficients to the test set in order to generate probability maps. To threshold probability maps and generate lesion segmentations masks, we applied the threshold determined from the optimal thresholding algorithm in each respective iteration. We iterated this training and validation process to yield 100 bootstrap cross-validated sets of predicted probability maps and estimated binary segmentation masks. We note MIMoSA extends the OASIS method by adding IMCo features in the model and by proposing an optimal thresholding algorithm for fully automated delineation.

In addition to comparing MIMoSA with OASIS, we also compared against LesionTOADS, a segmentation algorithm based on fuzzy c-means that incorporates both topological constraints and a statistical atlas. Lesions are detected as outliers to the clustering function. As LesionTOADS is an unsupervised learning method, we did not bootstrap the training and validation. Instead, we simply applied the LesionTOADS algorithm with default parameters using the Java Image Science Toolkit²⁹ to obtain binary lesion segmentations for all 94 subjects directly.

It is not uncommon for MRI studies in MS to exclude collection of PD and/or T2. To address this, we repeated the bootstrap cross-validation procedure as if PD, T2, and both PD and T2 were not collected. Additionally, we evaluated the method with the bootstrap cross validation when trained on only 20 subjects and tested on 74 subjects. These additional analyses evaluated the robustness of MIMoSA under different data collection schemes.

Calculation of Summary Statistics and Confidence Intervals

Using the cross-validated estimated lesion segmentation masks, we summarized performance results by subject-level partial area under the receiver-operator characteristic curve (pAUC, up to 1% false positive rate)¹⁹ and DSC comparing our proposed MIMoSA method, OASIS, and LesionTOADS with manual segmentations. We used pAUC as it only considers regions of the ROC space which correspond to clinically relevant values of specificity;³³ that is, we did not consider model performance under clinically irrelevant high false positive rates. We then averaged performance measures across test set subjects and 100 cross-validated folds. To compare performance statistically between MIMoSA and OASIS methods, we reported confidence intervals for the difference between MIMoSA and OASIS (MIMoSA-OASIS) DSC and pAUC. To accomplish this, within each test dataset we first found and recorded the average difference in pAUC and DSC quantities for MIMoSA and OASIS. After averages were obtained, we found the values associated with upper and lower 0.025 quantiles to provide confidence intervals. We also recorded the frequency with which each threshold was chosen in the optimal threshold algorithm in order to compare the optimal thresholding for MIMoSA and OASIS methods. The performance of MIMoSA and LesionTOADS was assessed by using the binary segmentations produced by the LesionTOADS algorithm to calculate the subject-level DSC and pAUC. To compare performance statistically between MIMoSA and LesionTOADS methods, we reported confidence intervals for the difference between MIMoSA and LesionTOADS (MIMoSA-LesionTOADS) DSC and pAUC, averaged over each test set.

In addition to DSC and pAUC, performance was assessed by determining the Pearson’s correlation of lesional volume estimated by manual segmentations and the automated pipelines. To assess the relationship between lesion volume and clinical phenotypes, correlations between disease duration (time from first symptoms) and EDSS score were calculated. Manually segmented volumes were also correlated with these covariates as a benchmark. To avoid overfitting, correlation measures were averaged across bootstrapped test sets to yield a single measure.

Segmentation Challenge Study

In this section we describe the application of MIMoSA to a Segmentation Challenge. These results can be used to compare MIMoSA with a variety of approaches as well as assess performance when multiple raters generate segmentation masks.

Data Description

The 2015 Longitudinal Multiple Sclerosis Lesion Segmentation Challenge provides neuroimaging data acquired at multiple time points from MS patients. All preprocessing was carried out by challenge coordinators. Details concerning image acquisition and preprocessing are available in the data brief.³⁴ For normalization, many subjects had high lesion volume and we found z-score normalization methods to have failed based on visual inspection of histograms. Therefore, we used WhiteStripe to normalize as it is robust to pathology.²⁵ This data consists of 19 subjects each with FLAIR, T1, T2, and PD volumes collected longitudinally. The data was split by challenge coordinators into a training set and a testing set where each sequence acquired in the training set has manual segmentations. WML were delineated by two human expert raters, the first with 4 years of experience in manual segmentation and the second with 10 years of experience in manual segmentation and 17 years of experience in structural MRI analysis.³⁵ The training data consist of images acquired at 16 study visits for 5 subjects imaged longitudinally. For testing, data from 14 subjects imaged at 61 study visits were provided. Segmentation masks were provided for the training data; manual segmentations from the testing data were not distributed, but an online interface provides performance summaries for uploaded automated segmentations.³⁶ The total cerebral volume of WML was 11.6 mL as measured by rater 1 and 17.9 mL by rater 2.

Validation in Challenge Data

We trained and tested MIMoSA using data from the Challenge Data (2015). Since multiple manual segmentations were provided for this data we trained three distinct models: (1) a model using rater 1 segmentations, (2) a model using rater 2 segmentations, and (3) a model using rater 1 and rater 2 labels fused with STAPLE.³⁷ In addition, we label-fused MIMoSA segmentation masks from models trained on rater 1 and trained on rater 2 using STAPLE. We refer to this as post-hoc STAPLE. We fit the model using the same procedure as described in Section 2.1. After training the models we applied each respective model to the test data in order to generate probability maps. A threshold was applied using the optimal threshold generated from each training procedure found using an input range of probabilities from 5% to 35% by 1%.

The test data provided do not contain manual segmentations. In order to assess performance we submit MIMoSA predicted lesion segmentation masks based on all three (3) trained models through the online submission. Additionally, we submit lesion segmentation masks generated using STAPLE on predicted lesion masks trained using rater 1 and predicted lesion masks trained using rater 2. Performance is displayed in Figure 4.

Figure 4.

In the first row we compare Sørensen-Dice coefficient (DSC) scores for the Challenge Data when using rater 1 and rater 2 as the manual segmentation, respectively. In the second row we compare MIMoSA segmentation volume with manual segmentation volume reported by the Challenge in mL. Each column depicts the models trained using rater 1, rater 2, the label-fused STAPLE segmentations, and the predicted segmentations from training on rater 1 and rater 2 label-fused post prediction. Solid lines represent $y=x$ while dashed lines indicate the fitted linear regressions also provided as equations in the bottom-right of each panel.

Results

Johns Hopkins Cohort

Optimal Threshold Results

Table 1 shows the frequency of optimal thresholds chosen by the optimizing DSC algorithm for MIMoSA and OASIS models using threshold values of 20% to 35% by 1%. We found the optimal threshold with OASIS ranged from 24% to 28%. Within this range, we obtained a mode of 25%. MIMoSA utilizes a slightly wider spread of optimal thresholds ranging from 26% to 32%. Results for the replication of the bootstrap cross-validation when PD, T2, PD and T2 were excluded are similar and thus not provided here. For the cross-validation with only 20 subjects in the training set, thresholds are also similar and thus are not provided here.

Table 1.

Frequency of optimal thresholds applied to the subjects in each test set (100 iterations total) from MIMoSA and OASIS.

Threshold	24%	25%	26%	27%	28%	29%	30%	31%	32%
MIMoSA	0	0	1	14	37	30	10	7	1
OASIS	13	25	30	16	6	0	0	0	0

In the OASIS algorithm, a recalibration of the population-level segmentation threshold was necessary and required manual adjustment. With the optimal threshold algorithm proposed here, this manual adjustment step is no longer required and allows fully automated segmentation of images from a new imaging center if training data are available.

Summary Statistics Results

MIMoSA took 17.5 hours to train on 47 subjects on a single core in a high-performance computing environment. Applying the trained model to each single subject in the test set took approximately 22 minutes.

Table 2 shows average DSC and pAUC across test samples and confidence intervals for the difference between MIMoSA and OASIS. MIMoSA outperforms OASIS and LesionTOADS in both average DSC and pAUC. The confidence interval for differences with OASIS do not contain 0, indicating that the observed improvement of DSC and pAUC in MIMoSA are statistically significant. The confidence intervals for differences with LesionTOADS indicate a statistically significant difference in DSC but comparable pAUC. The DSC performance for MIMoSA indicates superiority in segmentation, and visual inspection of Figure 4 demonstrates accurate delineation. This is further evidenced by the strong correlation between the manually segmented volumes and MIMoSA-estimated volumes presented in Table 3.

Table 2.

Average Sørensen-Dice coefficient (DSC) and partial AUC (pAUC) for MIMoSA, OASIS, and LesionTOADS as well as confidence intervals for their differences estimated using bootstrapped cross-validation.

	DSC	pAUC
MIMoSA	0.57	0.68
OASIS	0.54	0.63
LesionTOADS	0.50	0.65
MIMoSA - LesionTOADS (95% CI)	(0.03,0.10)	(−0.01, 0.05)
MIMoSA - OASIS (95% CI)	(0.02,0.04)	(0.03,0.06)

Table 3.

Clinical-MRI associations using manual lesion volume $\rho \left(\mathit{Manual}\right)$, average MIMoSA lesion volume across bootstrap iterations $\rho \left(\mathit{MIMoSA}\right)$, average MIMoSA lesion volume across bootstrap iterations $\rho \left(\mathit{OASIS}\right)$, and LesionTOADS $\rho \left(\mathit{TOADS}\right)$ volumes are shown for the Johns Hopkins data. Lesion volumes were correlated separately with Expanded Disability Status Scale (EDSS) and disease duration. Additionally, the correlations between MIMoSA, OASIS, and LesionTOADS with manual segmentation volume are presented.

Disease Measures	$\mathrm{\rho }\left(\mathrm{Manual}\right)$	$\mathrm{\rho }\left(\mathrm{MIMoSA}\right)$	$\mathrm{\rho }\left(\mathrm{OASIS}\right)$	$\mathrm{\rho }\left(\mathrm{TOADS}\right)$
EDSS	0.31	0.30	0.29	0.40
Disease Duration	0.45	0.47	0.49	0.31
Manually Delineated Lesion Volume	1.00	0.96	0.95	0.81

Table 4 shows average DSC and pAUC across bootstrapped test samples when PD and T2 images were excluded from analysis. Additionally, results are presented for bootstrapped samples where we trained on 20 subjects and test on 74. Across all settings, DSC and pAUC changes were negligible and did not result in statistically different quantitative results.

Table 4.

Sørensen-Dice coefficient (DSC) and partial AUC (pAUC) values for the MIMoSA models in replication of bootstrap cross-validation under exclusion of the Proton Density-weighted (PD) sequence, the T2-weighted (T2) sequence, both PD and T2, and reducing the training set sample size to 20 subjects.

	DSC	pAUC
No PD	0.56	0.66
No T2	0.55	0.65
No PD and T2	0.54	0.64
20 Subjects	0.56	0.67

Segmentation metrics are often employed to evaluate patient disease burden and to evaluate the efficacy of therapeutics. To investigate whether MIMoSA-estimated volumes could replace manually measured volumes in such settings, we report the relationship between segmentation volumes and clinical measures in Table 3. The correlation between lesion volume and EDSS is approximately equal across the automatic methods and manual volume. LesionTOADS yielded the highest correlation. For disease duration, a similar pattern was observed except LesionTOADS correlated less closely; rather, OASIS showed the highest correlation. Manual lesion volume was also highly correlated with the various automatic volumes with correlation coefficients uniformly larger than 0.80, indicating a strong linear relationship between the manual segmentations and automatic segmentations. LesionTOADS-estimated volumes showed the weakest association with manually assessed volume, while MIMoSA showed the strongest correlation with the gold standard.

Qualitative Results

MIMoSA shows a significant improvement in performance over OASIS and LesionTOADS. Figure 3 displays example probability maps and binary segmentations from all models in axial slices. The results show that MIMoSA is able to identify lesions that OASIS and LesionTOADS were unable to detect. Additionally, Figure 3 shows MIMoSA better separates lesions that are spatially close and which OASIS and LesionTOADS could not distinguish as distinct lesions. Furthermore, Figure 3 shows OASIS and LesionTOADS tend to exhibit more false positive regions than MIMoSA, which is also reflected quantitatively in the ROC analysis.

Validation on Challenge Data

Table 5 shows the thresholds chosen by the optimal thresholding algorithm separated by the models trained using rater 1 manual segmentations, rater 2 manual segmentations, and STAPLE label-fused manual segmentations. In this case, we used threshold values of 5% to 35% by 1%.

Table 5.

Optimal threshold for MIMoSA shown for each all trained models with validation set 2.

Model	Threshold
Rater 1	0.29
Rater 2	0.29
STAPLE	0.31

In Figure 4 we display results for the Challenge data. In the first row, notice that DSC tends to improve as total lesion volume increases across all trained models. Additionally, DSC and volume agreement tend to favor segmentations provided by rater 1 independent of the manual segmentations chosen to train. This result is consistent with plots in the second row which display manual segmentation volume versus MIMoSA predicted volume. As manual segmentations are not provided by the Challenge to evaluate performance, visual comparisons are not possible.

Discussion

MIMoSA is a fully automated segmentation method that utilizes the changes in inter-modality covariance structure that occur in white matter pathology, and can be used to assist in WML detection or replace manual segmentation. MIMoSA removes the variability associated with manual and semi-automated WML segmentation. The model can be easily adapted and trained for cases when fewer imaging sequences are available. We show that MIMoSA yields superior segmentation results compared to OASIS and LesionTOADS, which are competitive in performance to the state-of-the-art machine learning methods.³⁸ Estimated lesional volume from automated methods showed very strong correlation with manually segmented volume, with MIMoSA showing the highest correlation coefficient. Additionally, all automated methods performed comparably in associations between clinical variable and volume.

In the application of MIMoSA on the Challenge Data, we found that performance of models place in the top 25 for the 2015 Longitudinal Multiple Sclerosis Lesion Segmentation Challenge. In these analyses, MIMoSA tended to segment subjects with high total lesion volume with more accuracy. Additionally, no matter which manual segmentations were used, the MIMoSA segmentations consistently were more similar to those produced by the more experienced rater’s manual lesion segmentations.

The optimal thresholding algorithm can be utilized in numerous ways. In this application, it was used to determine a threshold to apply to subjects in each test set. Estimated optimal thresholds applied using MIMoSA were larger than those for OASIS. This is likely due to MIMoSA’s higher sensitivity to lesion, which resulted in lesional tissue being assigned greater estimated probabilities than OASIS. If investigators have a priori information about reasonable threshold values for their data they can simply create a finer threshold grid around the known value. If investigators are unsure about a reasonable threshold level, a wider grid search can be utilized and then improved using finer grids. During the implementation of the optimal thresholding algorithm, results should include a variety of thresholds chosen from the interval as well as minimal thresholding at the boundary of the interval. In the event of thresholding at the boundaries, users should widen the grid and re-run the model procedure. Since the optimal thresholding algorithm is based on DSC, it will favor large lesions and could induce more lesional confluence. After manually inspecting subjects in testing sets, however, we did not note excess confluence in the MIMoSA segmentation results.

Lesion segmentation methods, whether sophisticated deep learning methods or simpler methods such as intensity-based regression models, depend on the development and refinement of discriminative, reliable imaging features. IMCo regression aims to detect biological changes reflecting processes occurring inside WML captured in the different scanning modalities. IMCo modeling facilitates new opportunities for feature extraction for the purpose of WML segmentation, but also promising new measures of pathological severity and repair processes.³⁹ These results are shown to be robust when fewer subjects are available to train, and if certain imaging modalities such as PD and T2 are not available. Since MIMoSA is reliable in these settings, studies can cut cost by reducing the number of MRI modalities acquired to T1 and FLAIR as well as by manually segmenting fewer subjects for training. This will additionally save time during image acquisition and in manual segmentation steps. As such, IMCo regression features could not only be useful for volumetric analyses but also hold promise for monitoring disease and quantifying effects of disease-modifying therapies.

For generalizations to data from different imaging centers or protocols, the recalibration of a threshold can be achieved automatically and optimally using the proposed cross-validation scheme. This novel algorithm estimates the threshold that produces segmentations which maximize similarity with manual segmentations. MIMoSA can thus easily be applied in a fully automated manner to new datasets when manual segmentations on training subjects are available.

The MIMoSA model is sensitive to manual segmentations. That is, the model is highly sensitive and specific to the manual segmentations used when training the model. Using the DSC metrics provided in Figure 4, we note that each trained MIMoSA model performs best when the training and testing manual segmentations are from the same rater. That is, we noted that when we train using rater 1, the DSC is higher for rater 1 test subjects than for rater 2 test subjects. In the application of automated segmentation methods, manual segmentations should be delineated carefully by expert consensus.

The MIMoSA method may be sensitive to the thresholds applied to remove CSF and during the voxel selection procedure. MIMoSA uses empirically recommended thresholds on the FLAIR modality, and imaging sequences with differing contrast level may necessitate adjustments to these thresholds. The method also requires that data be normalized and the power to detect lesion will be reduced if normalization technique is unsuccessful. In the implementation of the method, we suggest visual inspection of normalization through histograms to ensure normalization is successful.

Future work includes further validation of MIMoSA under variations in imaging protocols in order to show the replicability of IMCo measures and segmentation performance. Additional opportunities for performance improvement may also include the refinement of IMCo regressions for lesion segmentation by including complex modeling of nonlinear IMCo relationships, as well as the use of multiple neighborhood sizes in multi-scale IMCo analyses. An investigation can also be done on whether all pairwise combinations of modalities are necessary using model selection procedures. Furthermore, MIMoSA could be a useful tool in lesion segmentation in longitudinal studies, but should be evaluated under different training schemes to ensure validity. Beyond binary segmentation maps, the method shows promise in providing information about WML with different intermodal information that might aid in elucidating the causes of lesions, for example, by comparing vascular to demyelinating contributions. Moreover, IMCo regression coefficients can be useful features in longitudinal studies for modeling prediction of lesion behavior and progression.