Abstract
There is increasing evidence that many GWAS risk loci are molecular QTL (eQTL, hQTL, sQTL, and/or meQTL). Here, we introduce a new set of functional annotations based on causal posterior probabilities of fine-mapped molecular cis-QTL, using data from the GTEx and BLUEPRINT consortia. We show that these annotations are far more strongly enriched for heritability (e.g. 5.84x for eQTL; P=1.19×10−31) across 41 independent diseases and complex traits than annotations containing all significant molecular QTL (1.80x for eQTL). eQTL annotations that were obtained by meta-analyzing all GTEx tissues generally performed best, but tissue-specific eQTL annotations produced stronger enrichments for blood- and brain-related diseases and traits. Notably, eQTL annotations restricted to loss-of-function intolerant genes from ExAC were even more strongly enriched for heritability (17.06x; P=1.20×10−35). All molecular QTL except sQTL remained significantly enriched in a joint analysis, implying that each of these annotations is uniquely informative for disease and complex trait architectures.
Introduction
Although Genome-wide association studies (GWAS) have been extremely successful in detecting thousands of risk loci for diseases and traits1,2,3, our understanding of disease architecture is far from complete as most risk loci lie in non-coding regions of the genome4,5,6,7,8,9. Leveraging molecular phenotypes such as gene expression10,11,12,13,14 or chromatin marks15,16,17,18 can aid in understanding the disease architecture: in particular, previous studies have shown that cis-eQTL are enriched in GWAS loci as well as genome-wide heritability of several diseases5,6,19,20, motivating further work on colocalization21–23 and transcriptome-wide association studies24–26. Partitioning heritability using raw genotypes/phenotypes27–31 or summary association statistics32–34 can aid our understanding of disease architectures, but it is currently unclear how to best leverage molecular QTL from rich resources such as GTEx12,14 and BLUEPRINT18 using these methods.
Here, we introduce a new set of annotations constructed from eQTL, hQTL, sQTL, and meQTL data that are very strongly enriched for disease heritability across 41 independent diseases and complex traits. We construct these annotations by applying a fine-mapping method35 (allowing for multiple causal variants at a locus) to compute causal posterior probabilities for each variant to be a causal cis-QTL. We show that our annotations are far more enriched for disease heritability than standard annotations. We further show that our eQTL annotations produce tissue-specific enrichments (despite high cis-genetic correlations of eQTL effect sizes across tissues12,36, and produce much larger enrichments when restricted to loss-of-function intolerant genes from ExAC37. Finally, we quantify the extent to which annotations constructed from eQTL, hQTL, sQTL, and meQTL provide complementary information about disease.
Results
Overview of Methods
Our goal is to construct molecular QTL-based annotations that are maximally enriched for disease heritability. For a given molecular QTL data set, we construct a probabilistic (continuous-valued) annotation as follows. First, for each molecular phenotype (e.g. each gene) with at least one significant (FDR 5%) cis-QTL (e.g. 1Mb from TSS), we compute the causal posterior probability (CPP) of each cis SNP in the fine-mapped 95% credible set, using our CAVIAR fine-mapping method35 (see URLs). Then, for each SNP in the genome, we assign an annotation value based on the maximum value of CPP across all molecular phenotypes; SNPs that do not belong to any 95% credible set are assigned an annotation value of 0. We refer to this annotation as MaxCPP. For comparison purposes, we also construct three other molecular QTL-based annotations. First, we construct a binary annotation containing all SNPs that are a significant (FDR 5%) cis-QTL for at least one molecular phenotype19,20; we refer to this annotation as AllcisQTL. Second, we construct a binary annotation containing all SNPs that belong to the 95% credible set (see above) for at least one molecular phenotype; we refer to this annotation as 95%CredibleSet. Third, we construct a binary annotation containing the most significant SNP for each molecular phenotype with at least one significant (FDR 5%) QTL. We refer to this annotation as TopcisQTL (see Online Methods).
We apply a previously developed method, stratified LD score regression (S-LDSC)32,33, to partition disease heritability using functional annotations. We use two metrics to quantify an annotation’s contribution to disease heritability: enrichment and standardized effect size ( ). Enrichment is defined as the proportion of heritability explained by SNPs in an annotation divided by the proportion of SNPs in the annotation32; here, we generalize this definition to probabilistic annotations such as MaxCPP. Standardized effect size ( ) is defined as the proportionate change in per-SNP heritability associated to a one standard deviation increase in the value of the annotation, conditional on other annotations included in the model33. Unlike enrichment, quantifies effects that are unique to the focal annotation (see Online Methods).
We constructed MaxCPP and other annotations using eQTL data from the GTEx Consortium12,14 and eQTL, hQTL, sQTL and meQTL data from the BLUEPRINT Consortium18 (Table 1; see URLs). We included a broad set of 75 functional annotations from the baselineLD model (Supplementary Table 1) in most analyses. We have made our annotations and partitioned LD scores freely publicly available (see URLs).
Table 1. List of molecular QTL data sets analyzed.
GTEx includes eQTL for a wide range of tissues. BLUEPRINT includes eQTL, two hQTL, sQTL and meQTL for 3 blood cell types. Sample sizes for each tissue are provided in Supplementary Table 5 (GTEx) and Supplementary Table 26 (BLUEPRINT).
| Dataset | QTL Type | Number of Tissues | (per tissue) | (total) |
|---|---|---|---|---|
| GTEx | eQTL | 44 | 70-361 | 7014 |
| BLUEPRINT | eQTL | 3 | 169-194 | 555 |
| BLUEPRINT | hQTL (H3K27ac) | 3 | 143-174 | 479 |
| BLUEPRINT | hQTL (H3K4me1) | 3 | 104-173 | 449 |
| BLUEPRINT | sQTL | 3 | 169-194 | 555 |
| BLUEPRINT | meQTL | 3 | 132-197 | 525 |
Simulations
We performed a comprehensive set of simulations to assess whether S-LDSC produces unbiased estimates of an annotation’s contribution to disease heritability for the AllcisQTL, 95%CredibleSet, TopcisQTL and MaxCPP annotations. We performed simulations using real genotypes from the UK Biobank, restricting to 749,024 SNPs on chromosome 1 (see Online Methods). In our main simulation, we simulated gene expression phenotypes for 500 individuals assuming that 10% of cis-variants for a gene are causal cis-eQTL (heritability=16%), simulated complex trait phenotypes for an independent set of 40,000 individuals assuming that the set of causal variants is exactly the set of causal eQTLs, with independent effect sizes (heritability=20%), and subsequently assumed that 10% of causal eQTL are missing from the data analyzed. We also performed secondary simulations under other genetic architectures and assumptions about missing data (see below). We estimated each annotation’s contribution to complex trait heritability using S-LDSC. We performed 400 independent simulations, and averaged results across simulations.
Enrichment estimates and true enrichments for each annotation are displayed in Figure 1 and Supplementary Table 2. We determined that S-LDSC estimates are severely upward biased for the TopcisQTL annotation On the other hand, S-LDSC estimates were slightly conservative for the AllcisQTL, 95%CredibleSet and MaxCPP annotations. Thus, we restrict our analyses to these three annotations in our analyses of real phenotypes below Of these three annotations, MaxCPP had the highest enrichment (Figure 1 and Supplementary Table 2). For comparison purposes, we also computed estimates using GCTA27,28 (see URLs), a method that has previously been applied to assess eQTL enrichment for complex traits19,20; we computed GCTA estimates for all annotations except MaxCPP, as GCTA is only applicable to binary annotations. We determined that GCTA estimates generally exhibited greater bias than S-LDSC estimates (Figure 1 and Supplementary Tables 2-3). We obtained similar results for both S-LDSC and GCTA at other simulation parameters (Supplementary Table 3). We also obtained similar results for both S-LDSC and GCTA using an alternative simulation framework, drawn from our previous work25, that directly uses simulated gene expression to generate complex trait phenotypes (see Online Methods and Supplementary Table 4).
Figure 1. S-LDSC and GCTA estimate for TopcisQTL are upward biased in simulations.
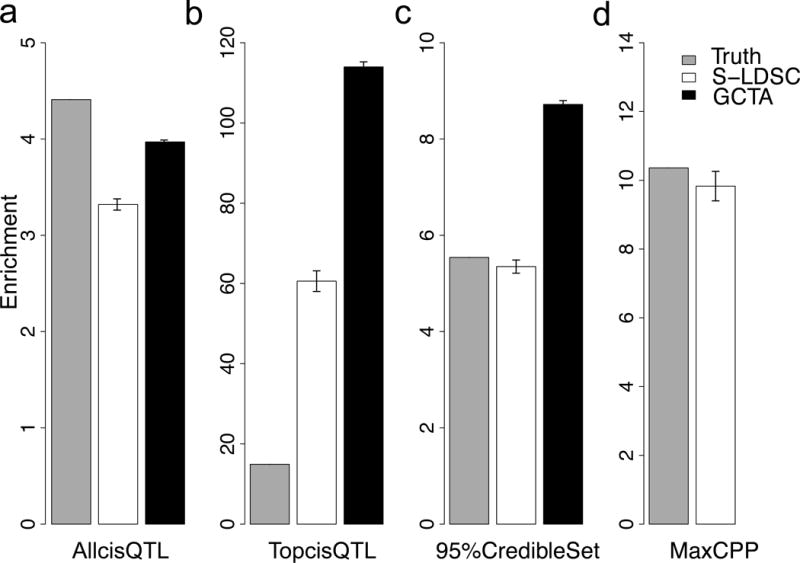
Panels (a), (b), (c), and (d) illustrate the true enrichment and S-LDSC and GCTA enrichment estimates for AllcisQTL, 95%CredibleSet, TopcisQTL, and MaxCPP annotations, respectively. GCTA is not applicable to continuous annotations (MaxCPP). The Y-axis indicates the mean of enrichment and error bars represent 95% confidence intervals that are computed for 400 simulations. Numerical results are reported in Supplementary Table 2. See Supplementary Table 3 and Supplementary Table 4 for additional simulation scenarios.
All functional enrichment methods (GCTA27,28, BOLT-REML30, S-LDSC32,33, and LDAK31) that we are currently aware of assume that causal disease effect sizes are independent and identically distributed (i.i.d) conditional on MAF, LD and function annotation values. However, this assumption may be violated for molecular QTL-based annotations when causal variants are sparse (see Online Methods for an example); in particular, this is a limitation of our S-LDSC method. Indeed, our simulations confirm these biases (Figure 1 and Supplementary Tables 2-4). We note that other functional enrichment methods are also subject to this limitation. Specifically, GCTA27,28 is shown by our simulations to exhibit greater biases than S-LDSC (Figure 1 and Supplementary Tables 2-4). BOLT-REML30 is a computationally efficient method that produces the same results as GCTA27,28, and LDAK31 has been shown in separate work to produce biased estimates in much simpler settings38. S-LDSC produces slightly conservative estimates across a comprehensive set of simulations for the AllcisQTL, 95%CredibleSet and MaxCPP annotations that we consider in our analyses of real phenotypes below.
Fine-mapped eQTL are enriched for disease heritability
We used the GTEx eQTL data set (Table 1) to construct AllcisQTL, 95%CredibleSet and MaxCPP annotations. We constructed annotations using each of the 44 tissues (Supplementary Table 5). We applied S-LDSC to assess each annotation’s contribution to disease heritability for each of 41 independent diseases and complex trait data sets (average =320K); for six traits we analyzed two different data sets, leading to a total of 47 data sets analyzed (see Supplementary Table 6). We meta-analyzed results across the 47 data sets, which were chosen to be independent (see Online Methods). We computed enrichment and for each annotation, in analyses that included 75 functional annotations (Supplementary Table 1) from the baselineLD model33. Results for whole blood, a widely studied tissue, are reported in Figure 2 and Supplementary Table 7. We determined that the MaxCPP annotation had far higher values of enrichment and than AllcisQTL or 95%CredibleSet; the enrichment estimates remain much higher for MaxCPP even after accounting for the fact that S-LDSC generally produces more conservative estimates for AllcisQTL and 95%CredibleSet than for MaxCPP in our simulations (1.10-1.58x and 0.76-1.23x more conservative respectively, across all simulations; Figure 2 and Supplementary Table 7). The MaxCPP annotation also had higher values of enrichment and in analyses that did not condition on the baselineLD model (Supplementary Figure 1 and Supplementary Table 8).
Figure 2. Fine-mapped eQTL are strongly enriched for disease/trait heritability.
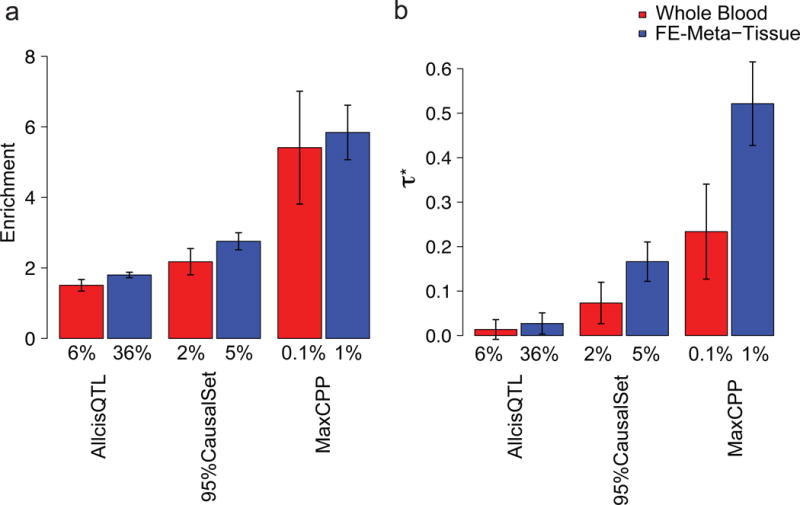
(a) Meta-analysis results across 41 traits of enrichment for whole blood and FE-Meta-Tissue from the GTEx data set conditioning on the baselineLD model. (b) Meta-analysis results across 41 traits of for whole blood and FE-Meta-Tissue conditioning on the baselineLD model. In each panel, we report results for AllcisQTL, 95%CredibleSet, and MaxCPP. Error bars represent 95% confidence intervals. The % value under each bar indicates the proportion of SNPs in each annotation; for probabilistic annotations (MaxCPP), this is defined as the average value of the annotation. Numerical results are reported in Supplementary Table 7.
We investigated whether the for MaxCPP in each respective tissue varied with sample size. We observed a correlation ( = 0.69, P = 1.36e-12) between sample size and (Figure 3 and Supplementary Table 9). We observed a similar pattern in simulations (Supplementary Figure 2). This suggests that the correlation between sample size and in GTEx data is related to statistical power and not because tissue-specific eQTL from tissues with larger sample size are more relevant for the 41 traits analyzed. Thus, annotations constructed from tissues with larger sample sizes are more informative for disease/trait architectures.
Figure 3. Relationship between eQTL sample size and the annotation effect size ( ).
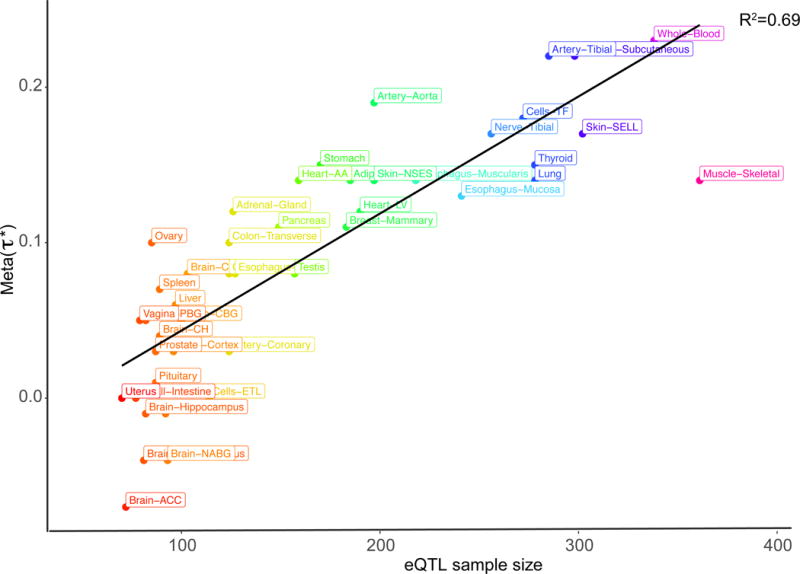
For each tissue, we plot the of the MaxCPP annotation, meta-analyzed across 41 traits, against the eQTL sample size. Numerical results are reported in Supplementary Table 10. For visualization purposes, we use the following abbreviations: Adipose Visceral Omentum (Adipose-Visceral), Brain Anterior cingulate cortex BA24 (Brain-ACC), Brain Caudate basal ganglia (Brain-CBG), Brain Cerebellar Hemisphere(Brain-CH), Brain Cerebellar Hemisphere (Brain-CH), Brain Frontal Cortex BA9 (Brain-FC), Brain Nucleus accumbens basal ganglia (Brain-NABG), and Brain Putamen basal ganglia (Brain-PBG), Cells EBV transformed lymphocytes (Cells-CETL), Cells Transformed fibroblasts (Cells-TF), Esophagus Gastroesophageal Junction (Esophagus-GJ), Heart Atrial Appendage (Heart-AA), Heart Left Ventricle (Heart-LV), Skin Not Sun Exposed Suprapubic (Skin-NSES), Skin Sun Exposed Lower leg (Skin-SELL), and Small Intestine Terminal Ileum (Small-Intestine).
To maximize sample size, we performed a fixed-effect meta-analysis of eQTL effect sizes across the 44 tissues (FE-Meta-Tissue)(see Online Methods). We determined that FE-Meta-Tissue annotations had slightly larger enrichments and much larger (due to larger annotation size) than annotations constructed from individual tissues (Figure 2, Supplementary Table 7 and Supplementary Table 10). As with individual tissues, the MaxCPP annotation had far higher values of enrichment (5.84x, s.e. = 0.40; P = 1.19e-31) and ( = 0.52, s.e. = 0.05; P = 2.73e-27) than AllCisQTL (enrichment = 1.80x and = 0.03) or 95%CredibleSet (enrichment = 2.75x and = 0.17). It is particularly notable that the for GTEx FE-Meta-Tissue MaxCPP (conditional on the baselineLD model) is much larger than the values of the 6 continuous annotations that we introduced in our previous work33 (Supplementary Table 11). A histogram of MaxCPP annotation values for GTEx FE-Meta-Tissue is provided in Supplementary Figure 3, and correlations with baselineLD model annotations and their LD scores are provided in Supplementary Figures 4 and 5.
Tissue-specific fine-mapped eQTL enriched for heritability
Although the FE-Meta-Tissue MaxCPP annotation outperformed each of the 44 tissue-specific MaxCPP annotations in the meta-analysis across 41 traits (Figure 2 and Figure 3), this was not the case for every trait. We examined six autoimmune diseases, five blood cell traits, and eight brain-related diseases and traits in detail (see Online Methods). We first analyzed the six autoimmune diseases, analyzing MaxCPP annotations for blood and FE-Meta-Tissue separately (conditional on the baselineLD model) and meta-analyzing results across the six diseases. We obtained higher estimates of (and higher or comparable estimates of enrichment) for blood than for FE-Meta-Tissue or any other individual tissue (Supplementary Table 12). We then analyzed MaxCPP annotations for blood and FE-Meta-Tissue jointly (conditional on the baselineLD model). We obtained a significantly positive estimate for blood ( = 0.91, s.e. = 0.34; P = 9.15e-03) (Figure 4 and Supplementary Table 13), implying that fine-mapped blood eQTL provides additional information about these six diseases conditional on fine-mapped FE-Meta-Tissue eQTL. We repeated these analyses for the five blood cell traits. When analyzing MaxCPP annotations for blood and FE-Meta-Tissue separately, we obtained higher estimates of (and higher or comparable estimates of enrichment) for blood than for FE-Meta-Tissue or any other individual tissue (Supplementary Table 14). When analyzing MaxCPP annotations for blood and FE-Meta-Tissue jointly, we obtained a significantly positive estimate for blood ( = 1.17, s.e. = 0.24; P = 1.77e-06) (Figure 4 and Supplementary Table 13), implying that fine-mapped blood eQTL provides additional information about these five traits conditional on fine-mapped FE-Meta-Tissue eQTL. The correlations of blood MaxCPP annotation values with baselineLD model annotations and their LD scores are provided in Supplementary Figures 6 and 7.
Figure 4. Tissue-specific fine-mapped eQTL enrichments for blood and brain related traits.
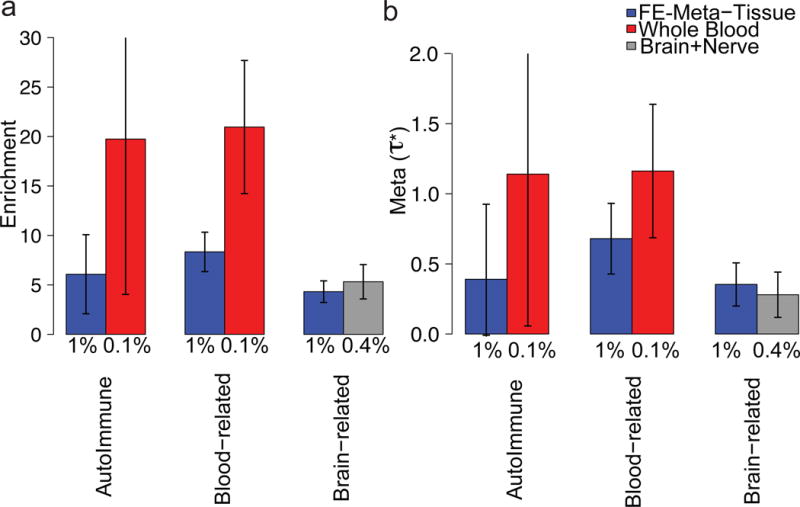
Meta-analysis results of (a) enrichment and (b) of FE-Meta-Tissue and tissue-specific MaxCPP annotations, conditional on each other and the baselineLD model, across six independent autoimmune diseases, five blood cell traits, and eight brain-related traits, respectively. The Y-axis is the meta-analyzed value and error bars represent 95% confidence intervals. The % value under each bar indicates the proportion of SNPs in each annotation, defined as the average value of the annotation. Numerical results are reported in Supplementary Table 13.
We then analyzed the eight brain-related diseases and traits. We performed a fixed-effect meta-analysis of eQTL effect sizes across the 10 brain tissues and one nerve tissue (Brain+Nerve). When analyzing MaxCPP annotations for Brain+Nerve and FE-Meta-Tissue separately, we obtained higher or comparable estimates of enrichment and for Brain+Nerve than for FE-Meta-Tissue or any individual tissue (Supplementary Table 15). When analyzing MaxCPP annotations for Brain+Nerve and FE-Meta-Tissue jointly, we obtained a significantly positive estimate for Brain+Nerve ( = 0.28, s.e. = 0.07; P = 9.81e-05) (Figure 4 and Supplementary Table 13), implying that fine-mapped Brain+Nerve eQTL provides additional information about these eight traits conditional on fine-mapped FE-Meta-Tissue eQTL. The correlations of Brain+Nerve MaxCPP annotation values with baselineLD model annotations and their LD scores are provided in Supplementary Figures 6 and 7. We repeated these analyses for each trait and each tissue separately, but determined that only three blood cell traits (white blood count, red blood cell distribution width, and eosinophil count traits), in conjunction with MaxCPP for blood, attained a significantly positive (FDR 5%) tissue-specific (Supplementary Tables 16 and 17). Overall, these results demonstrate that tissue-specific eQTL effects on steady-state expression can be significant for diseases and complex traits, despite the well-documented high cis-genetic correlations of eQTL effect sizes across tissues12,36.
MaxCPP signal is concentrated in disease-relevant gene sets
Recent studies have identified gene sets that are depleted for coding variants and enriched for de novo coding mutations impacting disease37,39,40. To investigate the importance of non-coding common variants in these gene sets, for each gene set we used GTEx FE-Meta-Tissue to construct a new annotation MaxCPP( ), defined as the maximum CPP restricted to genes in . For comparison purposes, we also constructed an annotation allSNP( ), defined as the set of all SNPs within 100Kb of genes in .
We first analyzed the ExAC gene set, consisting of 3,230 genes that are strongly depleted for protein-truncating variants37. We determined that MaxCPP(ExAC) was very strongly enriched in an analysis conditional on the baselineLD model, meta-analyzed across 41 independent traits (see Figure 5a and Supplementary Table 18). In particular, MaxCPP(ExAC) was much more strongly enriched (17.06x, s.e. = 1.28; P = 1.20e-35) than MaxCPP(All Genes) (5.84x) (P = 4.90e-17 for difference). This implies that eQTL for these 3,230 genes have a disproportionately strong impact on disease heritability, consistent with the fact that these genes are depleted for eQTL37. We then analyzed MaxCPP(ExAC) and MaxCPP(All Genes) annotations jointly (conditional on the baselineLD model). We obtained a significantly positive for MaxCPP(ExAC) ( = 0.41, s.e. = 0.04; P = 1.40e-23; Figure 5b and Supplementary Table 19), implying that MaxCPP(ExAC) provides additional information about disease heritability conditional on MaxCPP (All Genes). We observed that the effect size ( ) for MaxCPP(ExAC) conditional on MaxCPP (All Genes) and baselineLD is five times larger, and more statistically significant, than the of allSNP (ExAC) conditional on the baselineLD model (Supplementary Table 20). Thus, MaxCPP can increase power to identify enriched gene sets.
Figure 5. Heritability enrichment of fine-mapped eQTL is concentrated in disease-relevant gene sets.
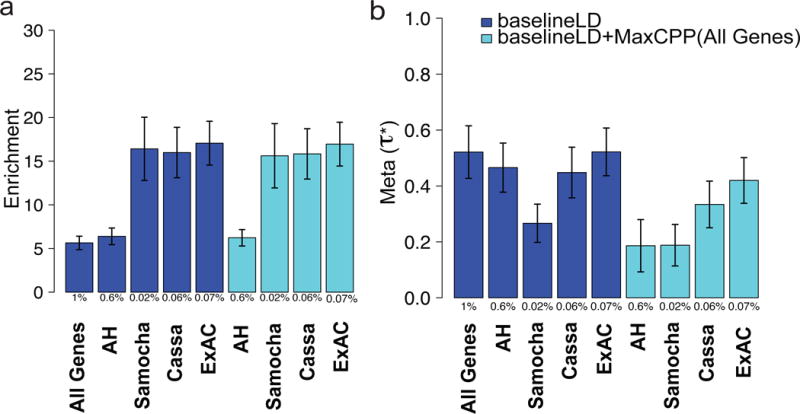
Meta-analysis results of (a) enrichment and (b) of MaxCPP(S) for various gene sets S. We report results conditional on the baselineLD model (dark blue) and results conditional on both the baselineLD model and MaxCPP(All Genes) (light blue), meta-analyzed across 41 traits. As expected, estimates are reduced by conditioning on MaxCPP(All Genes), but enrichment estimates are not affected. The Y-axis is the meta-analyzed value and error bars represent 95% confidence intervals that are computed over 41 traits. The % value under each bar indicates the proportion of SNPs in each annotation, defined as the average value of the annotation. Numerical results are reported in Supplementary Table 18.
We analyzed four additional gene sets : a set of 1,003 genes that are strongly depleted for missense mutations40 (Samocha); a set of 2,984 genes with strong selection against protein-truncating variants39 (Cassa); a set of 1,878 genes predicted to be essential based on CRISPR experiments in a human cancer cell line41 (Wang); and a set of 11,983 genes with evidence of allelic heterogeneity in analyses of GTEx gene expression data using our previously developed methods (AH)42. For each of these gene sets, MaxCPP( ) was strongly enriched in analyses conditional on the baselineLD model, meta-analyzed across 41 independent traits (Figure 5a and Supplementary Table 18). In addition, for each gene set except the Wang gene set, we obtained a significantly positive for MaxCPP( ) (after correcting for five gene sets tested) when analyzing MaxCPP( ) and MaxCPP(All Genes) jointly (conditional on the baselineLD model) (Figure 5b, Supplementary Table 19 and Supplementary Tables 21-25). As with the ExAC gene set, the for MaxCPP( ) conditional on MaxCPP(All Genes) and the baselineLD model were substantially larger than the of allSNPs (ExAC) conditional on the baselineLD model and were often more statistically significant (Supplementary Table 20), indicating that MaxCPP can increase power to identify enriched gene sets in which regulatory variants play an important role.
Fine-mapped molecular QTL are enriched for heritability
We analyzed five molecular QTL from the BLUEPRINT data set (Table 1), including eQTL, hQTL (H3K27ac and H3K4me1), sQTL and meQTL. In each case, we constructed AllcisQTL, 95%CredibleSet and MaxCPP annotations using each of the three immune cell types (CD14+ monocytes, CD16+ neutrophils, and naive CD4+ T cells; Supplementary Table 26) as well as a fixed-effect meta-analysis of molecular QTL effect sizes across the 3 cell types (FE-Meta-Tissue). We determined that for each QTL data set the MaxCPP annotation outperformed the AllcisQTL and 95%CredibleSet annotations (Supplementary Table 27). A histogram of MaxCPP annotation values for each QTL data set is provided in Supplementary Figure 8. MaxCPP for each molecular QTL was significantly enriched in an analysis conditional on the baselineLD model, meta-analyzed across the 41 traits: eQTL (5.44x, s.e. = 0.55; P = 3.26e-16), H3K27ac (4.28x, s.e. = 0.37; P = 2.59e-19), H3K4me1 (4.27x, s.e. = 0.36; P = 1.29e-20), sQTL (3.61x, s.e. = 0.40; P =1.39e-10), and meQTL (2.81x, s.e. = 0.19; P = 8.36e-22) (Figure 6a and Supplementary Table 28); the enrichment for BLUEPRINT eQTL was almost as large as the enrichment for GTEx eQTL (5.84x), despite the much smaller total sample size of FE-Meta-Tissue in BLUEPRINT. This implies that BLUEPRINT sample sizes, though small, are adequately powered for eQTL detection. Consistent with this finding, we observed a high replication rate between cis-QTL in GTEx and BLUEPRINT (see Supplementary Table 29), confirming that GTEx FE-Meta-Tissue provides increased power relative to GTEx blood (Supplementary Table 28). BLUEPRINT FE-Meta-Tissue generally attained higher enrichments and than MaxCPP computed using each of the three immune cell types individually (Supplementary Table 30), similar to our GTEx results (Supplementary Tables 7 and 10). MaxCPP computed using FE-Meta-Tissue also generally outperformed each of the three cell types in a meta-analysis across the six autoimmune diseases (Supplementary Table 31) and a meta-analysis across the five blood cell traits (Supplementary Table 32), in contrast to the stronger enrichments for tissue-specific GTEx blood eQTL annotations for blood cell traits (Supplementary Tables 12 and 14). FE-Meta-Tissue generally attained higher enrichments and than MaxCPP computed using each of the three immune cell types individually (Supplementary Table 30), similar to our GTEx results (Supplementary Tables 7 and 10). MaxCPP computed using FE-Meta-Tissue also generally outperformed each of the three cell types in a meta-analysis across the six autoimmune diseases (Supplementary Table 31) and a meta-analysis across the five blood cell traits (Supplementary Table 32), in contrast to tissue-specific results in GTEx (Supplementary Tables 12 and 14).
Figure 6. Fine-mapped eQTL, hQTL, sQTL, and meQTL annotations are enriched for disease/trait heritability.
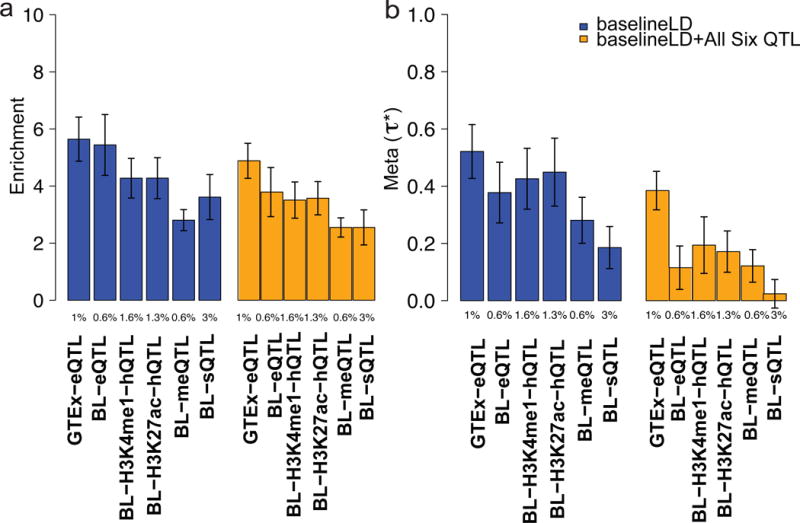
Meta-analysis results of (a) enrichment and (b) of MaxCPP for various molecular QTL from GTEx and BLUEPRINT (BL). We report results conditional on the baselineLD model (dark blue) and results conditional on both the baselineLD model and MaxCPP for all six molecular QTL (orange), meta-analyzed across 41 traits. As expected, estimates are reduced by conditioning on MaxCPP for all molecular QTL, but enrichment estimates are not affected. The Y-axis is the meta-analyzed value and error bars represent 95% confidence intervals that are computed over 41 traits. The % value under each bar indicates the proportion of SNPs in each annotation, defined as the average value of the annotation. Numerical results are reported in Supplementary Table 28 and Supplementary Table 33.
Finally, we jointly analyzed MaxCPP annotations for GTEx eQTL and each of the five BLUEPRINT molecular QTL (conditional on the baselineLD model). The purpose of this analysis was to determine whether each of these molecular QTL provides independent information about disease and complex trait architectures. We determined that remained statistically significant for all molecular QTL except sQTL (Figure 6b and Supplementary Table 33); a joint analysis of just the five BLUEPRINT molecular QTL (conditional on the baselineLD model) produced similar findings (Supplementary Table 34). LD scores of the sQTL annotation had the highest correlation with LD scores of the GTEx eQTL and BLUEPRINT eQTL annotations ( ; see Supplementary Figure 5), implying that much of the informativeness of sQTL in this analysis is captured by eQTL. However, eQTL, hQTL (H3K27ac and H3K4me1) and meQTL are each uniquely informative for disease and complex trait architectures.
Discussion
We have shown that annotations constructed using fine-mapped posterior probabilities for several different molecular QTL are strongly enriched for disease heritability. These results improve upon two previous studies that made key contributions in showing that annotations constructed using all significant cis-eQTL were significantly enriched for trait heritability19,20. Our findings provide additional motivation for colocalization studies21–23 and transcriptome-wide association studies (TWAS)24–26. Our fine-mapped eQTL annotations were able to detect tissue-specific enrichments for blood and brain related traits, despite high cis-genetic correlations12,36 of eQTL effect sizes across tissues and despite the fact that TWAS have generally concluded that their results “did not suggest tissue-specific enrichment”26.
We note that a previous study showed that cis-eQTL often lie close to the transcription start site (TSS) or transcription end site (TES)43, motivating us to investigate the orthogonal question of whether cis-eQTL that lie near the TSS/TES produce more disease signal than cis-eQTL that do not lie near the TSS/TES; we did not observe such an effect in the GTEx or BLUEPRINT data sets (see Supplementary Tables 35 and 36). Notably, our eQTL annotations produced particularly large enrichments when restricted to disease-relevant gene sets such as loss-of-function intolerant genes from ExAC, highlighting the potential to increase signal in analyses of gene sets harboring regulatory signals by prioritizing fine-mapped cis-eQTL. Our eQTL annotations may also prove useful in future analyses of gene pathways.
We also detected strong enrichments using annotations based on other molecular QTL, with eQTL, hQTL and meQTL all providing complementary information about disease, conditional on each other and on functional annotations from previous studies. These results motivate applying colocalization and TWAS methods to other molecular QTL; it may also be possible to prioritize other molecular QTL in gene set analyses by connecting regulatory regions to genes44,45. Although annotations constructed from sQTL were not conditionally significant in our analysis, previous work has shown that sQTL can contain information that is independent from eQTL46, motivating further investigation in larger sQTL data sets.
We note several limitations of our work. First, we restrict our analyses to common variants, as S-LDSC is not currently applicable to rare variants47. Recent work has shown that rare variants can have substantial effects on gene expression50, motivating ongoing work to extending S-LDSC to rare variants. Second, the CAVIAR fine-mapping method allows up to six causal variants per locus; this may limit power at loci that harbor more than six causal variants, although this would not lead to spurious signals. We determined that our results were very similar when modifying CAVIAR to allow up to three causal variants per locus (Supplementary Figures 9 and 10 and Supplementary Table 37), suggesting that modeling only six causal variants per locus is unlikely to greatly impact our results. Third, we show that S-LDSC is generally unable to produce unbiased enrichment estimates for molecular QTL based annotations when causal variants are sparse, due to violations of model assumptions (which also impact other functional enrichment methods, including GCTA27,28, BOLT-REML30 and LDAK31, which also assume that causal disease effect sizes are i.i.d conditional on MAF, LD and functional annotation values); S-LDSC produces slightly conservative enrichment estimates for the MaxCPP annotation that we focus on here; however, the S-LDSC estimates should not be viewed as rigorous lower bounds, because our simulations do not include all possible genetic architectures. We caution that the TopcisQTL annotation produces large upward biases and should be avoided (Figure 1). Fourth, our results are a function of the molecular QTL sample size (Figure 3) and set of tissues; although current molecular QTL sample sizes are clearly informative, analyses of larger sample sizes and/or different tissues or contexts may produce larger enrichments in the future. Fifth, we performed a fixed-effect meta-analysis of molecular QTL effect sizes across tissues (FE-Meta-Tissue) that does not account for overlapping samples and heterogeneity across tissues in eQTL effect sizes, which could in principle limit our power48. However, noise is largely uncorrelated across tissues (despite pervasive sample overlap), and recently developed random-effect cross-tissue eQTL meta-analysis methods48,49 are not applicable in the current setting (see Online Methods). Sixth, our approach cannot distinguish causal mediation from horizontal pleiotropy (i.e. independent effects on molecular QTL and disease), thus our molecular QTL enrichment results should not be viewed as a quantification of mediated effects. Despite these limitations, our results indicate that fine-mapped QTL annotations are strongly enriched for disease heritability and can help elucidate the genetic architecture of diseases and complex traits.
Online Methods
Molecular QTL-based annotations
We construct four annotations for any given QTL data set using the observed marginal association statistics. The four annotations are MaxCPP, AllcisQTL, 95%CredibleSet, and TopcisQTL. Each annotation is a vector that assigns a value to each SNP. Let indicate our annotation for one QTL data set where indicates the value assigned to SNP . For binary annotations (AllcisQTL, 95%CredibleSet, and TopcisQTL) , and indicates that SNP is not included in the annotation, while indicates that SNP is included in the annotation. For continuous probabilistic annotations (MaxCPP), .
Let indicate an ( ) matrix of the observed marginal association statistics obtained for each QTL data set, where is the number of SNPs and is the number of eGenes (e.g., genes that have at least one significant cis-eQTL). Let be the vector of marginal association statistics of gene for all the cis-variants. Utilizing and the LD structure, we can compute the causal posterior probability (CPP) for each variant. CPP is the probability that a variant is causal. Let be the posterior probability that the SNP is causal for the gene . We obtain the CPP values from CAVIAR35. In addition to the CPP values, CAVIAR provides a 95%credible set that contains all of the causal variants with probability at least 95%. Let indicate whether SNP is in the 95%credible set for the gene (i.e., =1 indicates that the SNP is in the gene 95%credible set and =0 otherwise). We construct the MaxCPP annotation for SNP by computing the maximum value of CPP over all genes where SNP is in the 95%credible set of the gene . More formally, we have: where the maximum is over genes with .
AllcisQTL annotation is a binary annotation, where any variant whose marginal association statistic for at least one gene passes the significance threshold (FDR 0.05) has annotation value 1, and each other variant has annotation value 0. Let indicate whether the SNP is statistically significant for the gene ( when FDR(j) 0.05 and otherwise). More formally, we have: .
95%CredibleSet is a binary annotation, any variant that is in a 95%credible set of at least one gene has annotation value 1 and each other variant has annotation value 0. More formally, we have: .
TopcisQTL is a binary annotation where any variant that is the most significant variant for at least one gene has annotation value 1 and each other variant has annotation value 0. Let indicate whether the SNP is the most significant SNP for the gene (i.e., =1 if SNP is the most significant SNP among all cis-variants for the gene and =0 otherwise). More formally, we have: .
Enrichment and effect size ( ) metrics
We use two metrics to measure the importance of an annotation in the context of diseases and complex traits: Enrichment and standardized effect size ( ) of annotation. We use S-LDSC32,33 to compute enrichment and standardized effect size ( ). Let indicate the annotation value of the SNP for the annotation . S-LDSC32,33 assumes that the variance of each SNP is a linear additive contribution to each annotation:
| (1) |
where is the contribution of the annotation to per-SNP heritability. S-LDSC32,33 estimates using the following equation:
| (2) |
where is the GWAS sample size and is the LD score of the SNP for the annotation . S-LDSC computes the LD scores as follow: where is the genetic correlation between the SNPs and .
Since depends on the trait heritability and the size of the annotation, ref.33 defined for an annotation as the standardized annotation effect size:
| (3) |
where is the standard deviation of the annotation , is the SNP-heritability, and is the number of variants used to compute . In our experiments, is equal to 5,961,159 (see below).
The enrichment of an annotation is defined as the fraction of heritability captured by the annotation divide by the fraction of SNPs in that annotation. We extend the definition of enrichment to continuous probabilistic annotations with values between 0 and 1:
| (3) |
where is the heritability captured by the c-th annotation. We can compute this quantity as follows:
| (4) |
Although both enrichment and are computed using a model that includes all annotations, quantifies effects that are unique to the focal annotation (after conditioning on all other annotations in the model), whereas enrichment quantifies effects that are either unique and/or non-unique to the focal annotation. For example, consider a model that includes two annotations, where the first annotation is a highly disease-informative functional annotation and the second annotation is the first annotation plus a random set of SNPs. Only the first annotation will have significant , but both annotations will be significantly enriched. We confirmed via simulation that, under a generative model in which only the baselineLD and GTEx FE-Meta-Tissue MaxCPP annotations directly influence trait heritability, estimates for the GTEx-Whole-Blood MaxCPP annotations are equal to 0 on average, with a correctly calibrated null distribution of P-values for nonzero (Supplementary Figure 11).
We computed the statistical significance level (p-value) of enrichment for each annotation via block-jackknife, as described in our previous studies32,33,50. We computed the statistical significance (p-value) of standardized effect size ( ) for each annotation by assuming that follows a normal distribution with mean 0 and variance of 1 ( )33.
Simulation framework
Main simulation framework
We simulated both gene expression and trait phenotypes. We utilized UK Biobank genotypes from chromosome 1, which consists of 749,024 variants, for our simulation. We used 40,000 individuals to generate the trait phenotypes and a non-overlapping set of 500 individuals to generate gene expression phenotypes. Let and indicate the total heritability of gene expression and trait phenotypes, respectively. We simulated causal trait effect sizes using a polygenetic model, , where is the causal (true) effect size of the -th causal variant and is the number of causal variants for the trait. Similarly, we simulated causal gene expression effect sizes using a polygenetic model, , where is the causal (true) effect size of the -th causal variant on gene expression of gene and is the number of causal variants. We use the following model to simulate the gene expression and traits:
| (5) |
where is environmental and measurement noise, is the simulated trait phenotypes, is the gene expression of gene , and is the environmental and measurement noise for gene . In the case of gene expression, we simulated 1,860 phenotypes to represent our simulated gene expression data as 1,860 genes lies on chromosome one. We simulated three different data sets where is set to 1 causal variant, 10 causal variants, or 10% of cis-variants that are causal for each gene. The default value of is set to 10% of cis-variants. In the case of trait phenotypes, we set to be the union of causal variants for all genes on chromosome 1 ( where is the set of causal variants for gene ). In our simulated data sets, we set to 0.2 and considered different values of to test our results on different input parameters. We set to 0.1, 0.16, and 0.2 resulting in different simulated data sets. The default value of 0.16 is used for . For each simulated data set, we performed 400 simulations.
After simulating the gene expression and trait phenotypes, we obtained marginal association statistics for each variant using linear regression implemented in the PLINK software51 (see URLs). In the case of simulated trait phenotypes, we computed the association of each variant with the simulated trait phenotypes ( ). In the case of simulated gene expression phenotypes, we computed the marginal statistics for all variants within 1Mb of the TSS ( ). In some simulations, we assumed that a subset of the causal variants are missing (not measured). Let indicate the fraction of causal eQTL that are missing. In our simulated datasets, we set to 0% (no causal eQTL is missing), 5% (5% of causal eQTL are missing), 10% (10% of causal eQTL are missing), or 50% (half of the causal eQTL are missing). The default value of 10% is used for
Alternative simulation framework
We also considered an alternative simulation framework, drawn from our previous work25 that directly uses simulated gene expression to generate complex trait phenotypes. We utilized UK Biobank genotypes from chromosome 1, which consists of 749,024 variants, for our simulation. We used 40,000 individuals to generate the trait phenotypes and gene expression phenotypes. We assume that the trait phenotype is a mixture of direct genotype effects (effect not medicate through gene expression) and gene expression effects. Let indicate the phenotypic variance explained directly by genotypes, indicate the gene expression variance explained directly by genotypes, and indicate the phenotypic variance explained by gene expression. We simulated causal gene expression effect sizes using a polygenetic model, , where is the causal (true) effect size of the -th causal variant on the gene expression of gene and is the number of causal variants. We simulated causal trait effect sizes using a polygenetic model, , where is the causal (true) effect size of -th causal variant and is the number of causal variants for simulated trait phenotypes. As above, we simulated expression values for the 1,860 genes on chromosome 1. We simulated the effect size of gene expression on traits using polygenetic model, , where is set to 25. We use the following model to simulate the gene expression and traits:
| (6) |
After simulating the gene expression and trait phenotypes, we obtained marginal association statistics for each variant using linear regression implemented in the PLINK software52 (see URLs). In the case of simulated trait phenotypes, we computed the association of each variant with the simulated trait phenotypes ( ). In the case of simulated gene expression phenotypes, we computed the marginal statistics for all variants within 1Mb of the TSS ( ) where is the subset of genotype matrix restricted to 500 individuals. We assumed that 10% of the causal variants are missing (not measured), i.e we set to 10%.
We generated the four annotations as described above. We used CAVIAR35 to generate the 95%Credible set and MaxCPP annotations. We utilized European samples from the 1000 Genomes Project (1000G)52 (see URLs) to estimate the LD structure required as input to CAVIAR. We applied CAVIAR under a setting where we allowed up to six causal variants for each gene. We observed that the results for cases where we allowed up to six or three causal variants for each gene are not statistically different (Supplementary Figures 9 and 10 and Supplementary Table 37). We note that the 95% credible set is not guaranteed to be unique; in this work we use a single 95% credible set for each gene for three reasons: First, use of a single 95% credible set is consistent with the output of all existing fine-mapping methods of which we are currently aware. Second, computing all 95% credible sets for each gene is computationally costly. Third, taking the union of all 95% credible sets might reduce the enrichment and , whereas the goal of this paper is to construct annotations with highest possible enrichment and .
After obtaining the four annotations, we ran S-LDSC32 to generate the LD score of each variant in each annotation using the same procedure described in the previous studies32,33. Regression SNPs, which are used by S-LDSC to estimate from marginal association statistics, were obtained from the HapMap Project phase 353. These SNPs are considered as well-imputed SNPs. SNPs with marginal association statistics larger than 80 or larger than 0.001 and SNPs that are in the major histocompatibility complex (MHC) region were excluding from all the analyses. Reference SNPs, which are used to compute LD scores, were defined using the European samples in 1000G52. Heritability SNPs, which are used to estimate and , were defined as common variants (MAF 0.05) in the set of reference SNPs. Using the LD score for each annotation and the marginal statistics obtained from the trait phenotypes, we computed the enrichment and for each simulation. Then, we compared the S-LDSC estimated enrichment and true enrichment for each annotation. All results are averaged across 400 simulations.
In addition to S-LDSC, we used GCTA27,28 to compute the enrichment of each binary annotation. We first computed the GRM for each annotation using the set of all variants in that annotation. We then used the –reml option in GCTA to estimate the heritability explained by each annotation.
Concrete example for S-LDSC bias estimates of TopcisQTL
Let x be a SNP in the TopcisQTL annotation, let y be a SNP not in the TopcisQTL annotation that is in LD with x, and let z be a random SNP not in the TopcisQTL annotation. Then, in expectation, y has a larger causal disease effect size than z (violating S-LDSC model assumptions), because it is possible that y is a causal molecular QTL (tagged by x, which may be more significant due to statistical chance), and that y is also causal for disease. The fact that SNPs in LD with the TopcisQTL annotation have larger causal disease effect sizes may cause TopcisQTL enrichment to be overestimated by S-LDSC, which attributes higher statistics for such SNPs entirely to tagging of causal TopcisQTL enrichment. On the other hand, enrichments of more inclusive annotations may be underestimated by S-LDSC, because SNPs in the annotation with high LD to other SNPs in the annotation are expected to have lower causal disease effect sizes than random SNPs in the annotation (again violating S-LDSC model assumptions).
Set of 41 independent diseases and complex traits
We initially considered 34 GWAS summary association statistic data sets that are publicly available and 55 UK Biobank traits (see URLs) for which summary association statistics were computed using BOLT-LMM30,54 (see URLs; up to N=459K European-ancestry samples). We restricted our analyses to 47 data sets with z-scores of total SNP heritability at least 6 (Supplementary Table 6). The 47 data sets included 6 traits that were duplicated in two different data sets (genetic correlation of at least 0.9). Thus, we analyzed 41 independent diseases and complex traits. We ran S-LDSC using the same procedures described in previous studies32,33 (see above). All analyses that included the baselineLD model are based on baselineLD model v1.1, which is identical to the baselineLD model as previously described33 except that we fixed an error in the promoter annotation (inherited from previous studies32,33); we determined that fixing this error did not affect our results (see Supplementary Table 38). The z-score of total SNP heritability was computed using S-LDSC with the baselineLD model, and the genetic correlation between pairs of traits was computed using cross-trait LDSC55. The meta-analyzed values of enrichment and across the 47 data sets were computed using a random-effect meta-analysis, as implemented in the R package.
Fixed-effect meta-analysis of eQTL effect sizes (FE-Meta-Tissue)
Given a set of effect sizes for SNP for tissues, where is the eQTL effect size for tissue , we used fixed-effect meta-analysis (FE-Meta-Tissue) to compute inverse-variance weighted meta-analysis z-scores as follows:
| (7) |
where and is the standard error of . We note that equation (7) is equivalent to computing a weighted average of z-scores.
Our use of FE-Meta-Tissue has two limitations. First, expression levels in two tissues in the same individual are not independent (sample overlap). Second, true effect sizes in two tissues may be different (heterogeneity). We discuss each limitation in turn.
Regarding the sample overlap limitation, we determined that noise is largely uncorrelated across tissues. For example, the correlation of normalized gene expression (read count) between whole blood and brain hippocampus is 0.11. Furthermore, the genetic correlation between these two tissues is 0.6736 and the heritability explained by cis-eQTL is 0.12. This implies that the bulk of gene expression correlation is due to genetic correlation. Thus, the noise (environmental and measurement) in expression levels in two tissues in the same individual is close to independent.
Regarding the heterogeneity limitation, we determined that recently developed random-effect cross-tissue eQTL meta-analysis methods48,49,56,57 are not applicable to our problem. The Meta-Tissue method40 is computationally intractable for data sets as large as GTEx (number of tissues and sample size). Other existing methods49,56,57, which are Bayesian methods, do not produce summary statistics (e.g. z-scores) that are required to compute the MaxCPP annotation. Thus, these methods are not applicable to our work. Previous studies12,36 have shown that eQTL effects are highly correlated across tissues, suggesting that our fixed-effect meta-analysis approach is likely to be fairly close to optimal.
We note that the above limitations pertain only to power and not to false positives in our setting, which involves building eQTL annotations to apply to independent disease data. Our results (Figure 2 and Supplementary Tables 7 and 27) show that we have improved our results by utilizing FE-Meta-Tissue. Furthermore, utilizing FE-Meta-Tissue increases replication rates for both eQTL and hQTL (Supplementary Table 29).
Blood and brain related diseases and complex traits
We analyzed six autoimmune diseases: Crohn’s disease58, Rheumatoid arthritis (ref.59 and UK Biobank), Ulcerative colitis58, Lupus60, Celiac61, and all autoimmune and inflammatory diseases in UK Biobank).
We analyzed five blood cell traits: white blood cell count, red blood cell count, platelet count, eosinophil count, and red blood cell distribution width. All of these data sets were obtained from UK Biobank.
We analyzed eight independent brain-related diseases and complex traits: Age at menarche62, BMI (ref.63 and UK Biobank), Bipolar Disorder64, Depressive symptoms2, Neuroticism (UK Biobank), Schizophrenia1, Smoking Status (ref.65 and UK Biobank), and Year of education (ref.66 and UK Biobank). These traits are a subset of traits from Supplementary Table 6 that were reported to be brain-enriched32,50.
Data availability
The S-LDSC software, baselineLD, and MaxCPP QTL-based annotations, and a tutorial on how to use S-LDSC with QTL-based annotations are available online (see URLs). A Life Sciences Reporting Summary is available.
URLs
GTEx (Release v6, dbGaP Accession phs000424.v6.p1): http://www.gtexportal.org.
GCTA: cnsgenomics.com/software/gcta/
BLUEPRINT: ftp://ftp.ebi.ac.uk/pub/databases/blueprint/blueprint_Epivar/qtl_as/
baselineLD annotations: https://data.broadinstitute.org/alkesgroup/LDSCORE/
MaxCPP QTL-based annotations and partitioned LD scores: https://data.broadinstitute.org/alkesgroup/LDSCORE/LDSC_QTL/
95%Causal Set QTL-based annotations and partitioned LD scores: https://data.broadinstitute.org/alkesgroup/LDSCORE/LDSC_QTL/
1000 Genomes Project Phase 3 data: ftp://ftp.1000genomes.ebi.ac.uk/vol1/ftp/release/20130502
PLINK software: https://www.cog-genomics.org/plink2
BOLT-LMM software: https://data.broadinstitute.org/alkesgroup/BOLT-LMM
BOLT-LMM summary statistics for UK Biobank traits: https://data.broadinstitute.org/alkesgroup/UKBB
UK Biobank: http://www.ukbiobank.ac.uk/
UK Biobank Genotyping and QC Documentation: http://www.ukbiobank.ac.uk/wp-content/uploads/2014/04/UKBiobank_genotyping_QC_documentation-web.pdf
Supplementary Material
Acknowledgments
We are grateful to Soumya Raychaudhuri, Noah Zaitlen, Bogdan Pasaniuc, Michel Nivard, Jae-Hoon Sul, and Fereydoun Hormozdiari for helpful discussions. This research was funded by NIH grants U01 HG009379, R01 MH101244, R01 MH109978, T32 DK110919, and R01 MH107649. This research was conducted using the UK Biobank Resource under Application 16549.
Footnotes
Contributions
F.H. and A.L.P. designed experiments. F.H. performed experiments. F.H., S.G, B.V.G., H.K.F., C.J.J, P.-R.L., A.S., Y.K., X.L, L.O., A.G., E.E., analyzed data. F.H. and A.L.P. wrote the manuscript with assistance from all authors.
Competing interests
The authors declare no competing interests.
References
- 1.Schizophrenia Working Group of the Psychiatric Genomics Consortium et al. Biological insights from 108 schizophrenia-associated genetic loci. Nature. 2014;511:421–427. doi: 10.1038/nature13595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Okbay A, et al. Genome-wide association study identifies 74 loci associated with educational attainment. Nature. 2016;533:539–542. doi: 10.1038/nature17671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.10 Years of GWAS Discovery: Biology, Function, and Translation. - PubMed - NCBI. doi: 10.1016/j.ajhg.2017.06.005. Available at: https://www.ncbi.nlm.nih.gov/pubmed/28686856. (Accessed: 24th March 2018) [DOI] [PMC free article] [PubMed]
- 4.Hindorff LA, et al. Potential etiologic and functional implications of genome-wide association loci for human diseases and traits. Proc Natl Acad Sci USA. 2009;106:9362–9367. doi: 10.1073/pnas.0903103106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Nicolae DL, et al. Trait-associated SNPs are more likely to be eQTLs: annotation to enhance discovery from GWAS. PLoS Genet. 2010;6:e1000888. doi: 10.1371/journal.pgen.1000888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Nica AC, et al. Candidate causal regulatory effects by integration of expression QTLs with complex trait genetic associations. PLoS Genet. 2010;6:e1000895. doi: 10.1371/journal.pgen.1000895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Maurano MT, et al. Systematic localization of common disease-associated variation in regulatory DNA. Science. 2012;337:1190–1195. doi: 10.1126/science.1222794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Trynka G, et al. Disentangling the Effects of Colocalizing Genomic Annotations to Functionally Prioritize Non-coding Variants within Complex-Trait Loci. Am J Hum Genet. 2015;97:139–152. doi: 10.1016/j.ajhg.2015.05.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Roadmap Epigenomics Consortium et al. Integrative analysis of 111 reference human epigenomes. Nature. 2015;518:317–330. doi: 10.1038/nature14248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wright FA, et al. Heritability and genomics of gene expression in peripheral blood. Nat Genet. 2014;46:430–437. doi: 10.1038/ng.2951. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Zhang X, et al. Identification of common genetic variants controlling transcript isoform variation in human whole blood. Nat Genet. 2015;47:345–352. doi: 10.1038/ng.3220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.GTEx Consortium. Human genomics. The Genotype-Tissue Expression (GTEx) pilot analysis: multitissue gene regulation in humans. Science. 2015;348:648–660. doi: 10.1126/science.1262110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Zhernakova DV, et al. Identification of context-dependent expression quantitative trait loci in whole blood. Nat Genet. 2017;49:139–145. doi: 10.1038/ng.3737. [DOI] [PubMed] [Google Scholar]
- 14.GTEx Consortium et al. Genetic effects on gene expression across human tissues. Nature. 2017;550:204–213. doi: 10.1038/nature24277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.McVicker G, et al. Identification of genetic variants that affect histone modifications in human cells. Science. 2013;342:747–749. doi: 10.1126/science.1242429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Waszak SM, et al. Population Variation and Genetic Control of Modular Chromatin Architecture in Humans. Cell. 2015;162:1039–1050. doi: 10.1016/j.cell.2015.08.001. [DOI] [PubMed] [Google Scholar]
- 17.Grubert F, et al. Genetic Control of Chromatin States in Humans Involves Local and Distal Chromosomal Interactions. Cell. 2015;162:1051–1065. doi: 10.1016/j.cell.2015.07.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Chen L, et al. Genetic Drivers of Epigenetic and Transcriptional Variation in Human Immune Cells. Cell. 2016;167:1398–1414.e24. doi: 10.1016/j.cell.2016.10.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Davis LK, et al. Partitioning the heritability of Tourette syndrome and obsessive compulsive disorder reveals differences in genetic architecture. PLoS Genet. 2013;9:e1003864. doi: 10.1371/journal.pgen.1003864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Torres JM, et al. Cross-tissue and tissue-specific eQTLs: partitioning the heritability of a complex trait. Am J Hum Genet. 2014;95:521–534. doi: 10.1016/j.ajhg.2014.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hu X, et al. Regulation of gene expression in autoimmune disease loci and the genetic basis of proliferation in CD4+ effector memory T cells. PLoS Genet. 2014;10:e1004404. doi: 10.1371/journal.pgen.1004404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Giambartolomei C, et al. Bayesian test for colocalisation between pairs of genetic association studies using summary statistics. PLoS Genet. 2014;10:e1004383. doi: 10.1371/journal.pgen.1004383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Hormozdiari F, et al. Colocalization of GWAS and eQTL Signals Detects Target Genes. Am J Hum Genet. 2016;99:1245–1260. doi: 10.1016/j.ajhg.2016.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gamazon ER, et al. A gene-based association method for mapping traits using reference transcriptome data. Nat Genet. 2015;47:1091–1098. doi: 10.1038/ng.3367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Gusev A, et al. Integrative approaches for large-scale transcriptome-wide association studies. Nat Genet. 2016;48:245–252. doi: 10.1038/ng.3506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mancuso N, et al. Integrating Gene Expression with Summary Association Statistics to Identify Genes Associated with 30 Complex Traits. Am J Hum Genet. 2017;100:473–487. doi: 10.1016/j.ajhg.2017.01.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Yang J, Lee SH, Goddard ME, Visscher PM. GCTA: a tool for genome-wide complex trait analysis. Am J Hum Genet. 2011;88:76–82. doi: 10.1016/j.ajhg.2010.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lee SH, et al. Estimating the proportion of variation in susceptibility to schizophrenia captured by common SNPs. Nat Genet. 2012;44:247–250. doi: 10.1038/ng.1108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gusev A, et al. Partitioning heritability of regulatory and cell-type-specific variants across 11 common diseases. Am J Hum Genet. 2014;95:535–552. doi: 10.1016/j.ajhg.2014.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Loh PR, et al. Contrasting genetic architectures of schizophrenia and other complex diseases using fast variance-components analysis. Nat Genet. 2015;47:1385–1392. doi: 10.1038/ng.3431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Speed D, et al. Reevaluation of SNP heritability in complex human traits. Nat Genet. 2017;49:986–992. doi: 10.1038/ng.3865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Finucane HK, et al. Partitioning heritability by functional annotation using genome-wide association summary statistics. Nat Genet. 2015;47:1228–1235. doi: 10.1038/ng.3404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gazal S, et al. Linkage disequilibrium-dependent architecture of human complex traits shows action of negative selection. Nat Genet. 2017;49:1421–1427. doi: 10.1038/ng.3954. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Pasaniuc B, Price AL. Dissecting the genetics of complex traits using summary association statistics. Nat Rev Genet. 2017;18:117–127. doi: 10.1038/nrg.2016.142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hormozdiari F, Kostem E, Kang EY, Pasaniuc B, Eskin E. Identifying causal variants at loci with multiple signals of association. Genetics. 2014;198:497–508. doi: 10.1534/genetics.114.167908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Liu X, et al. Functional Architectures of Local and Distal Regulation of Gene Expression in Multiple Human Tissues. Am J Hum Genet. 2017;100:605–616. doi: 10.1016/j.ajhg.2017.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Lek M, et al. Analysis of protein-coding genetic variation in 60,706 humans. Nature. 2016;536:285–291. doi: 10.1038/nature19057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Gazal S, Finucane H, Price A. Reconciling S-LDSC and LDAK functional enrichment estimates. BioRxiv. 2018 doi: 10.1038/s41588-019-0464-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Cassa CA, et al. Estimating the selective effects of heterozygous protein-truncating variants from human exome data. Nat Genet. 2017;49:806–810. doi: 10.1038/ng.3831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Samocha KE, et al. A framework for the interpretation of de novo mutation in human disease. Nat Genet. 2014;46:944–950. doi: 10.1038/ng.3050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Wang T, et al. Identification and characterization of essential genes in the human genome. Science. 2015;350:1096–1101. doi: 10.1126/science.aac7041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hormozdiari F, et al. Widespread Allelic Heterogeneity in Complex Traits. Am J Hum Genet. 2017;100:789–802. doi: 10.1016/j.ajhg.2017.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Veyrieras JB, et al. High-resolution mapping of expression-QTLs yields insight into human gene regulation. PLoS Genet. 2008;4:e1000214. doi: 10.1371/journal.pgen.1000214. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Javierre BM, et al. Lineage-Specific Genome Architecture Links Enhancers and Non-coding Disease Variants to Target Gene Promoters. Cell. 2016;167:1369–1384.e19. doi: 10.1016/j.cell.2016.09.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Mumbach MR, et al. Enhancer connectome in primary human cells identifies target genes of disease-associated DNA elements. Nat Genet. 2017;49:1602–1612. doi: 10.1038/ng.3963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Li YI, et al. RNA splicing is a primary link between genetic variation and disease. Science. 2016;352:600–604. doi: 10.1126/science.aad9417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Li X, et al. The impact of rare variation on gene expression across tissues. Nature. 2017;550:239–243. doi: 10.1038/nature24267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sul JH, Han B, Ye C, Choi T, Eskin E. Effectively identifying eQTLs from multiple tissues by combining mixed model and meta-analytic approaches. PLoS Genet. 2013;9:e1003491. doi: 10.1371/journal.pgen.1003491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Flutre T, Wen X, Pritchard J, Stephens M. A statistical framework for joint eQTL analysis in multiple tissues. PLoS Genet. 2013;9:e1003486. doi: 10.1371/journal.pgen.1003486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Finucane H, et al. Heritability enrichment of specifically expressed genes identifies disease-relevant tissues and cell types. Nat Genet. doi: 10.1038/s41588-018-0081-4. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Purcell S, et al. PLINK: a tool set for whole-genome association and population-based linkage analyses. Am J Hum Genet. 2007;81:559–575. doi: 10.1086/519795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.1000 Genomes Project Consortium et al. A map of human genome variation from population-scale sequencing. Nature. 2010;467:1061–1073. doi: 10.1038/nature09534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.International HapMap 3 Consortium et al. Integrating common and rare genetic variation in diverse human populations. Nature. 2010;467:52–58. doi: 10.1038/nature09298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Loh P-R, et al. Mixed model association for biobank-scale data sets. Nat Genet. doi: 10.1038/s41588-018-0144-6. In press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Bulik-Sullivan B, et al. An atlas of genetic correlations across human diseases and traits. Nat Genet. 2015;47:1236–1241. doi: 10.1038/ng.3406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Urbut SM, et al. Flexible statistical methods for estimating and testing effects in genomic studies with multiple conditions. bioRxiv. 2016 doi: 10.1038/s41588-018-0268-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Park Y, et al. Multi-tissue polygenic models for transcriptome-wide association studies. bioRxiv. 2017 [Google Scholar]
- 58.Jostins L, et al. Host-microbe interactions have shaped the genetic architecture of inflammatory bowel disease. Nature. 2012;491:119–124. doi: 10.1038/nature11582. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Okada Y, et al. Genetics of rheumatoid arthritis contributes to biology and drug discovery. Nature. 2014;506:376–381. doi: 10.1038/nature12873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Bentham J, et al. Genetic association analyses implicate aberrant regulation of innate and adaptive immunity genes in the pathogenesis of systemic lupus erythematosus. Nat Genet. 2015;47:1457–1464. doi: 10.1038/ng.3434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Dubois PCA, et al. Multiple common variants for celiac disease influencing immune gene expression. Nat Genet. 2010;42:295–302. doi: 10.1038/ng.543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Day FR, et al. Genomic analyses identify hundreds of variants associated with age at menarche and support a role for puberty timing in cancer risk. Nat Genet. 2017;49:834–841. doi: 10.1038/ng.3841. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Speliotes EK, et al. Association analyses of 249,796 individuals reveal 18 new loci associated with body mass index. Nat Genet. 2010;42:937–948. doi: 10.1038/ng.686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Psychiatric GWAS Consortium Bipolar Disorder Working Group. Large-scale genome-wide association analysis of bipolar disorder identifies a new susceptibility locus near ODZ4. Nat Genet. 2011;43:977–983. doi: 10.1038/ng.943. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Tobacco and Genetics Consortium. Genome-wide meta-analyses identify multiple loci associated with smoking behavior. Nat Genet. 2010;42:441–447. doi: 10.1038/ng.571. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Rietveld CA, et al. GWAS of 126,559 individuals identifies genetic variants associated with educational attainment. Science. 2013;340:1467–1471. doi: 10.1126/science.1235488. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The S-LDSC software, baselineLD, and MaxCPP QTL-based annotations, and a tutorial on how to use S-LDSC with QTL-based annotations are available online (see URLs). A Life Sciences Reporting Summary is available.


