Membrane Position Dependency of the pKa and Conductivity of the Protein Ion Channel

Abstract

The dependency of current-voltage characteristics of the α-hemolysin channel on the channel position within the membrane was studied using Poisson-Nernst-Planck theory of ion-conductivity with soft repulsion between mobile ions and protein atoms (SP-PNP). The presence of the membrane environment also influences protonation state of the residues at the boundary of the water-lipid interface. In this work we predict that Asp and Lys residues at the protein rim change their protonation state upon penetration to the lipid environment. Free energies of protein insertion in the membrane for different penetration depths was estimated using the Poisson-Boltzmann/solvent accessible surface area (PB/SASA) model. The results show that rectification and reversal potentials are very sensitive to relative position of channel in the membrane, which in turn contributes to alternative protonation states of lipid penetrating ionizable groups. The prediction of channel position based on the matching of calculated rectification with experimentally determined rectification is in good agreement with recent neutron reflection experiments. Based on the results we conclude that α-hemolysin membrane position is determined by a combination of factors and not only by the pattern of the surface hydrophobicity as is typically assumed.

Introduction

Biological ion channels are integral membrane proteins that allow ion flow across the membrane [1]. Ion channels are essential for many vital functions of living organisms, among them: conversion of chemical or mechanical signals into electric ones, generation and transmittance of electric signals in neurons and maintenance of a membrane potential and intracellular ion concentrations [2]. In addition to their biological significance, several ion channels have been proposed as a foundation for nano-devices, including various molecular sensors and a DNA sequencer (see reviews [3, 4]). The ability to computationally predict ion-channel conducting properties will enable better understanding of the underlying phenomena as well as provide a valuable tool for rational drug design and molecular-based technologies. Indeed, an extensive literature exists on theoretical prediction of ion-channel conductance properties [5-9]. However, the problem is far from being solved. Most previous theoretical studies have concentrated on specifics of modeling protein-ion and ion-ion interactions. Thus far, little attention has been given to how properties of a lipid membrane and a channel position with respect to it influence ion conductance [10]. There is only limited experimental high resolution data where transmembrane proteins positioning within membrane is available along with protein 3-D atomic structure. And in many cases where such information exists, the structures of proteins were obtained in the absence of their natural environment, e.g. solubilized by a detergent [11-13]. Therefore, the atomic details of protein positioning in lipid bilayers are mainly unknown. Yet, it is well recognized that the membrane’s low dielectric medium may significantly influence electrostatic interactions in the proteins by affecting screening of partially charged protein atoms, and by changing the pK_a values (protonation states) of some protein residues. Thus, the problem of positioning of the protein with respect to bilayer merits special attention.

Typically, in theoretical studies of ion channels, the membrane is positioned by either matching a hydrophobic outer surface of the protein with the hydrophobic layer of the membrane, or by positioning the protein symmetrically with respect to the center of the membrane [5-8]. These, however, may not be best predictors of protein position. For example, according to a recent neutron reflection experiment, the center of the hydrophobic belt of the α-hemolysin (AHL) channel inserted in tethered bilayer was shifted from the center of the lipid bilayer by several angstroms [14]. In this paper, we examined theoretically how positioning of the AHL protein in the membrane affects predicted conductivity of the channel, and propose a scheme in which these very predictions of current-voltage (I-V) characteristics of the channel can be used to validate protein position in the membrane. We utilized a continuum electrostatics approach to determine pK_a of protonatable residues while varying the protein position in the membrane protein. Channel conductance was computed using a recently introduced Poisson-Nernst-Planck Soft Repulsion (PNP-SR) method [9]. Free energy of the AHL insertion in the membrane was computed using the continuum electrostatics and non-polar solvation model.

α-Hemolysin is a well studied large toxin protein secreted by Staphylococcus aureus. It can spontaneously form homo-heptameric channels [11, 15, 16] in a wide variety of natural and synthetic membranes (for a recent review see Ref. [17]) The insertion of AHL into the membrane of an affected cell can cause passive flow of ions and small molecules through the cell membrane, which in turn can lead to cell death [18]. AHL forms a relatively wide pore (12-24Å). Once formed the protein complex is stable under various conditions and the channel remains open for a relatively long period of time. Because of these properties, AHL has been proposed as the foundation for several nano-devices, including sensors and a DNA sequencer (for recent reviews see Refs. [4, 19]). These devices utilize changes in the current-voltage (I-V) dependencies of the channel upon complex formation with different molecules. Theoretical prediction of such modified I-V dependencies could aid further technological development, thus a number of modeling studies of AHL were performed by us [9] and others [20-25]. However, the utility of theoretical modeling is limited, in part by an ad hoc treatment of the membrane.

The paper is organized as follows. In Methods, we briefly summarize recently reported extension to the Poisson-Nernst-Planck (PNP) theory of ion-conductivity termed PNP-SR[9] where SR stands for the soft repulsion (SR) between protein atoms and mobile ions; then we briefly describe how position depended diffusion coefficients were computed. Next, we describe methods and protocol used for the calculation of the protonation states of ionizable residues in the presence of the membrane. This is followed by details on calculation of free energy profile of ion-channel positioning within the membrane. Finally, parameters used for the PNP-SR calculations are described. In Results, we report on the influence of the ion-channel position within the membrane on the protonation state of protein ionazable residues, the electrostatic potential along the channel pore and on ion-channel I-V characteristics including total current, current rectification, reversal potential and selectivity. Next, we report our prediction on the free energy profile of AHL insertion in the membrane. In Discussion and Conclusions influence of an AHL position in the membrane on ion-conductive properties is discussed. The Summary lists the main outcomes of this work.

Methods

The Poisson-Nernst-Planck Theory with Soft Repulsion (PNP-SR)

The PNP-SR model [9] is an extension of the Poisson-Nernst-Planck (PNP) theory [26, 27]. It differs from the PNP theory in that it uses soft, rather than hard, repulsion between mobile ions and protein atoms. PNP-SR has been introduced and described in detail in our recent work [9]. Briefly, PNP-SR is a continuum theory, in which mobile ions are represented by their average concentration as a function of space; the protein channel is treated as a rigid continuum body with a low dielectric constant and a fixed charge distribution; the solvent and the membrane are treated implicitly as high and low dielectric media respectively.

PNP-SR is based on Poisson and Nernst-Plank equations. The Poisson equation describes electrostatic interactions in the system and the Nernst-Plank equation describes the energy gradient dependent diffusion of the mobile ions. Flux of mobile ions is thus described by drift diffusion equations (Nernst-Planck equations) as follows:

$$\overline{j_i}(\mathbf{r})=-D_i(\mathbf{r})\left(\overline{\nabla }{C}_i(\mathbf{r})+\frac{1}{kT}{C}_i(\mathbf{r})\overline{\nabla }{\mathrm{\psi }}_i(\mathbf{r})\right),$$ (1)

where i stands for the type of mobile ions, r is a three dimensional (3D) position vector, k is the Boltzmann constant, T is the temperature, D_i(r) is the space dependent diffusion coefficient of the i^th type of mobile ions, C_i(r) is i^th ion concentration, and Ψ_i(r) is its potential of mean force (PMF). The first term of Eq. 1 describes free diffusion; the second one describes drift under the energy gradient. Continuity of flux under steady state condition requires divergence of flux to be zero:

$$\overline{\nabla }\cdot \left[D_i(\mathbf{r})\left(\overline{\nabla }{C}_i(\mathbf{r})+\frac{1}{kT}{C}_i(\mathbf{r})\overline{\nabla }{\mathrm{\psi }}_i(\mathbf{r})\right)\right]=0$$ (2)

The solution of Eq. 2 is an equilibrium distribution of mobile ion concentrations in the presence of an external force $(-\overline{\nabla }{\mathrm{\psi }}_i(\mathbf{r}))$.

In PNP-SR theory, Ψ_i(r) accounts for the electrostatic and short-range interactions (repulsion) of an ion with the protein:

$${\mathrm{\psi }}_i(\mathbf{r})=q_i\phi (\mathbf{r})+W_i^{SR}(\mathbf{r}),$$ (3)

where q_i is the electric charge of the i^th type of the mobile ions, φ(r) is electrostatic potential, and $W_i^{SR}(\mathbf{r})$ is a 3D repulsive potential between an ion of type i and the protein. In our model SR is a pair-wise additive function. $W_i^{SR}(\mathbf{r})$ is calculated by sequentially placing a probe ion in all possible positions and computing total repulsion energy between the protein and the ion at this position:

$$W_i^{SR}(\mathbf{r})={\displaystyle \sum _l{W}_{il}^{SR}(\mathbf{r})},$$ (4)

where $W_{il}^{SR}(\mathbf{r})$ is the pair-wise potential between the l^th protein atom and a probe ion of type i at the position r. The summation is made over all protein atoms. The pair-wise additive soft repulsion potential has the following form:

$$W_{il}^{SR-MD}(\mathbf{r})=\{\begin{array}{cc}\left({\left(\frac{A_{il}}{\left|{\mathbf{r}}_l-\mathbf{r}\right|}\right)}^{{\eta }_{il}}-1\right)kT,& \left|{\mathbf{r}}_l-\mathbf{r}\right|<A_{il}\\ 0,& \left|{\mathbf{r}}_l-\mathbf{r}\right|\ge A_{il}\end{array},$$ (5)

where r_l is the position of l^th protein atom and r is a trial position of i^th ion type, A_il and η_il are fitting parameters. The potential has previously been parameterized using all atom Molecular Dynamics (MD) simulations for each essential amino-acid residue [9].

Electrostatic potential in Eq. 4 is computed using the Poisson equation:

$$\overline{\nabla }\cdot \left(\epsilon \left(\mathbf{r}\right)\overline{\nabla }\phi \left(\mathbf{r}\right)\right)=-4\pi \left({\rho }_{\mathit{static}}\left(\mathbf{r}\right)+{\displaystyle \sum _{i=1}^{N_{\mathit{ions}}}{q}_i{C}_i\left(\mathbf{r}\right)}\right),$$ (6)

where ε(r) is a position dependent dielectric constant and ρ_static(r) is charge density on protein atoms. Thus, the electrostatic contribution to PMF of i^th type of ions is q_iφ(r).

Poisson and Nernst-Planck equations (Eqs. 2 and 6) are solved self-consistently subject to Dirichlet boundary conditions. Boundary conditions for ion concentrations are set to their respective bulk values at all points of the boundary accessible to ions. Electrostatic potential is set to zero at the boundaries of the cis-compartment (see Fig. 1) and to the value of an applied potential at the boundaries of the trans-compartment; the potential at the boundaries of the membrane region is set as a linear ramp between cis- and trans- compartments.

Figure 1.

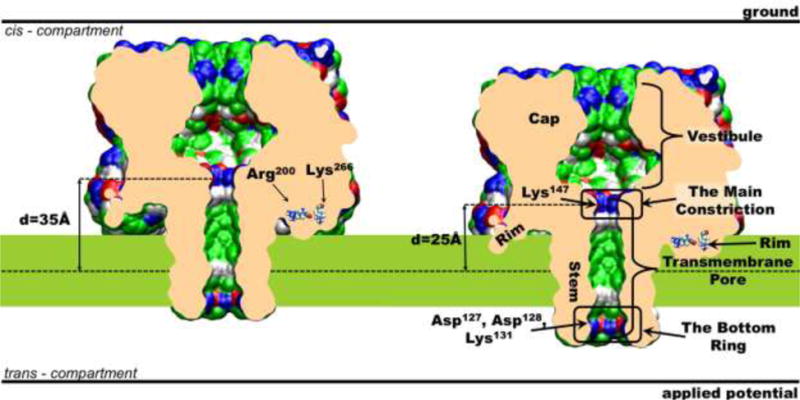
The structure and positioning of the AHL channel in the membrane. Two extreme positions are shown: the purple slab corresponds to deep insertion of AHL and the green slab corresponds to shallow insertion. The molecular surface of the channel represents ion accessible surface; the surface is colored by the residue types: white is used for hydrophobic residues, green - for polar residues, blue and red - for positively and negatively charged residues respectively. The shown system boundaries are not up to scale. This figure was prepared with the VMD program[53].

In our previous work [9] we tested four different methods of setting a distribution of the diffusion coefficients. We found that diffusion coefficients mainly affect total currents and have significantly smaller effect on other I-V properties, such as rectification, selectivity and reversal potential. Therefore, in this work we use a hydrodynamic approximation previously used by Noskov et al. [20] for calculation of position dependent diffusion coefficients in the AHL channel. For more details see section S1 in supplementary information (SI).

System setup for AHL and Parameters of PNP-SR

Initial coordinates for AHL were taken from the protein data bank (code 7AHL) [11]. The protein pore is aligned with the Z axis and its geometric center was moved to the coordinate system origin (the Z-coordinate of Lys141 N_ζ atoms is 0.96 Å). There were no geometry optimization or relaxation performed for protein structure. All crystal water molecules were removed. Membrane thickness was set to 28 Å, which corresponds roughly to the aliphatic region of the dipalmitoylphosphatidylcholine (DPPC) bilayer. The position of the membrane center was varied in order to model different penetration depths of the AHL channel. The penetration depth, d, is calculated as a distance between geometric center of AHL and the center of the membrane. In this coordinate system, the Z-coordinate of the geometrical center of the AHL hydrophobic belt (residues 116–126 and 132–142) is 28.6 Å. The dielectric constant was set to 4 for the protein, to 2 for the membrane and to 80 for the solvent. The atomic charges and radii were set using AMBER force field [28].

The simulation box was 171³ Ǻ³. The total current calculated for this box size differs by only 1% from that for the larger box of size of 301³ Ǻ³. The majority of the calculations were made with a grid scale of 1 grid/Å. Here, a typical calculation consisted of 2000 iterative PNP steps, where each PNP step comprised 20 steps over the Poisson solver and 20 steps over the Nernst-Planck solver. The relaxation parameter was 1.5 for both the Poisson and Nernst-Planck solvers for the majority of the calculations. It was found that these parameters allow efficient convergence of the current to less than 0.01%. The PB calculations typically consisted of 2000 iterations with a relaxation parameter of 1.6-1.8.

Calculation of the Protonation States of Protein Residues

Two methods were used here to compute protonation states of ionizable residues. Here we briefly introduce methods (for more details see section S2 of SI). The first method is PROPKA, an empirical method designed to predict pK_a values of ionizable groups in water soluble proteins [29, 30]. In this work PROPKA was used for the residues of the AHL’s water exposed cap region. The second method, which account for the membrane presence, is based on the work of Bashford and Karplus [31] and is usually referred to as FDPB due to the use of finite difference solver of the Poisson-Bolzmann equation (thus FDPB) for the evaluation of the electrostatic interaction within the system. pKa calculations with FDPB were done using a modified version of the pK_a and redox potential calculation module [32] of the HARLEM molecular modeling program[33]. Atomic charges were taken from Cornell et al. [28]. For atomic radii we have used parameters optimized for use with the Cornell et al. charges [32]. The concentration of KCl salt was 0.1M. The dielectric constants for the solvent, protein and membrane were set to 80, 10 and 2 respectively. A relatively high dielectric constant for the protein is used as is typical in practice of computing pKa of proteins with PB approach. Such choice of the dielectric constants provides higher accuracy of pKa prediction for a protein in a single conformation (a rigid) protein [34-36].

Dependency of Free Energy on the Position of AHL within the Membrane

In order to determine energetic landscape of AHL positioning within the membrane we calculated dependency of free energy on the AHL position in the membrane using the Poisson-Boltzmann solvent accessible surface area (PBSA) method [37, 38]. Here we briefly introduce variables and parameters for calculations, see section S3 of SI for more details. Free energy of insertion, ΔΔG, was calculated relative to a system where the AHL channel is completely exposed to the solvent. Electrostatic contribution was calculated using our Poisson equation solver. The non-polar contribution is calculated using the solvent accessible surface area approach. Solvent accessible surface area was calculated using MSMS [39], the molecular surface calculation program. In this part of the work we used PARSE/γ parameters [38, 40]. for atom charges, radii and surface tension coefficient (γ), the dielectric constants of protein, membrane and solvent were set to 2, 2 and 80, respectively.

Results

α-Hemolysin Protein Structure overview

The α-hemolysin (AHL) protein forms a transmembrane pore by self-assembly into a homo-heptamer. Its transmembrane pore region is formed by a β-barrel structure to which each monomer contributes a single β-hairpin. The AHL channel pore can be naturally divided into four structural parts (Fig. 1): the vestibule, the main constriction, the transmembrane (TM) pore and the bottom ring. The vestibule is the widest part of the channel. Although many charged residues are exposed into the vestibule these residues are surrounded and, therefore, effectively screened by the solvent. Thus, contribution of the vestibule to the ion conductance is expected to be relatively minor. The main constriction, located at the top entrance of the TM pore, is the narrowest part of the channel. This constriction is formed by side-chains of seven positively charged Lys147 residues. The narrowness of the main constriction and a positive charge of Lys147 make this part of the pore the most important contributor to the channel resistivity and selectivity. The bottom ring is a ring of charged residues consisting of Asp127, Asp128 and Lys131. It is located at the trans end of the TM pore (Fig. 1). The total charge of this ring is negative; thus, this region of the pore may also significantly influence channel conductance and selectivity. The exterior of the AHL stem has a distinct hydrophobic belt comprised of the residues 116–126 and 132–142. It seems natural to expect that when the protein is inserted in the membrane this hydrophobic belt is surrounded by the lipid bilayer hydrophobic core. However, if this is the case then the rim region of the protein located on the cis side of the bilayer (see Fig. 1) will be partially submerged to the hydrophobic membrane core. Since the rim has a set of residues with a non-zero charge at standard conditions such insertion may be unfavorable. Thus, three possibilities should be considered: 1) the whole structure is shifted with respect to the bilayer to avoid submersion of the charged and polar groups to the hydrophobic layer of the membrane, or 2) the residues in the rim change their protonation state upon membrane insertion to become neutral, or 3) the bilayer deformed in order to provide hydrophilic environment for charged groups. Therefore, an optimal position of AHL in the membrane needs to be determined by the balance of energies of a favorable desolvation of the hydrophobic stem and unfavorable transfer of the charged residues to the bilayer interior. In the following we will assess these factors.

Protonation States of Ionizable Residues

We will refer to a protonation state of a residue in its free form at neutral pH as a standard protonation state and to opposite form as alternative protonation state, e.g. the standard protonation state of lysine is protonated and the alternative state is deprotonated. In this work we calculated the I-V properties of the AHL channel under neutral pH (7.5). This significantly simplifies the problem, because for most ionizable residues the difference between standard pK_a and neutral pH is larger or equal to 3.2. Thus to change a protonation state of a residue a shift of pK_a value should be larger than 3.2. The only exceptions rom this rule of thumb are the N-terminal groups and histidines. Protonation states of these two types of ionizable groups are more sensitive to the pK_a shift at neutral pH because their standard pK_a are 8.0 and 6.5 respectively. Therefore, extra attention should be given to them.

Protonation states of ionizable residues were computed using two methods: PROPKA and FDPB (see Methods section for description of the methods). PROPKA gives higher accuracy but its applicability is limited to water-soluble proteins [41]. FDPB, in turn, allows for treatment of a protein embedded in the membrane. Here, PROPKA was used to predict protonation states of the residues located in the solvent exposed region of AHL, and to evaluate an effect of the protein environment in the absence of the membrane. FDPB was used to predict protonation states of individual residues in the protein in the presence of the membrane. Joint use of two methods improves reliability of results for residues located in the solvent exposed regions and allows for better characterization of pK_a shifts for residues submerged into the membrane.

In our analysis PROPKA predicted no change in the protonation states of any ionizable residue. At neutral pH protonation states of N-terminal and histidine residues may be shifted more readily than any other chemical group. PROPKA results show that the protein environment stabilizes both charged form of N-terminal (shifting its pK_a from 8.0 to 9.3), and the neutral form of all histidines. For His144 and His259 located near the membrane, we also used FDPB method to corroborate PROPKA prediction.

Table 1 in supplementary information reports on the FDPB predicted changes of the protonation states of the AHL residues at various depths of the protein membrane insertion. The table lists only residues that are in an alternative protonation state in at least one chain of the oligomers. All listed residues are located in the rim of the AHL. They all changed their state from a charged one to a neutral one. The result is consistent with the expectation that the hydrophobic membrane core favors neutral forms. Among all residues changing their protonation state upon deeper protein insertion into the membrane only Arg200 and Lys266 change their protonation state in the majority of oligomers. Therefore, in calculated I-V characteristics of the channel reported in the following sections Arg200 and Lys266 changed their protonation states upon deeper submergence of AHL into the membrane as follows. Up to penetration depth of 29 Å all residues retained their standard protonation states. At depths 29 Å and 27 Å Lys266 was in the alternative protonation form, and, finally, at deepest penetration (depths 25 Å and 23 Å) both Arg200 and Lys266 were in the alternative protonation form.

Variation of Electrostatic Potential at Different Penetration Depth of AHL

Electrostatic potential in the channel pore varies significantly with AHL position in the membrane (Fig. 2). At small penetration depth (depth 35 Å, Fig. 2 A), the electrostatic potential has one maximum which can be attributed to the positively charged main constriction and one minimum associated with the negatively charged bottom ring. When AHL is positioned deeper in the membrane the electrostatic potential well near the bottom ring becomes shallower (Fig. 2 A) due to an increased exposure of the protein trans side to the solvent. At the same time the barrier associated with the main constriction rises (Fig. 2 A) due to deeper penetration of this region to the low dielectric environment of the membrane. At penetration depth of 29 Å Lys266 changes its protonation state to a neutral form, leading to a significant drop in the electrostatic barrier at the main constriction (Fig. 2 B). At the penetration depth of 25Å the electrostatic potential in the pore (see Fig. 2 B) undergoes the second significant change because of the deprotonation of Arg200. At this protein position the barrier at the main constriction drops dramatically, while the well at the bottom ring changes little. The resulting profile exhibits significantly less variation along the whole channel pore than at other penetration depths. In summary, the height of barriers and the depth of wells of the electrostatic potential in the pore depend strongly on the positioning of AHL in the membrane and protonation states of the protein rim residues (note that both effects are strongly coupled). The properties of the channel ion conductivity are mainly determined by the above electrostatic potential profile. Figure 2B also shows electrostatic potential from all-atom MD simulations calculated by Aksimentiev and Schulten [22]. Because of different protonation states and salt concentration this profile cannot be directly compared to. However, there are some qualitative similarities: high barrier in main constriction, deep well in bottom ring and plato along vestibule.

Figure 2.

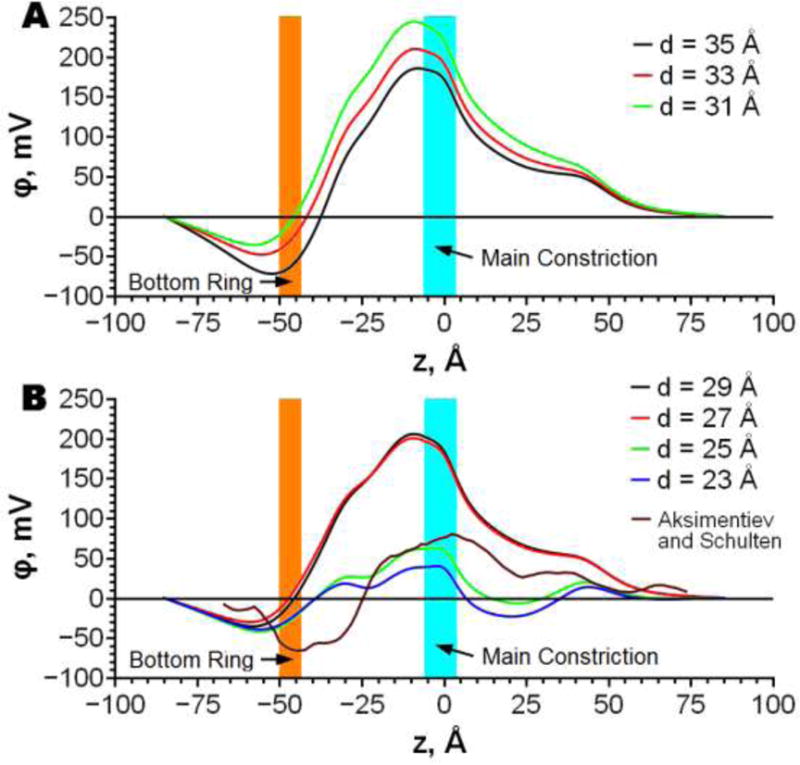
Dependencies of the electrostatic potential along the channel pore on penetration depth (d) of AHL to the membrane. Contributions of protein, membrane and water are shown. The protonation state is as used for I-V calculations. Continuum electrostatic potentials are also compared to the electrostatic potential from all-atom MD simulations calculated by Aksimentiev and Schulten [22].

Dependency of AHL conductivity properties on its membrane position

The current- voltage characteristics (or I-V) properties of AHL were calculated for seven AHL membrane insertion depths using the PNP-SR methodology as described in Methods section and elsewhere [9]. Figure 3A shows total channel currents at two applied voltages 80 mV and −80 mV as a function of the protein position in the membrane. Experimentally measured currents are also shown (horizontal lines in Fig.3A). [Note, that there is a significant discrepancy between reported experimental currents.] At positive applied voltage of 80 mV the PNP-SR calculated currents vary slightly with the protein insertion depth. [PNP-SR currents are overestimated compared to all experiments, which is expected, see e.g. discussion in Ref. [9]]. However, as the applied voltage reversed to −80mV, the predicted currents become strongly dependent on the depth of the channel membrane insertion. Moreover, the magnitude of predicted current is in the range of the experimental values when the channel is inserted at the depth 35 Å. As a result, rectification of the current shown in Fig. 3 B is highly sensitive to AHL positioning in the membrane. Rectification decreases almost monotonically from 2.3 to 1.2 and passes through the experimental range of values at penetration depths between 33 Å and 30 Å.

Figure 3.

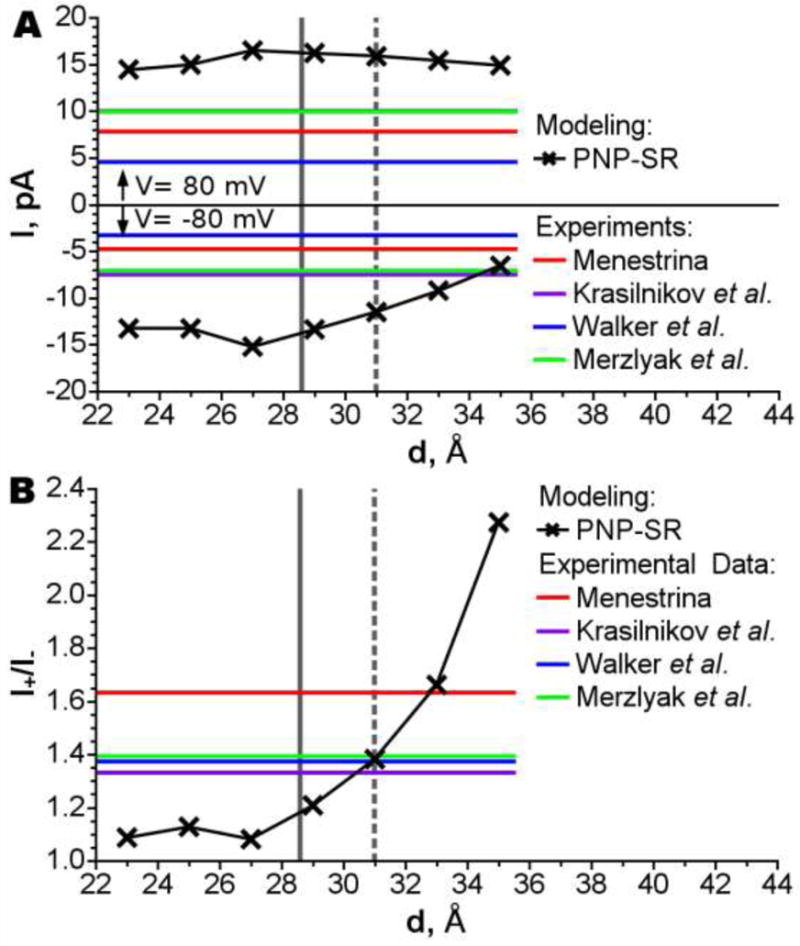
Total current (A) and rectification (B) versus position of AHL in the membrane. The position of the channel corresponding for the position when the center of channel’s hydrophobic belt center coincides with membrane center is shown by dark gray vertical solid line; the experimental position [14] of the channel is shown by dark gray vertical dashed line. The results of simulations are compared to experimental results of Menestrina [54], Merzlyak et al. [55], Krasilnikov et al. [56] and Walker et al. [57].

Selectivity (defined as a ratio of individual ion currents, I_K+/I_Cl−) and reversal potentials (an applied voltage at which there is no current through the channel) are also strongly affected by the AHL position and protonation (Fig. 4). However, unlike rectification, both selectivity and the reversal potential pass through their minima near penetration depth of 27 Å. The reversal potentials for concentrations in cis/trans compartments of 0.5M/0.05M and 1.0M/0.2M respectively show the best agreements with the experimental values in two distinct situations: when the channel is deeply submerged in the membrane, and at the smallest possible penetration (while the pore opens to the trans compartment). The reversal potentials for concentrations of 0.2M/1.0M show little dependency on the AHL position and overestimate experimental values at all membrane insertion depths. It is clear from these results that the channel bilayer position significantly influences its ion selectivity properties. At shallow penetration the bottom ring residues are surrounded by the membrane resulting in a deep electrostatic potential well (depth 35 Å, Fig. 2 A). This well partially compensates the electrostatic barrier at the main constriction resulting in weak anion selectivity. When the channel penetrates deeper better screening of the bottom ring by water results in shallower electrostatic potential well (depths 35-31 Å, Fig. 2 A), which leads to the higher anion selectivity (Fig. 4). This effect is so strong that even a neutralization of Lys266 does not overturn change of selectivity until the protein is inserted at depth of 27 Å. At such deep penetration the bottom ring is completely exposed to water, allowing neutralization of Lys266 and Arg200 and weakening anion selectivity (depths 25-23 Å, Fig. 4).

Figure 4.

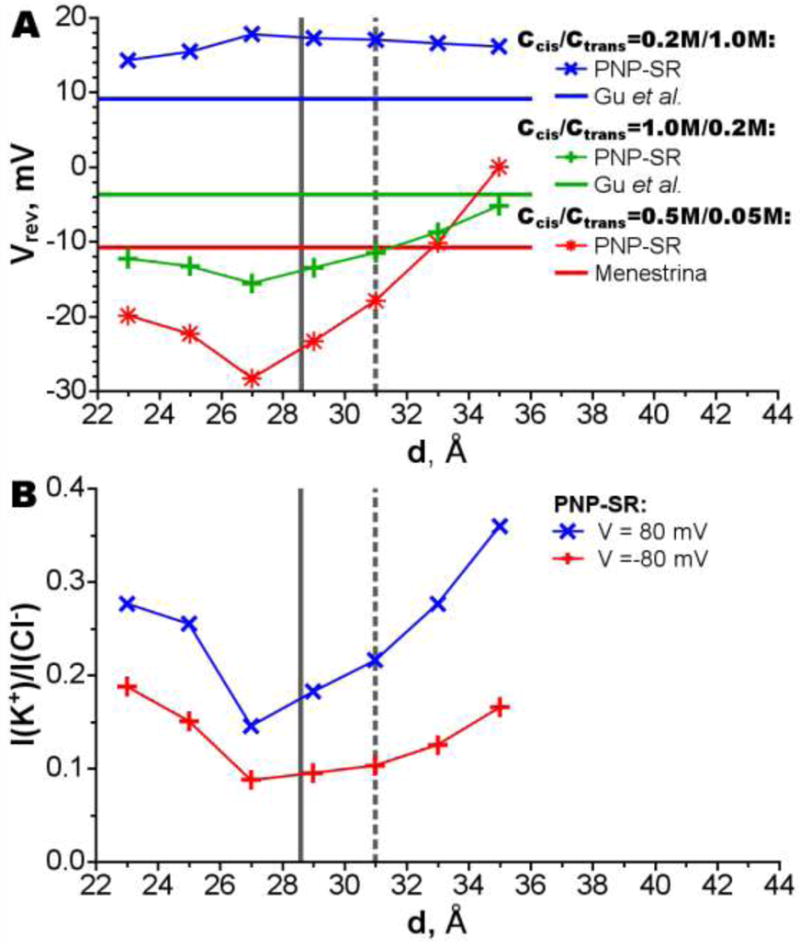
Dependency of the reversal potential (A) and the selectivity (B) on the AHL penetration depths. The position of the channel corresponding to the position when the center of channel’s hydrophobic belt center coincides with membrane center is shown by gray vertical line; the experimental position[14] of the channel is shown by gray vertical dashed line. The results of simulations are compared to experimental results: Menestrina[54] and Gu et al.[58]. The selectivity as current ratio (B) is shown for 0.1 M KCl.

Free Energy Profile of AHL Positioning in the Membrane

Free energy profile of the protein insertion in the membrane (computed as described in Methods section), its electrostatic and non-polar components are shown in Fig. 5. Electrostatic contribution to this free energy increases with the protein insertion depth, because at deeper insertion the charged residues located in the protein rim become submerged into the membrane low dielectric environment resulting in reduced screening of these charges, and thus, in increase of electrostatic energy. Non-polar contribution decreases upon the insertion because larger surface area of AHL becomes hidden from water. The total free energy goes through a shallow minimum at 29-31 Å.

Figure 5.

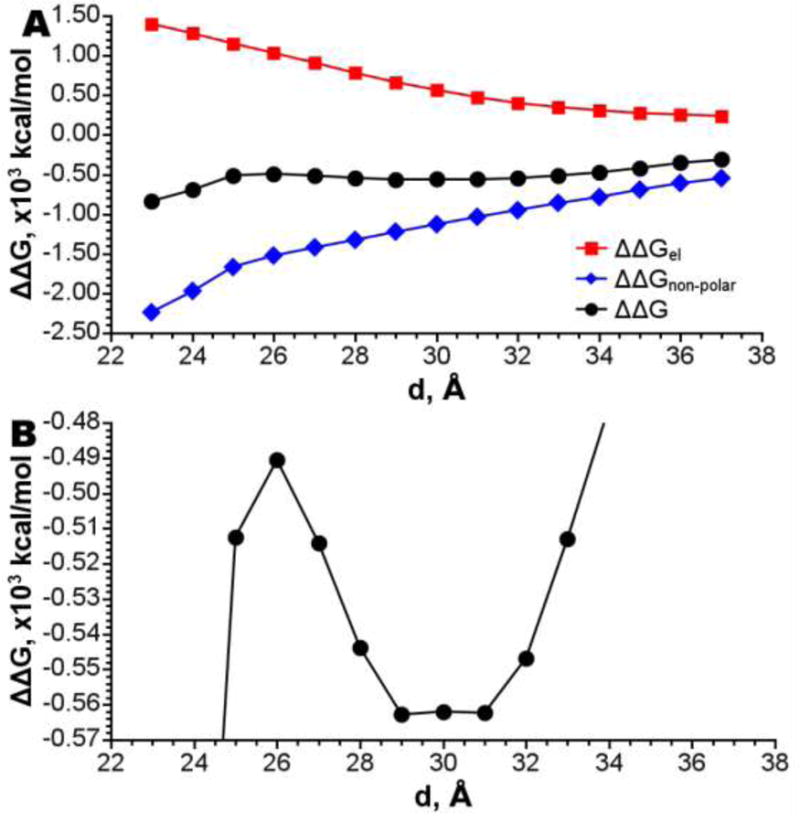
A - Change in free energy of insertion on the different levels of penetration of AHL to the membrane. B – Same, focused on the minimum at 30 Å.

It is worth to noting that in reality, a deep insertion of the AHL rim to the membrane may perturb packing of lipid; this should lead to an energetic penalty on such a deep insertion. However, the continuum PBSA model does not take this effect into account. Therefore, the predicted energy (Fig. 5 A) is perhaps underestimated at deep insertion.

Discussion and Conclusions

The purpose of the current work is three-fold: i) to determine influence of the AHL protein position in the membrane and protonation states of the its residues on the predicted current conduction properties of the channel; ii) to determine to what degree a mismatch of predicted I-V properties with experimental ones can be attributed to the membrane model; and iii) to predict the best AHL position in the membrane based on comparison of calculated I-V properties with experimentally measured ones.

Our calculations demonstrate that most electrophysiological properties of the pore including the total current, current rectification, and the reversal potential are sensitive to positioning of the AHL channel in the membrane. Therefore, a proper position of the channel within the membrane is an important characteristic for modeling its ionic conductance. In general, PNP-SR overestimates current selectivity and total current at all positions of the protein in the membrane. Therefore, this problem can not be completely attributed to the inadequate positioning of the channel in the membrane. Hence, in order to achieve more accurate results some PNP theory approximations should be reconsidered. Neglected by the PNP theory direct ion-ion correlation is probably the smallest unaccounted contributor because most calculations were done with low KCl salt concentrations. Most of our calculations were done at 0.1M KCl and only two reversal potential calculations were performed at 1M KCl. The third reversal potential calculation was done with smaller KCl concentration, and this calculation has a better agreement with experiment (Fig. 4B). PNP-SR also lack of protein flexibility treatment. Although AHL is a relatively rigid channel [11] the fluctuation of the side chains of some residues can have a significant contribution to PMF. For example, Lys147 side-chains can be bent towards the protein resulting in a lower barrier for the chloride. Probably the largest omission of the PNP theory is neglect with dielectric self energy (DSE), the energetic penalty that arises upon a transfer of charged particle from high dielectric media (bulk solvent) to low dielectric environment (pore of channel). It was shown previously that accounting for the dielectric self-energy in narrow channel results in significant increase of the barrier inside the channel and leads to smaller current [42]. Because of the complex form of electrostatic potential in the pore the inclusion of DSE can also affect channel selectivity. However, for wide channels DSE with pore radii larger then 3.8 Å is less or equal to 2 kT in the center of a pore [43]. The AHL radius is 5.1 Å in the narrowest part of the channel (as measured by the Hole program [44]), therefore DSE should not be the most dominating contributor. Although protein flexibility and DSE in such a wide channel may cause minor effects, the selectivity of AHL itself is small, and thus is a result of a fine balance between many factors. Neglect of any of those factors may lead to significant change in prediction. Therefore, further work is needed to address weather selectivity is indeed sensitive to these factors. To account for both channel flexibility and DSE of the ions it is necessary to calculate PMF of ions, e.g. directly from the MD simulations [45]. However, calculation of ions’ PMF for all possible positions in AHL is a task that is computationally demanding to the extreme.

In general, several scenarios for the AHL dynamics within the membrane are possible: 1) the AHL channel has one stable position with small oscillation around this position; 2) the AHL channel has several stable positions with small oscillation around each position and with transitions among them; or 3) the AHL can move relatively freely within a relatively large distance across the membrane. The calculated dependency of the reversal potential and free energy on the AHL position in the membrane indicates two possible stable positions. The first one is characterized by a relatively shallow penetration. The second one is characterized by a deep penetration of AHL to the membrane with submergence of the AHL rim into the membrane core. We can rule out the deep insertion based on the following reasoning. i) In the case of a deep penetration both Arg200 and Lys266 will be de-protonated. However, because of its high pKa value arginine residue is deprotonated and the free energy of transfer of arginine from water to a completely non-polar environment is high [46, 47]. ii) Our free energy calculations of the protein insertion do not account for any change in the packing of tails near inserted protein; thus, the energy for deep penetration is most probably underestimated. Therefore, taken into account together, both required protonation of arginine, and underestimation of free energies of insertion indicate that deep penetration is probably less favorable than the shallow insertion point. In addition, rectification shows only one favorable insertion position which corresponds to a shallow penetration. The best match of predicted rectification with experimental rectification occurs when the protein is inserted at the depth of 30.5 Å. This conclusion is also in very good agreement with the neutron reflection experiment on tethered bilayer lipid membranes [14] which gives penetration depth of 31 ± 2 Å (distance from the geometrical center of the protein to the center of membrane core). The experimental uncertainty of 2 Å can be explained by the size of the energy valley found in our PBSA calculations, which is around 3 Å. Therefore AHL probably has one unique position in the membrane with oscillation about 1.5 Å around it.

In this work we use a low dielectric media slab model. This slab represents the hydrophobic region of the lipid bilayer. Such simplification is feasible because the pore wall is mainly formed by the protein and the membrane is located sufficiently far from the pore region. Because of these two facts it is possible to neglect the fine atomic structure of the membrane and approximate membrane-ion interactions by the interaction of the ion with the averaged membrane structure. Similar to membrane hydrophobic region the membrane polar region was modelled implicitly as well with dielectric constant of 80 (in other words it was set to have same dielectric properties as water), large concentration of water molecules and polar nature of lipid’s head makes it a reasonable approximation. Throughout all positions calculated in this work the AHL rim is partially submerged to the hydrophobic membrane core. In case of deep penetration the residues located in the rim may perturb the membrane to such a degree that the applicability of the membrane slab model becomes questionable. However, recent neutron reflection experiments on tethered bilayer lipid membranes [14] supports applicability of the membrane slab model. According to these experiments thickness of the hydrophobic membrane region changed by only 1 Å upon insertion of the AHL. Thus, the membrane slab model is still a reasonable choice for the case of AHL.

It is important to discuss the choice of dielectric constants in the models presented here as this property is used as a fitting parameter in various molecular modeling sub-fields resulting in a large range of chosen values that we adopt in this work. All calculations presented in this work used continuum electrostatics approaches (PB or PNP based), which include protein dielectric constant as a parameter. We computed three different properties of the protein: ion currents, pKa values of residues, and energy of insertion (PBSA model). All three approaches include Poisson equation but consider protein model differently. Therefore the choice of the dielectric constant as a parameter in the Poisson equation varied appropriately with the approach, namely: four was used in PNP-SR for calculation of ion-currents, twenty in pK_a that use a single protein structure, and two in PBSA calculations that account explicitly for protein flexibility. The choice of an effective dielectric constant of the protein is determined by the best practice specific to an application. In general, the dielectric constant is a catch-all parameter that is used to compensate for model specific unaccounted contributions to energy and entropy, for example, when the protein remains rigid in a standard pKa calculation. The weights of the contributions from the omitted properties of the protein structures are different when the continuum theory applied to a variety of problems, and therefore an optimal dielectric constant value may be different. In ion-permeation studies the dielectric constant often set conservatively to 2-4 [9, 20, 27, 45, 48, 49] and treated as a fitting parameter to reproduce experimental data [50], while it was established that there is no significant difference in predicted currents between dielectric constant of 2 to 10. While it is commonly agreed that the dielectric constant of a globular protein core is 3-6 [51, 52] it is reasonable to assume a dielectic constant of 4 for the membrane protein of interest in this work for the PNP-SR calculation. Relatively high dielectric constants 10-20 are typically used for the pK_a calculations, due to better reproduction of experimental results for a variety of proteins [34, 36]. For estimation of channel protein positioning within the membrane we use Poisson-Boltzmann solvent accessible surface area (PBSA) approach. This calculation was done with PARSE/γ force field (FF) [38, 40]. This FF was parameterized with dielectric constant of 2 against the experimental solvation energies.

Summary

In this study we found that current conducting properties of AHL protein channel are extremely sensitive to the channel position in the membrane and protonation states of titratable residues that come close to the lipid bilayer. Even a few angstrom shift of the protein can result in significantly different I-V properties. Overall, PNP-SR model gives a good semi-quantitative prediction of current conducting properties of the channel, but systematically overestimates both ion selectivity and total current. Most probably due to its treatment of the protein in a single conformation and neglect of the dielectric self energy term (addressed in PMF-PNP or DSE-PNP approximations). Based on our I-V predictions and PBSA calculations we found a single best position of AHL in the membrane. This position is characterized by an electrostatic potential well with almost flat bottom of 3 Å width. The optimal position based on the match of rectification is in excellent agreement with the experimental results. In most works, little attention is given to proper positioning of the protein in the membrane and computing protonation states of the titratable residues that change their environment when inserted in the lipid bilayer. In this paper we have demonstrated clearly that in order to achieve accurate results on predicting protein conductance properties, both membrane position and protonation of the titratable groups need to be computed better than positioning of the protein in the middle of the hydrophobic region, which is a typical practice.

Table 1.

Dependency of the AHL residue protonation state on the channel position in the membrane.

Resedue*	Alternative State	Number of Residues in Alternative State†
		Penetration Depth, Å
		35	33	31	29	27	25	23
71 GLU	Protonated	0	0	0	0	0	1	1
75 LYS	Unprotonated	0	0	0	0	0	0	3
200 ARG	Unprotonated	0	0	0	1	3	6	6
266 LYS	Unprotonated	0	0	0	5	7	6	6

^*Only residues changing their protonation state are shown.