Computed free energies of peptide insertion into bilayers are independent of computational method

Abstract

We show that the free energy of inserting hydrophobic peptides into lipid bilayer membranes from surface-aligned to transmembrane inserted states can be reliably calculated using atomistic models. We use two entirely different computational methods: high temperature spontaneous peptide insertion calculations as well as umbrella sampling potential-of-mean-force (PMF) calculations, both yielding the same energetic profiles. The insertion free energies were calculated using two different protein and lipid force fields (OPLS protein/united-atom lipids and CHARMM36 protein/all-atom lipids) and found to be independent of the simulation parameters. In addition, the free energy of insertion is found to be independent of temperature for both force fields. However, we find major difference in the partitioning kinetics between OPLS and CHARMM36, likely due to the difference in roughness of the underlying free energy surfaces. Our results demonstrate not only a reliable method to calculate insertion free energies for peptides, but also represent a rare case where equilibrium simulations and PMF calculations can be directly compared.

Introduction

Membrane-protein insertion into a lipid bilayer typically occurs via one of two pathways. The simplest is direct partitioning from the aqueous environment, a pathway taken predominantly by single-transmembrane (TM)-spanning helices such as pore-forming toxins (Schlamadinger et al., 2012) and antimicrobial peptides (Bechinger, 1997; Sato & Feix, 2006; Ulmschneider, 2017; Upadhyay et al., 2015; Wang et al., 2016) due to their opportunistic and adventitious nature. For natively synthesized membrane proteins, the most common pathway in all organisms relies on the protein translocon, itself a membrane protein that provides a route to the hydrophobic core of the bilayer through its lateral gate (Frauenfeld et al., 2011; Park et al., 2014; van den Berg et al., 2004).

Although both pathways lead to the same fate for a protein, stable incorporation in the membrane, differences in energetics of the initial states (Gumbart, Chipot & Schulten, 2011b) and kinetics of the processes (Gumbart et al., 2013; Zhang & Miller III, 2012a) can lead to one pathway being favored over the other. Thus, a complete biophysical description of these pathways will ultimately depend on a quantitative measure of the interactions between the inserting protein and its three possible environments: water, membrane, and translocon. While experiments have been quite successful at probing the translocon-mediated pathway (Hessa et al., 2005; Hessa et al., 2007), direct partitioning has proven more difficult to systematically study due to the aggregation tendencies of many hydrophobic peptides (Wimley & White, 2000).

Computer simulations present an appealing alternative to experiments for understanding membrane-protein insertion, because all facets of the process being simulated are available for detailed scrutiny. Nonetheless, their utility is heavily dependent on the accessible time scales and the accuracy of the underlying force fields. The former concern can be met either through increasing the computational efficiency of simulations, e.g., by using the latest supercomputers such as Anton (Hu et al., 2016), or through enhanced sampling methods that permit calculation of free energies from biased simulations, e.g., umbrella sampling. Despite apparent successes of both approaches (Gumbart et al., 2013; Horn, Romo & Grossfield, 2013), recent work has indicated sampling difficulties for membrane-peptide interactions may have been drastically underestimated previously (Neale et al., 2011). The latter concern, that of the force fields, also represents an unsettled issue, in which different approaches in development have led to apparently different outcomes (Piggot, Piñeiro & Khalid, 2012).

Free energies of insertion for individual amino acids have been determined experimentally using an approach where insertion occurs via Sec61 (Hessa et al., 2005; Hessa et al., 2007) as well as an approach in which a guest residue is incorporated in OmpLA, a β-barrel membrane protein that can spontaneously fold and insert (Moon & Fleming, 2011). A number of simulation studies have followed these approaches, focusing on side-chain analogs (Johansson & Lindahl, 2008; MacCallum, Bennett & Tieleman, 2007) or single amino acids embedded in proteins (Dorairaj & Allen, 2007; Gumbart et al., 2011b; Gumbart & Roux, 2012). Although challenging due to aggregation tendencies as noted above, insertion energies for small α-helical peptides have been measured experimentally in limited cases, e.g., for toxins (Ladokhin & White, 2004), antimicrobial peptides (Ladokhin & White, 1999), and designed peptides (Wimley & White, 2000), as well as computationally (Babakhani et al., 2008; Irudayam, Pobandt & Berkowitz, 2013; Lyu et al., 2017; Sandoval-Perez, Pluhackova & Bockmann, 2017; Yeh et al., 2008).

In order to evaluate the consistency of various approaches and force fields to understanding lipid-protein interactions, we have calculated the energetics and kinetics of membrane partitioning for short polyleucine helices, denoted Ln (n=5–10). We used two completely unrelated protein (OPLS and CHARMM36) and lipid (united-atom and all-atom) force fields, as well as both long equilibrium simulations and potential-of-mean-force calculations to resolve the energetic landscape of the partitioning process. The results are found to be almost uniformly in quantitative agreement across methods and force fields. The only exception is in the rate of transitions between states, likely due to the simplified (united-atom) lipid model used in the OPLS force field. Our results demonstrate that peptide partitioning simulations are reliable and that the energetics of partitioning depend little on force field parameters and simulation techniques; however, the kinetics, in particular the diffusivity, does depend on the lipid model used.

Methods

Equilibrium molecular dynamics (MD)

Peptide sequences of the form ac-L_n-nme (Ln, n = 5–10) were constructed and embedded into the water phase of a box containing a preformed POPC (palmitoyloleoyl-phosphocholine) lipid bilayer. The initial conformation was an ideal α-helix, placed 10 Å from the bilayer surface. Equilibrium simulations run at 50, 120, and 160 °C were run on the Anton 1 machine at Pittsburgh Supercomputing Center (Shaw et al., 2009) and analyzed with VMD (Humphrey, Dalke & Schulten, 1996), while all others were performed and analyzed using Gromacs version 4.5 (www.gromacs.org) (Berendsen, van der Spoel & van Drunen, 1995) and hippo beta (http://www.biowerkzeug.com/). The CHARMM36 protein (Best et al., 2012) and lipid (Klauda et al., 2010) force fields were used along with TIP3P for water (Jorgensen et al., 1983) for all equilibrium simulations.

For Gromacs simulations, electrostatic interactions were computed using the particle-mesh Ewald method (PME); a cutoff of 10 Å was used for van der Waals interactions. Bonds involving hydrogen atoms were restrained using LINCS (Hess et al., 1997). Simulations were run with a 2-fs integration time-step. All simulations were performed in the NPT ensemble, with no additional applied surface tension. Water, lipids, and the protein were each coupled separately to a heat bath with time constant τ_T = 0.1 ps using weak temperature coupling (Bussi, Donadio & Parrinello, 2007); atmospheric pressure of 1 bar was maintained using weak semi-isotropic pressure coupling with compressibility κ_z = κ_xy = 4.6 · 10⁻⁵ bar⁻¹ and time constant τ_P = 1 ps (Berendsen et al., 1984).

In Anton simulations, a 2.5-fs time step was used. Temperature and pressure control were enabled through application of the Multigrator approach (Lippert et al., 2013) using a semi-isotropic Martyna-Tuckerman-Klein barostat (Martyna, Tobias & Klein, 1994) and Nosé-Hoover thermostat (Hoover, 1985; Martyna, Klein & Tuckerman, 1992). Short-range and long-range non-bonded interactions were updated every time step and every three time steps, respectively. For all simulations on Anton, the cutoff was automatically chosen to be around 13–14 Å.

The insertion propensity p_TM of each peptide was calculated as the probability of the peptide being in the TM state. To distinguish the TM state from the S state, a criterion of z < 8 Å and θ < 50° was found to be optimal. The free energy of S→TM partitioning was then calculated as ΔG_S→TM = +kT ln (1/p_TM − 1). Sufficient transition events were captured by using elevated temperatures. No loss of helical structure occurred even at temperatures as high 150 °C, for any sequence tested. We used helical restraints for T > 150 °C.

Free-energy calculations

All simulations used for potential-of-mean-force (PMF) calculations, denoted “US” in Table 1, were run with NAMD (Phillips et al., 2005). Simulations were run using either the CHARMM36 or the OPLS force field. In the case of OPLS, protein parameters were taken from the CHARMM-formatted file par_opls_aa.inp (Jorgensen, Maxwell & Tirado-Rives, 1996), distributed along with the CHARMM force field, while lipid parameters were taken from Ulmschneider et al. (Ulmschneider, Smith & Ulmschneider, 2010b). In all cases, the TIP3P force field for water was used (Jorgensen et al., 1983).

Table 1.

List of all simulations performed. C36 refers to CHARMM36 force field for both protein and lipids; OPLS refers to that force field for protein and the united-atom lipids. Under simulation type, MD is purely equilibrium, while US refers to replica-exchange umbrella sampling. “[R]” indicates the use of helical restraints on the peptide. Error bars are derived from block averaging over five blocks of equal length. The aggregate simulation time is over 71 μs.

Sequence	Force field	Simulation Type	T [°C]	Length [μs]	ΔGS→TM [kcal/mol]
L8	C36	MD	50	10.0	−0.98 ± 0.18
L8	C36	MD	120	7.2	−0.79 ± 0.43
L8	C36	MD	150	5.0	−0.54 ± 0.43
L8	C36	MD	160	2.5	−1.08 ± 0.09
L8	C36	MD [R]	180	5.0	−0.92 ± 0.30
L8	C36	MD [R]	210	5.0	−1.14 ± 0.19
L8	C36	US [R]	50	3.8	−2.86 ± 0.07
L8	C36	US [R]	120	3.0	−1.27 ± 0.14
L8	C36	US [R,x2]	120	1.0	−1.48 ± 0.14
L8	C36	US [R]	160	3.0	−1.38 ± 0.12
L8	OPLS	US [R]	50	3.0	−1.27 ± 0.18
L8	OPLS	US [R]	120	3.0	−1.00 ± 0.18
L8	OPLS	US [R]	160	3.0	−1.61 ± 0.03
L5	C36	MD	150	2.1	3.29 ± 0.20
L6	C36	MD	150	2.2	1.44 ± 0.26
L7	C36	MD	120	3.0	0.61 ± 0.28
L7	C36	MD	150	2.2	0.57 ± 0.48
L7	C36	MD	160	2.4	0.99 ± 0.18
L9	C36	MD [R]	210	2.0	−2.03 ± 0.39
L10	C36	MD [R]	210	2.8	−2.65 ± 0.59

For PMF calculations run using the CHARMM36 force field, a cutoff of 12 Å was used for short-range non-bonded interactions with a force-based switching function starting at 10 Å. For simulations with the OPLS force field, a cutoff of 10 Å was used for short-range non-bonded interactions with a potential based switching function starting at 8 Å; interactions between atoms separated by three bonds (“1–4 interactions”) were scaled by 0.5. Lennard-Jones interactions were calculated using an arithmetic combination rule for CHARMM36 and a geometric combination rule for OPLS. In all simulations in this section, a 2-fs time step was used with long-range electrostatics calculated using PME every other time step. Temperature was controlled with a Langevin thermostat with a damping constant of 0.1 ps⁻¹; pressure was maintained at 1 atm separately in the xy and z dimensions using a Langevin piston (Feller et al., 1995).

PMFs were calculated using umbrella sampling with replica exchange (REMD-US), which permits swapping periodically between neighboring windows to enhance conformational-space sampling (Sugita, Kitao & Okamoto, 2000), as implemented in NAMD. Two reaction coordinates were used. The first is the position of the peptide helix along the membrane normal z, which was divided into 12 windows spaced every 1.5 Å from −0.5 Å to 16.0 Å; z is calculated as the distance between the centers-of-mass of the peptide backbone and of the phosphorus atoms of the lipids. The angle of the peptide’s helical axis with the membrane normal is the second coordinate, with 8 windows spaced evenly over 90 degrees used. Thus, for 2D REMD-US, 96 windows were needed. After a 1-ns equilibration per window, 31 ns/window was run for most PMFs, making the typical net simulation time 3 μs/PMF (see Table 1).

Diffusivity calculations

Diffusivity was calculated through use of a generalized Langevin approach (Gaalswyk, Awoonor-Williams & Rowley, 2016). For each window from the REMD-US simulations, an additional 2-ns simulation was run in which the L8 peptide was harmonically restrained to that window’s center, (z_i, θ_i). From this simulation, the velocity autocorrelation function is calculated and input into the formula for D(z_i, θ_i) derived by Schumaker et al. (Schumaker, Pomès & Roux, 2000) as implemented in the stand-alone code ACFCalculator (Gaalswyk et al., 2016). A total of 1.15 μs of additional simulations (192 ns per temperature and force field) were needed to compute the full diffusivity maps.

Results

Equilibrium simulations

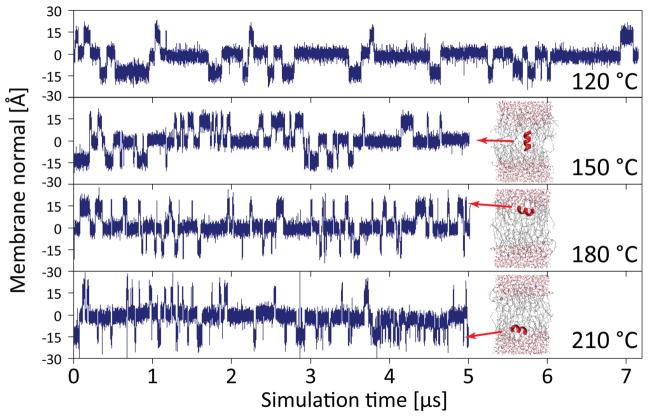
The Ln peptides studied here via long simulation timescales (multi-μs) can be seen to spontaneously transition between surface aligned (S) and transmembrane inserted (TM) conformations (Fig. 1), similar to the results reported previously with simulations using the OPLS force field and united atom lipid parameters (Ulmschneider, Andersson & Ulmschneider, 2011a; Ulmschneider et al., 2011b; Ulmschneider et al., 2010b). However, these transitions require much higher temperatures to occur for CHARMM36; for example, L8 at 120 °C has 31 transitions/μs using the OPLS force field (Ulmschneider et al., 2011b) but only 5 transitions/μs using the C36 force field (Fig. 1). At least 120 °C is needed to accumulate sufficient switching events, and the dwell time of the peptides at this temperature is observed to be in the μs range, much longer than what was seen with OPLS. The kinetics can be accelerated by further heating, where - in contrast to the OPLS simulations - the CHARMM36 simulations are fully helical even at 150 °C. Peptides do not unfold, nor is the bilayer disrupted at this superheated temperature (Ulmschneider et al., 2009; Ulmschneider et al., 2010a), although the area per lipid increases significantly, ranging from ~65 Ų at 50 °C to as much as 85 Ų at elevated temperatures. For T > 150 °C, we saw some temporary breakage of a few backbone hydrogen bonds, so we used helical restraints as we are not interested in the CHARMM36 melting curve of polyleucine at extreme (unphysiological) temperatures, but solely in its rigid-body S to TM transition behavior.

Figure 1.

The L8 peptide spontaneously switches between surface (S) and transmembrane (TM) states during equilibrium simulations using the CHARMM36 force field, shown here via plots of the center of mass position of the peptide along the membrane normal. The frequency of these switches increases rapidly with temperature. Very high temperature can be used without dissolving the membrane, and the peptides remain fully helical at 120 °C and 150 °C (for T > 150 °C, helical restraints were used). The kinetics are too slow for T < 120 °C to obtain convergence of ΔG_S→TM on the simulated time scales.

Despite the greatly reduced kinetics of the simulations as compared to OPLS, the observed orientations of the peptides are exactly the same for the two force fields: there are four dominant states, two surface aligned and two transmembrane – one with the N-terminus in the upper leaflet, and one with the C-terminus in the upper leaflet. Other orientations are energetically highly unfavored. The only difference between the force fields is that peptides are embedded slightly more deeply in the S-state when using OPLS as compared to CHARMM36, which is likely related to differences between the UA and AA lipids used, respectively.

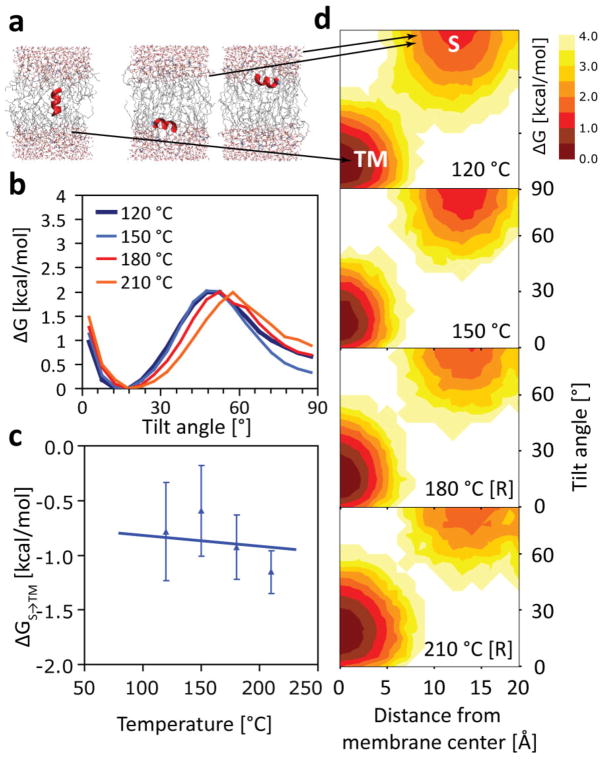
One of the surprising results of the OPLS simulations was the lack of a temperature dependence of the S→TM partitioning free energy, with ΔG_S→TM = const., and ΔS_S→TM = 0.(Ulmschneider et al., 2011b) When we calculate ΔG_S→TM here for CHARMM36, we observe the same lack of temperature dependence (Fig. 2). The result for L8 is ΔG_S→TM ≈ −0.9 ± 0.2 kcal/mol, independent of temperature, which is within roughly 0.6 kcal/mol of the OPLS value found previously (ΔG_S→TM ≈ −1.5 ± 0.2 kcal/mol).(Ulmschneider et al., 2011b) Thus, the two very different protein and lipid force fields agree surprisingly well. The simulation lengths of 5–7 μs allow for a sufficient number transitions for T > 120 °C, leading to fully converged free energy surfaces and excluding the possibility that insufficient sampling could play a role (Fig. 3).

Figure 2.

(a) Temperature independence of hydrophobic S→TM partitioning for the L8 peptide in equilibrium simulations using the CHARMM36 force field. No pronounced temperature effect is visible over the range 120–210 °C. Each simulation plotted here is at least 5-μs long, so one-dimensional free energy profiles (b), and the overall transfer free energy ΔG_S→TM (c), are well converged. Note that barrier in (b) is not a true transition state, which is undersampled in our equilibrium simulations. Simulations using helical restraints are denoted with [R]. No unfolding is observed otherwise, and both unrestrained and restrained simulations yield the same ΔG_S→TM ≈ −0.9 ± 0.2 kcal/mol (c). Two-dimensional free energy profiles (as a function of membrane insertion and tilt angle) reveal almost no variation with temperature (d).

Figure 3.

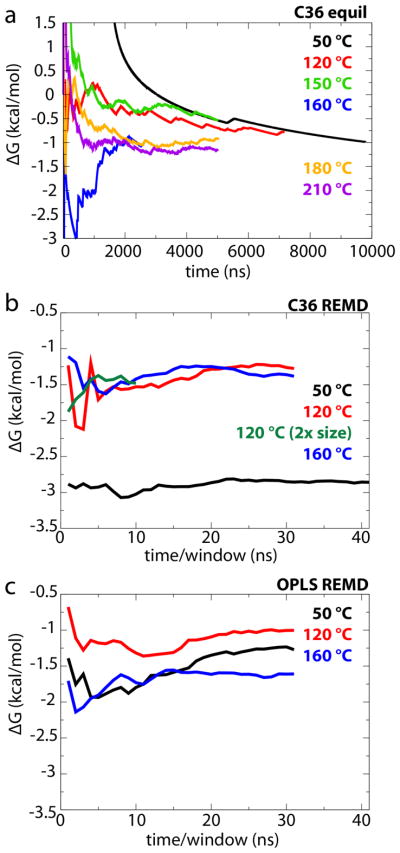
Convergence of ΔG_S→TM. (a) ΔG_S→TM as a function of time for all L8 equilibrium simulations. (b, c) ΔG_S→TM as a function of sampling time per window for (b) CHARMM36 REMD calculations and (c) OPLS REMD calculations.

Free-energy calculations

To determine the reliability of the long time-scale equilibrium simulations in predicting the free-energy difference between transmembrane and surface-associated states, we next turned to replica-exchange umbrella sampling (REMD-US). Two degrees of freedom relevant to the peptide were selected for biasing, the tilt angle of the helix and its position with respect to the membrane center. Potentials of mean force (PMFs) for both the CHARMM36 force field and the OPLS force field were determined at three temperatures each, 50 °C, 120 °C, and 160 °C. Each PMF calculation was run for 3 μs in total, with the exception of CHARMM36 at 50 °C, which was run for 3.8 μs (see Methods).

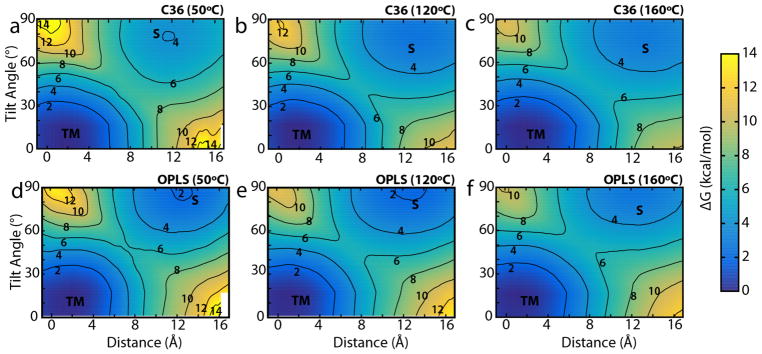
The PMFs in Fig. 4 reveal the same general behavior observed for the equilibrium simulations in Fig. 2d, namely there are two preferred states (TM and S) with TM being slightly favored over S. To calculate ΔG_S→TM for these two states, the 2D PMFs were integrated using Boltzmann weighting over the respective basins surrounding the two minima. With the exception of CHARMM36 at 50 °C, rough agreement between the PMF-derived ΔG_S→TM values and the equilibrium values was found; for CHARMM36 above 50 °C, ΔG_S→TM ranges from −1.4 to −1.3 kcal/mol, while for OPLS, the range is −1.6 to −1.0 kcal/mol (see Table 1). Thus, the transfer free energy of L8 is still found to be both force-field and temperature independent (within less than 1 kcal/mol), at least above 50 °C. However, for CHARMM36 at 50 °C, ΔG_S→TM = −2.86 kcal/mol is much lower than the other values. There is little change, however, over time after the first few ns (see Fig. 3). Insufficient sampling (41 ns/window) of long-time-scale membrane rearrangements remains a possible issue, as the 10-μs simulation using CHARMM36 at 50 °C gives ΔG_S→TM = −0.98 kcal/mol, similar to the other calculations for L8. Indeed, sampling up to 205 ns/window was insufficient to accurately determine the free energy of binding of n-propylguanidinium to a DOPC bilayer, although the average of 36 independent calculations did converge to the expected result (Neale et al., 2011).

Figure 4.

Two-dimensional PMFs as a function of the L8 helix position along the membrane normal and its tilt angle. The transmembrane and surface-associated states are indicated by “TM” and “S”. Contour lines are drawn every 2 kcal/mol and are labeled. (a–c) Plots for the CHARMM36 force field at (a) 50 °C, (b) 120 °C, and (c) 160 °C. (d–f) Plots for the OPLS force field at the same temperatures, respectively.

When the protein is in its S state, there is a difference in area/lipid between the two leaflets of the bilayer, one containing the protein and one not. This difference is either not present or not as pronounced for the TM state. Thus, finite-size effects may shift the free energies measured, by adding a surface-tension dependent term. To determine if such effects are manifest here, we repeated the REMD-US simulations for L8 in a bilayer of approximately twice the area as that used previously (91×91 Ų vs. 64×64 Ų), using CHARMM36 and a temperature of 120 °C. Although run for a shorter time (1 μs vs. 3 μs), the resulting value of ΔG_S→TM was almost identical to that found for the smaller membrane, −1.5 kcal/mol vs. −1.3 kcal/mol, respectively. Thus, finite-size effects are not apparent here.

The similar transfer free energies for both the CHARMM36 and OPLS force fields, at least at temperatures above 50 °C, do not resolve the question of why the rate of transitions at equilibrium is significantly higher using OPLS over CHARMM36. To address this question, we calculated the least free-energy path (LFEP) (Ensing et al., 2005) for each 2D PMF and extracted the activation energy. All cases exhibited a single barrier, indicating first-order kinetics. For OPLS, the TM→S activation energies are 6.2 kcal/mol at 50 °C (9.6 kT), 5.8 kcal/mol at 120 °C (7.5 kT), and 5.8 kcal/mol at 160 °C (6.7 kT). The activation energies found using CHARMM36 are almost identical for temperatures above 50 °C, namely 5.9 kcal/mol at 120 °C (7.5 kT) and 5.6 kcal/mol at 160 °C (6.5 kT).

Diffusivity calculations

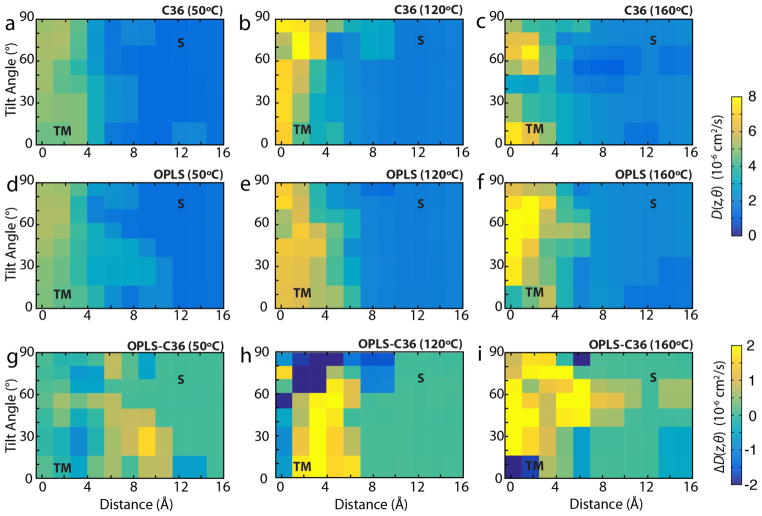
In addition to the size of the activation energy for transition between states, the kinetics of the process, specifically the diffusivity, also contributes to the rate of transitions. We calculated the diffusivity for both CHARMM36 and OPLS force fields at all three temperatures used for the REMD-US simulations, i.e., 50 °C, 120 °C, and 160 °C, plotted in Fig. 5. Diffusivity of the L8 peptide is consistently greater in the membrane than at the surface, where it is approximately two orders of magnitude less than in pure TIP3 water (Takemura & Kitao, 2007). We also calculated the difference in diffusivities between OPLS/UA-lipids and CHARMM36/AA-lipids, shown in Fig. 5g–i. The diffusivity in the membrane with UA lipids is greater than that in AA lipids for most orientations and positions of the L8 peptide. Although at T = 50 °C, the difference between the two force fields is mixed, this difference grows with temperature. Greater diffusivity will lead to increased transition rates between states in OPLS/UA vs CHARMM36/AA, as observed in the equilibrium simulations described above.

Figure 5.

Diffusivity as a function of position and tilt angle. (a–c) Diffusivity for CHARMM36 at (a) 50 °C, (b) 120 °C, and (c) 160 °C. (d–f) Diffusivity for OPLS at (d) 50 °C, (e) 120 °C, and (f) 160 °C. (g–i) The difference in diffusivities (D^OPLS – D^C36) at (g) 50 °C, (h) 120 °C, and (i) 160 °C. TM and S states are the same as indicated in Fig. 4. Values in (a)–(f) are colored on a scale of 0–8×10⁻⁶ cm²/s.

The roughness of the energy landscape can have a significant effect on the diffusivity, with rougher landscapes resulting in slower dynamics due to the presence of small barriers along the reaction coordinate. This roughness is governed by the relation D^* = D₀ exp[−(ε/kT)²], where D₀ is the diffusion coefficient in a smooth potential, D^* is the diffusion coefficient in the true rough potential, ε is the roughness of the potential, k is Boltzmann’s constant, and T is the temperature (Zwanzig, 1988). This effect has been observed both computationally and experimentally. For example, in simulations of small peptides, explicit solvents increase the roughness of the torsional energy landscape by ~1.0 kcal/mol over implicit solvents without affecting energy barriers or the location of local minima (Hamelberg, Shen & McCammon, 2006). As a result, inter-residue ω-angle cis/trans isomerization rates were up to 10⁴ times higher in the implicit solvent than the explicit solvent (Hamelberg et al., 2006). Changes in energetic roughness can also be critical mechanisms in biological processes, such as the increase in roughness of the environment by ~1.0 kcal/mol as aminoacyl-tRNA transitions from free solution into the A-site of the ribosome, decreasing the diffusion constant by ~20x (Whitford et al., 2013). A similar phenomena has also been observed in prion aggregation, where single molecule force microscopy experiments have shown that dimerization of the prion protein, PrP, increases the energy landscape roughness by ~3.0 kcal/mol over the monomeric state, resulting in a 1000-fold decrease in the diffusion coefficient and 300-fold decrease in the unfolding rate for the misfolding pathway of the dimer versus the folding pathway of the monomer (Yu et al., 2015).

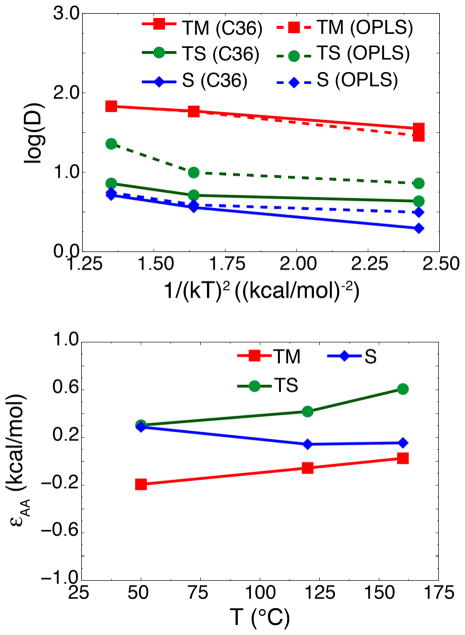
For united-atom lipid membranes, the lack of explicit hydrogens in the aliphatic tails should smooth the energy landscape, resulting in faster dynamics and more transitions of the helix than in all-atom lipid membranes. Transition rates in UA lipid membranes are ~40x that in the all-atom lipid membranes at 120 °C: 31 transitions in 1 μs (Ulmschneider et al., 2011b) vs. 5 transitions in 7 μs (this work), respectively. Using Kramer’s rate formula, given that the free energy landscapes are nearly identical between united-atom and all-atom lipids, diffusivity alone could explain the stark difference is transition rates. Since it is quite noisy (Fig. 5), we averaged the diffusivity in three distinct regions: the transmembrane region (TM), the surface-associated region (S), and the transition state region (TS) (see Fig. 6, top graph). Typically, to calculate energetic roughness, one computes a linear fit to ln(D) vs. 1/(kT)² for each system, where the slope is equal to −ε² (Hamelberg et al., 2006). However, calculating diffusivity in membranes is notoriously prone to convergence issues. Diffusivities of solutes permeating through a lipid bilayer typically require μs to ms to converge (Neale et al., 2011), and autocorrelation functions may not decay fast enough, leading to an underestimation of the diffusion coefficients (Lee et al., 2016). Given that some of the windows in Fig. 5 may not be fully converged, fitting to the three temperatures may yield inaccurate results.

Figure 6.

Average diffusivities and energetic roughness. (Top) Average diffusivities for transmembrane (“TM”, red curves), surface-associated (“S”, blue curves), and transition (“TS”, green) states for AA- (solid lines) and UA- (dashed lines) lipid membranes. TM and S states were defined as two potential wells observed in Fig. 4, with the TS state defined as the barrier region separating the two wells. Regions where the diffusivity calculations did not converge were excluded from the averages. Results are plotted as log(D) vs. 1/(kT)². (Bottom) Energetic roughness of AA-lipid membranes, approximated as ε_AA ≈ kT[log(D_UA) − log(D_AA)]^1/2, calculated for TM (red lines, squares), S (blue lines, diamonds), and TS (green lines, circles) states.

Instead of fitting, we can approximate the difference in roughness between UA- and AA-lipid membranes by assuming that the roughness of the UA-lipid membrane is negligible, i.e., that diffusion in the UA-lipid is essentially free diffusion. Although an implicit lipid membrane would better represent free diffusion as shown by Hamelberg et al. (2006), one would need to find such a model that produces the same free energy landscape as the AA-lipid force fields in order to calculate a true free diffusion constant. The UA-lipid force field is a good approximation of free diffusion in this case since it is the simplest model that reproduces the AA-lipid free energy landscape. Therefore, we approximate the roughness of the AA-lipid membrane at each temperature as ε_AA ≈ kT[log(D_UA) − log(D_AA)]^1/2 if D_UA > D_AA or −kT[log(D_AA) − log(D_UA)]^1/2 if D_UA < D_AA. These results are plotted in Fig. 6, bottom graph. At higher temperatures, the roughness of the transition-state (TS) region is ~0.4–0.6 kcal/mol in the AA-lipid membrane, whereas the roughness of the S and TM states is smaller (<0.2 kcal/mol). Increased roughness in the transition-state region between the TM and S states may be driving the decrease in transition rates in the AA-lipid membrane, as was the case for prion misfolding (Yu et al., 2015). The roughness values also appear to be in line with the modest increase in transition rates between UA-lipid membranes and AA-lipid membranes; previous studies have found ~300x–10,000x for 1.0–3.0 kcal/mol (Hamelberg et al., 2006; Yu et al., 2015), whereas we only observe ~40x increase in transitions for 0.5 kcal/mol.

Ln insertion curve

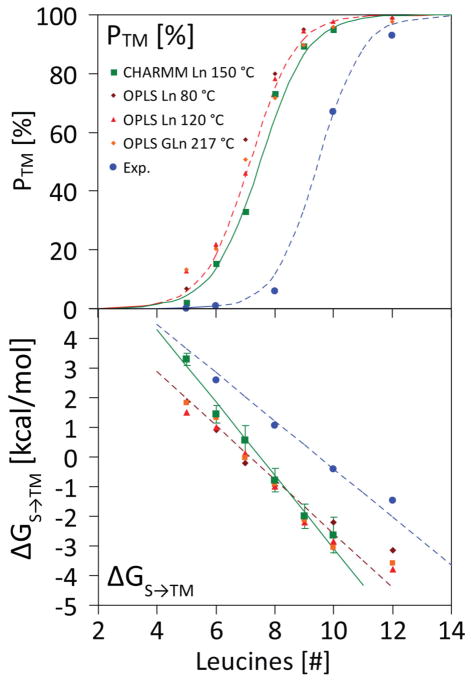
We further calculated L5, L6, L7, L9 and L10 insertion using direct partitioning simulations at 150–210 °C, to complete a length scan for CHARMM36, similar to the one performed for OPLS before. The results are shown in Fig. 7. The insertion curve is very similar for both force fields (upper panel). The free energy can be reliably calculated for sequences with |ΔG_S→TM|< 5 kcal/mol (lower panel). The same linearity of ΔG_S→TM with peptide length is found with the CHARMM36 parameters, albeit with a slightly larger slope of ΔΔG_S→TM = −1.23 kcal/mol, as compared to the OPLS value of ΔΔG_S→TM = −0.91 kcal/mol (Ulmschneider et al., 2011b). The similarity of two entirely different force fields is remarkable, and we believe these values accurately represent the spontaneous insertion behavior of polyleucine in a lipid bilayer. The shift with respect to the translocon curve is due to the structural details of the translocon, where a different equilibrium is sampled.

Figure 7.

Membrane insertion efficiency as a function of peptide length n for spontaneous partitioning of polyleucine (Ln) peptides into POPC lipid bilayers. (top) Insertion propensity. The computed values for the OPLS/UA-lipid force field at 80 and 120 °C (red) and GGPG-(L)_n-GPGG at 217 °C (brown) are shown. CHARMM36/AA-lipid results are also shown in the same figure (green). The results of the CHARMM36 simulations are very close to the OPLS results, and both show perfect two-state Boltzmann behavior (R² > 0.99), with a transition from a surface to TM state upon lengthening of the peptide. The experimental values are for translocon mediated insertion into dog pancreas rough microsomes of GGPG-(L)_n-GPGG constructs embedded into the leader peptidase carrier sequence (Jaud et al., 2009). (bottom) Free energy of TM insertion from the surface ΔG_S→TM as a function of peptide length n (insertion for negative ΔG). The straight lines indicate the two-state Boltzmann fit, while the data points show the computed (red, green) and experimental (blue) values for the individual peptides.

Discussion

From the results of the simulations, one can conclude that, a) direct partitioning simulations and PMF calculations give similar results using roughly equivalent sampling effort, b) hydrophobic peptide partitioning is independent of temperature and appears isentropic, c) ΔG_S→TM is independent of the force field used in the simulations, and d) the kinetics of partitioning depends on the force field. This last observation appears to be due to the difference between UA lipids and AA lipids. UA-lipid tails have no charge and behave like a pure Lennard-Jones fluid, allowing for a smooth energy landscape for partitioning. In contrast, AA-lipid tails consist of small polar CH₂ groups, and the additional hydrogens generate a rougher energy landscape, as demonstrated by the roughness calculations above (Fig. 6). Given that the transition is isentropic and independent of the force field, the total enthalpic contribution to the free energy barrier, including protein-lipid, lipid-water, and protein-water interactions, must be similar. As it is highly unlikely that differences in all these interactions between the two force fields would exactly cancel each other out to produce a similar free energy, these interactions individually are probably similar as well. Therefore, the energetic roughness is likely the underlying factor for the observed differences in kinetics between the UA- and AA-lipid membranes.

With the exception of CHARMM36 REMD-US simulations at 50 °C, the net result of the simulations of L8 is that ΔG_S→TM=−1.1±0.3 kcal/mol, supporting the conclusion that ΔG_S→TM is largely independent of the force field and temperature. The present work is also a demonstration that PMF calculations of peptides in lipid bilayers often agree with direct simulations if sufficient sampling is performed, which has previously been debated (Neale et al., 2011; Neale et al., 2014); albeit, both may yet suffer some unknown sampling deficiency, as suggested by the anomalous result for CHARMM36 REMD-US simulations at 50 °C. As noted before (Ulmschneider et al., 2011b; Ulmschneider et al., 2014), there is a shift between the spontaneous insertion and the translocon-based scale (Hessa et al., 2007), with the latter being ~2 kcal/mol higher (less favorable). This shift can be explained in part by structural details of the translocon, which is apparently less polar than a purely aqueous environment (Bol, de Wit & Driessen, 2007; Demirci et al., 2013; Gumbart, Chipot & Schulten, 2011a), and possibly also by the kinetics of the biological insertion process (Gumbart & Chipot, 2016; Gumbart et al., 2013; Zhang & Miller III, 2012b). Regardless of the precise origins, we have demonstrated here that errors in the simulation protocol are not responsible for the distinct energies found for the two processes. Furthermore, our results provide additional evidence that the energies measured in the translocon-based experiments do not represent an equilibrium partitioning between water and membrane, but something more complex (Gumbart et al., 2011b; Schow et al., 2011).

The equivalence of the calculated free energies using both two distinct force fields and two disparate methods imparts a degree of confidence in the quantitative accuracy of MD simulations, at least for the energetics of protein-lipid interactions. While it may be claimed that both force fields, CHARMM36/AA and OPLS/UA, are producing identical differences from the translocon-based scale, such a coincidence seems unlikely. However, the importance of reaching convergence in the measured properties cannot be understated, and membranes in particular can be slow to equilibrate (Neale et al., 2011). Nonetheless, the results presented here demonstrate the utility of MD simulations for studying other spontaneous-insertion processes applicable to, e.g., the design of novel antimicrobial peptides.