State-dependent risk-taking

Abstract

Who takes risks, and when? The relative state model proposes two non-independent selection pressures governing risk-taking: need-based and ability-based. The need-based account suggests that actors take risks when they cannot reach target states with low-risk options (consistent with risk-sensitivity theory). The ability-based account suggests that actors engage in risk-taking when they possess traits or abilities that increase the expected value of risk-taking (by increasing the probability of success, enhancing payoffs for success or buffering against failure). Adaptive risk-taking involves integrating both considerations. Risk-takers compute the expected value of risk-taking based on their state—the interaction of embodied capital relative to one's situation, to the same individual in other circumstances or to other individuals. We provide mathematical support for this dual pathway model, and show that it can predict who will take the most risks and when (e.g. when risk-taking will be performed by those in good, poor, intermediate or extreme state only). Results confirm and elaborate on the initial verbal model of state-dependent risk-taking: selection favours agents who calibrate risk-taking based on implicit computations of condition and/or competitive (dis)advantage, which in turn drives patterned individual differences in risk-taking behaviour.

1. State-dependent risk-taking

Who engages in risk-taking, and under what conditions? Risk—exposure to outcome or payoff variance—is inherent in every domain of life. Such diverse behaviours as cooperation, conflict and aggression, resource acquisition, mating, parenting and harm avoidance (among many others) all involve exposure to outcome variance, in that such behaviours involve exposure to both potential benefits and potential costs. Two distinct functional accounts explain why individuals take risks: the need-based account posits that organisms take risks when they are desperate and risk-taking is the only way to meet a need (consistent with risk-sensitivity theory; [1–7]); the ability-based account predicts that risks will be taken by individuals who are in good condition (e.g. stronger, richer, more intelligent) and are thus more likely to succeed. Both accounts have received empirical validation, but often make opposing predictions (see [8,9]). In the following, we (i) briefly define risk, (ii) summarize evidence and theorizing that gives rise to need-based and ability-based accounts of risk-taking, (iii) describe the relative state model, which is a framework of state-dependent risk-taking that reconciles the two pathways to risk-taking, and (iv) present a mathematical formalization of state-dependent risk-taking, with the goal of providing a tool for deriving specific (and new) testable hypotheses for future research.

(a). Dual pathways to risk-taking: need-based and ability-based

Risk-taking is behaviour that exposes an agent to outcome or payoff variance (e.g. [4,5,10–12]). What dictates when agents are willing to expose themselves to relatively higher or lower variability in outcomes? Previous research and theorizing suggests that there are two pathways to risk-taking—need-based and ability-based—that reflect different patterns in the costs and benefits of exposure to variance.

Need-based risk-taking is derived from risk-sensitivity theory [1–5,7]. According to this framework, decision-makers favour risky options under conditions of high need, where need describes disparity between an individual's present state and their goal (or required) state [4,13]. Low-risk options often cannot provide sufficient benefits to meet extreme needs, so risk-taking allows for obtaining outcomes that might otherwise be unattainable. Accordingly, the need-based account predicts that risks will be taken by individuals who are in poor condition, especially if they are competitively disadvantaged (e.g. weaker, poorer, less intelligent, injured) and cannot compete through relatively low-risk means (reviewed in [8]).

A classic example of risk-sensitive decision-making is someone without money stealing bread to feed their hungry family—their need for food cannot be met through the low-risk option of purchasing food, so the riskier option of thievery offers the only possibility of meeting the need. Just as temporary disadvantage (e.g. starvation) favours temporarily escalated risk-taking (e.g. stealing food; exposing oneself to predation risk when foraging), chronic disadvantage can favour persistently escalated risk-taking. For example, life-course persistent offending describes a pattern of persistent antisocial behaviour across the lifespan that is a product of developmental adversity (e.g. from head trauma, poor developmental environments) leading to chronic need-based risk-taking (e.g. [14]).

The ability-based account of risk-taking suggests that organisms choose risky options when they possess abilities or traits that facilitate relatively higher expected payoffs for risky options (over lower-variance alternative behaviours). That is, the ability-based account predicts that risks will be taken by individuals who are in good condition (e.g. stronger, richer, more intelligent, healthier) and are thus more likely to succeed. One ability-based route to higher payoffs is from an increased likelihood of the risk succeeding. For example, larger organisms (or those with allies present) are more willing to risk injury in fights over resources because they are more likely to win (e.g. [15,16]). Another ability-based route to higher payoffs involves better ‘buffering’ against the downsides of failed risks; examples include ‘high rollers’ being willing to risk large sums of money in casino games where such losses would still be only a small fraction of their total wealth, or animals only foraging in variable patches when they have enough energy reserves such that they will not starve if the patch is empty [17,18]. A third ability-based route to higher payoffs is if the gains of a successful risk are higher for those who are in better condition; an example is males with high sperm count benefiting more from a successful mating than males with low sperm count, because the former have a higher chance of fertilizing the female's egg(s) (reviewed in [19]).

The ability-based account is also useful for understanding risk-taking as a costly signal of underlying traits, skills, resources or abilities that are relevant to others (e.g. [20–23]), allowing the risky agent higher payoffs in future social interactions. For example, observers might infer that someone who is always willing to fight must be a good fighter (otherwise, they would often get injured; [24]), or that someone who regularly gambles for high stakes must have access to a lot of money (e.g. [25]). These eager fighters and gamblers might then receive better treatment in future social encounters (e.g. deference to the fighters in resource contests; profitable social opportunities for the wealthy). That is, such agents receive an ability-based ‘revenue stream’ attributable to their investment in a risky display.

The need-based and ability-based accounts of risk-taking both describe functional logic: selection favours organisms taking risks when the expected inclusive fitness benefits outweigh the costs (e.g. [26]); the mechanisms underlying such calculations need not be conscious (e.g. [27,28]). However, the two accounts lead to different predictions about patterns of individual differences in risk-taking. The need-based account suggests risk-taking is a product of one's desperation, whereas the ability-based account suggests that risk-taking is a product of one's capabilities. Accordingly, the need-based account suggests that selection should favour an escalation of risky behaviour among poor-condition or competitively disadvantaged individuals, who are more likely to be in a state of need, whereas the ability-based account suggests that selection will favour more risky behaviour among good condition or competitively advantaged individuals whose abilities improve the expected payoffs of risky behaviour. Our goal is to formally model how these opposing selection pressures interact.

(b). State-dependent risk-taking: integrating need and ability-based accounts

Our first step towards modelling the relationship between condition and risky behaviour was the relative state model [8]. This verbal conceptual model begins with the straightforward functional premise that selection favours decision-making processes that result in risky behaviour when the (expected) benefits exceed the costs, then specifies two very different functional contingencies—the need-based and ability-based pathways—that select for risk-taking behaviour. The model described how both pathways hinge on a single concept of state, which represents a barometer of (dis)advantage for a particular individual relative to its particular environment. The model was originally conceptualized around direct or indirect competition (hence ‘relative’ state), but is easily generalized to situations far removed from direct competition (simply ‘state’).

One's state has two key inputs—embodied capital and situational factors. Embodied capital describes attributes inherent to an individual (e.g. health, intelligence, strength) plus social capital (e.g. alliances). These characteristics are sometimes referred to as one's ‘condition’ (e.g. [29–31]) or biological ‘quality’ (e.g. [32,33]). Situational factors describe aspects of one's environment that moderate the positive or negative effects conferred by embodied capital (i.e. environmental features which affect the relationship between condition and biological fitness). For example, physical strength confers a larger competitive advantage on a battlefield relative to in a classroom. Being full of calories (i.e. on a positive energy budget) is more important in food-poor environments or for individuals with a high metabolism [5,7].

Together, the interaction of one's own embodied capital and aspects of one's situation or environment give rise to an individual's state, which is an index of how (dis)advantaged one is in one's environment. One's state in turn influences four key parameters that determine the costs and benefits of risk-taking in any given circumstance: (i) the probability of successful versus unsuccessful risk-taking; (ii) the expected value (payoff) of successful risk-taking; (iii) the expected value (payoff) of unsuccessful risk-taking; and (iv) the expected value (payoff) of the non-risky or ‘safer’ option [8]. Importantly, one's state can be relative to one's circumstances, relative to alternate states within the same individual or relative to others. A starving individual, for example, is disadvantaged compared to that same individual with a full belly, and is more disadvantaged in food-poor environments than in food-rich environments. Anyone engaging in social conflict is advantaged when they are healthy and have allies, relative to that same individual injured or alone. In other words, ‘state’ can refer to a competitive (dis)advantage within direct competition, but can also apply to situations far removed from direct competition or comparison to rivals.

Advantages of our model of state-dependent risk-taking [8] include intuitive explanations of certain patterns of risk-taking (e.g. domain-specificity versus domain-generality of risk) and the ability to generate qualitative predictions of when risk-taking will be observed. However, like all verbal models, it is presently somewhat imprecise and/or vague in its operationalization. For example, the verbal model is useful for explaining broad patterns of individual differences in certain types of risk-taking as functions of need (e.g. anti-social risk-taking) or ability (e.g. non-anti-social risk-taking), but verbal reasoning falls short when attempting to apply the model towards analysing situations where both need and ability are relevant. In general, verbal models are useful for explanation, but much more limited for prediction. The purpose of the present examination is to provide a mathematical model that formalizes our previous verbal model, generalizes it to situations without direct competition or comparison and provides a means of generating precise and testable quantitative hypotheses under complex combinations of explicitly specified parameters.

(c). The general model

We model a decision between a high-variance ‘risky’ option that succeeds with probability p (with 0 ≤ p ≤ 1) and a zero-variance ‘safe’ option that can be thought of as sitting out the risk or as continuing a current behavioural trajectory. Expected fitness values are denoted by E. Not taking the risk (n) has an expected lifetime inclusive fitness value of E_n, successful (s) risk-taking has a value of E_s, and failing (f) at the risk has a value of E_f. We are only interested in cases where E_s ≥ E_n ≥ E_f, because scenarios where E_f > E_n or E_n > E_s unequivocally favour the risky option and the safe option, respectively. Let w_r and w_n be the payoffs associated with taking the risk versus not taking the risk, respectively, which are calculated as:

1.1

and

1.2

We want to quantify when the payoff for the risky option outweighs the payoff for the safe option, i.e. when w_r > w_n. Thus, the net expected fitness consequence for choosing the risky option over the safe option (henceforth the ‘benefits of risk-taking’) is:

1.3

Thus, when pE_s + (1 − p)E_f − E_n > 0, it pays to take the risk.

E_s, E_f, E_n and p will vary between individuals within a species based on interaction of embodied capital and situational factors—what we earlier defined as one's state—an index of how (dis)advantaged one is in a local fitness landscape (including relative to one's circumstances, to other individuals or to the same individual in a different state or condition) [8]. For example, some individuals will have high or low expected fitness without taking the risk (high or low E_n, respectively): their current trajectory is favourable or unfavourable for reasons such as current energy resources, already having a mate, or being healthier, stronger or more intelligent compared to competitors. Similarly, individuals will vary in how much success or failure will impact their fitness: some individuals may benefit greatly or very little from success (high or low E_s, respectively) or may have a high or low ‘buffer’ against failure such that their fitness is high or low if they fail at the risk (high or low E_f, respectively). Thus, these are all functions of one's state, which we denote as x: p(x), E_s(x), E_f(x) and E_n(x). We want to know if and how the benefits of risk-taking (r) vary with one's state (x); that is, whether the slope of r is positive or negative with respect to x. We do this by taking the partial derivative of r with respect to an organism's state, x; this involves using the product rule in calculus. The partial derivative is:

1.4

where ∂p/∂x is the slope of p with respect to x (i.e. how strongly the probability of success p is affected by one's state, x), and ∂E_s/∂x, ∂E_f/∂x and ∂E_n/∂x are the slopes of E_s, E_f and E_n with respect to x, respectively (i.e. how strongly one's state affects these payoffs). When the partial derivative ∂r/∂x is positive, the slope of r with respect to x is positive, which means that risk-taking pays off more for those in a favourable state. When ∂r/∂x is negative, the slope of r with respect to x is negative, such that risk-taking pays off more for those in a poor state. The values of the parameters will affect whether ∂r/∂x is positive or negative, which determines whether risk-taking pays off more for those in good versus poor state, and thus who is more likely to take the risk.

Risk-taking by those in good state is more likely to occur when:

• — the risk involves very high variance in outcome (high E_s−E_f) and those in good state are particularly likely to succeed at it (high ∂p/∂x); the importance of each of these factors depends on the other, such that high variance in outcomes is irrelevant if one's state does not affect success, and state-based probabilities of success are irrelevant for low-variance choices;¹

• — individuals in good state earn much more if they succeed than do individuals in poor state (high ∂E_s/∂x); these differential benefits for success become more important for risks with high baseline success rates (high p) because then more individuals succeed at the risks; and

• — individuals in good state suffer less from failure than do individuals in poor state (high ∂E_f/∂x); differential costs for failure become more important for risks with low baseline success rates (low p).

Each of the above conditions makes risks more likely to result in superior payoffs for individuals in favourable states (e.g. those who are competitively advantaged). By contrast, risks are more likely to result in superior payoffs for those in poor states (e.g. those who are competitively disadvantaged) when:

• — individuals in good state are on a much better ‘current trajectory’ by having much better-paying non-risky options (high ∂E_n/∂x).

The relative importance of these four effects will determine whether individuals in good state take more risks than individuals in poor state, or vice versa. We note that this model is very general and makes no assumptions about the shapes of p(x), E_s(x), E_f(x) and E_n(x). In the next section, we present an example of how this general model can be applied in a case where there are linear effects of risk-taking on fitness.

(d). Model application: linear effects

We can illustrate the general model above with a more specific model (below) that uses simple parameters and linear effects. In the following model, p is the probability of success, and s, f and n are the payoffs for succeeding, failing and not taking the risk, respectively. Here, we assume that each of these four parameters has a baseline level for an individual at zero state (e.g. an individual who is in the worst possible condition to be alive; someone who is extremely competitively disadvantaged) (p₀, s₀, f₀ and n₀) and a linear effect which determines how much that variable is affected by increasing state (p₁, s₁, f₁ and n₁), as follows:

• — probability of succeeding at the risk: p = p₀ + p₁x (individuals in good state have higher probability of success);

• — expected value if an agent succeeds: E_s = s₀ + s₁x (individuals in good state have higher benefits if they do succeed);

• — expected value if an agent fails: E_f = f₀ + f₁x (individuals in good state have a greater buffer against failure); and

• — expected value if an agent does not take a risk: E_n = n₀ + n₁x (individuals in good state have a better ‘current trajectory’ without the risk, i.e. more to lose if they take the risk and fail).

Inserting these values into the fitness function above (equation (1.3)), the benefits for taking risks (r), relative to no risks, becomes:

1.5

which we can rewrite as:

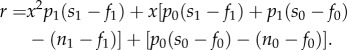1.6

Again, agents will take risks when r > 0. The function r results in a quadratic relationship of the form ax² + bx + c. This means that depending on the parameters, the payoff for risk-taking (relative to no risk) could be convex, concave, increasing monotonically or decreasing monotonically. As such, the result can be risk-taking by only those in good state, only those in poor state, intermediate-state individuals only, extremes only (i.e. very good and very poor state but not intermediates), no one or everyone, depending on how strongly state affects the probability of success (p₁), payoff from success (s₁), buffering against failure (f₁) and outside options without the risk (n₁).

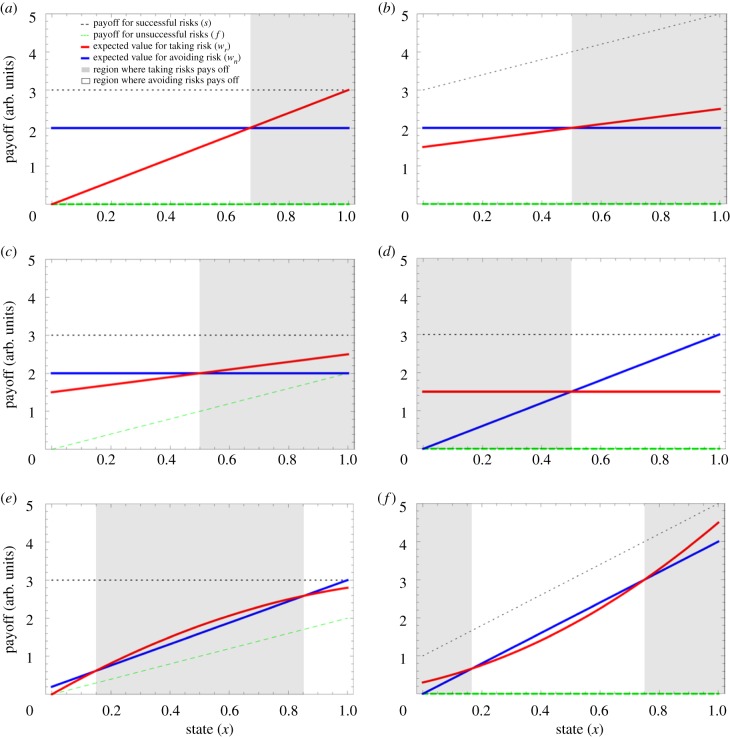
The electronic supplementary material, table S1 examines the conditions where individual differences can exist, and if they do exist, who tends to take risks; figure 1 graphs these modelled outcomes. In particular, when p₀(s₀−f₀) − (n₀−f₀) < 0, individuals in poor state avoid taking risks because they have something to lose (n₀) and either low probability of success (p₀) or gains from success (s₀). If anyone takes risks in that case, it is usually individuals in good state only (figure 1a–c), but can be individuals in intermediate state only if those in excellent state have much more to lose (high n₁) (figure 1e). By contrast, when p₀(s₀−f₀)−(n₀−f₀) > 0, individuals in poor state take risks because they have little to lose (low n₀), some gains from success (s₀) and some probability of succeeding (p₀). If anyone avoids risks in that case, it is usually individuals in relatively good state because they have more to lose (high n₁) (figure 1d). However, sometimes only intermediates avoid risks (i.e. risk-taking by extremes—very good and very poor states; figure 1f) because intermediates have something to lose (n₁), whereas those in excellent state have sufficiently high probability and payoffs for success (very high p₁ and s₁) to compensate for having more to lose. See the electronic supplementary material, table S1 for full conditions and rationales.

Figure 1.

Examples of state-dependent risk-taking. The lines represent: the payoff if one succeeds at the risk (black dotted line); the payoff if one fails at the risk (green dashed line); the payoff if one does not take the risk (thick blue line); and the expected value of taking the risk (thick red line) including one's probability of success versus failure. Individuals take risks (shaded region) if the expected payoff for risk-taking outweighs the payoff for non-risk-taking, i.e. when the red line is higher than the blue line. Risk-taking is performed only by individuals in: (a) good state (because of higher probability of success); (b) good state (because of higher benefits from success); (c) good state (because of higher buffer against failure); (d) poor state (because they have little to lose); (e) intermediate state (because individuals in poor state avoid risks because of having something to lose, little chance of success and little buffer against failure, whereas individuals in good state avoid risks because of little additional gains from risk); and (f) extremely poor and extremely good state (the former take risks because they have nothing to lose, the latter take risks because they have very high probability of success and extra gains if they succeed). The x-axis could represent different individuals in different states, or the same individual in different states. The parameters displayed are p₀ = 0.5, p₁ = 0, s₀ = 3, s₁ = 0, f₀ = 0, f₁ = 0, n₀ = 2 and n₁ = 0, except for changing the following: (a) p₀ = 0, p₁ = 1 (probabilities of success); (b) s₀ = 3, s₁ = 2 (payoffs if succeed); (c) f₀ = 0, f₁ = 2 (payoffs if fail); (d) n₀ = 0, n₁ = 3 (payoffs if avoid risk); (e) p₀ = 0, p₁ = 0.8, f₁ = 2, n₀ = 0.2 and n₁ = 2.8; and (f) p₀ = 0.3, p₁ = 0.6, s₀ = 1, s₁ = 4, n₀ = 0 and n₁ = 4.

We should note that risk-taking by individuals in good state (e.g. the relatively advantaged) alone or by individuals in poor state (e.g. the relatively disadvantaged) alone can arise under conditions that are easier to satisfy than risk-taking by intermediate- or extreme-state individuals alone. The former two situations require variation in one parameter alone, whereas the latter two situations require particular combinations of parameters. As such, we predict that the latter two conditions will be much rarer. Furthermore, risk-taking tends to pay much better or worse than risk-avoidance in the good-only and poor-only situations, whereas it tends to pay only slightly better or worse than risk-avoidance in the intermediate-only and extreme-only situations; organisms are less likely to detect such small payoff differences, making intermediate-only and extreme-only risk-taking less likely to arise.

2. Discussion

Natural selection should be expected to favour risk-taking by individuals in good state when their abilities facilitate high expected fitness returns on their investment, and by individuals in poor state when low-risk options cannot meet key fitness-relevant goals. Our general model of state-dependent risk-taking can help researchers understand how these competing selection pressures interact to determine which individuals take the most risks in various biological systems. The general form of the model is based on four parameters that affect the fitness payoffs of risk-taking behaviour: the probability of success versus failure, the expected value of success, the expected value of failure; and the expected value of the non-risky alternative. The general model makes no assumptions about the shape of the function between one's state and these four parameters, allowing for a broad understanding of how the four parameters interact to determine who takes the most risks.

The model suggests that risk-taking pays off more for individuals in good state (e.g. the relatively advantaged) when: (i) the advantaged are more likely to succeed at particularly high-variance risk-taking; (ii) the advantaged can expect higher expected values from success (if they succeed) compared to those who are disadvantaged; and (iii) the advantaged incur lower failure costs (if they fail) than those who are disadvantaged. The general model also predicts that individuals in poor state (e.g. the relatively disadvantaged) will take more risks than individuals in good state when the latter have much better non-risky options (e.g. advantaged individuals benefit from ‘staying the course’). Furthermore, the general model identifies conditions under which each of these factors are most important in determining who takes risks or when to do so.

We next made simple, reasonable linear assumptions about the specific relationship between one's state and each of the four parameters. This subsequent linear model revealed four categories of risk-state relationships that can emerge under various combination of parameters: risk-taking concentrated among (i) agents in good state (e.g. the relatively advantaged), (ii) agents in poor state (e.g. the relatively disadvantaged), (iii) those who are moderately (dis)advantaged but not extremely so, and (iv) those who are extremely (dis)advantaged (i.e. those who possess extremely good or extremely poor state) but not moderately so. The model also predicts the conditions under which each of these patterns will emerge. The mathematical combinations of parameters that produce these patterns can be translated back into intuitive concepts from familiar verbal models, e.g. ‘more likely to succeed’, ‘having more to lose’ and ‘having better outside options'. These four patterns will appear not only with linear functions of p(x), E_s(x), E_f(x) and E_n(x), but often also with more complex functions (e.g. quadratic, exponential). The linear assumptions were just one illustrative specification of the function shapes (which remained deliberately unspecified in the general model to increase generality). In fact, intermediate-only and extreme-only risk-taking are more likely to occur when these functions are nonlinear, such that steeper fitness curves occur.

The original relative state model proposed by Mishra et al. [26] suggests that there are dual, non-independent pathways to risk-taking: need-based and ability-based. The model further suggests that actors make decisions around their state, which includes a computation of competitive (dis)advantage within a particular pool of competition. The present mathematical model formalizes the predictions of the relative state model, generalizes it to situations without direct competition and provides further evidence of the use of the two-pathway model for explaining individual differences in risk-taking. In particular, the linear model reveals two possible patterns of risk-taking we did not predict in our previous verbal model: risk-taking by intermediates-only and risk-taking by extremes-only, and the types of conditions under which these patterns are expected to arise.

(a). Proximate currency conversions to fitness

Our model of state-dependent risk-taking is based on parameters that represent ultimate (fitness) costs and benefits. However, organisms do not necessarily directly make decisions around explicit fitness considerations (especially not humans); rather, individuals seek to optimize proxies of fitness—that is, outcomes or currencies that are (or were) associated with reproductive success and fitness (e.g. in the positive domain: mates, resources, status, reputation, calories, information; in the negative domain: illness, injury, low resources, low status) [4,17,18,26,34–37]. The equation by which proximate currencies are converted to fitness outcomes will necessarily vary based on a wide variety of situational factors and embodied factors.

There is substantial evidence indicating cross-taxa sex differences in risk-taking behaviour (e.g. [34,38–40]). The standard explanation for this phenomenon is that the sex facing higher reproductive variance (typically males) takes more risks, because the higher variance means that ‘big wins’ can be accessed via a ‘high risk/high reward’ strategy (reviewed in [34,41]). Such sex differences can be accounted for by modelling different functions for converting proximate currencies into ultimate reward, such that the marginal fitness benefit for an extra unit of any given fitness proxy (calories, mating opportunities) is greater for the sex with higher reproductive variance. For example, consider a species exhibiting extreme polygyny (e.g. elephant seals) such that males experience extremely high reproductive variance compared to females. In such a species, female fitness rises slightly with successful risk-taking, but not greatly so, because fitness proxies provide a smaller marginal fitness benefit (that is, competition is weaker among females). Also, the ‘non-risky’ payoff for females increases somewhat with better state (but not greatly so), such that there are few females desperate enough to take deadly risks and few benefits for doing so [41].

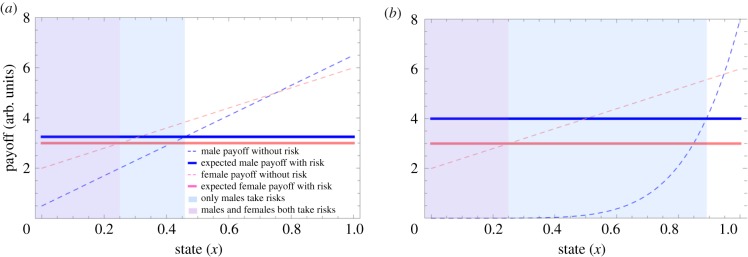
By contrast, male fitness can increase greatly with successful risk-taking: each unit of a fitness proxy provides high marginal fitness benefits because it makes a male more competitive, and competitiveness is crucial for reproductive success in highly polygynous systems (figure 2). In addition, the ‘non-risky’ payoff is low for all but the most competitively advantaged males (who have a very good ‘current trajectory’), such that all but the most securely dominant males benefit from taking dangerous risks to acquire such additional fitness proxies as additional calories, larger body size or weaponry or novel mating opportunities (e.g. attracting new mates). The logic of extreme polygyny extends to systems with milder polygyny, and our model allows us to compare different classes (e.g. males versus females) to see what proportion of each class will take risks and to predict how this varies with the level of monogamy versus polygyny (i.e. whether both sexes experience similar or different conversion of fitness proxies to actual fitness).

Figure 2.

Illustrative graphing of dangerous risk-taking by two classes (male: blue; female: pink) in: (a) a weakly polygynous system; and (b) a highly polygynous system. In both systems, males and females both have a 50% chance of succeeding at the risk (p_♂ = p_♀ = 0.5) and have zero fitness if they fail (E_f,♂ = E_f,♀ = 0). In both systems, a female's payoff without risk is somewhat affected by her state (E_n,♀ = 2 + 4x, dotted pink line); her maximum fitness is 6, obtainable either from being in the best possible state (x = 1) or from taking a successful risk (E_s,♀ = 6). Correspondingly, dangerous risk-taking is only worth it for the bottom 25% of females (pink shaded area) in both systems. Male payoffs are more variable than female payoffs, but to different degrees in the different systems. (a) In the weakly polygynous system, the maximum male fitness (6.5) and the benefits of a successful risk (E_s,♂ = 6.5) are slightly higher than for females, and one's state affects the non-risky payoff for males (E_n,♂ = 0.5 + 6x, dotted blue line) slightly more than females. Correspondingly, slightly more males than females have little to lose and something to gain—approximately 46% of males take dangerous risks (blue shaded area). (b) In the highly polygynous system, the maximum male fitness (8) and benefits of successful risk-taking (E_s,♂ = 8) are even higher, and one's state strongly affects the non-risky payoff for males such that males in poor state do not reproduce but males in very good state have disproportionately high fitness (E_n,♂ = 0 + 8x⁶, dotted blue line). Correspondingly, many males have little to lose and much to gain from taking dangerous risks, so almost 89% of males do so (blue shaded area). Intensifying the polygyny will exacerbate these sex differences further. In addition to examining sex differences, our state-dependent risk-taking model can be applied to any two (or more) classes, to predict what proportion of each class will take risks, and how this depends on the payoffs for risky and non-risky options in each class.

Threshold-based outcomes represent another broad class of conversion functions leading from proxies to fitness to actual fitness. Organisms who are disadvantaged because of low caloric reserves (i.e. in a negative energy budget; [6,7]) face a step function in the conversion of proximate calories into ultimate fitness: starving creatures must surpass a starvation threshold to have any chance at increasing their fitness. Risk-taking depends on how far from the threshold one is, and how much time remains to pass the threshold [17,18]. However, acquiring resources simply for survival is not enough; foraging animals must also pass another threshold to convert resources into actual reproductive success and fitness. So-called twin-threshold models have been constructed to address the issue of separate thresholds for survival and reproduction [42,43]. It would be interesting to examine how such thresholds would influence individual differences in risk-taking within the broader structure of the relative state model.

One example of where thresholds are useful is when investigating cooperation, which is often risky because one can help others yet receive no help in return. It is currently unclear whether cooperation will be performed by individuals in good state (because they have a better buffer against being ‘suckered’) or by individuals in poor state (because they are desperate enough that risky cooperation is their only chance at survival and reproduction). Our model of state-dependent risk-taking can solve this puzzle, especially when thresholds are included (e.g. sharing food to avoid a starvation threshold; [44,45]). Individuals will pursue risky cooperation if they are often below a threshold that successful cooperation could put them over, and will avoid risky cooperation if they are often just above a threshold that unsuccessful cooperation would put them below.

The exact functions that translate fitness proxies to fitness will vary for different proxies (e.g. calories versus status), different species, different classes within a species (e.g. sexes) and different environments. Furthermore, some failed risks are costlier than others [26]. A full discussion of the functions that govern the conversion of proxies of fitness into actual fitness in each system, and how they change over time, is beyond the scope of the present model. However, researchers who understand a particular system or species can approximate these functions to apply our model. For example, how is male fitness affected by status, body size or resources in a given species or culture—does it increase slightly, greatly, exponentially or not at all? Would a (un)successful risk have a large or small effect on fitness? Are individuals close to a threshold for survival or reproduction, and on what side are they currently? Even an approximation of these parameters is useful for generating predictions.

(b). Strengths and limitations

Unlike previous verbal models, our state-dependent mathematical model highlights key interactions between parameters of risk-taking and individual differences. Some parameters only affect who takes risks when other parameters are high; for example, buffering against failure matters most for risks that are intrinsically likely to fail, and the degree of outcome variance (E_s−E_f) only affects who takes risks when one's state affects the probability of success (and vice versa). Furthermore, our model unexpectedly revealed that under some conditions, risk-taking should be exclusively engaged in by individuals of intermediate competitive advantage; in other circumstances, risk is most incentivized for individuals who experience either extreme (but not moderate) competitive advantage or disadvantage. The former cases presumably model scenarios in which the logic of both ability-based and need-based pathways interact; it would be difficult to analyse such scenarios based only on intuition derived from a verbal model.

Like all models, ours is obviously a simplification. Our model quantified a single binary ‘succeed’ or ‘fail’ outcome, whereas real outcomes can have varying degrees of success, and are part of an ongoing series of decisions whose consequences extend beyond a single interaction. Other models of risk-taking (using stochastic dynamic modelling techniques) produce results interpretable as risk-taking ‘for survival’ versus risk-taking ‘as a luxury’ (i.e. poor-state desperation and good-state buffering; [17,18]). These similar results from different methods offer convergent evidence for the need-based and ability-based pathways to risk.

Real payoffs are measured in proxies of fitness (e.g. calories, mating opportunities), all of which translate to biological fitness via different functions (e.g. linear, sigmoid, threshold), as noted above. Furthermore, in social competitions, instead of ‘competitive advantage’ being a single scalar variable, it could be a vector of multiple qualities (e.g. attractiveness, strength, health, coalitional support; [46]) that are weighted differently in different social contexts. Future research examining these varied conversion functions would be illuminating. However, we do not anticipate that the basic findings will change in any meaningful way because our general model contains very few assumptions. Our model—although a simplification—can still help to generate quantitative predictions of who will take risks when. After all: ‘essentially, all models are wrong, but some are useful’ [47, p. 424].

Our model is based on functional cost–benefit analysis and should not be mistaken for a literal description of biological decision-making mechanisms. Evolved mechanisms do not perfectly execute functional logic; instead, natural selection produces heuristics or ‘rules of thumb’ that approximate the functional logic. One way to use such models to guide the study of mechanisms is to attempt to quantify the relevant functional parameters for one or more systems, compare the expected decisions of agents to actual decisions and analyse deviations. It is extremely challenging to operationalize fitness, especially with slow-reproducing organisms in field conditions, but one can still make directional predictions about how decision-making will change in response to relative changes in the relevant parameters.

3. Conclusion

The state-dependent risk-taking model helps predict who will take risks, and when. We have highlighted four factors that are affected by one's state and thus determine who takes risks, based on how much being in good or bad state results in: (i) a greater probability of success; (ii) higher payoffs if one does succeed; (iii) better buffering if one fails; and (iv) a better current trajectory without risk. The state-dependent model predicts the conditions under which risk-taking will be most prevalent among the advantaged only, disadvantaged only, intermediate-(dis)advantaged only and extremely (dis)advantaged only. It can also be used to compare two or more classes (e.g. males versus females) to predict the proportion of each class who takes risks, and how that varies with the degree of competition within each class (e.g. degree of polygyny).

Risk occurs in many domains of social life: cooperation, trust, foraging, status acquisition, aggression, mating, parenting, harm and disease avoidance, and more [48]; state-dependent risk-taking can predict who takes risks in any of these domains. Risk-taking should generalize across domains whenever one's state affects our four key parameters (p, E_s, E_f and E_n) in the same way across domains, and should be domain-specific whenever one's state affects those parameters differently in different domains [8]. We look forward to further research applying our state-dependent risk-taking model in each of these domains.

Data accessibility

This is a mathematical model and has no data.

Authors' contributions

P.B. conceived of the idea, created the model, wrote the analytical sections and led the project, S.M. and A.M.S. developed the ideas, contributed to the model and wrote introductory and discussion sections.

Competing interests

We declare we have no competing interests.

Funding

This work was funded by a Social Sciences and Humanities Research Council of Canada grant to P.B. (grant no. 430287). A.M.S. benefitted from the support of the US Air Force Office of Scientific Research (award FA9550-15-1-0137).