Antithetic proportional-integral feedback for reduced variance and improved control performance of stochastic reaction networks

Abstract

The ability of a cell to regulate and adapt its internal state in response to unpredictable environmental changes is called homeostasis and this ability is crucial for the cell's survival and proper functioning. Understanding how cells can achieve homeostasis, despite the intrinsic noise or randomness in their dynamics, is fundamentally important for both systems and synthetic biology. In this context, a significant development is the proposed antithetic integral feedback (AIF) motif, which is found in natural systems, and is known to ensure robust perfect adaptation for the mean dynamics of a given molecular species involved in a complex stochastic biomolecular reaction network. From the standpoint of applications, one drawback of this motif is that it often leads to an increased cell-to-cell heterogeneity or variance when compared to a constitutive (i.e. open-loop) control strategy. Our goal in this paper is to show that this performance deterioration can be countered by combining the AIF motif and a negative feedback strategy. Using a tailored moment closure method, we derive approximate expressions for the stationary variance for the controlled network that demonstrate that increasing the strength of the negative feedback can indeed decrease the variance, sometimes even below its constitutive level. Numerical results verify the accuracy of these results and we illustrate them by considering three biomolecular networks with two types of negative feedback strategies. Our computational analysis indicates that there is a trade-off between the speed of the settling-time of the mean trajectories and the stationary variance of the controlled species; i.e. smaller variance is associated with larger settling-time.

1. Introduction

The design and implementation of artificial in vivo biomolecular controllers has gained significant recent interest [1–6] due to their potential applications for the tight and robust control of gene expression [1], the optimization of metabolic networks for the efficient production of biomolecules [7,8], or the development of new treatments for certain genetic diseases [9]. Indeed, many of the instances of those problems can be interpreted from an homeostatic point of view in the sense that they may all be solved by achieving or restoring homeostasis in the corresponding genetic network using synthetic regulatory circuits [1,7–10]. In this regard, those problems essentially reduce to the design and the implementation of robust and reliable regulatory circuits that can optimize an inefficient network or correct a malfunctioning one—an observation which strongly suggests that ideas from control theory and control engineering [11] could be adapted to biochemical control problems [1,12–14]. A cornerstone in control theory and engineering is the so-called integral controller that can ensure precise constant set-point regulation for a regulated variable in a given system. Such a mechanism, where the action onto the controlled system depends on the integral of the deviation of the regulated variable from the desired set-point, is to be contrasted with the so-called proportional controller where the system is simply actuated proportionally to the deviation of the regulated variable from the desired set-point. Unlike integral control, the latter strategy is unable to achieve robust constant set-point regulation for the controlled variable and to reject constant disturbances. In other words, integral control has the capacity for ensuring perfect adaptation for the regulated variable. The downside, however, is that it may have a destabilizing effect on the dynamics (emergence of oscillations or even diverging trajectories) of the overall controlled system. This may be remedied by adjoining a proportional action, thus giving rise to the so-called proportional-integral (PI) controller [15].

Motivated by the above, an integral controller referred to as the antithetic integral controller was proposed in [1] for the control of the mean level of some molecular species of interest in a given biochemical reaction network. This controller requires a pair of species that exhibit stoichiometric inactivation. Such pairs have been reported and include toxin/antitoxin [16,17], sigma factor/anti-sigma factor [5,18], mRNA/antisense RNA [19] and scaffold/anti-scaffold [20], among others. Using the antithetic integral feedback motif [1,6] has recently presented the first rationally designed integral feedback control system in a living cell and demonstrated its robust perfect adaptation properties.

Even if this motif was proposed in [1] as a potential synthetic controller, it is now well understood that this motif is also naturally present in endogenous networks [1,21,22] where sequestration is involved, which makes it very important from a systems biology point of view. Understanding this network better will bring some new light on biological regulation mechanisms. A very important feature of this network is that it is fully functional in noisy environments and, hence, in the low copy number regime, which is of fundamental importance as cells often involve low molecular counts. It was notably shown that, under some reasonable conditions, the ergodicity properties of the controlled network are independent of the parameters of the antithetic integral controller—a surprising key property that has no counterpart in the deterministic setting and that dramatically simplifies its implementation. A drawback, however, is the increase of the stationary variance of the regulated species compared with the constitutive variance that would be obtained by using a static open-loop strategy, even though the latter one would be unable to ensure regulation and perfect adaptation for the mean level of the regulated species. This phenomenon is seemingly analogous to the destabilizing behaviour of the deterministic integral controller mentioned in the previous paragraph. This variance increase can hence be interpreted as the price to pay for perfect adaptation at the mean species level.

The goal of this paper is to investigate the effect of adding a negative feedback to the antithetic integral motif in a way akin, yet different, to deterministic PI controllers. As discussed above, adding a proportional action in the deterministic setting compensates for the destabilizing effect of the integrator. Comparatively, it may seem reasonable to think that, in the stochastic setting, a proportional action could have an analogous effect and would result in a decreased variance for the controlled variable (this is, for instance, what happens when considering certain linear systems driven by white noise). In fact, it has been shown that negative feedback at a transcriptional level in a gene expression network leads to a variance reduction in the protein levels; e.g. [23–26] and references therein. In this regard, it would be interesting to verify whether in endogenous networks implementing an antithetic integral feedback structure a negative feedback loop is present and whether knocking it down would lead to a variance increase in the controlled species.

Two types of negative feedback are considered in the present paper: the first one consists of an ON/OFF proportional action whereas the second one is governed by a repressing Hill function. First, we theoretically prove using a tailored moment closure method that, in a gene expression network controlled with an antithetic integral controller, the stationary variance in the protein copy number can be decreased by the use of a negative feedback. In this specific case, the steady-state variance is decreasing monotonically as a function of the strength of the negative feedback. An immediate consequence is that it is theoretically possible to set the steady-state variance to a level that lies below the constitutive steady-state variance, which is the value of the steady-state variance that would have been obtained using a constitutive (i.e. open-loop) control strategy. The theoretical prediction will also be observed by exact numerical predictions using Gillespie's algorithm (Stochastic Simulation Algorithm (SSA) [27]). A caveat, however, is that setting the gain of the negative feedback very high will likely result in a very low steady-state variance but may also result in a regulation error for the mean of the controlled species and in a loss of ergodicity for the overall controlled network. In this regard, reducing the steady-state variance below its constitutive level may not always be physically possible. Finally, it is also emphasized that a low stationary variance for the controlled species is often associated with higher settling-time for the controlled species. Hence, there is a trade-off between variability and fast dynamics/small settling-time. The two negative feedback actions also exhibit quite different behaviours. Indeed, while the ON/OFF proportional feedback seems to be efficient at reducing the stationary variance through an increase of its gain, the dynamics of the mean gets first improved by reducing the settling-time but, after the gain goes beyond a certain threshold, the settling-time gets dramatically deteriorated by the appearance of a fast initial transient phase followed by a very slow final one resulting then in a high settling-time. On the other hand, the Hill controller leads to very homogeneous mean dynamics for different feedback strength but the steady-state variance is also much less sensitive and does not vary dramatically. It is proposed that those differences may find an explanation by the presence of zeros in the dynamics. Another possible reason is that the effective proportional gain (which will be denoted by β) is much less sensitive to changes in the feedback strength for the Hill controller than for the ON/OFF controller.

Approximate equations for the stationary variance are then obtained in the general unimolecular network case. The obtained expressions shed some light on an interesting connection between the covariances of the molecular species involved in the stochastic reaction network and the stability of a deterministic linear system controlled with a standard PI controller, thereby unveiling an unexpected, yet coherent, bridge between the stochastic and deterministic settings. Applying this more general framework to the a gene expression network with protein maturation allows one to reveal that the steady-state variance may not be necessarily a monotonically decreasing function of the negative feedback strength. In spite of this, the same conclusions as in the gene expression network hold: the variance can sometimes be decreased below its constitutive level but this may also be accompanied with a loss of ergodicity. The same qualitative conclusions for the transient of the mean dynamics and the properties of the controller also hold in this case.

Even though the proposed theory only applies to unimolecular networks, stochastic simulations are performed for a gene expression network with protein dimerization; a bimolecular network. Once again, the same conclusions as in for previous networks hold with the difference that the constitutive variance level is unknown in this case due to openness of the moment equations. These results tend to suggest that negative feedback seems to operate in the same way in bimolecular networks as in unimolecular networks.

Table 1.

Notation.

Xi, i = 1, …, d	ith species of the controlled reaction network
K	number of reactions in the controlled reaction network
, i = k, …, K	kth reaction of the controlled reaction network
S	stoichiometric matrix of the controlled reaction network
λ( · )	vector of propensity functions of the controlled reaction network
X1	actuated species
Xℓ	controlled species
Zi, i = 1, 2	ith species of the antithetic reaction network
k	actuation reaction rate
η	comparison reaction rate
θ	measurement reaction rate
μ	reference reaction rate
Kp	feedback strength of the negative feedback
β	effective feedback strength of the negative feedback

1.1. Reaction networks

Let us consider a stochastic reaction network involving d molecular species X₁, …,X_d interacting through K reaction channels defined as

1.1

where is the reaction rate parameter of the propensity function λ_k of the mass-action kinetics reaction which is given by (note that this expression is always well defined due to terms cancellation in the numerator and denominator) and are the source/product complex of the reaction . The corresponding stoichiometric vector is hence given by indicating that when this reaction fires, the state jumps from x to x + ζ_k. The stoichiometric matrix of this reaction network is defined as S: = [ζ₁ … s ζ_K]. Note that the reaction rates ρ_k are not necessarily constants but are also allowed to be functions of the state of the network. Under the well-mixed assumption, the above network can be described by a continuous-time Markov process (X₁(t), …, X_d(t))_t≥0 with the d-dimensional non-negative lattice as state space; see [28].

1.2. The regulation/perfect adaptation problems and antithetic integral control

Let us consider here a stochastic reaction network . The regulation problem consists of finding another reaction network (i.e. a set of additional species and additional reactions) interacting with in a way that makes the interconnection well behaved (i.e. ergodic) and such that the mean of some molecular species X_ℓ for some given ℓ ∈ {1, …, d} converges to a desired set-point (given here by μ/θ for some μ, θ > 0) in a robust way; i.e. irrespective of the values of the parameters of the network .

It was shown in [1] that, under some assumptions on the network and the fact that the species X_ℓ can be produced from X₁ through a sequence of reactions, the antithetic integral controller defined as

1.2

solves the above regulation problem. This regulatory network consists of two additional species Z₁ and Z₂, and four additional reactions. The species Z₁ is referred to as the actuating species as it is the species that governs the rate of the actuation reaction which produces the actuated species X₁ at a rate proportional to Z₁. The species Z₂ is the sensing species as it is produced at a rate proportional to the controlled species X_ℓ through the measurement reaction. The first reaction is the reference reaction as it encodes part of the set-point μ/θ whereas the third reaction is the comparison reaction that compares the population of the controller species and annihilates them accordingly, thereby closing negatively the loop while, and at the same time correlating the populations of the controller species. The comparison (or titration) reaction is the crucial element of the above controller network and, to realize such a reaction, one needs to rely on intrinsic strongly binding properties of certain molecules such as sigma- and anti-sigma-factors [1] or small RNAs and RNAs [3,29,30]. An illustration of the interconnection of the controlled network and the antithetic integral controller is depicted in figure 1.

Figure 1.

A reaction network controlled with an antithetic integral controller.

1.3. Variance amplification in antithetic integral control

We discussed above about the convergence properties of the mean level of the controlled species X_ℓ when network is controlled with the antithetic integral controller (1.2). However, it was remarked in [1] that while the mean of X_ℓ converges to the desired steady state, the stationary variance of the controlled species could be much larger than its constitutive value that would be obtained by simply considering a naive constitutive production of the species X₁ that would lead to the same mean steady-state value μ/θ. This was interpreted as the price to pay for having the perfect adaptation property for the controlled species. To illustrate this phenomenon, let us consider the following gene expression network:

1.3

where X₁ denotes mRNA and X₂ denotes protein. The objective here is to control the mean level of the protein by acting at a transcriptional level using the antithetic controller (1.2); hence, we set k_r = kZ₁. Using a tailored moment closure method, it is proved in the electronic supplementary material, Section S2, that the stationary variance Var^I_π(X₂) for the protein copy number is approximately given by the following expression

1.4

The rationale for the assumption k/η ≪ 1 is that it allows for closing the moments equation (which is open because of the presence of the comparison reaction) and obtain a closed-form solution for the stationary variance. On the other hand, the constitutive (i.e. open-loop) stationary variance Var^OL_π(X₂) for the protein copy number obtained with the constitutive strategy

1.5

is given by

1.6

It is immediately seen that the ratio

1.7

is greater than 1 for all k, θ > 0 such that the denominator is positive. Note that the above formula is not valid when k = 0 or θ = 0 since this would result in an open-loop network for which set-point regulation could not be achieved. This expression is also a monotonically increasing function of the gain k, a fact that was numerically observed in [1]. This means that choosing very small k will only result in a small increase of the stationary variance of the controlled species when using an antithetic integral feedback. However, this will very likely result in very slow dynamics for the mean of the controlled species.

Finally, it is important to stress that while this formula is obviously not valid when the denominator is non-positive, we know from [1] that in the case of the gene expression network, the closed-loop network will be ergodic with converging first- and second-order moments for all k > 0 and all θ > 0 (assuming that the ratio μ/θ is kept constant). This inconsistency stems from the fact that the proposed theoretical approach relies on a tailored moment closure approximation that will turn out to be connected to the Hurwitz stability of a certain matrix that may become unstable when the gain k of the integrator is too large. This will be elaborated more in the following sections.

1.4. Negative feedback action

We will consider in this paper two types of negative feedback action. The first one, referred to as the ON/OFF proportional feedback, is essentially theoretical and cannot be exactly implemented, but it may be seen as a local approximation of some more complex (e.g. nonlinear) repressing function. It is given by the reaction

1.8

together with the propensity function where K_p is the so-called feedback gain/strength. It is similar to the standard proportional feedback action used in control theory with the difference that a regularizing function, in the form of a max function, is involved in order to restrict the propensity function to non-negative values. Note that this controller can still be employed for the in silico control of single-cells using a stochastic controller as, in this case, we would not be restricted any more to mass-action, Hill or Michaelis–Menten kinetics. This was notably considered in the case of in silico population control in [31–33].

The second type of negative feedback action, referred to as the Hill feedback, consists of reaction (1.8) but involves the non-cooperative repressing Hill function F(X_ℓ) = K_p/(1 + X_ℓ) as a propensity function. This type of negative feedback is more realistic as such functions have empirically been shown to arise in many biochemical, physiological and epidemiological models (e.g. [34]).

In both cases, the total rate of production of the molecular species X₁ can be expressed as the sum kZ₁ + F(X_ℓ), which means that, at stationarity, we need to have that , where u* is equal to the value of the constitutive (i.e. deterministic) production rate for X₁ for which we would have that . Noting now that for both negative feedback functions, we will necessarily have that , then this means that if the gain K_p is too large, it may be possible that the mean of the controlled species does not converge to the desired set-point implying, in turn, that the overall controlled network will fail to be ergodic. This will be notably the case when . In particular, on the basis of theorem 2 in [1], a very conservative sufficient condition for the closed-loop network to be ergodic when is that K_p < u*/μ whereas it becomes K_p < u* when F(X_ℓ) = K_p/(1 + X_ℓ). These conditions can be determined by considering the worst-case mean value of the negative feedback strategies, i.e. K_pμ and K_p, respectively.

2. Results

2.1. Invariants for the antithetic integral controller

We describe some important invariant properties of the antithetic integral controller (1.2) which are independent of the parameters of the controlled network under the assumption that these invariants exist, i.e. they are finite. Those invariants, proved in the electronic supplementary material, are given by

2.1

2.2

2.3

2.4

and they play an instrumental role in proving all the theoretical results of the paper. Interestingly, we notice that , which seems rather coincidental. From the second invariant we observe that, if η ≫ μ, then , which indicates that the values taken by the random variable Z₂(t) will most of the time be equal to 0. Note that Z₁(t) cannot be taking zero values since Z₁ is the actuating species whose mean must be non-zero (assuming here that the natural production rates of the molecular species in the controlled network are small). Similarly, setting η large enough in the third expression will lead to a similar conclusion. Note that is independent of η here and only depends on the set-point μ/θ, the integrator gain k and the parameters of the network which is controlled. The last expression again leads to similar conclusions. Indeed, if η is sufficiently large, then and, hence, which implies that Z₂(t) needs to be most of the time equal to 0. These properties will be at the core of the moment closure method used to obtain an approximate closed-form formula for the covariance matrix for the closed-loop network.

2.2. An approximate formula for the stationary variance of the controlled species

Let us assume here that the open-loop network is mass-action and involves, at most, unimolecular reactions. Hence, the vector of propensity functions can be written as

2.5

for some non-negative matrix and non-negative vector . It is proved in the electronic supplementary material, Section S3, that, under the assumption k/η ≪ 1, we can overcome the moment closure problem arising from the presence of the comparison reaction in the antithetic controller and show that the exact stationary covariance matrix of the network given by

is approximatively given by the matrix Σ solving the Lyapunov equation

2.6

where

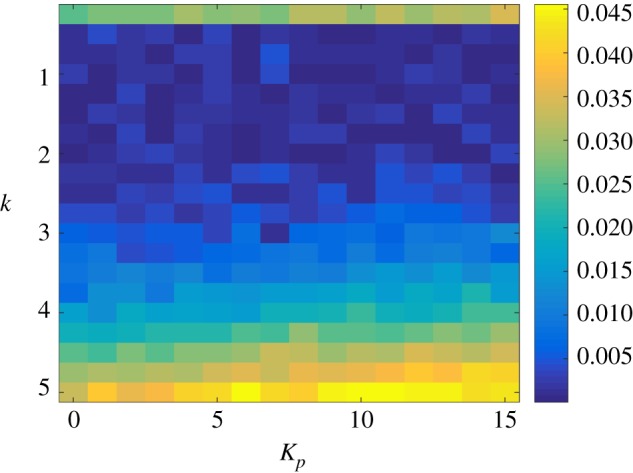
and {e_j}^N_j=1, for some positive natural number N, stands for the natural basis for 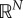. Note that since the function F is decreasing then the effective proportional gain, β, is always a positive constant and seems to mostly depend on K_p but does not seem to change much when k varies (e.g. electronic supplementary material, figures S1 and S2). It can also be seen that for the Lyapunov equation to have a positive definite solution, we need the matrix R to be Hurwitz stable; i.e. all its eigenvalues have negative real parts. In parallel with that, it is known from the results in [1] that the closed-loop network will remain ergodic when β = 0 even when the matrix R is not Hurwitz stable. In this regard, the formula (2.6) can only be valid when the parameters β and k are such that the matrix R is Hurwitz stable. When this is not the case, the formula is out its domain of validity and is meaningless. The stability of the matrix R is discussed in more detail in the electronic supplementary material, Section S4.

2.3. Connection to deterministic proportional-integral control

Interestingly, the matrix R coincides with the closed-loop system matrix of a deterministic linear system controlled with a particular proportional-integral controller. To demonstrate this fact, let us consider the following linear system

2.7

where x is the state of the system, u is the control input and y is the measured/controlled output. We propose to use the following PI controller in order to robustly steer the output to a desired set-point μ/θ

2.8

where θ is the sensor gain, β/θ is the proportional gain and k is the integral gain. The closed-loop system is given in this case by

2.9

where we can immediately recognize the R matrix involved in the Lyapunov equation (2.6).

2.4. Example: gene expression network

We present here the results obtained for the gene expression network (1.3) using the two negative feedback actions. In particular, we will numerically verify the validity of the formula (1.4) and study the influence of the controller parameters on various properties of the closed-loop network. The matrix R is given in this case by

2.10

It can be shown that the above matrix is Hurwitz stable (i.e. all its eigenvalues are located in the open left half-plane) if and only if the parameters k, β > 0 satisfy the inequality

2.11

Hence, given k > 0, the matrix R will be Hurwitz stable for any sufficiently large β > 0 illustrating the stabilizing effect of the proportional action. When the above condition is met, then the closed-loop stationary variance Var^PI_π(X₂) of the protein copy number is approximately given by the expression

2.12

For any fixed k > 0 such that (2.11) is satisfied, the closed-loop steady-state variance is a monotonically decreasing function of β. As a consequence, there will exist a β_c > 0 such that

2.13

for all β > β_c. In particular, when β → ∞, then we have that

2.14

We now analyse the results obtained with the antithetic integral controller combined with an ON/OFF proportional feedback. The first step is the numerical comparison of the approximate formula (2.12) with the stationary variance computed using 10⁶ SSA simulations with the parameters k_p = 2, γ_r = 2, γ_p = 7, μ = 10, θ = 2 and η = 100. The absolute value of the relative error between the exact and the approximate stationary variance of the protein copy number for several values for the gains k and K_p is depicted in figure 2. We can observe there that the relative error is less than 15% except when k is very small where the relative error is much larger. However, in this latter case, the mean trajectories do not have time to converge to their steady state value and, therefore, what is depicted in the figure for this value is not very meaningful. In spite of that, we can observe that the approximation is reasonably accurate.

Figure 2.

Absolute value of the relative error between the exact stationary variance of the protein copy number and the approximate formula (2.12) when the gene expression network is controlled with the antithetic integral controller (1.2) and an ON/OFF proportional controller. (Online version in colour.)

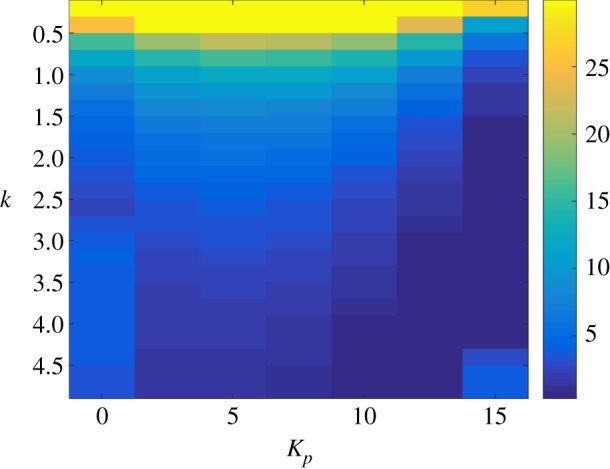
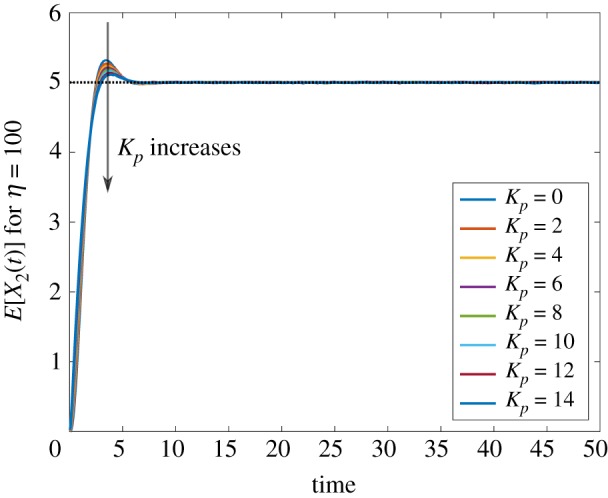
We now look at the performance of the antithetic integral controller combined with an OF/OFF proportional feedback. Figure 3 depicts the trajectories of the mean protein copy number while figure 4 depicts the trajectories of the variance of the protein copy number, both in the case where k = 3. Regarding the mean copy number, we can observe that while at the beginning increasing K_p seems to improve the transient phase, then the dynamics gets more and more abrupt at the start of the transient phase as the gain K_p continues to increase and gets slower and slower at the end of the transient phase, making the means very slow to converge to their set-point. On the other hand, we can see that the stationary variance seems to be a decreasing function of the gain K_p. More interestingly, when the gain K_p exceeds 20, the stationary variance becomes smaller than its constitutive value, which is equal to 6.1111. Figure 5 helps at establishing the influence of the gains k and K_p onto the stationary variance of the protein copy number. We can see that for any k, increasing K_p reduces the stationary variance while for any K_p, reducing k reduces the variance, as predicted by the approximate formula (2.12). Hence, a suitable choice would be to pick k small and K_p large. We now compare this choice for the parameters with the one that would lead to a small settling-time for the mean dynamics (figure 6). We immediately see that a small k is not an option if one wants to have fast mean dynamics. A sweet spot in this case would be around the right-bottom corner where the settling-time is the smallest. Interestingly, the variance is still at a quite low level even if sometimes higher than the constitutive value.

Figure 3.

Mean trajectories for the protein copy number when the gene expression network is controlled with the antithetic integral controller (1.2) with k = 3 and an ON/OFF proportional controller. The set-point value is indicated as a black dotted line. (Online version in colour.)

Figure 4.

Variance trajectories for the protein copy number when the gene expression network is controlled with the antithetic integral controller (1.2) with k = 3 and an ON/OFF proportional controller. The stationary constitutive variance is equal to 6.1111 and is depicted in black dotted line. (Online version in colour.)

Figure 5.

Stationary variance for the protein copy number when the gene expression network is controlled with the antithetic integral controller (1.2) and an ON/OFF proportional controller. (Online version in colour.)

Figure 6.

Settling-time for the mean trajectories for the protein copy number when the gene expression network is controlled with the antithetic integral controller (1.2) and an ON/OFF proportional controller. (Online version in colour.)

We now perform the same analysis for the antithetic integral controller combined with the Hill feedback and first verify the accuracy of the approximate formula (2.12). We can observe in figure 7 that the formula is very accurate in this case. To explain this, it is important to note that the gain K_p in both controllers are not directly comparable, only the values for the parameter β are. For identical K_p's, the value of β for the ON/OFF proportional feedback is much larger than for the Hill feedback (electronic supplementary material, figure S1 and S2). Figures 2 and 7 together simply say that the formula is very accurate when β is small.

Figure 7.

Absolute value of the relative error between the exact stationary variance of the protein copy number and the approximate formula (2.12) when the gene expression network is controlled with the antithetic integral controller (1.2) and a Hill controller. (Online version in colour.)

We now look at the performance of the antithetic integral controller combined with a Hill feedback. Similarly to previously, figure 8 depicts the trajectories of the mean protein copy number while figure 9 depicts the trajectories of the variance of the protein copy number, both for the case k = 3. Regarding the mean copy number, we can observe than the dynamics are much more homogeneous than in the previous case and that increasing K_p reduces the overshoot and, hence, the settling-time. This can again be explained by the fact that β is much smaller in this case. Similarly, the spread of the variances is much tighter than when using the other negative feedback, again because of the fact that β is small in this case. This homogeneity is well illustrated in figures 10 and 11 where we conclude the existence of a clear trade-off between settling-time and stationary variance.

Figure 8.

Mean trajectories for the protein copy number when the gene expression network is controlled with the antithetic integral controller (1.2) with k = 3 and a Hill controller. The set-point value is indicated as a black dotted line. (Online version in colour.)

Figure 9.

Variance trajectories for the protein copy number when the gene expression network is controlled with the antithetic integral controller (1.2) with k = 3 and a Hill controller. The stationary constitutive variance is depicted in black dotted line. (Online version in colour.)

Figure 10.

Stationary variance for the protein copy number when the gene expression network is controlled with the antithetic integral controller (1.2) and a Hill controller. (Online version in colour.)

Figure 11.

Settling-time for the mean trajectories for the protein copy number when the gene expression network is controlled with the antithetic integral controller (1.2) and a Hill controller. (Online version in colour.)

As can been seen in figures 3 and 8, the mean dynamics are quite different and it would be interesting to explain this difference in terms of control theoretic ideas. A first explanation lies in the sensitivity of the parameter β in terms of the feedback strength K_p. In the case of the ON/OFF proportional feedback, this sensitivity is quite high, whereas it is very low in the case of the Hill feedback (electronic supplementary material, figures S1 and S2). This gives an explanation of why the mean trajectories are very different in the case of the ON/OFF proportional feedback for different values of K_p while the mean trajectories are very close to each other in the case of the Hill feedback. A second explanation lies in the type of feedback in use. Indeed, the ON/OFF proportional feedback is an error-feedback and, when combined with the antithetic integral controller, may introduce a stable zero in the mean dynamics. On the other hand, the Hill feedback is an output-feedback that does not seem to introduce such a zero. When increasing the negative feedback gain K_p, this zero moves towards the origin. Once very close to the origin, this zero will have an action in the closed-loop mean dynamics that is very close to a derivative action, leading to abrupt initial transient dynamics. A theoretical basis for this discussion is developed in more detail in the electronic supplementary material, Section S5 and Section S6.

2.5. Example: gene expression network with protein maturation

The results obtained in the previous section clearly only hold for the gene expression network and it would be quite hasty to directly generalize those results to more complex unimolecular networks. Hence, this motivates the consideration of a slightly more complicated example, namely, the gene expression network involving a protein maturation reaction given by

2.15

where, as before, X₁ denotes mRNA, X₂ denotes protein and, now, X₃ denotes the mature protein. In this case, the goal is to control the average mature protein copy number by, again, acting at a transcriptional level. As this network is still unimolecular, the proposed framework remains valid. In particular, the matrix R is given by

2.16

and is Hurwitz stable provided that the two following conditions are satisfied

2.17

and

2.18

where

2.19

Considering, for instance, the following parameters k_p = 1, γ_r = 2, γ_p = 1, k′_p = 3, γ ′_p = 1, μ = 10, θ = 2 and η = 100, the above conditions reduce to

2.20

and

2.21

The intersection of these conditions yield the stability conditions

2.22

It can be verified that for values on the boundary of at least one of those intervals, the matrix R has eigenvalues on the imaginary axis. Standard calculations on the moments equation show that the open-loop variance is given by

2.23

With the numerical values for the parameters previously given, the open-loop variance is approximately equal to . The closed-loop variance, however, is approximately given by

2.24

where

2.25

and

2.26

An expression that is more complex than, yet very similar to, formula (2.12) obtained for the simple gene expression network. For the considered set of parameter values, the approximated variance is a non-monotonic function of the parameter β as can be theoretically observed in the electronic supplementary material, S3. It turns out that this behaviour can also be observed in the numerical simulations depicted in the electronic supplementary material, figure S5, where we can see that the variance exhibits this non-monotonic behaviour. However, it should also be pointed out that the increase of K_p is accompanied by the emergence of a tracking error for the mean dynamics (electronic supplementary material, figure S5) and a loss of ergodicity for the overall controlled network as emphasized by diverging mean dynamics for the sensing species (electronic supplementary material, figure S7). This contrasts with the gene expression case where the variance was a monotonically decreasing function of β. Note, however, that this non-monotonic behaviour is not observed on figure 13 for the considered range of values for K_p. Regarding the mean dynamics, we can see that increasing K_p and, hence, β, to reasonable levels improves the settling-time as depicted in figure 12 for the special case of k = 3. However, this is far from being the general case since the settling-time can exhibit quite complex behaviour for this network (figure 14). The stationary variance depicted in figure 15 exhibits here a rather standard and predictive behaviour where a small k and a large K_p both lead to its reduction. Similar conclusions can be drawn when the network is controlled with a Hill negative feedback controller (electronic supplementary material, figure S8–S11).

Figure 13.

Variance trajectories for the mature protein copy number when the gene expression network with protein maturation is controlled with the antithetic integral controller (1.2) with k = 3 and an ON/OFF proportional controller. The stationary constitutive variance is depicted in black dotted line. (Online version in colour.)

Figure 12.

Mean trajectories for the mature protein copy number when the gene expression network with protein maturation is controlled with the antithetic integral controller (1.2) with k = 3 and an ON/OFF proportional controller. The set-point value is indicated as a black dotted line. (Online version in colour.)

Figure 14.

Settling-time for the mean trajectories for the mature protein copy number when the gene expression network with protein maturation is controlled with the antithetic integral controller (1.2) and an ON/OFF proportional controller. (Online version in colour.)

Figure 15.

Stationary variance for the mature protein copy number when the gene expression network with protein maturation is controlled with the antithetic integral controller (1.2) and an ON/OFF proportional controller. (Online version in colour.)

2.6. Example: gene expression network with protein dimerization

The proposed theory is only valid for unimolecular networks but, in spite of that, it is still interesting to see whether similar conclusions could be obtained for a network that is not unimolecular. This motivates the consideration of the following gene expression network with protein dimerization:

2.27

where, as before, X₁ denotes mRNA, X₂ denotes protein but, now, X₃ denotes a protein homodimer. In this case, the Lyapunov equation (2.6) is not valid any more because of the presence of the dimerization reaction but we can still perform stochastic simulations. The considered parameter values are given by k_p = 1, γ_r = 2, γ_p = 1, k_d = 3, γ_d = γ_d′ = 1, μ = 10, θ = 2 and η = 100. We can see in figures 16–19 as well as in the electronic supplementary material, figures S12–S15, that similar conclusions hold.

Figure 17.

Variance trajectories for the homodimer copy number when the gene expression network with protein dimerization is controlled with the antithetic integral controller (1.2) with k = 3 and an ON/OFF proportional controller. (Online version in colour.)

Figure 18.

Stationary variance for the homodimer copy number when the gene expression network with protein dimerization is controlled with the antithetic integral controller (1.2) and an ON/OFF proportional controller. (Online version in colour.)

Figure 16.

Mean trajectories for the homodimer copy number when the gene expression network with protein dimerization is controlled with the antithetic integral controller (1.2) with k = 3 and an ON/OFF proportional controller. The set-point value is indicated as a black dotted line. (Online version in colour.)

Figure 19.

Settling-time for the mean trajectories for the homodimer copy number when the gene expression network with protein dimerization is controlled with the antithetic integral controller (1.2) and an ON/OFF proportional controller. (Online version in colour.)

3. Discussion

Adjoining a negative feedback strategy to the antithetic integral controller was shown to reduce the stationary variance for the controlled species, an effect that was expected from previous studies and predicted by the obtained theoretical results. The structure of the negative feedback strategy was notably emphasized to have important consequences on the magnitude of the variance reduction. Indeed, the ON/OFF controller can be used to dramatically reduce the variance while still preserving the ergodicity of the closed-loop network. This can be explained mainly because the proportional effective gain β is very sensitive to changes in the feedback strength K_p and can reach reasonably large values (still smaller than K_p) (electronic supplementary material, figure S1). The preservation of the ergodicity property for the closed-loop network comes from theorem 2 in [1] and the fact that remains smaller than the value of the nominal stationary control input (the constant input for which the stationary mean of the controlled species equals the desired set-point) for a wide range of values for K_p. Regarding the mean dynamics, this feedback leads to a decrease of the settling-time but also leads to abrupt transient dynamics for large values of K_p because of the presence of a stable zero in the mean closed-loop dynamics that is inversely proportional to β (which is very sensitive to changes in K_p in this case and which can reach high values). Unfortunately, this controller cannot be implemented in vivo because it does not admit any reaction network implementation. However, it can still be implemented in silico for the stochastic single-cell control for the control of cell populations using, for instance, targeted optogenetics (e.g. [35]). On the other hand, the Hill feedback, while being practically implementable, has a much less dramatic impact on the stationary variance and on the mean dynamics. The first reason is that the effective proportional gain β is less sensitive with respect to changes in K_p and remains very small even when K_p is large (electronic supplementary material, figure S2). The absence of zero in the mean dynamics does not lead to any abrupt transient dynamics even for large values for K_p but this may also be due to the fact that β always remains small as opposed to the ON/OFF proportional feedback case. A serious issue with this feedback is that ergodicity can be easily lost since very quickly becomes larger than the value of the nominal control input as we increase K_p. The properties of both feedback strategies are summarized in table 2.

Table 2.

Effects of the different feedback strategies on the mean dynamics and the stationary variance.

	ON/OFF proportional feedback	Hill feedback
ergodicity	robust (+)	fragile (−)
β	very sensitive (+)	poorly sensitive (−)
	wide range (+)	small range
mean dynamics	reduce settling-time (+)	reduce settling-time (+)
	zero dynamics (−)	no zero dynamics (+)
stationary variance	dramatic reduction (++)	slight reduction (+)

To prove the main theoretical results, a tailored closure method had to be developed to deal with the bimolecular comparison reaction. A similar one has also been suggested in [36] for exactly the same purpose. These methods rely on the assumption that the molecular count of the controller species Z₂ is, most of the time, equal to 0, a property that is ensured by assuming that k/η ≪ 1. This allowed for the simplification and the closure of the moment equations. The theory was only developed for unimolecular networks because of the problem solvability. However, the extension of those theoretical results to more general reaction networks, such as bimolecular networks, is a difficult task mainly because of the moment closure problem that is now also present at the level of the species of the controlled network. In this regard, this extension is, at the moment, only possible using existing moment closure methods (e.g. [37–39]) which are known to be potentially very inaccurate and would then compromise the validity of the obtained approximation. We believe that obtaining accurate and general theoretical approximations for the stationary variance for bimolecular networks is currently out of reach. It is also unclear whether the obtained qualitative and quantitative results still hold when the assumption k/η ≪ 1 on the controller parameters is not met.

Interestingly, the results obtained in the current paper provide some interesting insights on an unexpected connection between deterministic PI control and its stochastic analogues. In particular, it is possible to observe that the destabilizing effect of deterministic integral control is analogous to the variance increase due to the use of the stochastic antithetic integral controller. In a similar way, the stabilizing property of deterministic proportional controllers is the deterministic analogue of the property of variance decrease of the stochastic proportional controller (table 3).

Table 3.

The effects of the proportional and integral actions on the dynamics of a system in both the deterministic and stochastic setting.

	integral action	proportional action
deterministic setting	tracking (+)	no tracking (−)
	destabilizing (−)	stabilizing (+)
stochastic setting	regulation (+)	no regulation (−)
	increases variance (−)	decreases variance (+)

The controller considered in this paper is clearly analogous to PI controllers. A usual complemental element is the so-called derivative action (or a filtered version of it) in order to add an anticipatory effect to the controller and prevent high overshoot [15]. So far, filtered versions of the derivative action have been proposed in a deterministic setting. Notably, the incoherent feedforward loop locally behaves like a filtered derivative action. More recently, a reaction network approximating a filtered derivative action was proposed in [40] in the deterministic setting. It is unclear at the moment whether a stochastic version for the derivative action can be found but it is highly possible that such a stochastic derivative action can be implemented in terms of elementary reactions.

The negative feedback strategy considered here is an ideal/simplified one. Indeed, it was assumed in this paper that the controlled species was directly involved in the negative feedback. However, it is very likely that, the controlled species may not be directly usable in the feedback, that intermediary species may be involved (e.g. a gene expression network is involved in the feedback) or that the feedback is in terms of a species upstream the controlled species (for instance, feedback uses a protein while the controlled species is the corresponding homodimer). The theory may be adapted to deal with such cases as long as the controlled network is unimolecular. It is, however, expected that the same qualitative behaviour will be observed. The reason for that is that in unimolecular networks, species cooperate in the sense that they act positively on each other. Hence, decreasing the variance of one species will also decrease the variance of all the species that are created from it. For instance, in a gene expression network, if the mRNA variance is decreased, the protein variance will also decrease and vice versa.

From a systems biology viewpoint, it would be interesting to witness a qualitative experimental validation of the proposed theory. Indeed, a first question would be the identification of such negative feedback loops in endogenous networks implementing an antithetic integral controller structure. The next question would be verifying whether we would observe an increase in the variance when knocking this feedback loop down. This would strongly suggest that the role of this feedback loop is indeed to reduce the variance.

Finally, in a more synthetic biology perspective, the implementation of such negative feedback loops is an important, yet elusive, task. It is unclear at the moment how in vivo experiments could be conducted. Preliminary experimental results to validate the theoretical/computational ones could be obtained using optogenetics and single-cell control for population control. In vivo experiments will certainly require a lot more effort.

Data accessibility

This article has no additional data.

Authors' contributions

M.K. and C.B. conceived the study. C.B. and A.G. performed the research. C.B. performed the numerical simulations. M.K. supervised the research and secured the funding. C.B., A.G. and M.K. wrote the paper.

Competing interests

We declare we have no competing interests.

Funding

This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (grant agreement 743269) and from the Swiss National Science Foundation (grant 200021-157129).