Abstract
PURPOSE:
To theoretically compare the corneal stress distribution of laser in situ keratomileusis (LASIK) with the stress distribution of small-incision lenticule extraction.
SETTING:
Cleveland Clinic Cole Institute, Cleveland, and The Ohio State University, Columbus, Ohio, USA.
DESIGN:
Computational modeling study.
METHODS:
A finite-element anisotropic collagen fiber–dependent model of myopic surgery using patient-specific corneal geometry was constructed for LASIK, small-incision lenticule extraction, and a geometry analog model with unaltered material properties from preoperative but with postoperative geometry including thickness. Surgical parameters, magnitude of myopic correction, LASIK flap thickness, and lenticule depth in small-incision lenticule extraction were varied. Two sets of models, 1 with uniform and 1 with depth-dependent material properties, were constructed.
RESULTS:
Stress distribution between small-incision lenticule extraction simulations and the geometry analog model were similar. In contrast, LASIK consistently reduced stress in the flap and increased stress in the residual stromal bed (RSB) compared with the geometry analog model. An increase in flap thickness or lenticule depth resulted in a greater increase in RSB stress in the LASIK model than in the small-incision lenticule extraction model.
CONCLUSIONS:
Small-incision lenticule extraction may present less biomechanical risk to the residual bed of susceptible corneas than comparable corrections involving LASIK flaps. Deeper corrections in the stroma may be possible in small-incision lenticule extraction without added risk for ectasia.
The biomechanical impact of laser in situ keratomileusis (LASIK) on the cornea is a critical component affecting postoperative refractive outcomes.1,2 The human cornea is an anisotropic soft tissue with a distinct collagen distribution and 3-dimensional (3-D) fiber orientation3 that confers greater stiffness to the anterior stroma than the posterior stroma.4 The advent of the femtosecond laser has led to improvements in the consistency of flaps and the predictability of LASIK compared with the use of mechanical microkeratomes.5-8 However, the LASIK flap is created in the anterior stroma and its thickness is known to affect the biomechanical response of the cornea.9-11 Disruption of the most resilient portion of the corneal stroma may contribute to the risk for post-LASIK ectasia, a rare but serious complication related to postoperative structural and refractive instability.3,12
Femtosecond laser-assisted LASIK requires the use of 2 lasers; that is, a femtosecond laser for flap creation and an excimer laser for ablating the tissue beneath the flap to induce curvature change. Recently a method for the correction of myopia and myopia with astigmatism using a single femtosecond laser called refractive lenticule extraction was introduced. Two approaches to refractive lenticule extraction have been described; that is, femtosecond lenticule extraction,13,14 which involves cutting a hinged flap to remove the lenticule, and small-incision lenticule extraction,15,16 which involves removal of the lenticule through a small incision with no flap lift. In both approaches, 2 cuts are made in the anterior stroma using a femtosecond laser without tissue ablation. The tissue between the cuts is referred to as the lenticule. The shape of the lenticule is programmed into the femtosecond laser based on the magnitude of the spherical and astigmatism correction desired. The difference between femtosecond lenticule extraction and small-incision lenticule extraction lies in the arc length of the vertical side cuts that are created and the method by which the lenticule is removed from the stroma. These new procedures have potential benefits over femtosecond laser-assisted LASIK. Lenticule creation and removal in the small-incision lenticule extraction approach are hypothesized to protect most of the anterior stiffer corneal stroma fibrillar connectivity and cellular integrity, and thus the elastic strength,17-19 because the procedure is flapless. A few early clinical studies13-16 report that femtosecond lenticule extraction and small-incision lenticule extraction compare favorably with femtosecond LASIK in terms of the manifest refraction achieved less than 1 year after surgery.
The goal of this study was to evaluate the differences in stresses in the treated stroma and untreated stroma in patient topography-derived finite-element models of the postoperative state resulting from femtosecond laser-assisted LASIK and small-incision lenticule extraction. Using in vivo boundary conditions and anisotropic hyperelastic material property assumptions in the model, the depth of the treated zone and refractive correction parameters were varied in the model to evaluate its effect on stress in the treated and untreated stromal regions. As a comparison, we also modeled the same cornea with the postoperative geometry of the simulated refractive correction while maintaining the preoperative corneal material properties. This would represent a postoperative idealized model with unaltered material properties from the preoperative state and allow us to compare the biomechanical surgical responses to corneas with similar thickness. It was hypothesized that because small-incision lenticule extraction is a flapless procedure, as opposed to LASIK, the stresses in the cornea after the procedures will be distributed differently between the flap/cap and the residual stromal bed. To evaluate the sensitivity of the stresses to depth-dependent variations in the material property constants, the above simulations were performed with depth-dependent and depth-independent material property assumptions.
MATERIALS AND METHODS
Model Geometry and In Vivo Stresses
The anterior and posterior corneal surface topography maps of a normal cornea were obtained in vivo from a commercial anterior segment imaging system (Pentacam, Oculus Optikgeräte GmbH). The central thickness of the cornea was 580 μm. The method used to create a 3-D model and finite-element mesh from patient tomography measurements has been described previously.20,21 Because the cornea is under physiologic stress due to the intraocular pressure (IOP), these stresses are estimated using an iterative finite-element scheme with appropriate boundary conditions described previously.20,21 An en face and a cross-sectional view of the corneal-scleral mesh in Figure 1, A, and Figure 1, B, respectively, show the LASIK flap and small-incision lenticule extraction cap layers. The 3-D geometry was meshed with 8-noded hexahedral elements customized for an incompressible material. An IOP of 15 mm Hg was applied to all models as a uniform pressure. The finite-element models were solved in Abaqus software (version 6.12, Dassault Sysèemes).
Figure 1.

A: En face and cross-sectional view of the finite element mesh for LASIK and small-incision lenticule extraction models. B: Schematic representation of LASIK and small-incision lenticule extraction finite element models. The schematic shows the LASIK flap or small-incision lenticule extraction cap (brown), RSB (dark green), anterior stroma adjacent to flap/cap (light green), and the healed wound layer along the interface between the flap/cap and RSB (dark line). Section A and Section B represent the cross-section view of the cornea along the vertical meridian and horizontal meridian, respectively (LASIK = laser in situ keratomileusis).
Material Model
The cornea is an anisotropic tissue with a collagen orientation and distribution that varies along the depth of the stroma. Hence, the cornea was modeled as an anisotropic fiber-dependent hyperelastic material.22 F and J are the deformation gradient (equation 1) and determinant (det) of F (equation 2), respectively.
| (1) |
| (2) |
The modified right Cauchy strain tensor () (equation 3) and left Cauchy strain tensor (equation 4) are given, respectively, by
| (3) |
| (4) |
The total corneal strain energy (equation 5) is modeled in the decoupled form as
| (5) |
where ψ is the total strain energy and the subscripts iso, fiber, and vol represent the strain energy of the cellular matrix, collagen fibers arranged in lamellae, and near incompressibility of the corneal stroma, respectively. The different strain energies are further given by
| (6) |
| (7) |
| (8) |
| (9) |
where C1, k14, k16, k24 and k26 are material constants and , , and are the strain invariants defined by Pandolfi and Holzapfel.22 The values of C1 and k14(=k16) were 0.1 MPa and 0.234 MPa, respectively. The value of κ14(=κ16) was 30.0; κ is the dispersion parameter that characterizes the distribution of the fibrils from an orthotropic orientation in the central cornea to a circumferential orientation at the limbus.22 The Cauchy stress tensor can be obtained from the deviatoric component of the matrix product of the left Cauchy strain tensor and the first-order derivative of ψ with respect to .22
An ex vivo study of human corneas3 showed that the tensile strength of the central cornea in the anterior stroma was nearly twice that of the posterior stroma. Therefore, 2 sets of ψ were used in each simulation as follows:
Model 1. Material constants (C1, k14, k24) were uniform through the depth.
Model 2. Material constants were linearly scaled in proportion to the experimental data from the ex vivo study3 such that peak values of the material constants in the anterior-most region of the stroma were the same as the uniform value in model 1.
In the finite-element model, the epithelium was also modeled as a layer of elements with a constant thickness of 53 μm with only the isotropic component of the total strain energy formulation (equation 1). Because the epithelium does not have collagen and is a cellular structure, C1 for the epithelium was set at 2% of the corresponding value for the corneal stroma in all the simulations.
Refractive Procedure Simulation
Figure 1, B, shows a schematic of the modeling features relevant to LASIK and small-incision lenticule extraction. Each model was assumed to have 4 distinct zones under the postoperative scenario. The wound layer was modeled as a thin layer of tissue of approximately 20 μm in thickness. The angle subtended by the hinge/slit at the geometric center of the cornea was set at 25 degrees. In addition, ex vivo measurements have shown that the tensile strength of the wound layer in LASIK is of the order of nearly 30% of that of the RSB.23 It was also assumed that once the flap/cap cornea tissue heals, its fiber-dependent anisotropic component (ψfiber) was no longer recruitable.
In addition to the 2 possible outcomes described above (LASIK with material property changes and small-incision lenticule extraction with material property changes), a hypothetical postoperative idealized model with unaltered material properties from the preoperative state was generated for comparison with the postoperative LASIK and small-incision lenticule extraction models. Henceforth, this model is referred to as the geometric analog model because the strain energy was left unchanged in all zones and only a shape change was simulated. In LASIK, the strain energy function for the different zones was modified as follows: For the flap,
| (10) |
For the RSB,
| (11) |
For the anterior stroma adjacent to flap,
| (12) |
For the wound layer,
| (13) |
In small-incision lenticule extraction, the strain energy function for the different zones was modified as follows: For the cap,
| (14) |
For the RSB,
| (15) |
For the anterior stroma adjacent to cap,
| (16) |
For the wound layer,
| (17) |
The scaling of ψfiber in the small-incision lenticule extraction models was computed in direct proportion to the arc length of the slit to the LASIK wound length assuming that in LASIK, the 335-degree arc cut resulted in loss of the fiber-dependent component of the strain energy function in that region. Using a biaxial stretching approximation for an incompressible material strip, the tangent modulus due to the isotropic component only was observed to be nearly equal to the modulus due to the anisotropic fiber component only up to a nominal strain of 4% with the material constants chosen for this study. Thus, ignoring fiber contribution in the total strain energy function resulted in a nearly 50% drop in the total strain energy in the range of physiologic strain. From these analyses, a scaling factor of 0.7 in the wound layer resulted in a 35% drop in the total strain energy. Additional modeling variables that were perturbed were the flap thickness and cap thickness (100 μm and 300 μm, respectively) and the magnitude of spherical myopic correction (−3.0 diopters [D] and −9.0 D, respectively). Ablation profiles in LASIK and extracted lenticule geometries in small-incision lenticule extraction were calculated using the full Munnerlynn algorithm.24
Comparison of Stresses in the Laser In Situ Keratomileusis Flap/Small-Incision Lenticule Extraction Cap and Residual Stromal Bed
Due to fiber directions, the local directions for normal stresses (σxx, σyy, σzz) varied spatially within the stroma. Hence, the invariant von-Mises stress, σM, was used to compare the effects of different simulated procedures.
| (18) |
where σ1, σ2, and σ3 are the eigenvalues of the Cauchy stress tensor evaluated at the centroid of each element. The Abaqus software uses the deviatoric version of Cauchy stress to calculate the von-Mises stress. The mean ± SD values of von-Mises stress in the central 2.0 mm diameter zone of the flap/cap and the RSB were also calculated for comparison. To enable direct comparisons of von-Mises stress in the anterior-most layers of the flap/cap, the number of layers of elements in the flap/cap region was varied to keep the element thickness in each layer at 50 μm. Thus, there were 2 layers and 6 layers of elements in the flap/cap region of the 100 model and 300 μm model, respectively. The von-Mises stress in the top-most layer of elements in the flap region and cap region were also compared.
RESULTS
The results are organized into 3 analyses designed to compare LASIK and small-incision lenticule with the geometric analog model, including the effect of flap/cap thickness, the effect of depth-dependent properties, and the effect of the level of correction. In general, LASIK reduced the stress in the flap and increased the stress in the RSB compared with stresses with the geometry analog model. In general, small-incision lenticule extraction showed stresses closer to those of the geometry analog model.
Stress Distribution in Geometry-Analog Models
Figure 2 and Figure 3 show the stresses in the LASIK flap, small-incision lenticule extraction cap and RSB of the simulated cornea with 100 μm and 300 μm flap/cap thicknesses, respectively, and nonuniform material properties. Similarly, Figure 4 and Figure 5 show the stresses in the LASIK flap/small-incision lenticule extraction cap and RSB of the simulated cornea with 100 μm and 300 μm flap/cap thicknesses, respectively, with uniform material properties. In the first column in Figures 2 to 5, the stresses in the flap/cap and RSB are shown for the geometry analog model corresponding to 100 μm or 300 μm flap/cap thicknesses. Although the 2 models are the same in theory, there were some differences in the stress in the flap/cap and RSB because these stresses were at 2 different depths of flap/cap thickness in the figures and there were 2 different stress distributions. These differences in the stresses in the flap/cap and the RSB were lower in Figures 4 and 5 due to the uniform property assumption.
Figure 2.
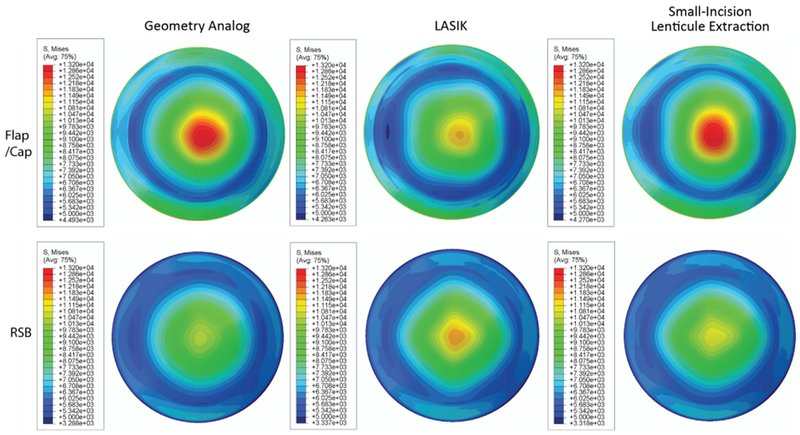
Comparison of von-Mises stresses in the flap/cap region and the RSB of the cornea with a −9.0 D correction, 100 μm flap/cap, and nonuniform material properties through the depth for the geometric analog model, LASIK with material property changes, and small-incision lenticule extraction with material property changes. The units of stress are Pa (LASIK = laser in situ keratomileusis; RSB = residual stromal bed).
Figure 3.

Comparison of von-Mises stresses in the flap/cap and the RSB with a −9.0 D correction, 300 μm flap/cap, and nonuniform material properties through the depth for the geometric analog model, LASIK with material property changes, and small-incision lenticule extraction with material property changes. The units of stress are Pa (LASIK = laser in situ keratomileusis; RSB = residual stromal bed).
Figure 4.

Comparison of von-Mises stresses in the flap/cap region and the RSB with a −9.0 D correction, 100 μm flap/cap, and uniform material properties through the depth for the geometric analog model, LASIK with material property changes, and small-incision lenticule extraction with material property changes. The units of stress are Pa (LASIK = laser in situ keratomileusis; RSB = residual stromal bed).
Figure 5.

Comparison of von-Mises stress in the flap/cap and the RSB with a −9.0 D correction, 300 μm flap/cap, and uniform material properties through the depth for the geometric analog model, LASIK with material property changes, and small-incision lenticule extraction with material property changes. The units of stress are Pa (LASIK = laser in situ keratomileusis; RSB = residual stromal bed).
Effect of Flap/Cap Thickness
Table 1 and Table 2 show the mean von-Mises stress values in the central 2.0 mm diameter zone in the flap/cap and the RSB, respectively. Figure 2 and Figure 3 show the stresses in the LASIK flap/small-incision lenticule extraction cap and the RSB of the simulated cornea with 100 μm and 300 μm flap/cap thicknesses, respectively, and nonuniform material properties. In the geometric analog model, the stresses were greater in the anterior region than in the posterior stromal bed. In the LASIK model, a thicker flap produced a greater increase in stress in the RSB from the stress value in the corresponding geometry analog model due to decreased RSB thickness. For example, in a −3.0 D LASIK correction with a 100 μm flap/cap thickness (Table 2), the increase in stress was 460 Pa (increased from 7966 to 7506 Pa). Similarly with a 300 μm flap/cap thickness (Table 2), the increase in stress was 1083 Pa (increased from 8424 to 7341 Pa). In the small-incision lenticule extraction model, the stresses were relatively unchanged from the stresses computed in the geometric analog model when the flap thickness was increased.
Table 1.
Mean von-Mises stress computed in the central 2.0 mm diameter zone of the LASIK flap region and small-incision lenticule extraction cap region.
| Flap Thickness/Spherical Correction | Mean Postop Stress (Pa) with No Material Change | Depth Dependent | LASIK |
Small-Incision Lenticule Extraction |
||
|---|---|---|---|---|---|---|
| Mean Stress (Pa) | Difference (%)* | Mean Stress (Pa) | Difference (%)* | |||
| 100 μm flap | ||||||
| 3.0 D | 8203 ± 265 | Yes | 7232 ± 231 | −11.8 | 8158 ± 281 | −0.5 |
| 9.0 D | 11 943 ± 586 | Yes | 10 585 ± 496 | −11.3 | 11 968 ± 606 | 0.2 |
| 3.0 D | 6666 ± 248 | No | 5876 ± 212 | −11.9 | 6612 ± 261 | −0.8 |
| 9.0 D | 10 004 ± 461 | No | 8874 ± 388 | −11.3 | 9999 ± 482 | −0.05 |
| 300 μm flap | ||||||
| 3.0 D | 7890 ± 251 | Yes | 7516 ± 291 | −4.7 | 7995 ± 254 | 1.3 |
| 9.0 D | 10 502 ± 915 | Yes | 10 218 ± 899 | −2.7 | 10 725 ± 898 | 2.1 |
| 3.0 D | 7151 ± 400 | No | 6807 ± 319 | −4.8 | 7244 ± 417 | 1.3 |
| 9.0 D | 9938 ± 341 | No | 9696 ± 320 | −2.4 | 10 165 ± 358 | 2.3 |
LASIK = laser in situ keratomileusis
Means ± SD
Percentage difference in stress from the postoperative without material change condition
Table 2.
Mean von-Mises stress computed in the central 2.0 mm diameter zone of the RSB region.
| Flap Thickness/Spherical Correction | Mean Postop Stress (Pa) with No Material Change | Depth Dependent | LASIK |
Small-Incision Lenticule Extraction |
||
|---|---|---|---|---|---|---|
| Mean Stress (Pa) | Difference (%)* | Mean Stress (Pa) | Difference (%)* | |||
| 100 μm flap | ||||||
| 3.0 D | 7506 ± 247 | Yes | 7966 ± 303 | 6.1 | 7738 ± 256 | 3.1 |
| 9.0 D | 9267 ± 834 | Yes | 10 123 ± 961 | 9.2 | 9669 ± 867 | 4.3 |
| 3.0 D | 7875 ± 491 | No | 8274 ± 484 | 5.1 | 8081 ± 501 | 2.6 |
| 9.0 D | 9899 ± 227 | No | 10 664 ± 291 | 7.7 | 10 271 ± 244 | 3.8 |
| 300 μm flap | ||||||
| 3.0 D | 7341 ± 150 | Yes | 8424 ± 214 | 14.8 | 7750 ± 154 | 5.6 |
| 9.0 D | 8291 ± 357 | Yes | 101 32 ± 464 | 22.2 | 8899 ± 376 | 7.3 |
| 3.0 D | 8452 ± 242 | No | 9594 ± 269 | 13.5 | 8906 ± 258 | 5.4 |
| 9.0 D | 9934 ± 155 | No | 12 032 ± 299 | 21.1 | 10 669 ± 175 | 7.4 |
LASIK = laser in situ keratomileusis
Means ± SD
Percentage difference in stress from the postoperative without material change condition
Overall, the greatest change in stress between the unoperated cornea and the LASIK and small-incision lenticule extraction models was in the RSB when the flap/cap thickness was increased from 100 μm to 300 μm. For example, in the 100 μm flap/cap thickness case with −9.0 D and depth-dependent material properties (Table 1), the mean stress values in the flap/cap were 11 943 Pa, 10 585 Pa, and 11 968 Pa in the geometry analog, LASIK model, and small-incision lenticule extraction model, respectively. In the RSB regions (Table 2), the mean values were 9267 Pa, 10 123 Pa, and 9669 Pa, respectively. In contrast, in the 300 μm flap/cap thickness case with −9.0 D and depth-dependent material properties (Table 1), the mean stress values in the flap/cap were 10502 Pa, 10 218 Pa, and 10 725 Pa in the geometry analog, LASIK model, and small-incision lenticule extraction model, respectively. In the RSB regions (Table 2), the mean values were 8291 Pa, 10 132 Pa, and 8899 Pa, respectively. Figures 4 and 5 show the stresses in the flap/cap and the RSB of the simulated cornea with a 100 μm and 300 μm flap/cap thickness, respectively, and uniform material properties. Although the magnitude of stresses differed when uniform material properties through the corneal depth were assumed, the patterns of response were similar to the case of nonuniform properties.
Effect of Depth-Dependent Material Properties
As discussed in the introduction, the anterior stroma has been shown to be stiffer than the posterior stroma in ex vivo studies. Figures 2 and 4 show the stresses in the LASIK flap/small-incision lenticule extraction cap and the RSB of the simulated cornea, respectively, with nonuniform material properties and uniform material properties and a 100 μm flap/cap thickness. In Figures 2 and 4, the plots in the first column show higher stresses in the anterior region, corresponding to the flap/cap of columns 2 and 4, and lower stresses in the region of the RSB with depth-dependent properties taken into account in the geometric analog model as well as with uniform properties. In the LASIK models, higher stress in the RSB was seen with the nonuniform material property assumption than with the uniform material property assumption. In the small-incision lenticule extraction models, the stress distributions and magnitudes were once again similar to the stresses computed in the geometric analog model and were affected by material property variation through the depth. Similar patterns can also be seen in Figures 3 and 5, which show the stress distributions with a 300 μm flap/cap thickness. Comparison of mean values of stress in Tables 1 and Table 2 show the effect of the depth-dependent material properties when the region of higher stress shifts from the RSB region to the flap/cap region.
Effect of Magnitude of Myopic Spherical Correction
In all simulations (geometric analog model, LASIK, and small-incision lenticule extraction), removal of a greater amount of tissue increased the stresses in the flap/cap and the RSB (Tables 1 and 2). Once again, small-incision lenticule extraction produced stresses closer to the geometric analog model than LASIK.
DISCUSSION
Laser in situ keratomileusis has been performed in millions of patients over the past decade with a satisfaction rate of nearly 95%. However, it is of immense importance for refractive surgeons to identify weaker corneas a priori to avoid postsurgical complications such as ectasia. Screening tools for identifying a predisposition to ectasia in the context of a wide variety of potential surgical risk factors have been developed but may lack sufficient sensitivity and specificity for effective prospective screening. In LASIK, the anterior stroma within the flap is largely decoupled from its anchoring boundaries to expose the underlying stroma, which is then ablated to produce a shape change. In contrast, small-incision lenticule extraction preserves much of the anterior stroma from mechanical disruption. Consistently, we observed the stress distribution in the postoperative simulations of small-incision lenticule extraction to be similar to that of the geometric analog model because the procedure preserves much of the stiffer anterior stroma. In contrast, LASIK consistently increased the stress in the RSB compared with the reference model. Furthermore, an increase in flap/cap thickness resulted in a greater increase in stress in the RSB in the LASIK model than in the small-incision lenticule extraction model. Although the link between corneal stress and ectasia has yet to be defined, these observations suggest that small-incision lenticule extraction could present less biomechanical risk to the RSB in susceptible corneas than comparable corrections involving LASIK flaps. They might even suggest that the correction could be placed deeper in the cornea without increasing the risk that would open the procedure to higher levels of correction that are not considered safe in LASIK.
The effect of flap/cap thickness on the stress distribution in LASIK and small-incision lenticule extraction models was interesting. A thicker flap in LASIK models resulted in a substantial increase in von-Mises stress in the RSB. However, a thicker cap in small-incision lenticule extraction models did not result in comparable changes in the von-Mises stress in the RSB. Smallincision lenticule extraction protected the RSB from an increase in stress, similar to the geometric analog model. This result can also be attributed to preservation of the anterior stroma in small-incision lenticule extraction. Clinical studies25-27 suggest that flaps with a planned thickness ranging from 90 to 160 μm provide comparable visual and refractive outcomes. In the present study, we simulated a larger difference in the minimum and maximum flap/cap thickness to increase the likelihood of detecting differences resulting from flap/cap effects. In addition, incorporation of a depth-dependent variation in material properties resulted in a significant redistribution of stress from the posterior stroma to the stiffer anterior stroma and supports the rationale of refractive surgical techniques that preserve the anterior stromal architecture.
This study has several possible future avenues of improvement. The small-incision lenticule extraction procedure uses a smaller cap diameter than a conventional LASIK flap. This could have further biomechanical impact on the stress redistribution because a smaller volume of tissue will be affected than in the simulated models. We estimated the changes in the strain energy function with LASIK and small-incision lenticule extraction. However, it is possible that the material property coefficients also change as a result of the procedures. Furthermore, in vivo data on depth-dependent variation in material properties and fiber directions are lacking and could enhance the accuracy of stress estimation in the postsurgical model. In summary, our analyses suggest that small-incision lenticule extraction tends to preserve a corneal stress distribution similar to that of a geometrically analogous model with unaltered corneal material properties by avoiding the more extensive circular keratotomy and disruption of the load-bearing anterior stromal collagen associated with LASIK flaps Additional simulation-based and clinical studies are needed to determine the degree to which these differences influence the precision and stability of refractive outcomes and the incidence of ectasia.
WHAT WAS KNOWN
No previous studies have presented a finite-element analysis of intrastromal femtosecond refractive surgery or compared the biomechanical effects of LASIK and small-incision lenticule extraction.
The depth dependency of corneal material properties has been shown in ex vivo studies; however, the effects of spatial material property differences on the response to LASIK, small-incision lenticule extraction, or other corneal refractive surgeries have not been quantified through computational modeling.
WHAT THIS PAPER ADDS
Stress distributions in simulations of postoperative small-incision lenticule extraction were more similar to those of the geometry-matched reference model than simulations of postoperative LASIK stress distributions.
Small-incision lenticule extraction could present less of a biomechanical risk to the RSB of susceptible corneas than comparable corrections involving LASIK flaps. Corrections involving greater depths of stromal tissue removal may be possible in small-incision lenticule extraction with a lower risk for ectasia than might be encountered in LASIK.
FINANCIAL DISCLOSURE(S)
Drs. Sinha Roy, Dupps, and Roberts received research funding from Carl Zeiss Meditec. Drs. Sinha Roy and Dupps are inventors on intellectual property filed through Cleveland Clinic Innovations pertaining to computational modeling methods used in this research.
Biography
Abhijit Sinha Roy, PhD
Cole Eye Institute, Cleveland Clinic Foundation, Cleveland, Ohio, USA

REFERENCES
- 1. Shah S Laiquzzaman M Yeung I Pan X Roberts C The use of the Ocular Response Analyzer to determine corneal hysteresis in eyes before and after excimer laser refractive surgery Cont Lens Anterior Eye 2009. 32 123–128 [DOI] [PubMed] [Google Scholar]
- 2. Ambrósio R Jr Dawson DG Salomão M Guerra FP Caiado ALC Belin MW Corneal ectasia after LASIK despite low preoperative risk: tomographic and biomechanical findings in the unoperated, stable, fellow eye J Refract Surg 2010. 26 906–911 [DOI] [PubMed] [Google Scholar]
- 3. Randleman JB Dawson DG Grossniklaus HE McCarey BE Edelhauser HF Depth-dependent cohesive tensile strength in human donor corneas: implications for refractive surgery J Refract Surg 2008. 24 S85–S89 [DOI] [PubMed] [Google Scholar]
- 4. Abahussin M Hayes S Knox Cartwright NE Kamma-Lorger CS Khan Y Marshall J Meek KM Accessed October 14, 2013 3D collagen orientation study of the human cornea using x-ray diffraction and femtosecond laser technology Invest Ophthalmol Vis Sci 2009. 50 5159–5164 Available at: http://www.iovs.org/content/50/11/5159.full.pdf [DOI] [PubMed] [Google Scholar]
- 5. Ahn H Kim J-K Kim CK Han GH Seo KY Kim EK Kim T-i Comparison of laser in situ keratomileusis flaps created by 3 femtosecond lasers and a microkeratome J Cataract Refract Surg 2011. 37 349–357 [DOI] [PubMed] [Google Scholar]
- 6. Chen S Feng Y Stojanovic A Jankov MR II Wang Q IntraLase femtosecond laser vs mechanical microkeratomes in LASIK for myopia: a systematic review and meta-analysis J Refract Surg 2012. 28 15–24 [DOI] [PubMed] [Google Scholar]
- 7. Gil-Cazorla R Teus MA de Benito-Llopis L Mikropoulos DG Femtosecond laser vs mechanical microkeratome for hyperopic laser in situ keratomileusis Am J Ophthalmol 2011. 152 16–21 [DOI] [PubMed] [Google Scholar]
- 8. Salomão MQ Wilson SE Femtosecond laser in laser in situ keratomileusis J Cataract Refract Surg 2010. 36 1024–1032 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Medeiros FW Sinha-Roy A Alves MR Dupps WJ Jr. Accessed October 14, 2013 Biomechanical corneal changes induced by different flap thickness created by femtosecond laser Clinics (Sao Paulo) 2011. 66 1067–1071 Available at: http://www.ncbi.nlm.nih.gov/pmc/articles/PMC3129968/pdf/cln-66-06-1067.pdf [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Knorz MC Vossmerbaeumer U Comparison of flap adhesion strength using the Amadeus microkeratome and the IntraLase iFS femtosecond laser in rabbits J Refract Surg 2008. 24 875–878 [DOI] [PubMed] [Google Scholar]
- 11. Potgieter FJ Roberts C Cox IG Mahmoud AM Herderick EE Roetz M Steenkamp W Prediction of flap response J Cataract Refract Surg 2005. 31 106–114 [DOI] [PubMed] [Google Scholar]
- 12. Randleman JB Post-laser in-situ keratomileusis ectasia: current understanding and future directions Curr Opin Ophthalmol 2006. 17 406–412 [DOI] [PubMed] [Google Scholar]
- 13. Sekundo W Kunert K Russmann C Gille A Bissmann W Stobrawa G Sticker M Bischoff M Blum M First efficacy and safety study of femtosecond lenticule extraction for the correction of myopia: six-month results J Cataract Refract Surg 2008. 34 1513–1520 erratum, 1819 [DOI] [PubMed] [Google Scholar]
- 14. Ang M Chaurasia SS Angunawela RI Poh R Riau A Tan D Mehta JS Accessed October 14, 2013 Femtosecond lenticule extraction (FLEx): clinical results, interface evaluation, and intraocular pressure variation Invest Ophthalmol Vis Sci 2012. 53 1414–1421 Available at:http://www.iovs.org/content/53/3/1414.full.pdf [DOI] [PubMed] [Google Scholar]
- 15. Sekundo W Kunert KS Blum M Small incision corneal refractive surgery using the small incision lenticule extraction (SMILE) procedure for the correction of myopia and myopic astigmatism: results of a 6 month prospective study Br J Ophthalmol 2011. 95 335–339 [DOI] [PubMed] [Google Scholar]
- 16. Shah R Shah S Sengupta S Results of small incision lenticule extraction: all-in-one femtosecond laser refractive surgery J Cataract Refract Surg 2011. 37 127–137 [DOI] [PubMed] [Google Scholar]
- 17. Riau AK Angunawela RI Chaurasia SS Lee WS Tan DT Mehta JS Accessed October 14, 2013 Early corneal wound healing and inflammatory responses after refractive lenticule extraction (ReLEx) Invest Ophthalmol Vis Sci 2011. 52 6213–6221 Available at: http://www.iovs.org/content/52/9/6213.full.pdf [DOI] [PubMed] [Google Scholar]
- 18. Mohamed-Noriega K Toh K-P Poh R Balehosur D Riau A Htoon HM Peh GSL Chaurasia SS Tan DT Mehta JS Accessed October 14, 2013 Cornea lenticule viability and structural integrity after refractive lenticule extraction (ReLEx) and cryopreservation Mol Vis 2011. 17 3437–3449 Available at: http://www.ncbi.nlm.nih.gov/pmc/articles/PMC3249438/pdf/mv-v17-3437.pdf [PMC free article] [PubMed] [Google Scholar]
- 19. Santhiago MR Wilson SE Cellular effects after laser in situ keratomileusis flap formation with femtosecond lasers: a review Cornea 2012. 31 198–205 [DOI] [PubMed] [Google Scholar]
- 20.Sinha Roy A, Dupps WJ. Patient-specific modeling of corneal refractive surgery outcomes and inverse estimation of elastic property changes. J Biomech Eng. 2011;133:011002. doi: 10.1115/1.4002934. [DOI] [PubMed] [Google Scholar]
- 21. Sinha Roy A Dupps WJ Accessed October 14, 2013 Patient-specific computational modeling of keratoconus progression and differential responses to collagen crosslinking Invest Ophthalmol Vis Sci 2011. 52 9174–9187 Available at: http://www.iovs.org/content/52/12/9174.full.pdf [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Pandolfi A, Holzapfel GA. Three-dimensional modeling and computational analysis of the human cornea considering distributed collagen fibril orientations. J Biomech Eng. 2008;130:061006. doi: 10.1115/1.2982251. [DOI] [PubMed] [Google Scholar]
- 23. Schmack I Dawson DG McCarey BE Waring GO III Grossniklaus HE Edelhauser HF Cohesive tensile strength of human LASIK wounds with histologic, ultrastructural, and clinical correlations J Refract Surg 2005. 21 433–445 [DOI] [PubMed] [Google Scholar]
- 24. Munnerlyn CR Koons SJ Marshall J Photorefractive keratectomy: a technique for laser refractive surgery J Cataract Refract Surg 1988. 14 46–52 [DOI] [PubMed] [Google Scholar]
- 25. Cheng Z-Y He JC Zhou X-T Chu R-Y Effect of flap thickness on higher order wavefront aberrations induced by LASIK: a bilateral study J Refract Surg 2008. 24 524–529 [DOI] [PubMed] [Google Scholar]
- 26. Bansal AS Doherty T Randleman JB Stulting RD Accessed October 14, 2013 Influence of flap thickness on visual and refractive outcomes after laser in situ keratomileusis performed with a mechanical keratome J Cataract Refract Surg 2010. 36 810–813 Available at: http://www.ncbi.nlm.nih.gov/pmc/articles/PMC3783967/?report=classic [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Moshirfar M Hatch BB Chang JC Kurz CJ Eugarrios MF Mifflin MD Prospective, contralateral comparison of 120-μm and 90-μm LASIK flaps using the IntraLase FS60 femtosecond laser J Refract Surg 2011. 27 251–259 [DOI] [PubMed] [Google Scholar]


