Hemoglobin A_1c Level and Cardiovascular Disease Incidence in Persons With Type 1 Diabetes: An Application of Joint Modeling of Longitudinal and Time-to-Event Data in the Pittsburgh Epidemiology of Diabetes Complications Study

Abstract

Type 1 diabetes (T1D) is associated with increased risk of cardiovascular disease (CVD), but hyperglycemia (measured by hemoglobin A_1c (HbA1c) level), which characterizes T1D, has itself been an inconsistent predictor of CVD incidence. However, only baseline HbA1c or a summary measure (e.g., mean level over follow-up) is usually analyzed. Joint models allow simultaneous modeling of repeatedly measured longitudinal covariates, using random effects, and time-to-event data. We evaluated data from the Pittsburgh Epidemiology of Diabetes Complications Study, an ongoing prospective cohort study of childhood-onset T1D that has followed participants since 1986–1988 and has repeatedly found little association between baseline HbA1c or mean follow-up HbA1c and coronary artery disease incidence. Of 561 participants without CVD at baseline, 263 (46.9%) developed CVD over a period of 25 years (1986–2014). In joint models, each 1% unit increase in HbA1c trajectory was associated with a 1.26-fold increased risk of CVD (95% confidence interval: 1.07, 1.45), after adjustment for baseline levels of other CVD risk factors, and a 1.13-fold increased risk (95% confidence interval: 0.99, 1.32) after adjustment for updated mean levels of other CVD risk factors. These findings, which support the need for good glycemic control to prevent CVD in persons with T1D, underscore the importance of utilizing methods incorporating within-subject variation over time when analyzing and interpreting longitudinal cohort study data.

Cardiovascular disease (CVD), comprising coronary artery disease (CAD), cerebrovascular disease, and peripheral vascular disease, is a major complication of type 1 diabetes (T1D). As in the general population, CVD is a significant contributor to morbidity and early mortality among persons with T1D; however, the risk of CVD is greatly increased in those with T1D (1). The reasons for this increased risk are not fully understood, since the hyperglycemia (measured by hemoglobin A_1c (HbA1c) level) that characterizes T1D is itself an inconsistent predictor of CVD incidence (2–10). In the Diabetes Control and Complications Trial (DCCT)/Epidemiology of Diabetes Interventions and Complications (EDIC) Study, persons in the intensive glycemic control arm of the study had significantly lower incidence of CAD than persons in the conventional therapy arm (11). In addition, updated mean HbA1c level was an important predictor of CVD incidence, second only to age (12). In contrast, observational studies have not found HbA1c to consistently predict CVD (4, 6, 7, 13–16). One potential explanation for these discordant results is that, in the DCCT, intensive therapy began early in the course of T1D, raising the suggestion that glycemia may be associated with the initiation of atherogenesis (17). In the Pittsburgh Epidemiology of Diabetes Complications (EDC) Study, a prospective cohort study of childhood-onset T1D, HbA1c level at baseline did not predict CAD incidence. However, decreasing absolute change between baseline HbA1c and most recent HbA1c was associated with lower CAD risk over 16 years of follow-up (8). In the Finnish Diabetic Nephropathy Study, HbA1c variability, but not mean HbA1c level over time, predicted CVD (16).

In contrast to this inconsistent relationship between HbA1c and CAD, glycemia has been more consistently associated with risk of lower-extremity arterial disease (LEAD) (4, 18, 19). This difference may indicate that hyperglycemia is more strongly associated with stable atherosclerosis, which characterizes LEAD, rather than plaque rupture, which precipitates acute coronary events (17). Stable atherosclerosis is characterized by plaques with high fibrous and lower macrophage and lipid content and evenly distributed atherosclerosis around the circumference of the vessel lumen (20). Unstable atherosclerosis is characterized by “vulnerable plaques,” with a necrotic core that is highly prone to producing a thrombus, or clot, and is covered by thin, fibrous caps (20). In the general population, most acute coronary events are precipitated by rupture of vulnerable plaques, with a small proportion resulting from erosion of more stable plaques (21, 22). In persons with T1D, these proportions are reversed, with most events being due to plaque erosion (21, 22), which is consistent with the hypothesis that hyperglycemia is associated with more stable atherosclerosis.

In observational cohort studies which examine these associations, baseline HbA1c level is most often used to predict CVD incidence. This approach, while generally providing valid results, does not account for changes in glycemic control over time that may affect risk (23). Both stability of predictors and change in predictors are relevant for estimating the likelihood of an event; thus, incorporation of within-subject patterns is important for understanding the risk factor–outcome relationship (23–26). Analyses of data from longitudinal cohort studies rarely make full use of serially measured risk factors. Failing to utilize all available data could lead to invalid results (23).

One common approach for accommodating changes in risk factors in statistical analyses is to model change directly (27). However, this approach does not account for the actual pattern of change, assumes a constant, linear increase or decrease over time, and may underestimate variance (28). Another approach for utilizing longitudinal data is to model the average level of the risk factor over the follow-up period. This method has similar drawbacks to modeling change, leading to a loss of important information regarding variability (29).

Joint modeling allows both longitudinal repeated covariates and time-to-event data to be modeled together, as detailed by Wulfsohn and Tsiatis (30). Comprehensive overviews of joint models have also been provided by Tsiatis and Davidian (26), Rizopoulos (31), and Diggle et al. (32). Briefly, a joint model consists of 2 submodels. A mixed-effects model characterizes the trajectory of the longitudinal covariate over time. The modeled random effects are simultaneously included in a survival model, so the relationship between the covariate trajectory and time to the event can be estimated (26). These random effects, or subject-specific deviations from the average effect, are assumed to be the underlying link between the longitudinal repeated measures and the subject-specific hazard for the time-to-event outcome (23).

While survival analyses and repeated-measures analyses employing mixed models have been performed separately using EDC Study data, joint modeling of both processes has not previously been carried out, to our knowledge. Thus, our objective in this study was to assess the relationship between serially measured HbA1c level and the incidence of CVD among persons with T1D using joint modeling. Additionally, we examined the specific manifestations of CVD separately to explore whether the relationship with HbA1c differs by type.

METHODS

Study population

The Pittsburgh EDC Study is a prospective cohort study of childhood-onset (age <17 years) T1D. All participants (n = 658) were diagnosed, or seen within 1 year of diagnosis, at Children’s Hospital of Pittsburgh (Pittsburgh, Pennsylvania) between 1950 and 1980. The cohort has been described in detail elsewhere (33, 34). Briefly, participants have been followed since 1986–1988, with biennial examinations being carried out for 10 years and with biennial questionnaires and further examinations being administered at 18 and 25 years postbaseline thereafter. Follow-up for the current analysis extended through October 31, 2014. Research protocols were approved by the University of Pittsburgh Human Research Protection Office, and all participants provided written informed consent.

Ascertainment of cardiovascular outcomes

Participants were followed for 25 years to assess incidence of total CVD, defined as the first instance of CAD (fatal CAD, myocardial infarction, revascularization procedure, blockage ≥50%, ischemic electrocardiogram, or angina), stroke, or LEAD (ankle-brachial index <0.8, lower-limb amputation due to vascular cause, or intermittent claudication). Fatal events were ascertained using medical records, death certificates, autopsy reports, and/or interviews with next of kin and were classified according to the system used in the Diabetes Epidemiology Research International Study (35). Myocardial infarction, revascularization/blockage, and stroke were self-reported by the participants and confirmed by medical records. Amputation was ascertained by self-report and/or physician examination. Ankle-brachial index was determined using a Doppler blood-flow detector with the subject lying supine. Ratios for each of the right and left tibialis posterior and dorsalis pedis systolic pressures were calculated, with arm systolic pressure as the denominator. Intermittent claudication was assessed using the Rose questionnaire (36). In addition to total CVD, each manifestation of CVD (CAD, stroke, and LEAD) was assessed as a separate outcome. Participants with prevalent CVD at baseline were excluded from analyses of the corresponding outcome.

Assessment of CVD risk factors

Risk factors for CVD were assessed at baseline and at 2, 4, 6, 8, 10, and 18 years of follow-up. Fasting blood samples were taken to measure levels of hemoglobin A1/HbA1c, lipids, and serum creatinine. From baseline through 10 years, HbA1 values were converted to DCCT-aligned HbA1c values using a regression equation derived from duplicate assays (DCCT HbA1c = 0.14 + 0.83(EDC HbA1)) (8). At 18 years, HbA1c was measured using the DCA 2000 analyzer (Bayer Healthcare LLC, Elkhart, Indiana) and converted to DCCT-aligned HbA1c by means of the equation DCCT HbA1c = (EDC HbA1c − 1.13)/0.81. Duplicate assays were performed to compare DCA and original DIAMAT HbA1 measures (Bio-Rad Laboratories, Hercules, California); the 2 methods had high agreement (8). From baseline through 10 years, serum total cholesterol and triglyceride concentrations were determined enzymatically (37, 38); high-density lipoprotein (HDL) cholesterol level was determined using a modified precipitation technique (39, 40). At 18 years, serum lipid levels were measured using the Cholestech LDX analyzer (Cholestech Corporation, Hayward, California). Non-HDL cholesterol level was calculated by subtracting the HDL cholesterol value from the total cholesterol value. White blood cell count was determined using a Coulter counter (Coulter Electronics, Inc., Hialeah, Florida). Three seated blood pressure readings were taken with a random-zero sphygmomanometer; the mean of the second and third readings was used in analyses, according to the Hypertension Detection and Follow-up Program protocol (41). Hypertension was defined as blood pressure ≥140/90 mm Hg or use of blood-pressure–lowering medication. Past and current smoking status was obtained by self-report.

At study visits, 3 timed urine samples (24-hour, overnight, and 4-hour collections taken over 2 weeks) were collected. Urinary albumin level was measured in each sample by immunonephelometry (42), and albumin excretion rate (AER) was calculated; the natural log-transformed median of the 3 AERs was used in analyses. Serum creatinine level was measured using an Ectachem 400 Analyzer (Eastman Kodak Company, Rochester, New York). Glomerular filtration rate was estimated by means of the Chronic Kidney Disease Epidemiology Collaboration creatinine equation (43). Positive baseline renal disease status was defined as AER ≥200 μg/minute in at least 2 of 3 timed urine samples, estimated glomerular filtration rate <60 mL/minute/m², or a history of renal transplant or dialysis.

Statistical analyses

Longitudinal HbA1c level and time to first CVD event were the outcomes of interest, and they were examined simultaneously using joint models (30, 43). To allow for curvature in the trajectory of HbA1c values at both the individual and cohort levels, we fitted the longitudinal HbA1c submodel with fixed and random linear and quadratic terms for time and random intercept. Thus, the population mean trajectory was assumed to be quadratic and the individual trajectories for subjects allowed for curvature, but in participants with fewer than 3 time points, the individuals’ curves were shrunk toward the population mean and fitted as a quadratic trajectory. Alternative forms of the models were also fitted, including 1) a model with linear fixed effects (no quadratic term), with both the intercept and linear terms allowed to be random, and 2) a linear fixed-effect model which allowed a random quadratic trajectory for each individual. Conclusions about the relationship of HbA1c to CVD risk did not differ, but an examination of the mean HbA1c plots indicated curvature in the cohort trajectories, so only results from the first parameterization described above are presented. HbA1c was censored at the time point prior to occurrence of the CVD event for cases, to avoid potential bias associated with glycemic control changing in response to a CVD event. For the survival submodel, we employed a Cox proportional hazards model. Interactions between longitudinal HbA1c and important predefined subgroups, specifically diabetes diagnosis cohort (diagnosed in 1950–1964 versus 1965–1980), sex, and renal disease status at baseline, were tested to determine whether the longitudinal HbA1c trajectory differed by group. Analyses were repeated separately with time to CAD, stroke, and LEAD as the outcome, respectively.

In primary analyses, all models adjusted for other baseline CVD risk factors; final models were selected using backward selection and likelihood ratio tests. The risk factors considered for adjustment were diabetes duration (years), non-HDL cholesterol level, hypertension, ln(AER), and white blood cell count, except in cases where collinearity was a concern (i.e., models including the diagnosis cohort indicator did not adjust for diabetes duration and those including the renal disease status indicator did not adjust for ln(AER)). In alternative analyses, models adjusted for the updated mean value of each factor (i.e., the mean value of all available measurements prior to event or censoring), instead of baseline values, as an estimate of mean exposure to the risk factors over the same follow-up period in which HbA1c was measured. This approach allowed a more direct comparison with the recent report from the DCCT/EDIC Study, where updated mean risk factors were found to be strongly associated with CVD (12). All joint modeling was performed using the joineR (44) routine in R (R Foundation for Statistical Computing, Vienna, Austria).

RESULTS

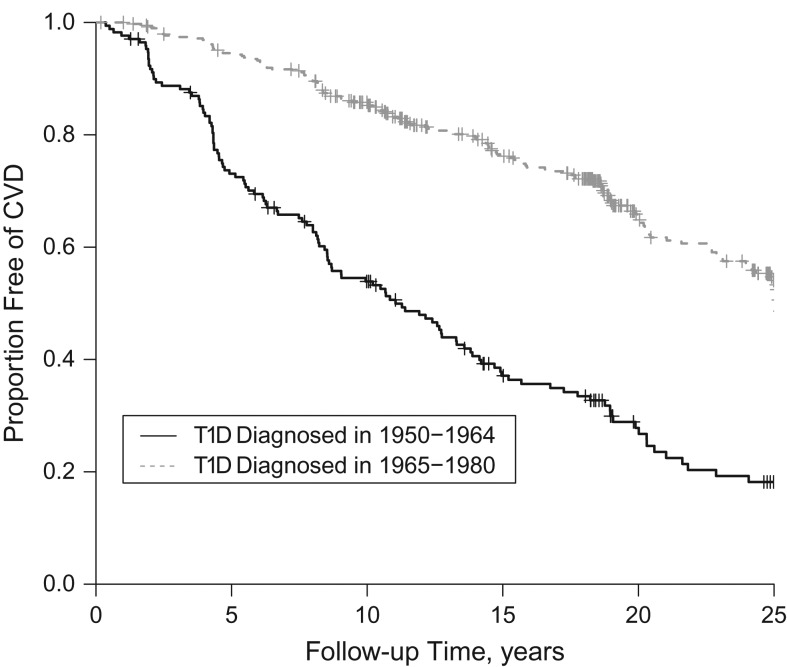
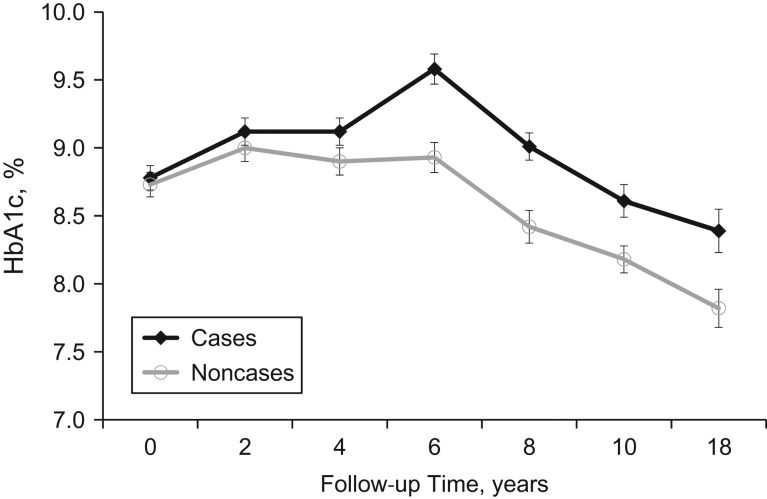
Of 561 participants without prevalent CVD at baseline, 263 (46.9%) developed CVD during the 25-year follow-up period (1986–2014). Baseline characteristics are shown in Table 1 according to CVD incidence status. The participants who developed CVD were older; had a longer duration of T1D; had higher body mass index, waist:hip ratio, non-HDL cholesterol level, triglyceride level, blood pressures, white blood cell count, and AER; and had a lower estimated glomerular filtration rate. They were also more likely to be taking blood-pressure–lowering medication, to have hypertension, and to have a history of smoking. The median follow-up time for CVD ascertainment was 15.0 years (range, 0.2–27.7 years). Participants had a median of 4 HbA1c measurements (interquartile range, 2–6) prior to their incident CVD event. The survival curve for total CVD by diabetes diagnosis cohort is shown in Figure 1. The observed mean longitudinal HbA1c profile by CVD incidence status is shown in Figure 2.

Table 1.

Baseline Characteristics of a Type 1 Diabetes Cohort by 25-Year Total Cardiovascular Disease Incidence Status (n = 561 Persons Free of Prevalent Cardiovascular Disease at Baseline)^a, Pittsburgh Epidemiology of Diabetes Complications Study, 1986–1988

	Incident CVD (n = 263)			No CVD (n = 298)
	Mean (SD)	No. of Persons	%	Mean (SD)	No. of Persons	%
Age, years	29.9 (7.4)			24.3 (7.0)
Duration of diabetes, years	21.5 (7.4)			16.2 (6.4)
Age at diabetes onset, years	8.4 (3.9)			8.1 (4.3)
Female sex		130	49.4		147	49.3
Nonwhite race		5	1.9		7	2.4
Body mass indexb	23.8 (3.2)			23.3 (3.2)
Waist:hip ratio	0.84 (0.07)			0.81 (0.07)
Hemoglobin A1c level, %	8.78 (1.50)			8.71 (1.53)
Cholesterol level, mg/dL
HDL cholesterol	53.7 (12.6)			54.9 (12.0)
Non-HDL cholesterol	146.5 (42.8)			122.7 (34.8)
Triglyceride level, mg/dLc	88.5 (65–131)			75.0 (56–102)
Systolic blood pressure, mm Hg	116.3 (16.2)			109.0 (11.4)
Diastolic blood pressure, mm Hg	74.1 (11.6)			70.6 (9.6)
Use of blood pressure medication		37	14.1	3.2% (9)	9	3.0
Hypertensiond		59	22.4	5.4% (16)	16	5.4
Hemoglobin, g/dL	15.0 (1.7)			15.3 (1.5)
White blood cell count, cells × 103/μL	6.77 (1.97)			6.17 (1.56)
Serum creatinine level, mg/dL	1.11 (1.18)			0.90 (0.61)
Albumin excretion rate, μg/minutec	27.8 (8.8–406.3)			10.9 (6.3–28.7)
Estimated glomerular filtration rate, mL/minute/1.73 m2	98.4 (33.2)			111.7 (28.4)
Insulin dose, units/kg of body weight	0.77 (0.27)			0.81 (0.24)
Smoking status
Never smoker		148	56.3		209	70.1
Former smoker		47	17.9		33	11.1
Current smoker		68	25.9		56	18.8

Abbreviations: CVD, cardiovascular disease; HDL, high-density lipoprotein; SD, standard deviation.

^a Total n = 658 persons examined at study baseline; 97 were excluded due to prevalent CVD at baseline.

^b Weight (kg)/height (m)².

^c Values are expressed as median (interquartile range).

^d Hypertension was defined as blood pressure ≥140/90 mm Hg or use of blood-pressure–lowering medication.

Figure 1.

Survival free of cardiovascular disease (CVD) among persons with type 1 diabetes (T1D) over 25 years of follow-up, by diabetes diagnosis cohort, Pittsburgh Epidemiology of Diabetes Complications Study, 1986–2014. Vertical lines represent censored observations.

Figure 2.

Observed mean hemoglobin A_1c (HbA1c) levels among persons with type 1 diabetes over 25 years of follow-up, by incident total cardiovascular disease (CVD) status, Pittsburgh Epidemiology of Diabetes Complications Study, 1986–2014. HbA1c was censored at the time point immediately prior to the CVD event for cases. Numbers of participants represented at each time point are given in Web Table 1 (available at https://academic.oup.com/aje). Bars, standard errors.

Three models were fitted to associate HbA1c trajectories (longitudinal component) with time to total CVD (survival component): 1) a joint model where both the longitudinal and survival submodels did not adjust for other covariates; 2) a joint model where both the longitudinal and survival submodels adjusted for baseline covariates; and 3) an alternative model where both the longitudinal and survival submodels adjusted for covariates averaged over the follow-up period (i.e., updated mean values) (Table 2). In model 1, the association parameter was 0.26 (95% confidence interval (CI): 0.07, 0.40), indicating that there was strong evidence of an association between the longitudinal and survival submodels. In other words, HbA1c was associated with CVD risk at any given time t. In model 2, after adjustment for baseline diabetes duration, non-HDL cholesterol level, hypertension, and ln(AER), the association parameter of 0.23 (95% CI: 0.07, 0.37) was only slightly attenuated. Thus, each 1% unit increase in HbA1c was associated with a 1.26-fold increase (exp(0.23) = 1.26) in the risk of CVD (95% CI: 1.07, 1.45), after covariate adjustment. In model 3, adjusted for diabetes duration and updated mean non-HDL cholesterol and ln(AER), the association parameter was 0.12 (95% CI: 0.006, 0.28), corresponding to a 1.13-fold increased risk of CVD (95% CI: 0.99, 1.32) per 1% unit increase in HbA1c.

Table 2.

Estimated Coefficients for Time to Total Cardiovascular Disease From a Joint Model With a Quadratic Longitudinal Hemoglobin A_1c Submodel and a Cox Survival Submodel, Pittsburgh Epidemiology of Diabetes Complications Study, 1986–2014

Submodel and Covariate	Estimatea	95% CI
Model 1b
Longitudinal HbA1c level
Intercept	8.88	8.74, 8.98
Time, years	0.05	0.02, 0.08
Time2	−0.005	−0.007, −0.004
Cox survival
Association parameter	0.26	0.07, 0.40
Model 2c
Longitudinal HbA1c level
Intercept	8.09	7.70, 8.43
Time, years	0.05	0.02, 0.08
Time2	−0.005	−0.007, −0.003
Type 1 diabetes duration	−0.03	−0.05, −0.02
Non-HDL cholesterol level	0.01	0.008, 0.01
Hypertension	−0.32	−0.67, 0.009
Cox survival
Type 1 diabetes duration	0.07	0.05, 0.09
Non-HDL cholesterol level	0.01	0.005, 0.01
Hypertension	0.56	0.16, 0.93
ln(AER)	0.16	0.07, 0.22
White blood cell count	0.09	0.03, 0.17
Association parameter	0.23	0.07, 0.37
Model 3d
Longitudinal HbA1c level
Intercept	7.82	7.39, 8.29
Time, years	0.05	0.02, 0.08
Time2	−0.006	−0.008, −0.004
Type 1 diabetes duration	−0.04	−0.05, −0.02
Non-HDL cholesterol level	0.01	0.006, 0.013
ln(AER)	0.11	0.04, 0.17
Cox survival
Type 1 diabetes duration	0.08	0.05, 0.10
Non-HDL cholesterol level	0.01	0.006, 0.01
ln(AER)	0.24	0.17, 0.33
Association parameter	0.12	−0.006, 0.28

Abbreviations: AER, albumin excretion rate; CI, confidence interval; CVD, cardiovascular disease; HbA1c, hemoglobin A_1c; HDL, high-density lipoprotein.

^a Per unit (see Table 1).

^b Unadjusted.

^c Adjusted for baseline levels of CVD risk factors.

^d Adjusted for updated mean levels of CVD risk factors.

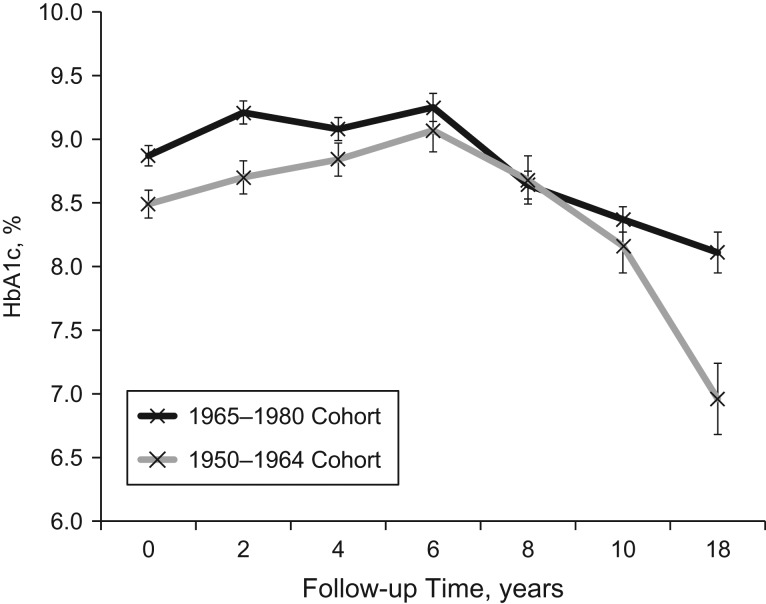
There was a significant interaction between diabetes diagnosis cohort and time, with respect to HbA1c trajectory (β_time×HbA1c = 0.13 (95% CI: 0.07, 0.19); ${\mathrm{\beta }}_{{\mathrm{time}}^2\times \mathrm{HbA1c}}=-0.01$ (95% CI: −0.19, −0.04)). The observed longitudinal trajectories of HbA1c by diabetes diagnosis cohort are depicted in Figure 3. HbA1c was generally lower in the earlier diagnosis cohort (1950–1964) throughout follow-up, and this cohort also experienced a more dramatic decline in HbA1c after 6 years of follow-up than the more recent diagnosis cohort (1965–1980). Despite this interaction between diagnosis cohort and time, with respect to HbA1c, the association between HbA1c trajectory and CVD risk was similar in both cohorts (1950–1964: per 1% unit increase in HbA1c, hazard ratio = 1.16 (95% CI: 0.92, 1.46); 1965–1980: per 1% unit increase in HbA1c, hazard ratio = 1.15 (95% CI: 0.94, 1.36)). There were no significant interactions between sex or baseline renal disease status and time with respect to HbA1c.

Figure 3.

Observed mean hemoglobin A_1c (HbA1c) levels among persons with type 1 diabetes, by diabetes diagnosis cohort, Pittsburgh Epidemiology of Diabetes Complications Study, 1986–2014. Numbers of participants represented at each time point are given in Web Table 2. Bars, standard errors.

The results from joint models of longitudinal HbA1c and the incidence of each specific manifestation of CVD, adjusted for baseline CVD risk factors, are shown in Table 3. The longitudinal trajectory of HbA1c was significantly associated with each manifestation of CVD, with a 1% unit increase in HbA1c being associated with approximately 1.2-fold increased risks of both CAD (95% CI: 1.04, 1.38) and LEAD (95% CI: 1.05, 1.43) and a 1.9-fold increased risk of stroke (95% CI: 1.32, 2.51). Adjustment for updated mean risk factor levels slightly attenuated these associations (Table 4). In these alternative models, a 1% unit increase in HbA1c was associated with a 1.1-fold increased risk of CAD (95% CI: 0.97, 1.31), a 1.7-fold increased risk of stroke (95% CI: 1.23, 2.10), and a 1.2-fold increased risk of LEAD (95% CI: 1.01, 1.40).

Table 3.

Estimated Coefficients for Time to Specific Manifestations of Cardiovascular Disease From Joint Models With a Quadratic Longitudinal Hemoglobin A_1c Submodel and a Cox Survival Submodel, Adjusted for Baseline Covariates, Pittsburgh Epidemiology of Diabetes Complications Study, 1986–2014

Submodel and Covariate	Estimatea	95% CI
Coronary Artery Disease
Longitudinal HbA1c level
Intercept	8.05	7.60, 8.40
Time, years	0.05	0.02, 0.08
Time2	−0.005	−0.007, −0.004
Type 1 diabetes duration	−0.03	−0.04, −0.02
Non-HDL cholesterol level	0.009	0.005, 0.01
Hypertension	−0.45	−0.80, −0.14
ln(AER)	0.08	0.02, 0.12
Cox survival
Type 1 diabetes duration	0.09	0.07, 0.11
Non-HDL cholesterol level	0.008	0.005, 0.01
Hypertension	0.50	0.09, 0.91
ln(AER)	0.15	0.05, 0.23
Association parameter	0.20	0.03, 0.36
Stroke
Longitudinal HbA1c level
Intercept	8.19	7.86, 8.51
Time, years	0.05	0.03, 0.08
Time2	−0.006	−0.007, −0.005
Type 1 diabetes duration	−0.02	−0.04, −0.04
Non-HDL cholesterol level	0.01	0.007, 0.01
Hypertension	−0.38	−0.68, −0.17
Cox survival
Type 1 diabetes duration	0.08	0.04, 0.11
Non-HDL cholesterol level	0.01	0.007, 0.02
ln(AER)	0.26	0.09, 0.37
Association parameter	0.62	0.28, 0.92
Lower-Extremity Arterial Disease
Longitudinal HbA1c level
Intercept	8.27	7.94, 8.62
Time, years	0.05	0.02, 0.08
Time2	−0.005	−0.007, −0.004
Type 1 diabetes duration	−0.03	−0.05, −0.02
Non-HDL cholesterol level	0.009	0.007, 0.012
Cox survival
Type 1 diabetes duration	0.06	0.05, 0.09
Non-HDL cholesterol level	0.01	0.008, 0.016
Association parameter	0.23	0.04, 0.32

Abbreviations: AER, albumin excretion rate; CI, confidence interval; HbA1c, hemoglobin A_1c; HDL, high-density lipoprotein.

^a Per unit (see Table 1).

Table 4.

Estimated Coefficients for Time to Specific Manifestations of Cardiovascular Disease From Joint Models With a Quadratic Longitudinal Hemoglobin A_1c Submodel and a Cox Survival Submodel, Adjusted for Updated Mean Covariates, Pittsburgh Epidemiology of Diabetes Complications Study, 1986–2014

Submodel and Covariate	Estimatea	95% CI
Coronary Artery Disease
Longitudinal HbA1c level
Intercept	7.79	7.33, 8.23
Time, years	0.05	0.02, 0.08
Time2	−0.006	−0.007, −0.004
Type 1 diabetes duration	−0.03	−0.05, −0.02
Non-HDL cholesterol level	0.010	0.006, 0.01
ln(AER)	0.12	0.06, 0.17
Cox survival
Type 1 diabetes duration	0.10	0.08, 0.12
Non-HDL cholesterol level	0.008	0.005, 0.01
ln(AER)	0.23	0.15, 0.30
White blood cell count	0.10	0.02, 0.17
Association parameter	0.11	−0.03, 0.27
Stroke
Longitudinal HbA1c level
Intercept	7.90	7.41, 8.27
Time, years	0.05	0.02, 0.08
Time2	−0.006	−0.007, −0.004
Type 1 diabetes duration	−0.03	−0.05, −0.02
Non-HDL cholesterol level	0.009	0.006, 0.01
ln(AER)	0.11	0.07, 0.16
Cox survival
Type 1 diabetes duration	0.07	0.03, 0.12
Non-HDL cholesterol level	0.01	0.005, 0.02
ln(AER)	0.43	0.25, 0.60
Association parameter	0.52	0.21, 0.74
Lower-Extremity Arterial Disease
Longitudinal HbA1c level
Intercept	7.96	7.53, 8.35
Time, years	0.05	0.02, 0.07
Time2	−0.005	−0.007, −0.004
Type 1 diabetes duration	−0.04	−0.05, −0.03
Non-HDL cholesterol level	0.009	0.006, 0.012
ln(AER)	0.11	0.06, 0.17
Cox survival
Type 1 diabetes duration	0.06	0.04, 0.08
Non-HDL cholesterol level	0.014	0.008, 0.018
ln(AER)	0.16	0.06, 0.24
Association parameter	0.19	0.01, 0.34

Abbreviations: AER, albumin excretion rate; CI, confidence interval; HbA1c, hemoglobin A_1c; HDL, high-density lipoprotein.

^a Per unit (see Table 1).

DISCUSSION

Our findings show that the longitudinal trajectory of HbA1c levels was associated with 25-year CVD incidence in this cohort of persons with long-standing childhood-onset T1D, and the associations were similar across the specific manifestations of CVD. The results from these joint models demonstrate that CVD risk is associated with the combination of a subject’s baseline Hba1c level and rate of HbA1c change over the course of follow-up, a longitudinal process best characterized by a quadratic curve. This model allows for both individual-level and cohort-level quadratic trajectories to be fitted and measures their effect on CVD risk. Taking into account the entire longitudinal trajectory of HbA1c, a 1% unit increase in the HbA1c trajectory is associated with a 26% increased risk of developing CVD, after adjustment for baseline CVD risk factors, and a 13% increased risk of CVD in alternative analyses adjusting for each participant’s updated mean values of CVD risk factors over follow-up.

Our results provide additional insight into the role of HbA1c in CVD risk in comparison with other methods, such as modeling of baseline HbA1c (8, 45), average HbA1c, change between the first and last measurements (8), or a measure of cumulative glycemic exposure (4) as predictors. In prior analyses of EDC data using baseline HbA1c, investigators were unable to demonstrate an association between glycemia and CAD incidence (4, 45). As the plots of HbA1c trajectories in Figure 2 show, baseline HbA1c did not differ between participants who subsequently developed CVD and those who did not. However, over time, the HbA1c trajectories between the 2 groups grew farther apart. Interestingly, in both groups, HbA1c level rose until 6 years of follow-up, albeit more so in the CVD cases, and began to decline steadily thereafter. This peak corresponds to the calendar years 1992–1994, and the subsequent decline probably reflects the implementation of intensive insulin therapy in clinical practice following publication of the results of the landmark DCCT (46). In another prior EDC analysis based on 16-year follow-up, absolute change in HbA1c was significantly associated with CAD risk (8). In those analyses, CAD cases had a mean HbA1c increase of 0.62% between the first and last measures, while noncases had a mean decrease of 0.09%. The current analyses added information by incorporating all available HbA1c measures and within-subject variability, allowing us to quantify the increase in CVD risk associated with each 1% unit increase in HbA1c trajectory while also adjusting for the mean levels of other risk factors over time. We were also able to account for the concave downward curvature of the HbA1c trajectory by incorporating quadratic terms into the longitudinal submodels.

Attenuation of the association between HbA1c trajectory and CVD incidence was greater when we adjusted for the updated mean values of other risk factors, as compared with adjusting for baseline values. Additional analyses carried out to determine which factors led to attenuation of the association between HbA1c and CVD incidence revealed that mean non-HDL cholesterol had the greatest impact (data not shown). Non-HDL cholesterol is traditionally an important CVD risk factor, regardless of diabetes status, and persons with T1D typically do not have higher non-HDL cholesterol levels than the general population. In a report using data from the National Health and Nutrition Examination Surveys, Carroll et al. (47) estimated that US adults had a mean non-HDL cholesterol concentration of 155 mg/dL (95% CI: 153, 157) between 1988 and 1994. This value is markedly higher than the mean non-HDL cholesterol level observed in the EDC cohort both at the 1986–1988 baseline (Table 1) and over the course of follow-up (mean level over all study cycles = 136.3 (standard deviation), 36.3) mg/dL); thus, non-HDL cholesterol itself does not seem to explain the increased CVD risk associated with T1D in this cohort. It is possible, however, that the effect of non-HDL cholesterol could be modified by diabetes, such that CVD risk is increased at lower levels of non-HDL cholesterol. Even given the observed attenuation of the association between HbA1c and CVD risk after adjustment for non-HDL cholesterol, these results demonstrate that glycemic control may explain more of the increased CVD risk than has previously been shown in observational studies. These findings are consistent with recent data from the DCCT/EDIC Study, where updated weighted-mean HbA1c level was found to be an important predictor of CVD incidence independent of lipid levels (12).

From a clinical perspective, these results provoke questions regarding how the observed relationship can be used to determine which patients should be targeted for CVD prevention based on their level of glycemic control. Data from a longitudinal cohort study can be used to examine etiological pathways that may take many years of follow-up to be revealed. This information is in contrast to what is clinically available, where often only a current snapshot of a risk factor level is accessible. An important unanswered question is whether some individuals are resistant to the benefits of intensive insulin therapy and continue to be at high risk for CVD, regardless of HbA1c control. As Figure 2 shows, in the Pittsburgh EDC Study, the pattern of glycemic control was generally worse over time in persons who developed CVD compared with those who did not. However, it is unclear whether hyperglycemia in CVD cases was undertreated or if this group is resistant to the benefits of appropriate treatment. The mean insulin dose between CVD cases and noncases did not differ at baseline (Table 1) or at any other point during follow-up (data not shown), suggesting the possibility that equivalent treatment for glycemia was less effective in persons who went on to develop CVD. It is possible that there are genetic factors driving both resistance to glycemic control and CVD risk. Identifying such factors is an important area of future research.

Our study had many strengths. The Pittsburgh EDC Study is a well-characterized, prospective cohort study with 25 years of follow-up that was designed to ascertain CVD incidence and clinical risk factors. CVD events were verified using death certificates and medical records by reviewers who were masked to participants’ risk factor status. Only HbA1c measurements taken prior to CVD incidence were included in these analyses, to minimize the potential for reverse causality. Using joint modeling, we were able to incorporate all HbA1c measurements and model the longitudinal trajectory while taking within-subject variability into account. The major advantage of joint modeling is that it allows the relationship between longitudinal repeated measures and a time-to-event outcome to be examined. As Lim et al. (23) emphasized, joint modeling may be particularly useful when the goal is to use longitudinal measures of biomarkers to improve prediction of an event. An objective of future research is to utilize this method to fit and validate a prediction equation for CVD that incorporates HbA1c trajectories. Another advantage of using joint modeling in this type of application is that it is able to reduce the potential for bias associated with event-free survival far beyond the last measurement of a longitudinal covariate by accounting for the subject-specific random effects (26). Use of simpler methods, such as modeling the two processes separately, may lead to bias if some subjects survive far beyond the most recent follow-up. Joint modeling is able to account for this differential follow-up time by including the subject-specific random effects within the survival model (23, 48).

One limitation of our study is that the cohort is 98% white, due to the demographics of Allegheny County, Pennsylvania (<15% African-American) and the lower incidence of T1D among African Americans during the period when the cohort was diagnosed. Consequently, it is unknown whether these results apply to more diverse groups. There was also a potential for “survivor bias,” particularly in the older diagnosis subcohort (1950–1964), because prevalent cases of CVD at baseline were excluded. A related issue is the potential problem of competing risks, particularly death from other causes. Here we presented results from cause-specific hazard models which estimated the association of HbA1c trajectory with the hazard function of CVD. It has been demonstrated that when the objective is to estimate the association between a risk factor and an outcome, rather than to predict the outcome, the cause-specific hazard provides a valid estimate (49). In the current study, the effect of competing risks was expected to be greater in the earlier diagnosis cohort (1950–1964), since this cohort was older, with greater mortality than the later diagnosis cohort (1965–1980). When stratified analyses were performed by cohort, we observed similar associations between HbA1c trajectory and CVD incidence in both cohorts, providing assurance that competing risks of death from non-CVD causes were not meaningfully influencing the results. Another limitation was the change in methodology for measuring non-HDL cholesterol at the 18-year time point. A sensitivity analysis excluding the 18-year non-HDL cholesterol data from the updated mean value produced estimates similar to those from the models including all data.

A limitation of joint modeling is that the censoring process is assumed to be independent of the random effects. If this assumption is violated, then parameter estimates may be biased (30). It is difficult to directly assess this assumption, as random effects are latent quantities and observed data do not provide adequate information for modeling the censoring mechanism. However, simulation studies have found that estimates resulting from joint models tend to be robust to misspecification of the distribution of random effects (31).

In conclusion, using joint modeling, we demonstrated that the longitudinal trajectory of HbA1c levels was associated with 25-year CVD incidence in this cohort of persons with long-standing childhood-onset T1D and that associations were similar across the specific manifestations of CVD. These results contrast with those of previous analyses that used only baseline or mean HbA1c as a predictor, which did not reveal a consistent relationship between glycemic control and CVD (8, 45). Thus, these findings underscore the importance of utilizing methods that incorporate within-subject variation when analyzing data from longitudinal cohort studies.

Abbreviations

AER

albumin excretion rate

CAD

coronary artery disease

CI

confidence interval

CVD

cardiovascular disease

DCCT

Diabetes Control and Complications Trial

EDC

Epidemiology of Diabetes Complications

EDIC

Epidemiology of Diabetes Interventions and Complications

HbA1c

hemoglobin A_1c

HDL

high-density lipoprotein

LEAD

lower-extremity arterial disease

T1D

type 1 diabetes