CalFitter: a web server for analysis of protein thermal denaturation data

Abstract

Despite significant advances in the understanding of protein structure-function relationships, revealing protein folding pathways still poses a challenge due to a limited number of relevant experimental tools. Widely-used experimental techniques, such as calorimetry or spectroscopy, critically depend on a proper data analysis. Currently, there are only separate data analysis tools available for each type of experiment with a limited model selection. To address this problem, we have developed the CalFitter web server to be a unified platform for comprehensive data fitting and analysis of protein thermal denaturation data. The server allows simultaneous global data fitting using any combination of input data types and offers 12 protein unfolding pathway models for selection, including irreversible transitions often missing from other tools. The data fitting produces optimal parameter values, their confidence intervals, and statistical information to define unfolding pathways. The server provides an interactive and easy-to-use interface that allows users to directly analyse input datasets and simulate modelled output based on the model parameters. CalFitter web server is available free at https://loschmidt.chemi.muni.cz/calfitter/.

INTRODUCTION

Proteins are the main building blocks of living organisms and are widely used in numerous biomedical and biotechnological applications. Since they are made up of only 20 amino acids, the enormous variety of their functions mainly stems from their unique structures. The interest in protein spatial organization is usually twofold: the exact position of active sites and connected residues can shed light on protein function such as enzymatic activity, intracellular transport or molecular signalling (1,2), and exact knowledge of structural elements provides methods of locating the possible sources of protein (in)stability and designing more stable variants using protein engineering (3,4). Moreover, protein misfolding and aggregation have also been reported as primary causes of several neurodegenerative diseases (5).

Streamlined protein denaturation experimental techniques to study protein (un)folding, misfolding, and aggregation include differential scanning calorimetry (DSC), fluorescence/absorbance spectroscopy, light scattering, and circular dichroism (CD) (6–10). They allow the recording of corresponding signals when a protein undergoes denaturation, e.g. due to an increase in temperature. Since those techniques produce an aggregated output from a highly complex underlying process of unfolding, they necessitate the development of software for data modelling and analysis (11,12). Such analysis usually involves the selection of an appropriate unfolding model that best fits the observed data and allows quantification of unfolding pathways in terms of the number of intermediate states, Gibbs free energy barriers separating those states, and corresponding melting temperatures (7,13,14). The importance of such information can hardly be overestimated: intermediates are often the culprits of aggregation, and energy barriers directly define protein half-lives. Hence, both provide attractive targets for protein engineering (15). Moreover, as far as molecular dynamic simulations are concerned, the number of unfolding intermediates can be used as input to cluster analysis in Markov state models, while experimental half-lives can provide guidance for the necessary length of simulations and their conditions (16,17).

Apart from general purpose but programming-intensive tools for data analysis, such as Matlab, Origin or Igor Pro, there are only a few software packages that handle different types of thermal denaturation experiments. These tools were designed to study kinetics or chemical equilibrium — KinTek Explorer, DynaFit — or are linked to a specific type of measurement — MicroCal DSC Origin and CDpal (18–20). Although the former are based on equations that can be adapted for unfolding, data and differential equations with a gradual temperature change are not supported, and the set of parameters offered requires additional manipulations for translation into those usually used to describe unfolding, e.g. Gibbs free energy differences and enthalpy changes. The latter tools offer a limited set of models for fitting, e.g. only reversible denaturation despite increasing cases of proteins unfolding irreversibly. Moreover, such tools are unable to fit global data from different sources, e.g. equilibrium and kinetic data, which may sometimes lead to simplified conclusions.

There are several advantages of global fitting over analyses of separate data sets. Fitting curves to multiple-step models is error-prone because the signal measured can be insensitive to some of the intermediates on the unfolding pathway. Moreover, consecutive steps sometimes overlap significantly and produce apparent single transition which cannot be resolved by fitting into just one data type, and different types of experimental signals must be analyzed simultaneously to overcome this problem (21). Modelling and data fitting of single experimental types individually may also fail to separate parameters enforcing re-parametrization of a model for available combinations of constants, e.g. the equilibrium constant K_eq instead of the rate ratios k_fwd/k_rev. Simultaneous fitting into a combination of different data types eventually leads to a single set of the original parameter values without any need for re-parametrization (22,23). Finally, many independent variables that have to be introduced in separate data fitting contributes to increased uncertainty and can be avoided in the global data fitting.

There is a need for a single, universal platform that handles thermal denaturation data analysis with multiple test models, a user-friendly interface, and the option to join different types of experimental data in one data fitting session. We have developed the web server CalFitter for an interactive data analysis of the commonly used thermal denaturation techniques, such as DSC, CD, and kinetic temperature-jump (T-jump) experiments. This first-of-a-kind web server offers flexible visualization of the data, quick data pre-treatment for removal of irrelevant and poor-quality data, data simulation, and fitting based on a wide range of fully reversible, irreversible, and partially-reversible unfolding models, as well as statistical data analysis of the goodness of fit. Its data fitting functionality was validated using denaturation data for six wild-type proteins from different structural families, and seven mutant proteins.

WORKFLOW

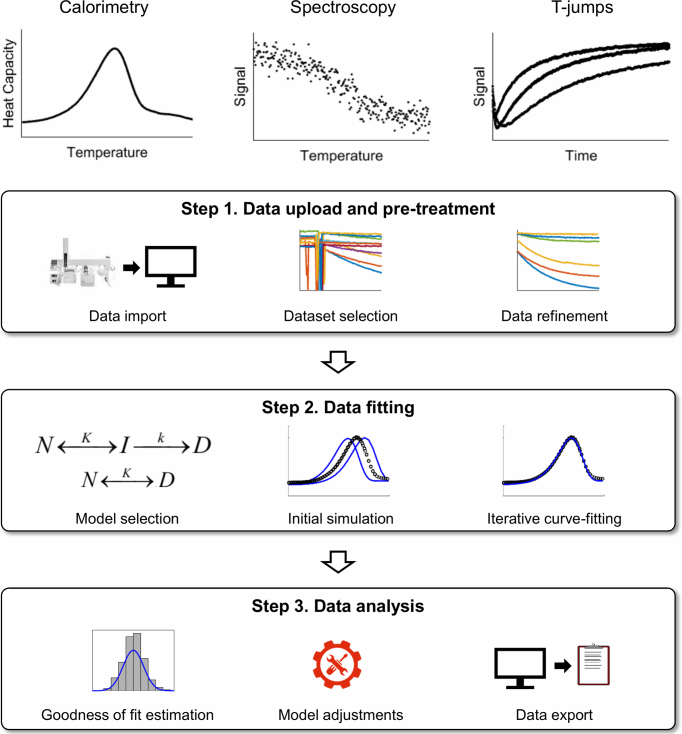
The basic workflow of CalFitter is outlined in Figure 1. There are three main phases in the process. First, the user uploads experimental datasets, plots them, and treats the data using built-in data pre-treatment options. Then the user selects a model for the data fitting, supplies initial parameter estimates, simulates the modelled dynamics, and starts the fitting process. The server performes numerical data fitting by minimizing the normalized sums of squared residuals. Once the data fitting is complete, the server returns optimal parameter values, confidence intervals calculated from asymptotic normal distribution, and statistical information about the goodness of fit. This information can be further used to estimate the outcome of the fitting and help identify the necessary adjustments to the selected model required for refitting. Different fitting sessions can be conducted in independent tabs after data uploading to compare the outcomes merely by switching the tabs. Once the fitting is complete, the results of the analysis can be exported to a single excel file for further use. Moreover, each session is given a unique ID and thus can be repeatedly accessed at the server.

Figure 1.

CalFitter workflow. The software provides an integrated analysis of data using three different types of experimental techniques: (I) calorimetry, (II) spectroscopy and (III) T-jumps. The procedure consists of three steps: (1) data upload and pre-treatment, (2) data fitting and (3) data analysis. A detailed description of the individual steps is provided in the text.

Step 1: Data upload and pre-treatment

The input to the server consists of experimental datasets of three types: (i) temperature-dependent heat capacity data from DSC, (ii) temperature-dependent spectroscopic signals (ellipticity, fluorescence, or absorbance) from spectroscopic scanning measurements, and (iii) time-dependent spectroscopic signals from folding/unfolding T-jumps. In the first step, the user interactively uploads datasets obtained from experiments and specifies the corresponding data columns, units, and experimental setup parameters such as scan rates for DSC and spectroscopy measurements or temperatures for T-jumps. In order to eliminate systematic errors during global fitting, all datasets must be collected under the same experimental conditions, e.g. pH, ionic strength, and buffer composition. The concentration dependence of protein unfolding must be verified to avoid aggregation or other association/dissociation effects.

The data files can be uploaded in either CalFitter native format (24), plain comma-separated values format (CSV), or several formats exported directly from the build-in software that comes with instruments, e.g. Chirascan or Bio-Kine. The user can select the units from the most widely used ones for temperature (°C or K), heat capacity difference (J, kJ, cal or kcal/mol K), and time (ns, μs, ms, s, min, h). There is no upper limit on the number of points in the datasets, although larger datasets take longer to calculate and can bias the fitting statistically. The web server provides a detailed Help page with guidelines about data formatting and uploading.

The user can then plot the uploaded datasets and select those that will be used for data analysis. Any combination of the dataset types can be used for global fitting. Moreover, the user can exclude some parts of the datasets such as temperature ranges with a poor experimental signal. Finally, visual data normalisation can be carried out at this step, which is of great importance in global fits, because collected experimental values usually have different units. In particular, DSC data for each scan rate can be superimposed using vertical shifts, spectroscopy data can be normalized by subtracting signal means and dividing by signal standard deviations for each dataset, and T-jump traces can be shifted vertically to the same starting point. This has only a visual effect since all the datasets are normalized automatically during the fitting as described in the section Global fitting of the Supplementary Data.

Step 2: Data fitting

Once the user is satisfied with the datasets selected and their quality, data fitting can be carried out. The procedure is similar to existing fitting software such as Origin or KinTek Explorer with a special focus on the determination of thermodynamic and kinetic parameters. First, a potential model is selected based on the desired number of steps on the unfolding pathway and their reversibility (Table 1). CalFitter currently offers models that are based on discreet macrostates on the unfolding pathways, i.e. native, intermediate, denatured, etc. Analysis based on the statistical free energy surface models of microstates (25) is beyond the scope of the web server. Second, initial parameter estimates are specified (Figure 1). The server produces initial values, however, the user needs to check and modify those values as there are currently no algorithms providing reliable initial parameter estimation for thermal denaturation models. The web server provides the option to simulate the output datasets based on the input initial parameters to assist the user at this stage. This allows the display of modelled and input data together on one graph. Finally, the user specifies whether some parameters should remain fixed during the fitting with an adjustable number of iterations. More details on mathematical modelling and data fitting can be found in the Supplementary Data and the relevant literature (11,12,24,26–28).

Table 1. The description of the models and the corresponding parameters implemented in CalFitter.

Model	Description	Model parametersa	Data sets
1 step
N −> D	A fully irreversible transition	T f, Ea, ΔH‡, ΔCp	All
N = D	A fully reversible transition with equilibrium	T m, ΔH, ΔCp	Calorimetry & spectroscopy
N = D (Van’t Hoff's)	A fully reversible transition with equilibrium and van’t Hoff's enthalpy	T m, ΔH, ΔHvh, ΔCp	Calorimetry & spectroscopy
N < = > D	A general transition with forward and reverse components	T fwd, Efwd, Trev, Erev, ΔCp	All
2 steps
N −> I −> D	A fully irreversible transition	Step 1: Tf, Ea, ΔH‡, ΔCp
		Step 2: Tf, Ea, ΔH‡, ΔCp	All
N = I −> D	A transition with a reversible step in equilibrium and an irreversible step	Step 1: Tm, ΔH, ΔCp Step 2: Tf, Ea, ΔH‡, ΔCp	Calorimetry & spectroscopy
N < = > I −> D	A general Lumry-Eyring model	Step 1: Tfwd, Efwd, Trev, Erev, ΔCp Step 2: Tf, Ea, ΔH‡, ΔCp	All
N = I = D	A fully reversible transition	Step 1: Tm, ΔH, ΔCp Step 2: Tm, ΔH, ΔCp	Calorimetry & spectroscopy
3 steps
N −> I1 −> I2 −> D	A fully irreversible transition	Step 1: Tf, Ea, ΔH‡, ΔCp	All
		Step 2: Tf, Ea, ΔH‡, ΔCp
		Step 3: Tf, Ea, ΔH‡, ΔCp
N = I1 −> I2 −> D	A transition with the reversible first step in equilibrium	Step 1: Tm, ΔH, ΔCp	Calorimetry & spectroscopy
	and the irreversible second and third steps	Step 2: Tf, Ea, ΔH‡, ΔCp
		Step 3: Tf, Ea, ΔH‡, ΔCp
N < = > I1 −> I2 −> D	A general Lumry-Eyring model with two intermediates	Step 1: Tfwd, Efwd, Trev, Erev, ΔCp	All
		Step 2: Tf, Ea, ΔH‡, ΔCp
		Step 3: Tf, Ea, ΔH‡, ΔCp
N = I1 = I2 −> D	A transition with two reversible steps in equilibrium	Step 1: Tm, ΔH, ΔCp	Calorimetry & spectroscopy
	and an irreversible step	Step 2: Tm, ΔH, ΔCp
		Step 3: Tf, Ea, ΔH‡, ΔCp
4 steps
N −> I1 −> D	A two-branch irreversible unfolding pathway	Step 1: Tf, Ea, ΔH‡, ΔCp	All
N −> I2 −> D		Step 2: Tf, Ea, ΔH‡, ΔCp
		Step 3: Tf, Ea, ΔH‡, ΔCp
		Step 4: Tf, Ea, ΔH‡, ΔCp

^a T _m – the melting temperature, T_f – the reference temperature of an irreversible step at which the corresponding rate is 1 (fwd. – forward rates; rev. – reverse rates), ΔH – the enthalpy change (at T_m if ΔC_p is nonzero; vh – van’t Hoff's); ΔH^‡– the activation enthalpy change (at T_f or T_m for irreversible and general steps, respectively, if ΔC_p is nonzero); E_a – the activation energy; ΔC_p – the heat capacity change. Since T-jumps are based on the relaxation kinetics, they cannot be simulated by the models with reversible steps assumed in equilibrium.

Step 3: Analysis of the results

Once the fitting is complete, the web server updates the parameter values, their confidence intervals and provides statistical information from the fitting such as Akaike (AIC) and Bayesian (BIC) information criteria and residual plots. At this point, the user can either accept the model or change it and carry out refitting. The most common strategy is to start from the simple model with a few steps and then add additional steps while checking the goodness of fit visually or using the AIC and BIC values (29). The common sign of over-parameterization is drifting parameter values and large confidence intervals. In this case, either the model should be simplified by removing some steps, or some fitting parameters should be held constant. Finally, the user can also check the sensitivity of the output to input parameters or undo the last fit before exporting the results in standard formats.

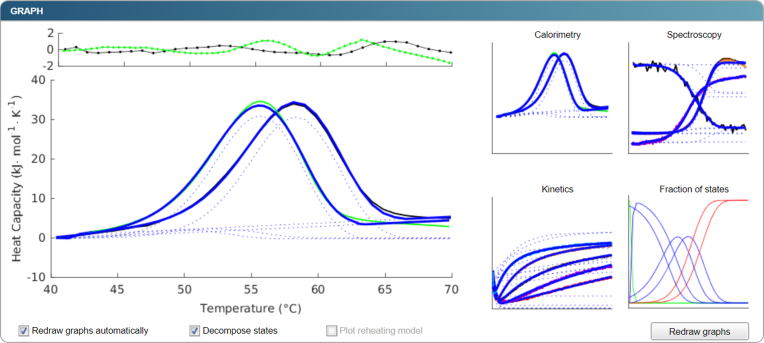
The output consists of the unfolding pathway, the updated parameter values that best describe the data included, their confidence intervals, and other statistical information from the fitting such as goodness of fit. There are four data types available for visualising the output (Figure 2). The first type is raw experimental and pre-treated data, each dataset being separate or combined with other datasets of the same type. The second type uses modelled signals matching the selected datasets given the current parameter values. A state decomposition may be carried out with this type whereby signal contributions from each step of the unfolding pathway to the overall modelled signal are shown. The third type uses the modelled protein state fractions as functions of temperature or time. Finally, the fourth type uses residuals from the fit, which might shed further light on the quality of the fit and main discrepancies between the modelled and experimental data. The user can then export the graphs and the corresponding datasets as an archive with figures and settings files or as an Excel file.

Figure 2.

An example of the graphical output. Initial datasets with modelled signal in blue are depicted as icons on the right-hand side and can be zoomed-in and displayed on the left-hand side. The zoomed-in version also depicts the residuals at the top so that a user can estimate the quality of the fit and the presence of any systematic errors or unexplained data variation. In the presented case, waves are apparent in the residual plot that are indicative of an approximately 5% misfit at high temperatures. When the option ‘Decompose states’ is selected, the contribution of each step to the overall signal is plotted in dotted lines. Apart from the plots of data and corresponding modelled signals, modelled fractions of states are presented in one of the graphs.

EXPERIMENTAL VALIDATION

The CalFitter performance was thoroughly validated with all the three data types. DSC data analysis was tested on previously published datasets: the thermograms of wild-type hen egg lysozyme, wild-type haloalkane dehalogenases LinB, DbjA, DhaA, fibroblast growth factor FGF2 and variants of DhaA and FGF2 engineered for higher thermostability (24,30). Calorimetry curves were curve-fitted and compared with the output from MicroCal DSC Origin and the standalone Matlab-based CalFitter 1 (24). Spectroscopy data analysis was tested on four variants of DhaA and compared with the output from CD-pal. Finally, T-jump data analysis was validated using four different global datasets consisting of several traces of DhaA wild-type and compared against the values obtained using KinTek Explorer. In all the cases, the output values produced by the CalFitter web differed from the previously published by <0.1% on average for temperature related parameters, and by <6.8% on average for energy and heat-related parameters (Table 2). Maximal discrepancies for the latter were mainly due to smaller parameter values and/or wide confidence intervals. Moreover, in those cases, the CalFitter web simulation with the parameters from the other tools produced visually the same quality of the fit suggesting that the differences stem from the numerical procedures used for fitting rather than from a different model behaviour.

Table 2. Experimental validation of CalFitter web server. Discrepancies are given in terms of absolute % difference for parameters obtained for energies and temperatures.

			Temperature variables (Tm, Tf)		Energy variables (Ea, ΔH, ΔHvh)
Data type	Software used for comparison	Number of datasets	Average discrepancy	Maximal discrepancy	Average discrepancy	Maximal discrepancy
DSCa	MicroCal DSC Origin	67	0.06%	0.42%	3.03%	15.06%
	Matlab-based CalFitter 1		0.00%	0.01%	0.00%	0.07%
CDb	CD-pal	44	0.01%	0.10%	0.05%	1.18%
T-jumpsc	KinTek Explorer	35	0.09%	0.21%	6.74%	10.87%

^abased on ΔH, ΔH_vh, and T_m from a non-two state model with ΔH_vh.

^bbased on T_m and ΔH for a one-step fully reversible model.

^cdata from global fitting based on E_a and T_a for a two-step fully irreversible model.

The global fitting provided by the web server was also used to analyse experimental data for stable variants of FGF2 protein designed recently using computer-assisted protein engineering (30). This analysis revealed new biophysical insights, namely the presence of an unfolding intermediate, and demonstrated a good agreement between the in silico predicted Gibbs free energy differences and the differences in the transition barriers for the first unfolding step estimated from experiments. Another case study of thermal denaturation of haloalkane dehalogenase DhaA112 engineered for stability is described in the Supplementary Data. This new case reveals an unfolding intermediate and provides quantitative estimates of unfolding rates.

CONCLUSIONS AND OUTLOOK

CalFitter is a web server that offers users a one-stop-shop for data analysis from commonly used temperature denaturation experiments. Not only does it offer a wider range of models for each separate data type when compared to most of the existing analogues, but it also enables the combination of different dataset types, such as equilibrium and T-jump data, in a single global data analysis. This feature has never been implemented for thermal unfolding studies before, to the best of the authors’ knowledge. The fitting procedures used were optimised and validated using several dozen datasets from different sources, including recently published data as well as cross-validation using the existing software for each data type analysis.

The server is complemented by an easy-to-use graphical interface that allows users to interactively pre-treat the data by excluding irrelevant parts or artefacts, selecting the desired subset for analysis and fitting, and simulating the behaviour of the models when parameters change. The hidden mathematical calculations and fitting makes the process of data analysis accessible to users without any prior expertise of mathematical modelling. The web server graphical output consists of four different plot types to provide the user with a full image of the modelled pathway and its correspondence to the supplied data.

In the future, we will implement an ‘advanced mode’ with a model editor that the users can manually input any model of their choice using a simple text entry with an intuitive syntax similar to KinTek Explorer or DynaFit. We are also working on a module for rapid initial parameter estimations. This module will estimate starting values based on the shape of the curves, rendering the web server even more user-friendly for researchers with limited experience in modelling data from thermal unfolding studies. Finally, we plan to add additional modelling capabilities to the existing modules, e.g., double T-jumps and singular value decomposition of CD spectra, as well as to develop modules for analysis of other types of experimental data, e.g., protein chemical denaturation and hydrogen-deuterium exchange mass spectrometry.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

Ministry of Education of the Czech Republic [LO1214, LQ1605, LM2015051, LM2015047 and LM2015055]; Czech Grant Agency [GA16-07965S]; European Union [720776 and 722610]; A.K. is a Brno Ph.D. Talent Scholarship Holder and funded by the Brno City Municipality. Funding for open access charge: Ministry of Education of the Czech Republic.

Conflict of interest statement. None declared.