Unimolecular Reaction Energies for Polycyclic Aromatic Hydrocarbon Ions

Abstract

Imaging photoelectron photoion coincidence spectroscopy was employed to explore the unimolecular dissociation of the ionized polycyclic aromatic hydrocarbons (PAHs) acenaphthylene, fluorene, cyclopenta[d,e,f]phenanthrene, pyrene, perylene, fluoranthene, dibenzo[a,e]pyrene, dibenzo[a,l]pyrene, coronene and corannulene. The primary reaction is always hydrogen atom loss, with the smaller species also exhibiting loss of C₂H₂ to varying extents. Combined with previous work on smaller PAH ions, trends in the reaction energies (E₀) for loss of H from sp²-C and sp³-C centres, along with hydrocarbon molecule loss were found as a function of the number of carbon atoms in the ionized PAHs ranging in size from naphthalene to coronene. In the case of molecules which possessed at least one sp³-C centre, the activation energy for the loss of an H atom from this site was 2.34 eV, with the exception of cyclopenta[d,e,f]phenanthrene (CPP) ions, for which the E₀ was 3.44 ± 0.86 eV due to steric constraints. The hydrogen loss from PAH cations and from their H-loss fragments exhibits two trends, depending on the number of unpaired electrons. For the loss of the first hydrogen atom, the energy is consistently ca. 4.40 eV, while the threshold to lose the second hydrogen atom is much lower at ca. 3.16 eV. The only exception was for the dibenzo[a,l]pyrene cation, which has a unique structure due to steric constraints, resulting in a low H loss reaction energy of 2.85 eV. If C₂H₂ is lost directly from the precursor cation, the energy required for this dissociation is 4.16 eV. No other fragmentation channels were observed over a large enough sample set for trends to be extrapolated, though data on CH₃ and C₄H₂ loss obtained in previous studies is included for completeness. The dissociation reactions were also studied by collision induced dissociation after ionization by atmospheric pressure chemical ionization. When modeled with a simple temperature-based theory for the post-collision internal energy distribution, there was reasonable agreement between the two sets of data.

1. Introduction

Polycyclic aromatic hydrocarbons (PAHs) have been under investigation for some time as molecules and ions of interstellar interest. This interest has spurred many laboratory studies on their formation and stability in simulated interstellar (and circumstellar) environments to attempt to get a better understanding of their potential role in astrochemistry.¹

The Lifshitz group were a major contributor to the discussion of large carbonaceous ion dissociation. Ho et al. studied the two primary channels, H loss and acetylene loss, of ionized naphthalene (NAP) using time resolved photodissociation mass spectrometry (TRPD-MS). ² They obtained activation energies of 4.48 eV for H loss and 4.41 eV for the loss of C₂H₂.² Ling et al. measured the energetics for ionized anthracene (ANT) and phenanthrene (PHE),³ pyrene (PYR)⁴ and fluoranthene (FLN),⁵ by the same method. They found in general that H loss required ≈4.4 eV, sequential H loss a much lower activation energy of ≈2.9 eV, and the C₂H₂ loss activation energy was found between 4 and 4.5 eV above the precursor ion.⁶ Computationally, Holm et al. studied several ionized PAHs (NAP, ANT, PYR and coronene (COR)) at the B3LYP/6-311++G(2d,p) level of theory.⁷ They determined that the H loss had the same activation energy for all molecules (≈4.7 eV) and that C₂H₂ loss had activations energies of 4.0 eV (NAP), 2.7 eV (ANT), 6.9 eV (PYR) and 8.0 eV (COR). Paris and co-workers calculated H₂ loss to be nearly isoenergetic with H atom loss in ionized coronene (5.04 eV compared to 4.86 eV for H loss).⁸ There has been very little work done on superhydrogenated PAHs. A theoretical study was conducted on protonated naphthalene which had the H loss at an activation energy of 2.71 eV which is in good agreement with that for H loss from dihydronaphthalene, DHN.⁹ Reitsma et al. have also shown the effect of hydrogenation on coronene using soft x-ray spectroscopy; they showed that the presence of hydrogenation under these high energy conditions act as a protector for the carbon backbone.¹⁰ To the contrary, Wolf et al. observed the opposite when they studied ionized hydrogenated pyrene via high energy collision-induced dissociation (CID) mass spectrometry and action spectroscopy. Here, they observed that the appearance energy for CH₃ loss decreased with increasing hydrogenation.^11–13

Previous work in our laboratory focused on the dissociative photoionization of small PAHs (naphthalene, anthracene, pyrene, 1,2-dihydronapthalene (DHN) and 9,10-dihydrophenanthrene (DHP)) and their fragments via imaging photoelectron−photoion coincidence spectroscopy (iPEPICO) and tandem mass spectrometry (CID) experiments.^14–18 In these studies, three distinct types of reactions were observed: the direct fragmentation of ionized PAHs by loss of H and C₂H₂ (and occasionally C₄H₂), the sequential dissociation from these PAH ions after the loss of the first hydrogen atom and the dissociation of hydrogenated PAHs (possessing at least one sp³ carbon center). Dehydrogenation and acetylene loss were the dominant channels with NAP also showing a small amount of H₂ and C₄H₂ loss.^{16, 17} For NAP and ANT, H loss was found to require 4.2 and 4.3 eV, respectively, in line with the results of Lifshitz.^{16, 17} Acetylene loss requires 4.1–4.2 eV, mildly lower than the results from TRPD-MS. Sequential H-loss dissociation from the [M–H]⁺ ion of NAP and ANT had E₀ values of 3.2 and 2.7 eV, respectively, consistent with those found by Lifshitz. However, it must be noted that what looks initially like a simple dissociation, particularly the ones involving H atom loss, have been revealed by computational chemistry to often involve complex structural rearrangement of the PAH ion skeleton and even ring-opening reactions. Case in point was our previous computational study on ionized naphthalene which showed that the primary H atom loss product is a ring-opened ion,¹⁹ and the extensive investigation of hydrogen and carbon-skeleton rearrangement by Trinquier et al.^{20, 21} Johansson et al. demonstrated that ionized anthracene likely isomerized to phenanthrene prior to C₂H₂ loss,²² but higher level calculations suggested this did not take place.¹⁶ These incongruities highlight the difficulty in deriving concrete answers for these systems computationally; even small changes in the level of theory used can result in kinetically significant changes in the reactions surfaces. Theoretical studies were also conducted on ionized pyrene (PYR), following the dissociation from the precursor ion (C₁₆H₁₀^+·) all the way to C₁₄⁺on the singlet surface.¹⁴ The calculated energies for hydrogen loss were similar to what has been observed, with the second hydrogen atom loss being substantially lower in energy than the first, and the initial H loss having a calculated activation energy of 5.10 eV and the second H loss lying only 3.5 eV higher. The relatively low level of theory used in this study results in the high E₀ for H loss. H₂ loss was also calculated with a dissociation energy of 4.12 eV, which would indicate that this might be a viable avenue for dehydrogenation. C₂H₂ loss from pyrene was reported at a very high energy of 6.02 eV, while C₄H₂ loss was a sequential fragmentation, following the initial loss of H, having an E₀ of 4.54 eV.

In this study, we explore the unimolecular reaction energetics for ionized acenaphthylene, fluoranthene, fluorene, cyclopenta[d,e,f]phenanthrene, perylene, dibenzo[a,e]pyrene, dibenzo[a,l]pyrene, coronene and corannulene and re-examine it for pyrene using iPEPICO spectroscopy and RRKM modeling. The goal is to establish clear, experimentally-derived trends in the reaction energies over a wide range of PAH ion sizes. We also employ CID mass spectrometry coupled with a simple temperature-based internal energy model to extract reaction energies based on experiments on a longer timescale than possible by iPEPICO.

2. Experimental Procedures

Acenaphthylene, fluoranthene, fluorene, cyclopenta[d,e,f]phenanthrene, coronene, corannulene, pyrene and perylene were all purchased from Sigma-Aldrich (Sigma-Aldrich, Oakville, Canada) and used without further purification. Dibenzo[a,e]pyrene, dibenzo[a,l]pyrene were synthesized at the PAH Research Institute in Greifenberg (Dr. Werner Schmidt).

2.1. iPEPICO

iPEPICO²³ experiments were conducted at the VUV beamline at the Swiss Light Source (Paul Scherrer Institut, Villigen, Switzerland) and the set-up has previously been described in detail.^24–27 Briefly, monochromatic VUV synchrotron radiation (4-8 meV resolution depending on the photon energy) is used as a photoionization source to ionize gaseous molecules introduced via a heated oven inlet system.²⁸ Ions are directed towards a time-of-flight mass spectrometer (TOF) while the ejected electrons are sent in the opposite direction towards an imaging microchannel plate (MCP) detector, with each event time and position stamped. Threshold electrons are focused onto the center of the MCP, and the non-zero kinetic energy electrons detected in a small ring region around this center spot give a good representation of the hot electron background of the threshold signal. The mass spectrum corresponding to this ring is subtracted from the center TOF distribution to obtain the threshold ionization mass spectra.²⁹

The time-of-flight mass spectrometer has two acceleration regions, and operates using a low and long draw-out field, which means that ions dissociating on the microsecond timescale do so in this region. The neutral fragment carries a portion of the kinetic energy, which means that the kinetic energy of the photoion will only be a fraction of its value based on its relative mass to the precursor ion. This results in an asymmetrically broadened daughter ion TOF peak characteristic of the dissociation rate constant.³⁰ However, if the leaving neutral is much lighter than the parent ion, the rate information may be obscured by the instrumental peak width, as is the case in most H-loss processes in PAHs. This can be counteracted to a degree by varying the total residence time in the acceleration region by changing the extraction field, and relying on the shift in the breakdown diagram as an indication for the rate constants. We measured each molecule using two acceleration fields, 120 and 60 V/cm. The resulting two breakdown diagrams provide two kinetic regimes under which to model the data, and are satisfied by a single set of kinetic parameters. The photon energies used in this experiment range from 12 to 22 eV with steps of 0.1 eV in the region where the relative abundances are changing rapidly.

Unresolved peaks in the mass spectra (such as M, M–H, M–2H etc.) were deconvolved to get accurate branching ratios. This was accomplished using the multi peak fitting protocol included in the IGOR PRO 4 (WaveMetrics, Lake Oswego, OR) software package. Once deconvolved, it was possible to correct the ion abundances for the ¹³C contribution of each peak to get a more accurate measurement of the branching ratios at each energy. The fractional abundance of the precursor ions and each fragment is then plotted versus photon energy in the breakdown diagram. The shape and slope of the breakdown curves are characteristic of the reaction mechanism, and establish parallel and sequential processes.^{31, 32} When applied to hydrogen loss from PAH cations, this also means that sequential hydrogen atom and hydrogen molecule losses can be distinguished unambiguously. However, there are two challenges that still lead to error bars on the activation energies sometimes even two orders of magnitude larger than ultimately possible using PEPICO.³³ First, the need to extrapolate the measured rate curve to its vanishing point, thus accounting for the kinetic shift, increases the uncertainty, and is further complicated by the limited rate information unless the first H-loss dissociation channel competes with a loss of a heavier hydrocarbon neutral fragment. Second, large competitive shifts (i.e., when a second, parallel process has a higher threshold and slowly starts competing as the energy is increased) are often encountered and lead to a poorly constrained activation energy for the higher lying channel.

Mass-selected threshold photoelectron spectra were acquired for selected compounds in the onset region to establish ionization energy values. These are listed in Table 1 and shown in Figure S1. Aside from hot bands, all but one of the molecules studied exhibit a strong, narrow, primary ionization peak which means the vertical and adiabatic ionization energies are essentially the same. For dibenzo[a,l]pyrene, the 0-0 band is somewhat broader (mostly due to difficulty in data accumulation) and thus the error limits are significantly larger.

Table 1.

Experimentally determined activation energies (E₀) and entropies of activation (Δ^‡S) for reactions R1-R25. The first column consists of iPEPICO results while the second column are APCI-CID results. The final column are the literature values found for comparison from (a) Zheng et al.³⁸ (b) Ling et al.⁵ and (c) Fugiwara et al.³⁹

		iPEPICO Results		APCI-CID results		Literature values
Reaction		E0 (eV)	Δ‡S1000K (J K-1 mol-1)	E0 (eV)	Δ‡S1000K (J K-1 mol-1)	E0 (eV)	Δ‡S (J K-1 mol-1)
Fluorene (IE = 7.895 ± 0.005 eV)d
R1	C13H10+· --> C13H9+ + H·	2.20 ± 0.50	-21 ± 43	2.30 ± 0.04	15 ± 7	2.43a
R2	C13H9+ --> C11H7+· + C2H2·	4.23 ± 0.77	-11 ± 42	3.8 ± 0.1	12 ± -4
R3	C13H9+ --> C9H8+ + C4H2	4.05 ± 0.68	-11 ± 36	3.74 ± 0.04	19 ± 4
R4	C13H9+ --> C13H8+· + H·	4.13 ± 0.68	13 ± 36	3.9 ± 0.1	25 ± 4
Cyclopenta[d,e,f]phenanthrene (IE = 7.775 ± 0.005 eV) d
R5	C15H10+· --> C15H9+ + H·	3.44 ± 0.86	84 ± 72	3.0 ± 0.1	4 ± 4
R6	C15H9+ --> C13H7+· + C2H2·	4.08 ± 1.3	-10 ± 74
R7	C15H9+ --> C15H8+· + H·	4.40 ± 0.74	37 ±41
Acenaphthylene (IE = 8.005 ± 0.005 eV) d
R8	C12H8+· --> C12H7+ + H·	4.41 ± 0.25	29 ± 13	4.2 ± 0.1	17 ± 6
R9	C12H8+· --> C10H6+· + C2H2	5.21 ± 0.34	46 ± 16	4.2 ± 0.1	29 ± 5
R10	C12H7+ --> C12H6+· + H·	3.50 ± 0.94	-11 ± 63
Fluoranthene (IE = 7.845 ± 0.005 eV) d
R11	C16H10+· --> C16H9+ + H·	4.86 ± 1.1	49 ± 68	3.75 ± 0.05	35 ± 2	4.38 ± 0.04b	12.1 ± 2b
R12	C16H9+ --> C16H8+· + H·	3.29 ± 0.85	10 ± 64			3.6	14.4
R13	C16H10+· --> C14H8+· + C2H2	2.59 ± 0.62	-43 ± 42	3.5 ± 0.1	-10 ± 6
Perylene (IE = 6.960 ± 0.001 eV)e
R14	C20H12+· --> C20H11+ + H·	4.75 ± 0.6	38 ± 35	4.75 ± 0.07	54 ± 4	4.62c
R15	C20H12+· --> C20H10+· + H2	4.58 ± 1.3	40 ± 69	4.7 ± 0.1	30 ± 5
R16	C20H11+ --> C20H10+· + H·	2.63 ± 1.2	-12 ± 84
Pyrene (IE = 7.42 ± 0.01 eV)f
R17	C16H10+· --> C16H9+ + H·	4.16 ± 0.69	-5 ± 37	4.1 ± 0.2	-37 ± 8	4.60 ± 0.04b	10.7 ± 2b
R18	C16H9+--> C16H8+· + H·	3.09 ± 1.22	-14 ± 84
Corannulene (7.83 eV) g
R19	C20H10+· --> C20H9+ + H·	4.24 ± 1.03	8 ± 58
Coronene (IE =7.29 ± 0.03 eV) g
R20	C24H12+· --> C24H11+ + H·	4.41 ± 0.83	12 ± 44	3.7 ± 0.1	-1 ± 5	4.64c
Dibenzo[a,e]pyrene (IE = 7.11 eV) e
R21	C24H14+· --> C24H13+ + H·	4.44 ± 0.56	48 ± 31
R22	C24H14+· --> C24H12+· + H2	4.46 ± 0.62	56 ± 34
R23	C24H13+ --> C24H12+· + H·	3.50 ± 0.65	66 ± 36
Dibenzo[a,l]pyrene (IE = 7.05 ± 0.02 eV) d
R24	C24H14+· --> C24H13+ + H·	2.85 ± 0.56	-3 ± 38
R25	C24H13+ --> C24H12+· + H·	2.35 ± 1.3	-4 ± 100

^dTPES measurement, present result. Data presented in Figure S3 of supporting information.

^eRef ⁴⁰

^fRef ⁴¹

^gRef ⁴²

2.2. APCI-CID

Atmospheric pressure chemical ionization (APCI) experiments were performed on a Micromass Quattro LC (Waters Micromass, Manchester, UK) triple quadrupole mass spectrometer equipped with a Z-spray source. 30 μL of sample solution was injected into the APCI source via a mobile phase of pure chlorobenzene or chloroform at a flow rate of 0.3 mL/min. The source block temperature was set at 150 °C while the probe temperature was kept at 400 °C. The corona and cone voltages were held steady at 3.4 kV and 30 V respectively. The first quadrupole resolution was held constant at a setting of 17 (as set in the Masslynx software) to provide baseline separation of all mass spectral peaks. Collision induced dissociation (CID) was carried out using argon as a collision gas (argon at a pressure of ≈1×10⁻³ mbar), and an energy range (E_lab) of 1–47 eV. During CID experiments, the second quadrupole resolution was held at a setting of 12 (slightly less than unit resolution) to increase sensitivity. The relative abundance of the precursor ions and each fragment is then plotted versus centre-of-mass collision energy (E_com) in order to generate the experimental breakdown diagram.

3. Computational Procedures

Precursor neutrals, ions and possible products were calculated using the Gaussian 09 suite of programs for all sample molecules presented here.³⁴ All structures were optimized at the B3-LYP/6-31G(d) level of theory. The extracted vibrational frequencies and rotational constants were employed in the RRKM modeling of the data (see below). For pyrene, coronene, corannulene and perylene, the precursor ion and first fragment ion (specifically the first hydrogen loss product) were calculated at the two lowest multiplicities. This was done to confirm whether the singlet or triplet state is lower in energy for the first fragment ion. For these molecules, UCCSD/6-31G(d) single point energy calculations were also completed to gain better accuracy for the comparison.

3.1. RRKM modelling

RRKM (Rice Ramsperger Kassel Marcus) theory was used to determine the 0 K activation energy (E₀) and entropy of activation (Δ^‡S, all values reported at 1000K) by fitting the experimental breakdown diagrams.

The rate of each dissociation channel, k(E), is calculated using the formula;

$$k(E)=\frac{\sigma N^{‡}(E-E_0)}{h\rho (E)}$$ (1)

σ represents the reaction degeneracy, h is Planck’s constant, N^‡ (E − E₀) is the sum of the number of internal states (vibrational and rotational states) for the transition state up to internal energy (E − E₀) and ρ(E) is the density of states for the reactant ion at internal energy (E) as calculated via the Beyer and Swinehart direct count algorithm.³⁵ The vibrational states of the transition state were approximated using the harmonic vibrational frequencies of the precursor ion. From this list an appropriate mode was deleted to account for the reaction coordinate. An example of this would be for the case of H loss from the precursor ion, where the vibrational frequency removed corresponded to that of a C−H bond stretch; this stretching normal mode corresponds best to the C−H bond breaking reaction coordinate. Of the remaining 3N − 7 modes for the transition state, the five modes with the lowest frequencies were scaled by a factor to adjust the entropy of activation (factors less than one increase Δ^‡S while values greater than one decrease Δ^‡S). The actual fitting of the experimental breakdown diagram was completed through the use of the minimal-PEPICO program.³⁰ In short, the program combines the physical parameters of the iPEPICO experimental set up at the SLS with temperature (for the initial neutral molecule internal energy distribution) and the RRKM k(E) values for each channel (adjusted through the choice of E₀ and Δ^‡S) to calculate experimental branching ratios for the ion dissociation as a function of photon energy, which are then compared to the experimental breakdown curves. Photon energies were converted to ion internal energies using the ionization energy of each molecule. The activation energies and entropies are then optimized to obtain the best fit to experiment. Error bars were established by finding the limits in E₀ and Δ^‡S that resulted in acceptable fits to the experimental data, which means 0.5% (max) from the relationship:

$$1-\frac{\Sigma ((Expt)(Calc))}{\sqrt{(\Sigma ((Expt)(Expt))\Sigma ((Calc)(Calc)))}}$$ (2)

Where Expt and Calc are the experimental and calculated data points in the breakdown curves.

In the case of modeling energy-resolved CID data, the only difference was the inclusion into the model of a changing internal energy distribution with E_com. Here the post-collision ions are assigned an effective temperature depending on the centre-of-mass collision energy, and thus a “thermal” vibrational energy distribution, according to the relationship:

$$T_{\text{eff}}=T_{\text{i}}+\alpha E_{\text{com}}$$ (3)

where T_i represents the initial temperature and α describes the relationship between the centre-of-mass collision energy (E_com) and the increase in the effective temperature (T_eff). This is clearly the “Achilles heel” of this present model and thus we previously only attempted to derive relative energetics and entropies for the systems under study.³⁶ As will be seen, modeling the E₀ for these reactions is quite precise when the error is only attributed to the quality of the theoretical fit to the experimental data. However, the systemic uncertainty due to the limitations in the model itself can only be assessed by comparison to the iPEPICO data.

4. Results and Discussion

4.1. Reaction summary

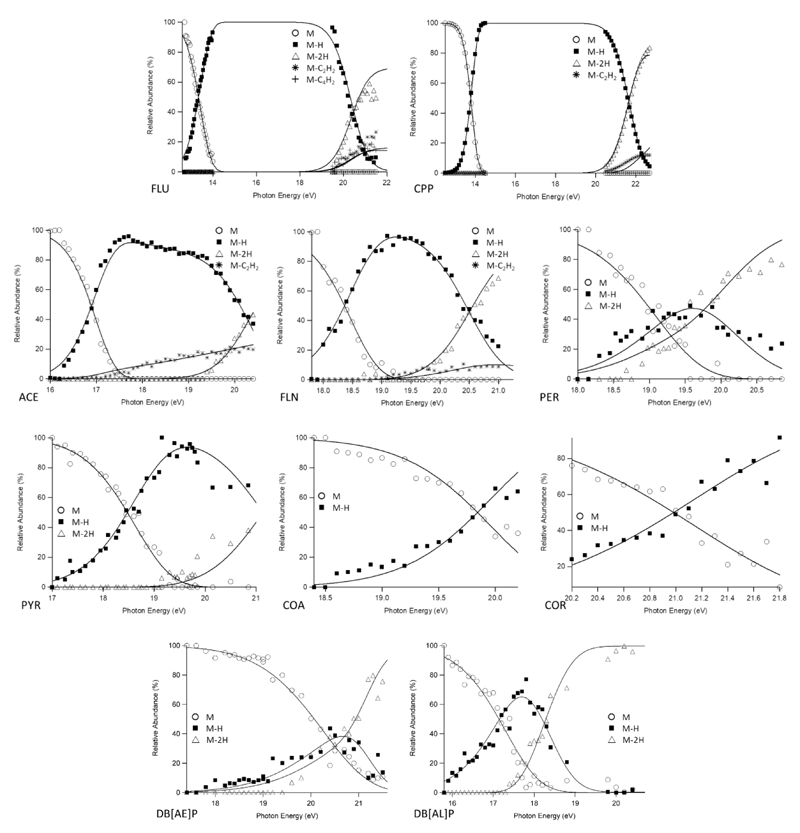
The observed unimolecular reactions are listed below (molecular ion structures can be found in supporting information Figure S2). Figure 1 summarizes the experimental breakdown curves for all of the ions probed herein, with the results of the RRKM modeling listed in Table 1. Since complete potential energy surfaces were not calculated for each system under study, the correspondence of the derived E₀ to a specific transition state or thermodynamic dissociation limits is not clear, and so we refer to these energies as simply “reaction energies”, that is, the minimum energy for a reaction to proceed to products.

Figure 1.

Experimental breakdown diagrams (points) measured with an extraction field of 120 V/cm. Solid lines are statistical fits created through RRKM modelling. Curves obtained at 60V/cm can be found in supporting information, Figure S3.

Fluorene (FLU)

R1       C₁₃H₁₀^+● → C₁₃H₉⁺ + H^●

R2       C₁₃H₉⁺ → C₁₁H₇^+● + C₂H₂

R3       C₁₃H₉⁺ → C₉H₇^+● + C₄H₂

R4       C₁₃H₉⁺ → C₁₃H₈^+● + H^●

Cyclopenta[d,e,f]phenanthrene (CPP)

R5       C₁₅H₁₀^+● → C₁₅H₉⁺ + H^●

R6       C₁₅H₉⁺ → C₁₃H₇^+● + C₂H₂

R7       C₁₅H₉⁺ → C₁₅H₈^+● + H^●

Acenaphthylene (ACE)

R8       C₁₂H₈^+● → C₁₂H₇⁺+ H^●

R9       C₁₂H₈^+● → C₁₀H₆^+● + C₂H₂

R10     C₁₂H₇⁺ → C₁₂H₆^+● + H^●

Fluoranthene (FLN)

R11     C₁₆H₁₀^+● → C₁₆H₉⁺ + H^●

R12     C₁₆H₉⁺ + → C₁₆H₈^+● + H^●

R13     C₁₆H₁₀^+● → C₁₄H₈^+● + C₂H₂

Perylene (PER)

R14     C₂₀H₁₂^+● → C₂₀H₁₁⁺ + H^●

R15     C₂₀H₁₂^+● → C₂₀H₁₀^+● + H₂

R16     C₂₀H₁₁⁺ → C₂₀H₁₀^+● + H^●

Pyrene (PYR)

R17     C₁₆H₁₀^+● → C₁₆H₉⁺ + H^●

R18     C₁₆H₉⁺ → C₁₆H₈^+● + H^●

Corannulene (COA)

R19     C₂₀H₁₀^+● → C₂₀H₉⁺ + H^●

Coronene (COR)

R20     C₂₄H₁₂^+● → C₂₄H₁₁⁺ + H^●

Dibenzo[a,e]pyrene (DB[AE]P)

R21     C₂₄H₁₄^+● → C₂₄H₁₃⁺ + H^●

R22     C₂₄H₁₄^+● → C₂₄H₁₂⁺ + H₂

R23     C₂₄H₁₃^+● → C₂₄H₁₂⁺ + H^●

Dibenzo[a,l]pyrene (DB[AL]P)

R24     C₂₄H₁₄^+● → C₂₄H₁₃⁺ + H^●

R25     C₂₄H₁₃^+● → C₂₄H₁₂⁺ + H^●

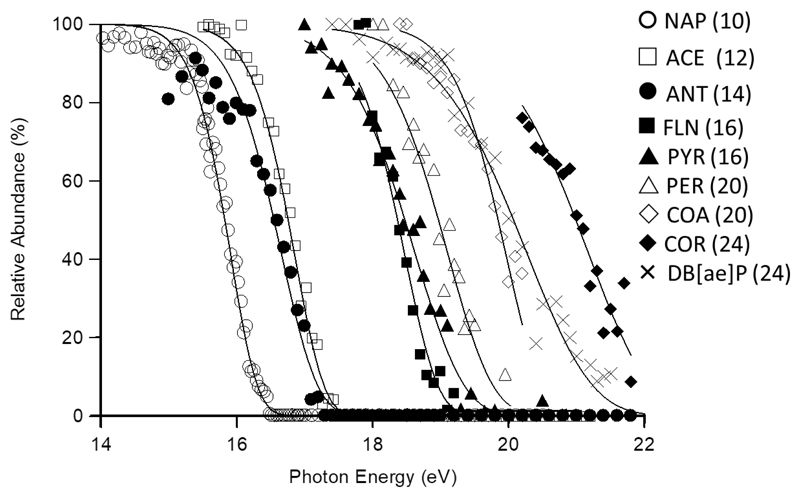
Figure 2 illustrates the role kinetic shift plays in the dissociation of PAH ions of increasing carbon number. The figure exhibits the precursor (M⁺) ion decay curves for PAHs ranging from naphthalene¹⁷ and anthracene¹⁶ through to coronene, and includes all species that share a common primary dissociation activation energy. Clearly the dissociation thresholds occur at increasingly higher photon (and thus internal) energy as the size of the PAH increases. So, any discussion of the reaction energies for these systems must take into account the reaction rates as done herein by employing the RRKM k(E) in the modeling process.

Figure 2.

Comparison of precursor ion decay curves for all unsaturated PAHs studied that have a common dissociation threshold (naphthalene and anthracene added for completeness, data from ref 16,17), illustrating the effect of kinetic shift moving the dissociation thresholds to increasingly higher photon (and hence internal) energy. The number in parenthesis corresponds to the number of carbon atoms in each molecule.

Overall, the dominant process is H atom loss, with all ions exhibiting this reaction. Fluorene (FLU) and cyclopenta[d,e,f]phenanthrene (CPP) are the only molecules studied in this paper which possess a sp³ carbon. In both cases, the first hydrogen loss preceded any further fragmentation by a large energy margin. They then go on to behave like the unsaturated PAH cations previously reported, namely they undergo the sequential loss of another H and a hydrocarbon unit, principally C₂H₂ (and C₄H₂ for FLU). The larger unsaturated PAHs only lose H, with some H₂ loss also observed for ionized perylene. For the loss of H from an sp³-C, the E₀ values are 2.20 ± 0.50 eV for FLU and 3.55 ± 0.86 eV for CPP, while the Δ^‡S for the two channels are -21 ± 43 J K^-1 mol^-1 and 84 ± 72 J K^-1 mol^-1, respectively. As mentioned, the sequential H losses (R2 and R6) are significantly higher with CPP coming in with E₀ = 4.40 ± 0.74 eV and Δ^‡S = 37 ± 41 J K^-1 mol^-1, while FLU has an E₀ value of 4.13 ± 0.68 eV and an activation entropy of 13 ± 36 J K^-1 mol^-1. The loss of C₂H₂ from the H-loss fragment ions (R3 and R7) is quite close in energy to the second hydrogen atom loss with E₀ values of 4.08 ± 1.3 eV for CPP and Δ^‡S, -11 ± 42 J K^-1 mol^-1 and -10 ± 74 J K^-1 mol^-1, respectively. The final reaction for fluorene, loss of C₄H₂ (R4), gave an E₀ of 4.05 ± 0.68 eV and a Δ^‡S of -11 ± 36 J K^-1 mol^-1. To date, there has not been anything reported in the literature for comparison and this channel was not observed in the CID work (see below). Another PAH has nevertheless been found to undergo the same fragmentation process at a similar energy, namely naphthalene at an E₀ of 4.27 ± 0.07 eV.¹⁷

Acenaphthylene (ACE) and fluoranthene (FLN) are related by the addition of a benzene ring to the former. For the primary dehydrogenation channels, R8 and R11, the E₀ values are 4.41 ± 0.25 eV for ACE and 4.86 ± 1.1 eV for FLN. In the case of FLN, Ling and Lifshitz determine the dehydrogenation energetics and found an E₀ of 4.38 eV,⁵ which is lower than our value but within the rather large associated uncertainty. The Δ^‡S values were both positive (29 ± 13 J K^-1 mol^-1 for ACE and 49 ± 68 J K^-1 mol^-1 for FLN), in agreement with the literature (12.1 J K^-1 mol^-1).⁵ Both molecules also exhibit a sequential dehydrogenation reaction (R10 and R12) for which E₀ = 3.50 ± 0.94 eV and Δ^‡S = -11 ± 63 J K^-1 mol^-1 (ACE) as well as E₀ = 3.29 ± 0.85 eV and Δ^‡S = 10 ± 64 J K^-1 mol^-1 (FLN) have been determined. Ling and Lifshitz derived an E₀ of 3.6 eV and Δ^‡S of 14.4 J K^-1 mol^-1 which are in very good agreement with the present results.⁵ The final reactions for this pair is the loss of acetylene, though for ACE it is a primary channel (R10) coming directly from parent molecule, whereas for FLN it comes from the first dehydrogenation product (R13). Looking at ACE first, the loss of C₂H₂ has an E₀ value almost 1 eV higher in energy than dehydrogenation (E₀ = 5.21 ± 0.34 eV) with a Δ^‡S value which is only slightly higher (46 ± 16 J K^-1 mol^-1). For fluoranthene, the loss of C₂H₂ comes after dehydrogenation (R13). The activation energy for this reaction is lower than the second dehydrogenation channel (E₀ = 2.59 ± 0.62 eV) while the entropy is quite negative (-43 ± 42 J K^-1 mol^-1), indicating a certain amount of reorganization is required prior to fragmentation.

Perylene (PER) and pyrene (PYR) cations do not lose hydrocarbon fragments. They sequentially lose hydrogen atoms instead (R14 and R16 for PER and R17 and R18 for PYR), and perylene also shows evidence for the loss of molecular hydrogen H₂ (R15). For the dehydrogenation channels in PER, R14 has E₀ = 4.75 ± 0.6 eV and Δ^‡S = 38 ± 35 J K^-1 mol^-1 and R16 has E₀ = 2.63 ± 1.2 eV and Δ^‡S = -12 ± 84 J K^-1 mol^-1. Pyrene energetics are an E₀ of 4.16 ± 0.69 eV and Δ^‡S of -5 ± 37 J K^-1 mol^-1 for the first dehydrogenation (R17) and E₀ = 3.09 ± 1.22 eV and Δ^‡S = -14 ± 84 J K^-1 mol^-1 for R18. Our previous iPEPICO data for pyrene was obtained at a single source voltage, and coupled with a less robust sample introduction system this led to vast uncertainty in the onset energy.¹⁴ The final reaction for this pair is the H₂ loss from perylene (R15): E₀ = 4.58 ± 1.3eV and Δ^‡S = 40 ± 69 J K^-1 mol^-1.

Coronene (COR) and corannulene (COA) only undergo dehydrogenation. The activation energy for both molecules are in the typical range for H loss from an sp²-C (COA E₀ = 4.24 ± 1.03 eV and COR E₀ = 4.41 ± 0.83 eV). The entropy of activation for both molecules are also very similar, being slightly positive (COA Δ^‡S = 8 ± 58 J K^-1 mol^-1 and COR Δ^‡S = 12 ± 44 J K^-1 mol^-1).

Dibenzo[a,e]pyrene ions exhibits a competition between H and H₂ loss from the molecular ion, the only ion other than perylene to do so (Table 1). The reaction energies for H and H₂ loss are 4.44 and 4.46 eV, respectively; so essentially the same. In contrast, dibenzo[a,l]pyrene does not yield H₂ since the reaction energy for H loss is so low, 2.85 ± 0.56 eV. This low E₀ is due to the unique geometry of the molecule in which the two benzo groups are twisted out of the molecular plane because of steric hindrance caused by bay hydrogen atoms (Figure S4).³⁷ Castillo et al. computationally demonstrated that the sequential loss of a second H atom can lead to a 5-member ring-containing structure.³⁷ Based on energetics arguments they concluded that DB[AE]P could exhibit a combination of H₂ and sequential 2H loss reactions, consistent with the present observations. They also left the door open to possible H₂ loss from DB[AL]P, but on the energy- and time-scale of the present experiment, we do not observe this channel.

4.2. Trends in the Overall Data

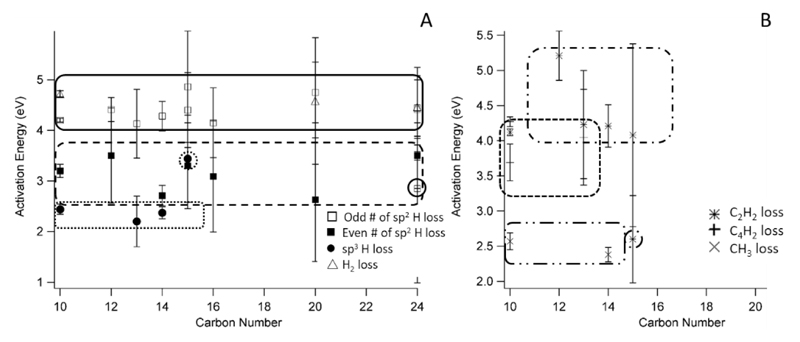
Figure 3 shows the various trends for activation energies (E₀) derived across all of the ions studied, including those previously published (for completeness).

Figure 3.

Activation energy (E₀) versus carbon number for all studied ionic reactions ranging from naphthalene (C₁₀) to coronene (C₂₄). Outlines highlight various groupings. Plot A shows dehydrogenation reactions while plot B illustrates the hydrocarbon loss channels. Outliers, discussed in the text, are circled.

The only reaction observed over the entire range of sizes is the loss of a single hydrogen atom from an sp² carbon site, with all energies lying within the range of ~4.40 eV.^{17, 18} This indicates that, for this reaction, the number of carbons as well as their layout (catacondensed versus pericondensed) has little to no effect on the energetics, consistent with the computed results of Holm et al. ⁷ The only exception was H loss from DB[a,l]P ions, which has a much lower energy due to the unique geometry of the ion. Three ions also underwent H₂ loss, naphthalene (C₁₀)¹⁷ perylene (C₂₀) and dibenzo[a,e]pyrene (C₂₄). Interestingly, the activation energies for these reactions are very close in energy to the first dehydrogenation channels (~4.65 eV) but, on the timescale of the iPEPICO experiment, this channel is minor and does not compete with hydrogen atom loss to any serious degree.

The loss of a second hydrogen atom from an sp² carbon is observed for molecules ranging from 10 (naphthalene) up to 20 carbons (perylene) in size. The activation energies for this channel have an average value of ~3.16 eV. This illustrates that the second hydrogen atom loss is energetically more favourable than the first. Pairing of the two unpaired electrons to make a triple bond would explain this trend. This “even-odd,” alternating higher and lower activation energy pattern is expected in hydrocarbons and has been previously observed in an earlier theoretically study of the dissociation of ionized pyrene.¹⁴

The final dehydrogenation channel is the loss from an sp³ carbon center. Four molecules have been studied with either 1 or 2 sp³ carbon centers.¹⁸ As would be expected, the energy required to remove a hydrogen atom is significantly lower (on average 2.34 eV) than the same loss from fully unsaturated PAHs. One exception to this energy range is CPP, which required over 1 eV more to remove the hydrogen atom (3.55 ± 0.86 eV) and has a large positive entropy of activation (84 ± 72 J K^-1 mol^-1). When the structures of the radical cations (Figure 4) are considered, the large positive Δ^‡S for CPP can be explained by the rigid structure of the molecule. The cyclopentadiene bond angle and the atomic distance between the carbon atoms on the rings adjacent to the 5-membered ring are highlighted in Figure 4. In FLU, when the H atom is lost, the bond angle decreases (from 108.8° to 106.9°) which has the effect of increasing the distance between the outer rings. CPP not only does not display this change, the bond angle actually increases with the loss of the hydrogen atom, thus forcing the outer rings even closer to one another – though the change is quite minor. This could explain why the values for H loss are so different – CPP requires more energy to overcome the rigidity of the molecule as the H atom must be released without significant skeletal relaxation. FLU, on the other hand, has a greater ability to flex the central ring which would allow for the lower E₀ and negative Δ^‡S.

Figure 4.

Molecular structure of fluorene (FLU), cyclopenta[d,e,f]phenanthrene (CPP) cations and their H atom loss product ions as determined by B3-LYP/6-31G(d). The key bond angles for the cyclopentadiene ring and the atomic distances are indicated.

Figure 3B shows the trends for hydrocarbon fragment loss. The only channel that was observed in more than 2 PAH ions was loss of acetylene.^{16, 17} The E₀ for this channel is quite close to the dehydrogenation and H₂ loss from ionized PAHs, with an average energy of 4.16 eV. Fluoranthene-H also loses C₂H₂ but as a sequential channel, thus the energy required is much lower. The only other dissociation observed directly from ionized PAHs is the loss of C₄H₂. This also has an energy above 4 eV (4.16 eV) though it has only been observed in two ions (naphthalene and fluorene-H).

The last observed fragment is the loss of methyl from the dihydro-PAHs. They are mentioned here to add to the complete picture though this work has been previously reported.¹⁸ The energy required for the proposed isomerization and dissociation is on average 2.48 eV.

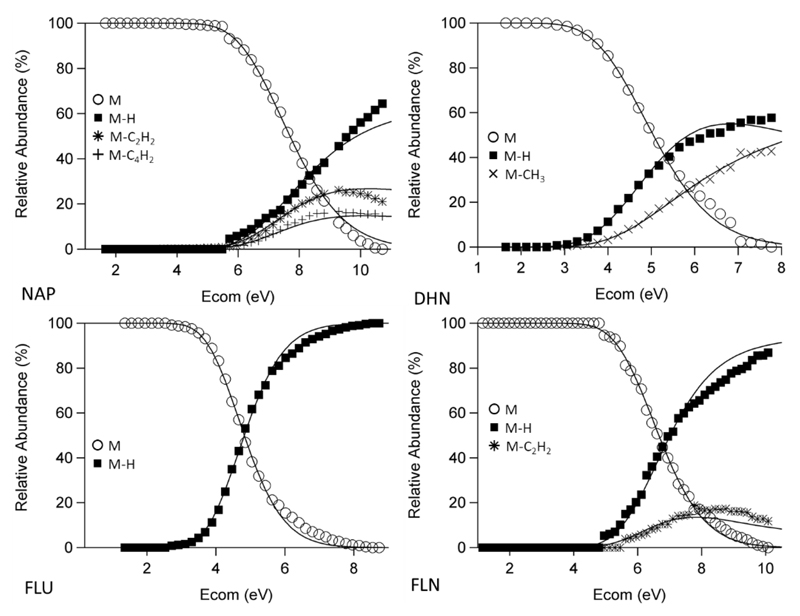
4.3. Comparison to APCI-CID Results

All molecules which have been studied by iPEPICO have also been looked at by APCI-CID. Figure 5 shows a select group of these results. All the energetics values for the molecules studied in this work are found in Table 1. Agreement between theory and experiment is quite good, but breaks down at higher E_com due to the linearity of eq. 3. The remaining APCI-CID results have been included in Figure S5. Figure 6 shows the comparison between the fitted activation energies between iPEPICO and APCI-CID experiments. It can be seen that they have fair agreement between the two methods, with CID results on average being either lower than or equal to the iPEPICO results. It seems that the higher in energy the transition the larger the difference between the E₀ values from both methods, likely due to the limitations in the model in describing the ion internal energy population over a large internal energy range. There is very good agreement for both sp³-C channels, the loss of H and CH₃, which are much lower in energy than all other reactions observed; conversely, the loss of H from sp²-C centres, are consistently lower for the APCI-CID results than the iPEPICO.

Figure 5.

Examples of APCI-CID experimental breakdown diagrams with theoretical curves of best fit. Included are naphthalene (NAP), 1,2-dihydronaphthalene (DHN), fluorene (FLU) and fluoranthene (FLN). Others can be found in supporting information. See text for experimental conditions.

Figure 6.

Comparison of activation energies derived from iPEPICO and APCI-CID data. The solid line indicates 1:1 agreement.

Even with the differences in the individual values, the trends still hold in both methods as the discrepancies are systematic, in that the majority of the reactions at a certain energy are affected to the same degree. The groupings also remain intact, though the spread is much larger than with the iPEPICO results. Even though the two methods are not in perfect agreement, the CID model described here is a quick way to get an idea of the reactions and energetics. It should also be noted that since the reaction time for CID processes on the triple quadrupole is significantly longer than it is for iPEPICO (milliseconds compared to microseconds), the CID results can exhibit reactions that are not seen in iPEPICO. An example of this would be for pyrene, where not only was H loss observed but also H₂ and C₂H₂ loss.

5. Conclusions

The unimolecular dissociation of seven radical cations have been investigated by iPEPICO spectroscopy. In total, 20 different reactions were observed and fit using RRKM modelling. For FLU and CPP, the dominant channel was the loss of H from an sp³-C centre and afterwards, these molecules behaved like typical unsaturated PAHs by losing H, C₂H₂ and for FLU C₄H₂. The remaining ions all lost a hydrogen atom as their primary dissociation channel. Acetylene loss was observed for ACE and FLN, though the former was a competing reaction to H loss and the latter lost it as a sequential dissociation. Sequential H loss was observed for all molecules other than COA and COR and H₂ loss was only observed for PER and DB[AE]P.

The results from this work were combined with our previous results in order to examine trends in the dissociation energies of ionized PAHs. Four main trends have been observed, the loss of hydrogen from a sp³-C centre, the first and second loss of H from a sp²-C centre and the loss of acetylene, and all trends indicated an independence of the reaction energy with respect to PAH size. The loss of hydrogen from an sp³-C centre is the lowest in energy as the molecule strives to regain the stability associated with an unsaturated PAH; this loss is ≈ 1 eV lower in energy than any other dissociation channel. The loss of acetylene is observed in smaller PAHs, with a cost of ≈ 4.16 eV. The first hydrogen loss from an sp²-C is the only reaction observed in all cases and it is consistently the primary avenue of dissociation, at ≈ 4.4 eV. The sequential loss of H has a lower energy requirement of only ≈ 3.16 eV which indicates that the ions gain stability from the pairing of unsaturation sites, which was predicted in previous computational results. Furthermore, the important role of kinetic shift in these systems was highlighted.

Finally, all of these results were compared with APCI-CID mass spectrometry modeled with a simple temperature-based description of the post-collision internal energy distribution. The CID results for the activation energies tend to be lower than those derived from iPEPICO but the trends observed in the iPEPICO results are maintained. The timescale for dissociation in the CID experiment is significantly longer than in the iPEPICO experiment, and this can result in reactions being observed that are different than those exhibited by the latter method.