Full dimensional potential energy surface and low temperature dynamics of the H₂CO+OH → HCO + H₂O reaction†

Abstract

A new method is proposed to represent analytically the potential energy surface of reactions involving polyatomic molecules capable to describe accurately long range interactions and saddle points, needed to describe low temperature collisions. It is based on two terms, a reactive force field term and a many body term. The reactive force field term describes accurately the fragments, long interactions among them and the saddle points for reactions. The many body term increase the desired accuracy everywhere else. This method has been applied to the OH + H₂CO → H₂O + HCO, giving a barrier of 27.4 meV. The simulated classical rate constants with this potential are in good agreement with recent experimental results [ Ocaña et al., Astrophys. J., 2017, submitted], showing an important increase for temperatures below 100K. The reaction mechanism is analyzed in detail here, and explains the observed behavior at low energy by the formation of long lived collision complexes, with roaming trajectories, with a capture observed for very long impact parameters, > 100 a.u., determined by the long range dipole-dipole interaction.

Introduction

Organic molecules have been widely detected in the interstellar medium (ISM), in hot cores, hot corinos, protoplanetary disks, etc¹. Being among the largest stable molecules detected in space when these molecules have more than 6 atoms they are commonly called Complex Organic Molecules (COMs)². The first organic molecules detected, and probably among the most abundant ones, are formaldehyde³ and methanol⁴. Formaldehyde and methanol are efficiently formed by irradiation of CO-H₂ mixture ices^5,6 and by successive hydrogenation of CO on dust grains^7–10, while in gas phase many of the sequential steps present reaction barriers and are typically neglected¹¹. At the colder regions at about 10K, these species can not thermally desorb, and they should pass to gas phase after absorbing high energy cosmic ray or UV radiation. Molecules like methanol, which forms very strong hydrogen bonds, are not easily desorbed by UV absorption, and instead they break and only the photofragments go to gas phase, as recently measured^12,13. Therefore, if methanol is produced in ices, its photofragments once in gas phase can react to form back methanol¹³. Another possibility, is that methanol desorbs as a photofragment of a larger molecule still not found¹².

The gas phase route to form COMs was recently opened by the measurement of a fast increase of the methanol with hydroxyl radical reaction rate constant at low temperature¹⁴, which was later confirmed by other experiments^15,16. This gas phase reaction rate constant allowed to model properly the abundance of CH₃O radical observed in Barnard 1b¹⁶. The CH₃OH + OH reaction has two barriers of ≈ 0.3 and 0.1 eV, respectively, and the increase of the rate constant was explained by a tunneling mechanism within a transition state theory (TST) formalism¹⁴. The tunneling was estimated by calculating the imaginary frequency along the reaction coordinate at the saddle point for the reaction.

A recent study¹⁷ has shown that this imaginary frequency was artificially too large, and that using a more realistic value yields too low reaction rate constants. Siebrand and co-workers also proposed an alternative model, in which a methanol dimer is formed which when colliding with OH gives rise to a OH-CH₃OH complex at energies below the OH + CH₃OH reactants threshold, so that it can only decay towards products by tunneling through the reaction barriers. This model was based on quasi-classical trajectory (QCT) simulations for the complex formation rate constants and TST with tunneling for the reaction probability. In their calculation, Siebrandt et al. assumed a proportion of methanol dimers of 0.3 in the experiments^14–16. A recent analysis by Shannon et al.¹⁸ showed that this proportion is at most one order of magnitude lower at the lowest studied temperature, 50 K.

In order to solve this apparent problem, further experimental studies are needed to address the probability of complex forming, which in the model of Siebrand and co-workers¹⁷ seems to be too high. In the experiments of Shannon and co-workers¹⁴ the CH₃O product was measured, appearing at a similar rate as the disappearance of the OH reactant. However, it is difficult to experimentally determine quantitatively the branching ratio to assess that the measured rate constant is completely assigned to the formation of CH₃O products. For this reason, realistic theoretical simulations are convenient to unravel this dichotomy, beyond the TST models with tunneling made until now, describing the full reaction dynamics.

Recently, the reaction rate constant of formaldehyde with hydroxyl radical was measured below 100 K using the CRESU technique¹⁹. As in the case of methanol, the reaction rate constant shows an important increase with decreasing temperature. These rate constants were used to model the formation of HCO in different astrophysical environments, with a modest impact, since there are many other routes to form this molecule. The fast increase of the rate constant with decreasing temperature was well reproduced by QCT calculations based on an accurate potential energy surface (PES). The aim of this work is to show the method developed to generate such PES and to discuss the low temperature reaction dynamics to understand the interesting rise of the rate constant in this regime.

The paper is organized as follows. First, in section II, the method used to calculate the PES and represent it by analytic functions is described. Section III is devoted to show and discuss the QCT dynamical results, and finally in section IV some conclusions are extracted.

Potential energy surface

Ab initio calculations

The H₂CO + OH → HCO + H₂O reaction involves the OH(²Π) radical and for its description a multiconfigurational method is required. The spin-orbit splitting between the ²Π_3/2 and ²Π_1/2, of 17.3 meV, is not taken into account in the electronic state calculation. The ²Π state of OH is doubly degenerate (without including spin-orbit couplings). The ground and first excited states of H₂CO + OH have been calculated at CASPT2 level, in order to determine if the first excited state may yield to products. The first excited state correlates with products in the excited HCO(1²A″) state, which correlates with CO(a³Π). This state has been well characterized²⁰ and it has a linear equilibrium geometry, while the ground HCO(X²A′) is bent (with an equilibrium angle close to the HCO angle in H₂CO). As a result, the saddle point for the excited electronic state is much higher (≈ 1 eV) than that of the ground electronic state. For this reason here we shall only consider the ground electronic state to study this reaction.

There are several previous ab initio calculations of the stationary points for the ground electronic state for this reaction^21–24, shown in Table 1. These works use different methods to optimize the geometry and/or to calculate the harmonic zero-point energy (ZPE). The barrier height including ZPE vary between them, from -5.2 meV to 173 meV, but all the energies without ZPE are always positive.

Table 1.

Stationary points and Zero Point Energies calculated using RCCSD(T)-F12a method in this work and comparison with previous results (with the basis set used in parenthesis). All energies are in meV relative to the reactants in their equilibrium configuration. In the E+ZPE column, the quantity in parenthesis corresponds to the energy of reactants including ZPE.

Method	Energy	ZPE	E+ZPE
H2CO+OH
This work VDZ-F12	0.0	957.0	957.0 (0.0)
CCSD(T)24 aug-cc-pVTZ	0.0	954.0	954.0 (0.0)
MP423 6-311++G(3df,3pd)	0.0	971.5	971.5 (0.0)
MP222 aug-cc-pVDZ	0.0	960.9	960.9 (0.0)
H2CO…OH
This work	-235.8	1045.8	810.0 (-147.0)
CCSD(T)24	-244.2	1041.3	797.1 (-156.9)
MP423	-157.8	1042.5	884.7 (- 86.8)
MP222	-227.0	1041.8	814.8 (-146.1)
Saddle point
This work	27.1	949.4	976.5 (19.5)
CCSD(T)24	2.4 × 10−2	948.8	948.8 (- 5.2)
MP423	70.1	932.4	1003.1 (31.6)
MP222	203.1	930.9	1134.0 (173.1)
HCO…H2O
This work	-1420.1	973.4	-446.7 (-1403.7)
CCSD(T)24	–	–	– (–)
MP423	-1450.3	1028.7	-421.7 (-1393.2)
MP222	-1582.6	983.7	-598.9 (-1559.8)
HCO+H2O
This work	-1301.1	937.9	-363.3 (-1320.3)
CCSD(T)24	-1260.6	934.3	-326.3 (-1280.3)
MP423	-1387.7	950.6	-437.1 (-1408.6)
MP222	-1456.2	937.1	-219.1 (-1180.0)

In this work we adopt the RCCSD(T)-F12a method²⁵, implemented in the MOLPRO package²⁶, using the VDZ-F12 basis set²⁷. Test calculations with larger basis set were done on the stationary points, obtaining essentially the same results. To check the adequacy of the RCCSD(T) method the T1 diagnostic²⁸ for a large variety of geometries being always smaller than 0.03, the larger value obtained at the saddle point, showing that multireference methods are not needed. This method is expected to be more accurate than all the previous ones, because the F12 method describes better the electronic correlation. All the geometries were optimized using the same RCCSD(T)-F12a method, and the results are shown in Table 1. We find a barrier of 19.5 and 27.1 meV, with or without ZPE, which we consider to be more precise than all previous values.

In all previous works^21–24 the reaction rate constants were calculated using the TST method with tunnelling based on the normal modes calculated at the saddle point. In order to go beyond TST methods, dynamical calculations have to be done, and in this work we shall use a QCT approach. In order to describe collisions at low temperature, a high correlated method as RCCSD(T)-F12 is required to have the proper accuracy of the PES. Ab initio molecular dynamics calculations are impractical because of the long computing time of a single point, and the high number of points on each individual trajectory at low collision energies. Thus an analytic fit is required to study the collision dynamics in these conditions, as described below.

Analytic fit of the PES

The fit of the PES of systems for more than 4 atoms is a challenging problem, specially when devoted to reactive collisions. The method of Bowman et al.²⁹, based on the direct fit with a many body term using permutationally invariant polynomials of the internuclear distances, has been applied to systems up to 10 atoms. For example, this method has been succesfully used to study S_N2 reactions³⁰ and water clusters³¹. However, this method is not applicable to low temperatures because of the difficulty of describing long range interactions properly. Instead, here we use a variation of an alternative recently used to describe the proton transfer in ${\text{H}}_4^{+}$ and ${\text{H}}_5^{+}$^32–34 considering properly the long range interactions.

In this approach, the electronic Hamiltonian matrix is separated in two terms as

$$H=H^{diab}+H^{MB},$$ (1)

where H^diab is an electronic diabatic matrix, in which each diagonal matrix element describes a rearrangement channel. Thus, reactants and products are properly described by these terms and also the long range interactions. In the case of ${\text{H}}_4^{+}$ and ${\text{H}}_5^{+}$ these terms were described by a triatomics-in-molecules method (TRIM)^32,34, which is an extension of the diatomics-in-molecule (DIM)^35,36. This allows to describe not only di- and triatomic products of physical relevance in those cases, but also a rather good description of the intermolecular interactions among them, including long range interactions. This method, however, is difficult to be extended to large polyatomic systems, as the one treated in this work. For this reason we shall use here a reactive force field (RFF)³⁷ approach, described below.

The H^MB term in Eq. (1) is a many-body term matrix added to get the desired accuracy. For describing the ground electronic state, a diagonal matrix with all elements being equal. This matrix element is expanded in terms of permutationaly invariant polynomials^38,39, as in the method of Bowman et al.²⁹. In this case, the RFF does not have all permutation symmetry, but only the physically allowed by energy, i.e., the permutation of the two equivalent hydrogen atoms of H₂CO reagent. As a consequence the MB term only consider this permutation symmetry. This term must vanish at long distance in any rearrangement channel³⁸.

Reactive force field

Here we use the Empirical Valence Bond method⁴⁰, which considers each rearrangement channel as a diabatic state that can be represented by an element of a matrix. The off-diagonal terms, V_eff, is an effective coupling term among the rearrangement channels, in such a way that the lowest eigenvalue of the matrix becomes continuous and describes the global potential for the ground electronic state. There are three rearrangement channels in this reaction, one for OH and H₂CO reagents, and two for HCO + H₂O products, leading to a 3×3 matrix representation of the RFF, represented as

$$H^{diab}=\left(\begin{array}{ccc}{H}_{11}& V_{eff}& V_{eff}\\ V_{eff}& H_{22}& 0\\ V_{eff}& 0& H_{33}\end{array}\right),$$ (2)

where H₁₁ = V^OH + V^H₂CO + V^OH+H₂CO, H₂₂= V^H_aCO + V^H₂O + V^{H_aCO−H₂O} + Δ and H₃₃ is equivalent to H₂₂ but replacing hydrogen H_a by H_b. The zero of energy is set at the minimum of the reactants at long distances and Δ= -1.30 eV corresponds the exothermicity of the reaction. Below we describe each of the terms separately.

a. PES of the fragments

The potential of isolated formaldehyde and water are described by a force field (FF) of the form

$$\begin{array}{l}{V}^A={\displaystyle \sum _b{D}_e{\left(1-e^{-\alpha \left(b-b_e\right)}\right)}^2+{\displaystyle \sum _{\theta }{k}_{\theta }{\left(\theta -{\theta }_0\right)}^2}}\\ +{\displaystyle \sum _{\varphi }{k}_{\varphi }\left(\varphi -{\varphi }_0\right)+{\displaystyle \sum _b{\displaystyle \sum _{b^{\prime }}{k}_{b{b}^{\prime }}\left(b-b_0\right)\left(b^{\prime }-b_0^{\prime }\right)}}}\\ +{\displaystyle \sum _{\theta }{\displaystyle \sum _{{\theta }^{\prime }}{k}_{\theta {\theta }^{\prime }}\left(\theta -{\theta }_0\right)\left({\theta }^{\prime }-{\theta }_0^{\prime }\right)}}\\ +{\displaystyle \sum _{\theta }{\displaystyle \sum _b{k}_{\theta b}\left(b-b_0\right)\left(\theta -{\theta }_0\right)}}\end{array}$$ (3)

with b corresponding to the internuclear distances of the bonds of the molecule, and θ are the angles beween the bonds. ϕ are the improper dihedral angles of formaldehyde, absent in the case of water molecule, and the subindex 0 refers to the equilibrium value of each coordinate. The parameters are optimized to reproduce the ab initio points calculated along several classical trajectories in the harmonic potential calculated from the ab initio normal modes. For those coordinates leading to dissociation, further points were added to better adjust this process. The summary of number of points, errors of the H₂CO and H₂O fragments are listed in Table 2.

Table 2.

Errors (number of points in the energy interval considered) of the H₂CO, H₂O, HCO and OH fragments obtained in the fit.

	Error (meV)
Fragment	E < 1 eV	E < 2 eV
H2CO	84.4 (3158)	111 (3781)
OH	4.42×10−3 (44)	6.33×10−3 (67)
HCO	93.0 (1322)	125 (2695)
H2O	63.8 (949)	393 (3029)

The PES for HCO presents several minima, and can not be properly described by such simple FF functional form. Instead, the HCO potential is represented by a many body expansion form fitting the parameters to reproduce the calculated ab initio points with the gfit3C program⁴¹. A summary of the fit is in Table 2.

Finally, the OH potential energy curve have been fitted to the ab initio points following the method of Aguado and Paniagua⁴².

b. Intermolecular PES

The V^OH−H₂CO and V^HCO−H₂O interactions between fragments, defined below Eq. 2, are described by two terms: a long range term, V_lr, and a short range, V_sr, on each arrangement. The transition between long and short range potentials in the entrance channel is done with a smooth switching function based on a hyperbolic tangent function.

The long range term, V_lr, has been introduced for the leading dipole-dipole interaction between OH and H₂CO systems, and neglected for the two HCO + H₂O products, because the reaction is exothermic and these terms are not expected to play an important role. The dipole of OH (d_OH) and H₂CO (d_H2CO) reagents with respect to their corresponding center-of-mass have been calculated at their equilibrium geometries, and is considered to be constant because the dipole of each fragment does not vary significantly with the vibrations. The long range potential is then given by the usual dipole-dipole interaction term⁴³

$$V_{lr}=\frac{R^2{\mathbf{\text{d}}}_{OH}\cdot {\mathbf{\text{d}}}_{H_{2}CO}-3({\mathbf{\text{d}}}_{OH}\cdot \mathbf{\text{R}})({\mathbf{\text{d}}}_{H_{2}CO}\cdot \mathbf{\text{R}})}{4\pi {\epsilon }_0{R}^5},$$ (4)

where R is the vector between the two centers of mass.

The short range term, V_sr, is represented by a sum of pair interactions between all atoms belonging to different fragments. Either Morse potentials, Lennard-Jones like or fully repulsive functions have been used to obtain the better fit to these interactions. The choice of the function is done by looking at the behavior of the ab initio calculations along several approaching geometries, and the parameters are fitted to reproduce in average the interaction on several of them.

c. Coupling between rearrangements

The V_eff terms in Eq. 2 introduce a coupling between the different rearrangement channels. These terms are carefully designed to reproduce the height and position of the saddle point, which should appear in the region where the "diabatic states" cross. In the present approach, we shall neglect the coupling between the two equivalent product channels 2 and 3. The couplings between the reactant channel 1 and the two product channels, 2 and 3, are equivalent, and we shall consider an unique effective coupling function V_eff, with the form

$$V_{eff}=C{e}^{-\alpha \Delta E^{2q}}g(r_{OH}-r_{CH})g(r_{CH}-r_{OH})$$ (5)

with C being the coupling strength, ΔE² the square of the difference in energy of the reactant and the closest product diabatic state, 2 or 3, and α and q are the parameters introduced to modulate the intensity as a function of the energy difference. Note, that q must be larger than 1 to avoid discontinuity in the derivatives when DeltaE = 0. Finally, g(x) is a damping function to localize the couplings in the region of the saddle point, where r_OH and r_CH are the distances of the breaking/forming bond.

Many-body term

The matrix element H^MB used to fit the ab initio energies is expanded as polynomials in the Rydberg variables expressed in terms of all the internuclear distances ({R_αβ}, α > β = 1, … , 6)³⁹. To make the potential invariant with respect to the interchange of indistinguishable nuclei, the polynomials are symmetrized using the Young operator corresponding to the totally symmetric irreducible representation of the S_n permutation group of n objects. The 3 × 3 H^diab matrix takes into account only the permutation of the two equivalent hydrogen atoms of H₂CO reagent. Hence the unnormalized Young operator, ω^[2] corresponds to the S₂ group,

$$w^{\left[2\right]}={\displaystyle \sum _P^{2}P}=1+P_{12}$$

where P₁₂ is the permutation operator that interchange the two equivalent hydrogen of H₂CO (named a and b). The application of ω^[2] to the product of the Rydberg variables ρ_αβ = R_αβ e^{−γ_αβ R_αβ}, gives the symmetry adapted functions (SAF) permutationally invariant with respect to the interchange of both equivalent hydrogen nuclei,

$${\rho }_r^{SAF}={\omega }^{\left[2\right]}{\displaystyle \prod _{\alpha >\beta }{\rho }_{\alpha \beta }^{i_{\alpha \beta }}}$$

where i_αβ are the power of the ρ_αβ variable of the polynomial, and r = {i_αβ}. The order of this polynomial is ∑_α>β i_αβ and will be used to select the terms included in the fit. In addition, the nonlinear γ_αβ exponents of the Rydberg variables must be optimized taking into account the permutation symmetry, that impose γ_1β = γ_2β for β = 3, … , 6.

The functional form for the six-body potential in terms of this SAF polynomials takes the form

$$H^{MB}(\{R_{\alpha \beta }\})={\displaystyle \sum _r{c}_r{\rho }_r^{SAF}}$$

where the sum run over r. In this sum we exclude the terms that correspond to two, three, four and five body potentials, that are included in the H^diab. This impose constrains on the r = {i_αβ} permitted values. With this restriction the number of terms of the polynomial are: 680 for the degree five and 5932 for the degree six. In order to use an intermediate number of parameters, we have imposed the restriction i_αβ = 0 or 1, that gives 2596 terms for the six order polynomial in the present case.

Fit procedure and results

In the fit procedure of the MB term it is necessary to reproduce the transition state region very accurately. For this reason, the intrinsic reaction coordinate (IRC) between the two deepest wells of the reactant and products channels have been calculated with the RCCSD(T)-F12a method (shown in Fig. 1). Also, the normal modes along the IRC were calculated, and ab initio points were calculated as a function of each normal coordinate. All these points were included in the fit with a larger weight (≈ 500 below 5 eV) to get a good accuracy at the transition state region.

Fig. 1.

Ab initio IRC, compared with the RFF and the RFF+MB complete fit. The insets indicate the geometry of the H₂CO…OH and HCO…OH₂ complexes and of the saddle point (with distances in Å). The points from the minima to the corresponding reactants and products asymptotes, respectively, are calculated with a steepest descent method from the asymptotes to the minima. The variable s is evaluated from the geometries as usually done for the IRC.

In total about 150000 ab initio points have been calculated, of which approximately 100000 have an energy lower than 10 eV (with respect to the asymptotic OH + H₂CO energy at the equilibrium geometry, here after consider as zero of energy). These points are introduced in the fitting procedure of the many bodyterm, H^MB, with a weight which decreases as energy increase over 5 eV over the reactant energy. The points have been calculated in different forms. First, regular grids in the reactant and products channels were calculated to characterize them at the equilibrium geometry of the fragments. Second, selected points chosen along classical trajectories run in different versions of the fit. Since the fit typically introduces oscillations in the potential, classical trajectories at 1eV (plus the ZPE) were used to locate the spurious minima. Ab initio calculations were performed at these points and introduced in a new fit. This procedure was repeated iteratively until no spurious minima were found running more the 10⁴ trajectories. Also, artificial barriers were located by running trajectories at low kinetic energies (1 meV plus ZPE), determinining the geometry of the rebound configuration, to add more points. Finally, random points were added at different geometries.

In the fitting procedure we optimize the 2596 linear c_r and 11 non-linear γ_αβ parameters. Because the non-linear optimization is computationally expensive, we have done the optimization of the non-linear parameters with the polynomial of order five. We have found that the fitted six-body term of the potential must correct both the short- and intermediate- regions of the potential. In order to warranty this, the non-linear parameter were set to be larger than 0.85. With this requirement the MB term of the potential goes to zero as any intenuclear distance goes larger than 10 a.u., ensuring the long range behavior of the potential given by V_lr.

The root-mean-square errors are listed in Table 3. For energies below 1eV (well above the saddle point) the error of the RFF+MB PES is 77.5 meV, about a half of the error of the RFF one. This energy is slightly higher than the energy of the reactant plus the ZPE as can be seen in Fig. 1, covering essentially all the energy range of interest in this work. This error is much lower along the IRC, as shown in this Fig. 1: the error of the RFF+MF fit is of 29.3 meV, and around the saddle point of only 11.8 meV, significantly lower than that of the RFF fit alone. The height of the saddle point of the RFF+MB PES is 26.3 meV while the ab initio value is 27.1 meV. This small error (less than 1 meV) was possible because the RFF saddle point is 27.4 meV by design. Also, at each intermediate fit made, the IRC was calculated and more ab initio points were added along the one-dimension cuts of the normal modes.

Table 3.

Analysis of the errors of the RFF and RFF+MB fits, in meV. The number of points in each energy interval considered is also shown.

Points	Energy	Error RFF	Error RFF+MB
228	IRC	75.8	29.3
101	IRC(−1 < s < 1)	55.3	11.8
240	NM (E < 1.0 eV)	68.2	11.5
27728	E < 0.0 eV	111.2	70.5
76486	E < 1.0 eV	146.7	77.5
95734	E < 5.0 eV	1218	126

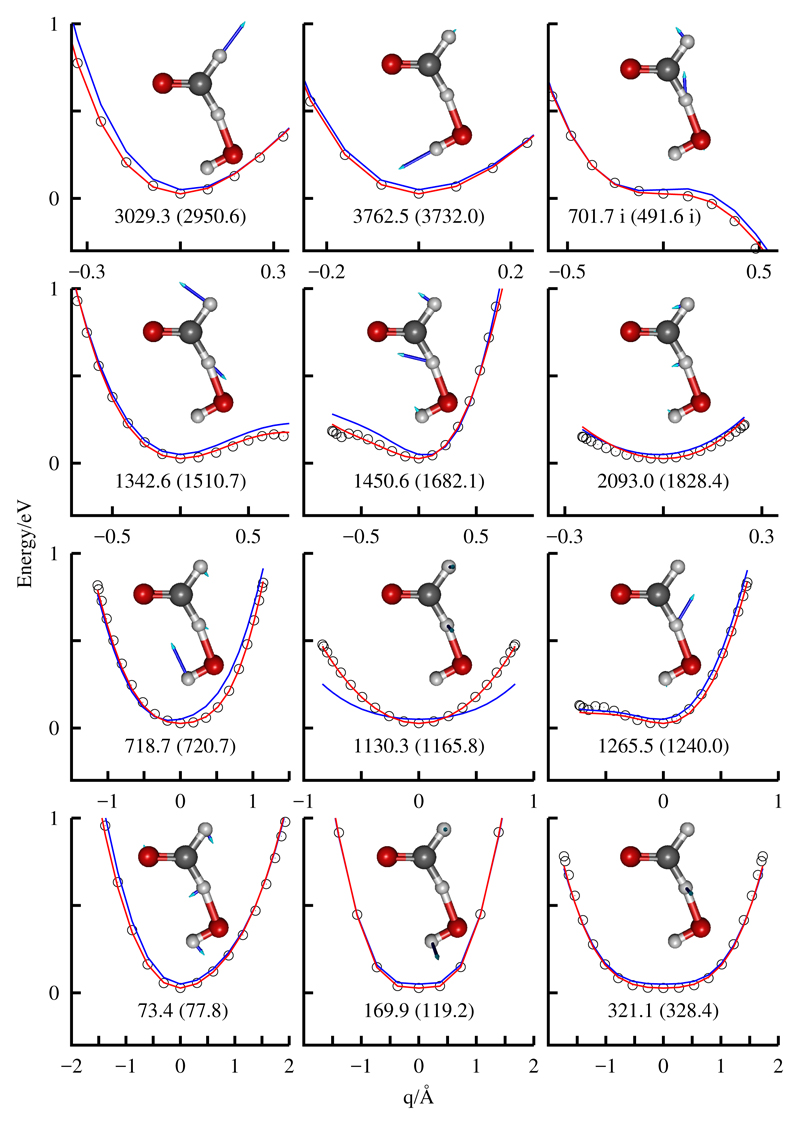
The dependence of the fits on the normal coordinates at the saddle point of the RFF+MB fit is shown in Fig. 2. It is seen that the RFF+MB fit describe very well the ab initio points up to a rather high energy, always improving the description of the RFF PES. The harmonic frequencies (real and imaginary) obtained at the saddle points of the RCCSD(T)-F12a and RFF+MF potentials are also shown for each of the normal mode. All this analysis demonstrate that the RFF+MB fit describe rather accurately the TS region, with an error lower that the overall error shown in Table 3. It can also be seen that some of the modes are very anharmonic, specially those with frequencies 1265.5, 1342.6, 1450.6, 3029.3 3762.5 and 701.7i cm⁻¹. The out-of-plane modes (with frequencies 169.9, 321.1 and 1130.3 cm⁻¹) are symmetric but very flat at the well, also indicating a behavior far from harmonic as $q_i^2.$ This indicate that the harmonic ZPE is not a good approximation, and anharmonic terms are expected to be rather important.

Fig. 2.

Ab initio points versus RFF (in blue) and RFF+MB (in red) fits along the monodimensional normal coordinates, q_i, obtained at the saddle point of the RFF+MB PES. In the inset each normal mode is shown. Also The harmonic frequency of the RFF+MB (ab initio) normal modes are indicated.

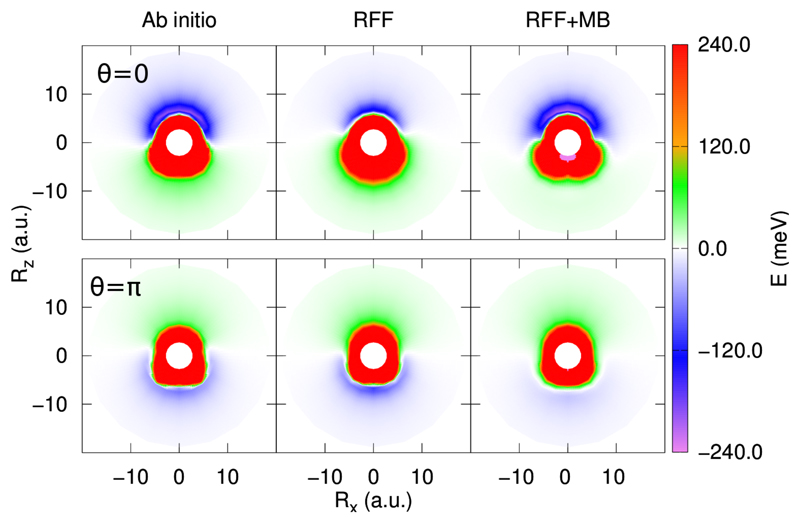
The long range region is of particular interest since it determines the dynamics at low energies, as will be discussed below. In Fig. 3 we compare the ab initio and the RFF potential for the long range part of the potential, for H₂CO in its equilibrium configuration and two different orientations of OH (in the equibrium distance) around the H₂CO, either with the H (θ=0 in top panels) or O (θ = π in bottom panels) atom pointing towards the H₂CO center-of-mass. The complete RFF+MB fit is identical to the RFF one in this region. The agreement between the ab initio and the RFF PES is excellent. It also shows that the interaction is about 0.5 meV at R ≈ 50 a.u.

Fig. 3.

Countour plots of the PES calculated with the RCCSD(T)-F12a ab initio points with the VDZ-F12 basis set (left panels) and the RFF (right panels). The H₂CO in its equilibrium geometry in the xz plane, with its center of mass at the origin and the CO bond along the z axis, as shown in the inset. R is the vector joining H₂CO and OH center-of-mass, with components R_x and R_z. The white circles in the figure indicate the region expanded in Fig. 4.

A detail of the PES is shown in Fig. 4 to analyze the quality of the fit, at the same orientation of the Fig. 3. The RFF (in the middle panels) is slightly too isotropic, being essentially attractive/repulsive for H/O pointing towads H₂CO. The addition of the MB term improves the description, allowing a better description of the anisotropy, in particular in the depth of the potential wells and extension in most of the cases. Some artifacts still remain at short distances. For example, in the bottom right panel, there is a repulsive ring, relatively low (< 10 meV) but absent in the ab initio case (left bottom panel). This artificial ring is surounded by an attractive ring, in agreement with the ab initio results. We finally conclude, that the present RFF+MB PES has a high accuracy at the saddle point and the long range region.

Fig. 4.

Countour plots of the PES calculated with the ab initio points (left panels), the RFF (middle panels) and and RFF+MB fit (right panels), for comparison. The geometries are the same of Fig. 3, but for shorter distances.

Quasi-classical trajectory calculations

Reactive cross section

Quasi-classical trajectory (QCT) calculations on the H₂CO + OH → HCO + H₂O reaction have been done on the RFF+MB PES in a recent publication¹⁹. In this work we shall analyze in more detail those results to get further physical insight of the reaction mechanism. The calculations were done with an extension of the miQCT code^44,45 applied to N atoms, and the details of the method and parameters used were described before¹⁹ and are omitted here. For H₂CO and OH in their ground vibrational and rotational states, the reactive cross section at fixed collision energies were calculated as⁴⁶

$${\sigma }_{\nu j}(E)=\pi b_{\text{max}}^2{P}_r(E)\text{with}{P}_r(E)=\frac{N_r}{N_{tot}},$$ (6)

where N_t is the maximum number of trajectories with initial impact parameter lower than b_max, the maximum impact parameter for which reaction takes place, and N_r is the number of trajectories leading to products. The initial conditions were sampled using a Monte Carlo method¹⁹, and the initial impact parameter is randomly set in the interval [0, B], with B being set according to a capture model⁴⁷ as

$$B=\sqrt{3}{\left(\frac{A}{2E}\right)}^{1/3},$$ (7)

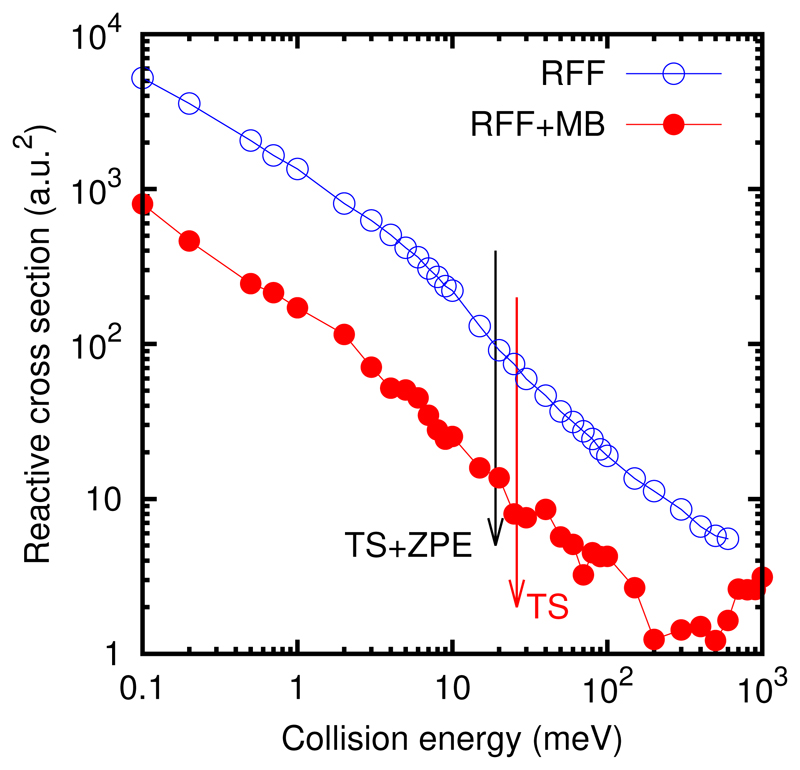
for a dipole-dipole interaction, Eq. (4), varying as −A/R³ for long distances R between the center-of mass of the two reactants (with A = 4 d_OH d_H2CO corresponding to the optimal orientation between the permanent dipoles of the two reactants). About 10⁵ trajectories have been calculated for each collision energy between 0.1 meV and 250 meV, and the cross section obtained is shown in Fig. 5.

Fig. 5.

Integral reactive cross section for the H₂CO + OH → HCO + H₂O reaction with the two reactants initially in their ground vibrational and rotational state.

The reactive cross section increases by nearly 3 orders of magnitude when collision energy reduces from 1000 to 0.1 meV. The energy of the transition state, with or without ZPE, does not affect at all to this behavior, and this happens for the two PESs. However, the RFF results are nearly 10 times larger than those obtained with the full RFF+MB PES. In order to explain these surprising results we shall use Eq (6) and discuss separaterely the effect of the impact parameter, b, and the reaction probability, P_r, in the cross section.

Capture and impact parameter

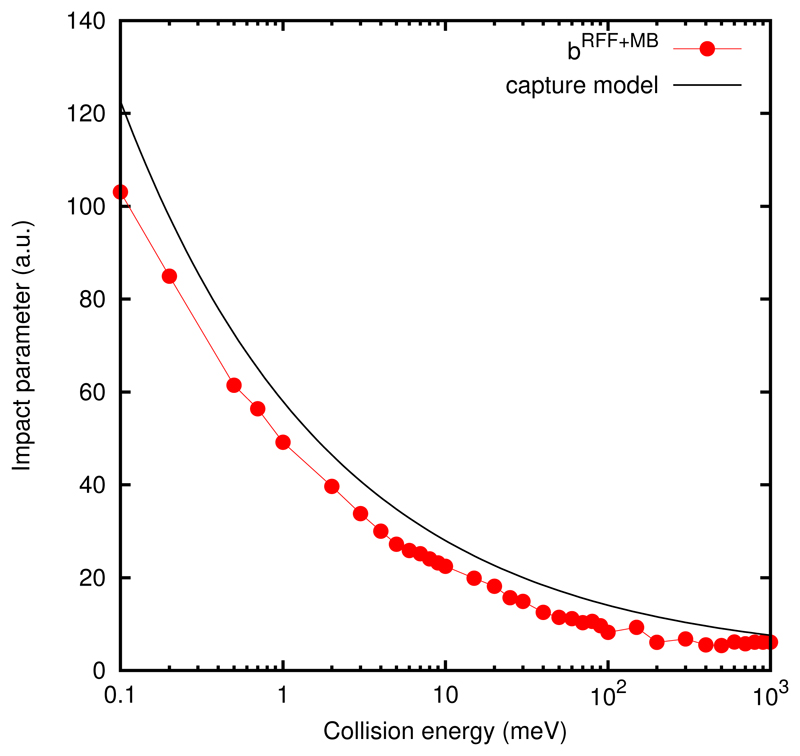
The impact parameter, b, shown in Fig. 6, increases continuously with decreasing collision energy, and closely mimic the results obtained with the capture model. As collision energy decreases, the potential is able to deviate the trajectories from longer distances to make the reactants approach each other. This increase of the impact parameter is clearly the responsible for the increase of the cross section as energy decreases.

Fig. 6.

Maximum impact parameter for the H₂CO + OH → HCO + H₂O reaction with the two reactants initially in their ground vibrational and rotational state.

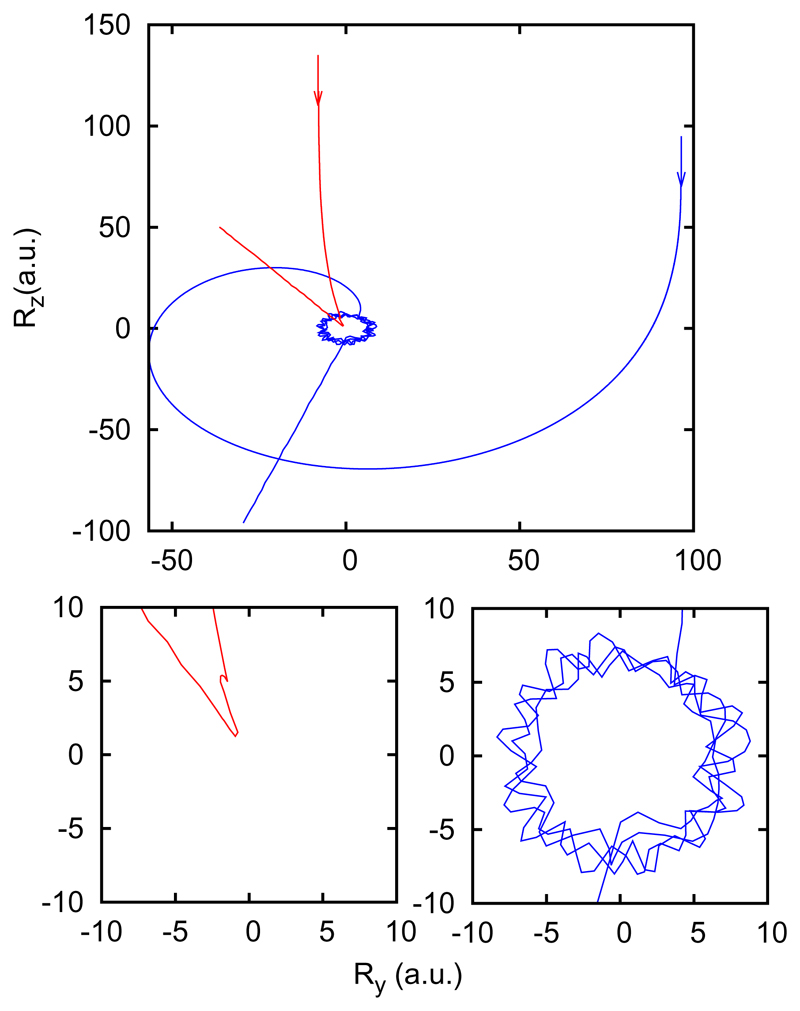
The capture process is illustrated in Fig. 7 for two typical trajectories, with large and small initial impact parameter. In trajectories with small impact parameter, the two reactants approach each other, rebound a couple of times and then the reactants or products fly apart. However, trajectories with large initial impact parameter, and hence large end-over-end angular momentum 𝓵, follow a long circular orbit, until a complex between reactants is formed. Within this complex, the two reactants continue rotating while they collide many times.

Fig. 7.

Typical trajectories at collision energy of 0.1 meV with large (blue) and small (red) initial impact parameter, as a function of R_x and R_y in the system of coordinates described in Fig. 3. The insets show each individual trajectory at shorter R values.

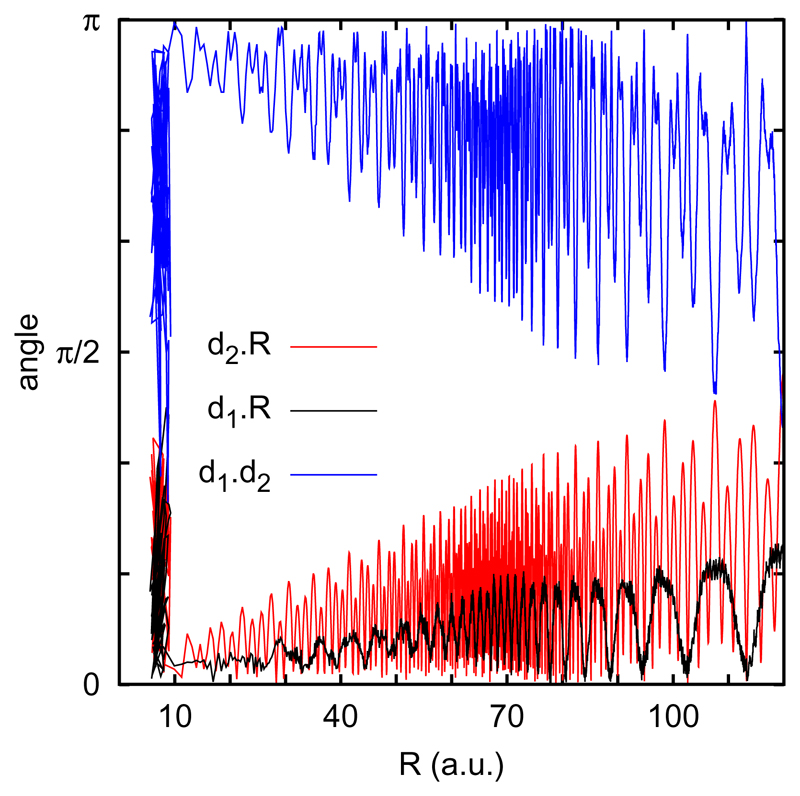
During this long approaching orbits, the relative orientation of the reactants also changes, as it is shown in Fig. 8. The d_OH and d_H2CO electric dipoles are along the OH and CO bonds, respectively. For the long trajectory of Fig. 7, the angles formed by the electric dipoles and the vector R vary around 0 for d_OH and d_H2CO, respectively. These geometries correspond to the situation in which the interaction gets more attractive, and since this interaction grows as R decreases, the amplitude of the oscillations decreases. Similarly, the angle between the two dipoles also varies around π, orientation at which the dipole-dipole interaction is more attractive.

Fig. 8.

Variation of the angles between R and d₁ (black), R and d₂ (red) and d₁ and d₂ (blue) for the trajectory of large impact parameter of Fig. 7

Because of this reorientation along the approaching trajectories, the two reactants start to rotate, and this rotational motion is accelerated as the reactants get closer. The rotational energy of the two fragments may get significant values as compared to the very low initial collision energies simply because the available kinetic energy is of the order of the well depth.

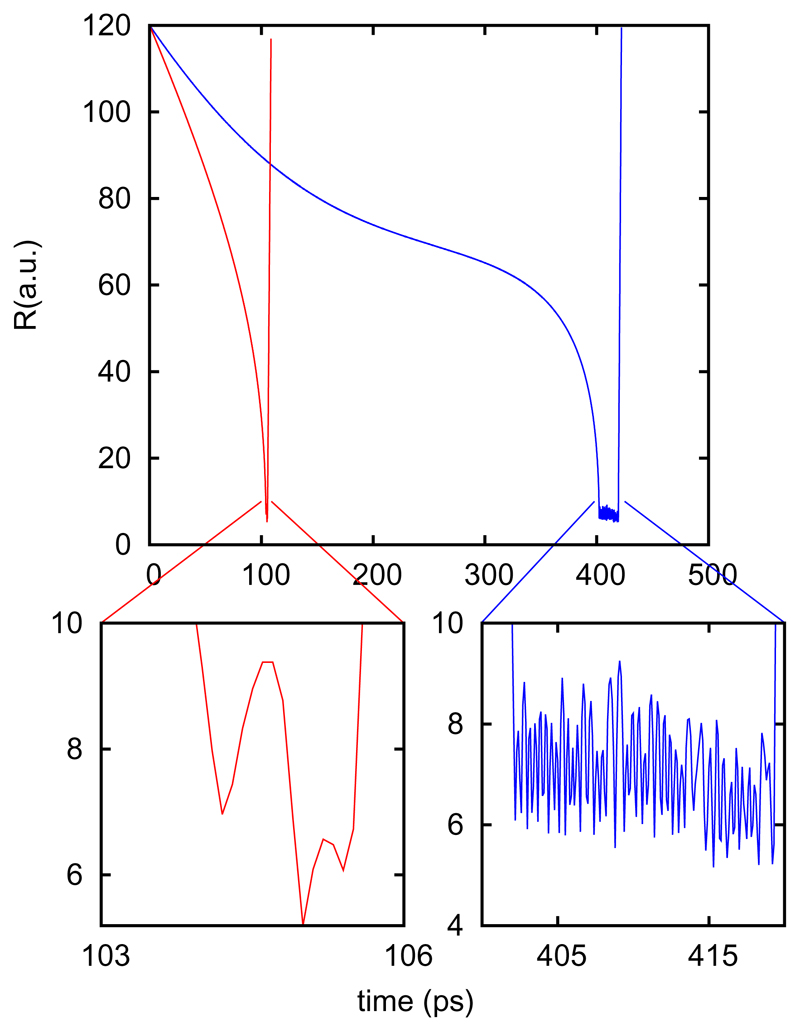
Once a molecular system starts to rotate, it is difficult that the rotation stops completely by colliding with the other partner. The rotational energy is larger than the collision energy required to escape back again, since a single rotational quantum of the OH (≈ 2.5 meV) is much larger than the energy required to fly apart. Therefore the system can not separate again because it does not have available energy in the translation degrees of freedom and the system becomes trapped in the well for a long time. In Fig. 9 the evolution of the trajectories with time shows that the complex time for large initial parameter is rather long, of the order to 10-20 ps. This time is however about one order of magnitude shorter than the time the reactants require to approach each other, of the order of several hundreds of ps.

Fig. 9.

Trajectories of Fig. 7 showing the evolution of R with time. The insets shows the evolution of the collision complex.

Collision complex lifetime and reaction probability

The trajectories trapped forming the complex, sample a large region of the configuration space (see Figs. 7 and 9) and may be considered to become ergodic. According to the RRKM statistical theory^48,49, the lifetime of the collision complex depends on the number of open channels, N_o, as

$$\tau =2\pi \hslash \frac{\rho (E)}{N_o(E)},$$ (8)

where ρ(E) is the density of states of the complex at energy E. This situation is analogous to the situation of ultracold collisions⁵⁰, where just one or very few open channels are available. Thus the collision complex have very long lifetimes, and virtually explore all the states contributing to ρ(E).

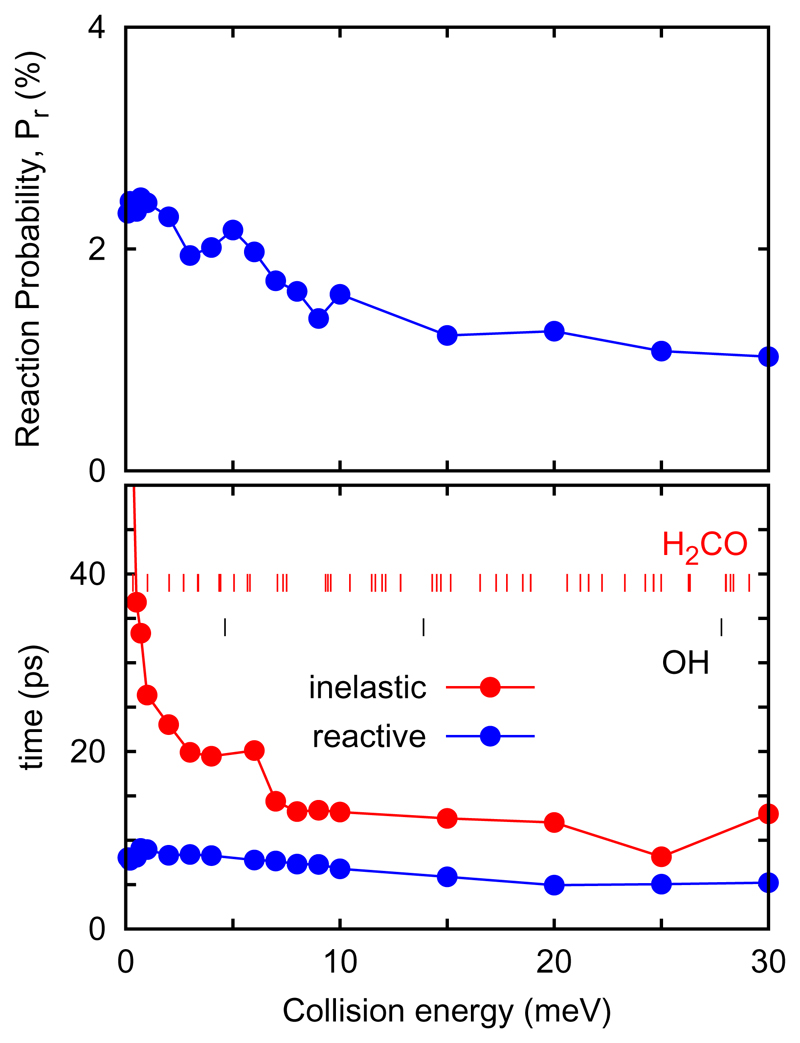
In Fig. 10 the average lifetimes for the ensemble of trajectories reacting or not are shown separately. The collision complex lifetime of non-reactive trajectories shows a sudden increase when the number of OH rotational levels reduces to just 1, what also reduces significantly the accesible levels of H₂CO by angular momentum conservation.

Fig. 10.

Top panel: reaction probability associated to the cross section shown in Fig. 5. Bottom panel: Average complex lifetimes for trajectories reacting (blue) and non-reacting (red). The rotational energies of OH and H₂CO are also shown.

On the contrary, for reacting trajectories, the collision complex lifetime is rather smooth and do not depend on the rotational levels of the OH and H₂CO reactants, but instead it may be considered that it depends on the products density of levels: the number of open products channels is considerably large and constant in this energy interval because the reaction is highly exothermic.

The structure of the collision complex lifetime for reacting trajectories closely mimic the reaction probability shown in the top panel of Fig. 10. This may indicate that there is a a connection between collision complex lifetime of reacting trajectories and reaction probability. The question that remains to answer is why the reaction probability is non zero at energies below the top of the barrier.

Considering the ZPE of reactants, the system has enough total energy to overcome this barrier. If the reactants ZPE remains in the coordinates orthogonal to the reaction coordinate, the reaction could not take place, since there would not be enough energy in the reaction coordinate. Clearly, this is not the case, and there must be couplings between the reaction coordinate to the remaining degrees of freedom, producing an energy transfer which explains the non zero reaction probability even at 0.1 meV of collision energy.

Such situation is typical in non-IRC trajectories⁵¹, since they explore large regions of the configuration space, far from the minimum energy path determined by the IRC where the anharmonicity is larger. The trajectory shown in Figs. 7 and 9 clearly show a roaming behavior^52,53 in which the fragments explore geometries very far from the IRC where the anharmonicity of the PES is higher producing energy transfer among all the degrees of freedom. Moreover, the ZPE at the transition state is calculated in the harmonic approximation, and it is expected to be considerably reduced when anharmonic effects, as those discussed in Fig. 2, are considered.

The reaction probability obtained for the RFF PES is much larger than that for the RFF+MB PES, and this is the reason of the large difference observed in the corresponding cross sections in Fig. 5. This difference is clearly not due to the height of the saddle point, since the higher TS is for the RFF, as can be seen in Fig. 1. Since for the two PES’s the trajectories are trapped by the long range term of the potential, the difference should be associated to the access from the well in the entrance channel to the saddle point for the reaction. The RFF is by far more simple, and does not describe properly the anisotropic character of the PES, giving an easier access to the TS region.

Quantum effects

As reaction probability is related to the lifetime of the collision complex, and this depends on the number of open channels, it is expected that quantum effects are important in this energy regime. Traditional quantum methods are not applicable for so many degrees of freedom and so low energies. On the other hand, a traditional way to correct QCT calculations is to neglect those trajectories which do not fulfill the ZPE requirement. However, in doing so most of inelastic trajectories will be discarded, while reactive trajectories not, and hence the reaction probability and reactive cross section would increase too much. One alternative is to use semiclassical methods, such as the ring polymer molecular dynamics approach^54–57 or centroid dynamics^58,59, both based on the path integral method. It is however a challenge to use these methods for such low temperatures of interest here.

Nevertheless we shall discuss about the qualitative behavior of QCT based methods to describe the reaction dynamics in this case. It is noticeable, that rotational excitation plays an important role in the dynamics in the entrance channel, through the dipole-dipole long range interaction that make the system form a long lived collision complex. The OH + F → HF + O reaction has a similar dynamics and energy profile and, being a triatomic system, exact quantum wave packet and QCT calculations have been perfomed^60–62. It was found that in this exothermic reaction, the quantum reactive cross section increases significantly at low energies^61,62. This increase was due to the formation of long lived resonance in the entrance channel in which OH was rotationally excited as in H₂CO +OH. The reaction probabilities calculated with a QCT method in this triatomic system showed peaks, which were associated to quasi-periodic orbits, and these peaks were in semiquantitative agreement with the corresponding quantum calculations. These resonance structures persist in OH+F reaction for high partial waves, and manisfest in an increase of the cross section at low collision energies, in both quantum wave packet and QCT calculations^60–62. However, the QCT results yielded a lower increase in the cross section, what was attributed to a lack of accuracy in describing resonance lifetime.

Analogously, in the H₂CO + OH results we expect also an underestimation of the cross section at low energies based on the previous example. Work in this direction is in progress.

Rate constants and comparison with experiment

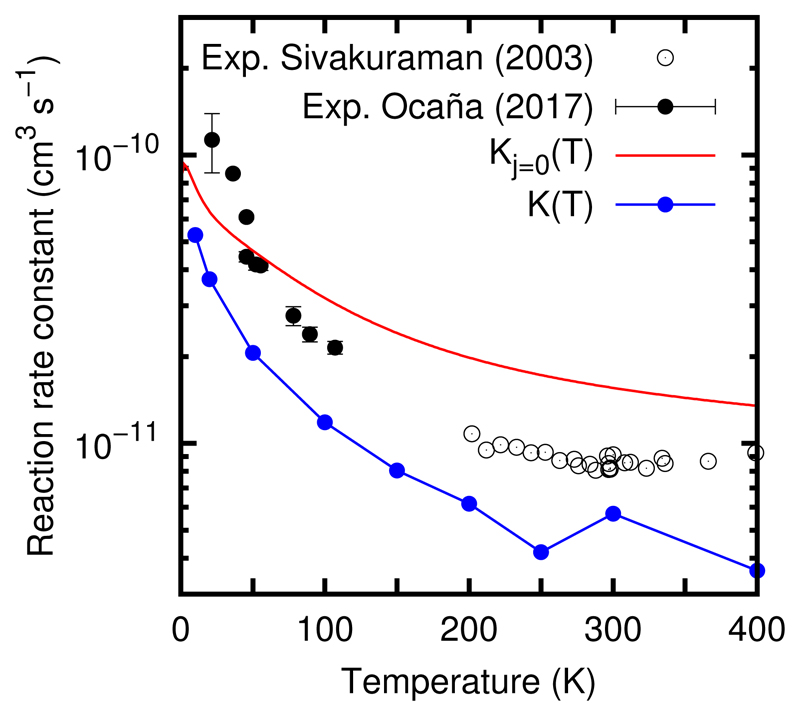
The initial state selected rate constant (corresponding to OH and H₂CO in their ground vibrational and rotational state) is obtained by integrating the cross section over a Boltzmann distribution. The spin-orbit splitting of the electronic states of OH(²Π) states (into the F₁(²Π_1/2) and F₂(²Π_3/2), with an energy separation of 200.279 K) should be taken into account. Assuming that two states correlating to the ground F₂(²Π_3/2) react, and the other two do not, the rate constant has to be multiplied by the factor q_e(T) = 1/(1 + exp(−200.3/T), arising from the electronic partition function, where k_B is the Boltzmann constant. The final state selected rate, K_j=0(T), is shown in Fig. 11, and it decreases with increasing temperature in the range studied. This behavior is expected after the analysis of the cross section, in Fig. 5, but, for T > 50K, the decrease is also due to the q_e(T) factor.

Fig. 11.

Calculated reactive rate constants (thermal K(T) and state-selected K_j=0(T) as described in the text) versus the experimental results of Ocaña et al.¹⁹ and Sivakuraman et al.⁶³.

In order to compare with the experiment, the thermal rate constant is also calculated running more the 1 million of trajectories for each temperature in the macracanonical ensemble¹⁹ as,

$$K(T)=q_e(T)\sqrt{\frac{8k_{B}T}{\pi \mu }}\pi b_{max}^2(T)P_r(T),$$ (9)

where µ = m_OHm_H2CO/(m_OH + m_H2CO) is a reduced mass. b_max(T) and P_r(T) are the maximum impact parameter and reaction probabilities defined above, but now for each temperature. The results obtained are shown in Fig. 11 and compared with the recent experimental rate constants of Ocaña et al.¹⁹.

The state-selected K_j=0(T) rate constant is always larger than the thermal rate constant K(T). The reason is that the capture mechanism described here is disrupted for excited rotational states of OH. First, the relatively high rotational energy of OH(j=1) (≈ 5 meV) makes more difficult to orient this fragment making less efficient the capture. Second, the higher rotational energy open more channels, specially significant in the reactant rearrangment channels, what reduces the lifetime of the collision complex. All this make less efficient the reaction as the rotational excitation grows higher, and this effect is now under study.

The calculated thermal rate constant is aapproximately a factor of 2 lower than the two sets of experimental data, but the overall descrease is semiquantitatively correct, demonstrating that this reaction does not show a threshold for temperatures above 10K. The lack of complete agreement between the theoretical and experimental results can be attributed at least to two reasons. First, the PES, due to the difficulty of getting a potential with an accuracy better than 10K. The zero point energy of the reagents is ≈ 1 eV, and the exothermicity is 1.3 eV. This would imply a relative error below 0.1% for a system with 12 internal degrees of freedom, which is now a days a challenge. Second, quantum effects are expected to increase the lifetimes of the collision complexes, as discussed above. This would produce an increase of the reaction rate. Work in these two directions is now in progress.

Conclusions

In this work a method has been developed to represent the multidimensional potential energy surface of reactions, like OH + H₂CO, with analytical functions, describing accurately the long range interaction and the saddle point. This kind of potentials are required to describe the collisions at the low temperatures of the interstellar medium (of ≈ 10K) and it has been applied to the study OH + H₂CO → H₂O+ HCO reaction. The reactive rate constants have been calculated using a Quasi-classical trajectory method between 10 and 400 K, and the results are in good agreement with the experimental data.

This reaction presents a low barrier for the reaction, of 27.4 meV≈ 318 K, but the measurements and calculations show that the reaction rate constant increases as the temperature decreases down to ≈ 10-20 K. This fact was previously explained in the framework of transition state theory introducing tunnelling. In the present classical calculations, it is simply an energy transfer between the vibrational modes and the reaction coordinate, induced by the formation of a collision complex leading to long lived roaming trajectories.

Quantum effects are expected to play a role and should be analyzed. However, rotation plays a major role in the energy transfer mechanism and minimize the zero-point energy problem. This has been analyzed in a similar system like OH+ F, for which quantum results have been calculated, indicating that the reactive cross section increases with decreasing collision energy in both quantum and classical results, with classical ones being in general lower.

This reaction mechanism may have an important effect in astrophysical models of dense molecular clouds at temperatures of 10K, where many gas phase reactions have been neglected because they show a reaction barrier. Many of these reactions have to be readdressed in order to determine if this mechanism is possible and may give a noticeable rate constant. For this purpose, the method developed in this work to represent analytically the potential energy surface of polyatomic systems is of great importance.