Abstract
The circadian rhythms influence the metabolic activity from molecular level to tissue, organ, and host level. Disruption of the circadian rhythms manifests to the host’s health as metabolic syndromes, including obesity, diabetes, and elevated plasma glucose, eventually leading to cardiovascular diseases. Therefore, it is imperative to understand the mechanism behind the relationship between circadian rhythms and metabolism. To start answering this question, we propose a semimechanistic mathematical model to study the effect of circadian disruption on hepatic gluconeogenesis in humans. Our model takes the light-dark cycle and feeding-fasting cycle as two environmental inputs that entrain the metabolic activity in the liver. The model was validated by comparison with data from mice and rat experimental studies. Formal sensitivity and uncertainty analyses were conducted to elaborate on the driving forces for hepatic gluconeogenesis. Furthermore, simulating the impact of Clock gene knockout suggests that modification to the local pathways tied most closely to the feeding-fasting rhythms may be the most efficient way to restore the disrupted glucose metabolism in liver.
Keywords: circadian rhythms, clock genes, FOXO1, gluconeogenesis, metabolism, PGC-1α
INTRODUCTION
The circadian rhythms are the biological time-keeping mechanisms that maintain 24-h oscillations in cellular and physiological processes (1). In mammalian organisms, the circadian machinery is organized as a hierarchical, interconnected network of clocks (1). The master clock lies in the suprachiasmatic nuclei and is linked to the light-dark cycle, synchronizing the peripheral clocks distributed across all cells (8, 9). Since homeostatic circadian rhythms are required for proper functioning of many physiological activities, disruption of the rhythms can lead to physiological imbalance. In particular, numerous studies suggest that disrupted circadian rhythms are linked to metabolic diseases (16). Interestingly, the relationship between circadian rhythms and metabolic activities appears to be bidirectional. For instance, temporal restriction of feeding restored rhythmic transcription of genes in oscillator-deficient Cry1−/−;Cry2−/− mutant mice (51). Therefore, understanding the complex regulatory network that encompasses circadian rhythms and metabolism is of great interest. In particular, restoration of rhythms by temporal restriction of feeding motivates the question of how metabolism is influenced by competing signals of the light-dark cycle and nutrient availability.
To that end, we developed a semimechanistic, mathematical model to study the intertwined network of circadian clocks and metabolism, focusing on hepatic gluconeogenesis as the circadian-modulated metabolic activity. Mammals have an intricate system to maintain the blood glucose level within a tight bound despite the intermittent access to nutrients, and the level of gluconeogenesis responds to the feeding state of the host utilizing an anticipatory mechanism to produce glucose endogenously. As a first step toward answering this question, we have previously modeled the entrainment of peripheral clock genes to the feeding rhythms as well as the synergistic role of competing light-dark cycle and feeding-fasting cycle in the periphery (3). We demonstrated the re-entrainment of clock genes to rhythmic feeding, where the dynamics of key clock components reach a new state on changes to the feeding cycle. Our model consists of a central compartment, which takes in the environmental (light) and behavioral (food) cues as inputs, and a peripheral compartment, which represents a human hepatocyte. The central compartment includes the hypothalamic-pituitary-adrenal (HPA) axis that secretes cortisol to the periphery, and the peripheral compartment encompasses the core clock machinery that oscillates autonomously, and cortisol and human sirtuin 1 (SIRT1)-mediated reactions that influence the rhythms of the peripheral clock genes and gluconeogenic gene expression.
Nutrient sensors such as AMP-activated protein kinase, poly(ADP-ribose) polymerase 1, and SIRT1 exhibit circadian behavior and interact with the key molecules of the core clock genes (24, 43). In our model, the cytosolic nicotinamide adenine dinucleotide (NAD+)-to-NADH ratio conveys the information of food availability to the peripheral clocks through SIRT1 for simplicity. Alternative models involving AMP-activated protein kinase, cAMP response element-binding proteins, or poly(ADP-ribose) polymerase 1 have also successfully described the feeding entrainment of clock genes (48, 52). SIRT1 is best characterized for its histone deacetylation activity (7), which is coactivated by NAD+. The changing NAD+ levels due to fasting state of the host change the transcription of gluconeogenic genes such as G6pc and Pck1 to control the generation of glucose (12). Although we recognize that alteration of Pck1 and G6pc expression may not be enough to describe changes in gluconeogenesis, we use it to represent hepatic gluconeogenesis since alterations in expression lead to changes in enzymatic activity (32). During long-term fasting (>6 h), SIRT1 activity results in increased transcription of these two genes. SIRT1-mediated deacetylation activates peroxisome proliferator-activated receptor-γ coactivator-α (PGC-1α) and Forkhead box O1 (FOXO1; Ref. 42). These two proteins, along with hepatic nuclear factor-4α (HNF-4α), are required for transcription of gluconeogenic genes (55). Furthermore, it is well-established that serum cortisol level increases gluconeogenesis in humans (17).
Based on the aforementioned observations, we propose a mathematical model that describes the interactions among various signaling molecules such as cortisol, SIRT1, and PGC-1α and their influence on hepatic gluconeogenesis to study the effects of light and feeding cycles on circadian dynamics of the peripheral metabolism. We validated the model by generating predictions under various combinations of feeding and light patterns and comparing them with known behaviors under ad libitum feeding and time-restricted feeding conditions. Then, we used the model to test the effects of circadian disruption on transcription of gluconeogenic genes and to investigate various nonpharmacological methods to overcome the effects of circadian disruption. We analyzed the model using three different approaches: local sensitivity analysis, global sensitivity analysis using the Morris method, and uncertainty analysis using the random-sampling high-dimensional model representations (RS-HDMR). From these analyses, we identify local targets that can overcome the effects of genetic clock knockout. Our model predicts that abnormally high level of fasting gluconeogenesis caused by Clock gene knockout can be returned to the wild-type level by changing the feeding time relative to the light-dark cycle. Furthermore, the sensitivity analyses consistently show that the dynamics of peripheral clocks (PER/CRY complex), cortisol-receptor complex, and PGC-1α are the most influential in rhythmic expression of gluconeogenic genes.
METHODS
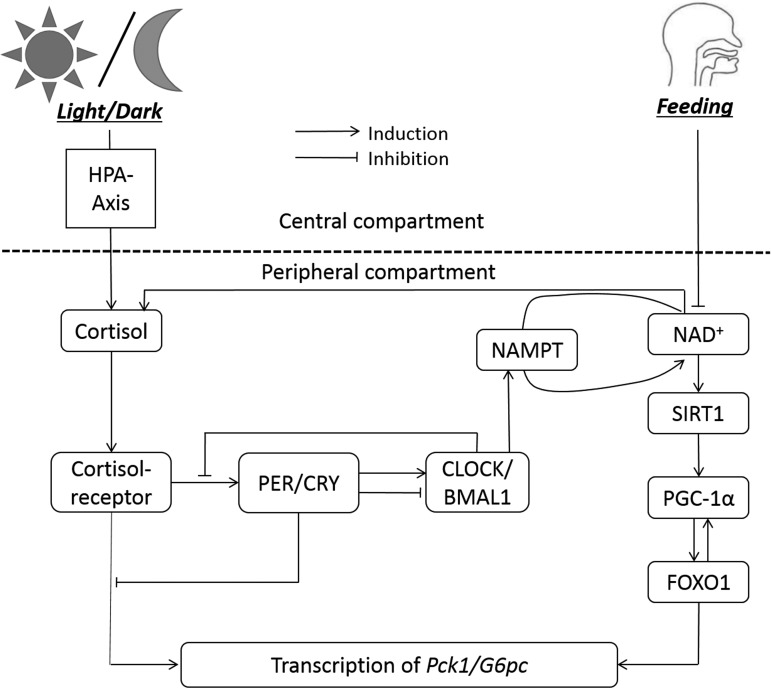
We developed a mathematical model that represents a sequence of events describing the circadian dynamics of clock genes and metabolic activities in a human hepatocyte to study the manifestation of two external stimuli, the light-dark cycle and feeding-fasting cycle. The model was built on our (3, 26, 27) previous works and is composed of a central compartment that receives and processes the environmental cues and a peripheral compartment that encompasses the core clock machinery and metabolic gene expression. Only the essential parts of the model directly relevant to gluconeogenic gene expression are described in this section. A simplified schematic showing the major driving forces for gluconeogenic gene expression is shown in Fig. 1. A detailed schematic displaying the network of signals transmitted from light and feeding to the downstream peripheral components along with the working version of the model can be accessed in the endnote.
Fig. 1.
Simplified schematic diagram of the model. The HPA axis is entrained to the light-dark cycle, and NAD+ availability is entrained to feeding rhythms. Transcription of gluconeogenic genes (Pck1/G6pc) is regulated by cortisol-receptor complex, peripheral clocks, and FOXO1. NAMPT, nicotinamide phosphoribosyltransferase.
Incorporation of Environmental Signals
The photic input from the light-dark cycle is received and processed by the HPA axis and entrains the daily rhythms of cortisol release to the periphery (26, 27). The light-dark cycle is modeled as a step function in our model as shown in Eq. 1, much like earlier studies incorporating a similar zeitgeber (3, 27, 33, 40). In the HPA axis, corticotrophin-releasing hormone (CRH), ACTH, and cortisol are modeled with a Goodwin oscillator modified with Michaelis-Menten kinetics with self-sustained oscillations, entrained by the light-dark cycle (Eqs. 2–4). Estimated parameter values and descriptions are reported in Table 1 in the repository (see endnote). Briefly, in Eq. 2, kp1 is the rate constant for CRH production, and Kp1 is the dissociation constant. Vd1 controls the enzymatic degradation of CRH, and kfp represents the efficiency of proinflammatory cytokine P on production of F. FR(N)HPA is the cortisol-receptor complex in the HPA axis, which negatively feeds back to the production of CRH. Cortisol dynamics are influenced by EntF, a transit compartment representing the electric signal from the periphery transmitted to the suprachiasmatic nucleus via ventromedial arcuate nucleus.
The feeding-fasting cycle is represented as a step function in Eq. 5, similarly to the light-dark cycle. Feeding signal is processed through two transit compartments shown in Eqs. 6 and 7, each with a delay of 3 h, eventually controlling the NAD+ oscillations in the periphery by modifying the oxidation-reduction relations and changing the cellular NAD+-to-NADH ratio. The purpose of the transit compartment in the model is to reflect the experimental observation that peak of NAD+ level occurs 5–6 h after the beginning of the active phase in rat liver (38). The dynamics of NAD+ level is governed by Eq. 8. In the first term of this equation, nad represents the sum of NAD+ and NADH amount; therefore, the quantity (nad − NAD) represents the NADH available for conversion to NAD+. The second term of Eq. 8 represents the NAD+ amount recovered from the NAD+ salvage cycle. In this term, NMN represents the nicotinamide mononucleotide, the precursor to NAD+ in the salvage cycle. The third term incorporates the effect of nutrient availability to the NAD+ dynamics, and the fourth term represents NAD+ lost due to entering the salvage pathway. Equation 9 describes the activation of SIRT1 by coenzyme NAD+ (5). In this equation, sirtT represents the total (active and inactive) amount of SIRT1 available in the cell; therefore, the quantity (sirtT − SIRT1) indicates the availability of inactive SIRT1 to be activated by NAD+. This term was constructed because the protein concentration stays constant throughout the day while its activity level fluctuates (4). The second term of this equation represents the degradation, and the third and fourth terms describe the binding of SIRT1 to the CLOCK/BMAL1 complex, which is a critical component in the peripheral clock machinery. The details for bidirectional interaction between SIRT1 and clock genes as well as the description of peripheral clock network of the model are available in our (3) previous work and the online repository (see endnote).
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
Expression of Gluconeogenic Genes
In our model, PGC-1α is a key molecule that incorporates the effects of feeding to the transcription of gluconeogenic genes. In mitochondria, it stimulates oxidative metabolism in brown fat and skeletal muscles (36). It is also involved in expression of genes associated with mitochondrial uncoupling and energy expenditure (35). Since glucose uptake is influenced by the rates of mitochondrial oxidation (39), PGC-1α is expected to play a significant role in glucose homeostasis. Indeed, diabetic mice show an enhanced activity of PGC-1α (42). Studies show that PGC-1α expression in liver increases under fasting condition (13, 55). Moreover, primary hepatocytes infected with adenoviruses encoding for PGC-1α stimulated phosphoenolpyruvate carboxykinase (PEPCK) and glucose-6-phosphatase (G6PC; Ref. 55). Studying the PEPCK promoter structure elucidated that coactivation of HNF-4α, FOXO1, and glucocorticoid response element (GRE) appears to be necessary in initiating transcription of the Pck1 (53).
Equation 10 describes the dynamics of PGC-1α mRNA. Equation 11 represents the translated PGC-1α protein. The dynamics of PGC-1α protein are dependent on the transcription rate (kg3b) of PGC-1α mRNA, degradation rate (kg3d) of the protein, and import (kg3t) and export (kg4t) rates to the nucleus. Equation 12 governs the dynamics of PGC-1α once the protein is translocated to the nucleus. Finally, Eq. 13 represents the SIRT1-activated PGC-1α protein. The binding (kg5) and dissociation (kg8d) of SIRT1 as well as the degradation (kg8) of active PGC-1α are modeled in a linear manner. Then, the coactivation of FOXO1 and HNF-4α is lumped for simplicity into a single variable, FOXO1, in Eq. 14. The level of FOXO1 is dependent on the activation by PGC-1α (kg9) and deactivation (kg10) of activated FOXO1. The activated FOXO1 binds to a DNA motif upstream of the gluconeogenic genes and activates the transcription (Refs. 34, 53; Eq. 15).
Glucocorticoid receptor is also required along with HNF-4α and PGC-1α for full activation of PEPCK promoter, as reflected in the first term of Eq. 15. The cortisol-receptor complex binds to the GRE region in the promoter of the gluconeogenic genes to stimulate transcription (53). This binding reaction appears to be under the influence of CRY proteins in the nucleus (nuc; Ref. 19), incorporated into Eq. 15 in a Hill-type function, with s as the Hill coefficient.
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
Uncertainty and Sensitivity Analyses
In a model-building process, uncertainty and sensitivity analyses play a very important role in quantifying the output variability and describing the relative importance of each input in determining the output variability (6). Recognizing that our model involves a complex network of transcription, translation, and cellular reactions, we analyzed our model using a series of uncertainty and sensitivity analysis methods: 1) local sensitivity analysis, 2) Morris method, and 3) RS-HDMR. Each of the three methods has its own strength and weakness and offered different insights into our model. Local sensitivity analysis is a one-at-a-time method that assesses how uncertainty in one factor influences the model output while keeping other factors fixed. Although this method is quick and straightforward, it fails to capture any interactions among the parameters. Morris method is a one-at-a-time method and is still computationally efficient, but it explores the input design space in such a way that the existence of interaction effects can be identified. However, this method does not identify which specific parameter pair interacts with each other. Finally, RS-HDMR provides the interaction effects of specific pairs of factors while also giving information about the primary effects. For all three methods, analysis was performed under the light and feeding synchronized (both signals on 6 AM to 6 PM at 1) condition for consistency. The amplitude of Pck1/G6pc mRNA was measured as the response.
Local sensitivity analysis.
The local sensitivity analysis was performed on all 130 parameters of the model. The relative sensitivity coefficient for every parameter was calculated using the following equation (40):
| (16) |
In Eq. 16,
| pk = tested parameter |
| y = measured response. |
Each parameter was varied by 1% in the positive direction, and the relative local sensitivity coefficients for each parameter based on the amplitude of Pck1/G6pc mRNA were computed.
Morris method.
The Morris method is a computationally effective screening method that identifies a few important parameters in models involving many parameters. The method first computes elementary effects or the changes in an output due solely to changes in a particular input (29). The elementary effects were calculated with the following equation (6) for k = 112 peripheral parameters:
| (17) |
In Eq. 17, Y is a deterministic function of k input factors (parameters). Because each input parameter (xi) is scaled in the interval [0, 1], the right side of the equation is divided by Δi, which is a value in {1/(p − 1),…,1 − 1/(p – 1)}. Here, p is the number of levels. The mean (Eq. 18) and variance (Eq. 19) of the elementary effects are considered together to determine the ranking of factors in the order of importance.
| (18) |
| (19) |
Since radial sampling strategy has proved effective for efficiently covering the input space, Sobol’s quasirandom numbers (44, 45) were used to generate radial sampling points between ±20% of the nominal values, adapting from the implementation methods presented in Ref. 6. The repetition r = 100 was used for analyzing our model. With the use of this method, the mean and variance of the elementary effects for the peripheral parameters were considered together to sort the factors in the order of importance. This resulted in 20 factors exhibiting the mean of elementary effects >1.5. These factors were further analyzed using RS-HDMR for both primary and interaction effects of input variables in output variance.
RS-HDMR uncertainty analysis.
HDMR is a variance-based method developed by Rabitz and coworkers (37) aimed to reduce the computational cost for representing input-output relationships in high-dimensional systems. We followed the RS-HDMR uncertainty analysis method presented in Ref. 23 to analyze the 20 selected parameters from sensitivity analysis using the Morris method. The basis for uncertainty analysis using RS-HDMR method is that output f(x) can be expressed as a combination of the input x using statistical ANOVA decomposition, as Eq. 20 shows. Here, x is the set of all input parameters.
| (20) |
In Eq. 20, f0 is a constant representing the mean response to f(x). First-order component function fi(xi) gives the independent contributions to f(x) by the ith input variable acting alone. Second-order component function fij(xi,xj) gives the pair-correlated contribution to f(x) by the input variables xi and xj. The last term contains any residual nth-order correlated contribution of all input variables. For most real-world applications, HDMR expansion to the second order is sufficient, and Eq. 20 reduces to Eq. 21.
| (21) |
The variables xi were sampled between ±20% of the nominal values using Sobol’s quasirandom sequence and then were rescaled such that 0 ≤ xi ≤ 1 for all i by performing transformation of the input variables. The individual component functions have a direct statistical correlation interpretation, which leads to the decomposition of model output variance into its individual input variable contributions. Because of the orthogonality of the component functions, the variance can be expressed as Eq. 22.
| (22) |
To reduce the sampling effort, the component functions were approximated orthonormal polynomials as basis functions (22).
RESULTS
Our in silico studies aim to explore the effects of circadian disruption and metabolic re-entrainment on the rhythms of hepatic gluconeogenesis. The expression of gluconeogenic genes (Pck1/G6pc in our model) is under the modulation of two independent zeitgebers, light-dark cycle and feeding-fasting cycle. The simplified schematic of the model encompassing the HPA axis and the periphery representing human hepatocyte is shown in Fig. 1. The schematic depicts the signal transduction from the environment (light and feeding) to the transcription of Pck1/G6pc. Cortisol level in the periphery is mediated by the light and the feeding signals and induces the transcription of Pck1/G6pc when bound to its receptor. Induction by cortisol is inhibited by the PER/CRY, one of the key components of the circadian clock machinery. The changing concentration of NAD+ following the feeding-fasting cycle regulates FOXO1 through SIRT1 and PGC-1α.
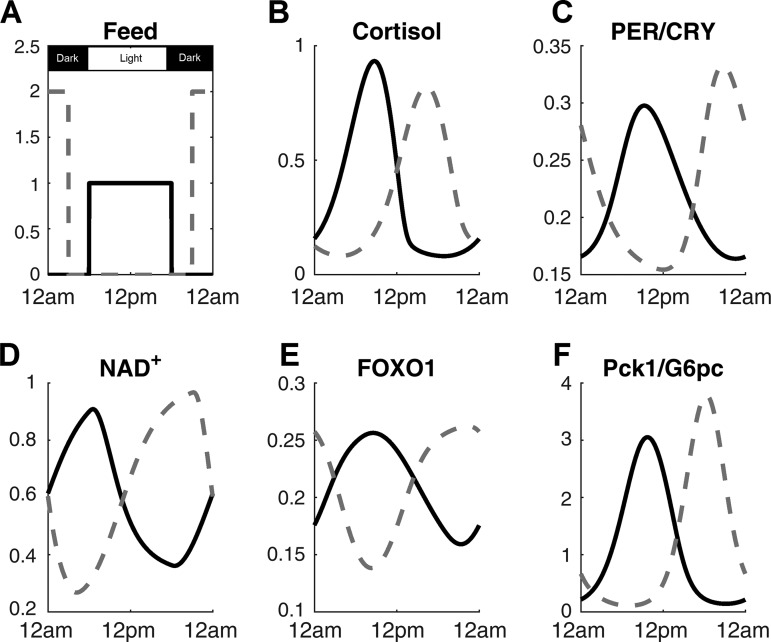
In Fig. 2, the behavior of the model throughout the 24-h day on synchronized (light and feeding schedules are identical) and time-restricted feeding (TRF) schedules are shown. Light signal was at 1 from 6 AM to 6 PM and at 0 for the rest of the day. Feeding signals for both conditions are shown in Fig. 2A. For the light-feeding synchronized condition, feeding signal was at 1 from 6 AM to 6 PM and at 0 for the other 12 h. To make sure that the system is provided with identical amount of feeding signal, which represents the amount of food available to the system at a given time, the area under the curve for feeding was identical between the light-feeding synchronized condition and TRF condition. As such, feeding signal was at 2 from 9 PM to 3 AM and at 0 for the rest of the time for TRF condition. The cortisol (Fig. 2B) and PER/CRY protein (Fig. 2C), both regulators of Pck1/G6pc transcription, peak in the morning time for the synchronized schedule and evening time for the TRF schedule. For both cases, cortisol and PER/CRY peak in the early active phase, consistent with restricted feeding studies on mice, which show ~12-h phase shift in cortisol and clock gene levels in the anticipation of meal time (10, 11, 46). NAD+ (Fig. 2D) peaks 4–5 h after the beginning of feeding time, agreeing with previous experimental work (30). The circadian rhythm of FOXO1 (Fig. 2E) closely follows that of SIRT1. Although no experimental data confirm this, the results are expected within the structure of our model because FOXO1 is activated by SIRT1-activated PGC-1α. The expression of Pck1/G6pc mRNA (Fig. 2F) also peaks in the early active phase according to our model. In ad libitum fed rats, both G6Pase and PEPCK activity peak slightly before the dark (active) phase in rats subjected to 12:12-h light-dark cycle (2, 32). When rats are moved to TRF schedule, G6Pase activity peaks slightly before the feeding start time. G6Pase protein amount still oscillates rhythmically but becomes bimodal, with the major peak slightly before the feeding time and a minor peak in the middle of the dark phase (32). For PEPCK, the enzymatic activity becomes bimodal with the major peak at the transition from dark to light phase and a minor peak in the middle of the dark phase. The PEPCK protein amount peaks ~2 h after the feeding start time (32). Although the phase changes that occur for the PEPCK and G6Pase enzymatic activities and protein amounts slightly differ in detail, the common theme for all of them is that the gluconeogenic gene expression is the highest around the transition time from inactive to active phase, consistent with our model. In terms of amplitude change on adjustment to feeding schedule, our model was constructed to follow most closely the experimental finding that amplitude of PEPCK protein amount increases when rats are switched from ad libitum feeding to TRF (32).
Fig. 2.
The time profiles of key components throughout the day on synchronized (solid line) and time-restricted (dotted line) feeding schedules. Light signal was at 1 from 6 AM to 6 PM and at 0 for the rest of the day. Feeding signals for both conditions are shown in A. The corresponding cortisol (B), PER/CRY protein (C), NAD+ (D), FOXO1 (E), and Pck1/G6pc mRNA (F) are also shown.
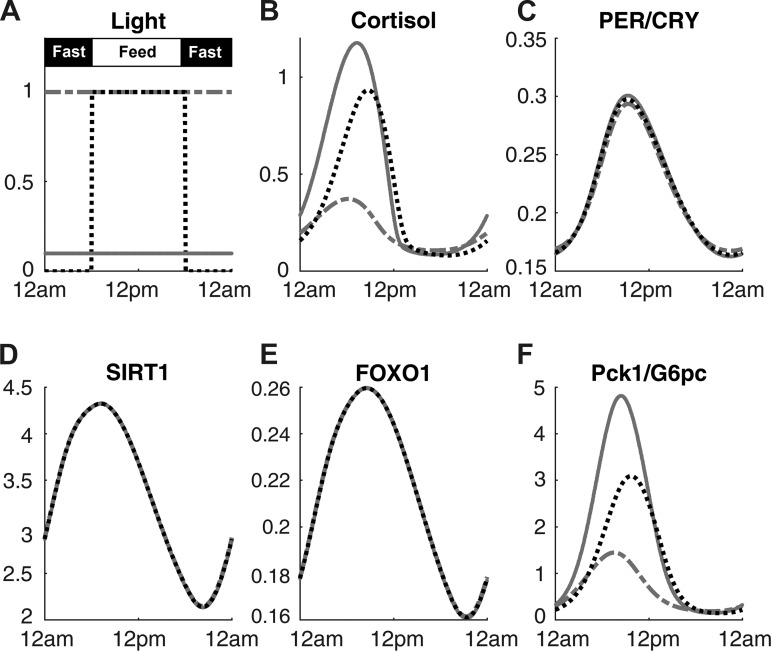
Figure 3 shows the modifications to gluconeogenic gene expression when the model experiences different types of light signals. In this figure, the responses of the model to constant dim light and constant bright light are compared with 12:12-h light-dark cycle while the feeding schedule is fixed to 12:12-h feeding-fasting cycle for all three conditions (Fig. 3A). Imposing constant bright light results in reduced amplitude of cortisol (Fig. 3B), whereas it increases the amplitude of Pck1/G6pc (Fig. 3F). An animal study conducted in voles confirmed the model prediction (2). When G6Pase activity was measured over a 24-h period, animals in constant dark environment showed statistically significant oscillation, whereas the animals in constant light environment did not. The PER/CRY (Fig. 3C) oscillation amplitude is slightly decreased when constant bright light is imposed, qualitatively in agreement with experimental observations in mice (47). SIRT1 (Fig. 3D) and FOXO1 (Fig. 3E) dynamics are not influenced by the light schedule change.
Fig. 3.
Time profiles of key components under constant light schedule at different intensities are compared. Feeding signals was at 1 from 6 AM to 6 PM and at 0 for the rest of the day (A). Constant bright light (dotted-dashed line) and constant dim light (solid line) are shown in A along with a control (dotted line), in which feeding and light are synchronized. The cortisol (B), PER/CRY protein (C), SIRT1 (D), FOXO1 (E), and Pck1/G6pc mRNA (F) under the different light intensities are also presented.
Next, we examined the effect of cortisol shock and CRY overexpression against experimental findings. Sharp increase in serum cortisol level increases glucose production due to gluconeogenesis in humans (17). When peripheral cortisol level is elevated in our model while the central compartment is conserved, PER/CRY, CLOCK/BMAL1, and Pck1/G6pc levels are all increased (data available in the repository; see endnote). The peripheral cortisol level was increased by doubling the secretion from the central compartment. Since our model does not consider PER and CRY separately, CRY overexpression was simulated by doubling the transcription rate of Per/Cry mRNA (V1b). The resulting profiles under ad libitum feeding and TRF are available in the repository (see endnote). Under both feeding schedules, modulating the transcription rate did result in increased expression of PER/CRY protein and resulted in decreased expression of Pck1/G6pc. The results are consistent with recent findings that CRY1 and CRY2 inhibit gluconeogenesis by cortisol-receptor complex in the nucleus from binding to the GRE region of the gluconeogenic genes (19).
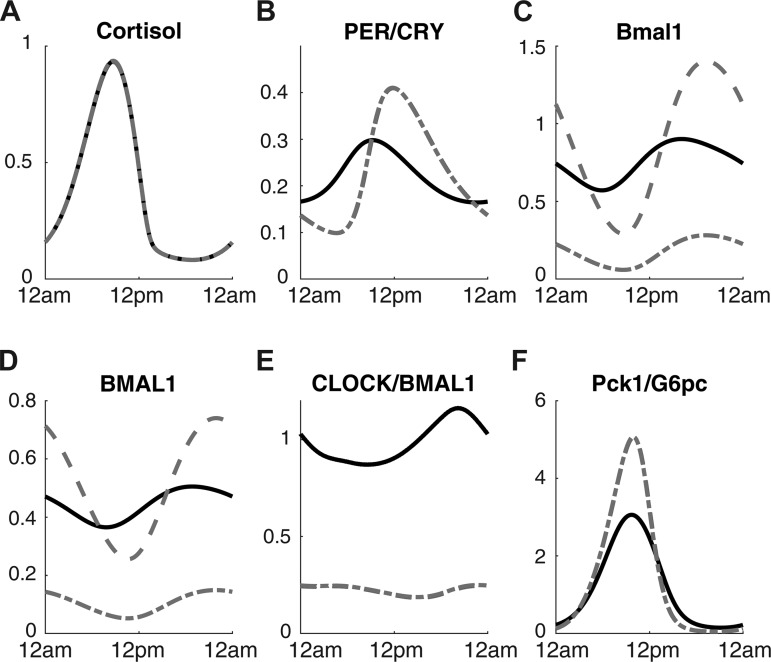
To simulate genetic circadian disruption, we tested the model under very low CLOCK and BMAL1 expression and showed the results in Fig. 4. CLOCK and BMAL1 knockouts were simulated by multiplying the synthesis term for each component by a factor of 0.2. As Fig. 4E shows, the concentration of CLOCK/BMAL1 is lower in both knockout conditions compared with the nominal condition. Circadian cortisol profile (Fig. 4A) is unaffected by the knockout in our model. BMAL1 protein (Fig. 4D) and Bmal1 mRNA (Fig. 4C) levels are suppressed for the BMAL1 knockout model, but the same components are expressed with increased amplitude for CLOCK knockout model. PER/CRY protein (Fig. 4B) oscillation amplitude becomes greater under the knockout conditions, and Pck1/G6pc (Fig. 4F) also oscillates with a higher amplitude. Experimental studies on whole body CLOCK knockouts give conflicting results depending on the experimental/environmental conditions as well as the genetic background of the animals (14). Some studies show that knockout of CLOCK results in decreased or normal blood glucose level (31, 41), whereas others report increased blood glucose level (25, 49) and impaired glucose tolerance. Our model supports the latter case where fasting glucose level is elevated on CLOCK knockout due to higher amplitude of gluconeogenesis.
Fig. 4.
Time profiles of cortisol (A), PER/CRY protein (B), Bmal1 mRNA (C), BMAL1 protein (D), CLOCK/BMAL1 complex (E), and Pck1/G6pc mRNA (F) are shown under nominal condition (black lines), Bmal1 knockout condition (gray dotted-dashed lines), and Clock knockout condition (gray dashed lines).
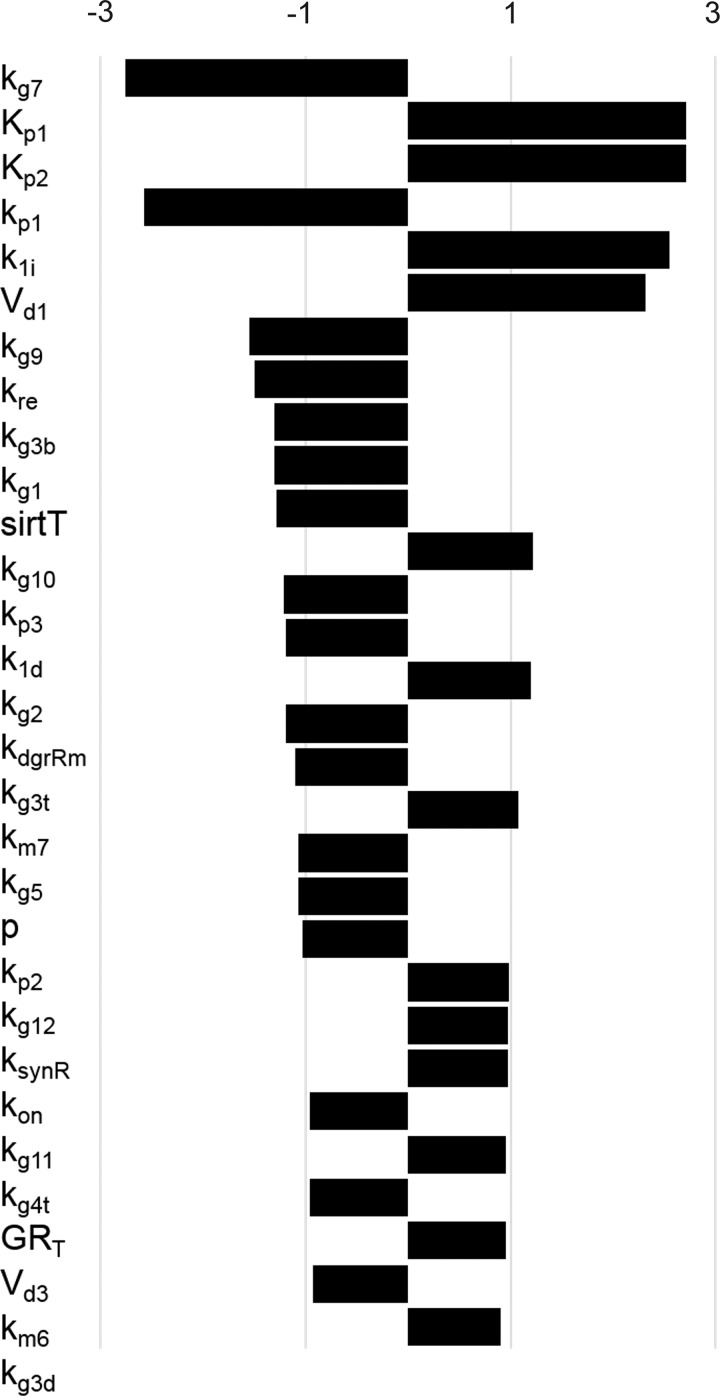
Next, we investigated whether the increased amplitude of Pck1/G6pc in Clock knockout condition can be adjusted back to the nominal amplitude by changing the feeding rhythm relative to the light-dark cycle. To examine the effect of phase relations between light and feeding, we simulated 12-h feeding period starting at different times of the day while fixing the light period from 6 AM to 6 PM. In Fig. 5, the amplitude of Pck1/G6pc for different feeding schedules normalized by the wild-type amplitude under synchronized condition is plotted. The x-axis represents the start time of the feeding period. The figure shows that amplitude of Pck1/G6pc under Clock knockout condition changes with the feeding start time. Amplitudes are greater when feeding is started in the dark phase. If feeding starts in the afternoon (3 to 6 PM), the amplitude for knockout model reaches below the wild-type amplitude under synchronized condition. Next, we present the analysis of the model using the uncertainty and sensitivity analyses on the amplitude of Pck1/G6pc. In Fig. 6, the sensitivity coefficients computed from local sensitivity analysis using Eq. 16 are shown for the 30 most sensitive parameters. The sensitivity coefficients for all parameters are available the repository (see endnote). Among the parameters with high-sensitivity coefficients, Kp1, Kp2, kp1, Vd1, and Vd3 mediate the dynamics of the HPA axis. A group of parameters that control the dynamics of PGC-1α and FOXO1, such as kg7, kg9, kg1, kg10, kg2, kg3t, kg4t, and kg3d, also had high-sensitivity coefficients. Other than these two groups, parameters associated with Per/Cry transcription (k1i and p) cortisol-receptor dynamics (kre, kdgrRm, and ksynR) also exhibited high-sensitivity coefficients.
Fig. 5.
Amplitude of Pck1/G6pc for Clock knockout model normalized by the wild-type amplitude under light-feeding synchronized schedule. Normalized amplitudes are plotted against the feeding start time. For all cases, feeding lasted for 12 h, and light schedule was fixed to be on from 6 AM to 6 PM.
Fig. 6.
Sensitivity coefficients for 30 most sensitive parameters using local sensitivity analysis. GRT, total glucocorticoid receptor protein; kon, 2nd-order rate constant for glucocorticoid receptor binding.
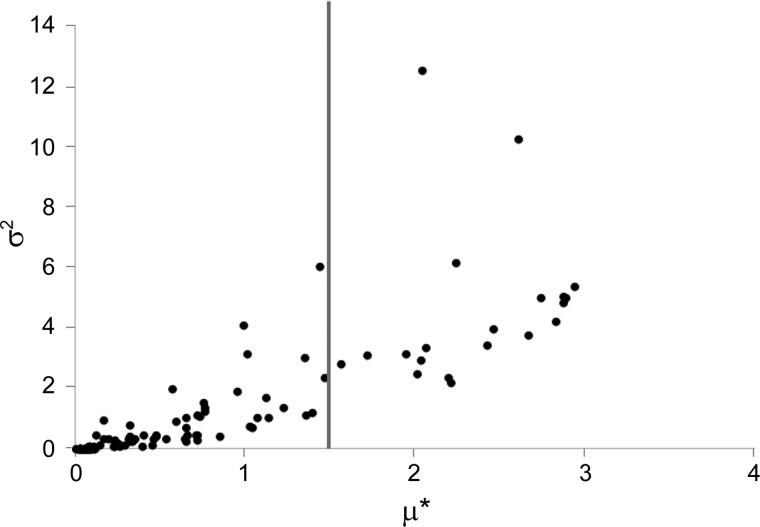
In Fig. 7, the results from sensitivity analysis using Morris method performed on peripheral parameters is visualized on a variance (σ2) vs. absolute mean (μ*) plot. Morris method was used as a screening method for identifying the most important parameters because this method will compute both elementary and interaction effects without high computational cost. In general, the parameters that had greater mean elementary effects also had greater variance. We selected 20 samples that had μ* values >1.5 as important parameters and listed them in Table 1 along with the σ2 values. As shown in the table, the parameters pertaining to the dynamics of PGC-1α, FOXO1, Per/Cry transcription, Bmal1 transcription, and cortisol receptor had the greatest elementary effects.
Fig. 7.
Sample results from sensitivity analysis using Morris method performed on the amplitude of Pck1/G6pc mRNA amplitude. One hundred repetitions of sampling were used to generate this figure. The variance (σ2) is plotted against μ*. Parameters with µ* > 1.5 were selected for further analysis.
Table 1.
Sensitivity metrics for 20 most sensitive parameters identified using Morris method on amplitude of Pck1/G6pc
| Rank | Parameter | μ* | σ2 | Rank | Parameter | μ* | σ2 |
|---|---|---|---|---|---|---|---|
| 1 | kg10 | 2.9330 | 5.4027 | 11 | kg8 | 2.2431 | 6.1479 |
| 2 | kg9 | 2.8870 | 4.9604 | 12 | kg11 | 2.2097 | 2.1702 |
| 3 | kg1 | 2.8673 | 4.8427 | 13 | kg12 | 2.1902 | 2.3458 |
| 4 | kg2 | 2.8631 | 5.0442 | 14 | sirtT | 2.0553 | 3.3711 |
| 5 | kg3b | 2.8250 | 4.2164 | 15 | k4b | 2.0430 | 12.5589 |
| 6 | kg3d | 2.7314 | 4.9744 | 16 | GRT | 2.0307 | 2.9139 |
| 7 | kg3t | 2.6627 | 3.7803 | 17 | kon,GR | 2.0089 | 2.4504 |
| 8 | k1i | 2.6072 | 10.242 | 18 | kre,GR | 1.9427 | 3.1098 |
| 9 | kg4t | 2.4582 | 3.9920 | 19 | kg7 | 1.7077 | 3.1010 |
| 10 | kg5 | 2.4166 | 3.4337 | 20 | km1 | 1.5650 | 2.8073 |
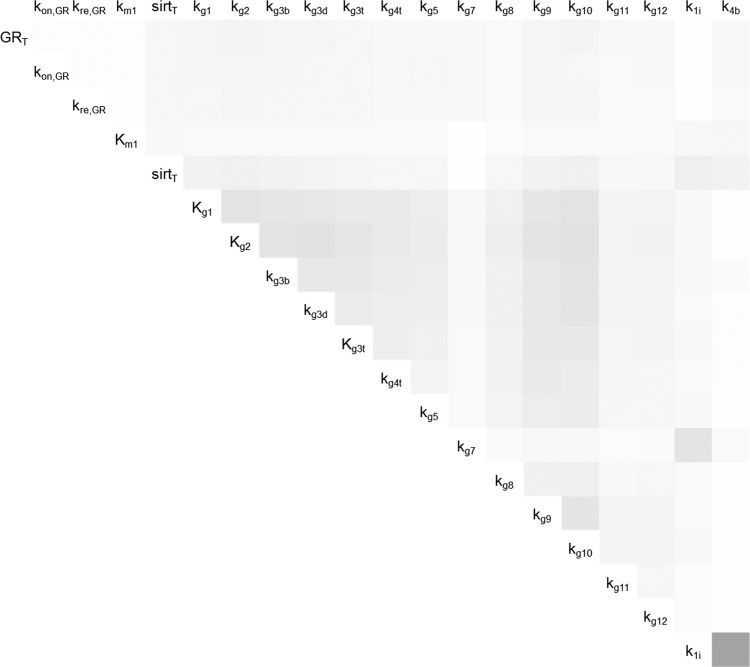
The parameters in Table 1 were further analyzed with RS-HDMR uncertainty analysis. Since our model is expected to be highly nonlinear, we first tried to identify the appropriate sample size for analyzing our model. Table 2 reports the main results from RS-HDMR uncertainty analysis for different sample sizes: output (mean amplitude of Pck1/G6pc); the total variance in output (σ2); the sum of all 1st-order variances (); and the sum of all 2nd-order variances (). For Eq. 22 to hold true, the condition has to be met. Therefore, only the sample sizes of 20,000 and 100,000 yield valid uncertainty analysis. Since greater sample size should provide the most accurate results, only the analysis resulting from the sample size of 100,000 is presented in Table 3 and Fig. 8. In Table 3, the 1st-order variance for the 20 tested parameters is presented in the order of importance. Parameters related to the dynamics of PGC-1α and FOXO1 are the most important parameters in determining the variance in amplitude of Pck1/G6pc according to the RS-HDMR method. In Fig. 8, the 2nd-order interaction effects to output variance are shown in a color scheme, with bigger interaction effects in darker color and smaller interaction effects lighter color. The pair k1i and k4b shows the largest 2nd-order interaction, whereas the parameters pertaining to the PGC-1α and FOXO1 level show the next largest 2nd-order interaction.
Table 2.
Summary of results from HDMR uncertainty analysis on amplitude of Pck1/G6pc
| Sample Size | f0 | σ2 | ||
|---|---|---|---|---|
| 1,000 | 5.8266 | 15.9072 | 11.4909 | 34.9030 |
| 2,000 | 5.8149 | 14.5537 | 10.8716 | 15.0472 |
| 3,000 | 5.7970 | 13.8447 | 10.4087 | 10.4486 |
| 5,000 | 5.8049 | 14.1645 | 10.5303 | 7.3712 |
| 10,000 | 5.7963 | 13.2363 | 10.1985 | 3.9241 |
| 20,000 | 5.7881 | 12.6472 | 9.9297 | 2.5715 |
| 100,000 | 5.7884 | 12.6021 | 9.9391 | 2.0946 |
Table 3.
First-order variance from HDMR uncertainty analysis
| Parameter | (from HDMR) | Correction Factor | Influence on PGC-1α (N) |
|---|---|---|---|
| kg2 | 0.836349 | 1.58 | Decrease |
| kg10 | 0.833797 | 1.57 | Decrease |
| kg9 | 0.793650 | 0.64 | Increase |
| kg1 | 0.792885 | 0.63 | Increase |
| kg3b | 0.790013 | 0.63 | Increase |
| kg3d | 0.720930 | 1.62 | Decrease |
| kg3t | 0.686181 | 0.62 | Increase |
| kg4t | 0.575706 | 1.69 | Decrease |
| kg5 | 0.556384 | 0.59 | Increase |
| kg12 | 0.450824 | 1.73 | |
| kg11 | 0.449879 | 0.58 | |
| kg8 | 0.409953 | 1.82 | Decrease |
| sirtT | 0.398856 | 0.59 | |
| GRT | 0.359445 | 0.64 | |
| kon,GR | 0.347152 | 0.64 | |
| kre,GR | 0.317100 | 1.60 | |
| kg7 | 0.233719 | 1.71 | |
| k1i | 0.191373 | 1.18 | |
| km1 | 0.166523 | 1.65 | |
| k4b | 0.028383 | 0.45 |
Correction factor to get nominal Pck1/G6pc amplitude for CLOCK knockout model is also presented. PGC-1α (N), nuclear PGC-1α.
Fig. 8.
Second-order interaction contributions to output variance from RS-HDMR uncertainty analysis. Darker gray indicates higher interaction effect.
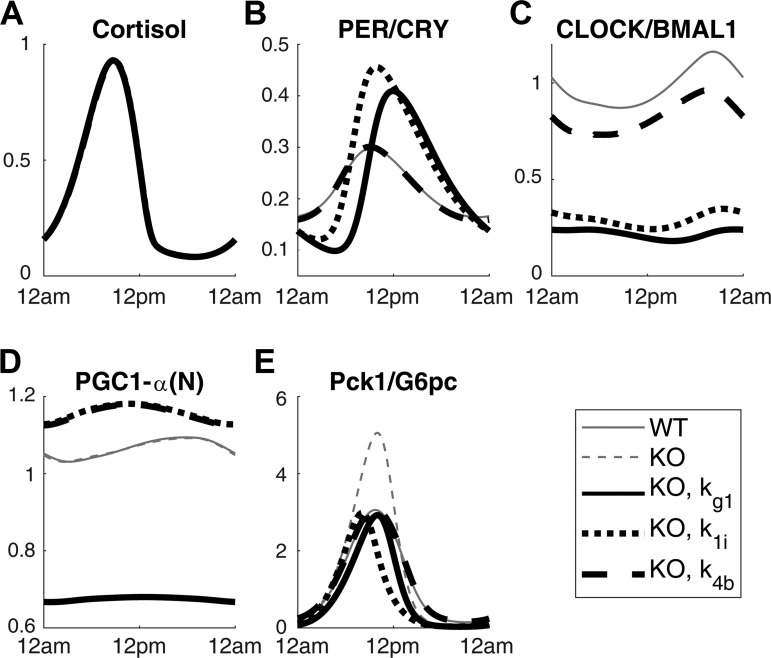
Finally, we attempted changing the amplitude of Pck1/G6pc of the Clock knockout model by applying a correction factor to different parameters. The correction factor that most closely adjusts the Pck1/G6pc amplitude back to the nominal amplitude for each parameter was calculated. These factors are listed in Table 3. The parameters that contribute to either increasing or decreasing level of nuclear PGC-1α are indicated. The correction factors for these parameters show that parameters with larger first-order variance require a correction factor with a smaller percentage change of the original value of the parameter. Time profiles for the Clock knockout model with select correction factors are shown in Fig. 9. Adjusting kg1 (PGC-1α transcription rate) reduced the amplitude of the Clock knockout model by decreasing the nuclear PGC-1α level (Fig. 9D), which is a direct activator of FOXO1 that stimulates the expression of gluconeogenic genes (Fig. 9E). Adjusting k1i (inhibition constant for Per/Cry transcription) increased the PER/CRY (Fig. 9B), CLOCK/BMAL1 (Fig. 9C), and nuclear PGC-1α (Fig. 9D) level. Finally, adjusting k4b returned the PER/CRY profile (Fig. 9B) to the wild-type condition and increased the CLOCK/BMAL1 (Fig. 9C) level and nuclear PGC-1α (Fig. 9D) level.
Fig. 9.
Time profiles of cortisol (A), PER/CRY protein (B), CLOCK/BMAL1 complex (C), nuclear (N) PGC-1α (D), and Pck1/G6pc mRNA (E) are shown under nominal condition and Clock knockout (KO) condition. The rest of the profiles show Clock knockout condition adjusted by correction factor for certain parameters: kg1, k1i, and k4b. The light and feeding schedule are synchronized for all profiles. WT, wild-type.
DISCUSSION
The circadian rhythms modulate important metabolic pathways, including gluconeogenesis (20, 56) and lipid metabolism (21, 54). Because of the intimate relationship between circadian rhythms and metabolism, disruption in the daily rhythms often results in metabolic syndromes such as obesity and high triglycerides (16). In mammals, it is important that plasma glucose level stays within a physiologically relevant bound since some key biological functions such as neuronal activity and balancing of electrolytes depend on homeostatic plasma glucose level (50). Various clock gene knockout studies support that plasma glucose homeostasis is under the regulation of circadian components (20, 56). These studies motivate the need to elucidate the mechanisms of how circadian rhythms modulate glucose homeostasis throughout the day. Since glucose homeostasis is maintained through a complex network of processes, we chose to focus on hepatic gluconeogenesis specifically to simplify the problem while drawing meaningful conclusions.
Figure 2 shows that the fasting level of Pck1/G6pc (Fig. 2F) will be elevated under TRF compared with that of ad libitum feeding. The dynamics of Pck1/G6pc are driven by three different forces in our model: 1) FOXO1 binding to a DNA motif on the promoter region and stimulating the transcription, 2) nuclear cortisol-receptor complex binding to the GRE region on the promoter and stimulating the transcription, and 3) PER/CRY inhibiting the binding of nuclear cortisol-receptor complex from binding to the GRE. Since cortisol peak at the light-dark transition period is decreased while PER/CRY level is decreased, the Pck1/G6pc level should decrease. However, Fig. 2E shows that FOXO1 amplitude and level increase when the model is exposed to TRF condition. These competing effects ultimately result in an increased amplitude and level in the expression of Pck1/G6pc, suggesting that the influence of FOXO1 is stronger than the effects of cortisol and PER/CRY. The increased amplitude of FOXO1 can be attributed to the higher amplitude of feeding signal, which transduces down to FOXO1 via SIRT1 (Fig. 2D) and PGC-1α. The phase of all major components is re-entrained to the feeding rhythm, since cortisol, clock genes, and FOXO1 are all phase-shifted. When the increase in amplitude and phase change of PEPCK protein was observed for the TRF condition (32), animals were given a 2-h window during the rest period for food consumption, which would have resulted in high caloric intake during a short period of time, similarly to the simulation condition.
Overexpression of PER/CRY and elevated peripheral cortisol validated that the model produces expected behavior. Increased level of PER/CRY protein does result in a decreased expression of Pck1/G6pc, for both ad libitum feeding and TRF, agreeing with animal studies (19, 56). Increase in peripheral cortisol also results in an increased expression of Pck1/G6pc. A side effect of increase in peripheral cortisol is the increased level CLOCK/BMAL1 complex, which activates the expression of PER/CRY protein. Stimulation of Pck1/G6pc expression by increased cortisol amount outperforms the increased inhibition by PER/CRY protein, resulting in a behavior consistent with experimental findings (17).
Constant exposure to bright light abolishes the rhythms for G6Pase activity, as shown in Ref. 2. From this study, we hypothesized that imposing a constant bright light on our model would result in a decreased amplitude for Pck1/G6pc. Figure 3F shows that our hypothesis is true, mainly due to the decline in the cortisol level and amplitude (Fig. 3B). The dampening of the rhythm in cortisol for the bright light condition is due to light-mediated degradation of CRH (15, 18, 28), which results in decreased secretion of cortisol from the HPA axis.
Our model predicts that the amplitude of Pck1/G6pc is higher for the Clock knockout model compared with the wild-type model (Fig. 4). CLOCK/BMAL1 complex in the nucleus influences the dynamics of PER/CRY protein in two opposing ways as depicted in Fig. 1. It binds to the E-box enhancer on the promoter of Per and Cry genes and stimulates the expression of PER/CRY. It can also inhibit the expression of PER/CRY by preventing the cortisol-receptor complex in the nucleus from binding to the GRE of the promoter and preventing the expression of PER/CRY. CLOCK knockout studies report conflicting findings where some result in decreased or normal blood glucose level (31, 41), whereas others report increased blood glucose level (31); our model supports the latter case.
Since animal experiments (32) and our model support the idea that feeding pattern can re-entrain the expression of gluconeogenic genes, we hypothesized that the increased amplitude of Pck1/G6pc under Clock knockout condition can be returned to the nominal level by adjusting the feeding schedule. Figure 5 shows the amplitude change for Clock knockout model normalized by the wild-type amplitude for different feeding schedules. Figure 5F shows that there exists a feeding schedule that produces amplitude for Pck1/G6pc very similar to the nominal amplitude. Although it should be noted that the decrease in Pck1/G6pc amplitude was accompanied by a wide phase shift, such behavior is expected since the phase relationship between feeding-fasting cycle and the Pck1/G6pc remained unchanged, which would leave the fasting level of gluconeogenesis similar to the nominal case in physiological situations.
The uncertainty and sensitivity analyses indicate that the local pathways that directly interact with the promoter of the Pck1/G6pc (PGC-1α and FOXO1 dynamics, cortisol-receptor dynamics, and PER/CRY dynamics) are the most influential in changing the amplitude of Pck1/G6pc. Local sensitivity analysis, the simplest and computationally the most efficient method of the three, alone, was sufficient for coming to this conclusion. However, local sensitivity analysis failed to identify parameters that have high interaction effect and low primary effect, such as the Michaelis constant for Bmal1 (k4b). RS-HDMR uncertainty analysis combined with the Morris method for identifying important parameters were able to identify the interaction of this parameter with inhibition constant for Per/Cry transcription (k1i).
Finally, we utilized the results from the sensitivity and uncertainty analyses to alter the behavior of Clock knockout model. The PGC-1α parameters listed in Table 3 and the accompanying correction factors indicate that the combination of uncertainty and sensitivity analyses were successful in identifying and ranking the parameters that have the greatest influence on Pck1/G6pc amplitude. Applying these correction factors influenced the system in various ways depending on the local pathways that the parameters belonged to, as shown in Fig. 9.
In summary, our model qualitatively captures the dynamics of hepatic gluconeogenesis represented by the transcription of Pck1/G6pc entrained to the light-dark cycle and feeding-fasting cycle. The dynamics of Pck1/G6pc mRNA are governed by three main driving forces in our model, the cortisol-receptor activating transcription, PER/CRY inhibiting transcription, and FOXO1 mediated by PGC-1α activating transcription. With the use of the semimechanistic model, we were able to simulate a clock gene knockout condition. Subsequently, we demonstrated that the abnormally high level and amplitude of Pck1/G6pc in the knockout model can be modified to resemble the nominal level by either targeting specific local pathways in our model and modifying parameters identified through the uncertainty analyses or imposing modifications to the feeding patterns relative to the light-dark cycle. Comparing the correction factors revealed that within a specific local pathway, uncertainty analyses are successful in identifying possible targets that have the most influence on gluconeogenic gene expression. Furthermore, our model predicts that exposure to constant bright light is detrimental to the robust oscillations of metabolic gene expression. Of course, our model is limited since it does not describe the enzymatic activity of PEPCK and G6PC, changes in glucose and glycogen levels, and other features of hepatic gluconeogenesis. Furthermore, a number of important questions still remain, such as the impact of nutritional composition and the duration of light signal, et cetera. In the future, we plan to address these questions and incorporate the role of insulin.
GRANTS
We gratefully acknowledge financial support from the National Science Foundation Graduate Research Fellowship under Grant DGE-1433187 and the National Institute of General Medical Sciences of the National Institutes of Health under Awards T32-GM-008339 and GM-024211.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
S.-A.B. and I.P.A. conceived and designed research; S.-A.B. performed experiments; S.-A.B. analyzed data; S.-A.B. and I.P.A. interpreted results of experiments; S.-A.B. prepared figures; S.-A.B. drafted manuscript; S.-A.B. and I.P.A. edited and revised manuscript; I.P.A. approved final version of manuscript.
ENDNOTE
At the request of the authors, readers are herein alerted to the fact that additional materials related to this manuscript may be found at a public repository, which at the time of publication the authors indicate is: https://github.com/AndroulakisGrp/SB_Gluconeogenesis. These materials are not a part of this manuscript and have not undergone peer review by the American Physiological Society (APS). APS and the journal editors take no responsibility for these materials, for the Web site address, or for any links to or from it.
REFERENCES
- 1.Albrecht U. Timing to perfection: the biology of central and peripheral circadian clocks. Neuron 74: 246–260, 2012. doi: 10.1016/j.neuron.2012.04.006. [DOI] [PubMed] [Google Scholar]
- 2.Ashman PU, Seed JR. Biochemical studies in the vole, Microtus montanus–II. The effects of a Trypanosoma brucei gambiense infection on the diurnal variation of hepatic glucose-6-phosphatase and liver glycogen. Comp Biochem Physiol B 45: 379–392, 1973. doi: 10.1016/0305-0491(73)90072-2. [DOI] [PubMed] [Google Scholar]
- 3.Bae SA, Androulakis IP. The synergistic role of light-feeding phase relations on entraining robust circadian rhythms in the periphery. Gene Regul Syst Bio 11: 1177625017702393, 2017. doi: 10.1177/1177625017702393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bellet MM, Orozco-Solis R, Sahar S, Eckel-Mahan K, Sassone-Corsi P. The time of metabolism: NAD+, SIRT1, and the circadian clock. Cold Spring Harb Symp Quant Biol 76: 31–38, 2011. doi: 10.1101/sqb.2011.76.010520. [DOI] [PubMed] [Google Scholar]
- 5.Bordone L, Guarente L. Calorie restriction, SIRT1 and metabolism: understanding longevity. Nat Rev Mol Cell Biol 6: 298–305, 2005. doi: 10.1038/nrm1616. [DOI] [PubMed] [Google Scholar]
- 6.Campolongo F, Saltelli A, Cariboni J. From screening to quantitative sensitivity analysis. A unified approach. Comput Phys Commun 182: 978–988, 2011. doi: 10.1016/j.cpc.2010.12.039. [DOI] [Google Scholar]
- 7.Cao D, Wang M, Qiu X, Liu D, Jiang H, Yang N, Xu RM. Structural basis for allosteric, substrate-dependent stimulation of SIRT1 activity by resveratrol. Genes Dev 29: 1316–1325, 2015. doi: 10.1101/gad.265462.115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Cardone L, Hirayama J, Giordano F, Tamaru T, Palvimo JJ, Sassone-Corsi P. Circadian clock control by SUMOylation of BMAL1. Science 309: 1390–1394, 2005. doi: 10.1126/science.1110689. [DOI] [PubMed] [Google Scholar]
- 9.Cassone VM. Effects of melatonin on vertebrate circadian systems. Trends Neurosci 13: 457–464, 1990. doi: 10.1016/0166-2236(90)90099-V. [DOI] [PubMed] [Google Scholar]
- 10.Filipski E, Innominato PF, Wu M, Li XM, Iacobelli S, Xian LJ, Lévi F. Effects of light and food schedules on liver and tumor molecular clocks in mice. J Natl Cancer Inst 97: 507–517, 2005. doi: 10.1093/jnci/dji083. [DOI] [PubMed] [Google Scholar]
- 11.Hara R, Wan K, Wakamatsu H, Aida R, Moriya T, Akiyama M, Shibata S. Restricted feeding entrains liver clock without participation of the suprachiasmatic nucleus. Genes Cells 6: 269–278, 2001. doi: 10.1046/j.1365-2443.2001.00419.x. [DOI] [PubMed] [Google Scholar]
- 12.Hatori M, Vollmers C, Zarrinpar A, DiTacchio L, Bushong EA, Gill S, Leblanc M, Chaix A, Joens M, Fitzpatrick JA, Ellisman MH, Panda S. Time-restricted feeding without reducing caloric intake prevents metabolic diseases in mice fed a high-fat diet. Cell Metab 15: 848–860, 2012. doi: 10.1016/j.cmet.2012.04.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Herzig S, Long F, Jhala US, Hedrick S, Quinn R, Bauer A, Rudolph D, Schutz G, Yoon C, Puigserver P, Spiegelman B, Montminy M. CREB regulates hepatic gluconeogenesis through the coactivator PGC-1. Nature 413: 179–183, 2001. doi: 10.1038/35093131. [DOI] [PubMed] [Google Scholar]
- 14.Kalsbeek A, la Fleur S, Fliers E. Circadian control of glucose metabolism. Mol Metab 3: 372–383, 2014. doi: 10.1016/j.molmet.2014.03.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Kalsbeek A, van der Vliet J, Buijs RM. Decrease of endogenous vasopressin release necessary for expression of the circadian rise in plasma corticosterone: a reverse microdialysis study. J Neuroendocrinol 8: 299–307, 1996. doi: 10.1046/j.1365-2826.1996.04597.x. [DOI] [PubMed] [Google Scholar]
- 16.Karlsson B, Knutsson A, Lindahl B. Is there an association between shift work and having a metabolic syndrome? Results from a population based study of 27,485 people. Occup Environ Med 58: 747–752, 2001. doi: 10.1136/oem.58.11.747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Khani S, Tayek JA. Cortisol increases gluconeogenesis in humans: its role in the metabolic syndrome. Clin Sci (Lond) 101: 739–747, 2001. doi: 10.1042/cs1010739. [DOI] [PubMed] [Google Scholar]
- 18.Kow LM, Pfaff DW. Vasopressin excites ventromedial hypothalamic glucose-responsive neurons in vitro. Physiol Behav 37: 153–158, 1986. doi: 10.1016/0031-9384(86)90398-7. [DOI] [PubMed] [Google Scholar]
- 19.Lamia KA, Papp SJ, Yu RT, Barish GD, Uhlenhaut NH, Jonker JW, Downes M, Evans RM. Cryptochromes mediate rhythmic repression of the glucocorticoid receptor. Nature 480: 552–556, 2011. doi: 10.1038/nature10700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lamia KA, Storch KF, Weitz CJ. Physiological significance of a peripheral tissue circadian clock. Proc Natl Acad Sci USA 105: 15172–15177, 2008. doi: 10.1073/pnas.0806717105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lau P, Nixon SJ, Parton RG, Muscat GE. RORα regulates the expression of genes involved in lipid homeostasis in skeletal muscle cells: caveolin-3 and CPT-1 are direct targets of ROR. J Biol Chem 279: 36828–36840, 2004. doi: 10.1074/jbc.M404927200. [DOI] [PubMed] [Google Scholar]
- 22.Li GY, Wang SW, Rabitz H. Practical approaches to construct RS-HDMR component functions. J Phys Chem A 106: 8721–8733, 2002. doi: 10.1021/jp014567t. [DOI] [Google Scholar]
- 23.Li GY, Wang SW, Rabitz H, Wang SY, Jaffe P. Global uncertainty assessments by high dimensional model representations (HDMR). Chem Eng Sci 57: 4445–4460, 2002. doi: 10.1016/S0009-2509(02)00417-7. [DOI] [Google Scholar]
- 24.Luna A, McFadden GB, Aladjem MI, Kohn KW. Predicted role of NAD utilization in the control of circadian rhythms during DNA damage response. PLOS Comput Biol 11: e1004144, 2015. doi: 10.1371/journal.pcbi.1004144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Marcheva B, Ramsey KM, Buhr ED, Kobayashi Y, Su H, Ko CH, Ivanova G, Omura C, Mo S, Vitaterna MH, Lopez JP, Philipson LH, Bradfield CA, Crosby SD, JeBailey L, Wang X, Takahashi JS, Bass J. Disruption of the clock components CLOCK and BMAL1 leads to hypoinsulinaemia and diabetes. Nature 466: 627–631, 2010. doi: 10.1038/nature09253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Mavroudis PD, Corbett SA, Calvano SE, Androulakis IP. Circadian characteristics of permissive and suppressive effects of cortisol and their role in homeostasis and the acute inflammatory response. Math Biosci 260: 54–64, 2015. doi: 10.1016/j.mbs.2014.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Mavroudis PD, Corbett SA, Calvano SE, Androulakis IP. Mathematical modeling of light-mediated HPA axis activity and downstream implications on the entrainment of peripheral clock genes. Physiol Genomics 46: 766–778, 2014. doi: 10.1152/physiolgenomics.00026.2014. [DOI] [PubMed] [Google Scholar]
- 28.Mazzocchi G, Malendowicz LK, Rebuffat P, Tortorella C, Nussdorfer GG. Arginine-vasopressin stimulates CRH and ACTH release by rat adrenal medulla, acting via the V1 receptor subtype and a protein kinase C-dependent pathway. Peptides 18: 191–195, 1997. doi: 10.1016/S0196-9781(96)00294-X. [DOI] [PubMed] [Google Scholar]
- 29.Morris MD. Factorial sampling plans for preliminary computational experiments. Technometrics 33: 161–174, 1991. doi: 10.1080/00401706.1991.10484804. [DOI] [Google Scholar]
- 30.Nakahata Y, Kaluzova M, Grimaldi B, Sahar S, Hirayama J, Chen D, Guarente LP, Sassone-Corsi P. The NAD+-dependent deacetylase SIRT1 modulates CLOCK-mediated chromatin remodeling and circadian control. Cell 134: 329–340, 2008. doi: 10.1016/j.cell.2008.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Oishi K, Atsumi G, Sugiyama S, Kodomari I, Kasamatsu M, Machida K, Ishida N. Disrupted fat absorption attenuates obesity induced by a high-fat diet in Clock mutant mice. FEBS Lett 580: 127–130, 2006. doi: 10.1016/j.febslet.2005.11.063. [DOI] [PubMed] [Google Scholar]
- 32.Pérez-Mendoza M, Rivera-Zavala JB, Díaz-Muñoz M. Daytime restricted feeding modifies the daily variations of liver gluconeogenesis: adaptations in biochemical and endocrine regulators. Chronobiol Int 31: 815–828, 2014. doi: 10.3109/07420528.2014.908898. [DOI] [PubMed] [Google Scholar]
- 33.Pierre K, Schlesinger N, Androulakis IP. The role of the hypothalamic-pituitary-adrenal axis in modulating seasonal changes in immunity. Physiol Genomics 48: 719–738, 2016. doi: 10.1152/physiolgenomics.00006.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Puigserver P, Rhee J, Donovan J, Walkey CJ, Yoon JC, Oriente F, Kitamura Y, Altomonte J, Dong H, Accili D, Spiegelman BM. Insulin-regulated hepatic gluconeogenesis through FOXO1-PGC-1α interaction. Nature 423: 550–555, 2003. doi: 10.1038/nature01667. [DOI] [PubMed] [Google Scholar]
- 35.Puigserver P, Rhee J, Lin J, Wu Z, Yoon JC, Zhang CY, Krauss S, Mootha VK, Lowell BB, Spiegelman BM. Cytokine stimulation of energy expenditure through p38 MAP kinase activation of PPARγ coactivator-1. Mol Cell 8: 971–982, 2001. doi: 10.1016/S1097-2765(01)00390-2. [DOI] [PubMed] [Google Scholar]
- 36.Puigserver P, Spiegelman BM. Peroxisome proliferator-activated receptor-γ coactivator 1α (PGC-1α): transcriptional coactivator and metabolic regulator. Endocr Rev 24: 78–90, 2003. doi: 10.1210/er.2002-0012. [DOI] [PubMed] [Google Scholar]
- 37.Rabitz H, Alis OF, Shorter J, Shim K. Efficient input-output model representations. Comput Phys Commun 117: 11–20, 1999. doi: 10.1016/S0010-4655(98)00152-0. [DOI] [Google Scholar]
- 38.Ramsey KM, Yoshino J, Brace CS, Abrassart D, Kobayashi Y, Marcheva B, Hong HK, Chong JL, Buhr ED, Lee C, Takahashi JS, Imai S, Bass J. Circadian clock feedback cycle through NAMPT-mediated NAD+ biosynthesis. Science 324: 651–654, 2009. doi: 10.1126/science.1171641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Randle PJ, Priestman DA, Mistry SC, Halsall A. Glucose fatty acid interactions and the regulation of glucose disposal. J Cell Biochem 55, Suppl: 1–11, 1994. doi: 10.1002/jcb.240550002. [DOI] [PubMed] [Google Scholar]
- 40.Rao R, DuBois D, Almon R, Jusko WJ, Androulakis IP. Mathematical modeling of the circadian dynamics of the neuroendocrine-immune network in experimentally induced arthritis. Am J Physiol Endocrinol Metab 311: E310–E324, 2016. doi: 10.1152/ajpendo.00006.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Rudic RD, McNamara P, Curtis AM, Boston RC, Panda S, Hogenesch JB, Fitzgerald GA. BMAL1 and CLOCK, two essential components of the circadian clock, are involved in glucose homeostasis. PLoS Biol 2: e377, 2004. doi: 10.1371/journal.pbio.0020377. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Schwer B, Verdin E. Conserved metabolic regulatory functions of sirtuins. Cell Metab 7: 104–112, 2008. doi: 10.1016/j.cmet.2007.11.006. [DOI] [PubMed] [Google Scholar]
- 43.Shi M, Zheng X. Interactions between the circadian clock and metabolism: there are good times and bad times. Acta Biochim Biophys Sin (Shanghai) 45: 61–69, 2013. doi: 10.1093/abbs/gms110. [DOI] [PubMed] [Google Scholar]
- 44.Sobol’ IM. On the distribution of points in a cube and the approximate evaluation of integrals. Zhurnal Vychislitel’noi Matematiki i Matematicheskoi Fiziki 7: 784–802, 1967. [Google Scholar]
- 45.Sobol IM. Uniformly distributed sequences with an additional uniform property. USSR Comput Math Math Phys 16: 236–242, 1976. doi: 10.1016/0041-5553(76)90154-3. [DOI] [Google Scholar]
- 46.Stephan FK. The “other” circadian system: food as a Zeitgeber. J Biol Rhythms 17: 284–292, 2002. doi: 10.1177/074873002129002591. [DOI] [PubMed] [Google Scholar]
- 47.Sudo M, Sasahara K, Moriya T, Akiyama M, Hamada T, Shibata S. Constant light housing attenuates circadian rhythms of mPer2 mRNA and mPER2 protein expression in the suprachiasmatic nucleus of mice. Neuroscience 121: 493–499, 2003. doi: 10.1016/S0306-4522(03)00457-3. [DOI] [PubMed] [Google Scholar]
- 48.Tareen SH, Ahmad J. Modelling and analysis of the feeding regimen induced entrainment of hepatocyte circadian oscillators using Petri Nets. PLoS One 10: e0117519, 2015. doi: 10.1371/journal.pone.0117519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Turek FW, Joshu C, Kohsaka A, Lin E, Ivanova G, McDearmon E, Laposky A, Losee-Olson S, Easton A, Jensen DR, Eckel RH, Takahashi JS, Bass J. Obesity and metabolic syndrome in circadian Clock mutant mice. Science 308: 1043–1045, 2005. doi: 10.1126/science.1108750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Tzamaloukas AH, Ing TS, Siamopoulos KC, Raj DS, Elisaf MS, Rohrscheib M, Murata GH. Pathophysiology and management of fluid and electrolyte disturbances in patients on chronic dialysis with severe hyperglycemia. Semin Dial 21: 431–439, 2008. doi: 10.1111/j.1525-139X.2008.00464.x. [DOI] [PubMed] [Google Scholar]
- 51.Vollmers C, Gill S, DiTacchio L, Pulivarthy SR, Le HD, Panda S. Time of feeding and the intrinsic circadian clock drive rhythms in hepatic gene expression. Proc Natl Acad Sci USA 106: 21453–21458, 2009. doi: 10.1073/pnas.0909591106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Woller A, Duez H, Staels B, Lefranc M. A mathematical model of the liver circadian clock linking feeding and fasting cycles to clock function. Cell Reports 17: 1087–1097, 2016. doi: 10.1016/j.celrep.2016.09.060. [DOI] [PubMed] [Google Scholar]
- 53.Yabaluri N, Bashyam MD. Hormonal regulation of gluconeogenic gene transcription in the liver. J Biosci 35: 473–484, 2010. doi: 10.1007/s12038-010-0052-0. [DOI] [PubMed] [Google Scholar]
- 54.Yang X, Downes M, Yu RT, Bookout AL, He W, Straume M, Mangelsdorf DJ, Evans RM. Nuclear receptor expression links the circadian clock to metabolism. Cell 126: 801–810, 2006. doi: 10.1016/j.cell.2006.06.050. [DOI] [PubMed] [Google Scholar]
- 55.Yoon JC, Puigserver P, Chen G, Donovan J, Wu Z, Rhee J, Adelmant G, Stafford J, Kahn CR, Granner DK, Newgard CB, Spiegelman BM. Control of hepatic gluconeogenesis through the transcriptional coactivator PGC-1. Nature 413: 131–138, 2001. doi: 10.1038/35093050. [DOI] [PubMed] [Google Scholar]
- 56.Zhang EE, Liu Y, Dentin R, Pongsawakul PY, Liu AC, Hirota T, Nusinow DA, Sun X, Landais S, Kodama Y, Brenner DA, Montminy M, Kay SA. Cryptochrome mediates circadian regulation of cAMP signaling and hepatic gluconeogenesis. Nat Med 16: 1152–1156, 2010. doi: 10.1038/nm.2214. [DOI] [PMC free article] [PubMed] [Google Scholar]