Phase reorganization leads to transient β-LFP spatial wave patterns in motor cortex during steady-state movement preparation

Abstract

Previous studies on the origin and properties of spatial patterns in motor cortex β-local field potential (β-LFP) oscillations have focused on planar traveling waves. However, it is unclear 1) whether β-LFP waves are limited to plane waves, or even 2) whether they are propagating waves of excito-excitatory activity, i.e., primarily traveling waves in excitable media; they could reflect, instead, reorganization in the relative phases of transient oscillations at different spatial sites. We addressed these two problems in β-LFPs recorded via microelectrode arrays implanted in three adjacent motor cortex areas of nonhuman primates during steady-state movement preparation. Our findings are fourfold: 1) β-LFP wave patterns emerged as transient events, despite stable firing rates of single neurons concurrently recorded during the same periods. 2) β-LFP waves showed a richer variety of spatial dynamics, including rotating and complex waves. 3) β-LFP wave patterns showed no characteristic wavelength, presenting instead a range of scales with global zero-lag phase synchrony as a limiting case, features surprising for purely excito-excitatory waves but consistent with waves in coupled oscillator systems. 4) Furthermore, excito-excitatory traveling waves induced by optogenetic stimulation in motor cortex showed, in contrast, a characteristic wavelength and reduced phase synchrony. Overall, β-LFP wave statistics differed from those of induced traveling waves in excitable media recorded under the same microelectrode array setup. Our findings suggest phase reorganization in neural coupled oscillators contribute significantly to the origin of transient β-LFP spatial dynamics during preparatory steady states and outline important constraints for spatially extended models of β-LFP dynamics in motor cortex.

NEW & NOTEWORTHY We show that a rich variety of transient β-local field potential (β-LFP) wave patterns emerge in motor cortex during preparatory steady states, despite stable neuronal firing rates. Furthermore, unlike optogenetically induced traveling waves, β-LFP waves showed no characteristic wavelength, presenting instead a range of scales with global phase synchrony as a limiting case. Overall, our statistical analyses suggest that transient phase reorganization in neural coupled oscillators, beyond purely excito-excitatory traveling waves, contribute significantly to the origin of motor cortex β-LFP wave patterns.

INTRODUCTION

Transient β-local field potential (β-LFP; ~20 Hz) oscillations are a prominent feature of motor cortex local field potential activity (Baker et al. 1997; Feingold et al. 2015; Jackson et al. 2003; Murthy and Fetz 1996; Rule et al. 2017; Sanes and Donoghue 1993), appearing during movement preparation periods, e.g., instructed delay tasks, or during postural maintenance, e.g., isometric force tasks. The power of β-LFP oscillations is attenuated during movement initiation, execution of reach-and-grasp actions and locomotion (Bansal et al. 2012; Best et al. 2017; Chatrian et al. 1959; Jasper and Penfield 1949; Kühn et al. 2006; Pfurtscheller et al. 2005; Rule et al. 2015a). Overall, the role of β-LFP remains enigmatic and has been connected to diverse mechanisms (Brittain and Brown 2014; Engel and Fries 2010; Spitzer and Haegens 2017). Previous studies have shown that β-LFP oscillations appear as planar traveling waves, the spatial structure of which relates to movement initiation (Best et al. 2017) and communication during movement preparation (Brovelli et al. 2004; Rubino et al. 2006; Takahashi et al. 2015). In this article, we address two main questions regarding the origin of the spatial dynamics in β-LFP waves during movement preparation: 1) are plane waves the primary spatiotemporal structure in motor-cortex β-LFP? and 2) what mechanisms might give rise to observed spatial patterns of β-LFP activity?

First, although previous studies have focused on β-LFP traveling planar waves, a systematic study of spatial dynamics and patterns in β-LFP oscillations has not been published. Spatial patterns in cortex can take many forms, including zero-lag spatial synchrony, standing waves, traveling waves, rotating spiral waves, radiating waves, and irregular spatial dynamics (Benucci et al. 2007; Besserve et al. 2015; Huang et al. 2004; Prechtl et al. 1997; Rule et al. 2015b). Furthermore, spatial dynamics in cortex can appear as transients changing rapidly over time: Townsend et al. (2015) characterize delta waves in anesthetized marmosets that transition into complex waves via intermediate wave patterns such as plane, rotating, or radiating waves. Schiff et al. (2007) report a similar phenomenon in slice preparations. We address whether β-LFP spatial patterns exhibit similar diversity and examine whether different spatial patterns occur within the same transient β-LFP event.

Second, the origin of observed β-LFP spatial wave patterns is unknown. Different mechanisms may yield superficially similar LFP spatiotemporal dynamics. In particular, traveling waves may arise via three main scenarios (Ermentrout and Kleinfeld 2001): 1) Initially localized oscillations can propagate via lateral interactions, generating excitatory traveling waves as seen in excitable media (Fig. 1A). The statistics of such waves are an emergent property of the excito-excitatory dynamics and patterns of lateral connectivity. 2) A shared input can drive adjacent sites in cortex with different conduction delays, yielding a spatial gradient in response latencies and phases that mimics a traveling wave (Fig. 1B); Finally, 3) many different sites in a cortical patch may oscillate with similar frequencies, forming a coupled-oscillator system. Reorganization of the oscillation phases across the sites into spatial gradient patterns can appear as traveling waves (Fig. 1C). Such phase reorganization could arise from inputs or changes in parameters controlling the local neural dynamics, or from metastability in the intrinsic dynamics. In the latter case, a rich variety of complex transient patterns can be generated (e.g., Deco and Jirsa 2012; Laing 2016; Panaggio and Abrams 2015; Shanahan 2010). Importantly, such coupled oscillator waves are not excito-excitatory traveling waves (1st scenario). They need not exhibit a characteristic wavelength, and their spatiotemporal statistics emerge from the organization of relative phases.

Fig. 1.

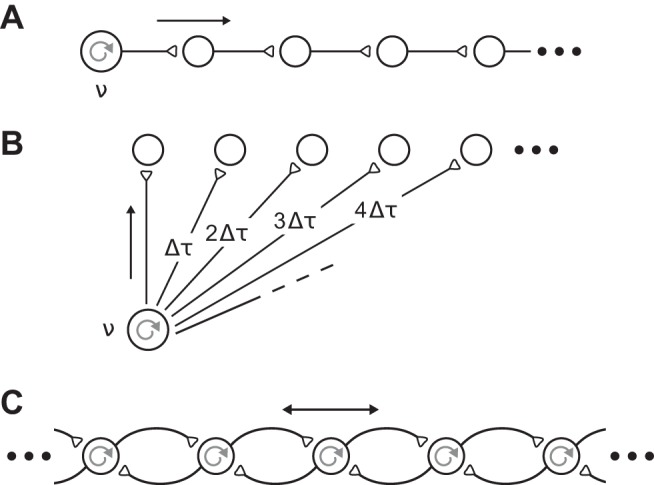
Multiple underlying mechanisms can explain traveling waves. A: excitatory waves. Waves may propagate as traveling waves in an excitable medium, driven by a local oscillatory source (frequency ν). B: anatomical conduction. β-Local field potential (β-LFP) oscillations may propagate from a common source (frequency ν) with varied delays (Δτ), leading to apparent traveling waves in the cortex. C: coupled oscillators. Phase gradients in local β-LFP oscillations can create phase waves. Each cortical patch generates oscillations, and the effective wavelength, phase velocity, and spatial patterns are emergent properties that arise from coupling of nearby neural oscillators. [Redrawn from Ermentrout and Kleinfeld (2001) with permission.]

Understanding the diversity and properties of β-LFP wave spatial patterns in primate motor cortex is important for constraining models of communication, computation, and encoding in motor cortex. For example, diversity in phase relation arising from rich spatiotemporal neural dynamics could support the segregation of parallel information streams in the cortex (Maris et al. 2016). Better statistical characterizations can also constrain biophysical models of β-LFP spatiotemporal dynamics in motor cortex (Heitmann and Ermentrout 2015; Heitmann et al. 2012). Beyond its relevance to basic neuroscience, understanding the origin of spatial patterns in motor cortex β-LFP oscillations has translational implications: if β-LFP spatial patterns carry information about planned movements, they could be useful for decoding in brain-computer interfaces for restoring movement and communication in people with paralysis (Bansal et al. 2012; Best et al. 2017; Hochberg et al. 2006, 2012; Milekovic et al. 2015; Truccolo et al. 2008). Finally, β-LFP spatial patterns could inform the development of closed-loop brain stimulation approaches for treating movement disorders such as Parkinson’s disease (Little et al. 2013).

To address both 1) the diversity and 2) the origins of β-LFP spatial waves, we examined the spatiotemporal structure of beta oscillations during the initial 1-s movement preparation periods in a reaching and grasping task. Neural recordings were obtained simultaneously from three motor cortex areas [primary motor (M1), ventral premotor (PMv), and dorsal premotor (PMd) cortices] of Macaca mulatta. These three cortical areas are known to be critical for the planning and execution of voluntary reach-and-grasp movements and can be used to decode the kinematics and kinetics of these actions (e.g., Aghagolzadeh and Truccolo 2016; Bansal et al. 2012; Milekovic et al. 2015; Saleh et al. 2012; Takahashi et al. 2017; Vargas-Irwin et al. 2010, 2015). By the experimental task design, neural activity during the selected 1-s movement preparation periods was steady and unperturbed by visual cues related to task instructions or motor transients related to movement initiation. In this sense, we refer to these periods as steady-state movement preparation periods, despite ongoing variability as evidenced by the β-LFP transients studied.

In addition, we compared the statistics of spontaneous β-LFP waves with the statistics of optogenetically induced traveling ~50-Hz LFP waves reported in Lu et al. (2015). These traveling waves were recorded in a setup that matched the brain region, species, and electrical recording setup of the examined β-LFP waves. This provides a superior reference compared with, for example, traveling waves in simulation or in another preparation. The optogenetically induced traveling waves emerged during constant stimulation and involved waves propagating away from the localized stimulation site. These waves thus reflect the intrinsic dynamics of wave propagation in motor cortex (Lu et al. 2015). This is in contrast to periodically driven electrically or optogenetically induced wave pulses, which may momentarily excite the tissue but might not reflect physiological mechanisms of excito-excitatory traveling waves. The analyses of the optogenetically induced traveling waves validates the statistical methods used to extract spatiotemporal LFP structure from Utah arrays with 400-μm spacing in primate motor cortex, despite the small size of such preparations. These two data sets allowed us to compare phenomena involving induced traveling waves in excitable media and spontaneous β-LFP waves, avoiding confounds from differences in spatial samplings or microelectrode properties.

METHODS

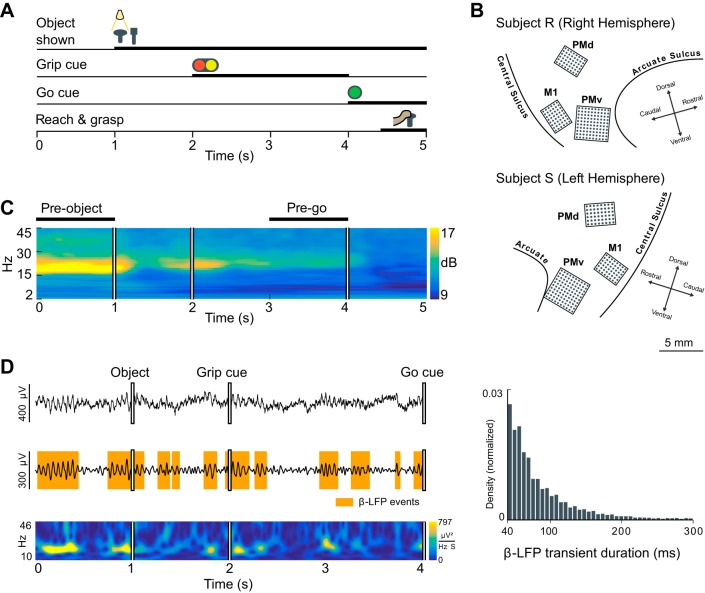
Spatiotemporal β-LFP wave data were recorded from nonhuman primate subjects (rhesus macaques, M. mulatta) during the steady-state period in a cued reach-to-grasp with instructed delay (CGID) task. Experimental procedures were conducted as approved by the local Institutional Animal Care and Use Committee (IACUC), and these data were previously used in Vargas-Irwin et al. (2015) and Aghagolzadeh and Truccolo (2014, 2016), which describe the CGID task in greater detail and analyze these data from the perspective of collective low-dimensional spiking population dynamics. Briefly, this task exhibited two steady-state 1-s movement preparation periods: an attentive waiting period before the presentation of visual cues, and a motor preparatory period following visual cues but before the reach and grasp action. The task required the subjects to reach toward, grasp, and raise one of two objects, using either a power grip, key grip, or precision grip, as instructed by cue lights and depending on the object (Vargas-Irwin et al. 2015). After presentation of visual cues, a 1-s hold period was required before a visual “go” cue was given, indicating that the subject should then reach out and lift the cued object using the cued grip. A schematic for the task organization is shown in Fig. 2A. In this study, we examine beta oscillations during the 1-s period preceding the first visual cue (object presentation) and the 1-s period preceding the go cue.

Fig. 2.

β-Local field potential (β-LFP) oscillations occur in transient events during the steady-state periods of a cued reach-and-grasp task. A: schematic of the cued grasping with instructed delay (CGID) task. Objects were presented to the subject, followed by a cue light instructing the subject how to manipulate the object. A 2-s planning and hold period was required before movement execution (see methods). B: β-LFP data were recorded from triple microelectrode array (MEA) implants in primary motor (M1), ventral premotor (PMv), and dorsal premotor cortex (PMd) areas in 2 subjects (R and S). C: example LFP spectrogram averaged over trials from area PMv in subject S. Task time is on the horizontal axis and frequency on the vertical axis. Beta oscillations can be seen throughout the task, in this subject most prominently in the pre-object period. The pre-go period was also free of cue or motor-evoked potentials and typically exhibited elevated β-LFP. D: inspection of single trials reveals that β-LFP occurred as transient events. Shown is trial 35 from session 1 of subject S in area M1. Top left, broadband LFP trace; β-LFP transients are visible superimposed on slow evoked potentials. Middle left, β-LFP transients can be identified from the amplitude envelope of bandpass-filtered LFP. Bottom left, wavelet spectrogram visualization of β-LFP transients. Right, the durations of these β-LFP transients do not exhibit a characteristic duration, but rather appear to be an exponentially distributed random process as illustrated by the histogram.

Neural Recordings

Spatiotemporal beta activity was recorded from two subjects (R and S) using triple implants of microelectrode arrays (MEAs) from Blackrock Microsystems. A single 10 × 10 MEA was implanted in area PMv, and smaller 6 × 8 electrode arrays were implanted in areas M1 and PMd. The electrode length of 1.5 mm targeted layers 3–5 of motor cortex, and electrodes were spaced 400 μm apart. In the PMv implants, four electrodes were connected to ground. In area PMv of subject S, an additional two electrodes exhibited unusual impedance spectra and were excluded from this study. Data for these missing electrodes were interpolated from their nearest neighbors. All electrodes were used in the area M1 and PMd implants. For both β-LFP and optogenetic data sets (see below), broadband LFPs were recorded at 30 kilosamples/s (0.3 Hz–7.5 kHz) and subsequently downsampled (zero-phase fourth-order Butterworth, ≤250 Hz) to 1 kilosample/s for analysis. See Vargas-Irwin et al. (2015) for additional details of the neural recordings for spatiotemporal β-LFP.

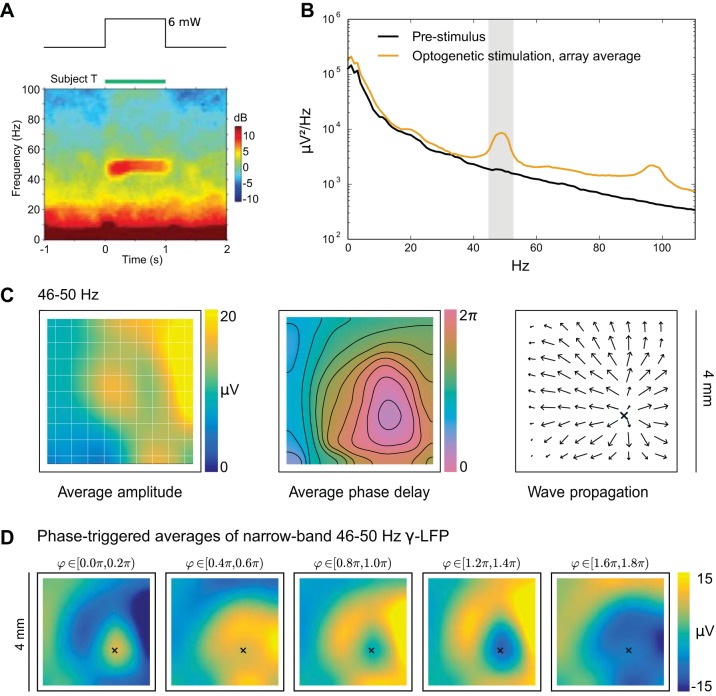
Optogenetically induced waves in motor cortex were examined from a third subject (T) during quiet wakefulness, as reported and described in Lu et al. (2015) (see Fig. 8). Neurons were transfected with the chimeric opsin C1V2_T/T under the CaMKIIα promoter, which is known to preferentially express in excitatory cells, with some expression also likely in inhibitory cells (Lu et al. 2015). Data were recorded from a single 10 × 10 array implanted in primary motor cortex and modified to contain an optical fiber at the center for delivery of laser light. The spatial domain of direct light stimulation was <1 mm (Lu et al. 2015). In the data presented in this article, constant-pulse optical stimulation at 561 nm and 6 mW was provided for 1 s during the rest state. See Lu et al. (2015) for details of the optogenetic recordings.

Fig. 8.

Constant optogenetic stimulation of motor cortex induces excitatory traveling waves. A: ~50-Hz oscillations emerged abruptly during a constant 1-s pulse of 6-mW light stimulation, as shown on the local field potential (LFP) spectrogram. [Reproduced from Lu et al. (2015) with permission.] B: compared with prestimulation background activity, power in ~50- and ~100-Hz oscillations was elevated. C: ~50-Hz LFP amplitude increased across many sites in the multielectrode array (left). The direct optical stimulation area was <1 mm in diameter, and the ~50-Hz oscillations propagated beyond the stimulation site via network interactions, as expected for traveling waves in excitable medium. Unwrapping phases relative to a reference electrode near the center of optical stimulation yielded an average phase delay map (middle). The induced ~50-Hz LFP oscillations organized as radiating waves, with an origin near the source of the optical stimulation. The average phase-gradient direction (right) was consistent with the average phase-delay map and confirms the radiating wave structure. D: phase-triggered averages of induced LFP oscillations over all stimulation trials, triggered on the phase (φ) of 50-Hz LFP oscillations on the channel closest to the radiating wave origin (near the lower boundary of the optically stimulated region of cortex).

LFP Phase Extraction

The beta-frequency band was identified separately for each subject and area. Multitaper spectra (Mitra and Pesaran 1999; 5 tapers, 5-Hz time bandwidth parameter for 1 s of data) were computed from the first second of the CGID task for all channels and trials, and the beta band was defined as the 5-Hz band centered at the largest spectral peak between 15 and 45 Hz during this period. Area PMd of subject R exhibited multiple harmonically related beta peaks. We restricted analysis to the lower (fundamental) frequency. The higher frequency peak showed cross-frequency coupling to the lower β-LFP frequency consistent with a summation of 2:1 and 3:2 overtones of the fundamental frequency, reflecting changes in the β-LFP waveform shape rather than a distinct oscillation. Narrow-band oscillation peaks in the optogenetically induced oscillations were identified from wavelet spectrograms averaged over all stimulation trials. Wavelet methods were appropriate in this case because the larger number of repeated trials in optogenetic stimulation obviated the need for reducing variance with the use of multitaper methods and offered better balance between time resolution at high frequencies and frequency resolution at low frequencies. The amplitude envelope and instantaneous phase for narrow-band LFP oscillations were extracted similarly for both the spontaneous beta oscillations and the induced oscillations: raw LFPs at 1 kilosample/s were bandpass filtered using a zero-phase fourth-order Butterworth filter, and the resultant narrow-band signal a(t) was passed through the Hilbert transform to generate an analytic signal z(t) = |z(t)| exp[i·φ(t)], which has both an instantaneous magnitude |z(t)| and phase φ(t) = arg[z(t)].

Spatial Synchrony

We used the circular standard deviation of the instantaneous Hilbert phase to assess zero-lag spatial phase synchrony over the recorded cortical patch, defined as (e.g., Berens 2009)

$${\mathrm{S}}_{\phi }(t)=\sqrt{-2\ln \left[R(t)\right]},$$ (1)

which corresponds to the standard deviation of a circularly wrapped normal distribution and can be obtained by a transformation of the first moment for circularly distributed data R(t). In our case, R(t) is defined as the normalized average (across channels) of the analytic signal vectors at a given time

$$R(t)=\frac{\left|{\displaystyle \sum {}_k}{\hspace{0.17em}z}_k(t)\right|}{{\displaystyle |\sum {}_k}{\hspace{0.17em}z}_k(t)|},$$ (2)

where k indexes channels. LFP spatial activity can show large variations in amplitudes across time, and yet potentially show the same level of spatial synchrony. To attenuate the effect of amplitude differences, we normalized the magnitude of the average vector by the sum of the magnitudes of each analytic signal vector z_k(t). We defined spatially synchronized states as those times for which S_φ(t) < π/4 such that ~95% of phase vectors were concentrated within one-quarter cycle.

Spatial Gradient of the Hilbert Phase

The local phase gradient provides an estimate of the wave propagation velocity. We computed the gradient of the phase ∇φ(t) as the (circularly wrapped) discrete difference of the Hilbert phase between adjacent electrode sites. The propagation velocity v and wavelength λ can also be extracted from the phase gradient using the relationship in Eq. 3 (see Rubino et al. 2006 for details):

$$\frac{\partial \phi }{\partial t}=-\nabla \phi ·v\mathrm{.}$$ (3)

Instantaneous estimates of local propagation speed were computed as the average magnitude of the local phase gradient (in radians/mm) divided by the median angular frequency (in radians/s). Plane waves were detected as time points when the distribution of phase-gradient vector directions was concentrated, as assessed by a phase-gradient directionality (PGD) measure (Rubino et al. 2006)

$$\text{PGD}(t)=\frac{\left|{\displaystyle \sum {}_k\nabla {\phi }_k(t)}\right|}{{\displaystyle \sum {}_k\left|\nabla {\phi }_k(t)\right|}},$$ (4)

where k indexes spatial location. For intuitive visualization, we show a transformed PGD measure with units of radians: the circular standard deviation of the Hilbert phase gradient. A version of this measure that is weighted by the amplitudes of the phase-gradient vectors can be computed as

$${\mathrm{S}}_{\nabla \phi }(t)=\sqrt{-2\ln [\text{PGD}(t)]}\mathrm{.}$$ (5)

For categorization, we adopt the same conventions as Rubino et al. (2006) and classify nonsynchronous wave events with PGD > 0.5 as plane waves. For purposes of measuring wavelength, we use the stricter threshold of S_∇φ(t) < π/4, i.e., 95% of phase-gradient vectors point within π/2 radians of each other. This corresponded to a PGD threshold of ~0.73. The more stringent cutoff addresses noise-induced biases in estimating wavelength.

For the analysis of plane waves in β-LFP, the wavelength was estimated from the magnitude of the average phase gradient. Taking the magnitude after averaging the phase-gradient vectors reduces the influence of noise on the estimation of plane-wave wavelength, as opposed to averaging the local phase-gradient magnitudes. Asymmetric radiating waves with a high signal-to-noise ratio that could not be described as a simple planar or radiating wave were common in the optogenetically induced activity, and in this case wavelength was estimated from the local gradient of the Hilbert phase and then averaged over the array.

Critical Point Analysis

We classified complex waves structures on the basis of critical points in a smoothed estimate of the phase-gradient field. Data were denoised via smoothing by convolving the analytic signals in each frame using a sinc function with a wavelength cutoff of 2 mm. Analytic signals were upsampled in the spatial frequency domain via a discrete cosine transform type I. The sinc kernel was constructed in the frequency domain with anti-aliasing to reduce numerical artifacts related to the small spatial domain. The phase gradient was extracted by convolving the Hilbert phase with 2 × 2 discrete difference kernels in the x and y directions.

Minima, maxima, and saddle points were identified by locating zeros in the phase gradient. These points can be distinguished by the direction of sign change in the gradient. Equivalently, one may examine the determinant and trace of the Jacobian at each critical point (Townsend et al. 2015). The centers of rotating waves were identified by taking a line integral of the Hilbert phase gradient surrounding each point. Points around which this line integral equals nonzero multiples of 2π are singularities in the Hilbert phase gradient and are the centers of rotating waves. Numerically, this integral was computed for every point by representing the Hilbert phase gradient as a complex number and representing the line integral around each point as a convolution.

We briefly note some carefully considered caveats to this analysis. The analysis focuses on mesoscopic β-LFP structure above 2 mm, consistent with previously reports (Rubino et al. 2006; Takahashi et al. 2011). Therefore contributions to β-LFP variability smaller than 2 mm were indistinguishable from noise for the purposes of this analysis and could be safely removed. However, at low signal-to-noise ratio (low β-LFP power), high spatial frequencies arising from channel-independent noise can alias into lower frequencies and confound the analysis. We addressed this by restricting analyses of wavelength to periods of high beta power and ordered planar wave activity, and emphasize that conclusions based on events with low amplitude or disordered wave structure are descriptive, not quantitative (see Figs. 5 and 6). We confirmed that modest variations in smoothing scale, amplitude, and phase-gradient concentration cutoffs do not alter the conclusions of this work. Additionally, we repeated the analysis cropping the 10 × 10 area PMv arrays down to the 8 × 6 size used in other motor areas, to confirm that MEA size was not responsible for the differences observed across areas. The limitations of current MEA technology preclude estimating the contribution of SNR-dependent aliasing artifacts to the observed trends for low LFP amplitudes and high spatial frequencies. Example code for spatial phase statistics is available online at https://github.com/michaelerule/CGID_waves_example.

Fig. 5.

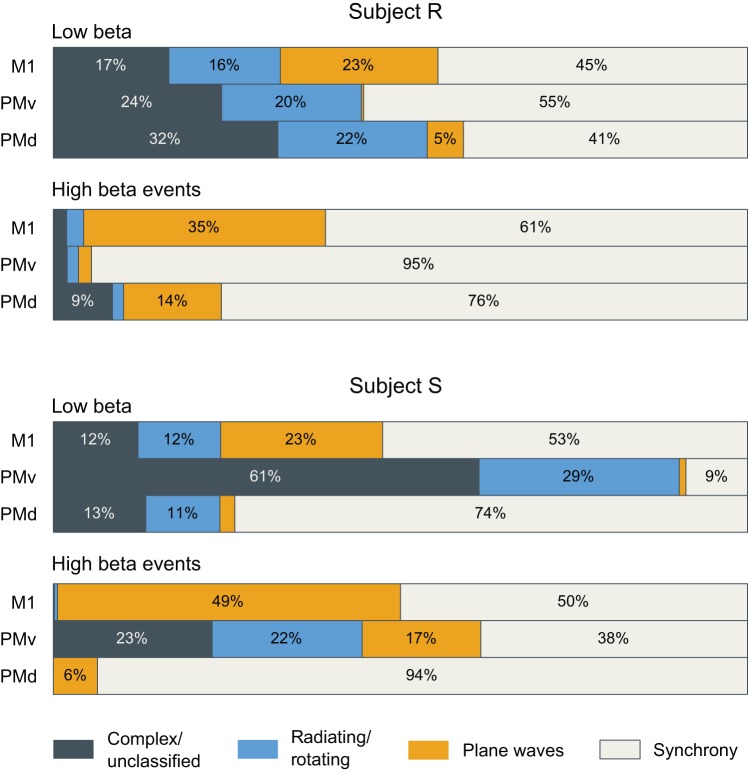
β-Local field potential (β-LFP) wave patterns are diverse, and ventral premotor cortex (PMv) area differs substantially from primary motor (M1)/dorsal premotor cortex (PMd) areas. Categorization of beta-wave spatiotemporal patterns during the 1-s movement preparation periods before object presentation and before the go cue shows a rich diversity of spatial patterns. Consistent with previous studies, areas M1 and PMd exhibited plane-wave activity. However, globally synchronized states were more common. The wave structure in area PMv differed from that in previously studied areas M1 and PMd, and also differed between subjects. Subject S displayed abundant complex wave activity, whereas area PMv in subject R was largely synchronous. β-LFP spatiotemporal activity was sampled every 50 ms, or ~1 β-LFP cycle. Plane-wave events were detected as times when the wave propagation directions (based on the phase gradients ∇φ; see also Fig. 3) were concentrated (PGD < ½). Synchronous events were likewise detected as times when the instantaneous β-LFP phase (φ) was concentrated (σ < π/4). Radiating and rotating waves were identified on the basis of critical points in the phase-gradient field. Times containing multiple radiating or rotating wave centers were classified as complex.

Fig. 6.

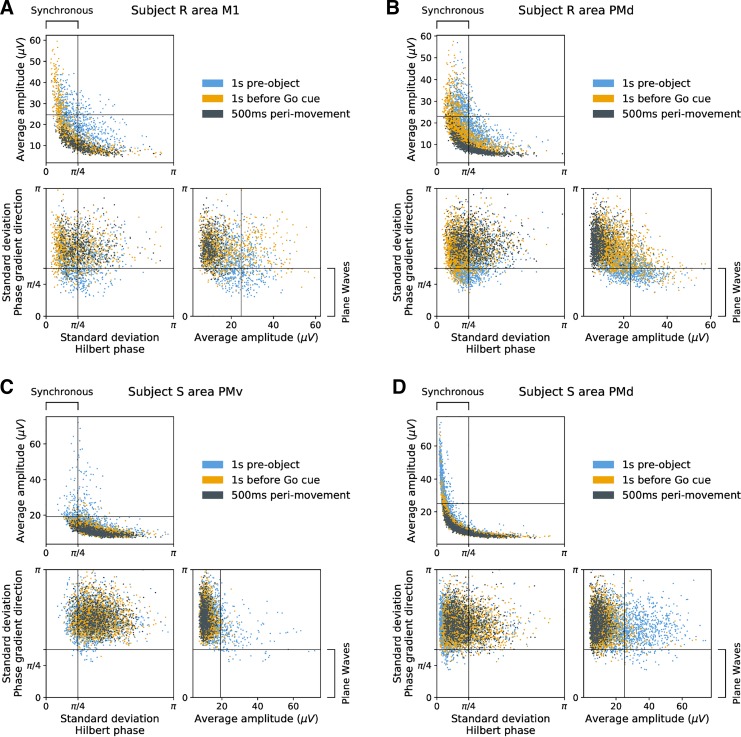
Wave properties transition continuously during motor steady states: variability does not reflect discrete states. Scatter plots illustrate variations in amplitude, synchrony (standard deviation of Hilbert phase), and plane-wave characteristics (standard deviation in phase-gradient direction), for representative data sets. Wave properties transitioned continuously, rather than clustering into multiple distinct states, implying that variability in spatiotemporal patterns in motor cortex β-local field potential did not arise from switching between discrete network states (bifurcations). Nevertheless some trends were evident: higher beta amplitudes were associated with increased synchrony (top left, all subplots) and were associated also with an increased tendency toward plane waves (bottom right, all subplots). Wave statistics were taken every 50 ms during 3 task stages: the 1-s hold period in anticipation of a visual cue (blue), the 1-s hold period leading up to a go cue (yellow), and the 500 ms surrounding movement onset (black). Amplitude was taken as the average Hilbert amplitude over the array. A: subject R, session 1, primary motor cortex (area M1). B: subject R, session 3, dorsal premotor cortex (area PMd). C: subject S, session 2, ventral premotor cortex (area PMv). D: subject S, session 3, area PMd.

Phase Maps for Induced Traveling Waves

The wave response to optogenetic stimulation was reproducible across trials, which allowed us to compute summaries of wave activity averaged over trials and time. For computing the average phase gradient, local phase-gradient fields were smoothed by convolution with a sinc kernel to remove structure finer than 1.8 mm. These phase gradients were averaged over time (see Fig. 8, C and D). To compute averaged phase-delay maps, phases were unwrapped relative to a reference electrode near the center of the radiating wave. Average phase delay was then computed as the average over time of the phase delay relative to this channel.

RESULTS

In this study, we characterize the spatiotemporal dynamics of waves in motor cortex β-LFP transient oscillations to clarify the collective neural dynamics underlying these oscillations. We first demonstrate that well-controlled steady-state movement preparation periods in the cued grasp with instructed delay (CGID; see methods) task reliably evoked beta oscillations, which occurred as transients with considerable trial-to-trial variability in terms of onset times and durations. We focused on the 1-s movement preparation periods preceding the object presentation in the CGID task. These “steady-state” periods were not perturbed by sensory- or motor-evoked components related to task cues or movement initiation, respectively, in either LFP or neuronal spiking activity. We show that the spontaneous transient beta oscillations corresponded to diverse types of wave dynamics and summarize the prevalence of various wave patterns. Next, we examine summary statistics of beta spatiotemporal oscillations and relationships among these statistics. We conclude by contrasting these statistics to those of traveling waves induced by 1-s constant-pulse optogenetic stimulation in motor cortex.

We analyzed three CGID data sets resulting from three different experimental sessions, each including recordings from areas M1, PMv, and PMd in subjects R and S. For both subjects, all examined data sets were recorded within 8 days of each other. Each session yielded between 46 and 114 successful 7-s CGID trial repetitions, collected over 20 min to 1 h. For the comparison to optogenetically induced traveling waves, we analyzed the spatiotemporal waves in primary motor cortex observed in subject T, previously reported in Lu et al. (2015).

Motor-Evoked Potentials and Beta Oscillations in the CGID Task

Consistent with previous studies of motor cortex LFPs, the CGID task reliably elicited task-related activity in all three motor areas (M1, PMd, PMv) from both subjects studied during the planning and preparatory phases (Fig. 2, A and B). The movement period of the CGID task was marked by slow motor-evoked potentials, increased single-unit firing rates, and beta suppression. Motor-evoked potentials were dominated by slow <2-Hz components and also contained peaks in the theta (2–7 Hz) band in all areas except subject S area PMv. In subject S, the beta band peaked at 21 Hz. In subject R, the beta band peaked at 17 Hz. Beta oscillations were prominent during the first second of the task (i.e., before object presentation) and also occurred during the period preceding the go cue (Fig. 2C). In subject S, beta power was highest before object presentation. In subject R, beta power was greatest during the delay preceding the go cue.

Although beta power was enhanced during the steady-state movement preparation periods of the CGID task, we found that β-LFP activity occurred in transient events with durations that exhibited considerable intra- and intertrial variability (Fig. 2D). We defined β-LFP transient events as events where the beta amplitude exceeded a threshold of 1.5 times the standard deviation for the filtered β-LFP signal within a given session. Large-amplitude transients did not necessarily occur on every trial: between 37% and 97% of trials exhibited β-LFP transients exceeding the defined threshold, depending on the subject and motor area.

The duration of beta transients was broadly distributed, with some trials showing sustained elevation of β-LFP for as long as 1 s (subject R: 184 ± 134 ms; subject S: 196 ± 146 ms). Overall, these transient β-LFP events occupied 26% and 22% of the examined 1-s movement preparation periods in subjects R and S, respectively (summarized over 3 motor cortical areas and 3 sessions per subject). During visual inspection of these transients, we observed diverse wave patterns. For illustration, we show examples of wave activity in Fig. 3. We observed states ranging from spatially synchronous states, to plane waves, to more complex activity such as radiating or rotating waves, to complex states that cannot be easily categorized. This illustrates that beta events can be associated with a diversity of wave patterns. Importantly, wave patterns appeared to transition continuously from desynchronized states, to more locally synchronized wave activity, to globally synchronized states.

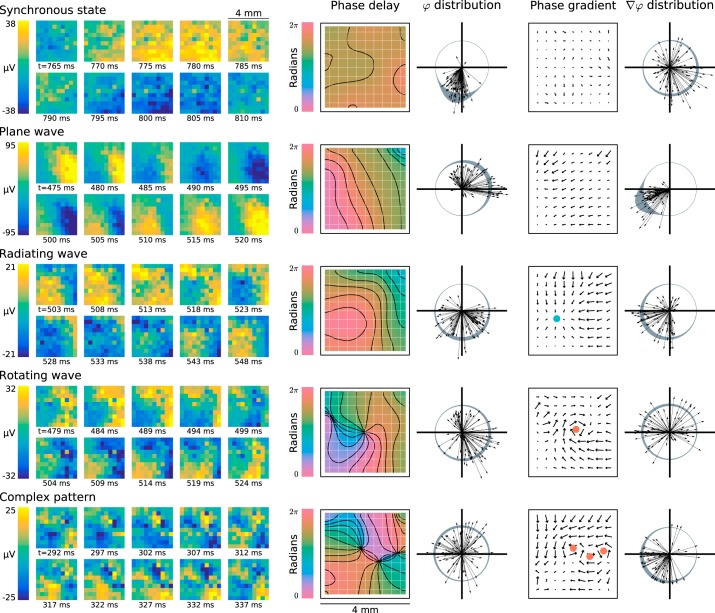
Fig. 3.

Transient β-local field potential (β-LFP) oscillations exhibit a rich variety of spatiotemporal wave patterns. In addition to traveling plane waves, beta spatiotemporal dynamics showed synchronous states, radiating and rotating waves, and other more complex wave patterns. Each example was taken from the 4 × 4-mm² area sampled by the 10 × 10 multielectrode array in ventral premotor cortex area of subject S. Missing electrodes were interpolated from nearest neighbors. Average phase-delay maps were computed by unwrapping Hilbert phases at the median frequency of the wave event before computing the average analytic signal. The mean analytic signal was smoothed at a 2-mm scale to generate the phase-delay maps pictured. The smoothed Hilbert phase (φ) was differentiated to extract critical points from the wave dynamics, shown as a blue dot for a radiating wave and red dots for rotating waves (see methods, Critical Point Analysis). Spatially synchronized states were detected as patterns where the angular distribution of analytic signals was concentrated as shown by the first (top to bottom) example (see methods, Spatial Synchrony). Plane-wave states were detected as spatial patterns where the angular distribution of the phase gradient (∇φ) direction was concentrated, as shown by the second example (see methods, Spatial Gradient of the Hilbert Phase).

In contrast to the transient nature of beta events, single-neuron spiking activity was typically sustained throughout the 1-s steady-state movement preparation periods (Rule et al. 2017). Forty-two percent (292/699) of well-isolated single units fired during steady-state delay periods, most of which exhibited either rhythmic spiking (66%; 192/292) or rhythmic bursting (25%; 72/292). Between 60% and 76% of these rhythmic units exhibited β-rhythmic mode firing frequencies between 10 and 45 Hz, depending on subject and task epoch. We considered the possibility that beta transients reflect changes in the underlying firing rates of these β-rhythmic neurons but detected no significant differences in firing rates within vs. outside of beta transients (Wilcoxon signed-rank tests for difference in the median, corrected for multiple comparisons using the Benjamini-Hochberg procedure for a false discovery rate of 0.05). For further results, refer to Rule et al. (2017). This β-LFP spiking rhythmicity suggests that the mesoscopic spatiotemporal β-LFP patterns might arise from synchronization dynamics among oscillatory subpopulations, motivating further examination of β-LFP spatiotemporal statistics.

Figure 4 illustrates a representative β-LFP transient. Local wave structures evident in each motor area were part of an overall global pattern. We observed that β-LFP wave events involved changes in both amplitude and phase: waves emerged not only by rearrangements of ongoing high-amplitude β-LFP oscillations but also by complex phase-amplitude dynamics during transient events. This suggests that the evolution of β-LFP phase patterns may be closely related to the concurrent modulations in amplitude. Below, we further investigate the relationship between β-LFP amplitude and wave patterns, and characterize in detail the diversity in wave patterns that were found in each motor area.

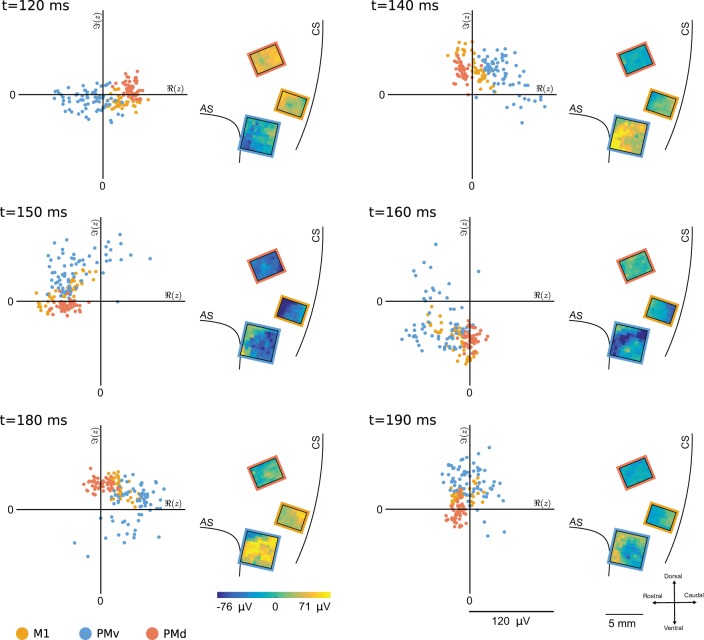
Fig. 4.

Evolution of a β-local field potential (β-LFP) wave event in the analytic-signal phase space. The evolution of the β-LFP analytic signals is visualized in phase space, in which the ongoing phase and amplitude at each electrode are plotted in polar coordinates (scatter plots). $\Re (z)$ and $𝔍(z)$ denote the real and imaginary parts of the complex-valued analytic β-LFP signal, respectively. The β-LFP signal is also visualized across the 3 motor areas (images). Beta-wave events tended to begin by excitation of oscillations in a subset of channels (first frame). In this example, initial amplitude differences progressed into a traveling wave in which the phase of ventral premotor cortex (PMv; blue dots) area lagged behind that of dorsal premotor cortex (PMd; red) and primary cortex (M1; (yellow) areas. This event lasted only a few cycles of the beta oscillation before collapsing back to an asynchronous state. Note that although this is a traveling wave event, it is not a plane-wave event. In this instance, the PMv activity was classified as a radiating wave, and the M1 and PMd activities were classified as synchronous. This example was taken from trial 2 of subject S, session 1.

Categorization of β-LFP wave patterns.

To investigate whether diversity in β-LFP wave patterns was widespread in our data, we qualitatively categorized wave states as either synchronous (in the sense of spatially uniform zero-lag phase synchrony), plane waves, radiating or rotating waves, or complex patterns. Figure 5 shows a breakdown of the prevalence of different classes of wave patterns for all areas in both subjects R and S. We identified synchronous states as those spatial patterns where the circular standard deviation of β-LFP phase was less than π/4 such that ~95% of electrodes on the array fell within the same quarter cycle (π/2 radians) of the oscillation (see methods, Spatial Synchrony). We classified plane waves using the same criterion as Rubino et al. (2006), requiring a phase-gradient directionality (PGD) > 0.5 (see methods, Spatial Gradient of the Hilbert Phase). For the purpose of assigning each beta cycle a unique classification, waves were classified as synchronous only if they were not also classified as plane waves. More complex wave patterns such as rotating and radiating waves were classified by identifying critical points in the spatially smoothed phase gradient (see methods, Critical Point Analysis).

The spatiotemporal structure varied considerably across motor areas. Area PMd in both subjects was typically highly synchronous, displaying few traveling waves. Area PMv in subject S showed more complex wave activity, even during beta transients with high power. In both subjects, organized plane wave activity was apparently rarer in area PMv, an area that has not been examined in previous studies. However, area PMv in subject S displayed other organized traveling wave states such as radiating and rotating waves (Fig. 5). These differences between areas were not due simply to the different sizes of the arrays, because the classification trends did not change when data from the 10 × 10 PMv arrays were spatially cropped to match the 6 × 8 size of the M1 and PMd arrays. High beta power corresponded to spatially synchronized states, whereas more complex activity was seen in lower beta power transient events.

Though we adopted a classification of beta wave activity into the above discrete types, we also emphasize an important aspect of the spatiotemporal dynamics that should not be overlooked: beta spatiotemporal dynamics appeared to transition smoothly between these different patterns. In other words, transitions among patterns could occur within the same β-LFP transient event, i.e., without an intermediate quiescent period in between the onset of different patterns, and typically the transitions did not appear to be abrupt. Corroborating this, we also explored dynamical mode decomposition (cf. Brunton et al. 2016), which recovered spatiotemporal oscillatory modes that generated sinusoidal basis functions similar to Fourier components. This suggested that spatiotemporal patterns in β-LFP are diverse and that their dynamics reflected a spatiotemporally bandpass stochastic or chaotic process, rather than consisting of a small set of distinct modes dictated by the anatomy and task. Nevertheless, in particular for complex, radiating, rotating, and plane waves, once a spatiotemporal pattern set in, it was clearly distinguishable from the other types and persisted for multiple β-LFP cycles. A potential ambiguity remained for the case of synchronous vs. long-wavelength waves. Although the thresholds for classification of synchrony and plane waves reflect the common intuition about synchronized and planewave activity, the data did not cluster into nonoverlapping “synchronous” and “asynchronous” or “planar” and “nonplanar” clusters. For example, long-wavelength waves would have appeared as spatially synchronous over the limited aperture of the MEA. This indicates that zero-lag spatial synchrony may be considered a limiting case of long-wavelength plane-wave activity.

β-LFP wave statistics correlate with amplitude.

The spatiotemporal properties of beta oscillations varied throughout the stages of the CGID task. Statistics of beta spatiotemporal activity exhibited trial-to-trial variability but tended to track task-related changes in the amplitude of beta oscillations. During task stages in which beta power was elevated, spatial synchrony was also higher and beta phase-gradient magnitude, which is inversely related to wavelength, was lower. PGD, a measure of how planar wave activity is (see methods, Spatial Gradient of the Hilbert Phase), was also higher during times when beta power was high. The number of critical points in the phase-gradient map, a measure of wave complexity, increased during task phases with weaker beta power. These observations suggested that the task-related changes in the properties of beta spatiotemporal waves were correlated with variations in beta amplitude and that changes in beta spatiotemporal organization may relate to transient modulations in beta power. However, β-LFP activity was highly variable. In our inspection of the data, the precise nature and timing of beta spatiotemporal patterns was seldom identical across trials. To better understand the spatiotemporal structure of β-LFP oscillations, we therefore assessed the instantaneous relationship between various statistics of spatiotemporal activity on a trial-by-trial basis.

We compared the average instantaneous Hilbert amplitude of β-LFP across the array to the circular standard deviations of both the Hilbert phase and the Hilbert phase gradient (Fig. 6). We found that beta amplitude and beta synchrony were positively correlated for all areas in both subjects. The correlation between beta amplitude and the standard deviation of the phase-gradient direction varied across areas. Overall, traveling wave states existed on a continuum between asynchronous and spatially synchronized states. Nevertheless, as stated above, once a complex, radiating/rotating plane wave set in, it was clearly distinguishable from a spatially synchronized state.

Because of the inherent challenges in differentiating signal and noise in these LFP recordings, there is the possibility for changes in signal-to-noise ratio to create spurious correlations between apparent spatial synchrony or phase gradient and amplitude (see methods, Critical Point Analysis). To address this confound, we further analyzed wavelength from planar wave events that showed an extremely high degree of phase-gradient order unlikely to occur by chance.

β-LFP wavelength correlates with amplitude.

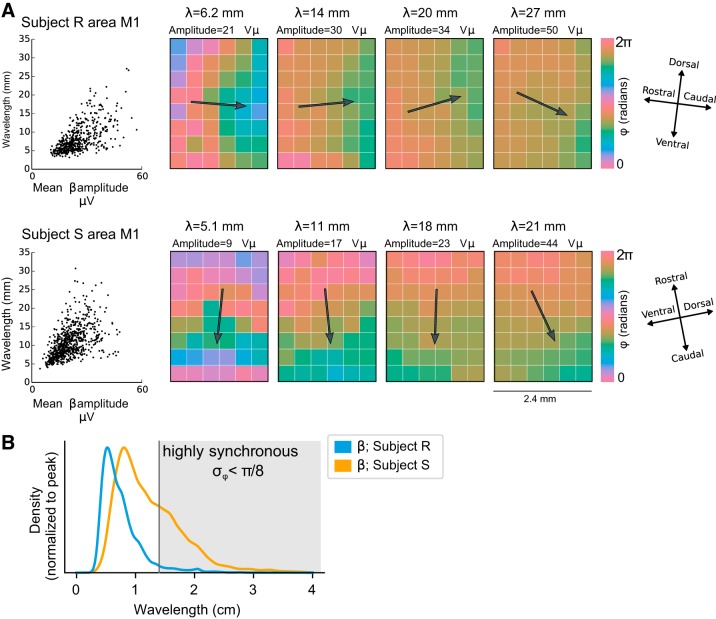
We analyzed the correlation between planar traveling wavelength and beta amplitude in the M1 arrays of both subjects, which displayed the largest number of planar traveling waves. To avoid effects of signal-to-noise ratio on the measured wavelengths, we considered only wave events for which the circular standard deviation of the Hilbert phase gradient was less than π/4 (see methods, Spatial Gradient of the Hilbert Phase). For both subjects, organized plane wave activity was rare in area PMd, which tended to be synchronous, and area PMv, which tended to show more complex wave activity in subject S and synchrony in subject R (see Fig. 5). We note that these results are not inconsistent with the findings of Rubino et al. (2006), who reported traveling waves in area PMd, because of the more stringent inclusion criterion used to avoid bias in our estimation of the correlation of amplitude and wavelength (see methods, Spatial Gradient of the Hilbert Phase).

With this approach (Fig. 7) we found that larger beta amplitudes corresponded to longer wavelengths (Pearson ρ = 0.64 for subject R, ρ = 0.53 for subject S). In subject R, wavelengths ranged from 3.2 to 28 mm, with a median of 7.2 mm. In subject S, wavelengths ranged from 3.5 to 31 mm, with a median of 10 mm. High beta power [amplitude envelope >1.5 standard deviations (σ) of the beta-band signal] was associated with a median wavelength of 11 mm in subject R and 13 mm in subject S, and low beta power (<1.5σ) was associated with a median wavelength of 6.8 in subject R and 8.8 in subject S. In summary, the wavelength of beta waves was not fixed but varied across the spontaneous β-LFP transient events during ongoing activity, contrary to the predictions of models based on center-surround lateral interactions (Heitmann and Ermentrout 2015; Heitmann et al. 2012). There was a continuum between desynchronized activity at low amplitudes and spatially synchronous states at higher amplitudes.

Fig. 7.

Variability in β-local field potential (β-LFP) wavelength correlates with amplitude. A: planar traveling waves exhibited a correlation between beta amplitude and wavelength λ (left plots; Pearson ρ = 0.64, subject R; ρ = 0.53, subject S). Only primary motor cortex (area M1) exhibited sufficient highly planar wave events to facilitate correlation analysis. Specific examples illustrate the progression (left to right) from shorter wavelengths at lower amplitudes to longer wavelengths at higher amplitudes. Long wavelengths cannot be distinguished from spatial synchrony because of the size of the microelectrode array. These plots indicate that traveling waves transition continuously into synchronized states, with the LFP phase tending toward greater spatial homogeneity at higher amplitudes. Samples were taken every 50 ms (1 beta cycle), and only those time points displaying a high degree of alignment in the phase gradient (i.e., plane waves) were considered for the analysis (see methods, Spatial Gradient of the Hilbert Phase). All sessions for each subject were combined in the scatter plots. The hue scale is doubled to resolve longer wavelength patterns. B: variability in wavelength. Zero-lag spatial phase synchrony exists as a limiting case of long wavelengths (wavelengths corresponding to a phase variance <π/8 are shaded). Variation from local wave dynamics at small amplitudes to zero-lag global synchrony at high amplitudes is consistent with a synchronization phenomenon among local, coupled oscillatory patches.

Incidentally, long-wavelength phase gradients can appear as fast-traveling waves. For example, phase velocities in excess of 67 cm/s were observed for the longest 1% of waves in subject S. Although such extreme waves were rare, they occurred at high β-LFP amplitudes where noise contamination is minimal and likely reflect a true description of the phase organization in the cortical patch. These speeds are difficult to reconcile with excito-excitatory traveling wave fronts, as examined below. We were only able to analyze planar traveling waves with this approach, because correlations between amplitude and the spatial scale of complex patterns could be confounded with variations in signal-to-noise ratio (see methods, Critical Point Analysis, and discussion).

Overall, the variability in apparent wavelengths is difficult to reconcile with traveling wave phenomena in excitable media, but can be explained if β-LFP waves arise from transient phase reorganization in coupled-oscillator systems. To further clarify the origins of these transient β-LFP waves, we next contrast it to an example of traveling wave phenomenon in excitable neural media (Fig. 1A) measured via the same recording setup.

Contrast to Traveling Waves in Excitable Media: Optogenetically Induced Traveling Waves

We next address the origin of spatial patterns in transient β-LFP oscillations in the context of the possible scenarios described in the Introduction and by the schematics in Fig. 1. The variety of spatial patterns observed was inconsistent with a simple common input with a single spatially organized gradient of time delays (2nd scenario in Introduction; Fig. 1B). For this reason, we focused on whether observed β-LFP waves were consistent with propagation of excitation in excitable media (1st scenario; Fig. 1A) or, alternatively, with phase reorganization in neural coupled-oscillator systems in motor cortex (3rd scenario; Fig. 1C). To distinguish between these two scenarios, we contrasted the statistics of spontaneous beta spatiotemporal oscillations with those of traveling waves in excitable media. We examined traveling waves induced by optogenetic stimulation as first reported in primate motor cortex by Lu et al. (2015). Lu et al. (2015) showed that a 1-s constant pulse of optogenetic stimulation elicits sustained ~50-Hz LFP oscillations, which travel as radial waves across the cortical patch recorded by the 4 × 4-mm² MEA (Fig. 8). These spatial waves were induced well beyond the <1-mm-diameter site of stimulation, requiring propagation through network lateral interactions (Lu et al. 2015).

We emphasize that induced oscillations were obtained via constant stimulation, not periodic driving. The oscillation onset was likely due to a bifurcation in the network’s intrinsic dynamics, and the traveling waves reflect excitatory conduction of these oscillations into the surrounding tissue (Heitmann et al. 2017). Induced LFP responses were reproducible across trials (Lu et al. 2015). Figure 8C explores two statistics of the average wave activity: the average phase delay and the average zero-lag spatial phase gradient (see methods, Phase Maps for Induced Traveling Waves) . The ~50-Hz oscillations showed spatial structure in the form of a radiating wave, as summarized by averages of LFP activity triggered on the phase of induced narrow band oscillations in Fig. 8D.

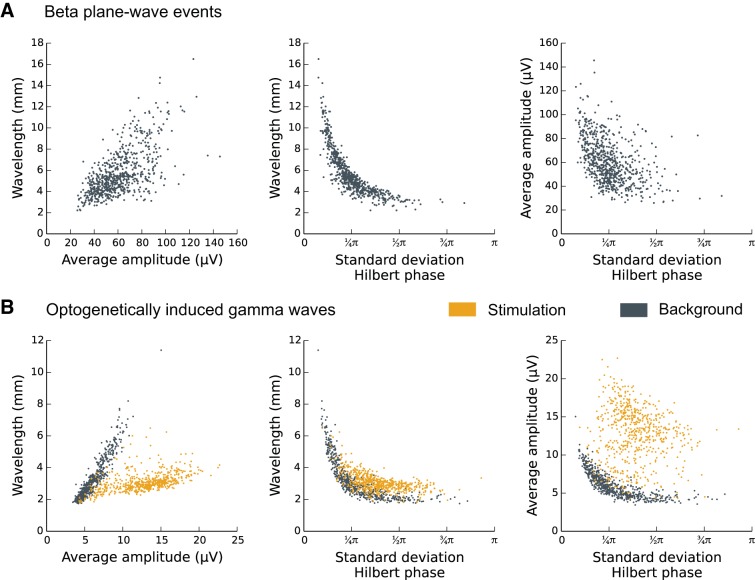
Similar to the beta-wave analysis, we examined the correlations between the amplitude of the optogenetically induced oscillations and the degree of spatial synchrony, as assessed by the standard deviation of the Hilbert phase angles across the array. Because this is not a plane-wave phenomenon, we did not examine correlations between the amplitude and the degree of alignment of phase-gradient vectors. However, there was very good signal-to-noise ratio during the induced oscillations such that we were able to estimate the local phase gradient. This allowed us to extract a local estimate of wavelength, and the spatial scale of the induced wave could be estimated by averaging this wavelength over the array (see methods, Spatial Gradient of the Hilbert Phase). The spatiotemporal statistics of optogenetically induced waves and prestimulation background spontaneous waves showed two different clusters (Fig. 9B). The induced waves showed a characteristic 2- to 4-mm wavelength, elevated amplitude, and reduced spatial synchrony. Compared with the prestimulation background ~50-Hz activity, the induced waves showed reduced variability in the estimated wavelength. Additionally, the optogenetic stimulation disrupted zero-lag spatial phase synchrony over the cortical patch, which need not have been the case. These statistics are consistent with abrupt appearance of a excitatory traveling wave with a characteristic wavelength and are to be contrasted with the spatiotemporal statistics of the spontaneous transient β-LFP waves detected during the movement preparation stages of the CGID task.

Fig. 9.

Unlike spontaneous β-local field potential (β-LFP) waves, induced traveling waves display a discrete transition and characteristic wavelength. Scatter plots compare amplitude, wavelength, and spatial synchrony for the β- and γ-LFP wave phenomena. Amplitude was taken as the average Hilbert amplitude over the array. Wavelength was computed from the average phase-gradient magnitude. Spatial synchrony was assessed by the circular standard deviation of zero-lag oscillation phase (smaller values are more synchronous). Each dot in the scatter plot represents a single wave cycle (20 ms for γ-LFP, 50 ms for β-LFP). A: β-LFP plane-wave events from subject R area M1; nonplanar wave events were excluded to avoid biased wavelength estimates. Left, amplitude varied continuously, and larger amplitudes exhibited longer wavelengths. Middle, spatial synchrony emerged as a limiting case of long-wavelength waves over the aperture of the microelectrode array. Right, spatially asynchronous states occurred at a range of amplitudes, but the highest amplitude events tended to be synchronous. B: optogenetically induced ~50-Hz oscillations in subject T were associated with abrupt emergence of spatial structure in the form of radiating traveling waves. Left, in contrast to the spontaneous β-LFP wave activity, induced LFP waves exhibited a narrow 2- to 4-mm wavelength that varied little with amplitude. Middle, both the background and induced LFP wave activity were superficially similar to the β-LFP in the sense that longer wavelengths were more spatially synchronized. However, the induced traveling waves had shorter wavelength events and less spatial synchrony compared with background, whereas high-beta events exhibited the opposite trend: elevated β-LFP state increased synchrony and wavelength. Right, induced LFP oscillations caused a transition to large-amplitude waves with a concurrent reduction in spatial synchrony. Spontaneous β-LFP waves showed continual variation.

In contrast to the optogenetically induced waves, the spontaneous transient β-LFP waves showed a continuous variation in amplitude and a tendency for increased spatial synchrony at higher amplitudes (Fig. 9A). Induced oscillations were associated with an abrupt increase in amplitude and decrease in spatial synchrony, compared with the background activity. We also note that the induced traveling waves had a characteristic fixed wavelength that varied little with amplitude relative to the background activity. In contrast, the wavelength of β-LFP oscillations increased linearly with amplitude such that the largest amplitude beta events were effectively synchronous over the recorded cortical area. This finding highlights that simple summary statistics such as amplitude and spatial synchrony can distinguish different types of traveling wave phenomena and can reflect differences in their underlying dynamics. Importantly, the optogenetically induced traveling waves served as a control for the statistical methods used to analyze β-LFP waves, ensuring that the wavelength and amplitude variability of β-LFP waves were not an artifact of our MEA recording setup or statistical analysis. Overall, whereas the induced waves were excitatory traveling waves induced by a local (<1 mm) direct optogenetic perturbation (1st scenario; Fig. 1A), our findings are consistent with the hypothesis that β-LFP spatial patterns during steady movement preparation periods resulted from phase reorganization of transient beta oscillations across the recorded neocortical patch (3rd scenario; Fig. 1A).

DISCUSSION

In this study, we characterized spontaneous transient beta waves appearing during the steady-state movement preparation periods of an instructed delay reaching and grasping task. These waves were contrasted with excitatory traveling waves induced by optogenetic stimulation. To our knowledge, our study is the first to report such systematic analysis of the range of spatiotemporal waves in motor cortex. We found that transient β-LFP dynamics transition spontaneously among a rich variety of spatiotemporal patterns ranging from spatially synchronized states and traveling plane waves to rotating, radiating and other more complex wave patterns. Although the anatomic connectivity in motor cortex may favor plane waves (Takahashi et al. 2011), our results indicate that a richer variety of wave patterns exists. Despite sustained β-rhythmic firing rates in the recorded single neurons (Rule et al. 2017), β-LFP wave patterns appeared as transient events with varied durations (sometimes up to several hundred milliseconds). In addition, during a single transient, beta oscillations could transition spontaneously among different spatial wave patterns.

The optogenetically induced propagating waves in primate motor cortex provide a reference for excitatory traveling waves in excitable media (1st scenario in Introduction; Fig. 1A) against which to compare the statistics of spontaneous β-LFP wave spatial patterns. Because both induced traveling waves and spontaneous βLFP waves were obtained via the same recording setup, confounds related to differences in spatial sampling and microelectrode electronics were minimized. Induced spatiotemporal patterns were globally organized, consisting of radial waves that propagated beyond the stimulation site. Unlike the spontaneous β-LFP patterns, these traveling waves exhibited a characteristic wavelength (2–4 mm). In contrast, spontaneous β-LFP waves showed wide variability in apparent wavelength. In spontaneous β-LFP spatiotemporal activity, diverse wave states (complex, planar, radiating, rotation, synchronous) existed on a continuum and correlated with amplitude. For example, synchronous states appear as a limiting case of long-wavelength activity at high β-LFP amplitudes. This suggests that various β-LFP spatiotemporal patterns did not reflect discrete shifts in network state or external inputs. The positive correlation between wavelength and amplitude observed in this study is also consistent with the emergence of waves in spatially extended oscillator systems close to a Hopf bifurcation (Kopell and Howard 1973). Overall, these findings are consistent with spatiotemporal β-LFP waves arising from reorganization in relative phases in spatially distributed neuronal oscillations.

We also examined β-LFP spatiotemporal dynamics in area PMv, a premotor area thought to be involved in grasping but not previously studied in the context of beta spatiotemporal waves. We found that it differed from areas M1 and PMd. In subject S, area PMv exhibited complex wave activity, even during transient periods of elevated β-LFP power. In contrast, in subject R, PMv exhibited synchronous beta oscillations, with few plane waves. Overall, although area PMv did not exhibit the plane-wave phenomena previously reported in M1 and PMd (Rubino et al. 2006), it did exhibit organized radiating and rotating waves. PMv may also have a relatively different anatomical structure, leading to functional differences and the observed diversity in wave patterns. These results motivate the need for further studies to explain how β-LFP spatiotemporal waves might change across anatomical or functional boundaries in the motor cortex.

Spatial Sampling, Phase Extraction, and Other Caveats

Multielectrode array recording approaches have limitations that should be considered when analyses of spatiotemporal wave dynamics are interpreted. Because cortex is curved, the depth of the electrodes could change across the array. The phase of motor cortex beta varies across layers (Murthy and Fetz 1996), and changes in the depth of the electrodes could create a phase gradient in the MEA recordings that mimics a traveling wave. However, this scenario cannot yield rotating or complex waves and so cannot explain the spontaneous beta and optogenetically induced wave patterns we have reported above. β-LFP phase is difficult to interpret at lower amplitudes due to reduced signal to noise. We addressed this confound by restricting quantitative analyses to periods of high signal-to-noise ratio. However, there is a need for improved methods that can account for the complex nature of neural signals recorded from MEAs, in particular interrelated structures in time, frequency, space, and spatial frequency. It remains unclear whether descriptions of spatiotemporal dynamics based on phase alone are sufficient. Indeed, recent work by Best et al. (2017) shows that spatiotemporal patterning of β-LFP amplitude fluctuations are also important in motor cortex.

The difference between spontaneous beta and induced traveling wave experiments should be interpreted with care. Differences in the statistics of these phenomena could arise from the more localized nature of optogenetic stimulation and the chosen level of stimulation. Nevertheless, our previous work (Lu et al. 2015) also reports ramp stimulation results and shows that induced traveling waves emerge at a critical level of stimulation intensity and grow with increasing amplitude at a fixed frequency, suggesting a supercritical Hopf bifurcation. Because the induced waves propagated in the surrounding medium well beyond the <1-mm spatial domain of direct light stimulation, these waves serve as a reference for excitatory traveling waves (Fig. 1A). These induced excitatory waves were successfully modeled using a neural field approach (Heitmann et al. 2017), which accurately predicted the phenomenon of mode-locking resonance in excitable neural media, i.e., where wave emission will skip cycles depending on the level of stimulation. Our modeling work suggests that this mode-locking resonance is not a property of the type of stimulation (optogenetic or other). Rather, it is a property of the surrounding neocortical tissue when driven by any source of oscillatory activity. Additional studies should explore in more detail the relationship between stimulation amplitude and spatiotemporal structure.

We note that task-related information becomes available in the local neural population after the object and grasp cues are presented. This information is then sustained across time (Vargas-Irwin et al. 2015). In this study we have examined two steady-state periods: one before the object cue, where there is no specific task information, and another corresponding to the interval starting 1-s after the grasp cue and ending at the go-cue presentation. The second period contains information about both object and grasp type (Vargas-Irwin et al. 2015). There is an important distinction between these steady-state instructed delay periods, during which we believe the prepared motor plan is maintained locally, and active processing periods, where information arrives in and is distributed within motor areas. Thus the steady-state periods we examined in this study are unlikely to directly address information flow among motor areas. The potential relationship between β-LFP phase reorganization and information storage or communication remains to be explored in further studies.

The Origin of Transient Spatiotemporal β-LFP Wave Patterns

We speculate that β-LFP transients in motor cortex may arise from a number of nonexclusive scenarios. The recorded cortical β-LFP oscillations may have multiple origins, reflecting both local sources of beta rhythmicity (e.g., Kopell et al. 2011; Roopun et al. 2006), as well as corticothalamic interactions and rhythmic inputs from other brain areas (e.g., Jones et al. 2009; Sherman et al. 2016 for the case of beta in somatosensory areas). Changes in the apparent spatial organization of motor cortex β-LFP may reflect changes in the contributions of different sources to the β-LFP signal. For example, a remote synchronous source may mix with local, asynchronous beta oscillations. If fluctuations in beta power reflect fluctuations in this synchronous source, it could explain the observed correlation between beta synchrony and amplitude. However, the correlation between the plane-wave wavelength and β-LFP amplitude found in this study contradicts this scenario: such globally organized states cannot be explained as chance occurrences in an asynchronous population. Spatially correlated inputs from other cortical or subcortical (e.g., thalamus) areas could also contribute to transient increases in β-LFP power over different sites of the recorded cortical patches, which could explain the correlation between the level of β-LFP power and the degree of spatial synchronization.

Alternatively, the observed variations in β-LFP power and spatial patterns may arise intrinsically in motor cortex. This variability could result from metastability in the phase synchronization between weakly coupled neuronal populations exhibiting transient oscillations with either homogeneous or slightly heterogeneous intrinsic frequencies (Deco and Jirsa 2012; Laing 2016; Panaggio and Abrams 2015; Shanahan 2010). Pyramidal tract neuron pools with different muscle fields are known to show different synchronization properties (Jackson et al. 2003), and variability in coupled-oscillator frequency can lead to entrainment that manifests as radiating waves (e.g., Kheowan et al. 2007). The variability in spatiotemporal patterns may also reflect fast coupling changes among these populations. For example, coupling between sources of beta may be higher when beta power is increased, leading to greater overall synchronization. Conversely, when local beta oscillations become more synchronous, their related extracellular field potentials would be expected to interfere constructively and generate a larger LFP signal.

If phase reorganization in coupled-oscillator systems plays an important role in the observed transient β-LFP wave patterns, a natural question then is, where are the oscillators? Our previous study has shown that recorded neurons exhibited sustained firing rates during the same steady-state periods, despite the transient β-LFPs (Rule et al. 2017). In addition, several single units also exhibited β-rhythmicity in their spiking activity, and spike-LFP phase locking increased during β-LFP transients. These neurons could play the role of oscillators (Rule et al. 2017). However, we emphasize that this β-rhythmicity in spiking activity could potentially also appear as rhythmic transients within otherwise irregular background activity. Further experiments will be required to address this issue. One possibility is that these coupled-oscillator systems are themselves transiently formed, lasting only tens to hundreds of milliseconds. Although the system is in a roughly steady-state with respect to the absence of strong sensory perturbations, it has its own spontaneous ongoing dynamics. During their transient existence, coupled-oscillator systems would undergo different phase reorganization dynamics, leading to different β-LFP spatiotemporal wave patterns. We do not exclude the possibility that the spatiotemporal dynamics result from a combination of both coupled-oscillator dynamics and excitable media effects. More work is needed to clarify this issue, including recordings of spiking activity and LFPs simultaneously obtained from motor-related areas in cortex and associated deep brain structures.

Implications for Models of β-LFP Spatiotemporal Dynamics

The contrast between the statistics of spontaneous β-LFP waves and the excitatory traveling waves highlights differences in the neural mechanisms underlying these phenomena and constrains spatially extended models of neural dynamics in motor cortex. The optogenetically induced ~50-Hz waves emerged with a characteristic wavelength (2–4 mm) that varied little with amplitude and disrupted phase synchrony across the cortical patch. On the other hand, spontaneous beta waves showed the opposite trend of increased synchrony at higher amplitudes and lacked a characteristic wavelength, instead showing a gradual lengthening of plane waves at larger amplitudes. This variable wavelength is inconsistent with models of oscillatory spatial pattern formation that rely on center-surround lateral interactions that exhibit wave activity emerging at a fixed spatial frequency (e.g., Heitmann and Ermentrout 2015; Heitmann et al. 2012; Rule et al. 2011), revealing a need for alternative models for motor cortex β-LFP. The variability in the spatial scale of beta spatiotemporal activity is, however, consistent with a model in which beta waves arise from transient reorganization of the relative phases of transient local beta oscillations (cf. chapter 8 in Ermentrout and Terman 2010).

Future Directions

Previous studies have emphasized traveling planar waves and their potential link to spiking communication (Besserve et al. 2015; Lubenov and Siapas 2009; Rubino et al. 2006; Takahashi et al. 2011, 2015; Wu et al. 2008) and movement initiation (Best et al. 2017). Further work is needed to investigate the implications of the diversity of spatiotemporal wave patterns found in this study, especially in terms of the functional roles of traveling waves vs. globally synchronized states, which both occur during high beta power. Neuroimaging studies could elucidate global coordination of beta phase and its relation to local dynamics, e.g., calcium imaging (O’Shea et al. 2017) or magnetoencephalography (Bonaiuto et al. 2018; Troebinger et al. 2014). Locally silencing the transient β-rhythmic activity in a small cortical patch could clarify the relationship between coupled-oscillator phase organization and propagating activity. Additionally, the relationship between spatiotemporal organization of beta and modulation in beta amplitude may hold important clues as to how beta power is modulated in motor cortex and how changes in beta power may impact computation and communication in neural systems.

The observation that motor cortex beta phase exhibits complex spatial dynamics has implications for our understanding of collective dynamics and single-unit activity in motor cortex. In particular, the relationship between spatiotemporal phase dynamics and single-unit spiking remains to be clarified (Okun et al. 2015), and beta waves could induce spatially patterned correlations at the single-unit level. The findings reported presently predict that β-LFP traveling waves during steady-state movement preparation arise from phase gradients within a system of coupled oscillators. Because these β-LFP oscillations are transient events, the coupled-oscillator system could itself be transiently formed. Overall, the functional or computational role of β-LFP phase reorganization across motor cortex remains an important open problem whose investigation may reveal the neural mechanisms associated with motor cortex preparatory steady states.

GRANTS

This research was supported by National Institute of Neurological Disorders and Stroke (NINDS) Grant R01 NS25074 (to J. P. Donoghue; co-investigator W. Truccolo) and NINDS Career Award K01 NS057389 (to W. Truccolo), Defense Advanced Research Projects Agency Reorganization and Plasticity to Accelerate Injury Recovery Grant N66001-10-C-2010 (to J. P. Donoghue and W. Truccolo), a National Science Foundation Predoctoral Fellowship (to M. E. Rule), and the Pablo J. Salame ’88 Goldman Sachs Endowed Assistant Professorship of Computational Neuroscience (to W. Truccolo).

DISCLAIMERS

The contents do not represent the views of the U.S. Department of Veterans Affairs or the United States Government.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

M.E.R., C.V.-I., J.P.D., and W.T. conceived and designed research; C.V.-I. performed experiments; M.E.R. analyzed data; M.E.R. and W.T. interpreted results of experiments; M.E.R. prepared figures; M.E.R., C.V.-I., and W.T. drafted manuscript; M.E.R., C.V.-I., J.P.D., and W.T. edited and revised manuscript; M.E.R., C.V.-I., J.P.D., and W.T. approved final version of manuscript.