Abstract
Acquiring new movements requires the capacity of the nervous system to remember previously experienced motor patterns. The phenomenon of faster relearning after initial learning is termed “savings.” Here we studied how savings of a novel walking pattern develops over several days of practice and how this process can be accelerated. We introduced participants to a split-belt treadmill adaptation paradigm for 30 min for 5 consecutive days. By training day 5, participants were able to produce near-perfect performance when switching between split and tied-belt environments. We found that this was due to their ability to shift specific elements of their stepping pattern to account for the split treadmill speeds from day to day. We also applied a state-space model to further characterize multiday locomotor savings. We then explored methods of achieving comparable savings with less total training time. We studied people training only on day 1, with either one extended split-belt exposure or alternating four times between split-belt and tied-belt conditions rapidly in succession. Both of these single-day training groups were tested again on day 5. Experiencing four abbreviated exposures on day 1 improved the performance on day 5 compared with one extended exposure on day 1. Moreover, this abbreviated group performed similarly to the group that trained for 4 consecutive days before testing on day 5, despite only having one-quarter of the total training time. These results demonstrate that we can leverage training structure to achieve a high degree of performance while minimizing training sessions.
NEW & NOTEWORTHY Learning a new movement requires repetition. Here, we demonstrate how to more efficiently train an adapted walking pattern. By compressing split-belt treadmill training delivered over 4 days to four abbreviated bouts of training delivered on the first day of training, we were able to induce equivalent savings over a 5-day span. These results suggest that we can manipulate the delivery of training to most efficiently drive multiday learning of a novel walking pattern.
Keywords: adaptation, gait, motor learning, multiday savings, split-belt treadmill
INTRODUCTION
Our ability to smoothly navigate our environment relies on the capacity to adapt our motor behavior to new environments and store a motor memory of the adapted movement. Consider the seemingly trivial transition of stepping from a boardwalk onto compliant sand. Transitioning between these walking environments poses a problem that the nervous system must solve for us to maintain balance and stay upright. When presented with predictable changes in the environment, the nervous system possesses the ability to change its motor output via motor adaptation—a process in which sensorimotor mappings update in response to systematic errors caused by new environmental demands (Martin et al. 1996; Mazzoni and Krakauer 2006; Shadmehr and Mussa-Ivaldi 1994; Tseng et al. 2007). Once these mappings are updated, it is equally crucial that the nervous system possesses the ability to store a motor memory of the new mapping so that it can be retrieved at a later point for successful navigation. Imagine if every time we step onto the sand, we have to adapt our walking pattern over the course of hundreds of steps as if we have never experienced anything similar before. The fact that we can smoothly transition from one walking environment to the next underscores the importance of storing a motor memory.
Prior work on motor adaptation in both reaching and walking has focused largely on adaptation over short timescales (e.g., learning within one session; Mazzoni and Krakauer 2006; Reisman et al. 2007; Shadmehr and Mussa-Ivaldi 1994; Tseng et al. 2007). While these studies are useful in uncovering the mechanisms underlying motor adaptation, we rarely come across truly novel environments in our everyday lives. More often than not, we rely on experience to readapt to the demands of previously encountered environments; alternatively, we are able to generalize previously learned movement patterns to new but similar environments. Just as a golfer can select from a number of clubs in his or her golf bag for a club best-suited for a given shot, we can call on an expansive collection of remembered movements to traverse a wide range of environments quickly and successfully. In the current study, we seek to understand how we can best incorporate a novel motor pattern into our repertoire of movements over multiple days of training.
Several studies have shown that people who have previously adapted to a perturbation can achieve faster learning when reexposed to the same perturbation, a motor learning phenomenon termed “savings” (Herzfeld et al. 2014; Mawase et al. 2014; Roemmich and Bastian 2015; Shadmehr and Brashers-Krug 1997). Savings has been well studied in the context of motor adaptation but these studies are often limited to two within-day training exposures (Haith et al. 2015; Huang et al. 2011; Morehead et al. 2015; Roemmich and Bastian 2015; Smith et al. 2006). Previous studies show savings to be sensitive to the structure of training (Malone et al. 2011; Roemmich and Bastian 2015; Shadmehr and Brashers-Krug 1997). Specifically, savings in locomotor adaptation is driven by previous exposure to similar abrupt changes in the environment as well as the amount of exposure in the new environment (Roemmich and Bastian 2015). Importantly, the balance of these two factors that leads to optimal savings across days has yet to be explored. Therefore, it is important that we understand how new movement patterns are learned over longer timescales (e.g., multiple days) and how different learning schedules affect the ability to store the newly learned pattern from day-to-day.
The ability to shape savings using the structure of training provides a promising tool for gait rehabilitation. Many patients face tight time and financial restrictions that limit their exposure to therapy, and thus it is critical that therapy is delivered as efficiently as possible. When undergoing adaptive training to learn a new gait pattern, patients look to build on what was learned from the previous training sessions. Knowledge of how to prescribe rehabilitation schedules for fastest day-to-day learning could lead to more efficient therapy whereby patients achieve the desired outcome with fewer training sessions.
Here, we studied how altering the training schedule influenced savings of a split-belt walking pattern over multiple days. Specifically, we altered the frequency and duration of split-belt treadmill training within days 1 to 4 of training and tested savings on day 5. While some participants received extended split-belt training with continuous exposure to the split-belt environment, others received a condensed training schedule consisting of short bouts of training in which they switched between the split-belt and tied-belt environments. Furthermore, we varied the delivery of these training regimes across groups such that some participants only trained on day 1 and returned to the laboratory for testing on day 5 while others trained for 4 consecutive days before testing for savings on day 5. We demonstrate that we can reduce the training load from 4 days to 1 day by implementing a switch training schedule and still achieve equivalent learning. Moreover, the savings observed following the switch training schedule followed a similar behavioral trajectory (i.e., altered kinematics) as that of savings observed following extended multiday training. Our findings indicate that we can leverage the structure of training to create an optimal training schedule that minimizes training time while still maintaining the integrity of the learned movement across multiple days.
MATERIALS AND METHODS
Participants.
Forty young, healthy adults were recruited for this experiment (12 men, 28 women; mean age ± SD: 22 ± 4 yr). All participants provided written, informed consent before taking part in the experiment. The experimental protocol was approved by the Johns Hopkins Medicine Institutional Review Board. All participants were free of any neurological and musculoskeletal conditions. Leg dominance was determined by asking the participants which leg they would use to kick a soccer ball.
Split-belt treadmill.
Adaptive learning was studied by having participants walk on a split-belt treadmill in which an independently controlled belt was located under each foot (Woodway USA, Waukesha, WI). The two belts were controlled by custom MATLAB (MathWorks, Natick, MA) software and could move at the same speed (i.e., tied belt) or at different speeds (i.e., split belt). Participants were instructed to stand in the middle of the treadmill with one foot on each belt. They wore a safety harness that was suspended from the ceiling to protect against the risk of falling. The harness did not provide any body weight support. Participants were not made aware of the speeds of the belts in subsequent trials and were given a handrail at the front of the treadmill to provide stability when the treadmill belts abruptly started. They were told to lift their hands off of the rail within the first few strides, walk with their arms across their chest, and avoid looking downward at the treadmill belts for the entirety of the experiment. Participants remained on the treadmill for the duration of each session.
Motion analysis.
We recorded participants’ kinematics as they walked using an Optotrak Certus motion capture system (Northern Digital, Waterloo, ON). Kinematic data were collected at 100 Hz from 12 infrared-emitting diodes placed bilaterally on the foot (fifth metatarsal head), ankle (lateral malleolus), knee (lateral joint space), hip (greater trochanter), pelvis (iliac crest), and shoulder (acromion process). Marker placement is displayed in Fig. 1A.
Fig. 1.
A: General experimental setup in which participants walked with one foot on each independently controlled belt. Step length was calculated as the anteroposterior distance between ankle markers at heel strike. Foot position was calculated as the hip-centered anteroposterior coordinate of the toe marker. B: experiment protocol diagrams for extended (top) and switch (bottom) training. Dashed and solid lines indicate the speeds of the fast and slow belt, respectively, while red solid lines indicate tied-belt walking. C: split-belt exposure schedules for each condition. Each box indicates a separate split-belt adaptation block. The width of each box is proportional to the time spent walking with split belts (i.e., a wide block denotes extended training, four abbreviated blocks denotes switch training). The colors of each exposure remain consistent throughout subsequent figures. We thank Tziporah Thompson for illustrations within Fig. 1.
Experimental paradigm.
The goal of this study was to investigate how various perturbation schedules contribute to the accumulation of savings of a newly learned walking pattern over multiple days. To characterize this, participants were randomly assigned to one of four groups (n = 10/group). The experimental paradigms are displayed in Fig. 1B. All groups experienced the same baseline period in which they underwent tied belt walking for 2 min at 0.7 m/s, 2 min at 1.4 m/s, and then another 2 min at 0.7 m/s. The four groups differed in how the split-belt adaptation period was delivered over the multiday testing. Participants in the Multiday and Single Day groups were trained for 30 min of split-belt walking per day (abrupt 2:1 split-belt perturbation). Their self-reported dominant leg was placed on the “slow belt” set to 0.7 m/s while the nondominant leg was placed on the “fast belt” set to 1.4 m/s. This was followed by a deadaptation period that consisted of 10 min of walking with both belts set to 0.7 m/s followed by 10 min of walking with both belts set to 1.4 m/s. The Multiday group performed this protocol on 5 consecutive days whereas the Single Day group performed it only on day 1 and day 5, with no training on intervening days (Fig. 1C).
To determine whether we could reduce the total amount of training time but still attain similar savings as in the Multiday group, we studied a switch training paradigm. On day 1 of training, participants in the Switch and Switch Short groups experienced four bouts of 7.5-min adaptation periods (30 min total adaptation). Like previous groups, the perturbation was a 2:1 split with the dominant leg placed on the slow belt set to 0.7 m/s and the nondominant leg placed on the fast belt set to 1.4 m/s. The four periods of adaptation were interleaved with 5-min deadaptation blocks in which participants experienced tied belts set to 0.7 m/s. The baseline periods and final deadaptation blocks were identical across all four groups. After day 1 switch training, we assessed learning in the Switch group on day 5 with no training on intervening days, and in the Switch Short group on day 2. These retests followed the same extended split-belt training paradigm (30 consecutive minutes of split-belt adaptation) as described above for the Multiday and Single Day groups. Importantly, the test paradigm to assess the effects of prior training was identical for all four groups (i.e., day 5 for Multiday, Single Day, Switch; day 2 for Switch Short).
Data analysis.
The primary outcome measure used to quantify adaptation during split-belt walking was step length asymmetry. Step length asymmetry (SLA) was calculated by normalizing the difference in bilateral step lengths (SLF = fast belt step length, SLS = slow belt step length) to their sum:
A step length asymmetry of zero therefore represents “perfect” symmetry, whereas a positive step length asymmetry value indicates the fast leg took a larger step than the slow leg, and vice versa for negative values. During treadmill walking, step length was calculated as the anteroposterior distance between the ankle markers at heel strike (Fig. 1A). The heel strike and toe off events were determined using a custom MATLAB program that extracted the gait events from the kinematic data. We targeted step length asymmetry for this experiment for two primary reasons. First, it is a parameter that has been shown to adapt during split-belt walking and results in aftereffects when the belts are returned to the same speed (Reisman et al. 2005). Second, this normalized parameter allows us to fairly compare individuals of different height and stride length.
The rate of learning throughout the experiment was determined by measuring the step length asymmetry over key time periods in the experiment. For example, the size of the initial perturbation of each subject was defined as the average step length asymmetry of strides 1–5 during adaptation. Early change was defined as the average step length asymmetry of strides 6–30 during adaptation. Measuring the early change on different days allows us to determine the amount of savings from day to day and provides a measure of the rate of learning without assuming any stride-dependent relationship (i.e., exponential, double exponential) on step length asymmetry. The same trial epochs were used to quantify changes in unlearning during deadaptation.
We know that step length asymmetry can result from differences in spatial control (i.e., where we place our feet), temporal control (i.e., the timing between foot strikes), or the externally applied perturbation (Finley et al. 2015). A model formulated by Finley et al. 2015() allowed us to separate the gait kinematics into spatial, temporal, and perturbation contributions to step length difference so that we could analyze how these features develop over exposures to the split-belt perturbation. Similar to step length asymmetry, we use the early change epoch (strides 6–30) to quantify savings of each of these features across multiple exposures to the split-belt treadmill.
Finally, we investigated what spatial features of gait were being saved from one training session to the next using foot position and velocity. Foot position was defined as the hip-centered anteroposterior coordinate of the toe marker (Fig. 1A). Thus, foot position was zero when directly below the hip marker, positive when the toe marker was ahead of the hip marker, and negative when the toe marker was behind the hip marker during the gait cycle.
Descriptive modeling of savings over multiple days.
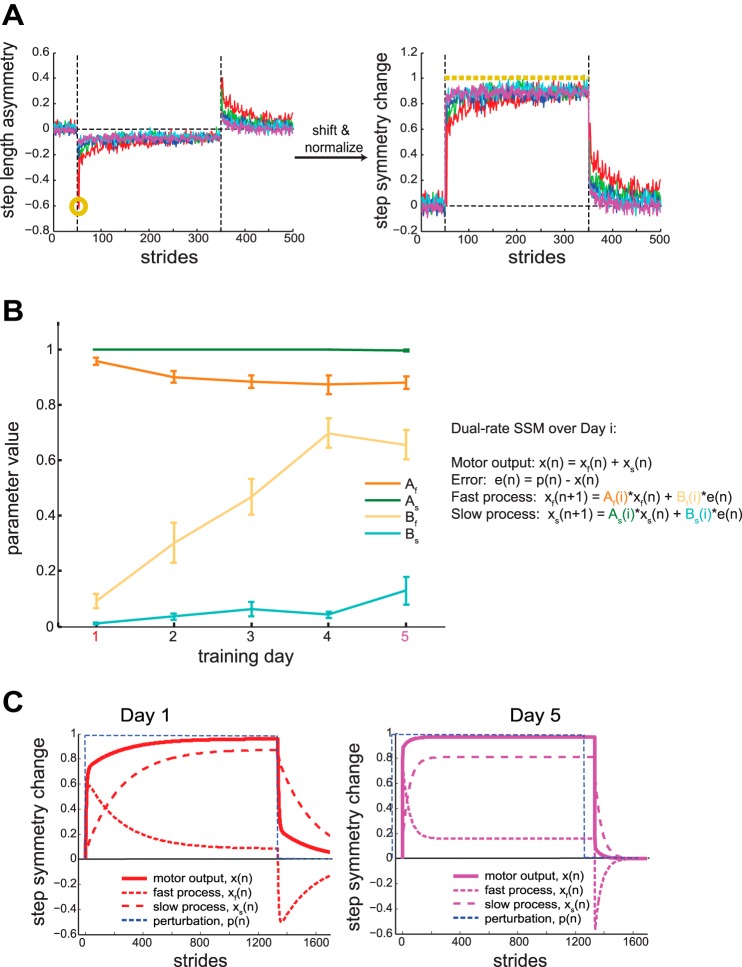
Several studies have aimed to derive computational models for savings in motor adaptation tasks. Of particular prevalence is the dual-rate state space model (SSM), composed of two linearly independent hidden states that combine to give the total motor output (Smith et al. 2006). These states are comprised of a fast state that learns quickly from error but is not retained well and a slow state that learns slowly from error but has high retention. Importantly, such a dual-rate SSM with time-invariant parameters cannot explain savings after prolonged washout, in which the hidden states have decayed to baseline values (Zarahn et al. 2008). When modeling savings in locomotor adaptation, Mawase et al. (2014) demonstrated that a change in the learning parameters following initial learning can best explain savings observed during two within-day blocks of adaptive learning. Within this framework, not only are the motor states updating trial by trial, but the learning parameters that govern the state updating rules are also updating with prior experience to the perturbation. Here, we apply this model to observe how learning parameters vary over multiple exposures to a split-belt perturbation over multiple days. The equations of the model are as follows:
On any trial n, x is the motor output, p is the external perturbation (0 for tied belts, 1 for split belts), and e is the error. The total motor output x is divided into a fast component, xf, and slow component, xs. Each of these components updates trial-by-trial with a retention factor, A(i), and a learning factor, B(i). These retention and learning factors vary across exposure i to the split-belt perturbation.
We fit the model to individual symmetry change data (Roemmich et al. 2016). Transforming step length asymmetry to symmetry change allowed us to convert our error signal (i.e., asymmetry) to a motor output form, which gradually updates in the presence of a perturbation and gradually returns to baseline from the adapted state once the perturbation is removed. We calculated symmetry change by shifting and normalizing step length asymmetry by each participant’s maximal asymmetry during the adaptation block on exposure 1. That is, symmetry change data during adaptation is a measure between 0 and 1, where 0 indicates that symmetry is maximally perturbed and 1 indicates that symmetry has been restored. The converse applies to the deadaptation block. As such, x(n) denotes what proportion of the perturbation p(n) has been restored on a given trial. We determined the parameters for individual subjects on each exposure by simultaneously fitting the entirety of adaptation and deadaptation blocks.
Statistical analysis.
To confirm there were no differences in baseline performance across groups, we ran one-way ANOVA of baseline step length asymmetry. Furthermore, we performed one-sample t-tests to confirm that the participants walked symmetrically (i.e., did not perform significantly differently from zero step length asymmetry). To measure whether baseline performance or initial perturbation differed across days within a single group, we ran repeated measures ANOVA and compared pairwise differences across days while correcting for multiple comparisons. To measure the rate of adaptation and deadaptation, we used step length asymmetry during early change (strides 6–30). We performed a series of repeated-measures ANOVAs to observe any main exposure effects on early change measures in each group across exposures to the split-belt perturbation. Post hoc analyses using the Studentized Range distribution (i.e., Tukey’s test) to correct for multiple comparisons revealed any pairwise differences in savings between any two adaptation blocks. Repeated-measure ANOVAs were used throughout to assess main effect of exposure on our measures of learning (e.g., early change step length asymmetry, temporal/spatial contributions, fitted SSM parameters, etc.).
We used correlation analysis to determine the relationship between specific kinematic parameters within the gait cycle (e.g., heel strike/toe off position) and the rate of step length asymmetry adaptation. Correlation analyses were also used to help explain which parameters in the dual-rate SSM best explained our observed savings across days. Additionally, repeated-measures ANOVA were performed to investigate effects of exposure on heel strike/toe off locations as well as dual-rate SSM parameters. The α-level for all analyses was set at 0.05.
We were interested in how varying the training structure from day 1 to day 4 of training would influence savings on the testing day (i.e., day 5). We performed a one-way ANOVA with the day 5 step length asymmetry during early change of Multiday, Switch, and Single Day to measure a group effect of savings. We performed post hoc analysis with Tukey’s honestly significant difference (HSD) correction for multiple comparisons to observe difference between any two groups. We used an independent sample t-test to confirm the time-decay resistance of savings following extended split-belt training. To test for the time-decay resistance of savings following switch training, we used a similar independent sample t-test to compare exposure 5 step length asymmetry values. Additionally, we performed a mixed-design, repeated-measures ANOVA with group and exposure as factors to observe whether savings differentially decayed between training and testing. For all repeated-measures ANOVA, we performed Mauchly’s test of sphericity and used the Greenhouse-Geisser correction of degrees of freedom if sphericity was violated. All analyses were performed using SPSS 24.0 (IBM, Armonk, NY) and α-level was set at 0.05. All data are reported as means ± standard error (SE).
RESULTS
Multiday savings.
In this experiment, we sought to determine how savings of a novel walking pattern developed over multiple days of training (30 min each day for 5 days; Fig. 1C, top row), and how different kinematic components of the gait cycle contributed to savings. Figure 2A shows group data from this experiment. Day 1 baseline asymmetry did not differ from zero (t9 = 0.04, P = 0.972), indicating participants walked symmetrically on the treadmill when belts were tied. Furthermore, baseline step length asymmetry on subsequent days did not differ from day 1 baseline performance (all P > 0.25), demonstrating that subjects were fully washed out from training on the prior day. Day 1 adaptation showed the typical initial perturbation and learning curve, so that by the end of adaptation subjects showed near zero step length asymmetry. Day 1 deadaptation showed the expected large aftereffect and subsequent error reduction, which eventually returned to baseline performance.
Fig. 2.

A: comparison of step length asymmetry across all exposures for the Multiday group. Mean curves across participants denote mean ± SE. Baseline (BL; last 50 strides), adaptation, and deadaptation mean curves are shown. Data points following adaptation and deadaptation curves indicate mean plateau values (mean ± SE of last 50 strides) for each block. B: early change step length asymmetry (mean ± SE of strides 6–30; shaded region in A) across all exposures of the Multiday group displayed in purple. Individual participant data is grayed in behind group mean with color indicating exposure number. ***Significant difference between early change values with α-level set to 0.05 as determined by repeated-measures ANOVA, corrected for multiple comparisons.
Subject performance on the first stride during adaptation remained consistent across days (repeated-measures ANOVA; F1.99,17.92 = 1.54, P = 0.242). However, performance on days 2–5 showed progressively smaller step length asymmetry during the initial perturbation epoch (strides 1–5; F2.00,18.04 = 18.41, P < 0.001) despite the fact that the split-belt parameters remained consistent across days. This is due to subjects’ ability to more rapidly compensate for the treadmill perturbation within early strides (each stride takes ~1 s, which allows for feedback control to partially change the walking pattern). Learning is more rapid in days 2–5 compared with day 1 and then reaches the same level at the end of adaptation. Deadaptation followed a similar pattern across days, with smaller aftereffects and a faster rate of unlearning.
Figure 2B shows our primary measure of savings across days (step length asymmetry during early change: mean of strides 6–30) for the entire Multiday group overlaid on individual subject performance. A decrease in mean asymmetry during early change suggests a faster rate of error reduction (i.e., savings). Our analysis revealed that savings increased across days (F1.29,11.59 = 36.51, P < 0.001) as participants performed extended split-belt training on 5 consecutive days. Participants reached the same level of learning at plateau in each of the days (F4,36 = 2.19, P = 0.090), indicating that while they learned at a faster rate from one day to the next, participants consistently reduced their errors to the same extent by the end of training on each day.
Following adaptation to the split-belt environment, the belts returned to the same speed to evaluate the presence of an aftereffect. The Multiday group showed a significant aftereffect on day 1 (initial perturbation epoch; t9 = 9.56, P < 0.001). Similar to the savings demonstrated with learning to walk symmetrically in the split-belt environment, we also found savings in unlearning when the belts were tied back to the same speeds. Analysis of the early change epoch revealed that participants reduced their error at a faster rate across successive days of training during deadaptation (F4,36 = 23.44, P < 0.001). We focused the remainder of our analyses on the kinematic data during the adaptation block because we found the magnitude and rate of learning and unlearning to be similar. Specifically, a mixed-methods repeated-measures ANOVA comparing absolute magnitude of early change in step length asymmetry during adaptation and deadaptation blocks revealed no significant main effect of block (F1,9 = 0.795, P = 0.396) or block-exposure interaction (F1.56,14.06 = 1.88, P = 0.192). This indicates savings in both adaptation and deadaptation showed similar magnitude and time course across days.
Spatiotemporal analysis.
Spatial (i.e., where we step) or temporal (i.e., when we step) features of gait both contribute to step length asymmetry while walking on a split-belt treadmill (Finley et al. 2015; Malone et al. 2012). We were interested in understanding how these spatial and temporal contributions changed across days as participants minimized their errors more quickly. As detailed in materials and methods, we separated step length difference into spatial, temporal, and perturbation components (Finley et al. 2015). Figure 3A displays each component during the adaptation block for each of the training days. Figure 3B shows the proportion of the perturbation corrected for by the spatial and temporal components during the early change epoch. Subjects showed savings in both the spatial and temporal contributions to step length difference: repeated-measures ANOVA revealed a significant main effect of Exposure on proportion corrected for step length difference (F1.47,13.19 = 31.93, P < 0.001), the spatial contribution (F1.49,13.37 = 17.10, P < 0.001), and the temporal contribution (F4,36 = 11.65, P < 0.001), with spatial providing a greater contribution than temporal (F1,9 = 18.60, P = 0.002). We performed further analysis to determine how the spatial and temporal components contributed to the corrected step length difference during the early change epoch. To do this, we normalized each participant’s proportion corrected spatial and temporal contribution by the step length difference proportion corrected. Figure 3C demonstrates that although participants are able to correct a larger proportion of the perturbation, the proportion of spatial and temporal contributions to this correction scaled equally across days (~70 and 30%, respectively). Repeated-measures ANOVA revealed no significant main effect of Exposure for either spatial or temporal proportion of step length difference (F1.06,9.58 = 0.01, P = 0.940 and F1.06,9.56 = 0.01, P = 0.945, respectively). In sum, the spatial and temporal components scale equally with savings of step length difference across days.
Fig. 3.
A: comparison of motor adaptation parameters (step length difference, spatial contribution, temporal contribution, perturbation) across exposures in the Multiday group. Mean curves during adaptation are shown. Data points following the curves represent the mean plateau values during each exposure. All data are shown as mean ± SE. B: proportion of the perturbation corrected for by step length difference, spatial contribution, and temporal components during the early change epoch (stride 6–30; shaded region in A) across training days. Note participants were able to reduce early change step length difference (i.e., error) across training days. C: contribution of spatial (gold) and temporal (teal) features to step length difference across training days. Note that the spatial and temporal components scale equally with the reduction of step length difference. All error bars denote SE.
Since the spatial domain drives a majority (~70%) of the correction in step length difference across days, we next analyzed specific spatial features of gait to observe what was saved across days. While the spatial contribution described above is an interlimb measure, we wanted to know how each leg’s kinematics contributed to savings across days. Figure 4A displays the kinematic features in phase plane space (anteroposterior foot position and velocity) of an average gait cycle for each leg during the early change epoch of the adaptation block. Note that time is not represented in this phase plane space. Heel strike and toe off position were calculated as the maximum and minimum foot position of each leg relative to the hip. A full gait cycle (i.e., stride) on the split-belt treadmill is composed of two steps: one step when the leg on the fast belt leads and one step when the leg on the slow belt leads. Positive foot velocity indicates forward motion (i.e., swing) and negative foot velocity indicates backward motion (i.e., stance). Heel strike and toe off locations occur approximately where foot velocity is zero. The leg cycles from stance to swing in a clockwise motion around this phase plane. Note that the overall shape of the trajectory for either leg is generally similar across days, though specific points change in a systematic manner.
Fig. 4.
Kinematic analysis of the Multiday group during the early change epoch of adaptation. A: average kinematics in phase plane (top) and treadmill (bottom) space. Phase plane plots average anteroposterior foot position and velocity during early change. Colors represent the exposure number shown in the split-belt schedule block diagram. Solid lines indicate the foot walking on the fast belt while dashed lines indicate the foot walking on the slow belt. Heel strike and toe off locations when the fast leg leads are marked with solid and open squares, respectively. Heel strike and toe off locations when the slow leg leads are marked with solid and open circles, respectively. The treadmill schematic displays the progression of heel strike and toe off position across exposures. Fast heel strike (top row) denotes the portion of the gait cycle when the fast leg leads while slow heel strike (bottom row) denotes the portion of the gait cycle when the slow leg leads. Symbols and colors are consistent with the phase plane. B: summary plots of heel strike (blue lines; mean ± SE) and toe off positions (green lines; mean ± SE) during the early change epoch on each training day. Solid lines/closed points indicate the foot walking on the fast belt while dashed lines/open points indicate the foot walking on the slow belt. Note the change in heel strike and toe off locations during fast heel strike (left), indicating savings is a result of participants learning to take longer steps early on in adaptation when the fast legs leads.
We investigated which portion of the stride contributed to savings over days by investigating whether heel strike or toe off locations correlate with step length asymmetry savings. We found that the fast heel strike and slow toe off locations were most important to savings. This was tested by correlating matrices containing step length asymmetry and heel strike/toe off locations for the early change epoch (strides 6–30) across days. Separate analyses were done for these foot locations when the fast leg led vs. when the slow leg led (Fig. 4A). These locations are displayed schematically in treadmill space in the bottom half of Fig. 4A. Our results indicate that the locations of heel strike and toe off when the fast leg leads significantly correlate with step length asymmetry (r = 0.81, P < 0.001; r = −0.65, P < 0.001, respectively). That is, as participants adapted faster across days, the fast leg stepped further forward (F4,36 = 15.35, P < 0.001) and slow limb trailed further backward (F4,36 = 9.51, P < 0.001; Fig. 4B, left). Conversely, the locations of slow leg heel strike and fast leg toe off did not correlate with step length asymmetry (r = 0.26, P = 0.073; r = 0.05, P = 0.730, respectively) across training days and did not show a progressive change from day to day (Fig. 4B, right). While ANOVA revealed a significant main effect of Exposure on slow limb heel strike location (F4,36 = 3.19, P = 0.024, Fig. 4B, right), this main effect was not a product of a progressive change in slow heel strike location from day to day. This measure did not change systematically with training day, as shown by a nonsignificant within-subjects linear contrast of days (F1,9 = 1.49, P = 0.253). In total, these results demonstrate that savings from one day to the next is due to participants learning to take longer steps when the fast leg leads (via the fast leg stepping farther forward and the slow leg toeing off farther back).
While participants learned to take longer steps when the fast leg led from one day to the next, the velocity profile of their movement for either leg did not change significantly from day to day. ANOVA of maximum swing velocity during the early change epoch of adaptation revealed no significant main effect of Exposure for either the fast leg (F4,36 = 0.56, P = 0.696) or the slow leg (F1.87,16.82 = 2.94, P = 0.083). Because participants learned to take longer steps when the fast leg leads and swung their fast foot at equivalent rates across days, we can conclude that participants learned to spend increasing amounts of time in stance on the slow belt across days. This increased time spent standing on the slow belt allows for the fast leg to extend further out for heel strike and the slow leg to be pulled further back by the treadmill belts before toe off, thus normalizing step length asymmetry.
Effects of training structure on savings.
We next investigated whether compressed training schedules could produce comparable savings to the Multiday group. Participants within the Switch group experienced four short bouts of split-belt adaptation on day 1 and then returned on day 5 to test for savings (Fig. 1C). We also tested a Single Day group to observe whether switch training provided additional benefit over extended training while controlling for the 4 days between training and testing. Participants within the Single Day group experienced extended training on day 1 and then returned on day 5 to test for savings. Note that regardless of the training structure, all participants experienced 30 total minutes of split-belt walking each day.
Figure 5 displays the group mean learning curves for the Switch (Fig. 5A) and Single Day groups (Fig. 5B). Naive performance (i.e., exposure 1) for either group did not differ from day 1 of the Multiday group (adaptation block displayed in Fig. 6A). Our analysis revealed no group differences in naive performance across baseline values (F2,27 = 0.81, P = 0.456), initial perturbation (F2,27 = 1.54, P = 0.233; Fig. 6A, inset), early change step length asymmetry (F2,27 = 0.77, P = 0.473; Fig. 6A, inset), or aftereffect magnitude (F2,27 = 1.58, P = 0.224). Thus, similar to the Multiday group, participants in the Switch and Single Day groups showed typical adaptation behavior on exposure 1; they walked symmetrically when belts were tied at baseline, experienced perturbed asymmetry when the belts were split, reduced their error during the course of the adaptation block, and showed significant aftereffects during the deadaptation block.
Fig. 5.
A: comparison of step length asymmetry across all exposures for the Switch group. Mean curves across participants denote mean ± SE. Baseline (BL; last 50 strides), adaptation (first 300 strides), and deadaptation (first 150 strides) mean curves are shown. Data points following adaptation and deadaptation curves indicate mean plateau values (mean ± SE of last 50 strides) for each block. B: comparison of step length asymmetry across exposures for the Single Day group. C: summary of early change step length asymmetry (mean ± SE of strides 6–30; shaded region in A) across all exposures of the Switch group displayed in orange. Individual participant data are grayed in behind group mean with color indicating exposure number. D: summary of early change step length asymmetry (mean ± SE of strides 6–30; shaded region in B) for the Single Day group. ***Significant difference between early change values with α-level set to 0.05 as determined by repeated-measures ANOVA, corrected for multiple comparisons when appropriate.
Fig. 6.

Effects of training structure on savings over a 5-day span. A: comparison of step length asymmetry on day 1 of training for Multiday, Switch, and Single Day groups. Mean curves during the adaptation block (strides 1–300) are shown. Data points following the curves represent the mean plateau values (last 50 strides) for each group. Inset displays a summary of first stride, initial perturbation (perturb.; mean strides 1–5), early change (mean strides 6–30), and plateau (mean last 50 strides) step length asymmetry across groups. B: comparison of step length asymmetry on day 5 of training for Multiday, Switch, and Single Day groups. Mean curves during the adaptation block (strides 1–300) are shown. Data points following the curves represent the mean plateau values (last 50 strides) for each group. Inset displays a summary of first stride, initial perturbation, early change, and plateau step length asymmetry across groups. C: summary of early change (strides 6–30) step length asymmetry across all exposures for Multiday, Switch, and Single Day groups. Note the difference in savings between groups on day 5 of training. The Switch group attains comparable savings as the Multiday group, despite having a quarter of the training time while both the Switch and Multiday group display greater savings than the Single Day group. ***Significant difference between step length asymmetry values with α-level set to 0.05 as determined by one-way ANOVA, corrected for multiple comparisons.
The Switch and Single Day groups both showed significant savings across subsequent exposures to the split-belt perturbation. Figure 5 displays the group mean of early change step length asymmetry overlaid on individual subject performance across exposures for Switch (Fig. 5C) and Single Day groups (Fig. 5D). Participants within the Switch group showed a significant main effect of Exposure on the early change measure (F2.14,19.22 = 35.99, P < 0.001), indicating that participants learned at a faster rate from one exposure of the split-belt perturbation to the next. Next, a comparison of early change on day 1 to that of day 5 in Single Day revealed less step length asymmetry during early change on day 5 (F1,9 = 38.46, P < 0.001), indicating significant savings following a single day of extended split-belt training.
Next, we were interested in understanding how savings varied across groups on our test day (i.e., day 5). Figure 6B displays day 5 performance during the adaptation block for Multiday, Switch, and Single Day groups. Figure 6C displays how savings evolves across exposures for each group. Our measure of interest was early change step length asymmetry on our test day (i.e., day 5) to observe whether training schedule influenced participants’ ability to save over this time span. A one-way ANOVA comparing step length asymmetry during early change on day 5 for all three groups revealed a significant main effect of Group (F2,27 = 7.27, P = 0.003). Post hoc analysis with Tukey’s HSD correction for multiple comparisons revealed greater savings in the Multiday and Switch groups on day 5 compared with the Single Day group (P = 0.002 and P = 0.050, respectively) while Multiday and Switch experienced similar savings on day 5 of testing (P = 0.422). Notably, this Group effect (F2,27 = 13.78, P > 0.0001) and post hoc comparisons hold for the initial perturbation epoch (strides 1–5) of day 5 adaptation as well (Fig. 6B, inset).
Importantly, all groups were equally perturbed (i.e., day 1 first stride; F2,27 = 0.66, P = 0.523; Fig. 6A, inset) and learned at the same rate when they were naive to the split-belt perturbation (i.e., day 1 early change; F2,27 = 0.77, P = 0.473; Fig. 6A, inset). Additionally, analysis of step length asymmetry during the first stride of day 5 adaptation revealed no difference in performance across conditions (one-way ANOVA; F2,27 = 3.16, P = 0.058; see Fig. 6B inset). Therefore, switch training provides a significant boost in savings over a 5-day span compared with a single day of extended training. Moreover, switch training can result in similar savings to that achieved over 4 consecutive days of training with just a quarter of the training load.
To confirm that the Switch group learned a similar movement pattern over the course of training, we performed a similar kinematic analysis as we did in the Multiday group. That is, we compared the spatial and temporal components of gait (Finley et al. 2015) to ensure the integrity of the movement was maintained across training conditions. Indeed, in day 5 of testing, Multiday and Switch had similar contributions from the spatial (t18 = 0.90, P = 0.381) and temporal (t18 = 0.67, P = 0.510) components to counteract the split-belt treadmill perturbation. Moreover, the proportions of spatial and temporal components toward the step length difference on day 5 were equivalent in both groups (t18 = 0.07, P = 0.946; ~70% spatial, 30% temporal) indicating that the learned movement in Switch shared similar spatiotemporal characteristics to those observed in the Multiday group on day 5 of training.
Time resistance of savings.
We observed similar savings in the Single Day group tested with a 4-day lag compared with that of the Multiday group on day 2 with a 1-day lag (t18 = 0.121, P = 0.905; compare day 5 to day 2 in Fig. 6C). Recall that in both of these groups day 1 training structure was the same 30 min of split-belt walking. This comparison is important because it shows that this training protocol is resistant to time decay over multiple days.
To observe whether the time resistance of savings was sensitive to the structure of training, we studied a new Switch Short group. The Switch Short group experienced four short bouts of split-belt adaptation on day 1 and then returned on day 2 to test savings (Fig. 1C, bottom row). Figure 7A displays the Switch Short adaptation behavior and Fig. 7B shows the early change in step length asymmetry. Similar to previous groups, Switch Short showed a significant main effect of Exposure across five exposures to the split-belt perturbation on step length asymmetry during the early change epoch (F1.77,15.88 = 45.64, P < 0.001; Fig. 7B), indicating increasing savings from one exposure to the next.
Fig. 7.

A: comparison of step length asymmetry across all exposures for the Switch Short group. Mean curves across participants denote mean ± SE. Baseline (BL; last 50 strides), adaptation (first 300 strides), and deadaptation (first 150 strides) mean curves are shown. Data points following adaptation and deadaptation curves indicate mean plateau values (mean ± SE of last 50 strides) for each block. B: summary of early change step length asymmetry (mean ± SE of strides 6–30; shaded region in A) across all exposures of the Switch Short group displayed in dark green. Individual participant data are grayed in behind group mean with color indicating exposure number. ***Significant difference between early change values with α-level set to 0.05 as determined by repeated-measures ANOVA, corrected for multiple comparisons. Inset displays the difference in early change step length asymmetry from exposure 4 to exposure 5, indicating savings following switch training is resistant to decay on this timescale. Note there is no savings lost for either the Switch or Switch Short group. n.s., Nonsignificant difference as determined by mixed-design, repeated-measures ANOVA.
We then compared the fifth exposure in Switch Short (collected on day 2) to the fifth exposure of Switch (collected on day 5) to observe the effects of additional days away from the laboratory on savings following a switch-training protocol (compare Figs. 6 and 7). We found no significant difference in measures of savings between groups (t18 = −1.044, P = 0.310), indicating that savings is also resistant to time decay over multiple days following switch-training on day 1. Analysis of exposure 4 and exposure 5 of Switch Short and Switch via a mixed-design, repeated-measures ANOVA yielded no significant main effects of Exposure (F1,18 = 1.49, P = 0.238) or Group (F1,18 = 1.81, P = 0.195, Fig. 7B, inset) and no Exposure-Group interaction (F1,18 = 0.35, P = 0.562). Additionally, early change differences between exposure 4 and exposure 5 in both Switch Short and Switch were not different from zero (t9 = −0.47, P = 0.649 and t9 = −1.22, P = 0.255, respectively). Our analysis shows both groups saved to a similar extent while the time between training and testing had no effect on the degree of savings we observed on our testing day (i.e., day 2 or day 5). Moreover, negligible savings were lost between training and testing for both groups.
Dual-rate state space model of savings over multiple days.
We used a dual-rate state space model to understand how savings developed in the Multiday group—did savings result from improved retention of what had been learned or faster relearning driven by increased sensitivity to error? We used a dual-rate state space model with time varying parameters similar to that used by Mawase et al. (2014). To observe how the model parameters evolved over subsequent exposures to a split-belt perturbation, we fit the four parameters (Af, Bf, As, Bs) to individual participant symmetry change data for each day of split-belt learning and unlearning within the Multiday group. Conversion of step length asymmetry to symmetry change is displayed in Fig. 8A and detailed in materials and methods. The fast state, which updates based on retention factor Af and learning factor Bf, is characterized by a rapid learning rate and weak retention. The slow state, which updates based on retention factor As and learning factor Bs, is characterized by a slow learning rate and strong retention. Figure 8B summarizes the fitted parameter values across days for the Multiday group.
Fig. 8.
Modeling savings in the Multiday group with a dual-rate state space model (SSM). A: conversion of step length asymmetry to step symmetry change for a representative subject. Individual step length asymmetry data (left) is shifted and normalized by the individual’s maximal asymmetry during the adaptation block on exposure 1 (gold circle). Step symmetry change (right) is a measure where 0 indicates that symmetry is maximally perturbed and 1 (gold dashed line) indicates that symmetry has been restored during adaptation. B: summary of dual-rate parameter values fitted to individual subjects across training days. Af and Bf are the retention and learning factor for the fast process, respectively. As and Bs are the retention and learning factor for the slow process, respectively. Each point represents mean ± SE. C: comparison of model fits of step symmetry change on day 1 (left) and day 5 (right) for adaptation and deadaptation to an abrupt perturbation using the mean parameters shown in B for the respective day. The motor output is calculated as the addition of the fast and slow processes.
Our analysis showed that multiday savings was largely due to increased sensitivity to error in the fast state (i.e., Bf). Specifically, a repeated-measures ANOVA revealed no significant main effects of Exposure on Af (F1.65,14.86 = 2.27, P = 0.144), As (F1.16,10.45 = 1.21, P = 0.307), or Bs (F1.21,10.88 = 4.54, P = 0.051). Meanwhile, ANOVA revealed a significant Exposure effect on Bf (F4,36 = 32.36, P < 0.001). Bf increased from 0.091 ± 0.027 on day 1 to 0.655 ± 0.053 on day 5 (comparison of day 1 to day 5 fits in Fig. 8C). Post hoc analysis on Bf revealed significant pairwise differences between day 1 values and the values of days 2–5 (all P < 0.025). Furthermore, correlational analysis reveals Bf has the strongest correlation (r = 0.70) with early change of step length asymmetry (i.e., our measure of savings) compared with Af, As, and Bs (r = −0.09, 0.07, and 0.37, respectively). These results suggest that the increase in Bf values can best explain the observed savings in the symmetry change data.
DISCUSSION
Learning a new movement pattern requires practice. For practice to be useful, it is crucial that we are able to remember what we learned from previous sessions. Whether learning a new golf swing or improving a dysfunctional gait pattern, training can be laborious and presents a significant time and often financial burden. As such, coaches and clinicians often focus on how to get the greatest improvement in performance in the least amount of time. Here, we investigated how to manipulate the delivery of training of a novel walking pattern to increase the time efficiency of training.
We demonstrated that participants could learn a novel walking pattern over the course of 5 days such that they have minimal error when transitioning from novel (i.e., split-belt) to natural (i.e., tied-belt) environments. Participants achieved this level of learning via day-to-day savings such that they learned to counter the novel environment more rapidly across exposures. We also showed that we could induce similar savings by compressing a four day training regimen into a 1 day intervention with four abbreviated training exposures delivered in succession. Specifically, our Switch group displayed equivalent savings as our Multiday group despite having one quarter of the training time.
Multiday savings.
This study aimed to determine how much savings could be induced during 5 consecutive days of split-belt training and what aspects of the motor pattern were being saved. Few studies have looked at multisession savings of an adapted movement and most have focused on arm movements using visuomotor tasks (Martin et al. 1996; Ruitenberg et al. 2017; Seidler et al. 2017). Additionally, studies of savings during split-belt walking have been largely limited to just two exposures to the training environment (Mawase et al. 2014, 2016; Roemmich and Bastian 2015). We were interested in how savings of a new walking pattern emerges on a longer timescale as split-belt training has proven to produce clinically meaningful improvements in pathological gait (Reisman et al. 2013). Interestingly, these lasting improvements were only observed following repeated practice (Reisman et al. 2013) whereas effects following just one session of training quickly diminished (Reisman et al. 2007). Thus, a full understanding of the timescale of this learned pattern over repeated training sessions is needed to inform the most efficient and effective training of a novel walking pattern.
Our participants were able to save a substantial portion (~85%; Fig. 2B) of the split-belt adaptation task by day 5 of training. Our analysis revealed that these savings accrued over days due to participants’ ability to change both spatial (i.e., where they step) and temporal (i.e., when they step) elements of their gait pattern early on in the adaptation blocks. Globally, this allowed participants to more quickly increase the length of their steps when the fast leg led to counter the perturbation (i.e., step farther forward with the fast leg and trail farther back with the slow leg). These behavioral changes upon reexposure reflect the nervous system’s ability to retrieve a motor memory and adopt a set of kinematics best suited for a given environment.
From a clinical point of view, it is encouraging that people save both the spatial and temporal features of walking. Paretic gait in persons poststroke has shown to be patient specific, resulting from either deficits in spatial control, temporal control, or a combination of both (Finley et al. 2015; Malone and Bastian 2014). Thus, the current work demonstrating that healthy individuals save both features bodes well for the possibility that stroke patients can do the same. It is important that the utility of multiday split-belt treadmill training is not limited to a subset of patients but has the potential to address all sources of paretic gait, regardless of whether the deficits are spatial or temporal.
Recent studies of reaching adaptation have suggested that savings is linked to conscious or strategic planning because it is abolished when preparation time is limited (Haith et al. 2015) and because savings can be accounted for by engaging an aiming strategy upon reexposure (Morehead et al. 2015). Such findings are difficult to compare with savings in locomotor tasks because walking is a more automatic process and may not be as explicitly accessible as reaching. For example, we recently reported that the walking adaptation process is unaffected by explicit error correction (Roemmich et al. 2016). Specifically, when subjects were given visual feedback of their stepping error, they could rapidly correct it. However, this correction was lost as soon as the feedback was removed and adaptation proceeded unaffected (Roemmich et al. 2016). Thus, our interpretation is that locomotor adaptation operates in parallel to a more conscious correction process. Feedback of stepping error during adaptation also does not affect savings on a subsequent exposure to the split-belt perturbation (Leech KA and Roemmich RT, unpublished observations). Furthermore, the current work demonstrates that savings of locomotor adaptation involves savings of temporal features of gait, which have previously been shown to be resistant to cognitive manipulations (Malone and Bastian 2010). We therefore speculate that locomotor savings is less reliant on conscious or strategic processes compared with savings in reaching.
Improving the time efficiency of training.
Our results indicate that we are able to shape the perturbation schedule to more efficiently train a novel walking pattern. By compressing training to four abbreviated bouts of adaptation, we induced similar savings to a training schedule consisting of 4 consecutive days of extended adaptation. Furthermore, 1 day of switch training produced more savings than 1 day of extended training. Two factors have been previously shown to influence savings in locomotor tasks: 1) abrupt exposures to the adaptive environment and 2) time spent in the adapted state (Roemmich and Bastian 2015). Here, we demonstrate that we can leverage these two factors to create a balance in our delivery of the perturbation that will more efficiently train the movement. That is, by maintaining the amount of abrupt exposures (i.e., four blocks) but reducing the total amount of time (i.e., reducing from four 30-min blocks to four 7.5-min blocks), we did not lose any training effects when testing on day 5, despite the reduced training time and the extended period between training and testing.
These results highlight the importance of early adaptation trials—and accompanying large errors—to the formation of a motor memory. Savings has been observed in both reaching and locomotor adaptation tasks as long as participants reach asymptotic performance during initial exposure (Huberdeau et al. 2015; Roemmich and Bastian 2015). Thus, experiencing a high frequency of these early adaptation trials (as did the Switch group) may strengthen the motor memory for subsequent exposures (Malone et al. 2011). Although we wanted to control for the within-session time participants spend on split belts (i.e., 30 min), it is feasible that with a higher frequency of switching in environments we could reduce this within-session time and make training even more efficient. We anticipate, however, that decreasing the amount of time within a single adaptation block will eventually have diminishing or even counterproductive effects. Previous work suggests that repetition of the adapted movement at plateau is necessary for maximum savings (Huang et al. 2011; Roemmich and Bastian 2015). Future work should aim at further characterizing this point of diminishing return.
It should be noted that savings during this locomotor task could be due to a combination of an immediate improvement in step symmetry within the first stride and a faster rate of improvement over subsequent strides. The present study reveals a trending difference (P = 0.058) in first stride performance across training conditions. Considering that all training conditions were fully washed out before adaptation, this appears to be different than what is seen during reaching adaptation studies, where there is no immediate improvement in the first reach following a period of washout (Herzfeld et al. 2014; Huang et al. 2011; Morehead et al. 2015; Orban de Xivry and Lefèvre 2015). We have reported this first stride phenomenon in several previous studies of split-belt walking (Leech et al. 2018; Malone et al. 2011; Roemmich and Bastian 2015), which differs from reaching tasks. Specifically, measurement of error during walking (i.e., step length asymmetry) is an interlimb measure that is collected stride-by-stride whereas the error in reaching (i.e., angular error) is a discrete measure observed following a relatively ballistic movement. As such, participants have a full walking stride (lasting ~1 s) to make online corrections in their movements to counter the perturbation. We speculate that this observed (albeit trending) reduction in initial error could be a product of online feedback within the first stride and that we can assume that participants are equally perturbed across exposures and training conditions. Only during the initial perturbation epoch (strides 1–5) is a statistically significant difference realized across training conditions (Fig. 6B, inset). Thus, while our training effect is largely driven by a faster stride-to-stride learning, it is possible that the training effects are twofold: faster online correction within a stride accompanied by a faster stride-to-stride adaptation.
Alternatively, participants may be more effectively responding to the abrupt nature of the split-belt perturbation across exposures. Studies of slip-perturbations in walking have shown that repeated slip-perturbation training shifts the stability response from a reactive (i.e., feedback) to a proactive (i.e., feedforward) control of center of mass (Lee et al. 2016; Pai and Bhatt 2007; Wang et al. 2011; Yang et al. 2013). Additionally, the training structure of the repeated slip-perturbation can alter the degree to which participants retain their slip response (Bhatt et al. 2012; Pai et al. 2010). Thus, it is possible that participants in the present study are proactively shifting their center of mass as they become more familiar with the adaptation environment across exposures, resulting in less asymmetry during the first stride. Future work is needed to dissect the balance of feedforward/feedback control within the first stride of split-belt adaptation and the effect of multiple exposures on this response.
Dual-rate state space model of multiday savings.
Recent results suggest that motor adaptation, in both locomotion and reaching, is a result of multiple learning processes operating on differing timescales to reduce error (Herzfeld et al. 2014; Malone et al. 2011, Mawase et al. 2014; Roemmich and Bastian 2015; Smith et al. 2006). Savings represents our ability to form long-term motor memories of a previously experienced environment (Shadmehr and Brashers-Krug 1997) and has been explained computationally as a change in learning parameters following initial exposure (Mawase et al. 2014). Savings within a dual-rate SSM framework was thought to be the result of a residual slow state that has been retained from previous exposure (Smith et al. 2006). Savings over multiple days, however, cannot be explained by such a mechanism (Zarahn et al. 2008). Thus, if we model the multiday savings as a change in learning parameters across days, a change in the learning rate of the fast process best explains the data. It is also worth noting that the learning rate of the slow process trended toward changing across days (P = 0.051). Thus, prior exposure to the perturbation may change how we respond to error on a trial-by-trial basis on subsequent exposures (Herzfeld et al. 2014; Orban de Xivry and Lefèvre 2015; Roemmich and Bastian 2015). Moreover, our behavioral results indicate that these changes in our nervous system’s ability to respond to error on subsequent exposures may be insensitive to time decay (e.g., compare Multiday group day 2 vs. Single Day group day 5), perhaps due to maintenance of increased learning rates. Indeed, the ability to save a locomotor task has been reported to be maintained over 2 mo later (Ruitenberg et al. 2017), although participants were not washed out within-session in this prior work. This time invariance suggests that savings is not a result of a residual hidden state that is governed by an invariant retention factor but rather a change in the updating rules that lasts for days and perhaps weeks following initial exposure.
Conclusion.
We think these results have important implications for adaptive learning in rehabilitation. By using switch training on day 1 of testing, we were able to achieve equivalent learning to 4 consecutive days of extended training, thereby reducing the training time and sessions. Across many forms of learning (adaptation included), therapeutic approaches for gait rehabilitation often focus on the amount of training as the manipulable factor for achieving improved rehabilitation outcomes, particularly in persons poststroke (Kwakkel et al. 2004; Van Peppen et al. 2004; Lohse et al. 2014). Specifically, we contend that how adaptive training is delivered is of equal or possibly even greater importance than the amount of practice. The nervous system’s ability to differentially respond to different parts of adaptive training (i.e., early training vs. asymptotic performance) can allow us to tailor training regimes that can produce the most efficient and effective learning. Ultimately, we aim to apply these findings to inform training schedules for the rehabilitation of gait disorders so that we may achieve the desired rehabilitation outcome and maximize training efficiency.
GRANTS
This work was supported by NIH grant R37 NS103356 to A. J. Bastian and K. A. Day, 5 T32 HD007414 23 to K. A. Leech, and F32 NS090751 to R. T. Roemmich.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
K.A.D., K.A.L., R.T.R., and A.J.B. conceived and designed research; K.A.D. and K.A.L. performed experiments; K.A.D. analyzed data; K.A.D., K.A.L., R.T.R., and A.J.B. interpreted results of experiments; K.A.D. prepared figures; K.A.D. drafted manuscript; K.A.D., K.A.L., R.T.R., and A.J.B. edited and revised manuscript; K.A.D., K.A.L., R.T.R., and A.J.B. approved final version of manuscript.
REFERENCES
- Bhatt T, Yang F, Pai YC. Learning to resist gait-slip falls: long-term retention in community-dwelling older adults. Arch Phys Med Rehabil 93: 557–564, 2012. doi: 10.1016/j.apmr.2011.10.027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finley JM, Long A, Bastian AJ, Torres-Oviedo G. Spatial and temporal control contribute to step length asymmetry during split-belt adaptation and hemiparetic gait. Neurorehabil Neural Repair 29: 786–795, 2015. doi: 10.1177/1545968314567149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haith AM, Huberdeau DM, Krakauer JW. The influence of movement preparation time on the expression of visuomotor learning and savings. J Neurosci 35: 5109–5117, 2015. doi: 10.1523/JNEUROSCI.3869-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herzfeld DJ, Vaswani PA, Marko MK, Shadmehr R. A memory of errors in sensorimotor learning. Science 345: 1349–1353, 2014. doi: 10.1126/science.1253138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang VS, Haith A, Mazzoni P, Krakauer JW. Rethinking motor learning and savings in adaptation paradigms: model-free memory for successful actions combines with internal models. Neuron 70: 787–801, 2011. doi: 10.1016/j.neuron.2011.04.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huberdeau DM, Haith AM, Krakauer JW. Formation of a long-term memory for visuomotor adaptation following only a few trials of practice. J Neurophysiol 114: 969–977, 2015. doi: 10.1152/jn.00369.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwakkel G, van Peppen R, Wagenaar RC, Wood Dauphinee S, Richards C, Ashburn A, Miller K, Lincoln N, Partridge C, Wellwood I, Langhorne P. Effects of augmented exercise therapy time after stroke: a meta-analysis. Stroke 35: 2529–2539, 2004. doi: 10.1161/01.STR.0000143153.76460.7d. [DOI] [PubMed] [Google Scholar]
- Lee A, Bhatt T, Pai YC. Generalization of treadmill perturbation to overground slip during gait: effect of different perturbation distances on slip recovery. J Biomech 49: 149–154, 2016. doi: 10.1016/j.jbiomech.2015.11.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leech KA, Roemmich RT, Bastian AJ. Creating flexible motor memories in human walking. Sci Rep 8: 94, 2018. doi: 10.1038/s41598-017-18538-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lohse KR, Lang CE, Boyd LA. Is more better? Using metadata to explore dose-response relationships in stroke rehabilitation. Stroke 45: 2053–2058, 2014. doi: 10.1161/STROKEAHA.114.004695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malone LA, Bastian AJ. Thinking about walking: effects of conscious correction versus distraction on locomotor adaptation. J Neurophysiol 103: 1954–1962, 2010. doi: 10.1152/jn.00832.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malone LA, Bastian AJ. Spatial and temporal asymmetries in gait predict split-belt adaptation behavior in stroke. Neurorehabil Neural Repair 28: 230–240, 2014. doi: 10.1177/1545968313505912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malone LA, Bastian AJ, Torres-Oviedo G. How does the motor system correct for errors in time and space during locomotor adaptation? J Neurophysiol 108: 672–683, 2012. doi: 10.1152/jn.00391.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malone LA, Vasudevan EV, Bastian AJ. Motor adaptation training for faster relearning. J Neurosci 31: 15136–15143, 2011. doi: 10.1523/JNEUROSCI.1367-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin TA, Keating JG, Goodkin HP, Bastian AJ, Thach WT. Throwing while looking through prisms. II. Specificity and storage of multiple gaze-throw calibrations. Brain 119: 1199–1211, 1996. doi: 10.1093/brain/119.4.1199. [DOI] [PubMed] [Google Scholar]
- Mawase F, Bar-Haim S, Joubran K, Rubin L, Karniel A, Shmuelof L. Increased adaptation rates and reduction in trial-by-trial variability in subjects with cerebral palsy following a multi-session locomotor adaptation training. Front Hum Neurosci 10: 203, 2016. doi: 10.3389/fnhum.2016.00203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mawase F, Shmuelof L, Bar-Haim S, Karniel A. Savings in locomotor adaptation explained by changes in learning parameters following initial adaptation. J Neurophysiol 111: 1444–1454, 2014. doi: 10.1152/jn.00734.2013. [DOI] [PubMed] [Google Scholar]
- Mazzoni P, Krakauer JW. An implicit plan overrides an explicit strategy during visuomotor adaptation. J Neurosci 26: 3642–3645, 2006. doi: 10.1523/JNEUROSCI.5317-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morehead JR, Qasim SE, Crossley MJ, Ivry R. Savings upon re-aiming in visuomotor adaptation. J Neurosci 35: 14386–14396, 2015. doi: 10.1523/JNEUROSCI.1046-15.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orban de Xivry JJ, Lefèvre P. Formation of model-free motor memories during motor adaptation depends on perturbation schedule. J Neurophysiol 113: 2733–2741, 2015. doi: 10.1152/jn.00673.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pai YC, Bhatt T, Wang E, Espy D, Pavol MJ. Inoculation against falls: rapid adaptation by young and older adults to slips during daily activities. Arch Phys Med Rehabil 91: 452–459, 2010. doi: 10.1016/j.apmr.2009.10.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pai YC, Bhatt TS. Repeated-slip training: an emerging paradigm for prevention of slip-related falls among older adults. Phys Ther 87: 1478–1491, 2007. doi: 10.2522/ptj.20060326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reisman DS, Block HJ, Bastian AJ. Interlimb coordination during locomotion: what can be adapted and stored? J Neurophysiol 94: 2403–2415, 2005. doi: 10.1152/jn.00089.2005. [DOI] [PubMed] [Google Scholar]
- Reisman DS, McLean H, Keller J, Danks KA, Bastian AJ. Repeated split-belt treadmill training improves poststroke step length asymmetry. Neurorehabil Neural Repair 27: 460–468, 2013. doi: 10.1177/1545968312474118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reisman DS, Wityk R, Silver K, Bastian AJ. Locomotor adaptation on a split-belt treadmill can improve walking symmetry post-stroke. Brain 130: 1861–1872, 2007. doi: 10.1093/brain/awm035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roemmich RT, Bastian AJ. Two ways to save a newly learned motor pattern. J Neurophysiol 113: 3519–3530, 2015. doi: 10.1152/jn.00965.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roemmich RT, Long AW, Bastian AJ. Seeing the errors you feel enhances locomotor performance but not learning. Curr Biol 26: 2707–2716, 2016. doi: 10.1016/j.cub.2016.08.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruitenberg MFL, De Dios YE, Gadd NE, Wood SJ, Reuter-Lorenz PA, Kofman I, Bloomberg JJ, Mulavara AP, Seidler RD. Multi-day adaptation and savings in manual and locomotor tasks. J Mot Behav 1–11, 2017. doi: 10.1080/00222895.2017.1371110. [DOI] [PubMed] [Google Scholar]
- Seidler RD, Gluskin BS, Greeley B. Right prefrontal cortex transcranial direct current stimulation enhances multi-day savings in sensorimotor adaptation. J Neurophysiol 117: 429–435, 2017. doi: 10.1152/jn.00563.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadmehr R, Brashers-Krug T. Functional stages in the formation of human long-term motor memory. J Neurosci 17: 409–419, 1997. doi: 10.1523/JNEUROSCI.17-01-00409.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadmehr R, Mussa-Ivaldi FA. Adaptive representation of dynamics during learning of a motor task. J Neurosci 14: 3208–3224, 1994. doi: 10.1523/JNEUROSCI.14-05-03208.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith MA, Ghazizadeh A, Shadmehr R. Interacting adaptive processes with different timescales underlie short-term motor learning. PLoS Biol 4: e179, 2006. doi: 10.1371/journal.pbio.0040179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tseng YW, Diedrichsen J, Krakauer JW, Shadmehr R, Bastian AJ. Sensory prediction errors drive cerebellum-dependent adaptation of reaching. J Neurophysiol 98: 54–62, 2007. doi: 10.1152/jn.00266.2007. [DOI] [PubMed] [Google Scholar]
- Van Peppen RP, Kwakkel G, Wood-Dauphinee S, Hendriks HJ, Van der Wees PJ, Dekker J. The impact of physical therapy on functional outcomes after stroke: what’s the evidence? Clin Rehabil 18: 833–862, 2004. doi: 10.1191/0269215504cr843oa. [DOI] [PubMed] [Google Scholar]
- Wang TY, Bhatt T, Yang F, Pai YC. Generalization of motor adaptation to repeated-slip perturbation across tasks. Neuroscience 180: 85–95, 2011. doi: 10.1016/j.neuroscience.2011.02.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang F, Bhatt T, Pai YC. Generalization of treadmill-slip training to prevent a fall following a sudden (novel) slip in over-ground walking. J Biomech 46: 63–69, 2013. doi: 10.1016/j.jbiomech.2012.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zarahn E, Weston GD, Liang J, Mazzoni P, Krakauer JW. Explaining savings for visuomotor adaptation: linear time-invariant state-space models are not sufficient. J Neurophysiol 100: 2537–2548, 2008. doi: 10.1152/jn.90529.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]