Photoacoustic tomography of blood oxygenation: A mini review

Abstract

Photoacoustic tomography (PAT) is a hybrid imaging modality that combines rich contrast of optical excitation and deep penetration of ultrasound detection. With its unique optical absorption contrast mechanism, PAT is inherently sensitive to the functional and molecular information of biological tissues, and thus has been widely used in preclinical and clinical studies. Among many functional capabilities of PAT, measuring blood oxygenation is arguably one of the most important applications, and has been widely performed in photoacoustic studies of brain functions, tumor hypoxia, wound healing, and cancer therapy. Yet, the complex optical conditions of biological tissues, especially the strong wavelength-dependent optical attenuation, have long hurdled the PAT measurement of blood oxygenation at depths beyond a few millimeters. A variety of PAT methods have been developed to improve the accuracy of blood oxygenation measurement, using novel laser illumination schemes, oxygen-sensitive fluorescent dyes, comprehensive mathematic models, or prior information provided by complementary imaging modalities. These novel methods have made exciting progress, while several challenges remain. This concise review aims to introduce the recent developments in photoacoustic blood oxygenation measurement, compare each method’s advantages and limitations, highlight their representative applications, and discuss the remaining challenges for future advances.

1. Introduction

Photoacoustic (PA) Tomography (PAT), also referred to as optoacoustic tomography, is a hybrid imaging modality that combines optical contrast and ultrasound image formation. In PAT, the target is illuminated by a short laser pulse and the absorbed photon energy is converted into heat, leading to a transient local temperature rise. The temperature rise induces a thermal-elastic expansion that generates a local pressure rise and emits acoustic waves. Therefore, PAT detects the acoustic signals generated by optical absorption from either endogenous chromophores (e.g., oxygenated (${\mathrm{H}\mathrm{b}\mathrm{O}}_2$) and deoxygenated hemoglobin ($\mathrm{H}\mathrm{b}\mathrm{R}$)), or exogenous contrast agents (e.g., nanoparticles and organic dyes) [1,2]. As acoustic waves are much less scattered in tissue than photons, PAT can generate high-resolution images in both the optical ballistic and diffusive regimes. Two major implementations of PAT exist: photoacoustic computed tomography (PACT) and photoacoustic microscopy (PAM) [[1], [2], [3], [4], [5]]. PACT reconstructs the image in the diffusive regime with wide-field illumination and acoustic detection at multiple locations using a transducer array. PAM images targets in the quasi-ballistic and quasi-diffusive regime with focused excitation light and/or a focused single-element ultrasonic transducer for direct image formation [1,6].

The wide choices of contrast agents allow PAT to play an increasingly important role in both preclinical research and clinical practice with its applications in vascular biology [[7], [8], [9]], oncology [[10], [11], [12]], neurology [[13], [14], [15]], ophthalmology [[16], [17], [18]], dermatology [[19], [20], [21]], gastroenterology [22,23], and cardiology [24,25]. Among all the endogenous chromophores, hemoglobin is one of the major absorbers at wavelengths below 1000 nm. Using HbO₂ and HbR, PAT can image vascular structure, oxygen saturation of hemoglobin (sO₂) [26], blood flow speed [27], and metabolic rate of oxygen [28]. sO₂, or blood oxygenation, is defined as the fraction of HbO₂ relative to total hemoglobin concentration in blood. At wavelengths between 650 nm and 900 nm, both HbR and HbO₂ have an optical absorption coefficient that is at least one magnitude larger than those of other chromophores such as lipids and water at physiologically realistic concentrations (Fig. 1) [29,30]. Although within this wavelength range melanin has a higher absorption coefficient than HbR and HbO₂, it is highly localized in the skin or retina and thus does not contribute to the oxygenation quantification. Such strong preferential absorption of HbO₂ and HbR allows high-contrast visualization of the blood-perfused vasculature in PAT images [31].

Fig. 1.

Absorption coefficient spectra of endogenous tissue chromophores. HbO₂ and HbR, 150 g/L in blood; Water, 80% by volume in tissue; Lipid, 20% by volume in tissue; Melanin, 14.3 g/L in medium human skin. Figure adapted with permission from [30].

The measurement of oxygen saturation of hemoglobin (sO₂) is no doubt one of the most important applications of PAT. Normal oxygenation levels range between 95%–100% in the arteries and 60% to 80% in the veins [32]. In many cases, disease processes alter the balance of oxygen delivery and consumption and change the blood oxygenation level and oxygen distribution [33]. For example, a fast-growing tumor has a high oxygen consumption rate, leading to new blood vessel development (angiogenesis) but an overall low oxygenation level (hypoxia) in the core region. The irregular blood perfusion network (torturous vascular path, interrupted blood flow, and leaky vessel wall) in the tumor results in limited oxygen supply to the tissue and elevated oxygen extraction, which in turn reduces the overall blood oxygenation in the tumor region. As a result, sO₂ plays an important role in tumor progression, and a large region of hypoxic core typically indicates a poor prognosis. By using fluence-compensated PA measurements at multiple wavelengths, the concentrations of oxygenated (${\mathrm{C}}_{{\mathrm{H}\mathrm{b}\mathrm{O}}_2}$) and deoxygenated hemoglobin (${\mathrm{C}}_{\mathrm{H}\mathrm{b}\mathrm{R}}$) can be mathematically estimated, from which the total hemoglobin concentration (HbT) and sO₂ can be computed [1]. PA imaging of sO₂ is expected to help improve cancer screening, cancer diagnosis, and therapy monitoring [1]. Moreover, the brain is highly sensitive to the changes in blood flow and oxygenation, as continuous oxygen delivery and CO₂ clearance are paramount in maintaining normal brain functions. Monitoring sO₂ inside the brain using PAT is of great interest in neurophysiology, neuropathology, and neurotherapy [34,35].

Compared to other blood oxygenation imaging modalities, PAT has the following merits: (1) Compared to functional magnetic resonance imaging (fMRI), PAT allows noninvasive in vivo oxygenation imaging at high spatial-temporal resolutions with a relatively low cost [36,37]. (2) Compared to positron emission tomography (PET), PAT uses nonionizing laser illumination and provides a much higher spatial resolution. (3) Compared to other high-resolution optical imaging methods, PAT can reach much deeper into tissue while maintains a reasonably high resolution [38]. These advantages readily make PAT a powerful fit-in-line tool for blood oxygenation measurement.

Nevertheless, PAT still faces certain challenges in measuring blood oxygenation in deep tissue beyond the optical diffusion limit (∼1 mm in soft tissue). Since PAT’s acoustic signal amplitude is proportional to the local optical absorption, the wavelength-dependent optical attenuation limits the ultimate imaging depth and confounds the spectral unmixing of HbO₂ and HbR. Measuring local optical fluence is a longstanding challenge faced by quantitative PAT, and several methods were proposed to solve this problem. For example, Guo et al. used the acoustic spectra of PA signals to quantify the absolute optical absorption and thus the blood oxygenation level [39]. Kirchner et al. utilized machine learning to deduce the corresponding optical absorption [40]. Xia et al. monitored sO₂ transition with multiple wavelength measurements to cancel out the contribution of optical fluence [41]. Tzoumas et al. demonstrated improved blood oxygenation measurement by modeling several fundamental optical absorption spectra (eigenspectra) in the tissue, with the consideration of unknown optical fluence [42]. Daoudi et al. showed the feasibility of compensating for optical fluence by acoustically tagging photons in deep tissue [43]. In this concise review, we introduce the principles of and recent advances in PAT of blood oxygenation. The advantages and disadvantages of different methods are compared, with representative applications. We also opine the current technical challenges of PAT of blood oxygenation, which point to further potential breakthroughs.

2. The progress in PAT of blood oxygenation

Fundamentally, quantifying blood oxygenation requires measurement of the PA absorption spectra of the blood. By extracting key parameters such as peak amplitudes (maximum signal strength of the received RF signal) from the detected signal at multiple wavelengths, photoacoustic spectra of the blood can be determined. Given the known molar absorption coefficients of HbR and HbO₂, ${\mathrm{C}}_{{\mathrm{H}\mathrm{b}\mathrm{O}}_2}$ and ${\mathrm{C}}_{\mathrm{H}\mathrm{b}\mathrm{R}}$ can be recovered from the measured photoacoustic spectra using different methods, which will be discussed in the following sections and summarized in Table 1. Then, sO₂ can be calculated as [44]:

$$s{O}_2\left(x,y\right)=\frac{C_{Hb{O}_2}\left(x,y\right)}{C_{Hb{O}_2}\left(x,y\right)+C_{HbR}\left(x,y\right)}\times 100\%,$$ (1)

where x and y denote the spatial coordination.

Table 1.

Summary of different methods in photoacoustic measurement of blood oxygenation.

Method	Principle	Demonstrated depth	Main advantages	Shortcomings
Linear model [10,44,45]	The PA signals at multiple wavelengths are directly used for linear unmixing HbO2 and HbR, without compensating the local fluence.	∼0.7 mm	Mathematically simple and easy to implement on most PAT systems.	Assuming the wavelength-independent optical fluence, the model is inaccurate at depths beyond 1 mm.
Optical transport model based method [45,46,47]	Forward optical transport models based on Beer’s law or diffusion finite-element method were used to estimate optical fluence distribution in tissue.	10 mm	Considering wavelength-dependent optical attenuation, these models are more accurate than the linear model at large depths.	The tissue structure is oversimplified to be adapted for complex tissue types such as the brain and tumor.
Acoustic spectrum based model [39,48]	The acoustic frequency spectrum of the received PA signals at different wavelengths are extracted to quantify the absolute absorption coefficient based on Beer’s law.	1.6 mm	Self-calibrated and less sensitive to the wavelength-dependent local optical fluence.	The assumption of flat blood vessel surface is not valid for vessels that are not much larger than the resolution.
Diffuse optical tomography (DOT) enhanced method [49,50]	The tissue’s optical properties and local optical fluence are estimated using DOT to correct the optical fluence inhomogeneity in the PAT measurement.	12 mm	DOT is highly compatible with PAT. The optical fluence at large depths can be compensated.	DOT is a low-resolution imaging modality, and optical fluence compensation lacks the spatial accuracy.
Statistical model for unmixing chromophores [51,52]	The number of major absorbers in the tissue is blindly estimated using statistical methods, such as singular value analysis.	Not mentioned	No requirement for the knowledge of local optical fluence and less sensitive to noise.	This method is mostly used to identify the number of absorbers instead of calculating the concentrations of HbR and HbO2.
Fluorescence lifetime based pO2 measurement [33,53,54,55]	Oxygen-sensitive fluorescent dye is excited by a pump laser and its excitation-state lifetime is measured by a probe PA method, which has a linear dependence on the local oxygen partial pressure.	∼12 mm	Capable of suppressing the background signals from hemoglobin, and less sensitive to the local optical fluence.	This method is slow. Repeated pump-probe excitation also induces photobleaching and changes in the molecular environment.
The absorption-saturation based sO2 measurement [56,57]	This method explores the difference in the non-radiative absorption lifetime between HbO2 and HbR, and quantifies their relative concentrations based on the absorption saturation at a single wavelength.	0.5 mm at 532 nm in vivo	Fast and less affected by the wavelength-dependent optical attenuation by using single wavelength.	The imaging depth is limited by optical attenuation to the point where absorption saturation becomes insufficient.
Eigenspectral multispectral fluence model [42]	Eigenspectra are identified using training datasets of known tissue components. Any fluence spectrum can then be predicted by combining these eigenspectra.	10 mm	Capable of estimating the local optical fluence and has shown a higher accuracy for targets at depths.	The method’s performance is likely affected by the complexity of the tissue compositions, which requires a large pool of training datasets for different disease models.

2.1. Linear-model-based sO2 measurement

The most commonly employed method of sO₂ measurement is the linear spectral fitting, such as the least square method (LLS) [10,44,45].

$$P({\lambda }_i,x,y)=\Phi \left(\lambda \right)\left({\epsilon }_{HbR}\left({\lambda }_i\right)C_{HbR}\left(x,y\right)+{\epsilon }_{Hb{O}_2}\left({\lambda }_i\right)C_{Hb{O}_2}\left(x,y\right)\right)$$ (2)

Here Φ(λ) is local optical fluence, $\mathrm{P}({\mathrm{\lambda }}_{\mathrm{i}},\mathrm{x},\mathrm{y})$ is the reconstructed PA image at a specific wavelength ${\mathrm{\lambda }}_{\mathrm{i}}$, ${\mathrm{\epsilon }}_{\mathrm{H}\mathrm{b}\mathrm{R}}({\mathrm{\lambda }}_{\mathrm{i}})$ and ${\mathrm{\epsilon }}_{{\mathrm{H}\mathrm{b}\mathrm{O}}_2}({\mathrm{\lambda }}_{\mathrm{i}})$ are the known molar extinction coefficients (cm⁻¹M⁻¹) of HbR and HbO₂ at wavelength ${\mathrm{\lambda }}_{\mathrm{i}}$, respectively. $\mathrm{\hspace{0.17em}}{\mathrm{C}}_{{\mathrm{H}\mathrm{b}\mathrm{O}}_2}\left(\mathrm{x},\mathrm{y}\right)$ and ${\mathrm{C}}_{\mathrm{H}\mathrm{b}\mathrm{R}}\left(\mathrm{x},\mathrm{y}\right)$ are the molar concentrations of HbR and HbO₂, respectively. After optical fluence normalization, by employing multiple wavelengths, ${\mathrm{C}}_{{\mathrm{H}\mathrm{b}\mathrm{O}}_2}\left(\mathrm{x},\mathrm{y}\right)$ and ${\mathrm{C}}_{\mathrm{H}\mathrm{b}\mathrm{R}}(\mathrm{x},\mathrm{y})$ can be estimated by solving the following linear equations [10]:

$$\left[\begin{array}{l}{C}_{HbR}\left(x,y\right)\\ C_{Hb{O}_2}\left(x,y\right)\end{array}\right]={\left({\epsilon }^T\epsilon \right)}^{-1}{\epsilon }^{T}P,$$ (3)

in which

$$P=\left[\begin{array}{c}\hfill P\left({\lambda }_1,x,y\right)\hfill \\ \hfill P\left({\lambda }_2,x,y\right)\hfill \end{array}\right]$$

is the PA measurement matrix at two wavelengths, and

$$\epsilon =\left[\begin{array}{cc}\hfill {\epsilon }_{HbR}\left({\lambda }_1\right)\hfill & \hfill {\epsilon }_{Hb{O}_2}\left({\lambda }_1\right)\hfill \\ \hfill {\epsilon }_{HbR}\left({\lambda }_2\right)\hfill & \hfill {\epsilon }_{Hb{O}_2}\left({\lambda }_2\right)\hfill \end{array}\right]$$

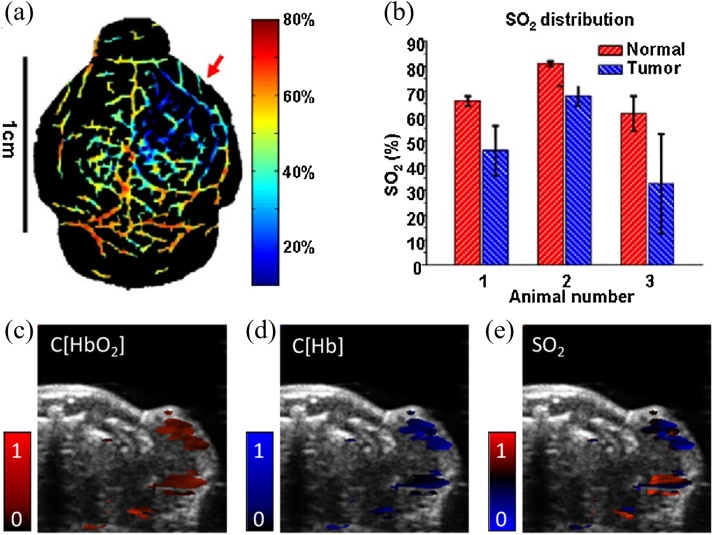
is the molar extinction coefficient matrix. Fig. 2(a) shows one example of sO₂ map of the mouse brain vasculature using LLS, in which different colors represent different oxygenation levels in the blood vessels [10,46]. Fig. 2(b) shows the sO₂ distribution in normal and tumor blood vessels.

Fig. 2.

PAT of blood oxygenation using a linear-model. (a) sO₂ image of a mouse brain acquired by using LLS spectral fitting. (b) Comparison of sO₂ in normal and tumor blood vessels. (c–e) HbO₂, HbR and sO₂ maps using a 2D skin-tissue layer model and minimum mean square error method. Figures adapted with permissions from [10,46].

However, the working assumption of the linear model is that the local optical fluence is the same at different wavelengths after normalization of incident light energy. Yet in biological tissue, the local optical fluence is easily affected by multiple factors such as optical properties of the tissue, light delivery pattern and the optical wavelength [46]. All these factors can induce substantial inaccuracy in oxygenation measurement, especially for targets in deep tissues, where the optical attenuation heavily depends on the optical wavelength. Therefore, this method can work most accurately only on PAT systems with superficial penetration depths [28,58,59].

2.2. Optical transport model based method

An upgraded linear spectral fitting method is to employ Beer’s law to calculate the local optical fluence [46]. A few steps are implemented. The imaged tissue is first segmented into skin and background tissue, which have different optical scattering coefficients. The skin thickness can then be determined from the concurrent ultrasound imaging. After segmentation, the optical fluence is estimated using a 2D skin-tissue layer model based on Beer’s law:

$$F\left(\lambda ,r\right)=F_0\left(\lambda \right)e^{-{\mu }_{eff}\left(\lambda ,r\right)\left|r\right|}$$ (4)

where F₀ is the incident optical fluence (mJ/cm²), |r| is the distance between skin surface and location of interest, and ${\mu }_{eff}=\sqrt{3{\mu }_a\left({\mu }_a+{\mu }_s^{\text{'}}\right)\hspace{0.17em}}$ is the effective attenuation coefficient (cm⁻¹), which is wavelength and tissue-type dependent. The absorption and scattering coefficient can be obtained from literatures. The PA signals can then be corrected at each wavelength by measuring the incident light energy at the skin surface, and a more accurate sO₂ measurement can be obtained. A minimum mean square error (MMSE) method is introduced to improve the reliability (Fig. 2(c–e)). In vivo experimental results indicated that this upgraded linear method was more robust than the previous method assuming homogenous tissue optical properties. Yet in vivo biological tissue is much more sophisticated than the two-layer model, which may eventually fail for deep-tissue imaging.

Laufer et al. reported a more comprehensive model considering wavelength-dependent optical attenuation in the capillary bed [45,47]. In the forward model of this method, a diffusion finite-element (FE) based optical transport model is applied to estimate the initial optical absorption, from which the initial acoustic pressure is calculated and fed into an acoustic propagation model. To quantify the chromophore concentrations, an inversion scheme is performed to minimize the discrepancies between the forward model results and the measurements. However, the FE optical transport model is constructed in a 2D geometry and assumes an infinite light beam in the third dimension, and thus overestimates the optical fluence and reduces the sO₂ measurement accuracy. Besides, it is also challenging to construct an accurate forward model for in vivo applications with unknown optical and acoustic properties.

2.3. Acoustic spectrum based method

An alternative method of minimizing the adverse effect of inhomogeneous optical fluence distribution is to analyze the acoustic spectra of PA signals [39,48]. The acoustic frequency spectrum S(ω) of the received PA signals depends upon three factors: the real object spectrum O(ω), the system dependent impulse response H(ω) and the acoustic attenuation factor a(ω). Based on the linear assumption, the detected PA signals in the frequency domain can be expressed as:

$$S\left(\omega \right)=F\left({\lambda }_1\right)O\left(\omega \right)H\left(\omega \right)a\left(\omega \right)$$ (5)

where F(${\mathrm{\lambda }}_1$) is the local optical fluence distribution at wavelength $\hspace{0.17em}{\mathrm{\lambda }}_1$. When using two different optical wavelengths to excite one blood vessel using the same PA system, the last two terms are cancelled out by dividing the two PA spectra. Using optical-resolution PAM (OR-PAM) in which the incident light is focused via an objective lens, the surface of a large blood vessel can be roughly regarded as a flat surface, since the beam size is exceedingly small.

In an optically homogeneous tissue condition, the local fluence on the blood vessel obeys Beer’s law, and the original target absorption is independent of incident light fluence and can be written as the following equation:

$$O\left(t\right)=\Gamma {\mu }_a\exp \left(-{\mu }_{a}ct\right)$$ (6)

where c is the speed of sound in biological tissue and $\Gamma$ is the Gruneisen coefficient. When PA signals in blood vessels are measured at two different wavelengths, the ratio of the two spectra can be written as:

$$\frac{S_1\left(\omega \right)}{S_2\left(\omega \right)}=\frac{F\left({\lambda }_1\right)O_1\left(\omega \right)H\left(\omega \right)a\left(\omega \right)}{F\left({\lambda }_2\right)O_2\left(\omega \right)H\left(\omega \right)a\left(\omega \right)}=\frac{F\left({\lambda }_1\right)\sqrt{{\left(\omega /{\mu }_{a2}\right)}^2+c^2}}{F\left({\lambda }_2\right)\sqrt{{\left(\omega /{\mu }_{a1}\right)}^2+c^2}}$$ (7)

The last two factors in Eq. 5 can be cancelled out, and O(ω) is the Fourier transform of Eq. 6 while F (${\mathrm{\lambda }}_1)$ and F(${\mathrm{\lambda }}_2)$ are the local optical fluence. The absolute values of F(${\mathrm{\lambda }}_1)/\mathrm{F}({\mathrm{\lambda }}_2)$, ${\mathrm{\mu }}_{\mathrm{a}1}$ and ${\mathrm{\mu }}_{\mathrm{a}2}$ can be derived by fitting Eq. 7, and the HbO₂ and HbR concentrations can be obtained in absolute units as shown in Fig. 3 [39]. The method was validated in bovine blood phantom and in a mouse ear in vivo. However, the major drawback is the assumption of a flat surface that is needed for applying Beer’s law. The small blood vessels cannot be approximated as a flat surface as the spatial resolution degrades with depth [48]. Therefore, deep sO₂ measurement remains challenging using the acoustic spectrum based method.

Fig. 3.

Optical absorption coefficients calculated based on acoustic spectra. (a) Theoretical fitting (dashed line) and experimental (solid line) acoustic spectra ratio of oxygenated bovine blood at two wavelengths. (b) The fitting of acoustic spectra ratio in an artery (V₁) and a vein (V₂) at two wavelengths in a mouse ear. Figures adapted with permission from [39].

2.4. Diffuse optical tomography (DOT) enhanced method

In addition to the efforts on estimating the optical fluence distribution using mathematical methods, other imaging modalities can also be used to improve the PA measurements of blood oxygenation. For example, diffuse optical tomography (DOT) has been applied to measure optical fluence [60]. With the knowledge of the illumination pattern at the tissue surface, the spatially-varying absorption and scattering maps acquired by DOT can be incorporated into the diffuse photon density wave equation [49]:

$$\nabla \cdot \left[D\left(r\right)\nabla \Phi \left(r\right)\right]-v{\mu }_a\left(r\right)\Phi \left(r\right)=-vS\left(r\right)$$ (8)

In Eq. 8, Φ(λ) is the optical fluence distribution D(r) is the diffusion coefficient, S(r) is the PA excitation source, and ${\mathrm{\mu }}_{\mathrm{a}}(\mathrm{r})$ is the optical absorption coefficient. Note that DOT and PAT can operate at the same wavelengths. Fluence information can then be provided by DOT to improve PA measurements of optical absorptions. More accurate concentrations of HbO₂ and HbR can then be calculated [50].

Enhanced PA reconstruction images were obtained by using the DOT-based method on phantom experiments (three optically-identical capillary tubes at 1.2 cm depth), as shown in Fig. 4 [49]. The targets at three different locations with different local optical fluence have consistent brightness after fluence-compensation calculated from DOT. These results demonstrated that DOT-facilitated PAT has reduced fluence-related errors in sO₂ measurement. Yet DOT is a low-resolution (2∼3 mm) imaging method, which has limited its use in high-resolution PAT applications.

Fig. 4.

Optical fluence compensation using DOT. (a) Original PA image of a cross-section of a phantom containing three tubes. (b) Fluence-compensated PA image of the same cross-section, showing improved signal consistency. (c) Volume-integrated PA signals of the three tubes. (d) Volume-integrated absorption coefficients of the three tubes after fluence correction. (e) The fluence distribution map measured by DOT. (f) Optical fluence profile at the tube depth, showing significant inhomogeneity along the azimuth direction. Figures adapted with permission from [49].

2.5. Statistical model for chromophore unmixing

Most quantitative PAT methods assume that the absorbers are known as a prior information, yet cases become more perplexing for in vivo studies in which other absorbers besides HbO₂ and HbR are co-existing in biological tissues. Neglecting the unknown absorbers would lead to errors in estimating blood oxygenation levels. To address this issue, multivariable data analysis and matrix factorization algorithms such as principal component analysis (PCA) and independent component analysis (ICA) are adopted for unaided or blind spectral unmixing in quantitative PAT [51,52].

PCA is a blind unmixing technique used to identify statistically uncorrelated source components from the correlated measurements [60]. By using singular value decomposition (SVD) of the multispectral measurement M, or by calculating the eigenvalue decomposition of its covariance matrix, correlated data is projected orthogonally into a new coordinate by using the transformation matrix${\mathrm{\hspace{0.17em}}\mathrm{U}}_{\mathrm{P}\mathrm{C}\mathrm{A}}^{\mathrm{T}}$:

$$R_{PCA}=U_{PCA}^{T}M$$ (9)

The largest variance is projected as the first principal component, and the second largest one as the second principal component, and so on. Once the number of principal components reaches the number of types of the interested absorbers, the remaining components can be discarded, which contain mostly noise and artifacts.

ICA is another blind source separation technique assuming that the source components are independent [61]. According to the central limit theorem, the mixed multispectral measurements are expected to be more Gaussian-like than the unmixed components, so the key is to maximize the non-Gaussianity of the measurement M by seeking a transformation ${\mathrm{\hspace{0.17em}}\mathrm{U}}_{\mathrm{I}\mathrm{C}\mathrm{A}}^{\mathrm{T}}$:

$$R_{ICA}=U_{ICA}^{T}M$$ (10)

In most cases, the datasets are too large to be separated, so a reasonable solution is to use PCA as a preprocessing step to discard noise and then analyze the data using ICA. However, this method is most applicable to identify the number of major absorbers in tissues instead of providing quantitative values of the absorber concentrations. Therefore, it is useful to separate arteries and veins, but less capable of quantifying the blood oxygenation.

2.6. The fluorescence lifetime based oxygen partial pressure (pO₂) measurement

pO₂ is another static parameter for quantifying the blood oxygenation level, and is closely related to sO₂ via the hemoglobin-oxygen disassociation curve. The PA lifetime imaging (PALI) can measure pO₂ by using an oxygen-sensitive dye whose life time depends on the local oxygen content. The technique uses a pump-probe approach: the fluorescent dye molecule is first excited by a pump laser pulse to a higher energy state, and then returns to the ground state under the interrogation of a delayed probe laser pulse at a different wavelength. For example, Ashkenazi et al. have demonstrated PALI using methylene blue (MB) [33]. MB is an FDA-approved water-soluble dye with a strong absorption at 660 nm. As an oxygen-sensitive agent, MB has a high quantum yield for triplet state transition with a long triplet lifetime of 79.5 μs in degassed water. The lifetime reduces sharply to 2 μs in air saturated water due to the transfer of energy and formation of singlet oxygen. Fig. 5 shows the lifetime dependence of MB on the oxygen content [33].

Fig. 5.

PA signal amplitude as a function of pump-probe delay at four different pO₂ levels. pO₂ levels 0.4 mmHg (circle), 8.6 mmHg (square), 40 mmHg (triangle), and 153 mmHg (diamond). The PA signal decay rate (up right corner) is also plotted as a function of pO₂ (R² = 0.9914). Figure adapted with permission from [33].

The major advantage of pump-probe excitation is the suppression of the overwhelming background signals generated by non-fluorescent, endogenous absorbers, such as hemoglobin. The imaging depth depends on the penetration depth of the pump and probe light in tissue, and the quantification accuracy is less sensitive to the absolute local fluence [33,53]. However, this technique also has its limitations. The measurement is slow due to multiple pump-probe pulse pairs with various time separations, and thus may suffer from motion artifacts for in vivo studies. Furthermore, the excessive excitation light may bleach the molecules. Finally, the prolonged imaging time may result in changes in the molecular environment such as temperature, pH, and ion concentration, which can affect the lifetime measurements [54].

2.7. The absorption-saturation based sO₂ measurement

Oxygen binding changes not only the absorption coefficient of hemoglobin but also its non-radiative absorption relaxation time [56]. Recent work by Yao et al. has demonstrated a single-wavelength (532 nm) pulse-width-based method for sO₂ measurement (PW-sO₂) [57]. The method explores the difference in HbO₂ and HbR saturation intensities, which are defined as the excitation intensity that reduces the absorption coefficient to half of the original value. The saturation intensity of hemoglobin is determined by its non-radiative absorption relaxation time. In PW-sO₂, hemoglobin was excited first by a picosecond laser pulse and then by a nanosecond laser pulse, with the same pulse energy. As shown in Fig. 6, HbO₂ can be saturated more with the picosecond laser pulse than the nanosecond pulse, while HbR responses similarly to the two types of pulses [57]. ${\mathrm{C}}_{{\mathrm{H}\mathrm{b}\mathrm{O}}_2}$ and ${\mathrm{C}}_{\mathrm{H}\mathrm{b}\mathrm{R}}$ are quantified based on the PA signals acquired with the following formulas [57]:

$$P_{ns}=\ln \left(10\right)kF\left({\epsilon }_{HbR}{C}_{HbR}+{\epsilon }_{Hb{O}_2}{C}_{Hb{O}_2}\right)$$ (11)

$$P_{ps}=\ln \left(10\right)kF\left(r_{HbR}{\epsilon }_{HbR}{C}_{HbR}+r_{Hb{O}_2}{\epsilon }_{Hb{O}_2}{C}_{Hb{O}_2}\right)$$ (12)

where P_ns and P_ps are respectively the PA signal amplitudes with nanosecond and picosecond excitations; F is the local fluence; k is the proportionality coefficient related to the detection system; ${\mathrm{\epsilon }}_{\mathrm{H}\mathrm{b}\mathrm{R}}$ and ${\mathrm{\epsilon }}_{{\mathrm{H}\mathrm{b}\mathrm{O}}_2}$ are the extinction coefficients of HbR and HbO₂; ${\mathrm{r}}_{\mathrm{H}\mathrm{b}\mathrm{R}}$ and ${\mathrm{r}}_{{\mathrm{H}\mathrm{b}\mathrm{O}}_2}$ are the saturation factors of HbR and HbO₂. With several approximations, sO₂ can be estimated as:

$$s{O}_2=\frac{C_{Hb{O}_2}}{C_{HbT}}=\frac{1-\frac{P_{ps}}{P_{ns}}}{1-r_{HbO2}(F)}=k_2(1-\frac{P_{ps}}{P_{ns}})$$ (13)

where

$$k_2=\frac{1}{1-r_{HbO2}(F)}$$

Fig. 6.

Absorption saturation of HbR and HbO₂. (a–b) PA signal amplitudes as a function of the energy of nanosecond (3 ns) and picosecond (3 ps) pulse excitation. (c) Saturation factors of HbR and HbO₂. The saturation factor is defined as the ratio of PA signal amplitude with picosecond and nanosecond excitation. Figures adapted with permission from [57].

Using a single wavelength, PW-sO₂ has achieved a one-dimensional imaging speed of 100 kHz. Moreover, PW-sO₂ is less affected by the wavelength-dependent optical attenuation. However, the imaging depth of PW-sO₂ is strongly limited by optical attenuation to the point where saturation becomes insufficient, which is about 0.5 mm at 532 nm.

2.8. Eigenspectral multispectral model based sO₂ measurement

The issue of unknown optical fluence distribution at depths and at different wavelengths can also be addressed by employing the PCA method as demonstrated in eigenspectral multispectral optoacoustic tomography (eMSOT) [42,62]. The working assumption is that only a small number of fundamental spectra exist in biological tissues, and any fluence spectrum can be predicted by combining these spectra. After applying PCA on 1470 optical fluence spectra simulated from light propagation with 21 uniform blood oxygenation levels at 70 depths, four significant base spectra (an averaged optical fluence spectrum ${\mathrm{\varphi }}_{\mathrm{M}}(\mathrm{\lambda })$ and three fluence eigenspectra: ${\mathrm{\varphi }}_1(\mathrm{\lambda })$, $\mathrm{\hspace{0.17em}}{\mathrm{\varphi }}_2(\mathrm{\lambda })$ and ${\mathrm{\varphi }}_3(\mathrm{\lambda })$) were produced:

$$\Phi \left(r,\lambda \right)={\Phi }_M\left(\lambda \right)+m_1\left(r\right){\Phi }_1\left(\lambda \right)+m_2\left(r\right){\Phi }_2\left(\lambda \right)+m_3\left(r\right){\Phi }_3\left(\lambda \right)$$ (14)

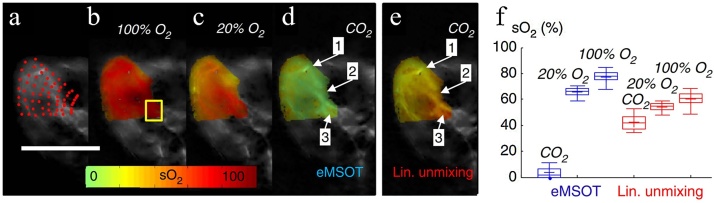
here, m_1, m_2, and m₃ are scalars, termed eigenfluence parameters. Together with Eqs. (1) and (2) with measurements at multiple optical wavelengths, ${\mathrm{C}}_{{\mathrm{H}\mathrm{b}\mathrm{O}}_2}$, ${\mathrm{C}}_{\mathrm{H}\mathrm{b}\mathrm{R}}$, m₁, m_2, and m₃ can be estimated using constrained optimization. The superior performance of eMSOT was demonstrated in the hindlimb muscle area of a mouse (Fig. 7(a)), showing the oxygenation gradient measurement in vivo after 100% O₂ breathing (Fig. 7(b)) and 20% O₂ breathing (Fig. 7(c)). Strong agreement can be observed from the eMSOT results and the expected physiological states. Fig. 7(d) and (e) compare the oxygenation measurement using eMSOT and the linear unmixing method in post mortem after CO₂ breathing, in which the linear unmixing method overestimated the sO₂ as tissue depth increased and showed a much smaller change in sO₂ (Fig. 7(f)). Therefore, eMSOT has shown higher accuracy compared with conventional spectral unmixing methods. However, it is still not clear how to confirm the performance of eMSOT for in vivo studies with unknown tissue compositions. Moreover, a large pool of training datasets is required to interrogate different physiological models such as in cardiovascular, diabetes and cancer research.

Fig. 7.

Comparison of sO₂ estimation using eMSOT and linear spectral fitting method. (a) The image area that eMSOT was applied on hindlimb muscles. (b–d) sO₂ estimation using eMSOT, under 100% O₂ breathing air (b), 20% O₂ breathing air (c), and post mortem (d). (e) sO₂ estimation using linear spectral unmixing method post mortem. Scale bar, 1 cm. (f) Estimated sO₂ values in a deep tissue area (yellow box in (b)) using eMSOT (blue) and linear unmixing method (red) under different breathing conditions. Figures adapted with permission from [42].

3. Conclusion and outlook

PAT has been demonstrated as a powerful tool to provide reliable anatomical and functional imaging. Various methods have been explored to further improve PAT’s performance in resolution, contrast, imaging speed, and penetration depth [1,29,31,45]. Among them, accurate measurement of blood oxygenation at depths larger than 1 mm is undoubtedly one of the most promising subjects. The conventional way of calculating sO₂ by using linear spectral fitting has insufficient accuracy due to the incorrect assumption of light fluence distribution in tissues. A number of new approaches have emerged to tackle this problem by constructing better optical fluence models in tissue (e.g., acoustic spectrum based method and eigenspectra based method). So far, the most promising method in measuring sO₂ in deep tissue is the eigenspectra method, yet more comprehensive mathematical analysis and disease-model validations should be implemented to reinforce this method. In addition, more efforts should also be made to boost other aspects of quantitative PAT beyond oxygenation detection, such as blindly unmixing chromophores by using statistical algorithms, and measuring the absorption relaxation times by exploiting the optical saturation effect. Besides the optical fluence, when the ultrasound transducer’s receiving angle cannot enclose the object, PAT’s limited-view problem needs to be addressed as well [[63], [64], [65], [66]]. All these technological advancements can potentially enable not only the oxygenation quantification but also other functional and molecular applications. Although challenges remain, none of them are beyond reach. Future improvement can be made by combining multiple methods to obtain more accurate oxygenation map in deep organs. For example, the limited-view problem in PAT with a linear transducer array can be addressed by adding acoustic mirrors to acquire more accurate signal amplitude at each wavelength for oxygenation quantification [64]. More phantom and in vivo validations should be performed to strengthen these methods with the tissue heterogeneity taken into consideration.

Conflict of interest

None.

Biographies

Mucong Li received her B.S in Automation and M.S. in Control Science and Engineering from Harbin Institute of Technology, China. She is currently a Ph.D. student in the Department of Biomedical Engineering at Duke University. Her research focuses on the development PACT system for preclinic and clinic applications.

Yuqi Tang received her B.S. in Bioengineering from Rice University in 2017. She is currently a Ph.D. candidate in the Department of Biomedical Engineering at Duke University. Her research interests include functional brain imaging, early cancer theragnostic, and imaging processing.

Junjie Yao is an assistant professor of Biomedical Engineering at Duke University, and a faculty member of Duke Center for In-Vivo Microscopy, Fitzpatrick Institute for Photonics, and Duke Cancer Institute. He received his B.E. and M.E. degrees at Tsinghua University, and his PhD in Biomedical Engineering at Washington University, St. Louis. His research interest is in photoacoustic tomography technologies in life sciences, especially in functional brain imaging and early cancer detection.