Abstract
Adaptive immunity relies on the generation and maintenance of memory T cells to provide protection against repeated antigen exposure. It has been hypothesised that a self-renewing population of T cells, named stem cell–like memory T (TSCM) cells, are responsible for maintaining memory. However, it is not clear if the dynamics of TSCM cells in vivo are compatible with this hypothesis. To address this issue, we investigated the dynamics of TSCM cells under physiological conditions in humans in vivo using a multidisciplinary approach that combines mathematical modelling, stable isotope labelling, telomere length analysis, and cross-sectional data from vaccine recipients. We show that, unexpectedly, the average longevity of a TSCM clone is very short (half-life < 1 year, degree of self-renewal = 430 days): far too short to constitute a stem cell population. However, we also find that the TSCM population is comprised of at least 2 kinetically distinct subpopulations that turn over at different rates. Whilst one subpopulation is rapidly replaced (half-life = 5 months) and explains the rapid average turnover of the bulk TSCM population, the half-life of the other TSCM subpopulation is approximately 9 years, consistent with the longevity of the recall response. We also show that this latter population exhibited a high degree of self-renewal, with a cell residing without dying or differentiating for 15% of our lifetime. Finally, although small, the population was not subject to excessive stochasticity. We conclude that the majority of TSCM cells are not stem cell–like but that there is a subpopulation of TSCM cells whose dynamics are compatible with their putative role in the maintenance of T cell memory.
Author summary
The human immune system remembers previously encountered pathogens so that, on meeting the same pathogen a second time, the response is quicker and more effective. This immune memory is the basis of all vaccinations. Immune memory persists for decades, but how memory is maintained is unclear. It has been hypothesised that there is a dedicated population of cells called stem cell–like memory T (TSCM) cells that have stem cell–like behaviour and are responsible for the persistence of T cell memory. Here, we show that a subset of TSCM cells, in healthy humans in vivo, have the dynamic properties of self-renewal and clonal longevity necessary to maintain long-lived immune memory.
Introduction
The maintenance of long-lived T cell memory is one of the hallmarks of adaptive immunity [1, 2]. Multiple studies have shown that the recall response to a previously encountered antigen has a half-life of the order of decades [3, 4]. It has been hypothesised that this T cell memory is dynamically maintained by differentiation of a precursor stem cell–like memory population [5]. Alternative, nonexclusive explanations include replacement by proliferation of differentiated memory T cells or the existence of a putative subpopulation of long-lived memory T cells that has not yet been identified, either because such cells are very rare or because they reside primarily outside of the peripheral blood [6–9].
Central memory T (TCM) cells (CD45RA―CCR7+ in humans) were previously thought to constitute the stem cell–like memory precursor population. Evidence supporting the ‘stemness’ of TCM cells includes their capacity to differentiate into effector memory T (TEM) cells and T effector (TEFF) cells [10, 11]. This hypothesis was further strengthened by cell fate–tracking experiments in mice (using genetic barcoding and single-cell transfer), showing that TCM cells had the capacity to self-renew and that a single TCM cell could reconstitute immune protection against an otherwise lethal pathogen [12, 13].
However, the concept of TCM as the stem cell population has been challenged by the identification of ‘stem cell–like’ memory T (TSCM) cells—which have enhanced stem cell–like properties compared to TCM cells—in mice [14], nonhuman primates [15], and humans [16]. In humans, like naïve cells, TSCM cells are CD45RA+CD45RO―, and they express high levels of CD27, CD28, interleukin 7 receptor alpha (IL-7Rα), CD62L, and C-C chemokine receptor 7 (CCR7). Unlike naïve cells, TSCM cells are clonally expanded and express the memory markers CD95 and CD122 [1, 16]. TSCM cells exhibit enhanced proliferative capacity compared to TCM cells, the potential to differentiate into all other classically defined T cell memory subsets (including TCM), and the ability to retain their phenotype following proliferation both in vitro and in mice in vivo [1, 14–16]. In light of these observations, it has been suggested that TSCM cells are the main stem cell memory population and play a key role in maintaining long-term memory in vivo [15–18].
There are 3 basic prerequisites for T cell memory stemness: multipotency, self-renewal, and clonal longevity. In this study, we focus on the related dynamic properties of self-renewal and clonal longevity. Self-renewal of human TSCM cells has been demonstrated in vitro [19], but it remains a concern that the local microenvironment, which may crucially affect the degree of self-renewal, will be different in vivo and in vitro. However, proving self-renewal of human TSCM cells in vivo has so far not been possible because of ethical and technical limitations. The second property we investigate is clonal longevity. Long-lived T cell memory requires that memory T cell clonotypes expressing the same T cell receptor (TCR) persist for several decades in vivo. For example, influenza immunity has been shown to last for several decades [20], and small pox vaccine–induced T cell memory has a half-life of 8–15 years [3, 4]. For TSCM cells to constitute a potential precursor population for T cell memory in vivo, the survival of TSCM clones needs to be consistent with those estimates. A number of studies suggest that TSCM clones can survive for several years. Biasco and colleagues [17] observed that genetically engineered TSCM cells could persist for many years in patients suffering from severe combined immunodeficiency disease. Fuertes Marraco and colleagues [21] identified a yellow fever virus (YFV)-specific TSCM population up to 25 years after vaccination. Finally, in leukaemia patients who had undergone haematopoietic stem cell (HSC) transplantation, Oliveira and colleagues [22] reported that gene-modified TSCM cells could be detected in the circulation up to 14 years after treatment. These studies support the concept of TSCM longevity, albeit in scenarios of lymphocyte depletion or profound CD8+ T cell expansion. However, it has been shown that the dynamics of posttransplant haematopoiesis in mice differs significantly from normal, unperturbed haematopoiesis [23–25], and so it cannot be assumed that these transplantation studies in humans necessarily recapitulate the healthy human system. In short, TSCM longevity has not been quantified in normal, unperturbed homeostasis in humans, and the related question of the ability of TSCM to self-renew has not been addressed in any human in vivo system.
In order to investigate human TSCM cells in homeostasis, we previously performed stable isotope labelling of healthy volunteers and analysed label uptake in CD4+ and CD8+, naïve T and TSCM cells. We found that the TSCM population was rapidly turning over (median 0.02 per day, interquantile range 0.016–0.037 per day, half-life < 1 year) and concluded that the TSCM population is dynamically maintained [26]. However, in this previous study, only labelling data were modelled, and so it was not possible to address the central question of the ‘stemness’ of the TSCM pool. First, to constitute a stem cell population, it is not enough to have a stably maintained population of cells; stemness requires long-term clonal persistence [18]. That is, whilst the size of the TSCM population as a whole may be stably maintained, the lifespan of any given antigen-specific precursor population could be short; such limited lifespans would be difficult to reconcile with the hypothesis that TSCM cells are the repository of T cell memory. Second, the high turnover rates obtained in this labelling study [26] do not necessarily indicate that the majority of the TSCM population is replaced by the self-renewal of the TSCM pool; frequent naïve cell differentiation could also be responsible. Indeed, given the very large size of the naïve pool compared to the TSCM pool [19], a relatively low proportion of proliferating naïve cells would be sufficient to replace lost TSCM cells. In this scenario, TSCM cells would simply represent transit cells on the differentiation pathway from naïve to effector rather than self-renewing stem cells.
Here, we investigate whether the dynamics of TSCM cells in healthy humans are consistent with their putative role as memory stem cells. Specifically, we investigate both the capacity of TSCM cells to self-renew and the longevity of TSCM clones. It is challenging to address these questions in humans, and they cannot be answered using stable isotope labelling alone, since different scenarios (e.g., ‘all new TSCM cells come from naïve cell differentiation’ versus ‘all new TSCM cells come from TSCM proliferation’) can give rise to very similar levels of label in the TSCM population. To enable us to deconvolute these possibilities, we performed telomere length analysis and utilised cross-sectional TSCM cell data from YFV vaccine recipients. Deterministic and stochastic mechanistic mathematical modelling were then used to analyse all 3 datasets. This novel approach allows us to investigate human TSCM cell dynamics in vivo and to address questions previously only investigated in animal models.
Results
To investigate the dynamics of TSCM cells in humans in vivo, we analysed experimental data that we obtained in a 7-week stable isotope–labelling study of 5 healthy individuals [26], in which label incorporation into CD4+ and CD8+ naïve (CD45RAbrightCD27brightCCR7+CD95−) and TSCM (CD45RAbrightCD27brightCCR7+CD95+) cells was measured at multiple time points (Fig 1). In addition, we performed single-telomere length analysis of each cell population in the same individuals. We then constructed an ordinary differential equation (ODE)-based mathematical model to describe both stable isotope (heavy water) labelling and telomere length, in which we assumed a linear differentiation pathway from naïve to TSCM cells (Fig 2, Methods [27]).
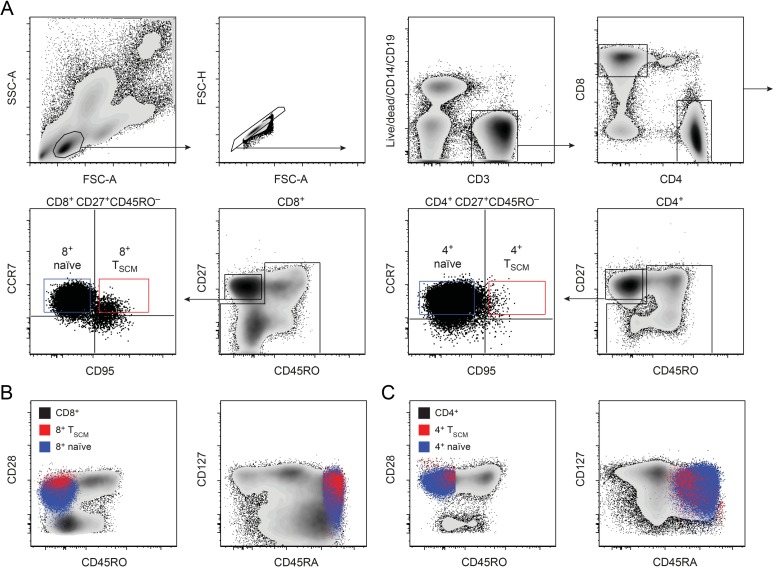
Fig 1. Cell surface phenotype of naïve and TSCM populations.
(A) Gating strategy used to sort CD4+ and CD8+ naïve and TSCM cells for isotope label and telomere length analysis: the top panels show the consecutive gating to detect CD8+ or CD4+ T cells; the bottom panels show the further gating to detect naïve or TSCM cells within CD8+ or CD4+ populations. (B) Expression of CD45RO, CD28, CD127, and CD45RA on CD8+ CCR7+ CD95− naïve cells (blue cloud) and CD8+ CCR7+ CD95+ TSCM cells (red cloud) compared with bulk CD8+ T cells (black cloud). (C) as for B but depicting CD4+ naïve and CD4+ TSCM compared to bulk CD4+ T cells. FSC-A, forward scatter area; FSC-H, forward scatter height; SSC-A, side scatter area; TSCM, stem cell–like memory T.
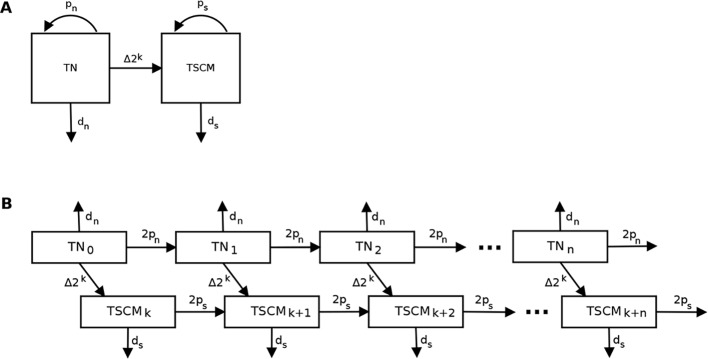
Fig 2. Model to describe the TN and TSCM populations.
(A) Schematic representation of the model for TN and TSCM populations. (B) Schematic representation of the model for telomere length data for TN and TSCM populations when C = k (inactive telomerase). TNi (or TSCMi) represent the number of TN (or TSCM) cells which have divided i times; pn, ps, dn, and ds are the proliferation and disappearance rates of TN and TSCM populations; Δ is the fraction of TN cells recruited per day, and k is the number of divisions that occur during clonal expansion. TN, naïve T; TSCM, stem cell–like memory T.
Heterogeneity in the TSCM population
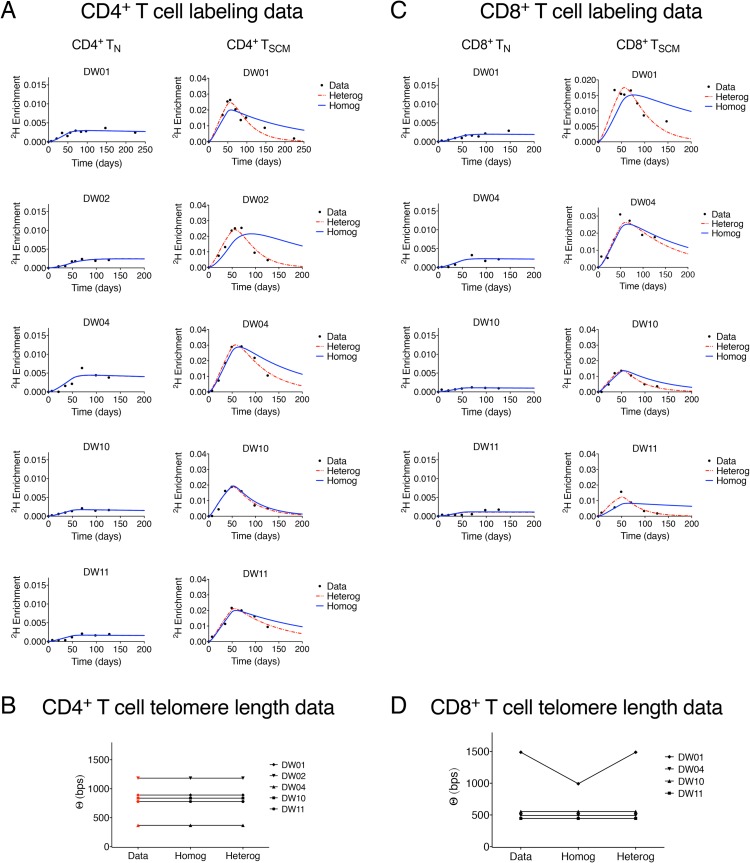
Estimates of the rate of TSCM renewal and TSCM clonal lifespan will depend upon the kinetic structure of the TSCM pool. We therefore first asked whether there was evidence for kinetic heterogeneity (i.e., existence of subpopulations with differing kinetics) within the TSCM pool by comparing the quality of fit of a homogenous and heterogeneous version of the mathematical model. In the homogeneous version of the model, we constrain the input rate (proliferation rate + rate of new entrants due to differentiation from naïve cells) of the whole TSCM population to be equal to the disappearance rate of labelled TSCM cells; this condition will be met for a kinetically homogenous population of constant size. In the heterogeneous version of the model, this constraint was relaxed to allow for the possibility of kinetic heterogeneity in the TSCM pool (Methods, [28]). We used this implicit description of kinetic heterogeneity rather than an explicit description of the subpopulations because it requires fewer parameters (2 compared with 3 for the explicit model [28–30]) and furthermore does not suffer from the parameter identifiability issue inherent in the explicit kinetic heterogeneity model, which arises due to the very strong correlation between the proliferation rate and size of a subpopulation [31]. A total of 9 datasets were included in this analysis, representing CD4+ and CD8+ T cells (naïve and TSCM) from 5 individuals (1 CD8+ TSCM cell dataset from 1 subject was not available). We found that, in 7 out of the 9 cases, constraining the TSCM population to be homogeneous resulted in a substantially worse description of the data (Fig 3); and there was strong evidence to reject the assumption of homogeneity P = 5.8 × 10−7, P = 4.1 × 10−6 (median of p-values calculated using Fisher’s F-test for nested models between the homogeneous and heterogeneous models for CD4+ and CD8+ TSCM, respectively), indicating considerable support for the heterogeneous description of the TSCM pool in both CD4+ and CD8+ T cell populations (S1 Table). In contrast, there was no evidence to reject the null hypothesis of homogeneity in the naïve cell pool (P = 0.6, P = 0.5, for CD4+ and CD8+ TN, respectively; median of p-values calculated using Fisher’s F-test for nested models between the homogeneous and heterogeneous models; S1 Table).
Fig 3. Label incorporation and telomere length in CD4+ and CD8+ naïve T and TSCM cells.
(A) Experimental labelling data (black dots) and best fit of model to the data assuming kinetic homogeneity (blue solid line) and kinetic heterogeneity (red dashed line) of the CD4+ TN pool (left column) and the CD4+ TSCM pool (right column). (B) Experimental measurement (red symbol) and best fit of the homogeneous (‘homog’) and heterogeneous (‘heterog’) models (black symbols) to the average telomere length differences (Θ) between CD4+ TN and CD4+ TSCM cells. Labelling data and telomere length data were fitted simultaneously. We found strong evidence to reject the null hypothesis of homogeneity in the CD4+ TSCM population (median P = 5.8 × 10−7, pooled P = 3.5 × 10−23) but not in the CD4+ TN population (median P = 0.6, pooled P = 0.9). (C) and (D) as for A and B but for CD8+ cells rather than CD4+ cells. Again, for CD8+ cells as for CD4+, we found strong evidence to reject the null hypothesis of homogeneity in the TSCM population (median P = 4.1 × 10−6, pooled P = 6.1 × 10−15) but not in the TN population (median P = 0.5, pooled P = 0.7). Experimental data depicted in this figure can be found in S1 Data. TN, naïve T; TSCM, stem cell–like memory T.
Magnitude of clonal expansion
The size of a newly generated TSCM clone will be an important determinant of clonal longevity, as this determines not just the initial magnitude of a new clone but also the rate at which an existing clone is displaced by new entrants bearing different TCRs. Unfortunately, the size of the clonal expansion accompanying the differentiation of naïve to TSCM cells (k in the model; Fig 2, Methods) was not identifiable. Different fitting runs to the same dataset (with different initial conditions or different random seeds) gave different estimates of the clonal expansion parameter k. Consistent with this, we found that if k was fixed to different constant values in the range 0–20, then, with the exception of 1 individual for which the sum of squares increases dramatically for k above 15, the sum of squares remained constant in every case for all values of k (Fig 4A and Fig 4E). Henceforth, we systematically repeat all analyses for multiple values of k in the range 0–20 to ensure that results are robust despite uncertainty in the clonal expansion parameter. Values of k above 20 were not considered biologically plausible [13, 32, 33].
Fig 4. Estimates of TSCM cell parameters from the implicit kinetic heterogeneity model.
(A-H) Estimates of TSCM cell parameters as a function of k in the CD4+ (top row: A—D) and CD8+ (bottom row: E—H) lineages. Isotope labelling and telomere length data were fitted simultaneously, fixing the clonal expansion size k to values between 0 and 20 and leaving the remaining parameters free. (A) and (E) show the variation in the sum of squared residuals (‘SSR’) with k in CD4+ and CD8+ T cells respectively; (B) and (F) show the variation in the fraction of newly generated TSCM cells originating from self-renewing TSCM proliferation computed as (psTSCM) / (2kΔTN + psTSCM); (C) and (G) show the variation in TSCM half-lives for CD4+ and CD8+ T cells, respectively, and (D) and (H) the variation in TSCM antigen-specific precursor lifespans (time until the last cell specific for a given antigen dies or differentiates). In all cases, k is plotted on the x axis. All results depicted are provided in S1 Data. TSCM, stem cell–like memory T.
In summary, we were not able to estimate the size of the clonal expansion k upon differentiation of naïve cells to TSCM cells and instead utilised a strategy to investigate TSCM dynamics despite uncertainty in this parameter.
TSCM clonal longevity
Next, we quantified TSCM clonal longevity. We fitted the mathematical model (implicit heterogeneous version) simultaneously to the telomere length and isotope labelling data, with k fixed sequentially at different values in the range 0–20. We found that, with the exception of 1 dataset (CD8+ T cells in DW01), the contribution of naïve cells to TSCM replacement was never less than 20% and could be as much as 90% (Fig 4B and 4F). Correspondingly, the average half-life of a TSCM clone was short: the maximum ever observed (across all values of k and across all individuals) was 4 years, but typically, it was much shorter and in the range 0–500 days (Fig 4C and 4G). These conclusions about short clonal longevity were robust to assumptions regarding the activity of telomerase. Specifically, for all values of telomerase compensation considered in the range 0–k, the estimated average clonal half-lives were never higher than those estimates reported above (in which compensation was a free parameter). Importantly, this half-life represents the duration of memory to an antigen (Methods), not the conventional population half-life.
It is possible that a very small number of surviving TSCM cells is sufficient to generate a substantial recall response, and so a short clonal half-life is not necessarily incompatible with long-lived recall responses. Moreover, extinction of some clones specific for a given antigen is not necessarily problematic if other clones (bearing different TCRs) specific for the same antigen survive. To assess this possibility, we used the exact Gillespie algorithm (Methods) to quantify the time for the last cell of an antigen-specific precursor population to disappear. This is reported as the precursor lifespan in Fig 4D and 4H. Whilst this did lead to a considerable increase in longevity (stochastic estimates of total antigen-specific precursor lifespan were typically 3 times longer than the deterministic clonal half-life), maximum estimates were still only of the order of 2,000 days (about 5 years) for most individuals.
In summary, although individual parameters were poorly identifiable, all parameter combinations able to describe the experimental data were associated with average clonal half-life estimates, which were much lower than the 8–15 year half-life of the recall response [3, 4]. Even total precursor lifespans (times until the last cell of an antigen-specific precursor population disappears) were lower than those values in most cases. We conclude that the average TSCM population is replaced too rapidly for it to be the stem cell population responsible for maintaining memory.
Subpopulation kinetics: YFV-specific responses
The model used up to this point allows for heterogeneity but nevertheless reports population averages (i.e., the proliferation rate and clonal half-life averaged across the whole TSCM population). This averaging could be hiding a small, long-lived population within the bulk short-lived population. Expanding our model, which deals with heterogeneity implicitly (and thus averages across the population), to one that deals with heterogeneity explicitly (and thus provides estimates for the half-lives of all subpopulations) is problematic, as even the simplest version of the explicit heterogeneity model suffers from severe identifiability issues [30] and fails to deliver the parameters of interest when fitted to labelling data. We confirmed that, for our more complex system with both naïve and TSCM cells, an explicit description of heterogeneity provided no information. To address this problem, we therefore sought an alternative class of data.
We analysed published data of the vaccine-induced YFV-specific TSCM response in humans from Fuertes Marraco and colleagues [21]. In brief, the magnitude of the CD8+ TSCM cell response to the HLA-A*02-restricted YFV nonstructural protein 4b (NS4b214−222) epitope was measured by HLA class I tetramer at different time points (range 0.27–35.02 years) postvaccination in a cross-sectional study of 37 recipients of the YF-17D YFV vaccine.
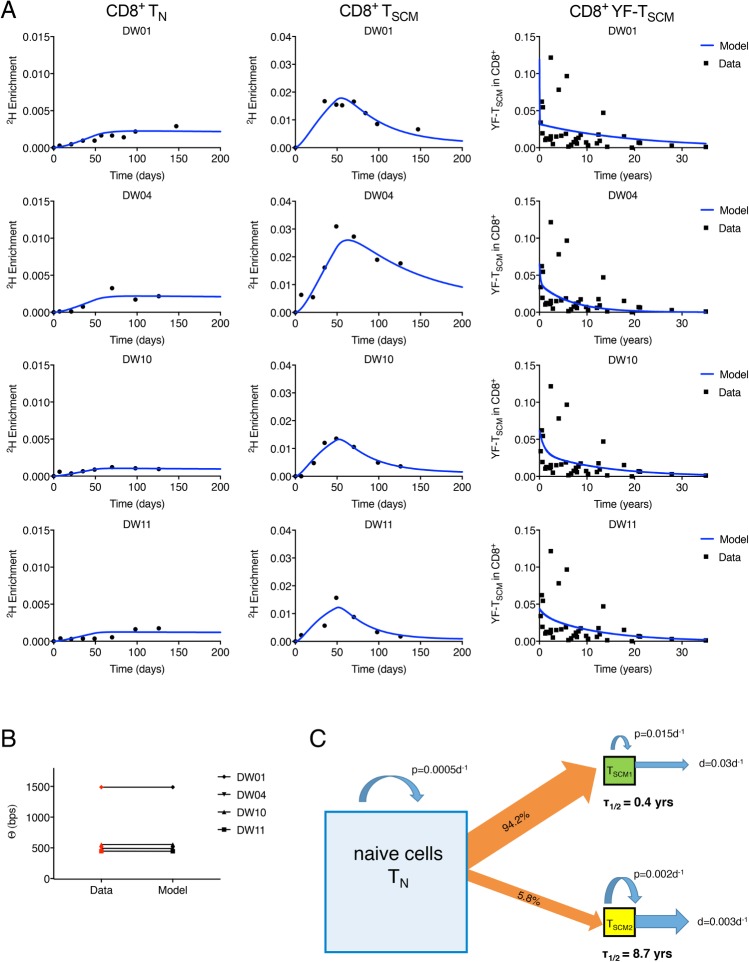
We fitted the explicit heterogeneity version of the naïve T (“TN”) and TSCM model to all 3 types of CD8+ T cell data (isotope labelling, telomere length, and YFV) simultaneously (Supplementary Methods in S1 Text). The fits are shown in Fig 5. As for the implicit heterogeneity model, the fraction of new TSCM cells originating from naïve cells was high (minimum 10%, median 44%). We found evidence for at least 2 subpopulations of CD8+ TSCM cells (designated TSCM1 and TSCM2 for the purposes of this discussion). The majority of the TSCM cells generated upon clonal expansion of naïve cells differentiated into the TSCM1 subpopulation, characterised by a short half-life (≤1 year) and a high replacement rate (median 0.02 per day, interquantile range 0.024–0.045 per day), slightly higher than the average rates estimated by the previous model. The remaining fraction of the generated clone was observed to enter a long-lived subpopulation with a median half-life of 9 years (Table 1, S2 Table). Surprisingly, although the fraction of naïve cells entering the TSCM2 pool was low, because of its low death/differentiation rate, the number of long-lived TSCM2 cells in the circulation at any given time could be as high as, or even higher than, the number of rapidly proliferating TSCM1 cells. Results are summarised schematically in Fig 5C. Four other weighting strategies (of the different types of data) yielded the same conclusions in all cases (S1 Fig, S3 Table).
Fig 5. Label incorporation, telomere length, and YFV predictions for CD8+ TN and TSCM cells.
(A) Fit of the explicit heterogeneity model to isotope labelling data from CD8+ TN and TSCM cells and to the YFV-specific TSCM data. Experimental data are represented by solid black symbols. (B) fits to the average telomere length differences (Θ) between the CD8+ TN and TSCM pools, experimental data shown in red. The number of bps lost per division was taken to be δ = 50 bp/division. Isotope labelling, telomere length, and the YFV data were fitted simultaneously. (C) Schematic summary of estimated TN and TSCM dynamics. Estimates are the medians across subjects obtained from the fits shown in panels A and B. Parameter estimates for each subject are provided in Table 1 and S2 Table. The size of the squares is proportional to the population size. Labelling data and telomere data are provided in S1 Data; the YFV tetramer data were previously published [21]. bp, base pair; TN, naïve T; TSCM, stem cell–like memory T; YFV, yellow fever virus.
Table 1. Parameter estimates for CD8+ TSCM cells from the explicit heterogeneity model.
Parameter estimates with 95% CIs (in parentheses) obtained by fitting the explicit heterogeneity model to isotope labelling, telomere length, and YFV datasets simultaneously. Table shows estimated half-life of the 2 subpopulations, the relative size of the long-lived TSCM2 subpopulation (TSCM2/TSCM), and the fraction of cells from each clonal burst that enter the TSCM2 subpopulation (f). Additional parameters are given in S2 Table.
| half-life TSCM1 [years] |
half-life TSCM2 [years] |
TSCM2/TSCM [TOTAL] | f | |
|---|---|---|---|---|
| DW01 | 0.02 (95% CI 0.02–6.74) | 13.92 (95% CI 2.26–20.68) | 0.25 (95% CI 0.14–0.89) | 5.6 × 10−4 (95% CI 7.6 × 10−4–7.2 × 10−1) |
| DW04 | 0.14 (95% CI 0.01–2.79) | 4.59 (95% CI 2.13–20.41) | 0.58 (95% CI 0.20–0.98) | 4.1 × 10−2 (95% CI 2.0 × 10−2–7.6 × 10−1) |
| DW10 | 0.69 (95% CI 0.05–0.77) | 9.09 (95% CI 2.33–16.50) | 0.51 (95% CI 0.37–0.74) | 7.4 × 10−2 (95% CI 1.9 × 10−2–1.5 × 10−1) |
| DW11 | 0.90 (95% CI 0.03–3.98) | 8.39 (95% CI 3.75–17.01) | 0.82 (95% CI 0.46–0.95) | 3.3 × 10−1 (95% CI 2.1 × 10−2–7.3 × 10−1) |
| MEDIAN | 0.41 (95% CI 0.02–3.39) | 8.74 (95% CI 2.30–18.71) | 0.55 (95% CI 0.28–0.92) | 5.8 × 10−2 (95% CI 1.9 × 10−2–7.3 × 10−1) |
Abbreviations: TSCM, stem cell–like memory T; YFV, yellow fever virus
Long-lived CD8+ TSCM cells: Degree of self-renewal and clonal stability
The long-lived TSCM subpopulation identified in the previous section (Subpopulation kinetics) is a potential candidate for the stem cell population responsible for the maintenance of immune memory. We therefore investigated the degree of self-renewal and clonal stability within this long-lived TSCM compartment. The degree of self-renewal of a population at steady state, 1 / (death rate + differentiation rate–proliferation rate), quantifies the upstream input necessary to maintain a population. If there is a large upstream contribution, then the degree of self-renewal will be low [34]. A perfectly self-renewing population (e.g., HSCs) will have an infinite degree of self-renewal. We quantified the degree of self-renewal for the long-lived population and found a median of 4,600 days, with the range 2,400–7,300 days (S2 Table). This implies that, on average, a TSCM cell (or its progeny) from the long-lived subpopulation resides in the TSCM compartment without dying or differentiating for 4,600 days.
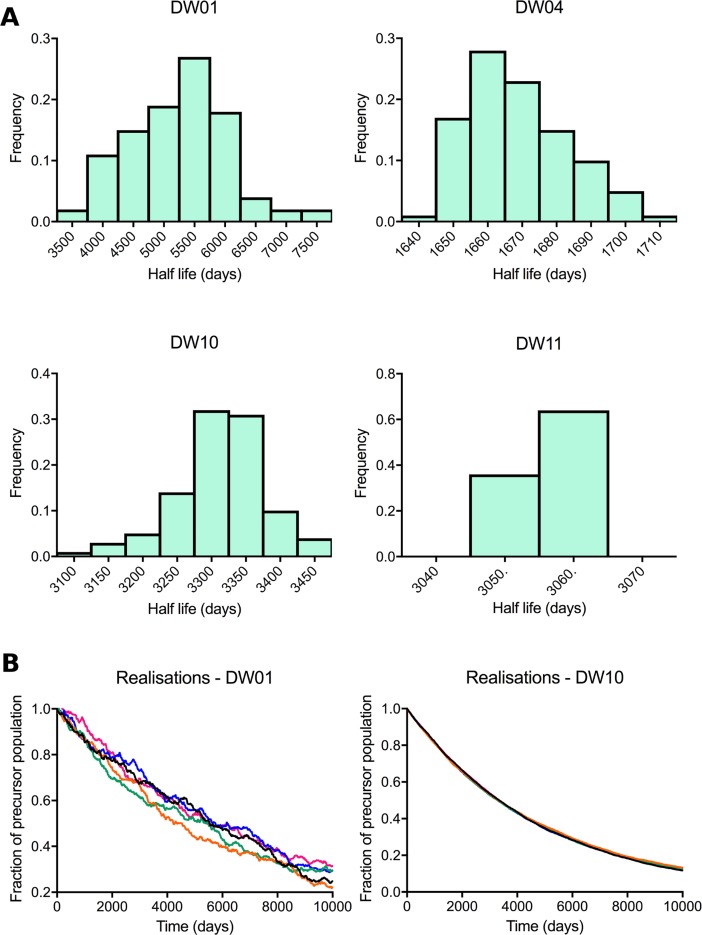
The total CD8+ TSCM population is small (2%–3% of circulating CD8+ lymphocytes [19], 1%–5% of lymph node–resident CD8+ T cells [35]). If only a proportion of this already small population is responsible for maintaining memory, then this raises the issue that, although the precursor population specific for a given antigen may have a long half-life, the small size of that population could mean that its dynamics are highly stochastic. That is, there may be wide ranges in the length of memory, and some antigen-specific precursor populations would be predicted to be lost by stochastic extinction soon after generation—i.e., memory would be erratic and fallible. To investigate the stochasticity of the length of memory within the long-lived TSCM pool, we performed Gillespie simulations of the size of the antigen-specific precursor population based on the parameter estimates derived from model fitting for each of the 4 individuals with CD8+ T cell data. Although there was stochasticity in the half-lives of antigen-specific precursors across different runs, the variation was not large (Fig 6A), and the different trajectories were tightly clustered (Fig 6B).
Fig 6. Stochastic dynamics of the long-lived antigen-specific TSCM populations.
Gillespie simulations of the change in size of antigen-specific precursor populations within the long-lived TSCM pool were performed for each individual. (A) Distribution of antigen-specific precursor population half-lives. (B) Five randomly chosen Gillespie simulations for the 2 subjects exhibiting the most interrealisation variation (DW01 and DW10). Simulations were performed using the TSCM parameters estimated by fitting the explicit heterogeneity model (Table 1 and S2 Table). All results depicted are provided in S1 Data. TSCM, stem cell–like memory T.
Subpopulation kinetics: Compatibility with long half-lives between 5 and 15 years
Concerned that the YFV vaccine, which is known to generate an exceptional CD8+ T cell response, may not be representative of a typical antigen, we also sought to study TSCM dynamics independent of the YFV dataset. Guided by the concept that there may be a long-lived TSCM subpopulation, we fitted the explicit kinetic heterogeneity model to the isotope labelling and telomere length data, ignoring the YFV data but imposing a half-life greater than 5 years on the long-lived TSCM subpopulation. As expected, parameters could no longer be reliably identified, but we were able to conclude that the dynamics of CD8+ TSCM cells were compatible with long subpopulation half-lives between 5 and 15 years (S2 Fig). This approach also allowed us to study CD4+ TSCM cells (which were not measured in the YFV study). Again, we found that the dynamics of CD4+ TSCM cells were compatible with the presence of a similarly long-lived subpopulation with a half-life between 5 and 15 years (S3 Fig).
Discussion
One leading explanation for the maintenance of long-term immunological memory is the existence of a stem cell–like population of memory T cells, able to both self-renew and to differentiate into all other subsets of the T cell memory pool [12, 17, 21]. It has been suggested that the recently discovered TSCM population is the main stem cell population responsible for maintaining T cell memory [18, 36].
In a previous study, we used stable isotope labelling to investigate TSCM dynamics at equilibrium in healthy subjects [26]. This revealed unexpectedly high rates of turnover in the CD4+ and CD8+ TSCM compartments. Whilst supporting the concept that the TSCM population as a whole is stable, it did not establish whether new TSCM cells were generated from naïve cells or by TSCM proliferation. Moreover, the key parameters of clonal longevity and self-renewal, which are prerequisites for stemness, could not be deconvoluted. Given that TSCM cells were found to die and be replaced rapidly, the source of the replacing cell becomes critical. Even a small contribution from naïve cells can result in a weakly self-renewing population and loss of memory as existing clones are replaced by cells specific for a different antigen.
In the present study, we overcame these limitations by simultaneously fitting telomere length and tetramer data to constrain the space of possible models and improve parameter identifiability. We report that firstly, the TSCM population is kinetically heterogeneous, with at least 2 kinetically distinct subpopulations turning over at different rates; and secondly, the dynamics of a subpopulation of TSCM cells are compatible with their hypothesised role as the main stem cell–like T cell precursor responsible for the maintenance of T cell memory. The best description of the data is one in which the kinetically heterogeneous TSCM population, despite its high average replenishment rate of approximately 2% per day, contained a fraction of long-lived TSCM cells. The half-life of this slower subpopulation was approximately 9 years, consistent with the 8–15 year half-life estimated for the recall response to a given antigen [3, 4]. Furthermore, although this subpopulation was small, the dynamic behaviour of individual clones was not excessively stochastic, and the half-life of a given antigen-specific precursor population was tightly distributed. Finally, we estimated that the degree of self-renewal of the long-lived TSCM subpopulation was approximately 4,600 days.
The quantification of the dynamics of TSCM cells is not easily addressed in humans, and different studies invariably involve different compromises. An advantage of our study is that it examines the natural dynamics of TSCM cells in healthy, lymphocyte-replete individuals. A disadvantage is that many of the model parameters were poorly identifiable; nevertheless, firm conclusions about clonal longevity and self-renewal can be drawn. A second disadvantage is that it utilises vaccination data generated using a vaccine (the YFV-17D vaccine) known for its ability to generate an exceptional CD8+ T cell response and which may not be representative of average immunity. To address this potential caveat, we repeated our analysis without reference to the YFV vaccination data. Whilst this reduced our ability to estimate individual parameters, it did confirm the conclusion that the TSCM population consists of subpopulations with different kinetics and that high turnover and short half-lives of the bulk TSCM population do not rule out the existence of a slowly turning over subpopulation with the dynamic properties required for TSCM cells to maintain both CD4+ and CD8+ T cell memory. Finally, it should be noted that our study was confined to circulating TSCM cells. In mice, it has been shown that memory T cell dynamics can vary across different anatomical compartments (spleen versus bone marrow) [37]. For human studies, ethical and technical considerations mean that repeated sampling of cells must be limited to the peripheral blood compartment. However, this does enable direct comparison with previously reported data, including the seminal description of human TSCM cells [16], which was based on circulating cells.
Our findings of kinetic heterogeneity in the human TSCM population are reminiscent of the proliferative heterogeneity described for transplanted HSCs in lethally irradiated mice [38], in which levels of Kit receptor distinguished cell subpopulations with different expansion capacities. Similarly, studies of human CD4+ and CD8+ TSCM cells cultured in the presence of cytokines (either interluekin 15 [IL-15] or interluekin 7 [IL-7] + IL-15) in vitro have also reported that a fraction of cells proliferated rapidly, while the majority remained quiescent [39] [19]. Finally, in rhesus macaques, circulating TSCM cells had a level of Ki-67 expression that the author remarked was ‘unexpectedly large’ (mean > 10%) [36]; this is consistent with our finding that, on average, the TSCM population in peripheral blood turns over rapidly. Our proliferation rate estimates for naïve and TSCM cells can be compared with proliferation rate estimates of other T cell subsets obtained using stable isotope labelling. We found that the proliferation of naïve T cells is slowest, p = 0.0005d−1, and comparable with previous estimates [40], though in this latter study, the gating strategy would have inadvertently included TSCM cells in the naïve cell gate. Next is the slow TSCM subpopulation with a proliferation rate an order of magnitude faster than naïve cells (p = 0.002d−1), then the fast TSCM subpopulation with a median proliferation rate of p = 0.015d−1 comparable with that of memory cells (0.006d−1–0.02d−1 [29, 41]). Giving the following rank order of proliferation rates: naïve < slow TSCM < fast TSCM ≲ memory. Our estimate of the degree of self-renewal is more difficult to place in context. To the best of our knowledge, this parameter has only been quantified previously for murine HSCs. Our estimate of 4,600 days for the degree of self-renewal of the long-lived TSCM subpopulation is naturally less than the corresponding estimate for murine HSC—which is, by definition, infinite—but is greater than the degree of self-renewal of compartments immediately adjacent to HSCs in the differentiation pathway—namely, short-term HSCs (degree of self-renewal of 90–150 days in mice) and multipotent progenitors (MPPs; degree of self-renewal of 7–28 days in mice) [23, 34]. If we convert to ‘animal lifespans’ (80 years for human, 2 years for mice; a scaling which appears valid for T cell kinetics [41]), then we see that the degree of self-renewal of TSCM cells is 0.15 lives; i.e., a long-lived TSCM cell resides without dying or differentiating for approximately 15% of our lifespan. This is similar to the degree of self-renewal of short-term HSCs (0.12–0.2 lives) and greater than the degree of self-renewal of MPPs (0.01–0.04 lives). It is remarkable that a peripheral cell population that is towards the end of the haematopoietic differentiation pathway should have a degree of self-renewal that is comparable with short-term HSCs.
Unexpectedly, we found strong evidence for continual differentiation of naïve T cells into the TSCM cell pool despite the study volunteers being healthy with no symptomatic infection. For both the implicit and the explicit heterogeneity models, the contribution of naïve cells to TSCM replacement was typically about 50% and never less than 10% (Fig 4B and 4F). This may represent differentiation of naïve cells in response to continual low-level exposure to novel environmental antigen and/or to persistent antigen. Considerable recruitment of naïve cells to the memory pool in the apparent absence of novel antigen has been previously described for mice persistently infected with Polyoma virus [42] or lymphocytic choriomeningitis virus [42] and for healthy mice [43].
The role of the short-lived TSCM subpopulation that we identify is unclear. Potentially, it is activated naïve cells rapidly transitioning to effectors whilst others are retained to form the long-lived TSCM pool that is the basis of memory. This is consistent with recent evidence that TSCM cells may pass through a phase in which they express effector molecules [44].
This work suggests a number of future directions. One important direction is to establish phenotypic markers to distinguish the ‘true’ TSCM subpopulation. A second is to develop a model to predict the TCR repertoire of the true TSCM subpopulation and whether this differs from bulk TSCM cells and the functional consequences of any such difference. Finally, it is important to know whether or not murine TSCM populations are similarly heterogeneous, since this would facilitate a whole range of experiments not possible in humans.
Our results show that substantial kinetic heterogeneity exists within the TSCM pool, encompassing a long-lived subpopulation with the dynamic properties required to maintain both CD4+ and CD8+ T cell memory. Further characterisation of these bona fide TSCM cells may illuminate the mechanistic basis of durable immune protection and facilitate translational efforts to develop more effective vaccines and immunotherapies.
Methods
Experimental data
Ethics statement
Approval was granted by the Cardiff University School of Medicine and London-Chelsea Research Ethics Committees (REC: 13/LO/0022. IRAS: 109455). All studies were conducted according to the Principles of the Declaration of Helsinki, and all subjects gave written consent.
Study participants
Five healthy adults were studied (DW01, age 32; DW02, age 64; DW04, age 83; DW10, age 34; DW11, age 29). All subjects were CMV-seropositive and HIV-1-seronegative.
Stable isotope labelling in vivo
We have previously described the labelling protocol in detail [26]. Briefly, participants were given oral doses of 70% deuterated water (2H2O) over a 7-week period (50 ml 3 times daily for 1 week, then twice daily thereafter). Saliva samples were collected for evaluation of body water labelling. Venous blood was drawn at successive time points during and after labelling. Peripheral blood mononuclear cells were sorted at high purity, using a custom-modified BD FACSAria II flow cytometer, into CD4+ and CD8+ naïve and TSCM cells on the basis of cell surface expression (naïve: CD45RO―CD27brightCCR7+CD95― TSCM: CD45RO―CD27brightCCR7+CD95+). Both subsets were further assessed for expression of other cell surface markers; TSCM cells were found to be CD45RA+, CD28+, CD127+, and CD57― (Fig 1). Deuterium enrichment in the DNA of the sorted T cell subsets was measured by gas chromatography/mass spectrometry [45].
Single-chromosome telomere length analysis
DNA from CD4+ and CD8+ naïve and TSCM cells (sorted as for stable isotope labelling analysis) was extracted, and single-telomere length analysis was carried out at the XpYp telomere as described previously [46].
Yellow fever vaccine data
Published data were acquired from a cross-sectional study of 37 healthy adults who received a single dose of the yellow fever vaccine YF-17D [21]. Time since vaccination ranged from 3 months to 35 years. Four subjects who received multiple YFV vaccinations were excluded from the analysis. CD8+CD45RA+CCR7INT TSCM cells specific for the HLA-A*02-restricted YFV NS4b214-222 epitope were quantified by tetramer staining and flow cytometry.
Mathematical modelling
Homogeneous and implicit heterogeneous models
To study the dynamics of TSCM clones, we developed an ODE model of the linear differentiation pathway between naïve and TSCM cells (Fig 2). Nonlinear models of differentiation were not considered [47]. In the classical model of TSCM formation, dedifferentiation of TCM, TEFF, and TEM cells to TSCM is infrequent [48–50], so we assumed a one-way differentiation pathway. Immunological memory has been shown to be generated by clonal expansion, in which naïve cells encountering antigen in lymphoid tissue undergo several rounds of division [1, 51–53]. We assume that newly generated TSCM cells can arise in 2 ways: either they are the product of self-renewal (proliferation of TSCM cells, ps), or they result from the differentiation of naïve cells following antigen exposure at a rate Δ. We assume that naïve and TSCM cells are in constant recirculation between lymph and blood [15, 19], giving the following equations:
| (1) |
| (2) |
in which TN and TSCM are the total number of cells in the naïve and TSCM populations, respectively; pn, dn, ps, and ds the proliferation and disappearance rates of naïve and TSCM cells, respectively; Δ is the fraction of naïve cells activated by antigen exposure per day; and k is the number of divisions occurring during clonal expansion in the differentiation from naïve to TSCM cells (resulting in 2k TSCM cells generated from each naïve cell). A value of k equal to 1 indicates that naïve cells divide only once after priming, and a value of k equal to 0 indicates that no divisions occur after antigen exposure. Deuterium-labelling experiments measure the fraction of deoxyadenosine nucleosides (dAs) with incorporated deuterium, so we construct the model in terms of dAs. The absolute numbers of labelled dAs derived from Eqs 1 and 2 are
| (3) |
| (4) |
in which and represent the absolute numbers of labelled dAs from naïve and TSCM cells, respectively; and are the disappearance rates of labelled naïve and TSCM cells, respectively; c is the amplification factor for enrichment; and U(t) is an empirical function describing label availability as measured in saliva [40]:
| (5) |
| (6) |
in which τ represents the time at which the administration of label is stopped, fr represents the fraction of deuterium in water, δ the turnover rate per day of body water, and β the baseline saliva enrichment. Parameters fr, β, and δ are known to vary between individuals, and their values were obtained by fitting Eqs 5 and 6 to successive measurements of label enrichment in saliva from each subject. The measured body water enrichments with best fits are shown in S4 Fig; estimates of fr, β, and δ are provided in S4 Table. The equations for the fraction of labelled dAs are then
| (7) |
| (8) |
While the naïve pool has been observed to be kinetically homogeneous [40], the heterogeneity of the TSCM population has not yet been explored. We have previously argued [28] that if a cell population is kinetically heterogeneous, the rate of label uptake during a labelling experiment will not be equal to the rate at which the label is lost. This scenario arises because the labelled population (and therefore the disappearance rate estimated from it) will not be representative of the whole population, as subpopulations with faster kinetics divide faster and will be overrepresented in the labelled cells. We can therefore impose kinetic homogeneity on the TSCM pool (‘homogenous model’) by constraining where 2kΔTN + psTSCM = dsTSCM. Removal of this constraint is equivalent to allowing the TSCM pool to be heterogeneous (‘implicit heterogeneity model’). Assuming kinetic homogeneity in the naïve pool, the equations for the fractions of labelled DNA at steady state are therefore
| (9) |
| (10) |
in which yields the homogeneous version of the model, and, if is free, then this yields the implicit heterogeneity version of the model. We also tested a version of the model in which the assumption of homogeneity for naïve cells (dn* = dn) was relaxed.
The explicit heterogeneous model
The implicit heterogeneous model (Eqs (9) and (10)) describes the average population dynamics of a heterogeneous TSCM pool. However, to estimate the sizes, the proliferation, and the disappearance rates of each of the TSCM subpopulations, these subpopulations need to be modelled explicitly. The explicit heterogeneous model describes 2 kinetically distinct subpopulations of TSCM cells. Additional subpopulations could not be resolved with the available data. If there are more than 2 subpopulations with distinct kinetics, then the subpopulation 1 and subpopulation 2 that we measure will have kinetics that represent the average of their smaller constituent subpopulations. The equations for the total numbers of cells in each of the modelled pools are
| (11) |
| (12) |
| (13) |
in which f is the proportion of cells from the clonal burst (of size 2k) that differentiate into the second TSCM subpopulation; ps1, ds1, ps2 and ds2 are the proliferation and disappearance rates of TSCM1 and TSCM2 cells, respectively; and the remaining parameters are as described for Eqs (3) and (4). The absolute number of labelled dAs derived from Eqs 11, 12, and 13 are
| (14) |
| (15) |
| (16) |
and the fractions of labelled DNA assuming steady state for cell population sizes are
| (17) |
| (18) |
| (19) |
Telomere length model (for homogeneous and implicit heterogeneity models)
Following de Boer and Noest [54], we derived an ODE model to describe the progressive shortening with division of the average telomere lengths in the naïve and TSCM cell populations (Fig 2B) for the homogenous and implicit heterogeneity models. The equivalent derivation for the explicit heterogeneity model follows the same pattern and is presented in the SI.
TN and TSCM cell populations were modelled as a series of n compartments, with TNi (or TSCMi) representing the number of TN (or TSCM) cells that have divided i times. If δ is the number of base pairs lost per cell division, then the cells in TNi (or TSCMi) have decreased their telomere lengths by δi base pairs. From Eqs (1) and (2) above, the number of cells in the TNi and TSCMi compartments are
| (20) |
| (21) |
in which pn, Δ, dn, ps, ds, and k are as in Eqs 1 and 2, and C is a parameter to allow for the impact of telomerase. If C = 0, then no shortening of telomeres occurs during clonal expansion (total compensation by telomerase); if C = k, then there is no compensation by telomerase. Experimental evidence suggests that, both for HSCs and peripheral T cells, telomerase attenuates, but does not prevent, telomere loss [55], i.e., 0 < C < k. The equations for the average number of divisions undergone by the cells in the naïve and the TSCM pools in our model (Eqs 20 and 21) follow trivially from the derivation in [54] and are given by
| (22) |
| (23) |
Average telomere lengths are obtained by multiplying μTN and μTSCM by δ. We define the difference between the average telomere lengths in the TN and the TSCM pool (in units of base pairs). The dynamics of Θ are then given by
| (24) |
Finally, when Eq 24 reaches steady state (shown numerically to have occurred for all subjects), then
| (25) |
We use an estimate of δ = 50 bp/division, within the reported range of 35–70 bp/division [54]. Including the telomere data helps to constrain the model fit by placing a bound on the maximum number of divisions occurring between an average naïve T cell and an average TSCM cell.
Computing clonal lifespans and half-lives
We computed the half-life of a clone deterministically from the TSCM parameters estimated by fitting the ODE models. We are interested in the half-life of the memory (rather than the classically reported population half-life), and so this is defined as
| (26) |
Antigen-specific precursor lifespans (time until the last cell of an antigen-specific memory precursor population disappears) were computed stochastically using the exact Gillespie algorithm [56, 57]. At each step of the algorithm, either a division or a disappearance event is chosen, with respective probabilities of x(t)p/S(t) and x(t)d/S(t), in which p and d are the proliferation and disappearance rates of the TSCM population; x(t) is population size at time t; and S(t) is the sum of x(t)p and x(t)d. At the end of each step, time t is incremented by a number of days sampled from an exponential distribution with rate S(t). As the naïve T cell population in an adult human has an approximate size of 1011 cells [58], we estimate the initial size of a TSCM clone in the long-lived subpopulation as
| (27) |
in which k is the number of divisions that occur during clonal expansion in the differentiation from TN to TSCM, Δ is the fraction of naïve cells activated by the same antigen, and f is the fraction of a newly generated clone that enters the long-lived pool. Antigen-specific T cell precursor frequency has been estimated in the naïve cell pool at <1 to 352 per 105 naïve CD8+ cells [59]. For estimates of precursor lifespan in the implicit heterogeneity model, we fixed Δ to a representative value of 1 × 10−5 (and as we are considering average lifespan, f = 1). For estimates of precursor lifespan of the long-lived TSCM subpopulation obtained using the explicit heterogeneity model, the values of Δ and f estimated by model fitting were used. Calculations of the initial size of a long-lived TSCM clone are provided in S5 Table.
Model of the frequency of YFV-specific CD8+ TSCM cells
The proportion of tetramer+ TSCM cells expressed as a fraction of CD8+ CD16− lymphocytes as a function of time since vaccination was modelled, allowing for 2 kinetically distinct subpopulations with exponential decay kinetics:
| (28) |
Degree of self-renewal
The degree of self-renewal of the long-lived TSCM subpopulation (TSCM2) is defined as
| (29) |
Fitting procedures
Models were fitted to the experimental data by minimizing the sum of squared residuals, using the pseudoOptim algorithm from the FME package in R [60, 61]. Details of the fitting procedure, the different models, data fitted, and rationale are summarised in the Supplementary Methods in S1 Text.
Script availability
The scripts used for fitting the homogenous model, the implicit heterogeneous model, and the explicit heterogeneous model, as well as the script for running the Gillespie simulation, are all freely available at Zenodo DOI 10.5281/zenodo.1253178 [27].
Statistics
The fit of the homogenous and heterogeneous model was compared using Fisher’s F-test for nested models. This test compares the goodness of fit of nested models to data, taking into account the different number of parameters in the models [62].
Supporting information
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
Acknowledgments
This work was facilitated by the Imperial College High Performance Computing Service.
Abbreviations
- CCR7
C-C chemokine receptor 7
- dA
deoxyadenosine nucleoside
- FSC-A
forward scatter area
- FSC-H
forward scatter height
- HSC
haematopoietic stem cell
- IL-7
interleukin 7
- IL-7Rα
interleukin 7 receptor alpha
- IL-15
interleukin 15
- MPP
multipotent progenitor
- NS4b
nonstructural protein 4b
- ODE
ordinary differential equation
- SSC-A
side scatter area
- TCM
central memory T
- TCR
T cell receptor
- TEFF
T effector
- TEM
effector memory T
- TSCM
stem cell–like memory T
- YFV
yellow fever virus
Data Availability
All relevant data are within the paper and its Supporting Information files.
Funding Statement
Wellcome Trust (grant number 103865 and 093053/Z/10/Z). B.A. is a Wellcome Trust Investigator (103865). The generation of the labelling data was partially funded by the Wellcome Trust (093053/Z/10/Z). The funder had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. Medical Research Council UK (grant number J007439 and G1001052). B.A. is funded by the Medical Research Council UK (J007439 and G1001052). The funder had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. European Union Seventh Framework Programme (grant number 317040 [QuanTI]). B.A., P.C.d.A, and J.L.B are funded by the European Union Seventh Framework Programme (FP7/2007–2013) under grant agreement 317040 (QuanTI). The funder had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. Wellcome Trust (grant number). D.A.P. is a Wellcome Trust Senior Investigator. The funder had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. Cancer Research UK (grant number C17199/A18246). D.M.B is funded by Cancer Research UK (C17199/A18246). The funder had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Farber DL, Yudanin NA, Restifo NP. Human memory T cells: generation, compartmentalization and homeostasis. Nat Rev Immunol. 2014;14(1):24–35. doi: 10.1038/nri3567 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ahmed R, Gray D. Immunological memory and protective immunity: understanding their relation. Science. 1996;272(5258):54–60. [DOI] [PubMed] [Google Scholar]
- 3.Crotty S, Felgner P, Davies H, Glidewell J, Villarreal L, Ahmed R. Cutting edge: long-term B cell memory in humans after smallpox vaccination. J Immunol. 2003;171(10):4969–73. [DOI] [PubMed] [Google Scholar]
- 4.Hammarlund E, Lewis MW, Hansen SG, Strelow LI, Nelson JA, Sexton GJ, et al. Duration of antiviral immunity after smallpox vaccination. Nat Med. 2003;9(9):1131–7. doi: 10.1038/nm917 [DOI] [PubMed] [Google Scholar]
- 5.Fearon DT, Manders P, Wagner SD. Arrested differentiation, the self-renewing memory lymphocyte, and vaccination. Science. 2001;293(5528):248–50. doi: 10.1126/science.1062589 [DOI] [PubMed] [Google Scholar]
- 6.Macallan DC, Borghans JA, Asquith B. Human T Cell Memory: A Dynamic View. Vaccines. 2017;5(1):E5–57. doi: 10.3390/vaccines5010005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mackay LK, Stock AT, Ma JZ, Jones CM, Kent SJ, Mueller SN, et al. Long-lived epithelial immunity by tissue-resident memory T (TRM) cells in the absence of persisting local antigen presentation. Proceedings of the National Academy of Sciences of the United States of America. 2012;109(18):7037–42. doi: 10.1073/pnas.1202288109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Jiang X, Clark RA, Liu L, Wagers AJ, Fuhlbrigge RC, Kupper TS. Skin infection generates non-migratory memory CD8+ T(RM) cells providing global skin immunity. Nature. 2012;483(7388):227–31. doi: 10.1038/nature10851 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Di Rosa F. Maintenance of memory T cells in the bone marrow: survival or homeostatic proliferation? Nat Rev Immunol. 2016;16(4):271. [DOI] [PubMed] [Google Scholar]
- 10.Sallusto F, Geginat J, Lanzavecchia A. Central memory and effector memory T cell subsets: function, generation, and maintenance. Annu Rev Immunol. 2004;22:745–63. doi: 10.1146/annurev.immunol.22.012703.104702 [DOI] [PubMed] [Google Scholar]
- 11.Stemberger C, Neuenhahn M, Gebhardt FE, Schiemann M, Buchholz VR, Busch DH. Stem cell-like plasticity of naive and distinct memory CD8+ T cell subsets. Semin Immunol. 2009;21(2):62–8. doi: 10.1016/j.smim.2009.02.004 [DOI] [PubMed] [Google Scholar]
- 12.Graef P, Buchholz VR, Stemberger C, Flossdorf M, Henkel L, Schiemann M, et al. Serial transfer of single-cell-derived immunocompetence reveals stemness of CD8(+) central memory T cells. Immunity. 2014;41(1):116–26. doi: 10.1016/j.immuni.2014.05.018 [DOI] [PubMed] [Google Scholar]
- 13.Gerlach C, Rohr JC, Perie L, van Rooij N, van Heijst JW, Velds A, et al. Heterogeneous differentiation patterns of individual CD8+ T cells. Science. 2013;340(6132):635–9. [DOI] [PubMed] [Google Scholar]
- 14.Zhang Y, Joe G, Hexner E, Zhu J, Emerson SG. Host-reactive CD8+ memory stem cells in graft-versus-host disease. Nat Med. 2005;11(12):1299–305. doi: 10.1038/nm1326 [DOI] [PubMed] [Google Scholar]
- 15.Lugli E, Gattinoni L, Roberto A, Mavilio D, Price DA, Restifo NP, et al. Identification, isolation and in vitro expansion of human and nonhuman primate T stem cell memory cells. Nature Protocols. 2013;8(1):33–42. doi: 10.1038/nprot.2012.143 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Gattinoni L, Lugli E, Ji Y, Pos Z, Paulos CM, Quigley MF, et al. A human memory T cell subset with stem cell-like properties. Nature Medicine. 2011;17(10):1290–7. doi: 10.1038/nm.2446 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Biasco L, Scala S, Basso Ricci L, Dionisio F, Baricordi C, Calabria A, et al. In vivo tracking of T cells in humans unveils decade-long survival and activity of genetically modified T memory stem cells. Sci Transl Med. 2015;7(273):273ra13 doi: 10.1126/scitranslmed.3010314 [DOI] [PubMed] [Google Scholar]
- 18.Gattinoni L, Speiser DE, Lichterfeld M, Bonini C. T memory stem cells in health and disease. Nat Med. 2017;23(1):18–27. doi: 10.1038/nm.4241 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gattinoni L, Lugli E, Ji Y, Pos Z, Paulos CM, Quigley MF, et al. A human memory T cell subset with stem cell-like properties. Nat Med. 2011;17(10):1290–7. doi: 10.1038/nm.2446 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Fisman DN, Savage R, Gubbay J, Achonu C, Akwar H, Farrell DJ, et al. Older age and a reduced likelihood of 2009 H1N1 virus infection. N Engl J Med. 2009;361(20):2000–1. doi: 10.1056/NEJMc0907256 [DOI] [PubMed] [Google Scholar]
- 21.Fuertes Marraco SA, Soneson C, Cagnon L, Gannon PO, Allard M, Abed Maillard S, et al. Long-lasting stem cell-like memory CD8+ T cells with a naive-like profile upon yellow fever vaccination. Sci Transl Med. 2015;7(282):282ra48 doi: 10.1126/scitranslmed.aaa3700 [DOI] [PubMed] [Google Scholar]
- 22.Oliveira G, Ruggiero E, Stanghellini MT, Cieri N, D'Agostino M, Fronza R, et al. Tracking genetically engineered lymphocytes long-term reveals the dynamics of T cell immunological memory. Sci Transl Med. 2015;7(317):317ra198 doi: 10.1126/scitranslmed.aac8265 [DOI] [PubMed] [Google Scholar]
- 23.Busch K, Klapproth K, Barile M, Flossdorf M, Holland-Letz T, Schlenner SM, et al. Fundamental properties of unperturbed haematopoiesis from stem cells in vivo. Nature. 2015;518(7540):542–6. doi: 10.1038/nature14242 [DOI] [PubMed] [Google Scholar]
- 24.Sun J, Ramos A, Chapman B, Johnnidis JB, Le L, Ho Y-J, et al. Clonal dynamics of native haematopoiesis. Nature. 2014;514(7522):322–7. doi: 10.1038/nature13824 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sawen P, Lang S, Mandal P, Rossi DJ, Soneji S, Bryder D. Mitotic History Reveals Distinct Stem Cell Populations and Their Contributions to Hematopoiesis. Cell Reports. 2016;14(12):2809–18. doi: 10.1016/j.celrep.2016.02.073 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ahmed R, Roger L, Costa Del Amo P, Miners KL, Jones RE, Boelen L, et al. Human Stem Cell-like Memory T Cells Are Maintained in a State of Dynamic Flux. Cell Reports. 2016;17(11):2811–8. doi: 10.1016/j.celrep.2016.11.037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Costa Del Amo P. Scripts from "Human TSCM cell dynamics in vivo are compatible with long-lived immunological memory and stemness". Openly available from Zenodo DOI 105281/zenodo1253178. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Asquith B, Debacq C, Macallan DC, Willems L, Bangham CR. Lymphocyte kinetics: the interpretation of labelling data. Trends in Immunology. 2002;23(12):596–601. [DOI] [PubMed] [Google Scholar]
- 29.Macallan DC, Asquith B, Irvine AJ, Wallace DL, Worth A, Ghattas H, et al. Measurement and modeling of human T cell kinetics. European Journal of Immunology. 2003;33(8):2316–26. doi: 10.1002/eji.200323763 [DOI] [PubMed] [Google Scholar]
- 30.Ganusov VV, Borghans JA, De Boer RJ. Explicit kinetic heterogeneity: mathematical models for interpretation of deuterium labeling of heterogeneous cell populations. PLoS Comput Biol. 2010;6(2):e1000666 doi: 10.1371/journal.pcbi.1000666 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.De Boer RJ, Perelson AS, Ribeiro RM. Modelling deuterium labelling of lymphocytes with temporal and/or kinetic heterogeneity. Journal of the Royal Society, Interface / the Royal Society. 2012;9(74):2191–200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Buchholz VR, Flossdorf M, Hensel I, Kretschmer L, Weissbrich B, Graf P, et al. Disparate individual fates compose robust CD8+ T cell immunity. Science. 2013;340(6132):630–5. [DOI] [PubMed] [Google Scholar]
- 33.Kaech SM, Ahmed R. Memory CD8+ T cell differentiation: initial antigen encounter triggers a developmental program in naive cells. Nature Immunology. 2001;2(5):415–22. doi: 10.1038/87720 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hofer T, Busch K, Klapproth K, Rodewald HR. Fate Mapping and Quantitation of Hematopoiesis In Vivo. Annual Review of Immunology. 2016;34:449–78. doi: 10.1146/annurev-immunol-032414-112019 [DOI] [PubMed] [Google Scholar]
- 35.Hong H, Gu Y, Sheng SY, Lu CG, Zou JY, Wu CY. The Distribution of Human Stem Cell-like Memory T Cell in Lung Cancer. Journal of Immunotherapy. 2016;39(6):233–40. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Lugli E, Dominguez MH, Gattinoni L, Chattopadhyay PK, Bolton DL, Song K, et al. Superior T memory stem cell persistence supports long-lived T cell memory. The Journal of Clinical Investigation. 2013;123(2):594–9. doi: 10.1172/JCI66327 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Siracusa F, Alp OS, Maschmeyer P, McGrath M, Mashreghi MF, Hojyo S, et al. Maintenance of CD8(+) memory T lymphocytes in the spleen but not in the bone marrow is dependent on proliferation. European Journal of Immunology. 2017;47(11):1900–5. doi: 10.1002/eji.201747063 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Grinenko T, Arndt K, Portz M, Mende N, Gunther M, Cosgun KN, et al. Clonal expansion capacity defines two consecutive developmental stages of long-term hematopoietic stem cells. The Journal of Experimental Medicine. 2014;211(2):209–15. doi: 10.1084/jem.20131115 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Abdelsamed HA, Moustaki A, Fan Y, Dogra P, Ghoneim HE, Zebley CC, et al. Human memory CD8 T cell effector potential is epigenetically preserved during in vivo homeostasis. The Journal of Experimental Medicine. 2017;214(6):1593–606. doi: 10.1084/jem.20161760 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Vrisekoop N, den Braber I, de Boer AB, Ruiter AF, Ackermans MT, van der Crabben SN, et al. Sparse production but preferential incorporation of recently produced naive T cells in the human peripheral pool. Proc Natl Acad Sci U S A. 2008;105(16):6115–20. doi: 10.1073/pnas.0709713105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Westera L, Drylewicz J, den Braber I, Mugwagwa T, van der Maas I, Kwast L, et al. Closing the gap between T-cell life span estimates from stable isotope-labeling studies in mice and humans. Blood. 2013;122(13):2205–12. doi: 10.1182/blood-2013-03-488411 [DOI] [PubMed] [Google Scholar]
- 42.Vezys V, Masopust D, Kemball CC, Barber DL, O'Mara LA, Larsen CP, et al. Continuous recruitment of naive T cells contributes to heterogeneity of antiviral CD8 T cells during persistent infection. The Journal of Experimental Medicine. 2006;203(10):2263–9. doi: 10.1084/jem.20060995 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Gossel G, Hogan T, Cownden D, Seddon B, Yates AJ. Memory CD4 T cell subsets are kinetically heterogeneous and replenished from naive T cells at high levels. eLife. 2017;6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Akondy RS, Fitch M, Edupuganti S, Yang S, Kissick HT, Li KW, et al. Origin and differentiation of human memory CD8 T cells after vaccination. Nature. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Busch R, Neese RA, Awada M, Hayes GM, Hellerstein MK. Measurement of cell proliferation by heavy water labeling. Nature Protocols. 2007;2(12):3045–57. doi: 10.1038/nprot.2007.420 [DOI] [PubMed] [Google Scholar]
- 46.Capper R, Britt-Compton B, Tankimanova M, Rowson J, Letsolo B, Man S, et al. The nature of telomere fusion and a definition of the critical telomere length in human cells. Genes Dev. 2007;21(19):2495–508. doi: 10.1101/gad.439107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Wherry EJ, Teichgraber V, Becker TC, Masopust D, Kaech SM, Antia R, et al. Lineage relationship and protective immunity of memory CD8 T cell subsets. Nature Immunology. 2003;4(3):225–34. doi: 10.1038/ni889 [DOI] [PubMed] [Google Scholar]
- 48.Appay V, van Lier RA, Sallusto F, Roederer M. Phenotype and function of human T lymphocyte subsets: consensus and issues. Cytometry Part A: the Journal of the International Society for Analytical Cytology. 2008;73(11):975–83. [DOI] [PubMed] [Google Scholar]
- 49.Mahnke YD, Brodie TM, Sallusto F, Roederer M, Lugli E. The who's who of T-cell differentiation: human memory T-cell subsets. Eur J Immunol. 2013;43(11):2797–809. doi: 10.1002/eji.201343751 [DOI] [PubMed] [Google Scholar]
- 50.Cieri N, Oliveira G, Greco R, Forcato M, Taccioli C, Cianciotti B, et al. Generation of human memory stem T cells after haploidentical T-replete hematopoietic stem cell transplantation. Blood. 2015;125(18):2865–74. doi: 10.1182/blood-2014-11-608539 [DOI] [PubMed] [Google Scholar]
- 51.Alberts B, Johnson A, Lewis J, Raff M, Roberts K, Walter P. Molecular Biology of the Cell. 4 ed New York: Garland Science; 2002. [Google Scholar]
- 52.Murphy K. Janeway's Immunobiology 8 ed New York: Garland Science; 2012. [Google Scholar]
- 53.von Andrian UH, Mempel TR. Homing and cellular traffic in lymph nodes. Nat Rev Immunol. 2003;3(11):867–78. doi: 10.1038/nri1222 [DOI] [PubMed] [Google Scholar]
- 54.De Boer RJ, Noest AJ. T cell renewal rates, telomerase, and telomere length shortening. J Immunol. 1998;160(12):5832–7. [PubMed] [Google Scholar]
- 55.Rufer N, Brummendorf TH, Kolvraa S, Bischoff C, Christensen K, Wadsworth L, et al. Telomere fluorescence measurements in granulocytes and T lymphocyte subsets point to a high turnover of hematopoietic stem cells and memory T cells in early childhood. The Journal of Experimental Medicine. 1999;190(2):157–67. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Renshaw E. Stochastic population processes: analysis, approximations, simulations Oxford: Oxford University Press; 2011. xii, 652 p. p. [Google Scholar]
- 57.Wilkinson DJ. Stochastic modelling for systems biology Boca Raton, FL; London: Chapman & Hall/CRC; 2006. 254 p p. [Google Scholar]
- 58.Bains I, Antia R, Callard R, Yates AJ. Quantifying the development of the peripheral naive CD4(+) T-cell pool in humans. Blood. 2009;113(22):5480–7. doi: 10.1182/blood-2008-10-184184 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Neller MA, Ladell K, McLaren JE, Matthews KK, Gostick E, Pentier JM, et al. Naive CD8(+) T-cell precursors display structured TCR repertoires and composite antigen-driven selection dynamics. Immunol Cell Biol. 2015;93(7):625–33. doi: 10.1038/icb.2015.17 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.R: A language and environment for statistical computing. Available from: http://www.R-project.org/. 2014. [cited 2016]
- 61.Soetaert K. R Package FME: Inverse Modelling, Sensitivity,Monte Carlo–Applied to a Dynamic Simulation Model. Available from: https://cran.r-project.org/web/packages/FME/. [cited 2016]
- 62.Stauffer HB. Contemporary Bayesian and frequentist statistical research methods for natural resource scientists Hoboken, N.J.: Wiley-Interscience; 2008. xv, 400 p. p. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
(PDF)
Data Availability Statement
All relevant data are within the paper and its Supporting Information files.