Decoding cortical brain states from widefield calcium imaging data using visibility graph

Abstract

Widefield optical imaging of neuronal populations over large portions of the cerebral cortex in awake behaving animals provides a unique opportunity for investigating the relationship between brain function and behavior. In this paper, we demonstrate that the temporal characteristics of calcium dynamics obtained through widefield imaging can be utilized to infer the corresponding behavior. Cortical activity in transgenic calcium reporter mice (n=6) expressing GCaMP6f in neocortical pyramidal neurons is recorded during active whisking (AW) and no whisking (NW). To extract features related to the temporal characteristics of calcium recordings, a method based on visibility graph (VG) is introduced. An extensive study considering different choices of features and classifiers is conducted to find the best model capable of predicting AW and NW from calcium recordings. Our experimental results show that temporal characteristics of calcium recordings identified by the proposed method carry discriminatory information that are powerful enough for decoding behavior.

1. Introduction

One of the major goals in neuroscience is to understand the relationship between brain function and behavior [1–10]. Towards this goal, imaging techniques capable of recording large numbers of spatially distributed neurons, with high temporal resolution, are critical for understanding how neuronal population contribute to changes in brain states and behavior. Widefield fluorescence imaging of genetically encoded calcium indicators (GECIs) is one such technique [11]. Newly developed GECIs such as GCaMP6 have improved sensitivity and brightness [12, 13] that, when expressed in transgenic reporter mice, enable imaging of neuronal activity of genetically defined neuronal populations over large portions of the cerebral cortex [12, 14–17]. Although widefield imaging lacks the micrometer-scale spatial resolution of non-linear optical methods such as two-photon laser-scanning microscopy [18, 19], the use of epifluorescence optical imaging allows for easier implementation, higher temporal resolution, and much larger fields of view [20, 21]. Two-photon calcium imaging can be used to track individual neurons over time as animals learn [22, 23], but it is difficult to study neurons in spatially segregated cortical areas. Furthermore, long-term widefield imaging can be performed through either cranial windows or a minimally invasive intact skull preparation in living subjects over multiple weeks [9, 24]. These developments in widefield imaging have opened new possibilities for studying large-scale dynamics of brain activity in relation to behavior [9, 10], for example, during locomotion and active whisker movements in mice [6, 14, 25–29].

Inferring about the behavior, intent, or the engagement of a particular cognitive process, from neuroimaging data, finds applications in several domains including brain machine interfaces (BMIs) [30–32]. Depending on the type of physiological activity that is monitored, various computational techniques have been suggested to infer or decode the intent or the cognitive state of the subject from recorded brain activities. Methods based on functional specificity [33, 34], brain connectivity patterns [2, 3, 35], and power spectral density [36], to name a few, have been suggested. However, the estimation power of such methods has been limited to distinguishing very distinct classes of motor activities or cognitive processes [37]. As such the community has been searching for alternative methods to improve the power of inference.

Given the time-varying nature of the brain function, in this work, we focus on the time domain information. We hypothesize that there exist “characteristics” in the time course of cortical activities that are specific to the corresponding behavior. The key challenge is to develop methods that can reliably identify such discriminatory characteristics in cortical recordings. To test the hypothesis, we use transgenic calcium reporter mice expressing GCaMP6f specifically in neocortical pyramidal neurons to image neural activity in nearly the entire left hemisphere and medial portions of the right hemisphere in head-fixed mice, including sensory and motor areas of the neocortex. For behavior, we focus on active whisking (AW) and no whisking (NW). Quiet wakefulness, in the absence of locomotion or whisking, is associated with low frequency synchronized cortical activity, while locomotion and whisking are associated with higher frequency desynchronized activity in primary sensory areas of the cortex [6, 38–41]. Recent studies indicate that active, arousal-related behaviors such as locomotion and whisking are associated with widespread modulation of cortical activation [14, 29]. Therefore, prior evidence exists for differences in the time courses of activities related to changes in behavioral states.

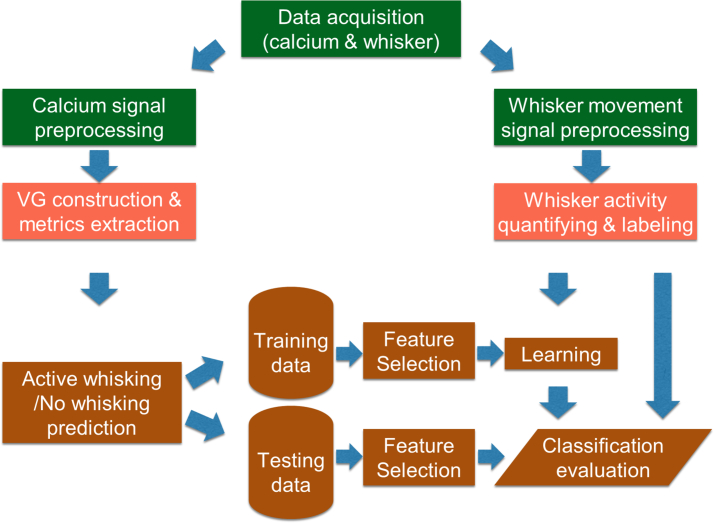
To identify features in calcium imaging data that would be unique to behavior (here AW or NW), we propose to use visibility graph (VG) [42]. As will be discussed, VG provides a means to “quantify” various properties of a given time series, enabling a path to extract temporal-based features that are unique to the characteristics of the time series. We construct the VG representation of the recordings for each region of interest (ROI), extract the graph measures, and build features based on the graph measures for all ROIs. We conduct an extensive study to identify the best model capable of inferring AW and NW for each subject, from cortical recordings. Fig. 1 provides a summary of the procedure.

Fig. 1.

Summary of the proposed analysis procedure.

The novelty of our work is the introduction of the visibility graph for extracting features that are related to the temporal characteristics of recorded calcium time series. It is shown that the temporal features of calcium recordings extracted through VG, carry discriminatory information for inferring the corresponding behavior. While in this study, we consider cortical signals from the entire left hemisphere and medial part of the right hemisphere, and focus on whisking condition, given the data-driven nature of the proposed approach, we expect that it would be also applicable to recorded activity from other areas of the brain, such as the thalamus and deep layers of motor cortex, for inferring other forms of behavior or cognitive states.

2. Materials and methods

Before discussing details of data collection and the analysis procedure, we provide clarification about some terminology used throughout the paper. Note that in this study we use the term “decode” and “infer” interchangeably.

The imaged area here refers to the optically accessible cortical area. The imaged area in this study covers the entire left hemisphere, and medial part of the right hemisphere of the cortex.

Behavior in this study is related to whisking condition. Two classes of behavior, active whisking (AW) and no whisking (NW), are considered here. We use the term “brain state” and “behavior” interchangeably.

Features are measures extracted from cortical recordings. To examine how well the proposed features from recorded calcium transients can discriminate the two classes of AW and NW, classification experiments are performed. In these experiments, a classifer refers to the algorithm that is used to perform classification.

A predictive model refers to a trained classifier. The ability of the model to correctly infer (or predict) the whisking condition (AW or NW) from features extracted from cortical recordings, is tested using k-fold cross validation.

We now discuss the widefield imaging experiments, and the methods used in the analysis.

2.1. Animals and surgery

Six mice expressing GCaMP6f in cortical excitatory neurons were used for widefield transcranial imaging [14, 44]. All procedures were carried out with the approval of the Rutgers University Institutional Animal Care and Use Committee. Triple transgenic mice expressed Cre recombinase in Emx1-positive excitatory pyramidal neurons (The Jackson Laboratory; 005628), tTA under the control of the Camk2a promoter (The Jackson Laboratory; 007004) or ZtTA (3/6 mice) under the control of the CAG promoter into the ROSA26 locus (The Jackson Laboratory; 012266) and TITL-GCaMP6f (The Jackson Laborotory; Ai93; 024103). At 7 to 11 weeks of age, mice were outfitted with a transparent skull and an attached fixation post using methods similar to those described previously [9, 14, 45]. Mice were anesthetized with isoflurane (3% induction and 1.5% maintenance) in 100% oxygen, and placed in a stereotaxic frame (Stoelting) with temperature maintained at 36 °C with a thermostatically controlled heating blanket (FHC). The scalp was sterilized with betadine scrub and infiltrated with bupivacaine (0.25%) prior to incision. The skull was lightly scraped to detach muscle and periosteum and irrigated with sterile 0.9% saline. The skull was made transparent using a light-curable bonding agent (iBond Total Etch, Heraeus Kulzer International) followed by a transparent dental composite (Tetric Evoflow, Ivoclar Vivadent). A custom aluminum headpost was affixed to the right side of the skull and the transparent window was surrounded by a raised border constructed using another dental composite (Charisma, Heraeus Kulzer International). Carprofen (5 mg/kg) was administered postoperatively. Following a recovery period of one to two weeks, mice were acclimated to handling and head fixation for an additional week prior to imaging. Mice were housed on a reversed light cycle and all handling and imaging took place during the dark phase of the cycle.

2.2. Widefield imaging of cortical activity and whisker movement recording

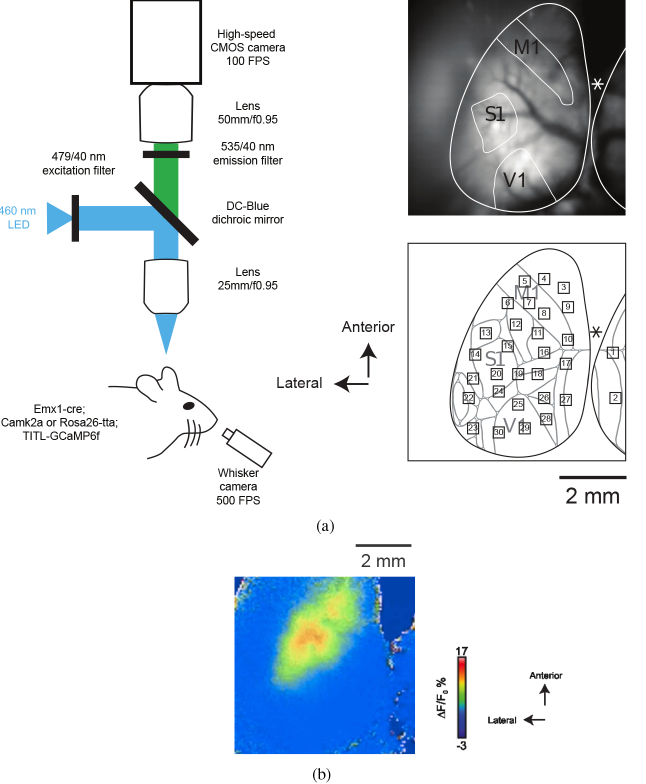
Imaging of GCaMP6f was carried out in head-fixed mice with the transparent skull covered with glycerol and a glass coverslip. A schematic of the imaging system is shown in Fig. 2(a). A custom macroscope [24] allowed for simultaneous visualization of nearly the entire left hemisphere and medial portions of the right hemisphere (as seen in Fig. 2(a)). The cortex was illuminated with 460 nm LED (Aculed VHL) powered by a Prizmatix current controller (BLCC-2). Excitation light was filtered (479/40; Semrock FF01-479/40-25) and reflected by a dichroic mirror (Linos DC-Blue G38 1323 036) through the objective lens (Navitar 25 mm / f0.95 lens, inverted). GCaMP6f fluorescence was filtered (535/40; Chroma D535/40m emission filter) and acquired using a MiCam Ultima CMOS camera (Brain vision) fitted with a 50 mm / f0.95 lens (Navitar). Images were captured on a 100 × 100 pixel sensor. Spontaneous cortical activity was acquired in 20.47 s blocks at 100 frames per second with 20 s between blocks (Fig. 3). Sixteen blocks were acquired in each session and mice were imaged in two sessions in a day. A sample frame obtained during a block is shown in Fig. 2(b). For the corresponding 20 s movie see Visualization 1 ^{(932.2KB, mp4)} .

Fig. 2.

a) Left: Illustration of the experimental setup used for widefield imaging of cortical activity of mice expressing GCaMP6f and simultaneous recording of whisker movement. Right, top: raw image of neocortical surface through transparent skull preparation. M1, S1, and V1 are schematically labeled. Asterisk indicates position of Bregma. Right, bottom: ROIs are superimposed on a map based on the Allen Institute common coordinate framework v3 of mouse cortex (brain-map.org; adapted from [43]). ROI: 1, Retrosplenial area, lateral agranular part (RSPagl); 2, Retrosplenial area, dorsal (RSPd); 3, 4, 9, Secondary motor area (MOs); 5, 7, 8, 10, Primary motor area (MOp); 6, Primary somatosensory area, mouth (SSp-m) / upper limb (SSp-ul); 11, 16, Primary somatosensory area, lower limb (SSp-ll); 12, SS-ul; 13, Primary somatosensory area, nose (SSp-n); 14, 20, Primary somatosensory area, barrel field (SSp-bfd); 15, SSp-bfd / Primary somatosensory area, unassigned (SSp-un); 17, Retrosplenial area, lateral agranular part (RSPagl); 18, Anterior visual area (VISa) / Primary somatosensory area, trunk (SSp-tr); 19, VISa / SSp-tr / SSp-bfd; 21, Supplementary somatosensory area (SSs); 22, Auditory area (AUD); 23, Temporal association areas (TEa); 24, SSp-bfd / Rostrolateral visual area (VISrl); 25, 29, 30, Primary visual area (VISp); 26, Anteromedial visual area (VISam); 27, RSPagl / RSPd; 28, Posteromedial visual area (VISpm). b) A sample 20 s movie obtained during a block. Frames corresponding to “AW” are identified by “W”, shown on the top left of frames (see Visualization 1 ^{(932.2KB, mp4)} ).

Fig. 3.

Experimental protocol that was followed for each subject. Each subject participated in two sessions per day. In each session, spontaneous activity was acquired for sixteen 20.47 s blocks, with 20 s of rest between blocks.

In addition, all whiskers contralateral to the imaged cortical hemisphere were monitored with high-speed video at 500 frames/s using a Photonfocus DR1 camera triggered by a Master-9 pulse generator (AMPI) and Streampix (Norpix) software. Whiskers were illuminated from below with 850 nm infrared light. The mean whisker position was tracked and measured as the changes in angle (in degree) using a well-established, automated whisker-tracking algorithm, freely available in MATLAB [46], that computes the frame-by-frame center of mass of all whiskers in the camera’s field of view. The angle of the center of mass of all whiskers is similar to the average angle of all whiskers tracked individually, because the whiskers do not move independently.

2.2.1. Preprocessing of calcium signals

Changes in GCaMP6f relative fluorescence (ΔF/F₀) for each frame within a recording were calculated by subtracting and then dividing by the baseline. The baseline was defined as the average intensity of the first 49 frames. Two blocks (one from subject #2 and one from subject #3) were excluded from further analysis due to loss of whisker movement data. The length of blocks were shortened to 20 s from 20.47 s for the remaining parts of analysis.

Thirty 5 × 5 pixel regions of interest (ROIs) distributed over the cortex (see Fig. 2(a)) in each frame were defined based on location relative to the bregma point on the skull. In 5/6 mice, whisker stimulation by piezo bending element was used to map the location of S1 barrel cortex. The 30 ROIs were positioned to cover and fill space between areas including somatosensory, visual and motor areas of the cortex (S1, V1, M1) (see Fig. 2(a)). Each pixel is 65 μm side length, and 5 × 5 pixel ROI is 325 × 325 μm. This size ROI is the approximate dimension of a cortical column in sensory cortex, and is consistent with the standard practices in the field [15, 47]. These studies, which examined sensory mapping, spontaneous activity, and task-related activation, have shown that widefield calcium signals do not display signals with resolution better than these dimensions, and therefore, smaller ROIs are not beneficial. The choice of ROI size is therefore, suitable and standard for comparison across different existing datasets. ROI locations were kept the same across subjects. Time series associated with each ROI were obtained by finding the average of pixel intensities within the corresponding ROI.

2.2.2. Labeling data related to active whisking and no whisking conditions

In order to investigate the relationship between behavior and the cortical activity, it is necessary to identify the duration in the recordings that are related to “active whisking” (AW) and “no whisking” (NW) conditions. Here we developed a method to automatically label the duration related to each condition, according to the whisker movement recordings.

The whisker movement time series was segmented using a sliding window. For a given segment i, the standard deviation (SD) of the signal (σ_wi) is computed as ${\sigma }_{w_i}={\sum }_{j=1}^N{\left(x_j-{\mu }_i\right)}^2$, where μ_i represents the mean and N denotes the number of samples within the segment. This procedure generates a new time series of σ_wi s, representing the extent to which the whisker is in motion over the course of observation. A threshold was then set to identify whether the recordings correspond to active whisking (above the threshold) or no whisking (below threshold) conditions. After testing different threshold values and visually inspecting the raw whisker movement signals, a threshold value of 10 was used.

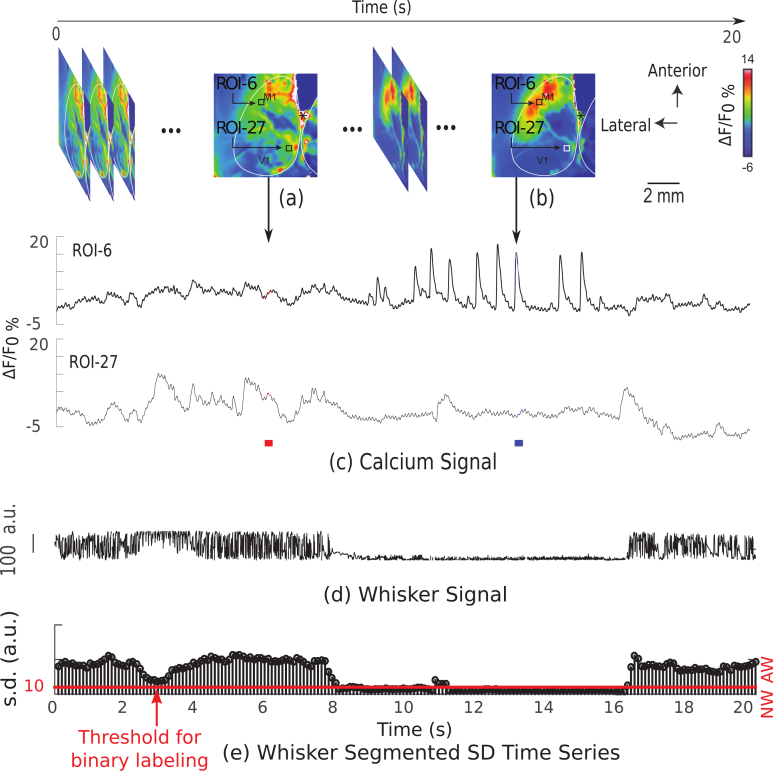
As an example, sample images and time series corresponding to two ROIs (6 and 27) along with whisking movement signal, recorded in block #1 from subject #1, are shown in Fig. 4. The top row illustrates a series of baseline-corrected images. Shown also are the averaged image for the duration of (6.01 − 6.20) s (labeled in red in Fig. 4(c)), where no clear calcium transients are present, and the averaged image for the duration of (13.21 − 13.40) s (labeled in blue in 4(c)), where calcium transients are present.

Fig. 4.

Sample images and time series recorded from block #1 of subject #1. (a)–(b) baseline-corrected images, (c) time series corresponding to ROI-6 and ROI-27, (d) measured angle corresponding to whisker movement signal recorded from the same block, and (e) standard deviation-based time series of the signal, (d) where the threshold level used for labeling AW and NW conditions is shown as a red line.

The measured angle corresponding to whisker movement recordings of the same block is shown in Fig. 4(d), and in Fig. 4(e) the time series obtained based on the standard deviation calculation of sliding window approach discussed in Section 2.2.2 is plotted. The threshold level for determining AW and NW conditions over time, is visualized by a red horizontal line.

2.3. Visibility graph

Here, we first describe the procedure used to construct the visibility graph for a given time series and extracting graph measures.

2.3.1. VG construction

Visibility graph is an effective tool that can be employed to reveal the temporal structure of the time series at different time scales [42, 48–50]. Recently, VG has been receiving increased attention in various studies related to human brain function such as those involving sleep [51], epilepsy [52, 53], Alzheimer’s disease [54], and differentiating resting-state and task-execution states [55]. In these studies, VG has been applied to time series obtained from various imaging modalities such as electroencephalography (EEG) [51–54, 56], functional near-infrared spectroscopy (fNIRS) [55], and functional magnetic resonance imaging (fMRI) [57].

VG maps a time series to a graph, thereby, providing a tool to “visually” investigate different properties of the time series [42, 50]. The VG associated with a given time series x = [x(1), · · · , x(N)] of N points is constructed as follows. Each point in x is considered as a node in the graph (i.e. for an N-point time series, the graph will have N nodes). The link between node pairs is formed only if the nodes are considered to be naturally visible. That is, in the graph, there will be an undirected and unweighted link between nodes i and j, if and only if, for any point p (i < p < j) in the time series, the following condition holds

$$x(p)<x(j)+[x(i)-x(j)][\frac{t(j)-t(p)}{t(j)-t(i)}],$$ (1)

where t(j), t(p) and t(i) are the time corresponding to points j, p, and i [42]. That is, two nodes i and j are connected, if the straight line connecting two data points (t(i), x(i)) and (t(j), x(j)), does not intersect the height of any data point (t(p), x(p)) that exists between them. Accordingly, in the adjacency matrix A_x = {a_i,j} (i, j = 1, · · · , N), the element a_i,j will be set to 1 if the nodes i and j are connected given the definition above, and 0 if otherwise.

2.3.2. Graph measures as features

Once the time series x of N points is mapped to a graph with adjacency matrix A_x = {a_i,j} (i, j = 1, · · · , N) via VG, the topological measures of the graph can be utilized to investigate different properties of the time series. Here, we consider three of such measures: Edge Density (D), Averaged Clustering Coefficient (C), and Characteristic Pathlength (L), as defined below.

• Edge Density (D) measures the fraction of existing edges in the graph with respect to the maximum possible number of edges [58]. The edge density is obtained as

  $$D=\frac{1}{N(N-1)}\sum _{i,j}{a}_{i,j}.$$ (2)

  It can be shown that for a globally convex time series, the value of D would be 1, and for a time series with large number of fluctuations, the value of D would be small. Therefore, the edge density can be considered as a measure of irregularity of fluctuations in the time series [59].
• Averaged Clustering Coefficient (C) is obtained as the average of local clustering coefficients of all nodes in the graph. The local clustering coefficient of the node i (C_i) is defined as the fraction of its connected neighboring nodes to the maximum number of possible connections among the neighboring nodes [58]. The averaged clustering coefficient is computed as

  $$C=\frac{1}{N}\sum _{i=1}^N{C}_i=\frac{1}{N}\sum _{i,j,l}\frac{a_{ij}{a}_{il}{a}_{jl}}{K_i(K_i-1)},$$ (3)

  where K_i represents the degree of node i (the number of edges connected to node i). A large value of C indicates dominant convexity of the time series [59].
• Characteristic Pathlength (L) is found as the average of the shortest pathlength between all node pairs in the graph. The characteristic pathlength is obtained as

  $$L=\frac{1}{N(N-1)}\sum _{i,j}{l}_{ij},$$ (4)

  where l_ij denotes the shortest pathlengh between nodes i and j.

2.4. Classification

To learn models of inferring behavior (as measured by AW and NW) from recordings obtained via widefield calcium imaging of cortical activity, classification experiments are performed. Specifically, we wish to learn classifiers in the following form:

$$f:\text{VG measures}(t_0,t_0+w)\to \left\{\mathit{AW},\mathit{NW}\right\},$$ (5)

where VG Measures (t₀, t₀ +w) represents graph measures that are extracted from VGs associated with calcium signals within the segment [t₀, t₀ + w], and w denotes the window length used for segmentation 3.1.

Here, we briefly describe the feature extraction process, the classifiers, and the measures used to evaluate the classification performance. Classification experiments were executed using GraphLab [60].

2.4.1. Feature extraction

Three graph measures were extracted from the VG associated with each segment (identified by the sliding window) of recordings obtained from individual ROIs. To extensively investigate which measures will result in a better model, seven types of feature vectors were formed. These were D, C, L, D + C, D + L, C + L, and D + C + L. In all cases, feature vectors were constructed using measures from all the ROIs. For example, when considering D as features, for each segment, a feature vector of 30 × 1 is constructed (where 30 represents the number of ROIs).

Five different sliding window duration (1, 1.5, 2, 2.5, and 3 s) were considered for segmentation. As such, the number of segments per recording block varies based on the sliding window duration (39 for 1 s window, 38 for 1.5 s window, 37 for 2 s window, 36 for 2.5 s window, and 35 for 3 s window). There are 32 blocks for subject #1, 4, 5, 6, and 31 blocks for subject #2 and 3. Table 1 summarizes the number of blocks, and the number of AW/NW segments for each subject, when the window duration of 2 s, and window step of 0.5 s are used.

Table 1.

Number of blocks and number of AW/NW segments for each subject, when the window length of 2 s with a step size of 0.5 s is used.

Subject ID	1	2	3	4	5	6	Total	% Total Segments
# Blocks	32	31	31	32	32	32	190
# AW Segments	238	360	240	416	227	153	1634	23.24
# NW Segments	946	787	907	768	957	1031	5396	76.76

2.4.2. Classifiers and evaluation measures

Three commonly-used classifiers were used to perform classification: 1) k-nearest neighbor (kNN), 2) regularized logistic regression (LR), and 3) random forest (RF). These classifiers have been shown to offer good performance with neuroimaging data in several studies [61–69]. Here, for kNN, k in the range of 1 and 10 is used, for LR, ℓ₂-norm regularization is used, and the weight of the regularization was set between 10⁻² and 10^1.5, and for RF, the subsampling ratio is selected to be 40%, 70% or 100%.

To evaluate the classification performance, three measures, accuracy (AC), sensitivity (SE), and specificity (SP), were used [70].

First, separate classifiers were trained for each subject. A ten-fold cross-validation was used to test the performance of the models. For each subject, the data were randomly partitioned into ten subsamples. Classification experiments were repeated ten times, where during each, one subsample was assigned as the testing dataset, and the remaining subsamples were assigned as training dataset. For every subject, the classification performance was evaluated using the measures described above, and then results were averaged across the ten repetitions.

3. Results

3.1. VG construction from calcium signals

The preprocessed calcium signals were segmented using sliding windows with the fixed step of 50 time points (0.5 s). Five different window lengths were used: 100, 150, 200, 250, and 300 time points (corresponding to 1, 1.5, 2, 2.5, and 3 s, respectively). The VG was constructed for each segment of the time series obtained from each ROI. For each VG, three graph measures, D, C, and L were extracted. As a result, for a given sliding window length, recordings from each ROI of each recording block, result in three time series for D, C and L. Our objective is to use these information and develop models to predict the behavior of active whisking and no whisking, from recorded calcium signals.

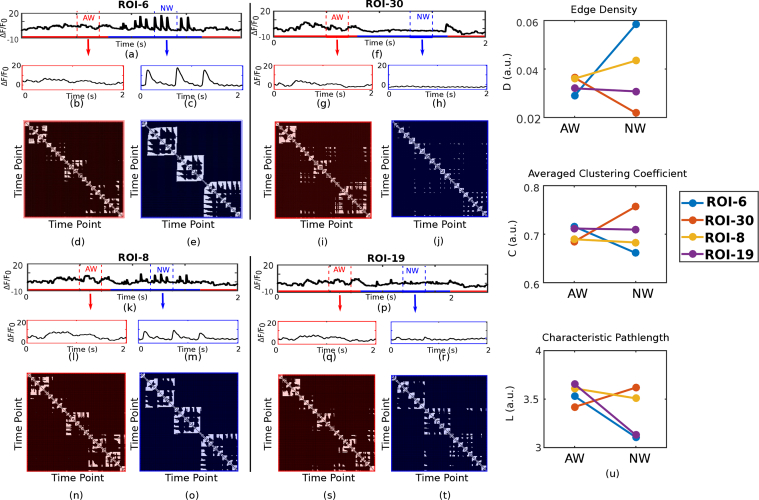
Representative preprocessed calcium signals from four ROIs (6, 8, 19 and 30) of the recording block #1 from subject #1 are shown in Fig. 5. For signals from each ROI, two segments of 2 s duration, corresponding to AW and NW, are also shown. For each of these segments, the VG is constructed and their corresponding adjacency matrices are presented. As segments have the same duration (2 s or 200 time points), the number of nodes in all graphs will be the same. In these matrices, the dark color represents no connection, and the light color represents the existence of an edge. For each ROI, the distinctions between the patterns of the matrices related to AW and NW can be revealed via the three graph measures D, C and L. The values for these measures are compared for AW and NW and each ROI in Fig. 5(u).

Fig. 5.

Preprocessed calcium signals of recording block #1 from subject #1 from ROI-6 (a), ROI-8 (f), ROI-30 (k) and ROI-19 (p). For each case, 2 s segments of signals corresponding to AW (shown in red in (b), (g), (l) and (q)) and NW (shown in blue in (c), (h), (m) and (r)) conditions as determined from whisker movement recordings. For each ROI, the adjacency matrices for 2 s AW are shown in (d), (i), (n), and (s), and for 2 s NW are shown in (e), (j), (o), and (t). Measures extracted from VG of 2 s duration of AW time series (shown in red) and from VG of 2 s NW time series (shown in blue) are also shown in (u) for each ROI.

As can be seen, distinct patterns (e.g. in terms of amplitude and width of calcium transients), for the same whisking condition (AW or NW) are observed in signals obtained from different ROIs distributed over the cortex, suggesting that different cortical regions have potentially different relationships with behavior. For example, for ROIs in or close to M1 (ROI-6 and ROI-8) the measure D is larger during NW compared to AW, suggesting that there are more number of edges in the VG representation of recordings from this region for NW as compared to AW. For ROIs close to S1 (ROI-19) the measure L appears to be smaller during NW compared to AW, suggesting that there are less connections in the VG representation of recordings from this region for NW as compared to AW. In V1 (e.g. ROI-30), the measure C is larger during NW as compared to AW, indicating the presence of smaller clusters in the VG representation of recordings from this region during AW as compared to NW. These results suggest that different regions of the brain follow different temporal dynamics during behavior, and such differences can be revealed and quantitatively described via VG measures D, C and L.

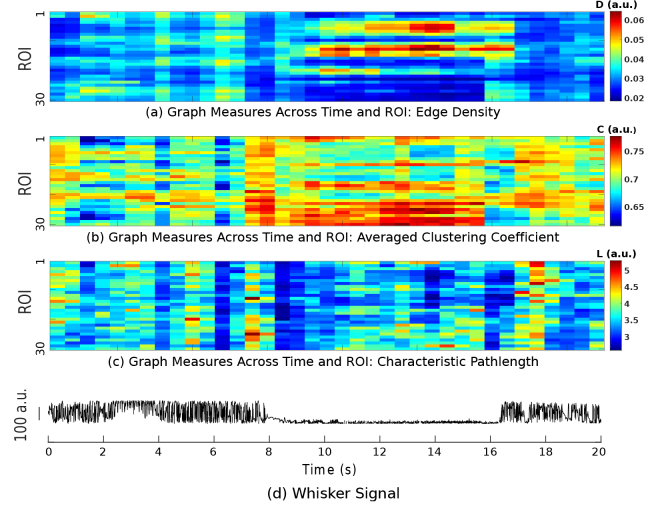
The graph measures shown in Fig. 5(u) correspond to two segments of the time series for each of the four ROIs. Using the sliding window of length 2 s, VGs can be constructed for each segment of the time series, and from each VG, the three mentioned graph measures can be extracted. Figs. 6(a) to (c) show the results of such analysis for all ROIs, illustrating the temporal evolution of D, C and L, respectively. The simultaneously obtained whisker movement recording is also shown in Fig. 6(d). It can be clearly seen that different patterns are observed for VG measures for duration corresponding to AW and NW across all ROIs.

Fig. 6.

Color-coded graph measures for all ROIs as a function of time during a recording block. (a) Edge density (D), (b) Averaged clustering coefficient (C), and (c) Characteristic pathlength (L). (d) Whisker movement recording obtained simultaneously in the same block.

3.2. Classification results

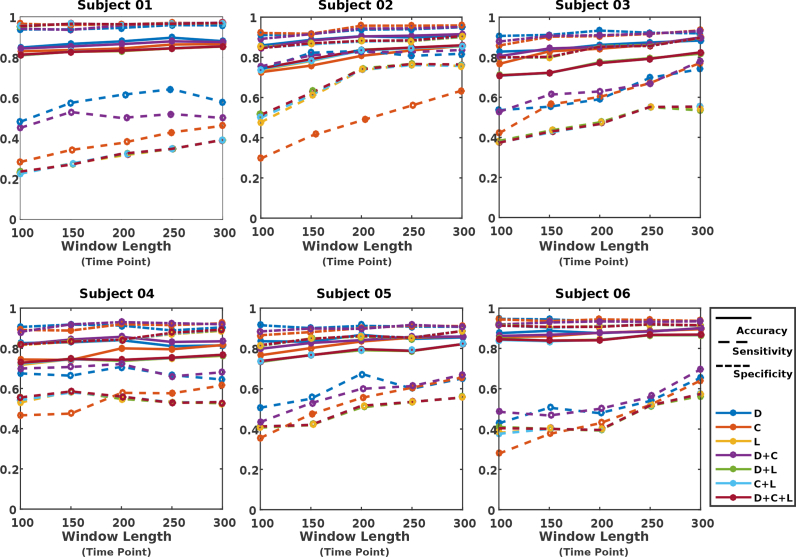
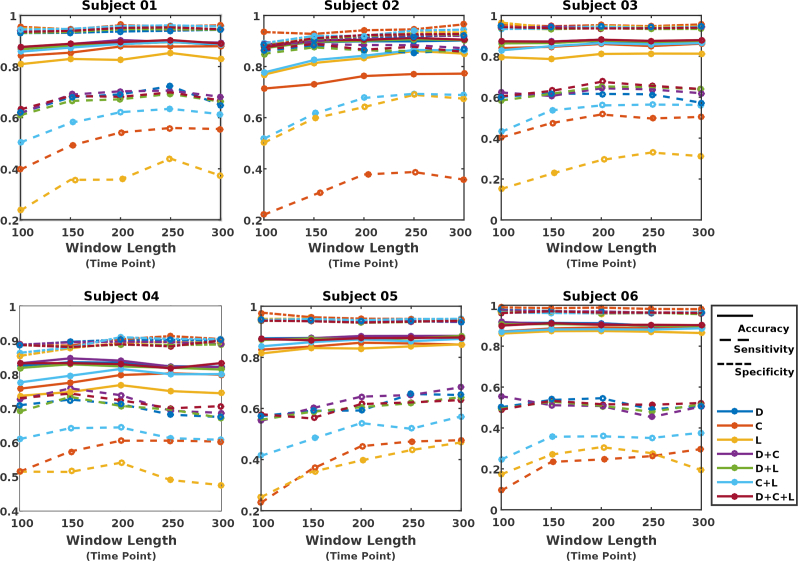
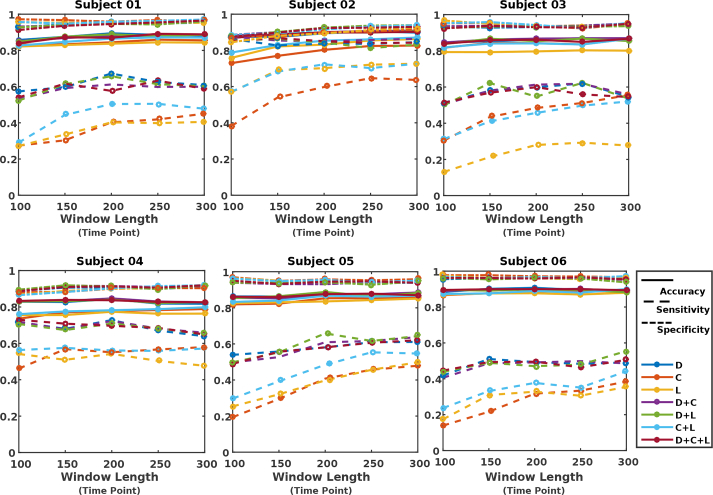
For each subject, we performed comprehensive investigation on how the selection of various parameters (e.g. various window sizes for extracting VG measures, and performing classification based on different selection of feature types) will impact the classification results. For each choice of window size, features were constructed based on individual or a combination of measures from the corresponding VG. Figs. 7, 8 and 9 illustrate the evaluation measures obtained for each subject when kNN, LR, and RF were used as the classifier, respectively.

Fig. 7.

Classification results when using kNN as classifier.

Fig. 8.

Classification results when using regularized logistic regression (LR) as classifier.

Fig. 9.

Classification results when using random forest (RF) as classifier.

It was found out that while the performance is subject dependent (due to individual variability as well as variability in whisking behavior across subjects (see Table 1)), with a proper choice for features and window length, all classifiers result in high levels of accuracy and specificity for all subjects. The sensitivity remains to be relatively modest, however, considering the imbalanced dataset between AW and NW (e.g. only 23% of the samples belonged to the AW condition for 2 s window duration), the obtained significantly better accuracy than naive classifier (in which all the testing samples are assigned the label associated to the majority class in the training set), demonstrating the effectiveness of the VG measures in providing features that carry discriminatory information for AW and NW. In majority of scenarios, classification based on either C or L did not result in good performance, while classification based on feature D + C or D led to the best sensitivity results for majority of the subjects.

For each classifier, information about the choice of window length (w), features, and parameters that have resulted in the best sensitivity among all the explored options, are summarized in Table 2. Consistent with the observation made from Figs. 7, 8, and 9, it can be seen that, in all cases, the graph measure D, either individually or jointly with others, has been identified as the optimum feature. For classifiers kNN and LR, the feature D + C across most subjects has resulted in the best sensitivity results, while for the RF classifier, the measure D by itself has worked as the optimum feature. In terms of duration of segments for constructing VGs, window duration of equal or larger than 2 s has resulted in the optimum performance. In addition, for most cases, the sensitivity measure dropped as the window size for extracting features goes below 150 points.

Table 2.

Classification results for best sensitivity obtained for each subject when using kNN, regularized logistic regression (LR), and random forest (RF) as classifier. Features, window lengths (w), and related parameters from which the optimum results have been obtained are also listed (SS is short for subsample). Note that “+” in the “Feature” rows represent using multiparametric approach for performing the classification.

Classifier	Performance Measure	1	2	3	4	5	6
k NN	AC (%)	89.84	91.52	89.78	85.72	86.74	90.09
	SE (%)	64.33	83.64	78.01	72.18	67.42	69.66
	SP (%)	96.08	95.15	93.03	93.01	91.20	93.47
	Feature	D	D + C	D + C	D + C	D	D + C
	w (points)	250	300	300	200	200	300
	k	7	3	1	5	1	1
LR	AC (%)	89.66	88.75	88.14	84.70	88.39	91.83
	SE (%)	72.36	89.54	67.53	75.89	68.30	55.58
	SP (%)	94.02	88.37	93.64	89.43	93.89	97.49
	Feature	D	D + C	D + C + L	D + C	D + C	D + C
	w (points)	250	100	200	150	300	100
	ℓ 2	0.01	0.5623	0.01	0.0178	0.010	0.0316
RF	AC (%)	88.93	91.94	87.00	84.37	88.77	88.21
	SE (%)	67.57	87.80	62.03	72.82	65.81	55.48
	SP (%)	94.15	93.73	93.91	90.68	94.20	93.74
	Feature	D	D	D	D	D + L	D + L
	w (points)	200	250	250	200	200	300
	Row SS Ratio	0.7	1.0	1.0	0.7	0.7	0.7
	Col. SS Ratio	1.0	0.4	0.7	1.0	0.4	1.0

Overall, kNN and LR deliver almost always slightly better performance than RF, but using the right features, all classifiers are able to successfully differentiate the whisking conditions, demonstrating that features based on visibility graph carry discriminatory information. To summarize the performance of the classifiers, we repeated the classification across subjects by using unified parameters that led to the best classification performance in majority of the subjects in Table 2. We used D + C as the feature, and 2 s as the window length. The results are presented in Table 3, where as can be seen, on average, an accuracy larger than 86% is achieved across all subjects.

Table 3.

Classification performance using unified parameters across subjects and classifiers. D + C is used as the feature, and w = 200 points is used as the window length for extracting features in all cases.

Classifier	Performance Measure	Mean	SD
k NN	AC (%)	86.54	2.86
	SE (%)	66.42	11.68
	SP (%)	91.67	2.82
	AUC	0.774	0.057
LR	AC (%)	88.76	2.67
	SE (%)	68.65	11.93
	SP (%)	93.81	2.34
	AUC	0.927	0.025
RF	AC (%)	87.48	2.16
	SE (%)	64.37	13.07
	SP (%)	93.31	1.78
	AUC	0.912	0.026

4. Discussions and conclusions

Measuring brain states over wide areas of cortex is of central importance for understanding sensory processing and sensorimotor integration. Changes in brain states influence the processing of incoming sensory information. For example, data from several sensory modalities including somatosensation, vision, and audition, indicate that the cortical representations of stimuli vary depending on the neocortical state when the stimulus arrives [71–74]. In mice, natural spontaneous behaviors such as locomotion and self-generated whisker movements influence brain states through increased behavioral arousal and activation of ascending neuromodulator systems [40, 75]. Studies in mice using widefield imaging of voltage and calcium sensors during whisking or locomotion have provided important information on the spatiotemporal modulations of brain states [14, 29], and relating these dynamic optical signals to behavior is an area of great interest. This line of research will be advanced by the development of several new transgenic calcium reporter mice [76, 77] and cranial window methods [16].

Studies from several sensory modalities including somatosensation, vision, and audition have reported changes in the cortical representation of stimuli that vary depending on the neocortical state when the stimulus arrives.

The VGs constructed here corresponded to segments of recordings as identified by the moving window of length w. We performed a comprehensive study (five different window lengths, seven types of features per choice of window length, and three classifiers) to find the model that can be used to infer the behavior (AW or NW) from calcium imaging data. All classifiers delivered high accuracy and specificity and moderate sensitivity, with kNN and LR offering better performances than RF. Considering the imbalanced dataset between AW and NW (e.g. only 23% of the samples belonged to the AW condition for 2 s window length), the obtained significantly better-than-naive-classifier demonstrates the effectiveness of the VG measures in providing features that carry discriminatory information for AW and NW. Other techniques for learning from imbalanced data, such as [78], can also be incorporated to achieve an even better performance. Regardless, as it was shown, the obtained performance was comparable to the scenario in which the number of spikes, inferred from calcium signals, are used as features.

Additionally, among the three considered visibility graph measures (D, C and L), it was observed that the measure D, was identified as the feature providing the best sensitivity results, for all subjects and all choice of classifiers, either individually or jointly with other measures (e.g. D + C)). This observation indicates that the measure D carries the strongest discriminatory information among the three considered VG measures. Given that D is related to the number of edges in the graph that are associated with the fluctuations in the time series, this result shows that variations in the patterns, and in the relative timing of the fluctuations with respect to one another, play key roles in differentiating the two states. Furthermore, it was demonstrated that the proposed method is capable of providing features common across subjects, which result in successful classification performance.

It is worth noting that, the three different classifiers were implemented independently, to demonstrate the robustness of the VG measures as features. The logistic regression classifier is robust to noise and can avoid overfitting by using regularization. The random forest classifier can handle nonlinear and very high dimensional features. The kNN classifier is considered computationally expensive but it is simple to implement and supports incremental learning in data stream. As presented, all classifiers were able to successfully differentiate the whisking conditions demonstrating the robustness of the VG metrics in capturing the temporal characteristic of optical imaging data.

4.1. Comparison with spike rate inference-based feature extraction approach

The proposed approach was applied directly to the recorded calcium signals, without using methods such as template matching [79, 80], deconvolution [81, 82], Bayseian inference [83, 84], supervised learning [85], or independent component analysis [86]. Here, we compare the classification performance of the proposed approach with the scenario in which the number of spikes are used as features for each condition.

To infer the spiking events from calcium recordings, we used the FluoroSNNAP [80] toolbox in MATLAB, which utilizes a commonly-used template-matching algorithm. The same window sizes that were considered in VG-based analysis, were also considered for spike-based analysis. For each segment, feature vectors were constructed by concatenating the number of detected spikes from all ROIs. The regularized logistic regression was used as the classifier, with the same ℓ₂ penalty weights as was set before. Similar to the VG-based feature extraction technique, the performance was evaluated using the same cross-validation procedure described earlier.

Results for the area-under-the-ROC-curve (AUC) are presented in Table 4 for each window size. It is shown that the VG-based approach provides a better performance. This result further confirms the capabilities of VG-based measures in identifying discriminatory features related to different behavior from calcium recordings.

Table 4.

Performance comparison of classification experiments based on i) VG-based feature extraction from all ROIs, ii), Spike-based feature extraction from all ROIs, iii) Variance-based feature extraction from all ROIs, iv) VG-based feature extraction only from ROI-20, and v) VG-based feature extraction from ROIs 25–30.

Window Size (s)	1	1.5	2	2.5	3
AUC (All ROIs VG-based)	0.916	0.923	0.927	0.923	0.923
AUC (Spike-based)	0.849	0.882	0.868	0.894	0.896
AUC (Variance-based)	0.914	0.919	0.920	0.915	0.916
AUC (ROI-20, VG-based)	0.841	0.856	0.860	0.857	0.857
AUC (ROIs 25-30, VG-based)	0.825	0.846	0.853	0.857	0.854

4.2. Comparison with signal variance-based feature extraction approach

We carried out another analysis to compare the classification performance of the proposed approach with the scenario in which the variance of the signal is used as features for all candidate window sizes. For each segment, feature vectors were constructed by concatenating the variance from all ROIs. The same classifier and regularization optimization process similar to VG-based approach was used. The AUC values based on 10-fold cross validation was used to compare the classification performance. The results are summarized in Table 4 for each window size, which shows the VG-based method provides a better performance regardless of the selection of window sizes.

4.3. Comparison with VG-based features from the somatosensory cortex

We carried out an additional analysis to examine whether the classification results will be different if only signals recorded from the ROIs located in the primary somatosensory cortex are considered, since layer 4 “barrels” in primary somatosensory cortex receive sensory input from the whiskers. Among the ROI locations, the ROI-20 was in close proximity of the primary somatosensory cortex, according to the location of bregma and functional mapping experiments in a subset of mice. Using the same parameter settings used earlier, classification was performed based on VG measures extracted from ROI-20 signals. Results for AUC are shown in Table 4. It can be seen that when features from all ROIs (covering large area of the cortex) are used, the classification performance is significantly better. This result is consistent with previous work [14, 26, 29, 87], which suggest that brain state modulation is widespread across many cortical regions.

In a related analysis, we further used VG-based features extracted from ROIs 25–30, which did not show the epileptiform-like events during NW (as seen in signals obtained from ROI 6). Results are summarized in Table 4, suggesting that VG is capable of decoding behavior from ROIs with various dynamic properties. It should be noted that VG analysis in this paper, uses a relatively fast time scale (2 s) compared to the blood-flow related signals that can reduce fluorescent calcium signals. Contamination is particularly strong for sensory-evoked signals [11, 77], but less of a concern here for signals related to spontaneous behavioral state transitions.

4.4. Concluding remarks

To the best of our knowledge, this work is the first study demonstrating that it is possible to infer behavior from the temporal characteristics of calcium recordings, extracted through visibility graph. As such the proposed method could have applications in BMIs involving human [30], or in rodents and primates [31, 32], where from brain recordings subject’s intention should be inferred. Due to differences in the nature of recorded signals or experimental conditions, a direct and fair comparison with these studies and the results shown here cannot be made, but the classification results for accuracy presented here are comparable to the results that have been reported in [30, 88, 89]. Additionally, the proposed methodology in combination with widefield optical imaging of ensembles of neurons in awake behaving animals, can open up several new opportunities to study various aspects of brain function and its relationship to behavior. It could also be employed to develop quantitative biomarkers based on VG measures. While here we considered three VG measures (D, L and C), a wide range of other graph measures [90] could also be used to possibly improve the classification performance. It can be concluded that VG is very effective in providing “quantitative” measures that can reveal differences in recorded calcium time series.

Future work will include 1) exploring the inclusion of other graph measures as features, 2) expanding VG to multilayer VG [49], where information about the dependency of time series will also be incorporated in the models, and 3) employing deep learning in developing predictive models, and 4) applying the methods to experiments involving learned behaviors and diverse cortical cell types.

Funding

Siemens Healthineers; National Science Foundation (NSF 1605646); New Jersey Commission on Brain Injury Research (CBIR16IRG032); National Institutes of Health (R01NS094450).

Disclosures

The authors declare that there are no conflicts of interest related to this article.