Multiwavelength time-resolved near-infrared spectroscopy of the adult head: assessment of intracerebral and extracerebral absorption changes

Abstract

An optical technique based on diffuse reflectance measurement combined with indocyanine green (ICG) bolus tracking is extensively tested as a method for the clinical assessment of brain perfusion at the bedside. We report on multiwavelength time-resolved diffuse reflectance spectroscopy measurements carried out on the head of a healthy adult during the intravenous administration of a bolus of ICG. Intracerebral and extracerebral changes in absorption were estimated from an analysis of changes in statistical moments (total number of photons, mean time of flight and variance) of the distributions of times of flight (DTOF) of photons recorded simultaneously at 16 wavelengths from the range of 650–850 nm using sensitivity factors estimated by diffusion approximation based on a layered model of the studied medium. We validated the proposed method in a series of phantom experiments and in-vivo measurements. The results obtained show that changes in the concentration of the ICG can be assessed as a function of time of the experiment and depth in the tissue. Thus, the separation of changes in ICG concentration appearing in intra- and extracerebral tissues can be estimated from optical data acquired at a single source-detector pair of fibers/fiber bundles positioned on the surface of the head.

1. Introduction

Currently, a variety of optical techniques for brain imaging are tested in clinical diagnostics [1]. One of such methods is near-infrared spectroscopy (NIRS) [2, 3]. Near-infrared light can penetrate into the human brain through the skin and skull and return to the surface of the head in reflectance geometry. This allows for evaluation of absorption changes in chromophores such as oxy- and deoxyhemoglobin circulating through the tissues because of their different spectral properties in the near infrared range of wavelengths [4]. Thus, the technique has a good potential for noninvasive assessment of cerebral perfusion and oxygenation at the bedside [5, 6]. It is a relatively low cost technique and is characterized by compactness of the instrumentation as compared to other available brain imaging methods. Three optoelectronic NIRS approaches have been proposed for brain’s hemodynamic changes measurements: continuous wave (CW) [7], frequency-domain [8, 9] and time-resolved (time-domain) [10, 11].

During classical CW NIRS, after the light propagates through the human head, the changes in attenuation of detected light are analyzed at two or more wavelengths and changes in oxy- and deoxyhemoglobins can be calculated [7, 12–14]. The distinct drawback of this technique is that the measured brain oxygenation signals are contaminated by the changes in oxygenation of the extracerebral tissue. A modified technique based on multi−distance detection was developed to distinguish these two layers (exta- and intracerebral) [15–17].

Two advanced NIRS techniques are applied for the discrimination of signals originating from the brain: (i) frequency-domain method in which the light emitted to the tissue is modulated at subGHz frequency and the path length of photons between source and detector located on the surface of the studied tissue is derived by estimation of the phase shift between emitted and detected light wave [18]; (ii) time-resolved technique (TR-NIRS) which is based on emission of ultra short (typically picosecond) laser pulses into the tissue and analysis of broadening of these pulses during penetration in the tissue [10, 19–24]. The latter technique is technically advanced and expensive but potentially allows us to assess optical properties of the studied tissue and to estimate the changes in concentrations of the chromophores with depth discrimination [11]. Methods for discrimination of superficial and deep absorption changes from data obtained by TR-NIRS were developed by several research groups [20, 22, 25–28] and recently, subtraction-based approach was proposed to enhance selective sensitivity to a layer at a specific depth [29, 30].

Beside oxygenation studies, optical methods based on NIRS have been tested in combination with the application of an intravascular flow tracer in order to assess cerebral perfusion parameters. Indocyanine green (ICG) is an optical contras agent of low toxicity revealing high absorption at the near-infrared wavelengths. After intravenous injection, ICG can be successfully monitored during its circulation through the brain [31–34]. Similarly to the NIRS-based oxygenation studies, the technique based on monitoring of ICG bolus passage suffers from extracerebral contamination. Several algorithms and optical techniques have been used to discriminate superficial and cerebral circulation of the contrast agent through the human head. One of the algorithms is based on several source-detector separations [35]. It was shown that the algorithm can be further enhanced when used along with time-resoled NIRS technique [20]. In TR-NIRS, analysis of changes in the statistical moments (zeroth, first, and second centralized moments) of distributions of times of flight of photons (DTOFs) acquired at different source-detector separations allow for estimation of absorption changes at various depths. Experiments in healthy volunteers have shown that the depth-dependent changes in absorption could be derived using measured changes in moments of DTOFs and sensitivity factors obtained using Monte Carlo modeling [21, 34]. Furthermore, this technique was used for bedside assessments of cerebral perfusion deficits in patients with acute ischemic stroke [36, 37], during endarterectomy [38], in patients with posttraumatic brain injury [39] and brain death [40]. Recent experiments carried out on piglets confirmed that time-resolved optical monitoring of inflow of the ICG is a promising tool for detecting cerebral perfusion insufficiencies [41].

In the present paper, we extend described previously concept based on analysis of changes in moments of DTOFs [20] and exploit additional information available from time-resolved measurements with the registration of the optical signal at multiple wavelengths (spectral TR-NIRS) and with simultaneous administration of optical contrast agent (ICG). The aim of this study was to demonstrate that the multiwavelength time-resolved measurements are feasible and allow to derive the depth-dependent changes of the absorption coefficient after the passage of the optical contrast agent. In contrast to previous study of Liebert et al. [20], we propose to acquire data at only single source-detector separation and record simultaneously the DTOFs at 16 wavelengths from near-infrared region (650-850 nm). It will be shown that depth-resolved changes in absorption can be deduced from analysis of statistical moments (total number of photons, mean time of flight and variance) of the DTOFs and sensitivity factors of the moments of DTOFs calculated by diffusion approximation using a layered model of the studied medium. In contrast to previously reported studies in which multidistance or single distance time-resolved measurements were carried in order to discriminate changes in absorption in two-layered tissue model, the method applied in our study based on application of multiple wavelengths may allow to resolve changes in absorption in a multilayered tissue structure.

2. Method of depth-resolved analysis of absorption changes

The human head under investigation is an inhomogeneous medium and can be modeled by a layered structure [42]. In a simple two-compartment model of the head, two main compartments: extracerebral tissues (consisting of scalp and skull) and intracerebral compartment (in particular the brain cortex) can be distinguished. To estimate changes in absorption in multiple layers of the head, we used a procedure based on analysis of statistical moments of DTOFs of photons acquired at multiple wavelengths. The analysis of the DTOF’s is based on derivation of changes in their statistical moments which are: N_tot - total number of photons (zeroth order moment – integral of the DTOF), <t> - the mean time of flight of photons (first moment of the DTOF), and the variance V of the DTOF (second centralized moment). In preprocessing of the DTOFs, the background signal was subtracted. Influence of the instrumental response function (IRF) was considered by subtracting the moments of the IRFs from the moments of DTOFs measured on phantoms or during in-vivo experiments (as described elsewhere [43]).

Previously, Liebert et al. used changes in the moments of DTOFs measured at multiple interoptode separations for estimation of changes of the absorption coefficient in a multilayered model of the tissue [20]. The changes of the absorption coefficient (Δμ_a) were obtained for 10 layers from changes in moments of the DTOFs measured at four emitter-detector separations. As a result, a linear system of 12 equations was build in which the changes in moments were linearly related to the unknown changes in absorption at different depths and to DTOFs moments’ sensitivity factors (SF): mean partial path length MPP, the mean time of flight sensitivity factor MTSF, and the variance sensitivity factor VSF. These factors describe sensitivity of changes in the corresponding moments of the DTOFs to changes in absorption in defined layer of the tissue penetrated by the photons [20]. This system of equations was solved using singular value decomposition (SVD).

In the present work, we proposed a modified concept based on the acquisition of DTOFs for the single source-detector pair and at multiple wavelengths. The changes in the concentration of ICG in each tissue layer (indexed by j) were estimated using an algorithm based on the assessment of changes of moments of the DTOF’s measured at 16 wavelengths (λ) from the near-infrared spectral region at single source-detector separation.

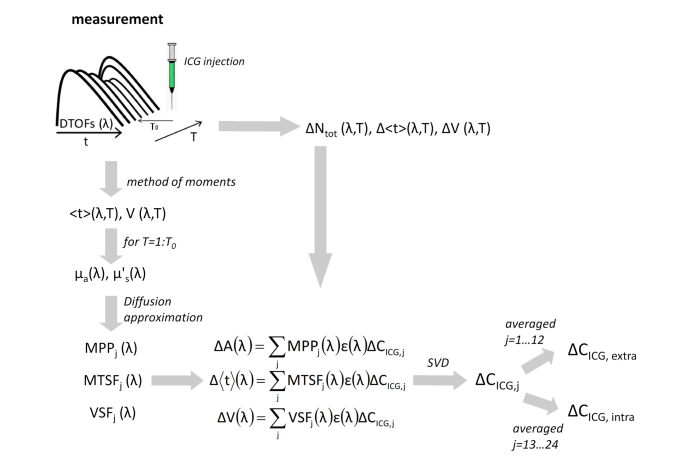
The implemented algorithm is schematically presented in Fig. 1 and consists of following steps:

Fig. 1.

The algorithm used for estimation of changes in the ICG concentration in intra- and extracerebral layers of the head (ΔC_ICG,intra, ΔC_ICG,extra). The acquired DTOFs contain a number of counted photons vs. time t which is typically in ns range. The DTOFs were acquired during the experiment lasting several minutes (time of experiment T). The ICG was injected at time instance T₀.

2.1 Estimation of the background optical properties of the medium

The absorption coefficients μ_a and reduced scattering coefficients μ'_s were evaluated from the measured DTOFs with the assumption of the homogeneity of the medium under investigation. The DTOFs used in this analysis were obtained by averaging of 100 DTOFs corresponding to the period of measurement preceding the ICG injection, acquired during the 30 s, and contained at least 1.5e + 6 photon counts. The optical coefficients were directly calculated from the analytical expressions in which the moments of the DTOFs for semi-infinite media were used [43]:

$$\begin{array}{l}{\mu }_a(\lambda )=\frac{<t{>}^3(\lambda )}{2cV(\lambda )(<t{>}^2(\lambda )+V(\lambda ))},\\ {{\mu }_s}^{\prime }(\lambda )=\frac{2<t>(\lambda )c(<t{>}^2(\lambda )+V(\lambda ))}{3r^{2}V(\lambda )}\end{array}$$ (1)

where: c is the speed of light in the medium, r – source-detector separation. The moments of DTOFs (<t> and V) were estimated by integrating the DTOFs in the limits of 1% of their maximum.

2.2 Calculation of the sensitivity factors

The sensitivity factors (SF) were obtained using the diffusion approximation described previously by Kacprzak et al. [28]. The changes in the moments of DTOFs related to defined changes in absorption located in voxels of the medium indexed by i were calculated and SFs were obtained for all considered wavelengths λ:

$$\begin{array}{l}MP{P}_i(\lambda )=\frac{\text{Δ}A(\lambda )}{\text{Δ}{\mu }_{a,i}(\lambda )}\\ MTS{F}_i(\lambda )=\frac{\text{Δ}<t>(\lambda )}{\text{Δ}{\mu }_{a,i}(\lambda )}\\ VS{F}_i(\lambda )=\frac{\text{Δ}V(\lambda )}{\text{Δ}{\mu }_{a,i}(\lambda )}\end{array}$$ (2)

where Δμ_a,i is the change in absorption coefficient appearing in the i^th voxel defined in the medium for each of λ, and ΔA is the change in attenuation:

$$\text{Δ}A(\lambda )=-\text{log}\left(\frac{N_{\mathit{\text{tot}}}(\lambda )}{N_{\mathit{\text{tot}},0}(\lambda )}\right)$$

The SFs were estimated using diffusion approximation on the basis of the experimentally determined background optical properties μ_a(λ) and μ_s´ (λ) in a homogeneous medium structure consisting of voxels x × y × z of size 0.2 × 0.2 × 0.1 cm (where z is the depth). Furthermore, the sensitivity factors MPP_j, MTSF_j, and VSF_j were obtained for 24 layers (of the thickness of 0.1 indexed by j) by summing up the sensitivity factors of the voxels contained in the layers.

2.3 Building up a system of equations

The wavelength-dependent absorption coefficient changes are proportional to a product of wavelength-independent ICG concentration ΔC_ICG,j and wavelength-dependent molar extinction coefficients of the ICG ε_ICG:

$$\text{Δ}{\mu }_{a,j}(\lambda )={\epsilon }_{ICG}(\lambda )\text{Δ}{C}_{ICG,j}$$ (3)

A system of equations with unknowns ΔC_ICG,j which are changes in ICG concentration as a function of depth and knowns represented by changes in three moments of DTOFs (∆A, ∆<t> and ∆V), together with their corresponding sensitivity factors for each layer and wavelength (MPP_j, MTSF_j, and VSF_j), was build:

$$\begin{array}{l}\text{Δ}A(\lambda )={\displaystyle \sum _{j}MP{P}_j(\lambda )\epsilon (\lambda )\text{Δ}{C}_{ICG,j}}\\ \text{Δ}<t>(\lambda )={\displaystyle \sum _{j}MTS{F}_j(\lambda )\epsilon (\lambda )\text{Δ}{C}_{ICG,j}}\\ \text{Δ}V(\lambda )={\displaystyle \sum _{j}VS{F}_j(\lambda )\epsilon (\lambda )\text{Δ}{C}_{ICG,j}}\end{array}$$ (4)

The molar extinction coefficients ε_ICG presented by Landsman et al. were used for the calculations [44].

2.4 Solution of the system of equations

The system of equations described above consists of 24 equations related to the three moments obtained at eight selected wavelengths (698, 710, 723, 735, 748, 760, 772 and 785 nm). The wavelengths utilized in this analysis were selected from all measured wavelengths to avoid the influence of the fluorescence of the ICG on diffuse reflectance signals. This effect is significant at longer wavelengths and was discussed in detail in Discussion section. The time-courses of ∆A, ∆<t> and ∆V were smoothed by sliding-average with a time-window width of 10 s. As the system of Eqs. (4) represents an ill-posed problem, its solution needs a regularization algorithm. Singular value decomposition truncated to three singular values was applied.

2.5 Estimation of changes in the ICG concentration in intra- and extracerebral layers of the head

The ICG concentration change in the extracerebral tissue ΔC_ICG,extra was obtained by the averaging of changes in concentration obtained in top 12 layers of the model forming the tissue compartment of thickness 1.2 cm which can be considered as the thickness of the extracerebral tissue structures. Consecutive layers were assumed to correspond to intracerebral tissue, and the change in ICG concentration ΔC_ICG,intra for this layer was calculated by averaging of the data obtained in the next 12 layers located at depths of 1.3 to 2.4 cm.

3. Experimental methods

3.1 Instrumentation

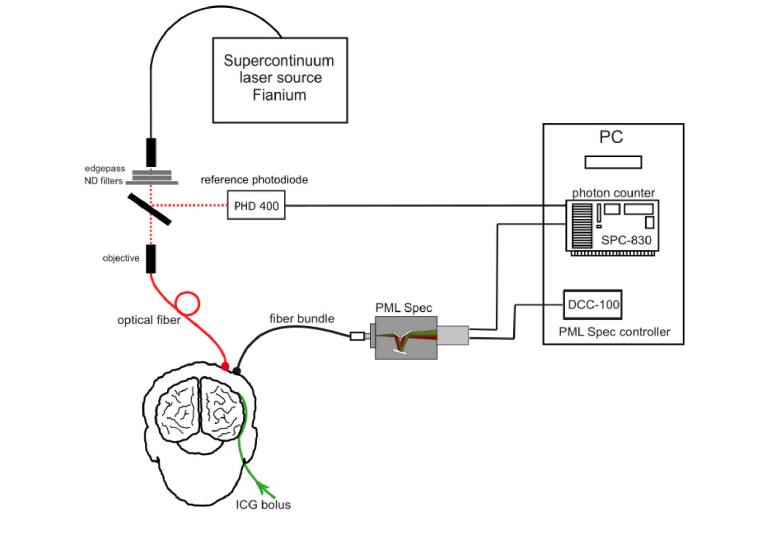
We constructed a multichannel time-resolved spectral system based on time-correlated single photon counting (TCSPC) electronics [45] for broadband measurements of diffuse reflectance (Fig. 2). A supercontinuum light was generated by fiber lasers SC450-4 or SC480 WhiteLase (Fianium, UK) operating at a repetition frequency of 40 MHz (used in in-vivo measurements) and 80 MHz (used in phantom studies), respectively.

Fig. 2.

The setup for multiwavelength time-resolved diffuse reflectance measurements.

The near-infrared light was delivered to the surface of the phantoms or tissue with the use of an optical fiber with length = 2 m (NA = 0.22, diameter 400 μm, QP400-2-VIS-NIR, Ocean Optics, USA). The power of light at the tip of source fiber was about 20 mW. The optode was constructed in such a way that the power density of the light on the surface of the skin was not higher than 2 mW/mm².

The remitted photons were transmitted to the detection system with the use of fiber bundle (Profile Cross Convertor FBPRS150xUV200-220, length 1.5 m, NA = 0.22, Art Photonics GmbH, Germany) terminated with a circular tip (diameter 3.6 mm) on the tissue side and line-shaped tip (1.4x7.3 mm) fitting to the slit of the polychromator. The fiber bundles consist of silica fibers with core/cladding 200/220μm and step index with effective collection area approximately 10.2 mm² and fill factor ca. 70%. This fiber bundle composition allowed us to maximize light detection efficiency which is crucial for the diffuse reflectance measurements on the head. The source fiber and detection bundle were positioned at source-detector separation r (r = 3 cm in in-vivo measurements and r = 1, 2, 3 and 4 cm in phantom studies) and fixed to the surface of the medium with the use of home-made optode holder made of flexible black rubber and Velcro stripes. The diffusely reflected photons were acquired using an integrated detector module PML Spec (Becker & Hickl, Germany), equipped with polychromator MS125 (Oriel Instruments, USA) which has NA = 0.135 and uses 77414 diffraction grating (Grating Groove Density is 600 I/mm) and 16-channel photomultiplier tube detector PML-16-1-C (Becker & Hickl, Germany). The mismatch between numerical apertures of the detection bundles (0.22) and polychromator (0.135) causes additional losses of photons in the photodetection system, however, application of the fiber bundles with lower NA would cause photons losses at the tissue side.

Each single photon pulse related to single photon detection was counted using the routing electronics (included in the detection module). This allowed us to build up the photon distribution over the arrival time of the photons independently for the different detectors channels. The detection system acquired simultaneously distributions of times of flight of diffusely reflected photons for 16 spectral channels. The width of the spectral channel was approximately 12.5 nm. The spectral range of 200 nm was adjusted in such a way that the measurement covered wavelengths between 650 nm and 850 nm. The supercontinuum source light was spectrally limited using the set of the edgepass filters (longpass filter FEL0650 and shortpass filter FES0850 with cut-on wavelengths of 650 nm and cut-off wavelength of 850 nm, respectively, Thorlabs, Sweden) mounted between the tip of laser’s output fiber (length 1.5 m) which ends with collimator, and the fiber which delivers light to the surface of the phantom/human tissue (see Fig. 2).

Single photon pulses were counted using a time-correlated single photon counting PCI card SCP-830 (Becker & Hickl, Germany). Power supply to the multianode photomultiplier tube PML-16-1-C was provided from a DCC-100 card (Becker & Hickl, Germany) allowing for gain control and overload shutdown of the PML-16-1-C. Measured distributions of times of flight of diffusely reflected photons contained 1024 time channels with the width of Δt = 9.77 ps.

Synchronization of the laser pulses with the TCSPC electronics was provided with the use of a reference detecting photodiode (PHD 400, Becker & Hickl, Germany). Instrumental response function (IRF) containing the time profile of the light source and the time characteristics of the whole measurement system was measured by positioning the source fiber in front of the detecting bundle with a piece of paper placed in front of the bundle to fill out its numerical aperture [46]. The FWHM of the IRF was in the range of 130-150 ps for all spectral channels. Collection time for simultaneous acquisition of 16 distributions of times of flight of photons was 0.3 s.

The setup was mounted in a 19-inch rack and a trolley optimized for transport in clinical settings.

3.2 Phantom experiments

The time-resolved measurements of diffuse reflectance were carried out on a liquid phantom consisting of a fish tank (dimensions: 20 × 20 × 15 cm) filled with a light scattering solution of milk and water (1:3) with small amount of black ink-water solution (1:100, ca. 1 ml/l) added to obtain optical properties of the liquid (μ_a = 0.18 cm⁻¹, μ_s' = 19 cm⁻¹) close to those observed in living tissues. The measurement was carried out through a window in the wall of the fish tank made of a thin (50 μm) optically turbid Mylar film (DuPont Teijin Films, USA). In consecutive measurements, the optical signals were collected for 4 distances between the source fiber and detection bundle (r = 1, 2, 3 and 4 cm).

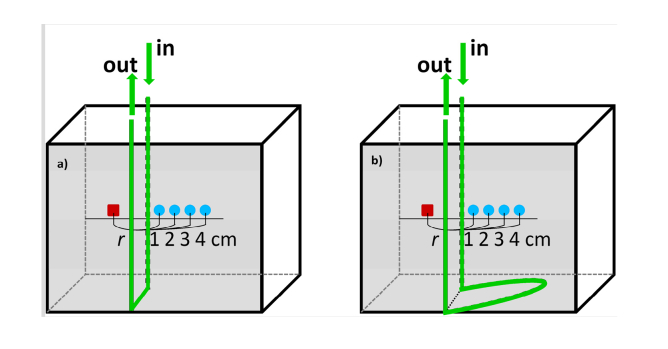
Silicon, optically turbid tube (inner diameter of 3 mm, outer diameter of 3.8 mm) was positioned inside the liquid medium. The tube inside the phantom was positioned in such a way that it formed a loop between two of its segments located at different depths in the liquid. The superficially located segment of the tube (outflow) was fixed next to the Mylar film, whereas the deeper located segment of the tube (inflow) was fixed at the distance of 2 cm from the Mylar film. Locations of the segments of the tube in respect to the optode holder were positioned to mimic the inflow of the dye to deeper layer of the human head corresponding to the brain and superficial layer corresponding to skin. The same mixture of water, milk, and ink was pumped through the tube with a rate of 0.6 ml/s using a peristaltic pump. Boli of 2 ml of the milk-water-ink mixture with ICG (Pulsion, Germany) were rapidly (<1 s) injected through the injection port into the tube in such a way that the bolus appeared first in the segment of the tube located deeper and then in the superficially positioned segment of the tube. In the series of measurements, the concentration of the injected dye was about 5 mg/L. The dye was injected into the tube at a distance of about 25 cm from the location of the optode holder on the surface of the phantom. The distributions of times of flight of diffusely reflected photons were collected within 0.3 s long intervals during 120 s long measurement.

In phantom measurements, the effect of the inflow of the ICG into the tube was studied in dependence of wavelengths (λ) and interoptode distance r. Experiments were carried out on the phantom with a dynamic inflow of ICG in two series of measurements. In the first kind of experiments, the loop between a deeper located segment of the tube and superficially located segment was so long that the boli appeared in these segments of the tube with approximately 27 s of delay. These measurements, called further long loop experiments allowed us to separate in time inflow of ICG to segments of the tube located deep and superficially. In the second kind of measurements, the loop was so short (short loop experiments) that the boli appeared to be overlapped: the dye was still present in the deeper located segment of the tube when it began to appear in the superficially located segment of the tube. The latter case resembles the inflow of the ICG into the human head tissue when the bolus appears first in the intracerebral layers, and then after a short time (seconds), it appears in extracerebral tissue layers [47]. The geometry of the liquid phantoms are presented in Fig. 3.

Fig. 3.

Geometry of the liquid phantom with a) short loop, b) long loop between segments of the tube located deeper and superficially. Boli with indocyanine green (ICG) were passing through the tube positioned in the fish tank at two depths in respect to the front wall of the phantom. Source fiber (red square) and detection fiber bundle (blue circle) were fixed on the surface of Mylar film which formed the front wall of the phantom. The segment of the tube located deeper was positioned at depth of 2 cm in respect to the front wall of the phantom.

3.3 In-vivo measurements

The measurements were carried out on the heads of healthy adults during intravenous injection of ICG. The ICG was administrated after obtaining written informed consent of the studied person. The study was approved by the Ethics Committee of the Medical University of Warsaw, Poland. The experiments were carried out under the supervision of an anesthesiologist. The volunteers were examined in the supine position. A bolus of 5-10 mg of ICG dissolved in 5 mL of water was administrated into the forearm vein. The ICG injection was rapid (about 1 s) and followed by injection of 10 ml of normal saline.

The optodes were located on the forehead close to the hairline above one of the hemispheres. In the in-vivo measurements, a single source-detector separation r = 3 cm was used.

4. Results

4.1 Phantom experiments

4.1.1 Analysis of statistical moments

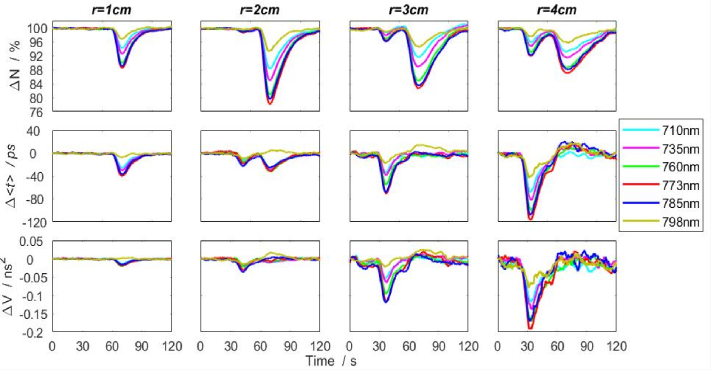
In phantom measurements (both long loop and short loop experiments), during the injection of the ICG, the reflectance signals were efficiently acquired at all 16 spectral channels. Signals representing changes in statistical moments of the DTOFs in long loop experiment acquired at different wavelengths are presented in Fig. 4 as a function of time of the experiment (T). The dye was injected into the tube at T₀ ≈24 s. We found large amplitudes of changes in the number of photons N_tot, mean time of flight of diffusely reflected photons <t> and variance V of the DTOF corresponding to the inflow into both deeper and superficially located segments of the tube. Maximum of absorption of the light caused by the inflow of ICG has appeared at about 798 nm. At wavelengths longer than 800 nm, we observed a significant influence of the fluorescence excited in ICG. This effect was clearly visible in changes of higher order moments Δ<t> and ΔV.

Fig. 4.

Long loop experiment: changes in statistical moments of the DTOFs of diffuse reflectance measured at source-detector separation r = 3 cm after injection of 6 mg/L solution of ICG into the tube of the phantom at T₀ = 24 s. The effect of the inflow of the dye to the segment of the tube located deeper can be observed at T ≈32 s. The dye inflows into the part of the tube located superficially later at T ≈50 s.

Considering this effect of contamination of the signals of diffuse reflectance by the fluorescence at longer wavelengths, in further steps of the study, the analysis was restricted to 8 wavelengths from the range of 650 nm to 800 nm.

Results of analysis of the DTOFs acquired in consecutive measurements of long loop experiments at four interoptode distances (1, 2, 3, 4 cm) and 8 wavelengths for the dose of injected ICG 5 mg/L are presented in Fig. 5. The presented signals were adjusted in such a way that the ICG inflows into the superficial segment of the tube appear at T ≈70 s (second peak in Fig. 5) in signals acquired at all source-detector separations.

Fig. 5.

Changes in statistical moments of DTOFs of diffuse reflectance measured after injection of 5 mg/L solution of ICG into the tube of the phantom at T₀ = 24 s. The peaks observed at T ≈35 s are related to the inflow of the dye to the segment of the tube located deeper whereas the peak appearing later (at T ≈70 s) is related to the dye inflow into the segment of the tube located superficially.

The flow of the dye through the two segments of the tube resulted in the appearance of two peaks in the measured signals related to the increased absorption during inflow of ICG. However, for r = 1 cm the inflow to the segment of the tube located deeper at T ≈35 s was not visible, whereas the second peak, related to the inflow of the dye into the segment of the tube located superficially (at T ≈70 s) was observed in all statistical moments of the DTOF’s with high amplitudes in ∆N_tot and low amplitudes in ΔV signals.

For interoptode distance of r = 2 cm, inflow of the dye into superficial tube was observed in ∆N_tot and ∆<t>, however signals of changes in mean time of flight ∆<t> and variance ∆V were more sensitive to changes in absorption related to the inflow of the dye to the segment of the tube located deeper. The early peaks were found in signals ∆<t> and ∆V at T ≈35 s and correspond to the bolus passage through the segment of the tube located deeper. However, in the signal ∆<t> the amplitude of changes was larger for the passage of ICG through the segment of the tube located superficially (peak appearing later) then through deeper segment, while in the signal of changes in variance ∆V the changes related to the passage of ICG through the superficial segment (at T ≈70 s) of the tube were hardly visible.

Furthermore, in signals of moments acquired at r = 3 cm and r = 4 cm the high amplitude peaks related to the inflow of ICG to the segment of the tube located deeper were clearly observed for Δ<t> and ΔV. For these moments the inflow into the superficially located segment of the tube cannot be observed whereas the amplitude of the signal change related to the superficially located segment in Δ N_tot is higher than for the segment located deeper.

In short loop experiment, the observed pattern of the inflow of the ICG into the tube was similar to long loop model, and the decrease of all moments was noted due to the increased absorption of the studied medium. Since the inner diameter of the tube is only 3 mm, the ICG bolus after injecting into the tube become broad, only one broad peak was observed due to overlapped superficial and deeper segments of the tube, which simulates inflow of the dye into the human brain. The amplitude of changes in ∆N_tot, ∆<t> and ∆V depended on the wavelengths, and the maximum of amplitude was found at 798 or 810 nm.

4.1.2 Estimation of the depth-resolved ICG concentration changes

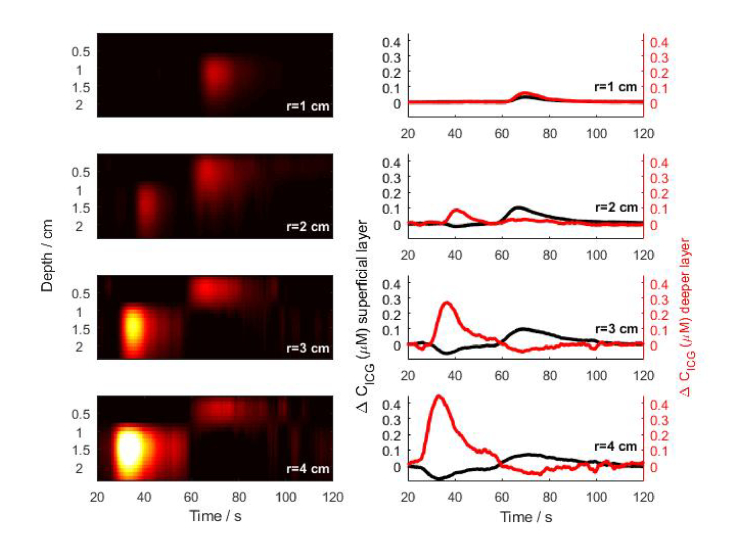
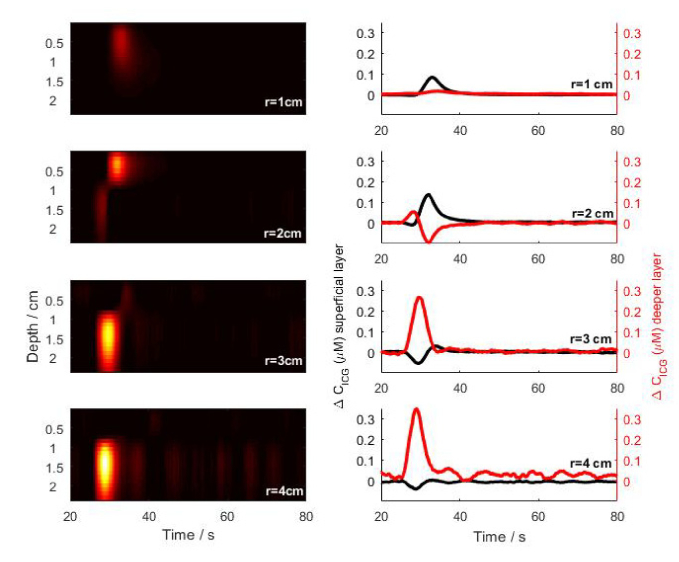
The changes in the ICG concentration (∆C_ICG) occurring at various depths were calculated by SVD using algorithm presented in Fig. 1. Results of this analysis were presented in Figs. 6 and 7 for the phantoms with a long and short loop between two segments of the tube, respectively. The time course of ∆C_ICG revealed that the signals recorded at shorter interoptode distances were sensitive to inflow to the segment of the tube located superficially whereas signals recorded at large source-detector separation were more sensitive to the inflow of the dye to the segment of the tube located deeper.

Fig. 6.

Phantom with long loop studies. Left panel: changes (colorbar) of the ICG concentration in all (24) layers of the model versus time before and after injection of an ICG bolus at T₀ = 24 s. The ΔC_ICG,j values were calculated from moments of DTOFs measured at multiple wavelengths and single source-detector separation (r = 1, 2, 3 and 4 cm). The colormaps were scaled in that way that all negative values were ignored for clarity. Right panel: the dynamics of ICG concentration changes in the deeper (first peak, red) and superficial (second peak, black) segments of the tube, obtained by averaging the ΔC_ICG changes in the layers of each segment (superficial and deeper).

Fig. 7.

Phantom with short loop studies. Left panel: changes (colorbar) of the ICG concentration in all (24) layers of the model versus time before and after injection of an ICG bolus at T₀ = 24 s. The ΔC_ICG,j values were calculated from moments of DTOFs measured at multiple wavelengths and single source-detector separation (r = 1, 2, 3 and 4 cm). The colormaps were scaled in that way that all negative values were ignored for clarity. Right panel: the dynamics of ICG concentration changes in the deeper (first peak, red) and superficial (second peak, black) segments of the tube, obtained by averaging the ΔC_ICG changes in the layers of each segment (superficial and deeper).

In the phantom with long loop measurement with r = 1 cm, implementation of the algorithm resulted in appearance of a single “joint” bolus at depth of ≈1.5 cm, appearing simultaneously in both signals related to the inflow of the dye into superficial (ΔC_ICG,extra) and deeper (ΔC_ICG,intra) part of the tube (Fig. 6, upper panel). In the phantom with a short loop, the algorithm differentiated ΔC_ICG,extra and ΔC_ICG,intra more precisely showing clear inflow only into the superficial part of the tube (Fig. 7, right panel).

The algorithm allowed us to reconstruct boli for deeper and superficial segments of the tubes for interoptode distances 2 and 3 cm with different sensitivity. For both phantoms loops, the separate boli inflows were observable in ΔC_ICG,extra and ΔC_ICG,intra signals, but with the predominance of the inflow into the superficial part of the tube in case of r = 2 cm: the reconstructed value of the ΔC_ICG,extra as averaged signal from top 12 layers of the model (see Section 2) was higher than ΔC_ICG,intra value as averaged signal from consecutive 12 layers of the model in the case of the short loop between segments (Fig. 7, right panel). In the phantom with a long loop, the reconstruction algorithm resulted in the properly separated boli for different tube segments, however, the amplitudes of the ICG concentration changes in signals ΔC_ICG,extra and ΔC_ICG,intra were smaller than the real ICG concentration values contained in the injected bolus. The predominance of the influence of the ICG boli present in the deeper part of the tube was observed in the reconstructed signals for r = 3 cm: ΔC_ICG,intra was 3 times higher than ΔC_ICG,extra. (Figs. 6 and 7, right panel)

At r = 4 cm only ICG concentration increase in the signal ΔC_ICG,intra related to inflow to the deeper part of the tube was observed. No traces of the ICG inflow into the superficial segment in the ΔC_ICG,extra signals were obtained in the phantom with short loop whereas only trace of such inflow was noted for the phantom with a long loop (right bottom panel in Fig.7 and 6, respectively). In Fig. 6, the peaks in the signals ΔC_ICG,intra and ΔC_ICG,extra corresponding to the inflow of the ICG into the different segments of the tube are broader than those presented in measurements on the phantom with shorter loop (as presented in Fig. 7) due to the slower speed of the peristaltic pump used in the long loop phantom experiments.

4.2 In-vivo measurements

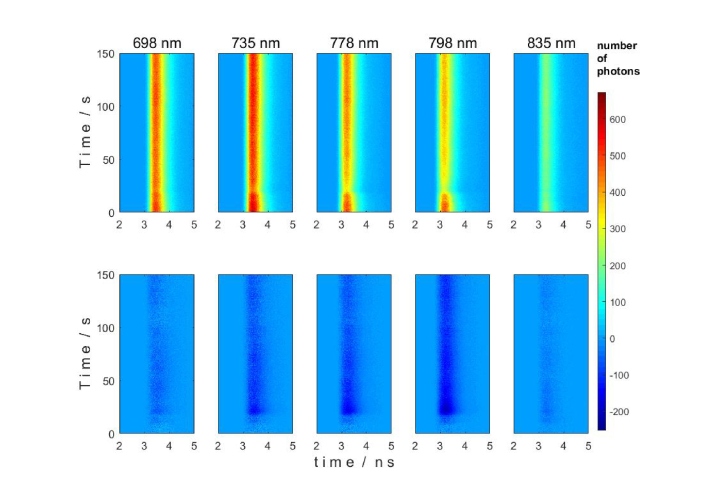
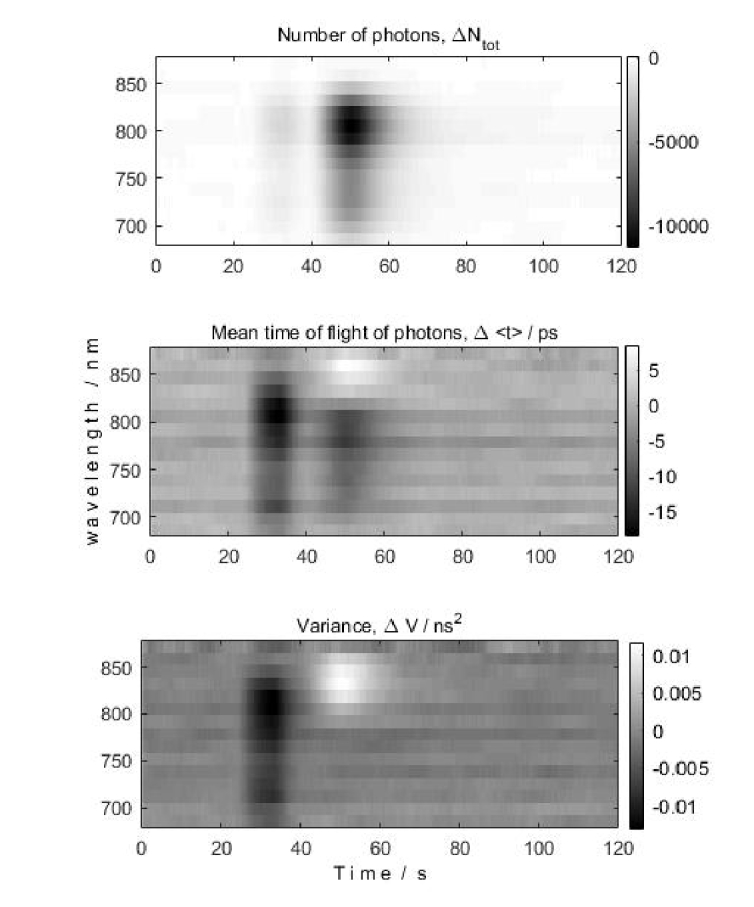
Example results of the in-vivo measurement carried out on the head of a healthy volunteer after ICG bolus injection are presented in Figs. 8 and 9. The reflectance signals were successfully detected in 15 spectral channels, covering about 200 nm in the range of 650-850 nm. Maximum of absorption of the light has been found at 798 nm. Changes in distributions of times of flight of diffusely reflected photons are shown in Fig. 8, upper row for selected wavelengths as a function of the time of passage of an ICG bolus (T). A progressive decrease in the number of detected photons starts about 17 seconds after injection of the dye and the minimum N is reached about 23 s after injection. This result matches well with time courses of signals obtained previously in fluorescence measurements [48]. In the bottom row of Fig. 8 the result of the subtraction of the DTOF averaged from time period T₀ before the ICG injection from every DTOF as a function of time of the experiment T is presented. This analysis allows to observe changes of the distributions of times of flight of photons caused by the increased absorption during ICG bolus inflow.

Fig. 8.

Upper panel: Changes in the number of diffusely reflected photons N shown as a function of time of experiment T and time t of the photon in respect to the laser pulse following injection of ICG bolus at T₀ = 0 s during the in-vivo measurement. Lower panel: difference colormaps demonstrating the changes of the DTOFs with respect to the first phase of the measurement (before ICG injection). Results of measurements carried out at 5 different wavelengths are presented.

Fig. 9.

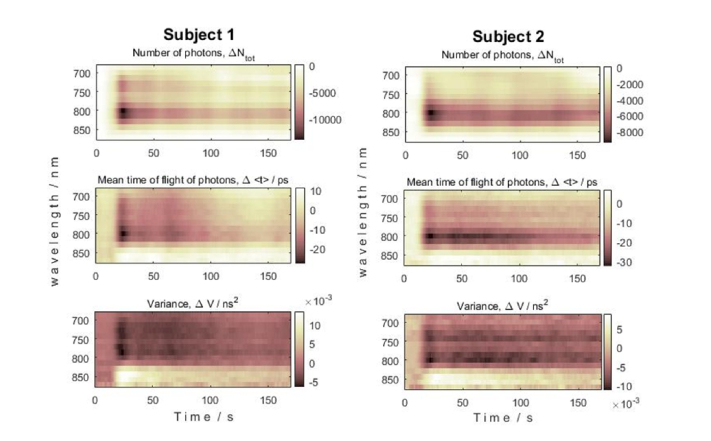
Changes in a total number of photons N_tot, mean time of flight <t> and variance V of diffusely reflected photons following the injection of ICG bolus at T = 0 in two healthy volunteers (left and right panels), measured for different wavelengths.

In Fig. 9, selected in-vivo results of the changes in statistical moments of distributions of times of flight of diffusely reflected photons (ΔN_tot, Δ<t>, ΔV) for two healthy volunteers following the injection of the bolus of ICG are presented. The inflow of the ICG into the head caused a rapid decrease in the total number of reflected photons N_tot due to the increased concentration of the dye, which led to the increased absorption in the studied tissue volume.

In the N_tot signals, the initial rapid decrease was observed during the inflow of the ICG bolus followed by an increase with a tendency to return of the signal to the initial level. The pattern of changes in higher statistical moments (mean time of flight of diffusely reflected photons <t> and variance V) calculated from DTOFs depended on the wavelength (Fig. 9). We noted increase in the amplitude of change in mean time of flight Δ<t> for the photons detected at longer wavelengths (for λ > 823 nm). For the variance V, this effect was even more pronounced - the increase of the variance of the DTOF was observed already at wavelengths longer than 810 nm.

In the in-vivo measurements, the bolus appears first in the brain and then in the extracerebral tissues with the delay of only a few seconds. The inflow and washout kinetics of ICG in deeper layers are rapid and much faster compared with superficial layers.

In our analysis, two-compartment model of the head was considered in which the intracerebral and extracerebral tissue compartments are represented. For analysis of in-vivo data, we assumed that the extracerebral compartment consisted of the 12 top layers covering 1.2 cm depths according to the observed transition in the dynamics of ΔC_ICG changes (Fig. 10, left panel). The dynamics of ICG concentration changes in the intracerebral and extracerebral compartments, obtained by averaging the ΔC_ICG changes among the layers representing extra- and intra-cerebral compartments are presented in Fig. 10a.

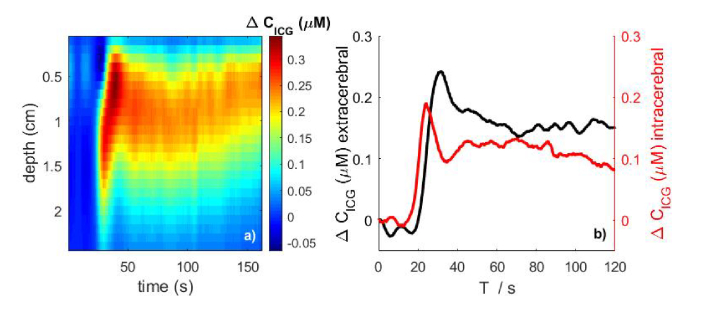
Fig. 10.

a) Changes (colorbar) of the ICG concentration ΔC_ICG,j in 24 layers of the head model (each 0.1 mm thick) versus time before and after injection of an ICG bolus at T₀ = 0 second. These changes were calculated from moments of DTOFs measured at multiple wavelengths and single source-detector separation (r = 3 cm). b) Changes in the ICG concentration averaged over the top 12 layers (extracerebral tissue compartment of the thickness of 1.2 cm) and the remaining 12 bottom layers (intracerebral tissue compartment).

We noticed a dynamic increase in ΔC_ICG in the intracerebral compartment followed by a fast decrease and return to initial level. This result was related to the fast inflow and washout of ICG in the cerebral tissue. In contrast, a delayed increase in ΔC_ICG in the extracerebral tissue compartment was followed by slower washout kinetics.

5. Discussion and conclusions

Recently, optical methods which utilize near-infrared spectroscopy are extensively tested in clinical trials [1, 6]. However, a significant challenge in applying these techniques in measuring clinically useful cerebral hemodynamic parameters in adult humans is that the light detected on the surface of the head must travel through the extracerebral layers (scalp, skull and cerebrospinal fluid) before interrogating the brain [5, 38, 49].

This problem significantly influences the potential of routine application of techniques based on NIRS in clinical practice. The techniques of assessment of cerebral perfusion or measurements of cerebral blood flow based on an assessment of inflow and washout of ICG also suffer from the problem of influence of extracerebral tissue on the results of measurements. It was shown in several studies carried out on adult subjects that the shape of ICG inflow and washout depends strongly on the perfusion of an extra-cerebral layer on the collected optical signals [18, 36, 37, 50, 51]. Previously, the optimal measurement conditions for assessment of brain perfusion with the use of optical contrast agent and time-resolved diffuse reflectometry were determined in multidistance time-resolved measurements carried out on phantoms and on the surface of the head at 16 source-detector separations during the injection of ICG: the source-detector separation of 6 cm is recommended for monitoring of inflow of optical contrast to the intracerebral brain tissue compartments with the use of continuous wave reflectometry, whereas the separation of 4 cm is enough when the higher-order moments of DTOFs are available [52].

The device developed for the present study was optimized for measurement of time-resolved spectrum of ICG in clinical conditions. This kind of measurement is challenging because of limited number of photons which reach the detection system and necessity to obey safety regulations. Thus, the trade-off between photon count rate and reasonable sampling frequency which allows to monitor inflow and washout of the dye in the head needs to be considered. Our results of liquid phantom measurements suggest that the optical signal detected at r = 3 cm (which is typically used in in-vivo studies) have proper quality for successful calculation of higher order statistical moments of the DTOFs. Furthermore, these results show that the signal originating from the deeper layers of the studied medium can be successfully separated in such measurement. In several NIRS studies, specific methods to minimize and correct the effect of extra-cerebral tissue were reported. A short source-detector separation measurement can be used to model the extracerebral contribution which is furthermore removed from larger separation measurements typically considered to contain brain-related components. However, in these studies CW-NIRS measurement method [54] was used or, (in the case of time-resolved studies) only functional NIRS measurements were carried out and changes in intra- and extracerebral hemoglobins concentrations were derived [55–59].

A multiwavelength NIRS approach was considered by several authors as a tool for assessment of cerebral oxygenation. A broadband light source [12, 13, 53, 54] or light sources with selected discrete wavelengths were applied for such measurements [14]. However, in the above-mentioned spectral approaches, the continuous wave light was utilized, and the discrimination of extra- and intracerebral components was not reported.

A few reports only proposed a time-resolved extension of the spectral approach for estimation of absorption and scattering parameters of the media as well as of chromophore concentration. It was demonstrated that evaluation of the chemical composition of the studied medium with higher precision was possible when broadband time-of-flight absorption and scattering spectra measurements were carried out [55]. Phantom studies were carried out [56, 57] as well as in-vivo breast [56] and abdomen [57] measurements with broadband time-resolved systems were performed. In brain studies, several multiwavelength time-resolved systems were presented, and results of functional studies were reported [58, 59]. However, the mentioned studies that use spectral time-resolved measurements are restricted to the determination of absorption coefficient as well as reduced scattering coefficient of the studied media and does not provide the depth-resolved information.

In the present work, we used broadband (spectral) time-resolved measurements in which the DTOFs were recorded at 16 wavelengths simultaneously but at single source-detector separation (r = 3 cm) during in-vivo tests carried out in healthy volunteers, or r = 1, 2, 3, 4 cm in phantom experiments during administration of a bolus of indocyanine green (ICG). Presented results show that the changes in wavelength-resolved reflectance signals related to the inflow of ICG can be successfully detected. The number of photons, mean time of flight and variance of the DTOF decreased with the increase of the tissue absorption related to the inflow of the dye. This effect was observed at wavelengths between 650 and 780 nm.

The observed increase of the <t> and V at longer wavelengths was related to the contribution of emitted fluorescence photons to the measured DTOFs. Along with strong absorption, ICG reveals fluorescence properties in near-infrared region [60]. However, proper filtration of the light remitted from the tissue is needed in order to observe the fluorescence signals because of limited quantum yield of the fluorophore and necessity to block the excitation light. In our setup, no filtration was used, and the fluorescence photons may influence the optical signals especially at longer wavelengths. At the wavelengths longer than 810 nm, at which the fluorescence of ICG is typically observed [48, 60] no influence of the fluorescence was observed in the N_tot signals for which rapid decrease during the inflow of the ICG bolus is caused by the increased absorption. However, in the signals of changes in higher order statistical moments (mean time of flight of diffusely reflected photons <t> and variance V) increases in amplitudes were noted which are related to the fluorescence emission. The fluorescence photons are expected to be appeared at longer times [61], thus influencing with higher probability the higher order moments of the measured DTOFs. Signals acquired at these longer wavelengths were not used in analysis of changes in ICG concentration at different depths in the medium. The influence of fluorescence on signals acquired during ICG bolus tracking was previously reported by Steinkellner et al. [37] and should be considered when the optical signal is detected by NIR reflectometry at a single laser source wavelength and broad-spectrum detection [62].

We have modified the proposed earlier method [20] to derive changes in the absorption coefficient from changes in the attenuation, mean time of flight and variance [20] measured at four source-detector separations, via replacing measurements at the multiple distances by measurements at multiple wavelengths. We proposed a method allowing for depth-resolved estimation of changes in the concentration of the ICG in the tissue by recording DTOFs of diffusely reflected photons and calculating their statistical moments for multiple wavelengths from the near-infrared region. The different sensitivities of the changes in moments to changes in absorption of the tissue appearing at different depths in the tissue were utilized, and the algorithm allowing for estimation of changes in ICG concentration as a function of depth was developed. The algorithm is based on (i) multilayered tissue model, (ii) calculation of sensitivities of the moments to changes in absorption appearing at different depth using diffusion equation solution and (iii) assumption of linear dependence of the measured quantities (moments) of the unknown changes in absorption appearing at different depths in the tissue.

The proposed in the present study method was first tested on the long-loop liquid phantom with a separated dynamic inflow of ICG into superficial and deeper segments of the tubes to extract a signal reflecting inflow to the deep layer of the medium. The next stage of the study was to shorten the loop between superficial and deeper segments of the tubes so that the signals from the deep and superficial segments of the tube were overlapping, as it occurs physiologically in the blood flow through the head in humans. After a successful calculation of changes in the optical contrast agent concentrations in the deep and superficial layer of the phantom, measurements were performed on healthy human subjects.

The derivation of the changes in absorption at different depths in the medium is performed by solving the system of linear equations and the calculation time is very short – it takes only few seconds on a standard PC for whole signal consisting of 1000 samples per channel in time. Thus, the proposed calculation method may allow for real-time ΔC_ICG estimation in extra- and intracerebral compartments.

Quantification of the derived changes in concentration of ICG in the different layers of the medium ΔC_ICG needs more deep discussion. In estimation of ICG concentration change as a function of time and depth during the phantom experiment we would expect appearance of two independent boli of similar amplitude related to the presence of the dye in deeper and superficial segments of the tube. The applied decomposition method resulted in different amplitudes of ΔC_ICG signals for these two compartments. This effect is clearly visible in Figs. 6 and 7 for different source-detector separations. This effect may be related to the assumptions made when the proposed method is used. The sensitivity factors were calculated using the assumption that initially the medium is homogeneous. Because the real optical properties of the two layers of the medium may differ significantly, the errors in the calculated values of absorption changes may appear. Another assumption is the linearity of the relationship between measured changes in moments and derived changes in concentration of the dye. This relationship holds true for small changes in absorption appearing in all layers of the medium [20]. For large changes in concentration of ICG and rather large changes in statistical moments of the DTOFs which were observed in phantom experiments this assumption may be not fulfilled. In in-vivo tests the assumption of the thickness of the extracerebral layer was made (1.2 cm), which may not properly reflect the real values (which in fact varies significantly from subject to subject). This assumption may also influence absolute quantification of the changes in ICG concentration obtained in both compartments of the studies tissues.

Results of the phantom experiments and in-vivo investigations show that application of the proposed algorithm based on monitoring of multiwavelength diffuse reflectance may allow us to derive depth-resolved kinetics of the ICG, thus, allowing potentially to assess blood flow in the brain cortex with higher precision.

The proposed method has an important practical advantage because it needs acquisition of the optical signals at only a single source-detector separation.

Funding

National Science Centre, Poland (UMO-2014/15/B/ST7/05276); National Centre for Research and Development (DOBR/0052/R/ID1/2012/03).

Disclosures

The authors declare that there are no conflicts of interest related to this article.