Abstract
Given that the neural and connective tissues of the optic nerve head (ONH) exhibit complex morphological changes with the development and progression of glaucoma, their simultaneous isolation from optical coherence tomography (OCT) images may be of great interest for the clinical diagnosis and management of this pathology. A deep learning algorithm (custom U-NET) was designed and trained to segment 6 ONH tissue layers by capturing both the local (tissue texture) and contextual information (spatial arrangement of tissues). The overall Dice coefficient (mean of all tissues) was 0.91 ± 0.05 when assessed against manual segmentations performed by an expert observer. Further, we automatically extracted six clinically relevant neural and connective tissue structural parameters from the segmented tissues. We offer here a robust segmentation framework that could also be extended to the 3D segmentation of the ONH tissues.
OCIS codes: (110.4500) Optical coherence tomography, (150.0150) Machine vision, (170.0170) Medical optics and biotechnology, (150.1135) Algorithms
1. Introduction
The development and progression of glaucoma is characterized by complex 3D structural changes within the optic nerve head (ONH) tissues. These include the thinning of the retinal nerve fiber layer (RNFL) [1–3]; changes in the minimum-rim-width [4], choroidal thickness [5, 6], lamina cribrosa (LC) depth [7–9], and posterior scleral thickness [10]; and migration of the LC insertion sites [11, 12]. If these parameters (and their changes) could be extracted automatically from optical coherence tomography (OCT) images, this could assist clinicians in the day-to-day management of glaucoma.
While there exist several traditional image processing tools to automatically segment the ONH tissues [13–20], and thus extract these parameters, each tissue currently requires a different algorithm (tissue-specific). Besides, they are computationally expensive [21], and are also prone to segmentation errors in images with pathologies [22–25] (e.g. glaucoma). In our previous study [26], while it was possible to isolate the connective and neural tissues of the ONH, we were unable to segment each ONH tissue separately.
Recently, with the advent of deep learning, several studies have shown the successful segmentation of retinal layers [27–30], choroid [31, 32], etc., from macular OCT images. However, the retinal layer segmentation technique proposed by Fang L. et al. [28], was able to capture only the local information (tissue texture), and was computationally expensive. Although the study by Venhuizen F.G. et al. [30] was able to capture both the local and contextual information (spatial arrangement of tissues), it was still limited by under-segmentation in images with mild-pathology (AMD). Also, current choroidal segmentation tools offered low specificity and sensitivity [31], and were slow [32]. With our recently proposed patch-based segmentation [33], we were able to simultaneously segment the individual neural and connective tissues, and offer significantly similar performance on healthy and glaucoma images. Yet, this approach was still limited as it failed to offer precise tissue boundaries, separate the LC from the sclera, and presented artificial LC-scleral insertions.
In this study, we present DRUNET (Dilated-Residual U-Net), a novel deep-learning approach capturing both the local and contextual information to segment the individual neural and connective tissues of the ONH. This algorithm can be used to automatically extract 6 structural parameters of the ONH. We then present a comparison with our earlier deep-learning (patch-based) approach to assert the robustness of DRUNET. Our long-term goal is to offer a framework that can be extended to the segmentation and the automated extraction of structural parameters from OCT volumes in 3D.
2. Methods
2.1. Patient recruitment
A total of 100 subjects were recruited at the Singapore National Eye Center. All subjects gave written informed consent. This study adhered to the tenets of the Declaration of Helsinki and was approved by the institutional review board of the hospital. The cohort consisted of 40 normal (healthy) controls, 41 subjects with primary open angle glaucoma (POAG) and 19 subjects with primary angle closure glaucoma (PACG). The inclusion criteria for normal controls were: an intraocular pressure (IOP) less than 21 mmHg, healthy optic nerves with a vertical cup-disc ratio (VCDR) less than or equal to 0.5 and normal visual fields test. Primary open angle glaucoma was defined as glaucomatous optic neuropathy (GON; characterized as loss of neuroretinal rim with a VCDR > 0.7 and/or focal notching with nerve fiber layer defect attributable to glaucoma and/or asymmetry of VCDR between eyes > 0.2) with glaucomatous visual field defects. Primary angle closure glaucoma was defined as the presence of GON with compatible visual field loss, in association with a closed anterior chamber angle and/or peripheral anterior synechiae in at least one eye. A closed anterior chamber angle was defined as the posterior trabecular meshwork not being visible in at least 180° of anterior chamber angle. We excluded subjects with any corneal abnormalities that would preclude reliable imaging. Note also that the patient cohort was the same as that in our previous patch-based study [33].
2.2. Optical coherence tomography imaging
The subjects were seated and imaged under dark room conditions after dilation with 1% tropicamide solution. The images were acquired by a single operator (TAT), masked to diagnosis with the right ONH being imaged in all the subjects, unless the inclusion criteria were met only in the left eye, in which case the left eye was imaged. A horizontal B-scan (0°) of 8.9 mm (composed of 768 A-scans) was acquired through the center of the ONH for all the subjects using spectral-domain OCT (Spectralis, Heidelberg Engineering, Heidelberg, Germany). Each OCT image was averaged 48× and enhanced depth imaging (EDI) was used for all scans.
2.3. Shadow removal and light attenuation: adaptive compensation
We used adaptive compensation (AC) to remove the deleterious effects of light attenuation [34]. AC can help mitigate blood vessel shadows and enhance the contrast of OCT images of the ONH [34, 35]. A threshold exponent of 12 (to limit noise over-amplification at high depth) and a contrast exponent of 2 (for improving the overall image contrast) were used for all the B-scans [34].
2.4. Manual segmentation
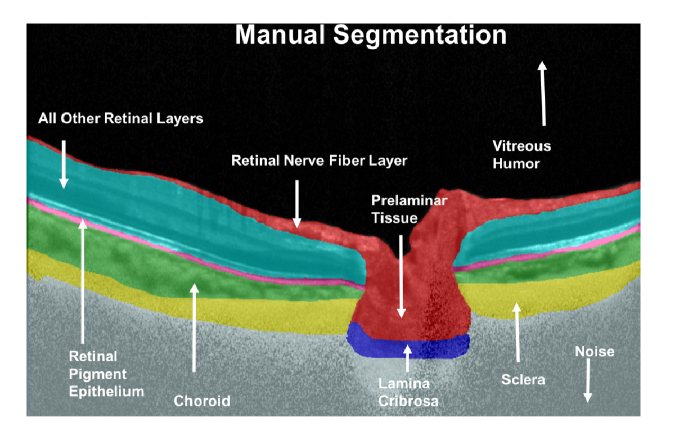
An expert observer (SD) performed manual segmentation of all OCT images using Amira (version 5.4, FEI, Hillsboro, OR). This was done to 1) train our algorithm to identify and isolate the ONH tissues; and to 2) validate the accuracy of the segmentations. Each OCT image was segmented into the following classes: (refer Fig. 1.): (1) the RNFL and the prelamina (in red); (2) the retinal pigment epithelium (RPE; in pink); (3) all other retinal layers (in cyan); (4) the choroid (in green); (5) the peripapillary sclera (in yellow); and (6) the (LC) (in blue). Noise (in gray) and the vitreous humor (in black) were also isolated. Note that we were unable to obtain a full thickness segmentation of the peripapillary sclera and the LC due to limited visibility [35]. Only their visible portions were segmented.
Fig. 1.
Manual segmentation of a compensated OCT image. The RNFL and the prelaminar tissue are shown in red, the RPE in pink, all other retinal layers in cyan, the choroid in green, the peripapillary sclera in yellow, the LC in blue, noise in grey and the vitreous humor in black.
2.5. Deep learning based segmentation of the ONH
While there already exist a few deep learning based studies for segmentation of retinal layers [27, 28, 30, 36] and choroid [31, 32] from macular OCT images, the simultaneous segmentation of the individual neural and connective tissues of the ONH still remains less explored. Although our recently proposed patch-based method, to the best of our knowledge, was the first to explore the simultaneous segmentation of the individual ONH tissues, its accuracy was still limited.
In this study, we developed the architecture DRUNET (Dilated-Residual U-Net): a fully convolutional neural network inspired by the widely used U-Net [37], to segment the individual ONH tissues. It exploits the inherent advantages of the U-Net skip connections [38], residual learning [39] and dilated convolutions [40], as also shown in [41], to offer a robust segmentation with a minimal number of trainable parameters. The U-Net skip connections allowed capturing both the local and contextual information [29, 30], while the residual connections offered a better flow of the gradient information through the network. Using the dilated convolutional filters, we were able to better exploit the contextual information: this was crucial as we believe local information (i.e. tissue texture) alone is insufficient to delineate precise tissue boundaries. DRUNET was trained with OCT images of the ONH and their corresponding manually segmented ground truths.
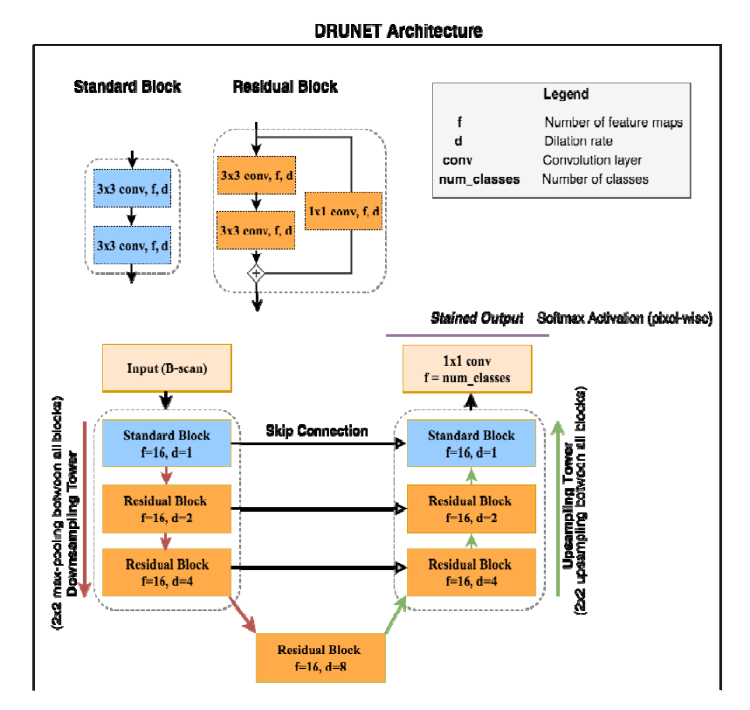
2.5.1. Network architecture
The DRUNET architecture was composed of a downsampling and an upsampling tower (Fig. 2), connected to each other via skip connections. Each tower consisted of one standard block and two residual blocks. Both the standard and the residual blocks were constructed using two dilated convolution layers, with 16 filters (size 3×3) each. The identity connection in the residual block was implemented using a 1×1 convolution layer, as described in Fig. 2. In the downsampling tower, the input image of size 496×768 was fed to a standard block with a dilation rate of 1 followed by two residual blocks with dilation rates of 2 and 4 respectively. After every block in the downsampling tower, a max-pooling layer of size 2×2 was used to reduce the dimensionality and exploit the contextual information. A residual block with a dilation rate of 8 was used to transfer the features from the downsampling to the upsampling tower. These features were then passed through two residual blocks with dilation rates of 4 and 2 respectively. A standard block with a dilation rate of 1 was used to restore the image to its original resolution. After every block in the upsampling tower, a 2×2 upsampling layer was used to sequentially restore the image to its original resolution. The output layer was implemented as a 1×1 convolution layer with the number of filters equal to the number of classes (8; 6 tissues + noise and vitreous humour). We then applied a softmax activation to this output layer to obtain the class-wise probabilities for each pixel. Finally, each pixel was assigned the class of the highest probability. Also, the skip connections [38] were established between the downsampling and upsampling towers to recover the spatial information lost during the downsampling.
Fig. 2.
DRUNET comprises of two towers: (1) A downsampling tower – to capture the contextual information (i.e., spatial arrangement of the tissues), and (2) an upsampling tower – to capture the local information (i.e., tissue texture). Each tower consists of two blocks: (1) a standard block, and (2) a residual block. The entire network consists of 40,000 trainable parameters in total.
In both towers, all the layers except the last output layer were batch normalized [42] and activated by an exponential linear unit function ELU [43]. In each residual block, the residual layers were batch normalized and ELU activated before their addition.
The entire network was trained end-to-end using stochastic gradient descent with Nesterov momentum (momentum = 0.9). An initial learning rate of 0.1 (halved when the validation loss failed to improve over two consecutive epochs) was used to train the network and the model with the best validation loss was chosen for all the experiments in this study. The loss function ‘L’ was based on the mean of Jaccard Index calculated for each tissue as shown below:
| (1) |
| (2) |
where is the Jaccard Index for the tissue ‘’, is the total number of classes, is the set of pixels belonging to class ‘’ as predicted by the network, and is the set of pixels representing the class ‘’ in the manual segmentation. The final network consisted of 40,000 trainable parameters. The proposed architecture was trained and tested on an NVIDIA GTX 1080 founder’s edition GPU with CUDA v8.0 and cuDNN v5.1 acceleration. With the given hardware configuration, each OCT image was segmented in 80 ms.
2.5.2. Data augmentation
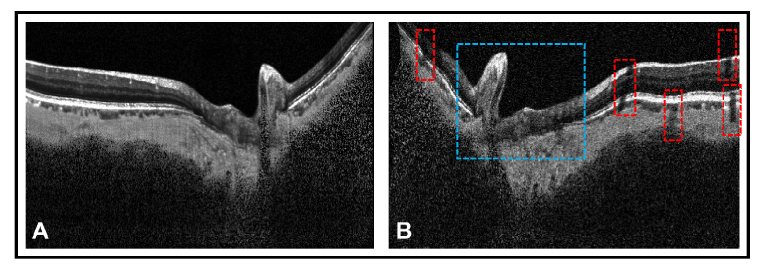
An extensive online data augmentation was performed to overcome the sparsity of our training data. Data augmentation consisted of rotation (8 degrees clockwise and anti-clockwise); horizontal flipping; nonlinear intensity shift; additive white noise and multiplicative speckle noise [44]; elastic deformations [45] and occluding patches. An example of data augmentation performed on a single OCT image is shown in Fig. 3.
Fig. 3.
Extensive data augmentation was performed to overcome the sparsity of our training data. (A) represents a compensated OCT image of a glaucoma subject. (B) represents the same image having undergone data augmentation. The data augmentation includes horizontal flipping, rotation (8 degrees clockwise), additive white noise and multiplicative speckle noise [44], elastic deformation [45] and occluding patches. A portion of the image undergoing elastic deformation and occlusion from patches is bounded by blue and red box respectively. The elastic deformations (combination of shearing and stretching) made our network invariant to images with atypical morphology (i.e., ONH tissue deformation in glaucoma [47]). The occluding patches reduced visibility of certain tissues, making our network invariant to blood vessel shadows.
Nonlinear intensity shift was performed using the following function:
| (3) |
where and are the image intensities (pixel-wise) before and after the nonlinear intensity shift respectively, and are random numbers between 0 and 0.1, and is an exponentiation factor (random number between 0.6 and 1.4). This made the network invariant to intensity inhomogeneity within/between tissue layers (a common problem in OCT images affecting the performance of automated segmentation tools [46]).
The elastic deformations [45] can be viewed as an image warping technique to produce the combined effects of shearing and stretching. This was done in an attempt to make our network invariant to images with atypical morphology (i.e., ONH tissue deformations as seen in glaucoma [47]). A normalized random displacement field representing the unit displacement vector for each pixel location in the image was defined, such that:
| (4) |
where and are the pixel locations in the warped and the original images respectively. The magnitude of the displacement was controlled by ( = 10 in the horizontal and = 15 in the vertical direction). The variation in displacement among the pixels was controlled by (60 pixels; empirically set), the standard deviation of the Gaussian that is convolved with the displacement field . Note that the unit displacement vectors were generated (randomly) from a uniform distribution between −1 and + 1.
Twenty occluding patches of size 60×20 pixels were also added at random locations to reduce the visibility in certain tissues, in an effort to make our network invariant to blood vessel shadowing that is common in OCT images. Each occluding patch resulted in the reduction of intensity in the entire occluded region by a random factor (random number between 0.2 and 0.8).
2.5.3. Demystifying DRUNET
In an attempt to understand the intuition behind each design element in the DRUNET architecture, four different architectures were trained and validated on the same data sets. The following architectures were used for training (with data augmentation):
Architecture1: Baseline U-Net (each tower consisted of only standard blocks with standard convolution layers).
Architecture 2: Modified U-Net v1 (each tower consisted of one standard block and two residual blocks with standard convolution layers).
Architecture 3: Modified U-Net v2 (each tower consisted of one standard block and two residual blocks with standard convolution layers; batch normalization after every convolution layer in the residual block).
Architecture 4: DRUNET (each tower consisted of one standard block and two residual blocks with dilated convolution layers; batch normalization after every dilated convolution layer in the residual block).
In all the architectures, the convolution layers (standard/dilated) had 16 feature maps, and were trained end to end using stochastic gradient descent with Nesterov momentum (momentum = 0.9).
The performance between different architectures was compared by assessing the training loss and the validation accuracy (accuracy on unseen images) obtained on the same training and testing data sets.
In an attempt to understand the importance of data augmentation, the entire process was repeated by training each architecture without data augmentation.
2.5.4. Training and testing of our network
The data set of 100 B-scans (40 healthy, 60 glaucoma) was split into training and testing data sets. The training set was composed of an equal number of compensated glaucoma and healthy OCT images of the ONH, along with their corresponding manual segmentations. The trained network was then evaluated on the unseen testing set (composed of the remaining compensated OCT images of the ONH and their corresponding manual segmentations). A training set of 40 images (60 testing images) were chosen for all the experiments discussed in this study.
To assess the consistency of the proposed methodology, the model was trained on five training sets of 40 images each and tested on their corresponding testing sets. Given the limitation of a total of only 100 OCT images, it was not possible to obtain five distinct training sets, thus each training set had some images repeated.
To study the effect of compensation on segmentation, the entire process (training and testing) was repeated with the baseline (uncompensated) images.
A comparative study was also performed between the DRUNET architecture and our previously published patch-based segmentation approach [33]. For this, we trained and tested both the techniques with the same data set.
We would like to assert that there was no overlap between the training and testing sets in each experiment. However, due to the scarcity of OCT images (100 images) and their manual segmentations, there was a small leakage of test/training sets across all experiments.
2.6. Qualitative analysis
All the DRUNET segmented images were manually reviewed by an expert observer (SD) and qualitatively compared with their corresponding manual segmentations.
2.7. Quantitative analysis
We used the following metrics to assess the segmentation accuracy of the DRUNET: (1) the Dice coefficient (DC); (2) Specificity (S.p); and (3) Sensitivity (S.n). For each image, the metrics were computed for the following classes: (1) RNFL and prelamina, (2) RPE, (3) all other retinal layers, and (4) choroid. Note that the metrics could not be applied directly to the peripapillary sclera and the LC as their true thickness could not be obtained from the manual segmentation. However, segmentation of the peripapillary sclera and of the LC was qualitatively assessed. Noise and vitreous humor were also exempted from such a quantitative analysis.
The Dice coefficient was used to measure the spatial overlap between the manual and DRUNET segmentation. It is defined between 0 and 1, where 0 represents no overlap and 1 represents a complete overlap. For each image in the testing set, the Dice coefficient was calculated for each tissue as follows:
| (5) |
where is the set of pixels representing the tissue ‘’ in the manual segmentation, while represents the same in the DRUNET segmented image.
Specificity was used to assess the true negative rate of the proposed method.
| (6) |
here and are the set of all the pixels not belonging to class ‘ ’ in the DRUNET segmented and the corresponding manually segmented image respectively.
Sensitivity was used to assess the true positive rate of the proposed method as is defined as:
| (7) |
Both specificity and sensitivity were reported on a scale of 0-1. To assess the segmentation performance between glaucoma and healthy OCT images, for each experiment, the metrics were calculated separately for the two groups.
2.7.1. Segmentation accuracy: comparison between glaucoma and healthy images
We used unpaired Student’s t-test to quantitatively compare the performance of DRUNET segmentation when tested on either glaucoma or healthy OCT images. In each of the five testing sets, unpaired t-tests were used to assess the differences in the Dice coefficients, specificities and sensitivities (means). The tests were performed in MATLAB (R2015a, MathWorks Inc., Natick, MA) and statistical significance was set at p<0.05.
2.7.2. Segmentation accuracy: effect of compensation
Paired t-tests were used to assess if the segmentation performance improved when trained with compensated images (as opposed to baseline or uncompensated images). In each of the five testing sets, paired t-tests were used to assess the differences in the Dice coefficients, specificities and sensitivities (means).
2.7.3. Segmentation accuracy: comparison with patch-based segmentation
The performance of DRUNET was compared with the patch-based approach by using paired t-tests to assess the differences in the quantitative metrics (means). For this experiment, both the approaches were trained and tested on the same data sets.
2.8. Clinical application: automated extraction of structural parameters
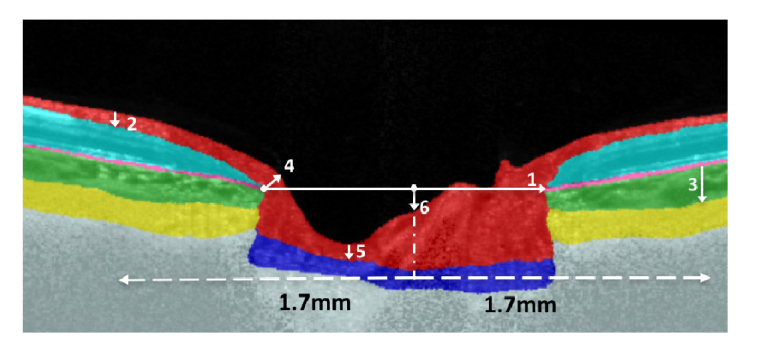
Upon segmenting the individual ONH tissues, six clinically relevant neural and connective tissue structural parameters (Fig. 4) were automatically extracted: The disc diameter, peripapillary RNFL thickness (p-RNFLT), peripapillary choroidal thickness (p-CT), minimum rim width (MRW), prelaminar thickness (PLT), and the prelaminar depth (PLD). Each parameter was calculated by computing the number of pixels representing them multiplied by the physical scaling factor.
Fig. 4.
Automated extraction of the ONH structural parameters. Upon segmenting the ONH tissues, six neural and connective tissue structural parameters were automatically extracted: (1) the disc diameter, (2) peripapillary RNFL thickness (p-RNFLT), (3) peripapillary choroidal thickness (p-CT), (4) minimum rim width (MRW), (5) prelaminar thickness (PLT), and the (6) prelaminar depth (PLD).
The disc diameter was defined as the length of the Bruch’s membrane opening (BMO) reference line. The BMO points were identified as the end tips of the RPE in the central scans of the ONH. The BMO reference line was obtained by joining the two BMO points. The segmented images were then rotated to ensure the BMO reference line was horizontal.
The p-RNFLT was defined as the distance between ILM and the posterior RNFL boundary measured at 1.7 mm from the center of the BMO reference line in the nasal and temporal regions.
The p-CT was defined as the distance between the posterior RPE boundary and the choroidal-scleral interface measured at 1.7 mm from the center of the BMO reference line in the nasal and temporal regions.
The MRW was defined as the minimum distance between each BMO point and the inner limiting membrane (ILM). The global values for the p-RNFLT, p-CT, and MRW were reported as the average of the measurements taken in the nasal and temporal regions.
The PLT was defined as the perpendicular distance between the deepest point on the ILM and the anterior lamina cribrosa surface (ALC) boundary.
The PLD was defined as the perpendicular distance between the mid-point of the BMO reference line and the ILM. An arbitrary plus and minus sign was used to differentiate elevation and depression of the ONH surface. When the ILM dipped below the BMO, a positive value was used to indicate depression. When the ILM was elevated from the BMO, a negative value was used.
Each parameter was also manually assessed by two expert observers (SD and GS) using ImageJ [48] for all the images. The structural measurements were then validated by obtaining the absolute percentage error (mean) between the automatically extracted values and the ground truth obtained from each expert observer for all the parameters.
For the same testing data set, the above procedure was repeated for the segmentations obtained from the patch-based method. Paired t-tests were used to assess the differences (means) in the percentage error obtained from both methods.
3. Results
3.1. Qualitative analysis
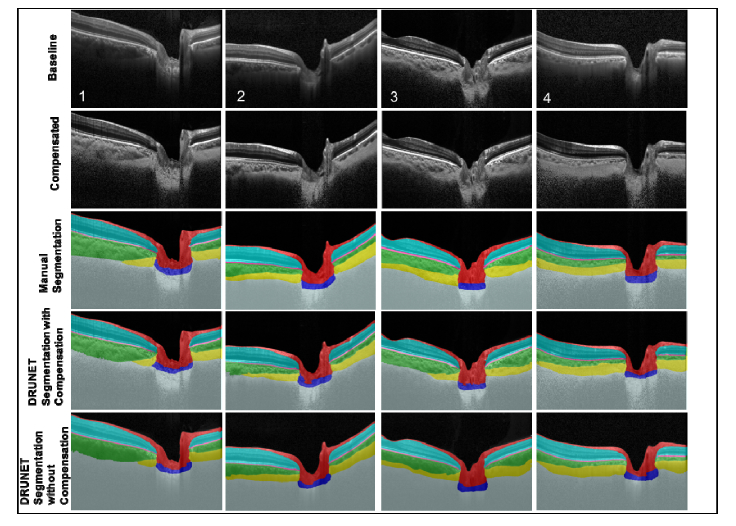
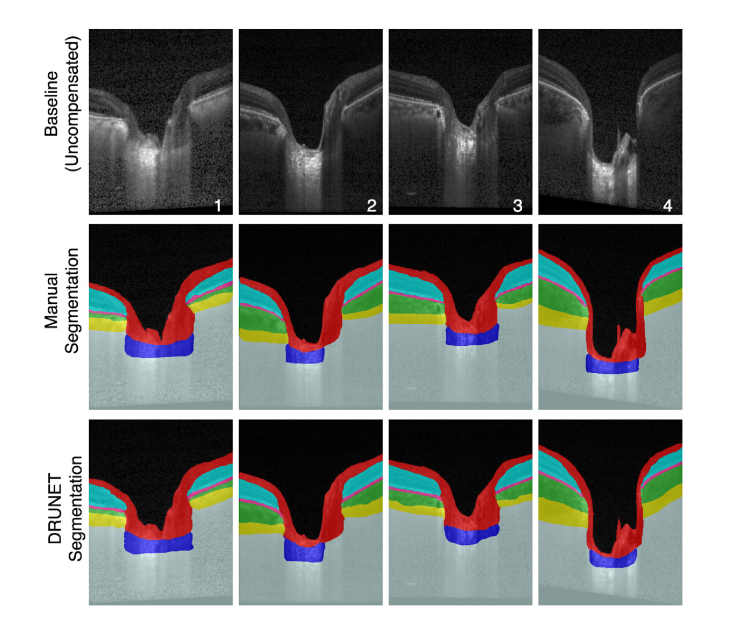
The baseline, compensated, manually segmented, and the DRUNET segmented images for 4 selected subjects (1&2: POAG, 3: Healthy, 4: PACG) are shown in Fig. 5. When trained with the compensated images (Fig. 5, 4th Row) or the uncompensated images (Fig. 5, 5th Row), DRUNET was able to simultaneously isolate the different ONH tissues, i.e. the RNFL + prelamina (in red), the RPE (in pink), all other retinal layers (in cyan), the choroid (in green), the sclera (in yellow) and the LC (in blue). Noise and vitreous humor were isolated in gray and black respectively. In both cases, the DRUNET segmentation of the ONH tissues was qualitatively similar, comparable and consistent with the manual segmentation. A smooth delineation of the choroid-sclera interface was obtained in both cases.
Fig. 5.
Baseline (1st row), compensated (2nd row), manually segmented (3rd row), DRUNET segmented images (trained on 40 compensated images; 4th row), and DRUNET segmented images (trained on 40 baseline images; 5th row) for 4 selected subjects (1&2: POAG, 3: Healthy, 4: PACG).
Irregular (Fig. 5, Subject 2 and 4) LC boundaries that were inconsistent with the manual segmentations were obtained in few images irrespective of the training data (compensated/uncompensated images).
When validated against the respective manual segmentations, there was no visual difference in the segmentation performance on healthy or glaucoma OCT images across all experiments.
3.2. Quantitative analysis
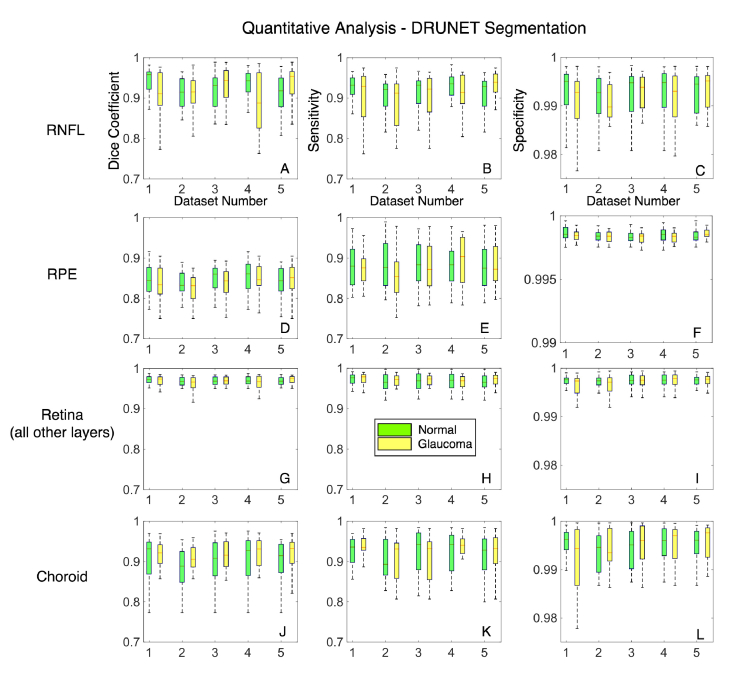
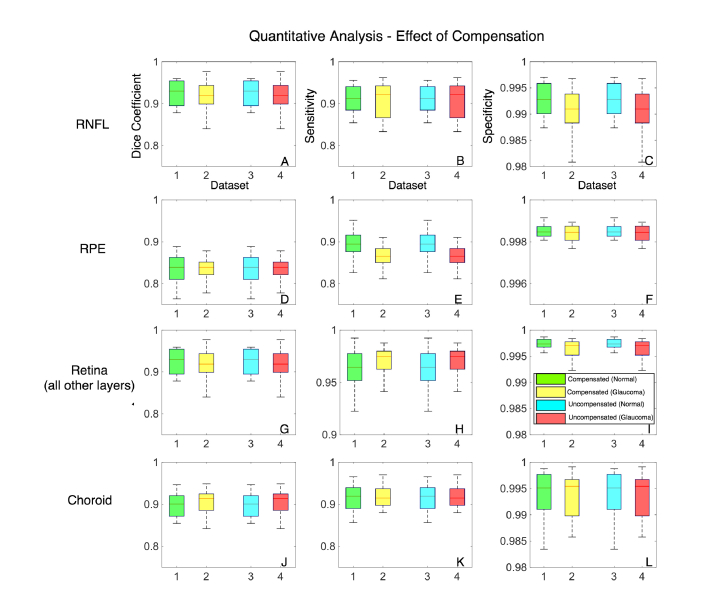
When trained with compensated images, across all the five testing sets, the mean Dice coefficients for the healthy/glaucoma OCT images were: 0.92 ± 0.05/0.92 ± 0.03 for the RNFL + prelamina, 0.83 ± 0.04/0.84 ± 0.03 for the RPE, 0.95 ± 0.01/0.96 ± 0.03 for all other retinal layers, and 0.90 ± 03/0.91 ± 0.05 for the choroid. The mean sensitivities for the healthy/glaucoma OCT images were 0.92 ± 0.01/0.92 ± 0.03 for the RNFL + prelamina, 0.87 ± 0.04/0.88 ± 0.03 for the RPE, 0.96 ± 0.04/0.96 ± 0.03 for all other retinal layers, and 0.89 ± 0.06/0.91 ± 0.02 for the choroid respectively. For all the tissues, the mean specificities were always above 0.99 for both glaucoma and healthy subjects. In all experiments, there were no significant differences (mean Dice coefficients, specificities, and sensitivities) in the segmentation performance between glaucoma and healthy OCT images (p>0.05; Fig. 6). Further, the segmentation performance did not significantly improve when using compensation (p>0.05; Fig. 7). Overall, the DRUNET performed significantly better (p<0.05) for all the tissues compared to the patch-based approach, except for the RPE, in which case it performed similar (Table 1 ).
Fig. 6.
A quantitative analysis of the proposed method is presented to assess the consistency and segmentation performance between glaucoma and healthy images. A total of 5 data sets were used for training (40 images) and its corresponding testing (60 images). (A-C) represent the Dice coefficients, sensitivities and specificities as box plots for the RNFL + prelamina for healthy (in green) and glaucoma (in yellow) images in the testing sets. (D-F) represent the same for the RPE, (G-I) represent the same for all other retinal layers and (J-L) represent the same for the choroid.
Fig. 7.
The effect of compensation on the segmentation accuracy is presented. A total of 5 compensated and uncompensated data sets were used for training (40 images) and its corresponding testing (60 images). Box plots (1-4) represent the mean of the 5 compensated (normal in green; glaucoma in yellow) and uncompensated (normal in cyan; glaucoma in red) data sets. (A-C) represent the Dice coefficients, sensitivities and specificities for the RNFL + prelamina. (D-F) represent the same for the RPE, (G-I) represent the same for all other retinal layers and (J-L) represent the same for the choroid.
Table 1. Performance Comparison Between DRUNET and Patch-Based Segmentation.
| Metrics | Tissue | DRUNET | Patch-Based | ||
|---|---|---|---|---|---|
| Healthy | Glaucoma | Healthy | Glaucoma | ||
| Dice coefficient (Mean ± SD) |
RNFL | 0.922 ± 0.052 | 0.921 ± 0.031 | 0.821 ± 0.040 | 0.814 ± 0.038 |
| Retinal Layers (all others) |
0.951 ± 0.010 | 0.960 ± 0.030 | 0.872 ± 0.034 | 0.863 ± 0.081 | |
| RPE | 0.831 ± 0.045 | 0.841 ± 0.034 | 0.857 ± 0.018 | 0.861 ± 0.060 | |
| Choroid | 0.906 ± 0.035 | 0.912 ± 0.050 | 0.862 ± 0.013 | 0.859 ± 0.025 | |
|
| |||||
| Sensitivity (Mean ± SD) |
RNFL | 0.923 ± 0.012 | 0.925 ± 0.032 | 0.897 ± 0.041 | 0.883 ± 0.012 |
| Retinal Layers (all others) |
0.960 ± 0.038 | 0.966 ± 0.032 | 0.981 ± 0.010 | 0.983 ± 0.002 | |
| RPE | 0.870 ± 0.043 | 0.888 ± 0.033 | 0.915 ± 0.052 | 0.899 ± 0.090 | |
| Choroid | 0.890 ± 0.060 | 0.911 ± 0.020 | 0.882 ± 0.021 | 0.871 ± 0.062 | |
|
| |||||
| Specificity (Mean ± SD) |
RNFL | 0.993 ± 0.005 | 0.994 ± 0.002 | 0.989 ± 0.002 | 0.988 ± 0.001 |
| Retinal Layers (all others) |
0.995 ± 0.001 | 0.996 ± 0.001 | 0.991 ± 0.004 | 0.989 ± 0.003 | |
| RPE | 0.993 ± 0.000 | 0.993 ± 0.004 | 0.989 ± 0.003 | 0.990 ± 0.000 | |
| Choroid | 0.996 ± 0.022 | 0.994 ± 0.004 | 0.993 ± 0.002 | 0.991 ± 0.005 | |
3.3. Clinical application: automated extraction of structural parameters
Six neural and connective tissue structural parameters were automatically extracted from the DRUNET segmentations. The percentage errors (vs. manual extraction; mean standard deviation) in the measurements when validated against both the observers (average for both) were: 2.00 2.12% for the disc diameter, 8.93 3.8% for the p-RNFLT, 6.79 4.07% for the p-CT, 5.22 3.89% for the MRW, 9.24 3.62% for the PLT, and 4.84 2.70% for the PLD.
When measured from the patch-based segmentations, the percentage errors (mean) were always greater than 10.30 6.28% for all the parameters irrespective of the observer chosen for validation.
The percentage errors (mean) between the observers were: 3.50 0.85% for the disc diameter, 5.94 2.30% for the p-RNFLT, 5.23 3.91% for the p-CT, 6.03 1.30% for the MRW, 4.85 1.99% for the PLT, and 5.18 0.67% for the PLD.
A significantly lower (p<0.05) percentage error in the automated extraction of the structural parameters was observed when extracted from DRUNET segmentations, as opposed to patch-based segmentations (Table 2 ).
Table 2. Clinical Application: Automated Extraction of Structural Parameters of the ONH.
| Percentage Error (Mean ± Standard Deviation) | |||||
|---|---|---|---|---|---|
| Parameter | DRUNET vs. Observer 1 (%) | Patch-Based vs. Observer 1 (%) | DRUNET vs. Observer 2 (%) | Patch-Based vs. Observer 2 (%) | Observer 1 vs. Observer 2 (%) |
| Disc Diameter | 2.03 ± 1.50 | 10.43 ± 6.05 |
1.98 ± 2.75 | 11.86 ± 5.78 |
3.50 ± 0.85 |
| p-RNFLT (global) | 8.85 ± 3.40 | 14.30 ± 9.74 |
9.01 ± 4.20 | 16.20 ± 8.33 |
5.94 ± 2.30 |
| p-CT (global) | 7.03 ± 4.50 | 21.65 ± 11.05 |
6.55 ± 3.65 | 19.36 ± 10.91 |
5.23 ± 3.91 |
| MRW (global) | 5.09 ± 4.00 | 19.86 ± 12.45 |
5.35 ± 3.78 | 22.30 ± 14.34 |
6.03 ± 1.30 |
| PLT | 9.15 ± 3.22 | 15.73 ± 8.24 |
9.34 ± 4.02 | 16.12 ± 9.03 |
4.85 ± 1.99 |
| PLD | 4.56 ± 2.85 | 11.23 ± 7.23 | 5.12 ± 2.55 | 10.30 ± 6.28 | 5.18 ± 0.67 |
3.4. Demystifying DRUNET
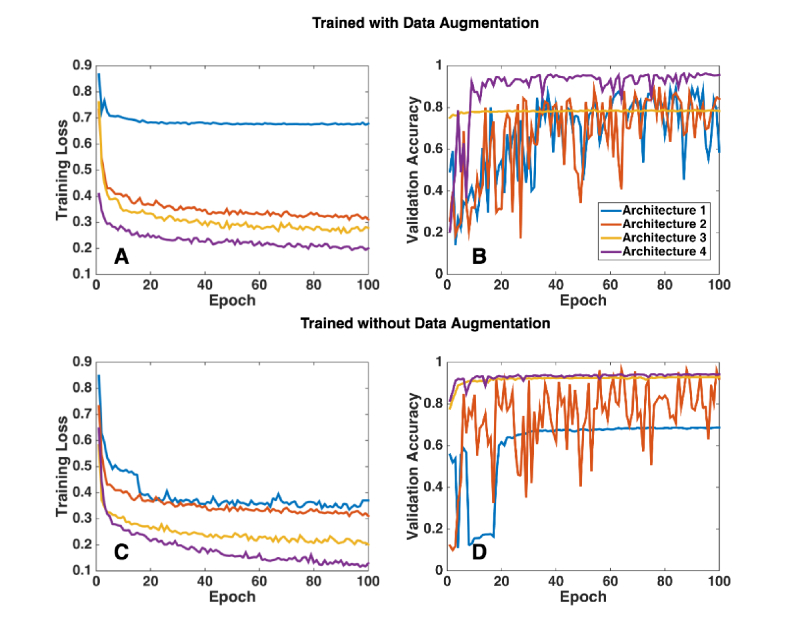
The performance (training loss and the validation accuracy) of all the four architectures is shown in Fig. 8. With the baseline U-Net (architecture 1), the training loss was the highest (best model training loss = 0.67) and the validation accuracy was highly inconsistent. Upon the addition of residual blocks to the baseline U-Net (architecture 2), the training loss nearly halved (0.31), and the model converged relatively faster. However, the validation accuracy was still inconsistent. When batch normalization was added (architecture 3), the training loss decreased further (0.26), and we obtained a consistent and fairly good validation accuracy (best model validation accuracy = 0.79) as well. Further, with the addition of dilated convolution layers along with batch normalization (architecture 4; DRUNET), we observed the lowest training loss (0.19), and the model converged the fastest. We also observed a 20% increase in the validation accuracy (to 0.94), when compared to the best model obtained in architecture 3.
Fig. 8.
In an attempt to understand the significance of each design element in the DRUNET better, four different architectures were trained with and without data augmentation. Architecture 1: Baseline U-Net (each tower consisted of only standard blocks; standard convolution layers); Architecture 2: Modified U-Net v1 (each tower consisted of one standard block and two residual blocks; standard convolution layers); Architecture 3: Modified U-Net v2 (each tower consisted of one standard block and two residual blocks with standard convolution layers; batch normalization after every convolution layer in the residual block); Architecture 4: DRUNET (each tower consisted of one standard block and two residual blocks with dilated convolution layers; batch normalization after every dilated convolution layer in the residual block). (A & B) represent the training loss and the validation accuracy respectively for all the four architectures, when trained with data augmentation. (C & D) represent the same, when trained without data augmentation.
In the absence of data augmentation, all the architectures overfitted in general and models converged slower. As for the validation accuracy, DRUNET performed better than rest (0.91), but relatively lower than DRUNET trained with data augmentation. The performance of DRUNET (without data augmentation) was poor especially in images with thick blood vessel shadows and intensity inhomogeneity.
4. Discussion
In this study, we present DRUNET, a custom deep learning approach that is able to capture both local and contextual features to simultaneously segment (i.e. highlight) the connective and neural tissues in OCT images of the ONH. The proposed study leverages on the inherent advantages of skip connections, residual learning and dilated convolutions. Having successfully trained, tested and validated on the OCT images from 100 subjects, we were able to consistently achieve a good qualitative and quantitative performance. Thus, we may be able to offer a robust segmentation framework, that can be extended to the 3D segmentation of OCT volumes.
Using DRUNET, we were able to simultaneously isolate the RNFL + prelamina, the RPE, all other retinal layers, the choroid, the peripapillary sclera, the LC, noise and the vitreous humor with good accuracy. When trained and tested on compensated images, there was good agreement with manual segmentation, with the overall Dice coefficient (mean of all tissues) being 0.91 ± 0.04 and 0.91 ± 0.06 for glaucoma and healthy subjects respectively. The mean sensitivities for all the tissues were 0.92 ± 0.04 and 0.92 ± 0.04 for glaucoma and healthy subjects respectively while the mean specificities were always higher than 0.99 for all cases.
We observed that DRUNET offered no significant differences in the segmentation performance when tested upon compensated (blood vessel shadows removed), or uncompensated images, as opposed to our previous patch-based method [33], which performed better on compensated images. This may be attributed to the extensive online data augmentation we used herein that also included occluding patches to mimic the presence of blood vessel shadows. In uncompensated images, the presence of retinal blood vessel shadows typically affects the automated segmentation of the RNFL [49, 50], that can yield incorrect RNFL thickness measurements. This phenomenon may be more pronounced in glaucoma subjects that exhibit very thin RNFL. Our DRUNET framework, being invariant to the presence of blood vessel shadows, could potentially be extended to provide an accurate and reliable measurement of RNFL thickness. We believe this could improve the diagnosis and management of glaucoma. However, given the benefits of compensation in enhancing deep tissue visibility [35], and contrast [34], it may be advised to segment compensated images for a reliable clinical interpretation of the isolated ONH tissues.
When trained and tested with the same cohort, DRUNET offered smooth and accurate delineation of tissue boundaries with reduced false predictions. Thus, it performed significantly better than the patch-based approach for all the tissues, except for the RPE, in which case it performed similarly. This may be attributed to DRUNET’s ability in capturing both local (tissue texture) and contextual features (spatial arrangement of tissues), compared to the patch-based approach that captured only the local features.
DRUNET consisted of 40,000 trainable parameters as opposed to the patch-based approach that required 140,000 parameters. Besides, DRUNET also eliminated the need for multiple convolutions on similar sets of pixels as seen in patch-based approach. Thus, DRUNET offers a computationally inexpensive and faster segmentation framework that only takes 80 ms to segment one OCT image. This could be extended to the real-time segmentation of OCT images as well. We are currently exploring such an approach.
We found that DRUNET was able to dissociate the LC from the peripapillary sclera. This provides an advantage as opposed to previous techniques that were able to segment only the LC [51, 52], or the LC fused with the peripapillary sclera [33]. To the best of our knowledge, no automated segmentation techniques have been proposed to simultaneously isolate all individual ONH connective tissues. We believe our network was able to achieve this because we used the Jaccard Index as part of the loss function. During training, by computing the Jaccard Index for each tissue, the network was able to learn the representative features equally for all tissues. This reduced the inherent bias in learning features of a tissue represented by a large number of pixels (e.g., retinal layers) as opposed to a tissue represented by a small number of pixels (e.g., LC/RPE).
We observed no significant differences in the segmentation performance when tested on glaucoma or healthy images. The progression of glaucoma is characterized by thinning of the RNFL [1–3] and decreased reflectivity (attenuation) of the RNFL axons [53], thus reducing the contrast of the RNFL boundaries. Existing automated segmentation tools for the RNFL rely on these boundaries for their segmentation and are often prone to segmentation artifacts [22–25] (incorrect ILM/ posterior RNFL boundary), resulting in inaccurate RNFL measurements. This error increases with the thinning of the RNFL [50]. Thus, glaucomatous pathology increases the likelihood of errors in the automated segmentation of the RNFL, leading to under- or over-estimated RNFL measurements that may affect the diagnosis of glaucoma [50]. An automated segmentation tool that is invariant to the pathology is thus highly needed to robustly measure RNFL thickness. We believe DRUNET may be a solution to this problem, and we aim to test this hypothesis in future works.
Upon segmenting the individual ONH tissues, we were able to successfully extract six clinically relevant neural and connective tissue structural parameters. For all the parameters, a significantly lower (p<0.05) percentage error (mean) was observed when measured from the DRUNET segmentations compared to our earlier patch-based approach. Thus, a robust segmentation approach can reduce the error in the automated extraction of clinically relevant parameters that follow. With the complex morphological changes occurring in glaucoma, a robust in vivo extraction of these structural parameters could eventually help clinicians in the daily management of glaucoma, thus increasing the current diagnostic power of OCT in glaucoma.
We attribute the significant improvement in the performance of segmentation and the automated extraction of structural parameters of DRUNET over the patch-based method to its individual design elements. By improving the information gradient flow along the network, residual connections helped the network learn better (lower training loss), while the addition of batch normalization yielded consistent and fairly good validation accuracy. With an enhanced receptive field, dilated convolution layers allowed the network to better understand the spatial arrangement of tissues, thus offering a robust segmentation with a limited amount of training data. Lack of data augmentation, in general, resulted in overfitting of all the architectures and poor generalizability. While the addition of each design element to the baseline U-Net improved the performance, a combination of all them (DRUNET: residual connections, dilated convolutions, and data augmentation) indeed offered the best performance.
While there exist several deep learning based retinal layer segmentation tools [27–30], they generally required a larger amount of training data (few volumes; we used only 40 images) [28, 30], and was unable to capture both the local and contextual information simultaneously [28]. While [27, 30] were able to capture both these features, there was still under-segmentation in images with mild-pathology [30], and [27] offered a relatively lower Dice coefficient (0.90) for the segmentation of the entire retina (ours = 0.94). We were unable to directly compare the performance with [28–30], as the validation metrics used were different (contour error, error in thickness map, mean thickness difference, etc.) from ours (Dice coefficient, specificity, and sensitivity). Recently developed deep learning techniques for the segmentation of the choroid [31, 32] from macular scans have shown superior performance [31] over the original U-Net [37]. Yet, it [31] still offered a lower specificity (0.73) and sensitivity (0.84) compared to the proposed DRUNET (sensitivity: 0.90; specificity: 0.99). However, we believe, a straightforward comparison of the segmentation performance between tissues extracted from the macular and ONH centered scans wouldn’t be fair given the difference in quality, resolution and deep tissue visibility between them.
While there exists a deep learning based study [54] for the segmentation of the Bruch’s membrane opening (BMO) from 3D OCT volumes, we rather follow a simple and straightforward approach to identify the BMO points as the extreme tips of the segmented RPE in central B-scans. Finally, to the best of our knowledge, while there exists a study for the demarcation anterior LC boundary [55] from ONH images, there exists no technique yet for the simultaneous isolation of individual connective tissues (sclera and LC; visible portion).
In this study, several limitations warrant further discussion. First, the accuracy of the algorithm was validated against the manual segmentations provided by a single expert observer (SD). The future scope of this study would be to provide a validation against multiple expert observers. Nevertheless, we offer a proof of concept for the simultaneous segmentation of the ONH tissues in OCT images.
Second, the algorithm was trained with the images from a single machine (Spectralis). Currently, it is unknown if the algorithm would perform the same way if tested on images from multiple OCT devices. We are exploring other options to develop a device-independent segmentation approach.
Third, we observed irregular LC boundaries that were inconsistent with that of the manual segmentations in few images. When extended for the automated parametric study, this could affect the LC parameters such as LC depth [56], LC curvature [57], and the global shape index [58]. Given the significance of LC morphology in glaucoma [12, 56, 58–64], a more accurate delineation of the LC boundary would be required to obtain reliable parameters for a better understanding of glaucoma. This could be addressed using transfer learning [65, 66] by incorporating more information about LC morphology within the network. We are currently exploring such an approach.
Fourth, a quantitative validation of the peripapillary sclera and the LC could not be performed as their true thickness could not be obtained from the manual segmentations due to limited visibility [67].
Fifth, we were unable to provide further validation to our algorithm by comparing it with data obtained from histology. This is a challenging task, given that one would need to image a human ONH with OCT, process it with histology and register both data sets. However, it is important to bear in mind that the understanding of OCT ONH anatomy stemmed from a single comparison of a normal monkey eye scanned in vivo at an IOP of 10 mm Hg and then perfusion fixed at the time of sacrifice at the same IOP [68]. Our algorithm produced tissue classification results that match the expected relationships obtained in this above-mentioned work. The absence of published experiments matching human ONH histology to OCT images, at the time of writing this paper, inhibits an absolute validation of our proposed methodology.
Sixth, a robust and accurate isolation of the ganglion cell complex (GCC) [69] and the photoreceptor layers [70], whose structural changes are associated with the progression of glaucoma was not possible in both compensated and uncompensated images. The limitation of an accurate intra-retinal layer segmentation from ONH images can be attributed to the inherent speckle noise and intensity inhomogeneity which affects the robust delineation of the intra-retinal layers. This could be resolved by using advanced pre-processing techniques for image denoising (e.g. deep learning based) or a multi-stage tissue isolation approach (i.e., extraction of retinal layer followed by the isolation of intra-retinal layers).
Seventh, given the limitation of a small data set (100 images), and the need for performing multiple experiments (repeatability), we were able to use only 40 images for training (60 images for testing) in each experiment. It is currently unknown if the segmentation performance would improve when trained upon a larger data set. Also, we would also like to emphasize again that there was no mixing of the training and testing sets in a given experiment. However, across all the experiments, there was indeed a small leakage of the testing/training sets. Nevertheless, we offer a proof of principle for a robust deep learning approach to isolate ONH tissues that could be used by other groups for further validation.
In conclusion, we have developed a custom deep learning algorithm for the simultaneous isolation of the connective and neural tissues in OCT images of the ONH. Given that the ONH tissues exhibit complex changes in their morphology with the progression of glaucoma, their simultaneous isolation may be of great interest for the clinical diagnosis and management of glaucoma.
Appendix
DRUNET robustness
To test the robustness of the proposed technique, we included 100 more subjects (40 normal, 60 glaucomatous), the details of which can be found from our previous studies [61, 71–73]. For each subject, 3D OCT scans centered on the ONH were obtained using a spectral domain OCT (Spectralis, Heidelberg Engineering, Heidelberg). All the images were noisier (20× signal averaged) than those used in the manuscript (48× signal averaged). The entire process (training and validation) was repeated with central horizontal slice obtained from each volume.
All the segmented images were qualitatively assessed by an expert observer (LZ). The baseline, manually segmented, and the DRUNET segmentations for 4 selected subjects (1&2: POAG, 3: Healthy, 4: PACG) are shown in (Fig. 9
Fig. 9.
Baseline (1st row), manually segmented (2nd row), and DRUNET segmented images (3rd row) for 4 selected subjects (1&2: POAG, 3: Healthy, 4: PACG).
). In all the cases, the segmentations obtained were qualitatively similar, comparable and consistent with the manual segmentation. The mean Dice coefficients (Table 3
Table 3. DRUNET Robustness.
| Metrics | Tissue | Test Data set |
|
|---|---|---|---|
| Healthy | Glaucoma | ||
| Dice coefficient (Mean ± SD) |
RNFL | 0.901 ± 0.043 | 0.903 ± 0.022 |
| Retinal Layers (all others) |
0.939 ± 0.008 | 0.920 ± 0.01 | |
| RPE | 0.821 ± 0.034 | 0.839 ± 0.019 | |
| Choroid | 0.891 ± 0.017 | 0.900 ± 0.050 | |
|
| |||
| Sensitivity (Mean ± SD) |
RNFL | 0.901 ± 0.008 | 0.900 ± 0.003 |
| Retinal Layers (all others) |
0.942 ± 0.023 | 0.931 ± 0.009 | |
| RPE | 0.882 ± 0.055 | 0.880 ± 0.010 | |
| Choroid | 0.902 ± 0.043 | 0.912 ± 0.009 | |
|
| |||
| Specificity (Mean ± SD) |
RNFL | 0.989 ± 0.005 | 0.984 ± 0.001 |
| Retinal Layers (all others) |
0.991 ± 0.003 | 0.993 ± 0.002 | |
| RPE | 0.989 ± 0.001 | 0.992 ± 0.004 | |
| Choroid | 0.992 ± 0.001 | 0.994 ± 0.005 | |
) for healthy/glaucoma OCT images were: 0.90±0.04/0.90±0.02 for the RNFL + prelamina, 0.82±0.03/0.84±0.02 for the RPE, 0.94±0.00/0.92±0.01 for all other retinal layers, and 0.89±0.02/0.90±0.05 for the choroid. For all the tissues, the mean sensitivities and specificities were always greater than 0.88 and 0.98 respectively for all images.
While the training and testing images described in the manuscript were 48× signal averaged, the robustness of the DRUNET was assessed by repeating the same on noisier (20× signal averaged) central horizontal slice obtained from each OCT volume. We obtained a good qualitative and quantitative performance on all the baseline (uncompensated) images despite reduced signal averaging and poor contrast. Thus, our technique may be applicable to a wide variety of OCT scans. Further validation with additional scan types may still be required.
Funding
Singapore Ministry of Education Academic Research Funds Tier 1 (R-155-000-168-112 [AHT]); R-397-000-294-114 [MJAG]); National University of Singapore (NUS) Young Investigator Award Grant (NUSYIA_FY16_P16; R-155-000-180-133; AHT); National University of Singapore Young Investigator Award Grant (NUSYIA_FY13_P03; R-397-000-174-133 [MJAG]); Singapore Ministry of Education Tier 2 (R-397-000-280-112 [MJAG]); National Medical Research Council (Grant NMRC/STAR/0023/2014 [TA]).
Disclosures
The authors declare that there are no conflicts of interest related to this article.
References and links
- 1.Bowd C., Weinreb R. N., Williams J. M., Zangwill L. M., “The retinal nerve fiber layer thickness in ocular hypertensive, normal, and glaucomatous eyes with optical coherence tomography,” Arch. Ophthalmol. 118(1), 22–26 (2000). 10.1001/archopht.118.1.22 [DOI] [PubMed] [Google Scholar]
- 2.Miki A., Medeiros F. A., Weinreb R. N., Jain S., He F., Sharpsten L., Khachatryan N., Hammel N., Liebmann J. M., Girkin C. A., Sample P. A., Zangwill L. M., “Rates of retinal nerve fiber layer thinning in glaucoma suspect eyes,” Ophthalmology 121(7), 1350–1358 (2014). 10.1016/j.ophtha.2014.01.017 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ojima T., Tanabe T., Hangai M., Yu S., Morishita S., Yoshimura N., “Measurement of retinal nerve fiber layer thickness and macular volume for glaucoma detection using optical coherence tomography,” Jpn. J. Ophthalmol. 51(3), 197–203 (2007). 10.1007/s10384-006-0433-y [DOI] [PubMed] [Google Scholar]
- 4.Gmeiner J. M. D., Schrems W. A., Mardin C. Y., Laemmer R., Kruse F. E., Schrems-Hoesl L. M., “Comparison of Bruch’s membrane opening minimum rim width and peripapillary retinal nerve fiber layer thickness in early glaucoma assessment BMO-MRW and RNFLT in early glaucoma assessment,” Invest. Ophthalmol. Vis. Sci. 57, 575–584 (2016). 10.1167/iovs.15-18906 [DOI] [PubMed] [Google Scholar]
- 5.Jonas J. B., “Glaucoma and choroidal thickness,” J. Ophthalmic Vis. Res. 9(2), 151–153 (2014). [PMC free article] [PubMed] [Google Scholar]
- 6.Lin Z., Huang S., Xie B., Zhong Y., “Peripapillary choroidal thickness and open-angle glaucoma: a meta-analysis,” J. Ophthalmol. 2016, 1 (2016). 10.1155/2016/5484568 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Park S. C., Brumm J., Furlanetto R. L., Netto C., Liu Y., Tello C., Liebmann J. M., Ritch R., “Lamina Cribrosa Depth in Different Stages of Glaucoma,” Invest. Ophthalmol. Vis. Sci. 56(3), 2059–2064 (2015). 10.1167/iovs.14-15540 [DOI] [PubMed] [Google Scholar]
- 8.Quigley H. A., Addicks E. M., “Regional differences in the structure of the lamina cribrosa and their relation to glaucomatous optic nerve damage,” Arch. Ophthalmol. 99(1), 137–143 (1981). 10.1001/archopht.1981.03930010139020 [DOI] [PubMed] [Google Scholar]
- 9.Quigley H. A., Addicks E. M., Green W. R., Maumenee A. E., “Optic nerve damage in human glaucoma. II. The site of injury and susceptibility to damage,” Arch. Ophthalmol. 99(4), 635–649 (1981). 10.1001/archopht.1981.03930010635009 [DOI] [PubMed] [Google Scholar]
- 10.Downs J. C., Ensor M. E., Bellezza A. J., Thompson H. W., Hart R. T., Burgoyne C. F., “Posterior scleral thickness in perfusion-fixed normal and early-glaucoma monkey eyes,” Invest. Ophthalmol. Vis. Sci. 42(13), 3202–3208 (2001). [PubMed] [Google Scholar]
- 11.Lee K. M., Kim T. W., Weinreb R. N., Lee E. J., Girard M. J. A., Mari J. M., “Anterior lamina cribrosa insertion in primary open-angle glaucoma patients and healthy subjects,” PLoS One 9(12), e114935 (2014). 10.1371/journal.pone.0114935 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yang H., Williams G., Downs J. C., Sigal I. A., Roberts M. D., Thompson H., Burgoyne C. F., “Posterior (outward) migration of the lamina cribrosa and early cupping in monkey experimental glaucoma,” Invest. Ophthalmol. Vis. Sci. 52(10), 7109–7121 (2011). 10.1167/iovs.11-7448 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Al-Diri B., Hunter A., Steel D., “An active contour model for segmenting and measuring retinal vessels,” IEEE Trans. Med. Imaging 28(9), 1488–1497 (2009). 10.1109/TMI.2009.2017941 [DOI] [PubMed] [Google Scholar]
- 14.Almobarak F. A., O’Leary N., Reis A. S. C., Sharpe G. P., Hutchison D. M., Nicolela M. T., Chauhan B. C., “Automated segmentation of optic nerve head structures with optical coherence tomography,” Invest. Ophthalmol. Vis. Sci. 55(2), 1161–1168 (2014). 10.1167/iovs.13-13310 [DOI] [PubMed] [Google Scholar]
- 15.Lang A., Carass A., Hauser M., Sotirchos E. S., Calabresi P. A., Ying H. S., Prince J. L., “Retinal layer segmentation of macular OCT images using boundary classification,” Biomed. Opt. Express 4(7), 1133–1152 (2013). 10.1364/BOE.4.001133 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Mayer M. A., Hornegger J., Mardin C. Y., Tornow R. P., “Retinal Nerve Fiber Layer Segmentation on FD-OCT Scans of Normal Subjects and Glaucoma Patients,” Biomed. Opt. Express 1(5), 1358–1383 (2010). 10.1364/BOE.1.001358 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Naz S., Ahmed A., Akram M. U., Khan S. A., “Automated segmentation of RPE layer for the detection of age macular degeneration using OCT images,” in Proceedings of Sixth International Conference on Image Processing Theory, Tools and Applications (IPTA), 2016), 1–4. 10.1109/IPTA.2016.7821033 [DOI] [Google Scholar]
- 18.Niu S., Chen Q., de Sisternes L., Rubin D. L., Zhang W., Liu Q., “Automated retinal layers segmentation in SD-OCT images using dual-gradient and spatial correlation smoothness constraint,” Comput. Biol. Med. 54, 116–128 (2014). 10.1016/j.compbiomed.2014.08.028 [DOI] [PubMed] [Google Scholar]
- 19.Tian J., Marziliano P., Baskaran M., Tun T. A., Aung T., “Automatic segmentation of the choroid in enhanced depth imaging optical coherence tomography images,” Biomed. Opt. Express 4(3), 397–411 (2013). 10.1364/BOE.4.000397 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zhang L., Lee K., Niemeijer M., Mullins R. F., Sonka M., Abràmoff M. D., “Automated segmentation of the choroid from clinical SD-OCT,” Invest. Ophthalmol. Vis. Sci. 53(12), 7510–7519 (2012). 10.1167/iovs.12-10311 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Alonso-Caneiro D., Read S. A., Collins M. J., “Automatic segmentation of choroidal thickness in optical coherence tomography,” Biomed. Opt. Express 4(12), 2795–2812 (2013). 10.1364/BOE.4.002795 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Liu Y., Simavli H., Que C. J., Rizzo J. L., Tsikata E., Maurer R., Chen T. C., “Patient characteristics associated with artifacts in Spectralis optical coherence tomography imaging of the retinal nerve fiber layer in glaucoma,” Am. J. Ophthalmol. 159(3), 565–576 (2015). 10.1016/j.ajo.2014.12.006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Asrani S., Essaid L., Alder B. D., Santiago-Turla C., “Artifacts in spectral-domain optical coherence tomography measurements in glaucoma,” JAMA Ophthalmol. 132(4), 396–402 (2014). 10.1001/jamaophthalmol.2013.7974 [DOI] [PubMed] [Google Scholar]
- 24.Alshareef R. A., Dumpala S., Rapole S., Januwada M., Goud A., Peguda H. K., Chhablani J., “Prevalence and distribution of segmentation errors in macular ganglion cell analysis of healthy eyes using cirrus HD-OCT,” PLoS One 11(5), e0155319 (2016). 10.1371/journal.pone.0155319 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kim K. E., Jeoung J. W., Park K. H., Kim D. M., Kim S. H., “Diagnostic classification of macular ganglion cell and retinal nerve fiber layer analysis: differentiation of false-positives from glaucoma,” Ophthalmology 122(3), 502–510 (2015). 10.1016/j.ophtha.2014.09.031 [DOI] [PubMed] [Google Scholar]
- 26.Mari J.-M., Aung T., Cheng C.-Y., Strouthidis N. G., Girard M. J. A., “A digital staining algorithm for optical coherence tomography images of the optic nerve head,” Transl. Vis. Sci. Technol. 6(1), 8 (2017). 10.1167/tvst.6.1.8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.S. C. Abhijit Guha Roy, S. Phani, K. Karri, D. Sheet, A. Katouzian, C. Wachinger, and N. Navab, “ReLayNet: retinal layer and fluid segmentation of macular optical coherence tomography using fully convolutional networks,” arXiv:1704.02161v2 [cs.CV] (2017). [DOI] [PMC free article] [PubMed]
- 28.Fang L., Cunefare D., Wang C., Guymer R. H., Li S., Farsiu S., “Automatic segmentation of nine retinal layer boundaries in OCT images of non-exudative AMD patients using deep learning and graph search,” Biomed. Opt. Express 8(5), 2732–2744 (2017). 10.1364/BOE.8.002732 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Pekala N. J. M., Freund D. E., Bressler N. M., Cabrera DeBuc D., Burlina P., “Deep learning based retinal OCT Segmentation,” arXiv:1801.09749 [cs.CV] (2018). [DOI] [PubMed]
- 30.Venhuizen F. G., van Ginneken B., Liefers B., van Grinsven M. J. J. P., Fauser S., Hoyng C., Theelen T., Sánchez C. I., “Robust total retina thickness segmentation in optical coherence tomography images using convolutional neural networks,” Biomed. Opt. Express 8(7), 3292–3316 (2017). 10.1364/BOE.8.003292 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Al-Bander B., Williams B. M., Al-Taee M. A., Al-Nuaimy W., Zheng Y., “A novel choroid segmentation method for retinal diagnosis using deep learning,” in Proceedings of 10th International Conference on Developments in eSystems Engineering (DeSE) (2017), 182–187. 10.1109/DeSE.2017.37 [DOI] [Google Scholar]
- 32.Sui X., Zheng Y., Wei B., Bi H., Wu J., Pan X., Yin Y., Zhang S., “Choroid segmentation from Optical Coherence Tomography with graph-edge weights learned from deep convolutional neural networks,” Neurocomputing 237, 332–341 (2017). 10.1016/j.neucom.2017.01.023 [DOI] [Google Scholar]
- 33.Devalla S. K., Chin K. S., Mari J. M., Tun T. A., Strouthidis N. G., Aung T., Thiéry A. H., Girard M. J. A., “A deep learning approach to digitally stain optical coherence tomography images of the optic nerve head,” Invest. Ophthalmol. Vis. Sci. 59(1), 63–74 (2018). 10.1167/iovs.17-22617 [DOI] [PubMed] [Google Scholar]
- 34.Mari J. M., Strouthidis N. G., Park S. C., Girard M. J. A., “Enhancement of lamina cribrosa visibility in optical coherence tomography images using adaptive compensation,” Invest. Ophthalmol. Vis. Sci. 54(3), 2238–2247 (2013). 10.1167/iovs.12-11327 [DOI] [PubMed] [Google Scholar]
- 35.Girard M. J., Tun T. A., Husain R., Acharyya S., Haaland B. A., Wei X., Mari J. M., Perera S. A., Baskaran M., Aung T., Strouthidis N. G., “Lamina cribrosa visibility using optical coherence tomography: comparison of devices and effects of image enhancement techniques,” Invest. Ophthalmol. Vis. Sci. 56(2), 865–874 (2015). 10.1167/iovs.14-14903 [DOI] [PubMed] [Google Scholar]
- 36.M. H. Donghuan Lu, S. Lee, G. Ding, M. V.,Sarunic, and M. F. Beg, “Retinal fluid segmentation and detection in optical coherence tomography images using fully convolutional neural network,” arXiv:1710.04778v1 [cs.CV] (2017). [DOI] [PubMed]
- 37.O. Ronneberger, P. Fischer, and T. Brox, “U-Net: Convolutional Networks for Biomedical Image Segmentation,” in Proceedings of Medical Image Computing and Computer-Assisted Intervention, MICCAI 2015 18th International Conference, Munich, Germany, October 5–9, 2015, Proceedings, Part III, N. Navab, J. Hornegger, W. M. Wells, and A. F. Frangi, eds. (Springer International Publishing, 2015), pp. 234–241. 10.1007/978-3-319-24574-4_28 [DOI] [Google Scholar]
- 38.E. V. Michal Drozdzal, G. Chartrand, S. Kadoury, and C. Pal, “The importance of skip connections in biomedical image segmentation,” arXiv:1608.04117 [cs.CV] (2016).
- 39.X. Z. Kaiming He, S. Ren, and J. Sun, “Deep residual learning for image recognition,” arXiv:1512.03385 [cs.CV] (2015).
- 40.V. K. Fisher Yu, “Multi-Scale Context Aggregation by Dilated Convolutions,” arXiv:1511.07122 [cs.CV] (2016).
- 41.Zhang Q., Cui Z., Niu X., Geng S., Qiao Y., “Image segmentation with pyramid dilated convolution based on ResNet and U-Net,” in Neural Information Processing (Springer International Publishing, 2017), 364–372. [Google Scholar]
- 42.S. Ioffe and C. Szegedy, “Batch normalization: accelerating deep network training by reducing internal covariate shift,” in Proceedings of the 32nd International Conference on International Conference on Machine Learning - Volume 37 (JMLR.org, Lille, France, 2015), pp. 448–456. [Google Scholar]
- 43.T. U. Djork-Arné Clevert, and S. Hochreiter, “Fast and accurate deep network learning by exponential linear units (elus),” arXiv:1511.07289 [cs.LG] (2015).
- 44.Girard M. J., Strouthidis N. G., Desjardins A., Mari J. M., Ethier C. R., “In vivo optic nerve head biomechanics: performance testing of a three-dimensional tracking algorithm,” J. R. Soc. Interface 10(87), 20130459 (2013). 10.1098/rsif.2013.0459 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Patrice D. S., Simard Y., John C. Platt “Best Practices for Convolutional Neural Networks Applied to Visual Document Analysis,” in Proceedings of the Seventh International Conference on Document Analysis and Recognition (ICDAR 2003) (2003). [Google Scholar]
- 46.Lang A., Carass A., Jedynak B. M., Solomon S. D., Calabresi P. A., Prince J. L., “Intensity inhomogeneity correction of macular OCT using N3 and retinal flatspace,” Proc. IEEE Int. Symp. Biomed. Imaging 2016, 197–200 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Wu Z., Xu G., Weinreb R. N., Yu M., Leung C. K., “Optic nerve head deformation in glaucoma: a prospective analysis of optic nerve head surface and lamina cribrosa surface displacement,” Ophthalmology 122(7), 1317–1329 (2015). 10.1016/j.ophtha.2015.02.035 [DOI] [PubMed] [Google Scholar]
- 48.Rueden C. T. S., Schindelin J., Hiner M. C., DeZonia B. E., Walter A. E., Arena E. T., Eliceiri K. W., “ImageJ2: ImageJ for the next generation of scientific image data,” BMC Bioinformatics 18(1), 529 (2017). 10.1186/s12859-017-1934-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Ye C., Yu M., Leung C. K., “Impact of segmentation errors and retinal blood vessels on retinal nerve fibre layer measurements using spectral-domain optical coherence tomography,” Acta Ophthalmol. 94(3), e211–e219 (2016). 10.1111/aos.12762 [DOI] [PubMed] [Google Scholar]
- 50.Mansberger S. L., Menda S. A., Fortune B. A., Gardiner S. K., Demirel S., “Automated segmentation errors when using optical coherence tomography to measure retinal nerve fiber layer thickness in glaucoma,” Am. J. Ophthalmol. 174, 1–8 (2017). 10.1016/j.ajo.2016.10.020 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Campbell I. C., Coudrillier B., Mensah J., Abel R. L., Ethier C. R., “Automated segmentation of the lamina cribrosa using Frangi’s filter: a novel approach for rapid identification of tissue volume fraction and beam orientation in a trabeculated structure in the eye,” J. R. Soc. Interface 12(104), 20141009 (2015). 10.1098/rsif.2014.1009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Tan M. H., Ong S. H., Thakku S. G., Cheng C.-Y., Aung T., Girard M., “Automatic feature extraction of optical coherence tomography for lamina cribrosa detection,” Journal of Image and Graphics 3, 2 (2015) [Google Scholar]
- 53.Gardiner S. K., Demirel S., Reynaud J., Fortune B., “Changes in retinal nerve fiber layer reflectance intensity as a predictor of functional progression in glaucoma,” Invest. Ophthalmol. Vis. Sci. 57(3), 1221–1227 (2016). 10.1167/iovs.15-18788 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Miri M. S., Abràmoff M. D., Kwon Y. H., Sonka M., Garvin M. K., “A machine-learning graph-based approach for 3D segmentation of Bruch’s membrane opening from glaucomatous SD-OCT volumes,” Med. Image Anal. 39, 206–217 (2017). 10.1016/j.media.2017.04.007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Belghith A., Bowd C., Medeiros F. A., Weinreb R. N., Zangwill L. M., “Automated segmentation of anterior lamina cribrosa surface: How the lamina cribrosa responds to intraocular pressure change in glaucoma eyes?” in Proceedings of IEEE 12th International Symposium on Biomedical Imaging (ISBI) (2015), 222–225. 10.1109/ISBI.2015.7163854 [DOI] [Google Scholar]
- 56.Sawada Y., Hangai M., Murata K., Ishikawa M., Yoshitomi T., “Lamina cribrosa depth variation measured by spectral-domain optical coherence tomography within and between four glaucomatous optic disc phenotypes,” Invest. Ophthalmol. Vis. Sci. 56(10), 5777–5784 (2015). 10.1167/iovs.14-15942 [DOI] [PubMed] [Google Scholar]
- 57.Kim Y. W., Jeoung J. W., Kim D. W., Girard M. J. A., Mari J. M., Park K. H., Kim D. M., “Clinical assessment of lamina cribrosa curvature in eyes with primary open-angle glaucoma,” PLoS One 11(3), e0150260 (2016). 10.1371/journal.pone.0150260 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Thakku S. G., Tham Y. C., Baskaran M., Mari J. M., Strouthidis N. G., Aung T., Cheng C. Y., Girard M. J., “A global shape index to characterize anterior lamina cribrosa morphology and its determinants in healthy indian eyes,” Invest. Ophthalmol. Vis. Sci. 56(6), 3604–3614 (2015). 10.1167/iovs.15-16707 [DOI] [PubMed] [Google Scholar]
- 59.You J. Y., Park S. C., Su D., Teng C. C., Liebmann J. M., Ritch R., “Focal lamina cribrosa defects associated with glaucomatous rim thinning and acquired pits,” JAMA Ophthalmol. 131(3), 314–320 (2013). 10.1001/jamaophthalmol.2013.1926 [DOI] [PubMed] [Google Scholar]
- 60.Han J. C., Choi D. Y., Kwun Y. K., Suh W., Kee C., “Evaluation of lamina cribrosa thickness and depth in ocular hypertension,” Jpn. J. Ophthalmol. 60(1), 14–19 (2016). 10.1007/s10384-015-0407-z [DOI] [PubMed] [Google Scholar]
- 61.Girard M. J., Beotra M. R., Chin K. S., Sandhu A., Clemo M., Nikita E., Kamal D. S., Papadopoulos M., Mari J. M., Aung T., Strouthidis N. G., “In vivo 3-dimensional strain mapping of the optic nerve head following intraocular pressure lowering by trabeculectomy,” Ophthalmology 123(6), 1190–1200 (2016). 10.1016/j.ophtha.2016.02.008 [DOI] [PubMed] [Google Scholar]
- 62.Lee E. J., Kim T. W., Kim M., Girard M. J. A., Mari J. M., Weinreb R. N., “Recent structural alteration of the peripheral lamina cribrosa near the location of disc hemorrhage in glaucoma,” Invest. Ophthalmol. Vis. Sci. 55(4), 2805–2815 (2014). 10.1167/iovs.13-12742 [DOI] [PubMed] [Google Scholar]
- 63.Sigal I. A., Yang H., Roberts M. D., Grimm J. L., Burgoyne C. F., Demirel S., Downs J. C., “IOP-induced lamina cribrosa deformation and scleral canal expansion: independent or related?” Invest. Ophthalmol. Vis. Sci. 52(12), 9023–9032 (2011). 10.1167/iovs.11-8183 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Abe R. Y., Gracitelli C. P. B., Diniz-Filho A., Tatham A. J., Medeiros F. A., “Lamina Cribrosa in Glaucoma: Diagnosis and Monitoring,” Curr. Ophthalmol. Rep. 3(2), 74–84 (2015). 10.1007/s40135-015-0067-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Hosseini-Asl E., Ghazal M., Mahmoud A., Aslantas A., Shalaby A. M., Casanova M. F., Barnes G. N., Gimel’farb G., Keynton R., El-Baz A., “Alzheimer’s disease diagnostics by a 3D deeply supervised adaptable convolutional network,” Front. Biosci. (Landmark Ed.) 23(2), 584–596 (2018). 10.2741/4606 [DOI] [PubMed] [Google Scholar]
- 66.Tajbakhsh N., Shin J. Y., Gurudu S. R., Hurst R. T., Kendall C. B., Gotway M. B., Jianming Liang, “Convolutional neural networks for medical image analysis: full training or fine tuning?” IEEE Trans. Med. Imaging 35(5), 1299–1312 (2016). 10.1109/TMI.2016.2535302 [DOI] [PubMed] [Google Scholar]
- 67.Girard M. J. A., Tun T. A., Husain R., Acharyya S., Haaland B. A., Wei X., Mari J. M., Perera S. A., Baskaran M., Aung T., Strouthidis N. G., “Lamina cribrosa visibility using optical coherence tomography: comparison of devices and effects of image enhancement techniques,” Invest. Ophthalmol. Vis. Sci. 56(2), 865–874 (2015). 10.1167/iovs.14-14903 [DOI] [PubMed] [Google Scholar]
- 68.Strouthidis N. G., Grimm J., Williams G. A., Cull G. A., Wilson D. J., Burgoyne C. F., “A comparison of optic nerve head morphology viewed by spectral domain optical coherence tomography and by serial histology,” Invest. Ophthalmol. Vis. Sci. 51(3), 1464–1474 (2010). 10.1167/iovs.09-3984 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Bhagat P. R., Deshpande K. V., Natu B., “Utility of ganglion cell complex analysis in early diagnosis and monitoring of glaucoma using a different spectral domain optical coherence tomography,” J Curr Glaucoma Pract 8(3), 101–106 (2014). 10.5005/jp-journals-10008-1171 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Fan N., Huang N., Lam D. S. C., Leung C. K.-S., “Measurement of photoreceptor layer in glaucoma: a spectral-domain optical coherence tomography study,” J. Ophthalmol. 2011, 264803 (2011). 10.1155/2011/264803 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Tun T. A., Atalay E., Baskaran M., Nongpiur M. E., Htoon H. M., Goh D., Cheng C. Y., Perera S. A., Aung T., Strouthidis N. G., Girard M. J. A., “Association of functional loss with the biomechanical response of the optic nerve head to acute transient intraocular pressure elevations,” JAMA Ophthalmol. 136(2), 184–192 (2018). 10.1001/jamaophthalmol.2017.6111 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Tun T. A., Thakku S. G., Png O., Baskaran M., Htoon H. M., Sharma S., Nongpiur M. E., Cheng C. Y., Aung T., Strouthidis N. G., Girard M. J., “Shape changes of the anterior lamina cribrosa in normal, ocular hypertensive, and glaucomatous eyes following acute intraocular pressure elevation,” Invest. Ophthalmol. Vis. Sci. 57(11), 4869–4877 (2016). 10.1167/iovs.16-19753 [DOI] [PubMed] [Google Scholar]
- 73.Wang X., Beotra M. R., Tun T. A., Baskaran M., Perera S., Aung T., Strouthidis N. G., Milea D., Girard M. J. A., “In vivo 3-dimensional strain mapping confirms large optic nerve head deformations following horizontal eye movements,” Invest. Ophthalmol. Vis. Sci. 57(13), 5825–5833 (2016). 10.1167/iovs.16-20560 [DOI] [PubMed] [Google Scholar]