Super-multiplexed fluorescence microscopy via photostability contrast

Abstract

Fluorescence microscopy is widely used to observe and quantify the inner workings of the cell. Traditionally, multiple types of cellular structures or biomolecules are visualized simultaneously in a sample by using spectrally distinct fluorescent labels. The wide emission spectra of most fluorophores limits spectral multiplexing to four or five labels in a standard fluorescence microscope. Further multiplexing requires another dimension of contrast. Here, we show that photostability differences can be used to distinguish between fluorescent labels. By combining photobleaching characteristics with a novel unmixing algorithm, we resolve up to three fluorescent labels in a single spectral channel and unmix fluorescent labels with nearly identical emission spectra. We apply our technique to organic dyes, autofluorescent biomolecules and fluorescent proteins. Our approach has the potential to triple the multiplexing capabilities of any digital widefield or confocal fluorescence microscope with no additional hardware, making it readily accessible to a wide range of researchers.

1. Introduction

Fluorescence microscopy is widely used in biological research for high contrast imaging with unrivalled specificity [1]. In a typical assay, 2-4 cellular targets are each labeled by fluorescent species with distinct spectral emission [2]. Combinations of different excitation sources and emission filters are then used to provide spectral contrast between the fluorescent species. In practice, there is inevitable mixing between fluorescent channels because fluorophores are excited and emit over a finite bandwidth. Fluorescent emission from a given fluorescent species contributes to the signal in multiple emission channels. This spectral cross-talk can be significant when using more than 3 fluorescent probes, necessitating unmixing algorithms for successful separation [3,4]. Generally, spectral unmixing procedures work well, however, one cannot isolate more fluorescent probes than one has spectral channels. High-end filter-based fluorescence microscopes have at most five excitation/emission filter combinations and can therefore spectrally separate up to 5 fluorescent species. Alternatively, spectrometer-based imaging systems can in principle acquire dozens of spectral channels, at the added cost of a large filter set or spectral imaging module. Unfortunately, even with a large number of spectral channels it is extremely challenging to identify more than 4-5 fluorescent species in a sample, regardless of the spectral measurement scheme [5,6]. This is because of the wide spectral width of each fluorophore (~40-50 nm with broad tails), the need for excitation windows (~20 nm minimum per excitation source) and the finite spectral bandwidth of the visible spectrum (300 nm). However, in many areas of biology there is a growing need to separate more objects or structures or to perform several fluorescence-based sensing experiments simultaneously to increase the information content derived from fluorescence microscopy assays.

Here we introduce a method for expanding the number of fluorescent species that can be simultaneously multiplexed in an image, without resorting to large filter sets or spectral detectors. We show that one may discriminate between fluorescent species by leveraging a photophysical process inherent in all organic fluorophores – photobleaching. Instead of using spectral signatures to distinguish fluorescent species, we use their photobleaching behaviour as an identifying property. This technique, which we call bleaching-assisted multichannel microscopy (BAMM), can be applied either by itself or in conjunction with spectral filters and is even capable of discriminating between fluorophores with nearly identical emission spectra.

Fluorescence photobleaching refers to a decrease in emission intensity of a fluorescent sample over time under illumination. This decrease is the result of chemical reactions between optically excited fluorescent molecules and the surrounding medium [7]. Bleached fluorophores are irreversibly “turned off” and are no longer able to emit light. The emission intensity (I) of an ensemble of fluorophores decreases exponentially over time ($t$) according to $I\left(t\right)=I\left(0\right)e^{-kt}$. The bleaching constant $k$ depends on a myriad of experimental and environmental parameters in addition to the electronic structure of the fluorophore itself [1]. For example, excitation power, excitation wavelength, oxygen concentration, and a fluorophore’s energy level structure all affect its bleaching rate [7,8]. This means that spectrally identical fluorophores can have very different bleaching rates.

A variety of microscopy techniques rely on photobleaching. For example, photo-imprint microscopy can increase resolution beyond the diffraction limit in both in-plane and axial dimensions [9,10]. Another super-resolution method called bleaching/blinking assisted localization microscopy (BALM) uses discrete photobleaching events to localize single molecules [11]. The resulting images are similar to that created by stochastic optical reconstruction microscopy (STORM) or photoactivated localization microscopy (PALM) [12,13], but sample preparation is greatly simplified because of the universal occurrence of fluorescence photobleaching. Yet another technique, fluorescence recovery after photobleaching (FRAP), has become a standard tool for investigating diffusion kinetics in living cells [14,15].

In the mid-1990s, photostability was briefly investigated as a contrast mechanism for multi-probe fluorescence microscopy [16,17], but suffered due to a lack of sophisticated unmixing algorithms and inadequate computing power. Though multicolor photobleaching-enabled super resolution imaging has recently seen interest [18], these photobleaching-based approaches have yet to be generalized and combined with modern unmixing techniques. We take advantage of modern developments in non-negative unmixing approaches [19,20], and introduce a specialized non-negative matrix factorization algorithm for photobleaching data. Moreover, we show that multiplexing can be further increased by combining spectral and photostability dimensions. Our work establishes photostability as a bona fide optical dimension for extended multiplexing without specialized sample preparation or additional microscope hardware.

2. Methods

2.1. Timelapse acquisition

The first step in BAMM is to record a timelapse of sample bleaching. The sample is repeatedly imaged with one or multiple lasers (or light emitting diodes, LEDs), causing the sample to fade. We record a timelapse movie, followed by background subtraction and drift compensation pre-processing steps [21]. We use unmodified commercial confocal and widefield fluorescence microscopes (confocal: Nikon AR1, Olympus FV1200; widefield: Thermo Fisher Scientific CellInsight CX7 High Content Analysis (HCA) platform) for timelapse acquisition. Sample-specific imaging parameters and filter combinations are given in the Results section.

2.2. Unmixing

2.2.1 Non-negative least-squares

Assuming that several fluorescent species are present in a sample, they can all potentially contribute to the signal collected in a given pixel. In principle, determining the relative abundances of these fluorophore species via bleaching can be achieved by fitting the amplitudes of a multi-exponential decay at each pixel. This basic problem occurs in many arenas from magnetic resonance imaging [22] to fluorescence lifetime imaging [23,24] and nuclear physics [25]. There are a wide range of computational approaches to this challenge, such as maximum likelihood estimation [25], the method of least-squares [26], method of moments [27] and the Gardner Transform [28]. However, our problem is more general as it can include both spectral and bleaching information. Accordingly, we extract the spectral and photobleaching characteristics from the data set itself. This self-calibrated approach avoids using physical models of photobleaching that may not be consistent with real world samples. We will refer to the spectral-bleaching characteristic of a fluorophore as its spectral-bleaching fingerprint. An analogous quantity has recently been used to unmix fluorescent probes based on their fluorescence lifetime and emission spectra [24]. Though the combination of spectral and photostability information is the most general form of our technique, we note that we can also use photostability information by itself, as will be seen in the Results section.

To separate pixel-by-pixel contributions of each fluorescent label, we use the MATLAB non-negative least-squares (NNLS) function lsqnonneg to solve the relevant linear unmixing problem [19]:

$$I_k\left(x,y\right)={\displaystyle \sum }_{i=1}^N{a}_i(x,y)v_{ik},k=1,2,\dots ,T$$ (1)

where $I_k\left(x,y\right)$ is the (measured) intensity at pixel $(x,y)$ for frame index $k$ (spectrally concatenated if spectral information is included), $a_i(x,y)\ge 0$ is the relative scalar abundance of fluorophore species $i$ at pixel $(x,y)$ and $v_{ik}$ is the $k$^th entry of the T-element (spectral-) bleaching fingerprint for fluorophore type $i$. Note that the system is overdetermined when T > N (N is the number of fluorescent labels in the sample). The extra information in this overdetermined system is crucial for noise suppression. The non-negativity prior for $a_i$ prevents the unmixed abundances from reaching nonphysical negative values and improves unmixing fidelity. The $i$^th image - the abundance map of fluorophore type $i$ - is given by $a_i(x,y)$ and ideally contains only signal from the $i$^th fluorescent species.

2.2.2 Non-negative matrix factorization

If there are regions of the sample where each fluorescent probe exists in isolation, then the (spectral-) bleaching fingerprints $v_{ik}$ can be manually identified. However, for many samples, this is not the case.

For such situations (typically cellular samples), the bleaching fingerprint of each fluorophore along with their pixel-by-pixel abundances, are simultaneously estimated by non-negative matrix factorization (NMF) [20]. This algorithm attempts to find non-negative bleaching traces and fluorophore abundances that solve the mixing problem of Eq. (1) in the least squared sense, using the alternating least squares (ALS) procedure [20]. The non-negativity constraint restricts possible solutions for the bleaching traces and the abundance maps to those with only positive values. As with NNLS above, this guarantees that the result is consistent with the fact that the intensity is a non-negative quantity. We perform NMF by using the built-in MATLAB non-negative matrix factorization function nnmf. We supply the nnmf function with the principal components of photobleaching curves as the initial estimates of the bleaching characteristics. For added robustness, we take the optimal solution out of three replicates – the first seeded with principal components as initial solutions and the following two with random initial guesses. Typical results required no more than 25 iterations.

2.2.3. Non-increasing non-negative matrix factorization

For highly multiplexed samples, the NMF approach above may converge to unphysical solutions where bleaching traces increase in intensity over time, yielding incorrect unmixing results. This can be mitigated by imposing additional restrictions to the solution space. To this end, we implement a modification to the standard ALS NMF procedure, which we call non-increasing NMF (NI-NMF). At each iteration, if the value of a bleaching trace estimate $B(t)$ at time $t=t_{n+1}$ exceeds the value of the bleaching trace estimate at time $t_n$, then we set $B\left(t_{n+1}\right)=B(t_n)$. This is modification is performed for each time point in succession so that the value of the bleaching trace is monotonically decreasing. We run NI-NMF for 25 replicates, with the first one being seeded with the principal components, and select the result with the lowest mean-squared error. For all NI-NMF and NMF procedures it was found to be beneficial to exclude dim pixels to reduce the influence of noise and decrease computation time. We typically exclude all pixels with that are dimmer than 1-10% of the brightest pixel in the data set. Once the estimate for the bleaching curves is found, the least squares solution for the abundances at every pixel in the image is found by using the timelapse data and the estimated bleaching curves together with the MATLAB backslash operator (a QR solver), and then setting negative abundances to zero. This is equivalent to including all pixels on the final iteration of the ALS (NI-) NMF algorithm.

3. Results

3.1. Working principle

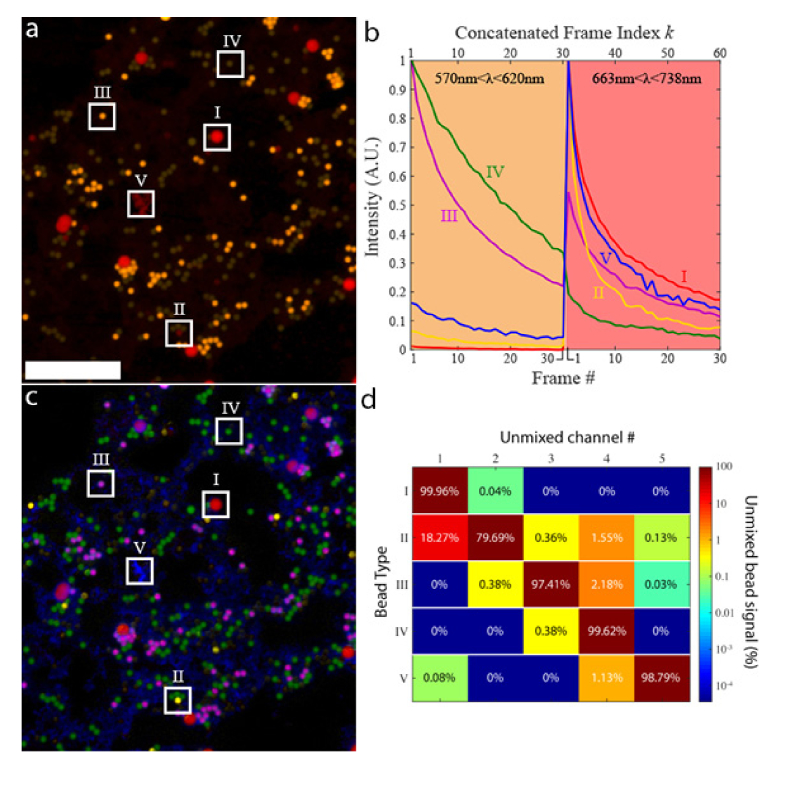
In this section, we demonstrate the working principle of BAMM using a model system consisting of five different types of fluorescent beads. The beads have peak emission wavelengths ranging from 500 - 700 nm, and are imaged simultaneously in yellow (570 - 620 nm) and red (663 - 738 nm) spectral channels using a confocal microscope (Fig. 1(a)). Bead types I-IV are Spherotech “Sky Blue”, “Blue”, “Purple”, and “Yellow”, respectively. Bead type V are “Chromeon 642” beads from Sigma Aldrich. Bead types I-IV are all > 2μm in diameter and are therefore easily resolvable by the confocal microscope. However, bead type V is only 80nm in diameter, and therefore appears as a dim amorphous red background since the beads themselves are spatially unresolvable.

Fig. 1.

BAMM with beads. a) The first frame of a 30-frame photobleaching experiment, with each frame consisting of a yellow/red dual spectral channel image of a mixture of 5 different fluorescent beads. Examples of different bead types are boxed and labeled as I-V. The red channel is gamma corrected to enhance dim pixels (for display only). Boxes II, IV and V have increased brightness for visibility. Scale bar is 50 μm. b) Time traces of beads I-V in (a), during the photobleaching experiment. Concatenated frames # 1-30 correspond to frames 1-30 in the yellow channel (570-620 nm) of image (a). Concatenated frames #31-60 correspond to frames 1-30 from the red channel (663-738 nm) of image (a). Each bead type has a unique spectral-bleaching “fingerprint”. c) False-coloured unmixed image of all five bead types. Abundance maps for bead types I-V are coloured red, yellow, purple, green and blue, respectively. d) The cross-talk matrix of the unmixing process. Cross-talk is generally low across all bead types except for bead type II into channel 1 (bead type I). This is due to the similarity in their bleaching rates, and low signal from type II beads (see (a) and (b)). For all other bead types, more than 97% of the bead signal is unmixed into the correct channel.

The bleaching timelapse for this sample was acquired using a Nikon AR1 confocal microscope, equipped with continuous wave (CW) excitation lasers at λ = 405, 488, 561 and 640 nm. Images were acquired using a 40x, 0.95 NA microscope objective, with a pixel dwell time of 1 μs and 2x line averaging. Figure 1(a) shows the first frame of the bleaching timelapse. This image is color coded with yellow and red channels corresponding to emission windows 570-620 nm and 663-738 nm, respectively. All emission channels are recorded simultaneously, and all 4 lasers excite the sample simultaneously with laser powers of (0.20, 1.10, 1.20, 0.09) mW for (405, 488, 561, 640) nm lasers, respectively. The confocal pinhole was set to 80% of the diffraction limit at 640 nm.

To supply the spectral-bleaching fingerprints of each bead, we manually identify 5 pixels in Fig. 1(a), each of which contains signal from only one of each of the fluorophore types in the sample. At each pixel, we have an associated 30-frame bleaching curve in each of the two emission channels, for a total of 60 data points across spectral and temporal dimensions. The photobleaching traces for the two spectral channels are concatenated into the 60-frame spectral-bleaching fingerprint curves shown in Fig. 1(b): concatenated frames 1-30 originate from the yellow spectral channel, concatenated frames 31-60 are from the red spectral channel. The abundance maps are subsequently obtained as described in Methods – Unmixing – Non-negative least-squares. The result is a 5-channel image consisting of 5 independent fluorophore abundance maps (Fig. 1(c)), each of which indicates the relative concentration of given fluorescent species. Abundance maps for bead types I-V are colored red, yellow, purple, green and blue, respectively. Cross-talk between abundance maps is shown in Fig. 1(d). Unmixing fidelity is generally high (<2.5% cross-talk) except for Type II beads (18.27% bleed through into Channel 1), due to the weak fluorescence of Type II beads. Though this sample contains mostly spatially non-overlapping objects, the mathematics employed here are fully capable of accounting for overlapping signals, as is shown in the following section. We note that using standard spectral unmixing techniques, it would only be possible to isolate $N$ fluorescent species using $N$ spectral channels. In Fig. 1, we improve on this limit by a factor of 2.5, unmixing 5 independent fluorophore abundance maps from two spectral channels. Spectral information, however, is not necessary for BAMM, which can separate spectrally identical fluorescent species provided their bleaching rate differs.

3.2. BAMM in fixed cells

The unmixing methods used in BAMM are also capable of separating spatially overlapping objects often encountered in biological samples. To demonstrate this capability, we imaged muntjac skin fibroblasts (FluoCells Prepared Slide #6, Thermo Fisher Scientific) labeled with Alexa Fluor 488 (actin) and Alexa Fluor 555 (mitochondria). For this experiment, we use an Olympus FV1200 confocal microscope equipped with a 20x 0.75NA air objective. A 473 nm laser excites both dyes and a single detector collects the dye emission over a spectral range that includes the peak emission wavelengths of both dyes (500-600 nm). Pixel dwell time was 8 μs and laser power was measured to be 0.27mW at the sample plane. The confocal aperture was set to the diffraction limit at 473nm.

The first frame of this monochromatic image series is shown in Fig. 2(a). In general, overlapping structures preclude the possibility of finding pixels that contain each of the fluorophores in isolation. Thus, we cannot use the manual method of Fig. 1 for identifying the bleaching fingerprint of a fluorescent species. Instead, we use a non-negative matrix factorization (NMF) algorithm [20] in MATLAB for simultaneous estimation of the bleaching behaviour of both dyes along with their spatial distribution (See Methods – Unmixing - Non-negative matrix factorization). The non-negativity constraint helps to restrict possible solutions for both the abundance maps and bleaching traces to those with only positive values. This guarantees that the result is consistent with the fact that the intensity is a non-negative quantity.

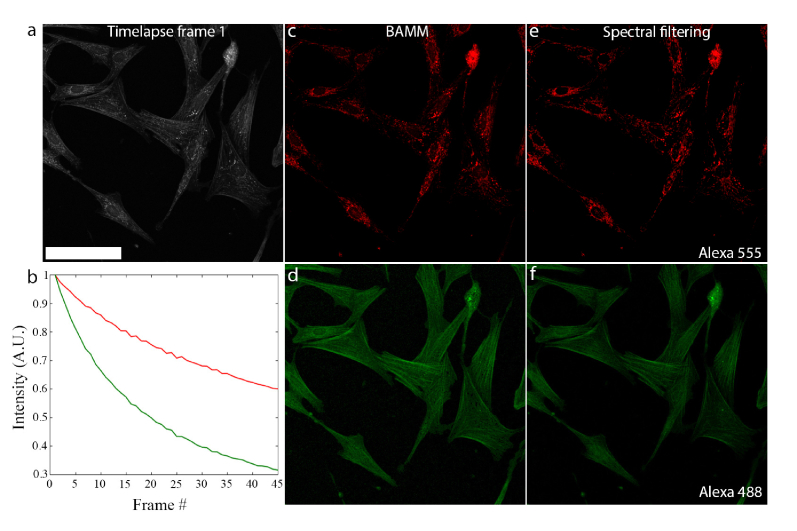
Fig. 2.

BAMM produces the correct abundance map with overlapping structures. a) First frame of a 45-frame bleaching timelapse of muntjac skin fibroblast cells under 473 nm illumination. A wide emission window is used (500-600 nm) to capture emission from both Alexa Fluor 488 and Alexa Fluor 555 dyes. Scale bar is 100 μm. b) Bleaching traces of Alexa Fluor 555 (red) and Alexa Fluor 488 (green) as estimated by NMF. c) and d) Alexa Fluor 555 and Alexa Fluor 488 abundance maps extracted from the single-channel timelapse (a) using the estimated bleaching curves in (b) along with the entire 45-frame bleaching timelapse. Even though structures in both channels overlap spatially, they are unmixed successfully. e) Image of Alexa Fluor 555 distribution acquired using spectral filtering (570-670 emission window). f) Image of Alexa Fluor 488 distribution acquired using conventional spectral filtering (480-542 nm emission window). Both (e) and (f) were recorded before bleaching.

The NMF-estimated bleaching behaviours are shown in Fig. 2(b): Alexa Fluor 555 (red) bleaches more slowly than Alexa Fluor 488 (green). The abundance maps of both dyes generated by NMF are shown in Figs. 2(c) and 2(d). Crucially, features are not duplicated between channels as occurs with incomplete unmixing. The spatial overlap between both fluorophore species is maintained. Reference images, acquired using spectral emission filters prior to bleaching (Figs. 2(e) and 2(f)) are nearly identical to those obtained using BAMM, demonstrating BAMM’s ability to produce high-quality multiplexed images of biological samples.

Single-spectral-channel dual-labeling BAMM experiments can also be performed with fluorophores that are traditionally not separable using spectral filters. For BAMM, one particularly attractive application is the separation of spectrally overlapping traditional organic dyes from fluorescent proteins. These two types of emitters have very different photostabilities, and are thus readily unmixed using BAMM using either reference curves with NNLS estimation or NMF.

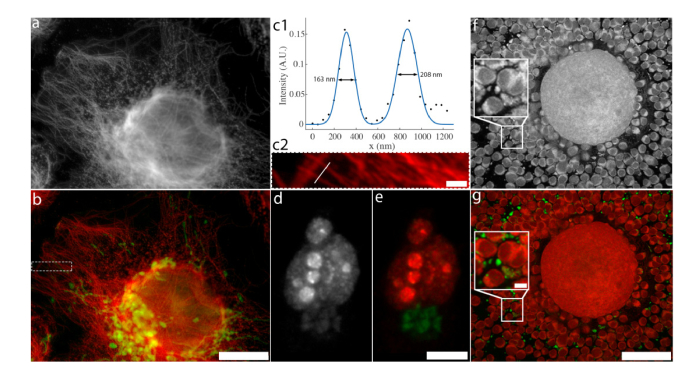
To demonstrate this capability, we imaged two samples each containing spectrally overlapping fluorophores in Figs. 3(a)-(e), with a widefield fluorescence microscope (Thermo Fisher Scientific CellInsight CX7 HCA Platform). The first sample (Figs. 3(a-c2) is labeled with Alexa Fluor 514 (tubulin) and GFP (mitochondria). The first frame of the monochromatic bleaching timelapse is show in Fig. 3(a) and 2-channel unmixed result is shown in Fig. 3(b). This sample was also processed for Expansion Microscopy [29,30], indicating BAMM’s compatibility with a super resolution technique. Here, we use a 20x/0.7 NA objective, with 227 nm pixel size in image space. Excitation was provided by a 485nm LED excitation with a 20nm FWHM bandpass filter and fluorescence emission was detected through a 27nm FWHM bandpass filter centered at 542nm. Integration time was 6.0s/frame. Bleaching data were unmixed using the NNLS procedure outlined in Methods. Reference bleaching curves obtained were obtained with singly-labeled samples under the same imaging conditions. We achieve an effective (pre-expansion) resolution of 163 nm (note, with a 0.7 NA objective), as measured by the width of an isolated microtubule in the dual channel BAMM image (Fig. 3(c1) and (c2)). This resolution is slightly lower than the raw image data before BAMM processing (137 nm), likely due to imperfect dedrifting correction.

Fig. 3.

Dual-channel BAMM in cells. a) First frame of a single spectral channel bleaching timelapse of a U2OS cell processed for Expansion Microscopy, labeled with Alexa Fluor 514 (tubulin) and GFP (mitochondria). b) Dual-channel BAMM image of (a) using NNLS with reference bleaching curves (40 frames) for GFP and Alexa Fluor 514. Alexa Fluor 514 is colored red and GFP is colored green. Color histograms are modified for visibility of dim features. Dotted white border indicates region shown in (c2). Scale bar indicates 60 μm after expansion (13 μm before expansion). c1) Intensity trace along the white line in (c2), intersecting two isolated microtubules. The black dots indicate data points and the blue curve is a Gaussian fit to the intensity profile. The full width at half maximum of each peak is indicated on the plot. c2) Magnified version of the region within the dotted region in (b). The white line indicates the path of the intensity trace in (c1). GFP channel not shown for clarity. Scale bar is 5 μm after expansion (1.09 μm before expansion). d) First frame of a single spectral channel bleaching timelapse of a HeLa cell labeled with Alexa Fluor 555 (Ki67) and RFP (Golgi). e) Dual-channel BAMM image of (c) using NMF (45 frames). Alexa Fluor 555 is coloured red and RFP is colored green. Scale bar is 10 μm. f) First frame of a bleaching timelapse mouse cumulus-oocyte-complex autofluorescence. The boxed region is enlarged 2.5x in the inset. g) False-coloured BAMM image using NMF (50 frames). Scale bar is 50 μm, inset scale bar is 5 μm.

For Figs. 3(d) and 3(e), we use the same Thermo Fisher Scientific CellInsight CX7 HCA Platform, but with a 40x/0.75NA objective. The sample (HeLa cell labeled with Alexa Fluor 555 (Ki67) and RFP (Golgi)) was sequentially illuminated and imaged with 386nm, 485, 549 and 560nm LEDs for exposure times of 3.0s, 3.0s, 1.0s and 1.0s, respectively. Software autofocus was performed before each iteration of the LED illumination sequence with 386nm excitation. Bleaching timelapse processed for BAMM used only information from 549nm excitation images, which were collected through a 5-band bandpass filter (transmission bands of the 5-band emission filter are (center wavelength/FWHM bandpass): 438/47 nm, 521/22 nm, 604/30 nm, 704/54 nm, and 810/85 nm).

In addition to exogenous dyes and genetically engineered fluorescent proteins, many biomolecules are naturally autofluorescent. These molecules are not inherently designed for photostability or multichannel imaging, and therefore have highly overlapping spectral profiles and display a wide range of bleaching behavior. The former makes them particularly hard to unmix spectrally and the latter is appealing for BAMM. To demonstrate the utility of BAMM to autofluorescent imaging, we acquire a bleaching timelapse of an unlabeled mouse cumulus-oocyte-complex (COC) within a wide yellow-to-red emission window (575-675 nm). Here, we used the Olympus FV1200 confocal microscope with a 60x 1.3 NA silicone immersion objective lens. The sample was excited with 473 and 559 nm CW lasers simultaneously (power 0.14 mW for each laser) with a pixel dwell time of 2 μs. The confocal aperture was set to 60% of the diffraction limit at 559 nm.

The first image of the resulting monochromatic bleaching stack is shown in Fig. 3(f). Analysis with NMF reveals two distinct fluorescent populations with different photostability. In the unmixed image (Fig. 3(g)), photostable foci (green) can be seen amongst the less photostable autofluorescence of the oocyte and cumulus cells (red). This result suggests that photostability may be a valuable, yet overlooked form of fluorophore identification, particularly in spectrally crowded samples.

3.3. Non-increasing non-negative matrix factorization

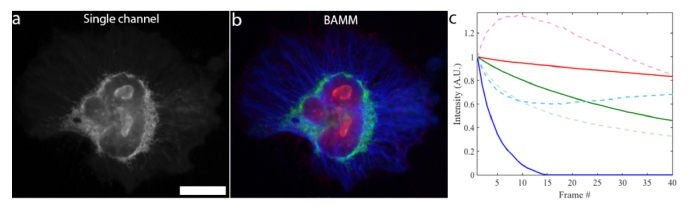
Blind unmixing three types of fluorophores via bleaching requires a priori information beyond non-negativity in order to reduce the solution space. To this end, we modify MATLAB’s ALS NMF algorithm to force the solution to the bleaching curves to be monotonically non-increasing at the start of each iteration (see Methods – Unmixing - Non-increasing non-negative matrix factorization). This guarantees that the NMF solution is physically consistent with the knowledge that fluorescent intensity must decrease over time. We call this approach the non-increasing NMF algorithm (NI-NMF). This added restriction of monotonically decreasing basis functions (the bleaching trace estimates) is crucial for 3-component unmixing using BAMM. Figure 4(a) shows a HeLa cell with 3 fluorescent labels (Alexa Fluor 555 (Ki67), GFP (mitochondria) and Alexa Fluor 430 (microtubules)) in a single spectral channel, while the 3-pseudo-color NI-NMF BAMM image is shown in Fig. 4(b). Here, imaging was performed using the Thermo Fisher Scientific CellInsight CX7, with a 40x/0.75NA objective. The sample was sequentially illuminated and imaged with 386nm, 485, 549 and 560nm LEDs for exposure times of 1.5s, 2.0s, 0.75s and 0.75s, respectively. Software autofocus was performed before each iteration of the LED illumination sequence with 386nm excitation. Bleaching timelapse processed for BAMM used only information from 485nm excitation images, which were collected through the same 5-band bandpass filter as Figs. 3d&e.

Fig. 4.

BAMM unmixing of 3 fluorescent labels from a single spectral channel. a) The first frame (of 40) of the BAMM bleaching timelapse, using 485nm LED excitation. This LED excites Alexa Fluor 555 (Ki67), GFP (mitochondria) and Alexa Fluor 430 (microtubules). Scale bar is 20 μm. b) False-color BAMM image obtained via NI-NMF, showing the fluorescent emitter distributions. Alexa Fluor 555 in red, GFP in green and Alexa Fluor 430 in blue. c) Bleaching traces for each fluorophore type estimated by NI-NMF (solid) and NMF (dotted). Solid curve colors match the color scheme in (b).

The unmixing result in Fig. 4b represents a 3-fold increase over the traditional multiplexing limit with only one spectral channel. The associated estimated bleaching traces for this data set are shown in Fig. 4c, for both NMF and NI-NMF unmixing. The NI-NMF algorithm correctly returns bleaching traces that only decrease over time whereas the unmodified NMF algorithm estimates bleaching behavior that increases over certain time intervals, leading to incomplete and physically inconsistent unmixing results.

4. Discussion and conclusions

We have shown that BAMM is compatible with both laser scanning confocal and widefield microscopes. Widefield illumination has the advantage that all fluorophores in a weakly absorbing 3D sample receive the same peak excitation power. In a confocal microscope this is not the case – the excitation intensity is highest in the middle of the focal spot. Fluorophores above and below the focal plane accumulate the same total dose during image acquisition, but experience a smaller peak excitation power. If nonlinear photobleaching effects are large, this could cause a depth-dependent photobleaching response. However, this effect could be mitigated by the confocal aperture, which blocks out–of-plane emission from reaching the detector. We did not observe any depth dependent artifacts arising from nonlinear photobleaching with the standard pinhole setting of ~1 Airy disc. Such artifacts would be apparent as systematic variations around 3D structures (e.g. the edge of a fluorescent bead would be observed to bleach at a different rate from the center of the bead, as their average depths are different). We observe no such halos in Fig. 1, nor in the rest of the data sets in this work.

The excitation illumination profile is critical for BAMM because the bleaching rate is a function of excitation intensity. Two species at different locations in the field-of-view can experience the same photobleaching rate if they are subject to different excitation intensities. If the illumination profile is known a priori, this effect could be mitigated by adjusting the temporal binning at each pixel to compensate for the spatially dependent excitation dose. A more straightforward approach is to simply crop the field of view so that the illumination profile is uniform within a smaller region.

In our experiments with fixed cells, we do not observe any systematic variation in bleaching rates both within cells (e.g. center vs. periphery of cell) and between cells. This is not surprising since fixed cell samples are subject to chemical treatment to prevent degradation and to allow fluorophores to pass through certain cellular structures. The chemical environment, which affects the bleaching rate, is therefore likely quite homogeneous, as opposed to the live cell case.

We have shown that BAMM is compatible with Expansion Microscopy [29,30], a relatively new route towards super resolution microscopy. We expect that BAMM will also be suitable for use with structured illumination, so long as accurate de-drifting correction is applied. Compatibility with fundamentally nonlinear techniques such as two photon and stimulated emission depletion is less clear as they are more susceptible to nonlinear bleaching [31]. Single molecule localization microscopy (SMLM) techniques such as stochastic optical reconstruction microscopy [12] are fundamentally different because they identify single molecules. On this scale, bleaching is a discrete process. Instead of calculating abundances at each pixel, an SMLM approach to BAMM might instead classify a fluorophore based on how many photons it emitted before bleaching (or the photobleaching recovery rate for fluorescent proteins). This could not only simplify multi-label SMLM but also allow more efficient photon collection and lower system cost by reducing the number of filters and light sources needed.

In summary, we have introduced a novel microscopy method, BAMM, which uses photobleaching as a contrast mechanism. Though photobleaching is usually thought of as being detrimental to fluorescence imaging, here we harness this ubiquitous effect to multiplex up to three fluorescent labels into a single spectral channel. BAMM reports on a fundamentally different property of fluorophores (their photostability) than standard spectral filter based fluorescence microscopy. As such, BAMM can be used to distinguish multiple fluorescent species given only a single emission channel, and separate nearly spectrally identical fluorophores. Our work complements other recent reports of fluorescence super-multiplexing methods where fluorescent labels are distinguished based on properties beyond standard excitation and emission spectra, such as fluorescence lifetime [24] and stimulated Raman scattering [32]. Unlike these techniques, however, BAMM does not require any additional hardware and can be performed on a standard digital fluorescence microscope – widefield or confocal.

Funding

Australian Research Council (ARC) (CE140100003, FT110100225).

Disclosures

The authors declare that there are no conflicts of interest related to this article.