Volumetric optical coherence microscopy with a high space-bandwidth-time product enabled by hybrid adaptive optics

Abstract

Optical coherence microscopy (OCM) is a promising modality for high resolution imaging, but has limited ability to capture large-scale volumetric information about dynamic biological processes with cellular resolution. To enhance the throughput of OCM, we implemented a hybrid adaptive optics (hyAO) approach that combines computational adaptive optics with an intentionally aberrated imaging beam generated via hardware adaptive optics. Using hyAO, we demonstrate the depth-equalized illumination and collection ability of an astigmatic beam compared to a Gaussian beam for cellular-resolution imaging. With this advantage, we achieved volumetric OCM with a higher space-bandwidth-time product compared to Gaussian-beam acquisition that employed focus-scanning across depth. HyAO was also used to perform volumetric time-lapse OCM imaging of cellular dynamics over a 1mm × 1mm × 1mm field-of-view with 2 μm isotropic spatial resolution and 3-minute temporal resolution. As hyAO is compatible with both spectral-domain and swept-source beam-scanning OCM systems, significant further improvements in absolute volumetric throughput are possible by use of ultrahigh-speed swept sources.

1. Introduction

High-throughput imaging over extended volumes and durations is desirable in many cellular level biological studies. Such capabilities enable the study of biological dynamics over a wide range of spatiotemporal scales, and can be especially beneficial for the investigation of collective or emergent behavior, during processes such as embryonic development, tissue regeneration, or cancer metastasis [1–3]. Many efforts have been made to achieve high speed volumetric imaging at cellular resolution [4–6], but these methods each have their own limitations. For example, light sheet microscopy is excellent in high-throughput volumetric imaging [4], but its fluorescence-based detection scheme may encounter problems with photobleaching and/or phototoxity in long term live imaging. Fourier ptychography achieves a high space-bandwidth-time product (SBP-T) in 2D cell imaging [5, 6], but has limited performance in 3D imaging of thick samples.

Optical coherence tomography (OCT) can provide label-free imaging of 3D biological samples. Its ability to simultaneously acquire images at multiple depths without axial scanning of a beam focus makes OCT a good candidate to fill the gap as a high-throughput label-free 3D imaging modality. However, combining high-throughput OCT approaches with cellular resolution optical coherence microscopy (OCM) presents significant challenges. The application of traditional OCM to the imaging of cellular behavior [7, 8] suffers from the trade-off between resolution and depth-of-field (DOF), which stems from the propagation of a focused Gaussian beam for beam-scanned imaging.

Various hardware methods have been proposed to overcome this trade-off in OCM. One approach is to synthesize various OCM volumes acquired from multiple focus depths [9–14], but the resulting low temporal resolution makes it difficult to observe rapid dynamic processes. Illumination with a Bessel beam enables single-shot acquisition of volumetric images (due to the extended DOF of Bessel beams) [14–17], and can reach cellular resolution [18–22]. However, Bessel beams result in undesirable side lobes in the imaging PSF and exhibit lower contrast than Gaussian beams at the focal plane [23]. Alternatively, full-field OCM was developed to only acquire the in-focus en face signal [24, 25] by parallelizing acquisition in the transverse dimension, but can be more vulnerable to cross-talk [26–28]. On the other hand, since OCM provides access to the scattered optical field, computed imaging techniques were developed to provide depth-invariant focal plane resolution throughout the entire imaged volume [29–36], and have been applied to cellular-resolution imaging including in vitro cell studies [37, 38]. However, the reconstruction quality of data acquired by Gaussian-beam-scanning systems is limited by decreasing signal strength, due to the lower number of scattered photons collected with distance from focus, and thus the reconstructed image suffers outside the confocal gate where the collection of photons reflected/scattered from the sample is reduced dramatically. Furthermore, theoretical simulations suggest that, even when the measured OCT signal is above the shot noise, intensity noise, or thermal noise floor, the dynamic range of the OCT system (governed by detector dynamic range) can limit the effective imaging depth range [39].

To address the trade-offs faced by the above approaches, we propose a hybrid method which leverages the advantages of hardware-based beam manipulation and computational techniques. It utilizes hardware adaptive optics (HAO) to equalize the depth-dependent optical illumination intensity across depth by performing focusing shifting (similar with Gabor domain OCM [9]), and intentionally introducing astigmatism, whose resolution penalty can be circumvented with computational adaptive optics (CAO) [31]. The equalization of illumination intensity across depth reduces the dynamic range requirement of the spectrometer camera in spectral domain OCM (SD-OCM), which may provide benefits for cell imaging where a lower peak intensity can alleviate photo-thermal damage to the sample [40–42]. Using this hyAO approach, we demonstrate a higher throughput OCM imaging capability, quantified by an increase in SBP-T [5] from theoretical simulations, resolution phantom measurements, grape imaging, and volumetric time-lapse imaging of the dynamics of a fibroblast cell population in 3D cell culture.

2. Theory

The small spot size at the focus of a Gaussian beam results in a high intensity, thus limiting the allowable incident laser power to avoid damage in live samples. Meanwhile, an astigmatic beam splits the single high-intensity focal spot into two line foci, reducing the illumination intensity and enabling imaging with a higher incident laser power. In OCM, an astigmatic beam has been shown to exhibit an extended signal collection range compared to a Gaussian beam, at the cost of a reduced peak SNR [31]. Even though the astigmatic beam suffers from a lower SNR than the Gaussian beam at a fixed incident power, the SNR loss can in principle be compensated by increasing the incident laser power, as long as the peak illumination intensity does not exceed that of the Gaussian case. By applying CAO to mitigate defocus and optical aberrations (such as astigmatism) introduced by HAO, we can effectively ‘spread out’ the collection of optical energy across depth. As a result, the combination of hardware and computational approaches can raise SNR and resolution throughout an imaged volume. As discussed in Sect. 4.1, another important consequence of this approach is the reduction of the dynamic range required to measure and reconstruct OCM volumes with extended depth range.

The peak illumination intensity $I_{\text{ill}}(z;k)$ across depth at optical wavenumber $k$ of a Gaussian beam can be modelled as

$$I_{\text{ill}}(z;k)==\frac{2P_{\text{inc}}}{\pi w^2(z)},$$ (1)

in which $P_{\text{inc}}$ is the total incident power of the beam, and $w(z)$ is the effective beam radius of the optical field distribution $g(x,y,z;k)$ in the xy-plane (for the elliptical spot of an astigmatic beam, $w(z)$ is taken as the geometric mean of the major and minor axis lengths). The optical field distribution $g(x,y,z;k)$ is given by

$$g(x,y,z;k)=\underset{-\infty }{\overset{\infty }{{\displaystyle \iint }}}G\left(k_x,k_y,z=0;k\right)e^{i\varphi \left(k_x,k_y\right)}{e}^{i{k}_{z}z}{e}^{i(k_{x}x+k_{y}y)}\text{d}{k}_x\text{d}{k}_y.$$ (2)

In Eq. (2), $x,y,z$ represents the spatial coordinates with the focal plane at z = 0. $k_x,k_y,k_z$ indicate the corresponding spatial frequency coordinates and $k_z=\sqrt{k^2-k_x^2-k_y^2}$ at optical wavenumber $k$. $G(k_x,k_y,z;k)$ represents the angular spectrum of the complex field distribution$g(x,y,z;k)$. $\varphi (k_x,k_y)$ denotes the phase profile resulting from any wavefront aberrations present in the incident pupil plane.

Given an OCM imaging system with a double-pass geometry, the illumination field $g_{\text{ill}}$ and collection field $g_{\text{col}}$ can be written as $g_{\text{ill}}\left(x,y,z;k\right)=g_{\text{col}}\left(x,y,z;k\right)=g(x,y,z;k)$. Approximating that scattering results in spherical wave emission, the OCM imaging PSF is given in [39], as

$$h(x,y,z;k)=\sqrt{P_{\text{inc}}}{g}_{\text{ill}}\left(x,y,z;k\right)g_{\text{col}}\left(x,y,z;k\right)=\sqrt{P_{\text{inc}}}{g}^2(x,y,z;k)$$ (3)

In the post-processing stage, the aberration-corrected PSF $h_{\text{ac}}(x,y,z)$ can be obtained by correcting the wavefront curvature encoded in the phase of the virtual pupil function $H(k_x,k_y,z;k)$, which is approximated via a 2D transverse Fourier transform of the imaging PSF [31, 43], i.e.,

$$H\left(k_x,k_y,z;k\right)=\underset{-\infty }{\overset{\infty }{{\displaystyle \iint }}}h(x,y,z;k)e^{-i(k_{x}x+k_{y}y)}\text{d}x\text{d}y$$ (4)

Thus, the aberration free PSF can then be expressed as

$$h_{\text{ac}}(x,y,z;k)=\underset{-\infty }{\overset{\infty }{{\displaystyle \iint }}}H\left(k_x,k_y,z;k\right)e^{i{\varphi }_{\text{ac}}\left(k_x,k_y,z\right)}{e}^{i(k_{x}x+k_{y}y)}\text{d}{k}_x\text{d}{k}_y$$ (5)

The optimal aberration correction function ${\varphi }_{\text{ac}}(k_x,k_y,z)$ can be found via optimization with suitable metrics [44], such as the summation of the fourth power of the en face plane signal magnitude in this work. Finally, the peak reconstructed intensity for an uncorrected signal $I_{\text{rec}}$ and for an aberration corrected signal $I_{\text{rec,ac}}$ can be calculated as

$$I_{\text{rec}}\left(z;k\right)\propto \underset{x,y}{\max }\left\{{\left|h\left(x,y,z;k\right)\right|}^2\right\},$$ (6)

$$I_{\text{rec,ac}}\left(z;k\right)\propto \underset{x,y}{\max }\left\{{\left|h_{\text{ac}}\left(x,y,z;k\right)\right|}^2\right\}.$$ (7)

Based on the above formulation, numerical simulations were conducted to compare the expected imaging performance between Gaussian versus astigmatic beams, as discussed in Section 4.1. In practice, the wavenumber $k$above is set to central wavenumber $k_{\text{c}}$of the illumination source for simplicity.

3. Methods

3.1 Experimental setup

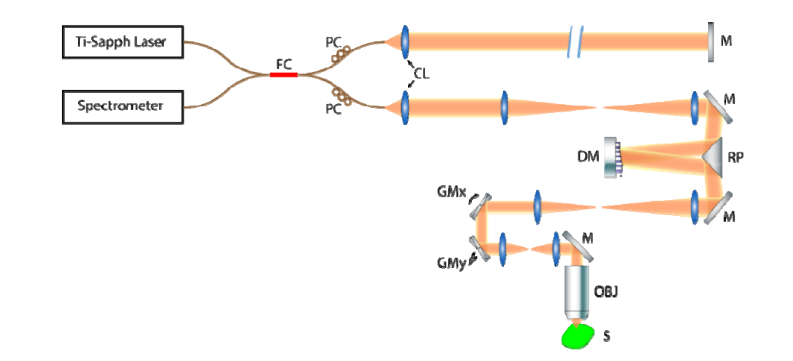
We used a SD-OCM system with adaptive optics (see Fig. 1). The system was illuminated by a Ti:Sapph broadband laser source (Femtolasers, Integral Element) with 810 nm central wavelength and 150 nm bandwidth. In the sample arm, the plane of the deformable mirror (Alpao, DM 97-15) was conjugate to the entrance pupil of the objective lens (Olympus, UMPlanFl 20XW) to shape the wavefront. The midpoint of the (coupled) X-scan and Y-scan galvanometer mirrors was conjugate to the back focal plane of the objective lens to minimize the scan path variation, described as coherence gate curvature [45, 46]. After the sample arm signal was superimposed with a reference arm signal at a 50:50 coupler, the net signal was collected by a spectrometer (Wasatch Photonics, Cobra 800) with a 12-bit line scan camera (e2v, Octopus). The laser and spectrometer combination offered a 2 μm full-width-at-half-maximum (FWHM) axial resolution. The total incident power on the sample was measured to be 23 mW, yielding a peak imaging sensitivity of 94 dB (at the Gaussian beam focus) at 300 μm below zero optical path delay (with a 5 dB/mm sensitivity fall-off). The hyAO method was first validated via bead phantom (TiO₂ in silicone) imaging by quantifying the depth-dependent SNR and resolution. Then, the technique was applied to imaging in a grape to demonstrate its advantage in imaging cellular structure. Finally, we used the hybrid AO approach to capture a 1mm × 1mm × 1mm FOV within a Matrigel sample containing live NIH-3T3 fibroblast cells to demonstrate the capability of the technique to perform high-throughput in vitro cell imaging.

Fig. 1.

System diagram for hybrid AO OCM. FC: 50-50 Fiber Coupler, PC: Polarization Controller, CL: Collimating Lens, M: Mirror, DM: Deformable Mirror, RP: Right-angle Prism, GMx and GMy: galvanometer mirror along x and y directions, OBJ: Objective Lens, S: Sample. All other unlabeled lenses are telescope pairs used for pupil conjugation.

The deformable mirror was used to physically adjust the astigmatism level and the corresponding separation distance between line foci. If a single axial beam position was inadequate to acquire an OCM volume with desired depth coverage, an additional amount of defocus was applied to the deformable mirror to shift the nominal focus (the plane of least confusion in the case of the astigmatic beam), to acquire multiple data sets with the plane of least confusion at different depths. The number of focus shifts is influenced by sample properties. In the following experiments for hyAO-OCM, one nominal focus position was adequate for imaging the phantom and grape samples over a 900 μm depth range. However, low scattering contrast necessitated the use of three nominal focus positions for imaging fibroblast cell dynamics across a 1 mm depth range. In post-processing, the resolution penalty of defocus and the intentionally applied astigmatism were compensated with CAO. In addition to the recovery of spatially invariant focal-plane resolution, this also resulted in an improvement of SNR associated with the restoration of constructive interference via CAO.

3.2 Different illumination approaches and comparison of imaging throughput

Gaussian and astigmatic beams have different peak intensities when imaging with a fixed illumination power. In cell imaging, peak illumination intensity must be limited in order to avoid thermal damage in the sample [40–42]. Therefore, a high-throughput imaging system must not exhibit a peak illumination intensity which exceeds a given maximum allowable value. For this study, we wished to compare the throughput of OCM imaging with Gaussian versus astigmatic beams under such a maximum allowable peak intensity constraint. Ideally, the two beam types should be compared when imaging with a constant reference arm signal and with equal peak illumination intensities between the two cases. However, this ideal comparison was not feasible with a fixed laser power and double-pass imaging configuration using only a single fiber-based coupler. Therefore, we adopted alternative illumination schemes to perform quantification of imaging throughput when using either beam type. We will refer to three illumination schemes in this paper: equal peak intensity illumination (EPII, ideal case), equivalent signal illumination (ESI), and equal power illumination (EPI), and they are summarized in Table 1 .

Table 1. Summary of different illumination approaches used for comparing Gaussian and astigmatic beams in the simulation and experiments.

		Incident power onto the sample	$I_{\text{ill,max}}$	$I_{\text{rec,max}}$
Equal peak intensity (EPII)	Gaussian beam	P0/α (α−1 laser power reduction)	$\propto P_0$	$\propto \alpha P_0$
	Astigmatic beam	P0		$\propto P_0$
Inter-mediate	Gaussian beam	P0/α (attenuated by α)	$\propto P_0$	$\propto P_0$(attenuated by α)
	Astigmatic beam	P0	$\propto P_0$	$\propto P_0$
Equivalent signal (ESI)	Gaussian beam	$P_0/\sqrt{\alpha }$(attenuated by α1/2)	$\propto \sqrt{\alpha }{P}_0$	$\propto \alpha P_0$(attenuated by α1/2)
	Astigmatic beam	P0	$\propto P_0$	$\propto P_0$
Equalpower (EPI)	Gaussian beam	P0	$\propto \alpha P_0$	$\propto {\alpha }^2{P}_0$
	Astigmatic beam		$\propto P_0$	$\propto P_0$

An EPII scheme compares system performance when the maximum peak illumination intensity using a Gaussian or astigmatic beam is kept constant. This is the ideal scheme under which we would like to compare the throughput of both beam types. Since an astigmatic beam has lower peak intensity than a Gaussian beam of the same power, EPII is achieved when using an astigmatic beam with higher incident power, such that its maximum peak intensity matches that of a Gaussian beam with lower power (i.e. the maximum peak illumination intensities $I_{\text{ill,max}}=\underset{z}{\max }\left\{I_{\text{ill}}(z)\right\}$ of both beam types match). In this scheme, both beams exhibit their best-case signal strength under a given maximum illumination intensity constraint, such as may be encountered in live cell imaging settings.

However, comparison with EPII was not practical with our imaging system. In a double-pass imaging configuration, this scheme requires the laser power to be altered. Ideally, we would increase the laser power to enable the optical intensity at the astigmatic beam line foci to be equal to the Gaussian beam case (and also attenuate the reference arm power to be equal to the Gaussian beam case). However, our OCT system was setup to perform standard Gaussian-beam imaging while operating our laser near its maximum output power. Therefore, an alternative ESI scheme was utilized as a substitute for conducting comparisons in a resolution phantom.

In this ESI scheme, the Gaussian beam power was attenuated with an ND filter, so that the maximum peak reconstructed intensities $I_{\text{rec,max}}=\underset{z}{\max }\left\{I_{\text{rec}}(z)\right\}$ of the Gaussian and astigmatic beams had the same ratio as in the ideal EPII case. As a result, the detected OCT images from this scheme can be used to infer the relative performance of the two beams in the ideal EPII case. In order to find the correct ND filter attenuation, an intermediate step was taken to equalize $I_{\text{rec,max}}$ at the Gaussian focal plane compared to either of the astigmatic line foci planes. We then determined the required attenuation value (linear scale) as the square root of the power attenuation from this intermediate step. Further explanation can be found in the following paragraphs and Table 1. In this way, although ESI uses a different Gaussian beam power compared to the ideal EPII scheme, the detected signal from the two schemes will still have the same ratio of$I_{\text{rec,max}}$, without changing the power of the laser source.

The drawback of inserting an ND filter into the sample arm is that, in a double-pass imaging configuration, the ND filter also attenuates the scattered light collected from the sample. This causes the SNR to drop, making signals from deep within a cellular sample fall below the OCT system noise floor. Therefore, illumination with the same incident power (EPI) was also used to simplify the comparison in the grape sample. However, it should be noted that under this scheme, the peak astigmatic beam intensity is lower than the Gaussian. In the live cell imaging experiment, the safety threshold is limited by peak intensity [40–42], so the astigmatic beam will perform below its potential capabilities during comparisons with this illumination scheme.

After utilizing these illumination schemes, imaging throughput was quantified via the SBP-T [5, 47]. For example, the cell imaging from hyAO covers a 1 mm³ FOV with 2 μm resolution in 3 minutes, giving a SBP-T of 5 mega-voxels per second. To determine the spatial coverage, we also define usable depth range as the depth range over which the transverse resolution is no worse than twice the Gaussian beam focal plane resolution, and an OCT SNR is at least 10 dB above the depth-dependent noise floor.

Detailed explanations for these schemes are shown in the following paragraphs, and summarized in Table 1.

Note that the astigmatic beam behaves identically in all three cases. It has an illumination power of $P_0$, yielding $I_{\text{ill,max}}\propto P_0$ and $I_{\text{rec,max}}\propto P_0$. Under the EPI scheme, $I_{\text{ill,max}}$ from a Gaussian beam is$\alpha$times greater than from an astigmatic beam of equal power, assuming $\alpha =\max \left({\left|g_{\text{gauss}}\right|}^2\right)/\max \left({\left|g_{\text{ast}}\right|}^2\right)$, where $g_{\text{gauss}}$ and $g_{\text{ast}}$ are the optical field distributions of the Gaussian and astigmatic beams, respectively. Given these relations, we may now describe the effects of each illumination scheme on a Gaussian beam.

For EPII, an incident Gaussian beam with illumination power $P_0/\alpha$ yields $I_{\text{ill,max}}\propto \max \left({\left|g_{\text{gauss}}\right|}^2\right)(P_0/\alpha )\propto \alpha \cdot (P_0/\alpha )=P_0$, and on the detection side provides $I_{\text{rec,max}}\propto \max \left({\left|g_{\text{gauss}}^2\right|}^2\right)(P_0/\alpha )\propto {\alpha }^2\cdot (P_0/\alpha )=\alpha P_0$ .

In order to determine the required ND filter value for achieving ESI, we performed an intermediate step. An ND filter was used to attenuate the sample arm beam power by $\alpha$ twice (once during illumination, and once during collection). An input illumination power of $P_0$ thus yields $I_{\text{ill,max}}\propto \alpha \cdot (P_0/\alpha )=P_0$ and $I_{\text{rec,max}}\propto {\alpha }^2\cdot [(P_0/\alpha )/\alpha ]=P_0$. This step gives the same$I_{\text{rec,max}}$at detection between the two types of beam, and provides an experimental means to measure $\alpha$, which is required to achieve the ESI scheme.

Once the linear-scale attenuation $\alpha$ was measured, we changed the ND filter to attenuate the power by $\sqrt{\alpha }$, which gives $I_{\text{rec,max}}\propto \alpha P_0$. Even though $I_{\text{ill,max}}$ differ between the Gaussian and astigmatic cases, this ESI scheme generates $I_{\text{rec,max}}$ equivalent to what would occur in the ideal EPII case.

For EPI, an input power of $P_0$ yields $I_{\text{ill,max}}\propto \alpha P_0$, and $I_{\text{rec,max}}\propto {\alpha }^2{P}_0$ for a Gaussian beam.

3.3 Sample preparation

The resolution phantom was made with 0.01% w/w TiO₂ particles inside a silicone medium. The silicone medium consisted of 1:10:100 w/w/w of RTVb, RTVa (Momentive, RTV615) and silicone oil, respectively.

Samples for imaging cellular dynamics consisted of NIH-3T3 fibroblasts embedded within a 3D Matrigel substrate. Fibroblasts were maintained in tissue culture flasks with media consisting of Dulbecco’s Modified Eagle Medium (Life Technologies) supplemented with 10% bovine calf serum (Life Technologies) and 1% penicillin-streptomycin (Life Technologies). To prepare samples, the cells were trypsinized, centrifuged, and re-suspended in chilled (4°C) culture media. This suspension was mixed with Matrigel (Corning) to achieve a final Matrigel concentration of 70%. The final cell concentration was 6.9 × 10⁵ cells/mL. The Matrigel-media-cell mixture was deposited in 100 µL aliquots on glass-bottomed petri dishes. Samples were placed in an incubator for 15 minutes to solidify before being covered in liquid culture media. Samples were maintained in an incubator for 3 days prior to imaging.

4. Results

4.1 Theoretical simulation

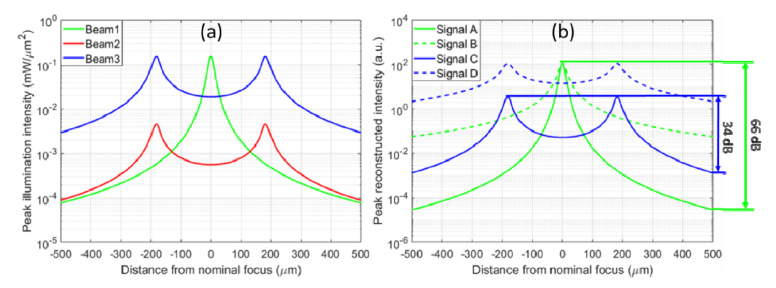
Beam intensity simulations in free space and the resulting OCT reconstructed intensities are shown in Fig. 2. The incident power was set to 0.7 mW for the Gaussian beam, and 23 mW for the astigmatic beam to achieve EPII. The aberration-free focal spot size was 2 μm (FWHM), and astigmatism had a RMS magnitude of 3 μm at the pupil plane. Following a CAO reconstruction for aberration removal, the astigmatic beam obtains an overall SNR enhancement across depth.

Fig. 2.

Simulation results showing the depth-dependent incident beam intensity and reconstructed OCT signals for a Gaussian versus astigmatic beam. (a) Depth-dependent illumination profile obtained with the following beam types. Beam1: Gaussian beam illumination. Beam 2: Astigmatic beam with EPI. Beam 3: Astigmatic beam with EPII. (b) Reconstruction of depth-dependent collection profile with CAO. Signal A: Depth-dependent OCM signal from Beam 1. Signal B: CAO reconstruction of Signal A. Signal C: Depth-dependent OCM signal from Beam 3. Signal D: CAO reconstruction of Signal C. The dynamic range occupied by Gaussian and astigmatic beam is labelled on the right side.

Besides, in order to collect signal over a 1 mm depth range, imaging with a Gaussian beam requires a 30 dB higher dynamic range across depth, compared to the astigmatic beam. Since scaling the space-domain signal corresponds to an equivalent scaling of spectral-domain fringe amplitude in SD-OCM, the reduction in dynamic range requirement for the line scan camera (which digitizes the fringes in the spectral domain) is the same as in the space domain. This additional benefit of 30 dB reduction in the dynamic range provided by hyAO was not experimentally demonstrated in this paper (since our Ti:Sapph laser was operated at a fixed (maximum) power level), but can have advantages in high throughput imaging as explained more in Section 5. From these simulation results, CAO-OCM with an astigmatic beam exhibits stronger signal collection across depth and has a lower requirement in camera dynamic range, compared to Gaussian beam illumination.

4.2 Performance comparison with a resolution phantom

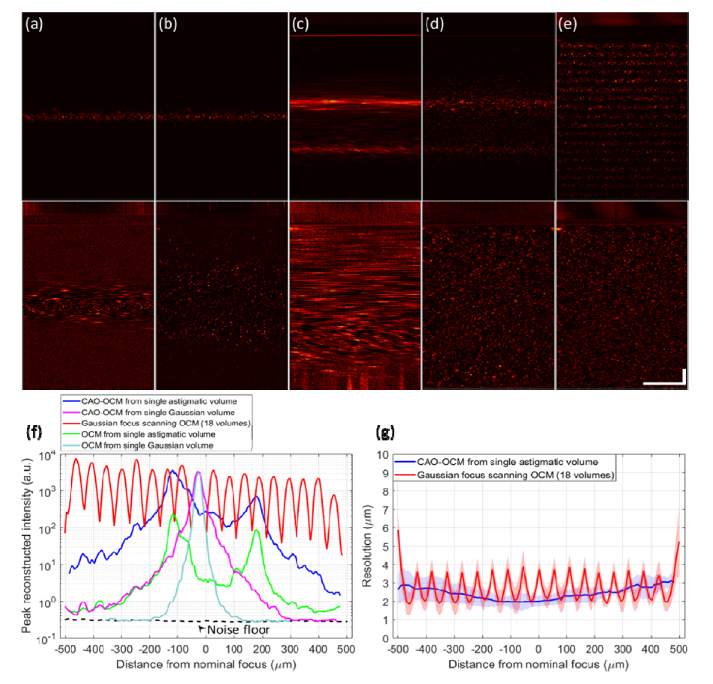
The comparison shown in Fig. 3 characterizes the depth-dependent PSF of standard OCM, the proposed hyAO technique, and focus scanning OCM using the ESI scheme. Since only a single hyAO acquisition is used in this case, hyAO reduces to CAO-OCM with an astigmatic beam. This comparison aims to quantify the SBP-T across different acquisition approaches for a given peak illumination intensity limit used for cellular imaging studies. The transverse FOV is 250μm × 250μm to capture the entire PSF across depth. The focus scanning OCM image was fused from volumes acquired at 18 focus depths, with 50 μm separation per step. The volume fusion process is analogous to the method used in Gabor-domain OCM [48]. Peak signal intensity was measured as the maximum of the magnitude-squared OCT signal across depth. Low signal regions outside the confocal gate from the multiple focus-scanned volumes were fused to estimate the effective depth-dependent noise floor. Such image-based noise floor measurement incorporates the sample dependent noises (multiple scattering, autocorrelation, resampling, aliasing, etc.), compared to using a reference spectrum to determine the noise floor (which does not capture these effects). The resolution was measured as the FWHM size of the sub-resolution TiO₂ scattering particles.

Fig. 3.

Performance characterization of Gaussian versus astigmatic illumination beams in a resolution phantom, using ESI. (a-e) Comparison of cross-sectional energy distribution across depth, from maximum intensity projection of a 250μm slice. The bottom row is the depth-normalized version of the top row (method explained in Sect. 4.2), with (a) OCM with Gaussian beam, (b) CAO-OCM with Gaussian beam, (c) OCM with astigmatic beam, (d) CAO-OCM with astigmatic beam, and (e) focus scanning OCM fused from 18 volumes. Scale bars indicate 100 μm for all images. (f) Quantitative measurement of peak reconstructed OCT signal intensity. (g) FWHM resolution for hyAO and focus scanning OCM. Color-filled regions indicate ± one standard deviation. In (f) and (g), the depth axis matches the portion of the cross sectional images that are below the sample surface.

As shown in Fig. 3, a broader depth coverage is observed for astigmatic imaging, and the relative behavior agrees with the simulations in Fig. 2. Requiring SNR >10 dB as usable signal, a single hyAO acquisition is able to cover a usable depth range that would require 18 focus scanning type acquisitions to obtain, thus reducing the imaging time for the entire volume by more than a factor of 10. Note that the last 120 μm depth of the volume was truncated from the window due to the dispersion artifacts from the conjugate image. Further depth coverage can be achieved by removing dispersion in the optical system. Moreover, if we normalize the intensity across depth, we can visualize more information in the hyAO acquisition than before normalization. This depth normalization approximates the noise floor and peak signal at each independent depth as the 30^th and 95^th percentiles, respectively. All intermediate values between these thresholds are linearly mapped to range from 0 to 1. Therefore, based on quantification of throughput via the SBP-T [5, 47], we get greater than 10 × improvement in throughput using the hyAO approach.

4.3 Application to a static biological sample

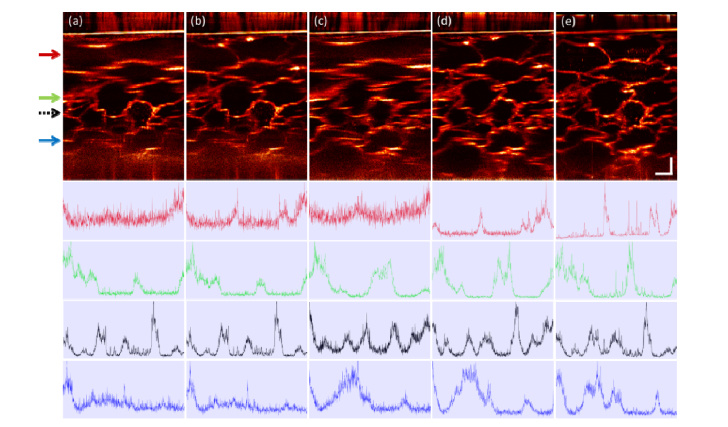
As a qualitative example of hyAO application in a biological environment exhibiting lower internal contrast than a TiO₂ phantom, we compare images from a grape with both hyAO (reducing to CAO-OCM with astigmatic illumination) and focus scanning OCM with EPI. The transverse FOV is 600μm × 200μm to capture the entire PSF across depth. The Gaussian control image was obtained by acquisition and fusion of focus scanning OCM with 18 focus positions. Even though the hyAO illumination has a lower peak intensity, it still offers a comparable signal and resolution with the conventional Gaussian focus scanning OCM. This can be seen in Fig. 4, where the cross-sectional images are compared and their corresponding SNR can be qualitatively visualized through the normalized intensity profiles. Therefore, we have demonstrated that a single hyAO volume can provide comparable performance to focus-scanning OCM with >10 volumes in a relatively low-scattering biological medium. In addition, since peak intensity will be the limiting factor rather than power in live imaging settings, SNR for hyAO is expected to be even better when using EPII or ESI, as demonstrated in the phantom results from Fig. 3.

Fig. 4.

Comparison of cross sectional energy distribution across depth in grape imaging, from maximum intensity projection of a 10 μm slice, in EPI. (a) OCM with Gaussian beam, (b) CAO-OCM with Gaussian beam, (c) OCM with astigmatic beam, (d) CAO-OCM with astigmatic beam, (e) Focus scanning OCM fused from 18 volumes. The line plots indicate the normalized intensity profile in the image at four depths, labelled by arrows with corresponding color, with black dashed arrow representing the focal plane position for the standard Gaussian acquisition. All images are depth-normalized with the same method as in the phantom results in Fig. 3. Scale bars indicate 100 μm for all images. A gamma correction with γ = 0.7 was applied to all images.

4.4 Large-volume imaging of cellular dynamics

Based upon the previous validation (Sect. 4.1-4.3), the hyAO approach is good at rapid volumetric imaging compared to focus scanning OCM under resolution priority mode, an essential characteristic for capturing fast cellular dynamics. In this experiment, we acquired a 3D time-lapse movie showing dynamics of fibroblast cells over a 5-hour duration. In order to maximize the signal collection over a 1 mm depth range, we used the deformable mirror to shift the nominal focus of the astigmatic beam across 3 depth positions (330 μm spacing) inside the sample. The number of shifted focus positions was determined from the depth coverage of each hyAO volume and the speed of desired cellular behaviors. For a fixed temporal resolution, we shifted the focal depth to as many positions as possible in order to maximize photon collection. The volumes with different focus locations were fused together with a trapezoidal window as described in [48]. The A-scan rate of the system was 50 kHz, and the 1mm × 1mm transverse FOV was spanned by 1500 × 1500 A-scans, giving a speed of 45 seconds per volume. Since a temporal resolution of 3 minutes is desired, fusion of 3 volumes per time point is allowed. After the fast dynamics are captured in the first hour, temporal resolution is reduced to 10 minutes for the remainder of the time-lapse acquisition (in order to conserve disk space).

As shown in the cellular dynamics visualizations, we are able to observe cell behavior in high resolution with large volumetric coverage and long duration under the hyAO approach. In Fig. 5 and Supplementary Visualization 1 ^{(17.9MB, mp4)} , biological processes including minute-scale intercellular interactions and hour-scale cell migration were captured in 3D across time. In Fig. 6 and Supplementary Visualization 2 ^{(18.2MB, mp4)} , filopodial extension dynamics and cell migration can be observed more clearly as an en face maximum intensity projection. The high-throughput imaging capability of hyAO enables the imaging of cellular dynamics over a wide range of spatiotemporal scales throughout the 1 mm³ volume, achieving a SBP-T up to 5 mega-voxels per second.

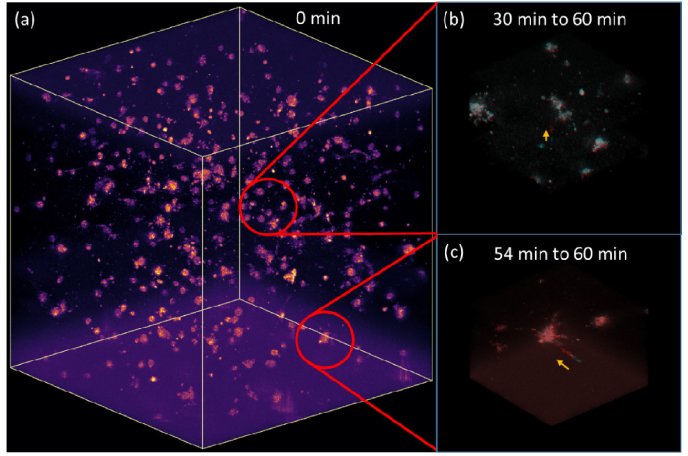
Fig. 5.

Volumetric visualization of fibroblast cell dynamics. (a) the entire volume with 1 mm × 1mm × 1mm FOV, extracted from Supplementary Visualization 1 ^{(17.9MB, mp4)} . (b) cell exhibits upward motion in a 30 min duration, (c) cell exhibits rapid sideways motion in a 6 min duration. Both (b) and (c) cover a 0.25mm × 0.25mm × 0.25mm volume, with the initial time point indicated by the cyan channel and final time point by the red channel.

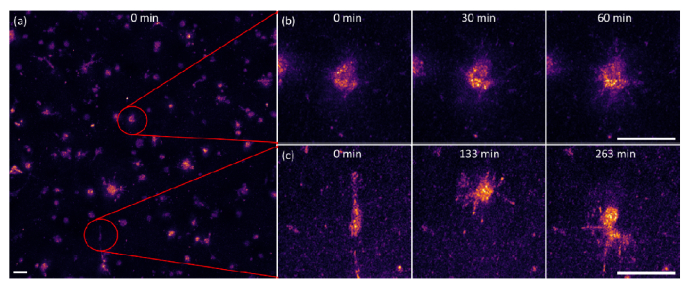
Fig. 6.

En face maximum intensity projection (400 μm slices) of fibroblast cell dynamics. (a) the entire 1mm × 1mm FOV, extracted from Supplementary Visualization 2 ^{(18.2MB, mp4)} . (b) cell extending filopodia across a 1 hour duration, (c) cell undergoing migration over a 263 minute period. Scale bar represents 50 μm for all groups.

5. Discussion

This paper presents a hybrid approach that leverages the advantages of physical beam manipulation and computational image formation. This approach is capable of acquiring millimeter-scale 3D cellular dynamics at minute-scale sampling rates. In this section, detailed issues in the theory and experiments are discussed below.

We note that the usable depth range obtained during the imaging of cellular dynamics was significantly lower than what we obtained in the TiO₂ phantom data. This is mainly due to the lower backscattering from the cell-Matrigel interface compared to the TiO₂-silicone interface. We measured a ~10 dB drop in overall SNR in the cell data set, and as a result this reduced the usable depth range by 300-400 μm. To overcome this signal reduction, focus shifting was applied via the DM to acquire volumes at three separate nominal focus positions. This demonstrates the SBP-T that can be achieved with hyAO is limited by the backscattering properties of the sample. Even though focus shifting was utilized in our hyAO in vitro cell imaging experiment, the acquisition time could still be reduced by a factor of 8-10 in hyAO-OCM compared to standard focus scanning OCM. In more turbid media, such as tissue, multiple scattering can have a large impact on the performance and benefit of hyAO because CAO only enables reconstruction of the singly scattered signals. Future work is needed to investigate the performance of hyAO in highly scattering tissues. However, within the context of imaging in vitro cellular dynamics in relatively sparse samples where multiple scattering is not significant, we have shown that hyAO can be an effective method to enhance volumetric throughput.

Astigmatic beam illumination spreads out a high-intensity Gaussian focal spot across depth, mitigating photo-thermal damage and reducing the dynamic range requirement of the camera. The former advantage can be useful in cell imaging where laser power is a concern for sample damage. The latter dynamic range advantage can benefit applications requiring large depth coverage with single-shot volumetric SD-OCM. However, this advantage was not fully realized in this paper since, for spectral-domain detection with a line scan camera, the DC background spectrum occupies a portion of the dynamic range. We estimate the interference fringes are confined to span 1/4 of the camera dynamic range, leaving the effective number of bits (ENOB) 2 bits less than the specified bit depth of the camera. Such a reduction of dynamic range by ${\text{20log}}_{\text{10}}{2}^2=12\text{dB,}$will further limit the usable depth range achievable with CAO-OCM (provided the signal is above the system noise floor). As shown in the simulation results in Fig. 2, astigmatic beam can reconstruct volumes in CAO with lower dynamic range than Gaussian beam. Therefore, astigmatic illumination can alleviate the effect of the ENOB reduction, besides the advantage of a more equalized signal collection across depth. Note that for a swept-source OCM (SS-OCM) system, this bit-depth reduction associated with SD-OCM detection is not present because the spectral background can largely be filtered out, allowing the full bit depth of the digitizer to span the interference fringes [49]. Nevertheless, the reduction in the dynamic range requirement offered from hyAO is still beneficial to SS-OCM for applications requiring large depth coverage.

From the biological perspective, hyAO-OCM may be used to help study cellular behavior over a large range of spatiotemporal scales, a key aspect in the investigation of collective cell behaviors. One area of research that could benefit from our hyAO approach is traction force microscopy (TFM). TFM has contributed to various studies of collective cell mechanobiology in both 2D and 3D settings [50–54], with expanded application likely in the future. Traction force optical coherence microscopy (TF-OCM) has demonstrated its application in tracking single-cell-induced 3D displacement fields [38], and has additional potential for time-lapse quantitative imaging of 3D cell traction forces. Current TF-OCM has already utilized CAO to extend the DOF [38]. The high volumetric throughput afforded by hyAO could enable TF-OCM to image 3D traction force dynamics in a larger-volume multi-cellular system.

In our implementation of hyAO, a few factors have limited the performance of our system. One major constraint is the amount of available laser power to be directed into the sample arm. Imaging throughput is ultimately limited by safety considerations, which limits the sample light exposure. Assuming any optical damage induced by an astigmatic beam is comparable to that of a Gaussian beam (with an equivalent peak intensity), a further increase in incident power is possible but not achieved in our setup. This enhancement in throughput can be accomplished via a more powerful laser to deliver greater incident power and/or a free space setup to reduce losses associated with coupling the free-space Ti:Sapph laser into fiber. However, the CAO-OCM results (Fig. 4) still demonstrate a partial advantage in depth coverage when using an astigmatic beam under the condition of equal illumination power.

Another factor that limits the volumetric update rate is the A-scan acquisition rate. The experimental setup in this study offered up to a 50 kHz A-scan rate, but with improvements to the data acquisition pipeline, an A-scan rate of up to 130 kHz is possible with our current line scan camera, leading to an increase in volumetric throughput 2.6 times faster than our current level. This higher A-scan rate can support the acquisition of volumes comparable to Fig. 5, but with higher temporal sampling of ~1 minute.

From the perspective of optimizing the absolute volumetric throughput, SS-OCM with MHz swept-source lasers [55–57] offers an acquisition speed tremendously faster than the confocal-type SD-OCM. If hyAO-OCM is implemented with a MHz-SS-OCM source, we still expect a significant improvement in volumetric throughput compared to standard OCM with Gaussian beam illumination. Thus, this integration can further improve the SBP-T of our current cellular-resolution studies by another order of magnitude. Also, we note that there are other OCM techniques demonstrating a large throughput, including line field [58, 59], full field [30, 36], and Bessel beam [14–22] illumination. Line-field and full-field OCM parallelizes the scanning beam for a faster acquisition, but these techniques are more vulnerable to cross-talk and multiple scattering than point-scanning methods [26–28]. Note that full-field OCM with spatially incoherent illumination reduces cross talk and is less sensitive to the deleterious effects of aberrations [60, 61]. However, this technique exhibits reduced sensitivity and is not as amenable to motion correction or post-processing techniques used by the other variations of OCM [28]. In a confocal acquisition scheme, extended focus OCM (xf-OCM) with Bessel beam illumination and Gaussian beam collection optics, and hyAO with astigmatic double-pass optics, can both support volumetric imaging with an extended depth coverage. At cellular resolution (< 3 μm), xf-OCM can achieve a greater depth coverage than a standard Gaussian beam [14–22] (as large as 800 μm in a resolution phantom [20]), while astigmatic hyAO shows >10 × enhancement in usable depth range and can achieve 1 mm depth coverage in a resolution phantom. However, both methods have their own drawbacks. Xf-OCM has undesirable sidelobes in its PSF that degrade the image quality, and hyAO-OCM has a stricter requirement on phase stability. In practice, both schemes can find their own suitable applications. For example, hyAO-OCM can be a good option for volumetric imaging of sparse biological cells, whereas xf-OCM is excellent at angiography [62] and optical coherence elastography [19]. In addition, there exists computational reconstruction in xf-OCM (xISAM) for DOF extension [63]. This is another example showing the synergistic utilization of hardware and computational approaches. Since they are based on similar principles, we expect that xISAM and the astigmatic hyAO would have comparable performances and similar applications. However, hyAO with an astigmatic beam can have a simpler implementation by adding a cylindrical lens, while xISAM needs to separate the illumination and collection path, and its PSF still contains sidelobes.

The function of the deformable mirror in our hyAO approach could in principle be performed with other alternatives. For example, a cylindrical lens in conjunction with a dynamical focus scanning setup would be able to produce a comparable PSF with common-place off-the-shelf hardware. The advantages of using a deformable mirror in a hyAO configuration include the ability to precisely and rapidly adjust the level of astigmatism (line foci spacing and/or orientation) in different samples, and to incorporate a wider range of aberrations in the future, including hardware AO correction of sample-induced aberrations [64–67]. In general, hyAO can incorporate real-time hardware AO aberration correction, or post-acquisition CAO [68]. This additional synergy provided by hyAO, where the ‘work’ of image formation is split in new ways between hardware and computation, merits further study in highly scattering media and could find future applications to volumetric OCM imaging in mouse brain, or in vitro tumor spheroid imaging in engineered cell cultures.

6. Conclusion

We have demonstrated hyAO as a novel approach for high-throughput OCM imaging, and achieved a 1mm × 1mm × 1mm field-of-view, 2 μm resolution volumetric imaging of cellular dynamics with 3-minute temporal resolution. Compared to Gaussian beam OCM, hyAO equalizes the illumination intensity across depth, and enhances the depth coverage and throughput by combining CAO with astigmatic illumination and rapid focus shifting. The large SBP-T provided by hyAO-OCM enables high-resolution imaging of cellular population dynamics over millimeter-scale volumes, with temporal scales spanning minutes-to-hours. This capability is potentially beneficial for various biomedical applications such as the study of collective cell behaviors in vitro, as well as time-lapse in vivo imaging studies of dynamic biological processes.

Funding

Cornell Discovery and Innovation Research Seed award (Adie); National Institutes of Health (NIBIB-R21EB022927, Adie; 1R21EY028389, Adie).

Disclosures

The authors declare that there are no conflicts of interest related to this article.