Suppression of photo-oxidation of organic chromophores by strong coupling to plasmonic nanoantennas

Strong coupling of organic chromophores to plasmonic nanoparticles was shown to markedly improve molecular photostability.

Abstract

Intermixed light-matter quasi-particles—polaritons—have unique optical properties owing to their compositional nature. These intriguing hybrid states have been extensively studied over the past decades in a wide range of realizations aiming at both basic science and emerging applications. However, recently, it has been demonstrated that not only optical but also material-related properties, such as chemical reactivity and charge transport, may be significantly altered in the strong coupling regime of light-matter interactions. We show that a nanoscale system, composed of a plasmonic nanoprism strongly coupled to excitons in a J-aggregated form of organic chromophores, experiences modified excited-state dynamics and, therefore, modified photochemical reactivity. Our experimental results reveal that photobleaching, one of the most fundamental photochemical reactions, can be effectively controlled and suppressed by the degree of plasmon-exciton coupling and detuning. In particular, we observe a 100-fold stabilization of organic dyes for the red-detuned nanoparticles. Our findings contribute to understanding of photochemical properties in the strong coupling regime and may find important implications for the performance and improved stability of optical devices incorporating organic dyes.

INTRODUCTION

Strong light-matter interactions in nanoscale objects have recently attracted considerable research attention. These interactions manifest themselves in emergence of new hybridized eigenstates of a strongly coupled system evidenced by coherent Rabi oscillations between the matter and the photonic subsystems (1, 2). This behavior is markedly different from weak light-matter coupling, which results in the conventional spontaneous emission process accelerated by the cavity through the Purcell effect. Strong coupling between optical and plasmonic cavity resonances and matter excitations has been recently realized in systems involving molecular (3–14) and semiconductor (15, 16) excitons, as well as vibrational transitions (17–19). Vasa et al. (20) have demonstrated strongly coupled systems to enable ultrafast optical switching and single-photon nonlinearities.

It is important to point out that in the strong coupling regime the photonic and excitonic components of the system cannot be treated as separate entities, as they form new polaritonic eigenstates having both light and matter characteristics. For this reason, not only electromagnetic but also material (microscopic) properties of a strongly coupled system can be modified. In particular, it has been shown recently that chemical reactivity (19, 21–23) and charge and exciton transport (24–26) can be modified under strong coupling conditions. Strong coupling has been demonstrated to tune the work function (27), as well as to control the Stokes shifts of hybridized molecules (28). Galego et al. (22) have theoretically described an increased stability in the strong coupling regime for a photoisomerization reaction. Herrera and Spano (23) showed that strong coupling can modify molecular reaction pathways via polaron decoupling. These observations open up new possibilities to use strong coupling for controlling chemical reactivity and other material-related properties. However, only a small number of chemical reactions in the strong coupling regime have been experimentally studied to date.

Here, we demonstrate that strong coupling between organic molecules and plasmonic nanocavities can significantly alter one of the most important classes of photochemical processes—the photobleaching reaction. Photobleaching limits applications of organic electronic devices, such as organic solar cells, electroluminescent devices, organic dye lasers, and molecular fluorescence, as it leads to irreversible photodegradation of organic molecules (29, 30). Therefore, it is important to seek ways to control and prevent photobleaching. Here, we observe that upon coupling of J-aggregates to a plasmonic nanocavity, the photobleaching rate can be markedly suppressed (up to 100-fold), which is evidenced by recording the evolution of the scattering response of the coupled systems over time. Moreover, our study reveals complex relations between the photobleaching rate and the plasmon-exciton detuning as well as the excitation conditions. These results point to a beneficial impact of strong coupling on photochemical properties and pave the way toward molecular optical nanostructures with increased photostability.

RESULTS

Concept

It is generally accepted that the mechanism of photobleaching involves photodynamic interactions between the excited triplet state of dye molecules and atmospheric triplet oxygen (³O₂). For fluorophores with a high quantum yield of intersystem crossing (ISC), a significant population transfer from the excited singlet state (S₁) to the long-lived triplet state (T₁) can occur (see Fig. 1C). Because the lifetime of the triplet state is long, the excited molecules have a higher chance to interact with environmental oxygen and thus undergo photobleaching. The interaction between molecular oxygen and triplet excitons occurs via energy or charge transfer mechanisms and leads to generation of several reactive oxygen species, such as singlet oxygen (¹O₂) and hydrogen peroxide (H₂O₂), which are highly unstable and therefore can chemically damage fluorophores and their surroundings (31, 32). When such a system interacts with a resonant cavity (see Fig. 1A), the relaxation pathways and therefore photobleaching may be drastically affected. Such interaction can be weak (that is, Purcell regime) or strong (that is, vacuum Rabi splitting). In both cases, the photochemical reaction can be modified, but when the system enters the strong coupling regime, the relaxation pathways of the hybrid can be modified to a very large degree. This is because strong coupling, as opposed to the weak counterpart, is a coherent effect that manifests itself through a buildup of collective states encompassing all participating molecules.

Fig. 1. Sketch and schematic diagram of photobleaching reaction in a strongly coupled system.

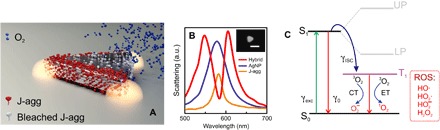
(A) Graphic sketch of the system under study. J-agg, J-aggregates. (B) Dark-field (DF) scattering spectra of the strongly coupled hybrid system (red), scattering spectrum from uncoupled J-aggregates (orange), and uncoupled individual plasmonic nanoprism (blue). The inset shows a SEM image of the corresponding nanoprism. Scale bar, 100 nm. a.u., arbitrary units. (C) Schematic diagram of a photobleaching reaction in the uncoupled molecular system and its possible modification in the strong coupling regime (light gray lines indicate upper and lower polaritonic states). ROS, reactive oxygen species; CT, charge transfer; ET, energy transfer.

Considerable progress on suppression of photobleaching has been achieved recently using inert ambient as well as oxygen scavenger reagents (33). Furthermore, plasmonic nanoantennas were shown to improve the photostability of organic dyes by quenching long-lived triplet states (34–36). Other important examples are known from surface-enhanced Raman and enhanced fluorescence experiments, where stability of single-molecule trajectories can often exceed several thousands of seconds, while the same molecules in free space typically photobleach in a matter of seconds. It is believed that enhanced spontaneous emission in the form of efficient competition with ISC is responsible for these observations (37–39). However, these experiments were performed in the weak coupling regime, whereas the potential of strong coupling for the purpose of photostability has not been explored.

Here, we suppress the photobleaching reaction in the strong coupling regime. Because polaritonic states are coherent mixtures of plasmons and excitons, their corresponding lifetime is extremely short (~10 fs) due to their partial plasmonic character. The typical ISC rate is many orders of magnitude slower (10⁻⁸ to 10⁻³ s) than that (40), and therefore, the polaritonic states are not able to populate the triplet efficiently. Thus, involvement of polaritonic states must be highly useful for suppressing the photobleaching reaction. The goal of this study is to elucidate the quantitative aspects of this problem.

System under study

We focus our study on the suppression of photobleaching of organic J-aggregate molecules strongly coupled to a plasmonic nanoantenna. A silver nanoprism surrounded by J-aggregates of 5,5′,6,6′-tetrachloro-di-(4-sulfobutyl) benzimidazolocarbocyanine (TDBC) organic dye molecules forms the hybrid system (see Fig. 1A and Materials and Methods for further details). The optical response of an individual hybrid system, bare plasmonic nanoprism, and uncoupled J-aggregates are furthermore characterized by their scattering spectra in Fig. 1B, together with a scanning electron microscopy (SEM) image of the corresponding individual silver nanoprism. The hybrid system shows Rabi splitting of the order of ~200 meV, which exceeds not only polariton but also the uncoupled plasmon resonance width. We have investigated several tens of individual hybrid systems, which showed reproducible Rabi splitting exceeding the plasmon linewidth. These observations unambiguously prove that the system under study is in the strong coupling regime, in agreement with our recent observations on qualitatively identical nanostructures (13, 14). We also note that mixing plasmonic and excited singlet states of J-aggregates forms the hybrid polaritonic states in our system. At the same time, the triplet state of J-aggregates has an extremely weak oscillator strength (41, 42), and so strong coupling between the plasmonic field and the triplet is not feasible.

Effect of Rabi splitting on photobleaching

To investigate the crucial impact of Rabi splitting on suppression of photobleaching in the hybrid system, we studied time-resolved photodegradation of several strongly coupled systems (see Fig. 2). To visualize photobleaching rates of the system, we recorded DF scattering spectra of individual hybrid systems as a function of exposure time upon irradiation with a spectrally flat broadband light beam at a constant intensity (see Materials and Methods). Figure 2 (A to E) shows the bleaching time-resolved DF scattering spectra as false-color plots for five individual hybrid structures, with similar plasmon-exciton detuning but different initial Rabi splitting values of 209, 200, 188, 170, and 154 meV, respectively. Electron microscopy data show that all the hybrid systems are composed of an individual silver nanoprism and J-aggregated molecules around (see insets in Fig. 2, A to E). Moreover, the size of the particles and their plasmon-exciton detuning are very similar, implying that the absorption cross sections are approximately the same. Figure S1 shows more examples. Figure 2 (A to E) shows the DF scattering spectra of the hybrid systems at 0, 240, and 480 s of bleaching time as blue, dark brown, and black lines, respectively. It is clear that Rabi splitting decreases with time for all samples, indicating degradation of organic molecules under optical excitation. For comparison, Fig. 2F shows much quicker degradation of scattering from uncoupled J-aggregates under the same experimental conditions.

Fig. 2. Photobleaching as a function of Rabi splitting.

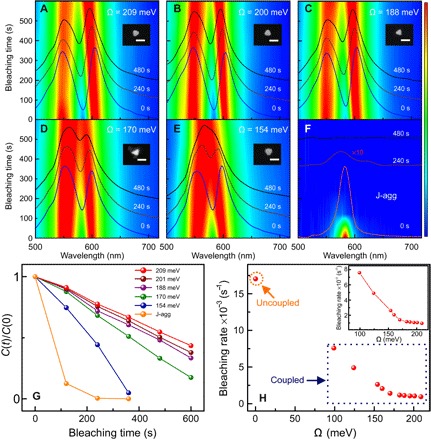
(A to E) Evolution of the DF scattering spectra of strongly coupled hybrid systems with different initial Rabi splitting energies of 209, 200, 188, 170, and 154 meV, respectively. Insets show the corresponding SEM images of the plasmonic silver nanoprisms. Scale bars, 100 nm. (F) Uncoupled J-aggregates as a function of irradiation/bleaching time under broadband excitation. (G) Photobleaching kinetics for the strongly coupled hybrid systems with different Rabi splitting energies of 209 meV (red), 200 meV (brown), 188 meV (violet), 170 meV (green), and 154 meV (blue), compared to the uncoupled bare J aggregates (orange). (H) Photobleaching rates for hybrid systems versus uncoupled J-aggregates as a function of Rabi splitting energy. The inset shows a zoomed-in plot of the photobleaching rates for the coupled systems.

The data presented in Fig. 2 (A to E) allow extracting the relative change in the concentration of active organic molecules C(t)/C(0) over time. To do that, we recall that the value of Rabi splitting at zero detuning is given by ${\mathrm{\Omega }}_{\mathrm{R}}=2\sqrt{({\mathrm{\omega }}_{+}-{\mathrm{\omega }}_0)({\mathrm{\omega }}_0-{\mathrm{\omega }}_{-})}$ with ω_± being the frequencies of the upper polariton (UP) and lower polariton (LP) that can be inferred directly from the recorded DF spectra and ω₀ being the exciton resonance energy. Then, we estimate the relative change in the concentration of active molecules as C(t)/C(0) ≈ [Ω_R(t)/Ω_R(0)]², since ${\mathrm{\Omega }}_{\mathrm{R}}~\sqrt{\mathit{N}/\mathit{V}}=\sqrt{\mathit{C}}$, where N is the number of active molecules residing within the mode volume V.

The obtained curves show one of the central results of our work: Photobleaching of the hybrid systems occurs at a much slower rate than that of the uncoupled systems (see Fig. 2G). Moreover, the hybrid system becomes more stable against photobleaching as the Rabi splitting is increased. Even after 600 s of continuous irradiation, the hybrid systems with the three largest Rabi splittings still show two hybridized modes in the DF scattering, indicating that many molecules still actively participate in the coupling process. In contrast to that, uncoupled J-aggregates are rapidly bleached, showing ~88% decrease in the intensity of DF scattering spectra within the first 120 s. The photobleaching dynamics is almost linear in the cases of hybrid particles, while it is exponential in the uncoupled J-aggregate case on the time intervals studied. This observation alone implies that photobleaching of hybrid systems is considerably slowed down. We will come back to this point later, when discussing the kinetics.

Results presented in Fig. 2 (A to F) confirm that strong coupling influences the photochemical processes, likely by alternating triplet state population and relaxation pathways. We stress that the particle sizes used were similar and thus their extinction cross sections and mode volumes are comparable (see SEM insets in Fig. 2). We performed the experiments under exactly the same illumination conditions. Therefore, variation of particle extinction and/or experimental conditions cannot explain these results.

For a further quantitative comparison of the hybrid systems, we analyze the photobleaching kinetics curves in Fig. 2G. We extract the bleaching rates as the slope of the kinetic curves assuming quasi-linear dynamics of the active-molecules concentration (see Fig. 2H). The extracted bleaching rates for the hybrid samples depend on the Rabi splitting, such that stronger coupled systems are more stable, while weaker coupled ones are less stable (see inset in Fig. 2H). The values of Rabi splitting in these experiments are in the range of 100 to 220 meV. By extrapolating the bleaching rate from 0- to 100-meV range of Rabi splitting values, we expect that the weakly coupled systems would be less stable than even the most unstable strongly coupled ones (see Fig. 2H). To interpret this behavior, we rely on several theoretical works where the transition dynamics between polaritonic and incoherent states were studied (23, 43–46). Within the strong coupling picture, a sequence of processes involving excitation of the UP state, its subsequent relaxation to the ground state and to the incoherent states, and decay of the incoherent states into the lower energetic states, which include both LP and triplet states, determines the photobleaching rate. We come back to this point in more detail, when discussing the photobleaching mechanism.

Concluding this section, we note that Fig. 2 evidently demonstrates suppression of the photobleaching rate due to strong coupling. Moreover, for larger Rabi splitting, this suppression is enhanced. These experiments have been performed with zero detuning hybrids and under a broadband optical excitation (350 to 715 nm). To shed more light on this effect, we have performed several additional experiments, where detuning between plasmons and excitons is varied and narrowband optical excitations across the visible range were used.

Effect of detuning on photobleaching

To get a deeper insight into the effect of different parameters on the photobleaching of the hybrid systems, we have investigated the influence of plasmon-exciton detuning on photobleaching dynamics. In Fig. 3, we show false-color scattering plots for several individual hybrid nanostructures with different plasmon-exciton detunings. We show DF scattering spectra in color plots using logarithmic scale to visualize both polariton peaks. Figure S2 shows more examples of the hybrid systems with different plasmon-exciton detunings. Figure 3 (A and B) shows the examples of low and high blue-detuned hybrid systems. For comparison, Fig. 3 (C and D) shows examples of low and high red-detuned hybrid systems. We observe that strongly coupled systems exhibiting red detuning of the plasmon resonance with respect to the exciton resonance experience much slower photobleaching than the blue detuned systems (see Fig. 3, E and F).

Fig. 3. Photobleaching as a function of plasmon-exciton detuning.

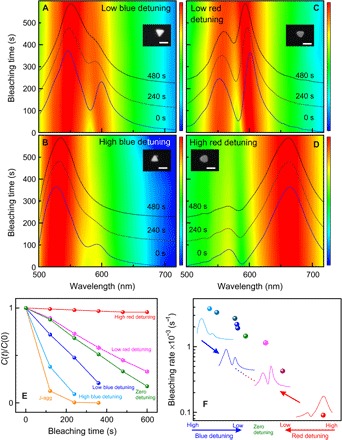
(A to D) Evolution of the DF scattering spectra of strongly coupled hybrid systems with time under broadband excitation for different blue (A and B) and red (C and D) detunings of plasmon resonance with respect to the exciton resonance of J-aggregates. Insets show corresponding SEM images of the individual silver nanoprisms. Scale bars, 100 nm. (E) Photobleaching kinetic curves and (F) the corresponding bleaching rates of the strongly coupled hybrid systems with different plasmon-exciton detunings. Note the logarithmic scale of the vertical axis in (F).

As can be seen in Fig. 3 (A and B), the weakly blue-detuned particle exhibits slower photobleaching than the strongly blue-detuned hybrid system. The LP peak in the strongly blue-detuned hybrid system disappears within the first 240 s of light irradiation, while the weakly blue-detuned one still shows Rabi splitting. Apparently, the strongly blue-detuned hybrid system exhibits a largely increased photobleaching rate; nonetheless, it is still slower than photobleaching of uncoupled molecules (see Fig. 3, E and F).

In contrast to the blue detuning cases, photobleaching occurs at a much slower rate in the red-detuned hybrid systems, as shown in Fig. 3 (C and D). In particular, the strongly red-detuned structure exhibits Rabi splitting even after 480 s of continuous irradiation. As the red detuning is increased, the photobleaching in the strongly coupled systems gets suppressed even more significantly, as shown in Fig. 3 (E and F). In particular, for strongly red-detuned Ag nanoprisms, the photobleaching rate is suppressed more than 100-fold in comparison to uncoupled J-aggregates. This is one of the central observations of our study. In the following sections, we focus on the explanation of these observations.

Effect of optical excitation

To evaluate contributions of each polaritonic state, namely, UP and LP, in the photobleaching, we performed experiments using narrowband variable wavelength optical excitations (see Fig. 4). We chose and excited three different hybrid systems with comparable initial Rabi splitting and plasmon-exciton detuning using narrowband light sources centered at 532, 568, and 640 nm aiming at selective excitation of the UP, uncoupled molecules, and the LP states, respectively (see Materials and Methods for further details). Figure 4 (A to C) presents the evolution of DF spectra for each system. Figure 4D shows the relative change in concentration of active molecules over time, which is extracted from the DF spectra for all three excitation wavelengths. In addition, we show the bleaching kinetics of uncoupled J-aggregates under the same illumination conditions for comparison. Last, we extract the bleaching rates for three excitation wavelengths from Fig. 4D and plot them against the initial DF and calculated absorption spectra of the coupled system (see Fig. 4E).

Fig. 4. Photobleaching as a function of excitation wavelength.

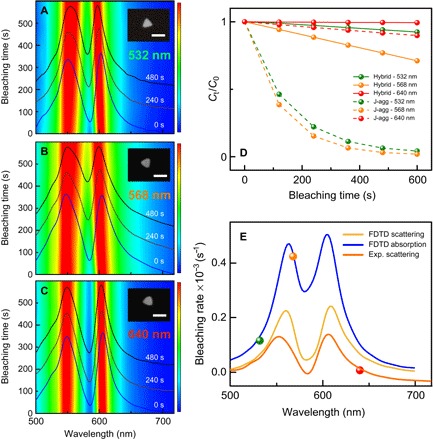
(A to C) DF scattering spectra of three identical hybrid systems at three different excitation resonances of 532, 568, and 640 nm, respectively. The insets in (A) to (C) show corresponding SEM images of the individual silver nanoprisms. Scale bar, 100 nm. (D) Photobleaching kinetics for the three nearly identical hybrid systems excited using 532-nm (green solid line), 568-nm (orange solid line), and 640-nm (red solid line) light sources. The corresponding dashed lines show the data for uncoupled J-aggregates. (E) Photobleaching rates of strongly coupled hybrid systems as a function of excitation wavelength for zero-detuned hybrids. The orange solid line shows a representative example of experimental DF spectrum for the coupled system. Calculated absorption and scattering spectra are also shown by the blue and yellow lines, respectively. FDTD, finite-difference time-domain; Exp., experimental scattering.

We observe that pumping the LP with 640-nm excitation causes the slowest bleaching (red solid line in Fig. 4D), whereas pumping at the wavelength of 568 nm causes the fastest bleaching of the coupled system. The reason for the fastest bleaching in this case is likely a better spectral overlap with the UP state absorption, which, in turn, populates the triplet state via long-lived intermediates. However, the strongly coupled system pumped with 568-nm excitation (orange solid line) still exhibits much slower photobleaching compared to uncoupled J-aggregates (orange dashed line) under the same experimental conditions, as shown in Fig. 4D. When the UP is excited by the 532-nm source (green solid line), the resulting photobleaching rate is slower than that at 568-nm excitation but faster than in the case of direct excitation of LP at 640 nm. This is because selective excitation of the LP cannot contribute directly to photobleaching due to its very short lifetime (~10 fs), whereas the UP does contribute to photobleaching due to inclusion of incoherent states into its relaxation pathway. Overall, strongly coupled systems exhibit slower photobleaching compared to uncoupled J-aggregates under the same experimental conditions for all studied excitations (see Fig. 4D).

In Fig. 4E, we observe that resonant excitation of the UP is more harmful for the coupled system than nonresonant high energy excitation (likely because of a larger extinction cross section of the former). We thus argue that the only efficient pathway for photobleaching of the coupled system is the resonant excitation of the UP state and its subsequent decay into the incoherent states. With this in mind, we now turn to the in-depth discussion of the photobleaching mechanism of the strongly coupled systems.

Photobleaching mechanism

The photobleaching process can formally be described by a set of differential rate equations (see section S4). Figure 5A schematically shows the relaxation pathways of the coupled system. We indicate the ground state, UP, and LP as G, UP, and LP, respectively. The Rabi splitting separates the UP and LP states. Moreover, the incoherent states (or exciton reservoir) are denoted as D. These states arise as a result of structural and orientation disorder of emitters in organic microcavities (43). The wavy lines joining the UP to D states and D states to the LP illustrate nonradiative energy transfer processes, which are described by the rates γ_UP→D and γ_D→LP, correspondingly. The full lines from the UP and LP to the G represent the direct decay of polaritonic states—γ_UP and γ_LP, correspondingly. All these states are singlet in terms of electron spin. In addition, there is an exciton triplet state, whose lifetime is relatively long. This state is populated via ISC at a rate γ_ISC and can decay via a combination of radiative and nonradiative processes with an effective rate of γ_T. It can also decay because of interaction with triplet oxygen from the environment, described by the second-order chemical reaction process—k[³O₂]. In principle, the LP may be found below the triplet state and thus activate reverse ISC, as well as enhance radiative triplet relaxation via the Purcell effect. However, in typical organic dyes, the energy gap between singlet and triplet is 0.5 to 1 eV (47, 48), which is significantly above the Rabi splitting in the current study. Therefore, these mechanisms are unlikely to affect the dynamics in the present study. We note that the triplet state in J-aggregates is nearly unaffected by dipole-dipole interactions because of the weak oscillator strength of the triplet state. Therefore, the J-aggregate triplet appears at the same energy as the triplet of the monomer band—0.5 to 1 eV below the monomer singlet state (41, 42). We also note that in Fig. 5A, we deliberately ignored the vibronic fine structure of all involved states. We performed this because TDBC J-aggregates are known to have a small Stokes shift.

Fig. 5. Scheme of photobleaching mechanism.

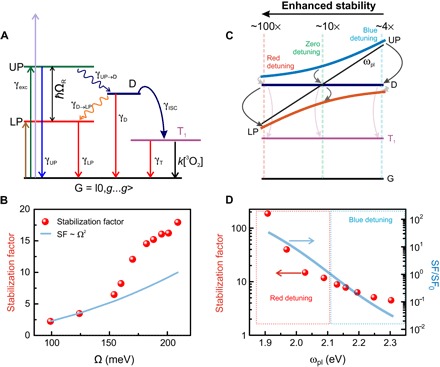
(A) Schematic representation of a strongly coupled system and transitions between various states. (B) SF as a function of Rabi splitting. Circles represent experimental results and are normalized by the bleaching rate of uncoupled J-aggregates. The solid blue line represents the theoretical dependence of the SF on the Rabi splitting. (C) Schematic representation of the photobleaching process as a function of plasmon-exciton detuning. The visibility/transparency of arrows represents high/low probability of the corresponding transition, demonstrating that highly red-detuned particles are much more stable than highly blue-detuned ones. (D) SF as a function of plasmon resonance frequency. Circles represent experimental results and are normalized by the bleaching rate of uncoupled J-aggregates. The solid blue line represents the relative SF (normalized by the SF at zero detuning) calculated using Eq. 4 at Ω_R = 200 meV. Note the logarithmic scale and different vertical axes for the experimental and theoretical data.

Under a quasi–steady-state operation, the equilibrium population of all intermediates, including the T, D, LP, and UP states, is reached. Thus, we may write γ_ISCn_D = (k[³O₂] + γ_T)n_T, where n_D and n_T denote equilibrium population of incoherent and triplet states, correspondingly. Within this model, the photobleaching process can be described by a gradual degradation of the strongly coupled molecules in accordance with $\frac{\mathit{d}\mathit{N}}{\mathit{d}\mathit{t}}=-{\mathrm{\gamma }}_{\text{bl}}\mathit{N}$, where N is the number of molecules participating in the coupling process and γ_bl is the photobleaching rate, which, in turn, reads (detailed derivation is provided in section S4)

$${\mathrm{\gamma }}_{\text{bl}}={\mathrm{\gamma }}_{\text{exc}}{\mathrm{\varphi }}_{\text{bl}}$$ (1)

where ${\mathrm{\varphi }}_{\text{bl}}=\left(\frac{{\mathrm{\gamma }}_{\text{UP}\to \mathrm{D}}}{{\mathrm{\gamma }}_{\text{UP}}+{\mathrm{\gamma }}_{\text{UP}\to \mathrm{D}}}\right)\left(\frac{{\mathrm{\gamma }}_{\text{ISC}}}{{\mathrm{\gamma }}_{\mathrm{D}\to \text{LP}}+{\mathrm{\gamma }}_{\mathrm{D}}+{\mathrm{\gamma }}_{\text{ISC}}}\right)\left(\frac{\mathit{k}[{}^3{\mathrm{O}}_2]}{\mathit{k}[{}^3{\mathrm{O}}_2]+{\mathrm{\gamma }}_{\mathrm{T}}}\right)$ << 1 is the quantum yield of photobleaching and γ_exc is the excitation rate of the UP (as shown in the previous section, the resonant excitation of UP is the most harmful process for the molecules). We notice that the bleaching rate does not depend on γ_LP as long as the LP relaxation is fast. Assuming that γ_bl does not depend on time, we obtain a simple exponent for the total number of coupled molecules: $\mathit{N}(\mathit{t})=\mathit{N}(0){\mathit{e}}^{-{\mathrm{\gamma }}_{\text{bl}}\mathit{t}}$. On the time scale of our experiments, the bleaching exhibits a quasi-linear behavior; thus, the solution can be approximated by $\frac{\mathit{N}(\mathit{t})}{\mathit{N}(0)}\approx 1-{\mathrm{\gamma }}_{\text{bl}}\mathit{t}$, in agreement with experimental observations in Figs. 2 to 4. The bleaching rate γ_bl can thus be directly assessed from experimental curves. In practice, γ_bl depends on the coupling strength, which, in turn, changes with time. Therefore, the slope of the photochemical reaction should increase with time, as observed (see Fig. 2G). In our analysis we have, however, ignored this dependence for the sake of simplicity.

For the case of uncoupled J-aggregates in the absence of any nanocavity, the bleaching dynamics is similarly given by $\frac{\mathit{d}{\mathit{N}}_0}{\mathit{d}\mathit{t}}=-{\mathrm{\gamma }}_{\text{bl}}^0{\mathit{N}}_0$, where N₀ is the number of molecules in the uncoupled J-aggregate and ${\mathrm{\gamma }}_{\text{bl}}^0={\mathrm{\gamma }}_{\text{exc}}^0{\mathrm{\varphi }}_{\text{bl}}^0$. Here, ${\mathrm{\varphi }}_{\text{bl}}^0=\left(\frac{{\mathrm{\gamma }}_{\text{ISC}}}{{\mathrm{\gamma }}_0+{\mathrm{\gamma }}_{\text{ISC}}}\right)\left(\frac{\mathit{k}[{}^3{\mathrm{O}}_2]}{\mathit{k}[{}^3{\mathrm{O}}_2]+{\mathrm{\gamma }}_{\mathrm{T}}^0}\right)$ is the quantum yield of photobleaching and ${\mathrm{\gamma }}_{\text{exc}}^0$ is the excitation rate for the uncoupled J-aggregates, correspondingly. The solution thus reads: ${\mathit{N}}_0(\mathit{t})={\mathit{N}}_0(0){\mathit{e}}^{-{\mathrm{\gamma }}_{\text{bl}}^0\mathit{t}}$. On the time scale of the experiment, this equation is exponential, which, in turn, implies that ${\mathrm{\gamma }}_{\text{bl}}^0\gg {\mathrm{\gamma }}_{\text{bl}}$. This is in agreement with experimental observations in Figs. 2 to 4. The bleaching rate ${\mathrm{\gamma }}_{\text{bl}}^0$ can thus be directly assessed from experimental exponential curves representing uncoupled J-aggregates.

To quantify the modification of the photobleaching dynamics, we introduce the stabilization factor (SF) as the ratio between the bleaching rates of strongly coupled and uncoupled molecules

$$\text{SF} =\frac{{\mathrm{\gamma }}_{\text{bl}}^0}{{\mathrm{\gamma }}_{\text{bl}}}=\frac{{\mathrm{\gamma }}_{\text{exc}}^0}{{\mathrm{\gamma }}_{\text{exc}}}\frac{{\mathrm{\varphi }}_{\text{bl}}^0}{{\mathrm{\varphi }}_{\text{bl}}}$$ (2)

Since the triplet state is energetically far away from any other state, we assume that the term $\left(\frac{\mathit{k}[{}^3{\mathrm{O}}_2]}{\mathit{k}[{}^3{\mathrm{O}}_2]+{\mathrm{\gamma }}_{\mathrm{T}}}\right)$ is not significantly altered by coupling and thus ${\mathrm{\gamma }}_{\mathrm{T}}^0\approx {\mathrm{\gamma }}_{\mathrm{T}}$. We also assume that the ISC rate γ_ISC is the same for uncoupled molecules and for the strongly coupled systems. Therefore, from Eqs. 1 and 2, it follows that, to increase the molecular stability, that is, to increase the SF, γ_UP and γ_D→LP must be maximized, whereas γ_UP→D and γ_exc (excitation of the UP state) should be minimized.

It is possible to measure SF experimentally (see Fig. 5, B and D). The data show that SF varies between ~200 for the strongly red-detuned particles and ~4 for strongly blue-detuned particles. For the zero-detuned particles, SF varies between ~2 and ~18 depending on the Rabi splitting. The exact values of the SF depend on the parameters of the coupled system, which we evaluate further.

To explain our experimental observations, we now turn to the relaxation dynamics and estimate the quantum yield of photobleaching in strong and weak coupling cases—ϕ_bl and ${\mathrm{\varphi }}_{\text{bl}}^0$. Dynamics of strongly coupled organic microcavities has been extensively studied theoretically by Agranovich et al. (43) and Litinskaya et al. (44) using Fermi’s golden rule approach, by Michetti and La Rocca (45) using numerical methods, and more recently by Herrera and Spano (23, 46) using the Holstein-Tavis-Cummings approach. From these works, it follows that the direct contribution of the UP and LP to photobleaching is likely negligible since their lifetime is extremely short (~10 fs), a few orders of magnitude shorter than the typical time scale of ISC γ_ISC⁻¹ of organic molecules, which lies in the nanosecond to millisecond range depending on the strength of spin-orbit coupling (40). The UP, however, can rapidly decay (~50 fs) into incoherent molecular states via a phonon-mediated process (43). There, the population can reside for a much longer time (~10 ps); thus, the impact of these states on the photo-oxidation must be crucial. The transition rate from UP to D is given by (43)

$${\mathrm{\gamma }}_{\text{UP}\to \mathrm{D}}\propto {\mathit{g}}^2{\mathrm{\omega }}_{\text{vib}}^2\frac{{({\mathrm{\Omega }}_{\mathrm{R}}/2)}^2}{{({\mathrm{\omega }}_{\text{UP}}-{\mathrm{\omega }}_0)}^2+{({\mathrm{\Omega }}_{\mathrm{R}}/2)}^2}{\mathit{e}}^{-{({\mathrm{\omega }}_{\text{UP}}-({\mathrm{\omega }}_0+{\mathrm{\omega }}_{\text{vib}}))}^2/{\mathrm{\gamma }}_0^2}$$ (3)

where g² is a dimensionless Huang-Rhys factor, which characterizes the strength of vibronic coupling, ω_vib is the phonon energy, ω₀ is exciton resonance frequency, and γ₀ is the total linewidth of the exciton resonance. The transition probability is maximized when ω_UP = ω₀ + ω_vib and thus depends on the density of available phonon modes in J-aggregates. Raman spectroscopy shows that the frequencies of molecular vibrations span over a broad range from 30 to ~430 meV (49, 50). At zero detuning, Eq. 3 reduces to ${\mathrm{\gamma }}_{\text{UP}\to \mathrm{D}}~{\mathit{g}}^2{\mathrm{\omega }}_{\text{vib}}^2{\mathit{e}}^{-{({\mathrm{\Omega }}_{\mathrm{R}}/2-{\mathrm{\omega }}_{\text{vib}})}^2/{\mathrm{\gamma }}_0^2}$, which shows that the optimum is achieved when $\frac{{\mathrm{\Omega }}_{\mathrm{R}}}{2}={\mathrm{\omega }}_{\text{vib}}$. In practice, this implies that there will always be a phonon matching the corresponding transition, even for rather large Rabi splittings. The rate of this transition is proportional to ${\mathit{g}}^2{\mathrm{\omega }}_{\text{vib}}^2$, and thus, it increases for high-frequency phonons provided the vibronic coupling is not negligible.

The degree of strong coupling also determines the subsequent relaxation of incoherent states. In particular, the nonradiative transition from relatively long-lived incoherent states to the short-lived LP via emission of an intramolecular phonon is accelerated because of an increased Rabi splitting. In this case, the energy is transferred from the excited incoherent state into the LP state with a single quantum of vibrational energy localized at the same molecule as the original electronic excitation. The matrix element of the corresponding exciton-phonon Hamiltonian is proportional to gω_vib. Thus, the probability of such a transition is given by (44): ${\mathrm{\gamma }}_{\mathrm{D}\to \text{LP}}\propto \langle {|{\mathit{a}}_{\mathit{s}}|}^2\rangle {\mathit{g}}^2{\mathrm{\omega }}_{\text{vib}}^2$, where 〈|a_s|²〉 is the contribution of the sth molecule into the LP state (averaged over all molecules). Therefore, photobleaching can be suppressed by depletion of the incoherent states population into the LP, where fast relaxation occurs. This depletion is especially accelerated by high-frequency phonons (see Fig. 5C).

With this at hand, we can now evaluate how the exciton-plasmon detuning, Rabi splitting, and excitation wavelength affect the SF. Recalling Eqs. 1 and 2, γ_UP and γ_D→LP should be maximized, whereas γ_UP→D and γ_exc should be minimized. This is in line with our experimental observations. In particular, highly red-detuned particles are very stable because of efficient depopulation of the D states and relatively small γ_exc due to the reduced plasmonic component of the UP (Fig. 5D). The highly blue-detuned particles are, on the contrary, very unstable because of inefficient depopulation of D, efficient γ_UP→D, and relatively high γ_exc due to increased plasmonic component of the UP (Fig. 5D). Furthermore, the expression for SF can be simplified to yield $\text{SF}\propto \frac{{\mathrm{\gamma }}_{\text{UP}}}{{\mathrm{\gamma }}_{\text{exc}}}\frac{{\mathrm{\omega }}_{\text{vib}(\mathrm{D}\to \text{LP})}^2}{{\mathrm{\omega }}_{\text{vib}(\text{UP}\to \mathrm{D})}^2}$, assuming γ_UP ≫ γ_UP→D, γ_D→LP ≫ γ_ISC, and equality of Huang-Rhys factors for the involved phonons. Further, we note that the ratio γ_UP/γ_exc is rather insensitive to detuning as γ_UP and γ_exc work against each other. In this simple case, the ratio of the phonon energies responsible for UP to exciton reservoir and exciton reservoir to LP relaxation rates determines the stabilization. Since the phonon energies for these two transitions must be equal to the difference between ω_UP and ω₀ and to ω₀ and ω_LP, correspondingly, we arrive to the following simple expression

$$\text{SF}\propto \frac{{({\mathrm{\omega }}_0-{\mathrm{\omega }}_{\text{LP}})}^2}{{({\mathrm{\omega }}_{\text{UP}}-{\mathrm{\omega }}_0)}^2}$$ (4)

Figure 5D shows this result as a blue solid line for Ω_R = 200 meV. Considering the extreme simplifications made and the absence of any free parameters, the agreement with experiment is remarkable. We note that Eq. 4 holds only under the assumption of strong coupling and for the corresponding kinetic model (see Fig. 5A), as well as a number of additional simplifications mentioned above. Thus, Eq. 4 will fail whenever the system is tuned out of the strong coupling regime, which may happen, for instance, because of excessive plasmon-exciton detuning and/or insufficient coupling strength.

In case of zero detuning, the phonon energies for the UP → D and D → LP transitions are equal. Hence, the interplay of the UP excitation and decay rates determines the relative stability: $\text{SF}\propto \frac{{\mathrm{\gamma }}_{\text{UP}}}{{\mathrm{\gamma }}_{\text{exc}}}$. For larger Rabi splitting, this ratio increases, leading to formation of more stable hybrids. This is due to the coherent nature of polaritonic states, which implies that the relaxation rate of the UP depends on the number of involved excitons as ${\mathrm{\gamma }}_{\text{UP}}=\frac{{\mathrm{\gamma }}_{\text{pl}}+\mathit{N}{\mathrm{\gamma }}_0}{2}$, while, at the same time, the excitation is shared between N sites resulting in ${\mathrm{\gamma }}_{\text{exc}}\propto \frac{{\mathrm{\sigma }}_{\text{ext}}}{\mathit{N}}$ to the first approximation (see section S4). This, in turn, implies that for the case of zero detuning, SF ∝ Ω². In the experiment, we observe even faster growth of the SF with the Rabi splitting (see Fig. 5B). This may happen because the white light excitation used here can also populate the exciton reservoir nonresonantly. The subsequent decay into the LP is more efficient for higher Rabi splitting, making particles with large Rabi splitting more stable.

DISCUSSION

To conclude, we have demonstrated that strong coupling of organic chromophores to metallic nanostructures can significantly stabilize the former against photobleaching. This is achieved by inhibiting the population of the triplet state by modifying relaxation pathways in the strong coupling regime. In particular, involvement of coherent polaritonic states speeds up relaxation, which, by efficiently competing with ISC, inhibits it and thereby blocks photobleaching.

Stabilization against photobleaching in the presence of strongly enhanced electromagnetic fields may come as a surprise, as one could expect a reaction to speed up instead of slowing down. Plasmonic nanoparticles and their arrays have been long known to boost photochemical reactions (51–54). In this “surface-enhanced photochemistry” regime, the interaction with the antenna, ${\mathrm{\gamma }}_{\text{exc}}>{\mathrm{\gamma }}_{\text{exc}}^0$, increases the excitation rate of the molecule, while the quantum yield of the corresponding photochemical process remains weakly perturbed (ϕ ≈ ϕ⁰). In our experiments, although enhanced fields are present (${\mathrm{\gamma }}_{\text{exc}}>{\mathrm{\gamma }}_{\text{exc}}^0$), the quantum yield of photobleaching is significantly reduced (${\mathrm{\varphi }}_{\text{bl}}\ll {\mathrm{\varphi }}_{\text{bl}}^0$), because of involvement of the collective UP and LP states. This enables significant stabilization of the strongly coupled system.

In addition, when molecules reside very close to a metal surface, their electronic orbitals may mix with the orbitals of the metal, resulting in charge transfer processes and renormalization of highest occupied molecular orbital–lowest unoccupied molecular orbital (LUMO) gaps (55). These processes can play an important role in surface chemistry. In addition to that, hot electrons (and holes) can affect molecular stability and, in particular, damage adsorbed molecules by populating their LUMO states (56). While it is hard to completely rule out the hot-electron scenario, we notice that hot electrons should additionally destabilize the molecules. In our experiments, the coupled system is, on the contrary, significantly more stable than uncoupled J-aggregates. We thus argue that hot-electron effects are likely minor. This may be explained by a protective ligand layer that is present between Ag nanoprisms and J-aggregates and that may hinder direct charge transfer (see Materials and Methods). In addition, because of the relatively large size of Ag nanoprisms used in this study, hot electrons are likely to thermalize within the metallic particle before reaching the surface.

Here, the incoherent states play a major role, as they are the only long-lived intermediates capable of populating the triplet states. We note, however, that in a situation where no long-lived intermediates exist, the hybrid system in the strong coupling regime could become completely immune to photobleaching. This hypothesis could experimentally be verified in the single-molecule strong coupling case, where no incoherent states exist (57). We also note that, in our study, the triplet state lies far below the LP state, and thus, the coupling does not directly affect its dynamics. However, the coupling potentially can be made so strong that the triplet and LP states can be co-aligned. This will enhance γ_T via activation of a reverse ISC process from the triplet to the LP. While this is not the case here, it can, in principle, be used to further increase the stability of these samples. Similar ideas have been previously verified both experimentally and theoretically in the weak coupling regime (34–36).

More generally, our findings indicate that, in the strong coupling regime, the kinetics of reactions can be markedly modified in comparison to the corresponding uncoupled case. This, in turn, implies that, for an arbitrary chemical reaction at equilibrium, where only one of the involved substances is strongly coupled to the vacuum field of the cavity, the equilibrium will be affected in favor of stabilization of the strongly coupled product (21–23).

In summary, our findings confirm that strong light-matter interaction plays an important role in determining the material properties of coupled systems and may have far-reaching implications for the development of nanophotonic devices incorporating organic molecules. We note that similar stabilization mechanisms can be important for other classes of molecules, such as perovskites and/or improved organic electronic devices where triplet population is undesirable. We also anticipate that stabilization by strong coupling can improve the performance of various organic optoelectronic devices, such as solar cells, organic light-emitting diodes, and others.

MATERIALS AND METHODS

Materials

Silver nitrate (AgNO₃, 99.9999%), trisodium citrate dihydrate, potassium bromide (KBr), sodium borohydride (NaBH₄, 99%), and bis(p-sulfonatophenyl)phenylphosphine dehydrate dipotassium salt (BSPP) were purchased from Sigma-Aldrich at the highest purity grade available. 5,6-Dichloro-2-[[5,6-dichloro-1-ethyl-3-(4-sulfobutyl)-benzimidazol-2-ylidene]-propenyl]-1-ethyl-3-(4-sulfobutyl)-benzimidazolium hydroxide, inner salt, sodium salt (TDBC; purchased from FEW Chemicals) was used without further purification. Transmission electron microscope (TEM) grids were purchased from Ted Pella Inc. All glassware and stir bars were thoroughly precleaned and dried before use. Ultrapure distilled water (18 megohms·cm; Millipore) was used in all preparations.

Synthesis of silver nanoprisms

Silver nanoprisms (AgNPs) were synthesized according to the literature (58). Briefly, a 3- to 5-nm silver seed nanoparticle solution was prepared by adding 1 ml of 30 mM trisodium citrate and 0.5 ml of 20 mM AgNO₃ solutions to 95 ml of ice-cold ultrapure distilled water. The solution was kept bubbling with N₂ under vigorous stirring in an ice bath for an additional 60 min in the dark. Then, 1 ml of ice-cold 50 mM NaBH₄ was added into the growth solution at which point the color of the solution turned pale yellow. Subsequently, 100 μl of 50 mM NaBH₄ was added to the solution and repeated three more times with 2-min break in between. The ice-cold and freshly prepared mixture of 1 ml of 5 mM BSPP and 1 ml of 50 mM NaBH₄ was added dropwise into the growth solution for seed nanoparticles. The solution was kept for 5 hours in an ice bath under gentle stirring and completed with aging overnight in an ice bath. For the photo-induced growth of AgNPs, 10 ml of the aged seed solution with a pH of 9.5 was irradiated with a 532-nm continuous-wave (CW) laser. The reaction was allowed to proceed for 24 hours at which point the AgNPs were washed two times by centrifugation at 3000 relative centrifugal force (rcf) for 5 min, discarding the supernatant, and redispersed in aqueous solution containing 0.3 mM trisodium citrate.

Synthesis of the hybrid nanostructures

For the hybrid nanostructures consisting of self-assembled J-aggregates of TDBC dye molecules on the individual AgNPs, we followed a previously reported method with slight changes (10). The freshly synthesized AgNPs (1 ml) were capped by mixing with 1 ml of the aqueous solution containing 0.1 mM TDBC dye molecules and 1 mM KBr under gentle stirring for 15 min. The resulting colloidal solution was washed once by centrifugation (3000 rcf for 5 min), redispersed in distilled water, and stored at 4°C until use.

Optical spectroscopy

The sample was prepared by drop-casting the 3 μl of hybrid nanoparticle solution on a polylysine-functionalized TEM (200 mesh) grid (90 μm × 90 μm). After 2 min, the solution was removed with dust-free tissue and dried with gentle nitrogen flow. Using a transparent and conductive TEM grid allows for spectroscopic and morphological correlation. A bare J-aggregate sample was prepared from the solution containing 0.1 mM TDBC dye molecules and 1 mM KBr with the same procedure as for the hybrid nanoparticles on the TEM grid. DF scattering spectra were recorded using an inverted microscope [Nikon TE-2000E equipped with an oil immersion 100×/numerical aperture (NA) of 0.5 to 1.3 objective] with a hyperspectral imaging technique based on a liquid-crystal tunable filter (13). The morphology characterization of hybrid nanoparticles was analyzed using a scanning electron microscope (Ultra 55 FEG SEM).

Photobleaching experiment

Photobleaching experiments under flat-broadband illumination were conducted with an irradiance of ~15 W/cm⁻² at the sample using a laser-driven white light source (EQ-99FC, high-brightness, flat-broadband spectrum) with a visible filter (350 to 715 nm, Thorlabs) in normal atmospheric conditions at room temperature. DF scattering spectra were recorded before and after iteratively 2 min of continuous photobleaching. The relative change of the DF scattering spectra was used to estimate photobleaching rates of the samples over 10 min using a linear fitting.

We noted that photobleaching using narrow excitation in Fig. 4 was considerably slower than a broad range source in Figs. 2 and 3. This is because the integrated power of the broad range source was significantly higher. In this experiment, three different band-pass filters with central wavelengths of 532, 568, and 640 nm were used for the photobleaching experiment with different excitation resonances of 532, 568, and 640 nm, respectively. The photobleaching rates for the different excitation resonances were normalized by the total irradiance to make a fair comparison.

To evaluate the contribution of molecular oxygen to the photobleaching in organic dye molecules, we performed a control experiment in the vacuum chamber (see fig. S3). The photobleaching experiment was performed using a 532-nm CW laser excitation (~200 W/cm⁻²) in an optical cryostat vacuum chamber and a long working distance objective (20×; NA, 0.45; Nikon). DF scattering spectra of pristine J-aggregates on a silicon substrate, inside and outside an optical cryostat vacuum chamber, were recorded before and after continuous photobleaching. While J-aggregates in the presence of oxygen were rapidly photobleached, they were highly stable and showed nearly unaffected optical response inside the vacuum chamber. We thus concluded that atmospheric oxygen plays a crucial role in our photobleaching experiments.

Numerical calculations

Finite-difference time-domain calculations were used to compute scattering and absorption spectra of silver nanoprisms coupled to J-aggregates. The dimensions of simulated nanoprisms were tuned using SEM images as guidance to obtain a plasmon resonance overlapping with the J-aggregate absorption line as well as red- and blue-shifted nanoprisms. The nanoprisms for zero detuning were 75 nm in length (side) with a corner rounding of 9 nm and edge rounding of 3 nm. The thickness was 19 nm in this case. Red-shifted nanoparticles had their thickness reduced to 13 nm, which is supported by SEM images indicating similar sizes (to zero-detuned particles) with a different contrast due to being thinner. In the case of blue-shifted nanoprisms, the thickness was increased to 29 nm, and the side length was reduced to 70 nm. These geometrical parameters with permittivity of silver taken from (59) yielded, together with a Lorentzian permittivity for J-aggregate, scattering spectra consistent with experimental measurements. The J-aggregate was modeled in every case by a Lorentzian permittivity function with a background refractive index of 1.45, absorption line at 590 nm, reduced oscillator strength of 0.07, and linewidth of 50 meV. The thickness in each case was uniform and equal to 2 nm, which is consistent with a single monolayer of J-aggregate. The particles were placed on a glass substrate with n = 1.45.

The particles were excited by a plane wave in the total-field/scattered-field configuration, which is appropriate for these thin particles whose out-of-plane resonance excited in a DF configuration is significantly detuned from the transverse plasmon. Total scattering and absorption cross sections were computed by integrating the Poynting vector outside and inside the total-field/scattered-field source, respectively. To assure convergence, a fine mesh of 0.5 nm was used around the nanoparticle.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/7/eaas9552/DC1

Section S1. Evolution of the DF scattering spectra of strongly coupled hybrid systems with different initial Rabi splitting energies

Section S2. Evolution of the DF scattering spectra of strongly coupled hybrid systems with different detuning of plasmon resonance with respect to the exciton resonance

Section S3. Contribution of molecular oxygen for photobleaching

Section S4. Coupled system rate equations

Fig. S1. Evolution of the DF scattering spectra of strongly coupled hybrid systems with different initial Rabi splitting energies.

Fig. S2. Evolution of the DF scattering spectra of strongly coupled hybrid systems with different detuning of plasmon resonance with respect to the exciton resonance.

Fig. S3. Contribution of molecular oxygen for photobleaching.