Oscillatory Switches of Dorso-Ventral Polarity in Cells Confined between Two Surfaces

Abstract

To maneuver in a three-dimensional space, migrating cells need to accommodate to multiple surfaces. In particular, phagocytes have to explore their environment in the search for particles to be ingested. To examine how cells decide between competing surfaces, we exposed single cells of Dictyostelium to a defined three-dimensional space by confining them between two planar surfaces: those of a cover glass and of a wedged microcantilever. These cells form propagating waves of filamentous actin and PIP3 on their ventral substrate-attached surface. The dynamics of wave formation in the confined cells was explored using two-focus fluorescence imaging. When waves formed on one substrate, wave formation on the other substrate was efficiently suppressed. The propensity for wave formation switched between the opposing cell surfaces with periods of 2–5 min by one of two modes: 1) a rolling mode involving the slipping of a wave along the nonattached plasma membrane and 2) de novo initiation of waves on the previously blank cell surface. These data provide evidence for a cell-autonomous oscillator that switches dorso-ventral polarity in a cell simultaneously exposed to multiple substrate surfaces.

Introduction

When eukaryotic cells are cultivated on a planar glass surface, they migrate with their ventral surface adhering to the glass and their dorsal surface extending into the fluid space. However, in their natural habitat, cells have to cope with irregular three-dimensional environments, implying the switching of dorsal and ventral sides. This is true for leukocytes and other cells that migrate in heterogeneous tissues (1, 2) and also for cells that, like those of Dictyostelium, are crawling between soil particles. In particular, these phagocytes need to explore three-dimensional spaces in the search for particles to be attached and ingested.

Here, we address the question of how cells react to confinement between two parallel surfaces: do they simultaneously interact with both opposing substrate surfaces, or do they select one of their substrate-attached surfaces to act as a ventral and the other as a dorsal side? In the latter case, the dorso-ventral polarity of the cell may be stable or may alternate between the two substrate surfaces. To confine the highly motile Dictyostelium cells between two planar surfaces, we used wedged microcantilevers that were kept at defined distances parallel to the surface of a glass coverslip using an atomic force microscope (AFM) (3). As markers for the ventral cell surface, we imaged waves of actin and PIP3 (phosphatidylinositol-(3,4,5)-trisphosphate or, in Dictyostelium, actually plasmanylinositol-(3,4,5)P3 (4)). In these patterns, propagating actin waves circumscribe a membrane territory rich in PIP3 and separate this inner territory from PIP3-depleted external membrane areas, which are decorated with the PIP3-degrading PI3-phosphatase PTEN (5, 6, 7).

The actin waves are sites of force generation against the substrate surface, as evidenced by cells migrating on a perforated film (8). Under these conditions, the cells form protrusions penetrating the holes in the substrate, specifically at the sites of actin waves and within the inner territory.

We used axenically growing cells of the AX2 strain of Dictyostelium discoideum because of their high capacity to form waves. These cells are mutated in neurofibromin, a Ras-GAP (9). The deregulation of Ras results in enhanced macropinocytosis on the free cell surface (10) and in the induction of actin waves in contact with a planar substrate. For quantitative recording of the wave pattern by confocal microscopy, we applied GFP-PHcrac (11), a fluorescent label of inositol-(3,4,5)P3 and inositol-(3,4)P2 (12).

Applying the wedged-cantilever technique, we found that confined cells can form propagating waves on both the glass and cantilever surfaces. However, waves propagating on one surface efficiently excluded wave formation on the other. Most of the confined cells entered an oscillatory mode in which the wave-forming surfaces alternated at regular intervals. Thus, cells symmetrically stimulated by confinement between two parallel surfaces, respond by the asymmetric formation of actin waves, and they periodically switch between the competing surfaces.

Switching the surfaces of interaction with a substrate is supposed to be essential for a motile cell to cope with the fabric of surfaces in its natural habitat. We discuss how in a natural environment with irregularly arranged surfaces, frequent switching may provide a cell with the flexibility required in the search for particles to be phagocytosed and in the response to signal gradients. For instance, the movement toward bacteria that release chemoattractant may require a cell to repeatedly change substrate surfaces to maintain direction toward the source of attractant. Similarly, when cells are guided by haptotaxis, responding to a gradient of matrix-bound signaling molecules (13), surface switching may assist them to readjust their direction of crawling in a three-dimensional texture of surfaces.

Materials and Methods

Cell culture and strains

Transformants from the AX2-214 strain of D. discoideum expressing mRFPM-LimEΔ (14) in combination with superfolding GFP-PHcrac (15) were used for imaging. The double-transformants were cultivated at 21 ± 2°C in 10 mL of nutrient medium (16) containing 10 μg × mL⁻¹ of blasticidin (Invitrogen, Life Technologies, Grand Island, NY) and 10 μg × mL⁻¹ of G418 (Sigma-Aldrich, St. Louis, MO).

For experiments, the cells were harvested before monolayers became confluent by gently suspending them in the nutrient medium of the petri dish. 1 mL of cell suspension was pipetted into an HCl-cleaned cover glass bottom dish (FluoroDish, World Precision Instruments, Sarasota, FL). After settling, the cells were washed twice with 1 mL 17 mM K/Na-phosphate buffer (pH 6.0) and subjected to confinement by a wedged cantilever.

Wedged cantilever technique for cell confinement

An AFM setup (CellHesion 200; JPK Instruments AG, Berlin, Germany) was mounted on an inverted confocal microscope (Observer Z1, LSM 700; Carl Zeiss Microscopy, Jena, Germany) equipped with a 63×/1.3 NA LCI Plan-Neofluar water immersion objective and the Zeiss software Zen Black. Cantilevers, 350 mm long, with a nominal spring constant of 150 mN m⁻¹ (NSC12/tipless/No Al, MikroMasch; Innovative Solutions Bulgaria, Sofia, Bulgaria) were modified with polydimethylsilane (PDMS; Sylgard 184; Dow Corning, Auburn, MI) wedges (3). The tilt angle was corrected such that the plane of the PDMS surface paralleled the cover glass. The spring constant of wedged cantilevers was determined using the thermal noise method (17).

For confinement, cells in the cover glass bottom dishes were covered by a wedged microcantilever. In the vicinity of a single motile cell, the cantilever was lowered until the wedge came into contact with the glass surface. To confine the cell, the wedge was raised by 20 μm, positioned over the cell, and lowered at 1 μm × s⁻¹ until an upward force of 10 nN was measured. Because the height of the cells decreased upon initial confinement, thus reducing the upward force, the wedge was lowered in steps of 1 or 0.5 μm until the 10 nN upward force no longer decreased. This occurred mostly at cell heights between 3 and 5 μm. Care was taken to avoid blebbing of the cells, which would be induced by stronger compression (18).

z-Stacks of two or three images were obtained with the focal plane of the first image on the bottom of the cell, i.e., the glass surface, and the last plane on the top of the cell, i.e., the wedge surface. The distance between the two surfaces was deemed the height of the confined cell. When needed, the position of the image frame was shifted between time points to capture the entire motile cell within each frame.

For force measurements, the wedge height was maintained after initial confinement, and the force acting on the cantilever was continuously recorded while fluorescent images were acquired. The automatic change of focus required for two-focus imaging caused artificial force peaks. During data processing, these peaks were replaced by linear interpolation of the data acquired immediately before and after the incidence of focusing.

Data analysis

Images were processed and analyzed using the image processing package Fiji (http://Fiji.sc/Fiji) developed by Schindelin et al. (19) on the basis of ImageJ (https://imagej.nih.gov/ij). Fast Fourier transformations were calculated using the Fourier Tool of the Analysis ToolPak. Force recordings were processed in IGOR Pro (WaveMetrics, Portland, OR). Data were copied in a Microsoft Office Excel sheet and displayed in tables and figures.

Results

Wave dynamics in cells sandwiched between two surfaces

Single cells expressing two markers for wave patterns—GFP-PHcrac as a label for PIP3 and mRFP-LimEΔ as a label for filamentous actin—were confined between two parallel surfaces: that of a coverslip and of a wedged cantilever (Fig. 1, A and B). The height of confinement was adjusted such that the cell initially resisted confinement with a force of ∼10 nN. This usually corresponded to a glass-cantilever distance of 3–5 μm and was below the compression that caused the cells to bleb (18). The cells tolerated the confinement, rarely escaping from the cantilever and even moving back under the cantilever. We maintained cells in confinement for up to 3 h.

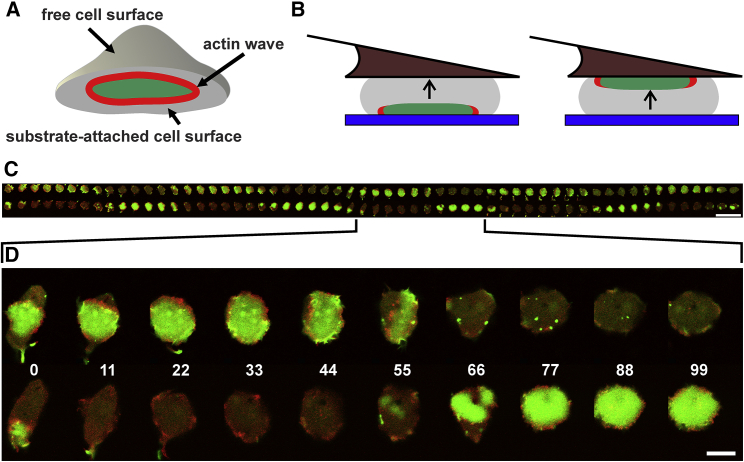
Figure 1.

Cell confinement and switching of wave formation between two substrate-attached cell surfaces. (A and B) Schemes of wave formation in a cell attached to a glass surface (A) and in a cell confined between a wedged cantilever (brown) and a glass surface (blue) (B) are shown. Actin is displayed in red, and PIP3 is displayed in green. A cell exposed to one substrate forms waves specifically on its substrate-attached membrane. A confined cell has the option of forming waves on both or either one of the two substrate surfaces. Arrows in (B) indicate the direction of force applied by the cell to the cantilever, which at the beginning of the experiments was adjusted to 10 nN. (C and D) Fluorescence images show PIP3/actin waves in a cell confined between a glass and a cantilever surface. The cell expressed mRFP-LimEΔ as a label for filamentous actin (red) and GFP-PHcrac as a label for PIP3 (green). The overview in (C) shows the temporal sequence of wave dynamics on the cantilever (top row) and on the glass surface (bottom row) at frame-to-frame intervals of 11 s. The indicated part of the sequence is zoomed in (D) to visualize the propagation and regression of actin waves and the enrichment of PIP3 in the territory circumscribed by an actin wave. Time is indicated in seconds. The entire sequence of cell 13 is also shown in Video S1. See also Table 1. Bars, 50 μm in (C) and 10 μm in (D).

Confocal fluorescence images of the two opposing substrate-attached membrane areas were acquired in tandem at intervals of 10–30 s. Under confinement, cells did form waves on each of the two planar surfaces. However, waves coexisted only rarely on both surfaces, as exemplified for one cell in Fig. 1, C and D and Video S1. Fig. 1 C shows this cell during a 10 min period of confinement, indicating that waves regularly alternated between the two surfaces. When a wave was initiated on either the glass or cantilever surface, it typically spread until the entire substrate-attached area was converted into a PIP3-rich state characteristic of the “inner territory” encircled by an actin wave (Fig. 1 D at 33 and 77 s). Subsequently, PIP3 decayed and the membrane area reverted to the PIP3-depleted state. In the following, the probability is examined for a new wave to appear either on the same surface as the previous wave or on the opposite surface.

In Table 1, we compiled the full set of recordings in which confined cells exhibited at least six phases of wave formation; this corresponded to three full cycles if the waves propagated alternately on the cantilever or the glass surface. All the 34 cells showed a preference for wave initiation and propagation on the opposite surface as compared to doing so on the same surface. Among the total 423 events recorded in which a wave appeared on a blank surface, in 378 events the wave formed on the opposite surface, and in only 10 events did it form on the same surface as the previous wave. As a measure of switching from one surface to the other, we determined a switching index I_s. The ratio of switching events to the opposed surface over the total onset of wave formation on either surface (including uncertain cases) yields I_s = 0.89. On the contrary, the number of nonswitching events over the total number of events yields a ratio of 0.02. These data indicate a strong propensity of the wave-forming state for regular switching from one surface to the other.

Table 1.

Switching of PIP3 Waves between Cantilever and Glass Surface

Cell	Switches		Nonswitches		Uncertain Cases
	From Cantilever to Cover Glass	From Cover Glass to Cantilever	Repetition on Cantilever	Repetition on Cover Glass
1	3	4	–	–	–
2	3	3	–	–	–
3	3	3	1	–	–
4	8	9	–	–	–
5	4	4	–	–	4
6	2	2	1	–	–
7	4	5	–	–	–
8	12	12	–	–	1
9	5	6	–	–	1
10	3	3	–	–	1
11	4	4	–	–	–
12	15	15	–	–	–
13	5	5	–	–	–
14	2	3	–	–	1
15	3	2	1	–	–
16	7	5	1	–	1
17	1	1	–	–	4
18	5	4	–	–	–
19	3	2	–	–	1
20	1	2	–	–	3
21	2	3	–	–	5
22	2	3	1	–	–
23	2	2	–	–	2
24	3	4	–	–	3
25	6	6	–	–	1
26	10	10	1	–	3
27	5	6	–	–	2
28	13	14	2	–	–
29	11	12	–	–	1
30	12	13	–	–	–
31	5	5	1	–	–
32	2	2	1	–	1
33	3	3	–	–	–
34	16	16	–	–	–
Sum	185	193	10	0	35

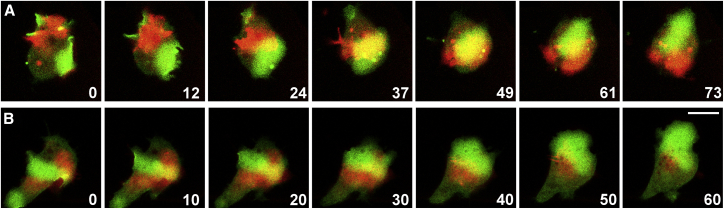
In the 35 cases (8%) that were classified as “uncertain” in Table 1, the PIP3 label remained most often at the cell border rather than spreading as a wave along either surface. However, in two cases, waves propagated simultaneously on both surfaces in different directions (Fig. 2). Video S2 displays one of these exceptional cases in which two waves crossed each other.

Figure 2.

Crossing of waves that propagate on separate surfaces. The two cells shown in (A) and (B) expressed GFP-PHcrac as a label for PIP3. The merged images display the PIP3 label on the glass surface in green and the PIP3 label on the cantilever surface in red. Time is indicated in seconds after the first frame of each series. The sequence in (A) is also shown in Video S2. The sequences of (A) and (B) illustrate cells 23 and 24, respectively, in Table 1. Bar, 10 μm.

As reported previously, the formation of actin waves can be enhanced by the pretreatment of cells with latrunculin A, a blocker of actin polymerization (20). During recovery from treatment with this drug, cells run through a period of profuse wave formation before they regain normal motility. We wish to emphasize that the slight compression of cells between the cantilever and glass surfaces renders the pretreatment unnecessary. Of the 34 cells registered in Table 1, only cells 2 and 3 were pretreated with latrunculin A; these cells exhibited surface switching similar to the untreated cells.

Modes of surface switching

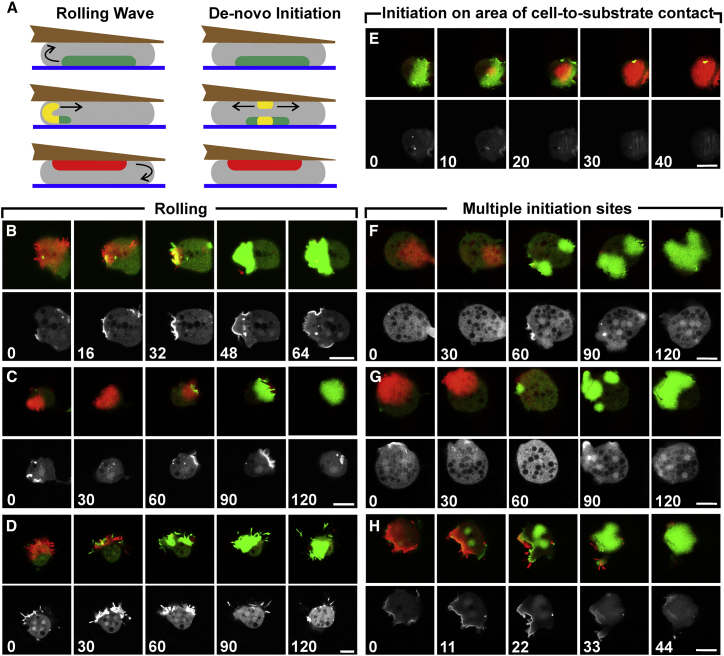
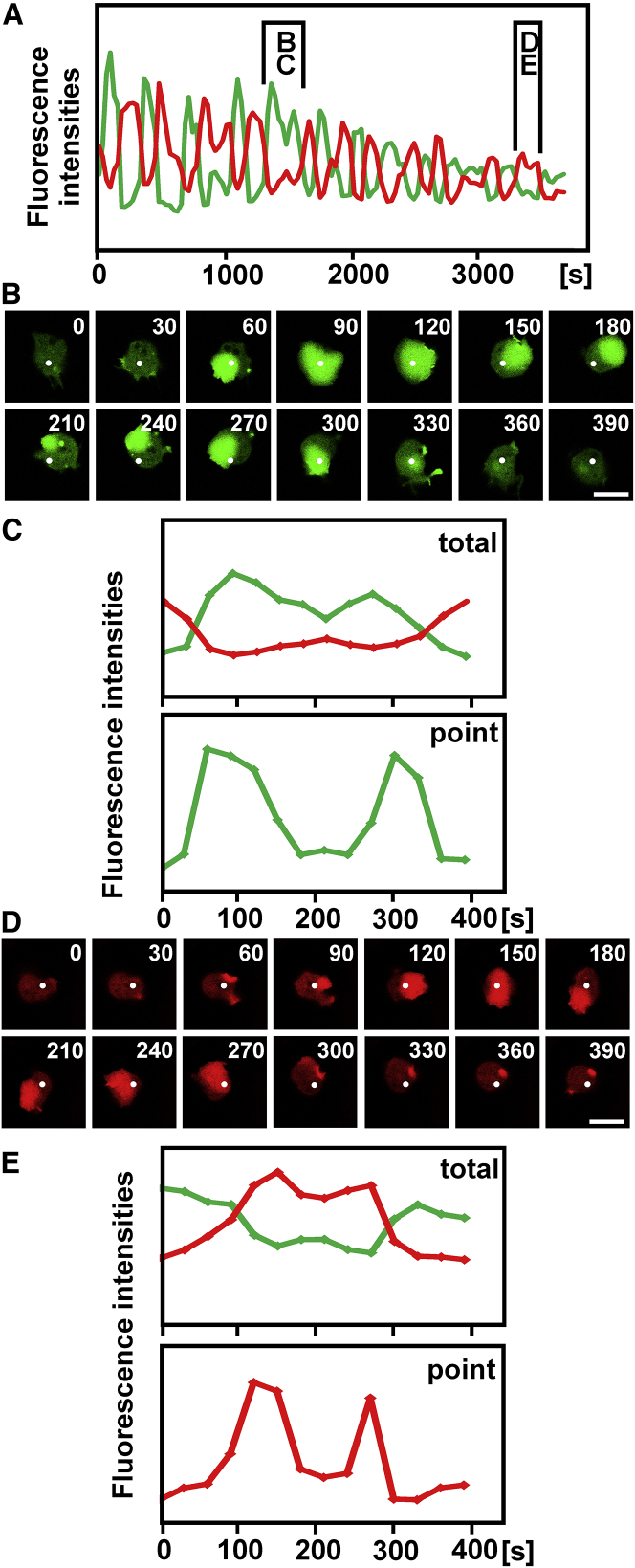
There are two possibilities of how the formation of PIP3 waves switches from one surface to the other. 1) A wave that arrives at the border of the substrate-attached area bridges the gap between the two substrate surfaces and subsequently expands on the opposed surface; this is depicted in Fig. 3 A as the rolling mode. 2) Another possibility is the de novo initiation of one or several waves on the new surface, meaning that wave formation starts on the opposed surface with no connection to the previous wave, as outlined in Fig. 3 A. In Fig. 3, B–H, examples of both modes of switching are shown.

Figure 3.

Modes of surface switching visualized by the labeling of PIP3 in the membrane of confined cells. (A) Diagrams outlining the rolling mode and de novo initiation in side views of cells sandwiched between a glass bottom (blue) and a wedged microcantilever (brown). These diagrams illustrate the color-coding of waves in the superimposed confocal images of (B)–(H), where PIP3 label on the glass-attached cell membrane is colored in green and that on the cantilever-attached membrane is colored in red. Positions at which labels on both attached membrane areas coincide in the merged images appear in yellow. (B–H) Image series of different modes of surface switching are shown. Each series displays PIP3 label in three confocal planes. The false-color panels in the top rows show merged fluorescence images focused either on the glass surface (green) or on the cantilever surface (red). The black-white panels in the bottom rows show the PIP3 label in a confocal plane midway between the two surfaces. Time is indicated in seconds after the first frame of each series. For cell 30 in (F) and (G), see also Fig. 7 and Video S3; for cell 13 in (H), see also Fig. 1, C and Video S1. See also Tables 1 and 2. Bars, 10 μm.

Rolling according to mode 1 is suspected when the site of wave decay on the cell border coincides with the site of wave expansion on the other surface. We observed the rolling of a wave along the unattached plasma membrane by recording a third plane of focus in between the two substrate surfaces. The presence of PIP3 label within this intermediate plane confirms a transient connection between the two labeled substrate-attached territories (Fig. 3, B–D).

The de novo initiation of waves (mode 2) is of interest because it indicates that each substrate-attached surface of a confined cell is not only capable of carrying on a propagating wave but is also predisposed to initiate new waves in a periodic manner. De novo initiation of waves is documented by lack of continuity between the decaying PIP3-rich territory on one surface and the expanding territory on the other. In Fig. 3, E–H, various configurations are displayed. When a wave is initiated within a substrate-attached area rather than on its border, it is obvious that the starting site of this wave is not connected to a remnant of the previous wave (Fig. 3 E). The same holds for the appearance of multiple initiation sites on one surface, which provides further evidence for surface switching by the programming of a substrate-attached membrane area for wave formation. Some of the multiple waves decay, whereas others expand and fuse with each other (Fig. 3, F–H; Video S3).

Frequency of oscillations

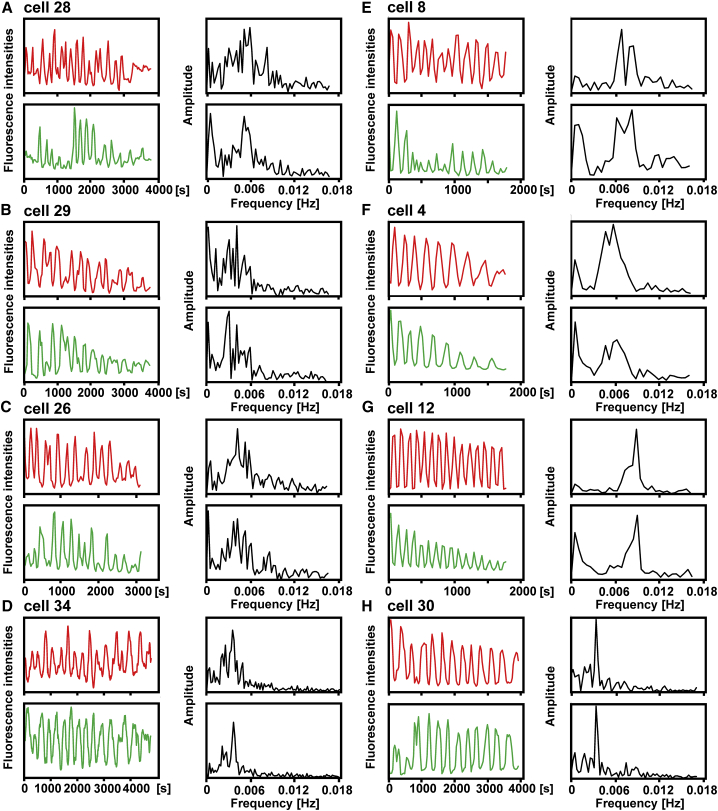
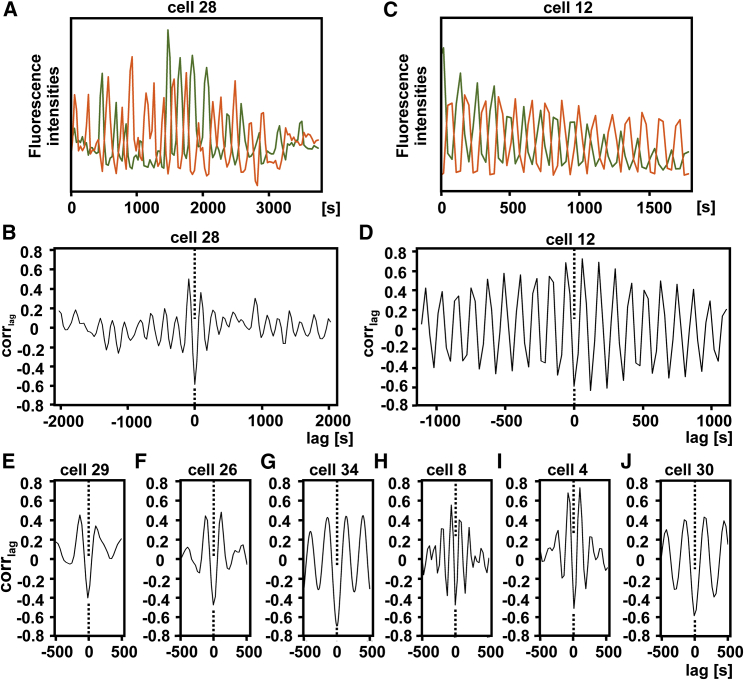
To quantify wave expansion and regression, we integrated at each time point the fluorescence intensities of the PIP3 label over the entire area of the cell surface attached to either the cantilever wedge or to the glass coverslip. Frequencies of oscillations were determined by Fourier analysis of all recorded runs with lengths of ≥10 periods. In Fig. 4, the plots of these eight runs are aligned roughly in the order of regularity of oscillations in each individual cell. All these plots show a high incidence of frequencies in the range of 0.003–0.009 Hz, corresponding to periods of 2–5 min (Table 2). In the most regular oscillations of cells 12 and 30, single peaks at 0.0089 and 0.0034 Hz, respectively, are prominent in the Fourier diagrams.

Figure 4.

Time series of fluorescence intensities of the PIP3 label on the cantilever (red) or the glass surface (green), and corresponding Fourier analysis of the oscillations (black). Data of eight cells that exhibited at least 10 periods of oscillation are shown. (A-H) Numbering of the cells corresponds to that in Tables 1 and 2. For cells 4 and 8, see also Fig. S1; for cell 29, see also Fig. 6; for cell 30, see also Figs. 3, F and G, 7, and Video S3; and for cells 28 and 12, see also Fig. 5.

Table 2.

Frequency Peaks and Derived Period Lengths of PIP3 Oscillations Obtained by Fourier Analysis of Single-Cell Recordings

Cell	Frequency [Hz] Cantilever	Frequency [Hz] Cover Glass	Period [min] Cantilever	Period [min] Cover Glass
4	0.0057	0.0063	2.91	2.67
8	0.0083	0.0083	2.00	2.00
12	0.0089	0.0089	1.88	1.88
26	0.0042	0.0042	4.00	4.00
28	0.0059	0.0051	2.82	3.24
29	0.0042	0.0042	4.00	4.00
30	0.0034	0.0034	4.92	4.92
34	0.0035	0.0037	4.74	4.49
Average	0.0055	0.0055	3.02	3.03

During a run of oscillations, the frequency tended to decline. This is obvious for cells 8 and 4, for which the analysis yielded a double peak (Fig. 4, E and F). When one of these runs was divided into two parts, the first part resulted in a peak corresponding to the higher frequency, and the second part resulted in a peak corresponding to the lower frequency (Fig. S1). We consider the initial higher frequencies to be representative of vital cells. The fluorescent label renders the cells sensitive to light such that oscillations finally stop when the contractile vacuoles arrest in a dilated state and cease from regulating osmolality.

Cross correlation of wave formation on the glass and the cantilever surfaces

The pairs of Fourier diagrams displayed in Fig. 4 indicate that for each of the cells analyzed, the frequency spectra obtained from the glass and the cantilever surface resemble each other, meaning that the fluctuations of the two surfaces are coupled. This notion was confirmed by cross correlation analysis (Fig. 5). The fluorescence intensities of the PIP3 labels on the glass and the cantilever surfaces correlated negatively; this means that high label on one surface coincided with low label on the other. The correlation became positive when the curves were shifted against each other by half of a period, which was consistent with the alternation of fluorescence intensities on the two surfaces.

Figure 5.

Cross correlation analysis of fluorescence intensities at the cantilever and the glass surfaces, showing alternation of PIP3 labeled with PHcrac-GFP. (A–D) Data of two cells are displayed, one shown as an example for irregular oscillations (A) and (B) and the other shown for regular ones (C)and (D). (A) Fluorescence patterns on the cantilever (red) and glass (green) surfaces for cell 28 are shown. (B) Cross correlation coefficients depend on shifting the two curves of (A) against each other. (C) The same as (A) is shown for cell 12. (D) The same as (B) is shown for the curves of (C). (E–J) Abbreviated cross-correlograms are displayed for oscillations of the six other cells shown in Fig. 4. All cross-correlograms reveal minima of correlation coefficients at 0-shift (dotted lines). See also Tables 1 and 2.

Patterns of wave initiation and propagation

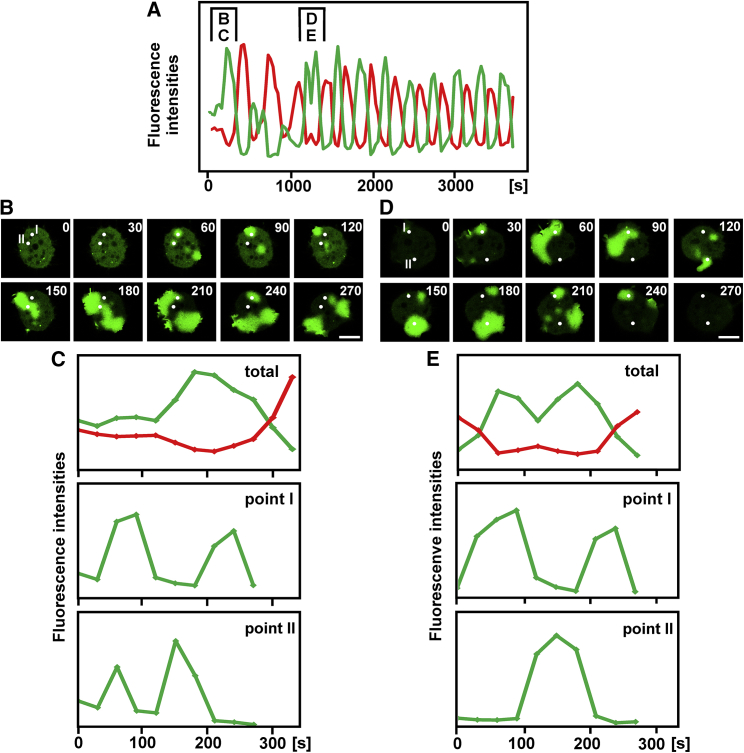
Surface switching might be considered as a consequence of refractoriness; if passage of a wave along one substrate-attached surface leaves this area in a refractory state, the opposite surface will be favored to carry a wave. However, previously published data obtained with cells attached to a single surface argue against this possibility; a wave can circulate on a substrate-attached surface without interruption for a length of time corresponding to multiple switching periods (5, 21). To support the notion that in confined cells refractoriness does not limit the time of wave propagation on either of the two surfaces, we have analyzed cases in which the waves passed certain points on a surface twice before they decayed (Figs. 6 and 7). These cases are often characterized by a split peak in the fluorescence signal of the PIP3 label (Figs. 6 A and 7 A).

Figure 6.

Circulating or reflected waves that repeatedly pass single points. This figure is related to Fig. 4B (cell 29). See also Tables 1 and 2. PIP3 labels on the glass surface are displayed in green, whereas those on the cantilever surface are shown in red. (A) Alternating wave formation on the glass and cantilever surfaces is shown. Brackets indicate sections of the run that are shown in (B) and (C) and in (D) and (E), respectively. (B and C) Circulating wave is shown. (D and E) A wave that reverses the direction of propagation is shown. White dots in (B) and (D) represent spots of 4 × 4 pixels in size, where local fluorescence intensities were measured. The top panels in (C) and (E), showing total fluorescence intensities on the entire cell surface, are expansions of the sections bracketed in (A). The bottom panels show point measurements at sites indicated by the white dots in (B) and (D), respectively. Time is indicated in seconds after the first frame of the bracketed sections. Scale bars, 10 μm.

Figure 7.

Multisite initiation of waves resulting in repeated wave passages over single points. This figure is related to Figs. 3, F and G, 4H, and Video S3 (cell 30). See also Tables 1 and 2. This figure is organized similarly to Fig. 6. Again, PIP3 labels on the glass are color-coded in green, and those on the cantilever are color-coded in red. (A) A run of oscillatory wave formation is displayed, with brackets indicating sections shown in (B) and (C) and in (D) and (E), respectively. (B) A wave pattern is shown in which two point measurements were taken (indicated by white dots I and II). (C) Total fluorescence intensities on the cell surfaces (top panel) and local fluorescence intensities at points I and II (middle and bottom panels) are plotted. Both points show the passage of two waves but at different intervals. (D) Another wave pattern in which two local measurements (white dots) were taken. (E) Total fluorescence intensities (top panel) and local intensities (middle and bottom panels) show the passage of two waves over point I and of a single wave over point II. Scale bars, 10 μm.

The repeated activation of PIP3 synthesis at a discrete point depends on the pattern of wave propagation and initiation. One possibility is that a wave circulates on the surface, passing a point twice (Fig. 6, B and C). Another possibility is that a wave is reflected at the cell border and then propagates in the reverse direction (Fig. 6, D and E). More complicated patterns are generated by the initiation of multiple waves and their fusion and by the splitting of waves (Fig. 7). Together, these data indicate that the refractory phase is shorter than the time that waves persist on one surface. Thus, refractoriness does not appear to limit the wave-switching period.

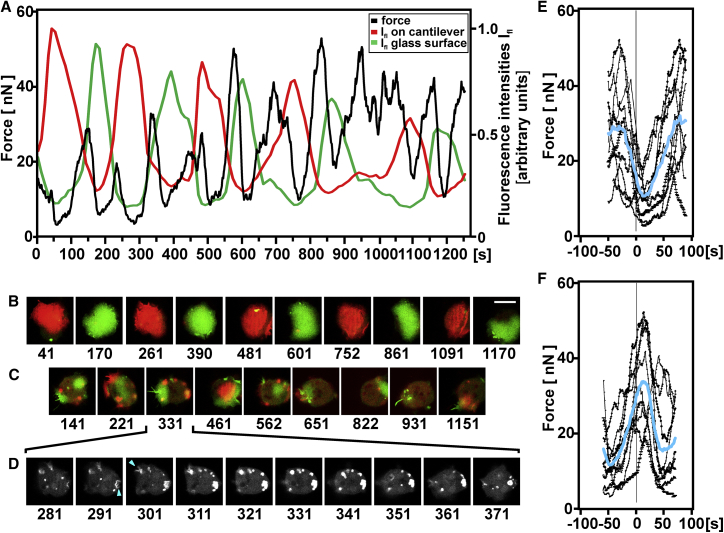
Is surface switching linked to force generation?

In addition to the fluorescence intensities on the glass and the cantilever surfaces, we measured fluctuations of the force that a confined cell applied to the cantilever (Fig. 8). The question was whether a component of the force fluctuations was phase-locked to the fluorescence oscillations. To elucidate such a component, we used two different reference points on the fluorescence curves: 1) the crossing points of fluorescence intensities on the glass and the cantilever surfaces and 2) the peaks of fluorescence intensities on each of the two substrate-attached cell surfaces. These reference points were set to zero on the time axis, and the force fluctuations aligned accordingly.

Figure 8.

Relation of vertical force generation to surface switching of PIP3 waves. Forces that a confined cell generates to a wedged cantilever were measured in parallel to recording of the fluorescent PIP3 label on the two substrate-attached membrane areas. (A) Time series of the fluorescence intensities of PHcrac-GFP on the glass (green) and cantilever (red) surfaces are shown, aligned with a force trace (black). (B and C) Merged fluorescence patterns on the glass (green) and cantilever (red) surfaces are displayed at the peaks of fluorescence intensities (B) or close to the crossing points of the fluorescence intensity curves (C). (D) Images show the PIP3 label midway between the two substrate surfaces. Blue arrowheads point to invaginations that develop into macropinocytotic vesicles. In (B)–(D), numbers indicate time in seconds corresponding to the timescale in (A). Bar, 10 μm. (E and F) Fluctuations of force adjusted either to the times of the peak PIP3 signals on the glass and the cantilever surfaces (E) or of the crossing points of the two fluorescence curves (F) are shown. These reference points were set to zero on the timescale. Individual force fluctuations are shown in black; averages of the 10 measurements in (E) or 9 measurements in (F) are plotted in blue. Data are from cell 31; see also Table 1.

The example shown in Fig. 8 A illustrates a general trend: force minima coincided with the peaks of fluorescence intensities, that is, at times when the waves were fully developed (Fig. 8, B and E). On the contrary, the force tended to be highest shortly after crossing of the fluorescence curves, close to the times of switching of a wave from one confining substrate surface to the other (Fig. 8, C and F). At these times of switching, the budding of macropinocytic vesicles was abundant at the free cell membrane between the two substrate surfaces (Fig. 8 D). A summary of force-to-fluorescence relationships for six cells is displayed in Fig. S2. We will address potential reasons for these relationships in Discussion.

Discussion

Periodic surface switches

Here, we examine the response of single cells to an easily reproducible three-dimensional arrangement of surfaces. Using a specific AFM-based technique, the cells were confined between two parallel substrate surfaces, a glass coverslip, and a wedged cantilever made of PDMS. The question was whether there is any pattern in the interaction of the cells with the two competing surfaces; do the cells engage both surfaces simultaneously or one after the other, and if so, do they alternate stochastically or periodically?

The Dictyostelium cells used formed territories rich in PIP3 on the cytoplasmic face of their substrate-attached membranes (5). These PIP3-rich territories are surrounded by actin waves and expand or decline depending on the direction of wave propagation, as revealed by fluorescent labeling (22). These PIP3/actin waves served as indicators of where the cells apply force to a substrate surface (8). To monitor wave formation in cells exposed to two opposing surfaces, the two membrane areas attached to the confining substrate surfaces were recorded in tandem by confocal fluorescence microscopy.

First, we explored whether the PIP3 patterns on the two substrate surfaces are aligned to each other, as it would be expected if a diffusing component acts as a common activator in the patterns generated on the two surfaces. The time series recorded did not provide evidence of a cytoplasmic factor that would link the wave dynamics on the upper and lower membrane sheets to each other. On the contrary, in the few cases in which waves coexisted on the two surfaces, they propagated independently and even crossed each other (Fig. 2; Video S2). In the vast majority of cases, the patterns were mutually exclusive. This means that expansion of a PIP3-rich territory on one surface coincided with the decline or absence of such a territory on the opposed surface. Importantly, the choice for one surface was not stable; wave formation preferentially switched from one surface to the other. Time series of sufficient length indicated that the switching resulted in regular antiphase oscillations of wave formation on the two surfaces.

Modes of surface switching

One mechanism by which an actin wave switches from one surface to the opposite one is to bridge the gap between the two surfaces when the wave arrives at the cell border. In this rolling mode of switching, the wave enters the new surface at the site where it left the previous surface (Fig. 3, B–D). In other cases, waves are initiated within the substrate-attached area rather than on its border (Fig. 3 E). This mode of de novo wave initiation provides evidence for the periodic programming of a surface for wave formation, in particular when the waves start at multiple sites (Fig. 3, F–H).

When a wave has passed a membrane area, it is followed by a state of reduced but not completely abolished excitability (23). The question is whether the relative refractoriness is responsible for switching the surface; silencing on one surface may favor wave formation on the other. There are two findings in cells attached to a single surface that argue against this view: a wave may change its direction, propagating into an area that it has passed before (23), and a wave may continually circulate for as long as 20 min (21) or even more than 30 min (5)—in any case, much longer than half a period of surface switching. The repeated passage of waves over defined points on the surface of a confined cell, as shown in Figs. 6 and 7, confirms that refractoriness is not key to surface switching.

Under our conditions, the cells switched almost symmetrically between the two surfaces, although one surface was made of PDMS and the other was made of clean glass. Nevertheless, it is conceivable that the switching probability can be modulated by the chemical or physical properties of the surfaces such that different persistence times enable the cell to favor one surface over another.

Surface switching in the context of cellular antiphase oscillations

The Dictyostelium system adds, to our knowledge, a new example to spatiotemporal patterns caused by out-of-phase oscillations in prokaryotic and eukaryotic cells. Mathematical principles of biological pattern formation on the basis of reaction-diffusion systems have been discussed by Meinhardt (24). A minimal model that accounts both for spatial and temporal patterns consists of a local activator that is autocatalytically amplified and two types of inhibitors: a long-ranging inhibitor and a slowly generated local inhibitor. Each inhibitor can be replaced by depletion of a precursor. The long-ranging inhibitor is proposed to antagonize the activator, and the local inhibitor is proposed to interrupt autocatalysis of the activator.

Two systems appear to be of immediate relevance to the oscillatory switching in Dictyostelium because they generate bipolar oscillations in single cells: the min system in Escherichia coli, which determines the cleavage plane of the bacteria (25), and the Cdc42 oscillator, which distributes symmetrically between the two cell poles in the fission yeast, Schizosaccharomyces pombe (26). In the min system, the proteins essential for the oscillations are minD and minE. The ATPase minD shuttles in a membrane-bound state between the two poles of the cell. For the minD propagation, the up-regulation of its ATPase activity by minE is required, an interaction that involves positive feedback (25). With a time delay, the high ATPase activity results in the detachment of minD from the membrane, thus enabling minD to propagate as a wave along the membrane.

Cellular pathways regulated by ATPases, as in the min system, or by small GTPases, such as Cdc42, are prone to generate spatiotemporal patterns by the implementation of positive and negative feedback circuits (27, 28). Explicitly, propagation of waves and oscillations have been predicted by Holmes et al. (29) under certain parameter regimes of a “pinning wave model” based on positive feedback in the activation of a Rho-GTPase and negative feedback mediated by polymerized actin. The induction of lamellipod retraction by myosin activation through Rho-kinase adds mechanochemical coupling to the repertoire of purely chemical feedback mechanisms (30).

A comprehensive mathematical treatment of antiphase oscillations in the eukaryotic cells of S. pombe has recently been published by Xu and Jilkine (31). In their ordinary differential equation model of the oscillations, the two cell poles compete for inactive Cdc42 as a common precursor. The model is based on fast diffusion of the small GTPase within the cytoplasm in its inactive state and on its activation upon immobilization by membrane-binding. Crucial for the oscillations is the interaction of Cdc42 with its activator, a guanine nucleotide exchange factor, by positive and negative feedback. For the positive feedback, autocatalytic promotion of Cdc42 binding to the membrane is proposed with a saturation effect due to depletion of cytosolic Cdc42. For the negative feedback, the best fit to the experimental data has been obtained by assuming that active Cdc42 negatively regulates the rates of guanine nucleotide exchange factor association with the cell poles. The model yields, in a certain parameter range, bipolar oscillations of Cdc42 with periods in the minute range.

Dictyostelium does not contain Cdc42 but notably several Ras isoforms, at least one of them being involved in the wave-generating system (32). Ras has been shown to be part of a positive feedback circuit that activates PI3-kinase (33, 34). Negative feedback is implemented in the Dictyostelium system by the PIP3-degrading enzyme PTEN, which binds to and is activated by its own product, PI(4,5)P2 (35, 36). In addition, PTEN-independent inhibition of PIP3 production contributes to wave propagation (37). Importantly, in both the PI3-kinase and PTEN circuits, inactive forms of the enzymes are cytoplasmic, whereas the active states are membrane bound. This means both enzymes are suited to drive wave propagation on one of the substrate-attached cell surfaces independently of the other surface, as found in the confined cells studied in this article.

A mathematical model of actin wave dynamics is based on a positive feedback loop between F-actin and PIP3, coupled with autocatalytic nucleation of actin filaments by the Arp2/3 complex (38). As an inhibitory factor, scarcity of the Arp2/3 complex or another essential constituent of the system is assumed. This model captures the propagation of actin waves at the border of a PIP3-enriched territory as well as the observed retraction of the waves. The nonlinear interactions in the wave-generating network of Dictyostelium cells manifest themselves in the excitability of the system, as outlined by Iglesias and Devreotes (39). A specified reaction-diffusion model by Knoch et al. (40) is based on experimental data showing that PIP3 synthesis and degradation are patterned in different ways. In this system, autocatalytic PIP3 synthesis followed by wave propagation is initiated beyond a threshold of excitation that is achieved only at sites of local PTEN depletion (37). The model of Knoch et al. takes this PTEN depletion into account by proposing the bistability of PTEN, undergoing transition from a high to a low membrane-bound state (40). The multiple initiation sites shown in Fig. 3 are in accord with this pattern of excitation.

PI3-kinase is recruited from the cytoplasm to initiate PIP3 synthesis at PTEN-depleted sites. In confined cells, depletion of cytoplasmic PI3-kinase may cause the wave-forming cell surface to exert long-range inhibition on the opposing surface. PTEN decorates the nonattached portion of the cell membrane. After a PIP3 wave has passed, PTEN enters from there onto the substrate-attached membrane area as a closed layer (7, 37), reminiscent of the minD propagation along the membrane. It appears, therefore, that the oscillatory switching system in Dictyostelium comprises characteristics of the min system (with respect to PTEN) and features of the Cdc42 system (as far as PI3-kinase and its regulator Ras are concerned).

Relation of wave switching to cellular force generation

Using a wedged cantilever, we measured the force a cell exerts on the confining surfaces together with the optical acquisition of the wave dynamics. Among the force fluctuations recorded, there was a component that correlated with the oscillations of the wave pattern; force reached peaks when wave formation switched from one surface to the other, and reached minima in the phases in between, when the waves became fully expanded on either one of the two surfaces (Fig. 8 E; Fig. S2). In the light of previous results, multiple factors will contribute to the force oscillations. When a wave propagating on the substrate-attached cell surface approaches the cell border, the membrane in front of the wave is pushed ahead, resulting in an expansion of the substrate-attached area (6, 21). This likely causes the cell to flatten and hence to lessen the force exerted on the cantilever. Myosin-IB is localized to the wave front (6, 41), where this single-headed motor protein is supposed to contribute to the flattening force in addition to the polymerization of actin that pushes against the membrane (8). Conversely, a regressing wave leaves behind an area rich in filamentous myosin II. This area contracts (21) similarly to the tail of a migrating cell (42). The contraction will cause an increase of force pushing in the vertical direction, in accord with the data shown in Fig. 8 F and Fig. S2.

Another activity that may contribute to force generation at times of wave switching is macropinocytosis. When a wave entered the interspace between the glass and the cantilever surfaces, the membrane was often invaginated to produce macropinocytic vesicles (Fig. 8 D). In phagocytes, the internalization of vesicles is accompanied by a transient increase of cortical tension, in particular if the membrane is prestretched (43, 44) as in the confined, slightly compressed cells. An increase in membrane tension should be reflected in an increase of force that the cell applies to the cantilever. It appears, therefore, that at least three factors can contribute to the periodic changes of force that the cells exert on the cantilever: flattening of the cells when waves are pushing against the cell border, contraction of the cells when waves disappear, and internalization of the membrane by macropinocytosis when a wave approaches the nonattached border of the cell.

Conclusions

When Dictyostelium cells are confined between two parallel surfaces, they maintain a dorso-ventral asymmetry; at any time, only one of the substrate-attached cell surfaces is predisposed to form patterns of actin/PIP3 waves, which are sites of force generation with an attempt to protrude in the direction of the substrate surface (8). The wave-forming capacity is controlled by an oscillatory switch mechanism, resulting in the regular alternation of wave formation on the two competing surfaces. We propose that this intrinsic dynamics allows a cell to keep its substrate interactions flexible and thus to cope with the diverse requirements of a three-dimensional environment where migrating cells are forced to make decisions about their interaction with surfaces of irregular geometry. In particular, this flexibility may assist a phagocyte in the search for particles to be taken up.

Author Contributions

J.H., D.J.M., and G.G. designed the project and wrote the article. J.H. and G.G. conducted the experiments. M.E. analyzed the data.

Editor: David Odde.