Coupling Magnetically Induced Electric Fields to Neurons: Longitudinal and Transverse Activation

Abstract

We present a theory and computational models to couple the electric field induced by magnetic stimulation to neuronal membranes. Based on the characteristics of magnetically induced electric fields and the modified cable equation that we developed previously, quasipotentials are derived as a simple and accurate approximation for coupling of the electric fields to neurons. The conventional and modified cable equations are used to simulate magnetic stimulation of long peripheral nerves by circular and figure-8 coils. Activation thresholds are obtained over a range of lateral and vertical coil positions for two nonlinear membrane models representing unmyelinated and myelinated straight axons and also for undulating myelinated axons. For unmyelinated straight axons, the thresholds obtained with the modified cable equation are significantly lower due to transverse polarization, and the spatial distributions of thresholds as a function of coil position differ significantly from predictions by the activating function. However, the activation thresholds of unmyelinated axons obtained with either cable equation are very high and beyond the output capabilities of conventional magnetic stimulators. For myelinated axons, threshold values are similar for both cable equations and within the range of magnetic stimulators. Whereas the transverse field contributes negligibly to the activation thresholds of myelinated fibers, axonal undulation can significantly increase or decrease thresholds depending on coil position. The analysis provides a rigorous theoretical foundation and implementation methods for the use of the cable equation to model neuronal response to magnetically induced electric fields. Experimentally observed stimulation with the electric fields perpendicular to the nerve trunk cannot be explained by transverse polarization and is likely due to nerve fiber undulation and other geometrical inhomogeneities.

Introduction

Background and motivation

Stimulation with a magnetically induced electric field (E-field) is a noninvasive technique that elicits or modulates neural activity. Transcranial magnetic stimulation (TMS) is widely used in neuroscience as a tool for probing brain function and connectivity (1). TMS is approved by the United States of America Food and Drug Administration for the treatment of depression and migraine, as well as for presurgical cortical mapping, and is under study for other neurological and psychiatric disorders (2, 3). Magnetic stimulation of peripheral nerves, which is also cleared by the Food and Drug Administration, is used for nerve conduction testing, neuromodulation, and neurorehabilitation (4, 5, 6, 7). The mechanisms determining the neural response to magnetic stimulation are still unclear, and experimental studies rely heavily on indirect, noninvasive measurements such as brain imaging and downstream neuromuscular responses (8, 9). Further, the strong electromagnetic coupling between the stimulus and electrophysiological recording systems presents challenges to direct in vivo recording from neurons, and recording latencies are typically longer than ∼1 ms after the stimulus (10).

Computational models of neuronal activation by magnetically induced E-fields provide an approach to understanding stimulation mechanisms and to optimizing stimulation parameters (11, 12, 13, 14, 15). Like electrical stimulation, a two-stage approach is commonly used to simulate magnetic stimulation (16). In the first stage, the macroscopic E-field distribution generated by magnetic stimulation is calculated under the quasi-static assumption (17, 18), for example by the finite element method (19, 20). This primary E-field ${\overrightarrow{E}}^{\prime }$ includes an induced component $\left({\overrightarrow{E}}_{\text{F}}^{\prime }=-\partial \overrightarrow{A}/\partial t\right)$ (21) and a conservative component $\left({\overrightarrow{E}}_{\text{q}}^{\text{'}}=-\nabla {\phi }^{\text{'}}\right)$ from charges associated with conductivity inhomogeneities (19, 22), which are represented by a vector potential $\overrightarrow{A}$ and a scalar potential φ′, respectively. In the second stage, the E-field is coupled to the cable equation (CE) that describes the neuronal response to stimulation (13, 14, 23, 24). The activating function f, which is proportional to the first spatial derivative of the E-field in the longitudinal direction of a neuronal process (typically an axon), is widely accepted as the term driving neural polarization (25). For magnetic stimulation, a hybrid CE was derived with the activating function generalized to include explicitly both E-field components (23, 24, 26):

$$f\left(z,t\right)=-{\lambda }^2\frac{\partial E_{\text{z}}^{\prime }}{\partial z}={\lambda }^2\left(\frac{{\partial }^2{A}_{\text{z}}}{\partial z\partial t}+\frac{{\partial }^2{\phi }^{\prime }}{\partial z^2}\right),$$ (1)

where z and λ are the axon’s longitudinal direction and length constant, respectively.

However, this approach raises several questions regarding the coupling between the two stages. Problems common to electrical and magnetic stimulation include the use of one-dimensional (1-D) cable representations of three-dimensional axons. Although this simplifies the computational implementation, the interaction between the field and the membrane, as well as some aspects of the membrane polarization, are not captured. Also, the E-field in the first stage is obtained with macroscopic conductivity values and therefore may not reflect the detailed field distribution on cellular scales (27, 28). The following two sections introduce issues specific to magnetic stimulation, which require resolution to improve the rigor and utility of models of magnetic stimulation.

Coupling of E-field to neuronal membrane in magnetic stimulation

Although CEs are used for magnetic stimulation (23, 24, 29), they have shortcomings in terms of theoretical justification and computational implementation. First, the use of potentials in magnetic stimulation models should be reevaluated. The primary scalar potentials φ′ can be ignored if the model has no external boundaries (29, 30, 31) or the induced E-field component is parallel to the boundary (23, 32, 33, 34). In other cases, however, φ′ is incorrectly ignored, for example, using field distributions for peripheral nerves to study the activation of cortical neurons (35). In response to the primary field, the cells generate a secondary E-field due to charge redistribution on the membrane, and this can be represented by a scalar potential, ${\overrightarrow{E}}^{″}=-\mathrm{\nabla }{\phi }^{″}$. The secondary potential φ″ is typically neglected by assuming its amplitude is small compared to the primary field (29), and only the latter is included in the conventional 1-D CE for magnetic stimulation (24). The exclusion of φ″ is justified theoretically in the conventional CE because the membrane potential it describes is the mean value averaged around the circumference of the cable and is not directly affected by the secondary field ${\overrightarrow{E}}^{″}$ (36, 37). However, ${\overrightarrow{E}}^{″}$ needs to be included to describe the behavior of the neural cable in the transverse dimension and/or ephaptic interactions with neighboring membranes (27, 28, 36, 37, 38, 39, 40). The vector potential is used together with the scalar potentials, especially the transmembrane potential, assuming that the latter behaves the same with a nonconservative E-field present (29). In the CE, the vector potential in the intracellular space is sometimes substituted with its extracellular value in analogy to the scalar potential (24). Although these are valid numerical approximations, their theoretical rigor requires further evaluation.

Furthermore, a simple and accurate computational implementation of magnetic stimulation in CE solvers has not been established. The primary E-field, and especially the magnetically induced component, is sometimes converted into an equivalent intracellular current injection (13, 41, 42, 43). The activating function at nodes of myelinated axons can be calculated using the integral of the E-field over neighboring internodes. However, these quantities are defined separately for each internode without establishing a global variable defined over the entire cell (32). As an alternative approach, Goodwin and Butson directly applied the total E-field solution obtained via the finite element method to cell models in the NEURON software and hence implicitly defined a global E-field integral (14). However, no other details were provided for the method, such as its computational implementation or distinction from electric potentials.

Activation of long nerves by transverse field in magnetic stimulation

Experiments with magnetic stimulation of peripheral nerves in vivo (44, 45, 46, 47) and in vitro (48, 49) showed cases of neural activation that were inconsistent with predictions by the activating function. To explain this discrepancy, the transverse component of the E-field was proposed to contribute to neural activation (44, 50), and Ruohonen et al. introduced a modified activating function f_M (44) by adding the steady-state transverse polarization of cylindrical fibers (51, 52)

$$f_{\text{M}}=-\alpha \times {\lambda }^2\partial E_{\text{z}}^{\prime }/\partial z+2E_{\text{x}}^{\prime }R.$$ (2)

Here α is a scaling factor, R is the axon’s radius, and the x axis is aligned with the transverse direction of the E-field. The experimentally fitted α suggested an equal or even dominant contribution to activation by the transverse component of the field (44).

However, whether the transverse field component indeed activates peripheral axons is unknown, because the modified activating function (44, 53, 54) and other studies (30, 31) used simplifying assumptions, including linear membrane models, unmyelinated axons, and neglecting the temporal integration required for membrane polarization. We derived a modified CE (37) and showed that modulation of the transmembrane potentials by the transverse E-field averages out to zero around the circumference of any neural compartment with a linear membrane (see Eqs. 3 and 6), thereby invalidating the use of the modified activating function as a simple predictor for neural activation. Our simulations with nonlinear membrane models also showed that the effect of the transverse E-field on activation thresholds is much smaller than estimated by linear membrane models, especially for myelinated axons (37). Nevertheless, the transverse field has the largest effect for short pulse duration and small spatial gradient of the extracellular field, two characteristics present in magnetic stimulation. Therefore, the modified CE should be used to examine whether the transverse field component induced by magnetic stimulation produces polarization and activation.

An alternate hypothesis to explain the experimental results is nerve undulation. Peripheral nerves exhibit undulation to accommodate compression and tension due to movement (55, 56, 57). The undulation of nerve fibers introduces short axonal segments that partially align with the E-field transverse to the nerve trunk and could be the mechanism underlying so-called transverse field activation (49, 54, 58). Previous studies of the effects of nerve undulation either used linear membrane models or investigated nonlinear membrane models for a limited number of coil types and positions. The activation due to undulation should be compared with that due to transverse fields in a straight axon under the same conditions to assess the relative contribution of the two activation mechanisms.

Aims and organization of the study

We present theoretical analyses and computational simulations to address the two questions described above, namely the coupling of magnetically induced potentials to neuronal membranes and transverse field activation.

The use of potentials is resolved by considering the characteristics of the E-field and electromagnetic-neuronal coupling on different timescales. The theoretical framework first uses the modified CE previously developed for electrical stimulation (37), which is based on asymptotic expansion of different temporal scales (36) and incorporates fast transverse polarization. The modified CE is used to analyze E-field coupling for magnetic stimulation to provide more rigorous theoretical justification for the use of the conventional CE for magnetic stimulation (24). Moreover, quasipotentials, a variable based on the integral of the E-field, are used in this theoretical analysis and for computational simulations of magnetic stimulation.

The transverse field activation of peripheral nerves by magnetic stimulation is quantified using the modified CE and quasipotentials. Unmyelinated and myelinated straight axons are simulated to obtain thresholds with both the conventional and modified CEs. The undulation of myelinated axons is also considered as an alternate factor contributing to activation by the transverse component of the E-field. The spatial distributions of the activation thresholds for circular and figure-8 coils for various positions with respect to an axon are presented, comparing modified versus conventional CEs for straight axons or undulating versus straight axons using the conventional CE.

Methods

Theoretical framework of electromagnetic-neuronal coupling

Modified CE

Previously, we modified the CE (37) for electrical stimulation to incorporate the transverse dimension into the 1-D longitudinal equation by assuming a local uniform-field solution for transverse polarization

$$c_{\text{m}}\frac{\partial {\overline{\phi }}_{\text{m}}}{\partial t}+\frac{1}{\mathit{\pi }}\sum _j\underset{0}{\overset{\mathit{\pi }}{\int }}{g}_{\text{m}}^{\left(j\right)}\left({\phi }_{\text{m}}-{\mathcal{E}}^{\left(j\right)}\right)\text{d}\theta =\frac{1}{2\mathit{\pi }R\times R_{\text{i}}}\left(\frac{{\partial }^2{\overline{\phi }}_{\text{m}}}{\partial z^2}+\frac{{\partial }^2{\overline{\phi }}_{\text{e}}^{\prime }}{\partial z^2}\right).$$ (3)

Here, c_m is the specific membrane capacitance, R_i = (σ_iπR²)⁻¹ is the longitudinal resistance per unit length that relates the longitudinal current I_i and its driving intracellular E-field (R_iI_i = E_z,i), σ_i is the intracellular conductivity, and the summation is over different types of ion channels j, each having reversal potential ${\mathcal{E}}^{\left(j\right)}$ and voltage-gated nonlinear conductance $g_{\text{m}}^{\left(j\right)}\left({\phi }_{\text{m}}\right)$. The transmembrane potential φ_m varies from its average value ${\overline{\phi }}_{\text{m}}$ by the steady-state transverse polarization for any longitudinal location (51, 52, 59)

$${\phi }_{\text{m}}\left(z,\theta ,t\right)={\overline{\phi }}_{\text{m}}\left(z,t\right)+2E_{\text{x}}^{\prime }\left(z,t\right)R\text{cos}\theta ,$$ (4)

where the x axis is defined locally by the direction of the transverse component of the quasi-uniform primary E-field and θ is the azimuthal angle on the axon’s circumference. The average transmembrane potential is ${\overline{\phi }}_{\text{m}}={\phi }_{\text{i}}-{\overline{\phi }}_{\text{e}}$, where φ_i is the uniform intracellular potential and ${\overline{\phi }}_{\text{e}}$ is the mean extracellular potential that is the same if calculated only for the primary field without accounting for the presence of the cell $\left({\overline{\phi }}_{\text{e}}={\overline{\phi }}_{\text{e}}^{\prime }\right)$ (37, 52). Along the axon, ${\overline{\phi }}_{\text{e}}^{\prime }$ varies according to the longitudinal component of the primary field

$${\overline{\phi }}_{\text{e}}^{\prime }\left(z,t\right)=-\underset{z_0}{\overset{z}{\int }}{\overline{E}}_{\text{z},\text{e}}^{\prime }\left(z,t\right)\text{d}z+{\overline{\phi }}_{\text{e}}^{\prime }\left(z_0,t\right),$$ (5)

where the z direction is the local longitudinal direction, z₀ is a reference point on the axon, and ${\overline{E}}_{\text{z},\text{e}}^{\prime }$ is the longitudinal component of the extracellular E-field averaged around the axon’s circumference (37).

The modified CE (Eq. 3) can be reduced to the conventional CE by converting the θ-dependent ionic currents of all channels into one equivalent channel with parameters $\overline{\mathcal{E}}\left(z,t\right)$ and ${\overline{g}}_{\text{m}}\left(z,t\right)$ at any longitudinal location (37)

$${\overline{\tau }}_{\text{m}}\frac{\partial {\overline{\phi }}_{\text{m}}}{\partial t}+\left({\overline{\phi }}_{\text{m}}-\overline{\mathcal{E}}\right)-{\overline{\lambda }}^2\frac{{\partial }^2{\overline{\phi }}_{\text{m}}}{\partial z^2}={\overline{\lambda }}^2\frac{{\partial }^2{\overline{\phi }}_{\text{e}}^{\prime }}{\partial z^2}\triangleq f,$$ (6)

with location- and time-dependent length and time “constants” $\overline{\lambda }\left(z,t\right)={\left(2\mathit{\pi }R{\overline{g}}_{\text{m}}\times R_{\text{i}}\right)}^{-1/2}$ and ${\overline{\tau }}_{\text{m}}\left(z,t\right)={\overline{g}}_{\text{m}}^{-1}{c}_{\text{m}}$. Because the extracellular potential varies around the neural cable, the activation by the longitudinal E-field should be calculated according to Eq. 5 using the primary extracellular field averaged around the neural compartment. The transverse field activation is through the integration of ionic currents in Eq. 3 or equivalent parameters $\overline{\mathcal{E}}$, ${\overline{\tau }}_{\text{m}}$, and $\overline{\lambda }$ in Eq. 6. The contribution of the transverse E-field is complex for a nonlinear membrane but averages out to zero for a linear membrane (37). Consequently, the simple addition of transverse and longitudinal E-field components in the modified activating function (Eq. 2) is invalid whether linear or nonlinear membranes are considered. The modified CE could be used to examine transverse field effects in magnetic stimulation using nonlinear membrane models. However, magnetically induced E-fields are nonconservative and cannot be described by scalar potentials. Therefore, the proper method to couple a magnetically induced E-field to the CE should be examined first.

Quasipotentials and CE for magnetic stimulation

The issue of coupling a nonconservative, magnetically induced E-field to a neural cable can be addressed by exploiting the low spatial variation of the E-field on microscopic scales. Both the transverse and longitudinal components of ${\overrightarrow{E}}_{\text{F}}^{\prime }$ can be considered quasi-uniform at any location on the neural cable (60), and the transversely uniform longitudinal component varies slowly along the cable’s axis. Therefore, quasipotentials ψ can be defined along the neural cable to combine the effect of both ${\overrightarrow{E}}_{\text{F}}^{\prime }$ and ${\overrightarrow{E}}_{\text{q}}^{\prime }$:

$$\psi =-\int \overrightarrow{E}\cdot \text{d}\overrightarrow{l}=\int \frac{\partial \overrightarrow{A}}{\partial t}\cdot \text{d}\overrightarrow{l}+\phi ,$$ (7)

in which the line integral starts from a point in the intracellular space and the E-field includes both the primary and secondary E-fields. In any transverse cross-section of the neuron, ψ_i is spatially uniform like φ_i due to the primary E-field being canceled by the secondary E-field of transverse polarization (37). Within the membrane, the primary E-field is similarly shielded by the secondary E-field from membrane polarization due to their orders-of-magnitude difference (∼10⁷ V/m for tens of millivolts across the nanometer-thick membrane versus <10³ V/m for typical neural stimulation). Therefore, ψ_m is the same as φ_m, and transmembrane quantities such as polarization and ionic current densities can still be described in their original forms (29). Similar to ${\overline{\phi }}_{\text{m}}={\phi }_{\text{i}}-{\overline{\phi }}_{\text{e}}^{\prime }$, the average ψ_m relates the intra- and extracellular quasipotentials

$${\overline{\psi }}_{\text{m}}={\psi }_{\text{i}}-{\overline{\psi }}_{\text{e}}^{\prime }.$$ (8)

Therefore, only ${\overline{\psi }}_{\text{e}}^{\prime }$ needs to be calculated at any longitudinal location, and quasipotentials can be considered an extracellular field parameter defined along the 1-D cable, with longitudinal variation given similar to Eq. 5:

$${\overline{\psi }}_{\text{e}}^{\prime }\left(\overrightarrow{s}\right)=-\underset{\mathcal{S}:{\overrightarrow{s}}_0\to \overrightarrow{s}}{\int }{\overline{\overrightarrow{E}}}_{\text{e}}^{\prime }\cdot \text{d}\overrightarrow{s}+{\overline{\psi }}_{\text{e}}^{\prime }\left({\overrightarrow{s}}_0\right).$$ (9)

Here, ${\overrightarrow{s}}_0$ is the location of the reference point on the neural cable to start the integration (typically the soma or the (main) axonal terminal, for convenience), $\overrightarrow{s}$ is the location of interest, S is the path of the integral from ${\overrightarrow{s}}_0$ to $\overrightarrow{s}$ along the neuron’s topology (i.e., along the sequence of neuronal segments between ${\overrightarrow{s}}_0$ and $\overrightarrow{s}$ rather than a straight line between the two points through extracellular space), and $\text{d}\overrightarrow{s}$ is the differential vector along S. As neurons typically have a tree-like topology that does not form connected loops on themselves, quasipotentials are well defined for individual neurons and should be calculated independently for each cell. Due to the low spatial variation of the E-field, the integration step is mostly determined by the morphology of the cell, e.g., distance between branching points and curvature of bends. For numerical computation, quasipotentials can be approximated by traversing the cell’s topology with sufficiently high resolution and adding the primary E-field component along each neural process in discrete steps

$${\psi }_{\text{c}}={\psi }_{\text{p}}-\frac{{\stackrel{\rightharpoonup }{E}}_{\text{c}}+{\stackrel{\rightharpoonup }{E}}_{\text{p}}}{2}\cdot {\stackrel{\rightharpoonup }{s}}_{\text{pc}},$$ (10)

where the subscripts c and p indicate the current (child) compartment and its previous (parent) compartment in the tree topology of the discretized neuron model (with the root of the tree having ψ₀ = 0); ${\stackrel{\rightharpoonup }{s}}_{\text{pc}}$ is the displacement vector between them; and the notations for primary field, averaging, and extracellular domain are ignored for simplicity.

The hybrid CE for magnetic stimulation, which uses an activation function defined by Eq. 1, has the correct mathematical form (24), but its theoretical justifications have limitations, especially accounting for transverse polarization. The transverse induced component −∂A_x/∂t is omitted and thought not to contribute to transmembrane current (24), whereas its contribution is implicitly contained in the form of E′_x when transverse polarization and the modified CE are considered. The longitudinal induced component −∂A_z/∂t is an additional term driving the intracellular current within the cable (23, 24, 26)

$$R_{\text{i}}{I}_{\text{i}}=E_{\text{z},\text{i}}=-\frac{\partial A_{\text{z},\text{i}}}{\partial t}-\frac{\partial {\phi }_{\text{i}}}{\partial z}=-\frac{\partial {\psi }_{\text{i}}}{\partial z},$$ (11)

and the extracellular value A_z,e is simply substituted for A_z,i, as they are considered identical because of the small radial distance between the two domains (24). Although the variation of the field is indeed small, the rigorous interpretation of this substitution is given by Eqs. 8 and 9, which together account for the averaging of extracellular quasipotentials around the cable’s cross-sectional circumference and the relationship of the average potentials in the longitudinal direction. Therefore, magnetic stimulation can use the CEs for electrical stimulation (Eqs. 3 and 6) by directly replacing the extracellular scalar potentials with extracellular quasipotentials, which provides significant convenience over the equivalent hybrid CE or other computational methods (see Discussion).

Computational quantification of transverse field activation by magnetic stimulation

The simulations were performed using custom code in MATLAB (versions 2016a and 2017b; The MathWorks, Natick, MA). The code and data are available online at https://doi.org/10.5281/zenodo.1186947.

Simulation setup for magnetic coils

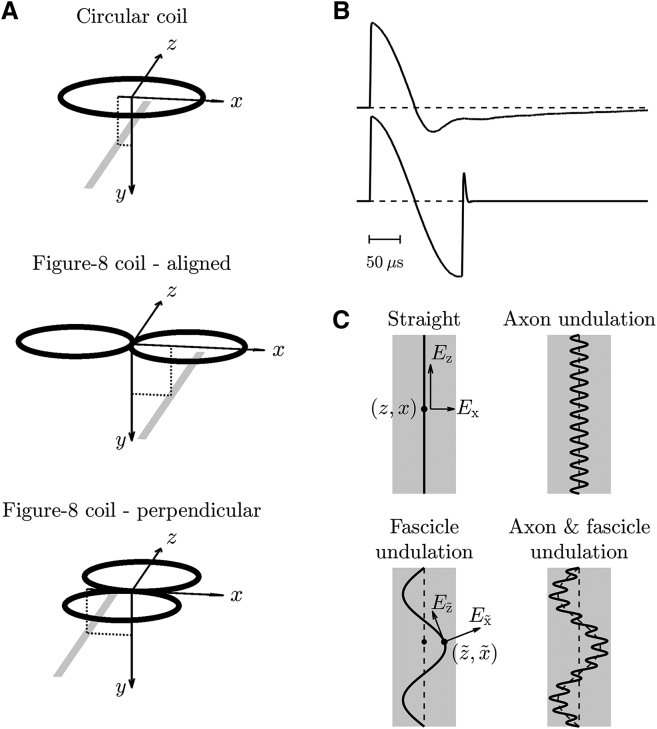
We quantified magnetic stimulation of peripheral nerves with a transverse E-field using the modified CE and nonlinear membrane models. The coils were placed parallel to the interface of a semi-infinite volume conductor in which the nerve was positioned parallel to the interface (Fig. 1 A). No secondary E-field was induced within the volume conductor, and the analytical solution for idealized circular coils (61) was used to calculate the E-field for a given rate of change of the coil current. The circular coil had a 5 cm diameter and 21 colocalized turns, similar to the one used by Ruohonen et al. (44). The figure-8 coil was simulated by combining the field solutions of two circular windings, each with a 4 cm diameter and 14 turns (44), in which the current directions were opposite and the coil was orientated with the peak field either aligned with or perpendicular to the nerve. The E-field was modulated temporally with either monophasic or half-sine waveforms recorded from a MagPro X100 device (MagVenture A/S, Farum, Denmark; Fig. 1 B). Both waveforms had peak amplitudes at pulse onset normalized to unity, a first phase with ∼75 μs duration, and a time integral of zero. The choice of the half-sine waveform was due to its similarity to biphasic waveforms in electrical stimulation, whereas a magnetic “biphasic” waveform has three phases and a significantly longer duration (62).

Figure 1.

Simulation setup. (A) Three configurations of magnetic stimulation coils (black) with a nerve (gray) underneath are shown. The coordinate system shows the nerve’s distance to the coil center in the vertical (y) and lateral (x) directions. (B) E-field waveforms of monophasic and half-sine magnetic stimulation pulses, with peak amplitude normalized to unity at pulse onset, are shown. (C) Four types of axon placement within the nerve trunk are shown. The wavelengths and amplitudes of the undulation are exaggerated for visualization.

Straight axons

The Hodgkin-Huxley (HH) model (63) and Richardson-McIntyre-Grill (RMG) model (64) were used to model unmyelinated and myelinated straight axons, respectively (Appendix A). The axon had a length of ∼30 cm, and its midpoint was aligned with the coil’s center in the z direction (Fig. 1 A). The axon’s distance to the coil was varied vertically (y) between 0.5 and 4 cm, and the lateral distance (x) for the three coil configurations was between −5 and 5 cm, −2.5 and 7.5 cm (range shifted because of symmetry of field distribution), or −5 and 5 cm, respectively, all with 2.5 mm intervals.

The E-field calculated along the axon (Fig. 1 C) was coupled to our custom modified CE solver directly for the transverse component E_x (37) and using quasipotentials for the longitudinal component E_z. For myelinated axons, E_x was only coupled to the nodes of Ranvier because transverse polarization was much smaller for the internodal axonal segments due to shielding by the myelin membranes (37) and the effect of transverse polarization averages out to zero for the passive internodes (Eq. 6). The simulation time step was 5 μs (HH model) or 2 μs (RMG model), and the membrane azimuthal discretization was set to 15 steps within θ ∈ [0,π] for the modified CE. To avoid action-potential initiation at the axon terminations, the activating function was set to zero at the ends of the axon. Activation thresholds were determined with 0.5% accuracy as the stimulation amplitude that elicited an action potential propagating to the axon terminal in the positive z direction and reported in units of amperes per microsecond (A/μs) for the coil current at the pulse onset. To quantify the effect of transverse polarization on activation thresholds, the percent difference of thresholds between the modified CE and the conventional CE was calculated.

Undulating axons

We simulated undulation of nerve fibers with the myelinated RMG-model axons using the conventional CE. The unmyelinated axons were excluded because they have very small diameters in mammalian nerves, and therefore their thresholds are too high to be excited by magnetic stimulation. The modified CE was not used due to the negligible influence of the transverse field on the thresholds of myelinated axons (see Results; (37)). The positioning of the nerve trunk (x, y) was the same as for the straight axon, and the undulation was assumed to be sinusoidal within the x-z plane (Fig. 1 C), consisting of a relatively short-wavelength undulation of the axon within the fascicle and a longer-wavelength undulation of the fascicle within the nerve trunk (54)

$$\tilde{x}=x+x_{\text{a}}\text{sin}\left(\frac{2\mathit{\pi }}{{\lambda }_{\text{a}}}z\right)+x_{\text{f}}\text{sin}\left(\frac{2\mathit{\pi }}{{\lambda }_{\text{f}}}z\right),$$ (12)

with z as the position along the nerve trunk and x_a,f and λ_a,f the amplitudes and wavelengths of the undulations, with subscripts a and f representing the axon and fascicle, respectively. The axon undulation had an amplitude of x_a = 40 μm and a wavelength of λ_a = 0.2 mm (49, 55, 57, 58). The E-field distribution along the axon was insensitive to a shift of the axon undulation because its wavelength was small compared to the spatial variation of the field, and therefore its phase was set to zero. The fascicle undulation had an amplitude of x_f = 0.8 mm and a wavelength of λ_f = 5 cm, and its phase was set to zero to maximize the amplification of the activating function (54). To investigate the contribution of the two undulation components, simulations were also performed on axons with either the axon or fascicle undulation only. For the undulating axons to have the same internodal distance as the straight axon, the arc length of Eq. 12 was first calculated as a function of z. Then, the inverse relationship between arc length and z was used to convert the compartment positions of a straight axon (x and z) to the corresponding undulating axon ($\tilde{x}$ and $\tilde{z}$). The longitudinal E-field $E_{\tilde{\text{z}}}$ was calculated according to the position and local orientation of the undulating axon and converted to quasipotentials. The discretization along the axon was increased by 10 times for the internodes to capture the increased spatial variation. To mitigate the increased polarization near the terminals due to the undulation, the axon’s length was extended by 20% in each direction without changing the location for action potential detection, and the surface area of the new terminal nodes was enlarged by 100 times to further suppress terminal polarization. All other neuronal parameters were the same as the straight axons (Appendix A). The effect of the undulation was quantified as the percent difference of thresholds between the undulating and straight axons, both obtained with the conventional CE.

Results

Distributions of E-field components relevant to neural activation

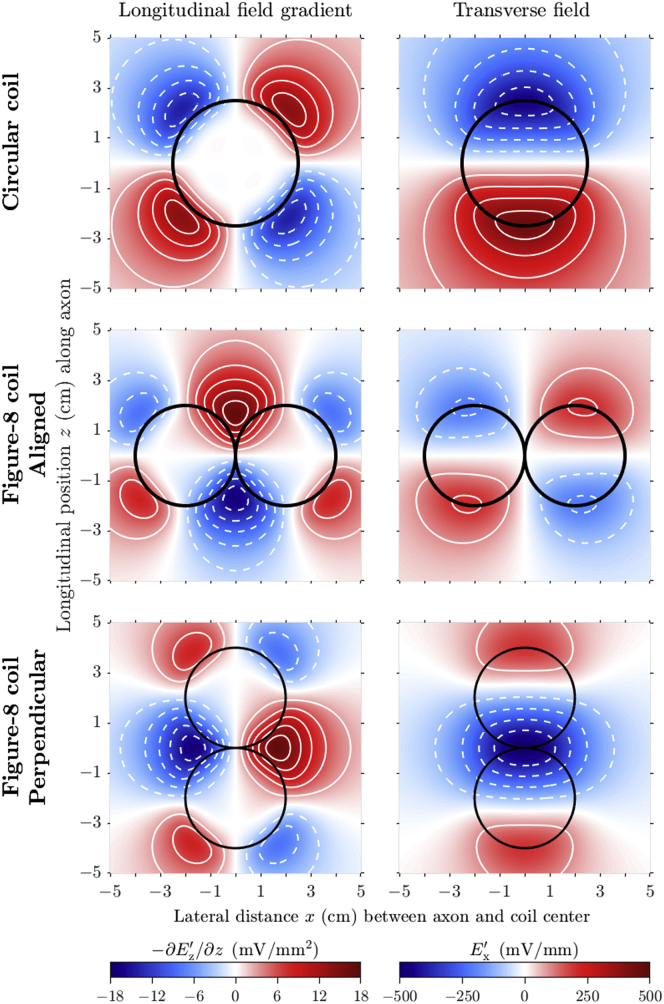
The distributions of the E-field calculated for the three coil configurations (Fig. 2) are in agreement with theoretical expectations and the results of Ruohonen et al. (44). The gradient of the longitudinal field and strength of the transverse field were largest for similar longitudinal locations along the nerve (z = ±2.5 cm for the circular coil, ±2 cm for the aligned figure-8 coil, and ±4 and 0 cm for the perpendicular figure-8 coil). In the lateral direction, the longitudinal field gradient was largest for the nerve trunk positioned tangential to the circular coil windings (x = ±2.5 cm for the circular coil, ±4 and 0 cm for the aligned figure-8 coil, and ±2 cm for the perpendicular figure-8 coil), whereas the transverse field amplitude was largest for the nerve trunk passing near the center of the windings (x = 0 cm for the circular coil and perpendicular figure-8 coil and ±2 cm for the aligned figure-8 coil).

Figure 2.

Distributions of E-field components contributing to neural activation in a plane 1 cm below a circular coil (top row) and a figure-8 coil aligned with or perpendicular to the nerve (middle and bottom rows, respectively). The coil current has a rate of change of 100 A/μs. The gradient of the longitudinal field (left column) and strength of the transverse field (right column) are shown along the nerve (z) for different lateral locations (x) relative to the coils (black outlines). The white contour lines, spaced at 3 mV/mm² and 100 mV/mm intervals, respectively, show positive and negative values with solid and dashed lines, respectively. To see this figure in color, go online.

Transverse stimulation of straight unmyelinated axons

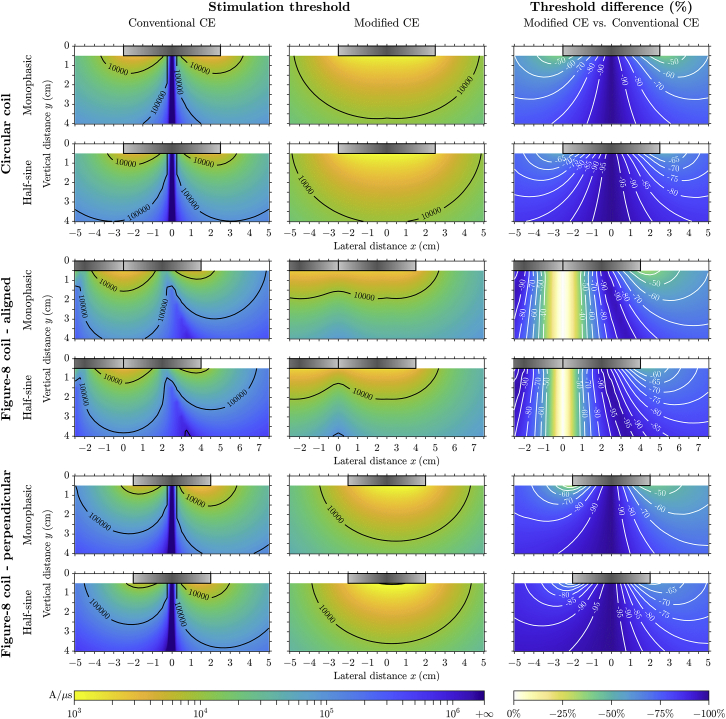
The thresholds for excitation of straight unmyelinated HH-model axons with monophasic and half-sine magnetic pulses were on the order of thousands of A/μs or more (Fig. 3), infeasible for practical magnetic stimulation devices. The conventional CE (left column) shows that thresholds were smallest at positions where the activating function was largest, i.e., at the edges for circular coils (top group) and perpendicularly orientated figure-8 coils (bottom group) as well as at the center for aligned figure-8 coils (middle group). The threshold increased with vertical distance from the coil and also when the axon was moved laterally. When aligned through the center of the coil windings, the activating function along the axon was zero for the circular coil or perpendicular figure-8 coil, and no action potential could be generated; for the aligned figure-8 coil, thresholds were much higher under the center of each circular winding. Threshold distributions were symmetric in the x direction for the circular and aligned figure-8 coils, whereas the perpendicular figure-8 coil had asymmetric threshold distributions due to the E-field gradient having different maximal amplitudes on the two sides (Fig. 2).

Figure 3.

Activation thresholds of straight unmyelinated HH-model axon for a range of vertical and lateral axon-coil distances. Rows show results for the monophasic and half-sine stimulation waveforms grouped by the three coil configurations. For the aligned figure-8 coil, the left region (negative x) is not fully shown because of the symmetry of the threshold distributions. The left and center columns show threshold values obtained with the conventional and modified CEs, respectively. The right column shows the threshold difference comparing modified and conventional CEs; any unmarked contour lines are spaced 10 and 5% apart for monophasic and half-sine waveforms, respectively. The outlines of the coils are illustrated as gray boxes, with the idealized windings located in the horizontal plane of y = 0. Color scales are the same within each column and shown at the bottom. To see this figure in color, go online.

Polarization of unmyelinated axons by the longitudinal and transverse field components (λ²∂E′_z/∂z and 2E′_xR) had similar amplitudes, given the field distribution presented in Fig. 2 and λ²/R = r_mσ_i/2 on the order of 10 mm for typical neuronal parameters. The modified CE (center column) indeed showed substantially different threshold distributions compared to the conventional CE; for a given vertical distance, stimulation thresholds at lateral positions with strong transverse field strength (i.e., under the center of the circular windings) were lower than thresholds at locations with large activating function (under the edge of the windings). Thresholds for the modified CE were substantially reduced compared to the conventional CE (right column), except when the axon was placed close to the center (within 1 cm lateral distance) of the aligned figure-8 coil.

The threshold distributions were qualitatively similar with the two waveforms, but quantitative changes were opposite for the conventional and modified CEs. Thresholds obtained with the conventional CE were higher for the half-sine waveform than the monophasic waveform due to the counteraction of the second phase on membrane polarization. For the modified CE, however, thresholds for the half-sine waveform were lower as a result of the transverse field activation (excluding axon locations close to the center of the aligned figure-8 coil). Therefore, threshold changes due to transverse polarization were even more prominent for the half-sine waveform.

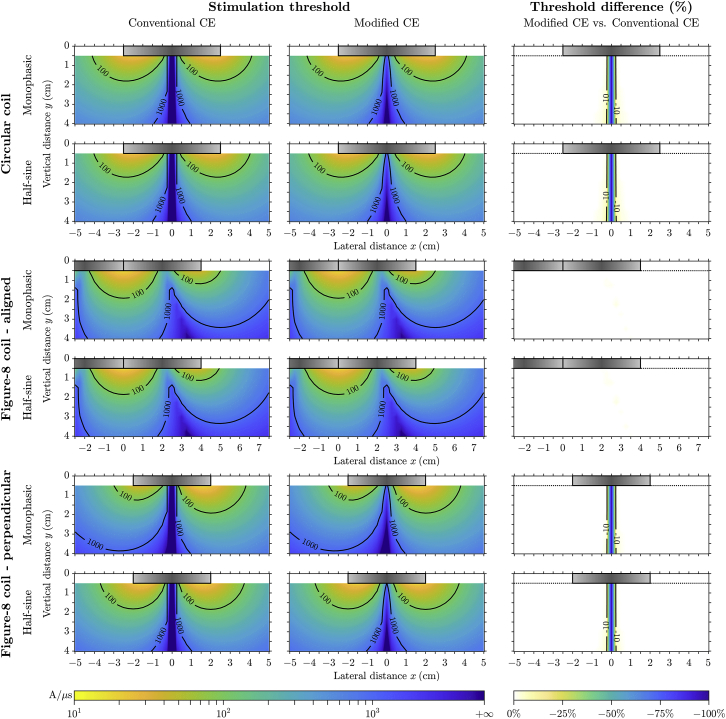
Transverse stimulation of straight myelinated axons

The activation thresholds of straight myelinated model axons (Fig. 4) were substantially lower than those for the unmyelinated axons (25) and readily achievable with conventional magnetic stimulation devices. This threshold difference was mainly due to the myelin, which insulated the internodal membrane and restricted the axial current driven by the extracellular stimulation to cross almost exclusively through the much smaller nodes. Quantitatively, the effective λ² of the myelinated axon, and hence the activating function, scaled approximately by the ratio of internodal distance and nodal length (∼10³) compared to that of an unmyelinated axon having the same membrane properties as the nodes (65) (see analysis in Appendix B). Therefore, the longitudinal polarization was much stronger in myelinated axons for a given E-field distribution and accounted for the lower thresholds. On the other hand, transverse polarization was present only at the nodes and did not affect thresholds except when the axon was placed within a few millimeters of the coil center for the circular and perpendicular figure-8 coils. For the half-sine waveform, threshold distributions were similar to those of the monophasic waveform, and the overall increase in threshold amplitude was in agreement with stimulation by the activating function. A qualitative difference occurred only for the perpendicularly orientated figure-8 coil, for which the half-sine waveform had a more symmetric distribution in the lateral direction. Due to the much faster ion channel kinetics of the myelinated axons, the second phase of the half-sine waveform activated axons with similar thresholds for negative positions of the coil along the x axis as for positive positions.

Figure 4.

Activation thresholds for straight myelinated RMG-model axon. These are presented in a similar format as Fig. 3, with a different color scale range for thresholds. To see this figure in color, go online.

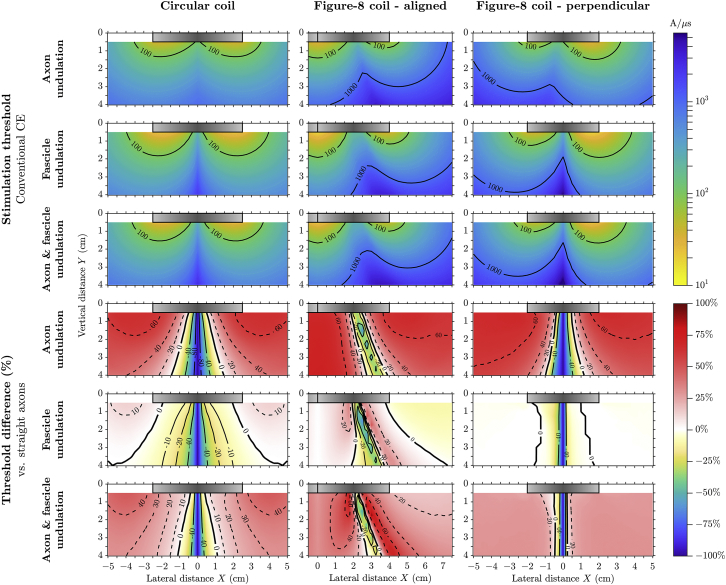
Effect of axon undulation on activation threshold

The threshold distributions of the undulating axon were more uniform compared to those of straight axons, due to the distribution of orientations of the axonal segments (Fig. 5, rows 1–3). The axon undulation, by itself or with fascicle undulation present, reduced thresholds for nerves located laterally near the center of the circular windings (Fig. 5, rows 4 and 6). The strong E′_x increased longitudinal activation (comparing $E_{\tilde{\text{z}}}^{\prime }$ versus E′_z), and “transverse field activation” by E′_x alone occurred when the nerve was perfectly aligned through the center of the circular and perpendicular figure-8 coils. Elsewhere, axon undulation increased thresholds because the projection of E′_z along the undulating path and weak E′_x resulted in smaller $E_{\tilde{\text{z}}}^{\prime }$ and decreased longitudinal activation. Fascicle undulation alone had weaker modulation effects on thresholds and mostly reduced thresholds under the center of coil windings (Fig. 5, row 5). For the half-sine waveform, the threshold distributions were qualitatively similar to those for monophasic stimulation; however, threshold modulation was weaker, and fascicle undulation only reduced thresholds (figure available online at https://doi.org/10.5281/zenodo.1186947.

Figure 5.

Activation thresholds of undulating myelinated RMG-model axon for the three coil configurations (columns) using monophasic waveform. The first, second, and third rows show the threshold values for axons having only axon undulation, only fascicle undulation, and both undulation components. The fourth, fifth, and sixth rows show the threshold difference compared to straight axons (versus left column of Fig. 4) for the three undulating axon models in the first, second, and third rows; contour lines for positive and zero difference are shown with dashed and thick solid lines, respectively. Color scales are the same within each row and shown on the right; the same colors as in Fig. 4 are used for the thresholds and negative threshold differences. To see this figure in color, go online.

Discussion

Transverse polarization and electromagnetic coupling to neuronal membranes

As in electrical stimulation, both the transverse and longitudinal components of a magnetically induced E-field can couple to neurons. Transverse polarization occurs on a sub-μs timescale and determines the deviation from the average membrane potential at a given longitudinal location of long neural cables. Based on analysis of transverse polarization, the modified CE incorporates the effects of both E-field components and defines the activating function according to the transversely averaged potentials in the longitudinal direction (37). By applying these transverse and longitudinal relationships to E-fields induced by time-varying magnetic fields, we provided a rigorous theoretical justification for the CE for magnetic stimulation, including the use of scalar potentials for the transmembrane quantities, the inclusion of the transverse E-field, and the substitution of the intracellular vector potential by the extracellular vector potential as well as the use of quasipotentials to drive the CE.

Quasipotentials for simulation of magnetic stimulation

We defined and theoretically justified the concept of quasipotentials that allow simple and practical computational implementation of the CE for magnetic stimulation, for example by using built-in functionality of CE solvers such as NEURON's extracellular mechanism (66). An alternative method for applying an exogenous E-field to neural cable models is to convert the activating function into equivalent intracellular currents applied to each neuronal compartment (13, 41, 42, 64). However, instead of the continuous first-order partial differential of the E-field, the activating function in computational models needs to be discretized as a first-order difference with asymmetric weights (i.e., intracompartmental conductance) along the cable due to variation in neuronal parameters (13, 64, 67), modified at terminals to reflect a sealed boundary condition ((13, 41, 67, 68); D. Elcin et al., 2017, Soc. Neurosci., abstract 202.04), and assigned additional terms at branching points governed by the current balance equation ((13, 41, 69); D. Elcin et al., 2017, Soc. Neurosci., abstract 202.04). Neglecting these considerations (35, 70) results in “leaky” compartments in which the longitudinal current driven by the induced E-field may arbitrarily enter or exit without crossing the membrane and may therefore lead to significant discrepancies in the interpretation and conclusions regarding activation of neurons by magnetic stimulation. Thus, the current injection approach is more complex and prone to implementation errors than the quasipotential approach, which does not require information about the neuron model properties other than the locations of the compartments and their topological connection.

Transverse field activation of peripheral nerves

The relative threshold distribution obtained with the modified CE for unmyelinated axons were seemingly in agreement with the experimental observation by Ruohonen et al. and their exploration using a modified activating function (44). However, the amplitudes required to activate unmyelinated axons were orders of magnitude larger than experimentally observed values. Indeed, as responses were characterized with electromyograms evoked from the median nerve (44), they were not due to activation of unmyelinated fibers, but rather large-diameter myelinated Aα axons. Similarly, in vitro electrical recordings of compound action potentials from phrenic nerves are unlikely to reflect contributions from unmyelinated axons (48, 49). Therefore, transverse field activation of unmyelinated axons cannot explain the experimental results, and the use of unmyelinated axons in magnetic stimulation models (23, 24, 29, 35) should generally be avoided unless specifically modeling such axons or diseased nerves with demyelination.

In contrast to the unmyelinated axon model, the myelinated axon model indicated that transverse stimulation did not affect thresholds in straight myelinated axons, and the threshold was always lowest for coil positions where the conventional activating function was largest. Therefore, the results from both membrane models indicated that the polarization due to transverse E-field alone cannot account for the experimental observations.

Apparent transverse field stimulation is likely the result of an E-field component along the axon that generates an activating function due to factors such as the geometry of the tissue surrounding and within the nerve, electrical inhomogeneity and anisotropy, and variations in the geometrical and/or electrical properties of the axon. For instance, the undulations of axons and fascicles result in short and curved axonal segments, locally aligned with E-field components that are globally transverse to the nerve (49, 54). The effect of undulation on thresholds was stronger for axon undulation, but fascicle undulation contributed as well. Undulations in the nerve reduced the thresholds for coil positions at which the activating function longitudinal to the overall nerve-trunk orientation was small, thereby creating apparent transverse field stimulation. Further, nerve undulation increased thresholds for coil positions where the longitudinal activating function was large. Therefore, nerve undulation flattened the threshold distributions for all coil configurations and reduced the sensitivity of threshold to coil position. For a fixed vertical axon-coil distance, the differential effect of undulation on the thresholds for various lateral coil positions resulted in threshold profiles resembling those recorded experimentally (44). The presence and role of nerve undulation is also consistent with experimental evidence that magnetic stimulation thresholds increase as the nerve is stretched (48), which can be interpreted to result from the reduction of axonal segments aligned with the transverse E-field.

Limitations

The simulation of magnetic stimulation in this study had several simplifying assumptions. Human unmyelinated axons are more sensitive to stimulation than the HH-model axons we used due to different membrane properties and higher temperature (71). However, unmyelinated axons typically have much smaller radii (≤1 μm) than myelinated fibers (3‒10 μm) (71, 72). Therefore, the orders-of-magnitude threshold difference for magnetic stimulation should remain and be comparable to the threshold difference reported for electrical stimulation (73, 74, 75). The E-field distributions were calculated using a semi-infinite volume conductor with homogenous conductivity (44) and therefore ignored the influence by the secondary charges on the boundary of the volume conductor and internal discontinuities. For example, both the shape of the forearm and the perineurium of individual fascicles reduce the field amplitude but have less effect on the relative distribution (44, 76). Considering the attenuation of the E-field amplitude due to the perineurium, especially in the transverse direction, the contribution of the transverse field to the activation of straight axons would be further reduced. Therefore, the conclusion that transverse polarization alone is insufficient for transverse stimulation remains valid even with these simplifications.

For undulating axons, the reduced transverse field also affects the E-field but to a lesser extent. The undulation of axons is not confined to one plane and can, for example, exhibit helical shapes that manifest as bands of Fontana (55, 56). As axons leave and join the nerve or the number and arrangement of fascicles changes over distance, the undulation of an individual axon is likely more irregular, not having steady sinusoidal variations with fixed amplitudes and wavelengths. The depth of the median nerve varies within the forearm, and the variation of the distance to the coil could further affect stimulation thresholds. The undulation of the axon was the major contributor to neural activation by the E-field transverse to the nerve trunk. However, the parameters for the undulation were drawn from previous histological measurements that could deviate from the actual geometry due to tissue deformation. Especially, shrinkage of the nerve could result in underestimates of the amplitude and overestimates of the wavelength of the undulation, which would, in turn, affect thresholds (58).

Conclusions

Transverse polarization and the modified CE provided a rigorous theoretical foundation and an improved theoretical justification for the use of the CE and quasipotentials in simulations of magnetic stimulation. Using this theoretical framework, the effects of transverse polarization and nerve undulation on activation threshold were quantified. Although the thresholds for unmyelinated axons were affected by transverse polarization, this was not the case for myelinated axons. Therefore, the experimentally observed activation of nerves by transverse E-fields cannot be explained by transverse axonal polarization but is likely due to nerve fiber undulation and other spatial inhomogeneities that cause a local longitudinal E-field in the axon.

Author Contributions

A.V.P. and W.M.G. conceived and supervised the study. B.W. performed the theoretical analysis, computational models, and simulations; analyzed data; and generated figures. B.W. wrote the manuscript. A.V.P. and W.M.G. revised the manuscript. All authors approved the final submitted version.

Editor: Raimond Winslow.

Appendix A: Parameters of Neuronal Membrane Models

The HH model (63) was adjusted to room temperature (23.5°C) with Q₁₀ = 3, and a radius of 3 μm was used following previous studies (37, 38, 53), with longitudinal discretization set to 82.1 μm according to the d_lambda (dλ) rule of NEURON (66), with dλ = 0.1. The RMG model (64), based on human peripheral nerve fibers at body temperature (37°C), had fast sodium channels, persistent sodium channels, and slow potassium channels at nodes, which are each modeled as a single compartment. The passive internodes had the same radius as the unmyelinated axon and corresponded to a 10 μm outer fiber diameter including the myelin; the membrane properties were calculated for 120 myelin lamella, and the internodes were discretized into 10 and 100 compartments for straight and undulating axons, respectively. The axon geometry and passive electrical parameters for the two models are summarized in Table 1. For the active ion channel parameters and dynamics, please refer to the original publications of the respective membrane models (63, 64). Detailed information can also be found in the code available online at https://doi.org/10.5281/zenodo.1186947.

Table 1.

Parameters of the Unmyelinated HH-Model Axon and Myelinated RMG-Model Axon

Parameter	Units	HH	RMG
	–	–	Node	Internode
Radius R	μm	3	1.65	3
Length l, δa	μm	82.1	1	1150
Membrane capacitance cm	μF/cm2	1	2	4.2 × 10−4
Membrane resistance (at rest) rm	kΩ⋅cm2	1.48	0.096	240
Intracellular conductivity σi	mS/cm	28.3	14.3	14.3

^aThe discretized compartment length l is given for the HH model, and total lengths of the node δ and internodes l are given for the RMG model.

Appendix B: Length Constant Scaling of Myelinated Axons

Extracellular stimulation is driven by longitudinal polarization, and thresholds are therefore related to the activating function (25). For a given E-field distribution, (de)polarization is proportional to λ² (Eq. 6). Although the nodes and internodes have different length constants (λ_n and λ_m, assuming infinite length for each), the behavior of the myelinated axons can be homogenized on the scale of the internodal length and described by an equivalent CE and an effective length constant λ_eff (65). On such a scale, ${\lambda }_{\text{eff}}^2$ is given by the harmonic mean of λ² of the node and internode weighted by their respective lengths, δ and l (65),

$${\lambda }_{\text{eff}}^2={\left(\frac{\delta }{L}\frac{1}{{\lambda }_{\text{n}}^2}+\left(1-\frac{\delta }{L}\right)\frac{1}{{\lambda }_{\text{m}}^2}\right)}^{-1},$$ (A1)

where L = l + δ.

Due to the vastly different membrane resistance and capacitance of the nodes and myelin, myelinated axons are sometimes modeled with completely insulating myelin ($r_{\text{m}}\to +\infty$ and $c_{\text{m}}\to 0$, for example in the simplest of the three axon models used in (64)). Then ${\lambda }_{\text{eff}}^2=L/\delta {\lambda }_{\text{n}}^2$, and the scaling is intuitively explained by the fact that the membrane resistance increases by a factor of L/δ, but the longitudinal resistance does not change when the axon becomes myelinated. Considering noninsulating membrane properties, myelin has a combined specific membrane resistance r_m about 3‒4 orders of magnitude larger than that of the node r_n. On the other hand, the internode is about three orders of magnitude longer than the node, whereas their radii R_m and R_n are similar. Therefore, the internodal term in Eq. A1 is on the same order of magnitude as the nodal term

$$k=\frac{\left(1-\frac{\delta }{L}\right)\frac{1}{{\lambda }_{\text{m}}^2}}{\frac{\delta }{L}\frac{1}{{\lambda }_{\text{n}}^2}}\approx \frac{r_{\text{n}}{R}_{\text{n}}}{r_{\text{m}}{R}_{\text{m}}}\frac{L}{\delta }\approx 0.1\sim 1.$$ (A2)

Here, the constant k is defined by the axon geometry and membrane properties (0.25 for our myelinated axon model). Thus, for an order-of-magnitude analysis, the effective length constant is approximately

$${\lambda }_{\text{eff}}^2=\frac{1}{1+k}\frac{L}{\delta }{\lambda }_{\text{n}}^2\approx \frac{L}{\delta }{\lambda }_{\text{n}}^2.$$ (A3)