The averted infections ratio: a novel measure of effectiveness of experimental HIV pre-exposure prophylaxis agents

Abstract

There is clear evidence that tenofovir disoproxil fumarate combined with emtricitabine (TDF-FTC) is a highly efficacious oral pre-exposure prophylaxis agent for preventing the acquisition of HIV. This has consequences for the design and analysis of trials evaluating experimental pre-exposure prophylaxis regimens, which now generally include an active-control TDF-FTC arm rather than a placebo arm as a comparator. We point out major problems in the interpretation of the primary measure of effectiveness proposed for these trials, namely the ratio of the HIV incidence rates in the experimental agent and TDF-FTC arms. We argue that valid interpretation requires an assumption about one of two parameters: either the incidence rate that trial participants would have experienced had they not received pre-exposure prophylaxis or the effectiveness of the TDF-FTC within the trial. However, neither parameter is directly observed due to the absence of a no-treatment arm, requiring the use of external evidence or subjective judgement. We propose an alternative measure of effectiveness based on the concept of “averted infections”, which incorporates one of these parameters. The measure is simple to interpret, has clinical and public health relevance, and is a natural “preservation of effect” criterion for assessing statistical non-inferiority. Its adoption would also allow the use of smaller sample sizes, currently a major barrier to the evaluation of experimental pre-exposure prophylaxis regimens.

INTRODUCTION

Pre-exposure prophylaxis (PrEP) is a major advance in HIV prevention and could have a profound impact on the course of the HIV epidemic.(1, 2) Currently, the fixed dose combination of tenofovir disoproxil fumarate (TDF) with emtricitabine (FTC) (and generic equivalents) is the only drug that has been approved for pre-exposure prophylaxis. TDF-FTC has been shown to reduce of the risk of acquiring HIV infection by up to 86% in intention-to-treat analyses of randomised controlled trials.(3, 4) Further, most infections observed in individuals allocated to TDF-FTC have been attributed to sub-optimal adherence, and evidence suggests that biological protection is almost complete if sufficiently high drug concentrations are achieved.(5–7)

Despite the remarkable efficacy of TDF-FTC, there are good reasons to assess other potential pre-exposure prophylaxis agents. For example, two ongoing trials are evaluating tenofovir alafenamide (TAF), another prodrug of tenofovir which is preferentially absorbed and activated within peripheral blood mononuclear cells, and long-acting cabotegravir, which may be particularly advantageous for individuals who have difficulty in adhering to a daily oral drug (ClinicalTrials.gov IDs: NCT02842086, NCT02720094). Neither of these trials includes a placebo control arm as this would be widely deemed as unethical in view of the demonstrable efficacy of TDF-FTC.(8, 9) Instead, they have been designed as non-inferiority trials in which the experimental arm is compared with an active-control TDF-FTC arm.(10) Similar designs are likely to be employed for other trials of experimental pre-exposure prophylaxis agents for the foreseeable future.

The primary measure of efficacy proposed for these studies is the HIV rate ratio comparing the experimental and standard agents, generalising the approach used in earlier placebo controlled trials.(7, 10) In this paper we point out fundamental difficulties in the interpretation of this measure, argue that additional contextual information is needed, and propose an alternative measure of effectiveness which explicitly incorporates this information. Our new measure is conceptually simple, has clinical and public health relevance, and should allow the use of much smaller sample sizes in trials evaluating experimental pre-exposure agents.

AVERTED INFECTIONS AND AVERTED INFECTIONS RATIO (AIR)

We introduce the concept of “averted infections” using data from the Partners PrEP Study.(11) In this trial, HIV-seronegative partners in sero-discordant heterosexual couples were randomised to one of three study regimens: once-daily TDF, once-daily TDF-FTC, or matching placebo. In the modified intention-to-treat analysis, a total of 82 incident HIV infections were observed: 17 in the TDF arm, 13 in the TDF-FTC arm, and 52 in the placebo arm (Table 1). TDF and TDF-FTC were both highly effective compared with placebo. TDF was slightly less effective than TDF-FTC although the difference was not statistically significant (P=0·48).

Table 1.

HIV incidence data from Partners PrEP study with estimated risk ratios (RR) and averted infections ratio (AIR)

Trial arm (subscript)	HIV incidence rate (# events/PYFU)	RR (90% CI)	AIR (90% CI)
Placebo (P)	1·99 (52/2607)	–	–
TDF-FTC (C)	0·50 (13/2616)	0·251 (0·15, 0·42)	–
TDF (E)	0·65 (17/2604)	0·331 (0·21, 0·52) 1·312 (0·72, 2·41)	0·90 (0·70, 1·15)

$\text{AIR}=\frac{{\text{λ}}_{\text{P}}-{\text{ λ}}_{\text{E}}}{{\text{λ}}_{\text{P}}-{\text{ λ}}_{\text{C}}}=\frac{1.99-0.65}{1.99-0.50}=0.90$

^1.Relative to placebo

^2.Relative to TDF-FTC

Incidence rates expressed per 100 person-years.

Formula for confidence interval for the AIR is given in the supplementary appendix

As follow-up was very similar in the three groups we can essentially focus on the numbers of observed infections. Randomisation implies that participants in the TDF and TDF-FTC arms would have experienced the same (on average) HIV incidence as the placebo arm had they not received pre-exposure prophylaxis. Thus we predict that TDF has averted 35 (52 minus 17) infections compared with placebo, and that TDF-FTC has averted 39 (52 minus 13) infections compared with placebo. The fraction 35/39 (=0.90) can be interpreted as the proportion of infections that would be averted by using TDF rather than using TDF-FTC. We propose this as a measure of relative effectiveness, which we refer to as the averted infections ratio (AIR).

STATISTICAL FORMULATION

A practically useful measure of effectiveness or efficacy needs to allow for variability in follow-up between the groups being compared. More formally, let λ_E, λ_C, and λ_P denote the incidence rate in the experimental arm, the control arm, and the placebo arm, respectively. The AIR is calculated by

$$\text{AIR}=\frac{{\text{λ}}_{\text{P}}-{\text{ λ}}_{\text{E}}}{{\text{λ}}_{\text{P}}-{\text{ λ}}_{\text{C}}}$$

The numerator is the rate difference between the placebo and experimental arms, and the denominator is the rate difference between the placebo and control arms. AIR =1 implies that the two agents are equally effective, AIR <1 that the experimental agent is less effective than the control agent, and AIR >1 that the experimental agent is more effective than the control agent. Alternative interpretations of the AIR are: (a) the ratio of the number needed to treat (NNT) for the active control agent relative to the NNT for the experimental agent(12); (b) the ratio of the effectiveness of the experimental agent relative to the effectiveness of the active control agent.

The AIR can be expressed as

$$\text{AIR }=\frac{{\text{λ}}_{\text{C}}-{\text{ λ}}_{\text{E}}+{\text{θ}}_{\text{C}} {\text{ λ}}_{\text{E}}}{{\text{ θ}}_{\text{C}}{\text{ λ}}_{\text{C}}}$$

where θ_C is the proportionate reduction in incidence (effectiveness) achieved by the control arm agent compared with placebo${\mathrm{ }(\mathrm{\theta }}_{\mathrm{C}}=\mathrm{ }1-\mathrm{ }{\mathrm{\lambda }}_{\mathrm{C}}/{\mathrm{\lambda }}_{\mathrm{P}}$). In this formulation, λ_P is indirectly estimated from the observed incidence rate in the control and arm and the assumed effectiveness of the control arm agent. Here, it also possible to define the AIR in terms of the parameters from a Cox regression model, which does not rely on the assumption that incidence rates are constant over time.

In a more precise analysis of the Partners PrEP Study based on incidence rates, the AIR (90% CI) for TDF versus TDF-FTC is 0·90 (0·70, 1·15) (Table 1), indicating that TDF averts 90% of infections relative to the number averted by TDF-FTC. The observation that the rate ratio (1·31) exceeds one is consistent with an AIR value of less than one, since the two measures have different directionality. However, a pessimistic view of the effectiveness of TDF, based on the rate ratio, would focus on the 95% upper confidence limit of 2·41, suggesting it could be potentially markedly inferior to TDF-FTC. In contrast, the analogous AIR value of 0·70 (lower 5% confidence limit) indicates a comparatively small loss of effectiveness associated with the use of TDF rather than TDF-FTC.

TWO ARM TRIALS WITHOUT A PLACEBO ARM

The major challenge in adopting the AIR is that direct estimation is not possible in active-control trials that do not include a placebo arm. In this case it is necessary to specify a value for the placebo arm incidence or the control agent effectiveness that we predict would have been observed (sometimes described as the hypothetical, putative, or counterfactual value).(13) This entails the specification both of the value itself and the uncertainty in this value, the latter being required to obtain a valid confidence interval for the AIR. Bayesian analysis, which involves postulating prior distributions for the model parameters, is an attractive approach to this problem.(14) A worked illustrative example is given in the Appendix, although further research is required on how to best specify the prior distributions since these strongly influence the inferences that are drawn.

An alternative approach is to plug-in a range of plausible values for one of the unobserved parameters, estimating the AIR and confidence interval each time, assuming the parameter value to be fixed. We have applied this approach to the Partners PrEP Study, where we pretend this was a two arm active-active control trial and do not use the information in the placebo arm (Figure 1). Several important conclusions can be drawn from this analysis. First, if the active control agent is highly effective (or, equivalently, the true placebo incidence is much higher than the active control incidence) then a slight misspecification of the unobserved parameter is inconsequential since the curve is comparatively flat in this region. Second, low values for the unobserved parameter map to low values for the AIR. Third, the lower confidence limit is more sensitive to misspecification than the point estimate. Finally, the lower confidence limit can be used to determine the minimum value of the unobserved parameter that achieves a target threshold for the AIR. Thus, we can be reasonably confident that the true AIR is greater than 0·5 if the placebo incidence exceeds 1·31 per 100 PY or the active control effectiveness exceeds 74%.

Figure 1.

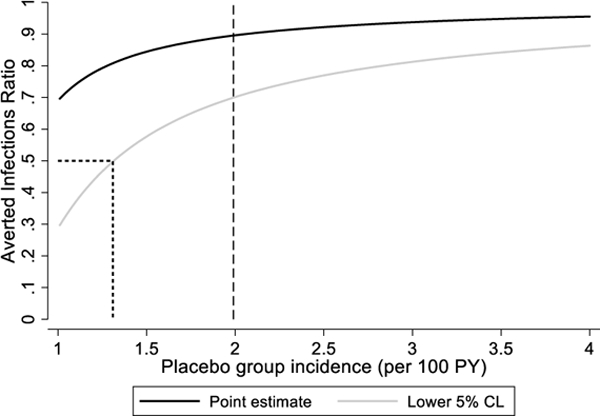
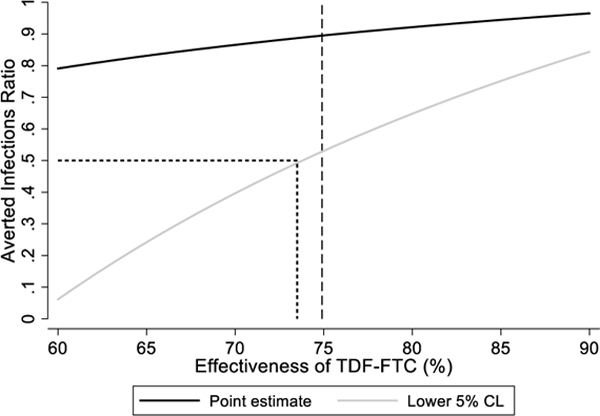
Sensitivity analysis of averted infections ratio (AIR) in Partners PrEP Study supposing there was no placebo arm. The estimated AIR and corresponding lower 5% CL are plotted as a function of (A) the assumed placebo incidence rate and (B) the assumed effectiveness of TDF-FTC.

Footnote

Dashed line shows the actual values observed in Partners PrEP Study. In actual applications of this approach this information would not be available.

Dotted line shows unobserved value corresponding to AIR of 50%.

ESTIMATING PLACEBO INCIDENCE OR CONTROL AGENT EFFECTIVENESS

Several empirical approaches for estimating the unobserved placebo incidence or control agent effectiveness are outlined in Table 2. All of these are subject to bias, imprecision, or both, but Figure 1 shows there is some leeway and that we can draw conservative inferences about the AIR by plugging-in a conservatively low value for the unobserved parameter. A detailed discussion of the approaches in Table 2 is beyond the scope of this article but we make a few general comments below.

Table 2.

Possible approaches for estimating HIV incidence in hypothetical placebo group or effectiveness of the control drug in an active-control trial

Unobserved parameter	Approach	Validity
HIV incidence in hypothetical placebo group	Run-in period without active treatment or Trial within a Cohort (TwiC) i.e. establish a cohort of individuals potentially interested in PrEP before trial drug becomes available.(7, 24)	Potential interest does not equate to agreement to be randomised. Number of infections usually small and estimates therefore imprecise. Potentially inaccurate if long period of follow-up and change in HIV incidence over time.
	Recent HIV prevention studies in the same geographic region in population with similar characteristics	Potentially unreliable if HIV incidence changing rapidly
	Estimates from epidemiological surveillance systems(4)	Likely to under-estimate incidence as diluted by low-risk individuals testing largely for reassurance
	Infer incidence from tests for recent infection on baseline samples(8)	Number of recent infections usually small and estimates therefore imprecise. Incidence just prior to trial entry may not reflect incidence over whole follow-up period.
	Measure STI incidence within trial, and calibrate from ecological association between incidence of HIV and other STIs	Ecological association not strong. HIV incidence possibly less stable than that of common STIs such as gonorrhoea.
Effectiveness of active control drug (versus placebo)	Meta-analysis of previous trials comparing active control to placebo(1)	Hinges on “constancy” assumption i.e. that effectiveness can be validly extrapolated from meta-analysis (but studies often highly heterogeneous)
	Measure adherence within trial and infer effectiveness from meta-regression or PK/PD models(7, 25)	Elicited adherence often inaccurate. Drug levels more reliable but expensive to collect samples.

We first consider estimation of placebo incidence. HIV prevention trials have traditionally been preceded by observational cohort studies to identify study populations with a sufficiently high HIV incidence.(15) The same approach could be considered for pre-exposure prophylaxis trials in settings without routine access to this intervention. Ethical issues are complex, however, since, unlike most other biomedical interventions to prevent HIV, pre-exposure prophylaxis is known to be highly efficacious. Nonetheless, there are often delays in securing investigational medical product, which provides a window of opportunity for estimating HIV incidence while not clearly breaching ethical boundaries. Second, estimates of HIV incidence from surveillance data may be available in some settings. However, the PROUD study under-scored the danger of relying exclusively on this source of information: national estimates of HIV incidence reported for MSM attending sexual health clinics were similar to the observed incidence among MSM randomised to immediate pre-exposure prophylaxis arm but 7-fold lower than the observed incidence among those randomised to deferred therapy.(4) Third, there is current research interest in measuring STI incidence during a trial and using this to predict HIV incidence based on models of ecological association. Although finding a high incidence of STIs is irrefutable evidence of risky sexual behaviour, it does not establish a high index of exposure to HIV, and it would be surprising if this association was sufficiently strong for useful quantitative prediction.

Estimating the effectiveness of TDF-FTC, the usual active control agent, is more straightforward in principle since we can draw upon the results of previous placebo controlled trials. However, highly variable results have been observed, thought to reflect variation in levels of adherence.(7) Thus the problem of estimating effectiveness in the current trial remains highly challenging. It would seem more appropriate to base predicted effectiveness on previous trials which are thought to be broadly analogous rather than an indiscriminate average of all previous estimates. An alternative approach which holds promise is to measure adherence in the current trial and to use meta-regression or the results of PK-PD models to infer effectiveness.(1, 5, 7)

LIMITATIONS OF THE RATE RATIO, CONTRAST WITH AIR

We consider a series of pairs of hypothetical two-arm active-control trials which highlight key problems in the interpretation of the rate ratio and show that these are obviated by using the AIR (Table 3). Note that the rate ratio is the same within each pair of studies. We also assume, for the purposes of exposition, that the unobserved placebo incidence is known.

Table 3.

Examples illustrating the rate ratio (RR) and the averted infections ratio (AIR) for hypothetical trials of prophylactic agents

Trial	Incidence rate (# events)		RR (90% CI)	Incidence rate, hypothetical placebo arm	AIR (90% CI)
	Experimental agent	Active control (TDF-FTC)
A	2 (40)	2 (40)	1.0 (0.69, 1.44)	5	1.0 (0.78, 1.28)
B	2 (40)	2 (40)	1.0 (0.69, 1.44)	2	ND
C	2 (40)	2 (40)	1.0 (0.69, 1.44)	5	1.0 (0.78, 1.28)
D	1 (20)	1 (20)	1.0 (0.59, 1.68)	5	1.0 (0.88, 1.14)
E	2 (40)	1 (20)	2.0 (1.27, 3.14)	2	0.0 (ND)
F	2 (40)	1 (20)	2.0 (1.27, 3.14)	5	0.75 (0.62, 0.91)

2000 person-years follow-up in experimental and active control arms in all trials.

Incidence rates expressed per 100 person-years.

Hypothetical placebo arm rate assumed to be known in derivation of CI for the AIR

ND, not defined

First, consider trials A and B which both find the same incidence rate (2 per 100 PY) in the experimental and active control arms. At face value, the rate ratio of 1·0 implies that the two agents are equally effective. In trial A, this is a logical conclusion since each arm shows 60% lower incidence compared with placebo (from 5 per 100 PY). However, in trial B the placebo incidence is the same as in the two treated arms. The only possible explanation of this finding, given the high known biological efficacy of TDF-FTC, was that this trial was conducted in a highly non-adherent population and has therefore produced no evidence about the comparative effectiveness of the two agents. Note that the AIR is, appropriately, undefined (zero divided by zero). In trials C and D the rate ratio is also 1·0 but trial C has a narrower 90% confidence interval (0·69–1·44) than trial D (0·59–1·68), a function of the higher incidence and larger number of events (40 per arm compared with 20 per arm). This suggests that trial C has produced the stronger evidence of prophylactic equivalence. However, the placebo incidence (5 per 100 person-years) reveals that effectiveness was higher in trial D (80% reduction in incidence) than in trial C (60% reduction). Paradoxically, the trial conducted in the more adherent population gives less precise inference on a rate ratio scale. The AIR does not suffer from this limitation, and yields a narrower 90% confidence interval for trial D (0·88–1·14) than trial C (0·78–1·28). Finally, consider trials E and F, where the rate ratio of 2·0 is correctly interpreted as evidence that the experimental agent is less effective than the active control agent. However, knowledge of the placebo incidence is essential to show that the experimental agent confers no protection at all as observed in trial E (AIR=0·0). Also, in trial F the rate ratio of 2·0 indicates that the experimental agent is substantially inferior, whereas the AIR of 0·75 indicates that it would nonetheless prevent most of the infections prevented by the active control agent, and might be a viable preventative option.

Finally, we note that the rate difference between the experimental and active control arms has also been proposed as a possible measure of effectiveness.(7) The rate difference has one important advantage over the rate ratio, in that its confidence interval becomes narrower rather than wider as the effectiveness of the agents increases (and the number of HIV endpoints decreases). However, the rate difference suffers from the same complication of interpretation as the rate ratio: it is close to zero either when the two agents are both highly effective or when the two agents have a minimal effect on HIV incidence. Although we have created artificial hypothetical trial results to illustrate points of principle, the findings from actual trials may not be that dissimilar, with the same challenges of interpretation.

DEFINING NON-INFERIORITY

Because of the high efficacy of TDF-FTC most active-control pre-exposure prophylaxis trials are being designed as non-inferiority studies. The primary aim of such studies is to show that HIV incidence is not unacceptably higher with the experimental agent than with TDF-FTC. This is formally judged by whether the observed confidence limit (lower or upper, as appropriate) for the primary outcome measure exceeds a pre-defined non-inferiority margin. A “preservation of effect” argument is often used as a basis for this margin i.e. to aim to show that the experimental agent preserves a minimum fraction of the effect of TDF-FTC relative to placebo or no treatment.(16, 17) Although this value is typically set at 50%, this is arguably too low given the high efficacy of TDF-FTC and the clinical and public health importance of preventing HIV infections.

It is also important to recognise that “effect” can be measured in several different ways and that the choice of this is arbitrary. The current, standard approach in pre-exposure prophylaxis trials is to assess non-inferiority based in terms of the logarithm of the rate ratio, but this lacks clear clinical interpretation.(7) In contrast, the AIR is a natural “preservation of effect” criterion for assessing non-inferiority, with the additional advantage of encouraging a focus on estimation rather than significance testing.(18)

SAMPLE SIZE

Sample size calculations based on the AIR depend on whether it is calculated via the assumed placebo incidence or the control agent effectiveness. If the latter is used we can make direct comparisons with sample sizes derived under the conventional approach, for equivalent values of statistical power and the non-inferiority margin. Under the usual assumption in non-inferiority trials that the experimental and active control agents are equally effective, the conventional approach requires a larger sample size (whether expressed as person-years follow-up or the number of events), with the magnitude depending on the effectiveness of the pre-exposure prophylaxis agents and the non-inferiority margin (i.e. the fraction of the effect of active control agent we aim to preserve) (Figure 2). If this is set at 50%, the same statistical power is achieved with a 27% to 46% smaller sample by using the AIR compared with the conventional approach, over a plausible range of values (50–80%) for the assumed active control agent effectiveness. Sample size savings are even larger if a more stringent non-inferiority margin is used.

Figure 2.

Ratio of sample sizes required under the standard analytical approach compared to using the AIR, for non-inferiority trials.

Footnote

See Appendix for mathematical derivation.

DISCUSSION

The key message of our paper is that the interpretation of active-control pre-exposure prophylaxis trials requires an implicit comparison with a hypothetical placebo group, to provide a context for the number of HIV infections observed in the active arms. This requires an assumption about one of two parameters: either the incidence rate that trial participants would have experienced had they not received pre-exposure prophylaxis or the effectiveness of the active control agent within the trial. Although neither parameter is directly observed due to the absence of a no-treatment arm, this problem needs to be confronted regardless of beliefs about the most appropriate statistical analysis. We strongly favour taking an explicit, quantitative approach, rather than simply conceding that the problem exists. If one is prepared to do this, the AIR provides an intuitive and clinically meaningful measure of the relative effectiveness of the experimental agent. We acknowledge the major challenge in reliably specifying either of the unknown parameters due to the wide variability between populations in HIV incidence and the effectiveness of TDF-FTC. A similar measure to the AIR was proposed ten years ago in the field of clinical depression but appears to have been rarely applied in practice.(19)

The AIR can be applied equally in regulatory trials, where the primary interest is estimating biological efficacy (i.e. outcomes under ideal conditions) and in non-commercial health services research trials, where the primary interest is estimating effectiveness (i.e. outcomes in real-life clinical practice). The key factor that differentiates efficacy and effectiveness in the context of pre-exposure prophylaxis is adherence to trial medication. Regulatory trials typically aim to equalise adherence between trial arms (e.g. through blinding) whereas differential non-adherence may be a natural phenomenon which one does not want to influence in non-regulatory trials.

The major challenge in using the AIR is specifying the unobserved parameter, and one objection from regulators might be that this is an inexact science which relies on non-randomised, external data. One solution might be to appoint an expert committee which is independent of the trial sponsors to review relevant external evidence. This issue should be less problematic in non-regulatory trials where there is no binary decision to be made (i.e. to approve or not approve the experimental agent). Here, sensitivity analyses similar to those shown in Figure 1, or a Bayesian analytical approach, could play an important role. It is also important to emphasise that TDF-FTC has set a very high bar and that other interventions which confer lower biological protection may nonetheless be cost-effective – for example, drug-containing vaginal rings in populations with difficulty in adhering to daily, oral TDF-FTC.(20) In this context, it is more relevant to estimate the absolute efficacy or effectiveness (compared with no treatment) of the experimental intervention. Finally, the use of the AIR is not limited to HIV pre-exposure prophylaxis, but could be applied to the evaluation of any prevention modality, for which there is a pre-existing effective intervention.

There is a widespread concern in the HIV prevention research community about the size, financial cost, and opportunity-costs of trials of experimental pre-exposure prophylaxis agents under the current design-analysis paradigm. In particular, very large sample sizes are required to generate sufficient HIV endpoints (typically more than 100) to establish non-inferiority as currently defined.(10) In light of evidence of recent rapid declines in HIV incidence in some MSM populations(21, 22) and the very high effectiveness of TDF-FTC(23), achieving such sample sizes is becoming impracticable. Our analyses indicate that adopting the AIR would allow the use of substantially smaller sample sizes and therefore produce significant cost savings. Creative thinking around new ways to assess pre-exposure prophylaxis potential agents, acceptable to researchers, sponsors, regulators, and patients, is urgently required. The AIR, while not a panacea, is an important contribution to this debate.