GW170817, general relativistic magnetohydrodynamic simulations, and the neutron star maximum mass

Abstract

Recent numerical simulations in general relativistic magnetohydrodynamics (GRMHD) provide useful constraints for the interpretation of the GW170817 discovery. Combining the observed data with these simulations leads to a bound on the maximum mass of a cold, spherical neutron star (the TOV limit): $M_{max}^{\text{sph}}\lesssim 2.74/\beta$, where β is the ratio of the maximum mass of a uniformly rotating neutron star (the supramassive limit) over the maximum mass of a nonrotating star. Causality arguments allow β to be as high as 1.27, while most realistic candidate equations of state predict β to be closer to 1.2, yielding $M_{\text{max}}^{\text{sph}}$ in the range 2.16–2.28M_⊙. A minimal set of assumptions based on these simulations distinguishes this analysis from previous ones, but leads a to similar estimate. There are caveats, however, and they are enumerated and discussed. The caveats can be removed by further simulations and analysis to firm up the basic argument.

I. INTRODUCTION

The long-sought premise of multimessenger astronomy was recently realized with the detection of a gravitational wave (GW) signal from a low-mass binary system by the LIGO/VIRGO detectors [1]. Event GW170817, which was accompanied by a short γ-ray burst (sGRB), revealed that if the compact objects have a low dimensionless spin (χ ≤ |0.05|), then the inferred masses of each component of the binary and its total mass are m₁ ∈ (1.36, 1.60)M_⊙, m₂ ∈ (1.17, 1.36)M_⊙, and $m_1+m_2={2.74}_{-0.02}^{+0.04}{M}_{\odot }$, respectively. This strongly suggests a merging binary neutron star system (NSNS) as the source of GW170817, although it cannot rule out the possibility that one of the binary companions is a stellar-mass black hole (BH). Evidence that such low-mass black holes (LMBHs) exist is very weak (see e.g. [2] for a summary of possible LMBH formation mechanisms and routes by which they may arise in binaries with NS companions). Since the usual mechanisms believed to generate stellar-mass BHs, such as the collapse of massive stars, result in BHs with masses significantly larger, we tend to rule out a BHNS merger as a possible source of GW170817.

The coincident sGRB (GRB 170817A) of duration T₉₀ = 2 ± 0.5 s was detected by the Fermi Gamma-Ray Burst Monitor [3,4] and INTEGRAL [5,6] 1.734 ± 0.054 s after the GW170818 inferred binary coalescence time, at a luminosity distance of ${40}_{-8}^{+8}$ Mpc in the galaxy NGC 4993. Here T₉₀ denotes the time during which 90% of the total counts of γ-rays have been detected. The burst exhibited an atypically low luminosity (L ~ 10⁴⁷ erg/s) and the absence of an afterglow during the first days, which has been attributed to the off-axis viewing of GRB emission (see e.g. [7,8]). It is likely that its volumetric value is much larger and comparable to typical sGRB values. Subsequent optical/infrared transients consistent with kilonova/macro-nova models were also observed (see e.g. [9–11]).

One of the most important puzzles in high energy astrophysics is the ground state of matter at zero temperature, which is closely related to the maximum gravitational mass, $M_{\text{max}}^{\text{sph}}$, of a nonrotating, spherical NS [12]. To date the largest pulsar masses observed are 2.01 ± 0.04M_⊙ for J0348 + 0432 [14], and 1.928 ± 0.017M_⊙ for J1614-2230 [15], but the quest for a firm upper limit on the mass of a NS has a long history [16] that started in 1974 by Rhoades and Ruffini [17]. Their argument involved a matching mass-energy density ρ_m below which the equation of state (EOS) is well known, while from that point on a causal EOS for the pressure P (P = ρ + const) is invoked. [18] This upper mass limit depends on the matching density [20], and assuming ρ_m = 4.6 × 10¹⁴ gr/cm³ ≈ 1.7ρ_nuc they obtained an upper limit of $M_{\text{max}}^{\text{sph}}=3.2M_{\odot }$. As the matching density increases the maximum mass for a spherical star decreases as ${\rho }_m^{-1/2}$. For example, in [21] where the confidence of the EOS was taken to be up to ρ_m = 2ρ_nuc, a maximum mass of 2.9 M_⊙ was obtained (see [22] for recent review). In [23] a parametrized piecewise-polytropic fitting was introduced in order to make a systematic study of different constraints placed on high density, cold matter, including the causality constraint. More recently and from another point of view, based on the sGRB scenario, a survey of a wide EOS parameter space and matching densities using plausible masses for a NS merger remnant concluded that $M_{\text{max}}^{\text{sph}}\approx 2-2.2M_{\odot }$ [24]. At high matching densities the core has negligible mass and the upper bound becomes independent of ρ_m. In [25] Newtonian merger simulations with different EOS, resulted in an upper bound of 2.4M_⊙.

With the discovery of GW170817, [26] used electromagnetic (EM) constraints on the remnant imposed by the kilonova observations after the merger, together with GW information, to make a tight prediction of $M_{\text{max}}^{\text{sph}}\le 2.17M_{\odot }$ with 90% confidence. They argued that the NSNS merger resulted in a hypermassive NS (HMNS; [27]) that collapses to a BH in ≈10–1000 ms, producing the observed kilonova ejecta expanding at mildly relativistic velocities. By contrast, [28] summarized a broad number of their relativistic hydrodynamic simulations favoring a long-lived, massive NS surrounded by a torus to support their inferred requirement of a strong neutrino emitter that has a sufficiently high electron fraction to avoid an enhancement of the ejecta opacity. To get such remnants one needs an EOS with a high value of $M_{\text{max}}^{\text{sph}}$, which they place between 2.15–2.25M_⊙. Although the authors disfavor the scenario of a BH-accretion disk system as a weak neutrino emitter, they remind us that there is no current consensus and more simulations are needed to address this point.

Here we introduce a new ingredient into the arguments put forward previously to narrow down possible merger outcomes. In particular we focus on GRMHD simulations that we performed recently, as well as some that we are currently performing, to argue that to have a sGRB as in GW170817 the merger remnant is likely an HMNS that undergoes delayed collapse. We also pinpoint how the GW170817 data can be combined with causality arguments to establish an interesting NS upper mass limit. In the process we identify the caveats that underlie this determination and thereby indicate areas for future investigation.

II. ASSUMPTIONS

In this work we make the following assumptions which we justify in the following section.

1. GW170817 and the associated sGRB result from the merger of an NSNS;

2. A BH arises following the formation of an HMNS that undergoes delayed collapse soon after the NSNS merger;

3. The sGRB is powered by the spinning BH accreting gas from a circumstellar, magnetized disk formed from NS tidal debris;

4. To trigger the sGRB a collimated, magnetically confined, helical jet was launched from the poles of the spinning BH remnant.

III. JUSTIFICATION AND CAVEATS

Here we discuss the above assumptions in order.

• (i)NSNS and BHNS mergers are the most promising and widely accepted models for a central engine capable of powering an sGRB [29–39], which is supported by the first detection of a kilonova associated with the sGRB “GRB 130603B” [40,41]. Given little evidence for LMBHs in the mass range compatible with either companion in GW170817 (≲1.6M_⊙), we consider only NSNS systems in our analysis.
• (ii)All GR simulations show that immediately after the NSNS merger the remnant is a differentially rotating NS that has undergone shock heating following contact. The configuration either settles into quasie-quilibrium in a couple of rotation periods, or undergoes prompt collapse. A combination of GWemission, magnetic winding, turbulent viscosity and neutrino cooling radiate away or redistribute some of its angular momentum, driving the core toward rigid rotation [42]. There are several possible final outcomes that can be split into two broad categories [43,44]:

  1. The NS remnant has a mass below the supramassive limit [45], which for a given EOS is the maximum mass of a uniformly rotating NS. This case can lead to the following possible scenarios:

     • (1a) If the mass is smaller than the maximum spherical limit, $M_{\text{max}}^{\text{sph}}$, then it will live for a very long-time as a spinning NS until, e.g., pulsar magnetic dipole emission causes its spindown once the tidal debris is cleared away. Without a BH and its ergosphere [46] to launch a collimated jet and power an sGRB after merger, this scenario is unlikely to have occurred in GW170817.
     • (1b)If the mass of the remnant is larger than $M_{\text{max}}^{\text{sph}}$ then the same mechanism as in (1a) will lead to BH formation close to the turning point [47,48]. This possibility is also unlikely since the spindown timescale to BH formation is longer than the observed times from GW170817 (~100 s [49]). [But see [7] for an alternative argument based on kilonova considerations.]

  2. The remnant has a mass above the supramassive limit, i.e., it is a (transient) HMNS supported primarily by differential rotation [27].

     • (2a)If its mass is below a critical threshold, M_thresh, which also depends on the EOS, the HMNS will persist for many orbital periods, but eventually will undergo delayed collapse as its angular momentum support is driven off by GWs, magnetic winding, etc. Little mass is ultimately ejected (numerical simulations indicate ≲0.01M_⊙ [7] although observations suggest that this number can be up to 0.05M_⊙ [50]) and ≲5% of the total rest-mass of the system goes into a disk around the BH [7,51], depending on the EoS.
     • (2b)Above M_thresh, the HMNS will undergo prompt collapse on a short dynamical time scale [43,52].

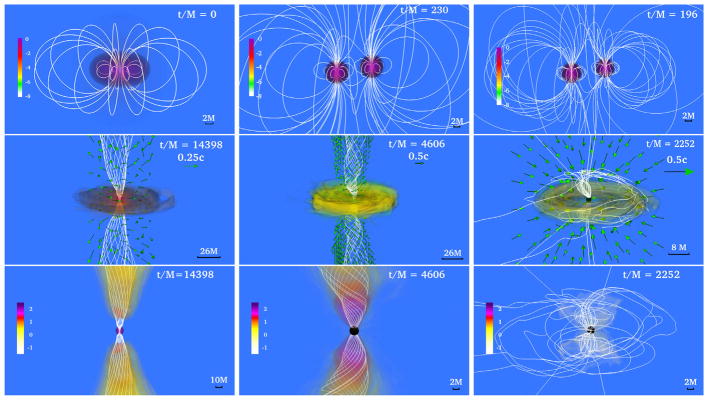
Case (1b) results when the merger remnant of an NSNS is a highly magnetized, supramassive NS [45]. We recently modeled this scenario by considering a differentially rotating NS seeded with an interior and exterior dipolelike magnetic field that is initially dynamically unimportant [53]. This case is depicted in Fig. 1, first column. Our preliminary numerical simulations do not exhibit evidence of jet formation, nor does a force-free magnetosphere arise, which is necessary for, e.g., the Blandford-Znajeck (BZ) mechanism to power a collimated jet Poynting luminosity. Thus remnant NS, which may arise and live arbitrarily long following the merger of a NSNS, probably cannot power an sGRB. However, very long simulations are required to completely rule out this scenario. On the other hand, depending on the strength of the magnetic field, the above remnant can be a long-lived magnetar. Now [26] points out that delayed x-ray emission observed after many sGRBs suggest the presence of magnetars and raise doubt about whether BH formation is a strict requirement to produce sGRBs. But GW170817 showed no evidence for such high-energy emission [10], which is a property of a long-lived magnetar [54,55]. A magnetar remnant can release part of its rotational energy through strong magnetic dipole radiation, which accelerates the ejected matter and produces very bright x-ray emissions [7]. These two features are not observed along with the optical/infrared transients in GW170817 [9,10], and therefore, the magnetar scenario is also unlikely [26]. Isolated NSs can, in principle, trigger the BZ mechanism if the NS spacetime exhibits ergoregions [46,56]. However, NSs supported by realistic EOSs probably cannot form ergoregions [57]. Since these configurations are unstable or marginally stable under scalar and EM perturbations [58] the probability of their significance is low.

FIG. 1.

Snapshots of the rest-mass density, normalized to its initial maximum value (log scale), for a supramassive remnant that persists, [first column, case (1b)], a HMNS remnant that undergoes delayed collapse [second column, case (2a)], a HMNS remnant that undergoes prompt collapse [third column, case (2b)]. First row shows NSs at the time of B-field insertion; second row shows the final quasistationary remnants. Third row shows the B²/(8πρ₀) field (log scale), the magnetic lines emanating from the remnant poles, and the fluid velocity flow vectors. The field lines form a tightly wound helical funnel and drive a jet in delayed collapse, but not in the other two cases. Here M = 0.0136(M_tot/2.74M_⊙)ms = 4.07(M_tot/2.74M_⊙)km.

Case (2a) is the scenario most favored by our GRMHD simulations and is depicted in Fig. 1, second column. It gives rise to an interesting upper mass limit which we discuss in Sec. IV.

For scenario (2b) our recent GRMHD simulations [59] show that remnants that undergo prompt collapse do not have time to sufficiently amplify their poloidal magnetic fields and overcome the ram pressure of the residual tidal debris near the polar regions of the star. As a result the polar regions above the resulting BH never achieve the necessary force-free conditions (characterized by B²/(8πρ₀) ≫ 1, as in a pulsar magnetosphere, where B is the magnetic field and ρ₀ is the rest mass density) capable of launching a jet and powering an sGRB. This case is depicted in Fig. 1, third column. Therefore these preliminary simulations tend to rule out the prompt collapse scenario as a possible origin of GW170817.

• (iii)A spinning BH-disk system is the most promising and widely accepted model for a central engine capable of powering an sGRB. Several distinct mechanisms invoking such a system have been proposed to trigger an sGRB [30,31,60–64]. One of the most successful and the subject of the most detailed studies is the BZ mechanism [65], which requires the disk to be threaded by a poloidal magnetic field that connects gas in the disk to footpoints near the BH poles. Alternative sGRB mechanisms driven by neutrinos alone appear to be inadequate [66,67], so magnetic fields likely play a crucial role. Many numerical simulations have been performed in GRMHD of magnetized disk accretion onto spinning BHs in stationary Kerr spacetimes [68–72]. The accretion exhibits BZ behavior and results in a significant Poynting jet luminosity. Our recent GRMHD numerical simulations of magnetized, merging NSNSs that form HMNSs and undergo delayed collapse track the late binary inspiral, through merger and BH-disk formation, and then continue until a quasistationary state is reached [51]. The result is a spinning BH remnant in a highly magnetized circumstellar disk that can power an sGRB via the BZ mechanism.
• (iv)Most models of sGRB require that the main conduit through which energy flows from the central BH engine to the outer regions where γ-rays and other forms of EM emission are generated is a relativistic jet. Such a jet is a key signature of the BZ mechanism. The jet is confined inside a force-free region by a tightly wound, helical magnetic field that emanates from the poles of the spinning BH and extends to very large radii. Our preliminary simulations show the clear formation of a bonafide incipient jet with these characteristics [51] (see Fig. 1, column 2). In particular, we found that NSNS mergers that undergo delayed collapse can launch a magnetically-driven jet after ~43(M_NS/1.625M_⊙)ms following the merger. The disk lifetime, which may be comparable to the burst duration, T₀, and its EM luminosity, were found to be τ_disk ~ 0.1 s and L_EM ~ 10⁵¹ erg s⁻¹, respectively, consistent with typical short sGRBs (see e.g. [73,74]). Different EOSs, NS mass ratios and spins, initial B-field topologies, and possibly neutrinos, affect the amount and composition of the ejecta during NSNS coalescences [75–80], and therefore, the ram pressure produced by the fall-back debris, as well as the mass of the accretion disk. The delay time for jet launching following the merger, as well as its lifetime, may therefore depend on these parameters. This may explain the delay time (~1.7 s) between the inferred merger time of GW170817 and the sGRB. Other processes associated with the sGRB γ-ray energy reprocessing mechanism may also contribute to the delay.

A few caveats remain regarding the GRMHD simulations in [51,59]. These preliminary equal-mass, irrotational binary studies adopt idealized, Γ-law EOSs (Γ = 2), adiabatic evolution (except for shocks), and aligned initial magnetic fields. They enabled us to provide a “proof of principle” regarding jet formation and Poynting jet luminosity beams. That GW170817 has an atypically low γ-ray luminosity (L ~ 10⁴⁷ erg/s) several orders of magnitude smaller than typical sGRBs, can be attributed to an off-axis viewing [7,8]. A more extensive parameter survey incorporating realistic hot, nuclear EOSs, different binary mass ratios and spins, different initial B-field topologies, and neutrino transport are required to corroborate the above conclusions.

IV. MAXIMUM MASS

Invoking scenario (2a) of Sec. III, favored by our GRMHD simulations, and noting that the total initial gravitational mass of the NSNS binary in GW170817 is M_NSNS ≈ 2.74M_⊙ we have

$$M_{\text{NSNS}}\approx 2.74\lesssim M_{\text{thresh}}\approx \alpha M_{max}^{\text{sph}}.$$ (1)

Here α ≈ 1.3–1.7 is the ratio of the HMNS threshold mass limit to the NS spherical maximum mass as gleaned from multiple numerical experiments of merging NSNSs [81–85]. We also have that

$$M_{\text{NSNS}}\approx 2.74\gtrsim M_{max}^{sup}\approx \beta M_{max}^{\text{sph}},$$ (2)

where β ≈ 1.2 is the ratio of the uniformly rotating supramassive NS limit to the nonrotating spherical maximum mass as determined by numerical studies of multiple candidates for realistic cold, nuclear EOSs [86–88]. Now if one uses a Rhoades-Ruffini causality argument for the maximum mass of a nonrotating as well as a uniformly rotating star [89,90], one obtains

$$M_{\text{max}}^{\text{sph}}=4.8{\left(\frac{2\times {10}^{14}\text{gr}/{\text{cm}}^3}{{\rho }_m/c^2}\right)}^{1/2}{M}_{\odot },$$ (3)

$$M_{max}^{sup}=6.1{\left(\frac{2\times {10}^{14}\text{gr}/{\text{cm}}^3}{{\rho }_m/c^2}\right)}^{1/2}{M}_{\odot },$$ (4)

from which β ≈ 1.27. Combining Eqs. (1), (2) we arrive at

$$2.74/\alpha \lesssim M_{max}^{\text{sph}}\lesssim 2.74/\beta .$$ (5)

Since α ≳ β > 1, Eq. (5) is self-consistent. Adopting the causal EOS above sets a TOV mass limit as low as $M_{max}^{\text{sph}}\lesssim 2.16$. However, most existing realistic EOS candidates give β = 1.2 (see [87,88,91], which gives a more conservative mass limit $M_{max}^{\text{sph}}\lesssim 2.28$.

Uncertainties in the EOS allow the high value of β that yields the low maximum mass. In particular, an EOS might be sufficiently stiff above a some (matching) density to produce a stiff core and still be compatible with current NS observations, including GW170817. Such a core is allowed by our causal EOS and is responsible for the high value of β. Our inability to calculate the dense matter EOS in QCD from first principles permits such a possibility. On the other hand, the discovery of a NS with a higher mass would rule out the presence of such a stiff core.

The error bar on this upper limit comes from the uncertainty in the remnant mass as well as the β parameter. According to the LIGO/VIRGO measurement, the mass on the numerator in Eq. (5) is ${2.74}_{-0.01}^{+0.04}$, i.e. it has an uncertainty of the order of 1.5%, and additionaly one has to take into account that a small percentage of the total mass will be ejected or radiated away. So, we can conservatively expect a total error less than 6.5% (1.5% from the LIGO/VIRGO mass measurement plus ~5% from possible ejecta and radiation) for the remnant mass that comes into Eq. (5). The uncertainty in the β parameter is more difficult to estimate since there is no systematic study of causal realistic EOSs currently. For a spread of realistic EOSs this error is close to 2% [88] and the expectation is that will remain the same when one considers causal EOS since both the spherical maximum and the Keplerian limit will be affected in the same way. Combining both errors one arrives at a maximum mass $M_{max}^{\text{sph}}$ between 2.16 ± 0.23 and 2.28 ± 0.23. In this analysis we considered low-spin priors |χ| < 0.05 since the fastest known pulsar in a binary has χ ≤ 0.05 and in general one does not expect spins higher than 0.5 [92]. If one assumes instead that χ ≤ 0.89 for which the remnant mass is ${2.82}_{-0.09}^{+0.47}$ [1] then the limit will be modified to give $M_{max}^{\text{sph}}$ between 2.22 ± 0.66 and 2.35 ± 0.66, but we regard this as unlikely.

Corroboration of the GRMHD scenario requiring delayed collapse of an HMNS remnant to generate a jet and a sGRB central engine will support this low estimate for the maximum mass.