A novel method for improved accuracy of transcription factor binding site prediction

Abstract

Identifying transcription factor (TF) binding sites (TFBSs) is important in the computational inference of gene regulation. Widely used computational methods of TFBS prediction based on position weight matrices (PWMs) usually have high false positive rates. Moreover, computational studies of transcription regulation in eukaryotes frequently require numerous PWM models of TFBSs due to a large number of TFs involved. To overcome these problems we developed DRAF, a novel method for TFBS prediction that requires only 14 prediction models for 232 human TFs, while at the same time significantly improves prediction accuracy. DRAF models use more features than PWM models, as they combine information from TFBS sequences and physicochemical properties of TF DNA-binding domains into machine learning models. Evaluation of DRAF on 98 human ChIP-seq datasets shows on average 1.54-, 1.96- and 5.19-fold reduction of false positives at the same sensitivities compared to models from HOCOMOCO, TRANSFAC and DeepBind, respectively. This observation suggests that one can efficiently replace the PWM models for TFBS prediction by a small number of DRAF models that significantly improve prediction accuracy. The DRAF method is implemented in a web tool and in a stand-alone software freely available at http://cbrc.kaust.edu.sa/DRAF.

INTRODUCTION

Information on the regulation of transcription forms a basis for understanding regulatory mechanisms of gene activation or repression in living organisms. Transcription factor (TF) proteins are a key component of gene regulatory networks (1). They bind promoters and other gene regulatory regions (2) in a sequence-specific manner and control gene expression through such interactions (3). TF binding sites (TFBSs) on DNA are short sequences located in the gene regulatory regions, typically from few to about 20 base-pairs (bp) in length. Accurate detection of TFBSs is frequently an intermediate step in the computational reconstruction of gene regulatory networks (4).

Both computational and experimental methods have been used for TFBS discovery. For experimental approaches, there are numerous in vivo and in vitro high-throughput methods that have been developed, as reviewed in (5). Significant progress has been made in the experimental technologies for this purpose, enabling large-scale studies of transcription regulation. For example, high-throughput ChIP-seq experiments from the ENCODE project (6) have investigated about 200 human TFs in less than a hundred cell lines. Despite the progress that has been made, these numbers are far lower than the estimated number of TFs that are encoded in the human genome or that might regulate a single tissue (7). Therefore, the need for efficient computational methods to predict TFBSs remains. Indeed, computational approaches for identifying TFBSs have been used successfully (8–11), varying from simple pattern matching methods to more complex models (12–15).

Pattern matching methods based on position weight matrices (PWMs) attempt to predict a TFBS by screening a candidate sequence of interest, with a model derived from experimentally determined binding sites for a TF (16). Although proposed a few decades ago PWM-type models remain the most widely used models for TFBS predictions, primarily due to their simplicity. However, a PWM model has several disadvantages. First, it is very sensitive to the quality and size of the set of TFBSs DNA sequences used to derive the PWM model (17). Second, the PWM prediction models of TFBSs frequently result in a high rate of false-positive predictions (18). Third, conventional PWMs do not model dependencies between individual positions within the TFBSs (19). Fourth, frequently one or more models for the TFBSs of a single TF are developed to capture variability among TFBS sequences and to improve individual model performance. This results in a significant number of TFBS models available in major bioinformatics resources. For example, 426 TFBS models are used to represent 401 TFs in HOCOMOCO (20), while 1082 TFBS models in JASPAR (21) represented 1059 TFs. In the TRANSFAC database (version 2012.2) (22), for 5760 TFs a total of 2170 TFBS models are used. One should note that PWM models of TFBSs do not include any information about the composition and structure of TFs that bind to them.

Obviously, there has been a challenge to develop models that predict TFBSs with high specificity and sensitivity. Classical TFBS PWM models have been improved to incorporate nucleotide k-mer relationships (23) or remote dependencies of nucleotide positions (24). Also, more flexible approaches have been implemented to develop customized models of TFBSs, such as those based on Bayesian networks (25), Hidden Markov Models (HMM) (14) and recently deep learning of Neural Networks (NN) (26). Various methods have incorporated sequence-specific and structural features of DNA for prediction of TFBSs, for example, DNA shape (27,28), or local chemical and structural properties (29). Some other approaches, like (30) used additional information such as DNA accessibility.

However, the approaches mentioned above do not use information from TFs that bind TFBSs. A lot of research has been done toward incorporating TFs properties into models for TFBS predictions with the hope to improve models and their prediction accuracy. Some examples of such work are the use of empirical protein–DNA binding energies or structure knowledge (31,32).

Also, a variety of computational approaches has been developed based on modeling TF-TFBS interactions. Qian et al. (33) used gene ontology (GO) annotations of TFs to denote the presence or absence of each GO term in the TF description in their predictive model of TF-TFBS links. This work was later extended (34) to include GO annotations of the TF target (TFT) genes in the TF-TFBS links, resulting in the use of TF-TFT-TFBS triplets that improved the accuracy of predictions. An apparent deficiency of this approach occurs when two TFs share the same GO descriptions but have different binding sites. The associated problem is that GO annotation of TFs does not have sufficient resolution and this further reduces the capability of predicting distinct TFBSs. Moreover, such methods are not applicable for studies of TFs that do not possess enough GO functional annotations. Another approach that includes the amino acid properties of TFs in a model was implemented in (35), where only six physicochemical properties of amino acids were used to describe a TF.

To reduce deficiencies of high false positive rates of the existing models and the need for a large number of models, in this study we developed a method, DRAF, for predicting TFBSs. DRAF combines in a novel manner: (i) physicochemical and structural properties of the DNA binding domains of TFs, specifically AAindex properties, the DNA binding domain family classification and the amino acid binding mode preference to DNA bases, and (ii) nucleotide sequences of TFs’ target TFBSs. To model the relationship between TFs and their associated TFBSs, DRAF uses random forests (RFs) machine learning models. Through a number of experiments, we show here that DRAF can significantly reduce the false positive rate of TFBS prediction while using small number of required TFBS prediction models. We developed only 14 DRAF models to encode the TF-TFBS relationships of 232 TFs. Each of these 14 models corresponds to one TFBS length (we used 14 models for TFBS lengths from 7 to 20). A DRAF model corresponding to one TFBS length encodes information of TF-TFBS relationships for several TFs whose binding sites are of that length. The TF-TFBS relationships of all 232 TF were possible to capture in these 14 models. Through a comprehensive comparison study, we demonstrated that for 98 human ChIP-seq datasets related to TF binding and obtained from ENCODE (6), the DRAF models generate at the same sensitivity level significantly less false positive predictions than PWM models from HOCOMOCO and TRANSFAC databases or the DeepBind (26) models. We believe that the structure and the incorporation of properties from the DNA binding domains of TFs and the way they have been used in the DRAF RF prediction models were the key to achieve this high prediction accuracy as compared to other models. The implementation of the DRAF prediction models of TFBSs is available at http://cbrc.kaust.edu.sa/DRAF.

MATERIALS AND METHODS

Datasets

TF and TFBS sequences

We used TFBS sequences from the HOCOMOCO (20) database version 9, whereby TFBSs were selected based on the PWM thresholds with a P-value < 0.0005 (as explained in (20)). P-values were computed by the MACRO-APE (http://autosome.ru/macroape, (36)). Consequently, 139,085 TFBS sequences of 426 TFBS models corresponding to 401 human TFs were obtained. Due to a larger number of parameters in the DRAF models that have to be tuned, as compared to the PWM models, we examined only TFs that have at least 15 associated TFBSs. We further discarded all TFs that did not have DNA binding domains in the Pfam database (37). This reduced the initial set of 426 TFBS models (associated with 401 TFs) to 250 TFBS models (associated with 232 TFs) with a total of 110,399 corresponding TFBS sequences (Supplementary Table S1). The amino acid sequences of these 232 TFs were obtained from UniProt (38).

TF domains

Protein domain information was obtained from the Pfam database. We used domains that are annotated as ‘DNA binding domain’ in at least three out of a total five annotation sections used in Pfam (Pfam, Seq-info, Pdb, GO and Interpro). We restricted our study to manually curated DNA binding domains (i.e. Pfam-A), having the highest significance score and an E-value of <0.1. As TFs may have multiple DNA binding domains, we selected for such TFs the domain of the lowest E-value. Finally, each TF was represented by the amino acid sequence of its associated DNA binding domain.

Modeling TF-TFBS links

Encoding TF properties

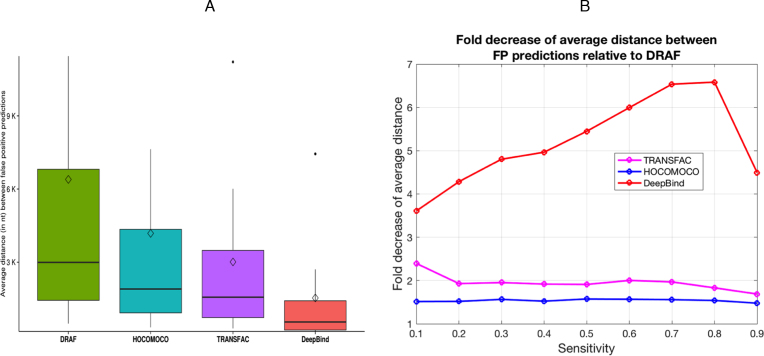
Each TF was encoded by three sets of characteristics: (i) (Properties A) the physicochemical properties obtained from the AAindex database version 9.1 (updated on 31 March 2008) (39) of amino acids within its associated DNA binding domain, (ii) (Properties B) the DNA binding domain family classification and (iii) (Properties C) the amino acid binding mode preference to DNA bases obtained from (40,41). For the first set of properties, we used numerical values of 544 physicochemical characteristics of amino acids available in the AAindex database. A feature 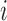of is the average value of the physicochemical property in the sequence of the DNA binding domain of weighted by the relative occurrences of individual amino acids in the sequence:

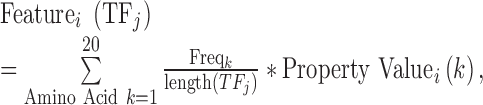(1)

where Freq_k is the number of times amino acid k is found in the sequence of the DNA binding domain of 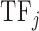; 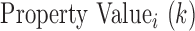is the numerical value of physicochemical property 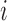for amino acid 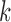; 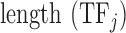is the number of amino acids in the sequence of the DNA binding domain of 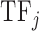. We used the same formula for each of the 544 features, which resulted in a 544-dimensional vector for each .

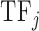Since all TF DNA binding domains that we obtained from the Pfam database belong to 72 domain families, we needed 7-binary digits (that can represent 2∧7 = 128 combinations) to encode them and this represents Properties B of TFs that we employed. While 55% of the TFs have only a single DNA binding domain, the remaining 45% have more than one and we selected one of these domains as explained earlier. Properties C of TF were determined and encoded as follows. Amino acids were classified into three categories according to their binding mode preference to DNA bases (41) (as shown in Supplementary Table S2). These categories are: (i) they bind to DNA bases through hydrogen bonds, (ii) they bind to DNA bases through van der Waals contacts or (iii) they do not have propensity to interact with DNA bases. Because the last three properties describe a TF, we used the weighted occurrence of amino acids in these three categories of amino acid binding preferences to DNA bases:

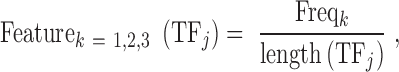(2)

where Freq_k is the total number of occurrences of amino acids that belong to category k (the three categories we described) in the sequence of the DNA binding domain of 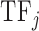; 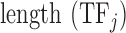is the number of amino acids in the sequence of the DNA binding domain of . Thus, the final set of features used to describe a TF consists of 554 ( = 544 + 7 + 3) features.

TFBS representation

Each TFBS that consists of L nucleotides was represented using a vector of length 4*L obtained as follows. Each of the four nucleotides (A, C, G, T) in the TFBS sequence was encoded by a four-digit binary number as follows: A as 0001, C as 0010, G as 0100 and T as 1000. A TFBS is then represented as a vector of length 4*L by concatenating the binary sequences corresponding to its nucleotide sequence as described. For example, ‘ACTCCGAT’ will be represented by ‘00010010100000100010010000011000’. The TFBSs of the selected 232 TFs (associated with 250 TFBS models) have 14 distinct lengths .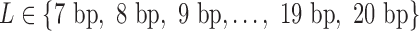

Combining TF and TFBS descriptions

Both TF and TFBS features were combined into one TF-TFBS feature vector as follows. Suppose that 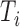and 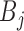are the feature row-vectors for 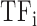and 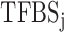, respectively. We define the combined TF-TFBS feature vector D as:

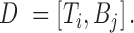(3)

For example, when 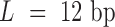, the TF-TFBS link is encoded by a 602-dimensional vector (554 TF features plus 12 × 4 TFBS features). If a TF is associated with N TFBSs, then we will have N TF-TFBS link vectors, where the first part, TF vector, remains the same across all N vectors.

Removal of duplicate feature vectors

After generating feature vectors, we kept all the 110,399 unique TF-TFBS features to train and test the DRAF models.

Data preprocessing

Normalization

To remove the bias that arises from different ranges of values used for TF and TFBS features, we normalized each feature by scaling minimum and maximum values to 0 and 1, respectively, as follows:

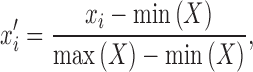(4)

where x_i is the original feature value and 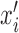is the value after normalization. X is the vector of feature values x_i across all samples. min(X) and max(X) are the minimum and the maximum values of X, respectively. In addition, the feature vectors are of different lengths due to varying TFBS lengths. Since a separate model is built for each of the 14 TFBS lengths, this does not cause any problems in the analysis.

TF feature selection

It is widely acknowledged that irrelevant and weakly relevant features may decrease the accuracy of predictions (42). We examined several feature selection methods on the training datasets, namely, the minimum redundancy maximum relevance (mRMR) method (43), individual feature ranking using the AUC (Area Under the ROC Curve) method, and the forward sequential feature selection method with 10-fold cross validation based on support vector machine (SVM) classifier and using accuracy as the evaluation function (44). Note that mRMR also uses the forward feature selection strategy combined with a backward feature selection strategy. We found that the mRMR method yielded the highest accuracy. Consequently, we used the mRMR method to identify TF properties of relevance to distinguish between the two classes of data (see the next section). We selected the top N features with the highest mRMR scores out of the initial set of 554 features. We evaluated different values of N (N = 10, 20, 30, …, 210), and found that N = 150 and N = 180 yielded the highest F-measure score (see Supplementary Figure S1). Thus, we used N = 150.

Positive (true) and negative (false) data

Positive data

The ‘positive’ dataset consists of 110,399 TF-TFBS links (‘positive’ links) that correspond to 232 TFs and their associated 110,399 TFBS sequences obtained from the HOCOMOCO data as explained earlier.

Negative data

For each TF-TFBS link we produced a presumably ‘false’ TF-TFBS link by preserving the TF feature part of the feature vector, but randomly selecting sequences from human chromosomes 4 and 22 to correspond to the ‘TFBS’ sequence part in the feature vector. These two chromosomes were used because chromosome 4 has the lowest (∼38%) GC content, while chromosome 22 is one of the two chromosomes that have the highest (∼48%) GC content among all human chromosomes. From the initial ‘negative’ TF-TFBS set, we excluded all TF-TFBS links that were also contained in the ‘positive’ dataset, which resulted in the final ‘negative’ data. ‘Positive’ and ‘negative’ data were given different class labels. Finally, for each ‘positive’ TF-TFBS link, we created 10 ‘negative’ TF-TFBS links to make the number of ‘negative’ samples 10 times higher than the number of ‘positive’ samples.

Training and test datasets

We split all data into 14 groups corresponding to the 14 different TFBS lengths that we considered. Then, separately for each of these groups, we generated training and test datasets, and based on that we developed one prediction model for each of the groups. Note that for 214 out of the 232 TFs, each of the groups was associated with mutually distinct sets of TFs assigned to the group based on length of their TFBSs, i.e. if a TF was associated with one of the groups, it did not appear associated with any of the other groups. The remaining 18 TFs were associated with two groups because they have two sets of TFBSs corresponding to different TFBS lengths. We pooled ‘positive’ and ‘negative’ datasets together, and using uniform random sampling selected 70% of the data for training and the 30% for testing. This division was made at random on the TF level, such that 70% of the TF-TFBS links of a particular TF were used for training and the remaining 30% were used for testing. Such training and testing data were pooled separately for each length of TFBSs. In addition, we performed 5- and 10-fold cross-validations for each length of TFBSs using the whole respective dataset, and reported the obtained results from each experiment. We set thresholds on the model outputs that yield the highest accuracy on the training dataset and used these thresholds when evaluating the model performance on the test datasets. The same is done in cross-validation experiments.

Random forests TFBS prediction model

DRAF uses RF (45) to model the relationship between TFs and their associated TFBSs. An RF model is an ensemble of decision tree (DT) models. The training data is divided between DTs in RF and each tree is trained with a subset of the data. This division of data occurs on the features (not the samples), such that each DT receives the entire training data for M randomly selected features (with replacement). In the testing phase, the class prediction of an unknown sample is provided by each DT and the RF model counts the votes and assigns the class label to the class with the most votes.

The TFs and the associated TFBSs are represented as TF-TFBSs links. The 250 TFBS models associated with 232 TFs fall into 14 groups according to the length of their TFBS sequences (Supplementary Table S1). We built 14 prediction models accordingly, such that one model represents all TF-TFBS links with a common TFBS length. Each prediction model is represented as an ‘RF’ composed of an ensemble of 80 decision trees. We tested a range (10, 20, …, 150) of the number of DTs in the ensemble and found that an RF composed of 80 DTs results in the highest accuracy on the training data (see Supplementary Figure S2). In the training phase, the model was trained with all TF-TFBS links in the training set that belong to ‘positive’ and ‘negative’ classes. In the testing phase, the trained model was used to predict the ‘positive’ or ‘negative’ class of a particular TF-TFBS link sample in the test dataset, after the features in the test dataset were normalized using parameters obtained from scaling of the training dataset. Tests by cross-validation were done in a standard way using the scaling as explained above, and the test results reported here were the average across all the folds.

Model evaluation metrics

The quality of the model was evaluated by accuracy, sensitivity, specificity, precision, F-measure and the Matthew’s correlation coefficient to allow for comparison with other existing prediction methods. These performance measures are defined as follows:

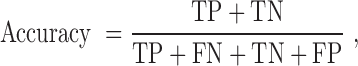(5)

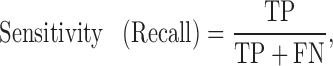(6)

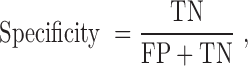(7)

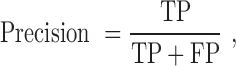(8)

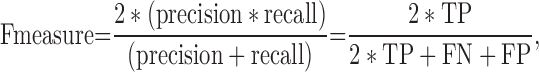(9)

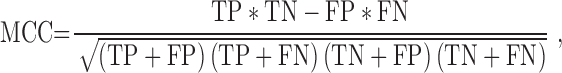(10)

TP (true positive) represents correctly predicted ‘positive’ TF-TFBS links, TN (true negative) represents correctly predicted ‘negative’ links, FP (false positive) represents ‘negative’ links incorrectly predicted as ‘positive’ links and FN (false negative) represents ‘positive’ links incorrectly predicted as ‘negative’ links.

Comparison of DRAF RF models with other machine learning model

We compared the prediction results of the DRAF RF models with three other types of machine learning models, namely NN, SVMs and Gaussian Mixture Regression (GMR) models. For each model, we set parameters to provide the highest accuracy on the training dataset. For NN, we tested the feed-forward back-propagation network with two and three hidden layers, each with either 100 or 200 neurons, and using sigmoid functions for hidden layers and a linear transfer function for the output layer. Based on the accuracy obtained from testing these options on the training data, we finally used the feed-forward back-propagation network with three hidden layers and the sigmoid transfer function, each layer with 100 neurons, and a linear output layer. The maximum number of epochs to train was set to 500 and the learning rate was set to 0.05 with the targeted maximum error of 1*10⁻⁵. For SVM (46), we tried four different types of kernels, namely linear, polynomial, radial basis and sigmoid. We used the radial basis function (46) within the LIBSVM (47) implementation of SVM, which provided the highest accuracy on the training data. We tested different values for the gamma (0.0625, 0.125, 0.25, 0.5, 1 and 2) and the regularization (cost) (0.5, 1, 2, 4 and 8) parameters. The kernel parameter values, which provided the highest accuracy on the training dataset, were set to 0.125 and 8 for the gamma and regularization parameters, respectively. For GMR, we used the implementation from (48) and tested a different number of Gaussian components (5, 10, 15, 20 and 25). We finally set the number of Gaussian components to 20 as it provided the best performance.

DRAF model validation on ChIP-seq data

ChIP-seq data

To measure the capability of the DRAF models to predict TFBSs with high sensitivity and specificity, we evaluated the DRAF models using independent ChIP-seq datasets. For this purpose, we used sequences of all human ENCODE ChIP-seq peaks that were processed and assigned signal scores by the ENCODE uniform processing pipeline (6). Consequently, we retrieved 690 ChIP-seq datasets that related to 165 unique TFs evaluated in different cell types, and 58 of these 165 TFs were among the 232 TFs we used to construct the DRAF models. For each of these 58 TFs, we selected all corresponding ChIP-seq datasets from all available cell types. From each dataset, we used the top 500 sequences, having the highest peak enrichment scores. We selected only ChIP-seq datasets that have not been used for derivation of any of the TFBS DRAF prediction models. This resulted in a total of 98 ChIP-seq datasets, each of which consists of 500 sequences. These 98 ChIP-seq datasets correspond to 27 distinct TFs.

TFBS extraction from ChIP-seq data

The TFBS part in the TF-TFBS feature vector was constructed from each ChIP-seq peak sequence of length N, using sliding windows of length L to extract sequences. Windows started from the first position of the peak sequence and were shifted by one nucleotide until the end of the peak sequence was reached. This resulted in a total of N-L+1 TFBS sequence parts from one ChIP-seq peak sequence. The same number of TFBS sequence parts was extracted from the reverse complement sequence of the ChIP-seq peak sequence, resulting in a total of 2*(N-L+1) TFBS sequence parts. This was done for each sequence of the ChIP-seq peaks. For example, if a particular ChIP-seq peak sequence had (N = 100 bp), and the TFBS length (L = 10), then we extracted 91 TFBS sequence parts from this ChIP-seq peak and 91 TFBS sequence parts from the reverse complement sequence. Then, each of these TFBS sequence parts was represented in the same binary representation explained above. The TF part of the feature vector consists of the features of the TF for which the ChIP-seq data are generated. Subsequently, TF-TFBS links were constructed by associating the TF part of the feature vector with each of the corresponding TFBS parts. Finally, we used the DRAF model to examine all these TF-TFBS links and predict correct TF-TFBS associations. A ChIP-seq peak sequence was declared to be correctly predicted (i.e. true positive) if at least one of the 2*(N-L+1) TF-TFBS links was identified by the DRAF model to be a positive link (i.e. the TFBS is a correct binding site for the associated TF). If none of the 2*(N-L+1) TF-TFBS links belonging to a particular ChIP-seq peak sequence was predicted by the DRAF model as a positive link, then this ChIP-seq peak sequence was considered as a false negative. To evaluate the quality of DRAF model predictions on the ChIP-seq dataset, we plotted the sequence logo for all the ChIP-seq predictions made by the DRAF model for each TF using the WebLogo tool (49), and compared the sequence logo with the standard TF sequence logo obtained from HOCOMOCO.

‘Negative’ data

The ChIP-seq data facilitated the estimation of the DRAF model sensitivity. However, to estimate the model’s specificity, we constructed the ‘negative’ (background, false) datasets for each ChIP-seq peak dataset. We want to point out that there is no good way to construct background sets for testing TF DNA binding. For this we used the whole human chromosome 21 (average CG content ∼41%) as follows. First, we excluded from chromosome 21 all TFBS sequences used for training, as well as all regions covered by the ENCODE ChIP-seq peaks for a specific TF that belongs to any cell type that was available in the ENCODE datasets. We also excluded the DNA accessible regions based on the data we downloaded from ENCODE (30) (the uniform DNAse I Hypersensitivity clusters merged from multiple cell types). The remaining portion of the chromosome 21 represent a good background test set since any TFBS prediction there will be more likely real false positive. We also note that none of the models we evaluated in this study uses information about accessibility of DNA (contrary, for example, to the model from (30)). The model that receives only DNA sequence as the input, as is the case with DRAF and other models we tested here, does not know if that sequence is accessible or not and could make predictions there anyway. This corresponds to the real scenario in which these models will be applied and using such background better reflects the actual performance, particularly in a genome-wide testing.

The remaining parts of chromosome 21 were used to extract negative data as follows. Let us assume that the considered ChIP-seq dataset corresponds to a TF that has TFBSs of length L. Then, we used sliding windows of length L to extract sequences. Windows started from the first position of chromosome 21 and were shifted by 1 nt until the end of the chromosome sequence was reached. Every such extracted sequence was discarded if it contained ambiguous nucleotides. Feature vectors describing potential TF-TFBS links were compiled in the same way as explained previously, by associating the TF properties with the TFBS representation for all extracted sequences and their reverse complements. After that, we removed from the TF-TFBS collection all links that were found in the training dataset of the corresponding DRAF model. The number of TF-TFBS links in the ‘negative’ dataset varies from one TF to another depending on the excluded regions from chromosome 21. This is due to: (i) the overlap with ChIP-seq peaks, (ii) the excluded TF-TFBS links because of the overlap with the training dataset and (iii) the TFBS length L. For these reasons, preparation of the ‘negative’ data from chromosome 21 differs from one TF to another. Finally, we used the DRAF models to predict if these presumed TF-TFBS links would correspond to the positive (true) or negative (false) links. If a particular TF-TFBS link of the ‘negative’ set was incorrectly predicted as ‘positive’, we considered this link as a false positive prediction; similarly, the TF-TFBS link correctly predicted as a ‘negative’ link, was considered a true negative prediction.

Comparison between the DRAF models, PWM models (HOCOMOCO, TRANSFAC) and DeepBind models on ChIP-seq peaks and their respective background datasets

Position weight matrix (PWM) models

We compared the predictive performance of the DRAF models with the PWM models obtained from the HOCOMOCO (version 9) and TRANSFAC (version 2012.2) databases. For each of the 27 TFs that we considered that correspond to the 98 ChIP-seq test dataset, we used the corresponding HOCOMOCO and TRANSFAC PWMs that model the respective TFBSs. After that, we scanned the ChIP-seq peaks and the chromosome 21 (as explained in the previous section) using MEME FIMO (50) to report PWM matching scores on these sequences. At different sensitivity levels (10, 20, …, 90%) we compared the predictions obtained from the DRAF models with those obtained from the PWM models.

DeepBind models

We repeated the same comparison that we performed between the DRAF models and the PWM models but this time with DeepBind models. We found 24 out of the 27 TFs that we tested using ENCODE ChIP-seq data to have a DeepBind model. This resulted in a comparison of the DRAF models with the DeepBind models in 87 out of the total 98 ChIP-Seq datasets that we retrieved from the ENCODE data.

RESULTS

New method for prediction of TFBSs

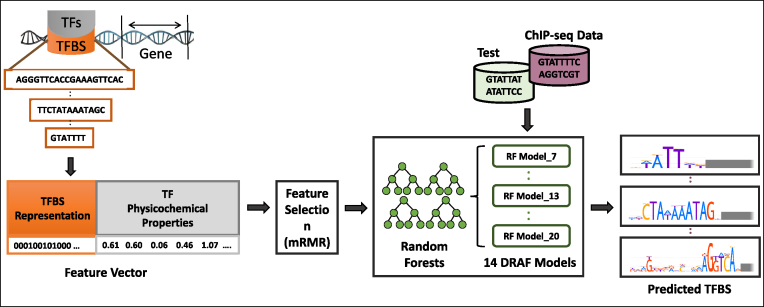
We developed a novel method, DRAF, for the prediction of TFBSs, which requires one predictive model per one length of TFBSs, irrespective of the number of TFs that have the binding sites of that length. Consequently, we developed 14 such models covering TFBS lengths from 7 to 20 bp. To describe TF-TFBS links, we used physicochemical properties of the DNA binding domains of TF proteins and combined them with the sequence properties of their DNA binding sites. From all these properties we derived feature vectors corresponding to each TF-TFBS link. We applied the mRMR (43) feature selection method to the features that correspond to the TF portion of the feature vector describing the TF-TFBS links. With features that remain, we developed RF models (45) for predicting TFBSs. Figure 1 depicts major steps in DRAF modeling. Details of the method are reported in the ‘Materials and Methods’ section.

Figure 1.

The input data, training procedure and usage of the DRAF models for prediction of TF-TFBS links. Sequences of TFs and their TFBSs are represented in TF-TFBS links using physicochemical properties of TFs and binary representation of TFBSs. Then, the DRAF models were constructed for each group of TFs depending on the TFBS length. Finally, the DRAF models were tested using the holdout test dataset and another set of ChIP-seq peak data and their associated background datasets. The DRAF models aim at predicting which TF-TFBS link suggests a valid TFBS for a particular TF.

Selected features of TFs

To describe each TF, 150 features, including AAindex (39) properties, DNA binding domain family classification (37), and amino acid binding mode preference to DNA bases (41), were selected using the mRMR feature filtering method. In the 14 models corresponding to different TFBS lengths, on average, out of the 150 selected features, 145 are AAindex properties, while 5 reflect other properties we introduced (see below). Therefore, on average, one out of four AAindex properties (27% = 145/544) and one out of two other features (50% = 5/10) were selected through this filtering. Of the 145 selected AAindex properties, on average, 115 can be classified into six groups, while 30 are ‘unclassified’ according to (39) (see Supplementary Figure S3). We notice that almost half of the selected features from AAindex (46%) are placed in the ‘hydrophobicity’ or ‘alpha and turn propensity’ groups. Although this may highlight the role of these two categories in predicting the TF affinity to TFBSs, we also notice that the distribution in groups of our AAindex selected features reflects well the distribution of all the 544 AAindex properties (see Supplementary Figure S3). The remaining five selected features represent the other properties we introduced, namely the DNA binding domain family classification and the amino acid binding mode preference to DNA bases. In particular, on average, four out of seven features (57%) used to describe the DNA binding domain family, and one out of three features (33%) used to represent the amino acid binding mode preference, were selected. This suggests that the features we added to those from AAindex have a high information value for predicting TF-TFBS links in the method we used.

TF-TFBS predictions by DRAF models

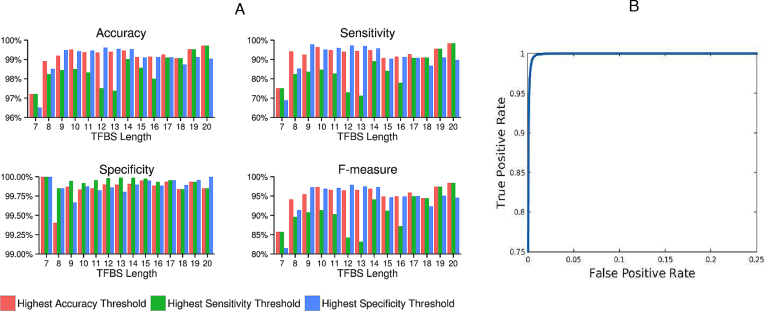
DRAF models were first trained using sets of ‘true’ TF-TFBS links, derived from HOCOMOCO and having DNA binding domains for TFs in the Pfam database (see ‘Materials and Methods’ section), and ‘false’ TF-TFBS links obtained by randomly selecting sequences from human chromosomes 4 and 22 for the TFBSs. They were then used to predict TFBSs of TFs. In order to measure the capability of the DRAF models to predict the TF-TFBS links, we used two different testing strategies, one based on holdout dataset and another based on cross-validation methods. In the holdout approach (see details in the ‘Materials and Methods’ section), the average accuracy, sensitivity, specificity and precision obtained from applying all 14 DRAF models to the test data were 99.16, 92.53, 99.86 and 98.57%, respectively (Figure 2A and Supplementary Table S3). These results were obtained using thresholds on the model output scores that provided the highest accuracy on the training data. We repeated the same experiments on the test data using the thresholds that provided the highest specificity and the highest sensitivity on the training data (Figure 2A; Supplementary Tables S4 and 5).

Figure 2.

The prediction performance of the DRAF models on the holdout test dataset. (A) The DRAF models were applied on the holdout test data using different threshold settings for the models’ prediction scores that provided the highest accuracy (pink bar), the highest sensitivity (green bar) and the highest specificity (blue bar), on the training dataset. (B) The ROC curve (true positive rate versus false positive rate) was performed for the predictions obtained from all the 14 DRAF models on the holdout test dataset. The AUC for the DRAF models is 0.9991.

In addition, Figure 2B depicts the receiver operating characteristic (ROC) curve for 14 models. The area under ROC is extremely high (AUC = 0.9991). This shows that the DRAF models could predict the TF-TFBS relationship with very high accuracy for all modeled TFs.

We repeated the evaluation experiments using also the 10- and 5-fold cross-validations. The average accuracy, sensitivity, specificity and precision obtained from applying all 14 DRAF models using a 10-fold cross-validation were 99.40, 97.71, 99.58 and 95.97%, respectively. Supplementary Tables S6–8 show the prediction results with a 10-fold cross-validation for all 14 models using the thresholds giving the highest accuracy, specificity and sensitivity, respectively, on the training data. Supplementary Tables S9–11 show similar results to those given in Supplementary Tables S6–8 but obtained using a 5-fold cross-validation.

Finally, we compared the prediction results of the DRAF models with NN, SVMs and GMR models (see ‘Materials and Methods’ section). DRAF models outperformed other models in terms of accuracy, specificity and precision (Supplementary Figure S4 and Table S12). That is, DRAF models yielded an average accuracy, specificity and precision of 99.16, 99.86 and 98.57%, respectively, which is better than the next best results of 99.06, 99.49 and 95.08%, respectively, obtained by the NN models. With the achieved accuracy and specificity being similar between the two models, the precision of DRAF models was higher. The DRAF models, however, yielded lower sensitivity than NN and SVM, but the sensitivity was higher than with the GMR models (Supplementary Figure S4 and Table S12).

As a final check, to assess the effect of the GC content on the DRAF predictive power, we repeated the training and testing experiment with background sequences extracted from chromosome 21, which has a GC content close to the average GC content of the human genome. The obtained average accuracy, specificity and precision (99.07, 99.82 and 98.04%, respectively) were extremely similar to those obtained with the background sequences extracted from chromosomes 4 and 22 (Supplementary Tables S13–15).

Evaluation of DRAF models using ChIP-seq data

We evaluated the predictive performance of the DRAF models on the 98 ENCODE ChIP-seq datasets (see ‘Materials and Methods’ section). We changed the thresholds on the model output scores to obtain the predictions at different sensitivity levels (10, 20, …, 90%) and monitored the capability of the DRAF models to recognize the background sequences as ‘false’ TFBSs (this was measured using the average distance between predictions made on the background sequences (51)). The results show that the DRAF models accurately predict TFBSs on sequences of ChIP-seq peaks, while maintaining high specificity of predictions on the background sequences (Supplementary Dataset 1). For example, using conventional performance measures, the DRAF models yield at the sensitivity level of 80%, with an accuracy and specificity (averaged over 98 ChIP-seq datasets) of 99.89 and 99.89%, respectively (Supplementary Dataset 1).

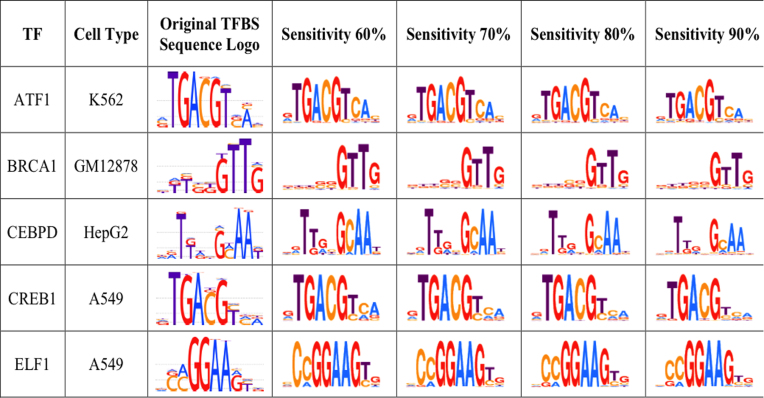
We examined the similarity of the predicted TFBSs in the ChIP-seq peaks with the known TFBSs for each TF used in this study. The sequence logos for TFBS predictions at different sensitivity levels show high levels of similarity to known sequence logos obtained from HOCOMOCO (20) for the corresponding TFs (Figure 3 and Supplementary Table S16). This suggests that each of the 14 DRAF models was capable of capturing the DNA binding patterns of the TFs encoded by the respective DRAF model.

Figure 3.

Sequence logos for the predicted TFBS sequences on the human ChIP-seq datasets using the DRAF models. The figure shows different sequence logos obtained from the DRAF-predicted TFBS sequences from ChIP-seq datasets at different sensitivity levels. The complete set of sequence logos for the 98 ENCODE ChIP-seq datasets are provided in Supplementary Table S16.

Next, we compared on the 98 ChIP-seq datasets the performance of the DRAF models with the HOCOMOCO PWM models, TRANSFAC PWM models and DeepBind models. For this purpose, we set thresholds on the DRAF model prediction scores that yielded the highest F-measure scores on the training data (see ‘Materials and Methods’ section). Note that this training data is independent from 98 ChIP-seq datasets and associated background sequences. We used these thresholds when evaluating the model performance on the ChIP-seq datasets (see ‘Materials and Methods’ section). The results show that the DRAF models achieve a higher specificity on the background data compared to the other three types of models, while having a better or at least the same sensitivity levels (Supplementary Datasets 2–4). The previous results were obtained by comparing the performance of DRAF and other models on ENCODE ChIP-seq datasets using thresholds that provided the highest F-measure scores on the training data. In addition, we repeated this comparison between the considered models by comparing their performance at different sensitivity levels (see ‘Materials and Methods’ section). At all studied sensitivity levels, the DRAF models outperformed HOCOMOCO, TRANSFAC and DeepBind models, providing a higher precision (positive predictive value) on the 98 background datasets (for HOCOMOCO, TRANSFAC) and 87 background datasets (for DeepBind), each corresponding to one of the ChIP-seq dataset (see ‘Materials and Methods’ section). Overall, for the individual ChIP-seq datasets, the DRAF models yielded precision on the background datasets (averaged over all sensitivity levels) higher than each of the HOCOMOCO, TRANSFAC and DeepBind models in 78.57% (77 out of 98 ChIP-seq datasets), 92.86% (91 out of 98 ChIP-seq datasets) and 91.95% (80 out of 87 ChIP-seq datasets), respectively (Supplementary Datasets 1, 5 and 6).

In 882 experiments (9 threshold values × 98 ChIP-seq datasets for HOCOMOCO and TRANSFAC), and 783 experiments (9 threshold values × 87 ChIP-seq datasets for DeepBind), the DRAF models yielded precision (averaged over all sensitivity levels) higher than each of the HOCOMOCO, TRANSFAC and DeepBind models in 69.05% (609 out of 882 experiments), 92.27% (820 out of 882 experiments) and 91.95% (720 out of 783 experiments), respectively.

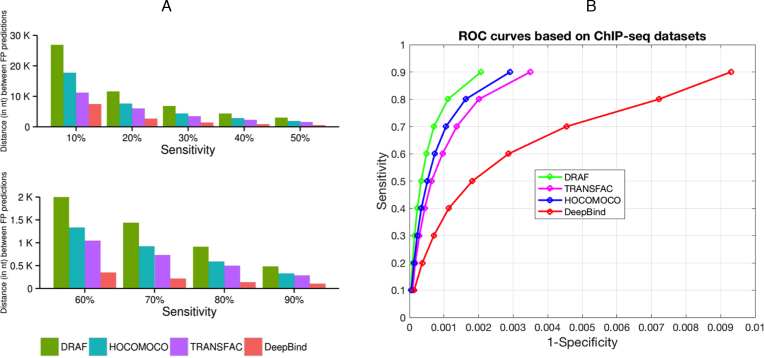
In the ‘Materials and Methods’ section, differences in the total number of ChIP-seq datasets related to TRANSFAC and DeepBind are described. Another measure that we used to compare the models was the average distance between false positive predictions on the background datasets (see ‘Materials and Methods’ section), averaged over all the tested background datasets. We found that at each of the tested sensitivity levels, DRAF models provided a significantly smaller number of false positive predictions than any of the other three types of models (Figures 4A, B and 5A; Supplementary Figure S5 and Supplementary Datasets 1, 5 and 6). The DRAF models provided on average 1.54-, 1.96- and 5.19-fold reduction of false positives at the same sensitivities compared to models from HOCOMOCO, TRANSFAC and DeepBind, respectively (Figure 5B, Supplementary Table S17, Supplementary Datasets 1, 5 and 6).

Figure 4.

Comparison of the DRAF, HOCOMOCO, TRANSFAC and DeepBind models. In (A) different sensitivity levels (averaged over all ChIP-seq datasets) were used. The X-axis represents the sensitivity level (Top: 10, 20…50% and Bottom: 60, 70…90%) and the Y-axis represents the average distance (in nt) between false positive prediction occurrences on the background sequences (from chromosome 21) averaged over the all corresponding tested ChIP-seq datasets. (B) ROC curves that correspond to DRAF, HOCOMOCO, TRANSFAC and DeepBind predictions per sensitivity averaged across the all corresponding tested ChIP-seq datasets.

Figure 5.

Summary of comparison between the DRAF, HOCOMOCO, TRANSFAC and DeepBind models. (A) Boxplots show the average distance (in nt) between FP predictions on the background sequences (from chromosome 21) at different sensitivity levels obtained from testing the corresponding models on the ChIP-seq datasets and averaged over all the datasets at each sensitivity level. The diamonds on the boxplots show the mean values. (B) Graph shows the fold decrease of the average distance between FP predictions on the background sequences (from chromosome 21) at different sensitivity levels for TRANSFAC, HOCOMOCO and DeepBind models relative to DRAF (Supplementary Table S17).

Reported performance of other models

Performance comparison of DRAF models with other relevant works is not straightforward, due to the differences between approaches and the criteria used in different studies. In some of the previous studies (13,31,52–54) models were assessed only for individual TFs or specific TF families. For example, the model created by Ellrott et al. (53) was evaluated on HNF4α; the model developed by Endres (31) was evaluated only on Zif268; Alamanova and colleagues (52) tested their model on few TFs such as P53 and NF-κB. Liu and Bader (54) reported results on Mat-α2 and GCN4 bZIP. Chen and others used six TFs to test their model (13).

Therefore, we focused on the performance comparison of the DRAF models and the reported results from (33–35). Each of these studies used more than 100 TFs in the assessment of models’ performances (Table 1). We used a much more comprehensive and significantly larger dataset with 1 214,389 TF-TFBS links (true and false) (Table 1, Columns 2, 3 and 4). Our dataset is 34-, 116- and 119-fold larger than the datasets used in (35), (34) and (33), respectively. The results show that the DRAF models, as evaluated on 30% of the holdout data (364,317 TF-TFBS links), achieve a significantly higher accuracy than the reported performance of models in (33–35) that were evaluated on much smaller datasets (Table 1).

Table 1. Reported prediction results from different studies.

Studya	Number of TFs	Number of unique TFBSs	Dataset size (Total TF-TFBS links)	True TF-TFBS links	False TF-TFBS links	Testing method	Highest accuracy
Qian Z. et al. (reported in (33))	480	2,341	10,206	3,356	6,850	Leave one out	76.6%
Qian Z. et al. (reported in (34))	143	571	10,430	3,430	7,000	Leave one out	87.9%
Cai, Y. et al. (reported in (35))	599	2,402	35,410	3,541	31,869	Leave one out	91.1%
DRAF models (on the datasets from this study)	232	44,710	1,214,389	110,399	1,103,990	30% holdout	99.16%

^aThis table shows the prediction accuracy of the DRAF models on the holdout dataset (30% of the total), and the other models as reported in the original references (33–35) that used different TF-TFBS test datasets. Our holdout dataset is 34-, 116- and 119-fold larger than the datasets from (35), (34) and (33), respectively. The test dataset for DRAF has 364 317 (positive and negative) TF-TFBS links which is more than 10 times larger than the next largest dataset used in (35).

DISCUSSION

We developed DRAF models to capture the relationship between TFs and their TFBSs. Each DRAF model is developed to capture relationships of all TFs whose TFBSs have the same length. Consequently, we needed only 14 DRAF models to represent TF-TFBS links that covered 232 human TFs and 250 TFBS sets. These TFBSs are grouped into 14 distinct lengths (7, 8, …, 20 bp). PWMs and other model types are typically developed for TFBSs for individual TFs, resulting in numerous models (usually one or more models for a single TF). However, in a much smaller number of cases TFBSs of TFs from the same family are used to develop one PWM model for that family. This is the reason why major TFBS model databases (HOCOMOCO, TRANSFAC and JASPAR) have a very large number of TFBS models. In contrast, DRAF successfully reduces the number of required models to only 14, based on the length of the TFBSs we considered. One such prediction model can thus be applied to a set of TFs whose TFBSs have the same length. For 232 TFs, DRAF requires only 14 models; this is ∼18 fold less than the corresponding 250 TFBS models in HOCOMOCO, ∼54 fold less than the corresponding 749 TFBS models in TRANSFAC (231 TFs of the 232 TFs were found TRANSFAC) and ∼50 fold less than the 704 TFBS models in DeepBind (124 TFs of the 232 TFs were found in DeepBind).

This reduction in the number of required models did not decrease performance. On the contrary, the results show that the DRAF models outperformed all three groups of models. Furthermore, the DRAF models increased specificity by making false positive predictions on the background datasets, on average 1.54-, 1.96- and 5.19-folds less frequent than the HOCOMOCO PWMs, TRANSFAC PWMs and DeepBind models, respectively. This confirmed the capability of DRAF models for the prediction of TFBSs. This is most likely due to the choice of features in the DRAF models, reflecting both the physicochemical and structural properties of the TFs and the sequences of their associated TFBSs and the more complex DRAF models than PWM models. Furthermore, the RF models used in DRAF may be able to capture nucleotide dependencies, thus overcoming an intrinsic limitation of the classical (mononucleotide-based) PWMs approach.

It should be noted that our testing approach relating to the ChIP-seq data involved validating models on background data composed of the entire chromosome 21 (excluding data used in training, those overlapped with ChIP-seq peaks when specific cell types were used, and those that corresponded to DNA accessible regions). Such chromosome-wide testing is useful in unbiased assessing TFBS prediction models, as it does not involve creation of artificial background sequences. For example, DeepBind models were evaluated on the ChIP-seq data using only the top 500 even-numbered ChIP-seq peaks that were randomly shuffled.

Although DRAF models demonstrate the lowest false positive rates among the tested models, the absolute number of false positive predictions is still noticeable (Supplementary Dataset 1). It is worth mentioning that our models predict binding sites in a non-cell-specific manner, thus some binding sites may not be available for binding in a given cell type and therefore do not intersect with the ChIP-seq peaks for that cell type. Chromatin structure interferes with TF binding via the modification of histones (6) and to a lesser extent, via DNA methylation (55). Commonly used computational strategies to compensate for the specifics of the chromatin structure could be applied to enhance predictions, using information from histone modification data or DNase I hypersensitivity regions (DNase-seq) for a cell type of interest (56,57).

CONCLUSION

In this work, we modeled TF-TFBS interactions using properties extracted from sequences of DNA binding domains of TFs, and TFs’ DNA-binding domains using a novel method (DRAF). RFs DRAF models were built for all TFs sharing a common TFBS length. That is, for all 250 TFBS models obtained from the HOCOMOCO database we developed 14 DRAF models representing 14 distinct TFBS lengths we considered. The average DRAF’s prediction accuracy of 99.94% is, to the best of our knowledge, the highest of those currently reported on large datasets and clearly demonstrates the advantages of the DRAF method for TFBSs prediction.

Using the DRAF method we reduced the number of required models, yet, we demonstrated that at the same sensitivity levels DRAF models achieve much higher specificities than the HOCOMOCO, TRANSFAC and DeepBind models.

DATA AVAILABILITY

DRAF is freely available as a web tool and as a standalone software at http://cbrc.kaust.edu.sa/DRAF.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

King Abdullah University of Science and Technology (KAUST) [BAS/1/1606-01-01 to V.B.B.]. Funding for open access charge: KAUST [BAS/1/1606-01-01].

Conflict of interest statement. None declared.