Errors in Energy Landscapes Measured with Particle Tracking

Abstract

Tracking Brownian particles is often employed to map the energy landscape they explore. Such measurements have been exploited to study many biological processes and interactions in soft materials. Yet video tracking is irremediably contaminated by localization errors originating from two imaging artifacts: the “static” errors come from signal noise, and the “dynamic” errors arise from the motion blur due to finite frame-acquisition time. We show that these errors result in systematic and nontrivial biases in the measured energy landscapes. We derive a relationship between the true and the measured potential that elucidates, among other aberrations, the presence of false double-well minima in the apparent potentials reported in recent studies. We further assess several canonical trapping and pair-interaction potentials by using our analytically derived results and Brownian dynamics simulations. In particular, we show that the apparent spring stiffness of harmonic potentials (such as optical traps) is increased by dynamic errors but decreased by static errors. Our formula allows for the development of efficient corrections schemes, and we also present in this work a provisional method for reconstructing true potentials from the measured ones.

Introduction

Video tracking of Brownian particles is an important technique that serves multiple purposes. It has been used for decades to study biological and soft matter and has indeed provided valuable information on the microscale dynamics and structures of these systems (1, 2, 3). With this technique, one can, for instance, probe live-cell microenvironments (4, 5), study the dynamics of individual proteins in natural settings (6, 7), or image the viral invasion of host cells (8, 9). Extracting mechanical properties of individual biological molecules has also been shown to be possible by measuring the thermal fluctuations of cytoskeletal and membrane filaments (10, 11, 12, 13) and of DNA (14, 15). Using single-molecule tracking, recent studies have further measured the trapping energetic landscapes confining the movements of membrane receptors (16, 17). Brownian-particles tracking has also been used extensively in synthetic-soft-matter physics. Hence, central applications of this technique have been to determine the microrheology, diffusion rates, or mechanical properties of complex fluids (18, 19, 20, 21). It has also been employed to measure colloidal interactions of electrostatic (22, 23) or entropic (24, 25) origins and more recently to map the trapping energies of microchannels (26, 27, 28, 29).

Statistical analysis of Brownian-particle trajectories is a prerequisite to extracting observables that can be physically interpreted (30). The mean-squared displacement (MSD) is often calculated as a measure of the time- or population-averaged dynamics of the tracked particles. For example, the MSD enables distinguishing between diffusive, driven, subdiffusive, hopping, or trapped motions (31).

Reconstructing the underlying energy landscape guiding the particles’ dynamics is another insightful analysis of Brownian trajectories, which has been exploited in many of the aforementioned applications (16, 17, 22, 23, 24, 25, 26, 27, 28, 29). To calculate this landscape, the statistics of the Brownian particles’ positions is measured at equilibrium and assumed to obey the Boltzmann distribution (23, 27, 32, 33). Note that this analysis requires only localizing particles in each frame of the video, whereas calculating the MSD involves the additional and often nontrivial step of linking the particles’ successive positions into trajectories (30).

Video particle tracking, however, suffers from various sources of errors. In particular, artifacts intrinsic to the imaging detectors can contaminate the trajectory measurements well beyond the statistical uncertainties arising from finite sampling. Several studies have compared the resilience of tracking methods to these errors (2, 34), and new Bayesian techniques notably tend to improve the robustness of the extracted trajectories (2, 35). Nevertheless, positioning and trajectory linking are irremediably suffering from errors, which have been recognized to propagate to the measured physical observables (18, 27, 33, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47).

Most detection errors may be classified into two categories: “static” and “dynamic” (48). The “static error” typically comes from video-signal noise (camera-specific noise, background autofluorescence, etc.) and would even affect the localization of an immobile particle (30, 48). The “dynamic error” is the result of motion blur due to finite camera exposure time and occurs when measuring the positions of a moving particle. The propagation of these errors to MSD calculations has been characterized in detail (37, 38, 43). However, no such systematic description exists for their effects on mapping energetic landscapes. Yet the need for such studies has been emphasized by the recent experimental work of Krishnan et al. (27), which notably shows that trapping potentials, extracted from video particle tracking via the Boltzmann distribution, are strongly influenced by the camera exposure time (26). On the other hand, inference schemes may be a promising approach to extract reliable measures of trapping potentials from noisy data (49, 50), and the consequences of generic localization errors on hopping energies have indeed been analyzed (51). Nevertheless, to the best of our knowledge, a rigorous account of the distinct effects of static and dynamic errors have not yet been fully incorporated into these Bayesian approaches.

The goal of this work is to explain how static and dynamic errors affect energetic mapping. We derive analytically a relationship between the true potential landscape and its apparent evaluation when measurements are contaminated by these errors. Our results notably show that static and dynamic errors cause systematic biases and misinterpretations in experimental results. We also explore means for postmeasurement corrections of these errors, which would allow experimentalists to revise their existing data. The implications of our work are relevant for a wide class of trapping and interparticle potentials. The article is organized as follows. Methods describes the model quantifying how localization errors affect the measured potentials and details the algorithm to verify these predictions (in Simulations). Results and Discussion presents the simulation data to confirm the validity of our formula for specific and pertinent potentials and further explains in Correction a possible strategy to correct experimental results for static and dynamic errors.

Methods

Static and dynamic errors

The relationship between the potential V probed by the trapped particles and the probability density function (PDF) of their positions $\mathbf{r}=\left({\text{x}}_1,{\text{x}}_2,{\text{x}}_3\right)$ is given at equilibrium by the Boltzmann distribution $f_{\mathbf{r}}\left(\mathit{r}\right)\propto e^{-\beta V\left(\mathit{r}\right)}$, where β = (k_BT)⁻¹ (k_B: Boltzmann constant; T: temperature). In our notation, f_r(r) is the joint PDF of r evaluated at $\mathit{r}=\left(x_1,x_2,x_3\right)$, the space coordinates. In principle, the Boltzmann distribution allows experimentalists to recover the energetic landscape by measuring the equilibrium distributions of positions of the trapped Brownian particles using video microscopy. In practice, however, cameras measure a moving average of positions over a shutter time σ, to which a zero-mean random vector ξ resulting from instrumental noise is added (10, 37, 38, 52):

$$\overline{\mathbf{r}}\left(t\right)=\frac{1}{\sigma }{\int }_{t-\sigma }^t\mathbf{r}\left(s\right)\text{d}s+\mathit{\xi }$$ (1)

at time t, with ξ independent of r. The time average in Eq. 1 results in motion blur or “dynamic errors,” whereas the added noise produces the “static errors” that would occur even when locating an immobile particle (37). The validity of the various assumptions (properties of ξ, statistics of illumination and detection, etc.) leading to Eq. 1 has been discussed elsewhere (37, 53).

Most relevant to quantify the static error is the noise covariance matrix, $\mathit{E}=\langle \mathit{\xi }{\mathit{\xi }}^{\mathrm{⊺}}\rangle$, where ${\mathit{\xi }}^{\mathrm{⊺}}$ is the transpose of ξ, and $\langle \cdots \rangle$ is the average. The noise covariance matrix can often be written E = ε²I (with I the identity matrix) in two-dimensional (2D) particle tracking, in which the static errors are isotropic in the observation plane (37). In that case, ε is the spatial resolution of the tracking method, and together with the detector exposure time σ, they quantify the two common sources of errors in particle tracking.

We denote the observed PDF of the measured positions given by Eq. 1 as $f_{\overline{\mathbf{r}}}$. Applying $f_{\overline{\mathbf{r}}}\left(\mathit{r}\right)\propto e^{-\beta \overline{V}\left(\mathit{r}\right)}$ to this “apparent” PDF does not measure the correct potential V in which the particles move but an apparent potential $\overline{V}$ via

$$\beta \overline{V}\left(\mathit{r}\right)=-\text{ln}{f}_{\overline{\mathbf{r}}}\left(\mathit{r}\right)+\text{constant,}$$ (2)

with an added, arbitrarily chosen constant that, unless stated otherwise, will be ignored in the remaining.

We illustrate in Fig. 1 the effects of errors ε and σ on a representative one-dimensional (1D) potential: the exact potential is shown by the line, and the measured potentials affected by motion blur or static positional uncertainty are given by the up and down triangles, which are obtained by Brownian dynamics simulations (our algorithm is explained in Simulations; for illustrative purposes, the errors used here are larger than in the actual experiments, where ε ≈ 4 nm and σ ≈ 1 ms). Although static errors tend to apparently widen the potential (down triangles in Fig. 1), dynamic errors produce the opposite (up triangles). These antagonistic effects were already revealed when studying the propagation of the tracking errors to the MSD (37). Near the potential’s minimum, static errors tend to slightly narrow it, whereas motion blur gives rise to secondary minima, similar to those observed by Krishnan et al. (27), whose experimental results are shown with the filled circles in Fig. 1. The resemblance of these artifacts indicates that motion blur is likely their cause in the measurements. The latter are obtained from three-dimensional (3D) tracking experiments, whereas the simulations are performed in 1D, and the observed discrepancy in amplitude between the up triangle and filled circle data may indeed come from this dimensional mismatch (see 2D Potentials in Results and Discussion).

Figure 1.

Effect of static and dynamic errors on a 1D potential mapping. The trapping energetic landscape, $\beta V_{\text{ES}}\left(x\right)=2.5\left[\text{tanh}\left(3x/a-4\right)-\text{tanh}\left(3x/a+4\right)\right]$, with a = 160 nm, is shown with the solid line and is chosen to resemble the slice of the 3D electrostatic potential in a microfluidic trap as measured by Krishnan et al. (27) using a 100 nm particle with diffusion coefficient D = 1.8 μm² s⁻¹ (filled circles are data reproduced from Fig. 3 of their study). The open symbols are results of our simulations (see Simulations). The effect of errors shown in their 3D experimental measurements is more pronounced than in our 1D simulations, as the dimension may indeed change the magnitude of the resulting artifacts (see 2D Potentials in Results and Discussion). To see this figure in color, go online.

Apparent potential

The apparent PDF $f_{\overline{\mathbf{r}}}$ of measured positions can be analytically related to its true counterpart f_r under two main assumptions. First, we assume that the tracked particle undergoes overdamped Langevin dynamics. Second, the trapping potential in which the particle moves is considered smooth enough to be approximated, within the typical width of static and dynamics positioning errors, by its second-order Taylor expansion. The approximation of an overdamped (i.e., inertialess) dynamics is valid for most video-tracked particles (micron-sized colloids or smaller globular objects such as proteins). The condition of potential’s smoothness imposes upper bounds for both σ and ε, as we shall see below. Under these assumptions, we can obtain an analytical relationship between $f_{\overline{\mathbf{r}}}$ and f_r, the derivation of which is detailed in Appendix A for an arbitrary number of dimensions. The resulting expression for the apparent potential $\overline{V}$ in multiple dimensions (the particular 1D case is given later in this section), as obtained from $f_{\overline{\mathbf{r}}}$ using Eq. 2, is

$$\overline{V}=V-\frac{\text{ln det}\left({\mathit{U}}_{\mathit{E},\sigma }\right)}{2\beta }+\frac{{\mathit{v}}^{\mathrm{⊺}}{\mathit{\Lambda }}^{-1}\left({\mathit{U}}_{\mathit{E},\sigma }-\mathit{I}\right)\mathit{v}}{2\beta D}.$$ (3)

Here $\text{det}(\cdots )$ designates the determinant of a matrix, D is the diffusion coefficient (assumed to be constant) of the particle, and we have introduced the convective velocity and the local relaxation matrix,

$$\mathit{v}=-\beta D\mathit{\nabla }V$$ (4a)

and

$$\mathit{\Lambda }=\beta D\mathit{\nabla }{\mathit{\nabla }}^{\mathrm{⊺}}V,$$ (4b)

respectively (with $\mathit{\nabla }$ the nabla vector and $\mathit{\nabla }{\mathit{\nabla }}^{\mathrm{⊺}}$ the symmetric Hessian matrix operator; Λ has the dimension of an inverse time). We have also defined the following error-propagation matrix:

$${\mathit{U}}_{\mathit{E},\sigma }={\left[2{\left(\sigma \mathit{\Lambda }\right)}^{-2}\left(\sigma \mathit{\Lambda }-\mathit{I}+e^{-\sigma \mathit{\Lambda }}\right)+\mathit{\Lambda E}/D\right]}^{-1}.$$ (5)

Note from this expression that ${\mathit{U}}_{\mathbf{0},0}=\mathit{I}$, indeed leading to $\overline{V}=V$ in Eq. 3 when both E and σ vanish in the absence of tracking errors.

Equation 3 is valid for both shutter times σ and static errors small enough so that, within the localization errors they induce via Eq. 1, third- and higher-order variations in V(r) may be neglected. We write these conditions, conservatively, as

$$D\sigma \Vert \beta \mathit{\nabla }V\Vert +\sqrt{D\sigma }\ll {\Vert \beta {\mathit{\nabla }}^{3}V\Vert }^{-1/3}$$ (6a)

and

$${\Vert \mathit{E}\Vert }^{1/2}\ll {\Vert \beta {\mathit{\nabla }}^{3}V\Vert }^{-1/3}.$$ (6b)

Here, the elements ${\left({\nabla }^{3}V\right)}_{ijk}={\partial }^{3}V/(\partial x_i\partial x_j\partial x_k)$, and $\Vert \cdots \Vert$ designates the maximum norm, that is, for a position-dependent matrix A(r) with elements $A_{ij\dots }\left(\mathit{r}\right)$,

$$\Vert \mathit{A}\left(\mathit{r}\right)\Vert =\underset{ij\dots ;\mathit{r}\in \mathit{\Omega }}{\text{max}}\left|A_{ij\dots }\left(\mathit{r}\right)\right|$$ (7)

is the maximal absolute value of any elements of the matrix over the observable space domain Ω. The left-hand side of the inequality (Eq. 6a) represents the typical displacement of the particle during the time σ, which can be caused by the drift imposed by the trap (first term) and diffusion (second term). Hence, the conditions (6) express the requirement for the potential to be “resolvable” to its second order within the localization errors corrupting the particle tracking. We verify in Appendix B that these nontrivial conditions indeed provide correct limiting values for σ and ε, below which Eq. 3 is valid.

Another requirement for Eq. 3 to be applicable is ${\mathit{U}}_{\mathit{E},\sigma }\mathrm{⩾}0$ (positive definite), which ensures that the logarithmic term is defined. The error matrix E is positive definite, and we indeed verify that the same holds for the σ-term in Eq. 5. However, Λ does not have this property around local maxima or saddle points of V(r). In these cases, and under the additional condition of a static error larger than a typical Brownian displacement during the time σ (i.e., $\epsilon >\sqrt{D\sigma }$), we find that ${\mathit{U}}_{\mathit{E},\sigma }$ may not be positive definite at these particular points (see an example in 1D Potentials, Fig. 2 h, in the next section).

Figure 2.

Comparison of Eq. 8 (lines) with BD simulations (symbols) for various σ and ε, and under different 1D trapping potentials: V(x) = x² (a and b), V(x) = x⁴ (c and d), V(x) = (−x + x⁴)/2 (e and f) and V(x) = −x² + 2x⁴ (g and h). The top panels (a, c, e, and g) investigate the motion blur with no static errors. The bottom panels (b, d, f, and h) concern static errors under a fixed shutter time σ = 0.1. The conditions in (11a), (11b) require $\sigma \ll 0.05$ and $\epsilon \ll 0.3$ for (c) and (d), $\sigma \ll 0.07$ and $\epsilon \ll 0.4$ for (e) and (f), and $\sigma \ll 0.03$ and $\epsilon \ll 0.3$ for (g) and (h). To see this figure in color, go online.

In 1D, we rename $x_1=x$, and Eq. 3 is written

$$\overline{V}=V-\frac{\text{ln}{u}_{\epsilon ,\sigma }}{2\beta }+\frac{v^2\left(u_{\epsilon ,\sigma }-1\right)}{2\lambda \beta D},$$ (8)

with the convective velocity and the local relaxation rate, (4a), (4b), defined in 1D using the first and second derivatives of V(x),

$$v=-\beta D{V}^{\prime }$$ (9a)

and

$$\lambda =\beta D{V}^{″},$$ (9b)

respectively. The error propagator, Eq. 5, now reads

$$u_{\epsilon ,\sigma }={\left[2\left(\sigma \lambda -1+e^{-\sigma \lambda }\right)/{\left(\sigma \lambda \right)}^2+\lambda {\epsilon }^2/D\right]}^{-1}.$$ (10)

Finally, in the 1D case, the conditions of validity become

$$D\sigma \Vert \beta V^{\prime }\Vert +\sqrt{D\sigma }\ll {\Vert \beta V^{″\prime }\Vert }^{-1/3}$$ (11a)

and

$$\mathit{\epsilon }\ll {\Vert \beta V^{″\prime }\Vert }^{-1/3},$$ (11b)

with $\Vert f\left(x\right)\Vert ={\text{max}}_{x\in \mathit{\Omega }}\left|f\left(x\right)\right|$, and are supplemented by the requirement that $u_{\epsilon ,\sigma }>0$.

One can linearize Eq. 3 under the more constraining conditions $\Vert \sigma \mathit{\Lambda }\Vert \ll 1\mathrm{and}\Vert \mathit{\Lambda E}/D\Vert \ll 1$, to obtain

$$\overline{V}=V+\frac{\text{tr}\left(\sigma \mathit{\Lambda }{\mathit{S}}_{\mathit{E},\sigma }\right)}{2\beta }-\frac{\sigma {\mathit{v}}^{\mathrm{⊺}}{\mathit{S}}_{\mathit{E},\sigma }\mathit{v}}{2\beta D},$$ (12)

with ${\mathit{S}}_{\mathit{E},\sigma }=\mathit{E}/\left(D\sigma \right)-\mathit{I}/3$ and $\text{tr}(\cdots )$ designating the trace. In particular, Eq. 12 shows the opposite effects of static and dynamic errors on the apparent potentials and that these errors can negate each other when ε² = Dσ/3, as also observed for the MSD of a diffusing particle (37).

Typical values of the errors are around ε ∼ 10 nm and exposure times σ in the range of 0.1–1000 ms for modern CMOS (complementary metal-oxide semiconductor) and CCD (charge-coupled device) cameras; the characteristic width a of measurable potentials ranges from 100 nm to several microns; and the usual diffusion coefficients of trackable microspheres in a liquid at room temperature are in the range of 0.1–1 μm² s⁻¹ (23, 24, 26, 27, 54). Hence, in many instances, $\epsilon \mathrm{\lesssim }\sqrt{D\sigma }\mathrm{\lesssim }0.1a$, and Eq. 3 should indeed be effective for most experimental settings.

Simulations

In the following, we verify the validity of Eq. 3 by comparing it with Brownian dynamics (BD) simulations for several examples of potentials. An explicit first-order time-stepping algorithm is used to advance the position r(t) of a particle at time t: $\mathbf{r}\left(t+\delta t\right)=\mathbf{r}\left(t\right)+\dot{\mathbf{r}}\left(t\right)\delta t$, where δt is the time step and $\dot{\mathbf{r}}\left(t\right)$ satisfies the following equation (55):

$$\dot{\mathbf{r}}\left(t\right)=-\beta D\nabla V\left(\mathbf{r}\left(t\right)\right)+\sqrt{2D/\delta t}\mathbf{w}\left(t\right),$$ (13)

which assumes the drag on the particle to be Stokesian and neglects any other hydrodynamic interactions. Here, w(t) is a stationary Gaussian process that satisfies $\langle \mathbf{w}\left(t\right)\rangle =\mathbf{0}$ and $\langle \mathbf{w}\left(t\right){\mathbf{w}}^{\mathrm{⊺}}\left(t^{\prime }\right)\rangle =\mathit{I}$ if $|t-t^{\prime }|\le \delta t$, 0 otherwise.

Each trajectory is 10⁹ time steps long and is then transformed by calculating the average positions over nonoverlapping sets of n time steps, $\overline{\mathbf{r}}\left(t\right)={(n+1)}^{-1}{\sum }_{k=0}^n\mathbf{r}\left(t-k\delta t\right)+\mathit{\xi }$, where σ = nδt defines the shutter time and where the added static error ξ is a random, normally distributed vector with $\langle \mathit{\xi }{\mathit{\xi }}^{\mathrm{⊺}}\rangle ={\epsilon }^2\mathit{I}$.

In the remaining, we work with dimensionless quantities, for which the unit distance a is the characteristic width of the potential trap (meaning V(|r| = a) − V(0) = β⁻¹), the unit energy is β⁻¹, and the unit time is a²/D. The dimensionless spatial resolution and shutter time are therefore expressed ε/a and Dσ/a², respectively. For example, with the values used in Fig. 1, one finds ε/a = 0.3 (ε = 50 nm and a = 160 nm) and Dσ/a² = 0.3 (σ = 4 ms and D = 1.8 μm² s⁻¹), as reported by the dashed lines in Fig. 5 d for the same simulation data. In these units, δt is chosen to be 5 × 10⁻³ or less and n to be 100 or greater. We further verify, for each simulation, that decreasing δt and/or increasing n (while keeping the value σ of interest conserved) does not significantly affect the results shown.

Figure 5.

Corrections of the errors using polynomial fitting. In all panels, the solid lines show the original potentials, and the dashed lines are polynomial fits of the apparent potentials (designated as “app.” in the legend) as measured from simulation data affected by the indicated dynamic and static errors. For each set of errors, the symbols show the corrected potentials (“corr.” in the legend) using polynomial coefficient fitting following Eqs. 15 and 16. (a) uses data for V(x) = x⁴ (see Fig. 2, c and d), (b) is for V(x) = (−x + x⁴)/2 (see Fig. 2, e and f), (c) for V(x) = −x² + 2x⁴ (from Fig. 2, g and h), and (d) for $V\left(x\right)=V_{\text{ES}}\left(x\right)$ as defined in the caption of Fig. 1, with a = 1. To see this figure in color, go online.

A histogram of the positions with a bin size ≤0.05 is then calculated, and we verified that the observed PDF is independent of the bin size when it is chosen in this range. The apparent potential is then extracted from the PDF via Eq. 2. For all the examples investigated next, we also perform BD simulations without dynamic and static errors and verify that the correct potential is returned by our algorithm (see Fig. 3 a and the open squares in Figs. 1, 2, and 4). Furthermore, in all the simulation results presented here, error bars are a fraction of the symbols’ size used in the plots.

Figure 3.

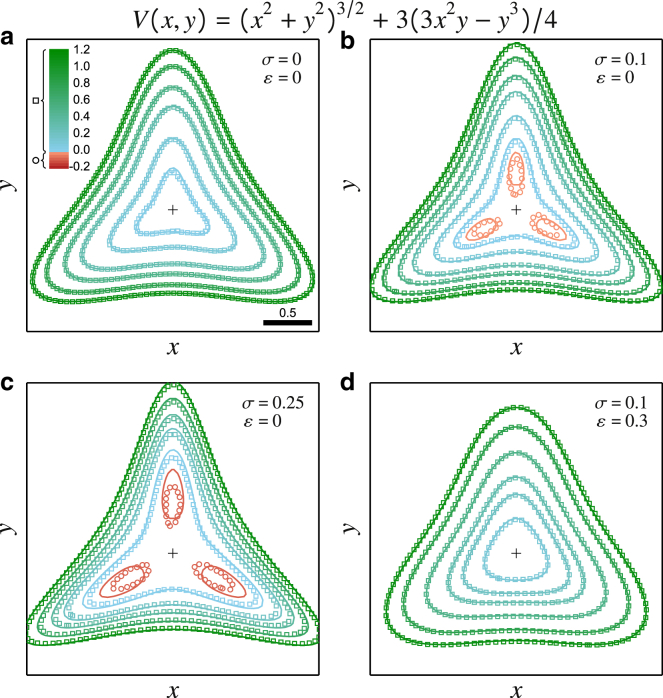
Comparison of Eq. 3 with BD simulations for various σ and ε in the 2D trapping potential V(x, y) = (x² + y²)^3/2 + 3(3x²y − y³)/4. The symbols are contours extracted from the simulations (squares for positive level contours, circles for negative ones), whereas the lines are their counterparts obtained using Eq. 3. (a)–(c) are for increasing dynamic errors but no static errors, whereas (d) includes both effects. The cross indicates the point (0,0), and the outermost contour is at V = 1.1 in all four panels. The conditions of (6a), (6b) require $\sigma \ll 0.1$ and $\epsilon \ll 0.5$ over the observed domain. To see this figure in color, go online.

Figure 4.

Comparison of Eq. 8 with the simulations of two identical Brownian particles interacting via the potential V(d) = (d − 10)² (a) and via $V\left(d\right)=V_{\text{DLVO}}\left(d\right)=250e^{-10d}/\left(d+10\right)-\left(50/3\right)/{\left(d+10\right)}^2-\left(50/3\right)/\left(d^2+20d\right)-\left(1/3\right)\text{ln}\left[\left(d^2+20d\right)/{\left(d+10\right)}^2\right]$ (b). In both panels, the symbols are BD results, and the lines are calculated using Eq. 8 with the substitutions $D\to 2D$ and ${\epsilon }^2\to 2{\epsilon }^2$. The conditions in (11a), (11b) require $\sigma \ll$ 0.01 and $\epsilon \ll$ 0.2 for (b). To see this figure in color, go online.

Results and Discussion

1D potentials

We now use Eq. 8 to predict the shape of the apparent potential for a few 1D examples presented in Fig. 2 and compare the results with the BD simulations described in the previous section. In this figure, the lines are obtained from Eq. 8, and the symbols are obtained from the simulations.

The first potential we consider is V(x) = x² (Fig. 2, a and b), for which Eq. 8 is exact and indeed matches the simulations for any values of ε and σ. This canonical harmonic potential, indicating a linear elastic interaction, is ubiquitous in soft biological systems (56) and in the optical tweezer technique commonly used to probe them (57, 58). For a general harmonic trap with constant k, V(x) = kx²/2, the apparent potential can be expressed, using Eq. 8, as $\overline{V}\left(x\right)=\overline{k}{x}^2/2$ with $\overline{k}=k/u_{\epsilon ,\sigma }$ and for the relaxation rate λ = βDk. Consequently, the apparent MSD of a particle trapped in such potential will reach, at a large lag time, a plateau $2/\left(\beta \overline{k}\right)=2g_{\sigma }/\left(\beta k\right)+2{\epsilon }^2$ with $g_{\sigma }=2\left(\sigma \lambda -1+e^{-\sigma \lambda }\right)/{\left(\sigma \lambda \right)}^2$, as already shown by Savin and Doyle (37, 38). Our formula in that case also justifies the corrective approach employed by Mojarad and Krishnan (26) to evaluate the stiffness of their trapping potentials via the dependency of the MSD plateau with the camera exposure time.

The second potential we examine is V(x) = x⁴, shown in Fig. 2, c and d, and which has been investigated as a possible confinement landscape for membrane proteins (12). This trapping potential also resembles the interaction restricting the motion of a particle attached to a substrate by a polymer tether (59, 60). The “tethered particle motion” technique has been used in recent years to probe the mechanical properties and interaction of various biological macromolecules (61). Unlike the previous case of a harmonic potential, Eq. 8 is an approximation that fails for large values of σ or ε when the conditions expressed by (11a), (11b) are not satisfied. Accordingly, we observe discrepancies between the predicted apparent potential and the simulations (see the up triangle and plus sign data in Fig. 2, c and d, respectively). However, our formula correctly returns the existence of two symmetric minima in the apparent potential as observed in the simulation results (and similar to the data presented in Fig. 1) and is accurate for lower (and typically more experimentally realistic) values of σ and ε. We also note that near the potential’s minimum, the dynamic errors tend to apparently widen the trap, with the static errors producing the reverse. This behavior is indeed the converse of what is seen on the higher parts of the trapping branches of the potential (about β⁻¹ above its minimum; see Fig. 1).

We also investigate an asymmetric potential, V(x) = (−x + x⁴)/2 in Fig. 2, e and f, for which Eq. 8 also returns an effective approximation of the simulation results when σ and ε satisfy the conditions (11a), (11b). We study, in Fig. 2, g and h, the potential V(x) = −x² + 2x⁴, which is a double-well trap similar to ones observed in several biological systems (61, 62). It is symmetric and displays a local maximum at x = 0, which can be apparently hidden by the static errors (see the diamond data, correctly predicted by our formula, in Fig. 2 h). Also in Fig. 2 h, we show an instance in which higher values of ε lead to $u_{\epsilon ,\sigma }<0$ and Eq. 8 is undefined around the local maximum of V(x) (dashed line), as explained in Apparent Potential of Methods.

We note that overall, Eq. 8 is returning an effective approximation of the apparent potential $\overline{V}$, unless the static and dynamic errors originate from particularly large values of ε and $\sqrt{D\sigma }$, respectively, that is, greater than ∼a/3.

2D potentials

We further extend our analysis to 2D potentials and confirm the applicability of Eq. 3 in that case. Such potential maps obtained in 2D (or 3D) can be used to characterize, for example, the pore geometries in protein gels (63) or receptors’ trapping in cell membranes (49, 51, 54, 64). In Fig. 3, we rename $\left(x_1,x_2\right)=\left(x,y\right)$ and study the potential V(r) = (x² + y²)^3/2 + 3(3x²y − y³)/4 (that is, $V\left(\mathit{r}\right)=r^3\left[1+\left(3/4\right)\text{sin}\left(3\theta \right)\right]$ in polar coordinates r = (r, θ)), which confines the particle in a trap shaped as a three-pointed star.

We show that BD simulations (symbols) are indeed effectively described by Eq. 3 (lines), even for values of σ and ε close to the limits set by (6a), (6b). We further observe that the effects of the dynamic errors share features of the 1D case. Hence, it also produces apparent local minima (see the contours shown with the circles in Fig. 3, b and c), but the magnitude of these 2D dents in the potential map tends to be larger than in their 1D counterparts under similar σ (compare Fig. 3 b with the circle data in Fig. 2 c). This amplification of motion blur artifacts at higher dimension, which we have not assessed in detail here, may indeed explain the difference between the experiments and simulations presented in Fig. 1. Motion blur also modifies the overall shape by sharpening and extending the corners while narrowing the side edges (compare Fig. 3, a–c with increasing σ and no static errors). This observation, in particular, does not qualitatively align with the results reported by Ritchie et al. (39) for particles trapped in a square well (region of free diffusion bounded by impenetrable walls; our model, derived for smooth potentials, cannot be applied for this situation), in which case the apparent potential tends to be harmonic like. These dissimilarities indeed highlight the nontrivial effects of motion blur.

The static errors have the opposite effect in the observed range of potential near its minimum, at which the corners appear flushed (compare Fig. 3, b and d) and the trap narrower. At higher values of the potential, this effect reverses and the potential indeed appears to be widened by the static errors (although, overall, narrowed by the dynamic errors).

Interaction potential

Equation 3 is written for a Brownian particle diffusing in a trapping potential V. However, it is also correct for a system of two Brownian particles with trajectories ${\mathbf{r}}_1\left(t\right)$ and ${\mathbf{r}}_2\left(t\right)$ in a mutual interaction potential $V\left(\left|{\mathit{r}}_1-{\mathit{r}}_2\right|\right)$. One only needs to replace in Eq. 3 the diffusion constant D with the sum of the diffusion constants of the two particles D₁ + D₂ and the noise covariance matrix with the sum of the individual noises E₁ + E₂. If the particles are identical and tracked in 1D or 2D, the substitutions are $D\to 2D$ and ${\epsilon }^2\to 2{\epsilon }^2$.

This reasoning is valid, because Eq. 1 can also be written identically for the two-particle system, with $\mathbf{r}={\mathbf{r}}_1-{\mathbf{r}}_2$ now representing the separation between the interacting particles and with the added individual noise vectors ${\mathit{\xi }}_1$ and ${\mathit{\xi }}_2$ assumed to be mutually independent. The system’s dynamics are now also governed by Eq. 13 for the particle separation r(t), with D replaced by D₁ + D₂, as obtained by subtracting each BD equation describing ${\mathbf{r}}_1\left(t\right)$ and ${\mathbf{r}}_2\left(t\right)$. From there, the derivation of Eq. 3, as described in Appendix A, proceeds in an identical manner.

We numerically verify Eq. 8 for two interaction potentials between identical particles in 1D motion, and the results are presented in Fig. 4. The first potential models two particles connected by a linear spring with rest length 10, V(d) = (d − 10)², where d is the distance between the particles’ surfaces. For this harmonic potential, Eq. 8 is exact (see Fig. 4 a) for all values of σ and ε. We perform this simulation to verify that the substitutions $D\to 2D$ and ${\epsilon }^2\to 2{\epsilon }^2$ are indeed correct.

A relevant interaction in colloidal science is modeled by the Derjaguin-Landau-Verwey-Overbeek (DLVO) theory. For a typical system of trackable particles, the potential may be written as (22):

$$V_{\text{DLVO}}\left(d\right)=A_{\text{y}}\frac{\rho e^{-d/{\lambda }_{\mathrm{D}}}}{d+2\rho }-\frac{A_{\text{c}}}{6}\left[\frac{2{\rho }^2}{{\left(d+2\rho \right)}^2}+\frac{2{\rho }^2}{d\left(d+4\rho \right)}+\text{ln}\frac{d\left(d+4\rho \right)}{{\left(d+2\rho \right)}^2}\right],$$ (14)

where ρ is the particles’ radius, d + 2ρ is the distance separating the two particles’ centers, λ_D is the Debye length, A_y is a constant of the screened Coulomb repulsion, and A_c is the Hamaker constant. For a realistic example, with ρ = 500 nm latex particles, having 10⁻⁴ Cm⁻² charge density, and immersed in a 1:1 electrolyte with 10⁻³ M ionic strength, then λ_D = 10 nm, A_y = 50 β⁻¹, and A_c = 2β⁻¹ (22, 65). To perform simulations of two Brownian particles interacting with this potential, we set the unit of length to a = 10λ_D (see the resulting dimensionless expression of $V_{\text{DLVO}}\left(d\right)$ in the caption of Fig. 4). The particles are further trapped by a parabolic branch for d ≥ 5a, which mimics the effect of the line-scanned optical tweezer used to perform experimental measurements of this kind (24).

The results of our simulations for the DLVO potential are shown in Fig. 4 b, and Eq. 8 is in reasonable agreement with these data. The effect of dynamic errors is to apparently deepen the interaction potential, shorten its range and steepen its variations around the minimum (see down triangles in Fig. 4 b). Such qualitative differences between true and observed potentials would also occur with interactions of similar profiles in the attractive range (e.g., depletion interaction). These discrepancies indeed resemble previously reported mismatches between the experiments and theory (25, 66), which may also be the result of dynamic errors in the measurements.

Corrections

In principle, Eq. 3 is a differential equation that could be solved numerically for V after measuring $\overline{V}$, with a set of boundary conditions (one of which would arbitrarily set the value of V at a particular location). We could not, however, implement a systematic and general solution using common solver packages. Instead, we have developed a provisional procedure, which first allows for preliminary assessing if positioning errors are significant in the measurements and then for obtaining an estimation of the true potential from the apparent potential if the role of these errors is estimated as important.

The measured potential must be first fitted by a power series, using any built-in package for polynomial fitting in the data analysis software. To assess if motion blur can be neglected, one can apply the transformation $V\stackrel{\mathrm{Eq}.3}{\to }\overline{V}$ described by Eq. 3 to the fitted apparent potential, that is, calculating the “transformed apparent” potential $\overline{V}$ via $\overline{V}\stackrel{\mathrm{Eq}.3}{\to }\overline{\overline{V}}$. If differences between $\overline{V}$ and $\overline{\overline{V}}$ are within experimental error bars, no correction needs to be applied. This reasoning is justified by the fact that the transformation described in Eq. 3 affects the function it is applied to by a comparable magnitude when applied for the second time compared to when it is applied for the first time, as we have numerically verified. Hence, if the differences between $\overline{V}$ and $\overline{\overline{V}}$ are negligible, so will be the changes between V and $\overline{V}$.

If applying Eq. 3 to the apparent potential recovered from data shows changes exceeding experimental error bars, one can estimate the true potential by applying a polynomial coefficient fitting of Eq. 3. For example, if in 1D $\Vert \sigma \lambda \Vert <1$ and ε² < Dσ, one can efficiently approximate Eq. 8 by the following:

$$\beta \overline{V}=\beta V+s_{\epsilon ,\sigma }\frac{\sigma \lambda -\sigma v^2/D}{2}+\left(1-6s_{\epsilon ,\sigma }^2\right)\frac{{\sigma }^2{\lambda }^2}{24}-\left(1-12s_{\epsilon ,\sigma }^2\right)\frac{{\sigma }^2\lambda v^2/D}{24}+\left(1+10s_{\epsilon ,\sigma }-60s_{\epsilon ,\sigma }^3\right)\frac{{\sigma }^3{\lambda }^2{v}^2/D}{120}+c ,$$ (15)

with $s_{\epsilon ,\sigma }={\epsilon }^2/\left(D\sigma \right)-1/3$, as obtained by a second-order expansion of $\text{ln}{u}_{\epsilon ,\sigma }$ and $\left(u_{\epsilon ,\sigma }-1\right)/\left(\sigma \lambda \right)$ in σλ (one order beyond Eq. 12). In the above equation, c is the constant found in Eq. 2. We next write $\beta \overline{V}\left(x\right)={\sum }_{k=0}^p{\overline{c}}_k{\left(x/a\right)}^k$ and $\beta V\left(x\right)={\sum }_{k=0}^p{c}_k{\left(x/a\right)}^k$ as two polynomial expansions of degree p and where ${\left\{{\overline{c}}_k\right\}}_{k=0\dots p}$ are the fitting parameters for the measured potential. Upon substituting these expressions into Eq. 15, and comparing the polynomial coefficients, we obtain a system of equations

$$\begin{array}{c}{f}_0\left(c,c_0,c_1,c_2\right)={\overline{c}}_0\\ f_1\left(c_1,c_2,c_3\right)={\overline{c}}_1\\ \dots \\ f_{p-3}\left(c_1,\dots ,c_{p-1}\right)={\overline{c}}_{p-3}\\ f_{p-2}\left(c_1,\dots ,c_p\right)={\overline{c}}_{p-2}\\ f_{p-1}\left(c_1,\dots ,c_p\right)={\overline{c}}_{p-1}\\ f_p\left(c_1,\dots ,c_p\right)={\overline{c}}_p\end{array},$$ (16)

where the functions ${\left\{f_k\right\}}_{k=0\dots p}$ can be obtained using a symbolic mathematical software. These are p + 1 equations for the p + 2 unknowns $c,c_0,c_1,\dots ,c_p$, the missing equation being the one that sets $c_0$, which can be assigned arbitrarily by choosing, for example, $V\left(0\right)=\overline{V}\left(0\right)$ (that is, $c_0={\overline{c}}_0$). This well-posed system can then be numerically solved to obtain the coefficients ${\left\{c_k\right\}}_{k=0\dots p}$ of the original potential from the fitting parameters ${\left\{{\overline{c}}_k\right\}}_{k=0\dots p}$ and the known values of σ, ε, and D.

We distribute through GitHub (https://github.com/savin-lab/potential-correction) an implementation of this method, which we apply in Fig. 5 to several of the canonical potentials investigated in this study. We observe that we can indeed recover the appropriate profiles, notably eliminating the apparent double potential wells (see Fig. 5 a for σ = 0.1 and ε = 0 and Fig. 5 d for σ = 0.3 and ε = 0), and, on the contrary, restoring lacking features of the true potential that are flushed by the static errors (see Fig. 5 c for σ = 0.1 and ε = 0.3). The residual discrepancies observed in Fig. 5, c and d may result from using the approximation given by Eq. 15 and/or the inaccuracy of the polynomial fits.

Here, the polynomial fits are obtained for power series with degree p between 6 and 12, chosen so as to obtain the best match with the original potential. However, a prior knowledge of the probed potential is normally not available. In practice, we anticipate that the best choice of p reflects a compromise between fitting the experimental data as accurately as possible without capturing features originating from statistical uncertainty over small length scales. A natural criterion for choosing the fitting length scale, and hence p, could be based on the terms of (11a), (11b) that sets the validity of Eq. 8 and that is verified in Appendix B.

We shall deal with this issue in more detail in the course of analyzing published experimental works that could be affected by tracking errors. Although our findings prove the validity of the inversion approach, more effort is required to offer a systematic and robust numerical method to recover V from $\overline{V}$.

Conclusions

We have determined the effects of dynamic (resulting from motion blur) and static (resulting from instrumental noise) errors on recovering energy landscapes from measured Brownian-particle position distributions. We have shown that these two phenomena are the source of nontrivial, systematic biases in the measurements, potentially leading researchers to read out and interpret an incorrect apparent potential. In particular, we have described the phenomenology of these effects in more detail on some canonical trapping potentials: harmonic, double well, asymmetric, and in 1D and 2D as well as interaction potentials. For the harmonic case, the contaminated potential is also harmonic with an apparent stiffness constant that can be exactly calculated.

Estimating if static and dynamic errors significantly skew measurements in a given system can be carried out using our results. Equation 3 for predicting the apparent potential is accurate for many setups and easily implemented for a wide class of examples. Inverting it to obtain the true potential from the apparent potential poses a challenge for numerical mathematics. We also proposed in this study a practical strategy to perform this task, although further work is needed to achieve a stable and accurate reconstruction method and assess its performances under real-world experimental conditions.

We conjecture that the effects of these measurement errors may have been overlooked in some existing experimental works (25, 66). Hence, we recommend that the effects of these errors should be assumed to be one of the possible explanations for unexpected results obtained when using particle-tracking methods. Including explicit information about the shutter times used, tracking parameters, and noise characterization (48) should now become a standard practice in reporting research involving Brownian-particle video tracking.

Further research needs to be carried out in this direction. Our study should be followed by a detailed review of existing experimental results. As already mentioned, it is also necessary to develop systematic algorithms to invert Eq. 3 for calculating the true from the apparent potential, $\overline{V}\to V$. Our provisional method has indeed significant shortcomings, which are explained in Correction. Furthermore, this type of error propagation analysis should also be made for the other observables (e.g., pair or van Hove correlation functions (67), two-point microrheology (68), etc.) that are extracted from Brownian-particle-tracking data.

Author Contributions

T.S. designed the research. M.J.B. and T.S. performed the research and wrote the article.

Editor: Julie Biteen.

Appendix A: Derivation of Eq. 3

For a single particle in an external potential, we start by writing the moving average of particle positions in Eq. 1, which represents data collected during a single shutter time, as the limit of a discrete series of n + 1 successive positions taken by the particle every σ/n time unit, added to a noise term

$$\overline{\mathbf{r}}\left(t\right)=\underset{n\to \infty }{\text{lim}}\frac{1}{n+1}\sum _{k=0}^n{\mathbf{r}}_k\left(t\right)+\mathit{\xi },$$ (17)

where ${\mathbf{r}}_k\left(t\right)=\mathbf{r}\left(t-\sigma +k\sigma /n\right)$ such that ${\mathbf{r}}_0\left(t\right)=\mathbf{r}\left(t-\sigma \right)$ and ${\mathbf{r}}_n\left(t\right)=\mathbf{r}\left(t\right)$. The particle is assumed to obey the inertialess (i.e., overdamped) limit of the Langevin equation in an external potential. Consecutive positions in the series forming $\overline{\mathbf{r}}\left(t\right)$ are almost surely located infinitesimally close to each other when n is large. Therefore, the motion between them can be treated via the BD,

$${\mathbf{r}}_k={\mathbf{r}}_{k-1}-\left(\sigma /n\right)\beta D\mathit{\nabla }V\left({\mathbf{r}}_{k-1}\right)+\sqrt{2D\sigma /n}\mathbf{w},$$ (18)

where w is a vector realization of a delta-correlated, stationary Gaussian process with zero mean. Hence, $f_{\mathbf{w}}\left(\mathit{w}\right)=\mathcal{N}\left(\mathit{w};\mathbf{0},\mathit{I}\right)$ and the autocorrelation $\langle \mathbf{w}\left(t\right){\mathbf{w}}^{\mathrm{⊺}}\left(t^{\prime }\right)\rangle =\mathit{I}$ if $|t-t^{\mathbf{\prime }}|\le \sigma /n$, 0 otherwise. We here employ the usual notation for the d-dimensional normal distribution with mean vector μ and covariance matrix Σ,

$$\mathcal{N}\left(\mathit{r};\mathit{\mu },\mathbf{\Sigma }\right)=\frac{e^{-{\left(\mathit{r}-\mathit{\mu }\right)}^{\mathrm{⊺}}{\mathbf{\Sigma }}^{-1}\left(\mathit{r}-\mathit{\mu }\right)/2}}{{\left(2\pi \right)}^{d/2}\text{det}{\left(\mathbf{\Sigma }\right)}^{1/2}}.$$

Each position ${\mathbf{r}}_k$ is now assumed to be in the vicinity of ${\mathbf{r}}_0$ so that we may linearize the force $\beta D\nabla V\left({\mathit{r}}^{\mathbf{\prime }}\right)=-{\mathit{v}}_0+{\mathit{\Lambda }}_0\left({\mathit{r}}^{\mathbf{\prime }}-{\mathit{r}}_0\right)$, where we have used the notations

$$\begin{array}{c}{\mathit{v}}_0\mathbf{=}\mathit{v}{|}_{\mathit{r}={\mathit{r}}_0}\\ {\mathit{\Lambda }}_0\mathbf{=}\mathit{\Lambda }{|}_{\mathit{r}={\mathit{r}}_0}\end{array}$$

for ν and Λ as defined by (4a), (4b) in Apparent Potential. The subscript “0” indicates that these are evaluated at ${\mathit{r}}_0$. The conditions for this second-order expansion of V to be valid are given by (6a), (6b).

The conditional PDF $f_{\mathbf{r}|{\mathbf{r}}^{\mathbf{\prime }}}\left(\mathit{r}|{\mathit{r}}^{\mathbf{\prime }}\right)=f_{\mathbf{r},{\mathbf{r}}^{\mathbf{\prime }}}\left(\mathit{r},{\mathit{r}}^{\mathbf{\prime }}\right)/f_{{\mathbf{r}}^{\mathbf{\prime }}}\left({\mathit{r}}^{\mathbf{\prime }}\right)$ is written in terms of the joint PDF $f_{\mathbf{r},{\mathbf{r}}^{\mathbf{\prime }}}$ and the marginal $f_{{\mathbf{r}}^{\mathbf{\prime }}}$. From Eq. 18, it follows that

$$f_{{\mathbf{r}}_k|{\mathbf{r}}_{k-1}}\left(\mathit{r}|{\mathit{r}}^{\mathit{\prime }}\right)=\mathcal{N}\left(\mathit{r};{\mathit{A}}_n{\mathit{r}}^{\mathit{\prime }}+{\mathit{b}}_n,2D\sigma \mathit{I}/n\right),$$

with ${\mathit{A}}_n=\mathit{I}-\sigma {\mathit{\Lambda }}_0/n$ and ${\mathit{b}}_n=\sigma \left({\mathit{v}}_0+{\mathit{\Lambda }}_0{\mathit{r}}_0\right)/n$. Recursively using $f_{{\mathbf{r}}_k|{\mathbf{r}}_{k-2}}\left(\mathit{r}|{\mathit{r}}^{\mathbf{\prime }}\right)=\int \int \int f_{{\mathbf{r}}_k|{\mathbf{r}}_{k-1}}\left(\mathit{r}|\mathit{\rho }\right)f_{{\mathbf{r}}_{k-1}|{\mathbf{r}}_{k-2}}\left(\mathit{\rho }|{\mathit{r}}^{\mathbf{\prime }}\right){\text{d}}^3\rho$ and exploiting the properties of Gaussian integrals, we get the following for any k > j ≥ 0:

$$f_{{\mathbf{r}}_k|{\mathbf{r}}_j}\left(\mathit{r}|{\mathit{r}}^{\mathit{\prime }}\right)=\mathcal{N}\left(\mathit{r};{\mathit{A}}_n^{k-j}{\mathit{r}}^{\mathit{\prime }}+\sum _{i=0}^{k-j-1}{\mathit{A}}_n^i{\mathit{b}}_n,2D\frac{\sigma }{n}\sum _{i=0}^{k-j-1}{\mathit{A}}_n^{2i}\right).$$

This equation allows us to calculate $f_{{\mathbf{r}}_k|{\mathbf{r}}_0}$ and $f_{{\mathbf{r}}_k,{\mathbf{r}}_j|{\mathbf{r}}_0}=f_{{\mathbf{r}}_k|{\mathbf{r}}_j}{f}_{{\mathbf{r}}_j|{\mathbf{r}}_0}$ for any k > j ≥ 1. All are normal distributions, and so will be $f_{\overline{\mathbf{r}}|{\mathbf{r}}_0}$. Further using the matrix’s geometric series ${\sum }_{j=0}^{k-1}{\mathit{A}}_n^j={\left(\mathit{I}-{\mathit{A}}_n\right)}^{-1}\left(\mathit{I}-{\mathit{A}}_n^k\right)$, the matrix exponential limit, ${\text{lim}}_{n\to \infty }{\left(\mathit{I}-\mathit{A}/n\right)}^n=e^{-\mathit{A}}$, and accounting for static errors by adding $\mathit{E}=\langle \mathit{\xi }{\mathit{\xi }}^{\mathrm{⊺}}\rangle$ to the covariance matrix of the measured position, we finally obtain

$$f_{\overline{\mathbf{r}}|{\mathbf{r}}_0}\left(\mathit{r}|{\mathit{r}}_0\right)=\mathcal{N}\left(\mathit{r};{\mathit{r}}_0+\frac{\sigma }{2}{\mathit{G}}_{\sigma }{\mathit{v}}_0,D\sigma {\mathit{H}}_{\sigma }+\mathit{E}\right),$$

where ${\mathit{G}}_{\sigma }=\mathit{G}\left(\sigma {\mathit{\Lambda }}_0\right)$ and ${\mathit{H}}_{\sigma }=\mathit{H}\left(\sigma {\mathit{\Lambda }}_0\right)$ with

$$\begin{array}{c}\mathit{G}\left(\mathit{X}\right)=2{\mathit{X}}^{-2}\left(\mathit{X}-\mathit{I}+e^{-\mathit{X}}\right),\\ \mathit{H}\left(\mathit{X}\right)=2{\mathit{X}}^{-2}-{\mathit{X}}^{-3}\left(3\mathit{I}-e^{-\mathit{X}}\right)\left(\mathit{I}-e^{-\mathit{X}}\right).\end{array}$$

We now use $f_{\overline{\mathbf{r}}}\left(\mathit{r}\right)=\int \int \int f_{\overline{\mathbf{r}}|{\mathbf{r}}_0}\left(\mathit{r}|{\mathit{r}}_0\right)f_{{\mathbf{r}}_0}\left({\mathit{r}}_0\right){\text{d}}^3{r}_0$, where $f_{{\mathbf{r}}_0}\left({\mathit{r}}_0\right)=f_0{e}^{-\beta V\left({\mathit{r}}_0\right)}$, with $f_0$ a constant, to calculate the apparent distribution. We may use again the expansion

$$\begin{array}{c}\beta DV\left({\mathit{r}}_0\right)=\beta DV\left(\mathit{r}\right)-{\mathit{v}}^{\mathrm{⊺}}\left({\mathit{r}}_0-\mathit{r}\right)+\frac{1}{2}{\left({\mathit{r}}_0-\mathit{r}\right)}^{\mathrm{⊺}}\mathit{\Lambda }\left({\mathit{r}}_0-\mathit{r}\right),\\ {\mathit{v}}_0=\mathit{v}-\mathit{\Lambda }\left({\mathit{r}}_0-\mathit{r}\right),\\ {\mathit{\Lambda }}_0=\mathit{\Lambda },\end{array}$$

where ν and Λ are evaluated at r. The resulting integral reads as follows, after the change of variable $\mathit{\rho }={\mathit{r}}_0-\mathit{r}$:

$$f_{\overline{\mathbf{r}}}=\frac{f_0{e}^{-\beta V}}{{\left(2\pi \right)}^{d/2}\text{det}{\left(D\sigma {\mathit{H}}_{\sigma }+\mathit{E}\right)}^{1/2}}\int \int \int \text{exp}\{-{\left[\mathit{\rho }+\frac{\sigma }{2}{\mathit{G}}_{\sigma }\left(\mathit{v}-\mathit{\Lambda }\mathit{\rho }\right)\right]}^{\mathrm{⊺}}{\left(D\sigma {\mathit{H}}_{\sigma }+\mathit{E}\right)}^{-1}\left[\mathit{\rho }+\frac{\sigma }{2}{\mathit{G}}_{\sigma }\left(\mathit{v}-\mathit{\Lambda }\mathit{\rho }\right)\right]+\frac{{\mathit{v}}^{\mathrm{⊺}}\mathit{\rho }}{D}-\frac{{\mathit{\rho }}^{\mathrm{⊺}}\mathit{\Lambda }\mathit{\rho }}{2D}\}{\text{d}}^3\rho .$$

The above Gaussian integral (with a linear term) can be calculated. After noting the relation [I − XG(X)/2]² = G(X) − XH(X), we finally obtain

$$f_{\overline{\mathbf{r}}}=\frac{f_0{e}^{-\beta V}}{\text{det}{\left({\mathit{G}}_{\sigma }+\frac{\mathit{\Lambda E}}{D}\right)}^{1/2}}\text{exp}\left\{-\frac{{\mathit{v}}^{\mathrm{⊺}}{\mathit{\Lambda }}^{-1}\left[{\left({\mathit{G}}_{\sigma }+\frac{\mathit{\Lambda E}}{D}\right)}^{-1}-\mathit{I}\right]\mathit{v}}{2D}\right\},$$

from which Eq. 3 can be readily deduced upon defining ${\mathit{U}}_{\mathit{E},\sigma }={\left({\mathit{G}}_{\sigma }+\mathit{\Lambda E}/D\right)}^{-1}$.

Appendix B: Conditions of Validity

We here assess the ranges of σ and ε for which Eq. 3 can be used. The examples investigated in the main text suggest that the conditions of validity (6a), (6b) provide appropriate estimates for the maximal values ${\sigma }_{\text{max}}$ and ${\epsilon }_{\text{max}}$ below which Eq. 3 can indeed be used. To assess these limiting values in a systematic manner, we simulated a Brownian particle trapped in the potential V(x) = x² + [cos(2πkx) − 1]/8, for k = 1...7, with increasing values of σ and of ε. Increasing k for this potential increases the level of details that needs to be resolved by the particle tracking methods (compare Fig. 6 a, where k = 2, with Fig. 6 b, where k = 6). For this potential, we test our predictions for ${\sigma }_{\text{max}}$ and ${\epsilon }_{\text{max}}$ obtained by equating both sides in each (11a), (11b), (11a), (11b), a and b,

$$\left(2+\pi k/4\right){\sigma }_{\text{max}}+{\sigma }_{\text{max}}^{1/2}={\left(\pi k\right)}^{-1}$$ (19a)

and

$${\epsilon }_{\text{max}}={\left(\pi k\right)}^{-1},$$ (19b)

respectively. The amplitude 1/8 of the oscillations around the term x² in the potential is such that no term may be neglected in (19a), (19b).

Figure 6.

Assessing the conditions (6a), (6b) by quantitatively comparing Eq. 8 to BD simulations for the trapping potential V(x) = x² + [cos(2πkx) − 1]/8, with k = 1...7. (a) and (b) show the simulated apparent potentials (symbols) and our approximated expression (lines) for increasing values of σ and with ε = 0 (k = 2 in (a), k = 6 in (b)). The discrepancy is quantified by $\text{min}{\chi }_{\text{red}}^2$, defined in Eq. 20, whose variations with σ and k are shown in (c) (values of k displayed on each corresponding line). (d) shows the range ${\sigma }_{\text{max}}$ (below which Eq. 8 is effective) as a function of k, as defined by the threshold $\text{min}{\chi }_{\text{red}}^2=10$ (symbols) and as obtained by Eq. 11a (line, see text). (e) and (f) give the same quantities as (c) and (d), respectively, to compare the range of static error ${\epsilon }_{\text{max}}$ evaluated from $\text{min}{\chi }_{\text{red}}^2=10$ and Eq. 11b for the displayed values of $\sigma <{\sigma }_{\text{max}}$. To see this figure in color, go online.

The simulation results (symbols in Fig. 6, a and b) are then compared to the apparent potential $\overline{V}$ predicted by Eq. 8 (lines in Fig. 6, a and b). Specifically, the discrepancy between the simulations and Eq. 8 is quantified by the reduced chi-squared ${\chi }_{\text{red}}^2$, defined as

$${\chi }_{\text{red}}^2=\frac{1}{N}\sum _{j=1}^N\frac{\mathit{\Delta }{\overline{V}}_j^2}{\text{var}{\overline{V}}_j}.$$ (20)

Here, ${\left\{\mathit{\Delta }{\overline{V}}_j\right\}}_{j=1\dots N}$ are the differences between the simulations and Eq. 8 at the N locations output by the simulations, and ${\left\{\text{var}{\overline{V}}_j\right\}}_{j=1\dots N}$ are the variances of the simulated data at these locations. The arbitrary constant in Eq. 2 is chosen beforehand to minimize ${\chi }_{\text{red}}^2$, so that we designate as $\text{min}{\chi }_{\text{red}}^2$ our measure of deviation of Eq. 8 from the simulations.

As σ increases, the approximation fails above a value ${\sigma }_{\text{max}}$ that is determined by $\text{min}{\chi }_{\text{red}}^2=10$, as indicated in Fig. 6 c (69). The results for ${\sigma }_{\text{max}}$ are compared favorably to the solution of Eq. 19a, shown by the line in Fig. 6 d for various values of k. The same procedure is applied to evaluate a maximal static error ${\epsilon }_{\text{max}}$ for each k = 1...7 (Fig. 6 e) and compare it with the result of Eq. 19b shown by the line (Fig. 6 f). We further verified that the latter results do not depend on $\sigma <{\sigma }_{\text{max}}$.

We have thus confirmed that (6a), (6b) provide effective estimates for the range of validity of Eq. 3.