Investigation of phonatory characteristics using ex vivo rabbit larynges

Abstract

Quantitative analysis of phonatory characteristics of rabbits has been widely neglected. However, preliminary studies established the rabbit larynx as a potential model of human phonation. This study reports quantitative data on phonation using ex vivo rabbit larynx models to achieve more insight into dependencies of three main components of the phonation process, including airflow, vocal fold dynamics, and the acoustic output. Sustained phonation was induced in 11 ex vivo rabbit larynges. For 414 phonatory conditions, vocal fold vibrations, acoustic, and aerodynamic parameters were analyzed as functions of longitudinal vocal fold pre-stress, applied air flow, and glottal closure insufficiency. Dimensions of the vocal folds were measured and histological data were analyzed. Glottal closure characteristics improved for increasing longitudinal pre-stress and applied airflow. For the subglottal pressure signal only the cepstral peak prominence showed dependency on glottal closure. In contrast, vibrational, acoustic, and aerodynamic parameters were found to be highly dependent on the degree of glottal closure: The more complete the glottal closure during phonation, the better the aerodynamic and acoustic characteristics. Hence, complete or at least partial glottal closure appears to enhance acoustic signal quality. Finally, results validate the ex vivo rabbit larynx as an effective model for analyzing the phonatory process.

I. INTRODUCTION

Investigation of the oral communication process in mammals and humans is within the scope of various scientific fields and motivated by a variety of different reasons. Studies can basically be separated into two categories. For the first group, vocal fold physiology is the primary scientific interest. The second group focuses on the progress and development of medical treatments to facilitate phonation. The principles of voice production or phonation are similar for many mammals and humans (Titze, 2017). An overview of principal vocalization mechanisms in mammals can be found in Elemans et al. (2015). The primary acoustic signal is generated in the larynx by two opposing vocal folds. During vocalization or phonation, vocal fold vibrations are induced by airflow coming from the lungs. During vibration, the vocal folds open and close, producing the primary acoustic signal. This signal is modulated in the vocal tract and then emitted from the mouth or nose. For mammals, investigations of the oscillation frequencies of the vocal folds have exhibited a wide range between 15 Hz for an elephant (Herbst et al., 2013) and 2100 Hz for elk calls (Titze and Riede, 2010). Even higher vocal fold oscillation frequencies were found for other mammals, as reported in Titze et al. (2016). For humans, dependent on age and gender, the fundamental frequency typically ranges between 100 Hz and 350 Hz for normal phonation (Patel et al., 2014). However, during singing, vocal fold vibration frequencies of up to 1568 Hz were reported (Echternach et al., 2013).

Different mammalian species have been investigated when studying the physiology of the voice source (i.e., oscillating vocal folds). The largest mammals considered were elephants (Herbst et al., 2012), elk (Riede and Titze, 2008), bovines (Regner et al., 2010), tigers (Titze et al., 2010), and lions (Klemuk et al., 2011). Mammalian species exhibiting similar laryngeal dimensions to humans were ovines (Alipour and Jaiswal, 2009), porcines (Bohr et al., 2016), and canines (Herbst et al., 2014; Ling et al., 2015). These latter models were studied as potential models of human vocal fold vibration, and their vocal fold dynamics were compared with human laryngeal dynamics (Döllinger et al., 2011). For smaller larynges, dynamical studies on rat (Welham et al., 2009) and rabbit (Novaleski et al., 2016) models have also been reported.

The rabbit larynx model seems specifically suitable for mimicking human voice production as the histology of the rabbit lamina propria (Thibeault et al., 2002) and the layer structure (Hertegard et al., 2003) were found to be similar to those of humans. However, to date, experiments analyzing the phonatory process using rabbit larynges are limited. One study focused on establishing the ex vivo, and another the in vivo, rabbit model as a feasible model for phonatory analysis (Maytag et al., 2013; Ge et al., 2009). Awan et al. (2014) analyzed in vivo nonlinear dynamic phenomena by varying flow rate and adduction levels. However, only one ex vivo study performed detailed parameter studies (Mills et al., 2017). They determined aerodynamic parameters [airflow, subglottal pressure (P_S), sound pressure level (SPL)], the fundamental frequency (f₀), and the vibrational amplitude as a function of vocal fold elongation. They showed that at phonation onset P_S, SPL, and f₀ increase as a function of elongation. Further studies were medically oriented and focused on surgical outcome (Kojima et al., 2014; Novaleski et al., 2016) and scarring (Hertegard et al., 2009; Mau et al., 2014). However, despite these previous studies on rabbit phonation, an in-depth, quantitative analysis reporting vocal fold vibratory parameters, the time-resolved acoustic and subglottal pressure signals, has not been performed yet. Hence, thus far, the correlation of vibratory characteristics with aerodynamic and acoustic parameters has largely been neglected for the rabbit model. To overcome this shortcoming, this study has the following two goals:

• (1)To present quantitative data and parameters computed from high-speed imaging (HSI) data, and time-resolved subglottal pressure and acoustic signals. A wide range of phonatory conditions is applied to investigate the phonatory range of rabbit larynges.
• (2)To identify and quantify dependencies between glottal closure insufficiency and phonatory parameters computed from the dynamic, acoustic, and pressure signals. The motivation and hypothesis for analyzing such dependencies is that glottis closure insufficiency is thought to be accountable for a variety of swallowing and breathing problems, as well as for breathy and weak voice (Schneider-Stickler et al., 2013; Giraldez-Rodriguez and Johns, 2013). When pathological glottis closure insufficiency is detected in humans, it is always the goal to restore glottis closure through vocal fold medialization by applying material injection (e.g., calcium hydroxyapatite) or material implantation (e.g., silicone blocks); see, e.g., Almohizea et al. (2016) and Dumberger et al. (2017). Despite the known negative effect of glottis closure insufficiency on the phonatory process, a quantitative analysis based on detailed parameter extraction is still missing.

II. MATERIALS AND METHODS

A. Specimen

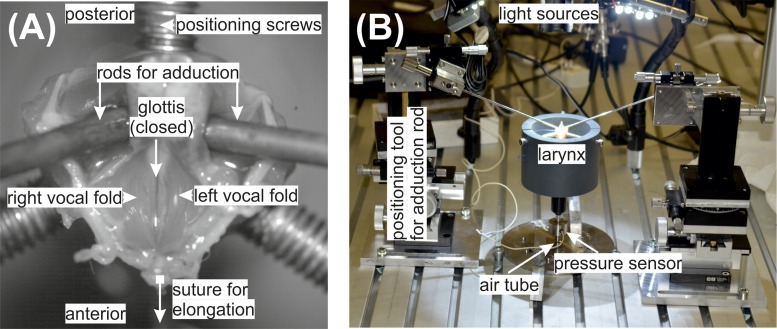
Altogether 12 rabbit ex vivo larynges (New Zealand White female rabbits, 4–5 kg weight, age 14–118 weeks) were available for investigation. The larynges were harvested right after the rabbits were sacrificed using Buprenorphin. Since the rabbits were primarily sacrificed for use in other scientific experiments (local ethical approval number 54-2532.1-54/12), no separate ethical approval was necessary. The larynges were dissected to expose the vocal folds, Fig. 1(A). The trachea was cut 3 cm below the larynx. Afterward the larynges were quick-frozen in liquid nitrogen and stored in a deep freezer at −80 °C, thus preserving the tissue characteristics (Chan and Titze, 2003). The night before the experiments, the larynges were slowly thawed in a refrigerator at 6 °C. One larynx showed tissue hemorrhage, and was therefore excluded from further experiments. The remaining 11 larynges showed no visible anatomical or other potential alterations.

FIG. 1.

(Color online) (A) A close-up of the ex vivo rabbit larynx and the experimental phonatory bench (B) are given.

B. Data acquisition

Figure 1 shows the experimental setup. The applied tools and data acquisition devices are explained in the following. The ex vivo larynges were mounted on an artificial, stainless steel, trachea with a diameter of 6 mm, dimensioned for the rabbit larynges. A hole was drilled in the artificial trachea for placement of the subglottal pressure sensor, 100 mm below the larynx. A custom-made support tool prevented the unintentional lateral displacement of the larynx. It consisted of a Polyvinylchloride (PVC) tube and three screws fixing the cricoid cartilages. The entire experimental setup is given in Fig. 1(B) and a close-up of the mounted larynx, as seen through the camera, is given in Fig. 1(A).

The time-resolved subglottal pressure was captured by a XCS-93-5PSISG pressure sensor (Kulite Semiconductor Products, Inc., Leonia, NJ), which was flush-mounted to the internal wall of the artificial trachea. The pressure sensor was driven by a PXIe-4330 bridge module (National Instruments, Austin, TX), offering a 24 bit resolution. The time-resolved acoustic pressure signal was captured by a 4189 1/2-inch free-field microphone (Brüel&Kjaer, 2850 Nærum, Denmark) mounted in coronal plane of the larynx with a 45° inclination toward the sagittal plane at a distance of 20 cm to the glottis. The microphone was driven by a Nexus 2690 microphone conditioning amplifier (Brüel&Kjaer, 2850 Nærum, Denmark). The amplified signal was captured by a PXIe-4492 dynamic signal acquisition module (National Instruments) with a 24 bit resolution. The vocal fold oscillations were recorded by a Phantom V2511 high-speed camera (Vision Research, Wayne, NJ) at 8000 fps and a spatial resolution of 768 × 768 pixel. To correlate the high-speed recordings with the acoustic and subglottal pressure signals, the camera state signals were captured by a PXIe-6356 multifunctional data acquisition module (National Instruments) with 16 bit resolution. The three National Instruments modules were integrated in a PXIe-1073 express (National Instruments). Both pressure signals and the camera state signals were synchronously sampled with a sampling rate of f_s = 96 kHz. The measurement was started with the start trigger of the high-speed camera that simultaneously started the PXIe system. The whole setup was controlled by a standard personal computer (PC) via scripts using the software LabView (National Instruments) as described in Birk et al. (2017a).

C. Experimental procedure for phonation

To modify the degree of longitudinal tension in the vocal folds, and thereby induce different phonatory conditions, a suture with three different weights (w₁ = 1 g, w₂ = 2 g, w₃ = 5 g) was attached anteriorly at the thyroid cartilage; see Fig. 1(A). The purpose of this suture was to simulate the action of the cricothyroid muscle by tilting the thyroid cartilage forward. Self-sustained vibrations were induced by an airflow generated and controlled by a 4000B digital power supply driving a MF1 mass flow controller (MKS Instruments, Andover, MA). The humidified (ConchaTherm Neptune, Teleflex, Morrisville, NC) and heated (37 °C) airflow passed through the artificial trachea and then through the glottis (i.e., the area between the two oscillating vocal folds).

The dynamic experiments were based on former ex vivo studies (Alipour and Jaiswal, 2009; Maytag et al., 2013) and were performed as follows: (1) A weight was attached to induce longitudinal tension. (2) To keep the larynx in position, three screws were tightened until they touched the larynx. (3) Two rods were symmetrically tightened posteriorly, simulating the adduction process, to bring the larynx in phonatory position, i.e., until the glottis was entirely closed. Then the phonatory threshold pressure (PTP) level was determined by manually and continuously increasing the air flow through the larynx until sustained phonation occurred (Birk et al., 2017b), i.e., PTP was determined as the subglottal pressure level at which the vocal folds initiated sustained vibration. From the PTP, the airflow was increased 14 times successively in steps of 0.5 lm⁻¹ (8.33 mls⁻¹). This was performed for each of the three weights w_i yielding a total of 45 experimental runs of sustained phonation per larynx. For each run, 125 ms of sustained phonation were recorded by the high-speed camera. This corresponded to 37–112 oscillation cycles depending on the oscillation frequency of the vocal folds. For each run, 35 oscillation cycles were considered for further analysis. For the acoustic and subglottal pressure signals, an additional 375 ms were recorded, yielding 500 ms of sustained oscillation or 148–448 cycles, to achieve the recommended number of cycles (i.e., at least 100 cycles) for reliable acoustic analysis (Titze, 1995; Karnell et al., 1995). To eliminate potential environmental noise, the acoustic and subglottal pressure signals were low pass filtered with a cut off frequency of 5 kHz. Due to the extremely large storage space for the high-speed data, a recording time of 500 ms was not practicable. However, the 35 cycles considered in our study constitutes a much larger data sample than used in similar ex vivo quantitative HSI studies (Herbst et al., 2012; Luegmair et al., 2015).

D. Data analysis of phonatory experiments

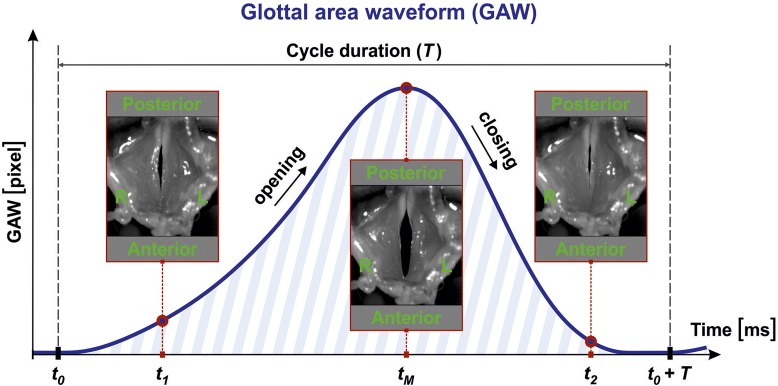
Before extracting parameters from the vocal fold dynamics, image processing was performed. The vocal fold dynamics are represented by the opening and closing of the vocal folds. Hence, the glottal area between the vocal folds was segmented within the HSI footage yielding the glottal area waveform (GAW) in pixels. The GAW is the function of the glottal area (number of pixels) over time. Figure 2 shows the GAW behavior over a typical oscillation cycle of length T. When the glottis is entirely closed at time step t₀, the glottal area contents contain zero pixels. During the opening process, the glottis, and therefore the number of pixels, increases until the maximum opening state is reached at time t_M. Then the glottis closes and the GAW becomes smaller again. Glottal segmentation was performed with a software tool developed in-house, known as Glottis Analysis Tools (GAT); the GAT tool is available upon request. This software has proven its functionality in previous quantitative HSI studies and is also used by international colleagues (Chen et al., 2013; Dippold et al., 2015; Patel et al., 2016).

FIG. 2.

(Color online) Images of the larynx during phonation as seen through the camera: phonatory cycle with length T and computed GAW.

From the GAW signal, parameters were computed reflecting main components of the glottal dynamics, as shown in Table I: (A) glottal closure insufficiency, (B) tissue characteristics, (C) opening and closing behavior, and (D) dynamic left-right symmetry. For the acoustic and time-resolved subglottal pressure signal, parameters reflecting harmonic components and perturbation were computed, as shown in Table II. Within Tables I and II, references are given to show where the parameters were derived.

TABLE I.

Group variable GGI and dynamic laryngeal parameters solely computed for the GAW; a.u. refers to arbitrary units.

Parameter (unit) and references	Abbreviation	Parameter description
(A) Glottis closure characteristic
Glottis gap index (a.u.; Patel et al., 2014)	GGI	Minimum glottal area/maximum glottal area:
		Glottis entirely closed [0–0.01]; glottis partially closed] 0.01–0.4[; no contact of vocal fold [0.4–1]
(B) Parameters on tissue characteristics
Amplitude-to-length-ratio (a.u.; Titze, 1994)	ALR	Dynamic range of GAW (max - min)/glottis length: the larger the more deformable the vocal folds
Stiffness (1/frames; Munhall et al., 1985)	Stiffness	Maximum absolute value of first derivative/dynamic range: the higher the value the stiffer the tissue
(C) Parameters on opening and closing behavior
Asymmetry Quotient (a.u.; Henrich et al., 2003)	ASQ	Speed quotient/(speed quotient + 1)
Closing quotient (a.u.; Holmberg et al., 1988)	CQ	Closing time/cycle duration
Open Quotient (a.u.; Baken and Orlikoff, 1999)	OQ	Glottis open time/cycle duration
Maximum area declination rate (pixel/frames; Titze, 2006)	MADR	Absolute value of negative peak in the first derivative of GAW, i.e., maximum GAW closing velocity
Speed quotient (a.u.; Baken and Orlikoff, 1999)	SQ	Opening time/closing time
(D) Parameters on left-right symmetry
Amplitude symmetry index (a.u.; Wang et al., 2016)	ASI	Spatial symmetry of GAW: rate between maximum left and right glottal area, the closer to 1 the more symmetric
Phase asymmetry index (a.u.; Qiu et al., 2003)	PAI	Symmetry in time: deviation in time between left and right GAW amplitude; the closer to 0 the higher the symmetry

TABLE II.

Parameters computed on both the acoustic and subglottal pressure signals reflecting the signal quality.

Parameter (unit) and references	Abbreviation	Description/formula
Perturbation measures
Jitter (%; Bielamowicz et al., 1996)	JT	Time periodicity of the signal, the lower the better
Shimmer (%;-(Bielamowicz et al., 1996)	SH	Amplitude periodicity of the signal, the lower the better
Harmonics components
Harmonic to noise ratio (dB; Yumoto et al., 1982)	HNR	Ratio between energies of harmonics-based signal and noise, the higher the better
Cepstral peak prominence (dB; Hillenbrand et al., 1994)	CPP	Development of harmonics, the higher the better

Furthermore, fundamental frequencies (f₀) of vocal fold oscillation were computed on the basis of the HSI data (GAW). Applied airflow (lm⁻¹) was measured. Averaged subglottal pressure (P_S) was computed from the time-resolved pressure signal. SPL (dB) was computed on the basis of the acoustic signal. The laryngeal flow resistance R_B (i.e., the ratio between the transglottal pressure difference and the mean glottal flow rate) was determined using the definition of van den Berg et al. (1957). In contrast to typical aerodynamic applications, a high flow resistance R_B is desired in phonation, yielding a high energy transfer from the glottal flow to the vocal fold tissues (Döllinger et al., 2016).

E. Statistical analysis

Question 1.

Do the glottal gap characteristics change for increasing pre-tension levels w_i and increasing applied airflow? The glottal gap occurrence during vibration was represented by the glottal gap index (GGI); see Table I. Analysis of the dependency of the GGI on elongation levels (w₁, w₂, w₃) and applied airflow level was performed using a univariate general linear model approach: The dependent variable was GGI, and the 2 fixed effect factors were pre-tension (3 levels) and airflow (15 levels). The random effect factor contained the individual larynges (11 levels). The Levene-test was not significant [F(44,369) = 1.269, p = 0.126]; hence, homogeneity of GGI for the different groups was assumed. Tukey's technique for post hoc comparison was applied. The significance level of p = 0.05 was used.

Question 2.

Is there a direct influence of the dynamic glottal gap (GGI) on other phonatory parameters? The effect of the glottal gap or glottal closure insufficiency during phonation on glottal dynamics, aerodynamic, and acoustic parameters was computed as follows:

• (1)All HSI recordings were visually inspected and divided into three visually easy to differentiate groups by one examiner: vocal folds completely closed, vocal folds partially closed, and vocal folds do not collide during phonation. Computing the GGI values for these subjectively allocated groups yielded the following intervals for GGI: GGI₁ ([0;0.01], entire closure during vibration), GGI₂ (]0.01;0.4[, partial closure), GGI₃ ([0.4;1], no visually recognizable contact of vocal folds). The visual inspection and group division was executed as reported before (Birk et al., 2017b). The only difference to that previous study was that, in the current work, only one group for partial glottal closure (GGI₂) was used due to reduced sample size. Representative examples for the three GGI groups are given in three mp4 format movie clips (Mm. 1, Mm. 2, and Mm. 3).

Mm. 1.

Download video file ^{(2.9MB, mp4)}

DOI: 10.1121/1.5043384.1

High-speed movie with GGI = 0.000 (entire closure). This is a file of type “mp4” (2993 KB). The video was re-sampled to 25 fps.

Mm. 2.

Download video file ^{(2.5MB, mp4)}

DOI: 10.1121/1.5043384.2

High-speed movie with GGI = 0.250 (partial closure). This is a file of type “mp4” (2579 KB). The video was re-sampled to 25 fps.

Mm. 3.

Download video file ^{(2.6MB, mp4)}

DOI: 10.1121/1.5043384.3

High-speed movie with GGI = 0.517 (no vocal fold contact). This is a file of type “mp4” (2626 KB). The video was re-sampled to 25 fps.

• (2)To investigate how the parameters differ between the three main GGI groups, the following steps were performed. Shapiro-Wilk tests showed that none of the vibrational, aerodynamic, harmonic, and noise parameters were normally distributed. Hence, Kruskal-Wallis tests were performed followed by post hoc tests (Mann-Whitney-U-test) with Bonferroni adjusted significance level with p = 0.05/3 = 0.017.

All statistics were performed using IBM SPSS version 21 (IBM, Armonk, NY).

F. Histological analysis

To confirm the use of healthy vocal folds, histological analysis was performed after the phonation experiments. The larynges were fixed for 24 h in 4% buffered formaldehyde and treated by the standard procedure of alcoholic dehydration and paraffin embedding. Serial horizontal cross sections (5 μm) were performed using a microtome. Two larynges were ruined during the cutting procedure and could not be further analyzed. For the remaining nine larynges, the sections were alternately stained with both van Gieson for collagen distribution and Gomori for reticular fiber distribution (Mulisch and Welsch, 2010). Van Gieson staining was performed in accordance with the manufacturer's instructions (Roth, Karlsruhe, Germany).

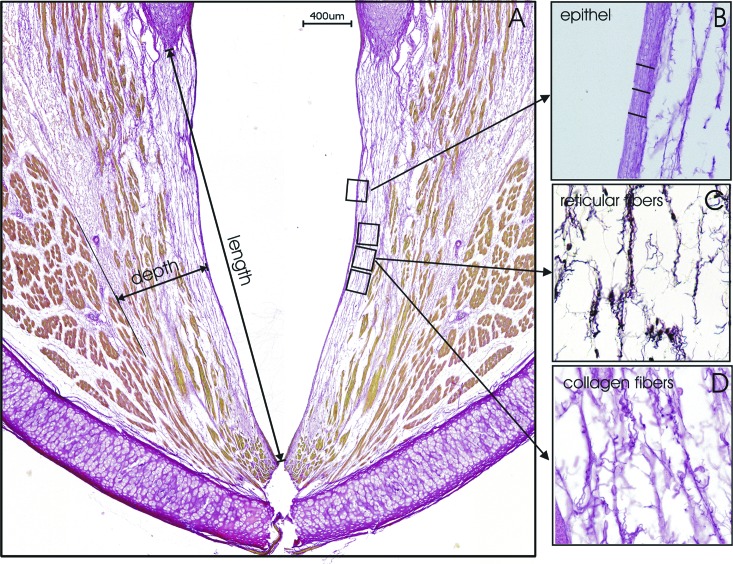
The stained sections were examined with a digital BZ-9000 microscope (Keyence, Neu-Isenburg, Germany) with the software BZ-II-Analyzer. For semi-quantitative analysis, the intensity of collagen and reticular staining from three typical regions within the lamina propria bordering the epithelium (Fig. 3) was assessed through densitometry (three measurements on each of three different slices, size: 200 μm × 150 μm). We collected the data from the nine larynges and calculated the average values and standard deviation in arbitrary units (a.u.). The length of the vocal folds and thicknesses of the epithelium and lamina propria were measured as the average over nine measurements (i.e., three measurements on each of three slices). The length of the vocal fold was measured from the arytenoid cartilage up to the thyroid cartilage.

FIG. 3.

Structures of collagen and reticular fibers were stained and analyzed with semiquantitative densitometry (three measurements on each of the three slices).

III. RESULTS

Altogether 414 (84%) of the 495 performed experimental runs could be analyzed. Experiments were excluded when the fundamental frequency could not be determined due to too high aperiodic vibrations (50 runs) and failure or insufficient accuracy of the image processing (31 runs). Hence, it must be noted that the presented results were restricted to periodic vocal fold oscillations, i.e., oscillations where the fundamental frequency was clearly defined, and could be determined reliably and consistently. An overview of the range of the fundamental phonatory parameters is given in Table III.

TABLE III.

Range of fundamental phonatory parameters; the values for phonation onset are given separately.

	F0 (Hz)	PS (Pa)	Flow (mls−1)	RB (Pa s l−1)	SPL (dB)
Phonation onset	494 ± 112	707 ± 346	61 ± 11	11967 ± 6293	64.8 ± 7.0
All recordings	605 ± 105	1436 ± 687	117 ± 34	12365 ± 4845	76.3 ± 7.6
Minimum values	315	123	42	1850	53.8
Maximum values	858	3287	180	21852	91.7

Question 1 (Is GGI influenced by pre-stress and airflow?).

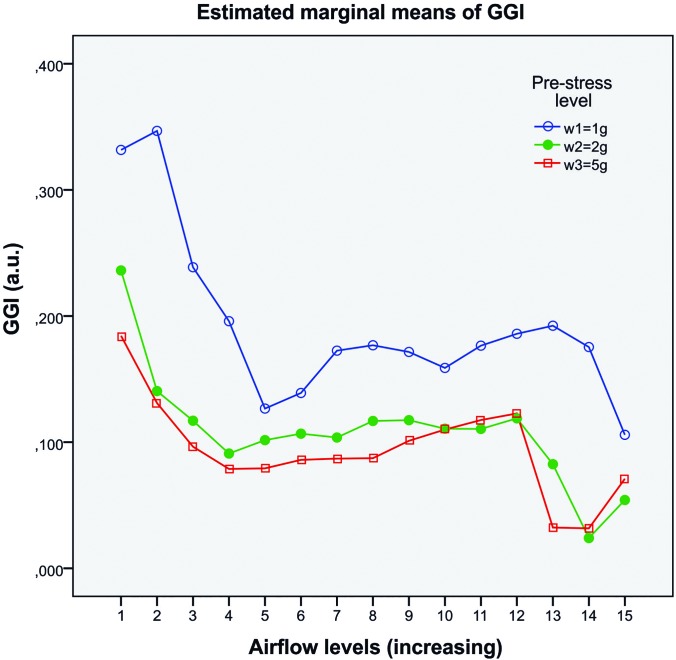
The estimated marginal means of the GGI separated for the two fixed effect factors, pre-stress and airflow, are given in Fig. 4. The statistics showed that pre-stress had significant influence on GGI [F(2,369) = 5.973, p = 0.009, partial η²= 0.372]. GGI clearly decreased from low pre-stress w₁ (blue) to w₂ (green) and then only slightly decreased to w₃ (red); see Fig. 4. Airflow also had a significant influence on GGI [F(14,369) = 6.203, p = 0.000, partial η²= 0.389]. GGI decreased over all three pre-stress levels for increasing airflow. Further, there was a significant interaction between pre-stress and airflow regarding GGI [F(28,369) = 1.604, p = 0.034, partial η²= 0.179]. The higher the flow, the less GGI changed for increasing pre-stress: The distance between the w_i curves became smaller for increasing airflow. The effect sizes f (Cohen, 1988) were large (f_pre-stress = 0.77) and medium (f_flow = 0.68, f_inter = 0.47).

FIG. 4.

Dependency of GGI toward pre-stress and airflow. The labels on the x axis correspond to phonation onset (number 1) and numbers 2–15 correspond to the successively increased flow steps with Δ = 8.33 mls⁻¹ between each run.

Question 2 (Does GGI influence phonatory parameters?).

The subdivision in the three GGI groups resulted in the following distribution of the experimental runs: GGI₁ (N = 148), GGI₂ (N = 216), GGI₃ (N = 50). The means and standard deviations for all parameters, separated for the three GGI conditions, are given in Table IV.

TABLE IV.

Means and standard deviations of all parameters separated for the three GGI conditions; a.u. refers to arbitrary units.

Parameters	GGI1 0.00 ± 0.00	GGI2 0.13 ± 0.11	GGI3 0.53 ± 0.09
Glottal dynamic parameters
ALR (a.u.)	15.2 ± 3.4	15.4 ± 3.9	7.8 ± 2.5
Stiffness (frames−1)	0.34 ± 0.05	0.28 ± 0.06	0.26 ± 0.05
ASQ (a.u.)	0.62 ± 0.07	0.61 ± 0.07	0.59 ± 0.05
CQ (a.u.)	0.32 ± 0.08	0.38 ± 0.07	0.41 ± 0.05
OQ (a.u.)	0.83 ± 0.10	0.99 ± 0.02	1.00 ± 0.00
MADR (px frames−1)	520 ± 220	520 ± 219	249 ± 117
SQ (a.u.)	1.73 ± 0.52	1.71 ± 0.57	1.52 ± 0.35
ASI (a.u.)	0.79 ± 0.13	0.83 ± 0.11	0.73 ± 0.09
PAI (a.u.)	0.13 ± 0.07	0.10 ± 0.06	0.13 ± 0.07
Aerodynamic parameters
RB (Pa s l−1)	15024 ± 3714	11683 ± 4791	7417 ± 2710
SPL (dB)	79.1 ± 6.4	76.1 ± 7.1	69.4 ± 7.5
PS (Pa)	1679 ± 646	1394 ± 691	897 ± 387
Acoustic signal: Harmonic and perturbation components
JTA (%)	2.7 ± 4.0	2.8 ± 3.6	5.7 ± 7.1
SHA (%)	23.2 ± 27.0	30.4 ± 30.4	55.7 ± 42.5
HNRA (dB)	15.6 ± 6.4	14.1 ± 6.7	10.8 ± 9.0
CPPA (dB)	24.0 ± 4.8	22.8 ± 4.8	19.4 ± 4.9
Subglottal pressure signal: Harmonic and perturbation components
JTP (%)	2.0 ± 2.9	2.1 ± 3.1	2.1 ± 2.9
SHP (%)	9.2 ± 14.9	10.0 ± 16.3	11.3 ± 17.9
HNRP (dB)	20.4 ± 6.6	21.1 ± 6.1	20.1 ± 6.4
CPPP (dB)	27.5 ± 3.9	26.4 ± 3.9	25.6 ± 3.2

The p-values of the statistics on GGI group differences for all parameters are given in Table V. All nine GAW parameters showed differences among the GGI groups. The most differences (eight) were found between complete glottis closure (GGI₁) and no vocal fold contact (GGI₃). The three main aerodynamic parameters (R_B, SPL, P_S) showed statistical significant differences between all three groups. In 9 out of 12 tests, the acoustic parameters showed significant differences between GGI groups. In contrast, the same parameters computed on the subglottal pressure signal only showed statistically significant differences for 2 out of 12 tests. These two statistically significant differences were both found for cepstral peak prominence (CPP_P).

TABLE V.

Computed p-values among the three GGI groups for the glottal dynamic parameters computed on the GAW, aerodynamic parameters, and parameters reflecting harmonic and perturbation in the acoustic and subglottal pressure signals.

Parameters	Post hoc tests (Mann-Whitney-U-test; p < 0.017)			Kruskal-Wallis (p < 0.05)
	GGI1 vs GGI2	GGI1 vs GGI3	GGI2 vs GGI3
GAW parameters
ALR	0.227	0.000	0.000	0.000
Stiffness	0.000	0.000	0.004	0.000
ASQ	0.301	0.009	0.074	0.044
CQ	0.000	0.000	0.042	0.000
OQ	0.000	0.000	0.001	0.000
MADR	0.519	0.000	0.000	0.000
SQ	0.242	0.006	0.078	0.034
ASI	0.000	0.000	0.000	0.000
PAI	0.000	0.939	0.002	0.000
Aerodynamic parameters
RB	0.000	0.000	0.000	0.000
SPL	0.000	0.000	0.000	0.000
PS	0.000	0.000	0.000	0.000
Acoustic signal: Harmonic and perturbation components
JTA	0.273	0.000	0.001	0.000
SHA	0.012	0.000	0.000	0.000
HNRA	0.021	0.000	0.027	0.001
CPPA	0.007	0.000	0.000	0.000
Subglottal pressure signal: Harmonic and perturbation components
JTP	—	—	—	0.335
SHP	—	—	—	0.980
HNRP	—	—	—	0.301
CPPP	0.009	0.000	0.046	0.001

Histology.

Figure 3(A) shows a histological slice with the positions of the densitometric analysis; positions for length, depth, and epithelial thickness measurements are indicated [Fig. 3(B)]. Histological analysis of the microstructure of the vocal fold showed no lesions, scarring, or bleeding. Figures 3(C) and 3(D) show the reticular and collagen staining, respectively. Both stainings showed a loose network of stained fibers. The average level of collagen was 849 ± 250 a.u. and of reticular fibers was 1975 ± 1236 a.u. Both fiber types were homogeneously distributed for all measurements over all larynges. The mean epithelial layer thickness was measured at 8.1 μm ± 1.2 μm and the mean lamina propria thickness was 602 μm ± 90 μm. The mean vocal fold lengths were measured at 4111 μm ± 426 μm. Elastin was not detected in the upper layer of the lamina propria. Only in the deep layer close to the vocalis muscle was possible to detect elastin bundles of longitudinal aligned fibers.

IV. DISCUSSION

Basic phonatory relationships were analyzed by performing 11 ex vivo rabbit experiments. It was shown that the GGI can be reduced by increasing vocal fold longitudinal pre-tension and applied airflow, yielding improved aerodynamic characteristics (i.e., higher R_B and SPL values) and an improved acoustical signal quality [i.e., increased harmonics-to-noise ratio (HNR_A) and CPP_A; decreased JT_A and SH_A].

A. Histology

Histologic analysis confirmed intact laryngeal tissue. Similar anatomical dimensions and similar distribution of two main extracellular matrix components (collagen and reticular fibers) were observed in all tested larynges. The measured thickness of the lamina propria was slightly thicker than previously described (Valerie et al., 2016), possibly depending on the age and sex of the animals, but also on the exact place of measurement position. The collagen and reticular fiber distribution looked similar to other investigations of the rabbit vocal fold extracellular matrix (Pitman et al., 2018; Rousseau et al., 2004).

However, the third main component, elastin, was not detected in the superficial region of the lamina propria; neither immunohistological nor Verhoeff staining exhibited any appearance of elastin. Small quantities of short, parallel elastin fibers in the longitudinal direction were found in the deeper region of lamina propria. This is in contrast with other publications in which elastin has been found in cross sections, also in the superficial layer of the vocal fold (Thibeault et al., 2002). One reason might be that we performed longitudinal cuts in which we may have missed the non-homogeneously distributed elastin fibers. Another reason might be that our vocal folds actually contained very little elastin, which could happen due to degradation as a result of reduced vocalization or due to the normal aging process (Roberts et al., 2011).

B. Fundamental phonatory parameters (Table III)

Mean PTP with 707 Pa ± 346 Pa (Table III) was found 57% lower than previously reported (1650 Pa ± 124 Pa) by Maytag et al. (2013). Accordingly, the averaged phonation threshold flow rate was also lower by 21% compared to their experimental data (76.8 mls⁻¹± 6.8 mls⁻¹). Mills et al. (2017) reported even lower phonation threshold flow rates down to 27.5 mls⁻¹, which are only 45% of ours, whereas their PTPs (647 Pa–839 Pa) were similar to the mean PTP from our experiments.

Similarly, Novaleski et al. (2016) reported lower mean flow rate (85.9 mls⁻¹) and subglottal pressure (900 Pa) compared to our overall mean values (Table III). Regarding the P_S range, our experimental results exhibited lower and higher values (123 Pa–3287 Pa) than given by Mills et al. (2017; approximately 500 Pa–2000 Pa). However, Mills et al. (2017) achieved phonation at lower flow rates starting from ∼17 mls⁻¹. Also the experiments reported by Awan et al. (2014) showed good consistency with our experiments regarding flow rates (85 mls⁻¹–144 mls⁻¹). However, we could apply flow rates of up to 180 mls⁻¹ (25% higher) yielding regular vibrations.

The SPLs (56.2 dB–68.5 dB) reported by Novaleski et al. (2016) were in the same range as those by Mills et al. (2017; 49.1 dB–59.3 dB). In contrast, we measured values between 53.8 and 91.7 dB; see Table III. Similar high SPLs (up to 85 dB) were also reported in in vivo studies by Ge et al. (2009).

The mean fundamental frequency f₀ was found higher than in Maytag et al. (2013; 451 Hz). Furthermore, f₀ achieved a higher range in our study (Table III) than previous investigations by Novaleski et al. (2016; 419 Hz and 728 Hz), but shows good accordance with the f₀ range found by Mills et al. (2017; approximately 300 Hz–850 Hz). Finally, Awan et al. (2014) reported potential fundamental frequencies of around 1000 Hz, which is higher than the maximum value (858 Hz) computed in our study.

To the best of our knowledge, no study has previously reported transglottal flow resistance R_B for rabbits; see Table III. Here the reported values of up to 21 852 Pa s l⁻¹ are nearly a factor of 3 higher than maximum values for other mammals such as porcines, ovines, and bovines, which had a maximum value of ∼7770 Pa s l⁻¹ (Alipour and Jaiswal, 2009) and ex vivo human models (Döllinger et al., 2016), which had a maximum value of ∼3000 Pa s l⁻¹. Thus, these high R_B values in rabbits suggest a highly efficient energy transfer from the airflow to the vocal fold tissues during phonation (Döllinger et al., 2016; Kniesburges et al., 2017).

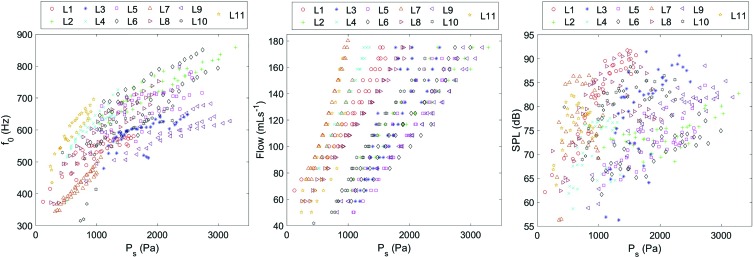
Tangentially, our study also confirmed previous observations that with increasing subglottal pressure, the airflow, f₀, and SPL increase (Mills et al., 2017); see Fig. 5.

FIG. 5.

Fundamental frequency, flow, and SPL over subglottal pressure P_S for all experiments of all 11 larynges L_i.

However, we could not confirm whether, at phonation onset, parameters P_S and f₀ increased for increasing elongation (i.e., longitudinal pre-stress), as reported by Mills et al. (2017); see Table VI. However, we did find increasing flow as a function of increasing elongation (not reported by Mills et al., 2017). In contrast to Mills et al. (2017), our data showed decreasing SPL; see Table VI. However, it must be noted that the absolute parameter variations at phonation onset were rather small, so interpretation was somewhat limited. Differences between both studies may also be based on different experimental setups.

TABLE VI.

Averaged values at phonation onset separated for the three pre-stress levels w_i.

Pre-stress	F0 (Hz)	PS (Pa)	Flow (mls-1)	SPL (dB)
w1	483 ± 137	683 ± 350	63 ± 4	64.6 ± 10.7
w2	477 ± 112	668 ± 384	64 ± 5	61.1 ± 11.8
w3	520 ± 97	764 ± 342	67 ± 10	58.3 ± 11.8

In summary, we could show that the dynamic range of the rabbit larynx is greater than previously reported: Normal phonation was observed (1) for lower P_S and for higher P_S and (2) for higher flow rates than reported in previous studies. Higher SPL values were measured than before, probably due to the greater P_S levels, as compared to previous studies. These differences may also be based on possible different ages and sexes of the animals, as compared to other studies. However, this is speculative, since none of the studies reported information on sex and age. Finally, the first data on transglottal flow resistance R_B were presented, suggesting a highly effective phonatory process for rabbit larynges. The high SPL and f₀ values in combination with large glottal resistance show that the rabbit phonation process is extremely efficient. This high efficiency is necessary because rabbits mainly phonate/vocalize at these high frequencies and loudness in extremely dangerous situations with the aim of baffling predators and warning conspecifics (Quesenberry and Carpenter, 2011; Bays et al., 2006).

C. Phonatory correlations and parameter dependencies

Statistics confirmed that the GGI can be reduced by increasing vocal fold longitudinal pre-tension and applied airflow (i.e., subglottal pressure); see Fig. 4. The glottal closure insufficiency represented by GGI highly influences glottal dynamic GAW parameters, quantitatively (Table IV) and statistically (Table V). Despite the fact that 19 out of 27 statistical post hoc tests were statistically significant for the GGI_i groups, the mean parameter value differences between Asymmetry Quotient (ASQ), SQ, and ASI only varied between 5% and 14%. However for stiffness, closing quotient (CQ), open quotient (OQ), and phase asymmetry index (PAI), the mean values varied between 20% and 31% and varied even more for amplitude-to-length-ratio (ALR) (97%) and maximumun area declination rate (MADR) (109%).

In our study, spatial dynamic left-right symmetry (ASI) seemed to be influenced more consistently by GGI than asymmetry in time (PAI). Whereas ASI showed statistically significant differences between all three GGI_i groups, interestingly, no statistically significant differences were found for PAI between GGI₁ vs GGI₃. Despite statistically significant differences, but due to the actual low range of the glottal asymmetry parameters ASI and PAI as compared to the rather high variation in acoustic parameters (Table IV), we encourage further studies to analyze the dependencies between dynamic vocal fold asymmetries and voice quality since this topic is still under discussion (Mehta et al., 2011). Nevertheless, dynamic asymmetry is often reported for voice disorders (Yamauchi et al., 2016; Samlan and Story, 2017).

According to its definition, the GGI is an appropriate measure to describe the degree of glottal closure insufficiency, which is a major cause of dysphonic voice (Inwald et al., 2011; Vaca et al., 2017). Thus, its influence on the acoustic parameters is obvious. The acoustic parameters JT_A, SH_A, HNR_A, and CPP_A are statistically different among the three GGI groups (Table V) and show a deterioration of the acoustic output signal with increasing degree of glottal closure insufficiency, as displayed in Table IV.

Smaller GGIs enhanced the quality of the acoustic signal; harmonic and perturbation components showed consistently better values for the entire closed glottis (GGI₁) compared to partial closure (GGI₂) or no vocal fold contact (GGI₃). Whereas the differences between GGI₁ and GGI₂ were statistically present but not as high, the deterioration of these two groups toward GGI3 was quantitatively large.

Most obvious, this acoustic deterioration is caused by massive decay of the glottal flow resistance R_B (Table IV), which is well-correlated with the energy transfer between the glottal air flow and the vocal folds. As a consequence, vocal fold oscillation, which is the primary acoustic source for phonation, is disturbed (i.e., see the change of dynamic glottal parameters as shown in Table IV).

For aerodynamic parameters, it could be shown that with increasing glottal closure insufficiency, the energy transfer flow-tissue was reduced (R_B), and the intensity (SPL) of the acoustic outcome signal and the subglottal pressure (P_S) also decreased.

The influence of GGI on parameters computed on the time varying subglottal pressure signal was only verified for CPP_P. There only statistical significant differences were present between full glottal closure and the other two groups. The CPP is a measure for the periodicity of the signal, i.e., development of the fundamental frequency and its harmonics (Hillenbrand et al., 1994; Birk et al., 2016). In contrast, JT and SH only considered disturbances within the fundamental frequency. This means that glottal closure insufficiency (groups GGI₂ and GG₃) mainly disturbed the development of the harmonics within the subglottal pressure signal but not amplitude (SH_P) or time variation (JT_P) of the fundamental frequency within the subglottal pressure signal. The harmonics-to-noise ratio (HNR_P) exhibited no statistical differences among GGI groups, although HNR also considers harmonics. However, HNR is computed in the time domain and involves the averaged signal, whereas the CPP is computed in the frequency domain. This suggests that HNR is not as sensitive to changes of the harmonics, as compared to CPP.

Hence, for the fluid–structure–acoustic interaction of the phonatory process, our data suggest that the structure–fluid interaction was detected in changing CPP_P values, but not in JT_P and SH_P for the three different GGI groups, i.e., little structure–fluid interaction. This means that the glottal closure gap induced slight disturbances in the subglottal signal harmonics that also resulted in great acoustic parameter changes, i.e., strong fluid–acoustic interaction. Hence, our data suggest that the harmonics within the subglottal pressure (airflow) are highly important for the acoustic signal quality. Also the results showed that the influence of glottal closure characteristics on the fundamental frequency of the subglottal signal was rather minor.

Regarding general relations within the phonation process found in our study (Tables IV and V), the data suggest the following. First of all, it was difficult to predict acoustic output quality based on the subglottal pressure signal. Whereas the acoustic signal showed high variations in the computed parameters, the subglottal signal seemed to vary only in the harmonic components. Second, glottal closure insufficiency highly influenced laryngeal dynamics, reducing the energy transfer from the airflow to the tissue vibrations, and yielding a reduced quality of the acoustic output signal. In turn, this suggested, third, that full glottis closure was necessary for an optimal interaction of fluid–dynamics and acoustics and therefore for good voice quality. Partial vocal fold closure (GGI₂) already interrupted this interaction. However, no contact of the vocal folds (GGI₃) during phonation resulted in highly reduced aerodynamic parameter values and acoustic quality.

V. CONCLUSIONS

Glottal closure characteristics appeared to exhibit a major influence on the phonatory process since all dynamic glottal, acoustic, and aerodynamic parameters were statistically and significantly influenced by GGI; see Table V. Complete glottal closure during phonation was desirable. While partial glottal closure during phonation already began to reduce aerodynamic and acoustic characteristics, contact-free oscillations of the vocal folds highly decreased acoustic and aerodynamic characteristics. The influence of glottal closure on the subglottal pressure signal appeared to be minor, but was recognizable in the CPP. Glottal closure insufficiency could be reduced by increasing the pre-tension of the vocal folds, the applied airflow, or both. Finally, the phonatory process in rabbits seemed more effective (i.e., in terms of higher R_B values) than in other mammalian species investigated so far and the phonatory range in rabbits was found to be larger than previously reported.