Not only size matters: Early-talker and late-talker vocabularies support different word learning biases in babies and networks

Abstract

In typical development, word learning goes from slow and laborious to fast and seemingly effortless. Typically developing 2-year-olds seem to intuit the whole range of things in a category from hearing a single instance named – they have word-learning biases. This is not the case for children with relatively small vocabularies (late talkers). We present a computational model that accounts for the emergence of word-learning biases in children at both ends of the vocabulary spectrum based solely on vocabulary structure. The results of Experiment 1 show that late talkers’ and early talkers’ noun vocabularies have different structures, and that neural networks trained on the vocabularies of individual late talkers acquire different word-learning biases than those trained on early talker vocabularies. These models make novel predictions about the word learning biases in these two populations. Experiment 2 tests these predictions on late- and early-talking toddlers in a novel noun generalization task.

There is extraordinary variability in the vocabularies of very young children. A two-year-old in the lower 10^th percentile may produce around 10 words whereas a two-year-old in the top 10^th percentile will produce well over 300 (Fenson, Dale, Reznick, Thal, Bates, Hartung, Pethick, & Reilly, 1993). In general, the course of word learning proceeds from slow, effortful learning of nouns, and of the range of things to which each noun refers, to quick, efficient noun learning. Indeed, typically developing 2-year-olds are so skilled at learning new nouns that they seem to intuit the whole range of things in a named category from a single naming experience – 2-year-olds demonstrate word learning biases. According to Linda Smith and colleagues’ Attentional Learning Account, children acquire these word learning biases as second-order generalizations over learned first-order noun categories, speeding up the task of learning new nouns (Smith, Jones, Landau, Gershkoff-Stowe & Samuelson, 2002). This shift from slow-to-fast does not necessarily occur for children below the 20^th percentile on productive vocabulary, who are defined as late talkers. Why do some children learn words quickly and early and others learn words slowly, maybe even showing effects that persist beyond childhood? (Rescorla, 2009) This paper looks at two possible contributing, and interrelated, factors: noun vocabulary composition and word learning biases.

Vocabulary Composition and Word Learning Biases

Children usually say their first word at around 12 months. Lexical learning at first is slow. However, the pace with which children add new words to their receptive and productive vocabulary increases over time such that by 24 to 30 months, they add words at a rate of 5 to 9 new words a day (e.g., Ganger & Brent, 2004). The evidence suggests that typically developing young children are skilled noun learners, at least in part, because they know about the different sorts of properties that are relevant in different domains. For example, when presented with a single never-before-seen thing and told its name (e.g., “This is a wug”), children systematically generalize that name to new instances in ways that accord with adult intuitions of category structure. Specifically, researchers using this novel noun generalization task (NNG) have consistently reported a shape bias for solid objects and a material bias for non-solid substances. That is, given a solid thing with multiple parts and constructed shape, children extend its name broadly to all things that match it in shape. Given a non-solid substance, children extend its name by surface properties, especially material. (e.g., Jones, Smith & Landau, 1991; Soja, Carey, & Spelke, 1991).

The relationship between vocabulary composition and word learning biases has been typically characterized in one of two ways: On the rationalist side, word learning biases are understood as abstract knowledge that guides, facilitates, and indeed allows word learning (e.g., Soja et al, 1991; Gelman & Bloom, 2000). On the empiricist side, the words that a child learns give rise to, create, and in fact constitute generalized knowledge about word learning leading to the observed biased behavior (e.g., Smith, 2000; Colunga & Smith, 2005, Samuelson, 2008). We would like to bypass the debate on whether word-learning biases are the egg to the vocabulary chicken or the other way around and focus instead on the interrelationship between these two factors.

In typical development, vocabulary structure and word learning biases are tightly coupled. First, the tendency to attend to shape in the specific context of naming solid objects emerges as children learn nouns, and becomes particularly robust around the time children have between 50 to 150 nouns in their productive vocabulary (Gershkoff-Stowe & Smith, 2004). Second, the developmental sequence and relative strength of these word learning biases reflects the statistical structure of early noun vocabularies in different languages (Samuelson & Smith, 1999; Colunga & Smith, 2005). In fact, individual differences in vocabulary composition predict individual differences in word learning biases (Perry & Samuelson, 2011). Third, changing 17-month-olds’ vocabulary composition by intensively teaching them names for shape-based categories yields an early shape bias, a bias to generalize names for artifacts by shape. At the same time, this trained early shape bias accelerates learning of object names outside of the lab, causing a dramatic increase in vocabulary size compared to control groups (Smith, Jones, Landau, Gershkoff-Stowe & Samuelson, 2002).

In addition to the behavioral work summarized above, computational modeling work has supported the idea of a relationship between vocabulary composition and word learning biases. Colunga & Smith (2005) trained a recurrent neural network on a vocabulary approximating the structure of the average 30-month-old noun vocabulary, in terms of the proportion of words that referred to solid things alike in shape (e.g., ball), material (e.g., cheese), and both shape and material (e.g., penny). After learning the nouns in the average child’s vocabulary, the networks were tested on an analog of the NNG task, using novel input patterns. The networks’ internal representations showed word learning biases akin to those of 30-month-old children. This model also made novel predictions regarding the effect of shape complexity and solidity, and accounted for effects of different syntactic frames, across languages, and more (Colunga & Smith, 2005; Colunga, Smith & Gasser, 2009). The modeling work presented here is an extension of these models beyond the average child, to model the relationship between vocabulary composition and word learning biases in children of different language abilities.

Late Talkers and Word Learning Biases

Altogether, the findings reviewed above suggest a developmental feedback loop between learning nouns, developing biases to attend to the relevant properties for objects and substances, and the learning of more nouns. In typical development, the nouns a child knows and what the child knows about learning nouns in general go hand in hand. This relationship is such that, in fact, learning names for categories of things organized by shape speeds up noun learning for typically developing children. However, this may not be the case for all children.

Late talkers are children who show a vocabulary delay in the absence of any sensory, cognitive or neurological deficit. It is well known that late talkers are not a homogenous group in terms of their developmental outcomes: some catch up, and some will experience persistent social and learning difficulties (Rescorla, 2002). A few late talkers will be diagnosed with Specific Language Impairment, for some the source of the delay may be processing speed (Fernald & Marchman, 2012), and for others the source of the delay may be environmental (Rescorla, Roberts, & Dahlsgaard, 1997; Thomas & Knowland, 2014). Importantly, although there is developmental continuity in vocabulary measures at the group level, the outcome for individual children cannot be accurately predicted on the basis of vocabulary production or comprehension (Thal, Bates, Goodman, & Jahn-Samillo, 1997; Desmarais, Meyer, Bairati & Rouleau, 2008). This paper presents a computational model that accounts for the relationship between vocabulary structure and word learning biases in children at different ends of the language spectrum.

Interestingly, unlike typically developing children, late talkers do not show systematic word learning bias. For example, 2- and 3-year-old late talkers extend the name of a novel solid object to other objects that match it in shape to a lesser extent than an age-matched typically developing control group (Jones, 2003). Similarly, pre-school children with specific language impairment (SLI) show no shape bias compared to age- and SES-matched typically developing controls (Collisson, Grela, Spaulding, Rueckl, & Magnuson, 2015). In fact, in one study, almost half of the late talkers systematically extended the novel name of a solid object to others matching in texture rather than shape (Jones, 2003).

The decoupling of vocabulary acquisition and word-learning biases may mean that late talkers are not just limited in their production of object names (the measure that defines them as late talkers) but also deficient in the processes that underlie the acquisition of new words, their word learning biases. If this were the case, one would expect the noun vocabularies of late-talkers to have a different structure than the noun vocabularies of typically developing children. Indeed, there is evidence that this is the case. For example, Beckage, Smith, & Hills (2011) showed that vocabularies of typically developing children show characteristics of small world structure, whereas vocabularies of late talkers show this pattern to a lesser extent.

In sum, the evidence suggests that learning names for things teaches children how to learn new nouns – how different kinds of properties are relevant for different kinds of things – and that in turn these word learning biases facilitate young children’s noun learning. To the extent that this interrelation holds true for children in opposite ends of the language spectrum – late talkers and early talkers – one might be able to leverage this developmental loop to predict outcome. The first step, however, is to show that 1) late talkers and early talkers know different sorts of nouns and that 2) these differences in vocabulary structure are related to corresponding differences in word learning biases. Thus, in Experiment 1 we examine the noun vocabulary composition of 18- to 30-month-old late- and early-talking children and show that neural network models trained on the vocabularies of individual late talkers learn different biases than those trained on individual early talker vocabularies. Experiment 2 tests the novel predictions made by these simulations about world learning biases in a novel noun generalization task with late- vs. early-talking toddlers.

Experiment 1

We first look at the relationship between vocabulary structure and word learning biases using vocabularies from age-matched late and early talkers and neural network simulations based on these vocabularies. Specifically, as a proxy for their vocabulary, we used the MacArthur-Bates Communicative Developmental Inventory toddler version (MCDI). The MCDI is a 680-word checklist that asks parents to indicate which words their child says. Although it is imperfect as a measurement instrument (Fenson, Dale, Reznick, Bates, Thal, & Pethick, 1994) it appears to be reliable and systematically related to children’s performances in a variety of laboratory measures of word learning, including especially their word-learning biases in the Novel Noun Generalization task (e.g., Landau, et al, 1988, Perry & Samuelson, 2011).

We characterize the words in the children’s vocabularies depending on whether they refer to solid or non-solid things that are alike in shape, material, or both. This is a grouping that has been shown to be informative both in behavioral and computational studies (e.g., Samuelson & Smith, 1999; Colunga & Smith, 2005; Perry & Samuelson, 2011). We then train individual neural networks on the noun vocabulary structure of each individual late-talking and early-talking child. If there are differences in vocabulary structure, and these differences can, to some extent, explain the differences in language ability, we would expect training on late talker vocabularies to yield different word learning biases than training on early talker vocabularies. More specifically, we would expect training on early talker vocabularies to result in word learning biases that would facilitate the learning of a vocabulary structured like the MCDI – highlighting shape similarities for solids and material similarities for non-solids. In contrast, we would expect networks trained on late talkers’ vocabularies to generalize more variable word learning biases, and perhaps even biases that would be unhelpful in learning early vocabularies.

Method

Participants

The vocabularies of 15 late talkers and of 15 early talkers were selected out of a pool of 148 MCDI forms completed by parents for children between 18-30 months of age. The criterion for inclusion was that there exist a vocabulary form from a child matching in age to within 5 days in both the late talker and the early talker groups. Late talkers scored at or below the 25^th percentile; early talkers were at or above the 75^th percentile according to the MCDI norms.

Age, percentiles, and vocabulary sizes for late and early talkers whose vocabularies were used in this study are summarized in Table 1. The ages for the two language groups ranged from 18.49 months to 28.26 months (M: 23.14/SD: 2.89 for late talkers and M: 23.15/SD: 2.85 for early talkers). Vocabulary sizes for the late talker group ranged between 15 and 425 words (M: 132.53/SD: 122.73); for the early talker group vocabulary size was between 158 and 664 words (M: 457/SD: 125.67).

Table 1.

Age, percentiles, and vocabulary sizes for late and early talkers whose vocabularies were examined in Experiment 1.

	Age	Percentile	Words	Nouns
Late Talkers	M: 23.14/SD: 2.89	M: 13.33/SD: 8.59	M: 132.53/SD: 122.73	M: 48.47/SD: 44.22
	(18.49-28.26)	(5-25)	(15-425)	(2-132)
Early Talkers	M: 23.15/SD: 2.85	M: 81.33/SD: 6.4	M: 457/SD: 125.67	M: 172.53/SD: 42.58
	(18.49-28.23)	(75-95)	(158-664)	(62-216)

As in Colunga & Smith (2005), we characterized each child’s vocabulary by the proportion of words they knew for the categories of: 1) solid things alike in shape (e.g., spoon), 2) solid things alike in material (e.g., chalk), 3) solid things alike in both shape and material (e.g., penny), 4) non-solid things alike in shape (bubble), 5) non-solid things alike in material (e.g., milk), 6) non-solid things alike in both (e.g., jeans). Since children were drawn from a wide age range (about 10 months), and the two language groups – late and early talkers – were matched by age, they naturally differed in their vocabulary size. Looking at the proportion of words in children’s vocabularies for each of the word types allowed us to get a sense of the variability in vocabulary composition (as opposed to vocabulary size) in children at different percentiles in vocabulary development. Nouns in children’s vocabularies were classified as falling in each of the different word type categories according to adult judgments made for each of the nouns in the MCDI reported in Samuelson & Smith, 1999.

The Model

Our models use the LEABRA algorithm (Local, Error-driven and Associative, Biologically Realistic Algorithm), which combines Hebbian and error-driven learning (O’Reilly, 2001). The Hebbian, self-organizing learning uses longer time-scale statistics about the environment and is useful for extracting generalities. However, Hebbian learning can have a hard time handling more complex patterns that include special cases and exceptions; these are more efficiently learned with supervised methods. LEABRA incorporates error-driven learning by using the differences between expectations and outcomes to adjust weights. The general function used in the Leabra algorithm is shown in Equation 1.

$$f_{\mathit{xcal}}\left(xy,{\theta }_p\right)=\{\begin{array}{c}xy-{\theta }_p xy<{\theta }_p{\theta }_d\\ -\frac{xy\left(1-{\theta }_d\right)}{{\theta }_d} \mathit{else}\end{array}$$ (1)

Where x is the sending activity, y is the receiving activity and θ_d and θ_p are floating thresholds which regulate how the weights change over the course of learning. The weight function of the network is the sum of that of the error-driven learning and that of the Hebbian learning.

The error-driven weight changes are updated based on the short-term average connection activity (<xy>_s) and the medium-time scale average connection activity (<xy>_m).

$$\mathrm{\Delta }{w}_{\mathit{error}}=f_{\mathit{xcal}}\left(<xy{>}_s,<xy{>}_m\right)=f_{\mathit{xcal}}\left(x_s{y}_s,x_m{y}_m\right)$$ (2)

Where <xy>_m represents the emerging expectation about a current situation and <xy>_s reflects the actual outcome and therefore the result of the received error information. In the simulator, there is a plus and minus phase in training. The minus phase comes first and represents the expectation of the network before it sees an outcome. Next, in the plus phase, the outcome is observed and influences activations.

The Hebbian weight changes are based on the short-term connection activity (xy_s) and long-term average activity of the receiving unit (<y>_l).

$$\mathrm{\Delta }{w}_{\mathit{Hebbian}}=f_{\mathit{xcal}}\left(x{y}_s,x<y{>}_l\right)=f_{\mathit{xcal}}\left(x{y}_s,x{y}_l\right)$$ (3)

Based on <y>_l, the threshold for weight change is adjusted, making the weight more likely to change in the direction given by xy_s. This creates the structure of generalization for the Hebbian learning mechanism. This algorithm is equivalent to contrastive Hebbian learning used in previous work (Movellan, 1990). For more details on network dynamics, see O’Reilly, Munakata, Frank, and Hazy (2012).

Architecture

The architecture is adapted from Colunga & Smith, 2005 as shown in Fig. 1. Words are represented discretely (as 24 localist single units) on the Word Layer. Referents are represented as distributed patterns over several dimensions on the Perceptual Layer. For example, the shape and material of an object (say the roundness of a particular ball and its rubbery material) are represented by an activation pattern along 12-unit shape and material layers. Solidity and non-solidity are represented discretely; one unit stands for solid and another for non-solid. Finally, there is a 25-unit hidden layer that is fully connected to all the other layers and recurrently to itself. Units in the Word Layer are connected to each other with negative weights; all other weights are initialized with random values between 0 and 1.

Figure 1.

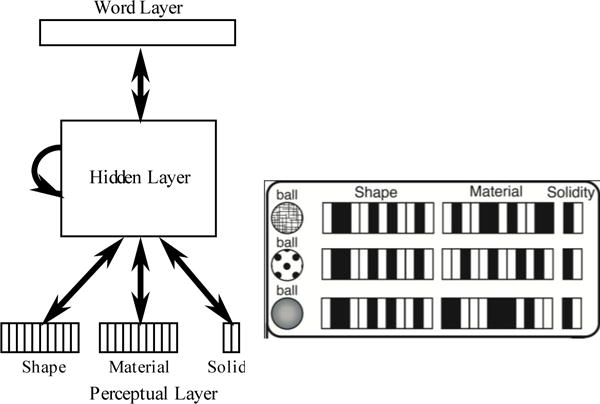
Network architecture and example training patterns used in Experiment 1.

Training

Because we are interested in the consequences of different vocabulary structures regardless of their size, all networks were trained to learn 24 nouns, proportionally structured like their corresponding child’s vocabulary. Thus, late- and early-talker networks had the same architecture, the same vocabulary size, the same learning and updating rules. In fact, the only differences among networks were the differences in vocabulary composition – the proportion of their vocabulary that referred to solid or non-solid things, alike in shape, material or both.

The networks are trained with categories presenting the same correlational structure as each individual child’s noun vocabulary. A training set consisting of 24 “words” was prepared for each child. For each type of word, a proportional number of training patterns was generated. For example, to represent a particular solid-shape word (e.g., a word like “ball”, which was judged to refer to things similar in shape but different in material), a 12-bit binary vector was randomly generated to be input in the shape layer. Similarly, to represent a particular solid-material word, a 12-bit binary vector was randomly generated to be input in the material layer. The irrelevant dimension was left unspecified, to be instantiated during run time. Note that this means a solid-both training pattern would involve no variability, as it would always present the same shape and material predetermined patterns. Patterns for non-solids were generated in a similar fashion, except that shapes were drawn from a more restricted part of the space: 4 out of the 12 shape units were always clamped to the same pattern. This represented the smaller range of shapes non-solids can take, compared to solids, and a prediction of this assumption was tested in previous work (Colunga & Smith, 2005).

On each training trial, a word was paired with a referent. That is, the corresponding, pre-determined 12-bit pattern was presented in the relevant dimension, paired with its corresponding word unit, solidity unit, and a randomly generated pattern on the irrelevant dimension. For example, Fig. 1 shows 3 training trials for a solid-shape word. On each epoch, we do this for each of the 24 nouns in the child’s training set. Networks were trained in this way until they reached asymptotic (and near perfect) performance. This part of the simulation is intended to put into the networks the lexical knowledge that the individual child would bring to the laboratory NNG task. Five networks were run for each child, with randomized initial weights. Learning rate was set at 0.01, and weights were updated after every epoch.

Note that all networks had the same vocabulary size (24 words), and vocabulary differences were only represented as the differences in proportions of each word type. That is, there was no attempt to represent in the model other likely relevant information, such as age or vocabulary size. This was done with the goal of isolating the contribution of vocabulary structure to word learning biases in the models, however, it is important to point out that the findings reported here do not encompass a thorough exploration of the space.

Testing

The testing set was kept constant for all networks and consisted of 10 novel solid exemplars and 10 non-solid novel exemplars; each exemplar had four instances matching in shape and differing in material, and four instances matching in material and differing in shape, for a total of 160 testing patterns. We used the network’s hidden layer activations for each of these patterns to assess the network’s word learning biases.

The question at hand is, what sort of word learning bias will the networks learn given different vocabulary structures? We address this question in a virtual version of the NNG task (Colunga & Smith, 2005). A test trial of the virtual NNG task, then, can be construed as presenting the network with three novel test patterns (one at a time) on the perception layer – an exemplar, and two choice items, one matching the exemplar in shape only and one matching in material only. For each of these three inputs, we recorded the resulting pattern of activation on the hidden layer, the network’s internal representation. If the network emphasizes the shape of the item then the similarities of the internal representations for the exemplar and its shape matching choice should be greater than the similarity of the internal representations for the exemplar and the material matching choice. If, however, the internal representations highlight the material of the items, then the similarity of the internal representations for the exemplar and the shape matching choice should be less than the corresponding similarity of the exemplar and the material matching choice. We used Luce’s choice rule to calculate probability of choice using these similarity measures to predict performance in the novel noun generalization task.

Results

Vocabulary Structure

Table 2 shows the means, standard deviation, and ranges for late talker and early talkers on raw counts, as proportion of total noun vocabulary, and as within-category proportions (e.g., what is the mean proportion of solid shape words late talkers know) for each of these five types of words: solid-shape, solid-material, solid-both, non-solid-material, and non-solid-both (there were zero non-solid-shape nouns). Because the neural networks were trained on vocabularies proportionally approximate to those of individual children, we focus this analysis on the children’s proportion of nouns of each word type. Although there are some commonalities between the two groups, there is greater variability in the composition of the vocabularies of the late-talker group (std.dev = .07) than the early talker group (std.dev = .01) for both solids and non-solids (all Levene’s test for equality of variances, F>6.5, p<.02).

Table 2.

Means, standard deviation, and ranges for late talker and early talkers on raw counts, as proportion of total noun vocabulary, and as within-category proportions for each of these five types of words: solid-shape, solid-material, solid-both, nonsolid-material, and nonsolid-both.

	Counts
	SolSh	SolMat	SolB	NsolMat	NsolB
MCDI	120	25	63	8	6
Late Talkers	M:26.93/SD:24.16	M: 5.2/SD: 5.15	M: 12.6/SD: 12	M: 1.8/SD: 1.97	M: 1.93/SD: 1.71
	(2-70)	(0-16)	(0-37)	(0-5)	(0-5)
Early Talkers	M:94.27/SD:24.46	M: 19.8/SD: 4.78	M: 48.33/SD: 12.66)	M: 5.2/SD: 1.01	M: 4.93/ SD:.88
	(29-117)	(8-25)	(19-62)	(3-7)	(3-6)
	Noun proportion
	SolSh	SolMat	SolB	NsolMat	NsolB
MCDI	0.54	0.11	0.28	0.04	0.03
Late Talkers	M: .61/SD: .16	M: .09/SD: .08	M: .23/SD: .08	M: .04/SD: .05	M: .04/ SD: .03
	(.3-1)	(0-.3)	(0-.36)	(0-.2)	(0-.1)
Early Talkers	M: .54/ SD: .03	M: .12/SD: .01	M: .28/SD: .02	M: .03/SD: .01	M: .03/SD: .01
	(.47-.59)	(.11-.13)	(.23-.31)	(.02-.05)	(.02-.05)
	Subcategory Proportion
	SolSh	SolMat	SolB	NsolMat	NsolB
Late Talkers	M: .22/SD: .2	M: .21/SD: .21	M: .2/ SD: .19	M: .23/SD: .24	M: .32/SD: .29
	(.02-.58)	(0-.64)	(0-.59)	(0-.63)	(0-.83)
Early Talkers	M: .79/SD: .2	M: .79/SD: .19	M: .77/SD: .2	M: .65/SD: .13	M: .82/SD: .15
	(.24-.98)	(.32-1)	(.30-.98)	(.38-.88)	(.5-1)

Children’s proportion of nouns were submitted to a 2(Language Group: early talkers, late talkers) × 2(Solidity: solid, non-solid) × 3(Dimension: shape, material, both) repeated measures analysis of variance (ANCOVA) with age in months as a covariate. The analysis yielded the expected main effects of solidity, F(1,27)=50.7, p<.0001, η² = .65, and dimension, F(2,54)=8.416, p=.001, η² = .24, indicating that, overall, there were more words for solids than for non-solids, and more words for shape-based categories than any other type. In addition, the expected interaction between solidity and dimension was significant, F(2,54)=12.37, p<.0001,η² = .31. There were more shape-based words for solids, and fewer shape-based words for non-solids. There was a marginally significant 3-way interaction between solidity, dimension, and age, F(2,54)=3.18, p=.05, η² = .11, as well as a marginally significant 3-way interaction between solidity, dimension and language group, F(2,54)=3.18, p=.055. Descriptively, compared to early talkers’ noun vocabularies, late talkers’ vocabularies have relatively fewer words for solids organized by both shape and material (t(28)=2.06, p=.049, two-tailed). No other main effects or interactions approached significance.

An ANCOVA using MCDI percentile as a continuous covariate, instead of as a categorical between-subjects variable, revealed a similar pattern of results: a main effect of solidity, F(1, 27) = 49.21, p<.001, η² = .65; main effect of dimension, F(2, 54) = 9.44, p<.001, η² = .26; a significant interaction between solidity and dimension, F(2, 54) = 13.784, p<.001, η² = .34; and a significant 3-way interaction between solidity, dimension, and percentile, F(2, 54) = 3.89, p=.026, η² = .13. No other main effect or interactions were significant.

Simulations

The networks’ predictions for each of the fifteen vocabularies of early talkers and each of the fifteen vocabularies of late talkers are shown in Figs. 2 and 3 respectively. In short, using a cut-off of at least two standard deviations above or below the 50% chance level mark, all networks in the early talker group show a shape bias for solids, and 12/15 early talker networks show a material bias for non-solids as well. In contrast, 12/15 late talker networks show a shape bias for solids and only 3/15 show a material bias for non-solids. Interestingly, 6/15 late-talker networks show a shape bias for non-solids, a novel prediction that has not been empirically tested so far. To further analyze the networks’ performance, networks were classified according to the observed generalization patterns: correct if they showed a shape bias for solids and a material bias for non-solids (12 out of 15 early talker networks; 2 out of 15 late talker networks), half-right if they showed the appropriate shape bias for solids but no consistent bias for material¹ (3 early talker networks; 7 late talker networks), or wrong, if they showed an incorrect overgeneralized shape biased to non-solids (no early talker networks; 6 late talker networks). A chi-square test showed these types of word learning biases were distributed differently in late talker and early talker networks, X²(2,15)=14.743, p=.0006 (Yates’ p=0.004).

Figure 2.

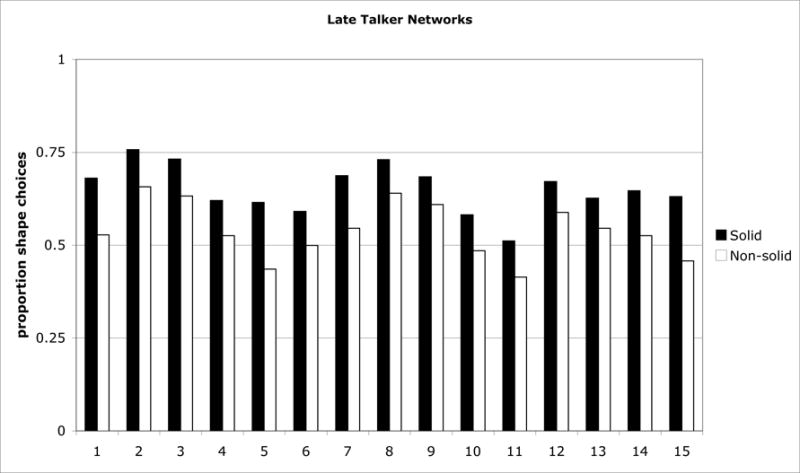
Predicted proportions of shape choices for solids and nonsolids for each of the late talker networks.

Figure 3.

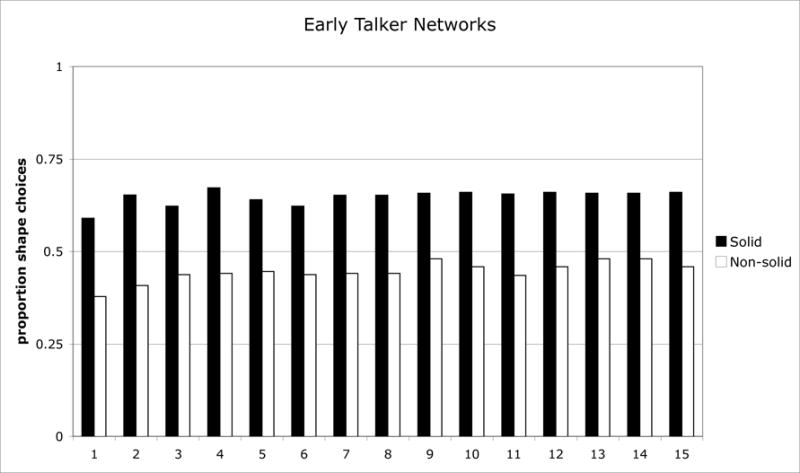
Predicted proportion of shape choices for solids and nonsolids for each of the early talker networks.

Discussion

Previous work has shown that the vocabularies of late talkers and early talkers show differences when characterized by connectivity measures in a network (directed graph) representation (Beckage et al, 2011). Perry & Samuelson (2011) found that the number of names for solid, material-based categories predicts performance in the novel noun generalization task with solids in typically developing children. Here we look at the structure of children’s vocabularies in the only way available to our computational model – their proportion of words referring to solids or non-solids alike in shape, material, or both. In this measure, too, the vocabularies of late talkers and early talkers show differences in the structure. This is true even though the two groups were matched by age one-to-one. Specifically, late talkers have vocabularies with a relatively smaller proportion of words for solid things that are similar in both shape and material than early talkers. These are words like book, carrot, jeans, and basket. As a group, late talkers show more variability in their vocabulary structures than early talkers. This is perhaps not strange given that, on average, the children in the late talker group have smaller vocabularies and thus many more ways of “selecting” the words they know out of the MCDI checklist. Put another way, as early talkers approximate mastery of the whole checklist, their vocabularies will tend to match the structure of the checklist. The crucial question, then, is whether these differences in vocabulary composition are differences that matter. Do the different nouns late- and early-talkers know yield different word learning biases? The results of the simulations answer this question and suggest novel predictions.

The results of the simulations suggest that the differences in noun vocabulary composition between late- and early-talking children may be associated with differences in word learning biases. The word learning biases learned by these networks can be interpreted as predictions at the group level. First, the networks make a novel prediction about early talkers. A majority of the early talker networks show material biases for non-solids. Previous findings have shown that children at this age (18- to 30-month-olds) show a material bias for non-solids only when offered extra supporting cues. For example, Soja (1992) showed older 2-year-olds have a material bias when offered supporting syntactic and visual cues by using mass syntax and presenting the material in pieces. Similarly, Colunga & Smith (2005) showed that even children as young as 18-months demonstrated an early material bias for non-solids when the non-solids were presented in simple shapes, but not when they were shaped into complex constructed shapes. However, children in general do not show a robust material bias for non-solids until around age 3 (Samuelson & Smith, 1999). Thus, this is a novel prediction that warrants testing: the networks predict that unlike the general population, early talkers (or children with vocabularies structured like those of early talkers) will show a robust material bias for non-solids at a relatively young age.

The networks also make predictions about the patterns of novel noun generalizations one should expect to see in young late talkers, between 18 and 28 months of age. According to these predictions, as a group, late talkers should show a shape bias for solids, with about half of them overgeneralizing this shape bias to non-solids as well. At first glance, this result may appear to contradict previous findings in which late talkers do not show a shape bias for solids (Jones, 2003). However, the children in the Jones, 2003 study were nearly a year older than the children in this study (25-41 months of age, M=33.25). It is possible that the shape bias for solids predicted by these simulations will disappear over the next year or that some of these children will not be late talkers a year later; late talkers may show different “signatures” at different ages.

To date, late talker’s novel noun generalizations for solid objects and non-solid substances have not been tested at this age. Thus, this is the second novel prediction made by the models: Late talkers will tend to have a shape bias for solids, with about half of them overgeneralizing this shape bias to non-solids. Experiment 2 tests the model’s predictions for early- and late-talking toddlers. The networks constructed for each individual child do not yield sufficiently fine-grained predictions to discriminate performance at the level of individuals, a point we consider in greater detail in the general discussion, and therefore we behaviorally test the predicted difference between the two groups of children in Experiment 2.

Experiment 2

The goal of this study was to test the predictions made by the neural network models in Experiment 1, based on late- and early-taker vocabularies. In Experiment 2, then, we replicate Experiment 1 with a smaller group of late- and early-talker children – examining their vocabulary structure and running simulations based on their individual vocabularies – but critically, we also test the children in the lab in a novel noun generalization task with solid objects and non-solid substances. Although the children whose vocabularies were examined in Experiment 1 ranged in age from 18 to 30 months, the models were age-less and all had the same vocabulary size, differing only in vocabulary structure. In Experiment 2 we chose to test children on the younger end of the age range, between 18 and 22 months, for two reasons. First, this is an age at which children do not typically show robust word learning biases yet, and we reasoned we might be able to notice individual differences. Second, as mentioned before, performance in the novel noun generalization task has been observed to change with age and vocabulary size, so limiting the age range is an attempt to deal with this potential confound. Any remaining small age differences were controlled for in the analyses.

Method

Participants

Nine late talkers (5 girls) and 8 early talkers (4 girls) between the ages of 18 and 22 months (M:19.36/SD:0.32 for late talkers; M:19.3/SD:0.33 for early talkers) were selected out of 32 children recruited as part of a larger study. As in Experiment 1, the criterion for inclusion was scoring at or below the 25^th percentile for late talkers and at or above the 75^th percentile for early talkers. MCDI scores ranged from 5^th to 20^th percentile (M:11.2/SD: 2.79) for the late talkers and between 75^th and 99^th percentile for early talkers (M:91.94/ SD:3.19). Vocabulary sizes for the late talker group ranged between 9 and 82 words (M:33/SD:8.77); for the early talker group vocabulary size ranged between 151 and 526 words (M:376.3/SD:45.31).

Stimuli

The stimuli consisted of a warm up set, a solid set and a non-solid set. The warm up set had an exemplar, a red plastic ball, two other balls (a tennis ball and a green and blue rubber ball), a plastic spoon, a toy carrot, and a toy cat.

The solid set consisted of an exemplar, an orange fuzzy round container, and 5 test items: two items matching the exemplar in shape alone (iridescent green bumpy round container and golden glittery round container), two items matching the exemplar in material (fuzzy blue irregular ring and fuzzy orange hook-like shape, and one matching in color (orange mesh polyhedron). The non-solid set was similarly structured and consisted of an exemplar (purple craft sand mixed into facial cream in a rounded elongated x-like shape), two material matches (green sand + facial cream in an asymmetric s-like shape and red sand + facial cream in a lollypop-like shape), two shape matches (elongated x-like shapes made out of sawdust or purple shaving cream), and a color match (purple hair gel in an hourglass shape. All non-solids were presented on flat, square, plastic foam boards.

Procedure

The procedure was modeled after Gershkoff-Stowe & Smith (2004). In the warm-up phase, the experimenter presented all six toys to the child and allowed him or her to look at them and handle and touch them for 30 seconds. Then the objects were removed and immediately placed back on the table outside of the child’s reach. The child was then shown the exemplar ball and told, “look at this ball.” Then they were asked to “get a ball” or get “another ball.” If the child failed to retrieve a ball, the child was asked one more time, and finally was told “here’s another ball,” handed the ball, and allowed to get it one more time on request. If the child got one of the non-ball distracter items, they were told, “that’s not a ball, that’s a ____”, then the distracter was replaced on the table, and the child was asked again, “is there another ball?”

The procedure during the test phase with the solid and non-solid novel sets was the same, except that no feedback was offered. Children were shown the exemplar and told, “Look at this dax” and then asked to “get a dax” or “get another dax” for the solid set or “get more dax” or “get some dax” in the non-solid set. Thus, solids were presented with count syntax supporting an object construal and non-solids were presented with mass syntax supporting a substance construal (Soja, 1992). Children were asked to get another (or more) until they indicated that there were no more, thus allowing children to accept or reject as few or as many items as they desired. The solid set was always presented before the non-solid set, and there was a 5-minute break and a change in testing rooms in between the two test sets to minimize carry-over effects.

Coding

To incorporate order information into children’s choices, and because all children made at least three choices for each test set, their choices were coded as follows: 3 points for the item that was 1^st choice, 2 points for the 2^nd choice, 1 point for the 3^rd choice, and 0 points for 4^th or 5^th choices.

Vocabularies and Neural Networks

Children’s vocabulary structures² were assessed as in Experiment 1, by categorizing nouns depending on whether they refer to things that are solid or non-solid, and alike in shape, material or both. Then these vocabulary structures were used to generate training sets for neural networks. The architecture, training set construction, testing set, and all parameters were the same as in Experiment 1. Individual networks were constructed based on the vocabulary of each child, and as in Experiment 1, the results presented below are based on averages over 5 runs per child, initialized with random weights.

Results

Vocabulary Structure and Simulations

Before analyzing the results of the behavioral experiments, the vocabularies of the children participating in the behavioral experiment were submitted to the same analyses as in Experiment 1, and neural networks were built for each of the participating children, except for one late talker who had no nouns in their vocabulary.

The noun vocabulary structure of the participating children showed a similar pattern to those found in Experiment 1. A 2 solidity × 3 dimension × 2 language group mixed ANCOVA, with age as a covariate, revealed a significant solidity by dimension interaction, F(2, 26) = 9.97, p = .001, η² = .43. There was also a significant three-way interaction between solidity, dimension, and age, F(2, 26) = 6.56, p = .005, η² = .34, and a significant three-way interaction between solidity, dimension, and language group, F(2, 26) = 11.2, p < .001, η² = .46. As in Experiment 1, late talker vocabularies had a relatively small proportion of words for solids that were alike in both shape and material compared to their early talker counterparts, t(14) = 3.89, p = .005. Again, the variance was greater in the late talker (std.dev = .12) than in the early talker group (std.dev = .01), all F’s for Levene’s test for equality of variance >10, all p<.01.

Similarly, the simulations showed patterns comparable to the ones in Experiment 1. For the early talker networks, 6/8 showed shape and material biases, and the other two showed only a shape bias and no robust material bias. None of the early talker networks showed incorrect biases. For the late talker networks, all eight networks showed a shape bias for solids, but only one showed a material bias for non-solids. In addition, 4/8 late talker networks showed an overgeneralized shape bias for non-solids. As in Experiment 1, a chi-square test showed these types of word learning biases were distributed differently in late talker and early talker networks, X²(2,8)=7.77, p=.02 (Yates’ X²= 4.54, p=0.103).

Word learning biases in behavioral study

The simulations in Experiment 1 predicted that early and late talkers would show different word learning biases, and predict specific patterns of novel noun generalizations for solids and non-solids for these two groups of children. First, children were classified based on their bias scores for solids and for non-solids, correct if the score was positive or incorrect if the score was negative. Given this classification, 7/8 early talkers showed a shape bias for solids and a material bias for non-solids (the other child showed a material bias for both solids and non-solids). In contrast, only 2/9 late talkers showed correct shape and material biases, 6/9 late talkers showed incorrect biases (5 showed a shape bias for non-solids, 1 showed a material bias for solids), and one showed no bias. A chi-square indicated that these types of biases were distributed differently in the two groups, X²(2,8)=7.32, p=.026 (Yates’ X²= 4.14, p=0.13).

Next, we look at the data of all children together and then evaluate the predictions for each language group. We submitted both groups of children’s scores for the shape and material test items for the solids and non-solid sets to a 2 (language group: early, late) × 2 (solidity: solid, non-solid) × 2 (dimension: shape, material) mixed ANOVA. Fig. 4 shows the average score for the items that matched the exemplar in shape or material for the solid and non-solid sets for both language groups. There was a main effect of dimension, F(1,29) = 4.77, p = .045, η² = .24; overall shape matches had higher scores than material matches. There was also a significant interaction between solidity and dimension, F(1,15) = 15.6, p=.001, η² = .51. Post-hoc tests showed that across both language groups, children were more likely to choose the shape over the material match for the solid set, t(16) = 4.03, p=.001, but not for the non-solid set, t(16) = -.613, n.s. The three-way interaction between language group, solidity, and dimension was marginally significant, F(1,15) = 4.33, p=.055, η² = .22.

Figure 4.

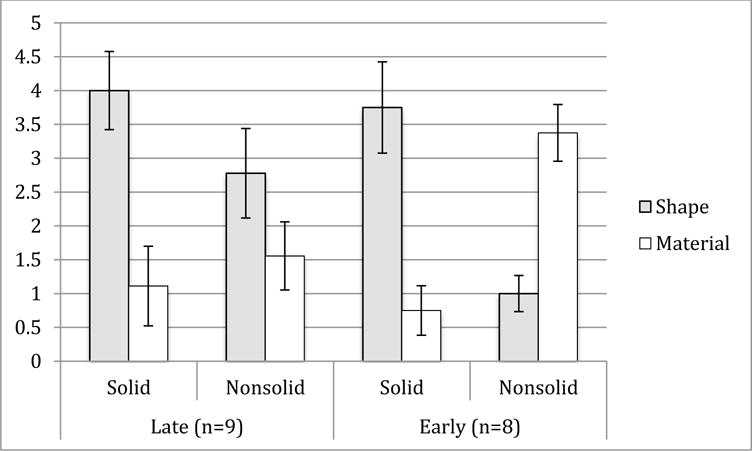
Scores for shape and material matches for solids and nonsolids for early- and late-talking children in Experiment 2.

The z-score transform of these data were further submitted to a 2 (solidity: solid, non-solid) × 2 (dimension: shape, material) ANCOVA, using age and percentile as covariates. The results show a significant effect of dimension, F(1,14) = 6.42, p = .024, η² = .31 and a significant age by dimension interaction, F(1, 14) = 5.97, p = .028, η² = .3. The critical three-way interaction between solidity, dimension, and percentile was also significant, F(1, 14) = 5.33, p = .037, η² = .28. No other main effects or interactions were significant.

The model’s predictions regarding each of the two language groups were further tested by analyzing the two groups separately. First, the prediction that early talkers would show a robust shape bias for solids and a robust material bias for non-solids was confirmed by a 2 (solidity) × 2 (dimension) ANOVA revealing a two-way interaction between solidity and dimension, F(1,7) = 26.15, p = .001, η² = .78. Furthermore, planned comparisons (all two-tailed) showed that this interaction came from early talkers’ shape bias for solids (t(7)=3.06, p=.018) and material bias for non-solids (t(7)=−4.46, p=.003). Second, a similar analysis on late talkers’ scores revealed a main effect of dimension, F(1,8) = 5.5, p=.047, η² = .41, and no other main effects or interactions. Planned comparisons showed that late talkers had a shape bias for solids, t(8) = 2.57, p=.033, but did not overgeneralize the shape bias to non-solids as a group, t(8) = 1.1, n.s. However, 5 out of the 9 late talkers in the study showed a robust shape bias for non-solids (a difference score of more than 3), and none of the early talkers did.

Discussion

The analyses on the vocabulary structure and neural network simulations based on the smaller, and on average younger, group of children in Experiment 2, replicate the findings in Experiment 1. Compared to early talkers, late talker vocabularies showed greater variance and had a relatively small proportion of words referring to categories of solid things alike in both shape and material. The simulations based on individual children’s vocabularies made qualitatively the same prediction as the simulations in Experiment 1: most early talker networks showed both a shape bias for solids and a material bias for non-solids, whereas half late talker networks showed an overgeneralized shape bias for non-solids.

The results of Experiment 2 are in line with the predictions of the simulations in Experiment 1. Early talkers show a shape bias for solids and a material bias for non-solids; late talkers show a shape bias for solids and a mixed pattern of generalizations for non-solids. It is important to note that these predictions work at the group level and not at the level of individuals. For example, although five late takers showed an overgeneralized shape bias for non-solids in both the behavioral tasks and in the network simulations, these were not the same children; only two children showed this bias in both the simulations based on their vocabularies and their performance in the behavioral task. The behavioral task, and probably the vocabulary measure as well, lack the finesse to make predictions at the individual level based on a single data point. However, as we will argue in the general discussion, looking at the relationship between vocabulary composition and word learning biases in the lab task over multiple sessions longitudinally may offer us the ability to make predictions about the trajectory or future growth of the individual.

The results of experiment 2 are in line with previous work noting a relationship between the number of nouns in a child’s vocabulary and their word learning biases, but they extend it in important ways. The finding that early talkers show robust word learning biases for both solids and non-solids at not even two years of age is new. Although one might have predicted this pattern of results a priori from the idea that early talkers might excel across tasks, the prediction came from the models. Harder to predict without the networks, however, is the pattern found for the late talkers. In fact, at first glance it seems to contradict what we know about late talkers; that 2- to 3-year-old late talkers lack a shape bias while their same-aged peers already have a well established bias. However, the prediction from the networks, and our findings on the patterns of word learning biases in very young late talkers, before the age of 2, may help us understand something new about the processes underlying word learning in general.

Gershkoff-Stowe and Smith (2004) followed eight children as they learned their first 100 nouns, looking at their word learning biases for solids and their vocabulary growth every three weeks. Their results show that as children’s noun vocabulary increases, so does their attention to shape. They set the emergence of the shape bias at around the time children acquire 50 nouns. The results from Experiment 2 suggest that this relationship may be different for late talkers. None of the late talkers in Experiment 2 reached the 50-noun mark (though a couple were on the cusp), and yet they overall showed a robust preference for shape for the solid set in our task. Curiously, although attention to shape increased with vocabulary size in Gershkoff-Stowe’s study, their lower vocabulary group did show a preference of shape over material. This suggests an intriguing possibility. These models do not make a distinction between naming and non-naming contexts. It is possible that the shape preference for solids here is not a true shape bias, but rather an overgeneralized heightened attention to shape. The fact that about half of the late talkers showed an overgeneralized shape bias for non-solids suggests that this may be the case. This sort of non-discriminating shape bias extended to solids and non-solids has been observed as an early stage in the development of biases in children between 2 and 4 years of age (Samuelson, Horst, Schutte, & Dobbertin, 2008). Similarly, in a 9-week training study, Perry and colleagues (2010) taught either high similarity or low similarity shape-based categories to young children, and only those children who had been taught categories based on more variable exemplars showed a discriminating shape bias. Children who were taught solid-shape words instantiated by highly similar exemplars tended to overgeneralize the shape bias to non-solids as well. Interestingly, in a follow-up a month later, the children in the low similarity condition, who showed the discriminating shape bias, had significantly larger noun vocabularies than the children in the high similarity condition (Perry, Samuelson, Malloy, & Schiffer, 2010).

General Discussion

The work presented here makes several contributions. First, the results of these studies add to the growing evidence that late talkers and typically developing children’s vocabularies differ in their structure. Specifically, we show that late talkers and early talkers know different sorts of nouns. This is a new finding, and critically, it suggests that the difference between late and early talkers – a classification given by counting the number of words produced by children – is not just quantitative, but also qualitative. Late and early talkers do not just know different numbers of words; they know different sorts of words. This is in line with recent work showing that the semantic networks formed from vocabularies of late talkers have different connectivity characteristics than the semantic networks of typically developing children (Beckage, Hills, & Smith, 2011). Beckage and colleagues suggest that the source of the structural difference they find in the semantic networks of the two groups of children could be in the children’s language environment, or in the way children sample words from their environment. The present computational models show one way in which the vocabulary composition – word learning bias feedback loop might operate, changing the ease with which subsequent words are learned and further skewing the vocabularies. However, evaluating the models will require looking at developmental trajectories and longitudinal data from children, as discussed below (Sims, Schilling, & Colunga, 2013a).

The finding that these differences in vocabulary composition lead to qualitatively different word learning biases in a computational model – a computational model that has been previously shown to capture various aspects of novel noun learning – suggests a promising use for process-level computational models. Efforts to tease apart the contributions of different factors to developmental outcome in late talkers have come up with some characteristics that put children at higher risk, but the underlying mechanisms are not well understood. The need to identify subgroups within late-talking toddlers remains. Recent work by Thomas and Knowland (2014) uses a population modeling approach to study how different simulated learner characteristics (processing capacity limitations and low plasticity) and different simulated environments alter language development trajectories, with different initial conditions resulting in either persistent or resolving delays. The models presented here are a promising first step in leveraging computational models to aid in understanding why some late talkers catch up and others do not. The work presented here falls short of characterizing mechanistic differences between late and early talkers, and instead focuses on the snapshot relationship between vocabulary composition and word learning biases, without attending to the developmental trajectory. However, we have begun work to expand these models to account for longitudinal trajectories and the dynamics of emergence of the different biases (Sims, Schilling, & Colunga, 2012; 2013b) and how these may be different for persistent and resolving late talkers (Sims, Schilling, & Colunga, in press).

Furthermore, these models represent an important extension over previous word-learning modeling efforts in that they go beyond modeling the performance of the mythical average child to making predictions based on the performance of individual children, and of children who are both at the top and at the bottom of the vocabulary spectrum. In so doing, the simulations presented here make novel and testable predictions about these two groups of children. The simulations predict that, between 18 and 30 months of age, early talkers will show an early material bias and that late talkers will show an overgeneralized shape bias in the novel noun generalization task. The fact that these novel predictions were in line with the behavior in the lab of a small group of early and late talker toddlers further suggests that these models are capturing something fundamental about the way young children learn nouns.

Finally, this work adds to what we know about word learning biases in late talkers and early talkers. Even before they turn two, children who excel in vocabulary acquisition show very consistent word learning biases not typically observed until a year or so later. The late talker toddlers in the study, on the other hand, show a different pattern of novel noun generalizations, and one that is less consistent.

The work presented here also has some limitations. First, the fact that we do not yet have outcome data for the children in these studies constrains what we can infer from these results and their potential use in early identification of at-risk children at the individual level – will the late talking children who show correct biases catch up? Or are the ones showing the overgeneralized shape bias the ones on the right track? Are these differences in vocabulary and in word learning biases predictive of outcome? Second, all of these networks are identical except for the vocabulary structure on which they are trained. Although this constraint makes these simulations the strongest possible demonstration of the relationship between vocabulary composition and word learning biases, allowing for pre-existing individual differences beyond words known in these models may increase their power, and come closer to presenting an account of what late talkers may be lacking (Thomas & Knowland, 2014). Finally, there is more to language, and even more to word learning, than learning nouns. Thus, these models capture only a sliver of language learning and may miss crucial differences between children with different linguistic endowment.

In spite of these limitations, the models presented here constitute an innovative approach to predicting and characterizing typical and atypical vocabulary acquisition in young children. The relationship between vocabulary composition and word learning biases modeled here – the words you know determine the way you learn new words, which constrains and facilitates the words you will know next, and so on – opens a new way of thinking about computational models, to capture not only averages and not only individuals, but individual trajectories. Thomas and colleagues have argued that using a trajectories approach can aid in understanding the underlying mechanism, especially in to characterizing atypical populations (Thomas, Annaz, Ansari, Scerif, Jarrold, & Karmiloff-Smith, 2009). If we can build computational models that can successfully capture this self-constructing developmental loop, we may be able to leverage these models to aid in the process of diagnosis and individualized interventions design.