Abstract
We report a water model, Bind3P (Version 0.1), which was obtained by using sensitivity analysis to readjust the Lennard-Jones parameters of the TIP3P model against experimental binding free energies for six host-guest systems, along with pure liquid properties. Tests of Bind3P against >100 experimental binding free energies and enthalpies for host-guest systems distinct from the training set show a consistent drop in the mean signed error, relative to matched calculations with TIP3P. Importantly, Bind3P also yields some improvement in the hydration free energies of small organic molecules, and preserves the accuracy of bulk water properties, such as density and the heat of vaporization. The same approach can be applied to more sophisticated water models that can better represent pure water properties. These results lend further support to concept of integrating host-guest binding data into force field parameterization.
Keywords: Drug design, binding free energy, binding enthalpy, host–guest, force field, water model, molecular dynamics, hydration, TIP3P, sensitivity analysis, attach-pull-release
Graphical abstract

INTRODUCTION
Predicting the binding affinities of small molecules for a specific protein target is a central challenge in the field of computer-aided drug design. Physics-based free energy methods using explicit-solvent molecular dynamics (MD) simulations have shown considerable promise in this application.1–3 However, problematic deviations between calculation and experiment persist4,5, and it can be difficult to determine how much of the errors that are observed results from inadequate conformational sampling, from problems in protein setup, such as in the assignment of histidine protonation states, or from inaccuracies in the force fields employed.
Host-guest systems are compact models for protein-ligand binding. Their simple structures mean that setup problems can often be avoided, and their small sizes enable faster numerical convergence of explicit-solvent binding thermodynamics calculations6–9. Thus, we have reported calculations of binding free energies and enthalpies with sub-kcal/mol numerical uncertainties, for a variety of host-guest systems, including cucurbit[7]uril (CB7)8,9, α- and β-cyclodextrin (αCD, βCD)10, octa acid (OA)11 and a derivative of octa acid, tetra-endo-methyl octa-acid (TEMOA)11. These computed results correlate moderately to strongly with the corresponding experimental data, but still yield root-mean-square errors (RMSE) from experiment greater than 1 kcal/mol. This pattern holds true in the broader computational chemistry community as well. For example, in the SAMPL5 blinded prediction challenge (2015–2016)12, two top-ranked methods both yielded absolute RMSE values on the order of 2 kcal/mol for OA and TEMOA host-guest systems11,13. Given the virtual absence of setup and convergence issues in these model systems, deviations from experiment trace to errors in the force fields.
For aqueous systems, the force field representation of water is a key determinant of properties computed with atomistic simulations14–16. Many studies have explored how the choice of water model affects hydration free energies and related quantities17–19, but studies that systematically examine the influence of the water model on binding thermodynamics have been less common. This might reflect a sense that binding calculations are too computationally demanding for use in evaluating force fields. Although this may still hold for many protein-ligand systems, varied host-guest systems and certain protein systems have shown great promise in validating the performance of force fields and explicit water models in binding calculations9,11,20,21. Accordingly, over the past few years, our group has explored the accuracy of water models8,10,11,21,22, force fields10,21,23 and partial charge assignment methods10,21 in predicting binding thermodynamics. These studies have frequently revealed systematic overestimation of binding free energies and enthalpies, especially for host-guest complexes that show medium to strong binding affinities. For instance, binding free energy calculations using the TIP3P water model24 yielded a mean signed error (MSE) relative to experiment of −8.2 kcal/mol, for CB7 with ammonium and alcohol guests25. A prospective study21 on CB7 with a series of hydrocarbon guests yielded an MSE of −5.0 kcal/mol for TIP3P water and AM1-BCC26,27 solute charges, and an MSE of −4.4 kcal/mol for the OPC water model with RESP28 charges. Another prospective study11, based on the OA and TEMOA hosts, yielded an MSE of −1.6 kcal/mol for binding free energies computed using TIP3P, and −2.1 kcal/mol using OPC29. Based on the systematic nature of these overestimates, we conjectured that improvement of a factor common to all the calculations, namely the water model, could improve accuracy of binding predictions. Furthermore, improvement might be possible by parameterizing the water model not only against properties of pure liquid water and the isolated water molecule, but also against binding data.
Here we describe the development of a three-site, rigid water model, Bind3P, as a proof of concept. We chose the TIP3P water model as a starting point for this work, for two reasons. First, we have often observed overestimation of affinities in binding calculations using TIP3P, and we conjectured that adjusting the water model could ameliorate this problem across many host-guest systems. Second, despite these overestimates, the accuracy of binding calculations with TIP3P has been about as good as that obtained with other water models, including ones that are more complex and computationally demanding, such as TIP4P-Ew30.
Traditionally, explicit water models have been parameterized against physical properties of bulk water such as densities and heats of vaporization24,30, along with quantum chemistry data in some cases31,32. In the present work, the sensitivity analysis approach33–36, which has been previously demonstrated as an effective tool for integrating host-guest binding data into force field parameterization25, is used to tune the original TIP3P Lennard-Jones parameters against both pure water properties and several host-guest binding data. The resulting Bind3P water model is then evaluated against a much larger test set of host-guest binding free energies and enthalpies. The favorable results support the utility of this initial model adjustment and further validate the overall approach of using host-guest binding data to optimize force fields.
METHODS
Attach-Pull-Release (APR) Calculation of Binding Thermodynamics
The attach-pull-release (APR) method for computing binding thermodynamics has been previously applied to host-guest9,37 and protein-ligand systems38. In the present APR calculations, the bound structure was aligned with the lab-frame z-axis and then solvated in an orthorhombic box that was aligned with the lab-frame axes and was longer in the z-axis than in the x- and y-axes. The number of water molecules ranged from 2000 to 2500, mainly depending on the size of the host molecule. The alignment of the host along the z-axis was maintained during the simulations by a set of six distance, angle, and torsion restraints between the host and three anchor particles. These translational and rotational host restraints do not perturb the internal conformational degrees of freedom of the host and remain unchanged during the entire APR process. Aligning the system with the long axis of the simulation box allows less solvent to be used, and thus speeds the calculations. The anchor particles also serve as an attachment point for restraints which function to remove the guest molecule gradually out of the host cavity along the z-axis (Figure S1). It is worth noting that the complete APR process provides the reversible work, and hence the free energy change, of going from the unrestrained, bound state to the unrestrained, unbound state, because it accounts for both the work for both imposing and removing all restraints applied along the way. The purpose of such restraints is to make sure that all windows along the pulling path well sampled.
The binding free energy of each host–guest pair was computed from the reversible work required to attach a set of restraints to the guest and, in some cases, the host (Wattach), pull the guest out of the binding pocket (Wpull), release all attached restraints (Wrelease−conf), and finally set the guest at standard concentration (Wrelease−std):
| (1) |
Because the six distance, angle, and dihedral restraints between the host atoms and anchor particles that fix the position and orientation of the host molecule are maintained during the entire calculation, and do not perturb the internal conformational degrees of freedom of the system, there is no need to compute the work of attaching and detaching them. For the guest, three distance and angle restraints were gradually turned on during the attach phase and released in the end. The work of releasing guest restraints was computed analytically.
For all cyclodextrin and CB7 systems, conformational restraints were gradually imposed on the host molecule to facilitate conformational sampling during exit of the guests in the “pull” simulation windows. These restraints were then released as previously detailed9, leading to the presence of a nonzero Wrelease−conf term, while the work of attaching these restraints is included in Wattach. Among the OA and TEMOA systems, conformational restraints were applied for TEMOA with G4, as well as OA with G5, where they were used to widen the narrow entryway of the host and thus facilitate the exit of this bulky guest11. Again, we included both the work of imposing and removing these restraints. The narrow ends of the OA and TEMOA hosts are essentially closed, so the guests can be only pulled out of the wider end; and we only considered guest orientations in the bound state where the ionized group projects into solvent, rather than into the hydrophobic cavity. A total of 15 windows were used for the attach phase, and 46 for the pulling phase. For the cyclodextrin and CB7 systems, 15 more windows were appended for the additional release phase needed to compute Wrelease−conf. During the pulling phase, the umbrella sampling windows were spaced at 0.4 Å intervals. The guest was pulled along the z-axis to a maximum of 18 Å away from its initial position, at which point it was considered to be fully unbound. (Test calculations in which additional windows were used to pull the guest further from the host yielded results that were the same to within the numerical uncertainties reported here.) For CB7, which has two symmetric openings, the guests were only pulled from one opening. Most of CB7 guests freely sampled both equivalent bound state orientations, but two guests, diamantine and perfluorohexane, did not flip orientations on the simulation timescale, and thus required a correction of −RTln(2) = −0.41 kcal/mol to account for the two equivalent binding poses. In the case of cyclodextrin, which can bind asymmetric guests in two non-equivalent orientations, the guests were pulled from both of the primary and the secondary faces of the host, and the binding free energy and enthalpy were computed separately for each orientation and appropriately combined account for their individual contribution to the Boltzmann ensemble, as previously described9. The thermodynamic integration (TI) approach39 was employed to calculate the work terms from the mean force in each window. Please refer to our previous study for more details9. The calculations were automated with a set of Python scripts that can be downloaded from the AMBER tutorial website or GitHub (see SI).
Binding enthalpies were computed by extending the simulation length of the first and last windows of the APR calculations to at least 750 ns, and computing the difference between their mean potential energies, as previously described9,11,25,40.
Parameter Adjustment by Sensitivity Analysis
Sensitivity analysis refers to analytical calculation of the gradient (i.e., the partial derivatives) of a simulated property with respect to force field parameters of interest. Here, we focus on the sensitivity of host-guest binding free energies to the Lennard-Jones parameters of the water model. The workflow of parameter adjustment by sensitivity analysis includes the following steps:
Use MD simulations to compute binding free energies, saving snapshots needed for subsequent calculation of partial derivatives;
Compute the gradients with respect to force field parameters of interest from the MD snapshots;
Use the gradients to select a change in parameters that will improve the agreement of computed binding free energies with experiment.
These steps may, optionally, be iterated to drive further improvements in accuracy. Note that the gradients in step 2 are computed analytically, rather than by the method of finite differences, so the method is relatively efficient.
As previously shown25, the derivatives of the binding free energy with respect to Lennard-Jones parameters of interest σi and εi are
| (2) |
| (3) |
Here refers to the total Lennard-Jones interaction energy of all atoms assigned the parameters of interest with all other atoms in the system, and the angle brackets indicate Boltzmann averages taken in the bound and unbound ensembles. Because the MD simulations of these states are sampled from the Boltzmann distribution, the averages here are computed as unweighted averages over MD snapshots. Based on AMBER’s LJ functional form and mixing rules
| (4) |
where rij is the distance between atoms i and j, the partial derivatives in Eq 2 and 3 have the following forms:
| (5) |
| (6) |
The gradients of binding free energies with respect to the Lennard-Jones parameters of the water oxygen were used to estimate the root mean square error (RMSE) of calculation versus experiment for the six host-guest pairs in the training set, n=1…6, following small changes in ε and σ, based on the first order truncation of the Taylor expansion:
| (7) |
| (8) |
Here, is the binding free energy computed for host n with the starting parameters, is the computed binding free energy predicted from the sensitivity analysis for the modified parameters, and is the experimental binding free energy. Note that, an overly large perturbation step can make the linear approximation inaccurate, and it is not known a priori how large a step will work well. Therefore, it is essential to run new simulations with the new parameters to validate the predicted changes in ΔG°. If the agreement is not satisfactory, a smaller step should be tried.
Simulation Details
OA and TEMOA Host-Guest Systems
The starting structures of OA and TEMOA were built manually and then energy minimized. The initial structures of the unbound guest molecules were obtained through the conformational search module in MOE41. Both OA and TEMOA were treated as fully deprotonated with a net charge of −8e, given that the experimental studies were carried out at high pH values (see footnotes of Table 1). Partial atomic charges were derived using the RESP procedure28 on the R.E.D. server42. Bonded and Lennard-Jones parameters were obtained from GAFF43 and assigned with AMBER's antechamber utility44. Most of the new calculations reported here used GAFF v1.8; test runs indicate that GAFF v1.7 and v1.8 provide virtually the same results for these systems. The starting bound configurations for APR calculations were obtained by docking the guests into the hosts with MOE, in accordance with the experimental observation that charged groups of the guests situate themselves at the entrance of the cavity, while the hydrophobic moieties are always inside the binding pocket45; these initial conformations were relaxed with preliminary MD simulations.
Table 1.
Measured and computed binding free energies (kcal/mol) of host OA with the six training set guest molecules. Expt: experimental data; TIP3P: computed with TIP3P11; Bind3P (pred): results predicted for Bind3P by applying sensitivity analysis to simulations using TIP3P; Bind3P: results obtained by using Bind3P in new simulations. MSE: mean signed error (kcal/mol); RMSE: root-mean-squared error (kcal/mol); R2: square of Pearson correlation coefficient; m: slope of linear regression. The error metrics are averages from resampling with replacement using 10,000 bootstrap cycles, and thus may be different from the values calculated directly from the means.
| Guest | Expt. | TIP3P | Bind3P (pred) | Bind3P | TIP4P-Ew | OPC | TIP4P-D |
|---|---|---|---|---|---|---|---|
| G1 | −5.4 | −6.5 | −5.1 | −5.2 | −7.1 | −6.1 | −6.1 |
| G2 | −4.7 | −5.4 | −3.9 | −3.8 | −5.7 | −5.2 | −3.7 |
| G3 | −4.5 | −6.8 | −5.5 | −5.7 | −8.2 | −7.8 | −7.2 |
| G4 | −9.4 | −12.3 | −10.6 | −10.6 | −12.9 | −11.4 | −10.4 |
| G5 | −3.7 | −4.5 | −3.1 | −3.5 | −7.8 | −6.4 | −5.8 |
| G6 | −5.3 | −6.5 | −4.9 | −4.8 | −7.4 | −6.4 | −5.4 |
|
| |||||||
| MSE | −1.5 | 0.0 | −0.1 | −2.7 | −1.7 | −0.9 | |
| RMSE | 1.7 | 0.8 | 0.9 | 2.9 | 2.0 | 1.5 | |
| R2 | 0.8 | 0.8 | 0.8 | 0.6 | 0.6 | 0.6 | |
| m | 1.2 | 1.1 | 1.0 | 0.7 | 0.5 | 0.6 | |
The experimental binding affinities were obtained from ITC measurements54 taken at 298 K in 50 mM sodium phosphate buffer with pH of 11.5.
Each system was solvated with 2500 water molecules in an orthorhombic box. The thickness of the water layer between any atom in the solute and the edge of the box was set as 10 Å in the X and Y direction. In the Z direction, the closest distance between the guest and the nearest periodic copy of the host was more than 20 Å, even in the last window where the guest is far from the host, to ensure that the interaction between them would be negligible. The box size was approximately 38 × 38 × 55 Å3 after constant pressure equilibration. Sodium ions were modeled with the TIP3P-specific sodium parameters of Joung and Cheatham46 in both TIP3P and Bind3P simulations. Sodium ions were only added to neutralize the system. Each sampling window was simulated for a minimum of 2.5 ns, with extension as needed to either bring the standard error of the mean (SEM) estimate of the forces under a specified threshold or to 50 ns, whichever came first.
Cucurbit[7]uril (CB7) Host-Guest Systems
The bonded and Lennard-Jones parameters for CB7 and its guests were taken from GAFF v1.843 and assigned with AMBER's antechamber utility44. Partial charge assignments were made using the RESP approach via the R.E.D. Server42. The initial conformations of the CB7-guest systems were obtained through manual placement of the guest in the center of the host cavity. The longest dimension corresponded to the extraction axis (i.e., the z-axis). Salt ions were not included, in order to match the experimental conditions which intentionally excluded salt to simplify comparison. Each sampling window was run at least 2.5 ns and was extended up 25 ns depending on whether further simulation was required to reduce the uncertainties in the restraint forces to a target level. The first and last windows in the process, corresponding respectively to the unrestrained bound conformation and the fully dissociated states were extended to 500 ns to calculate binding enthalpies, although experimental binding enthalpies were not available for these systems.
α- and β-Cyclodextrin (αCD, βCD) Host-Guest Systems
Force field parameters for the cyclodextrin hosts were taken from the Q4MD-CD model of Cezard et al.47 which combines portions of other AMBER force fields, along with RESP charges generated with the R.E.D. server42 to generate conformational properties that match experimental data. Guest molecules were parameterized via AMBER’s antechamber utility44 with bonded and Lennard-Jones parameters from GAFF v1.7, while partial charges were derived using the RESP approach via the R.E.D. Server. Unlike CB7, the two openings of the cyclodextrin cavity are not symmetrical, so guests can bind in two distinct orientations. Both orientations were constructed and simulated, and the reported results account for both orientations, as noted above. The simulation lengths of the sampling windows were set as done for CB7.
Hydration Free Energies
We computed hydration free energies for all twenty molecules which were contained in both our guest sets and the Freesolv database48. This was convenient because it provided vetted systems which we could use to validate our hydration free energy calculations. The solute force field parameters, derived from GAFF v1.7 bonded and LJ parameters along with AM1-BCC charges, were taken directly from the Amber prmtop/inpcrd files hosted on the Freesolv GitHub repository using Amber's parmed tool. The solute molecule was solvated with Amber's tleap tool in either TIP3P or Bind3P water using a 15 Å minimum buffer distance to the periodic boundary edge. The hydration free energy was computing using a three-stage alchemical approach using a series of λ windows: 1) the solute charges were reduced to zero, 2) the solute was decoupled from the solvent using a softcore LJ function, and 3) the charges were restored in a vacuum environment. Eleven λ windows were used for the decharging and recharging steps, spanning 0.0 to 1.0 with equal spacing. Sixteen λ windows were used for the decoupling step, with the additional windows focusing on areas of greater change in an identical fashion to the Freesolv protocol.
All simulations were performed using either the pmemd or pmemd.cuda MD engines for the gas and solvated phases, respectively, from a pre-release version of Amber18. All solvated simulations used a time step of 1 fs, a nonbonded cutoff of 8.0 Å, and default Amber PME settings. Temperature was regulated with a Langevin thermostat at 298 K and pressure was maintained at 1.0 bar with a Monte-Carlo barostat. Gas phase simulations used a time step of 1fs, an infinite cutoff, and a Langevin thermostat for temperature control at 298 K. Each lambda window was allowed to run up to 1 ns, unless it reached a ∂U/∂λ uncertainty convergence threshold of 0.15 kcal/mol and 0.01 kcal/mol for the solvated and gas phases, respectively, in which case the simulation was terminated.
The free energy of the transformation was computed via integration of the ∂U/∂λ points across the interval from 0 to 1 for each stage of the transformation. An overall estimate of the uncertainty was computed by boot-strapping the integration step for 10000 cycles and choosing a specific ∂U/∂λ value for each cycle from a distribution defined by the mean and uncertainty for the specific window. The uncertainty for each of the stages was then added in quadrature to arrive at the final uncertainty.
We confirmed that our hydration free energy calculations gave expected results by comparing our results for the TIP3P calculations with those available in the Freesolv database. The comparison statistics indicated excellent agreement: R2 = 0.9993, RMSE = 0.08 kcal/mol, MSE = −0.03 kcal/mol. The Python code for organizing and executing these calculations is available for download (see SI).
Properties of Pure Water
The thermodynamic properties of the TIP3P or Bind3P water model were computed from 100 ns NPT trajectory of OpenMM49. The orthorhombic simulation box was filled with 400 water molecules, and the dimensions were 23 × 23 × 24 Å3 after equilibration. Quantities including density, dielectric constant, isothermal compressibility, and thermal expansion coefficient were computed and exported through OpenMM reporter and MDTraj API50. The heat of vaporization was computed according to the equations provided in Horn et al.30
In addition, the radial distribution functions were computed from 20 ns NPT runs simulated by Amber44 with the same setting of the simulation box. The “radial” command in cpptraj51 was used to compute the O-O coordination number as a function of O-O distance with a spacing of 0.01 Å.
RESULTS AND DISCUSSION
This section first describes the use of sensitivity analysis to guide the efficient creation of a three-point water model, called Bind3P, which is based on TIP3P but adjusted to improve the accuracy of six OA-guest binding free energies while preserving the ability to reproduce properties of bulk water. We then compare Bind3P with other water models in calculations of binding free energies and enthalpies for an expanded set of OA-guest systems. Finally, we evaluate the performance of Bind3P in calculations of more than a hundred binding free energies and enthalpies for a more diverse set of host molecules, spanning TEMOA (see above), cucurbiturils, and cyclodextrins.
Parameterization of the Bind3P Water Model
The water model was trained against binding data for the OA host with guests G1–G6 (Figure 1), which first appeared in the SAMPL5 challenge12, along with experimentally determined pure water properties at 298K and 1 atm pressure: density, static dielectric constant, isothermal compressibility, coefficient of thermal expansion, and heat of vaporization. The fact that many computational groups have generated encouraging predictions for these six OA-guest systems13,52,53 supports the robustness of the experimental data and the utility of these systems as computational test cases. In addition, these six guests are reasonably diverse chemically, and include functional groups present in some of the test set systems (below). As a starting baseline, binding free energies that we previously computed11 with the TIP3P water model are listed in Table 1 as ΔG°(TIP3P). Despite a strong correlation with experiment (R2 0.8), the calculations overestimate the experimental binding affinities in all cases (MSE −1.5 kcal/mol).
Figure 1.
Chemical structures of octa acid (OA), tetra-endo-methyl octa-acid (TEMOA), and 20 guest molecules. All guests were measured with OA, and guests G1–G6 were measured with TEMOA. Silver: carbon; red: oxygen; Blue: nitrogen. Non-polar hydrogen atoms are omitted for clarity. Protonation states of all host and guest molecules shown in the figures were suggested by their pKas and the experimental pH values.
We used sensitivity analysis to select updated water Lennard-Jones parameters that should improve the accuracy of the computed binding free energies for the six training-set host-guest systems, while retaining good results for the bulk water properties, as follows. First, bound and unbound simulations of each training-set host-guest complex were used to compute partial derivatives of the six binding free energies with respect to the Lennard-Jones parameters of the TIP3P water oxygen (see Methods). The resulting derivatives are listed in Table 2. (There are no other Lennard-Jones interaction sites in the TIP3P model, and we did not add any in the Bind3P model.) We next used these derivatives to predict values of the training set RMSE for two-dimensional scans of σow ∈[2.9933, 3.3083] (±5% of the original σow) and εow ∈[0.1140,0.1900] (±25% of the original εow) in steps of 0.0158 (0.5% of the original σow) and 0.0008 (0.5% of the original εow), respectively (Figure 2). Note that these scans did not require additional simulations; instead, the predicted RMSE values were obtained by linear extrapolation, using the original TIP3P results and the derivatives of the binding free energies with respect to σow and εow. Combinations of these two parameters that yielded predicted RMSE values <1 kcal/mol were then used to run pure water simulations (T=298K, P=1 atm), from which the water properties listed above were computed. Regions of the (σow, εow) plane found in this manner to yield pure water properties with accuracy comparable to that of TIP3P, as well as low errors for the six host-guest binding free energies, were rescanned at finer resolution (0.2% of the original σow and εow), to yield additional combinations of σow and εow, for which pure water properties were again computed.
Table 2.
Derivatives of the binding free energies of host OA with the six training-set guest molecules with respect to the Lennard-Jones parameters of the TIP3P OW atom type (σow, εOW). Results are shown for the first rounds of adjustment (see text).
| Guest |
|
|
||
|---|---|---|---|---|
| G1 | 19.2 | 59.2 | ||
| G2 | 21.3 | 65.0 | ||
| G3 | 21.1 | 57.9 | ||
| G4 | 28.5 | 77.9 | ||
| G5 | 19.6 | 58.7 | ||
| G6 | 23.9 | 68.0 |
∂ΔG°/∂σow: kcal/(mol·Å); ∂ΔG°/∂εow: unitless.
Figure 2.
Contour plot of RMSE of computed host-guest binding free energies for the six training set cases, as a function of σow and εow, estimated by linear extrapolation of the sensitivity analysis. Regions with RMSE values larger than 2 kcal/mol are left blank. Green diamond: Bind3P; Red dot: TIP3P. Parameters that can lower the RMSE value to 0.6–0.8 kcal/mol were found, in separate calculations, to generate worse pure liquid properties compared to those yielded by the original TIP3P Lennard-Jones parameters.
This procedure led to identification of the parameters listed under Bind3P in Table 3, which represent a 0.6% reduction in σow, and a 19.6% increase in εow, relative to TIP3P. The training-set host-guest binding free energies predicted by sensitivity analysis have an RMSE of 0.8 kcal/mol (Bind3P (pred), Table 1), which is improved relative to the RMSE of 1.7 kcal/mol for unmodified TIP3P (Table 1). The pure water properties for the proposed parameters are similar in accuracy to those for unmodified (Bind3P vs TIP3P in Table 3): the density and isothermal compressibility predictions are slightly improved in Bind3P, while the dielectric constant and coefficient of thermal expansion are statistically indistinguishable (Tables 3, S5). In addition, although Bind3P yields a flatter oxygen-oxygen radial distribution function (RDF) than TIP3P at long range (Figure S2), the location and height of its first peak are in close agreement with recent experimental measurements55, and are a better match than those of TIP3P (Table 3 and Figure S2).
Table 3.
Parameters of the original TIP3P and Bind3P water models, and a comparison of bulk properties computed with both. The geometry of the water model and its partial charges are unchanged in Bind3P.
| Expt. | TIP3P | Bind3P | |
|---|---|---|---|
| σow (Å) | - | 3.1508 | 3.1319 |
| εow (kcal/mol) | - | 0.1520 | 0.1818 |
| q (e) | - | 0.417 | 0.417 |
| Density (g/cm3) | 0.997[57] | 0.985 (<0.001) | 0.990 (<0.001) |
| Static dielectric constant | 78.5[58] | 98 (2) | 102 (4) |
| Isothermal compressibility (10−6 bar−1) | 45.8[59] | 58 (1) | 55 (2) |
| Coeff. of thermal expansion (10−4 K−1) | 2.0[59] | 9.1 (0.4) | 9.5 (0.7) |
| Heat of vaporization (kcal/mol) | 10.52[60] | 10.09 (0.01) | 10.02 (0.02) |
| Position of first RDF peak (Å) | 2.82[55] | 2.78 (<0.01) | 2.81 (0.01) |
| Height of first RDF peak | 2.49[55] | 2.71 (<0.01) | 2.64 (<0.01) |
All bulk properties were computed at 298.15 K and 1 atm and reported as the mean, with the standard deviation across triplicate calculations given in parentheses. The properties of the TIP3P water model listed in this table were also computed in the present work, and are in good agreement with those reported in ref61.
New attach-pull-release calculations for the six training-set host-guest systems, using the proposed Bind3P parameters, yielded binding free energies (Bind3P, Table 1) that agree well with those predicted by linear extrapolation using the partial derivatives from sensitivity analysis; compare Bind3P and Bind3P (pred) in Table 1. Another round of optimization following the same procedure indicated that no significant improvement to the new RMSE value of 0.8 kcal/mol could be achieved by further perturbing the Lennard-Jones parameters, without sacrificing the accuracy of the pure water properties.
The Bind3P model yields improved agreement with experiment for the present training set. Bind3P corrects TIP3P’s tendency to provide overestimates of the binding free energy, as its MSE is only −0.1 kcal/mol, versus −1.5 kcal/mol for TIP3P (Table 1), while lowering the RMSE from 1.7 to 0.9 kcal/mol. Three other water models, TIP4P-EW, OPC, and TIP4P-D56, also overestimate the training set binding free energies (MSE −0.9 to −2.7 kcal/mol, Table 1), and provide results that are less accurate than Bind3P. However, the significance of these comparisons with experiment is limited by the fact that Bind3P was adjusted against these training set data. The following subsection therefore evaluates the new model with a much larger set of host-guest binding data, which were not used to adjust Bind3P.
Evaluation of Bind3P for Data Outside the Training Set
Additional Octa-Acid Binding Data
We further evaluated Bind3P by comparing it with the TIP3P, TIP4P-Ew, OPC and TIP4P-D water models, in calculations of OA-guest binding free energies and enthalpies outside the binding free energy dataset used to adjust the parameters of Bind3P. The binding enthalpy dataset includes all OA guests in Figure 1 for which ITC experiments were done, namely G1–G6 and a subset of the additional 14 guests in Figure 1 and Table 4. Note that, although G1–G6 appear in the training set, only their free energies were used to train the Bind3P model.
Table 4.
Comparison of experimental and calculated binding free energies (ΔG°) using four different water models for the host OA with guests (all in kcal/mol except for R2 and m, which are unitless). The uncertainties of the computed ΔG° values range from 0.2 to 0.3 kcal/mol. The uncertainties in RMSE and MSE are 0.3–0.4 kcal/mol and 0.1–0.3 kcal/mol, respectively, based on bootstrap resampling. Experiments were done with ITC or NMR, as indicated. MSE: mean signed error; RMSE: root-mean-squared error; R2: coefficient of determination, i.e., the square of the Pearson correlation coefficient; m: slope of linear regression. The error metrics are averages over 10,000 bootstrap cycles of sampling with replacement, and thus may be different from the values calculated directly from the means.
| Guest | Expta | Bind3P | TIP3P | TIP4P-Ew | OPC | TIP4P-D |
|---|---|---|---|---|---|---|
| L1 | −8.3 | −13.1 | −14.2 | −14.7 | −13.3 | −12.7 |
| L2 | −7.4 | −12.4 | −13.2 | −13.6 | −12.6 | −12.2 |
| L3 | −4.9 | −7.2 | −8.7 | −9.1 | −8.8 | −7.6 |
| L4 | −6.0 | −8.8 | −10.8 | −11.9 | −10.8 | −10.2 |
| L5 | −6.9 | −10.1 | −11.1 | −12.8 | −12.1 | −11.3 |
| O1 | −3.7 | −4.0 | −5.3 | −5.7 | −5.4 | −4.6 |
| O2 | −5.9 | −7.5 | −9.4 | −10.1 | −9.9 | −8.9 |
| O3 | −6.3 | −7.7 | −10.3 | −11.1 | −10.6 | −9.7 |
| O4 | −6.7 | −7.7 | −9.3 | −10.4 | −9.9 | −9.2 |
| O5 | −5.2 | −5.1 | −7.5 | −8.2 | −7.1 | −6.6 |
| O6 | −5.6 | −7.8 | −9.2 | −9.7 | −9.3 | −8.3 |
| O7 | −7.6 | −8.4 | −10.4 | −10.9 | −10.2 | −9.5 |
| O8 | −3.7 | −5.5 | −7.3 | −7.8 | −6.9 | −6.0 |
| O9 | −6.6 | −9.3 | −11.0 | −11.2 | −10.2 | −9.3 |
|
| ||||||
| MSE | −2.1 | −3.8 | −4.5 | −3.7 | −2.9 | |
| RMSE | 2.6 | 4.0 | 4.6 | 3.9 | 3.2 | |
| R2 | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 | |
| m | 1.4 | 1.4 | 1.4 | 1.3 | 1.4 | |
For the 14 OA test-set binding free energies, Bind3P provides greater accuracy (lowest RMSE) than the other four water models (Table 4 and Figure 3). As in the case of the training set (above), much of the improvement traces to a reduced tendency to overestimate the binding affinities, as evident from a less negative MSE. However, unlike the training set, where the MSE for Bind3P was near zero, the MSE here remains significantly negative, at −2.1 kcal/mol. The water model whose performance most resembles that of Bind3P is TIP4P-D, whose dispersion interactions were strengthened, relative to TIP4P, to reduce the tendency of proteins to collapse into unrealistically compact structures56. Evidently, the same adjustment also reduces the tendency to overestimate host-guest binding affinities. Overall, however, despite their greater level of detail, the four-site water models examined here do not provide greater accuracy than the three-site water models for the binding affinity calculations. In fact, TIP4P-Ew most strongly overestimates the affinities, and yields the largest errors.
Figure 3.
Computed versus experimental ΔG° for 14 test-set OA-guest systems, computed with five different water models. Green dots: Bind3P; Red squares: TIP3P; Yellow triangles: TIP4P-Ew; Blue crosses: OPC; Orange diamonds: TIP4P-D. Dashed lines are the trendlines for each water model. Solid black line is the line of identity.
For the 16 OA test-set binding enthalpies (Table 5), Bind3P again provides greater accuracy than TIP3P, with a lower RMSE (3.4 vs. 5.2 kcal/mol), due largely to a reduced tendency to overestimate heat release (MSE −1.3 vs −3.9 kcal/mol). Thus, adjusting water parameters to improve binding free energies led to improvement in binding enthalpies. Nonetheless, the correlation with experiment is not as good for the binding enthalpies, as R2 here is only 0.2, and the RMSE also is larger (3.4 vs 2.6 kcal/mol). Overall, the OPC model yields the most accurate binding enthalpies with an RMSE of 2.3 kcal/mol and R2 of 0.4, despite providing middling results for the binding free energies.
Table 5.
Comparison of experimental and calculated binding enthalpies (ΔH) using four different water models for the host OA with guests (kcal/mol except for R2 and m). uncertainties of the computed ΔH values range from 0.2 to 0.7 kcal/mol. See Table 4 for additional details.
| Expta | Bind3P | TIP3Pb | TIP4P-Ew | OPC | TIP4P-D | |
|---|---|---|---|---|---|---|
| G1 | −7.7 | −6.7 | −8.4 | −6.8 | −4.3 | −2.3 |
| G2 | −4.4 | −3.3 | −5.7 | −4.9 | −1.8 | −0.4 |
| G3 | −5.9 | −4.6 | −7.2 | −6.3 | −4.0 | −3.4 |
| G4 | −14.8 | −12.5 | −15.5 | −12.3 | −9.2 | −6.1 |
| G5 | −9.9 | −3.6 | −5.6 | −7.7 | −5.6 | −3.8 |
| G6 | −5.7 | −6.6 | −9.5 | −9.7 | −6.8 | −5.2 |
| L1 | −8.5 | −13.0 | −15.9 | −13.5 | −9.1 | −7.7 |
| L2 | −7.4 | −12.2 | −15.2 | −11.4 | −8.0 | −6.7 |
| L3 | −5.2 | −8.5 | −11.5 | −8.1 | −5.0 | −3.4 |
| L4 | −5.6 | −10.8 | −13.5 | −10.1 | −5.9 | −5.2 |
| L5 | −5.6 | −10.8 | −13.4 | −10.1 | −5.8 | −5.1 |
| O3 | −10.4 | −10.9 | −13.6 | −12.1 | −9.9 | −8.6 |
| O4 | −9.4 | −9.9 | −12.5 | −12.0 | −8.6 | −8.0 |
| O6 | −4.2 | −7.8 | −10.3 | −7.1 | −4.7 | −2.9 |
| O7 | −8.3 | −8.9 | −11.8 | −9.9 | −6.0 | −4.6 |
| O9 | −6.6 | −10.1 | −12.8 | −10.5 | −6.7 | −5.0 |
|
| ||||||
| MSE | −1.3 | −3.9 | −2.1 | 1.1 | 2.6 | |
| RMSE | 3.4 | 5.2 | 3.2 | 2.3 | 3.4 | |
| R2 | 0.2 | 0.2 | 0.3 | 0.4 | 0.3 | |
| m | 0.4 | 0.4 | 0.5 | 0.5 | 0.5 | |
The experimental ΔH values of OA with O1, O2, O5 and O8 are not available. The experimental data of OA with O3, O4, O7 and O9 are from personal communication with Dr. Bruce Gibb, and others are from references54 and62. Note that guest O6 (cyclohexanecarboxylate) in Ref45 was also measured in Ref62.
Tetra-Endo-Methyl Octa-Acid (TEMOA) and Six Guest Molecules
The tuned parameters were further tested on six TEMOA-guest pairs (Figure 1), which were not part of the training set. The TEMOA host is an OA analog with methyl groups in place of hydrogens para to the carboxylic acid groups on the benzoic acid moieties. Encouragingly, Bind3P yields substantially lower RMSEs than TIP3P for both the binding free energies and enthalpies (Table 6). Again, these changes result largely from decreased overestimation of affinity and heat release, as reflected in the MSE values. However, the correlation between experiment and calculation, as reflected in R2, change little, and, for the binding free energies, the slope of a linear regression fit is further from unity for the new water model (1.4 vs 1.0).
Table 6.
Comparison of experimental and calculated binding data using TIP3P and Bind3P water models for the TEMOA test set (kcal/mol except for unitless coefficient of determination, R2, and linear regression slope, m). MSE: mean signed error; RMSE: root-mean-squared error. The error metrics are averages over 10,000 bootstrap cycles of sampling with replacement, and thus may be different from the values calculated directly from the means.
| ∆G° | ∆H | |||||
|---|---|---|---|---|---|---|
|
|
|
|||||
| Expta | Bind3P | TIP3Pb | Expta | Bind3P | TIP3Pb | |
| G1 | −5.5 | −6.5 | −7.6 | −10.0 | −9.6 | −11.7 |
| G2 | −5.3 | −6.2 | −7.0 | −7.6 | −7.8 | −10.7 |
| G3 | −5.7 | −6.6 | −7.3 | −6.6 | −7.4 | −9.5 |
| G4 | −2.4 | −2.1 | −4.4 | - | - | - |
| G5 | −3.9 | −4.3 | −5.3 | - | - | - |
| G6 | −4.5 | −5.0 | −6.0 | −9.1 | −7.6 | −11.0 |
|
| ||||||
| MSE | −0.6 | −1.7 | 0.2 | −2.4 | ||
| RMSE | 0.8 | 1.8 | 1.0 | 2.5 | ||
| R2 | 0.9 | 0.9 | 0.6 | 0.7 | ||
| m | 1.4 | 1.0 | 0.5 | 0.5 | ||
The experimental values can be found in ref54. The NMR experiments (rows with ΔG° only) were carried out in 10 mM sodium phosphate buffer at a pH of 11.3, while the ITC experiments (rows with both ΔG° and ΔH) were performed in 50 mM sodium phosphate buffer at pH 11.5. All were measured at 298 K, except that G4 was measured at 278 K.
The computed ΔG° and ΔH values using the original TIP3P water model were reported in ref11.
Sixty-Nine Cyclodextrin and Cucurbituril Host-Guest Pairs
Finally, we tested the Bind3P water model for additional 69 binding interactions involving host molecules distinct from the octa-acids: cyclodextrins63–65 (CDs) and cucurbit[7]uril66–69 (CB7) (Figure 4). The CD test set includes binding free energies and enthalpies for 43 host-guest pairs, each with an ammonium, an alcohol, or a carboxylate functional group (Tables S1, S2). This set was used in our recent work assessing combinations of water models, partial charges, and general force field parameters in binding calculations10, and has been proposed as a benchmark to evaluate force fields and free energy methods20. Although we use GAFF force field parameters for the other molecules in this study (see Methods), we used Q4MD-CD parameters47 for the cyclodextrin hosts, as these have been tuned to generate more realistic cyclodextrin conformational distributions, based on experimental NMR data, and provided a more plausible conformational ensemble for free βCD in our prior study10. The CB7 test set is from the HYDROPHOBE blind prediction challenge21, which was based on newly measured binding free energies of 26 neutral hydrocarbons (Table S3). Evaluation statistics are provided in Table 7 for the CD-guest binding free energies and enthalpies, as well as the CB7-guest binding free energies; detailed results for each host-guest pair are provided in Tables S1 and S2.
Figure 4.
Structures of α-cyclodextrin (αCD), β-cyclodextrin (βCD), and cucurbit[7]uril (CB7). Gray: carbon; blue: nitrogen; red: oxygen. Nonpolar hydrogen atoms are omitted for clarity.
Table 7.
Comparison of error statistics between TIP3P and Bind3P results, for the CD and CB7 test sets. See prior tables for definitions and units. Results for each host-guest pair are provided in Tables S1 and S2.
| Cyclodextrins (CD) | Cucurbit[7]uril (CB7) | |||||
|---|---|---|---|---|---|---|
|
|
|
|||||
| ΔG° | ΔH | ΔG° | ||||
|
|
|
|
||||
| Bind3P | TIP3P | Bind3P | TIP3P | Bind3P | TIP3P | |
| MSE | −0.5 | −1.3 | −1.1 | −1.9 | −4.4 | −5.3 |
| RMSE | 1.3 | 1.8 | 1.5 | 2.2 | 5.5 | 6.3 |
| R2 | 0.40 | 0.37 | 0.72 | 0.69 | 0.87 | 0.88 |
| m | 0.9 | 0.9 | 0.9 | 1.0 | 2.2 | 2.3 |
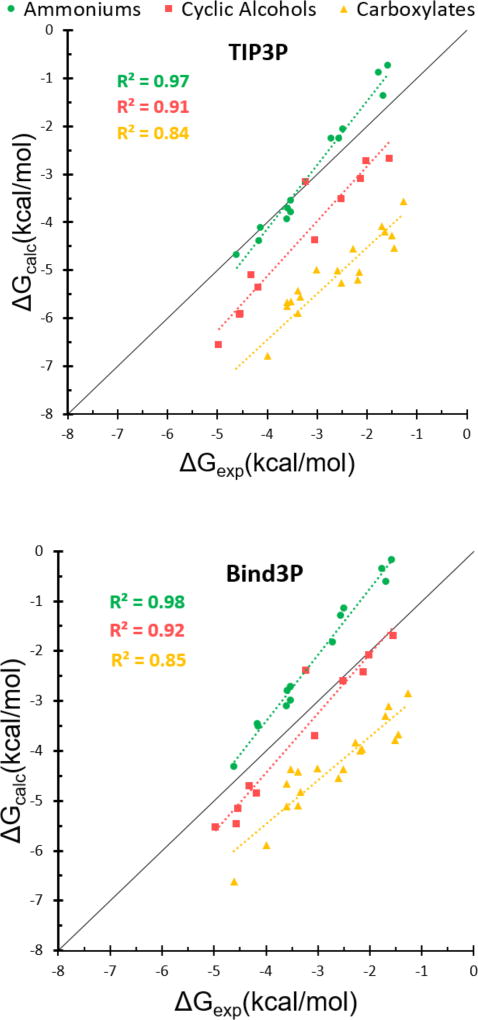
The trends in the summary statistics (Table 7) for this large test set are consistent with the results for OA and TEMOA. Thus, the TIP3P water model is associated with binding affinities and enthalpies that are consistently too negative (MSE −1.3 to −5.3), and Bind3P reduces these systematic errors, here by about 0.9 kcal/mol. The reduction in systematic error lead to reductions in RMSE, but not much change in the correlation (R2) of experiment versus calculation, or in the slope (m) of the linear regression. For the CD systems, the free energy correlations obtained for each separate group of guests – ammonium, alcohol, carboxylate – are much better than those for all guests considered together, not only for TIP3P, as previously observed (Figure 5, top panel), but also for Bind3P (Figure 5, bottom panel). We surmise that bringing all three sets of guests into alignment will require changes in parameters associated with their respective functional groups and or changes in the partial charges of the water model. It is also worth noting that, for the CB7 systems, the Bind3P model is still associated with severe overestimates of affinity, and an excessively high regression slope of calculation versus experiment. On the other hand, the correlation of calculation with experiment is higher for the CB7 cases than the CD cases.
Figure 5.
Comparison between calculated and measured binding free energies of cyclodextrin test set using the TIP3P (top) and Bind3P (bottom) water models. Green circles, red squares, and yellow triangles represent guests with ammonium, alcohol, and carboxylate functional groups, respectively. The upper left legends include the R2 values for each guest functional group colored consistently with data points. The solid black line is the line of identity.
Hydration free energies of small, organic molecules
To further test the Bind3P water model, we used it to compute the hydration free energies of all guest molecules in this study for which data are available in the FreeSolv database48, and compared with matched calculations using TIP3P. As detailed in Figure S3 and Table S4, both models provide high correlations with experiment (R2 0.92–0.93, with linear regression slopes of 0.9), but Bind3P yields somewhat lower RSME and MSE values (0.7 and 0.3 kcal/mol, respectively) than TIP3P (0.8 and 0.5 kcal/mol, respectively). Given that a host and guest are less solvent-exposed when bound than when free in solution, it makes physical sense that a water model which leads to stronger (more favorable) hydration of solutes would also tend to weaken host-guest binding, as observed in the present study. These hydration free energy results lend further support to the Bind3P model and, more generally, to the transferability of parameters adjusted based on binding data.
Conclusions and Outlook
This first use of host-guest binding data to optimize a water model yields consistent improvement in accuracy across a large test set of host-guest binding thermodynamics, including host molecules distinct from those in the training set. In particular, the new model, Bind3P (v0.1), leads to reduced overestimation of binding affinities and heat release on binding, relative to the starting TIP3P model. The fact that Bind3P also tends to improve the accuracy of hydration free energy calculations indicates that parameters based on binding data are transferable to other physical properties. Bind3P furthermore preserves the accuracy of properties of pure water at room temperature, much as previously observed for the TIP3P-MOD18 and TIP4P-D56 water models, which were adjusted, respectively, to improve the accuracy of hydration free energies and of the conformational distributions of unfolded proteins. Because Bind3P has the same form as the widely used TIP3P model, it can readily be tested and used in other applications. It will be interesting in future work to examine its predictions for additional pure water properties, such as the self-diffusion constant and properties at various temperatures; and to test it in the context of protein-small molecule binding, which is important in drug design. Based on such studies, it may well be possible to generate new versions of the water model that are further improved.
It is worth highlighting the large number of binding data used in this study, over 120 different host-guest binding free energies and enthalpies. The size of this dataset rivals and in some cases exceeds that of other datasets traditionally used to test and adjust force fields, such as the properties of pure liquids and the hydration free energies of small molecules. This use of host-guest binding data to test and tune force fields is enabled by advances in computing hardware and software that have greatly accelerated atomistic molecular simulations. It should be straightforward to expand this approach by using additional data from the experimental literature. In addition, we have embarked on a project to generate new experimental host-guest data specifically designed to generate a diverse collection of chemical interactions that will be useful to test and improve force fields70.
One of the key applications of molecular simulations is the prediction of protein-small molecule binding affinities in the setting of drug discovery. It seems likely that adjusting force field parameters against binding data, as done here, will be a particularly fruitful approach to generate potential functions suitable for computer-aided drug design. Unlike other data types used to adjust force fields, binding data challenges the ability of water models to replicate the complex properties of water in the confines of a binding site. It is also worth noting that, although hydration free energies are informative, getting them right requires a force field that works well not only in liquid water, but also in vacuo; and it is not clear that restraining force field parameters against in vacuo data is an optimal strategy for generating parameters for use in the condensed phase.
The present study also supports a broad conclusion that adjusting a force field based on binding thermodynamics need not lead to reduced accuracy in other experimental observables. In particular, there appears to be significant degeneracy in the water model parameters dictated only by the properties of pure water. That is, pure water properties do not tightly define the water model’s parameters, and the addition of binding data into the parameterization scheme helps break the degeneracy. This result is congruent with the conclusions of a prior study, which adjusted the parameters of the TIP3P water model to improve the accuracy of hydration free energies, rather than binding thermodynamics, while retaining the properties of pure water18. Similarly, the TIP4P-D model preserves key properties of pure water, while reducing the tendency of simulated disordered proteins to collapse into compact structures56.
Still, it might be argued that a water model should be adjusted to capture the properties of pure water as well as possible, and that solutes should then be parameterized in the context of this model to best capture the thermodynamics of hydration. However, it is not clear that it is ultimately the best approach if one’s goal is to best capture the properties of aqueous solutions. This is because the simplifications inherent in most current force fields mean that one cannot expect a single set of parameters to get everything right, and if one aims to model aqueous solutions, then some compromises in the treatment of pure water may be appropriate, particularly given that additional experimental data, such as the properties of organic liquids, constrain the solute parameters. That said, as just noted, there is some tolerance in water parameters, in the sense that one can adjust a water model to do well for pure water properties while also improving its treatment of hydration thermodynamics. We would also emphasize that it is far from clear that pure water properties provide enough information to determine how well a water model will perform for complex environments like the binding cavity of a host molecule or the active site of an enzyme. Only binding data, as used here, tests this aspect of water models, which is central to some of the most important applications of molecular simulations, such as computer-aided drug design.
Although Bind3P reduces the systematic overestimation of binding associated with TIP3P, it does not improve the correlation between calculation and experiment; and it does not bring the three classes of guest molecules in the CD test set (ammoniums, alcohols, and carboxylates) into line with each other. It may be possible to improve these aspects of the calculations in future versions of the Bind3P water model, such as by changing partial charges and/or the geometry. However, we anticipate that substantial reductions in scatter will require coordinated, consistent adjustments of both water and solute parameters. Using binding data to adjust solute force field parameters will require a larger dataset of binding thermodynamics, so, as noted above, our group is working to systematically expand the dataset by developing facile syntheses of cyclodextrin derivatives designed to probe diverse nonbonded interactions70. We anticipate that force fields adjusted based on the resulting data will improve the accuracy of computed free energies not only for host-guest systems, but also for protein-ligand interactions important in drug design and discovery.
Supplementary Material
Acknowledgments
M.K.G. acknowledges funding from National Institute of General Medical Sciences (GM061300). The contents of this paper are solely the responsibility of the authors and do not necessarily represent the official views of the NIH.M.K.G. has an equity interest in and is a cofounder and scientific advisor of VeraChem LLC. We thank Dr. David Slochower for his useful and thoughtful comments.
Footnotes
The authors declare no competing financial interest.
ASSOCIATED CONTENT
Binding free energies and binding enthalpies of the cyclodextrin test set (Table S1, S2); binding free energies of the CB7 test set (Table S3); hydration free energy calculations (Table S4); p values and statistical significance (Table S5).
Figure S1–S3; Table S1–S5 (PDF)
Table 1,2,4–6 with uncertainties provided (XLSX)
This information is available free of charge via the Internet at http://pubs.acs.org
References
- 1.Jorgensen WL. Efficient Drug Lead Discovery and Optimization. Acc. Chem. Res. 2009;42(6):724–733. doi: 10.1021/ar800236t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wereszczynski J, McCammon JA. Statistical Mechanics and Molecular Dynamics in Evaluating Thermodynamic Properties of Biomolecular Recognition. Q. Rev. Biophys. 2012;45(01):1–25. doi: 10.1017/S0033583511000096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Wang L, Wu Y, Deng Y, Kim B, Pierce L, Krilov G, Lupyan D, Robinson S, Dahlgren MK, Greenwood J, et al. Accurate and Reliable Prediction of Relative Ligand Binding Potency in Prospective Drug Discovery by Way of a Modern Free-Energy Calculation Protocol and Force Field. J. Am. Chem. Soc. 2015;137(7):2695–2703. doi: 10.1021/ja512751q. [DOI] [PubMed] [Google Scholar]
- 4.Gathiaka S, Liu S, Chiu M, Yang H, Stuckey JA, Kang YN, Delproposto J, Kubish G, Dunbar JB, Carlson HA, et al. D3R Grand Challenge 2015: Evaluation of Protein-Ligand Pose and Affinity Predictions. J. Comput. Aided. Mol. Des. 2016;30(9):651–668. doi: 10.1007/s10822-016-9946-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gaieb Z, Liu S, Gathiaka S, Chiu M, Yang H, Shao C, Feher VA, Walters PW, Kuhn B, Rudolph MG, et al. D3R Grand Challenge 2: Blind Prediction of Protein–Ligand Poses, Affinity Rankings, and Relative Binding Free Energies. J. Comput. Aided. Mol. Des. 2017:1–20. doi: 10.1007/s10822-017-0088-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Mobley DL, Gilson MK. Predicting Binding Free Energies: Frontiers and Benchmarks. Annu. Rev. Biophys. 2017;46:531–558. doi: 10.1146/annurev-biophys-070816-033654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Quevedo MA, Zoppi A. Current Trends in Molecular Modeling Methods Applied to the Study of Cyclodextrin Complexes. J. Incl. Phenom. Macrocycl. Chem. 2017:1–14. [Google Scholar]
- 8.Fenley AT, Henriksen NM, Muddana HS, Gilson MK. Bridging Calorimetry and Simulation through Precise Calculations of Cucurbituril-Guest Binding Enthalpies. J. Chem. Theory Comput. 2014;10(9):4069–4078. doi: 10.1021/ct5004109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Henriksen NM, Fenley AT, Gilson MK. Computational Calorimetry: High-Precision Calculation of Host-Guest Binding Thermodynamics. J. Chem. Theory Comput. 2015;11(9):4377–4394. doi: 10.1021/acs.jctc.5b00405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Henriksen NM, Gilson MK. Evaluating Force Field Performance in Thermodynamic Calculations of Cyclodextrin Host-Guest Binding: Water Models, Partial Charges, and Host Force Field Parameters. J. Chem. Theory Comput. 2017;13(9):4253–4269. doi: 10.1021/acs.jctc.7b00359. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Yin J, Henriksen NM, Slochower DR, Gilson MK. The SAMPL5 Host-Guest Challenge: Computing Binding Free Energies and Enthalpies from Explicit Solvent Simulations Using Attach-Pull-Release (APR) Approach. J. Comput. Aided. Mol. Des. 2016:1–13. doi: 10.1007/s10822-016-9970-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Yin J, Henriksen NM, Slochower DR, Shirts MR, Chiu MW, Mobley DL, Gilson MK. Overview of the SAMPL5 Host-Guest Challenge: Are We Doing Better? Journal of Computer-Aided Molecular Design. 2016:1–19. doi: 10.1007/s10822-016-9974-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Bosisio S, Mey ASJS, Michel J. Blinded Predictions of Host-Guest Standard Free Energies of Binding in the SAMPL5 Challenge. J. Comput. Aided. Mol. Des. 2017;31:61–70. doi: 10.1007/s10822-016-9933-0. [DOI] [PubMed] [Google Scholar]
- 14.Zhou R. Trp-Cage: Folding Free Energy Landscape in Explicit Water. Proc. Natl. Acad. Sci. U. S. A. 2003;100:13280–13285. doi: 10.1073/pnas.2233312100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Nutt DR, Smith JC. Molecular Dynamics Simulations of Proteins: Can the Explicit Water Model Be Varied? J. Chem. Theory Comput. 2007;3(4):1550–1560. doi: 10.1021/ct700053u. [DOI] [PubMed] [Google Scholar]
- 16.Omosun TO, Hsieh M-C, Childers WS, Das D, Mehta AK, Anthony NR, Pan T, Grover MA, Berland KM, Lynn DG. Catalytic Diversity in Self-Propagating Peptide Assemblies. Nat. Chem. 2017 Feb;:1–5. doi: 10.1038/nchem.2738. No. [DOI] [PubMed] [Google Scholar]
- 17.Shivakumar D, Williams J, Wu Y, Damm W, Shelley J, Sherman W. Prediction of Absolute Solvation Free Energies Using Molecular Dynamics Free Energy Perturbation and the Opls Force Field. J. Chem. Theory Comput. 2010;6(5):1509–1519. doi: 10.1021/ct900587b. [DOI] [PubMed] [Google Scholar]
- 18.Shirts MR, Pande VS. Solvation Free Energies of Amino Acid Side Chain Analogs for Common Molecular Mechanics Water Models. J. Chem. Phys. 2005;122(13):134508. doi: 10.1063/1.1877132. [DOI] [PubMed] [Google Scholar]
- 19.Hess B, van der Vegt NFa. Hydration Thermodynamic Properties of Amino Acid Analogues: A Systematic Comparison of Biomolecular Force Fields and Water Models. J. Phys. Chem. B. 2006;110:17616–17626. doi: 10.1021/jp0641029. [DOI] [PubMed] [Google Scholar]
- 20.Mobley DL, Heinzelmann G, Henriksen NM, Gilson MK. Predicting Binding Free Energies: Frontiers and Benchmarks (a Perpetual Review) eScholarship. 2017 doi: 10.1146/annurev-biophys-070816-033654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Assaf KI, Florea M, Antony J, Henriksen NM, Yin J, Hansen A, Qu Z, Sure R, Klapstein D, Gilson MK, et al. The HYDROPHOBE Challenge: A Joint Experimental and Computational Study on the Binding of Hydrocarbons to Cucurbiturils. J. Phys. Chem. B. 2017;121(49):11144–11162. doi: 10.1021/acs.jpcb.7b09175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gao K, Yin J, Henriksen NM, Fenley AT, Gilson MK. Binding Enthalpy Calculations for a Neutral Host–Guest Pair Yield Widely Divergent Salt Effects across Water Models. J. Chem. Theory Comput. Chem. theory Comput. 2015;11(10):4555–4564. doi: 10.1021/acs.jctc.5b00676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Muddana HS, Gilson MK. Prediction of SAMPL3 Host-Guest Binding Affinities: Evaluating the Accuracy of Generalized Force-Fields. Journal of Computer- Aided Molecular Design. 2012;26:517–525. doi: 10.1007/s10822-012-9544-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983;79(2):926–935. [Google Scholar]
- 25.Yin J, Fenley AT, Henriksen NM, Gilson MK. Toward Improved Force-Field Accuracy through Sensitivity Analysis of Host-Guest Binding Thermodynamics. J. Phys. Chem. B. 2015 doi: 10.1021/acs.jpcb.5b04262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Jakalian A, Bush BL, Jack DB, Bayly CI. Fast, Efficient Generation of High-Quality Atomic Charges. AM1- BCC Model: I. Method. J. Comput. Chem. 2000;21(2):132–146. doi: 10.1002/jcc.10128. [DOI] [PubMed] [Google Scholar]
- 27.Jakalian A, Jack DB, Bayly CI. Fast, Efficient Generation of High-Quality Atomic Charges. AM1-BCC Model: II. Parameterization and Validation. J. Comput. Chem. 2002;23:1623–1641. doi: 10.1002/jcc.10128. [DOI] [PubMed] [Google Scholar]
- 28.Bayly CCI, Cieplak P, Cornell WD, Kollman PA. A Well-Behaved Electrostatic Potential Based Method Using Charge Restraints for Deriving Atomic Charges: The RESP Model. J. Phys. Chem. 1993;97:10269–10280. [Google Scholar]
- 29.Izadi S, Anandakrishnan R, Onufriev AV. Building Water Models : A Different Approach. J. Phys. Chem. Lett. 2014;5:3863–3871. doi: 10.1021/jz501780a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Horn HW, Swope WC, Pitera JW, Madura JD, Dick TJ, Hura GL, Head-Gordon T. Development of an Improved Four-Site Water Model for Biomolecular Simulations: TIP4P-Ew. J. Chem. Phys. 2004;120(20):9665–9678. doi: 10.1063/1.1683075. [DOI] [PubMed] [Google Scholar]
- 31.Wang LP, Martinez TJ, Pande VS. Building Force Fields: An Automatic, Systematic, and Reproducible Approach. J. Phys. Chem. Lett. 2014;5:1885–1891. doi: 10.1021/jz500737m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Laury ML, Wang LP, Pande VS, Head-Gordon T, Ponder JW. Revised Parameters for the AMOEBA Polarizable Atomic Multipole Water Model. J. Phys. Chem. B. 2015;119(29):9423–9437. doi: 10.1021/jp510896n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Wong CF, Thacher T, Rabitz H. Rev. Comput. Chem. Wiley VCH; New York: 1998. Sensitivity Analysis in Biomolecular Simulation. [Google Scholar]
- 34.Zhu S-B, Wong CF. Sensitivity Analysis of Water Thermodynamics. J. Chem. Phys. 1993;98(11):8892–8899. [Google Scholar]
- 35.Di Pierro M, Elber R. Automated Optimization of Potential Parameters. J. Chem. Theory Comput. 2013;9(8):3311–3320. doi: 10.1021/ct400313n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Di Pierro M, Mugnai ML, Elber R. Optimizing Potentials for a Liquid Mixture: A New Force Field for a Tert-Butanol and Water Solution. J. Phys. Chem. B. 2015 doi: 10.1021/jp505401m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Velez-Vega C, Gilson MK. Overcoming Dissipation in the Calculation of Standard Binding Free Energies by Ligand Extraction. J. Comput. Chem. 2013;34:2360–2371. doi: 10.1002/jcc.23398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Heinzelmann G, Henriksen NM, Gilson MK. Attach-Pull-Release Calculations of Ligand Binding and Conformational Changes on the First BRD4 Bromodomain. J. Chem. Theory Comput. 2017;13(7):3260–3275. doi: 10.1021/acs.jctc.7b00275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kirkwood JG. Statistical Mechanics of Fluid Mixtures. J. Chem. Phys. 1935;3(5):300–313. [Google Scholar]
- 40.Fenley AT, Henriksen NM, Muddana HS, Gilson MK. Bridging Calorimetry and Simulation through Precise Calculations of Cucurbituril − Guest Binding Enthalpies. J. Chem. Theory Comput. 2014;10:4069–4078. doi: 10.1021/ct5004109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Molecular Operating Environment (MOE), 2013.08. Chemical Computing Group Inc.; 1010 Sherbooke St. West, Suite #910, Montreal, QC, Canada, H3A 2R7: 2016. [Google Scholar]
- 42.Vanquelef E, Simon S, Marquant G, Garcia E, Klimerak G, Delepine JC, Cieplak P, Dupradeau FYRED. Server: A Web Service for Deriving RESP and ESP Charges and Building Force Field Libraries for New Molecules and Molecular Fragments. Nucleic Acids Res. 2011;39(SUPPL. 2) doi: 10.1093/nar/gkr288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Wang J, Wolf RM, Caldwell JW, Kollman PA, Case DA. Development and Testing of a General Amber Force Field. 2004;25:1157–1174. doi: 10.1002/jcc.20035. [DOI] [PubMed] [Google Scholar]
- 44.Case DA, Cerutti DS, TE Cheatham I, Darden TA, Duke RE, Giese TJ, Gohlke H, Goetz AW, Greene D, Homeyer N, et al. AMBER. University of California, San Francisco: University of California, San Francisco p University of California, San Francisco; 2017. [Google Scholar]
- 45.Gibb CLD, Gibb BC. Binding of Cyclic Carboxylates to Octa-Acid Deep-Cavity Cavitand. J. Comput. Aided. Mol. Des. 2014;28(4):319–325. doi: 10.1007/s10822-013-9690-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Joung IS, Cheatham TE. Determination of Alkali and Halide Monovalent Ion Parameters for Use in Explicitly Solvated Biomolecular Simulations. J. Phys. Chem. B. 2008;112(30):9020–9041. doi: 10.1021/jp8001614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Cézard C, Trivelli X, Aubry F, Djedaïni-Pilard F, Dupradeau F-Y. Molecular Dynamics Studies of Native and Substituted Cyclodextrins in Different Media: 1. Charge Derivation and Force Field Performances. Phys. Chem. Chem. Phys. 2011;13(33):15103. doi: 10.1039/c1cp20854c. [DOI] [PubMed] [Google Scholar]
- 48.Mobley DL, Guthrie JP. FreeSolv: A Database of Experimental and Calculated Hydration Free Energies, with Input Files. J. Comput. Aided. Mol. Des. 2014;28(7):711–720. doi: 10.1007/s10822-014-9747-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Eastman P, Swails J, Chodera JD, McGibbon RT, Zhao Y, Beauchamp KA, Wang LP, Simmonett AC, Harrigan MP, Stern CD, et al. OpenMM 7: Rapid Development of High Performance Algorithms for Molecular Dynamics. PLoS Comput. Biol. 2017;13(7) doi: 10.1371/journal.pcbi.1005659. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.McGibbon RT, Beauchamp KA, Harrigan MP, Klein C, Swails JM, Hernández CX, Schwantes CR, Wang LP, Lane TJ, Pande VS. MDTraj: A Modern Open Library for the Analysis of Molecular Dynamics Trajectories. Biophys. J. 2015;109(8):1528–1532. doi: 10.1016/j.bpj.2015.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Roe DR, Cheatham TE. PTRAJ and CPPTRAJ: Software for Processing and Analysis of Molecular Dynamics Trajectory Data. J. Chem. Theory Comput. 2013;9(7):3084–3095. doi: 10.1021/ct400341p. [DOI] [PubMed] [Google Scholar]
- 52.Mikulskis P, Cioloboc D, Andrejić M, Khare S, Brorsson J, Genheden S, Mata RA, Söderhjelm P, Ryde U. Free-Energy Perturbation and Quantum Mechanical Study of SAMPL4 Octa-Acid Host-Guest Binding Energies. J. Comput. Aided. Mol. Des. 2014;28(4):375–400. doi: 10.1007/s10822-014-9739-x. [DOI] [PubMed] [Google Scholar]
- 53.Bell DR, Qi R, Jing Z, Xiang JY, Mejias C, Schnieders MJ, Ponder JW, Ren P. Calculating Binding Free Energies of Host–Guest Systems Using the AMOEBA Polarizable Force Field. Phys. Chem. Chem. Phys. 2016 Jun;18:30261–30269. doi: 10.1039/c6cp02509a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Sullivan MR, Sokkalingam P, Nguyen T, Donahue JP, Gibb BC. Binding of Carboxylate and Trimethylammonium Salts to Octa-Acid and TEMOA Deep-Cavity Cavitands. J. Comput. Aided. Mol. Des. 2016:1–8. doi: 10.1007/s10822-016-9925-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Soper AK. The Radial Distribution Functions of Water as Derived from Radiation Total Scattering Experiments: Is There Anything We Can Say for Sure? ISRN Phys. Chem. 2013;2013:279463. [Google Scholar]
- 56.Piana S, Donchev AG, Robustelli P, Shaw DE. Water Dispersion Interactions Strongly Influence Simulated Structural Properties of Disordered Protein States. J. Phys. Chem. B. 2015;119(16):5113–5123. doi: 10.1021/jp508971m. [DOI] [PubMed] [Google Scholar]
- 57.Kell GS. Precise Representation of Volume Properties of Water at One Atmosphere. J. Chem. Eng. Data. 1967;12(1):66–69. [Google Scholar]
- 58.Weast RC. CRC Handbook of Chemistry and Physics. Book. 1977 [Google Scholar]
- 59.Franks F. Water: A Comprehensive Treatise. Plenum Press; New York: 1972. [Google Scholar]
- 60.Wagner W, Pruss A. The IAPWS Formulation 1995 for the Thermodynamic Properties of Ordinary Water Substance for General and Scientific Use. J. Phys. Chem. Ref. Data. 2002;31:387. [Google Scholar]
- 61.Wu Y, Tepper HL, Voth GA. Flexible Simple Point-Charge Water Model with Improved Liquid-State Properties. J. Chem. Phys. 2006;124(2):024503. doi: 10.1063/1.2136877. [DOI] [PubMed] [Google Scholar]
- 62.Sun H, Gibb CLD, Gibb BC. Calorimetric Analysis of the 1:1 Complexes Formed between a Water-Soluble Deep-Cavity Cavitand, and Cyclic and Acyclic Carboxylic Acids. Supramol. Chem. 2008;20(1–2):141–147. [Google Scholar]
- 63.Rekharsky MV, Mayhew MP, Goldberg RN, Ross PD, Yamashoji Y, Inoue Y. Thermodynamic and Nuclear Magnetic Resonance Study of the Reactions of α- and β-Cyclodextrin with Acids, Aliphatic Amines, and Cyclic Alcohols. J. Phys. Chem. B. 1997;101(1):87–100. [Google Scholar]
- 64.Rekharsky MV, Inoue Y. Complexation Thermodynamics of Cyclodextrins. Chem. Rev. 1998;98(97):1875–1918. doi: 10.1021/cr970015o. [DOI] [PubMed] [Google Scholar]
- 65.Rekharsky M, Inoue Y. Chiral Recognition Thermodynamics of Beta-Cyclodextrin: The Thermodynamic Origin of Enantioselectivity and the Enthalpa-Entropy Compensation Effect. J. Am. Chem. Soc. 2000;122(33):4418–4435. [Google Scholar]
- 66.Kim H-J, Jeon WS, Ko YH, Kim K. Inclusion of Methylviologen in Cucurbit[7]Uril. Proc. Natl. Acad. Sci. U. S. A. 2002;99(8):5007–5011. doi: 10.1073/pnas.062656699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Moghaddam S, Yang C, Rekharsky M, Ko YH, Kim K, Inoue Y, Gilson MK. New Ultrahigh Affinity Host - Guest Complexes of Cucurbit [7] Uril with Bicyclo [2.2.2] Octane and Adamantane Guests : Thermodynamic Analysis and Evaluation of M2 Affinity Calculations. J. Am. Chem. Soc. 2011;133:3570–3581. doi: 10.1021/ja109904u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Muddana HS, Varnado CD, Bielawski CW, Urbach AR, Isaacs L, Geballe MT, Gilson MK. Blind Prediction of Host-Guest Binding Affinities: A New SAMPL3 Challenge. J. Comput. Aided Mol. Des. 2012;26(5):475–487. doi: 10.1007/s10822-012-9554-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Liu S, Ruspic C, Mukhopadhyay P, Chakrabarti S, Zavalij PY, Isaacs L. The Cucurbit[n]Uril Family: Prime Components for Self-Sorting Systems. J. Am. Chem. Soc. 2005;127(45):15959–15967. doi: 10.1021/ja055013x. [DOI] [PubMed] [Google Scholar]
- 70.Kellett K, Kantonen SA, Duggan BM, Gilson MK. Toward Expanded Diversity of Host-Guest Interactions via Synthesis and Characterization of Cyclodextrin Derivatives. ChemRxiv. 2018 [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.