Collaborative-controlled LASSO for constructing propensity score-based estimators in high-dimensional data

Abstract

Propensity score-based estimators are increasingly used for causal inference in observational studies. However, model selection for propensity score estimation in high-dimensional data has received little attention. In these settings, propensity score models have traditionally been selected based on the goodness-of-fit for the treatment mechanism itself, without consideration of the causal parameter of interest. Collaborative minimum loss-based estimation is a novel methodology for causal inference that takes into account information on the causal parameter of interest when selecting a propensity score model. This ‘‘collaborative learning’’ considers variable associations with both treatment and outcome when selecting a propensity score model in order to minimize a bias-variance tradeoff in the estimated treatment effect. In this study, we introduce a novel approach for collaborative model selection when using the LASSO estimator for propensity score estimation in high-dimensional covariate settings. To demonstrate the importance of selecting the propensity score model collaboratively, we designed quasi-experiments based on a real electronic healthcare database, where only the potential outcomes were manually generated, and the treatment and baseline covariates remained unchanged. Results showed that the collaborative minimum loss-based estimation algorithm outperformed other competing estimators for both point estimation and confidence interval coverage. In addition, the propensity score model selected by collaborative minimum loss-based estimation could be applied to other propensity score-based estimators, which also resulted in substantive improvement for both point estimation and confidence interval coverage. We illustrate the discussed concepts through an empirical example comparing the effects of non-selective nonsteroidal anti-inflammatory drugs with selective COX-2 inhibitors on gastrointestinal complications in a population of Medicare beneficiaries.

1. Introduction

1.1. Purpose

The propensity score (PS) is defined as the conditional probability of treatment assignment, given a set of pretreatment covariates.^1,2 The PS, which we will denote as g₀, is widely used to control for confounding bias in observational studies. In practice, the PS is usually unknown and PS-based estimators must rely on an estimate of the PS, which we will denote as g_n.

Accurately modeling and assessing the validity of fitted PS models is crucial for all PS-based methods. It is generally recommended that PS models be validated through measures of covariate balance across treatment groups after PS adjustment. In high-dimensional covariate settings, however, evaluating covariate balance on very large numbers of variables can be difficult. Using covariate balance to validate PS models in high-dimensional covariate settings is further complicated when applying machine learning algorithms and penalized regression methods to reduce the dimension of the covariate set, as it is not always clear on what variables balance should be evaluated. Cross-validated prediction diagnostics can greatly simplify validation of the PS model when applying machine learning algorithms for PS estimation in high-dimensional covariate settings.

Westreich et al.³ suggested that machine learning (ML) methods (e.g. support vector machines) could enhance the validity of propensity score estimation, and that “external” cross-validation (CV) can be used for model selection. Lee et al.⁴ further investigated PS weighted estimators when the PS was estimated by multiple ML algorithms, where the hyper-parameters of the ML algorithms were selected by minimizing the CV loss for treatment prediction. Estimation procedures that are based on external CV will result in estimated models that optimize the bias-variance tradeoff for treatment prediction (i.e. the true PS function), but they do not consider the ultimate goal of optimizing the bias-variance tradeoff for the treatment effect estimate. We conjecture that PS estimators that are selected by CV will tend to be under-fitted in order to reduce variability in the prediction of treatment assignment, and that the optimal estimator in reducing bias in the estimated treatment effect should be less smooth (or more flexible) compared to the estimator selected by external CV.

To address this limitation of external CV, we studied two recently proposed variations of the C-TMLE algorithm,^5,6 and compared them to other widely used estimators using multiple simulation studies. We focused on strategies that combined the C-TMLE algorithms with LASSO regression, an l–1 regularized logistic regression,⁷ for PS estimation. Previous studies have shown that LASSO regression can perform well for variable selection when estimating high-dimensional PSs.⁸ However, selecting the optimal tuning parameters to optimize confounding control remains challenging. Combining variations of the C-TMLE algorithm with LASSO regression provides a robust data adaptive approach to PS model selection in high-dimensional covariate datasets, but remains untested. We used quasi-experiments based on a real empirical dataset to evaluate the performance of combining variations of the C-TMLE algorithm with LASSO regression and demonstrate that external CV for model selection is insufficient.

The article is organized as follows. In section 1.2, we introduce the structure of the observed data, the scientific question, the parameter of interest, the average treatment effect (ATE), and the necessary assumptions for making the parameter of interest identifiable. In section 2 we briefly review some commonly used estimators of the ATE. In section 3, we review the targeted minimum-loss-based estimator. In section 4, we introduce two recently proposed C-TMLE algorithms which extend the vanilla TMLE algorithm. In section 5 we describe the electronic healthcare database used in the simulations and empirical analyses. In section 6 we describe how the simulated data are generated from the empirical dataset, and how results were analyzed from the simulation, including point estimation (subsection 6.3), confidence interval (subsection 6.4), and pair-wise comparisons (subsection 6.6) of estimators. In section 7 we apply the vanilla TMLE and novel C-TMLE algorithms to analyze the empirical dataset. Finally, in section 8, we discuss the results from the simulations and the scientific findings from the empirical data analysis.

1.2. Data structure, scientific question, and identification

Suppose we observe n independent and identically distributed (i.i.d.) observations, O_i = (Y_i, A_i, W_i), i ∈ 1,…, n, from some unknown but fixed data generating distribution P₀. Consider a simple setting, where W_i is a vector of some pre-treatment baseline covariates of the i-th observation, and A_i is a binary indicator taking on a value of 1 if observation i is in the treatment group and is 0 otherwise. Further, suppose that each observation has a counterfactual outcome pair, $(Y_i^{(0)},Y_i^{(1)})$, corresponding to the potential outcome if patient i is in the control group (A_i = 0) or the treatment group (A_i = 1). Thus, for each observation, we only observe one of the potential outcomes, Y_i, which corresponds with either $Y_i^{(0)}$ or $Y_i^{(0)}$, depending on whether the individual received treatment or remained untreated. For simplicity, we refer to Q₀(W) as the marginal distribution of W, go(W) as the conditional expectation of A|W, and ${\overline{Q}}_0(A,W)$ as the conditional expectation of Y|A, W. We will let g₀ represent the PS, under the data generating distribution P₀. In addition, we will let ${\mathbb{E}}_0$ represent the expectation under the unknown true data generating distribution P₀. Consider the ATE as the parameter of interest

$${\Psi }_0={\mathbb{E}}_0\left(Y^{(1)}\right)-{\mathbb{E}}_0\left(Y^{(0)}\right)$$

This parameter of interest is identifiable under following assumptions Assumption 1. (Consistency)

$$Y_i=Y_i^{(A_i)}=Y_i^{(0)}\left(1-A_i\right)+Y_i^{(1)}{A}_i$$

Assumption 2. (Conditional Randomization)

$$\left(Y^0,Y^{(1)}\right)╨A|W$$

Assumption 2 has also been called strong ignorability, or unconfoundedness.⁹ Under assumptions 1 and 2, the conditional probability of Y=y given A = a, W = w can be written as

$$P\left(Y=y|A=a,W=w\right)=P\left(Y^{(a)}=y|W=w\right)$$

Thus the conditional expectation of Y given A = a, W = w can be written as

$$\mathbb{E}\left(Y|A=a,W=w\right)=\mathbb{E}\left(Y^{(a)}|W=w\right)$$

and the parameter of interest, ATE, can be written as

$$\begin{array}{c}\begin{array}{c}{\Psi }_0=\mathbb{E}\left(Y^{(1)}\right)-\mathbb{E}\left(Y^{(0)}\right)\\ ={\mathbb{E}}_0\left({\mathbb{E}}_0\left(Y|A=1,W\right)\right)-{\mathbb{E}}_0\left({\mathbb{E}}_0\left(Y|A=0,W\right)\right)\end{array}\end{array}$$

Assumption 3. (Positivity)

$$0<g_0\left(W\right)<1$$

almost everywhere.

Assumption 3 is necessary for the identification. Otherwise, the model is not identifiable, as we can never observe one of the potential outcomes for the units with certain baseline covariates W.

2. Brief review of some common estimators

One of the well-studied estimators for the ATE in observational studies is the G-computation estimator (or outcome regression model), which estimates ${\overline{Q}}_0$ with ${\overline{Q}}_n$, and then estimates ATE by the following formula

$${\Psi }_n^{G-comp}=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left[{\overline{Q}}_n\left(A=1,W=W_i\right)-{\overline{Q}}_n\left(A=0,W=W_i\right)\right]}$$

As long as the aforementioned assumptions hold, and the conditional response model estimator ${\overline{Q}}_n$ for ${\overline{Q}}_0$ is consistent, the resulting estimator ${\Psi }_n^{G-comp}$ is also consistent.

Another widely used estimator is the Inverse Probability of Treatment Weighting (IPW) estimator. It only relies on the estimator g_n of g₀

$${\Psi }_n^{IPW}=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left[\frac{A_i{Y}_i}{g_n\left(W_i\right)}-\frac{\left(1-A_i\right)Y_i}{1-g_n\left(W_i\right)}\right]}$$

where g_n is usually fitted by a supervised model (e.g. logistic regression), which regresses A on the pre-treatment confounders W. Similar to G-computation, the IPW estimator is consistent as long as all of the aforementioned assumptions hold, and the estimated PS, g_n, is consistent. However, the IPW estimator can be highly unstable since extreme values of the estimated PS can lead to overly large and unstable weights for some units. This phenomenon is called the practical positivity violation. To overcome this issue, Hájek¹⁰ proposed a stabilized estimator

$${\Psi }_n^{Hajek-IPW}={\displaystyle \sum _{i=1}^n\left[\frac{A_i{Y}_i/g_n\left(W_i\right)}{{\displaystyle {\sum }_{i=1}^n{A}_i/g_n\left(W_i\right)}}-\frac{\left(1-A_i\right)Y_i/\left(1-g_n\left(W_i\right)\right)}{{\displaystyle {\sum }_{i=1}^n\left(1-A_i\right)/\left(1-g_n\left(W_i\right)\right)}}\right]}$$

where the denominator n is replaced by the weight normalization term A_ig_n(W_i) and (1 − Ai)(1 − g_n(Wi)). It is easy to show that this estimator is also consistent as long as g_n is a consistent estimator.

All of the estimators mentioned above are not robust in the sense that misspecification of the first stage modeling (of conditional outcome, or the PS) could lead to biased estimation for the causal parameter of interest. This is the reason why double robust (DR) estimators are preferable. DR estimators usually rely on the estimation of both ${\overline{Q}}_0$ and g₀. As long as one of them is estimated consistently, the resulting final estimator would be consistent. Weighted Regression (WR) is one of the commonly used DR-estimators^11,12 In comparison to G-computation, it estimates ${\overline{Q}}_0$ by minimizing the weighted empirical loss

$${\overline{Q}}_n^{WR}=\underset{\overline{Q}}{\arg \min }{\displaystyle \sum _{i=1}^n\left[{\omega }_i\left(g_n\right)L\left(\overline{Q}\left(A_i,W_i\right),Y_i\right)\right]}$$

where the weight is defined ω_i(g_n) = [A_i/g_n(W_i) + (1 − A_i)/(1 − g_n(W_i))], and L is the loss function. The estimator for the causal parameter is defined as

$${\Psi }_n^{WR}=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left[{\overline{Q}}_n^{WR}\left(A=1,W=W_i\right)-{\overline{Q}}_n^{WR}\left(A=0,W=W_i\right)\right]}$$

The WR estimator is also called the weighted least squares (WSL) estimator, if the loss function is the squared error L(x, y) = (x − y)².

Augmented IPW (A-IPW, or DR-IPW) is another DR-estimator which can be written as

$${\Psi }_n^{DR-IPW}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{H}_{g_n}\left(A_i,W_i\right)\left[Y_i-{\overline{Q}}_n\left(A_i,W_i\right)\right]}+{\overline{Q}}_n\left(1,W_i\right)-{\overline{Q}}_n\left(0,W_i\right)$$ (1)

where

$$H_{g_n}\left(A,W\right)=\frac{A}{g_n\left(W\right)}-\frac{1-A}{1-g_n\left(W\right)}$$

is designed based on the target parameter, ATE. ${\Psi }_n^{DR-IPW}$ also relies on both ${\overline{Q}}_n$ and g_n. It was first proposed by the authors in literature^13,14 where it was called the ‘‘bias-corrected estimator’’. It corrects the bias from the initial estimate, ${\overline{Q}}_n$, with the weighted residual from the initial fit. Robins et al.¹⁵ proposed a class of estimators which contains 1, and Robins and Rotnitzky¹⁶ further showed that 1 is a locally semiparametric efficient estimator.

Similar to the IPW estimator, A-IPW is also influenced by extreme weights, as it uses inverse probability weighting. However, a Hajek style stabilization could mitigate concerns of overly influential weights

$${\Psi }_n^{HBC-IPW}={\displaystyle \sum _{i=1}^n\left[\left(\frac{A/g_n(W)}{{\displaystyle {\sum }_{i=1}^{n}A/g_n\left(W\right)}}-\frac{\left(1-A\right)/\left(1-g_n\left(W\right)\right)}{{\displaystyle {\sum }_{i=1}^n\left(1-A\right)/\left(1-g_n\left(W\right)\right)}}\right)\left(Y_i-{\overline{Q}}_n\left(A_i,W_i\right)+\frac{1}{n}{\overline{Q}}_n\left(1,W_i\right)-\frac{1}{n}{\overline{Q}}_n\left(0,W_i\right)\right)\right]}$$ (2)

For simplicity, we will call the estimator in equation (2) the HBC (Hajek type bias-correction) estimator. Although this estimator no longer enjoys some attractive theoretical properties (e.g. efficiency) of A-IPW, it is still DR, and it can potentially improve finite sample performance. It is also possible that these modifications could improve the robustness of the estimated treatment effects when both of the models are misspecified.¹¹

3. Brief review of targeted minimum loss-based estimation

Targeted minimum loss-based estimation (TMLE) is a general template to estimate a user-specified parameter of interest, given a user-specified loss function, and fluctuation sub-model. In this study, we consider the ATE as our target parameter, the negative likelihood as the loss function, and the logistic fluctuation. Let Y represent a binary variable, or a continuous variable within the range (0, 1).^a The TMLE estimator for the ATE can be written as

$${\Psi }_n^{TMLE}=\frac{1}{n}{\displaystyle \sum _{i=1}^n\left({\overline{Q}}_n^{*}\left(1,W_i\right)-{\overline{Q}}_n^{*}\left(0,W_i\right)\right)}$$ (3)

In equation (3), ${\overline{Q}}_n^{*}$ (which is within the range (0, 1)) is updated from an initial estimate, Q_n, by a logistic fluctuation sub-model

$$\text{logit}\left({\overline{Q}}_n^{*}\left(A,W\right)\right)=\text{logit}\left({\overline{Q}}_n\left(A,W\right)\right)+ϵH_{g_n}\left(A,W\right)$$ (4)

The fluctuation parameter ϵ is estimated through maximum likelihood estimation, or equivalently, minimizing the negative log-likelihood loss

$$L(\in )={\displaystyle \sum _{i=1}^n{Y}_i({\overline{Q}}_n^{*}(A_i,W_i))+(1-Y_i)(1-{\overline{Q}}_n^{*}(A_i,W_i))}$$

If either the propensity model or outcome model is consistent, then the TMLE estimator is consistent. If both of them are consistent, then the TMLE estimator is also efficient. To consistently estimate ${\overline{Q}}_0$ and g₀, we suggest using Super Learner, a data-adaptive ensemble method, for prediction modeling.^17–22

In addition to double robustness and asymptotic efficiency, TMLE has the following advantages:

1. Equation (3) shows that TMLE is a plug-in estimator and, therefore, respects the global constraints of the model. For instance, suppose Y is binary. The ATE, therefore, should be between [−1, 1]. However, some competing estimators may produce estimates out of such bounds. Since TMLE maps the targeted estimate P* of P₀ into the mapping Ψ, it respects knowledge of the model.

2. The targeting step in TMLE is a minimum loss estimation,^b which offers a metric to evaluate the goodness-of-fit for g_n and ${\overline{Q}}_n$, w.r.t. the parameter of interest Ψ₀.

3. In the empirical/simulation studies by Porter et al.,²³ TMLE is more robust than IPW and A-IPW to positivity, or near positivity, violations, where g_n is too close to 0 or 1.

4. Brief review of collaborative TMLE

4.1. C-TMLE for variable selection

In the TMLE algorithm, the estimate of ${\overline{Q}}_0$ is updated by the fluctuation step, while the estimate of g₀ is estimated externally and then held fixed. One extension of TMLE is to find a way to estimate g₀ in a collaborative manner. Motivated by the second advantage of TMLE, collaborative TMLE was proposed to make this extension feasible.²⁴ Here we first briefly review the general template for C-TMLE:

1. Compute the initial estimate ${\overline{Q}}_n^0$ of ${\overline{Q}}_0$.

2. Compute a sequence of estimates g_n,_k and ${\overline{Q}}_{n,k}^{*}$ for g₀ and ${\overline{Q}}_0$ respectively, with k = 1,..., K. With k increasing, the empirical loss for both g_n,k and ${\overline{Q}}_{n,k}^{*}$ would decrease. In addition, we require g_n,K to be asymptotically consistent for g₀.

3. Build a sequence of TMLE candidate estimators, based on a given fluctuation model.

4. Use cross-validation for step 3 to select the ${\overline{Q}}_{n,k}^{*}$ that minimizes the cross-validated risk, and denote this TMLE estimator as the C-TMLE estimator.

This is a high-level template for the general C-TMLE algorithm. There are many variations of instantiations of this template. For example, the greedy C-TMLE was proposed by the authors in literature^24,25 for variable selection in a discrete setting. The following are some details of greedy C-TMLE:

• In step 2, the greedy C-TMLE algorithm starts from an intercept model (which fits the PS with its mean), and then builds the sequence of g_n,k by using a forward selection algorithm: during each iteration k, for each of the remaining covariates W_j, that have not been selected yet, we add it into the previous PS model g_n,_k−1, which yields a larger PS model $g_{n,k}^j$ and $H_{g_{n,k}^j}$. We then compute ${\overline{Q}}_{n,k}^{*,j}$ by equation (4). For all j, we select the PS model that corresponds to the ${\overline{Q}}_{n,k}^{*,j}$ with the smallest empirical loss. For simplicity we call this the forward selection step at the k-th iteration.

• For the initial estimate in equation (4), we start with ${\overline{Q}}_{n,1}={\overline{Q}}_n$. For each iteration k, we first try ${\overline{Q}}_{n,k}={\overline{Q}}_{n,k-1}$. If all of the possible ${\overline{Q}}_{n,k}^{*,j}$ mentioned above do not improve the empirical fit compared to ${\overline{Q}}_{n,k-1}$, we update ${\overline{Q}}_{n,k}={\overline{Q}}_{n,k-1}^{*}$ and rerun the forward selection step at the k-th iteration. Notice that as we use the last TMLE estimator as the candidate, all of the current candidate ${\overline{Q}}_{n,k}^{*,j}$ are guaranteed to have a better empirical fit compared to their initial estimate ${\overline{Q}}_{n,k}$. Otherwise if there is at least one candidate that improves the empirical fit, we just move to the next forward selection step. In this manner, we make sure that the empirical loss for each candidate ${\overline{Q}}_{n,k}^{*}$ is monotonically decreasing.

Ju et al.²⁶ also proposed scalable versions of the discrete C-TMLE algorithm as new instantiations of the C-TMLE template. These scalable C-TMLE algorithms avoid the forward selection step by enforcing a user-specified ordering of the covariates. Ju et al.²⁶ showed that these scalable C-TMLE algorithms have all of the asymptotic theoretical properties of the greedy C-TMLE algorithm, but with much lower time complexity.

4.2. C-TMLE for model selection of LASSO

To the best of our knowledge, C-TMLE has primarily been applied for variable selection. However, it can easily be adapted to more general model selection problems. In our recent work,^5,6 two instantiations of the C-TMLE algorithm were proposed for a general model selection problem with a one-dimensional hyper-parameter. In this study, we consider an example where the PS model is estimated by LASSO

$$\begin{array}{c}{\beta }_{n,\lambda }=\underset{\beta \in {ℝ}^p}{\min }\left(\frac{1}{n}{\displaystyle \sum _{i=1}^{n}L\left(A_i,\text{logit}\left(\beta W_i\right)\right)+\lambda {\Vert \beta \Vert }_1}\right)\\ g_{n,\lambda }\left(W_i\right)=\text{logit}\left({\beta }_{n,\lambda }{W}_i\right)\end{array}$$

where L is the negative log-likelihood for the Bernoulli distribution, as A is binary. We used C-TMLE to select the PS estimator, g_n,λ, with the best penalty parameter λ. We applied two C-TMLE algorithms for model selection of LASSO. Here, we provide a brief outline for each of the algorithms. Details are provided in the supplemental appendices.

• C-TMLE1: First, we briefly introduce the C-TMLE1 algorithm. According to the C-TMLE template outlined above, C-TMLE1 first builds an initial estimate for ${\overline{Q}}_n$ and a sequence of propensity score estimators, $g_{n,{\lambda }_k}$, for k ∈ 0,..., K, each with a penalty λ_k, where λ_k is monotonically decreasing. We recommend to set λ₁ = λ_CV because the cross-validation usually selects an ‘‘under-fitted’’ (e.g. a LASSO estimator with a regularization parameter, λ, that is too large) PS estimator; thus, it is unnecessary to consider λ₁ > λ_CV. Then, we just follow step 3 in the template described previously, and build a sequence of estimators, ${\overline{Q}}_{n,\lambda }^{*}$, each corresponding to g_n,_λ. We then select the best ${\overline{Q}}_{n,{\lambda }_{ctmle}}^{*}$ by using cross-validation, with its corresponding initial estimate ${\overline{Q}}_{n,{\lambda }_{ctmle}}$. Finally we fluctuate the selected initial estimate ${\overline{Q}}_{n,{\lambda }_{ctmle}}$ with each g_n,λ for λ_K < λ < λ_ctmle, yielding a new sequence ${\overline{Q}}_{n,\lambda }^{*}$. We choose ${\overline{Q}}_n^{*}={\overline{Q}}_{n,\lambda }^{*}$, which minimizes the empirical loss, as our final estimate. The final step guarantees that a critical equation

  $$\begin{array}{l}{P}_n{D}^{+}\left({\overline{Q}}_{n,\lambda }^{*},g_{n,\lambda }\right)\\ =\frac{\partial }{\partial \lambda }{\displaystyle \sum _{i=1}^n{H}_{g_{n,\lambda }}}\left(A_i,W_i\right)\left(Y_i-{\overline{Q}}_{n,\lambda }^{*}\left(A_i,Y_i\right)\right)=0\end{array}$$ (5)

  is solved.^5,6 This guarantees that the resulting C-TMLE estimator is asymptotically linear under regularity conditions even when ${\overline{Q}}_n$ is not consistent. A detailed description of C-TMLE1 is provided in Appendix 1.
• C-TMLE0: the C-TMLE0 algorithm does not select the PS estimator collaboratively. Instead, it is exactly the same as the TMLE algorithm, except it updates the estimate by equation (6)

  $$\text{logit}\left({\overline{Q}}_n^{*}\left(A,W\right)\right)=\text{logit}\left({\overline{Q}}_n\left(A,W\right)\right)+{ϵ}_1{H}_{g_{n,{\lambda }_k}}\left(A,W\right)$$ (6)

  where

  $$\begin{array}{c}{\tilde{H}}_{g_{n,\lambda }{}_{{}_k}}\left(A,W\right)=\frac{\partial H_{g_{n,\lambda }}\left(A,W\right)}{\partial \lambda }{|}_{\lambda ={\lambda }_k}\\ =\frac{1-A}{{\left(1-g_{n,{\lambda }_k}\left(W\right)\right)}^2}\frac{\partial \left(1-g_{n,\lambda }\right)}{\partial \lambda }{|}_{\lambda ={\lambda }_k}+\frac{A}{g_{n,\lambda }{\left(W\right)}^2}\frac{\partial g_{n,{\lambda }_k}}{\partial \lambda }{|}_{\lambda ={\lambda }_k}\end{array}$$

  Note we still call it C-TMLE as it solves the critical equation (6). Solving the additional clever covariate ${\tilde{H}}_{g_{n,\lambda }{}_{{}_k}}$ could be considered as an approximation of the collaborative selection in C-TMLE1.^5,6 More details of C-TMLE0 can be found in Appendix.

  Same as the discrete C-TMLE estimator in Gruber and van der Laan,²⁵ standard errors for both of the new C-TMLEs are computed based on the variance of the influence curve (IC). With the point estimate, $\widehat{\psi }$, and its estimated standard error, $\widehat{se}$, we construct the Wald-type α-level confidence interval: $\left[\widehat{\psi }-z_{1-\alpha /2}\widehat{se},\widehat{\psi }+z_{1-\alpha /2}\widehat{se}\right]$, where z_a is the α-percentile of the standard normal distribution. More details of IC and the IC based variance estimator can be found in the literature.^25,27

  The code for LASSO-C-TMLE algorithms (C-TMLE1 and C-TMLE0) can be found on the Comprehensive R Archive Network.²⁸

5. Data source

In previous work by Ju et al.,²⁰ Super Learner was applied to three electronic healthcare data sets for propensity score estimation. In two of the data sets (NOAC study and Vytorin study), the PS model showed strong nonlinearity patterns, where non-linear algorithms (gbm) outperformed main term LASSO (w.r.t. the predictive performance of the estimated PS) with the same covariate set. Thus the main term linear model may result in strong model misspecification for such a dataset. To better demonstrate C-TMLE for LASSO selection under mild model misspecification, we only considered the NSAID dataset, where the treatment mechanism could be estimated satisfactorily with main term linear models. Note that the methodology can be easily extended to highly non-linear data by adding more basis functions (e.g. high order interaction terms) in LASSO, or replacing vanilla LASSO with Highly Adaptive LASSO (HAL).²⁹ This data set was first created by Brookhart et al.³⁰ and further studied by the authors in literature.^31,32

5.1. Nonsteroidal anti-inflammatory drugs study

In this study, the observations were sampled from a population of patients aged 65 years and older who were enrolled in both Medicare and the Pennsylvania Pharmaceutical Assistance Contract for the Elderly (PACE) programs between 1995 and 2002. The treatment is a binary indicator taking on values of 1 for patients who received a selective COX-2 inhibitor and 0 for patients who received a non-selective nonsteroidal antiinflammatory drug. The outcome is also a binary indicator taking on values of 1 for patients who are diagnosed with gastrointestinal (GI) complications during the follow-up periods, and 0 otherwise.

To adjust for potential confounders, some predefined baseline pre-treatment covariates were collected (e.g. age, gender, race). To further adjust for confounding we implemented a widely used variable selection algorithm for healthcare claims databases, known as the high-dimensional propensity score (hdPS) (discussed further below).³¹ The dataset for this study included 9470 claims codes, which were clustered into eight categories, including ambulatory diagnoses, ambulatory procedures, hospital diagnoses, hospital procedures, nursing home diagnoses, physician diagnoses, physician procedures and prescription drugs. The value for each claims code denotes the number of times the respective patient received the healthcare procedure corresponding to the code during a 12-month baseline period prior to treatment initiation. Thus all of the claims data are non-negative integers. Table 1 shows some summary statistics for the NSAID study databases.

Table 1.

Brief summary of the NSAID study databases.

Sample size	49,653
No. of baseline covariates	22
No. of code resource	8
No. of claims code	9470

5.2. The high-dimensional propensity score (hdPS) to learn from health insurance data

Claims data are usually high-dimensional (p_c = 9470 in this study) due to large amounts of healthcare diagnoses and procedures. Further, claims data are often highly sparse as each patient often receives only a few diagnoses. To address these issues, the hdPS variable selection algorithm was introduced by Schneeweiss et al.³¹ to generate hundreds of baseline variables from claims codes, and then rank them by their potential confounding impact. Its core part is outlined in the following steps:

1. Cluster the codes according to their source^c: this is determined manually based on the origin and quality of data feeds and is unique to the database being used. In this study, the codes come from eight sources.

2. Identify candidate codes in each cluster: for each code count c, compute its empirical prevalence $p_{n,c}={\mathbb{E}}_{n}I\left(c>0\right)$, rank all covariates by max(p_n,c, 1 − p_n,_c), and select the top k₁ codes within each cluster. In the NSAID study, we have 8k₁ claims covariates left after this step.

3. Generate hdPS covariates: For each claims covariates, c_i, for each individual, i, construct three indicator variables where: $c_i^{\left(1\right)}$ is equal to one if and only if (iff) c_i is positive, $c_i^{\left(2\right)}$ is equal to one iff c_i is larger than the median of { c_i : 1 ≤ i < n}, and $c_i^{\left(3\right)}$ is equal to one iff c_i is larger than the 75%-quantile of { c_i : 1 ≤ i < n}. We denote these new covariates as ‘‘hdPS covariates”. For the empirical example in this study, this step results in 24k₁ generated hdPS covariates.

4. Select hdPS covariates for confounding adjustment: Use the Bross formula^31,33 to rank each hdPS covariate, c, by its potential for confounding bias:

   $$\text{Bias}\left(c\right)=\frac{{\mathbb{E}}_n\left(c=1|A=1\right)\left(r{r}_n\left(c\right)-1\right)+1}{{\mathbb{E}}_n\left(c=1|A=0\right)\left(r{r}_n\left(c\right)-1\right)+1}$$

with

$$r{r}_n\left(c\right)=\frac{{\mathbb{E}}_n\left(Y=1|c=1\right)}{{\mathbb{E}}_n\left(Y=1|c=0\right)}$$

where ${\mathbb{E}}_n$ denotes the empirical distribution of data.

Covariates are then ranked by descending order of log(Bias(c))|. We then select the first k₂ ordered hdPS covariates among the total 24k₁ hdPS (generated) covariates from step 3.

The hdPS algorithm has been used in studies evaluating the effectiveness of prescription drugs and medical procedures using healthcare claims data in the USA,^34–37 Canada,^38–40 Europe,^41–43 and electronic health records.^44,45 Schneeweiss et al.⁴⁶ evaluated a range of algorithms to improve covariate ranking based on the empirical covariate outcome relationship without any meaningful improvement over the ranking using the Bross formula. Ju et al.²⁰ evaluated various choices for the parameters k₁ and k₂ within the hdPS algorithm, and found that the performance of the hdPS was not sensitive to choices for k₁ and k₂ as long as the hyperparameter pair were within a reasonable range. For this study, we let k₁ = 100 and k₂ = 200. For simplicity, we denote the combined set of predefined baseline covariates and selected hdPS covariates as W.

6. Quasi-experiment

6.1. Simulation setting

In this simulation, we generated partially synthetic data based on the NSAID data set. We designed our own conditional distribution of the outcome, Y, given treatment, A, and baseline covariates, W, while keeping the structure of the treatment mechanism g₀(A|W) so that the relationships between covariates with treatment assignment were preserved.⁴⁷ In our study, the conditional distribution of the outcome was defined as

$$Y_i=2+\beta W_i+A_i+{ϵ}_i$$ (7)

Where ϵ_i is drawn independently from the standard normal distribution. We then selected 40 covariates that had the highest Pearson correlation with treatment A. The coefficient of β in equation (7) was set to zero for all the non-selected covariates. The coefficient for the selected covariates was sampled from separate and independent standard normal distributions and were fixed across all simulations. We define the marginal distribution of W as the empirical distribution of W_i for i ∈ 1... n. The parameter of interest is the ATE, thus it is identifiable if we know the distribution of the conditional response Y| A, W and marginal distribution of W.

In our simulation, we considered two settings. In the first setting, only the first 10 out of 40 confounders were used to estimate ${\overline{Q}}_0$. In the second setting, ${\overline{Q}}_0$ was estimated using the first 20 out of 40 confounders.

By the description above, we have the following:

• There are only 40 confounders in total.

• The true value of the parameter of interest (ATE) is 1.

• The treatment mechanism g₀(A| W) comes from a real world data generating distribution, which is usually non-linear. Ju et al.²⁰ showed that the PS in this example can be estimated well by linear models. Therefore, in this example the PS model is only mildly misspecified.

• Both ${\overline{Q}}_0$ and g₀ are estimated with a misspecified model: ${\overline{Q}}_0$ is estimated with an incomplete predictor set; g₀ is estimated with linear model, while there is no reason to believe it is truly linear.

The results are computed across 500 replications, each with sample sizes of 1000.

6.2. Competing estimators

In this study, we focused on PS-based estimators, including inverse probability of treatment weight (IPW) estimator, Hajek type IPW estimator, double robust (augmented) inverse probability of treatment weight (DR-IPW, or A-IPW) estimator, Hajek type Bias-correction (HBC) Estimator, weighted regression (WR) estimator, targeted maximum likelihood estimator (TMLE), and the proposed two collaborative-TMLE estimators.

For all PS-based estimators, we consider two variations. For the first variation, we first used the cross-validated LASSO (CV-LASSO) algorithm to find the regularization parameter λ_CV of LASSO for PS estimation, and then plugged it into the final estimators. In the second variation, we first applied C-TMLE1, and use LASSO with the regularization parameter λ_C–TMLE selected by C-TMLE1 to estimate the PS, and then plug it into the estimator. Taking IPW as example, we used ‘‘IPW’’ to denote the first variation, and ‘‘IPW*’’ for the second variation.

It is important to note that in this case, ‘‘TMLE*’’ is actually a variation of collaborative TMLE, as the PS model is selected collaboratively.^24,25 However, it is different from the proposed C-TMLE algorithms, as it does not solve the critical equation (5).

It is also important to note that both C-TMLE and CV-LASSO use cross-validation. For simplicity, and to avoid ambiguity, we use the term ‘‘CV’’ to denote the non-collaborative model selection procedure which relies on the cross-validation w.r.t. the prediction performance for the treatment mechanism itself (e.g. the model selection step in CV-LASSO).

In addition, we also compute an ‘‘oracle estimator’’ for comparison, which is given by a TMLE estimator with the PS estimated by a logistic regression with only confounders.

6.3. Point estimation

We first compared the variance, bias, and mean square error (MSE) for the point estimation from all the competing estimators in two settings.

Table 2 and figure 1 show the point estimation performance of all the competing estimators. It is not surprising that the oracle TMLE estimator has the best performance for both bias and variance. However, it is not achievable in practice as it is usually unknown which covariates are confounders. IPW has very large variance and bias, which might due to the practical violations of the positivity assumption. We can see that TMLE*, C-TMLE1, CTMLE0, and CTMLE0* outperformed other estimators, with each having similar performance. In addition, C-TMLE0* did not show any improvement compared to C-TMLE0. This is consistent with previous results.^5,6

Table 2.

Performance of Point Estimation for Estimators when the initial estimate ${\overline{Q}}_n$ of ${\overline{Q}}_0$ is estimated on 10 and 20 out of 40 confounders.

Initial Fit		unadj	G-comp	WR	WR*	Hajek-BC	Hajek-BC*
10/40	Bias	−59.29	−9.69	−5.68	−3.11	−15.54	−12.29
	SE	8.43	3.36	2.66	2.75	5.80	6.63
	MSE	35.87	1.05	0.39	0.17	2.75	1.95
20/40	Bias	−59.91	−4.72	−2.77	−2.12	−7.56	−5.47
	SE	8.36	2.73	2.27	1.92	4.10	4.54
	MSE	36.59	0.30	0.13	0.08	0.74	0.51
Initial Fit		IPW	IPW*	Hajek-IPW	Hajek-IPW*	DR-IPW	DR-IPW*
	SE	36.55	91.38	4.85	8.21	2.63	3.02
	MSE	104.40	249.69	6.92	2.53	0.44	0.19
20/40	Bias	97.11	125.85	−25.60	−13.70	−2.92	−1.95
	SE	35.98	90.85	4.77	8.56	2.26	2.17
	MSE	107.23	240.75	6.78	2.61	0.14	0.09
Initial Fit		TMLE	TMLE*	CTMLE1	CTMLE0	CTMLE0*	orcale
10/40	Bias	−5.49	−1.23	−1.40	0.70	−0.64	0.36
	SE	2.57	3.46	3.56	3.38	4.40	1.83
	MSE	0.37	0.13	0.15	0.12	0.20	0.03
20/40	Bias	−2.68	−1.28	−1.38	0.08	−0.95	0.04
	SE	2.19	2.53	2.53	2.85	3.07	1.35
	MSE	0.12	0.08	0.08	0.08	0.10	0.02

Note: The results are computed based on simulations across 500 replications, each with a sample size of 1000 based on the NSAID study. All of the numeric values are on a scale of 10⁻².

Figure 1.

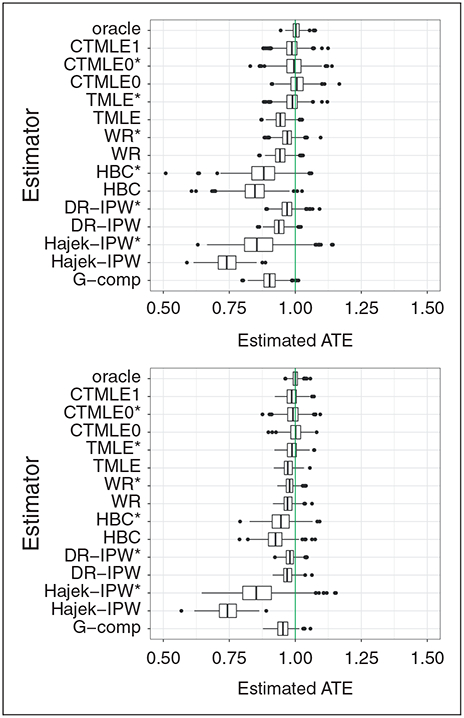
Boxplot of the estimated ATE for each estimator across 500 replications, when the initial estimate is fit on 10/20 out of 40 confounders.

We also evaluated the relative performance of other PS-based estimators with g_n selected by C-TMLE, compared with g_n selected by CV. For IPW, the performance was still poor. However, for all of the other estimators that rely on the estimated PS, the performance improved considerably. Taking the first setting as an example, the relative empirical efficiency of DR-IPW* compared to DR-IPW was $\frac{\text{MSE}\left(\text{DR}-\text{IPW}\right)}{\text{MSE}\left(\text{DR}-\text{IPW}*\right)}=1.52$, while for TMLE it was $\frac{\text{MSE}\left(\text{TMLE}\right)}{\text{MSE}\left(\text{TMLE}*\right)}=1.66$. The relative empirical efficiency for both of these estimators is improved with a reduction in bias and slight increase in variance. These empirical results are consistent with previous theory^5,6 showing that the model selected by external CV is usually under-fitted. These results illustrate the weakness of using ‘‘external’’ CV for PS model selection.

6.4. Confidence interval

In this section, we evaluate the coverage and the length of the confidence intervals (CIs) for all the double robust estimators.

Table 3 shows that the CIs of the oracle TMLE estimator are too conservative, as they achieved 100% coverage. In both settings, TMLE* and C-TMLE1 had the best coverage. We can see that for other estimators, the length of the CIs were usually smaller/under-estimated. This resulted in a less satisfactory coverage even though the point estimation had similar performance (e.g. compare C-TMLE0 to C-TMLE1). With collaboratively selected g_n, the coverage of TMLE and DR-IPW improved significantly. These empirical results illustrate that a more targeted propensity score model selection can improve both causal estimation and inference.

Table 3.

Coverage of the 95% confidence intervals for semi-parametric efficient estimators when the initial estimate ${\overline{Q}}_n$ of ${\overline{Q}}_0$ is estimated on 10 and 20 out of 40 confounders.

		CTMLE1	CTMLE0	CTMLE0*	DR-IPW	DR-IPW*	TMLE	TMLE*	oracle
10/40	Coverage	0.926	0.920	0.910	0.458	0.914	0.526	0.942	1.000
	Average Length	0.142	0.115	0.142	0.120	0.159	0.119	0.144	0.153
20/40	Coverage	0.934	0.872	0.898	0.748	0.928	0.790	0.946	1.000
	Average Length	0.105	0.087	0.103	0.088	0.112	0.087	0.106	0.111

Note: The results are computed across 500 replications, each with sample sizes of 1000 based on the NSAID study. All of the numerical values are multiplied by 100.

6.5. Variable selection from LASSO

Table 4 shows the average number of covariates selected by LASSO, with λ determined by CV and C-TMLE1. Recall that there are 222 covariates in total (22 baseline covaraites and 200 covariates generated by the hdPS algorithm), including 40 confounders. CV was too conservative: on average it only selected 36.6 covariates, and only included 13.2 confounders. C-TMLE1 selected much less regularization, which leads to a larger model: it successfully picked up more confounders than CV in both experiments.

Table 4.

Average number of covariates selected from CV and C-TMLE.

Initial Fit	CV	C-TMLE1
10/40	36.6 (13.2)	149.1 (35.1)
20/40	36.6 (13.2)	148.9 (31.4)

Note: The number in the parentheses is the average number of selected confounders among the selected covariates.

6.6. Pairwise comparison of efficient estimators

In this section, we studied the pairwise comparisons for several pairs of the efficient estimators, TMLE, C-TMLE, and DR-IPW, with different PS estimators. The purpose of these pairwise comparisons is to help in understanding the contribution of the collaborative estimation of the PS. We used the shape and color of the points to represent the coverage information of the CIs for each estimates.

6.6.1. Impact of collaborative propensity score model selection

We first compared the two pairs. Within the pair, both of the estimators were identical except each had a different PS estimator. The first pair compared TMLE to TMLE*, and the second pair compared C-TMLE0 to CTMLE0*.

From Figure 2(a) and (b), we can see that a more targeted PS model contributes substantially to the estimation. The vanilla TMLE underestimated the ATE, while TMLE* is close to unbiased. The variance of the two estimators is similar.

Figure 2.

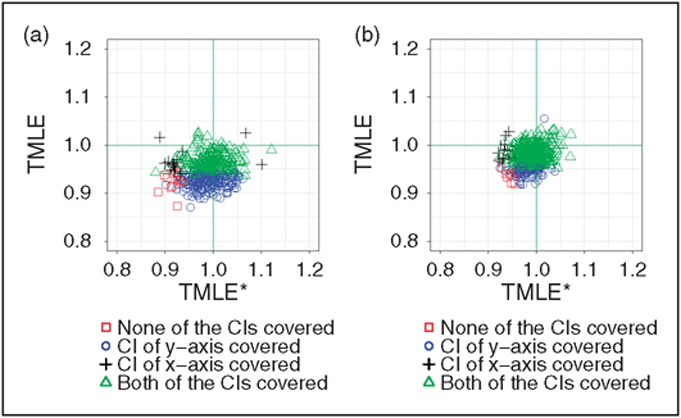
Comparison of TMLE wand TMLE*. The only difference within the pair the how the estimator g_n is selected. (a) Comparison of TMLE and TMLE*, with the initial estimate $Q_n^0$ adjusting for 10 out of 40 confounders. (b) Comparison of TMLE and TMLE*, with the initial estimate $Q_n^0$ adjusting for 20 out of 40 confounders.

From Figure 3(a) and (b) we can see that the improvement for the CTMLE0 pair is not as significant as the improvement for the TMLE pair. Interestingly, most of the poor performance in the CIs for CTMLE0 is from the over-estimated point estimate, while for CTMLE0* is mainly from under-estimation of the point estimate.

Figure 3.

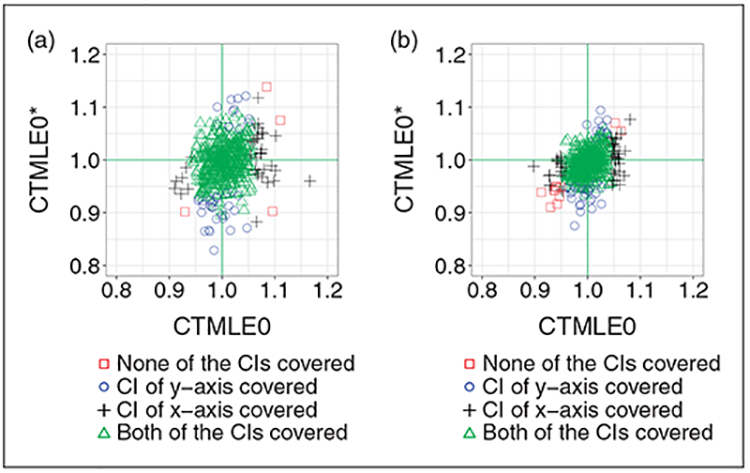
Comparison of CTMLE0 and CTMLE0*. The only difference within the pair the how the estimator g_n is selected. (a) Comparison of C-TMLE0 and C-TMLE0*, with the initial estimate $Q_n^0$ adjusting for 10 out of 40 confounders. (b) Comparison of C-TMLE0 and C-TMLE0*, with the initial estimate $Q_n^0$ adjusting for 20 out of 40 confounders.

As discussed in literature,^5,6 such ignorable improvement with collaboratively selecting g_n for the CTMLE0 pair might be due to the redundant collaborative estimation step. Thus, it is not necessary to both select the PS model using C-TMLE and solve for the extra clever covariate.

6.6.2. Contribution of solving extra critical equation

We compared TMLE with C-TMLE0. The only difference between these two estimators is that C-TMLE0 solves for the extra clever covariate, which guarantees that the critical equation is solved.

Figure 4 shows the improvement of solving an additional clever covariate. C-TMLE0 is less biased compared with TMLE. It is interesting to see that the performance of the estimator can improve substantially with such small change. In addition, this additional change almost requires no additional computation, which makes it more favorable among proposed C-TMLEs when the computation resources are limited.

Figure 4.

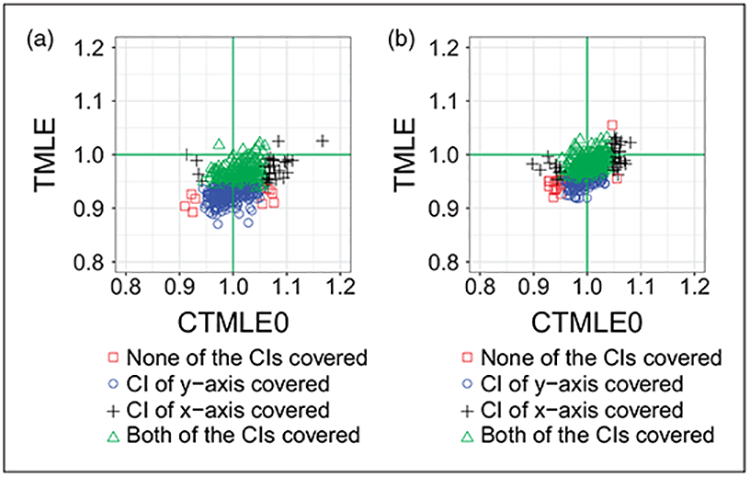
We compared TMLE with C-TMLE0, where the only difference between the two estimators is that C-TMLE0 solves the extra critical equation with additional clever covariates. (a) Comparison of TMLE and C-TMLE0, with the initial estimate $Q_n^0$ adjusting for 10 out of 40 confounders. (b) Comparison of TMLE and C-TMLE0, with the initial estimate $Q_n^0$ adjusting for 20 out of 40 confounders.

6.6.3. Comparison of variations of C-TMLE

We compared the two pairs of variations of C-TMLEs. We used C-TMLE1 as the benchmark, as it gave the best performance for both point estimation and confidence interval coverage.

Figure 5(a) and (b) shows the pairwise performance of C-TMLE1 and C-TMLE0. Both estimators performed well with respect to the MSE. Although the distribution of points looks similar and have variances that appear similar, there were more CIs from C-TMLE0 that failed to cover the truth. In addition, the failures from C-TMLE1 mainly resulted from the under-estimation of the estimates. In comparison, the failures from C-TMLE0 primarily came from both under/over-estimated estimates. This suggests that the relatively poor CI coverage of C-TMLE0 might be due to its under-estimated standard error.

Figure 5.

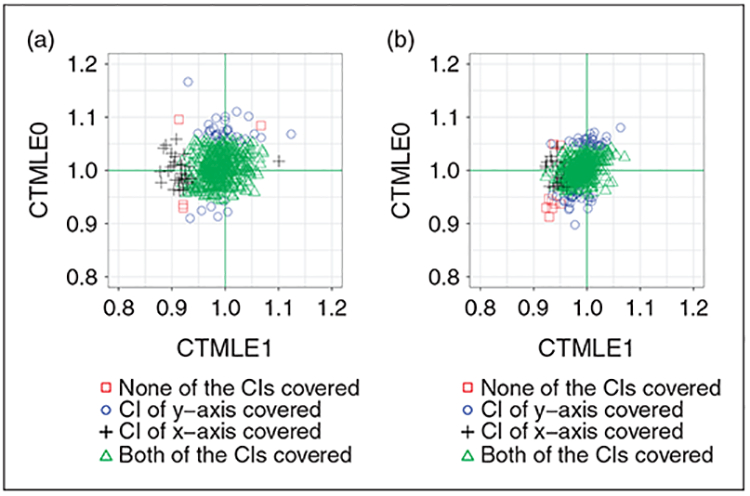
We compared C-TMLEI with C-TMLE0. (a) Comparison of C-TMLEI and C-TMLE0, with the initial estimate $Q_n^0$ adjusting for 10 out of 40 confounders. (b) Comparison of C-TMLE1 and C-TMLE0, with the initial estimate $Q_n^0$ adjusting for 20 out of 40 confounders.

7. Real data analysis

In this section, we applied the methods described previously to the NSAID study. As discussed previously, the goal of this study is to compare the effectiveness of two treatments on improving the risk (probability) of being diagnosed with severe gastrointestinal complications during the follow-up period. The treatment group was prescribed a selective COX-2 inhibitor, while the control group was prescribed a non-selective nonsteroidal anti-inflammatory drug. To compare the safety of the two treatments, we used the average treatment effect (ATE) as our target parameter.

7.1. Method

We followed the hdPS procedure in section 5.2, where we generated the hdPS covariates with k₁ = 100 and k₂ = 200.

We investigated three kinds of initial estimate ${\overline{Q}}_n^0$ for TMLE and C-TMLE:

• The initial estimate was given by the group means of the treatment and control group.

• The initial estimate was estimated by Super Learner with only baseline covariates.

• The initial estimate was estimated by Super Learner with both baseline covariates and hdPS covariates.

For Super Learners,^17,18 we used library with LASSO,⁴⁸ Gradient Boosting Machine,⁴⁹ and Extreme Gradient Boosting.⁵⁰

7.2. Results

Figure 6 shows the point estimates and 95% CIs for all TMLE and C-TMLE estimators. We use the blue line to denote the null hypothesis (H₀ : Ψ₀ = 0), the green line denotes the initial estimate, and use red line to denote the results from the naive difference in means estimator (${\Psi }_n^{\text{native}}=0.0949\%$).

Figure 6.

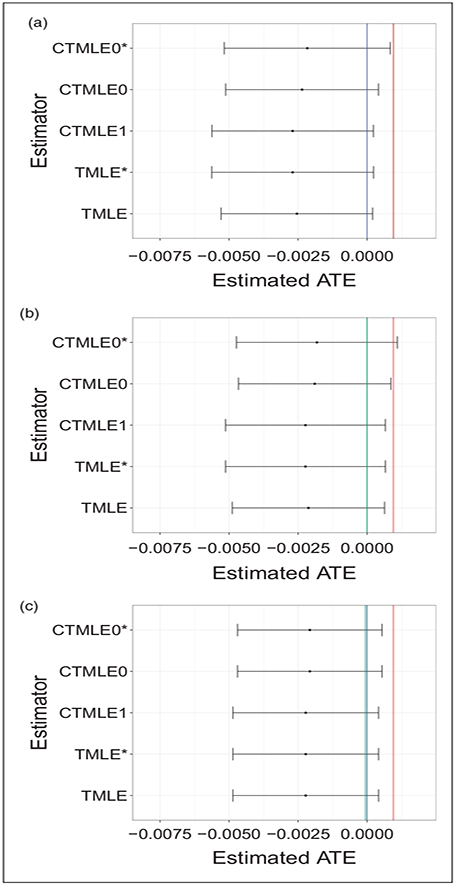
Confidence intervals for TMLE based estimators for the NSAID study. (a) Influence curve based confidence interval for all TMLE based estimators for NSAID study, with the group means as initial estimate. (b) Influence curve based confidence interval for all TMLE based estimators for NSAID study, with initial estimate provided by Super Learner with baseline covariates. (c) Influence curve based confidence interval for all TMLE based estimators for NSAID study, with the initial estimate provided by Super Learner with baseline covariates and hdPS covariates.

Figure 6(c) shows that, after adjusting for selection bias using the TMLE/C-TMLE algorithms, all the estimators have similar results, with the estimated ATE being in the negative direction. Similar to the results in simulation, the CIs for TMLE* and C-TMLE0* were wider with PS estimator selected by C-TMLE1, than with PS estimator selected by CV. The details of the point estimates and confidence intervals are reported in Table 5. We computed the analytic influence curve-based confidence interval. None of these intervals, except C-TMLE0*, covered the naive estimate. However, all of them covered the null hypothesis.

Table 5.

The point estimates and confidence intervals for all TMLE/C-TMLE estimators.

names	TMLE	TMLE*	CTMLE1	CTMLE0	CTMLE0*
Point Estimate	−0.2381	−0.2491	−0.2491	−0.2208	−0.2093
Analytic SE	0.1414	0.1487	0.1486	0.1417	0.1502

Note: All the values are on a scale of 10⁻².

In addition, we also compared the results from different initial estimator. Figure 6 shows the results for all estimators, with group means (6a), Super Learner with baseline covariates (6b), and Super Learner with both baseline and hdPS covariates (6c). The CV.LASSO PS estimator selected 137 covariates, with regularization parameter λ = 0.001159. The C-TMLE estimator with naive initial estimate selected 164 covariates, with λ = 0.000266. The C-TMLE estimator uses the initial estimate provided by SL with only baseline covariate have similar results: it selected 166 covariates with λ = 0.000238. For the C-TMLE with initial estimate provided by SL with all covariates, it selected the same model as CV.LASSO. It shows when the initial estimate is biased, C-TMLE selected model with less regularization, thus adjusted more potential confounders. In addition, all the covariates that are selected by LASSO-C-TMLE but not by C-TMLE but not by CV.LASSO are hdPS covariates. This suggests such additional hdPS covariates can be confounder. However, as they have relatively weaker predictive performance for treatment mechanism, they would be mistakenly removed by CV.LASSO.

Figure 7 shows the details of the CV loss for each selected PS estimator. The blue line is the λ selected by C-TMLE1 with naive estimator. Its CV binomial deviance (twice the binomial negative log-likelihood) is 1.199632. The purple line is the λ selected by C-TMLE1 with initial estimator provided by SL with only baseline covariates. Its CV binomial deviance is 1.199668. The red line is the λ selected by CV.LASSO, and C-TMLE1 with initial estimator provided by SL with both baseline and hdPS covariates. Its CV binomial deviance is 1.199288.

Figure 7.

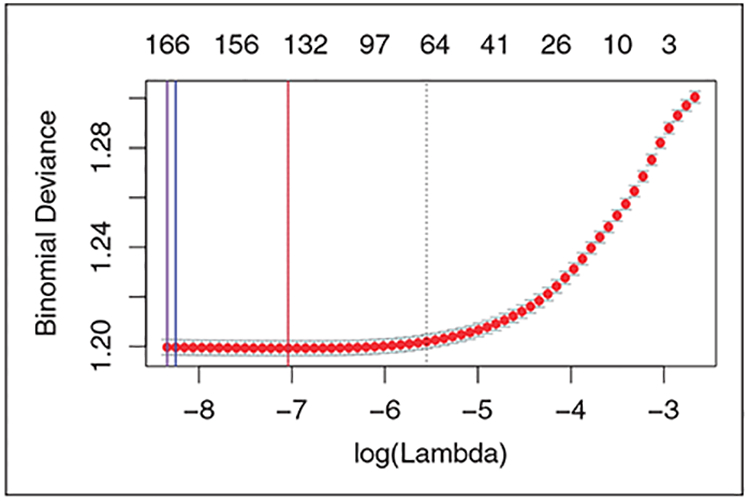
Binomial deviance for λ selected by CV.LASSO and C-TMLE with different initial estimators.

The estimates and confidence intervals were similar even with different initial estimators. This may be due to the signals in all the initial estimates are too weak: all the initial estimates of ATE are very close to 0. In addition, all the confidence intervals covered null hypothesis. The additive treatment effect in this study is not statistically significant.

7.3. Conclusions from the empirical study

Patients who received selective COX-2 inhibitors were less likely to get severe gastrointestinal complications during the follow-up period, compared to the patients who received a non-selective nonsteroidal anti-inflammatory drug. The average additive treatment effect was approximately −0.249%, which was estimated using TMLE* and C-TMLE1 (the two estimators achieved the best performance in simulations). The point estimates for other estimators were similar.

Based on the results, the additive treatment effect was not statistically significant. However, this does not necessary imply that there is no difference between the two treatments. More observations or better designed studies are necessary for further comparison of these treatments.

8. Conclusion

In this study, we described two variations of C-TMLE, and assessed their performance on quasi-experiments based on real empirical data. We assessed the performance of several well-studied PS-based estimators in settings where estimated models for both the conditional response $\mathbb{E}\left(Y|A,W\right)$ and the propensity score $\mathbb{E}\left(A,W\right)$ were misspecified. In particular, we focused on using the LASSO estimator for the PS model. In comparison to our previous work, this study provides a more detailed evaluation of all the estimators by not only assessing their point estimation, but also the confidence intervals for each of the estimators. Results showed that the C-TMLE1 and C-TMLE0 estimators had the best performance in terms of both point estimation and CI. We also evaluated the impact of directly applying the model that was collaboratively selected by C-TMLE1 to other PS non-collaborative estimators. Results showed that all of the PS-based estimators, except the vanilla IPW estimator, improved substantially, in terms of the point estimation, when the collaboratively selected model was applied to these estimators. However, C-TMLE0* did not improve when compared to C-TMLE0 for point estimation. Finally, pairwise comparisons of estimators were also evaluated to help in understanding the contribution of the collaborative model selection.

In comparison to previous work, this study is the first to thoroughly investigate and compare the confidence intervals coverage and length for the novel C-TMLE algorithms, as well as some commonly used competitors. Further, it offers detailed pair-wise comparisons with other competing estimators using different PS model selection procedures. Finally, this study utilizes the quasi-experiments based on a real electronic healthcare dataset and then makes inference on the same database. This makes the conclusions from the real data analysis more convincing.

In conclusion, this study introduces a new direction for PS model selection. It shows the insufficiency of using “external” cross-validation for the LASSO estimator. Thus, we conclude that the ensemble PS estimators, which rely on “external” cross-validation, are not optimal (w.r.t. the causal parameter) for maximizing confounding control. Ensemble learning that is based on C-TMLE is a potential solution to address this issue. We leave this for the future work.

Appendix 1

A C-TMLE 1

C-TMLE1 is a straightforward instantiation of the general C-TMLE template, which generates a sequence of PS estimators, with corresponding TMLE estimators. Then it selects the TMLE estimator with the smallest crossvalidated loss w.r.t. the causal parameter. Finally it takes one more targeting step to make sure the critical equation (5) is solved.^5,6 Algorithm 1 shows the details of the C-TMLE1 algorithm.

Algorithm 1: Collaborative Targeted Maximum Likelihood Estimation Algorithm I
1.	Construct an initial estimate ${\overline{Q}}_n^0$ for ${\overline{Q}}_0={\mathbb{E}}_0\left(Y|A,W\right)$.
2.	Construct a sequence of propensity score model gn,λ indexed by λ, where a larger λ implies a smoother/simpler estimator (e.g. larger regularization for LASSO, or larger bandwidth for kernel estimator). We further set λ within the set Λ = [λmin, λcv].
3.	Bound the estimated propensity score gn,λ = max{0.025, min{gn,λ, 0.975}}
4.	Set k = 0
5.	while Λ is not empty do
6.	Apply targeting step for each gn,λ, with λ ∈ Λ, with initial estimate ${\overline{Q}}_n^k$ and clever covariate $H_{g_{n,\lambda }}\left(A,W\right)=\frac{1-A}{1-g_{n,\lambda }\left(W\right)}-\frac{A}{g_{n,\lambda }\left(W\right)}$
7.	Select ${\overline{Q}}_{n,{\lambda }_k}^{*}$ with the smallest empirical risk $L\left({\overline{Q}}_{n,{\lambda }_k}^{*}\left(A,W\right)\right)$
8.	For λ ∈ [λk , λk−1], compute the corresponding TMLE using initial estimate ${\overline{Q}}_n^{k-1}$ and propensity score estimate gn,λ. We denote such estimate with ${\overline{Q}}_{n,\lambda }^{*}$ and record them.
9.	Set a new initial estimate ${\overline{Q}}_n^k={\overline{Q}}_{n,{\lambda }_k}^{*}$.
10.	Set Λ = [λmin, λk].
11.	Set k = k + 1.
12.	end while
13.	Select the best candidate ${\overline{Q}}_{n,{\lambda }_c{}_{tmle}}^{*}$ among ${\overline{Q}}_{n,\lambda }^{*}$, with the smallest cross-validated loss, using the same loss function as in the TMLE targeting step.
14.	Pick up the corresponding initial estimate ${\overline{Q}}_{n,{\lambda }_c{}_{tmle}}$ for ${\overline{Q}}_{n,{\lambda }_c{}_{tmle}}^{*}$
15.	Apply targeting step to ${\overline{Q}}_{n,{\lambda }_c{}_{tmle}}$ from the last step, with each gn,λ, λ ∈ [λmin, λctmle), yielding a new sequence of estimate ${\overline{Q}}_{n,\lambda }^{*}$.
16.	Select ${\overline{Q}}_n^{*}=\arg {\min }_{{\overline{Q}}_{n,\lambda }^{*}}L\left({\overline{Q}}_{n,\lambda }^{*}\right)$, λ ∈ [λmin, λctmle) with the smallest empirical loss from the sequence in last step as the final estimate.

B C-TMLE 0

In the C-TMLE0 algorithm, we only fluctuate the initial estimate using two clever covariates, $H_{g_{n,\lambda }}(A,W)$ and ${\tilde{H}}_{g_{n,\lambda }}(A,W)$, with propensity score estimate g_n,_λ = g_n,_λcv pre-selected by external cross-validation.

One of the main strength of this method is its computational efficiency: without generating sequence of TMLE estimators and applying cross-validation for model selection, it is much faster compared to C-TMLE1. Algorithm 2 shows the detail of the C-TMLE0 algorithm.

Algorithm 2. Collaborative Targeted Maximum Likelihood Estimation 0
1.	Construct an initial estimate ${\overline{Q}}_n^0$ for ${\overline{Q}}_0={\mathbb{E}}_0\left(Y|A,W\right)$.
2.	Estimate the propensity score and select the hyper-parameter using external cross-validation: $g_{n,\lambda }=g_{n,{\lambda }_{cv}}$.
3.	Apply targeting step in (4) with initial estimate ${\overline{Q}}_n^0$ and two clever covariates
	$H_{g_{n,\lambda }}\left(A,W\right)=\frac{1-A}{1-g_{n,\lambda }\left(W\right)}+\frac{A}{g_{n,\lambda }\left(W\right)}$
and
	${\tilde{H}}_{g_{n,\lambda }}=-\frac{1-A}{{\left(1-g_{n,\lambda }\left(W\right)\right)}^2}\left(g_{n,\lambda +\delta }-g_{n,\lambda }\right)+\frac{A}{g_{n,\lambda }\left(W\right)}\left(g_{n,\lambda +\delta }-g_{n,\lambda }\right)$
which gives a new estimate ${\overline{Q}}_{n,{\lambda }_{cv}}^{*}$
4.	Return the TMLE: ${\overline{Q}}_n^{*}={\overline{Q}}_{n,{\lambda }_{cv}}^{*}$