The intrinsic vulnerability of networks to epidemics

Highlights

• •We searched for properties making a network intrinsically vulnerable to epidemics.
• •We conducted simulations on both modelled and real-world contact networks.
• •Network properties may affect outbreak magnitude more than pathogen features.
• •We show how structural properties can be used to infer relative network vulnerability.

Abstract

Contact networks are convenient models to investigate epidemics, with nodes and links representing potential hosts and infection pathways, respectively. The outcomes of outbreak simulations on networks are driven both by the underlying epidemic model, and by the networks’ structural properties, so that the same pathogen can generate different epidemic dynamics on different networks. Here we ask whether there are general properties that make a contact network intrinsically vulnerable to epidemics (that is, regardless of specific epidemiological parameters). By conducting simulations on a large set of modelled networks, we show that, when a broad range of network topologies is taken into account, the effect of specific network properties on outbreak magnitude is stronger than that of fundamental pathogen features such as transmission rate, infection duration, and immunization ability. Then, by focusing on a large set of real world networks of the same type (potential contacts between field voles, Microtus agrestis), we showed how network structure can be used to accurately assess the relative, intrinsic vulnerability of networks towards a specific pathogen, even when those have limited topological variability. These results have profound implications for how we prevent disease outbreaks; in many real world situations, the topology of host contact networks can be described and used to infer intrinsic vulnerability. Such an approach can increase preparedness and inform preventive measures against emerging diseases for which limited epidemiological information is available, enabling the identification of priority targets before an epidemic event.

1. Introduction

Network analysis is a powerful approach for investigating epidemics, with nodes representing anything from individuals to countries, and links mapping transmission routes that pathogens can exploit to spread from one node to another (Newman, 2002, Keeling and Eames, 2005, Strona and Castellano, 2018). This general framework permits simulating different epidemiological scenarios over the same network (Pastor-Satorras et al., 2015), yielding disease-specific outcomes that could be important for informing management and intervention strategies (Rushmore et al., 2013, Yamin et al., 2014, Sun et al., 2014, Herrera et al., 2016). Although each scenario has its own characteristics and is expected to lead to specific outcomes, those are also constrained by network structure. Understanding to what extent such constraints can attenuate differences between different epidemiological scenarios may offer important insights into the ecology and dynamics of infectious disease spread (Keeling, 2005).

Common models that investigate epidemics in networks are based on identifying distinct categories (i.e., compartments) that define the health status of a host, and a set of specific rules dictating the probability of transition from one status to another. In a typical implementation of epidemic models, nodes can be in one of three different states at any given time: susceptible to the infection, S; infected, I; and recovered/removed from the system, R (following complete immunization or death). Different epidemic models are then formulated by varying the rules that permit hosts to transition from one state to another. For example, a very common model is the SI, where nodes can pass only from S to I. In the SIS models, infected nodes are allowed to roll back to the susceptible state without gaining immunity (I → S) according to a certain probability, which enables a disease to cycle in a host population by re-infecting individuals that have recovered from a previous infection. Simulating individuals gaining permanent or temporary immunity requires the addition of a third compartment that sees nodes removed from the network (I → R), which creates more complex models, such as the SIR and the SIRS (note that, besides immunization, the R status may indicate the death of a node) (Pastor-Satorras et al., 2015).

The classic compartmental epidemic models are flexible and simple, but moving beyond these particular formulations to establish more general topology-vulnerability relationships has been difficult, in part because they depict specific and distinct scenarios. As a result, the effects of network structure on disease outcomes are usually investigated by focusing on a particular type of network and pathogen whose features combine to determine disease dynamics (Pastor-Satorras et al., 2015). While precise, these constraints on model formulation limit our ability to compare dynamical outcomes across different networks configurations and across different pathogen types.

In an attempt to overcome these issues, we introduce here a generalization of classic compartmental models, which we named the ‘Synthetic Network Epidemic Spread’ (SNES) model. Despite its simple formulation, the SNES model permits the investigation of a wide range of epidemic scenarios in a continuous and controlled way, through tuning three parameters quantifying fundamental pathogen features: (1) the pathogen's transmission rate, τ; (2) the duration of infection (i.e., survival time of the pathogen in the host), ρ; and (3) the pathogen's immunization effect on hosts over repeated infections, ι. Such parameters (all bounded in [0, 1]) offer a straightforward way to perform comparisons across different epidemic scenarios.

Here we take advantage of this by applying the SNES model to a large set of simulated networks (representative of many different real world situations), and to a set of animal contact networks (representing potential encounters between field voles obtained from a mark/recapture study, Davis et al., 2015), with the aim to investigate to what extent network structure affects the outcome of an epidemic.

We found that, when a broad range of network topologies is taken into account, the epidemiological parameters of the model are in many cases less important than network structure in determining the magnitude of an epidemic outbreak. Of course, when similar networks are considered, as in the case of the field vole contact networks, epidemic parameters (and particularly transmission rate) became fundamental to determine epidemic magnitude. Nevertheless, even in the case of similarly structured networks, topological properties still permit an accurate assessment of relative network vulnerability towards a given class of pathogens (i.e. to pathogens whose spread can be modelled using similar epidemic parameters). These findings can help improve preparedness when limited epidemiological information is available and a fast response (for example in terms of prioritization) is needed, a situation that is expected to become ever more common in the future, due to the growing globalization, and the rapid emergence of new diseases.

2. Materials and methods

2.1. The Synthetic Network Epidemic Spread model (SNES)

At each time step, any node i can be infected by nodes pointing towards (or, in the case of an undirected network, connected to) it according to a given probability τ × S _i, with τ being the pathogen's transmission rate, and S _i being individual host susceptibility to the infection.

Concurrently, each node recovers with probability R _i, controlled by a parameter ρ, varying in [0, 1], and increasing with time since infection: R _i = (1 − 1/(1 + t)^ρ). Due to the purely theoretical nature of this study, the choice of the R _i function is arbitrary. This formulation of R _i, however, permits a smooth transition from situations where the probability of recovery increases very slowly with time (when ρ is close to 0), to opposite scenarios of fast recovery (when ρ is close to 1). It is intuitive that the concept behind the SNES model allows for maximum flexibility in the choice of R _i(t) function, making it possible to accommodate specific situations. Yet, to avoid adding further complexity to our analyses (and possibly complicating the interpretation of results), we used the above formulation in all of our epidemic simulations.

The susceptibility of a node following infection becomes S _i = S _i × ι, with ι being equal for all individuals (since theoretically dependent on the pathogen) and varying in [0, 1]. This accounts for a general property of immunizing diseases where individuals who have been infected and who have recovered are less likely to be re-infected, which is the basis of vaccination (though we note there is variation with respect to immunity which is unaccounted for in these models; e.g., waning immunity; Scherer and McLean, 2002). Interestingly, analogies can be drawn for very different contexts, such as that of information spread in social networks. The probability that a person will share a piece of information will rapidly decrease when receiving the same piece of information again. In the following, we will refer to this process as ‘immunization’, but it may also represent the path towards removal/death of an individual, corresponding to real world situations where repeated infections can be fatal. As in the case of R _i(t), S _i(ι) can also be adjusted to fit specific hypotheses.

The parameters ρ and ι combine to control disease behavior, for instance, the extent of disease spread in terms of number of infected nodes. These parameters also permit the model to be tuned to reflect typical epidemiological models such as SI (when ρ = 0, ι = 1), SIS (when ρ > 0, ι = 1), SIR(S) (when ρ > 0 and ι ≤ 1), or to explore epidemic scenarios in a continuous and controlled way. For example, the SNES framework makes it possible to track how epidemic outcomes compare between the SI scenario to a typical SIS scenario (Pastor-Satorras et al., 2015) by progressively increasing the probability that a host will recover and become susceptible again. Additionally, the SNES model can also be easily adapted to more specific scenarios. For example, the addition of a simple rule controlling the lapse between the time a node is infected and the time it becomes infectious enables the SNES to emulate compartment models that include latency (such as the SEIRS, which includes an ‘exposed’ class).

We note that the SNES is conceptually similar to a SIRS model were the transition probabilities S → I, I → R, and R → S are adjusted to particular values. Nevertheless, by departing from the typical compartmental scheme, the formulation of SNES offers some advantages in terms of clarity. In particular, while the different, typical compartmental models (and possibly a ‘tunable’ SIRS) focus on the possibility (and probability) of a host's transition from a health status to another, and use this constraint to identify different epidemic categories on the basis of permitted and forbidden transitions, the SNES attempts to remove the boundaries between different models. Those, in fact, simply represent different regions of an ideal, continuous three-dimensional space defined by ρ, ι and τ.

2.2. Generation of simulated networks

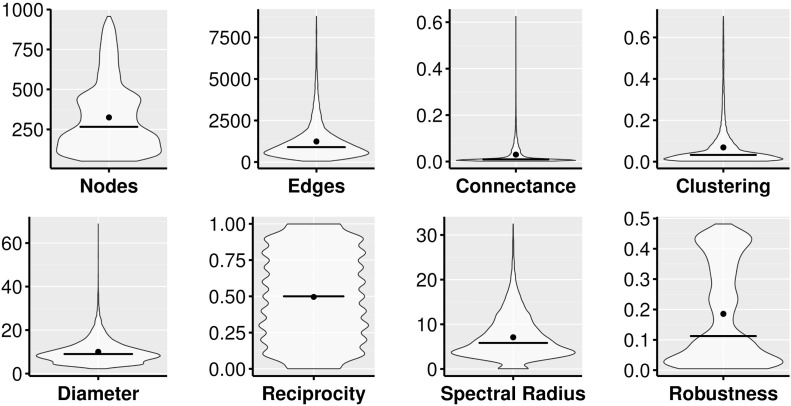
We tested our model on 10,000 simulated networks. To grow each network, we selected at random a model between four different well-known ones (configuration model; Erdos Renyi, ER; Barabasi–Albert, BA; and Watts–Strogatz, WS) (Strogatz, 2001). To build networks using the configuration model (Békéssy et al., 1972), we selected a random exponent for the power law degree distribution varying between 2 and 3. In ER networks we set the number of nodes (V) to a random integer in [50, 500] and the number of edges to a random integer in [V, 1000]. In BA networks, we set the number of nodes to a random integer in [500, 1000], and the number of outgoing edges generated for each node to (V × r × 0.01 + 1), with V being the number of nodes, and r being a random real number in [0, 1]. In WS networks, we set the dimension of the lattice to 1, the size of the lattice along all dimensions to a random integer in [50, 250], the distance within two nodes are connected to a random integer in [2, 10], and the rewiring probability to a random real number in [0, 1]. In this way, we obtained networks with a good variation in number of edges, nodes, connectance, clustering, and diameter (Fig. 1 ).

Fig. 1.

Structural properties of the randomly generated networks. Black horizontal lines indicate median value, while black dots indicates mean values. The shape of the violin plots indicates the density of observations.

2.3. Reciprocity

Instead of focusing on directed and undirected networks separately, we applied the following conceptualization: an undirected network is in fact a directed network where, given any link connecting node A to node B, a reciprocal link B → A exists. The relative abundance of reciprocal links determines how much a directed network differs from its undirected counterpart. Thus, we generated all networks as directed and simple (that is without loops and reciprocal links), and then we added reciprocal links until reaching a preselected degree of reciprocity, extracted at random in [0, 1] (with 0 corresponding to a directed network with no reciprocal links, and 1 corresponding to an undirected network).

2.4. Real world contact networks

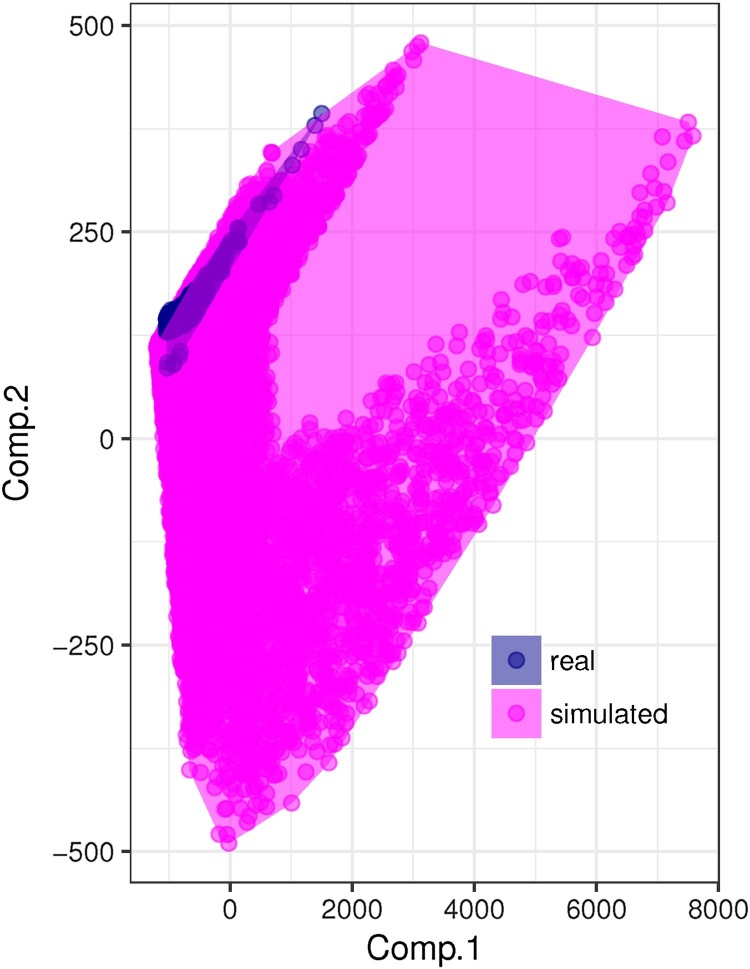
To verify the validity of our results in real-world situations, we replicated the analysis also on a set of empirical networks, all representing the same specific setting. In particular, we used mark-recapture data of field voles (Microtus agrestis) collected over 7 years in four different sites, which we obtained from (Davis et al., 2015). In the original study (Davis et al., 2015), captures were performed at each of the four sites using 100 traps placed at the nodes on a regular grid of 5 m² square cells. Trapping sessions were carried out every 28 days from March to November, and every 56 days from November to March (please refer to Davis et al., 2015 for a more complete description of the methodology and additional details). Starting from the raw data, which included a unique identifier for each field vole individual caught in a trap at least once, as well as the time (day) and location (node in the trap-grid) of capture, we built networks of potential contacts between voles by linking all individuals caught in the same cage, or in two neighbouring cages (i.e. at a distance smaller than 5 m), on the same day. We then retained only the networks including at least 100 edges. In this way, we built 296 networks, with relatively small variability in their structural properties (much smaller than that observed in the set of simulated networks, see Fig. 2 ).

Fig. 2.

Principal component analysis biplot showing the differences between the structure of simulated and real-world networks. The cumulative variance explained by the first two components was 0.99998.

2.5. Unique Robustness Measure (R)

Besides basic network properties such as clustering, connectance, diameter, number of nodes and edges, and spectral radius of the adjacency matrix (Wang et al., 2003), we also measured robustness as described in Schneider et al. (2011) for each network. Robustness is computed as: R $=1/N{\sum }_{r=1}^{N}Q$, where N is the total number of network nodes and Q is the fraction of nodes in the largest connected cluster after removing r nodes. Although this measure was developed in a completely different context (in particular, to assess the resilience of a network against node removal), it is also closely related to the concept of percolation, which has fundamental implications for studying epidemics (Moore and Newman, 2000, Boguná et al., 2003, Serrano and Boguná, 2006). In its original formulation, R was computed by removing nodes in decreasing order of their degree (i.e. their number of connections). The aim of sequentially removing nodes with the largest degree is to speed up the process of network disassembly, hence obtaining a conservative estimate of robustness in the worst case scenario of node removal. However, it has been pointed out that other criteria going beyond local properties (such as node degree) could offer more efficient ways to disrupt networks (Morone and Makse, 2015). Thus, we used PageRank (Page et al., 1999) to determine the order of node removal in the computation of R. Nevertheless, we also tested the sensitivity of R as a measure of intrinsic vulnerability (see section 2.10) to different criteria of node removal (namely, node degree and betweenness).

2.6. Node susceptibility

To investigate the potential effect of individual node susceptibility (S _i) on outbreak magnitude, we replicated the experiment on simulated networks in two alternative scenarios. In the first one (for which we report results in the main text), we attributed equal susceptibility (0.5) to all nodes in the network. In the second scenario, we attributed individual (S _i) values to nodes by sampling them from a normal distribution with mean 0.5 and standard deviation 0.1.

2.7. Model runs

For each model run, we varied ρ and ι at random in order to produce very different scenarios, ranging from situations where the probability of a node to recover from infection was very low (ρ = 0⁺) and where immunization required several repeated infections (ι = 1⁻), to situations of fast recovery (ρ = 1) and immunization (ι = 0⁻). In all cases, we set ρ > 0 and ι < 1, in order to produce contained epidemics. We ran each model until the infection disappeared from the network. In addition, we varied at random the disease transmission rate τ between (0, 1], in order to simulate different scenarios of pathogen infectivity. We simulated 100 epidemics on each network, starting from a randomly selected infected node, and then averaging the results (see next paragraph) over the 100 runs. For the set of real world networks, we performed 10000 replicates by randomly selecting one of the networks in the dataset (N = 296) and by averaging the outcomes of 100 epidemic spreads.

2.8. Outbreak magnitude measures

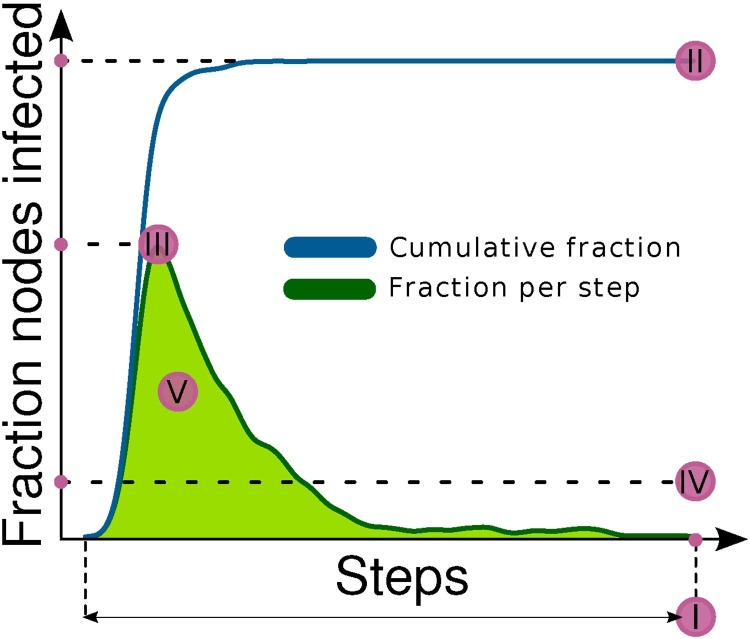
For each virus spread simulation, we recorded five different measures of outbreak magnitude (Fig. 3 , defined as follows: (I) epidemic persistence, i.e. the total number of performed simulation steps until complete immunization; (II) epidemic breadth, i.e. the fraction of nodes that have ever been infected over the total number of nodes; (III) epidemic peak, i.e. the ratio between the maximum number of simultaneously infected nodes, and the total number of nodes; (IV) epidemic strength, i.e. the mean fraction of infected nodes per step; (V) epidemic area, quantified as the area under the curve of the fraction of infected nodes over the total number of nodes vs. simulation time, rescaled to [0,1]. Although these measure are clearly not independent from one another, they still indicate different aspects of outbreak magnitude and, together, can depict subtle differences between different epidemic events.

Fig. 3.

Measures of outbreak magnitude. The green line corresponds to the fraction of nodes infected at each step of a single simulation, while the blue line corresponds to the cumulative fraction of infected nodes. For each simulation we recorded the duration (I), the cumulative fraction of nodes reached by the infection (II), the maximum and the average fraction of infected nodes per step (III, IV), and the area under the curve that depicts the fraction of infected nodes per step (the green line) (V). (For interpretation of the references to color in text/this figure legend, the reader is referred to the web version of the article.)

2.9. Statistical analysis

We used canonical correlation analysis (Hair et al., 2006) to compare the outbreak magnitude measures with the corresponding network structural properties and the epidemic parameters (ρ and ι), using the R package yacca (Butts, 2016). We standardized all data to z values as (x _i − μ)/σ, with x _i being the target value, and μ and σ being, respectively, the average and standard deviation of the variable x _i. We evaluated the strength of canonical relationships using canonical roots, and we used Rao's F test to assess significance of the relationships (Mardia et al., 1980). We evaluated the effects of dependent and independent variables on the respective canonical variates by examining cross canonical loadings, and we used redundancy analysis to evaluate the amount of variance in the set of dependent variables explained by independent variables (Hair et al., 2006). In both simulated and real-world networks, the redundancy values indicated that the first canonical dimension explained a consistent fraction of variance (respectively, 0.57 and 0.62), while the second canonical dimension added a limited contribution (0.04 and 0.05). Thus, in the main text, we limited our discussion the canonical loadings of the first dimension.

2.10. Testing R as a measure of intrinsic vulnerability

To assess the performance of the Unique Robustness Measure as an estimator of intrinsic network vulnerability to epidemic spread for a given class of pathogens (i.e. for pathogens whose spread can be modelled with similar epidemic parameters), we first ranked all the field vole contact networks according to their R. We then ran several sets of classical SIR models (Pastor-Satorras et al., 2015) under 100 different combinations of infection and recovery probabilities (with both ranging from 0.1 to 1 with a step of 0.1) on all networks. Each scenario correspond to a particular class of pathogens. For each network and model setting we replicated 100 epidemic simulations (each starting from a randomly selected infected node), averaging the total fraction of infected nodes throughout each simulation run. This value was used to rank networks within each set of simulations (i.e. for each combination of infection/recovery probability). Finally, we compared this rank with that provided by the Unique Robustness Measure (R). Networks for which the average fraction of infected nodes throughout the 100 simulations happened to be identical were ranked in random order.

2.11. Reproducibility

All the scripts and data needed to replicate the analyses in the present paper and reproduce figures are made freely available at: https://github.com/giovannistrona/network_intrinsic_vulnerability_to_epidemics.

3. Results and discussion

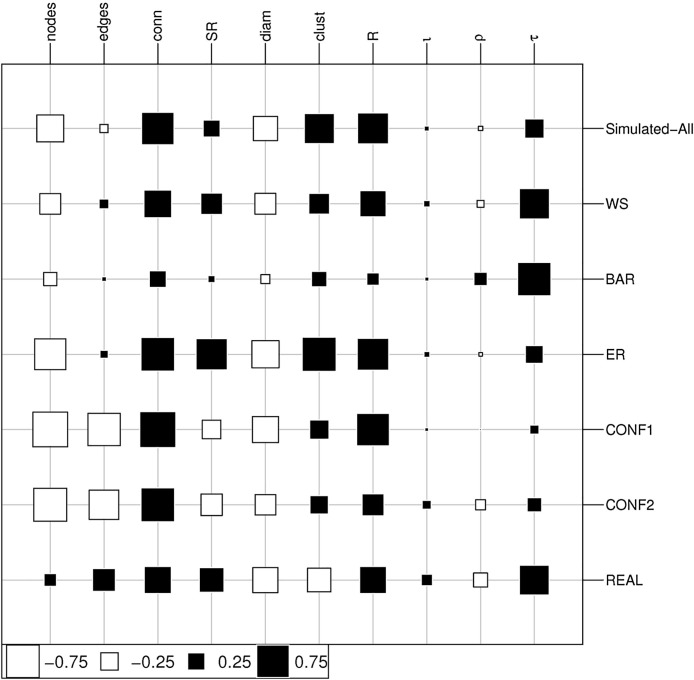
We conducted a large experiment to compare the vulnerability of a wide range of network topologies (Fig. 1) to a broad range of epidemic spread scenarios, that we obtained by varying randomly the three epidemic parameters of the SNES (ρ, ι and τ, see Section 2). In simulated networks, the magnitude of epidemic outbreaks (Fig. 3) was well explained by the combination of epidemic parameters and by network properties (Table 1 ). Surprisingly, topological properties, and particularly the density of infection pathways (quantified by network connectance), and their redundancy (quantified by network clustering, that is how often two nodes pointing to another one are linked, and by network robustness, see below) had a stronger effect on outbreak magnitude than the epidemic parameters when a broad range of network topology is considered (Fig. 4 ). Network robustness (R) resulted also more important than epidemic parameters (and the second most important factor). This result was very consistent in two different scenarios where we assumed, respectively, that all nodes had the same susceptibility to infection (0.5), or a random susceptibility extracted from a normal distribution with mean 0.5 and standard deviation 0.1. This suggests that outbreak magnitude is driven by average susceptibility more than by its variation across individuals. Thus, we report and discuss here only the results referring to the first scenario.

Table 1.

Effects of network properties and epidemic parameters on outbreak magnitude. The table reports the results of the Canonical Correlation analysis performed on the outcomes of simulations performed on both the set of randomly generated networks, and the set of real-world networks indicating contacts between field voles (n = 10,000 in both cases). I: epidemic duration; II: cumulated fraction of nodes reached by the infection; III–IV: maximum and average fraction of infected nodes per step; V: area under the curve of fraction of infected nodes per step); τ: pathogen's transmission rate; ρ: duration of infection (i.e., survival time of the pathogen in the host); ι: pathogen's immunization effect on hosts over repeated infections.

Networks	Simulated		Real
Canonical dimension	1	2	1	2
Correlation	0.88	0.65	0.91	0.78
Root	0.77	0.42	0.83	0.60
Redundancy	0.57	0.04	0.62	0.05
F test	539	254	1075	635
F	60	44	50	36
p-Value	<0.001	<0.001	<0.001	<0.001
Canonical loadings
Nodes	−0.54	−0.06	0.14	0.10
Edges	−0.07	−0.19	0.40	0.04
Connectance	0.75	0.18	0.54	−0.10
Reciprocity	0	−0.02
Spectral radius	0.24	−0.04	0.47	0.01
Diameter	−0.44	−0.03	−0.47	0.09
Clustering	0.65	−0.19	−0.42	0.07
Robustness	0.69	−0.2	0.54	−0.03
ρ	0.03	0.02	0.12	0.58
ι	−0.02	0.25	−0.17	−0.47
τ	0.31	0.05	0.65	−0.18
I	0.3	−0.33	0.24	0.43
II	0.82	−0.2	0.84	0.00
III	0.8	−0.14	0.90	0.12
IV	0.84	−0.09	0.87	0.15
V	0.84	−0.08	0.87	0.12

Fig. 4.

Effects of network structural properties and epidemiological parameters (ρ, ι, and τ) on outbreak magnitude measures for both the experiments on random and real-world networks. The area of squares represents the absolute value of canonical loadings, which represent the relative importance of independent variables in determining outbreak magnitude (see Methods), with white and black squares indicating, respectively, positive and negative values. For simulated networks we report both results for all aggregated networks, and the results for the different kinds of networks. Since in both simulated and real-world networks the amount of variance in the set of dependent variables explained by that of independent variables was consistent in the first dimension, but not in the second one (see Table 1), we focus here on the loadings of the first canonical dimension. The graph was generated using the table.value function from the R package adegraphics (Dray and Siberchicot, 2017). Conn: network connectance; SR: spectral radius; Diam: network diameter; Clust: network clustering; R: network robustness; τ: pathogen's transmission rate; ρ: duration of infection (i.e., survival time of the pathogen in the host); ι: pathogen's immunization effect on hosts over repeated infections.

We replicated the same procedure (as was applied to the simulated networks) using a set of real-world networks. The experiment with simulated networks explored a very broad range of network topologies, and demonstrated how network topology affects epidemic outbreak magnitude even more than epidemiological parameters. Conversely, for our test on real world scenarios, we focused on a set of networks representing independent replicates of the same exact real world setting, and that therefore exhibited a relatively low variability in their structural features (Fig. 2). This permitted us to investigate if (and to what extent) small variations in network properties may be major determinants of epidemic outbreak magnitude.

Even in this case, where network topological variability was limited, important epidemiological parameters, such as the one controlling the duration of the infective stage (ρ), and the one modelling the immunizing effect of pathogens (ι), had a negligible effect in determining outbreak magnitude (Fig. 4). Transmission rate (τ) emerged as the most important factor, although both network robustness and network connectance had very strong effects (much higher than those of ρ and ι). The other network parameters were less relevant, and their effects were not always consistent with those observed in the set of simulated networks. For example, clustering was positively associated to epidemic magnitude in simulated networks, but negatively associated in real world networks (Fig. 4), which highlights how the dynamics and outcome of an epidemic event are affected by network structure in complicated ways that cannot be captured by individual basic network properties, and that do not offer a straightforward interpretation.

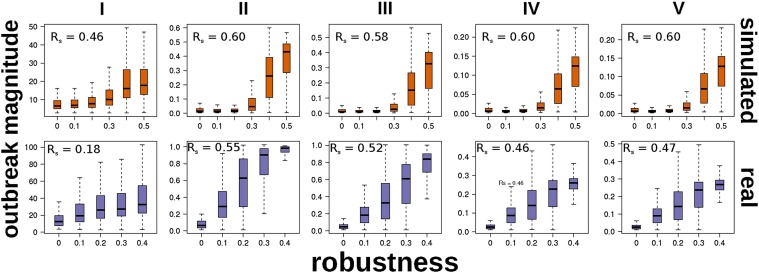
In both experiments, the Unique Robustness Measure (R) (Schneider et al., 2011) was consistently one of the most influential factors, and positively associated with outbreak magnitude (Figs. 4, 5 ). The R measure is computed by counting the number of nodes present in the largest connected component after nodes are progressively removed, thus representing the ability of a system such as a power grid or the Internet to delay collapse after subsequent failures (Schneider et al., 2011). In the context of epidemics, R may offer a synthetic picture of the redundancy of infection pathways. In a network with higher R, a pathogen will have many chances to spread between nodes and will be less affected by the immunization of many nodes (or their death, leading, in both cases, to their removal from the network).

Fig. 5.

Comparison between outbreak magnitude measures and network Unique Robustness Measure (R) in randomly generated and real-world networks. Vertical axes indicate the outbreak magnitude measures (I: epidemic duration; II: cumulated fraction of nodes reached by the infection; III–IV: maximum and average fraction of infected nodes per step; V: area under the curve of fraction of infected nodes per step), while boxplots group the outcomes of simulations according to the respective network's R value. The Spearman's rank correlation coefficient (r_s) was computed, for each plot, on the raw data (i.e. comparing all the outbreak magnitude values for a given measure with their corresponding R values).

This finding has two important implications. On the one hand, it indicates that the networks where a potential outbreak is predicted to be strongest will also be the most difficult to protect, since having a high R complicates immunization procedures based, for example, on targeted vaccination (Morone and Makse, 2015). On the other hand, it suggests that R's ability to synthesize various aspects of network structure in a single value might make it a useful index to rank networks on the basis of their intrinsic vulnerability, thereby offering a way to prioritize preparedness efforts by focusing preventive and surveillance actions on the most vulnerable networks.

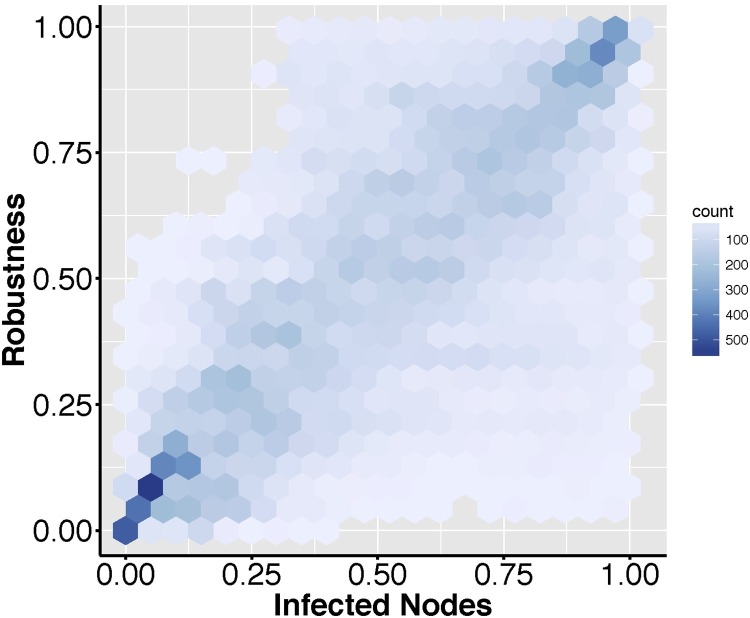
This idea was supported by our experimental results, which confirmed the Unique Robustness Measure, R as an efficient measure of intrinsic network vulnerability. In particular, the rank of field vole networks according to R was very consistent with the rank obtained by ordering networks on the basis of their vulnerability in a broad range of epidemic scenarios, that we modeled by running a set of classical SIR models (Pastor-Satorras et al., 2015) under different combinations of infection/recovery probabilities (Fig. 6 ; adjusted R-squared: 0.59, p < 0.00001, regression line y = 0.77x + 0.12). We quantified vulnerability in terms of the total fraction of nodes reached by the infection throughout the epidemic simulation (see Fig. 3-II). This result is particularly convincing when considering the limited topological variability of the field vole contact networks (see Fig. 2), which makes them a challenging benchmark to test the sensitivity of R as a vulnerability measure. Using different criteria of node removal to compute R (namely, node degree and betweenness) led to very consistent results (adjusted R-squared: 0.60, p < 0.00001, regression line y = 0.78x + 0.11 when node degree was used; adjusted R-squared: 0.61, p < 0.00001, regression line y = 0.78x + 0.11 when node betweenness was used).

Fig. 6.

The Unique Robustness Measure (R) as an index of network vulnerability to epidemic spread. The efficiency of (R) in ranking networks according to their vulnerability towards an unknown epidemic threat was evaluated by comparing the rank of the face-to-face contact networks (Isella et al., 2011) according to their R with their respective rank measured as the fraction of nodes reached by the infection in 100 different SIR scenarios (see Methods). The color scale maps the density of observations falling within each hexagon.

Intuition suggests that the outcome of an epidemic should be affected mainly by disease behaviour (in terms, for example, of transmission, infection dynamics, or latency) (Lloyd-Smith et al., 2009). Yet, our results paint a very different picture where the structure of the infected network influences outbreak magnitude more than epidemic parameters used to model pathogens’ features.

It should be highlighted that, in some cases, the structure of the network used to model a particular outbreak includes some implicit information about a pathogen's behavior, such as its transmission mode. For example, one will use a network of sexual contacts to model the spread of HIV within a community (Woodhouse et al., 1994), or a spatial network mapping crop distribution to model a plant pest spread (Strona et al., 2017), or again the air transportation network for describing airborne pathogens (Brockmann and Helbing, 2013). On the one hand, in such cases, looking at the pathogen and at the network as two separate entities would not be straightforward. On the other hand, however, the issue is more philosophical rather than applicative, since it does not prevent us from comparing network vulnerability both between and within broad classes of pathogen transmission strategies. Furthermore, it depicts more scenarios where our findings could be very useful. For example, one may generate different networks within the same context by considering different possible pathogen transmission strategies. Those could be either general ones, such as airborne or sexual transmission, or very specific strategies taking into account, for instance, vector vagility (Strona et al., 2017). Then, one may compare the structure of such networks in order to identify their relative risk towards different kinds of pathogens.

Our results are consistent with (and complementary to) previous studies that have shown how network structure can profoundly affect infectious disease dynamics (Keeling, 2005), and that taking this aspect into account may improve our ability to understand and predict epidemic patterns, and to implement intervention measures (Keeling and Eames, 2005). For example, the properties of the air-transportation-network have been identified as a main determinant of global patterns of emerging diseases, with complex features of the airline network being at heart of the global spread dynamics of diseases such as severe acute respiratory syndrome (Colizza et al., 2006). In addition, a more recent study showed that measuring the distance between the source and the target of an infection in network space can provide a more reliable prediction of epidemic spread rate than geographical distance, regardless of the nature of the disease (Brockmann and Helbing, 2013). Consistent with those ideas, our findings suggest that, in the face of many unmeasurable unknowns related to epidemiological parameters, focusing on network properties can facilitate the identification of vulnerabilities and the optimization of existing systems.