Optoacoustic signal excitation with a tone-burst of short pulses

Abstract

Individual light pulses with durations in the nanosecond range are most often employed in biomedical optoacoustic imaging. In this excitation regime, ultra-wideband acoustic responses are generated from tissues that cannot be efficiently captured with ultrasound transducers having a limited detection bandwidth. Here, we analyse a narrowband optoacoustic signal excitation mechanism consisting of a tone-burst of multiple equally-delayed pulses. The signal generation efficiency of single-pulse versus tone-burst excitation is compared for normal light exposure levels in the linear optoacoustic signal generation regime as well as when considering non-linearities associated with temperature increase or absorption saturation. The signal-to-noise ratio of the excited signals is also experimentally compared using a highly-absorbing ink phantom.

Optoacoustic imaging and tomography is based on the thermoelastic generation of pressure signals by absorption of intermittent light radiation. The generally low conversion efficiency from optical into acoustic energy can be maximized by inducing sharp variations in the excitation light intensity [1]. Thereby, short-pulsed lasers in the nanosecond range are typically used in biomedical optoacoustics to generate detectable responses [2]. The optimal energy per-pulse would usually depend on the target imaging depth. While sub-microjoule pulses are sufficient for optical-resolution microscopy at depths of up to about 1 mm, per-pulse energies in the millijoule to tens of millijoules range are required in order to achieve reasonable signal-to-noise ratio (SNR) at centimeter-scale depths [3].

The bandwidth of the collected optoacoustic signals depends on several factors, such as the shape and duration of the laser pulse as well as the size and shape of the absorbing structures [4], acoustic attenuation in the propagation medium [5] and the frequency response of the ultrasound detector(s) [6]. Although broadband detectors, e.g. based on polyvinylidene fluoride (PVDF) films [7], capacitive micromachined ultrasonic transducers (CMUTs) [8] or optical interferometers [[9], [10], [11]] are generally available, piezocomposite sensors remain the workhorse in optoacoustic imaging owing to their superior sensitivity and robustness. Most piezocomposite materials exhibit limited detection bandwidth and hence represent an inefficient approach to collect the very broadband optoacoustic responses, even when combining multiple sensors [12]. More narrowband excitation of optoacoustic signals can be achieved with low-power intensity modulated laser sources. Intensity modulation methods based on e.g. sinusoidal [13], chirped [14] or sinusoidal-burst [15] functions have been suggested. While intensity-modulated light sources represent an affordable alternative to short-pulsed lasers, the SNR of the generated optoacoustic signals is orders of magnitude lower as compared to those obtained with pulsed excitation [16,17].

In this work, we analyze the performance of an alternative narrowband optoacoustic excitation approach based on a tone-burst consisting of a train of equally-delayed short light pulses. Provided that the duration of each pulse is short enough to fulfill both the acoustic and thermal confinement regimes, the non-homogenous wave equation characterizing the pressure field ${\mathrm{p}}_{\mathrm{N}}(\mathrm{x},\mathrm{t})$ generated with a train of N pulses separated by Δt can be expressed as [1]

$$\frac{{\partial }^2{\mathrm{p}}_{\mathrm{N}}(\mathrm{x},\mathrm{t})}{{\partial \mathrm{t}}^2}-{\mathrm{c}}^2{\nabla }^2{\mathrm{p}}_{\mathrm{N}}\left(\mathrm{x},\mathrm{t}\right)=\mathrm{\Gamma }\mathrm{H}\left(\mathrm{x}\right)\sum _{\mathrm{n}=0}^{\mathrm{N}-1}\frac{\partial \mathrm{\delta }\left(\mathrm{t}-\mathrm{n}\Delta \mathrm{t}\right)}{\mathrm{\delta }\mathrm{t}},$$ (1)

where c is the speed of sound, Γ is the dimensionless Grüneisen parameter and H(x) is the absorbed energy per unit volume for each pulse. The solution of Eq. (1) is then given by

$${\mathrm{p}}_{\mathrm{N}}\left(\mathrm{x},\mathrm{t}\right)=\frac{1}{\mathrm{N}}\sum _{\mathrm{n}=0}^{\mathrm{N}-1}{\mathrm{p}}_1\left(\mathrm{x},\mathrm{t}-\mathrm{n}\Delta \mathrm{t}\right),$$ (2)

being ${\mathrm{p}}_1(\mathrm{x},\mathrm{t})$ the pressure wave field generated with a single pulse containing the same amount of optical energy as the entire burst sequence. The latter can be expressed via [18]

$${\mathrm{p}}_1\left(\mathrm{x},\mathrm{t}\right)=\frac{\mathrm{\Gamma }}{4\mathrm{\pi }\mathrm{c}}\frac{\partial }{\partial \mathrm{t}}{\int }_{\mathrm{S}\mathrm{\text{'}}(\mathrm{x},\mathrm{t})}\frac{\mathrm{H}({\mathrm{x}}^{\mathrm{\text{'}}})}{\left|\mathrm{x}-\mathrm{x}\mathrm{\text{'}}\right|}\mathrm{d}\mathrm{S}\mathrm{\text{'}}(\mathrm{x},\mathrm{t}),$$ (3)

where $\mathrm{S}\mathrm{\text{'}}(\mathrm{x},\mathrm{t})$ is a spherical surface for which $\left|\mathrm{x}-\mathrm{x}\mathrm{\text{'}}\right|=\mathrm{c}\mathrm{t}$. Eqs. (1)–(3) establish a linear relationship between the optical energy and the acoustic pressure. The acoustic energy of the generated ultrasound wave E_a,N in this linear optoacoustic regime, calculated from the acoustic wave intensity I_a,N(x,t) impinging upon a surface enclosing all the optoacoustic sources, is then given by

$${\mathrm{E}}_{\mathrm{a},\mathrm{N}}={\iint }_{\mathrm{S},\mathrm{t}}{\mathrm{I}}_{\mathrm{a},\mathrm{N}}\left(\mathrm{x},\mathrm{t}\right)\mathrm{d}\mathrm{S}\mathrm{d}\mathrm{t}={\int }_{\mathrm{S},\mathrm{t}}\frac{{{\mathrm{p}}_{\mathrm{N}}}^2(\mathrm{x},\mathrm{t})}{\mathrm{Z}}\mathrm{d}\mathrm{S}\mathrm{d}\mathrm{t}=\frac{1}{\mathrm{N}}{\int }_{\mathrm{S},\mathrm{t}}\frac{{{\mathrm{p}}_1}^2(\mathrm{x},\mathrm{t})}{\mathrm{Z}}\mathrm{d}\mathrm{S}\mathrm{d}\mathrm{t}=\frac{1}{\mathrm{N}}{\mathrm{E}}_{\mathrm{a},1},$$ (4)

where E_a,1 is the energy of the generated acoustic wave for the single-pulse excitation and Z is the acoustic impedance. It can be readily seen that the energy of the excited acoustic wave is inversely proportional to the number of pulses contained in the burst. This also makes sense from an energy conversion point of view as the transduction of light energy into acoustic energy is a non-linear process with its efficiency being proportional to the energy of the laser pulse [19]. On the other hand, the bandwidth of the signal generated with a tone-burst consisting of a train of equally-delayed pulses is reduced with respect to that of a single pulse, which affects the frequency spectrum of the generated signals. The Fourier transform of ${\mathrm{p}}_{\mathrm{N}}(\mathrm{x},\mathrm{t})$ can be expressed as

$${\stackrel{\sim }{\mathrm{p}}}_{\mathrm{N}}\left(\mathrm{x},\mathrm{f}\right)=\frac{1}{\mathrm{N}}\sum _{\mathrm{n}=0}^{\mathrm{N}-1}{\stackrel{\sim }{\mathrm{p}}}_1\left(\mathrm{x},\mathrm{f}\right){\mathrm{e}}^{-2\mathrm{\pi }\mathrm{f}\mathrm{n}\Delta \mathrm{t}\mathrm{j}}.$$ (5)

Eq. (5) indicates that the amplitude spectral density of the pressure wave field excited with a tone-burst is always lower or equal to that generated with a single pulse. Equal amplitude is only achieved for $\mathrm{f}=\pm \mathrm{m}/\Delta \mathrm{t}$, with m being an integer number.

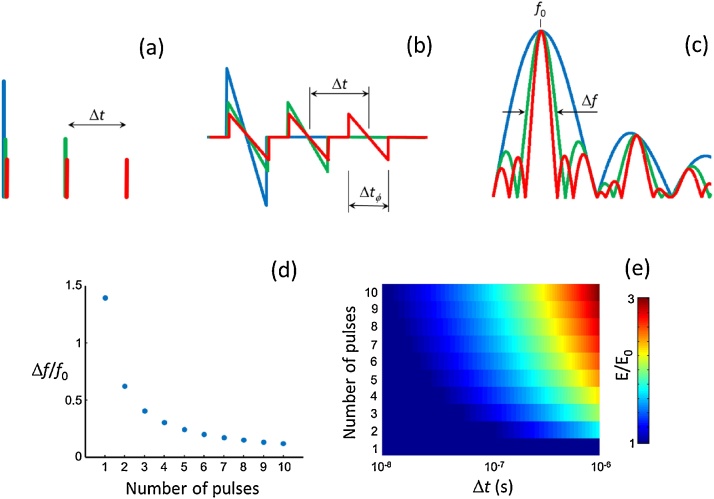
Fig. 1 illustrates the differences between signals generated with tone-burst and single pulse excitation. Fig. 1a displays the excitation time profiles for single pulse (blue) and for tone-bursts consisting of 2 (green) and 3 (red) pulses having the same optical energy. For simplicity and without loss of generality, the signals were generated by a uniformly absorbing sphere with diameter ϕ and optical absorption per unit volume H, where the separation between pulses was taken as Δt = 1/f₀, being f₀ the peak frequency for the acoustic wave excited with a single short laser pulse. The pressure signal emitted by a spherical absorber excited with a laser pulse can be calculated analytically via [1]

$${\mathrm{p}}_{1,\mathrm{\varnothing }}\left(\mathrm{r},\overline{\mathrm{t}}\right)=\{\begin{array}{c}\frac{-\mathrm{\Gamma }H\varphi }{4r}\overline{\mathrm{t}},\mathrm{\hspace{0.17em}}\mathrm{i}\mathrm{f}\mathrm{\hspace{0.17em}}\left|\overline{\mathrm{t}}\right|\le 1\\ 0,\mathrm{\hspace{0.17em}}\mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\end{array},$$ (6)

being $\overline{\mathrm{t}}=2(\mathrm{c}\mathrm{t}-\mathrm{r})/\varphi$ and Γ the Grueneisen parameter. The Fourier transform of $\mathrm{p}(\mathrm{r},\overline{\mathrm{t}})$ is given by

$$\stackrel{\sim }{\mathrm{p}}\left(\mathrm{x},\overline{\mathrm{f}}\right)=\frac{\mathrm{\Gamma }H\varphi }{2r}j\left[\frac{\mathrm{s}\mathrm{i}\mathrm{n}\left(2\mathrm{\pi }\overline{\mathrm{f}}\right)}{{\left(2\mathrm{\pi }\overline{\mathrm{f}}\right)}^2}-\frac{\mathrm{c}\mathrm{o}\mathrm{s}\left(2\mathrm{\pi }\overline{\mathrm{f}}\right)}{2\mathrm{\pi }\overline{\mathrm{f}}}\right],$$ (7)

where $\varphi$ is the sphere diameter and r is the distance from its center.

Fig. 1.

Optoacoustic excitation with a tone-burst consisting of equally-delayed short light pulses. (a) Time profile of the optical energy density for single pulse (blue) and tone-bursts consisting of 2 (green) and 3 (red) pulses separated by Δt. The corresponding optoacoustic waveforms generated by a spherical absorber and their frequency spectra are shown in (b) and (c), respectively. The absorber diameter was selected so that the central frequency of the signals emitted with single-pulse excitation is equal to the central frequency of the burst excitation. (d) Relative bandwidth of the generated signals as a function of the number of pulses contained in the burst. (e) Maximum permissible optical energy of the burst under ANSI safety standards [20] as a function of the number of pulses and Δt. The values were normalized with the corresponding maximal permissible energy for the single-pulse excitation.

The generated optoacoustic waveforms and their corresponding frequency spectra for the three excitation profiles are shown in Fig. 1b and c, respectively. As previously mentioned, the optoacoustic signal amplitude is inversely proportional to the number of excitation pulses. On the other hand, the generated signal bandwidth contracts as the number of pulses increases. This reduces the achievable resolution if this excitation approach is used for tomographic imaging, for which new reconstruction procedures are required. The axial resolution is also negatively affected by a lower bandwidth in raster-scan-based approaches. Fig. 1d shows the relative bandwidth of the signals calculated as the ratio between the full width at half maximum (FWHM) of the frequency spectra to the central frequency. Note that the optoacoustic signal bandwidth for the single-pulse excitation is determined by the dimensions and shape of the absorber, not by the profile of the excitation pulse. Furthermore, even though the optoacoustic signals generated with tone-burst excitation can better match the detection characteristics of narrowband transducers, the spectral amplitude is lower or equal for all frequencies. Hence, a higher SNR is expected with single-pulse excitation when using the same total optical energy. The laser exposure standards limit the maximum energy density (fluence) Φ_max in mJ/cm² at the skin surface to [20]

$${\mathrm{\Phi }}_{\mathrm{m}\mathrm{a}\mathrm{x}}=\left\{\begin{array}{c}20{\mathrm{C}}_{\mathrm{A}}\mathrm{\hspace{0.17em}}\mathrm{i}\mathrm{f}\mathrm{\hspace{0.17em}}{\mathrm{T}}_{\mathrm{e}\mathrm{x}\mathrm{p}}\le {10}^{-7}\mathrm{s}\\ 1100{\mathrm{C}}_{\mathrm{A}}{{\mathrm{T}}_{\mathrm{e}\mathrm{x}\mathrm{p}}}^{0.25}\mathrm{\hspace{0.17em}}\mathrm{i}\mathrm{f}\mathrm{\hspace{0.17em}}{\mathrm{T}}_{\mathrm{e}\mathrm{x}\mathrm{p}}>{10}^{-7}\mathrm{s}\end{array},\right)$$ (8)

where T_exp is the exposure time and C_A is a factor that depends on the optical wavelength. For typical pulsed nanosecond lasers, T_exp < 10⁻⁷s for a single pulse. However, T_exp = (N − 1)Δt for tone-burst excitation, which may exceed 10⁻⁷ s. Thereby, the maximum optical energy that can be delivered onto the tissue surface can be in principle made higher for tone-burst excitation. Fig. 1e shows the ratio of the maximum permissible optical energies for tone-burst and single-pulse excitation as a function of Δt and the number of pulses. Since the amplitude of the generated optoacoustic signals is proportional to the deposited optical energy, larger spectral amplitude can be achieved for certain frequencies with tone-burst excitation, particularly for larger Δt (lower central frequency of the burst). Thereby, a higher SNR of the collected optoacoustic signals can be achieved in some cases for tone-burst excitation under the safety limits on the total deposited energy onto the skin surface.

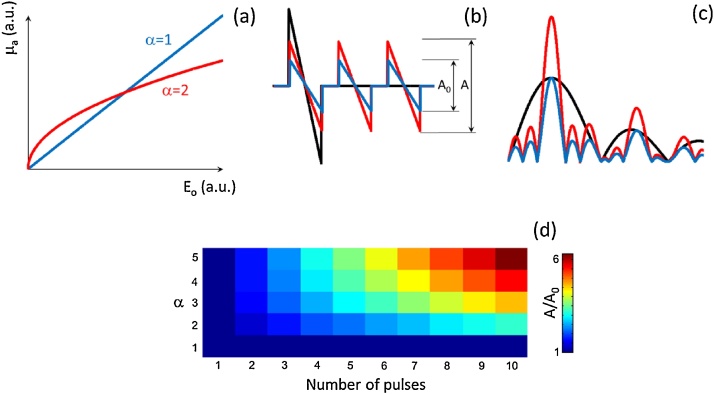
As previously mentioned, efficiency of the light-to-ultrasound energy conversion is proportional to the energy of the laser pulse. This implies that the optoacoustic signal amplitude cannot increase indefinitely with optical intensity, thus expected to saturate above a certain threshold. Optical absorption saturation was observed for oxygenated hemoglobin excited with picosecond duration pulses, which was exploited for oxygen saturation estimation as well as for super-resolution imaging [21]. When optical absorption saturates, the optoacoustic signal is no longer proportional to the laser energy. As an example and without loss of generality, we assumed that the optical absorption coefficient μ_a as a function of the optical energy of a single pulse E_o,1 can be approximated as

$${\mathrm{\mu }}_{\mathrm{a}}=\mathrm{k}{{\mathrm{E}}_{\mathrm{o},1}}^{1/\mathrm{\alpha }},$$ (9)

being k a constant and α an integer number. Fig. 2a displays the optical absorption coefficient as a function of the deposited optical energy for α = 1 and α = 2. The initial optoacoustic pressure is proportional to μ_a. The corresponding optoacoustic waveforms for a tone burst consisting of 3 pulses are plotted in Fig. 2b. For α = 1 (blue curve), the signal amplitude is reduced by a factor of 3 with respect to the signal generated with a single pulse with the same energy (black curve). The relative amplitude of the signals excited with a tone burst grows as a function of the non-linearity factor (see red curve for α = 2 in Fig. 2b) with the spectral density exceeding that of the single-pulse excitation for certain frequencies (Fig. 2c). The ratio between the amplitudes of the signals in the temporal or, equivalently, the spectral domain is shown in Fig. 2d as a function of α and the number of pulses. For certain frequencies, the spectral density of the optoacoustic signals for the tone-burst excitation may greatly exceed the signals produced with single pulse excitation.

Fig. 2.

Effects of optical absorption saturation on optoacoustic signals generated with tone-burst excitation. (a) Absorption coefficient as a function of optical energy modelled as μ_a=kE₀₁^1/α, where α = 1 corresponds to the linear optoacoustic signal generation regime. (b) Optoacoustic signals generated for single pulse excitation (black) versus tone-burst of 3 pulses with the same total energy for α = 1 (blue) and α = 2 (red). (c) The corresponding frequency spectra of the signals. (d) Amplitude of the optoacoustic signals generated with the tone-burst excitation normalized to the signal generated with a single pulse with the same total energy.

Another non-linearity that can potentially affect optoacoustic signal generation when employing tone-burst excitation is associated with the temperature dependence of the optoacoustic signals. Indeed, absorption of a laser pulse causes an instantaneous temperature elevation that is proportional to the energy of the pulse [1]. If a second pulse with the same energy is absorbed before the tissue relaxes to the original temperature, the generated optoacoustic signal will have a larger amplitude due to the dependence of the Grüneisen coefficient on temperature [22]. The corresponding non-linearity of the signal generated by two consecutive pulses has been exploited e.g. for super-resolution imaging [22] and for facilitation of light focusing through scattering samples [23]. Non-linearities associated to temperature increases have also been induced via ultrasound heating [24] or using longer light exposure times [25]. The non-linear effects caused by temperature changes in the tone-burst excitation mode are illustrated in Fig. 3. Here thermal relaxation in a spherical absorber was estimated with a thermal diffusion model. The spatio-temporal temperature distribution given an initial temperature rise T₀ at t = 0 and r = 0 is given by

$$\mathrm{T}\left(\mathrm{r},\mathrm{t}\right)={\mathrm{T}}_0\frac{1}{{(4\mathrm{\pi }\mathrm{D}\mathrm{t})}^{3/2}}\mathrm{e}\mathrm{x}\mathrm{p}\left(-\frac{{\mathrm{r}}^2}{4\mathrm{D}\mathrm{t}}\right),$$ (10)

where D is the thermal diffusivity (D ∼ 114 × 10⁻⁹ m² s⁻¹ in biological tissues). We assumed that the initial temperature distribution can be approximated as a Gaussian with a FWHM given by the diameter of the sphere, i.e., t = t₁ = φ²/ln(2)16D in Eq. (10). The temperature at the center of the sphere is then estimated as

$$\mathrm{T}\left(\mathrm{r},\mathrm{t}\right)={\mathrm{T}}_0\frac{1}{{(4\mathrm{\pi }\mathrm{D}(\mathrm{t}-{\mathrm{t}}_1))}^{3/2}}.$$ (11)

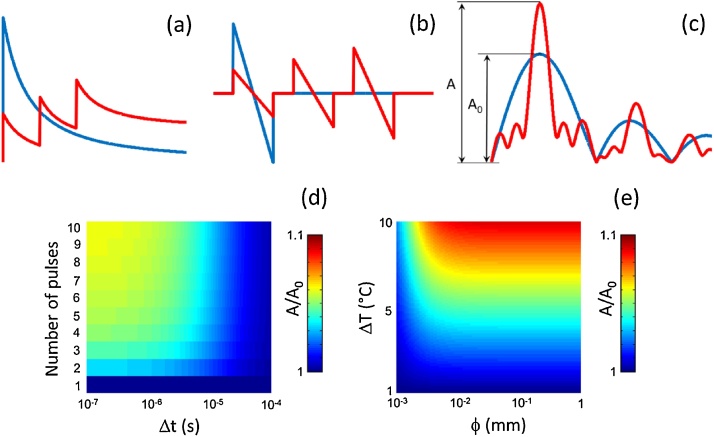
Fig. 3.

Effects of temperature increase in the signals generated with tone-burst excitation. (a) Temperature time profiles for single pulse (blue) and tone-burst excitation (red). (b) Optoacoustic signals generated for a significant temperature increase caused with each pulse. (c) Frequency spectrum of the signals. (d) Relative amplitude spectral density for the central frequency of the burst with respect to that of a single pulse for an absorber with ϕ = 5 μm and a temperature rise for single pulse excitation of 5 °C. (e) Relative amplitude spectral density for the central frequency of a burst of 3 cycles with Δt = 1 μs with respect to that of a single pulse.

The time dependence of the temperature of the sphere calculated in this manner is plotted in Fig. 3a for single-pulse (blue curve) and tone-burst (red curve) excitation. The maximum temperature reached with tone-burst excitation is lower than for a single pulse and is increased for Δt values below the thermal relaxation time. The optoacoustic signals generated by the tone burst were estimated by assuming that the temperature within the sphere is uniform and that the Grüneisen parameter significantly increases when the subsequent pulse is emitted. Fig. 3b and c shows the generated optoacoustic signals and their frequency spectra, respectively. It can be seen that optoacoustic amplitude increases for subsequent pulses, so that a higher spectral density is achieved for certain frequencies with respect to single-pulse excitation. This effect is further quantified in Fig. 3d and e. Specifically, Fig. 3d shows the peak value of the spectral density for tone-burst excitation normalized with the corresponding peak value for the single pulse excitation with the same total energy. The absorber was assumed to have ϕ = 5 μm and a temperature rise of 5 °C for a single pulse. Fig. 3e displays the same ratio for a tone-burst consisting of 3 cycles separated by 1 μs as a function of the diameter of the absorber and the temperature rise for a single pulse. Generally, a higher increase in the amplitude spectral density is produced for larger absorbers and for higher central frequencies of the burst, although it is generally rather reduced for relatively low temperature rises. If the temperature rise is relatively large, tissue damage may be produced. The degree of tissue damage is generally estimated from the peak temperature reached, although in some cases the exposure time is also taken into account [26]. In this regard, the peak temperature is higher for single pulse excitation than for excitation with a tone burst having the same optical energy, whereas the exposure time is higher when using a tone burst (Fig. 3a).

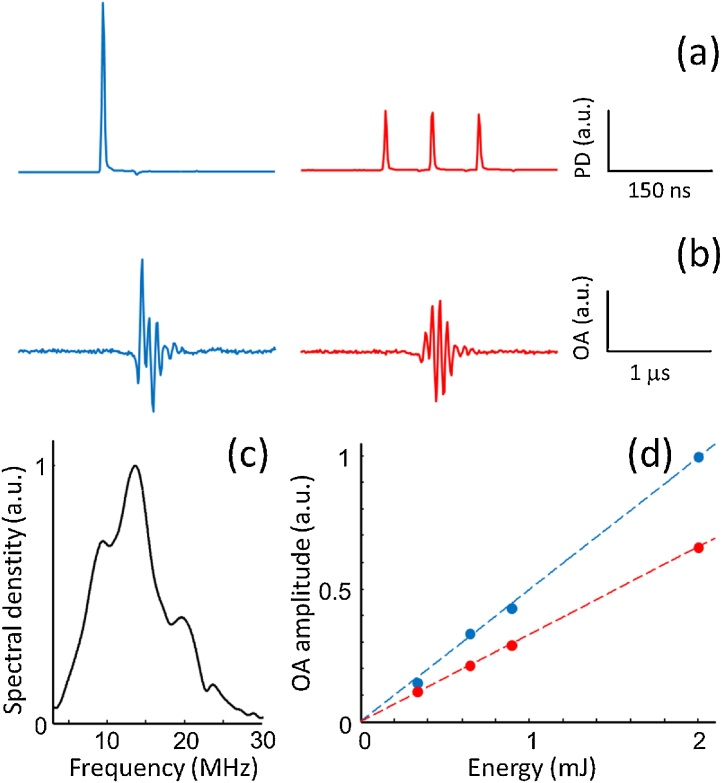
The SNR of the signals generated with single-pulse and tone-burst excitation was also compared experimentally (Fig. 4). A custom-made fiber bundle (Ceramoptec GmbH) was used to split an incident pulsed laser beam into multiple fibers with different lengths forming two outputs emitting a single pulse or a train of 3 pulses of equal energy separated by Δt ∼ 74 ns. The temporal profiles of the output beams for both outlets measured with a photodiode (Thorlabs, DET10A/M) are displayed in Fig. 4a. The total energy of the two output beams was approximately the same (∼2 mJ). A tunable optical parametric oscillator (OPO) laser (Innolas GmbH) set to 720 nm and 10 Hz was used as illumination source. The two outlets were subsequently positioned at a distance of ∼60 mm from a 0.86 μm inner diameter polyethylene tubing filled with undiluted black India ink (Higgins Inc.) with an approximate optical density (OD) of 2900 at 720 nm illumination wavelength. The light fluence was approximately 2 mJ/cm² at the tubing location. A narrowband piezoelectric transducer (Olympus, A313S-SU) was placed at a distance of ∼30 mm from the tubing to collect the generated optoacoustic responses. The signals were digitized with an embedded acquisition card (AlazarTech, ATS9351) having 50Ω input impedance, 12 bit vertical resolution and +-400 mV input range. No signal amplification was required due to the high absorption of ink. The effective bandwidth of the piezoelectric transducer in the detection mode was estimated by measuring an optoacoustic signal generated by a ∼20 μm diameter absorbing microsphere (Cospheric BKPMS 20-27). The Fourier transform of the signal, depicted in Fig. 4c, shows a central frequency of ∼14 MHz and a FWHM of ∼9 MHz. Neutral density filters (Thorlabs, φ1/2“) were positioned in front of the fiber outputs in order to vary the light energy absorbed by the tubings. The amplitude of the generated optoacoustic signals as a function of the pulse energy is depicted in Fig. 4d for single-pulse (blue dots) and tone-burst excitation (red dots). A linear dependence of the optoacoustic signal amplitude with laser energy was observed and a higher SNR was rendered with single pulse excitation. This is consistent with the fact that the spectral density is lower or equal at all frequencies for the tone-burst excitation in the linear optoacoustic generation regime.

Fig. 4.

Experimental comparison of single pulse and tone-burst excitation. (a) Photodiode signals at the output of the fiber bundle for single pulse (blue) and a tone-burst consisting of 3 pulses (red) with approximately the same energy. (b) Corresponding optoacoustic signals generated in a tubing of black India ink. (c) Spectral sensitivity of the ultrasound transducer for the detection of optoacoustic signals as determined with a single microsphere of ∼20 μm diameter. (d) Amplitude of the optoacoustic signals as a function of the optical energy for single pulse (blue) and tone-burst (red) excitation.

The optical density of the ink tubing is higher than that of blood (hemoglobin) for any optical wavelength, so that a linear behavior is also expected in blood for the same experimental parameters. Since other endogenous chromophores or extrinsically administered contrast agents are generally less absorbing than hemoglobin, it is expected that the linear relationship between the optoacoustic pressure and the optical energy is generally maintained for nanosecond duration pulses with energies below safety limits. Thereby, tone-burst excitation is expected to provide lower SNR for the same total energy delivered to the sample. However, the detected signal amplitude can readily be made higher if the total energy of the tone burst excitation in the above experiment is raised by ∼50%. As shown in Fig. 1, this can be done without exceeding safety exposure limits for a tone-burst frequency around 1 MHz. Generally, in case of total duration of the tone-burst exceeding 100 ns, the total energy delivered can be increased without compromising the safety standards. This may benefit a number of applications where the available detection bandwidth is severely limited, e.g. due to the use of air-coupled transducers for non-contact optoacoustic imaging [27]. Increasing the SNR in non-contact based approaches represents a substantial challenge in optoacoustic imaging. In addition, by exploiting the temperature dependence or the signals or optical absorption saturation, it may be possible to enhance the contrast and resolution of the images. It is also important to note that signal averaging can further enhance the SNR. However, optimum averaging is achieved for pulse repetition frequencies below 10 Hz due to safety exposure limits related to mean power density [20]. Hence, averaging equally benefits single-pulse and tone-burst excitation. Another potential application of the tone-burst excitation is Doppler-effect-based measurements of the blood flow. Reducing the bandwidth of the signals with an intensity modulated source based on a sinusoidal function of finite length has been previously shown to enable the detection of frequency shifts associated with the flow velocity [15], and tone-burst excitation based on a train of equally-delayed pulses may serve a similar purpose. In [15], excitation bursts of 5 pulses with central frequency of 1 MHz separated by 20 μs were used. If higher order harmonics are filtered out by the ultrasound transducer, approximately the same excitation bandwidth could be achieved by using 5 short pulses separated by 1 μs repeated every 20 μs.

In conclusion, while the optoacoustic signals generated with a tone-burst based on a train of equally-delayed pulses generally have lower SNR than those excited with a single pulse, some cases can be identified where the amplitude spectral density can be higher with tone burst excitation, which may benefit the sensitivity and imaging depth. Thereby, this excitation approach can become the method of choice for enhancing optoacoustic contrast in some applications.

Conflict of interest

The authors declare that there are no conflicts of interest.

Biographies

Daniel Razansky earned his B.Sc. and M.Sc.degrees in electrical engineering and his Ph.D. degree in biomedical engineering, all from the Technion – Israel Institute of Technology, and completed a postdoctoral training at the Harvard Medical School. Since 2007, he has been the Director of the Lab for Optoacoustics and Molecular Imaging Engineering at the Institute for Biological and Medical Imaging (IBMI), Helmholtz Center Munich and is also a Professor of Molecular Imaging Engineering at the Technical University of Munich. He has published more than 80 peer-reviewed journal articles and holds 10 patents and patent applications in bio-imaging and bio-sensing disciplines. He has also delivered more than 50 invited and plenary lectures worldwide and serves on a number of editorial boards of international journals and research council review boards. Professor Razansky is the recipient of a number of prizes and awards, among them the BioVaria spin-off Award and the ERC starting grant, and has been selected to appear in the “Young elite: Top 40 scientists under 40” list by the Capital magazine in 2011 and 2012.

Xosé Luís Deán Ben received the diploma in automatics and electronics engineering from the Universidade de Vigo in 2004. He received the PhD degree from the same university in 2009. Since 2010, he serves as a postdoctoral fellow at the Lab for Optoacoustics and Molecular Imaging Engineering at the Institute for Biological and Medical Imaging (IBMI), Helmholtz Center Munich. His major research interests are the development of new optoacoustic systems for preclinical and clinical applications and the elaboration of mathematical algorithms for fast and accurate imaging performance.