Energy Optimization in Gold Nanoparticle Enhanced Radiation Therapy

Abstract

Gold nanoparticles (GNPs) have been demonstrated as radiation dose enhancing agents. Kilovoltage external photon beams have been shown to yield the largest enhancement due to the high interaction probability with gold. While orthovoltage irradiations are feasible and promising, they suffer from a reduced tissue penetrating power. This study quantifies the effect of varying photon beam energies on various beam arrangements, body, tumour and cellular GNP uptake geometries. Cell survival was modeled based on our previously developed GNP-Local Effect Model (LEM) with radial doses calculated using the TOPAS-nBio Monte Carlo code. Cell survival curves calculated for tumour sites with GNPs were used to calculate the relative biological effectiveness (RBE) weighted dose. In order to evaluate the plan quality, the ratio of the mean dose between the tumour and normal tissue for 50 – 250 kVp beams with GNPs was compared to the standard of care using 6 MV photon beams without GNPs for breast and brain tumors. For breast using a single photon beam, kV+GNP was found to yield up to 2.73 times higher mean RBE-weighted dose to the tumour than two tangential MV beams while delivering the same dose to healthy tissue. For irradiation of brain tumors using multiple photon beams, the GNP dose enhancement was found to be effective for energies above 50 keV. A small tumour at shallow depths was found to be the most effective treatment conditions for GNP enhanced radiation therapy. GNP uptake distributions in the cell (with or without nuclear uptake) and the beam arrangement were found to be important factors in determining the optimal photon beam energy.

1. Introduction

Gold nanoparticles (GNPs) have been proposed as a radio-enhancers in radiation therapy. Hainfeld et al. first demonstrated improvements in tumour control in mice bearing subcutaneous EMT-6 mammary carcinomas receiving kilovoltage x-rays after injection of GNPs as compared to radiation alone(Hainfeld et al 2004). Subsequently, 11 nm diameter GNPs also showed radiotherapy enhancement after intravenous administration with orthotropic Tu-2449 malignant glioma in mice(Hainfeld et al 2013). Their long-term (>1 year) survival was 50% when combining GNPs and x-rays versus 0% for x-rays alone. This approach holds promise for the application of GNPs to human brain cancers in clinical radiation therapy. The GNP radio-enhancement is mainly attributed to secondary photoelectrons and the emission of Auger electrons which is maximized when kilovoltage x-rays are used.

The biological effectiveness of GNPs in the patient’s tumour must be predicted to make GNP radio-enhancement clinically applicable. Early theoretical studies have focused on macroscopic dose enhancement(Cho 2005). However, in vitro experiments, even with small concentrations of GNPs, have shown significantly greater radio-enhancement than macroscopic dose predictions(Jain et al 2011). Recently, the effects of GNPs in the dose enhancement have been investigated in the microscopic level to predict the biological endpoint(Koger and Kirkby 2016a, Lechtman et al 2013, Lin et al 2014, McMahon et al 2011, Sung et al 2016, Zygmanski and Sajo 2016). Especially, Local Effect Model (LEM)-based predictions of radio-enhancement were suggested based on the ideas of heterogeneous dose distributions inside the cell in GNP-enhanced x-ray therapy(Lin et al 2015, McMahon et al 2016, Sung et al 2017). The GNP-LEM predicts the survival fraction of cells treated with GNPs, which allows the calculation of relative biological effectiveness (RBE)-weighted dose distributions within the patient.

In radiation therapy, tumours are located at varying depths and have different sizes. The biological effect of GNP radio-enhancement is maximized with kilovoltage x-rays, which have less penetrating power in tissue. The use of kilovoltage x-rays may increase the surface dose and deliver radiation damage to normal tissue. Therefore, trade-off strategies between doses to tumour and normal organs are necessary to make GNP radio-enhancement clinically applicable.

This study calculated the dependency of cell survival for polychromatic photon energies, tumour depth, and GNPs distributions. Using those parameters, RBE-weighted dose distributions were calculated for clinically relevant scenarios, in which the target volume is located at several representative depth locations within various sizes of the patient.

2. Methods

2.1 Effect Modeling

Monte Carlo simulations were performed using the TOPAS/TOPAS-nBio version 3.0.p1(Agostinelli et al 2003, McNamara et al 2017, Perl et al 2012), which is based on Geant4 version 10.2.p01. The simulation and modeling procedures are briefly described in this paper. Detailed explanations can be found in our previous publications on GNPs radio-enhancement(Lin et al 2015, Lin et al 2014, Sung et al 2017).

Therapeutic x-rays with six different energies were incident on a water phantom. The spectra of polychromatic beams were acquired by SpekCalc 1.1(Poludniowski et al 2009). Different combinations of energies and filters were selected and modified from a study using various therapeutic x-rays with range from 50 kVp to 250 kVp(Ehringfeld et al 2005) as shown in Table 1.

Table 1.

Characteristics of the polychromatic x-rays used in this study.

	Filter material and thickness (mm)
Maximum Energy (kVp)	Tin	Copper	Aluminum	HVL (mm)	Mean Energy (keV)
50	-	-	1	0.9 Al	28.5
100	-	-	1.65	2.3 Al	45.6
150	-	-	2.4	4.4 Al	57.9
200	-	0.45	1	1.0 Cu	85.8
200	0.4	0.25	1.02	1.9 Cu	108
250	0.8	0.25	1.02	3.1 Cu	140

Fifty mm diameter phase spaces (files recording the position, momentum energy and particle type) perpendicular to the beam axis were acquired at selected depths (0.1, 2, 4, 8, 12, 16, 20 cm). For macroscopic simulations, the range cut was set to 1 μm and no step size limitation was applied. All particles reaching the phase space plane were included in the phase spaces.

The lengths of each phase space was manually adjusted to have the same diameter as a 15 nm single GNP. The angular distribution was also manually corrected using in-house python code. To ensure all particles are passing through the GNP, the direction for all particles were adjusted to be parallel to the primary beam directions. In order to not bias the result and consider contributions of laterally scattered electrons, each particle was given a weighting factor of 1/cos θ, where θ is the angle between the particle’s original direction and the primary beam direction to consider contributions of laterally scattered electrons (Lin et al 2015). These modified phases spaces were used to irradiate a single GNP. For this step the Geant4-Penelope physics list was used, which allows tracking of electrons down to 100 eV and 1 nm range cut was used for all particles. Only secondary outgoing electrons were recorded at the GNP surface in a second sphere-shaped phase space file.

This second phase space was used as the radiation source at the centre of a 60 × 60 × 60 μm³ water phantom to score radial doses in spherical shells of 1 nm radial thickness. Deposited dose was recorded and scored in spherical bins according to distance to the centre of the GNP. The Geant4-DNA physics list was used for this step and electrons were tracked down to 7 eV in water (Incerti et al 2010). The Geant4-DNA simulate all interactions explicitly and do not use any production cut. The default Geant4-DNA constructor was used, which includes the Champion elastic, Born excitation, Born ionisation, Sanche vibrational excitation, and Melton attachment models (Bernal et al 2015).

For both Geant4-Penelope and Geant4-DNA physics in microscopic simulations, the maximum step size was set to be 1 nm for all particles. For all simulation procedures, atomic de-excitation was activated including Auger production, particle induced x-ray emission (PIXE), and fluorescence.

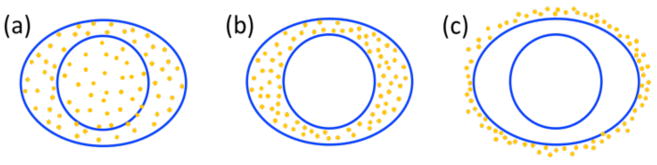
To predict the cell survival fraction, the radial dose was superimposed on each GNP location in the cell. To reduce calculation time, we found a fitting curve of Dose = a × (radius)^b + c such that a,b, and c are fitting parameters for several radial bins. The break points between radial ranges were 0.02, 0.1, 0.2, 0.6, 1, 2, 10, 15, and 20 μm with a maximum radius of 30 μm. At each location of a GNP, the radial dose was superimposed using this function. Since the cells investigated have a maximum diameter of 21.2 μm, the radial doses from single GNP dose overlay covers the entire cell in this study. Three GNP distributions were considered, i.e., GNPs located outside the cell membrane (media), in the cytoplasm (cyto), and homogeneously distributed inside the cell (homo). For this study we used human breast cancer (MDA-MB-231) and glioblastoma (T98G) cells which have previously been shown to be sensitive to GNP radio-enhancement in clonogenic assays(Butterworth et al 2010, Jain et al 2011). In addition, treatments for these tumours would benefit from a target dose escalation (or normal tissue dose reduction). To calculate the survival curves, we used the following parameters for the linear-quadratic equations: α = 0.019 and β = 0.052 for MDA-MB-231 cells(Jain et al 2011) and α = 0.04 and β = 0.03 for T98G cells(Butterworth et al 2010). The cells were represented by oval shapes with major/minor diameters of the cell membrane of 18.5/8.5 μm and 21.2/6.5 μm for MDA-MB-231 and T98G cells, respectively(Kaushik et al 2014, Liu et al 2015). The thickness of the cell is set to be 2 μm. The radiation sensitive nucleus at the centre was assumed to be 8 and 6 μm, respectively. An additional 2.5 μm thickness was added outside the cell to represent the extracellular media region. The number of GNPs was determined based on a 2% GNPs mass weight condition, which is comparable to gold concentrations achieved in vivo for tumour (1.5%) and blood (1.8%) (Hainfeld et al 2004, Hainfeld et al 2013). The GNP-LEM was implemented in 2D and the cell volume was assumed to be a cylinder with thickness of 2 μm. The 15 nm spherical GNPs were distributed without overlapping. This approximation is reasonable for in vitro cells because cells attached to a culture dish are flattened and similar to a 2D object. A schematic view of the cell shapes and GNP distributions is shown in figure 1.

Figure 1.

GNP distributions considered in this study. (a) homo: GNPs randomly distributed in the whole cell, (b) cyto: GNPs randomly distributed only in the cytoplasm, and (c) media: GNPs randomly distributed in the extracellular media

The cell survival curve was predicted based on the GNP-LEM as described in our previous work(Lin et al 2015, Sung et al 2017). For sparsely ionizing radiation, the dose-response curve (S_x) can be described with a threshold dose D_t and maximum slope S_max = α + 2βD_t (Eq. (1))

$${\mathit{S}}_{\mathit{x}}=\{\begin{array}{ll}{\mathit{e}}^{-\mathit{\alpha }\mathit{D}-\mathit{\beta }{\mathit{D}}^{\mathbf{2}}}\hfill & (\mathit{D}\le {\mathit{D}}_{\mathit{t}})\hfill \\ {\mathit{e}}^{-\mathit{\alpha }{\mathit{D}}_{\mathit{t}}-\mathit{\beta }{\mathit{D}}_{\mathit{t}}^{\mathbf{2}}}{\mathit{e}}^{-{\mathit{S}}_{\mathit{max}}(\mathit{D}-{\mathit{D}}_{\mathit{t}})}\hfill & (\mathit{D}>{\mathit{D}}_{\mathit{t}})\hfill \end{array}$$ Eq. (1)

This linear-quadratic-linear (LQ-L) model with two way representation was due to the overestimation of the single linear-quadratic model in the high-dose region(Astrahan 2008). The threshold dose D_t was set to 20 Gy for this study (Kramer et al 2000). The GNP-LEM assumed that equal local doses lead to equal lethal events. The lethal events (N) can be described using the above X-ray dose response curve (Eq. (2)).

$$\mathit{N}(\mathit{D})=-\mathit{ln}({\mathit{S}}_{\mathit{x}})$$ Eq. (2)

Increased effectiveness of densely ionizing radiation due to GNPs can be described by a combination of the dose response of sparsely ionizing radiation and the microscopic dose distribution(Katz 2003). Therefore, the average number of lethal events (N̄) in the nucleus describes the macroscopic surviving fraction with GNPs as follows:

$${\mathit{S}}_{\mathit{GNP}}(\mathit{D})={\mathit{e}}^{-\overline{\mathit{N}(\mathit{D})}}$$ Eq. (3)

The cell survival curve with GNPs was acquired for each depth, energy, and GNP distribution. Calculated survival curves up to 10 Gy were fitted using the linear-quadratic model (LQ model, e^{−αD−βD2}) to obtain α and β parameters for the cells with GNPs.

2.2 Patient dose calculations

A simple spherical phantom was used to represent the treatment sites of breast and brain cancer patients. For breast cancer patients, 11 and 13 cm diameter spheres were used to represent the minimum and maximum sizes of patients’ breasts (Huang et al 2011). For brain cancer patients, we used a diameter of 10 cm for a minimum paediatric head size, and 15, 17.5, and 20 cm for the adult minimum, mean, and maximum head sizes, respectively (Bushby et al 1992, Nguyen et al 2012, WHO 2007). Specific dose distributions for different field sizes were calculated by assigning a mask to the simple large field dose distributions. The source to isocentre distance was kept at 100 cm and the isocentre was placed at the centre of the spherical body.

When calculating the effective RBE for a given treatment, the values of RBE cannot be simply added when adding multiple treatment fields due to the dose dependency of RBE. A dose-weighted sum was applied to obtain the total α and β values using α_k and β_k for each condition (i.e., depth, incident photon energy, and GNP distributions) as shown below (Polster et al 2015). The α_k and β_k for a specific depth was interpolated using a look-up table of α_k and β_k for five depths with corresponding photon energy as described in equations 4 and 5.

$$\mathit{\alpha }=\frac{{\sum }_{\mathit{k}}^{\mathit{fields}}{\mathit{\alpha }}_{\mathit{k}}{\mathit{D}}_{\mathit{k}}}{{\sum }_{\mathit{k}}^{\mathit{fields}}{\mathit{D}}_{\mathit{k}}}$$ Eq. (4)

$$\mathit{\beta }={(\frac{{\sum }_{\mathit{k}}^{\mathit{fields}}\sqrt{{\mathit{\beta }}_{\mathit{k}}}{\mathit{D}}_{\mathit{k}}}{{\sum }_{\mathit{k}}^{\mathit{fields}}{\mathit{D}}_{\mathit{k}}})}^{\mathbf{2}}$$ Eq. (5)

The RBE corresponding to the delivered dose was calculated using the total α and β values. The RBE-weighted dose was calculated by multiplying the delivered dose and its corresponding RBE in each macroscopic voxel in the patient geometry.

To quantitatively evaluate the quality of the treatment modalities, the tumour to normal tissue ratio (TNR) was defined as the ratio of the mean dose delivered to the tumour and to healthy tissues:

$$\mathit{TNR}=\frac{\overline{{\mathit{D}}_{\mathit{tumour}}}}{\overline{{\mathit{D}}_{\mathit{healty}\mathit{tissue}}}}$$ Eq. (6)

Thus, the modality with higher TNR delivers less normal tissue dose for a given target dose. Also, to compare the effectiveness between treatment modalities, the enhancement factor (EF) was defined as the ratio of TNRs for a given energy (x) with GNPs and the standard of care MV photon therapy without GNPs, as shown below.

$${\mathit{EF}}_{\mathit{x}}=\frac{{\mathit{TNR}}_{\mathit{x},\mathit{GNP}}}{{\mathit{TNR}}_{\mathbf{6}\mathit{MV},\mathit{noGNP}}}$$ Eq. (7)

The standards of MV photon treatments were assumed to be two tangential and multiple arc fields for breast and brain, respectively. The EF provides an easy metric to show if the plan quality with GNPs is improved compared to the best treatment modalities without GNPs. An EF > 1 means that the dose distribution with kilovoltage GNPs radio-enhancement improves the plan over conventional 6MV treatment, while EF < 1 shows no potential of GNPs radio-enhancement for the corresponding treatment condition. For comparison purposes, all plans were normalized such that 90% of the relative RBE-weighted dose covered 90% of the tumour volume.

To obtain the plan quality dependency on the incident photon beam energy, variable parameters were used in the simulation: body diameter, tumour diameter, tumour location, GNP distribution, and treatment techniques. For breast cancer patients, diameters of 1, 3, and 5 cm tumour volume were considered. The depth along the radiation field axis (body surface to the closest tumour surface) was kept at 1 cm. For brain cancer patients, 0.25, 1, 2, and 3 cm radius tumours were treated. The brain cancer target was placed at the body centre or in the periphery region. For all patients, a constant 0.5 cm margin was added in all directions around the tumour volume.

Three GNP distributions were investigated: (a) homo: GNPs are randomly distributed in the whole cell including the nucleus and cytoplasm, (b) cyto: GNPs are randomly distributed in the cytoplasm only, and (c) media: GNPs are randomly distributed in the extracellular media only (see figure 1).

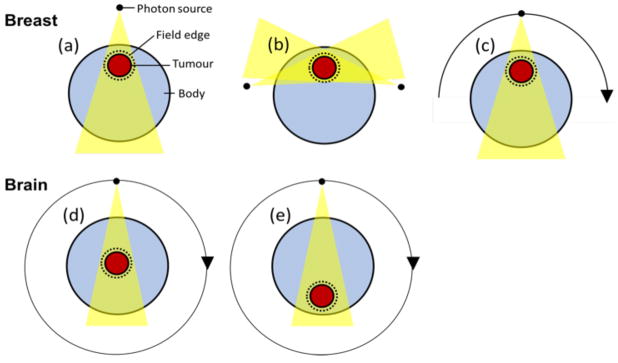
Three treatment techniques were investigated for breast cancer patients: (a) one port, (b) two port, and (c) half arc (photon source rotating 180 degrees) treatments. For brain tumour treatments, only full arc techniques, which used 40 beams with the photon source rotating 360 degrees, were considered for both, tumours located at the centre or in the periphery of the head (see figure 2).

Figure 2.

Treatment techniques considered for breast and brain cancer patients. (a) one port, (b) two port, and (c) half arc for breast cancer. Full arc for (d) central and (e) peripheral brain cancer patients.

3. Results

3.1 Breast

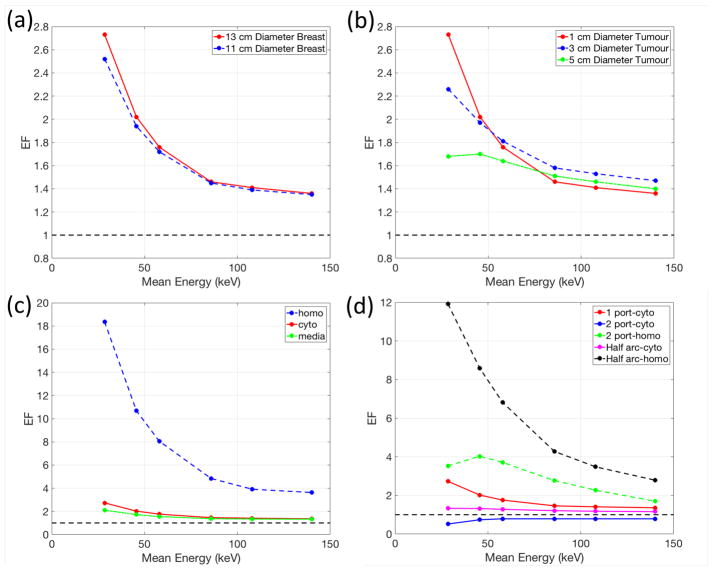
The effects of the incident photon beam energy on the breast plan quality with GNPs are shown in figure 3. The four breast cancer scenarios used to compare the plan quality are summarized in Table 2. For one port treatments, the EF is the largest at 2.73 for the lowest energy photon beams (figure 3(a)). All kilovoltage energy photon beams were superior to 6 MV. As the size of the tumour increases, higher energy photons were required to penetrate the tissue to cover the whole tumour volume (figure 3(b)). Therefore, the enhancement advantage of 50 kVp photons was reduced while high energy photons (≥200 kVp) became effective for certain sizes of tumours. Homogeneously distributed GNPs result in the maximum EF increase of up to 18.35 for the lowest photon energy (figure 3(c)). Each treatment technique induces different EF patterns depending on the incident photon energy and GNP distributions due to different required penetrating depths to deliver the dose to the tumour (figure 3(d)). Using two tangential photon beams (2 port) with the cyto GNP distribution was inferior to standard 6 MV treatments because of the short penetration depth of kV beams and the addition of GNPs did not increase the dose in the nucleus enough to compensate in this scenario. In other words, GNP radio-enhancement was less effective for all kilovoltage energies for a 2-port treatment compared to 6 MV unless the GNPs are internalized in the cell nucleus (homo). However, with different beam arrangements or GNP uptake inside the nucleus, the GNP radio-enhancement was able to overcome the limited penetrating power of kV beams.

Figure 3.

Dependency of the enhancement factor (EF) on the incident photon beam energy for various (a) sizes of the breast, (b) sizes of tumour, (c) GNP distributions, and (d) beam geometries. Note that the red solid line is for the same setup in all panels. Table 2 describes the settings for each panel.

Table 2.

Four clinical scenarios to compare between treatment modalities.

Figure 3 panel	Breast Diameter (cm)	Tumour Diameter (cm)	GNP Distributions	Beam Geometries
(a)	11, 13	1	cyto	one port
(b)	13	1, 3, 5	cyto	one port
(c)	13	1	homo, cyto, media	one port
(d)	13	1	homo, cyto	one port, two port, half arc

3.2 Brain

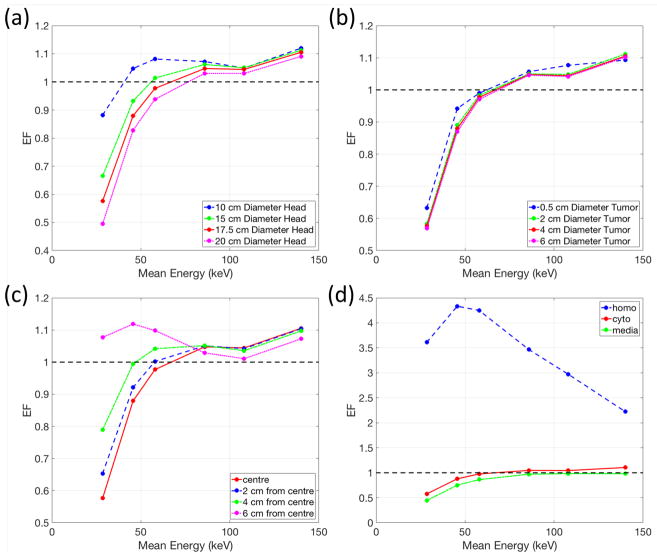
For brain cancer patients, the tumour was assumed to be treated with a full arc beam rotation. The three clinical scenarios used to compare the plan quality between treatment modalities are summarized in Table 3. Interplay effects between the penetrating power and dose enhancement with GNPs were observed (figure 4(a)). A higher photon energy has better penetrating power to deliver dose to the tumour at the centre while it decreases the amount of dose enhancement with GNPs. This conflict results in non-linear EF trends for all head sizes, even producing a local maximum EF around 50 keV for the 10 cm diameter head. However, for larger head sizes, the EF generally increases as the photon energy increases. The requirement to cover the whole tumour volume was not significantly affected by the size of tumour (figure 4(b)). Due to the reduced tumour to skin distance, a tumour located in the periphery of the body achieved higher EF with low energy photons around 50 keV (figure 4c)). The largest EF (up to 4.33) occurs with homogeneously distributed GNPs in the whole cell and low energy photon beams around 50 keV (figure 4(d)).

Table 3.

Four clinical scenarios used to compare different treatment modalities.

Figure 4 panel	Head Diameter (cm)	Tumour Diameter (cm)	Tumour Location from Centre (cm)	GNP Distribution
(a)	10, 15, 17.5, 20	4	0	cyto
(b)	17.5	0.5, 2, 4, 6	0	cyto
(c)	17.5	4	0, 2, 4, 6	cyto
(d)	17.5	4	0	homo, cyto media,

Figure 4.

Dependency of the enhancement factor (EF) on incident photon beam energy for various (a) sizes of head, (b) sizes of tumour, (c) location of tumour, and (d) GNP distributions. Note that the red solid line is for the same setup in all panels. Table 3 summarizes the settings for each panel.

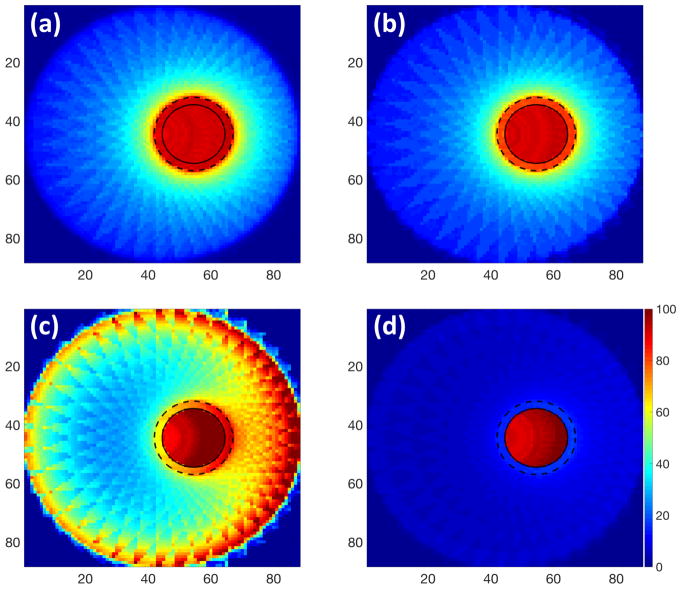
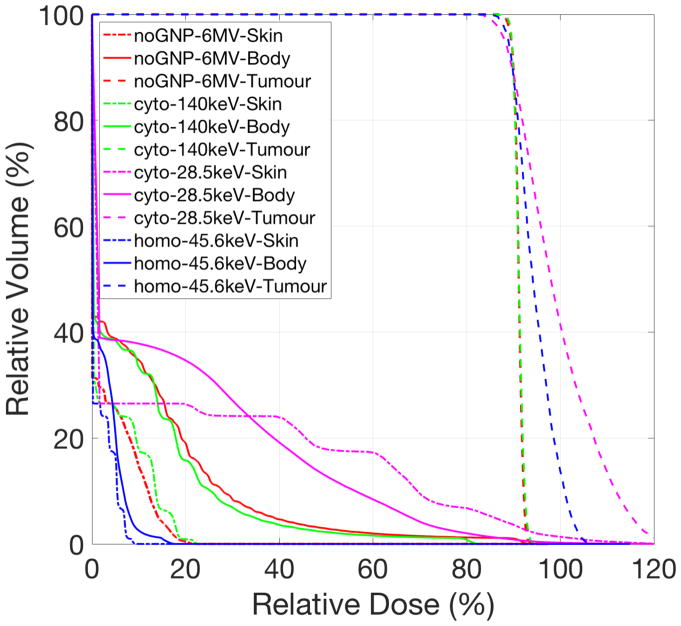
Figure 5 shows the RBE-weighted dose distributions for a 4 cm tumour in the pe riphery of a 17.5 cm head phantom. Figure 6 is the corresponding dose volume histogram. Using 6 MV photon beams, the TNR was 9.79 without GNPs which improved to 10.80 with GNPs distributed in cytoplasm and 250 kVp (figure 5(a) and (b)). The delivered dose to the body excluding the tumour region was reduced while maintaining the tumour coverage (figure 6). Even though the tumour cont ained GNPs in the cell cytoplasm, a large proportion of the healthy tissue received greater than 50% of the maximum dose if the photon beam energy was not op timized, for example using a 50 kVp (figure 5(c)). One particular concern for kVp photon treatments is the skin dose (0.5 cm thickness shell inside phantom surfa ce). We found that, for low energy photons (50 kVp) the skin dose was highly increased, however, for 250 kVp treatments with cyto GNP distribution, the skin dose was similar to conventional MV treatments, and could even be reduced if GNPs were taken up homogeneously (figure 6). If tumour cells take up GNPs in the whole cell (homo), the RBE-weighted dose was tightly conformed around the target (figure 5(d)) and, interestingly, 100 kVp was the optimal energy.

Figure 5.

Dose distribution maps for multiple photon beams treating a 4 cm diameter tumor in the periphery of a 17.5 cm diameter spherical head phantom. (a) 6 MV without GNPs, (b) 250 kVp (mean energy=140 keV) and (c) 50 kVp (mean energy=28.5 keV) with GNPs distributed in cytoplasm, and (d) optimal energy 100 kVp (mean energy=45.6 keV) with GNPs homogeneously distributed in the whole cell. The solid line indicates the tumour region. The dotted line represents the target region including tumour and margin.

Figure 6.

Cumulative dose-volume histogram (DVH) for photon beams treating a 4 cm diameter tumour in the periphery of a 17.5 cm diameter spherical head phantom. The curves correspond to the use of GNP cellular uptake (noGNP: without GNP uptake, cyto: GNPs distributed in cytoplasm, and homo: GNPs distributed in the whole cell), incident photon mean energy, and organs. Incident photon energies are 6 MV (mean energy=1.3 MeV), 250 kVp (mean energy=140.0 keV), 100 kVp (mean energy=45.6 keV), and 50 kVp (mean energy=28.5 keV). A shell thickness of 0.5 cm inside sphere surface was considered as the skin region. The dotted and solid lines indicate the DVH for the tumour and the body excluding the tumour volume, respectively. All plans were normalized such that 90% of the prescription dose covered at least 90% of the tumour volume.

Discussion

Several potential configurations were investigated for treatment planning with GNPs based on the GNP-LEM with Monte Carlo simulations. Effects of kilovoltage photon energies within clinically relevant ranges were studied. The EF was assessed as a function of the beam energy to compare GNP and no-GNP treatments. For breast cancer patients treated with one port beam, all photon energies were found to be effective with a maximum EF of up to 2.73. The EF tended to increase with decreasing tumour size with the lowest photon energy. On the other hand, for brain cancer patients treated with multiple beams, higher photon energies above 50 keV were more effective in increasing the tumour dose with GNPs. The EF was shown to increase as body size decreases as this allowed the selection of lower photon energies increasing the GNP radio-enhancement. For both cases, if the GNPs were homogenously distributed inside the cell, the EF was increased significantly up to 18.35 and 7.09 for breast and brain cancers, respectively (Table 4 and 5).

Table 4.

Maximum enhancement factor (EF) with corresponding mean incident photon energy for one port beam treating 13 cm diameter breast.

Tumour Diameter (cm)	GNP distribution
	cyto	homo	media
1	2.73 (28.5 keV)	18.35 (28.5 keV)	2.10 (28.5 keV)
3	2.26 (28.5 keV)	15.12 (28.5 keV)	1.75 (28.5 keV)
5	2.26 (45.6 keV)	11.11 (28.5 keV)	1.75 (57.9 keV)

Table 5.

Maximum enhancement factor (EF) with corresponding mean incident photon energy for multiple beams treating a 4 cm brain tumour.

Head Diameter (cm)	Tumour Location	GNP distribution
		cyto	homo	media
10	centre	1.12 (140 keV)	5.90 (28.5 keV)	0.99 (108 keV)
15	centre	1.11 (140 keV)	4.73 (45.6 keV)	0.99 (108 keV)
17.5	centre	1.11 (140 keV)	4.33 (45.6 keV)	0.98 (108 keV)
	6 cm from centre	1.12 (45.6 keV)	7.09 (28.5 keV)	0.96 (85.8 keV)
20	centre	1.09 (140 keV)	4.03 (57.9 keV)	0.97 (140 keV)
	6 cm from centre	1.09 (140 keV)	5.62 (28.5 keV)	0.98 (57.9 keV)

The calculation approach in this study has several limitations. First, the photon attenuation due to gold was not taken into account. The interaction of radiation with gold was considered only in the effect modeling but not in patient dose calculations. The RBE-weighting factor was separately derived from cell survival in GNP-LEM. In the last step, the macroscopic patient dose was independently calculated and multiplied by the RBE-weighting factor to acquire RBE-weighted dose distribution. Due to this omission of photon attenuation by gold, the delivered dose to normal organs behind the tumour is expected to be smaller than reported in this study. Thus, the TNR with GNP is expected to be higher if gold attenuation is considered. In other words, the TNR with GNPs could be slightly underestimated in this study. Second, we used a simple binary mask to calculate the dose distribution in a given volume for specific field sizes. This neglects the penumbra dose distributions and the scatter from out of fields regions. The delivered dose to normal organs would be overestimated in this study but the general trend of EF should not differ significantly. In our breast phantom, normal organs such as heart and lung doses were not fully considered; the dose to normal tissue is simply calculated in a sphere around the tumour. To fully assess the clinical impact one would have to model all relevant organs at risk. The development of a convolution-superposition algorithm for kilovoltage photon dose distributions may resolve the limitations of this study. Third, a radial dose symmetry was assumed in this study. This one-dimensional dose distribution approach may lead to errors due to the anisotropic angular emission of Auger and photoelectrons (Gadoue et al 2017). It was reported that the variation exceeds 8% at 100 nm distance for 50 nm GNPs exposed to 120 keV X-rays.

Another limitation of our study is the Geant4-Penelope model used for radiation interactions with GNPs. The Geant4-Penelope has limitations for dosimetry at the nanometer scale because this is condensed-history model (Lazarakis et al 2018). This study neglected the electrons of energies below 100 eV, which can travel distances up to 15 nm in liquid water (Kyriakou et al 2016). In addition to that, the Geant4-Penelope physics list ignores reduced dimensionality and exchange-correlation effects of the GNPs, which may influence electron transport at the nanometre scale (Emfietzoglou et al 2013, Emfietzoglou et al 2017, Kyriakou et al 2011). An upcoming release of Geant4-DNA physics models is expected to include a more detailed description of electron transport for gold. Such improved physics description of the interaction of the radiation field with gold would further improve the results of this study, in particular in close proximity to GNPs compared to the currently used low-energy extension of the condensed-history physics models (Livermore and Penelope) (Kyriakou et al 2017, Sakata et al 2016, Sakata et al 2018).

In our current study, we only investigated simple biological parameters although those values are sensitive to photon energy and cell lines. The α and β values for the survival curve without GNPs were produced from cell lines irradiated with 160 kVp in other GNP radio-enhancement studies (Butterworth et al 2010, Jain et al 2011). Those α and β values are dependent not only on energy but also on the in vivo cancer type. Also, the cell-specific threshold dose (D_t) in GNP-LEM has effects on the cell survival curve (Paganetti and Goitein 2001). While there is some expectation that D_t decreases as the magnitude of α/β decreases, extracting this value from experimental results may be difficult (Astrahan 2008). It has been also reported that the LQ approximation would be still reasonable at doses in the 20 Gy range (Brenner 2008, Sachs et al 1997). For biological modeling of GNP radio-enhancement, the dose response curve was reported to be sensitive to D_t in the range of 10 to 30 Gy for 2 nm GNP but was found to be much less sensitive for 50 nm GNP (Lin et al 2015). For 15 nm GNPs used in this study, the maximum difference of the area under the survival curve was found to change by only up to 1.6% in a range of 10 to 30 Gy for D_t. However, a successful translation of GNP-mediated radio-enhancement to clinical application requires not only the consideration of the physical aspect but has to also encompass the chemical and biological aspects of radiation action. (Cui et al 2017, Ngwa et al 2014). In addition, the current physical model still is subject to significant uncertainties in the low-energy domain (Nikjoo et al 2016). Nevertheless, our results can serve as qualitative estimates comparing various treatment modalities.

For arc treatment, the results were similar with the effect greatest near a mean source energy of 50 keV. However, we discovered that the effects were also dependent on beam geometry and GNP distributions. If treatment setups are not optimized, the skin dose can be a critical problem when using kilovoltage photon beams as observed in figure 5(c), especially for breast treatment. Intensity modulation may further improve the dose distribution in the normal tissue as in conventional MV treatments. The findings highlight the need of a specialized treatment planning system for GNP-enhanced radiation therapy. The development of inverse optimization is required to provide easy and rigorous beam geometry to acquire optimal GNP-RBE-weighted dose distributions as currently implemented clinically for intensity modulated radiation therapy (IMRT).

The distribution of GNPs was found to be the most significant factor influencing the dose enhancement as observed in our previous studies. If GNPs are randomly distributed in the whole cell, the EF was increased rapidly up to 18.35 and 7.09 for breast and brain cases, respectively. However, several studies have investigated that GNPs are rarely internalized to the cell nucleus(Chithrani et al 2006). Therefore, this study focused on GNPs distributions only in the cytoplasm. In addition, the concentration of GNPs is a significant factor. This study assumed a relatively high concentration of 2% w/w gold achieved by intravenous administration. Different GNP concentration throughout the phantom will influence the amounts of radio-enhancement.

For intravenous GNP delivery, the first barrier is the vascular tumour endothelial cell, which are thin cells with the nucleus in close contact with the cell membrane. As reported in previous studies, cell geometry is one of the crucial factors in GNP radio-enhancement and the effects could be increased as the nucleus to GNP distance decreases(Sung et al 2017). Moreover, in vivo cells are 3D structures while this study used a 2D computational model with constant 2 μm thickness because in vitro flat cell are attached to a cell culture dish. Further investigation is necessary to evaluate radio-enhancement in 3D in vivo cellular condition.

Koger and Kirkby have demonstrated the energy effects of GNP enhanced arc radiation therapy over the 6 MV treatment by converting dose-to-medium to dose-to-tissue(Koger and Kirkby 2016a, b). Instead, we developed a photon energy-dependent RBE-weighted dose calculation, which have been widely used in particle therapy treatment systems.

One additional consideration is, that our study was based on dose enhancements caused by the addition of GNPs, with the biological effect fitted using in vitro cell survival curves. The radiation response to the cells could be different between in vitro and in vivo systems. The in vitro RBE values are determined using colony formation while the in vivo RBE values are for tissue response endpoints in different conditions. However, in vivo effects of GNP enhanced radiation effects have been consistently reported to be higher than when studied in vitro(Butterworth et al 2012, Schuemann et al 2016). Our results already show the potential for a large increase of RBE-weighted dose for orthovoltage GNP-therapy. The in vivo effectiveness of GNPs may be even larger than reported here.

Conclusions

A simple treatment planning system was established to investigate the effects of varying parameters for GNP-enhanced radiation therapy. These parameters included body size, tumour size, tumour location, GNP distribution, beam geometry and photon energy. For GNPs distributed in the cell cytoplasm, the mean dose to the tumour for a constant tissue dose was found to vary significantly, resulting in an enhancement factor from 0.5 to 2.7 compared to 6 MV treatments, depending on the geometry and energy. The beam geometry was a crucial factor to find the optimal photon energy. The most effective treatment condition for GNP-enhanced radiation therapy occurred when the body and tumour sizes were smaller and GNPs were distributed in the whole cell.