A Small-Angle Scattering Environment for In Situ Ultrasound Studies

Abstract

Ultrasonic devices are common tools in laboratory and industrial settings to produce cavitation events for cleaning, emulsification, cell lysis and other materials applications. Effects of sonication at the macroscopic scale can be visible while effects at the molecular and nano-scales are not easily probed and, therefore, not fully understood. We present a new small angle scattering sample environment designed specifically to study structural changes occurring in various types of dispersions at the nano-scale due to ultrasonic acoustic waves. The sample environment features two face-to-face high-intensity focused ultrasound transducers coaxially aligned and normal to the neutron/x-ray beam propagation direction. A third broadband transducer is fixed beneath the scattering volume to acoustically monitor for cavitation events. By correlating acoustic data to scattering data, measured structural changes can be correlated to changes in parameters such as frequency, acoustic pressure, or cavitation pressure threshold. Several example applications of colloidal systems effectively influenced by ultrasound fields are also presented to demonstrate the capabilities of the device and to motivate future work on in-situ scattering analysis of ultrasound materials processing methods.

Graphical Abstract

We designed and tested a calibrated ultrasound sample environment for in situ small-angle X-ray and neutron scattering measurements.

Introduction

Although ultrasound is often associated with diagnostic imaging or sonar, ultrasonic baths and tip sonicators are commonly used tools in industrial and research laboratory settings. Sonication is often used for mechanical disruption for applications such as emulsification, cleaning, and resuspension of particles. The mechanical stresses used in sonication are the result of the formation and violent collapse of vapor cavities in a process known as cavitation.^1–3

Cavitation is often associated with high localized pressures, stresses, and temperatures in the vicinity of collapsing bubbles.^4–7 Under certain conditions, cavitation can also lead to free radical formation or even to light emission in a process known as sono-luminescence.^1,2,8–10 It has been estimated that the peak velocities achieved during bubble collapse are on the order of 1500 m/s while temperatures can exceed 3000 K.^3,5,11–13 Stresses from cavitation bubble collapse impinging on components can produce sufficient force for premature wear and failure of components in mechanical systems such as ship propellers, bearings and valves.⁶

Although sonication is most often associated with the breakdown of objects into smaller fragments (e.g. emulsification, dispersion, and cleaning), there have also been examples of using it to promote the assembly and growth of larger objects.^3,11,14–16 Fusing of metallic nanoparticles to form large porous metallic aggregates was one of the earliest demonstrations that acoustic cavitation could be used to promote the assembly of larger objects from microparticles. The fusion of metallic particles to form porous agglomerates was due to high temperatures within the immediate vicinity of the cavitation volume.^11,17,18

In the field of sono-crystallization, acoustic cavitation promotes the formation of crystalline nuclei that can accelerate crystallization. Several studies have demonstrated that a variety of proteins and pharmaceutical agents can be successfully crystallized with ultrasound.^14–16 Here, the acoustic conditions used can be tuned to control particle size by balancing sono-crystallization with sono-fragmentation.¹⁹ This is of particular interest in improving drug solubility as well as creating nanoparticle suspensions that can be aerosolized for pulmonary delivery.^14–16,19

In the field of sonochemistry, stresses and free radicals formed from cavitation drive reactions. This field can be separated into two categories.¹ The first are reactions that occur or are accelerated due to physical effects. A classic example of this is the acceleration of Ullman coupling in the reaction of 2-iodonitrobenzene in dimethylformamide in the presence of copper.²⁰ An acceleration of as much as a 50 times in reaction rates can be achieved by cavitation within the sample cell.²⁰ Here, acoustic fields enhance the reaction by both promoting mass transfer through acoustic streaming and localized heating in the vicinity of a bubble due to cavitation. The second class of sonochemical reactions are driven by free radicals formed during cavitation.¹ Sonochemical free radicals are formed from cavitation bubble collapse generating sufficiently high temperatures and stresses to dissociate solvent molecules or other dissolved solutes.^2,10,21 Sonochemcial free radical formation has been used in a variety of applications including free radical polymerization, environmental remediation, and nanoparticle synthesis.^21–30

In recent years, there has been an increasing number of studies using sonication to promote the assembly of micro and nano-structures. In the field of organic electronic devices, alignment of conductive polymers is critical to improving charge transport. Strategies such as electric field alignment, shear forces and gravity have all shown to enhance growth, alignment and charge transport for polymers such as poly-3-hexylthiophene (P3HT).^31–34 Recently, several studies have also suggested that sonication of P3HT solutions will produce long nanofibers, which can further improve charge transport and device performance.^35–38

Unfortunately, for many of these systems the underlying mechanisms driving structural modifications through acoustic forces are not fully understood. In this study, we present a new scattering sample environment to study physical changes in a complex fluid system exposed to a controlled ultrasound acoustic field. The new sample environment, which can be used for either in situ X-ray (SAXS) or neutron (SANS) scattering measurements, allows users to vary acoustic conditions (e.g. pulse repetition frequency, pulse duration, acoustic pressure, and frequency) while simultaneously monitoring structural changes in the sample via scattering. The system also integrates acoustic cavitation detection to assist in decoupling changes observed in the insonated system due to cavitation versus those that may occur simply due to the propagation of non-cavitating acoustic waves. In this work, we first discuss the design, use and characterization of the acoustic sample environment. This is then followed by several short examples demonstrating the functionality and limitations of the new sample environment.

Methods

The acoustic sample environment was designed while considering a number of important factors including the scattering volume, the acoustic beam profile, acoustic attenuation, acoustic standing waves, sonophoresis and cavitation detection. System validation was conducting using ultra-small-angle X-ray scattering (USAXS) as well as small-angle neutron scattering (SANS).

Assembly

The acoustic sample environment consists of three primary components: a sample holder, two transmitting spherical-focus transducers, and a receiving PVDF transducer (Figure 1 and supplemental material). The central sample holder contains X-ray and neutron transparent windows on the front and back surfaces. The X-ray/neutron windows could accommodate 100 μm thick Kapton films or 1 mm thick quartz disks 15 mm in diameter, sealed with Viton O-rings. The left and right sides of the sample environment has acoustically transparent Kapton film windows for efficient acoustic transmission and for facilitated sample changes. They are also sealed with Viton O-rings. Beneath the sample holder there is an in-house designed polyvinylidene difluoride (PVDF) wide-band acoustic transducer (unfocused, 28 μm thick) with nearly constant sensitivity up to a 40 MHz bandwidth to record and monitor acoustic signals due to cavitation. The PVDF transducer is in direct contact with the sample environment through a blind hole and acoustically coupled using ultrasound gel (Medline, Mundelein, IL, USA). A threaded hole on the top of the device is used for sample loading/unloading. The filling port can be sealed with an O-ring fitted thumb screw. Optional temperature monitoring can also be performed by threading a thermocouple through the sample filling port.

Figure 1.

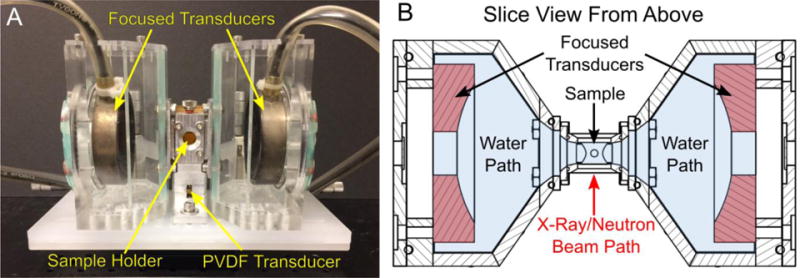
(A) The assembled focused ultrasound sample environment and (B) a top down slice view through the midplane of the sample environment. The sample is held in an aluminum sample holder in the center of the apparatus. 100 μm thin Kapton windows cover the front and back face of the sample holder where the X-ray or neutron beam must pass. Similarly, Kapton film windows are used on the left and right face of the sample holder for acoustic transmission. Beneath the sample holder is a custom built unfocused polyvinylidene (PVDF) transducer that is acoustically coupled to the aluminum body of the sample holder with ultrasound gel. Left and right of the sample holder are two chambers acoustically coupled to the primary sample holder with gel. Each chamber holds a focused transducer submerged in degassed water to insonate the sample.

Chambers containing the spherically-focused acoustic transducers were positioned left and right of the sample holder in a coaxially aligned configuration. Both chambers were in acoustic contact with the sample holder via medical ultrasound gel. The isolation of the transducers and the sample holder allows for quick sample changes and minimizes the required sample volume (~ 5mL). Degassed, filtered and deionized (DI) water was used as the coupling medium for the transducers. By degassing and filtering the water in the chambers it is possible to minimize cavitation in the coupling medium. The two acoustic chambers are tapered at a 55° angle to accommodate transducers with a f-number (focal length to transducer diameter ratio) as low as 0.95. Each transducer is bolted in place against the back of the acoustic chambers using an acrylic back plate fitted with silicone O-rings. The back plate is machined such that the focus point of the transducer coincides with the center of the sample holder. Virtually any transducer with diameter less than 70 mm and with a focal length greater than 18 mm could be adapted to the acoustic chamber by machining a back plate with the appropriate dimensions. In the experiments presented in this work, we use two identical spherically focused transducers (H-102, f-number 0.95, Sonic-Concepts Inc., Bothell, WA, USA) of 68 mm in diameter and 1.24 MHz frequency.

The sample holder, PVDF transducer, and acoustic transducer chambers were fixed onto a machined base plate that was magnetically coupled to the USAXS or SANS instrument. An aluminum mounting point with four alignment pins at the center of the base plate ensured repeatable positioning of the sample holder during sample changes. The transducer chambers were fixed to the slots in the base plate using four bolts allowing axial translation (along the acoustic beam axis) for quick coupling/decoupling from the central sample holder. Bolts on the left and right side of the sample holder sealing the acoustic windows were used to register consistent positioning of the transducer chambers to the sample environment (See supplemental material).

A laptop was used for control and data acquisition using MATLAB codes (Mathworks Inc., Watham, MA, USA). The transducers were driven using short N-cycle sine-wave bursts generated from a dual-channel arbitrary waveform generator (4154, BK Precision, Yorba Linda, CA, USA) amplified by 55 dB through a linear amplifier (A150, ENI, Rochester, NY, USA). A detailed block diagram of the sample environment can be found in supplemental figure 1. The transducers were activated in an alternating configuration to avoid sonophoresis from a single transducer (i.e. sample depletion in the scattering volume due to acoustic radiation force) or sample enrichment at acoustic standing wave antinodes (i.e. during simultaneous transducer activation). Sonophoresis is a significant concern in the design of ultrasound sample environments since it can result in the modification of the scattering intensity that could be incorrectly interpreted as a change in the structure. The pulse amplitude, pulse duration, pulse repetition frequency, and transducer switching frequency were controlled using the laptop through the waveform generator. In general, the acoustic sample environment is driven at peak-to-peak voltages between 0 V and 450 V (corresponding to peak negative pressure amplitudes from 0 to 7.2 MPa), pulse duration of 40 cycles (32.3 μs pulse length), pulse repetition frequency of 6.2 KHz, and switching between each transducer at a rate of 1 Hz.

Acoustic data used for cavitation detection was captured using a custom PVDF transducer connected to a wide band preamplifier (Precision Acoustics, Dorchester, UK). Waveforms from the PDVF transducer were sampled at 200 MHz using an oscilloscope (2190D, BK Precision) and transferred to the computer via USB connection. All acoustic data was time-stamped and settings were stored for possible co-registration with changes observed in scattering profiles.

A data acquisition card (USB-6001, National Instruments, TX, USA) was used to digitally synchronize the laptop controlling the acoustic sample environment with the X-ray or neutron scattering instrument. By detecting start and stop triggers from the scattering instrument, a series or sonication conditions could be queued to automate parameter scans and data acquisition.

Acoustic and Incident Scattering Beam Co-Alignment

The center of the acoustic field was found by identifying the maximum reflected signal off of a spherical target from the two transmit transducers. The reflective target was a 3 mm sphere made of steel (used in USAXS experiments) or a polymer bead (used in SANS experiments) attached to a 21-gauge blunt needle fixed to a bolt. Because the fill port of the sample holder was threaded, the vertical position of the spherical target was adjusted by simply turning the bolt attached to the spherical target (see supplemental figure 2). During the USAXS experiments the beam was aligned to the center of the acoustic field by moving the sample environment on a motorized stage such that the center of the spherical target was centered on the beam using radiography imaging. A beam-defining aperture for X-ray experiments was not necessary because the beam diameter of the USAXS instrument (0.8 mm × 0.8 mm) was smaller than the acoustic field dimensions (1.7 mm radial × 6.8 mm axial).

Because the beam diameter (12.5 mm diameter) during SANS experiments is considerably larger than the acoustic field area (1.7 mm radial by 6.8 mm axial), a slit-based beam defining aperture was used to co-align the neutron scattering volume to the acoustic beam focus. A set of micro-positioners were used to translate a 1 mm by 8 mm cadmium aperture to ensure the scattering volume coincided with the maximum acoustic field. After positioning the spherical target at the location of maximum acoustic reflectivity, neutron transmission measurements were collected at different aperture heights to locate the center of the spherical target. Because the spherical target attenuated the neutron beam, the position of minimum transmission was identified as the center of the acoustic field (see supplemental figure 2).

Simulations

The geometry of the sample environment was optimized through simulations of the acoustic field using COMSOL Multiphysics (COMSOL Multiphysics, COMSOL Inc., Burlington, MA, USA). The equations for linear acoustics were solved using a 2-dimensional domain representing the horizontal and vertical cross-section of the sample environment. For all simulations, a minimum of 7 elements per wavelength was used to resolve the acoustic field. The propagating medium was assumed to be water with a speed of sound of 1530 m/s and a density of 997 kg/m³. All results were obtained used conditions mimicking the 1.24 MHz spherically focused transducers used in the experiments.

Acoustic Beam Profiling & Calibration

A calibration curve of the acoustic pressure output from the transducers was measured using both a fiber optic hydrophone (FOPH 2000, RPI Acoustics, Germany) as well as a needle hydrophone (HN-1000, Onda Corp., Sunnyvale, CA, USA) in a degassed water tank. The beam profile along the axial and radial axes were profiled in free field using the needle hydrophone. Additional needle hydrophone measurements were made using the ultrasound chambers attached to the transducer and the sample holder in place to determine acoustic losses due to the membranes and geometric confinement.

Cavitation Analysis

Cavitation events are passively detected using a broadband PVDF transducer using methods adapted from Arnal et al. 2015 and Li et al. 2017.^39,40 A minimum of 270 acoustic waveforms were collected for each acoustic condition. The waveforms were divided according to which transducer was triggered at any instant in time. After pre-processing all of the data for each transducer, the results from the two transducers were averaged. The cavitation signal was isolated by subtracting an averaged background acoustic signal. A 40 μs window beginning 43 μs (one-way time of flight from the transducer face to the acoustic focus) after the transducer was fired was used to compare the time-averaged cavitation signal relative to background measurements. When the acoustic signal exceeded a value 9-times greater than background, they were flagged as cavitation events. The minimum threshold pressure needed to induce cavitation was defined as the point of 50% cavitation probability. This was numerically found by fitting a sigmoid curve to cavitation probability versus acoustic pressure.

Sonication of Pure Fluids

Pure fluid samples tested included filtered deionized (DI) water and ethanol during USAXS measurements. Each sample was sonicated with increasing acoustic pressures from 0 to 7.2 MPa peak negative pressure while simultaneously acquiring USAXS measurements at 90 second intervals.

Emulsification of Perfluorooctane in Water

To prepare emulsion samples, 3 % by volume of perfluorooctane (PFO) was introduced into DI water. A coarse PFO emulsion was synthesized by sonicating the sample using a tip sonicator (Digital Sonifier 450, Branson, Danbury, CT, USA) at 30% amplitude for 10 seconds with a 50% duty cycle (0.1 seconds on, 0.1 seconds off for a 5 second total sonication period). The PFO emulsion was loaded into the sample cell and exposed to varying pressures from 0 to 7.2 MPa while simultaneously acquiring USAXS measurements. At each pressure, the sample was exposed to 90 seconds of sonication with simultaneous USAXS data collection.

Resuspension of Dry Silica Particles in Water

A coarse silica particle dispersion was prepared by introducing 0.25 weight % of dry silica powder (Seahostar KE-P10, Nippon Shokubai Co., Chuo-ku, Osaka, Japan) in DI water and mixing via vortex mixing for 10 seconds. The sample was then loaded into the acoustic sample environment for 10 minutes of continued insonation at 7.2 MPa of peak negative acoustic pressure. An initial USAXS measurement was taken prior to sonication. During sonication, USAXS measurements were made at 30 second intervals.

Formation of Pickering Emulsions

The role acoustic forces play in the formation of Pickering emulsions was also demonstrated using a gold nanoparticle (GNP) and PFO emulsion system. GNP coated perfluorocarbon emulsion systems have been previously synthesized and characterized for sono-photoacoustic imaging as well as therapy.^40,41 The method was adapted from Arnal et al. 2015 and Larson-Smith et al. 2012.^40–43 Briefly, 12-nm diameter GNP dispersions were synthesized using a citrate reduction method. The GNP were then functionalized with 10 kDa thiol-terminated poly-(ethylene glycol)-methyl-ether (PEG-thiol) achieving a surface coverage of 8 PEG chains/nm². After PEGylation, butanethiol (~20 chains/nm² surface coverage) was added into the GNP solution and allowed to react overnight. The GNP solution was then added to a PFO emulsions (previously prepared using the abovementioned method) at a 50:1 PFO: GNP volume ratio. The samples were then immediately loaded in the acoustic sample environment and sonicated for 90 seconds with simultaneous USAXS measurements.

Sono-Crystallization of Fullerenes

Fullerenes are commonly used to enhance charge transport and performance in organic electronic devices. In recent studies, sonication been shown to assist in organizing phenyl-C61-butyric acid methyl ester (PCBM) into nanosheets.^44,45 Here, the crystallization of phenyl-C61-butyric acid methyl ester (PCBM) due to sonication was studied using SANS. PCBM (99%, Lot PC6-208, SES Research, Houston, TX, USA) was dissolved in d4-1,2-dichlorobenzene (Cambridge Isotope Laboratories, Cambridge, MA, USA) at a concentration of 5 mg/ml at 80°C. After cooling the PCBM solution to room temperature, an equal volume of d4-methanol (Cambridge Isotope Laboratories, Cambridge, MA, USA), a poor solvent, was added to the PCBM solution to achieve a 1:1 volume ratio of deuterated methanol to dichlorobenzene. The mixture was then mixed 5 minutes using a sonication bath. After allowing the sample to rest for 20 hours, the PCBM solution was then transferred to the acoustic sample environment. SANS measurements were then collected before and after 150 min of insonation at 6.8 MPa, which exceeded the cavitation threshold for the solution.

Scattering Measurements and Data Reduction

Sample environment testing and validating was performed on the 9ID-C USAXS beamline at the Advanced Photon Source (APS) at Argonne National Lab, NGB 30 m SANS beamline at the National Institute of Standards and Technology National Center for Neutron Research (NIST NCNR), and the GP-SANS CG-2 beamline in the High Flux Isotope Reactor at Oak Right National Lab (ORNL). SANS measurements were taken at three detector positions to cover a q-range of 3×10⁻³ Å⁻¹ to 8×10⁻² Å⁻¹. All data were reduced using standard techniques established by APS, NIST, and ORNL^46–48.

Results and Discussion

Simulations and Acoustic Characterization

Simulations of the acoustic field were used to guide the design of the sample environment (figure 2). The environment required a balance of maximizing acoustic transmission efficiency while minimizing the path length of X-ray or neutron scattering. The final design could accommodate the transducers with a diameter as large as 90 mm and a maximum focal length of approximately 80 mm. During experimental testing and validation, a pair of identical 1.24 MHz spherically focused transducers with a diameter of 68 mm and a focal length of 64.6 mm (f-number 0.95) were used to produce the acoustic field. These tightly focused transducers could generate a maximum peak negative pressure of 7.2 MPa with a measured full-width half maximum (FWHM) beam width of 1.7 mm and a focal length of 13.2 mm at the focus (see supplemental figure 3). Although the beam width was quite narrow, a much longer scattering path length was required to ensure the transmitted acoustic field was not significantly affected by the geometry of the sample holder. Ultimately, a 10 mm path length was used for all experiments reported here. However, depending on the acoustic field transmitted from the focused transducers, a narrower scattering path length acoustic cell could be accommodated to increase the contrast-to-background of the sonicated sample volume.

Figure 2.

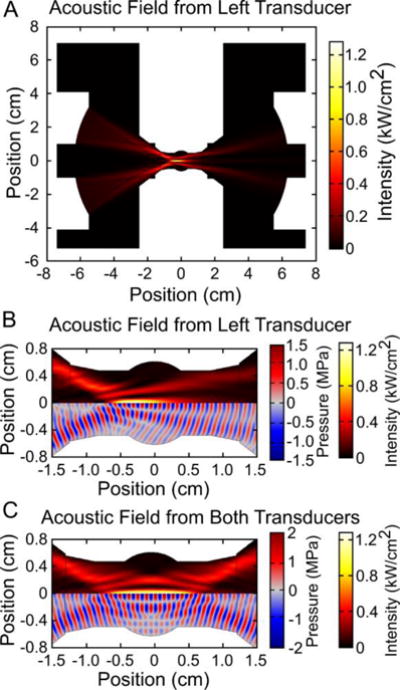
The acoustic field was simulated to guide the design of the acoustic sample environment. A mid-plane section view of the acoustic field from the left transducer can be seen in panel (A) with the cropped view at the sample holder location shown in panel (B). Because the acoustic field is symmetric along the horizontal center line, plots in panels (B) and (C) are split to show the acoustic intensity (hot color scale) and the acoustic wave field (red/blue color scale). According to the simulations, acoustic focus is within 3 mm of the center of the sample holder. The average acoustic intensity field from the two transducers, shown in panel (C), uniformly covers an ellipsoidal region in the center of the sample holder.

Experimentally measured beam profiles within the sample holder agreed well with simulation results (see supplemental figure 3). Minor discrepancies may be due to machining imperfections leading to acoustic scattering from the walls of the sample holder. Hydrophone measurements indicated that acoustic losses at the transducer focus due to the sample environment relative to free-field measurements were only 7.7 %.

Cavitation of Pure Fluids

USAXS measurements were obtained on pure ethanol and DI water samples exposed to acoustic pressures between 0 and 7.2 MPa. The measured cavitation thresholds for ethanol and water were 5.1 MPa and 7.3 MPa respectively. Even though cavitation was detected acoustically in several USAXS measurements, no significant changes to the scattering profile were observed (figure 3). Although gas bodies are known to strongly scatter X-rays, the lifetime of a cavitation event is only several microseconds, which would represent a small fraction of the integrated USAXS measurement acquisition period (60-90 seconds). Therefore, the long time-averaging of the USAXS measurement reduced the contrast and sensitivity to transient cavitation events. Based on these results, it was concluded that subtraction of scattering contributions from transient cavitation bubbles was not necessary to correct the data.

Figure 3.

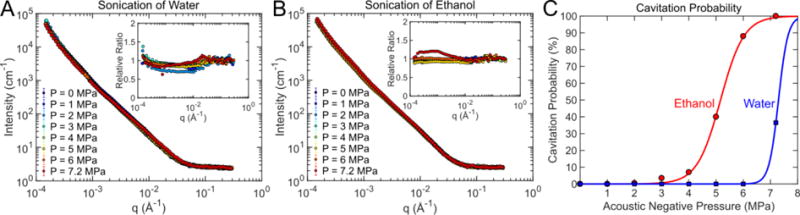
X-ray scattering profiles from (A) water and (B) ethanol showed little change with increasing acoustic pressure. The relative change in scattering intensity versus q is shown in the inset plots. (C) Cavitation was acoustically detected for both water and ethanol. The 50% cavitation threshold for water was 7.3 MPa and 5.1 MPa for ethanol. Although cavitation data suggested that cavitation was present at high acoustic pressures, it was not obvious in the 1-D scattering profiles.

Emulsification of Perfluorooctane in Water

Sonication is a common method used to emulsify two-phase liquid mixtures to produce nano-/micro-droplets through the mechanical disruption of the dispersed liquid phase in a solvent (figure 4). In general, sonication of oil-in-water mixtures will initially produce a polydisperse droplet distribution that will asymptotically decrease in size and increase in monodispersity with increasing sonication time and intensity.^49–53 As validation of the acoustic sample environment, the emulsification of PFO (oil phase) in water was chosen as a model system. USAXS measurements were collected during emulsification of PFO in water at acoustic pressures ranging of 0 MPa to 7.2 MPa. As acoustic pressure increased, a reduction in scattering intensity and slope was observed in the low-q region between 1.5×10⁻⁴ Å⁻¹ and 3×10⁻³ Å⁻¹ (figure 5). Decreased scattering intensity in the low-q region suggested a reduction in the number of large particles. At the highest acoustic pressures there was increased scattering intensity in the high-q region (~0.01 Å⁻¹), signifying a shift towards smaller droplet production.

Figure 4.

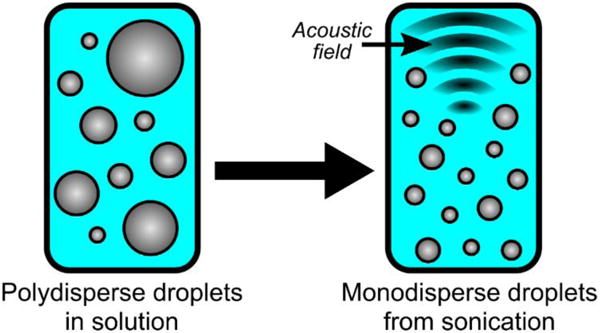
A coarse oil-in-water emulsion can be broken to form a monodispsed nanoemulsion using ultrasound.

Figure 5.

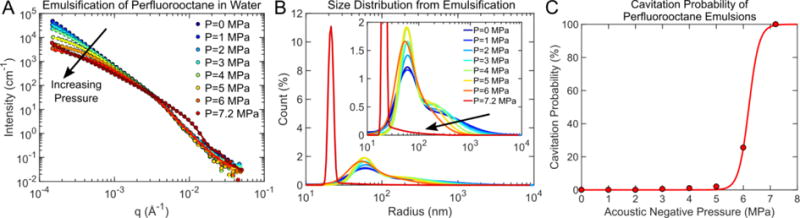
(A) 1-D USAXS scattering profiles during the emulsification of perfluorooctane (PFO) at increasing acoustic pressures and corresponding (B) distributions resulting from each acoustic pressure. In general, as the acoustic pressure increased, average droplet size decreased and monodispersity improved. However, beyond the cavitation threshold (6.2 MPa, panel (C)), the average droplet size decreased from approximately 60 nm to radius to 20nm to radius.

A USAXS scattering model was developed assuming that there are two droplet populations. We hypothesized that the acoustic forces from sonication disrupt larger micrometer-scale droplets to form nanodroplets. The first droplet distribution has a log-normal population, with mean diameter on the order of 1 μm, representing the initial coarse dispersion.^54,55 The second log-normal distribution (mean diameter on the order of 100 nm) represents smaller droplets produced through the breakdown of larger droplets during emulsification.^54,55

Based on the scattering fit of the initial droplet population prior to acoustic exposure, the majority of droplets had radius of approximately 60 nm (figure 5B). However, the initial droplet distribution has a long tail that extended well beyond a radius of 1 μm. As the applied acoustic pressure increased, the distribution became more monodisperse as the number of large droplets (R>200 nm) decreased while the number of droplets with a radius of approximately 60 nm increased (figure 5B). However, at the highest acoustic pressure (7.2 MPa), the droplets produced are considerably smaller (mean radius of approximately 20 nm) than those at lower pressures. According to acoustic data, cavitation only occurred consistently at high pressure conditions (50% cavitation threshold is 6.2 MPa, see figure 5C). Overall, these trends in producing monodisperse droplets with increasing acoustic pressure agrees well with previously published results.^51–53

From these results, we suspect two modes of emulsification are possible. The first mode occurs when the acoustic pressure is below the cavitation threshold. In this mode, stresses associated with the acoustic field are able to deform droplets to the point of fractionation. Currently, it is unclear what controls the final droplet diameter in this mode. The high acoustic wavelength to droplet diameter ratio is likely the limiting factor for this form of emulsification. However, a more exhaustive study is needed to determine the exact roles of acoustic frequency and pressure on various oil-in-water systems with different viscosity and interfacial tension values.

A second mode of emulsification occurs above the cavitation threshold. During this process, a cavitation vapor cavity is formed and rapidly collapsed. It is unclear if the cavitating medium is the solvent phase or the droplet phase. If droplets themselves are cavitating, then it is possible that the vaporized droplet fractures into small nanobubbles during the collapse phase and then condense into smaller nanodroplets. If the solvent is cavitating, the bubble collapse could create locally high stresses and gradients near the collapsed bubble, causing fine emulsification of the PFO droplets.

Resuspension of Dry Silica Particles in Water

Sonication is commonly used to overcome inter-particle forces preventing dry particles from freely dispersing into solution (figure 6). Dispersing dry silica nanoparticles in water by sonication was the second test case used to validate the function of the acoustic sample environment. The samples were sonicated at the maximum acoustic pressure (7.2 MPa) while USAXS measurements were acquired over 60 second intervals. In the scattering profiles there were three features observed. In the high-q region (>4×10⁻³ Å⁻¹), all samples contained a scattering pattern resembling monodisperse 120 nm diameter spherical silica particles (figure 7). A power-law dependence in the low-q region (~1.0×10⁻⁴ Å⁻¹ to 1×10⁻³ Å⁻¹) indicated that large structures from particle aggregates were present in the solution. Over time, the scattering intensity in the low-q range decreased due to sonication (figure 7). The reduction in the power-law exponent in the low-q scattering region over time suggested that particle aggregates were disrupted to form free particles. In the mid-q region (~1.5×10⁻³ Å⁻¹ to 4×10⁻³ Å⁻¹), a subtle slope change was observed. The feature change in the mid-q region was from particle-particle interactions in clusters.^56,57

Figure 6.

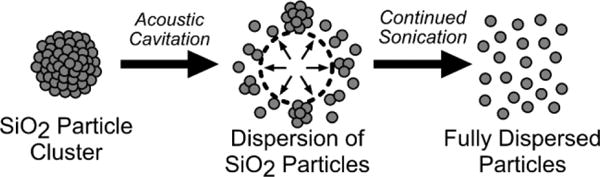
Dispersing dry particles in water typically results in a large number of particle aggregates. Acoustic cavitation from sonication sources are often used overcome the attractive forces between the particle aggregates, freely dispersing the particles in liquid.

Figure 7.

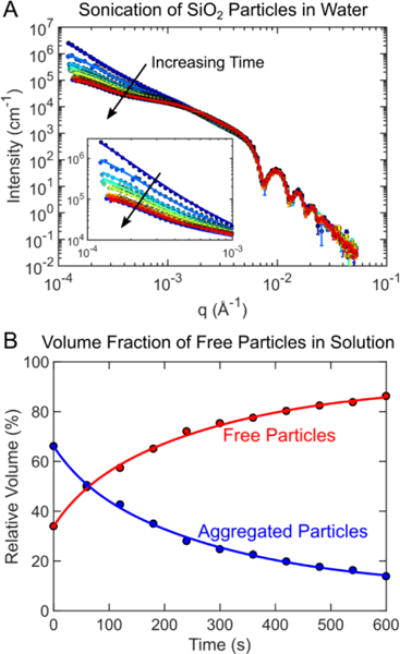
(A) USAXS measurements were collected at 60 second intervals as silica particle aggregates in water were redispersed using sonication. The scattering data was fit to obtain a volume fraction free particles versus particle aggregates. Over time, the volume fraction of free particles increased proportionally as the number of particle aggregates decreased.

A three-part model was needed to accurately capture the scattering profile from sonicated silica particles over time. The first part of the scattering model was a sphere model to described individual particles fully dispersed in water.^54,55 The next model was a Debye model used to describe small particle clusters of 2 to 10 particles.^54–57 Particle clusters of 10 particles or fewer are known to have energetically preferred packing arrangement that can be explicitly defined and modeled.^56,57 This is also essential for reproducing mid-q scattering features that arise from interparticle correlations within such clusters, which is not captured by fractal models. For clusters with more than 10 particles, a fractal model was used.⁵⁸ Without the addition of the Debye model or the fractal model, the low-q slope features could not be accurately captured.

From the fits, the ratio of fully dispersed free particles to aggregates was obtained (figure 7B). Approximately 67% of the particles were freely dispersed at the start of sonication while the rest were aggregated. As expected, the fraction of particle aggregates reduced monotonically with time as the number of free particles increased. This result confirmed that sonication does indeed assist in overcoming the inter-particle forces when resuspending particles and the acoustic sample worked as intended.

Formation of Pickering Emulsions

Pickering emulsions are emulsions whose interface is coated with solid particles instead of a surfactant (figure 8). Pickering emulsions were synthesized using 12 nm-diameter gold nanoparticles (GNP) stabilizing PFO droplets in water. USAXS measurements were collected on a GNP and PFO droplet suspension during sonication at low (1 MPa) and high pressure (7.2 MPa). The low acoustic pressure results produced a scattering pattern matching 12 nm spherical particles freely dispersed in solution in the high-q region, and a large secondary object with a linear slope in the low-q region (figure 9). The scattering profile was modeled using the linear combination of two polydisperse sphere models, which represented the 12 nm diameter GNP and the PFO droplets.^54,55 Based on the model fit, PFO droplets had a mean diameter of 876 nm. Transmission electron microscopy (TEM) images confirmed that the majority of GNPs were freely dispersed and no evidence of Pickering emulsions were seen (figure 9B). These results suggested that the GNPs do not spontaneously adsorb onto the PFO interface to form Pickering emulsions, most likely due to electrostatic repulsive forces.⁴¹

Figure 8.

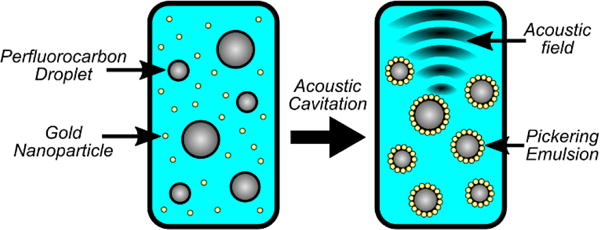
Pickering emulsions can be difficult to form due to repulsive forces preventing the interaction of particles on a droplet interface. Acoustic cavitation can assist in overcoming the energy barrier forcing particles onto a droplet interface forming Pickering emulsions.

Figure 9.

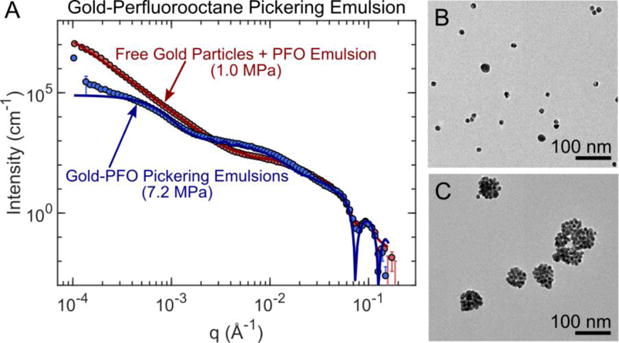
(A) Measured USAXS scattering profile of gold nanoparticles and perfluorocarbon droplets in water after low pressure (1 MPa) versus high pressure (7.2 MPa) insonation and the corresponding transmission electron microscopy (TEM) images (panels B and C). TEM images (panel B) and USAXS model fits confirm that the sample exposed to a low pressure is comprised of two non-interacting populations of 12 nm gold spheres and 876 nm diameter PFO droplets. Conversely, at high pressure the Pickering emulsions formed were visualized in TEM as particle clusters (panel C). Using a Debye model, it was determined that 90% of the Pickering emulsions had a mean diameter of 64 nm while the remaining emulsions had a mean diameter of 488 nm.

TEM images of samples exposed to high acoustic pressures showed Pickering emulsions formed from GNP clusters (Figure 9C). In USAXS scattering profiles, the inter-particle spacing along the emulsion interface produced the flat slope between the q values of 1.5×10⁻² Å⁻¹ and 5.0×10⁻² Å⁻¹. A Debye model of a PFO droplet decorated with gold nanoparticles was used to analyze the data.^55,59 From fitting results, it was clear that two Pickering emulsion populations existed in the sample after sonication. The majority, 90% of the Pickering emulsions by volume, had a mean diameter of 64 nm while the remaining 10% had a mean diameter of 488nm. Both Pickering emulsion distributions had a GNP coverage corresponding to approximately 80% of the total droplet surface area, which approaches the maximum close packing limit of 83%. The smaller Pickering emulsion population (diameter ~64 nm) matched well with the size observed in the TEM images (figure 9C).

The change in droplet distribution for two different acoustic pressures was similar to what was observed in the emulsification of PFO in water while excluding contributions from the gold nanoparticles. Without cavitation, the PFO droplets were relatively large with mean diameter of 876 nm. Because of cavitation, the large PFO droplets were fractionated to form smaller 64 nm Pickering emulsions. The results suggest that cavitation plays a key role in overcoming the repulsive force preventing spontaneous adsorption of the GNPs onto the PFO emulsion interface.

Although the acoustic sample environment helped identify that cavitation was needed, it is still unclear what specific aspect of cavitation is necessary. Similar to the emulsification experiment, there are two possible cavitating media: the solvent phase and the droplet phase. If the solvent phase cavitates exclusively, then the droplets and particles are likely pushed towards one another due to local stresses induced by cavitation. Alternatively, if it is the droplet that is cavitating, then changes in interfacial properties are probably the cause. During the cavitation process, the interfacial properties on the gaseous perfluorocarbon bubble may promote adhesion of the GNPs onto the bubble interface. During the compression phase of the acoustic wave the bubble decorated with GNPs would then recondense back into its liquid phase, forming a Pickering emulsion. Other effects such as locally high stresses and velocities in the vicinity of the cavitation bubbles would also play a role in conjunction with the changes in interfacial properties to promote Pickering emulsion formation.

With the current dataset, we are unable to differentiate between these two effects. However, with recent advancements in time resolved scattering methods we suspect that identifying the source of cavitation is possible. With modern free electron lasers and synchrotron sources, femtosecond time resolutions are possible, while millisecond time resolutions are feasible using SANS.^60–63 Using a time resolved method to obtain small-angle scattering measurements, the early stages of cavitation nucleation formation can be captured and fit using scattering techniques. Meanwhile, acoustic cavitation detection can be used to confirm if cavitation occurred.

Sono-Crystallization of Fullerenes

PCBM is frequently used in organic photovoltaic devices to enhance device performance. In such devices, fullerenes would be ideally organized into structures that enhance charge transport in the active layer. Recent studies have shown that PCBM can be assembled into nanosheets while in solution with the aid of sonication (figure 10).^44,45 Using a method adapted from Garcia-Espino et al. 2015⁴⁵, PCBM dissolved in a 1:1 deuterated methanol and dichlorobenzene sample was sonicated at 6.8 MPa for 150 min. A SANS measurement was taken before and after sonication. From the 1-D SANS scattering profiles, a significant increase in scattering intensity was observed in the low-q region while the high-q region (>0.2 Å⁻¹) appeared unchanged (figure 11). The increased low-q intensity suggests larger scale structures in the sample due to acoustic exposure. This was confirmed through Guinier analysis⁵⁵ (figure 11B), which showed an increased radius of gyration from 4.92 Å to 13.33 Å. Although Garcia-Espino et al. 2015⁴⁵ observed the formation of nano-sheets in TEM images, physical models attempting to fit a nanosheet structure from SANS data would not result in physically meaningful values. It is possible that the acoustic exposure volume was too small and the sonication time was insufficient to create the nanosheet structure or that the structures that are formed in dispersion are fundamentally different from those proposed by Garcia-Espino et al.

Figure 10.

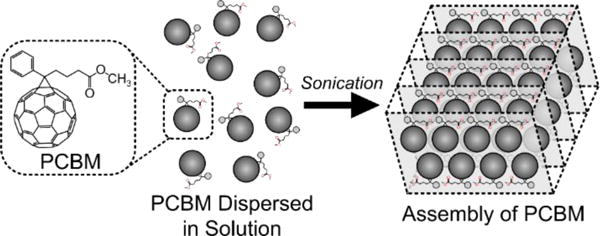
PCBM can be freely dispersed in organic solvents. Under the correct solvent conditions, acoustic forces can be used to facility organization of PCBM to form large scale sheets and fibers.^44,45

Figure 11.

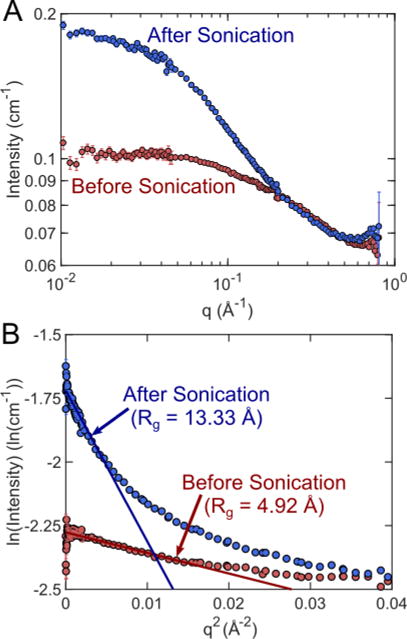
(A) SANS measurements before and after sonication at 6.8 MPa. A significant change in scattering intensity was observed in the low-q region after sonication, indicating larger structures present in the sample. (B) Gunier analysis confirmed that the radius of gyration in the sample increased from 4.92 Å to 13.33 Å due to insonation.

Future Work

The inability to detect transient cavitation events using X-ray or neutron scattering was due to a combination of spatial averaging and the short lifetime of cavitation events. We suspect that transient cavitation event could be observed in future measurements by making two adjustments. First, increase the spatial coordination of the acoustic exposure volume and the scattering volume to minimize contributions from parts of the sample that are not exposed to ultrasound. This can be achieved using transducers with a wider beam width or by reducing the sample volume in the scattering path. Second, use the ultrasound sample environment in time-resolved scattering instruments.^64–68 Free electron X-ray lasers and synchrotron sources now have the ability to resolve at up to femtosecond time resolutions, while SANS techniques that resolve millisecond time scales are also possible.^60–63 Depending on the acoustic conditions used, bubble lifetimes can vary from microsecond to millisecond time scale.^69–72 Using time resolved scattering techniques and instruments, the propagating acoustic wave and stages of cavitation may be fully resolved. On such instruments, the acoustic sample environment would allow us to measure and model the cavitation inception in the solvent versus the dispersed phase, and correlate any structural changes to the corresponding acoustic pressure and cavitation data. Such time resolved cavitation measurements would benefit the understanding of the changes and mechanisms observed in the cavitation process and sono-/mechano-chemistry.

Conclusions

In this study a new acoustic sample environment designed for in situ X-ray or neutron scattering was presented. Basic functions of the systems were validated and tested with simple use-case examples of cavitation, emulsification, and particle break-up. Although sonication and cavitation are often associated with breakup of large objects to form smaller objects, we were able to demonstrate the cavitation can also play a role in the assembly of complex nanostructures, with the examples of the formation of Pickering emulsions and PCBM aggregates.

The acoustic sample environment presented is a new tool that will benefit a broad range of fields including sono-/mechano-chemistry. This system can be used optimize acoustic parameters for efficiently processing materials that require sonication (e.g. emulsification, dispersion, denaturing proteins, etc.). Using this sample environment in small-angle scattering measurements, effects due to cavitation, acoustic pressure, frequency, exposure time, etc. can be studied while simultaneously monitoring the physical changes at length scales ranging from 0.1 to 1000 nm. Although electron microscopy techniques provide similar length scale measurements as small-angle scattering, the samples typically must be dried, possibly altering the structure of the sample.

To the best of our knowledge, the sample environment presented is the first ultrasonic sample environment enabling in situ structural studies at the nanoscale using small-angle scattering, while simultaneously monitoring for cavitation. Although physical changes due to sonication were clearly observed and successfully correlated to acoustic detection of cavitation, the exact source of the cavitation events could not be determined.