Personalized Diagnosis for Alzheimer’s Disease

Abstract

Current learning-based methods for the diagnosis of Alzheimer’s Disease (AD) rely on training a general classifier aiming to recognize abnormal structural alternations from homogenously distributed dataset deriving from a large population. However, due to diverse disease pathology, the real imaging data in routine clinic practices is highly complex and heterogeneous. Hence, prototype methods commonly performing well in the laboratory cannot achieve expected outcome when applied under the real clinic setting. To address this issue, herein we propose a novel personalized model for AD diagnosis. We customize a subject-specific AD classifier for the new testing data by iteratively reweighting the training data to reveal the latent testing data distribution and refining the classifier based on the weighted training data. Furthermore, to improve estimation of diagnosis result and clinical scores at the individual level, we extend our personalized AD diagnosis model to a joint classification and regression scenario. Our model shows improved performance on classification and regression accuracy when applied on Magnetic Resonance Imaging (MRI) selected from Alzheimer’s Disease Neuroimaging Initiative (ADNI) database. Our work pin-points the clinical potential of personalized diagnosis framework in AD.

1 Introduction

Alzheimer’s Disease is one of the most common neurodegenerative disorders, which leads to gradual progressive memory loss, cognition declines, loss of functional abilities, and ultimate death [1–4]. Modern imaging technique MRI offers a non-invasive way to observe the abnormal structure changes of AD progression in vivo. In order to facilitate the MRI diagnosis of AD, a number of machine learning approaches have been developed to recognize AD-related altered brain structure [5, 6].

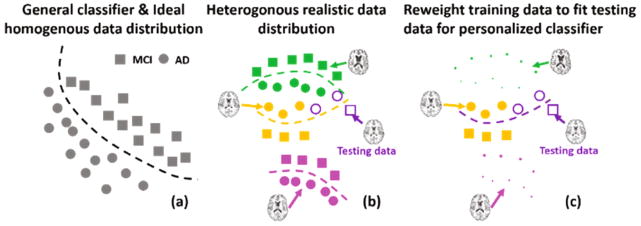
Most current learning-based methods train a general classifier (such as kernel Support Vector Machine) to find a hyper-plane to separate two groups in a high dimensional non-linear space, which is suitable for data of homogeneous distribution (as shown in (a)). However, it is evident that AD pathology is of heterogeneous characteristic. Therefore, real data distribution could be too complex to be represented by only one general model. As shown in (b), the real data distribution might have multiple sub-groups of distinct disease patterns due to inter-personal variance (different colors indicate different sub-groups). The incapability of a general classifier to fit heterogeneous data for precise classification prompts us to construct a specific classifier for each sub-group/person to achieve accurate classification. As shown in (b), the green, orange, and pink curves in are ideal classifiers for the green dataset, orange dataset, and pink dataset, respectively. Based on this strategy, we developed a personalized classification model specifically for each testing person desirable for real clinical applications.

The key to the personalized model is to reweight the training data to fit testing data distribution and train a person-specific classifier using the weighted training data. Figure 1(b) and (c) show a toy example on how to construct a personalized classifier. There are three sub-groups of different distributions in the training dataset (green, orange, and pink) and one testing dataset (purple). Although it seems that the center of the testing dataset is closer to the green dataset than the orange dataset, only the distribution of the orange dataset resembles the testing dataset. Therefore, the orange dataset is associated with high-value weights and others are assigned with small value weights (see Fig. 1(c), size is proportional to weights). This weighted dataset reveals the latent testing data distribution and a personalized classifier (purple curve in Fig. 1(c)) can be learned from the weighted training dataset. Furthermore, to optimize weights for building the classifier, we developed an integrated solution which makes learning the training data weights and training the personalized classifier simultaneous.

Fig. 1.

(a) Conventional methods with a general classifier applied on homogeneously distributed data; (b) Heterogeneously distributed realistic data requiring person-specific classification solution; (c) Proposed personalized classification model by re-weighting training data to fit testing data distribution. (Best viewed in color)

This personalized training strategy can sort out the data heterogeneity issue and produce more accurate diagnosis results at the individual level. Moreover, we extend the personalized diagnosis model to a joint classification (on the binary clinical labels) and regression (on the continuous clinical scores) such that we can further improve the accuracy of diagnosis by utilizing both imaging and phenotype data. We evaluated the proposed personalized AD diagnosis model on ADNI dataset and achieved more than 8% improvement on average in identifying AD and MCI (Mild Cognition Impairment) subjects, compared to using general classification models.

2 Methods

2.1 Generalized Classification Model

Suppose the training set X consist of N subjects, denoted by X = {x_i|i = 1, ···, N}, where each x_i is the feature vector extracted from MRI. Each training subject also has a clinical label l_i to identify whether the underlying subject is at MCI stage (‘−1’) or has converted to AD (‘+1’). These clinical labels form a set L = {l_i|i = 1, …, N}. Hereafter, we take the kernel SVM as the example of the generalized classification model to illustrate the idea of our personalized AD diagnosis. Kernel SVM seeks to learn a non-linear mapping φ to determine the label for the new testing data y, where φ is essentially the weighted kernel distances with respect to each known instance x_i in the training dataset X, i.e., $\phi (\mathit{y})={\sum }_{j=1}^N{\alpha }_i{k}_C({\mathit{x}}_i,\mathit{y})$, where k_C(x_i, y) denotes the kernel distance from x_i to y in the high dimensional non-linear space. The classification coefficient α = {α_i|i = 1, …, N} can be optimized from the training dataset X via the following classic energy function:

$$arg{min}_{\mathit{\alpha }}\frac{1}{2}{\mathit{\alpha }}^T{\mathit{K}}_C\mathit{\alpha }+\mu E_C(\phi ).$$ (1)

The first term is the regularization term where K_c is a N × N kernel matrix with each element k_C(x_i, x_j) measuring the distance between any two training data x_i to x_j (i, j = 1, …, N) in the high dimensional non-linear space. The second term is the misclassification error term $E_C(\phi )={\sum }_{i=1}^N{\Vert \phi ({\mathit{x}}_i)-l_i\Vert }_h$, where ||v||_h= max(0, v) is the hinge loss function. μ is a scalar balancing the regularization term and misclassification error term. The classification coefficient α is optimized to fit the whole population in Eq. (1). If the data distribution is as homogeneous as the example shown in (a), a generalized classifier can achieve good performance on classification. However, real clinical data usually has complex distribution due to heterogeneous characteristics of AD pathology. Hence, one general classifier alone is not sufficient to cover all individuals.

2.2 Personalized Classification Model

To address the issue of heterogeneity, we propose to learn a person-specific classifier by leveraging the most relevant data in the training dataset. The training data are reweighted to reveal the testing subject distribution. Compared to the general model, we measure the relevance degree of each training data x_i w.r.t. the new testing data y denoted by r = {r_i}_i=1,…,N. In contrast to the general model which treats all training data uniformly, here, we penalize the misclassification error for different training data w.r.t the relevance degree to testing data. To achieve personalized AD diagnosis, we adjust the energy function of general classification model to personalized classification model in three ways:

1. The misclassification errors are weighted based on the relevance degree r, it turns to the weighted average across all training data: $E_c(\phi ,\mathit{r})={\sum }_{i=1}^N{r}_i{\Vert \phi ({\mathit{x}}_i)-l_i\Vert }_h^2$.

2. The insight of personalized classifier is to re-weight each training data such that the difference between the distribution of testing data and weighted training data distribution is minimized. Therefore, we introduce the additional distribution mismatch term which is related to the relevance values r. First, we need to estimate the distribution for testing data y. Recall that the challenge in medical imaging area is the limited number of data with label information. Actually, it is not difficult to find a sufficient number of unlabeled data. Therefore, we propose to construct the distribution for the testing data y from another unlabeled dataset, denoted by U (U ∩ X = ∅). Specifically, we select the top similar M data to y from U to form the testing dataset Y = {y_j|y_j ∈ U, j = 1, …,M} (we set M = 4 in our experiment). Since the size of testing dataset is very small (M ≪ N), it is hard to calculate the data density in characterizing the distribution of Y. To avoid the unreliable estimation of data density, we resort to the Kernel Mean Matching (KMM) method [7], which is able to measure the distribution dissimilarity in the high dimensional or even infinite dimensional Reproducing Kernel Hilbert Space (RKHS) H. Specifically, we define the distribution mismatch term 𝒟(X,Y, r) as the function of r by:

   $$\mathcal{D}(\mathbf{X},\mathbf{Y},\mathit{r})={\Vert \frac{1}{N}{\sum }_{i=1}^N{r}_i\varphi ({\mathit{x}}_i)-\frac{1}{M}{\sum }_{j=1}^M\varphi ({\mathit{y}}_j)\Vert }_2^2,$$ (2)
   where ϕ is a non-linear mapping from image feature space to the RKHS. The intuition behind Eq. (2) is to adjust the distribution of training dataset X based on the relevance degrees such that the weighted distribution of training dataset (first term in Eq. (2)) can fit the distribution of testing dataset Y, i.e., X and Y are comparable in the RKHS. To make Eq. (2) solvable, “kernel trick” is used to compute the pairwise kernel distance in H, rather than the exact value ϕ(x_i). Thus, we use Π = [π_ij]_N×N (i, j = 1, ···, N) to denote the N × N kernel matrix where each element π_ij = k_D(x_i, x_j) measures the kernel distance between training data x_i and x_j in RKHS H. Similarly, we use θ = [θ_i]_i=1,…,N to denote a N-length column vector where the i-th element ${\theta }_i=\frac{N}{M}{\sum }_{j=1}^M{k}_D\left({\mathit{x}}_i,{\mathit{y}}_j\right)$ measures the average distance of the training data x_i to all testing data. It is worth noting that the kernel function k_D used here might be different with the kernel function k_c in kernel SVM (Eq. (1)). After that, we turn Eq. (2) into a quadratic term as:

   $$E_D(\mathit{X},\mathit{Y},\mathit{r})=\frac{1}{2}{(\mathit{r})}^T\mathbf{\Pi }\mathit{r}-{\mathit{\theta }}^T\mathit{r},$$ (3)

3. Since the training error term E_c(φ, r) and the distribution mismatching term E_D(X, Y, r) are both influenced by the relevance degrees r, we can leverage the r to jointly minimize the classification error and distribution difference. By doing so, we can guarantee that the relevance degrees are optimized towards the eventual goal of improving the classification accuracy for the new testing data.

Overall energy function

By integrating the above three modifications, the overall energy function for personalized AD diagnosis can be defined as:

$$arg{min}_{\mathit{\alpha },\mathit{r}}\frac{1}{2}{\mathit{\alpha }}^T{\mathit{K}}_C\mathit{\alpha }+\mu E_C(\phi ,\mathit{r})+\lambda E_D(\mathit{X},\mathit{Y},\mathit{r})$$ (4)

where λ is the scalar used to control the strength of distribution matching. Since the clinic label of the testing data is unknown yet, the estimation of the weights for training data is driven by the distribution mismatch term E_D(X, Y, r) in an unsupervised manner. In addition, the estimation of relevance degrees r are jointly driven by minimizing the classification error and distribution mismatch.

Optimization

Equation (4) is a bi-convex quadratic problem [8], i.e., E(α) is convex if r is fixed and E(r) is convex if α is fixed. Under these conditions, an alternate gradient search approach is guaranteed to monotonically decrease the objective function. Hence, we alternatively optimize Eq. (4) w. r. t. r and α until converge [9].

Discussion

Conventional subject selection approaches, however, are usually separately performed prior to train the classifier, and thus resulting in a sequential two-step strategy. Therefore, the selected training data in the two-step strategy might not be optimal for classification, since there is no chance to refine the subject selection procedure. Since the personalized classifier is free of the less relevant training samples, the customized mapping function in our personalized classifier is more robust to the new testing subject than the general classifier learned from entire training data, as demonstrated in (c).

2.3 Advance Personalized AD Diagnosis Model

In many medical applications, clinical scores such as Mini-Mental State Examination (MMSE) and Clinical Dementia Rating (CDR) scores are widely used to quantify memory loss and behavior abnormality and facilitate the clinical AD diagnosis. Since the clinical scores have higher correlations than the imaging features, there is an increasing trend to integrate classification (for the binary diagnosis labels) and regression (for the continuous clinical scores). Hence, we go one step further to present the advanced personalized AD diagnosis model. Suppose each training data x_i has the clinical scores c_i which forms the set of clinical scores C = {c_i|i = 1, …, N}. For consistency, we use the kernel Support Vector Regression (SVR) model to learn another non-linear mapping function $\psi (\mathit{y})={\sum }_{i=1}^N{\beta }_i{k}_R({\mathit{x}}_i,\mathit{y})$ to determine the scores for the new testing data y based on the weighted average of kernel distance k_R(x_i, y) to all training data. The regression coefficients β = {β_i|i = 1, …, N} can be optimized by:

$$arg{min}_{\mathit{\beta }}\frac{1}{2}{\mathit{\beta }}^T{\mathit{K}}_R\mathit{\beta }+\eta E_R(\psi ),$$ (5)

where η is the scalar balancing the regularization term and regression error term $E_R(\psi )={\sum }_{i=1}^N{\Vert \psi (x_i)-c_i\Vert }_2^2$. K_R is the N × N kernel matrix with each element k_R(x_i, x_j) measuring the kernel distance between x_i and x_j in the regression problem. To personalize the regression, we turn the regression error term E_R(ψ) into the weighted average across all training data as $E_R(\psi ,\mathit{r})={\sum }_{i=1}^N{r}_i{\Vert \psi ({\mathit{x}}_i)-c_i\Vert }_2^2$. Thus, the energy function of personalized regression can be derived as:

$$arg{min}_{\mathit{\beta },\mathit{r}}\frac{1}{2}{\mathit{\beta }}^T{\mathit{K}}_R\mathit{\beta }+\mu E_C(\psi ,\mathit{r})+\lambda E_D(\mathit{X},\mathit{Y},\mathit{r}),$$ (6)

Furthermore, we integrate personalized classification and regression and derive the overall energy function of advanced personalized AD diagnosis model as:

$$arg{min}_{\mathit{\alpha },\mathit{\beta },\mathit{r}}\frac{1}{2}{\mathit{\alpha }}^T{\mathit{K}}_C\mathit{\alpha }+\frac{1}{2}{\mathit{\beta }}^T{\mathit{K}}_R\mathit{\beta }+\mu E_C(\phi ,\mathit{r})+\eta E_R(\psi ,\mathit{r})+\lambda E_D(\mathit{X},\mathit{Y},\mathit{r}).$$ (7)

Equation (7) can be similarity solved by alternatively updating α, β, and r until converge.

3 Experiments

We evaluate our proposed personalized AD diagnosis model on 150 MCI and 150 AD subjects selected from ADNI database, each has the clinical scores such as ADAS-COG (Alzheimer’s Disease Assessment Scale-Cognitive Subscale) and MMSE. For each subject, we first segment each image into white matter (WM), gray matter (GM), cerebral spinal fluid (CSF). Then, we register the AAL template with 90 manually labeled ROIs (regions of interest) to the underlying subject image. We concatenate the tissue percentiles across 90 ROIs as the morphological feature for each subject.

The accuracy of classification and regression is evaluated by leave-one-out strategy. For each leave-one-out case, we divide the remaining subjects into five folds. One-fold data is used as the validation dataset for parameter turning, one-fold is used as the candidature dataset for augmenting testing data and the left three-fold data are use as the training dataset. The optimal parameters are learned by an exhaustive strategy on the validation dataset. The search range for parameters is set to [10⁻⁴, 10⁴]. Three statistical measures are used to evaluate classification, including accuracy (ACC), sensitivity (SEN) and specificity (SPEC). Root Mean Square Error (RMSE) and Correlation Coefficients (CC) are used to evaluate the regression performance for two popular clinical measurements, i.e., ADAS-Cog and MMSE.

Kernel SVM/SVR(generalized model) are the baseline methods in comparison. In the following experiments, we evaluate the classification and regression separately. We use the RBF kernel and the regularization parameters are tuned using five-fold inner cross-validation. In classification, we compare our personalized classifier (Eq. 4) with kernel SVM and convention subject selection (estimate the weight based on feature similarity) followed by kernel SVM called SS+SVM. Similarly, we evaluate the regression performance for the baseline kernel SVR, SS+SVR, and our personalized regressor. Our advance personalized AD diagnosis model (called Personalized SVM+SVR) is both evaluated in classification and regression tasks, in order to show the benefit from joint classification and regression.

Evaluation of classification performance

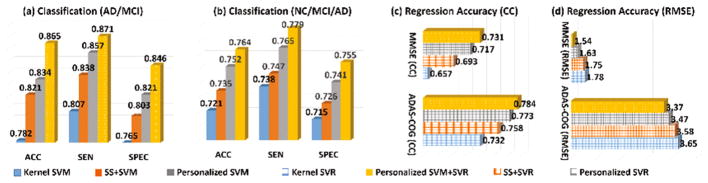
The ACC, SEN, and SPEC results in identifying MCI/AD and NC/MCI/AD subjects by kernel SVM, SS+SVM, personalized SVM, and personalized SVM+SVR are shown in Fig. 2(a). In general, all personalized approaches achieve higher accuracy than the baseline kernel SVM method which does not have any adjustment to the testing subject. Since our personalized SVM method can jointly select the most relevant subjects and train the classifier, it achieves overall 1.3% improvement in terms of ACC value over the naïve SS+SVM approach that selects training data and trains the classifier separately. Furthermore, our personalized SVM+SVR can obtain additional 3.1% improvement of ACC value over the personalized SVM method, which shows the substantial benefit of joint classification and regression. It is worth noting that our advanced personalized model (personalized SVM+SVR) achieves 8.3% improvement in terms of ACC value, compared to generalized model (kernel SVM).

Fig. 2.

Classification performance in identifying MCI/AD, NC/MCI/AD subjects and regression performance in estimating MMSE and ADAS-Cog scores. (CC represent correlation coefficients and RMSE represents root mean square error. Best viewed in color)

Evaluation of regression performance

Since the clinical scores of each testing subject are known, we calculate the RMSE and CC values between the ground truth and the estimated score by four competing methods. We show the MMSE and CC results of estimating MMSE and ADAS-Cog measurements by kernel SVR, SS+SVR, personalized SVR, and personalized SVM+SVR in Fig. 2(b) and (c), respectively. It is apparent that (1) all personalized method beat the generalized regression method (kernel SVR); (2) our personalized SVR outperforms the naïve SS+SVR method due to the advantage of joint weighting training data and regression; (3) personalized SVM+SVR has the minimal MMSE value and large CC value between the ground truth and estimated scores, indicate the advantage of allowing clinical labels to guide the regression of clinical scores.

Evaluation of personalized diagnosis model with respect to data heterogeneity

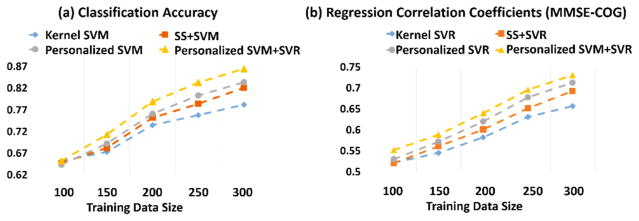
Since the main objective of our study is to address the heterogeneous issue of imaging data by using personalized model, we specifically evaluate the performance of the personalized model with respect to the heterogeneity in the observed imaging data. Here we assume that the data heterogeneity proportionally increases as the size of imaging data becomes larger and larger. Therefore, we examine the performance of classification and regression w.r.t. the different number of the training data, as shown in Fig. 3. We run the two-sample t-test for results in Fig. 3 and find the improvement is significant with p < 0.05. One can observe that (1) both general and personalized models perform at similar accuracy when the size of training data is small; (2) as the number of training subjects increases, the personalized model achieved much higher performance accuracy compared to general model in terms of both classification and regression tasks, although the performance accuracy of all methods increase consistently; (3) the improvement of personalized model over the generalized model becomes more prominent as the subject number increases. These results prove that the personalized model we propose is superior to the general model when applied on a large heterogeneous dataset and thus is of potential for clinical practice.

Fig. 3.

The performance of personalized model vs. general model with respect to different number of training data. (Best viewed in color)

4 Conclusion

To address the heterogeneous issue of image-based diagnosis of AD, we construct a personalized diagnosis model in this work. In this model, we establish a subject-specific AD classifier by reweighting training data to reveal the latent distribution for each testing data and simultaneously refining classifier. We further improve the diagnosis performance at the individual level by establishing a joint classification and regression scenario. Finally, we evaluate our method on ADNI dataset for both clinical label and clinical score estimation compared to the state-of-art counterpart methods and demonstrate the potential of our personalized model in translating computer assisted diagnosis method into routine clinical practice.