Contralateral Eye Comparison of SMILE and Flap-Based Corneal Refractive Surgery: Computational Analysis of Biomechanical Impact

Abstract

PURPOSE:

Computational analyses were performed to quantify and directly compare the biomechanical impact of flapless and flap-based procedures in a series of patients undergoing small incision lenticule extraction (SMILE) in one eye and flap-based femtosecond lenticule extraction in the other.

METHODS:

Tomographic data from 10 eyes of 5 patients undergoing femtosecond laser refractive lenticule extraction for myopic astigmatism with or without a stromal flap (femtosecond lenticule extraction in one eye, SMILE in the contralateral eye) were used to generate computational models. Inverse finite element analyses were performed at physiologic intraocular pressure followed by forward analyses at elevated intraocular pressure to assess corneal displacement and stress under differential loading. Case-specific treatment settings were incorporated. Preoperative material constants were obtained through inverse finite element analyses, and the surgically induced change in fiber stiffness within each flap was determined by minimization of the error between the simulated and actual 6-month topographic outcomes.

RESULTS:

Flap-based procedures produced a 49% (range: 2% to 87%) greater mean reduction in effective stromal collagen fiber stiffness within the flap region than contralateral SMILE cases. Lower stresses and deformations were observed within the residual stromal bed in SMILE cases than in flap-based cases. Stromal bed displacements and stresses were more affected by a loading increase in flap-based eyes than flapless eyes.

CONCLUSIONS:

Intrastromal flapless procedures had less impact on anterior stromal collagen mechanics and resulted in lower stromal bed displacements and stresses than flap-based procedures in contralateral eyes. However, biomechanical impact varied widely between individuals and this reinforces the need for individualized assessment of ectasia risk.

Refractive lenticule extraction¹ is a recently introduced technique that employs a femtosecond laser to fashion an intrastromal refractive lenticule. The lenticule is shaped based on the desired correction using geometric optics principles and then removed mechanically by the surgeon by either lifting a flap (femtosecond lenticule extraction) or pulling the lenticule through a side-cut incision (small incision lenticule extraction [SMILE]). Unlike LASIK and femtosecond lenticule extraction, SMILE disrupts only a subset of the collagen fibers in the anterior-most stroma when a small angle is subtended to gain access to the intrastromal lenticule, and this relative preservation of anterior fibrillar integrity has been proposed as a potential biomechanical advantage over comparable flap-based procedures in conceptual² and computational³ modeling studies.

Prior studies comparing the clinical biomechanical behavior of flap-based and flapless procedures using clinically available air-puff deformation responses have demonstrated insignificant^4,5 or inconsistent^6,7 differences. The purpose of the current study was to quantitatively compare the magnitude of surgically induced biomechanical changes in the anterior stroma of a clinical cohort of patients receiving a flap-based (femtosecond lenticule extraction) procedure in one eye and SMILE in the other. Inverse finite element analysis was applied to patient-specific tomography data to determine, in the setting of contralateral eye controls with similar refractive corrections, the change in corneal properties required to produce the observed postoperative changes in corneal curvature with each procedure. In addition, surgically induced residual bed deformations and stresses were compared at multiple intraocular pressures (IOPs) using the corneal material properties derived from the inverse analysis.

PATIENTS AND METHODS

Patients, Preprocessing, and No-load Calculations

Ten paired eyes of 5 patients were analyzed using individual geometry scans acquired preoperatively and 6 months postoperatively with a commercial Scheimpflug-based tomographer (Pentacam; Oculus Optikgerate, Wetzlar, Germany) during a previously completed prospective trial in Aarhus University Hospital (Aarhus, Denmark). A subset of patients from this series who received similar refractive treatments in both eyes were included in the study. The study was approved by the local institutional review board and adhered to the tenets of the Declaration of Helsinki. Patients enrolled in the prospective study signed informed consents for surgery and the study.

The tomographic x, y, and z coordinates of the anterior and posterior surfaces were exported and incorporated into finite element meshes with hexahedral 20-node hybrid elements using SpecifEye software (version 0.165; OptoQuest, Cleveland, OH). Four distinct depth-specific regions (Figure A, available in the online version of this article) were assigned to each patient-specific corneal geometry, including a 50-pm thick epithelium, the flap/cap zone, the lamellar wound zone, and the residual stromal bed. A spherical anterior half-sclera with thickness scaled per the patient-specific corneal thickness at the limbus was included in each geometric model to account for the effects of physiological limbal boundary conditions.

Figure A. Cross-section of an illustrative corneoscleral mesh.

Corneal geometries acquired in living eyes under physiological loading are different from those that would be obtained in an unloaded state. Finite element models need to account for this pre-condition by either estimating the pre-stresses⁸ or approximating the no-load geometry.⁹ We approximated the stress-free (no-load) geometry for each case using an iterative technique described elsewhere.^9,10 and modified by our group.^11,12 The patient-specific finite element mesh was built based on surface coordinates taken from the tomography (pre-treatment mesh [X_pre]). The nodes of X_pre were repositioned to X_post according to the lenticule extraction algorithm. The coordinates of the posttreatment mesh (including treatment zone, peripheral cornea, limbus, and sclera) were taken as a reference (X_ref). A negative pressure was applied to the inner surface of the corneoscleral model that reduced IOP to 10% of its physiological level (X_ref). The displacements calculated from the negative pressure (u_deflation) were added to X_ref to obtain the initial set of coordinates (X₀) to start the iterative no-load calculation (Equation 1):

$$X_0=X_{ref}+u_{deflation}$$ (1)

Following deflation, physiologic IOP (15 mm Hg) was applied to the posterior surface of the globe and the error (e) was calculated using the Euclidian norm according to the algorithm below (Figure B, available in the online version of this article). If the error (e) was not smaller than the le-5 threshold, the displacements of this simulation were added to the node’s initial structure and the simulation was repeated using the modified structure as the new initial structure and applying the physiologic IOP to the new initial structure. Iteration was continued until the error was below le-5 (Figure B).

Figure B. Algorithm for stress-free state calculation for post-ablation geometry. IOP = intraocular pressure.

MATERIAL MODEL

The stromal material formulation used in finite element simulations was an anisotropic (accounting for directional dependence of properties due to fiber orientation), hyperelastic, depth-dependent (describing the depth variation of stromal properties described in other experimental work), and incompressible material model.^3,9,13 The model was derived from Pandolfi and Holzapfel’s work⁹ and was originally developed to simulate the mechanical behavior of blood vessels by Holzapfel et al.¹⁴ The strain energy equation (Equation 2) for this model:

$$W_{anisotropic}=W_{ground}+W_{fiber}+W_{volumetric}$$ (2)

includes a fiber component (W_fiber) and an isotropic component (W_ground), where the latter is defined below in Equation 3 using a neo-Hookean material model and is dependent to the first invariant (Ī₁) of the isochoric right Cauchy deformation tensor (C̄) and transverse shear modulus of the isotropic matrix (C₁₀). W_fiber accounts for the collagen fiber contribution by computing the fourth and sixth strain invariants (Ī_4,6) of the isochoric right Cauchy deformation tensor (C̄), which includes the effect of the directions of two orthotropic fiber directions (nasal-temporal and superior-inferior) in the central cornea and primarily circumferentially oriented fibers in the peripheral cornea and a dispersion parameter (kappa [κ]), which includes the probable density of the preferred arrangement of these two fiber families in the central cornea (Equation 3):

$$W_{ground}=C_{10}\left({\stackrel{\_}{I}}_1-3\right)$$ (3)

The right Cauchy-Green strain tensor (C) is calculated as C = F^tF. The isochoric component of the tensor (C̄) modifies C by calculating C̄ = J^(−2/3) C. Thus, the total strain energy function is composed of three components described by the following equations:

$${\text{W}}_{\text{fiber}}={\displaystyle {\sum }_{i=4,6}\frac{k_{1i}}{k_{2i}}}\left\{exp\left[k_{2i}{\left({Ī}^{*}{}_i-1\right)}^2\right]-1\right\}{Ī}^{*}{}_i={\kappa }_i{Ī}_1+\left(1-3{\kappa }_i\right){Ī}_i$$ (4)

$$W_{volumetric}=\frac{{\left(J-1\right)}^2}{D}$$ (5)

where C₁₀ is the transverse shear modulus of the isotropic ground matrix, k_1(4–6) and k_2(4–6), are the small and large strain fiber moduli, respectively, in orthotropic directions, D is related to the bulk modulus, and k is the dispersion parameter. The small and large strain fiber moduli in both directions were considered equal to each other throughout the study (k₁₄ = k₁₆, k₂₄ = k₂₆). The definitions of the strain invariants Ī_i, Ī₄, Ī₆ and the calculation of dispersion parameter (κ_i) can be found elsewhere.⁹ The dispersion parameter for the preferred fiber alignment and local fiber coordinate systems were calculated at each integration point with a custom Fortran user subroutine.

Procedure Simulations

Patient-specific femtosecond laser treatment settings were documented for each eye. The treatment parameters were translated from the spectacle plane to the corneal plane assuming a vertex distance of 12.5 mm.¹⁵ The optical zone was 6.5 mm for each patient according to the operative reports. The lenticule shape required to produce the desired spherical correction was calculated from the Munnerlyn equation.¹⁶ The corresponding case-specific cylindrical treatment was calculated per Mrochen et al.,¹⁷ but with the wavefront optimized correction components removed from the cylindrical equation. The lenticule also contained an annular transition zone to taper the peripheral corneal tissue from the optical zone to the lenticule edge that is grasped by the surgeon during lenticule extraction. The thickness profile for the transition zone was calculated from the Munnerlyn equation by substituting the optical zone with 7.5 mm and reducing the reported spherical correction by 90% in the equation until the calculated lenticule thickness reached 15 pm at the lenticule edge where the surgeon grasps the lenticule during extraction. Flap (femtosecond lenticule extraction) and cap (SMILE) diameters were 7.9 and 7.3 mm, respectively, based on the actual treatment settings. The shape of the lenticule for each simulation was calculated with a custom Python script. The nodes of the corneal geometries were repositioned according to the reported correction calculation by the Python script prior to the no-load calculation to perform the refractive profiling on a loaded geometry.

The anisotropic material constants of the material formulation, k_1(4–6) and k_2(4–6), represent the stiffness of the collagen fibers during small strain (crimped) and large strain (completely un-crimped) states, respectively. We assumed that corneal collagen fibers do not completely uncrimp under the simulation conditions. The effect of a dimensionless k_2(4–6) value on corneal geometry at physiologic pressure was investigated with a sensitivity analysis in a single case within the range of 10 to 400 and the effect was found to be negligible. Thus, k_2(4–6) was held constant throughout the simulations. Depth-dependent corneal stromal properties were incorporated in the current modeling analysis based on prior cohesive tensile strength data.¹⁸ Both C₁₀ and k₁₄ were linearly scaled to 50% of their anterior stromal values for the posterior region during pre-load geometry calculations. Following the no-load calculation strain energy equation, parameters were modified for the fiap/cap and wound layers of the two contralateral procedure simulations. The modified parameters for each of the regions are given in Table A (available in the online version of this article).

TABLE A.

Material Parameters for Anatomic Components of the Contralateral Flap-Based (FLEx) and Flapless (SMILE) Eye Models

Procedure	C10 (MPa)	k14 (MPa)	k24
SMILE cap (7.3-mm diameter)	0.03	kpre × 0.93	30
FLEx flap (7.9-mm diameter)	0.03	kpre × Δfiber	30
Preoperative (flap/cap)	0.03	kpre	30
SMILE/FLEx wound	0.03 × 0.005	kpre × 0	30
SMILE/FLEx side cut	0.03 × 0.7	kpre × 0	30
Preoperative wound/side cut for FLEx/SMILE	0.03	kpre	30

K₁₄ = crimped fibril stiffness (MPa); k₂₄ = unitless fibril uncrimping constant; SMILE = small incision lenitcule extraction; C₁₀ = transverse shear modulus of the isotropic matrix; k_pre = preoperative crimped fibril stiffness; FLEx = femtosecond lenticule extraction; Δ_fiber = induced change in fibril stiffness within the FLEx flap region (central 7.9 mm)

The two unknown material parameters in Table A were determined using a two-step inverse finite element analysis approach. At step 1, preoperative fiber stiffness at small strain (crimped fiber state), kpre, was obtained for each SMILE eye through inverse finite element analysis of the no-flap lenticule extraction procedure with the assumption of a 7% reduction of the total fiber stiffness in the cap region. This assumption is derived directly from the dimensions of the small incision in SMILE³ and the relative impact attributable to the subpopulation of fibers transected by the incision. An assumption about the material change is required for at least one eye of a pair to facilitate the inverse calculation of the preoperative material properties using surgically induced tomographic changes, and any error in this assumption is likely to be lower for the small incision case than the larger cap/fiap edge incisions associated with femtosecond lenticule extraction and LASIK. At step 2, the resulting preoperative fiber stiffness value was assigned to the contralateral femtosecond lenticule extraction eye and the surgically induced biomechanical change of the fiber stiffness within the flap region (Δ_fiber) for that eye was determined by optimization. Specifically, the error between the postoperative anterior corneal curvature of simulated and actual 6-month postoperative results was minimized using a global pattern search optimization. The anterior corneal curvature error calculation was performed using 15 concentric rings with diameters that ranged from 0.1 to 1.5 mm spanning the central cornea and centered on the Scheimpflug tomography instrument axis. Mean tangential curvature was calculated at each ring for clinical and simulated surfaces using the first and second derivatives of the 12th order Zemike polynomials (Z) with respect to the radius (r) (Equation 6). The calculated tangential curvature values were converted to diopters (D) using Snell’s law and a corneal refractive index of 1.3375.

$$Ktan=\frac{{\left(1+{\left(\frac{dZ}{dr}\right)}^2\right)}^{\frac{3}{2}}}{\left|\frac{d^{2}Z}{d{r}^2}\right|}$$ (6)

An inverse finite element problem requires an objective function that is mini006Dized by running the forward problem iteratively until the global minimum is achieved with the optimization algorithm. The objective function (f) was determined as the root mean square of the differences of mean tangential curvatures between clinical and simulated rings at the same radii (Equation 7).

$$f=\sqrt{\frac{{\displaystyle {\sum }_{r=0.1}^{1.5}{(Mean(Ktanmode{l}_r)-Mean(Ktanatua{l}_r))}^2}}{15}}$$ (7)

The objective function was minimized using MATLAB optimization toolbox (version 2009; Mathworks, Natick, MA). All inverse analyses were run with a 15 mm Hg physiologic IOP applied homogenously to the posterior surface of the corneoscleral model. Following the inverse analyses, two forward finite element analyses were performed for each case using optimized pretreatment and posttreatment values at IOP loading equivalents of 15 and 30 mm Hg to elicit information on differential displacement and stress under greater loads in each case. Residual bed maximum displacement and maximum von Mises stress values were noted at the end of each simulation. Calculation of von Mises stresses was explained in detail in a previous study from our group.³ Von Mises stress is commonly used in finite element modeling to represent the total state of stress acting on a material at the specified location. The clinical importance of stress is its association with deformation (strain) in the same region. Finite element models were solved using Abaqus (version 6.11; Dassault Systemes Simulia Corp., Providence, RI) commercial finite element solver. Clinical simulated keratometry values of steep (K₁) and flat (K₂) meridians were derived from pretreatment and posttreatment geometries using VolCT (Sarver & Associates, Cookeville, TN) and the average of these two values were reported as K_ave. Tangential curvature maps of the geometries were plotted in VolCT. Statistical significance was determined by paired Student’s t tests for non-independent samples with a P value of .05 indicating significance.

RESULTS

The mean programmed refractive correction for all 10 eyes was −7.22 ± 1.44 D for the spherical component and −0.22 ± 0.22 D for the cylinder component. Table 1 presents the actual surgically induced change in spherical equivalent manifest refraction (ΔMRx), attempted spherical equivalent correction (Seq), and difference between Seq and ΔMRx (residual spherical equivalent refractive error) for each eye. Differences in spherical equivalent attempted correction and residual refractive error between flapless and flap-based eyes were not statistically significant (P = .60 and .40, respectively). Clinical pretreatment and posttreatment K_ave values are presented in Table B (available in the online version of this article) and corresponding tangential topography maps are provided in Figure 1.

TABLE 1.

Clinical ΔMRx, S_eq, and Postoperative Refractive Error^a for Contralateral Flap-Based (FLEx) and Flapless (SMILE) Cases^b

Patient	FLEx			SMILE
	ΔMRx	Seq	Residual Error	ΔMRx	Seq	Residual Error
1	−5.50	−6.00	−0.50	−5.25	−5.75	−0.50
2	−7.75	−8.00	−0.25	−8.25	−8.12	0.12
3	−6.62	−6.62	0.00	−6.37	−6.86	−0.49
4	−9.50	−9.25	0.25	−9.25	−9.25	0.00
5	−6.62	−6.50	0.12	−5.62	−6.00	−0.38
Mean ± SD	−7.20 ± 1.51	−7.27 ± 1.33	−0.07 ± 0.30	−6.95 ± 1.72	−7.20 ± 1.47	−.025 ± 0.29
P	–	–	–	–	.60	.40

ΔMRx = change in spherical equivalent manifest refraction; S_eq = attempted spherical equivalent correction; FLEx = femtosecond lenticule extraction; SMILE = small incision lenticule extraction

^aDifference between S_eq and ΔMRx.

^bExpressed as spherical equivalent refractive error in diopters (D).

TABLE B.

Clinical Preoperative and Postoperative K_ave Values

Patient	Procedure	Laterality	PreKave (D)	PostKave (D)	ΔK (D)
1	FLEx	OD	42.18	37.90	−4.28
	SMILE	OS	42.33	38.21	−4.12
2	FLEx	OS	42.24	37.09	−5.15
	SMILE	OD	42.21	36.45	−5.76
3	FLEx	OD	44.13	39.01	−5.13
	SMILE	OS	44.40	38.98	−5.42
4	FLEx	OD	44.09	37.54	−6.55
	SMILE	OS	44.20	37.48	−6.73
5	FLEx	OD	42.78	37.58	−5.20
	SMILE	OS	42.78	37.88	−4.90
Mean ± SD			43.13 ± 0.94	37.80 ± 0.78	−5.32 ± 0.84

K_ave = average keratometry value of the steep and flat meridians; D = diopters; ΔK = surgically induced change in K_ave values; FLEx = femtosecond lenticule extraction; OD = right eye; SMILE = small incision lenticule extraction; OS = left eye; SD = standard deviation

Figure 1. Preoperative (preop) and postoperative (postop) tangential curvature maps of the subjects. P = patient; FLEx = femtosecond lenticule extraction; SMILE = small incision lenticule extraction.

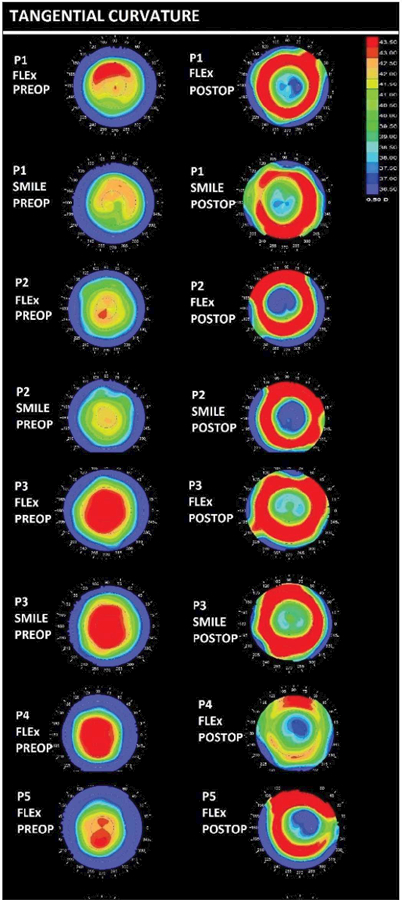
Table 2 demonstrates the converged preoperative fibril stiffness and Δ_fiber values for individual cases. Using identical preoperative corneal material property assumptions in each eye pair based on no-load state optimizations, a 56% (range: 9% to 94%) mean reduction in the fiber stiffness within the flap region of femtosecond lenticule extraction cases was computed when each fellow SMILE case was assumed to reduce cap fiber stiffness by 7% based on incision arc length (as described in the Methods section). The mean difference between eyes was 49% with a range of 2% to 87%. All femtosecond lenticule extraction cases produced greater calculated reductions in fibril stiffness than SMILE cases.

TABLE 2.

Material Property Solutions for Contralateral Flapless (SMILE) and Flap-Based (FLEx) Refractive Surgeries

Variable	Flapless Procedure		Flap-Based Procedure
	kpre (MPa) from iFEA Optimizations of Preoperative SMILE Eye	Assumed Change for Cap	kpre (MPa) from Preoperative Solution for Contralateral Eye	Δfiber from iFEA Optimization of Pre–Post Geometry Change in FLEx Eye
Patient 1	0.0295	−7%	0.0295	−94%
Patient 2	0.023	−7%	0.023	−9%
Patient 3	0.029	−7%	0.029	−77%
Patient 4	0.08	−7%	0.08	−65%
Patient 5	0.025	−7%	0.025	−35%
Mean ± SD	0.0373 ± 0.024	−7%	0.0373 ± 0.024	−56 ± 34%

SMILE = small incision lenticule extraction; FLEx = femtosecond lenticule extraction; iFEA = inverse finite element analysis; k_pre = preoperative crimped fibril stiffness; Δ_fiber = induced change in the fibril stiffness within the FLEx flap region (central 7.9 mm)

Table 3 and Table C (available in the online version of this article) display the maximum residual bed displacements and von Mises stresses, respectively, for each case based on forward finite element simulations using the optimized parameters given in Table 2 and calculated from the unloaded state to the specified IOP. Maximum residual stromal bed deformations were not significantly different at 15 mm Hg for femtosecond lenticule extraction and SMILE (P = .10), but were significantly lower in SMILE simulations at 30 mm Hg (P = .03). Femtosecond lenticule extraction simulations produced 5% higher residual bed von Misses stresses and displacements than SMILE cases in physiologic loading (P = .002) and 12% higher stresses at 30 mm Hg (P = .002). The difference in stresses and deformation in the residual stromal bed between SMILE and femtosecond lenticule extraction cases increased in simulations conducted at a load of 30 mm Hg. Figures 2–3 demonstrate the residual bed displacements and von Mises stresses, respectively, of patient 1 as a representative contralateral eye pair.

TABLE 3.

Maximum Residual Stromal Bed Displacements for Flap-Based (FLEx) and Flapless (SMILE) Refractive Surgery in Contralateral Eye Models as a Function of IOP Measured From the No-Load State to the Specified IOP Load^a

Variable	SMILE at 15 mm Hg	SMILE at 30 mm Hg	FLEx at 15 mm Hg	FLEx at 30 mm Hg
Patient 1	701	1,140	729	1,190
Patient 2	813	1,267	800	1,261
Patient 3	690	1,120	705	1,150
Patient 4	669	1,040	690	1,080
Patient 5	833	1,313	863	1,353
Mean ± SD	741 ± 76	1,176 ± 112 (+58.7%)	757 ± 73	1,207 ± 105 (+59.5%)
P (difference between  SMILE and FLEx)			.10	.03

SMILE = small incision lenticule extraction; FLEx = femtosecond lenticule extraction; IOP = intraocular pressure

^aMeasured in microns.

TABLE C.

Maximum Residual Stromal Bed von Mises Stresses for Flap-Based (FLEx) and Flapless (SMILE) Refractive Surgery in Contralateral Eye Models as a Function of IOP^a

Variable	SMILE at 15 mm Hg	SMILE at 30 mm Hg	FLEx at 15 mm Hg	FLEx at 30 mm Hg
Patient 1	0.0239	0.0545	0.0255	0.0643
Patient 2	0.0255	0.0595	0.0272	0.0641
Patient 3	0.0243	0.0556	0.0251	0.0622
Patient 4	0.0296	0.0664	0.0316	0.0756
Patient 5	0.0271	0.0659	0.0283	0.0718
Mean ± SD	0.0261 ± 0.0023	0.0604 ± 0.0055 (+128%)	0.0275 ± 0.0026	0.0676 ± 0.0057 (+146%)
P (difference between  SMILE and FLEx)	–	–	.002	.002

SMILE = small incision lenticule extraction; FLEx = femtosecond lenticule extraction; IOP = intraocular pressure

^aMeasured in MPa.

Figure 2. Residual stromal bed displacements (in millimeters) for case-specific models of patient 1 for (A) small incision lenticule extraction (SMILE) at 15 mm Hg, (B) femtosecond lenticule extraction (FLEx) at 15 mm Hg, (C) SMILE at 30 mm Hg, and (D) FLEx at 30 mm Hg. Displacements reported for each state relative to the unloaded state.

Figure 3. Residual stromal bed von Mises stresses (in MPa) for case-specific models of patient 1 for (A) small incision lenticule extraction (SMILE) at 15 mm Hg, (B) femtosecond lenticule extraction (FLEx) at 15 mm Hg, (C) SMILE at 30 mm Hg, and (D) FLEx at 30 mm Hg.

Table D (available in the online version of this article) demonstrates the mean tangential dioptric power within the central 3-mm region (Kmean) for contralateral eyes of all patients at 15 and 30 mm Hg IOP steps. Eyes that underwent flap-based procedures demonstrated more central steepening with an IOP increase than contralateral SMILE eyes (P < .05).

TABLE D.

Anterior Tangential Curvature Within the Central 3-mm Region (K_mean) for Flap-Based (FLEx) and Flapless (SMILE) Surgery in Contralateral Eye Models as a Function of IOP^a

Variable	SMILE at 15 mm Hg	SMILE at 30 mm Hg	Difference	FLEx at 15 mm Hg	FLEx at 30 mm Hg	Difference
Patient 1	37.79	40.65	2.86	37.90	41.08	3.18
Patient 2	36.20	39.66	3.46	36.02	39.50	3.48
Patient 3	38.91	41.69	2.78	39.08	42.08	3.00
Patient 4	36.85	38.72	1.87	37.11	39.15	2.04
Patient 5	38.15	40.41	2.26	37.77	40.14	2.37
Mean ± SD	37.58 ± 1.06	40.22 ± 1.11	2.64 ± 0.60	37.57 ± 1.12	40.39 ± 1.19	2.81 ± 0.59 (+6%)
P (difference  between SMILE  and FLEx)	–	–	–	–	–	.02

FLEx = femtosecond lenticule extraction; SMILE = small incision lenticule extraction; IOP = intraocular pressure

^aMeasured in diopters.

DISCUSSION

LASIK is one of the most frequently performed procedures globally and is associated with high patient satisfaction rates.¹⁹ However, the interest in small incision intrastromal surgery as an alternative to flap-based refractive surgery is driven in part by conservation of anterior stromal architecture and the potential to reduce the impact of refractive surgery on corneal biomechanical integrity. Depth-dependent differences in human corneal material strength have been noted in previous experimental mechanics studies^18,20 and are consistent with observations of preferential mechanical reinforcement of the anterior stroma through interlamellar weaving²¹ and transverse bridging fibers.^22,23 The relevance of this property gradient in relation to conservation of anterior stromal architecture in intrastromal surgery has been discussed by Reinstein et al.,² and a previous study from our group3 provided insight into the potential structural benefits of a flapless procedure with comparative forward finite element analyses of LASIK and SMILE in one eye.

In this clinical contralateral comparative study, we evaluated the biomechanical impact of flap-based and flapless lenticule extraction treatments on the anterior stromal cap/flap region and the residual stromal bed. The computational model used here has demonstrated high clinical predictive value in myopic LASIK²⁴ and is expected to have similar fidelity in highly analogous procedures such as femtosecond lenticule extraction and SMILE. The inverse finite element analysis approach is a commonly used method for estimating material properties and material property changes in biomedical applications. Our group previously used this approach in clinical datasets to estimate the material property changes caused by collagen cross-linking²⁵ and LASIK,²⁶ but it is entirely novel in the current context of comparing flap-based and flapless surgeries. Our purpose was to study the biomechanical impact of the two investigated procedures and to put numbers to this comparison based on actual clinical data. The goals of extending this work to refractive prediction or ectasia risk analysis are not dealt with here, although the study provides some information that is relevant to those objectives. Measuring the impact of each surgical method is an important early step to support subsequent model-based attempts to propagate those material changes to refractive outcome predictions and assessments of ectasia risk. Any structural model of the surgery for these later objectives requires assumptions about the surgically induced material changes so that the appropriate changes can be assigned to the material model. This study provides the first such estimates for SMILE and femtosecond lenticule extraction.

Computationally derived reductions in postoperative biomechanical properties of the anterior stroma were greater in the flap-based procedures than in the flapless procedures in every case. It is unlikely that these differences were driven by interocular differences in magnitude of attempted refractive correction because these differences were both clinically and statistically insignificant. Furthermore, there was no clinical tendency toward systematic overcorrection or undercorrection with either procedure relative to the contralateral eye, which suggests that this approach to differentiating the biomechanical impact of procedures is sensitive and does not rely on the presence of clinically evident refractive error differentials to detect differential material property changes. Because the computational analysis is driven by the change in the corneal geometry between the preoperative and 6-month examinations, the computed differences in biomechanical response are driven by the differences in the topographic response to each procedure. Six-month postoperative data and incorporation of a nominal wound layer at the lenticule interface in the model were used to represent the convalescent state when hydration changes and stromal and epithelial remodeling have typically stabilized.

Flap-based cases demonstrated higher residual bed stresses and displacements in postoperative forward simulations using patient-specific optimized material properties than SMILE cases. In a recent clinical modeling analysis of a case of unilateral post-LASIK ectasia, we found the eye that developed ectasia exhibited higher stromal bed stresses and strains (where strain is closely related to displacement) than its contralateral fellow eye both before and after LASIK.²⁷ A large-scale modeling study of ectasia risk from our group also supports the role of mechanical strain as a predictor of ectasia risk.²⁸ In light of these studies and others proposing elevated stress and strain as risk factors in corneal structural stability,²⁹ higher instantaneous stresses and displacements in the residual bed are more likely to favor biomechanical instability over time due to aberrant remodeling processes, viscoelastic creep, and other processes dependent on time and wound healing. The flap-based group also consistently demonstrated more central steepening than the Hapless group with provocative simulated IOP elevations. The magnitude of this change may be greater than what would be anticipated clinically because of the use of a sensitive tangential dioptric power algorithm, and could also be impacted by scleral elasticity and boundary condition assumptions. The latter are fully accounted for in the initial noload calculations and are treated identically between eyes of a pair to eliminate any associated error in relative/interocular results.

Reductions in corneal elastic modulus have been shown in prior computational modeling studies to be a driver of corneal ectasia development and progression,^11,30,31 and we postulate that higher focal stresses and strains could be a mechanical stimulus for further mechanical³² or maladaptive biological responses that could lead to structural failure. Ectasia after SMILE has been reported,^33–35 and it is important to note that ectasia risk exists on a continuum involving intrinsic predisposition and extrinsic surgical risk factors. Anterior fibr-sparing procedures may reduce relative risk but cannot eliminate risk in eyes with other predisposing factors or manifest disease.^36,37

Although a prior modeling study from our group compared LASIK and SMILE in a single theoretical case,³ the current study is the first clinically driven computational analysis of flap-based and Hapless surgical analogues. A major strength of this study is that it leverages a unique clinical dataset in which well-matched myopic refractive errors were treated with SMILE and femtosecond lenticule extraction in a prospective contralateral eye study design. This maximizes the validity of assumptions of parity with respect to preoperative corneal biomechanical properties, biological variables such as age and wound healing, environmental and surgical variables, and many other potential confounding variables. Non-idealities such as deviations in the delivered pulse profile and extracted lenticule geometry from a Munnerlyn model, decentration during lenticule formation (see Figure B), and torsional differences between preoperative and postoperative tomography scans represent potential sources of error and could impact the convergence behavior of the geometric optimization algorithm and final material property values. To the extent that these non-idealities manifest similarly between two eyes of a contralateral pair, the comparison of property changes as a function of procedure type remains valid. Interocular differences in collagen fiber distributions or biomechanical properties are less likely, but if present could introduce a source of error that has greater potential to affect the conclusions about the relative biomechanical impact of the procedures.

The assumption of a 7% reduction in SMILE cap fiber elastic properties was based directly on the anatomic relationship to the percentage of anterior fibers transected by the small incision and was required to allow computation of a common set of preoperative corneal properties for each eye pair. Error in the estimation of the percentage of fibers transected would affect the accuracy of preoperative property calculations but should not alter conclusions about the interocular differences in surgical impact because the study design applies the same preoperative properties to both eyes and convergence behavior in these simulations was robust and not prone to errors due to local minima. Each contralateral eye analysis allowed for a two-way outcome (either an increase or a decrease in elastic properties) and in every case supported the conclusion that flap-based surgery alters corneal biomechanical behavior more than SMILE does.

Fiber-sparing flapless procedures such as SMILE appear to have less impact on anterior stromal collagen mechanics and result in lower stromal bed displacements and stresses than flap-based procedures in contralateral eyes. Furthermore, simulated increases in pressure load result in smaller increases in stromal bed stresses and anterior corneal curvature in flapless procedures. These findings, which are derived directly from clinical tomographic outcomes, demonstrate quantifiable structural advantages for anterior fiber-sparing procedures. This study provides the first computationally derived measures of corneal material property changes in SMILE and femtosecond lenticule extraction and will inform future modeling attempts to simulate these procedures for refractive outcome prediction and structural risk analysis.