Temporally feathered intensity‐modulated radiation therapy: A planning technique to reduce normal tissue toxicity

Abstract

Purpose

Intensity‐modulated radiation therapy (IMRT) has allowed optimization of three‐dimensional spatial radiation dose distributions permitting target coverage while reducing normal tissue toxicity. However, radiation‐induced normal tissue toxicity is a major contributor to patients’ quality of life and often a dose‐limiting factor in the definitive treatment of cancer with radiation therapy. We propose the next logical step in the evolution of IMRT using canonical radiobiological principles, optimizing the temporal dimension through which radiation therapy is delivered to further reduce radiation‐induced toxicity by increased time for normal tissue recovery. We term this novel treatment planning strategy “temporally feathered radiation therapy” (TFRT).

Methods

Temporally feathered radiotherapy plans were generated as a composite of five simulated treatment plans each with altered constraints on particular hypothetical organs at risk (OARs) to be delivered sequentially. For each of these TFRT plans, OARs chosen for feathering receive higher doses while the remaining OARs receive lower doses than the standard fractional dose delivered in a conventional fractionated IMRT plan. Each TFRT plan is delivered a specific weekday, which in effect leads to a higher dose once weekly followed by four lower fractional doses to each temporally feathered OAR. We compared normal tissue toxicity between TFRT and conventional fractionated IMRT plans by using a dynamical mathematical model to describe radiation‐induced tissue damage and repair over time.

Results

Model‐based simulations of TFRT demonstrated potential for reduced normal tissue toxicity compared to conventionally planned IMRT. The sequencing of high and low fractional doses delivered to OARs by TFRT plans suggested increased normal tissue recovery, and hence less overall radiation‐induced toxicity, despite higher total doses delivered to OARs compared to conventional fractionated IMRT plans. The magnitude of toxicity reduction by TFRT planning was found to depend on the corresponding standard fractional dose of IMRT and organ‐specific recovery rate of sublethal radiation‐induced damage.

Conclusions

TFRT is a novel technique for treatment planning and optimization of therapeutic radiotherapy that considers the nonlinear aspects of normal tissue repair to optimize toxicity profiles. Model‐based simulations of TFRT to carefully conceptualized clinical cases have demonstrated potential for radiation‐induced toxicity reduction in a previously described dynamical model of normal tissue complication probability (NTCP).

1. Introduction

Since the advent of therapeutic radiotherapy, our understanding of radiation planning, delivery and effects have significantly grown. In parallel, the utilization of radiotherapy has increased, and currently it is estimated that about half of the cancer patients benefit from curative or palliative therapy at some point during the course of their disease.¹ The principle challenge in delivering safe, yet effective radiotherapy has been the balance of tumor control probability (TCP) against normal tissue complication probability (NTCP), termed the therapeutic ratio.² The so called “widening” of the therapeutic ratio has been subject to research since the early implementation of radiotherapy. Specifically, treatment planning techniques have evolved from 2D to 3D planning, and now intensity‐modulated radiation therapy (IMRT), which has allowed the optimization of physical dose distributions and avoidance of organs at risk (OARs).^{3, 4, 5} Moreover, clinicians can now also alter radiation dose to the target as well, such as in heterogeneously dosing across a tumor volume, promoting dose intensification.⁶ This is all done while abiding by conventional dose constraints to normal tissues to qualify plan safety before patient delivery.² The ability to spare organs and healthy tissues has been pivotal in improving quality of life during and following radiotherapy.⁷

Through these advancements, the four pillars of radiobiology have guided the understanding of radiation effect on tissue: (a) repair of sublethal damage, (b) reassortment of cells within the cell cycle, (c) repopulation, and (d) reoxygenation. We accept sublethal damage repair and repopulation as the main drivers of dose‐limiting acute toxicity and hence fractionated radiotherapy still predominates in the clinic. The consistent fractional dose of radiation administered daily, delivers consistent insult to tumor cells while allowing time for normal tissue recovery between treatment fractions.⁸ Yet clinically, not all radiation‐induced damage to organs at risk (OARs) is recovered with this interfractional interval. Taking the example of head and neck malignancies, treated to 70 Gy in 35 fractions, acute toxicities often still manifest mid‐way or toward the end of most treatment courses. Despite reversibility of acute toxicity, when severe, it can lead to treatment breaks and compromise tumor control.⁷ Additionally, well‐documented late effects contribute to the morbidity of radiation therapy, as these are often irreversible. The repopulation of normal tissues following peak acute toxicity can take weeks to months. We herein introduce a novel treatment planning strategy with the potential to reduce acute and late normal tissue toxicity.

Understanding basic radiobiology principles discussed above, we have developed a novel technique of optimizing radiation dose and fractionation, leveraging time to maximize normal tissue recovery, and therefore decrease toxicity without altering tumor dose. We hypothesize that if an organ at risk receives a once weekly higher than standard fractional dose of IMRT followed by lower fractional doses, the 1 week interval between the higher fractional doses will allow increased sublethal damage repair and repopulation. The novelty is in balancing normal tissue repair against radiation‐induced damage using a nonlinear model of dynamic NTCP. The focus of this study is introducing the theoretical radiation biology behind the advance. The proposed dynamical model of NTCP with a recovery term of normal tissue damage allows for the conceptual presentation of TFRT, and development of a predictor of TFRT benefit over conventionally planned IMRT. Possible clinical implications of reduced toxicity include improvement the quality of life issues, as well as potential for dose intensification to the tumor with similar toxicity profiles.

2. Methods

2.A. Temporally feathered radiation therapy

We present a novel treatment planning strategy, which we term temporally feathered radiation therapy (TFRT), in which the fractional radiation dose delivered to OARs is altered to allow for increased normal tissue recovery of radiation‐induced damage with respect to conventionally fractionated IMRT. A TFRT plan is generated as a composite of several iso‐curative (i.e., same tumor dose) plans each with altered constraints on particular OARs of interest. In each of these TFRT plans, a single OAR would be deprioritized, allowing the optimization algorithm to reduce radiation dose and thereby toxicity to all other OARs. In practice, let us assume a planning target volume (PTV) with five surrounding OARs of interest prescribed a standard dose of 70 Gy in 35 fractions, similar to that commonly implemented for head and neck cancers.⁷ Furthermore, let us consider that five treatment plans are developed, wherein each of the five OARs receives a relatively high fractional dose (d_H) compared to the standard fractional dose (d_S) once weekly, that is, 2.0 Gy. A relatively lower (d_L) fractional dose is then delivered the remaining 4 days of the week (see Fig. 1). With this treatment planning strategy, although greater radiation‐induced damage is induced by d_H once weekly, it is offset by the lower fractional dose, d_L, delivered over a greater amount of time, that is, during the remaining 4 days. We then compare the composite of d_H and d_L to the corresponding standard fractional dose d_S delivered to each OAR in a conventionally fractionated IMRT plan. In this hypothetical case, the TFRT plan is composed by 35 fractions, and each OAR of interest will receive 28 fractions of 0 < d_L < d_S and 7 fractions of d_H > d_S > 0. We consider that fractional doses d_L and d_H remain unaltered during the course of treatments. For demonstrative purpose, we focus on radiotherapy treatment plans which feather five OARs, though any number of OARs can be chosen for temporally feathering.

Figure 1.

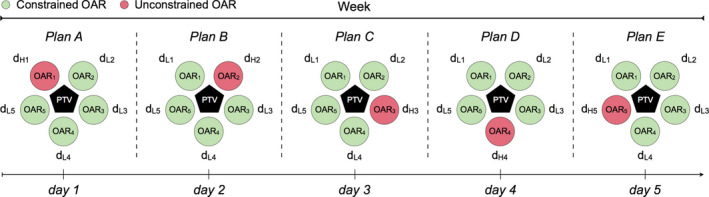
Schematic representation of treatment planning in temporally feathered radiation therapy (TFRT). The planning target volume (PTV) is in close proximity to five organs at risk (OARs). Each OAR i receives a higher fractional dose once weekly (d_{H i}), followed by lower fractional doses for the remaining 4 weekdays (d_{L i}), 1 ≤ i ≤ 5. The PTV is represented as a pentagon, and circles represent the surrounding OARs. For each weekday and treatment plan a single and different OAR is unconstrained, where the remaining are constrained. [Color figure can be viewed at wileyonlinelibrary.com]

2.B. Biologically effective dose model

The Linear‐Quadratic (LQ) model is currently the most widely used dose–response formulation in radiotherapy.^{8, 9} The LQ model fits to in vitro cell survival experiments and incorporates the LQ behavior of observed cell survival curves.⁹ The linear component accounts for cell killing by DNA double strand breaks (DSBs) due to a single hit of radiation, whereas the quadratic component represents the lethal effects of two separate ionizing events that eventually cause DSBs.^{8, 9, 10} The surviving fraction (SF) of cells after n fractions of a radiation dose d is given by

$$SF\left(d\right)=e^{-nd\left(\alpha +\beta d\right)},$$ (1)

where α (Gy⁻¹) and β (Gy⁻²) are tissue‐dependent radiosensitivity parameters. It follows directly from the LQ model that the biological effect (E) of n equally sized fractions of dose d is given by E = nd (α + βd). This equation can be manipulated to derive biologically effective dose (BED) calculations, which is a standard quantity allowing comparison of various radiotherapy fractionation schemes. BED is dependent on inherent biologic radiosensitivity of tissues, which is termed as the α to β ratio, α/β. This is also borrowed from the LQ model.^{9, 10, 11} The BED^{11, 12} is given by

$$BED=nd\left[1+\frac{d}{\alpha /\beta }\right].$$ (2)

The BED equation above applies to conventionally fractionated radiation plans in which a same fractional dose (i.e., standard dose) is daily delivered. The BED for a standard daily treatment fraction (BED_S) is given by

$$BE{D}_S=n_S{d}_S\left[1+\frac{d_S}{\alpha /\beta }\right]$$ (3)

where n_S is the number of treatment fractions and d_S is the radiation dose per fraction. The BED of temporally feathered plans BED_TF is defined as follows

$$BE{D}_{\mathit{TF}}=n_L{d}_L\left[1+\frac{d_L}{\alpha /\beta }\right]+n_H{d}_H\left[1+\frac{d_H}{\alpha /\beta }\right],$$ (4)

where n_L and n_H refer to the number of lower dose (d_L) fractions and number of higher dose (d_H) fractions, respectively. Lower dose fractions deliver a radiation dose less than what would be delivered in a conventionally fractionated IMRT plan, 0 < d_L < d_S. Similarly, higher dose fractions deliver a radiation dose higher than what would be delivered in a conventionally fractionated IMRT plan, d_H > d_S > 0. We consider that fractional doses d_L and d_H remains unaltered during the course of treatments, and are homogeneously distributed on each OAR. The total number of fractions and their time of delivery remains the same in conventionally fractionated IMRT and TFRT plans, that is, n_S = n_L + n_H, and we are not changing tumor dose, only dose to OARs.

2.C. BED‐based comparison of treatment plans

The difference in the BED delivered by a conventionally fractionated IMRT plan (S) of standard dose d_S and a temporally feathered (TF) radiation therapy plan is defined as ∆BED = BED_S − BED_TF, see Eqs. (3) and (4).

2.D. Dynamical model of normal tissue complication probability

We use a nonspatial dynamical model to simulate normal tissue response to radiation. This is a form of NTCP modeling, which is a quantitative measure of radiation‐induced detriment to normal tissues.^{13, 14, 15, 16, 17} The model is formulated as a logistic differential equation that describes the recovery of normal tissues (N) from sublethal radiation‐induced damage given by

$$\frac{\mathit{dN}}{\mathit{dt}}=\mu N\left(t\right)\left(1-N\left(t\right)\right)-\delta \left(t_i\right)RT\left(d\right)N\left(t\right)\left(1-N\left(t\right)\right),$$ (5)

where the organ‐specific parameter μ > 0 represents the recovery rate of radiation‐induced damage. We consider the case that before radiation, the simulated OAR is at tissue homeostasis with a 1% turnover rate, thus N(0) = 0.99. Then N(t) < N(0) represents the level of normal tissue damage by radiotherapy (small values of N(t) relate to severe damage), and (N(0) − N(t)) is used as an indication of the radiation‐induced toxicity. The logistic differential Eq. (5) used to model normal tissue recovery simulates a decay of toxicity to zero overtime. This is based on clinical observations revealing that not all patients develop late toxicities, and more importantly, that acute toxicities normally do go to zero on rather short time scales. Furthermore, this model is used to compare conventionally fractionated and temporally fathered radiotherapy plans under the same conditions, which does not influence the ability to compare planning techniques. The model was solved numerically in Matlab (www.mathworks.com).

The effect of radiation is included by the loss term $\delta \left(t_i\right)RT\left(d\right)N\left(t\right)\left(1-N\left(t\right)\right)$ in Eq. (5), where δ($t_i$) is the Dirac‐delta function equals to one at the time of irradiation $t_i$, and zero otherwise. The structure of this loss term models the growing effect of radiation therapy with increasing number of treatment fractions. In fact, it is known that as treatment fractions accumulate the observed radiation‐induced acute toxicities become increasingly apparent.¹⁸ Clinically, we observe normal tissue toxicities that increase in severity mid‐way and toward the end of radiation therapy treatments. The function $RT\left(d\right)=(1-e^{-\alpha d-\beta d^2})$ is based on the radiobiological LQ model in Eq. (1). More precisely, $RT\left(d\right)$ represents the “injured fraction” of normal cells receiving a radiation dose d, that is, 1 — surviving fraction of cells. Thus, for low radiation doses the injured fraction of normal cells due to radiation must be small, thereby $RT\left(d\right)$ must be close to zero. On the other hand, high radiation doses will result in more killed normal cells for which $RT\left(d\right)$ tends to one. Furthermore, we assume that both the delivery of each treatment fraction and response to radiation are instantaneous. We notice that similar dynamical models have been previously proposed to simulate the effect of radiation on brain^{19, 20, 21} and lung tumors,²² as well as to define an organ‐specific NTCP model.²³

2.E. NTCP‐based comparison of treatment plans

We denote by ∆NTCP = N_S(t_end) − N_TF(t_end), the difference between OAR toxicity induced by a conventionally fractionated IMRT plan (N_S(t_end)) and a TFRT plan (N_TF(t_end)) at the end of treatment t_end, see Eq. (5). This means that positive values (∆NTCP > 0) favor TFRT over IMRT plans.

2.F. Overall and maximum potential benefit of TFRT over conventionally fractionated IMRT

We estimate the normal tissue toxicity reduction of TFRT over conventionally planned IMRT by using a term referred to as overall potential benefit (OPB_TF). For any given combination of the organ‐specific recovery rate μ and the fractional radiation dose d_S delivered by a conventionally fractionated IMRT plan, OPB_TF is the ratio of simulated TFRT plans with 0 < d_m ≤ d_L ≤ d_S and 0 < d_S ≤ d_H ≤ d_M that result in ∆NTCP > 0 and deliver higher total doses than the corresponding IMRT plans. In this study, d_m and d_M are the minimum lower dose (d_L) and the maximum higher dose (d_H) considered to generate the TFRT plans.

The maximum potential benefit (MAX_TF) of TFRT over conventionally planned IMRT is defined as the maximum ∆NTCP > 0 of simulated TFRT plans delivering higher total doses than the corresponding IMRT plans.

3. Results

3.A. BED model simulations

We first consider the BED model to compare TFRT and conventionally fractionated IMRT under varying conditions. To that end, we considered an OAR at a physiologic equilibrium and characterized by a α/β ratio of 3 Gy. Furthermore, we simulated TFRT plans with d_m ≤ d_L ≤ d_S and d_S ≤ d_H ≤ d_M consisting of 28 fractions (n_L) of d_L < d_S and 7 fractions (n_H) of d_H > d_S, and the corresponding conventionally fractionated IMRT plans delivering d_S in 35 fractions. For illustrative purposes, we have chosen d_m = (d_S − 0.5 Gy) and d_M = (d_S + 2.5 Gy) with a dose increment of 0.01 Gy between d_m and d_S, as well as between d_S and d_M.

Figure 2 illustrates ∆BED = (BED_S − BED_TF) between different TFRT and conventionally planned IMRT plans, see Eqs. (3) and (4). Irrespective of d_S, TFRT plans result only in a lower BED when the total dose (28 d_L + 7 d_H) delivered to the OAR of interest is less compared to the standard IMRT plan (35 d_S). Furthermore, combinations of d_L and d_H exist in which BED_TF > BED_S even when the total dose by TFRT plans is less than in the conventionally fractionated IMRT plan. These results hold irrespective of the α/β ratio of the OAR of interest (see Fig. S1). The BED formulation does not account for the effect of interfractional normal tissue recovery of radiation‐induced damage, and therefore is not a suitable model to evaluate the potential benefit of TFRT. This highlights the need for models, which account for the dynamic of normal tissue recovery from radiation‐induced damage between treatment fractions to assess the feasibility of TFRT.

Figure 2.

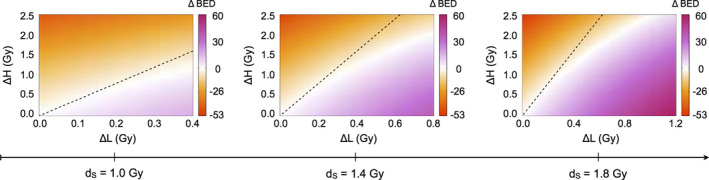
Comparison of conventionally fractionated IMRT and TFRT based on the biologically effective dose (BED) model. From left to right, ∆BED is represented in the divergent colormap for increasing doses d_S . The x‐ and y‐axes represent ∆L = d_S −d_L and ∆H = d_H −d_S , respectively. The regions below and above the dashed lines represent combinations of d_L and d_H in which TFRT plans deliver lower and higher total doses compared to the corresponding IMRT plan delivering a fractional dose d_S , respectively. [Color figure can be viewed at wileyonlinelibrary.com]

3.B. Dynamical NTCP model simulations

We now simulate normal tissue complication probability (NTCP) of TFRT compared to conventionally fractionated IMRT implementing the dynamical NTCP model presented in Eq. (5). As above, we consider an OAR with α/β = 3 Gy and a conventionally fractionated IMRT plan delivering a standard fractional dose d_S in 35 fractions. TFRT plans consist of 28 fractions (n_L) of d_L < d_S and 7 fractions (n_H) of d_H > d_S, with d_L and d_H varying in the ranges [d_S − 0.5 Gy, d_S] and [d_S, d_S + 2.5 Gy], respectively. Model simulations reveal a range of treatment planning conditions in which TFRT plans reduce radiation‐induced toxicity to OARs compared to conventional planned IMRT plans. These conditions are dependent on d_L and d_H, as well as on the organ‐specific recovery rates μ, associated with radiation‐induced damage. This is shown in Figs. 3 and 4, which represent ∆NTCP for TFRT and conventionally fractionated IMRT plans with varying μ and d_S values, respectively. We found that there exist combinations of d_L and d_H delivering higher total doses in TFRT plans as compared to conventionally fractionated IMRT plans (28 d_L + 7 d_H > 35 d_S) but yet reduce the overall radiation‐induced OAR toxicity. This is depicted by the regions above the dashed lines, but still in the beneficial (red: ∆NTCP > 0) regions, in the bottom panels of Figs. 3 and 4.

Figure 3.

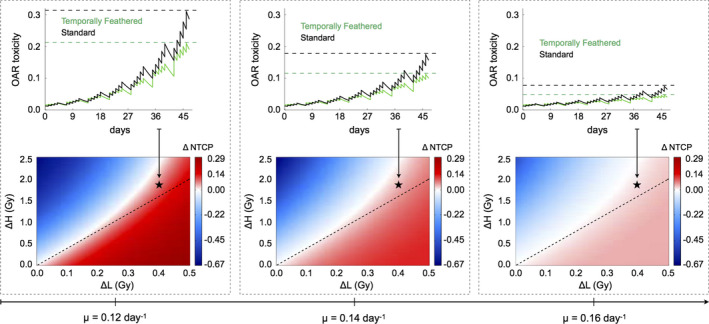
Comparison and representation of NTCP and radiation‐induced OAR toxicity between conventionally fractionated IMRT and TFRT with varying organ‐specific recovery rates (μ). Bottom panels, from left to right, ∆NTCP (colorbar: positive values are beneficial, negative values are detrimental) are represented for d_S  = 1.2 Gy and increasing values of μ. The x‐ and y‐axes represent ∆L = d_S −d_L and ∆H = d_H −d_S , respectively. The regions below and above the dashed lines represent combinations of d_L and d_H in which TFRT plans deliver lower and higher total composite doses compared to the corresponding IMRT plan delivering a fractional dose d_S , respectively. Top panels show the time‐evolution of OAR toxicity induced by the IMRT and TFRT plans corresponding to the location marked by stars in bottom panels. Dashed lines represent the time points at which NTCP of IMRT (higher OAR toxicity) and TFRT (lower OAR toxicity) plans are compared. [Color figure can be viewed at wileyonlinelibrary.com]

Figure 4.

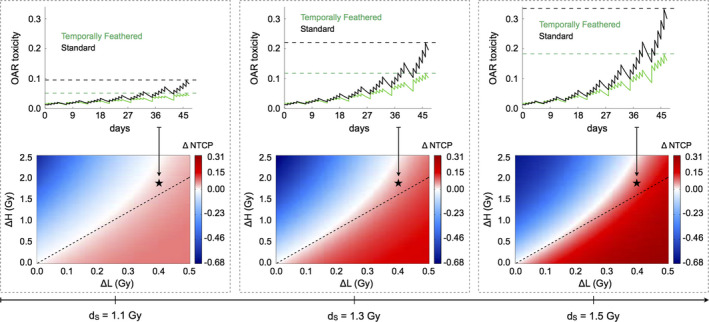
Comparison and representation of NTCP and radiation‐induced OAR toxicity between conventionally fractionated IMRT and TFRT with varying standard fractional doses (d_S ). Bottom panels, from left to right, ∆NTCP (colorbar: positive values are beneficial, negative values are detrimental) are represented for μ = 0.15 day⁻¹ and increasing fractional doses d_S IMRT plans. The x‐ and y‐axes represent ∆L = d_S −d_L and ∆H = d_H −d_S , respectively. The regions below and above the dashed lines represent combinations of d_L and d_H in which TFRT plans deliver lower and higher total composite doses compared to the corresponding IMRT plan delivering a fractional dose d_S , respectively. Top panels show the time‐evolution of OAR toxicity induced by the IMRT and TFRT plans corresponding to the location marked by stars in bottom panels. Dashed lines represent the time points at which NTCP of IMRT (higher OAR toxicity) and TFRT (lower OAR toxicity) plans are compared. [Color figure can be viewed at wileyonlinelibrary.com]

The therapeutic gain by TFRT plans increases as the treatment progresses. This is shown in the top panels of Figs. 3 and 4, where irrespective of the values of μ and standard fractional doses d_S considered, the difference in the radiation‐induced OAR toxicity, that is, N_S(t) − N_TF(t), see Eq. (5), by conventionally fractionated IMRT and TFRT plans, progressively increases with the number of treatment fractions. Furthermore, Figs. 3 and 4 show the difference between OAR toxicity induced by conventional planned IMRT and TFRT plans at the end of treatment (∆NTCP) is greater with decreasing values of μ and increasing fractional doses d_S. Thus, TFRT is more beneficial for reducing radiation‐induced toxicity in OARs with low recovery rates μ and receiving high standard fractional doses d_S with conventional planned IMRT.

Figure 5 summarizes the impact of organ‐specific and treatment parameters on the potential benefit of TFRT over conventionally fractionated IMRT. For each combination of μ and d_S considered, Figs. 5(a) and 5(b) show the overall potential benefit (OPB_TF) and maximum potential benefit (MAX_TF) of TFRT plans with (d_S − 0.5 Gy) ≤ d_L ≤ d_S and d_S ≤ d_H ≤ (d_S + 2.5 Gy) over the corresponding IMRT plans delivering a standard fractional dose d_S. Figure 5 shows that while keeping constant d_S or μ, and varying the other parameter, the OPB_TF and MAX_TF of TFRT increase until a maximum level and then decrease again. This suggests that for each OAR characterized by a specific recovery rate μ, TFRT plans can be designed to reduce OAR toxicity if the standard fractional dose d_S delivered by a conventionally fractionated IMRT plans lies in a certain range. Furthermore, there exists an optimal dose d_S in that range for which OAR toxicity reduction with TFRT is greater. Similarly, OARs receiving a specific standard fractional dose d_S with conventional planned IMRT can be temporally feathered if they have a recovery rate μ is in a certain range. This evidences that both d_S and μ must be considered together when determining the OAR toxicity reduction from TFRT over conventionally planned IMRT. Figures S2 and S3 show that OPB_TF and MAX_TF of TFRT over conventionally fractionated IMRT also depend on the specific α/β ratio of the OARs of interest. Those figures illustrate that, when applied on OARs characterized by different α/β ratios, TFRT continues to represent a theoretically valuable treatment planning strategy to reduce radiation‐induced OAR toxicity.

Figure 5.

Comparison of conventionally fractionated IMRT and TFRT with respect to the standard fractional dose (d_S ) and organ‐specific recovery rate (μ). (a) Overall potential benefit (OPB_TF ) and (b) maximum potential benefit (MAX_TF ) of TFRT over conventional planned IMRT. (I‐III) Top panels represent the single cases marked by stars in (a). The x‐ and y‐axes represent ∆L = d_S −d_L and ∆H = d_H −d_S , respectively. Bottom panels show time‐evolution of OAR toxicity induced by the IMRT and TFRT plans corresponding to the location marked by diamonds in the top panels. [Color figure can be viewed at wileyonlinelibrary.com]

4. Discussion

Through the years, researchers in the field of radiation oncology and medical physics have been innovating new ways of widening the therapeutic ratio by either increasing (TCP) or decreasing normal tissue complication probability (NTCP). Recent works have shown the potential of spatiotemporal fractionation schemes delivering distinct radiation dose distributions in different fractions to improve the therapeutic ratio.^{6, 24, 25} The goal has been to maximize the mean BED in the tumor and minimize the mean BED in normal tissues by hypofractionating parts of the tumor while delivering approximately identical doses to the surrounding normal tissue. This planning strategy has been shown to result in spatiotemporal fractionation treatments that can achieve substantial reductions in normal tissue dose. However, the effect of interfractional normal tissue recovery of radiation‐induced damage has not been taken into account, which when considered could lead to further reduce treatment side effects. In this study, we consider the nonlinear aspects of normal tissue repair to optimize toxicity profiles without compromising tumor control. We introduce TFRT as a novel treatment planning strategy that alters fractional radiation doses delivered to OARs over time with the hypothesis that this will lead to greater overall normal tissue recovery of radiation‐induced damage through the course of treatment. This paper is an exercise in theory that TFRT has the potential to reduce normal tissue toxicity if the assumptions made in Eq. (5) are valid, namely the normal tissue recovery term. Conceptually, TFRT planning capitalizes on the nonlinearity of normal tissue recovery, allowing nonintuitively for more occasional sublethal damage repair and prolonged repopulation phases even in the face of higher total dose delivered at the end of treatment. For this purpose, we used the LQ model to describe the immediate radiation response of normal tissue and a dynamical NTCP model to describe normal tissue repair of radiation‐induced damage during fractions and over the entire treatment time.

The dynamical NTCP model considered in this work parallels prior similar models which have been proposed to simulate radiation effects on different tumor types,^{19, 20, 21, 22} as well as in healthy tissues.²³ The current BED formulation is limited by the lack of a temporal recovery term of radiation‐induced damage, and therefore are not suitable models to compare radiation schema with various fractionations over time. Thus, a dynamical NTCP model with normal tissue recovery is pivotal to theoretically demonstrate potential toxicity reduction with TFRT. The proposed NTCP model is sensitive to parameter changes including OAR recovery rate μ, α/β ratio, and standard fractional dose d_S. As these parameters represent phenomenological values, this model is personalizable to different clinical scenarios, which is relevant for recent work on Genomic Radiation Dosing revealing a wide heterogeneity in response to radiation therapy.²⁶ Understanding the effect of TFRT on particular OARs allows for OAR prioritization to be used in optimization methods. Additional simulations under altered environments are included in the Supplementary Material. We emphasize that OAR‐specific parameters may crucially determine the potential benefit of TFRT in decreasing normal tissue toxicity, which has important implications for clinical trial design. The concept of overall potential benefit is used to determine the potential of TFRT plans in reducing normal tissue toxicity as compared to conventionally fractionated IMRT plans (see Fig. 5, and Figs. S2 and S3). Candidates for TFRT are patients with target volumes in close proximity to the organs at risk, in which conventionally planned IMRT leads to fractional doses to OARs near tolerance and with low recovery rates of radiation‐induced damage.

While the focus of the work herein is to introduce the theoretical concept of TFRT, future work will need to evaluate feasibility of patient‐specific TFRT plans with currently available treatment planning systems. Endpoints for TFRT plan dosimetry and safety evaluation should be defined including dose‐volume histogram (DVH)‐based metrics.^{27, 28, 29} Before application in the clinic, an optimized workflow must be developed. The radiation plans must be developed in tandem, otherwise the creation, optimization, evaluation, and quality assurance (QA) of five separate plans will not prove feasible in the clinic. Currently, organ‐defined recovery rates (μ) and radiosensitivity parameters α and β values are not reliably defined, limiting the utility of this model at this time for clinical decision‐making. However, after prospective clinical implementation and careful data gathering, efforts will be directed toward elucidating these parameters for various OARs. Based on radiobiological properties of the OARs involved, clinicians can be informed regarding the number of OARs to be feathered with optimized timing. In future work, temporal optimization will be combined with spatial optimization and evaluation of partial volumes of organs rather than their entirety. This has been described previously as different portions of the organs may preferentially contribute to toxicity.²⁹ These concepts can be applied to any disease site in which the target is within close proximity to multiple surrounding organs at risk and are not only limited to head and neck malignancies.

5. Conclusions

We introduce a novel strategy of treatment planning termed TFRT, by which the radiation dose to organs at risk is optimized through time, which suggests an opportunity to improve normal tissue recovery from radiation‐induced damage. In silico simulations using a dynamical NTCP model, accounting for normal tissue recovery demonstrate the potential of TFRT to reduce OAR toxicity compared to conventionally planned IMRT. Future work is focused on feasibility of TFRT planning using current treatment planning systems and ultimately translation to be prospectively evaluated in clinic.

Conflict of interest

The authors have no conflicts to disclose.

Supporting information

Fig. S1. Comparison of conventionally fractionated IMRT and TFRT based on the biologically effective dose (BED) model.

Fig. S2. Comparison of conventionally fractionated IMRT and TFRT with respect to the standard fractional dose (dS) and organ‐specific recovery rate (μ) for OARs with different α/β ratios.

Fig. S3. Comparison of conventionally fractionated IMRT and TFRT with respect to the standard fractional dose (dS) and organ‐specific recovery rate (μ) for OARs with different α values and the same α/β ratio.