Graphical abstract
Keywords: Magnetorheological brake, MATLAB Simulink model, Brake performance, Stopping distance
Abstract
Magnetorheological (MR) brakes, owing to their quick response, are being investigated as a possible candidate for substitution for the conventional hydraulic brakes of road vehicles. The MR brake system for a two-wheeler application was envisaged in this article. Based on analytical equations, the system was modelled in the MATLAB Simulink environment. The braking performance of the system in terms of the stopping distance was estimated with the help of the model. The output from the model was compared with the Indian Standard (IS) automotive brake standard requirement for two-wheelers. A single-disc MR brake system did not seem to satisfy this requirement. It took six or more MR disc brakes to meet the stopping distance requirement of the IS standard. Moreover, weight and space constraints may not allow these brakes to be used for automotive applications. With the current state of the technology, MR brakes do not fulfil the requirements of an automotive brake system.
Introduction
Automotive brakes have a large influence on vehicle safety and stability. The stopping time and stopping distance are the major performance parameters of a typical automotive brake system. The stopping time is the time elapsed between the moment the brake is actuated and the moment it comes to a standstill. The stopping distance is the distance traversed by the vehicle from the point of time when the brake is actuated until it comes to a standstill. Brake performance tests for determining the stopping time and distance have been standardized for various categories of vehicles and presented in various brake testing standards like the Indian Standards (IS in India), Federal Motor Vehicle Safety Standard (FMVSS in USA) and Economic Commission for Europe (ECE for European countries).
Conventional hydraulic brakes (CHBs) have been successfully used in road vehicles for decelerating in a similar manner. However, investigations are proceeding to find a substitute for CHBs, which have a response time of approximately 200–300 ms [1]. Magnetorheological (MR) brakes based on MR fluids are being explored for automotive applications since the response time for MR brakes is said to be 15–20 ms [1] compared with the time of 200–300 ms for CHBs. A reduction in the response time translates into a reduction in the stopping time and stopping distance, thereby providing significant improvements in the brake system performance. This paper presents an effort to simulate an MR brake system for a two-wheeler application in a MATLAB Simulink environment in order to estimate the performance parameters. The results from the simulation model have been compared with the performance measurements of IS standards to assess the feasibility of these brakes for automotive applications.
Li and Du [2] designed an MR brake for general purposes and evaluated its performance experimentally. This was one of the earliest works on MR brakes. Park et al. [1] presented the design and magnetostatic as well as thermal analysis for an MR brake meant for an automotive application. They assessed the brakes for sliding mode controls for an antilock braking system (ABS). Karakok et al. [3], in a continuation of the earlier work of Park et al., presented design considerations for a typical MR brake. Furthermore, they performed an experimental evaluation of an MR brake prototype designed for an automotive application. The current and the angular velocity were found to be influencing parameters for the performance of an MR brake. Park et al. [4] analysed the designed MR brake for magnetic intensity, fluid flow, and temperature analyses. They also used optimization techniques such as simulated annealing, subproblem approximation and a first-order method to arrive at the best possible design. Sukhawani and Hirani [5] proposed a high-speed MR brake and evaluated it experimentally to assess the effect of the influencing parameters such as the current, speed and MR gap on the braking torque. They found an MR gap of one mm to be optimal for the MR brake under consideration. Assadsangabi et al. [6] demonstrated the application of a genetic algorithm for the optimization of their MR brake, which was designed for a road vehicle. An effort was made to increase the braking torque and lower the weight of the MR brake. Younis et al. [7] demonstrated the successful use of the SEUMRE global optimization technique and compared it with genetic algorithm and simulated annealing techniques for solving the automotive MR brake design problem. FEA-based optimization was attempted by Nguyen and Choi [8] for an MR brake envisaged for a passenger car. Based on the results, the researchers presented discussions for an improvement of the MR brake’s performance. A novel bi-directional MR brake was proposed by Nguyen and Choi [9] along with a new approach for magnetic circuit modelling. Particle swarm optimization (PSO) along with a gradient repair method was used to optimize the design. Experiments were carried out to validate the accuracy of the approach. A different T-shaped drum-type configuration and the use of the radial as well the axial magnetic fluxes were proposed by Hung and Bok [10] for their MR brake, which was designed for a mid-sized motorcycle. The results of the FEA based optimization, taking into account the mass, space, braking torque, and temperature, were presented. Sarkar and Hirani [11] proposed a squeeze mode-based MR brake to improve the braking torque. During the experimentation, a maximum torque of 7 Nm was achieved at 1.25 A, which is not sufficient for an automotive application. They also compared an MR brake under a shear mode with an MR brake using compression plus shear [12] and found an increment in the braking torque in the second case.
It is evident from the above literature review that MR brakes for automotive applications have been designed, analysed and optimized. Experimental studies on prototypes have been performed to characterize their behaviour in terms of the torque output and influencing parameters. The torque magnitude and the weight of the brake seem to be major challenges despite optimization efforts and novel design approaches used by various researchers. However, major research has been conducted on the MR brake as an element rather than the system as a whole. The performance of the MR brake system in terms of the stopping time and stopping distance needs to be estimated if the system is used for a road vehicle in order to assess the feasibility of this brake system for vehicular applications in the future. The proposed MR brake system needs to meet the requirements of appropriate brake testing standards. Since earlier research has proven the inadequacy of MR brakes for a mid-sized car, in this work, the use of MR brakes has been envisaged for a two-wheeler application whose torque requirement will be low [3]. The major contribution of this work lies in an attempt to simulate the MR brake system in a MATLAB Simulink environment to assess its braking performance, which has not been witnessed in the earlier literature. The MR brake technology, along with the MR brake system, is presented in the beginning of this article. The modelling approach of the MR brake system using MATLAB Simulink is also described, followed by the simulation results and a discussion of these results.
Magnetorheological (MR) fluids and the MR brake system
This section presents the MR fluids and the MR brake technology in brief.
Magnetorheological (MR) fluids
MR fluids belong to the family of smart materials. These were discovered in the 1940s by Jacob Rabinov at the US National Bureau of Standards. The rheological behaviour of an MR fluid depends on the magnetic field [3]. These fluids behave like a liquid when they are not subjected to a magnetic field. However, they become viscous when a magnetic field is present. This change in the viscosity is controllable, since the strength of the magnetic field can be varied with the help of an input current to the electromagnet. The MR fluid is composed of an iron powder suspended in a carrier liquid, such as synthetic oil with some additives, to improve the properties of the fluid. Typically, carbonyl iron powders with particle sizes of less than 10 µm are preferred for MR fluids. Synthetic or silicone oils are used as a carrier medium. Stabilizers and surfactants are used as additives in MR fluids. Many of the MR fluid-based devices, called MRF device-like dampers, have been put to commercial use. MR brakes have not been commercialized yet. However, owing to their quick response time of approximately 15–20 ms, [1] MR brakes are being explored as a possible candidate for replacing conventional hydraulic brakes (CHBs) used in road vehicles. The MRF 132-DG from Lord Corp., USA is considered in this work owing to its broad operating temperature range, i.e., −40 °C to +130 °C [3]. The typical properties of this MR fluid are presented in Table 1.
Table 1.
Properties of MRF 132-DG [3].
| Property | Value/Limits |
|---|---|
| Base fluid | Hydrocarbon |
| Operating temperature | −40 to 130 °C |
| Density | 3090 kg/m3 |
| Colour | Dark grey |
| Yield stress | 45 kPa |
| Weight percent solid | 81.64% |
| Specific heat at 25 °C | 800 J/kg K |
| Thermal conductivity at 25 °C | 0.25–1.06 W/m K |
| Flash point | >150 °C |
| Viscosity at 40 °C | 0.09 (±0.02) Pa s |
| K (MRF-dependent constant parameter) | 0.269 Pa m/A |
| β (MRF-dependent constant parameter) | 1 |
MR brake technology
MR brakes use the shear mode of operation of MR fluids. A typical single disc MR brake is shown in Figs. 1a and 1b [13].
Fig. 1a.
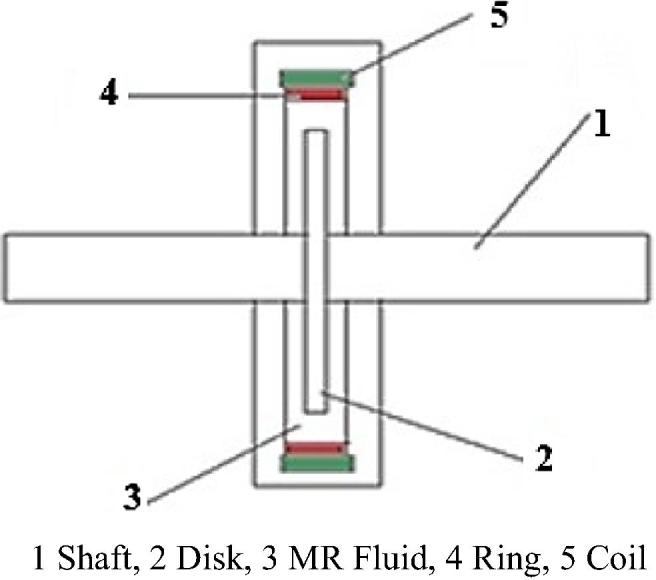
Typical MR brake.
Fig. 1b.
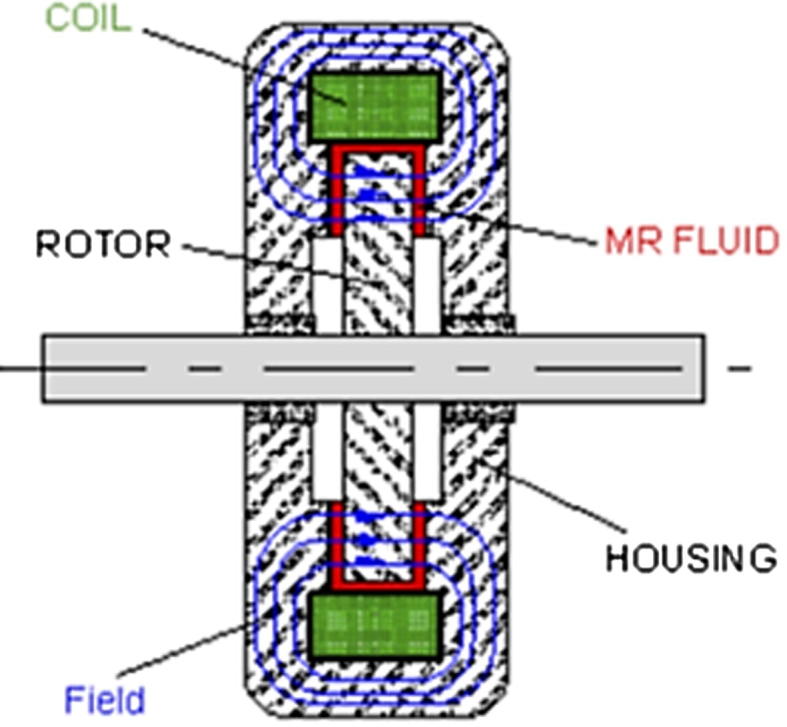
Typical MR brake [13].
The brake basically consists of a disc mounted on a shaft surrounded by the housing. The electromagnet is placed within the housing. There is a small radial gap, called an MR gap, between the disc and the housing, and it is filled by the MR fluid. The MR fluid, when subjected to a magnetic field, increases its viscosity and thereby develops a shear stress, by virtue of which the disc motion is decelerated, and the brake is applied. The response time of the brake is 15–20 ms [1]. The shear stress and therefore the braking torque can be varied by the current input to the electromagnet. The braking torque also depends on the angular speed, the MR fluid-dependent constant parameters, the MR fluid gap, the disc size and the number of discs of the brake, as evident from Eqs. (1), (2) presented below [3].
| (1) |
where TH is the torque due to the magnetic field, N is the number of discs, H is the magnetic field intensity, rz and rj are respectively the outer and inner radii of the disc, and K and β are the MR fluid-dependent constant parameters. Common values for K and β are 0.269 Pa m/A and 1, respectively [3].
| (2) |
where Tµ is the torque due to the plastic viscosity, h is the thickness of the MR fluid gap and w is the angular velocity of the disc.
The total braking torque of the MR brake is composed of the above two components, and it is given by Eq. (3) below [3].
| (3) |
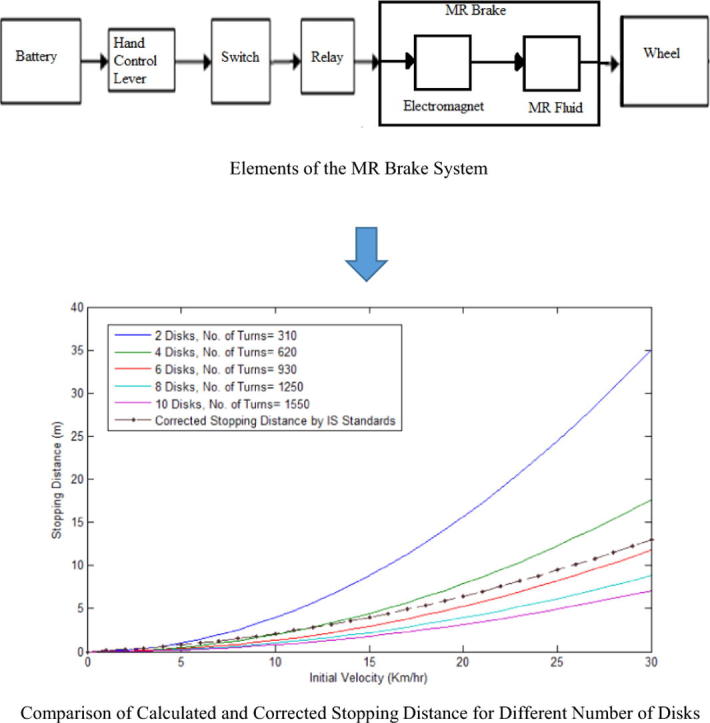
MR technology needs a 12-V supply; hence, it can be adopted for road vehicles. The MR brake system envisaged for such a vehicle is shown in Fig. 1c [14]. Upon pressing the control lever, the switch will be closed, and the current from the battery will be drawn and delivered to the electromagnet, thereby actuating the MR brake and decelerating the vehicle.
Fig. 1c.
Elements of the MR brake system.
Design configuration of an MR brake
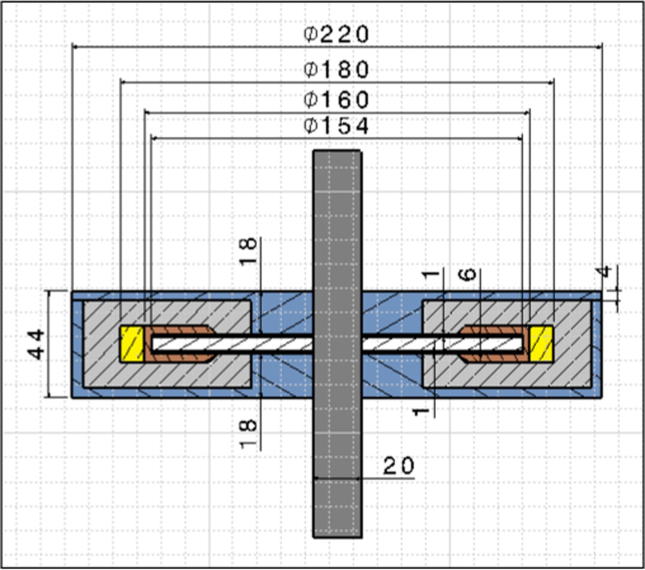
This section presents a brief description of an MR brake under consideration for this work. Table 2 presents the configuration of this brake. A single disc rotary-type MR brake with an MRF 132-DG working fluid and an MR gap of 1 mm is considered for this MR brake. The materials selected for the various elements of the brake are presented in Table 3.
Table 2.
Configuration of the MR brake under consideration.
| Parameter | Configuration selected |
|---|---|
| Type | Disc brake |
| Geometry | Rotary |
| Number of discs | One |
| MR fluid | MRF 132-DG |
| Gap size | 1 mm |
Table 3.
Materials selected for various components of the MR brake.
| Parts | Material | Behaviour |
|---|---|---|
| Shaft | 304 stainless steel | Non-ferromagnetic |
| Shear disc | AISI 1018 | Ferromagnetic |
| Casing | Aluminium/low carbon steel | Non-ferromagnetic |
| Magnetic circuit (core) | AISI 1018 | Ferromagnetic |
AWG 21 copper wire with a current density of 2.653 A/mm2 and a diameter of 0.77 mm is used for the electromagnet. The magneto-motive force is determined to be of 238.73 amp-turns, and hence, 160 turns are estimated at 1.5 A. Fig. 2 presents the sizing of the MR brake used in this study.
Fig. 2.
MR brake assembly under consideration.
Modelling of an automotive MR brake system in a MATLAB/Simulink environment
This section presents the modelling approach used in order to estimate the brake system performance parameters. The simulation study is performed in two stages. To characterize the braking behaviour in terms of the braking torque, a test of the proposed MR brake using the experimental setup is simulated. Thereafter, the MR brake system as a whole is simulated in a MATLAB/Simulink environment.
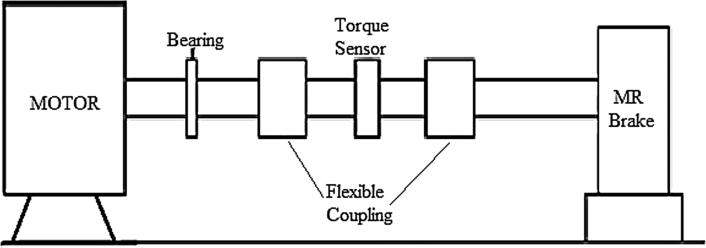
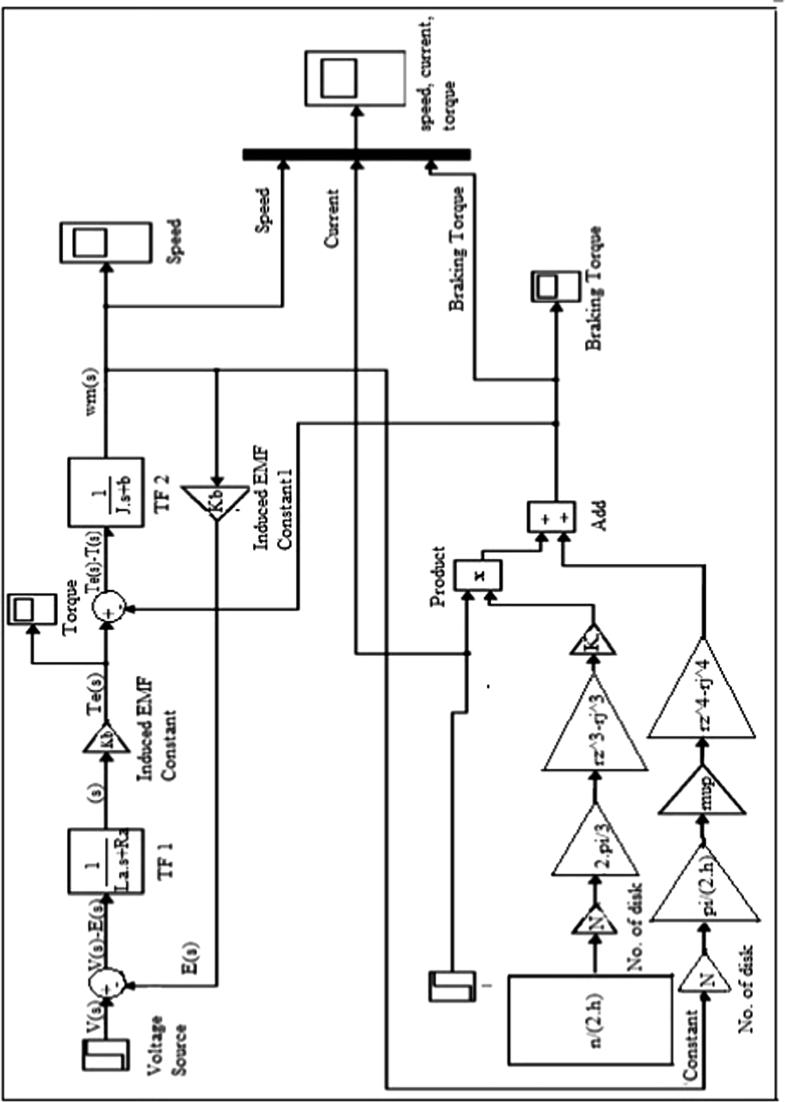
The proposed MR brake experimental setup is shown in Fig. 3a. It is composed of an electric drive, an MR brake, and a torque sensor in order to measure the braking torque at various current and speed levels. The Simulink model for the same setup is presented in Fig. 3b, while the numeric values used for modelling the brake and electric drive are presented in Table 4.
Fig. 3a.
Proposed MR brake experimental setup.
Fig. 3b.
Full Simulink model.
Table 4.
Numerical values for various modelling parameters.
| Sr. no. | Modelling parameter | Symbol | Numeric value |
|---|---|---|---|
| 1 | No. of turns in the electromagnet | N | 160 |
| 2 | MR fluid gap | H | 2 × 10-3 m |
| 3 | No. of discs | N | 1 |
| 4 | Outer radius of the disc | rz | 0.077 m |
| 5 | Inner radius of the disc | rj | 0.01 m |
| 6 | Viscosity of the MR fluid | µp | 0.1 Pa s |
| 7 | Wheel radius | R | 0.228 m |
| 8 | Angular velocity of the disc | W | 8.33 m/s |
| 9 | MR fluid-dependent constant K | K | 0.269 Pa m/A |
| 10 | MR fluid-dependent constant β | Β | 1 |
| 11 | Self-inductance | La | 0.003H |
| 12 | Armature resistance | Ra | 3.94 Ω |
| 13 | Viscous torque coupling | B1 | 2 Nm/(rad/sec) |
| 14 | Polar moment of inertia | J | 0.0167 kg-m2/s2 |
| 15 | Induced emf constant | Kb | 0.8 V/rad/s |
| 16 | Supply voltage | Vt | 230 V |
The major assumptions made during the modelling are as follows:
-
(1)
The stiffness of the shaft is very large. Thus, the angular speed of the electric motor is transmitted to the MR brake.
-
(2)
No reversible stresses due to the MR brake are induced in the motor; hence, there are no losses of the motor torque.
-
(3)
There is no external load on the MR brake; hence, the load torque is not considered.
-
(4)
Hysteresis losses within the motor are neglected.
-
(5)
The fluid velocity distribution across the gap is linear.
-
(6)
There are no slip conditions for the MR brake.
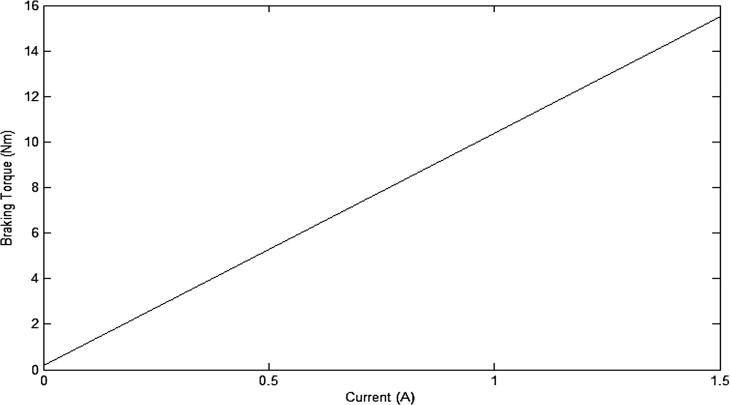
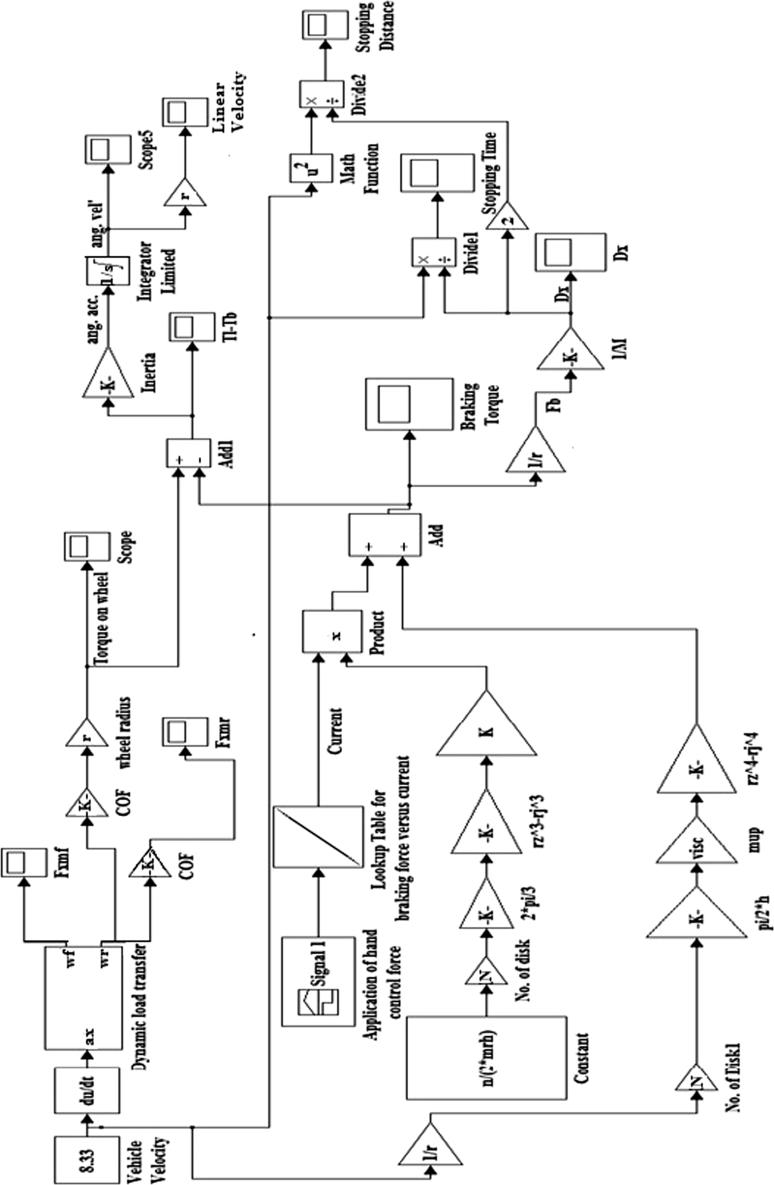
The full Simulink system model shown in Fig. 3b is composed of an electric motor subsystem model and an MR brake subsystem model. The speed of the motor considered is 20.61 rad/sec, and the step input of the voltage is provided after 1 sec. The inputs for the motor are the voltage (v(s)) and the load torque (TL), and the output is the angular speed. The inputs for the MR brake are the electric current supplied to the electromagnet and the speed of the motor shaft, whereas the output is the braking torque. The simulation results are presented in Figs. 4a and 4b. The variation in the braking torque with respect to the current and the angular speed are shown in Fig. 4a. At a speed of 20.63 rad/sec and with a current of 1.5 A, the braking torque obtained is 15.43 Nm. Fig. 4b shows the variation in the braking torque with the input current varying from 0 to 1.5 A. At 0 A, the braking torque shown is due to the viscosity of the MR fluid present in the MR brake, and its value is very low.
Fig. 4a.
Variations in the speed, current and braking torque.
Fig. 4b.
Braking torque versus current.
As mentioned earlier, the MR brake system is proposed for a two-wheeler applications like electric bicycles, whose torque requirements are low owing to their low weight. Hence, the braking requirement is considered to be met by the system. From a performance point of view, the parameters of interest are the stopping time and stopping distance, and the governing equations for these parameters are Eqs. (4), (5) below [15].
| (4) |
| (5) |
where
= Initial velocity (m/s)
= Linear deceleration value (m/s2) =
= Total of all longitudinal deceleration forces on the vehicle
= where
= Vehicle weight
= Front axle braking force
= Rear axle braking force
= Aerodynamic drag
= Uplift grade
For a two-wheeler application, since the frontal area is small and the speed is low, the aerodynamic drag and gradient forces can be neglected. The braking torque generated by the MR brake will be modelled using Eqs. (1), (2), (3) as mentioned above. However, this braking torque shall be subtracted from the driving torque, which is given by Eq. (6) as follows.
| (6) |
where is the maximum braking force on the front wheel that is limited by the weight component on the front wheel and the coefficient of friction between the road and the tyre surface, while r is the wheel radius. The velocity at the instant of braking can be obtained by integrating the angular acceleration of the wheel. The expression of interest is as given in Eq. (7) below.
| (7) |
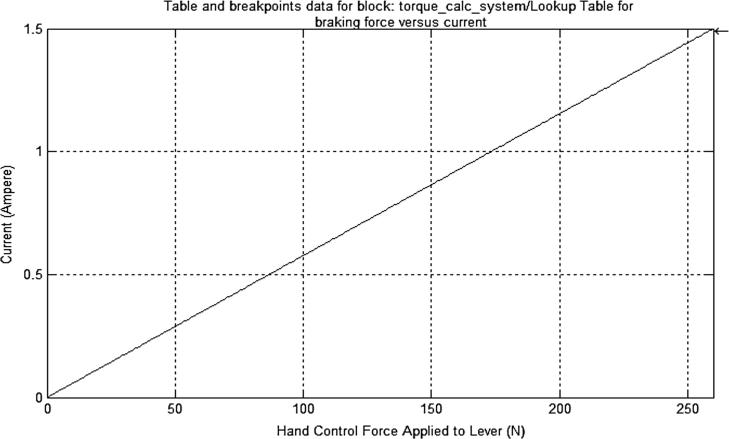
where J is the inertia and is the angular acceleration at the wheel. The wheel inertia is found experimentally using a torsional pendulum and the trifiler suspension method. The inertia found using the torsional pendulum method is 0.047 kg m2, and the inertia found using the trifiler suspension method is 0.069 kg m2. The value of 0.069 kg m2, being on the conservative side, is considered in this work. The constant initial velocity of 8.33 m/s corresponding to the speed of 30 kph is provided as an input to the model. The current is input to the MR brake, which influences the braking torque and is supplied as a function of the hand-operated control force. In view of ergonomic considerations, the maximum control force applied during braking for two-wheelers should not be greater than 260 N. Hence, corresponding to a maximum force of 260 N, it is assumed that the current supplied should be a maximum, i.e., 1.5 A. A look-up table establishing the correlation between the control force and the supply current is obtained as a part of the model. The plot for the application of the hand control force and the current supplied to the MR brake is shown in Fig. 5.
Fig. 5.
Look-up table for the hand control force and the current.
The braking torque obtained using to the MR brake is subtracted from the torque on a wheel and then divided by the mass moment of inertia in order to obtain the angular acceleration of the wheel. The angular speed is obtained by integrating the angular acceleration. Hence, a limited integrator block is used. Multiplying the angular velocity by the wheel radius (0.228 m), the linear velocity at the time of the application of the current is calculated. The stopping time and stopping distance are calculated and displayed in the scope block.
The Simulink model representing the whole MR brake system is shown in Fig. 6a and the numerical values of the parameters used for modelling are presented in Table 3, presented earlier.
Fig. 6a.
Simulink model for the MR brake performance estimation.
Validity of the simulation model
The output from the above simulation model in terms of the stopping time and distance is compared with the values of stopping time and distance obtained from the analytical equations for various input values of the current. Though the model is based on the same analytical equations, it is essential to check the correctness of the model so that it can be used for various input combinations. Table 5 confirms the correctness of the model, as the same output values are obtained from the model and the analytical equations.
Table 5.
Comparison of the outputs from the SIMULINK model and the analytical equations.
| I(A) | SIMULINK model values |
Results of analytical equations |
||
|---|---|---|---|---|
| Stopping time (s) | Stopping distance (m) | Stopping time (s) | Stopping distance (m) | |
| 0 | 835.93 | 3483.1 | 835.93 | 3483.1 |
| 0.4 | 6.34 | 26.40 | 6.34 | 26.40 |
| 0.8 | 3.18 | 13.30 | 3.18 | 13.30 |
| 1 | 2.55 | 10.60 | 2.55 | 10.60 |
| 1.5 | 1.68 | 7.10 | 1.68 | 7.10 |
Suitability of MR brake as a main service brake
To be used as a service brake for road vehicles, the MR brake system must satisfy the performance requirements as stated by brake testing standards. The correct stopping distance per IS 14664:1999 for a two-wheeler having a maximum speed of less than 45 kph is evaluated as shown in Table 6 [16].
Table 6.
Correct stopping distance as per the IS.
| Load condition | Test | Speed | Corrected stopping distance (m) |
|---|---|---|---|
| Laden | Front brake only | Initial speed (V) (kph) |
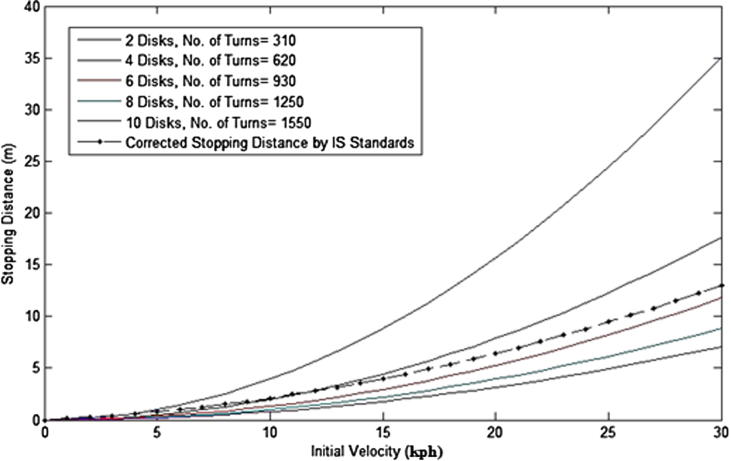
For a maximum speed of 30 kph, the correct stopping distance should be 13 m. When compared with the model outputs shown in Fig. 6b, where the variations in the stopping distance with respect to the initial velocity for various MR brake configurations ranging from two to ten discs and with a current of 1.5 A are presented, it is evident that an MR brake with two discs will not be able to meet the requirements of the braking standard. The requirement could be met with brakes having six or more discs, which may not be practically feasible from the viewpoint of weight and size considerations.
Fig. 6b.
Comparison of the calculated and corrected stopping distances for different numbers of disks.
Conclusions
This work presents an effort made to assess the feasibility of an MR brake proposed for road vehicle applications. The novelty of the work lies in simulations of the automotive MR brake system that have not been reported earlier. A MATLAB Simulink model was built, and the approach for the same has been presented. The inertia of the front wheel was found experimentally using a torsional pendulum and the trifilar suspension method. The correctness of the model was ensured by comparing the outputs from the model with the results from analytical equations. The model was used to estimate the stopping distance for a two-wheeler application. The output from the model in terms of the stopping distance was compared with Indian brake standard IS 14664:1999. It is evident from this study that the single-disc MR brake system proposed for a two-wheeler application will not be able to meet the requirements of the performance standard. An MR brake with six or more discs would be required to meet the requirements of the braking standard. However, size and weight constraints do not allow the use of such brakes for two-wheeler automotive applications. The model could be used for further investigations in the form of experimental studies to estimate the MR brake system performance for vehicular use.
Conflict of interest
The authors have declared no conflict of interest.
Compliance with Ethics Requirements
This article does not contain any studies with human or animal subjects.
Acknowledgements
The authors acknowledge the Rajarambapu Institute of Technology, Rajaramnagar, for supporting this study.
Footnotes
Peer review under responsibility of Cairo University.
References
- 1.Park E.J., Stoikov D., da Luz L.F., Suleman A. A performance evaluation of an automotive magnetorheological brake design with a sliding mode controller. Mechatronics. 2006;16:405–416. [Google Scholar]
- 2.Li W.H., Du H. Design and experimental evaluation of a magnetorheological brake. Int J Adv Manuf Technol. 2003;21:508–515. [Google Scholar]
- 3.Karakoc K., Park E.J., Suleman A. Design considerations for an automotive magnetorheological brake. Mechatronics. 2008;18:434–447. [Google Scholar]
- 4.Park E.J., da Luz L.F., Suleman A. Multidisciplinary design optimization of an automotive magnetorheological brake design. Comput Struct. 2008;86:207–216. [Google Scholar]
- 5.Sukhwani V.K., Hirani H. Design, development, and performance evaluation of high-speed magnetorheological brakes. Proc Inst Mech Eng, Part L: J Mater: Des Appl. 2008;222:73–82. [Google Scholar]
- 6.Assadsangabi B., Daneshmand F., Vahdati N., Eghtesad M., Bazargan-Lari Y. Optimization and design of disk-type MR brakes. Int J Auto Technol. 2011;12:921–932. [Google Scholar]
- 7.Younis A., Karakoc K., Dong Z., Park E., Suleman A. Application of SEUMRE global optimization algorithm in automotive magnetorheological brake design. Struct Multidiscip O. 2011;44:761–772. [Google Scholar]
- 8.Nguyen Q.H., Choi S.B. Optimal design of an automotive magnetorheological brake considering geometric dimensions and zero-field friction heat. Smart Mater Struct. 2010;19:115024. [Google Scholar]
- 9.Nguyen P.B., Lim S.G., Choi S.B. A new magneto-rheological brake for haptic applications. Adv Mater Res. 2011;317:581–585. [Google Scholar]
- 10.Hung N.Q., Bok C.S. Optimal design of a T-shaped drum-type brake for motorcycle utilizing magnetorheological fluid. Mech Des Struct Mach. 2012;40:153–162. [Google Scholar]
- 11.Sarkar C., Hirani H. Design of a squeeze film magnetorheological brake considering compression enhanced shear yield stress of magnetorheological fluid. In J Phys: Conf Series. 2013;412:012045. [Google Scholar]
- 12.Sarkar C., Hirani H. Theoretical and experimental studies on a magnetorheological brake operating under compression plus shear mode. Smart Mater Struct. 2013;22:115032. [Google Scholar]
- 13.Olabi A.G., Grunwald A. Design and application of magneto-rheological fluid. Mater Des. 2007;28:2658–2664. [Google Scholar]
- 14.Patil SR, Sawant SM. Reliability analysis of automotive magnetorheological brake: a qualitative approach. In: ASME 2014 12th Biennial Conf on Eng. Systems Design and Analysis; 2014. p. V003T10A003–V003T10A003.
- 15.Gillespie T.D. SAE International; Warrendale, Pennsylvania: 1992. Fundamentals of vehicle dynamics. [Google Scholar]
- 16.IS 14664:1999, Edition 1.1, (2003-12).