Comparison of Decision-Related Signals in Sensory and Motor Preparatory Responses of Neurons in Area LIP

Abstract

Neurons in the lateral intraparietal (LIP) area of Macaques exhibit both sensory and oculomotor preparatory responses. During perceptual decision making, the preparatory responses have been shown to track the state of the evolving evidence leading to the decision. The sensory responses are known to reflect categorical properties of visual stimuli, but it is not known whether these responses also track evolving evidence. We recorded neural responses from lateral intraparietal area of 2 female rhesus monkeys during a direction discrimination task. We compared sensory and oculomotor-preparatory responses in the same neurons when either the discriminandum (random dot motion) or an eye movement choice-target was in the neuron's response field. The neural responses in both configurations reflected the strength and direction of motion and were correlated with the animal's choice, albeit more prominently when the choice-target was in the response field. However, the variance and autocorrelation pattern of only the motor preparatory responses reflected the process of evidence accumulation. Simulations suggest that the task related activity of sensory responses could be inherited through lateral interactions with neurons that are carrying evidence accumulation signals in their motor-preparatory responses. The results are consistent with the proposal that evolving decision processes are supported by persistent neural activity in the service of actions or intentions, as opposed to high-order representations of stimulus properties.

SIGNIFICANCE STATEMENT Perceptual decision making is the process of choosing an appropriate motor action based on perceived sensory information. Association areas of the cortex play an important role in this sensory-motor transformation. The neurons in these areas show both sensory- and motor-related activity. We show here that, in the macaque parietal association area LIP, signatures of the process of evidence accumulation that underlies the decisions are predominantly reflected in the motor-related activity. This finding supports the proposal that perceptual decision making is implemented in the brain as a process of choosing between available motor actions rather than as a process of representing the properties of the sensory stimulus.

Introduction

The life of animals is a constant process of deciding what to do next based on, among other things, the perception of the world around them. In primates, perceptual decision making has evolved into an efficient mechanism of translating the perceived state of the world into possible motor actions (Cisek and Kalaska, 2005; Klaes et al., 2011; Kubanek and Snyder, 2015). The motor system receives continuous access to evolving perceptual decisions and maintains a graded level of preparedness based on the quality of the incoming evidence (Gold and Shadlen, 2000; Selen et al., 2012). This sensorimotor transformation is particularly evident in the parietal and prefrontal association cortices, where neurons encoding the motor actions associated with the choices on offer also represent evolving decisions (Kim and Shadlen, 1999; Roitman and Shadlen, 2002; Bollimunta and Ditterich, 2012; Ding and Gold, 2012; de Lafuente et al., 2015). Thus, perceptual decision making can be framed as a choice between available motor actions (Cisek, 2007; Shadlen et al., 2008; Cisek and Kalaska, 2010).

Yet, perceptual decisions do not feel like they are about potential actions but about propositions or stimulus properties. Indeed, one can make a decision without knowledge of the action that will be required to act on it. In such situations, one might expect neural circuits involved in motor planning to be irrelevant to the decision process (Gold and Shadlen, 2003). However, it has been shown that, even then, neurons in the parietal association areas carry a representation of the properties of the stimulus that will be relevant for future actions (Freedman and Assad, 2006; Bennur and Gold, 2011; Goodwin et al., 2012). It is possible that such “abstract” representations of decision relevant information, independent of the possible motor actions, coexist with representations of decisions as intended actions (Freedman and Assad, 2011). Whether such simultaneous representations exist in the same association area has not been investigated before. Consequently, it is also not known whether such abstract representations play a role in the decision-making process.

We used the random-dot motion (RDM) direction discrimination task (Newsome et al., 1989) to investigate these questions. In this task, the animals discern the net direction of a stochastic motion stimulus and report their decision by making a saccade to one of two choice targets that is along the direction of the perceived motion. This task is particularly well suited for our purposes. First, optimal performance on this task demands integration of motion evidence over time. This prolonged deliberation time allows characterization of whether a neural population is participating in the process of evidence accumulation or not. Second, there exists a theoretical framework, bounded accumulation of noisy evidence to a decision threshold (also known as drift diffusion) (Smith and Ratcliff, 2004; Palmer et al., 2005), which accounts quantitatively for the speed and accuracy of decisions in this task. Third, it has been shown that responses of neurons in several areas of the brain involved in planning saccadic eye movements represent the evolving decision in this task (Shadlen and Newsome, 1996; Horwitz and Newsome, 1999; Kim and Shadlen, 1999; Ding and Gold, 2010, 2012).

We focused on the parietal sensorimotor association area LIP. Many neurons in LIP respond to both the presence of a sensory stimulus in, and to a planned saccade into, their response fields (RFs) (Barash et al., 1991b). We recorded the responses of the same set of neurons during the RDM discrimination task in two configurations: when the RF contained the RDM stimulus and when it contained one of the choice targets. We show that the neurons represent the moment-by-moment accumulation of sensory evidence only in the latter configuration, that is, when they are involved in the planning of the motor action required to report the choice.

Materials and Methods

All training, surgery, and experimental procedures were conducted in accordance with the National Institutes of Health Guide for the care and use of laboratory animals and were approved by the University of Washington Institutional Animal Care and Use Committee (IACUC Protocol #2896-01).

Experimental design and statistical analysis

Neural recordings.

We recorded activity of 49 well-isolated single units from the ventral subdivision of area LIP (LIPv, Lewis and Van Essen, 2000) of two adult female rhesus monkeys (Macaca mulatta) trained on the RDM direction discrimination task. MRI was used to localize LIPv and to target recording electrodes. Within this putative LIPv, we screened for neurons that had both visual responses and spatially selective persistent activity. The persistent activity was assessed using a memory-guided saccade task (Gnadt and Andersen, 1988). In this task, a target is flashed in the periphery while the monkey fixates on a central spot. The monkey has to remember the location of the target and execute a saccade to that location when instructed. The RF of each neuron was identified as the region of visual space that elicited the highest activity during the interval between the target flash and the eventual saccade. For the majority of neurons in LIPv, this region also elicits the strongest visual response (Platt and Glimcher, 1998). During the recording sessions, visual and persistent activities were assessed qualitatively. We confirmed these properties by analyzing the following responses acquired during the experiment: (1) the response to RDM presented in the RF, 100–300 ms after onset and (2) delay period activity, 100–300 ms before a saccade into the RF. We confirmed that both proxies were greater than baseline activity, 0–200 ms before the appearance of a visual stimulus in the RF. For two neurons, post hoc analysis revealed that, in the Target-in-RF condition, the persistent response was higher for the target that we had initially considered to be out of the RF. The sensory responses were equally strong for both locations. We elected to not recode the target IDs ex post facto. These are the two significant points with β₂ < 0 in Figure 4A.

Figure 4.

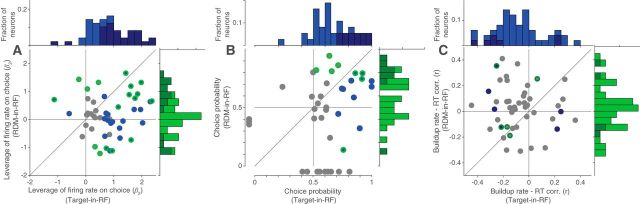
Leverage of neural activity on behavior. Scatter plot and histograms for the two stimulus configurations showing the distribution of β₂ term (A) of logistic regression (Eq. 5), CP (B), and coefficient of correlation (C) between slope of response buildup and RT. Neurons for which the metric was significant are shown with a blue fill (significant in the Target-in-RF configuration) and/or a green border (significant in the RDM-in-RF configuration) in the scatter plots and as darker colors in the histograms. B, Data points outside the axes indicate neurons where CP could be determined for only one of the two configurations. One and three such data points are not shown in the scatter plots of A and C, respectively.

Behavioral task.

The choice-reaction time direction discrimination task is similar to previous studies (Roitman and Shadlen, 2002). The animal initiates a trial by fixating on a point (fixation point) presented on an otherwise black screen. Two choice-targets then appear on the screen. After a variable delay (drawn from an exponential distribution of mean 750 ms), the RDM stimulus is displayed in an imaginary aperture (i.e., invisible borders) of 5°-9° diameter at a third location. The first three frames of the stimulus consist of white dots randomly plotted at a density of 16.7 dots · deg⁻² · s⁻¹. From the fourth frame, each dot from three frames before is replotted, either displaced in one direction along the axis connecting the two targets, or at a random location. The probability with which a dot is displaced in the direction of one of the targets determines the stimulus strength (coherence); and on each trial, this was randomly chosen from the set C = [0, 0.032, 0.064, 0.128, 0.256, 0.512]. The motion strengths and the two directions were randomly interleaved. Importantly, the monkey was allowed to view the stimulus as long as it wanted and indicate the perceived direction of motion with a saccade to the target that lay in that direction to obtain a liquid reward. Rewards were given randomly (p = 0.5) for the 0% coherence motion condition.

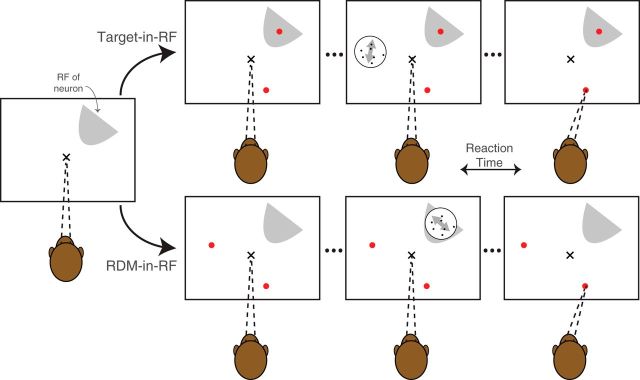
During recording from each isolated neuron, the choice-targets and the RDM were presented in two configurations (see Fig. 1). In the Target-in-RF configuration, one of the choice-targets overlay the neuronal RF. In the RDM-in-RF configuration, the RDM stimulus was presented in the RF. The two configurations were alternated in blocks (median block size 90, interquartile range 60–120). The order of blocks was randomized across neurons (23 started with Target-in-RF blocks; 26 with RDM-in-RF blocks), and each neuron was recorded with at least one block of trials in each configuration. For 33 of the neurons, the targets and the dot stimuli were placed 120° apart on an imaginary circle (see Fig. 1). For the remaining 16 neurons (in 1 monkey), the targets and the dot stimulus were aligned linearly in both configurations. In this arrangement, the targets were aligned to the direction of RDM when the RDM was in RF. The whole alignment was rotated close to 90° and translated to situate a target in the RF in the other configuration (Fig. 1-1). Because the directions of motion varied across sessions, we adopted the following conventions. In the Target-in-RF configuration, the direction of motion toward the target in the RF for each neuron was considered the “positive” direction. In the RDM-in-RF configuration, the positive direction was assigned post hoc from the neural recordings: the direction of motion that elicited the higher mean response.

Figure 1.

Behavioral task configurations. The monkey fixates at an instructed location (x) and then two choice targets (red dots) appear in one of two configurations: (1) Target-in-RF: One of the targets is situated in the RF of the neuron being recorded from. (2) RDM-in-RF: Both targets are situated outside the RF. In the next step, the RDM is presented either inside (RDM-in-RF) or outside the RF (Target-in-RF). The monkey is free to report its decision any time after the appearance of the RDM by making a saccade to one of the targets. The alignment of the RDM and targets used in 16 sessions was slightly different and is shown in Figure 1-1.

All statistical tests are described in the pertinent sections of Materials and Methods.

Analyses of behavioral data

The accuracy and reaction time (RT) of the monkeys were fit by a bounded evidence accumulation model (Shadlen et al., 2006). In the parsimonious application of this model used here, the instantaneous evidence about motion at each time step is assumed to arise from a normal distribution with variance Δt and mean κ(C − C₀)Δt, where C is the signed motion coherence, C₀ is a bias, and κ is a scaling parameter. This instantaneous evidence is accumulated over time, and the decision process terminates when the accumulated evidence reaches one of the bounds ±B, leading to the choice of one of the targets. The mean RT is the expectation of the time taken for the accumulated evidence to reach the bound plus a constant, the nondecision time t_nd comprising sensory and motor delays. To account for asymmetric RTs in some configurations, we used two different nondecision times (t_nd1 and t_nd2) for the two target choices. In this framework, the mean RT for the correct choices (i.e., choices consistent with the sign of the drift rate, κ[C − C₀]) is described by the following:

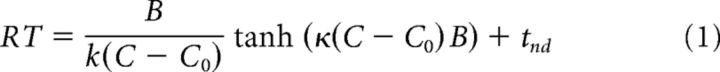Further, the choice distributions are described by the following:

where P₊ is the probability of choosing the target consistent with the “positive” direction of motion. We fit Equation 1 to the RT data and used the fitted parameters to predict the choice functions (Eq. 2) (Gold and Shadlen, 2002; Kang et al., 2017). We first established an estimate of C₀ from a logistic fit of the choices. Because the parsimonious model explains only the RT when the choice is consistent with the sign of the drift rate (Ratcliff and Rouder, 1998), we used the mean RT for positive choices at C − C₀ > 0 and negative choices for C − C₀ < 0. We then fit κ, B, t_nd1, and t_nd2 and used the values of κ and B in Equation 2 to establish predictions of choice (see Fig. 2).

Figure 2.

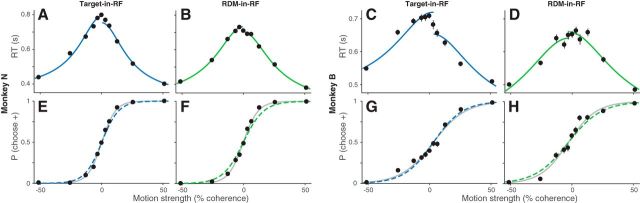
Predicting choices from diffusion-to-bound model fit to RTs. A–D, RTs of the two monkeys as a function of motion strength in the two task configurations (for convention on sign of motion strength, see Materials and Methods). Solid lines indicate the fits of a diffusion-to-bound model. Data include the trials at 0% motion strength in which the monkey chose the target consistent with its bias (established from logistic fits to the choice data) and correct trials at other motion strengths. E–H, The probability the monkey chooses the target consistent with positive motion direction, plotted as a function of motion strength. Dashed lines indicate predictions from the corresponding fits of the RTs. Gray lines indicate fits to the choice data (logistic regression). The data were also fit with a more elaborate diffusion-to-bound model. The fits are shown in Figure 2-1.

We evaluated the fidelity of these predictions by comparing the predictions with a logistic regression fit of the choice data. To demonstrate that these predictions were not a trivial result of monotonic ordering of RTs by motion strength, we compared them with predictions from 10,000 pseudorandomly generated RT versus coherence functions that preserved the order of RTs. To generate these functions, we retained the observed RTs for the minimum (−51.2%), maximum (51.2%), and 0% coherences and used ordered random values within this range for the other coherences. We quantified the magnitude of the perturbation as the average of the percentage change from the observed RT at each coherence. We then performed the steps above to fit these perturbed RTs to establish a new predicted choice function. We estimated the probability of obtaining a predicted choice function as good or better that the ones derived from data as a function of the size of the perturbation. We report the minimal perturbation at which p < 0.01.

To obtain a more precise estimate of decision times, we fit an elaborated version of the bounded evidence accumulation model (Fig. 2-1) simultaneously to both choices and RTs (including both correct and error trials). In this model, the decision bounds (B) collapse with time (t) such that:

where B₀ is initial bound height, B₁ is the rate of collapse, and B_del is the delay to onset of collapse. The nondecision time is modeled as a normal distribution with mean t_nd and SD σ_tnd. A separate nondecision time was used for decisions terminating at each of the two bounds. This model was fit by maximizing the log likelihood of the observed responses (choice and RT) on each trial to numerical solutions for the probability densities of terminating at ±B(t) (Churchland et al., 2008; Kang et al., 2017). The mean decision times were obtained from these fits and their SE estimated from fitting the model to resampled trials (i.e., the SD of the means from 100 iterations).

Analyses of neural data

Population responses were computed as the average of all trials from all neurons after smoothing each trial with a 75-ms-wide boxcar filter (see Fig. 3A–D). The smoothing was only for visualization, and all analyses were conducted on the raw spike data (1 ms resolution). To visualize the coherence-dependent buildup of activity (see Fig. 3A,C, insets), we detrended individual neuronal responses by subtracting the average responses across all coherences for the same neuron (separately for each task configuration).

Figure 3.

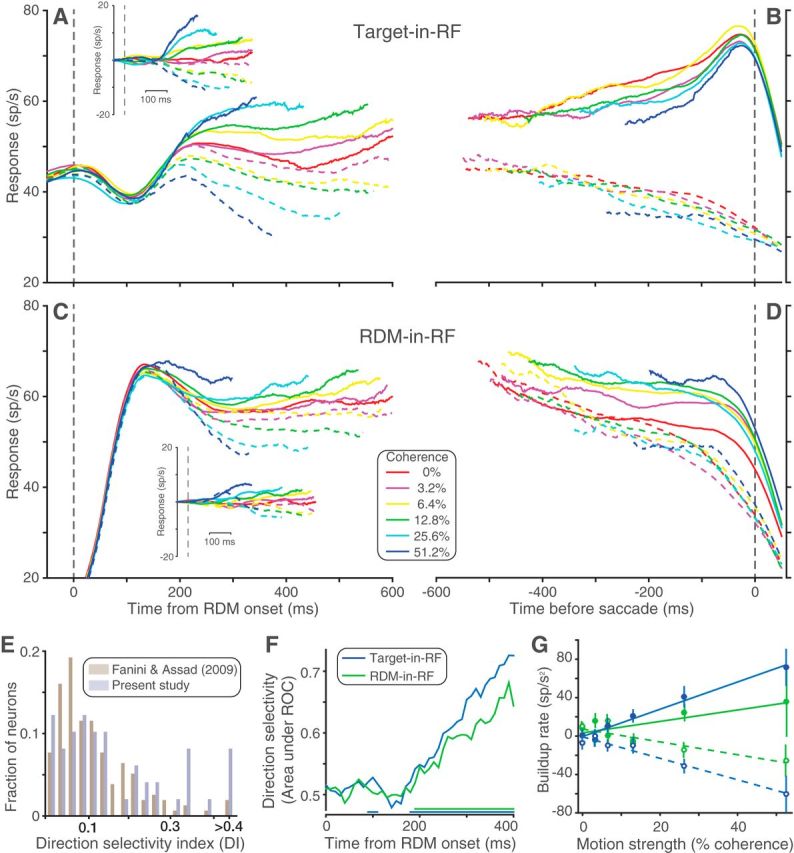
Neural population responses. Average response of the recorded neural population during Target-in-RF (A, B) and RDM-in-RF (C, D) configurations. A, C, Aligned to the onset of RDM and including all trials sorted by direction and strength of motion. Solid and dashed lines indicate responses to positive and negative motion directions, respectively (for conventions on sign of direction, see Experimental design and statistical analysis). Insets, Average of detrended responses (i.e., after subtraction of the mean response for all motion strengths, for each neuron). B, D, Aligned to the saccade and including correct trials (and 0% coherence trials sorted by the animal's choices). E, Histograms of the distribution of DI for the neural population recorded by Fanini and Assad (2009) and for the neural population in the RDM-in-RF configuration of the present study. F, Area under ROC for responses to the two directions of motion at 51.2% coherence computed in 40 ms bins. Colored lines at the bottom indicate the time bins in which this metric was significantly >0.5 for the corresponding configuration. G, The relation between the response buildup rate and motion strength. Filled circles represent data from trials with motion in the neuron's preferred direction. Open circles represent the opposite motion direction. Solid and dashed lines indicate corresponding linear regression model fits. Population responses pooled separately for the 2 monkeys are shown in Figure 3-1 and Figure 3-2.

We compared the strength of direction selectivity in our neural population with that reported by Fanini and Assad (2009) using their direction selectivity index (DI) as follows:

where R_n is the mean response to n^th direction θ_n in the time window 190 ms after RDM onset to 100 ms before saccade. DI was computed from responses to the 51.2% coherence motion trials in the two directions (π radians apart). We compared the distribution of the DI values in our population with those reported by Fanini and Assad (2009, their Fig. 3A), using a rank sum test (see Fig. 3E).

We used responses at the two strongest motion strengths (±51.2% coherence) to estimate the latency from motion onset to the time that direction selectivity was first apparent in a given neural population (see Fig. 3F). We averaged the responses in 40 ms bins on each trial at these coherences and derived receiver operating characteristics (ROC) from these response distributions at each time bin. The area under the ROC denotes the probability of the neuron responding more to the positive direction of motion. For each time bin, we applied a Wilcoxon rank sum test and estimated the response latency as the first of three successive bins that met statistical significance (p < 0.05). We used a bootstrap procedure to estimate the distribution of latencies under the two task configurations. For each configuration, we resampled trials with replacement, matching the number of trials in the original datasets, and obtained a latency using the same procedure as on the actual data. We repeated this procedure 1000 times for each configuration. The medians of these distributions recapitulated the latency estimated from the data (180 and 190 ms for the Target-in-RF and RDM-in-RF, respectively). We report the p value of a rank sum test (two-tailed) using the bootstrap-derived distributions to evaluate the null hypothesis that the latencies are the same for the two configurations. We obtained the same result by sampling neurons (instead of trials), with replacement. We used a similar area under ROC metric to estimate the degree of overlap between the responses to the two directions of motion in the RDM-in-RF configuration. Mean responses in a 200 ms time bin (100–300 ms before the saccade) was used for this estimation. We report the population average of this metric as in Swaminathan and Freedman (2012).

We quantified the effect of motion strength on the rate of increase of neural response (“buildup rate”) during the decision-making epoch as the slope of the response in the time window 180–380 ms after stimulus onset (see Fig. 3G). The start of the time window was chosen based on the latency of the direction selectivity of the responses. To exclude presaccadic activity, we discarded from each trial, the spikes occurring up to 100 ms before saccade onset. We computed by least-squares method, the slope for each neuron at each coherence from the mean detrended response in 10 ms time bins in the aforementioned time window. We then tested whether these buildup rates scaled with coherence across the population in each stimulus configuration by fitting a linear model regressing these buildup rates against signed coherence. We confirmed that the trends shown in Figure 3G were preserved when the analysis was performed using weighted regression.

Leverage of neural activity on behavior.

We measured the leverage of neural activity on the animal's choice in two ways (see Fig. 4). First, we fit the monkey's choices with logistic regression as follows:

where P₊ is the probability of choosing the “positive” direction target, C is signed coherence, and R is the z-scored mean neural response of each trial in the time window 100–300 ms before saccade (standardized separately for each configuration in each neuron). If the variations in firing rate of the neurons have leverage over choice even when the effect of motion coherence is accounted for, then β₂ ≠ 0. We compared β₂ across configurations with a signed rank test on their absolute values. We also quantified the additional leverage of the neural responses on choice beyond that of the motion strength, by measuring the difference in the deviance of the full model and the model without the R term (Λ). Comparisons of Λ provided similar results to the comparisons of the β₂ term that are presented in the results.

Second, we quantified the trial-by-trial correlations between neuronal response and the animal's choice in the 0% coherence trials by computing “choice probability” (CP) (Britten et al., 1996). For each neuron, we computed the mean responses on the 0% coherence trials in a time window 100–300 ms preceding the saccade. The trials were separated into two groups based on the animal's choice. We used the distributions of responses from the two groups to calculate the area under the ROC, termed the CP. We evaluated the null hypothesis that |CP−0.5| = 0 using a permutation test. We permuted the union of responses from both groups and assigned them randomly to the two choices (matching the number of trials in each group) and computed the CP. By repeating this procedure 2000 times, we established the distribution of |CP−0.5| under H₀ and report the p value as the area to the right of the observed CP minus 0.5.

To evaluate whether the CPs from the two configurations were different, we first converted responses to z scores (by neuron and configuration) and then combined the z scores across neurons. We then computed two CPs, as above, for the two configurations. To evaluate the null hypothesis that the two CPs are equal, we performed another permutation test, this time preserving the association with choice but permuting the association with configuration. We obtained the distribution of the difference in CP (|ΔCP|) under H₀ from 2000 repetitions of the permutation procedure and report the p value as the area of this distribution that is greater than the observed |ΔCP| from the data.

We also quantified the correlation between the buildup rates and RT. We used trials in which the monkey chose the “positive” direction target, including all such trials at 0% motion strength and only correct trials at positive motion strengths. For each trial, we computed the slope of the response between 180 and 420 ms after RDM onset (using 40 ms time bins) from the detrended responses. To remove the effect of coherence on RT, we standardized (i.e., z-scored) both the RTs and the buildup rates within each coherence and computed the correlation between them.

Variance and correlation analysis.

To evaluate whether the neuronal firing rates on individual trials during the decision-making epoch reflect a process of accumulation of noisy evidence, we analyzed the pattern of variance and autocorrelation of the responses (Churchland et al., 2011; de Lafuente et al., 2015). We were interested in the variance attributable to such an accumulation process. For the i^th time bin, this variance (s_<Ni>²) is the fraction of the total measured variance (s_Ni²) remaining after accounting for the point process variance (PPV), that is, the variance expected even if the underlying rates were constant. We refer to s_<Ni>², which is a variance of a conditional expectation of the counts, hence the variance of the underlying rate, simply as “variance” in the main text. Assuming the PPV is proportional to the mean count:

where ϕ is a constant that must be estimated.

Because our goal was to compare how well the firing rates conform to a diffusion process, we allowed ϕ to be a free parameter and fit it to obtain the best conformity to the autocorrelation pattern for a running sum of independent, identically distributed random numbers. Recall that the variance of the sum of n independent random samples of variance σ² is nσ². If the sum is extended for another m samples, the variance is (n + m)σ². The sum out to n shares a fraction of this variance: n/(n + m). This is the R², and its square root is the correlation, ρ. So, for an unbounded diffusion process, the correlation between the i^th and j^th time steps is as follows:

For six time bins, the 6 × 6 correlation matrix contains 15 unique values of ρ_i≠j.

We characterized the variance and autocorrelation from six 60 ms time bins between 180 and 540 ms after stimulus onset, ignoring any time bins that extended to within 100 ms of the saccade. To pool data across neurons, we used the residuals for each trial as follows. The mean response of a trial in each time bin was subtracted from the mean of the responses from all the trials for that neuron for the same signed coherence in that time bin. We computed the covariance matrix from the residuals for the six time bins.

We used an initial guess for ϕ to calculate the variance attributable to the diffusion process (s_<Ni>², Eq. 6) and substituted the raw variances for the diagonal of the covariance matrix. The correlation was derived from this covariance matrix by dividing each term by √(s_<Ni>²s_<Nj>²). We used Nelder-Mead simplex method (MATLAB function fminsearch) to find the ϕ that minimized the sum of squares of the difference between the 15 z-transformed calculated correlation (r_ij) and the z-transformed theoretically predicted correlation (ρ_ij). The values of ϕ were not constrained to be the same in the Target-in-RF (ϕ = 0.42) and RDM-in-RF (ϕ = 0.39) configurations.

We report the variance (s_<Ni>²) in Figure 5 using the fitted ϕ values and estimated the SEs from a bootstrap. We evaluated the effect of time on the variance using least-squares regression. We also performed these analyses over a range of plausible values of ϕ and confirmed that only the absolute values of the variances differed, whereas the shape of the variance function over time was unaffected. We similarly computed the variance and its SE for time bins aligned to the onset of the saccade.

Figure 5.

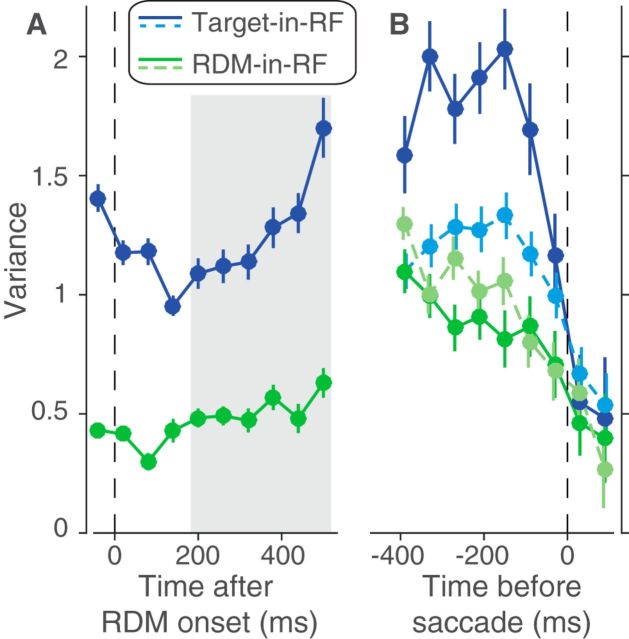
Variance of responses. The variance of neural responses aligned to the onset of RDM (A) or to the saccade (B). Total variance is computed in 60 ms bins and the point process variance subtracted from it (see Materials and Methods). B, Solid lines indicate data from trials in which the animal chose the preferred target of the neuron. Dashed lines indicate trials with the opposite choice.

We used a combination of Monte Carlo methods and parametric statistical tests to analyze the decline in variance preceding the saccade. For trials in which the monkey chose the target in the RF, we compared the variance in the two time bins immediately preceding the saccade, using the bootstrap-derived SEs. We report a t test. We made the same comparison for each of the other conditions: (1) unchosen Target-in-RF, (2) preferred direction choice with RDM-in-RF, and (3) nonpreferred direction choice with RDM-in-RF. None was significant (p > 0.05). We do not report these tests in the results and instead compare directly the estimates of variance decline in the four conditions. To do this, we computed the fractional difference in variance in the two time bins and estimated its SE using the same bootstrap. We compared this difference statistic in the four conditions using ANOVA. We report the maximum p value for the comparison of the chosen Target-in-RF condition with the other three conditions, using Tukey's test.

To quantify how well the measured correlation values conform to theoretical predictions, we formed a sum of square statistic from the 15 pairs of observed and theoretical correlations (after Fisher-z transformation; see Fig. 6D,E). We used a bootstrap procedure to estimate the distribution of this statistic by sampling with replacement from the data and following the steps above (100 iterations). We used a Kolmogorov–Smirnov test to determine the significance of the difference between the distribution of the sum of square statistics between the RDM-in-RF and the Target-in-RF configurations.

Figure 6.

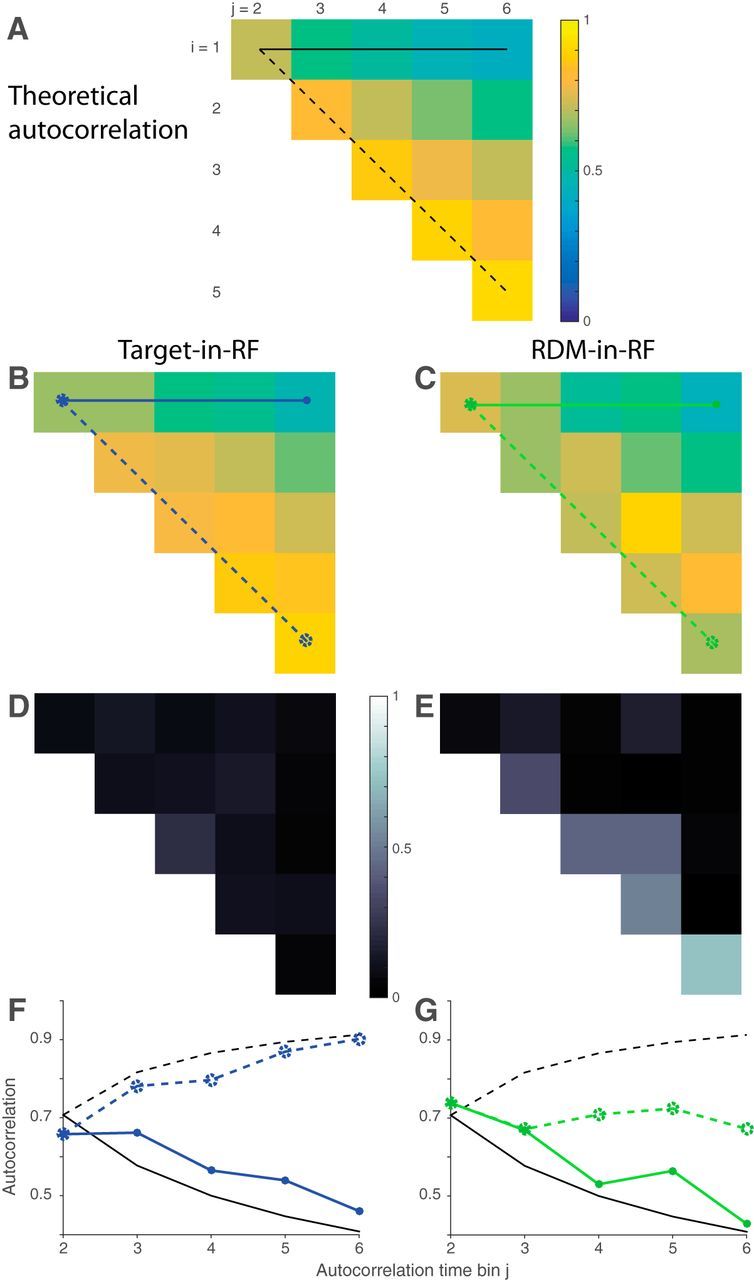
Autocorrelation of responses. A, Theoretical prediction of the autocorrelation matrix for six time bins (ρ_i,j) of a diffusion process. Only the 15 unique values (upper triangular matrix, i<j) are shown. B, C, Estimated autocorrelation for the neural responses in the two stimulus configurations. D, E, Deviation of B, C from the theoretical predictions shown in A. F, G, Comparison of correlation values in A–C between theory (black lines) and data (colored lines). Solid lines indicate correlation along the top row (between first and j^th time bins) and dashed lines indicate correlation along the first juxtadiagonal (between j^th and its preceding time bin). Line style and color correspond to those in A–C.

Model

We simulated the spike rates of three neural populations during the RDM epoch: one population with the RDM in its RF and two with targets in their RF. We devised two models that could account for direction selectivity seen in the RDM-in-RF population: (1) selectivity is inherited by means of divisive suppression from the Target-in-RF populations that are accumulating evidence (divisive suppression model), and (2) selectivity arises from an evidence accumulation process transpiring in the RDM-in-RF population itself (parallel diffusion model). Each model was implemented in two stages. In the first stage, our goal was to approximate the pattern of mean responses seen in the data. The models specify the predicted autocorrelation matrices for both neural populations. In the second stage, we compared the two models by assessing their capacity to explain the autocorrelation matrices derived from the neural data.

In the divisive suppression model (see Fig. 7A), the RDM-in-RF population was modeled as having an exponential rise in firing rate starting 50 ms after RDM onset and peaking at 130 ms (see Fig. 7C). The peak response varied from trial to trial, independent of RDM direction. The population then maintained the peak response through the end of the simulated epoch (540 ms after RDM onset). The two Target-in-RF populations were modeled as maintaining a steady response (R₀) up to 180 ms after RDM onset and then following drift diffusion dynamics (see Fig. 7B). The responses S in the dynamic epoch evolved at each time step Δt as follows:

Incorporating a deterministic drift component (K) and a diffusion component (N), a normally distributed random number with mean zero and SD $\alpha \sqrt{\Delta t}$. The drift component was positive for one target population (T₁) and negative for the other (T₂). The parameter K was chosen so that the drift rate in the T₁ population of the model after implementation of divisive suppression (see below, Eq. 9) matched the observed buildup of the neural response for the Target-in-RF neural population at the 25.6% coherence condition (see Fig. 7F, solid line). The parameter α was chosen such that the slope of the variance, after incorporation of suppression, mimicked that seen in data (see Fig. 5A, blue curve). For values of model parameters, see Table 1 .

Figure 7.

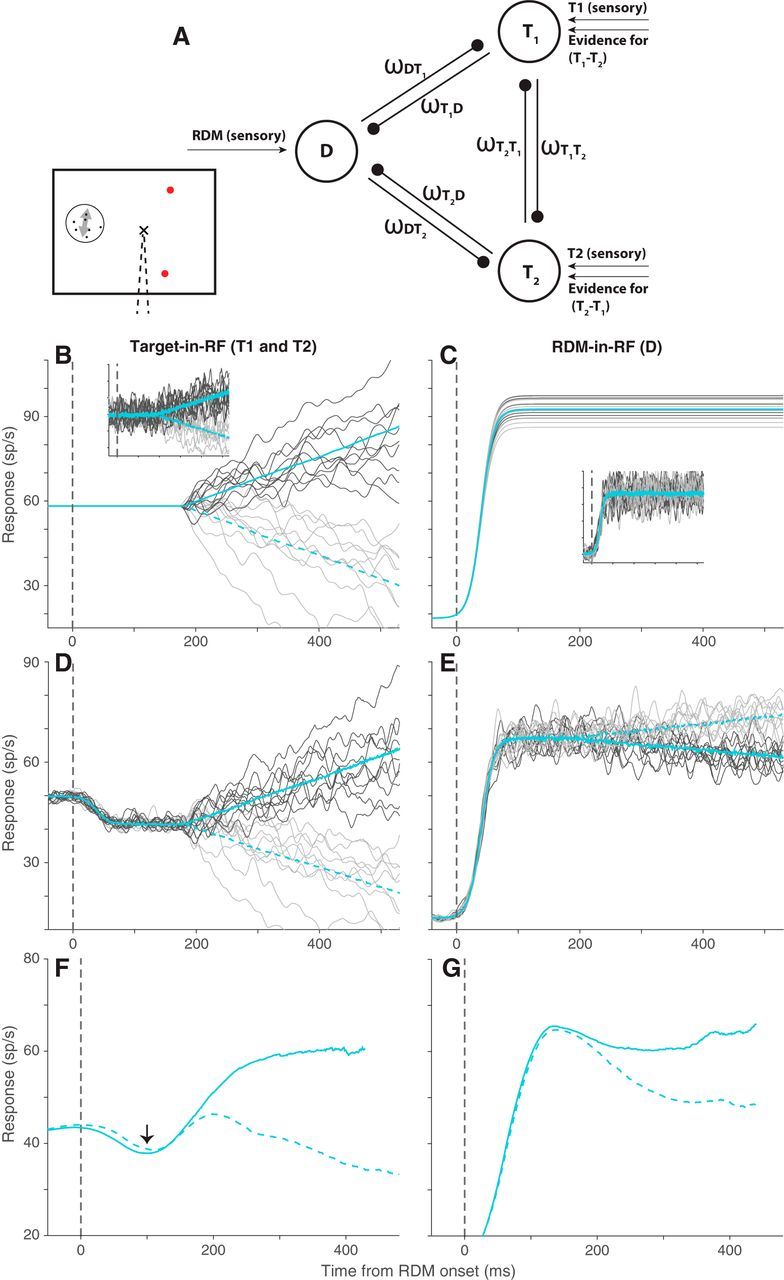
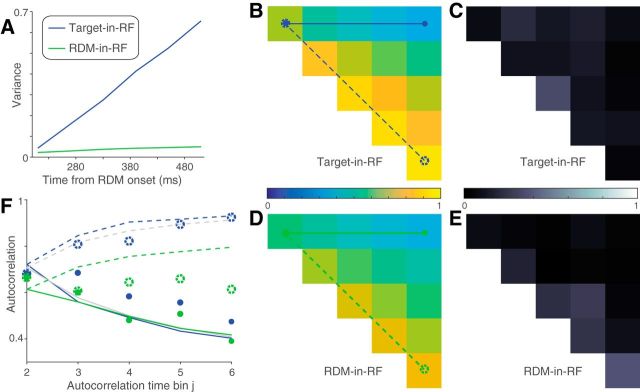
Divisive suppression model. A, Schematic of the three populations simulated in the model: one population representing the RDM (D) and two representing the targets (T₁ and T₂). The ω terms denote the suppressive influence of each population on the other two. B, Average response of simulated T₁ (solid cyan) and T₂ (dashed cyan) populations across trials in which the direction of motion supported T₁. Dark and light gray traces represent responses to 10 example trials for the two populations. C, The mean and example trial responses of the D population to the two directions of motion. Dark and light gray represent motion toward T₁ and T₂, respectively. Solid and dashed cyan lines indicate the corresponding average response traces, but they overlap, as the two populations do not distinguish between directions of motion. B, C, Insets, Noisy versions of the corresponding responses that furnish the divisive suppression. D, E, The responses of the three populations after implementation of divisive suppression. Color scheme is the same as in B, C. The simulated responses in B–E are smoothed with a 10 ms boxcar filter. F, G, The average responses of the recorded neural population to the 25.6% motion strength stimulus in the Target-in-RF and RDM-in-RF configurations that our simulations approximated. These traces are the same as the cyan traces in Figure 3A,C.

Table 1.

Parameter values for simulations

Parameter	Divisive suppression model	Parallel diffusion model
K (T)	80.4	52.8
α (T)	29.8	23.7
K (D)	NA	25.0
α (D)	NA	9.6
ωT2T1 = ωT1T2	2 × 10−3	NA
ωDT1 = ωDT2	4 × 10−3	NA
ωT1D	6 × 10−3	NA
ωT2D	1 × 10−3	NA
ϕRDM	0.38	0.39
ϕTar	0.43	0.43
VRDM	4.17	0

We simulated 10,000 trials and implemented divisive suppression between the three populations of the following form:

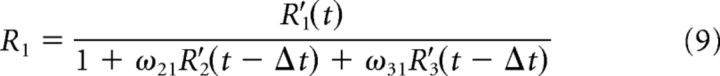where R′ and R denote the unsuppressed and suppressed responses, respectively, of the population indicated by the subscript, and ω_ij is the weight of the influence of the i^th population on the j^th. The suppressed responses at each time point (t) was computed based on the unsuppressed responses in the time window preceding it by Δt = 10 ms.

We first estimated the suppression of two target populations on each other (ω_T1T2 and ω_T2T1) from the peak and steady-state responses of the neurons to the appearance of a target in their RF. We then estimated the weight of suppressive influence of the RDM-in-RF population on the Target-in-RF populations (ω_DTx, x ∈ {1, 2}) using the firing rates at the trough of the response dip following the onset of RDM (see Fig. 7F, arrow) (Bollimunta and Ditterich, 2012). The influences of the two Target-in-RF populations on the RDM-in-RF population ω_TxD were adjusted around ω_DTx to mimic the observed separation in mean responses of the RDM-in-RF population to the two directions of motion. Such asymmetry of the influence of the two Target-in-RF populations might arise from the different spatial relationship they might have with the RDM-in-RF population. Similar asymmetries are likely for the other pairs of ω, too, but we set them to be equal here to simplify the model. We used the weights of suppression to estimate the underlying unsuppressed mean responses of each of the populations (see Fig. 7B,C).

In the parallel diffusion model, we implemented drift diffusion dynamics in the RDM-in-RF population as well as in the Target-in-RF population, and the populations had no suppressive interactions (see Fig. 9). The drift component in the RDM-in-RF population (K in Eq. 8) was set to mimic the observed separation of responses to the two directions of motion in the data (see Fig. 7G). The scaling factor for the variance of the diffusion component (α in Eq. 8) was adjusted to mimic the observed slope of the variance of the responses in the RDM-in-RF configuration (see Fig. 5A, green curve). Because of the absence of divisive interactions in this model, K and α for the Target-in-RF populations were recomputed to bring them in agreement with the data (Table 1).

Figure 9.

Alternative model with the RDM-in-RF population showing drift diffusion dynamics. This model assumes that there is no interaction between the RDM-in-RF neurons and the Target-in-RF neurons. A, B, Responses of model neurons (similar to Figure 7B, C, respectively). C–H, Variance and autocorrelation in the model and the data (conventions as in Figure 8A–F, respectively).

Up to here, all parameters were established from the neural data, allowing both models to approximate the mean responses in the data. To compare how well the two models can account for the pattern of autocorrelation in the data, we needed to consider other possible sources of variance and autocorrelation. In both models, the variance of the nondirectional sensory response of the RDM-in-RF populations was incorporated as a free parameter V_RDM. This parameter was constrained to not exceed the variance observed at the peak of the sensory neural response in the RDM-in-RF configuration. For the divisive suppression model, our hypothesis is that the noisiness of the suppression causes the autocorrelation pattern of the RDM-in-RF population to deviate from theoretical predictions. We instantiated this noisy process by corrupting the interaction signals so that they were not perfect replicas of the responses of the three populations in the model (see Fig. 7B,C, insets). This noise term was proportional to the square root of the response. We set the scaling term γ = 5 to represent a modest amount of noise (R² = 0.81 for the diffusion paths and their corrupted versions).

We attempted to achieve the best possible fit to the 30 correlations observed in the data in the two configurations (15 unique values each for the Target-in-RF and RDM-in-RF configuration) under each of the models. The models give rise to predicted correlations in the Target-in-RF and RDM-in-RF populations (varying with the free parameter V_RDM). As above, we allow for uncertainty in the PPV in the data (ϕ in Eq. 6). So we compute the correlations in the neural data with two additional degrees of freedom (parameters, ϕ_RDM and ϕ_Tar for the RDM-in-RF and Target-in-RF configurations, respectively). We estimated the set of parameters that maximized the log likelihood (L̂) of the 30 correlations in the data (Fisher z-transformed) under the model predictions. It was not possible to fit γ and ϕ_RDM simultaneously without imposing additional constraints (e.g., ϕ_RDM = ϕ_Tar). Instead, we fixed γ to establish a modest perturbation of the interaction signals, as noted above. This is the model illustrated in Figures 7 and 8 (parameters in Table 1). We compared models using the difference in Bayesian Information Criterion (BIC = − 2L̂ + k ln(n), where k is the number of free parameters and n is the number of data points). We explored a range of γ to confirm that the suppression model is favored even with subtle noise perturbation (e.g., ΔBIC > 100 for γ = 1, R² = 0.99). BICs were calculated by conservatively assuming 4 df for the divisive suppression model (ϕ_RDM, ϕ_Tar, γ, V_RDM) and just 2 df for the parallel diffusion model (ϕ_RDM, ϕ_Tar) because γ should be regarded as a free parameter and the best fit of the parallel diffusion model assigns V_RDM ≈ 0. We also fit to a model with γ as a free parameter under the constraint ϕ_RDM = ϕ_Tar. This implementation also favors the suppressive interaction model (ΔBIC > 6 × 10³; best fitting γ = 8.2). The implementation of V_RDM introduces autocorrelation of the rate that spans the duration of the analysis epoch (360 ms). Parametrization of the sensory responses with exponentially decreasing autocorrelation did not provide a significantly better fit to the data in either model.

Figure 8.

Variance and correlation of the simulated responses shown in Figure 7. A, Variance as a function of time in two of the simulated suppressed populations (D and T₁ for trials with motion supporting T₁ choice). B, Autocorrelation in the simulated suppressed Target-in-RF population T₁ (conventions as in Figure 6B). C, Deviation of the autocorrelation in the model from the autocorrelation estimated from the data in the Target-in-RF configuration. D, E, Same as B, C for the RDM-in-RF population. F, Comparison of correlation values along the top row (solid lines) and first juxtadiagonal (dashed lines) between the model (B, D) and the data. Circles represent the correlation estimated from data. Filled circles represent the values along the top row. Open circles represent the values along the juxtadiagonal. Gray lines indicate the correlation expected from a diffusion process.

Results

We recorded from 49 well-isolated single neurons in area LIP from 2 monkeys (28 neurons from Monkey N and 21 neurons from Monkey B) as they decided the net direction of a noisy RDM stimulus. On each trial, two choice targets indicated the two directions to be discriminated (e.g., up vs down). The monkeys reported their decision by making a saccade to the choice target along the perceived direction of motion. They were free to indicate their decision whenever ready, thus providing a measure of RT. The monkeys performed the task with the RDM and the targets arranged in two configurations (Fig. 1). In the Target-in-RF configuration, one of the choice targets was placed in the RF of the neuron under study. In the RDM-in-RF configuration, the RDM was placed in the RF. In this way, we obtained data from the same LIP neuron when it belonged either to the pool representing the RDM stimulus or to one of the two pools representing the choice targets.

Figure 1-1

Linear stimulus configuration. In 16 recording sessions, the targets and RDM were placed in a linear arrangement. Conventions are as in Figure 1. Download Figure 1-1, EPS file ^{(2.3MB, eps)}

We first establish that the animals integrate motion information over 100s of milliseconds to make their choices in both task configurations. This prolonged deliberation time offers a window in which to interrogate how the neural responses relate to the process of decision formation. We show that the firing rates of neurons represent the state of the accumulated evidence only when the neurons belong to a pool representing the targets.

Behavior in the two task configurations

The behavior of both monkeys exhibited an orderly dependence on the strength of the RDM in both task configurations. They took longer to report their decision when the motion strength was weaker (Fig. 2A–D), and their decisions were less accurate (Fig. 2E–H). The systematic relationship between RT and accuracy is well described by the accumulation of noisy evidence to a threshold, which determines both the time it takes to make a decision and which alternative the monkey chooses (Gold and Shadlen, 2002; Smith and Ratcliff, 2004). We support this assertion by fitting the RTs to a bounded evidence accumulation model and then using the fitted parameters to predict the choices (Shadlen and Kiani, 2013; Kang et al., 2017). Specifically, the curves in the top row of Figure 2 are fits to a parsimonious symmetrically bounded drift diffusion model, which uses four parameters to account for the effect of motion strength on the mean RT for correct choices (Eq. 1; see Materials and Methods). Two of the parameters (the bound height, ±B; and the sensitivity coefficient, κ) establish predictions for the proportion of choices as a function of motion strength (Eq. 2). Figure 2 (bottom, dashed curves) depicts these predictions. They are only slightly worse than logistic fits to the choice data themselves (gray curves), which are unconstrained by RT. To quantify the “goodness of prediction,” we compared the model predictions to those obtained from random perturbations of the mean RTs, which preserve their orderly dependence on motion strength. Small perturbations of the RT (mean 7.5%, range 1%–12% or equivalently, mean 48 ms, range 7–73 ms) are sufficient to produce substantially poorer predictions (p < 0.01). The fidelity of the predictions supports the assertion that the choices result from the same process of bounded evidence accumulation that explains the decision times. Importantly, this conclusion holds for both stimulus configurations.

Figure 2-1

Simultaneous fit of RT and choice with a diffusion-to-bound model. The probability of choosing the positive direction target (A,B) and the mean RTs (C,D) are plotted as a function of motion strength and direction (indicated by sign of coherence; see Methods) for the two monkeys in the two stimulus configurations. The curves are fits to the data from a diffusion-to-bound model with nonstationary bounds (see Methods). The fit parameters are shown in Table 1. E,F: Mean decision times (solid curves) derived from the model fits, plotted as a function of motion strength. Shading is ±1 S.E. Download Figure 2-1, EPS file ^{(2.7MB, eps)}

From this exercise, we conclude that the decision times (i.e., RT − the nondecision time) estimated from diffusion model fits can be used to identify an epoch in which noisy evidence was integrated to make the decision. To obtain more refined estimates of the integration times for the different task configurations, we fit a more elaborate bounded diffusion model (Fig. 2-1; for details, see Materials and Methods; for fit parameters, see Table 2). The small differences in RTs between the two configurations for Monkey N were accounted for by the nondecision time parameter. For Monkey B, a combination of increased sensitivity and decreased bound height contributed to the faster RTs in the RDM-in-RF configuration. Importantly, the fits established that both monkeys integrated evidence over hundreds of milliseconds in each configuration.

Table 2.

Bounded diffusion model best fit parameter values (± SE)

Parameter	Monkey N (Target-in-RF)	Monkey N (RDM-in-RF)	Monkey B (Target-in-RF)	Monkey B (RDM-in-RF)
κ	16.05 ± 0.38	13.86 ± 0.44	9.66 ± 0.39	12.00 ± 0.70
B0	0.72 ± 0.02	0.78 ± 0.02	0.52 ± 0.02	0.47 ± 0.04
Bdel	0.01 ± 0.00	0.00 ± 0.01	0.02 ± 0.01	0.02 ± 0.01
B2	0.67 ± 0.09	0.97 ± 0.08	1.16 ± 0.21	1.26 ± 0.38
tnd1	0.34 ± 0.01	0.29 ± 0.01	0.41 ± 0.01	0.45 ± 0.01
σtnd1	0.13 ± 0.00	0.11 ± 0.00	0.07 ± 0.00	0.08 ± 0.00
tnd2	0.38 ± 0.01	0.32 ± 0.01	0.47 ± 0.01	0.43 ± 0.01
σtnd2	0.12 ± 0.00	0.12 ± 0.00	0.07 ± 0.00	0.06 ± 0.00
C0	0.00 ± 0.00	0.00 ± 0.00	−0.02 ± 0.00	0.02 ± 0.01

LIP neuronal responses in the two task configurations

Neurons in area LIP can exhibit sensory-, memory-, and saccade-related responses (Gnadt and Andersen, 1988; Barash et al., 1991a). For example, in a task where a monkey must remember a visually cued location and make a delayed saccade to it, LIP neurons can show the following: (1) a short latency response to the visual cue if it appears in the RF, (2) a persistently elevated response during the delay period, and (3) a burst of activity preceding a saccade to the remembered location. Not all LIP neurons exhibit all three types of responses. Because our goal was to compare the decision-related activity in the same neurons when they belonged to the pool representing the sensory information and when they belonged to the pool involved in planning the motor action, we recorded from neurons that responded to visual stimuli in their RF and also showed persistent activity in association with saccadic motor planning. Each of our neurons increased their responses above baseline to the appearance of a visual stimulus in their RF (responses after RDM onset: median 5 SD above baseline, interquartile range 2.7–7.7). The strength of this sensory response was comparable with the highest responses observed during the delay period (median 4.3 SD above baseline, interquartile range 2.3–9.2, p = 0.49, Kolmogorov–Smirnov test).

During the direction discrimination epoch, the pattern of activity of the recorded neurons varied according to which pool they belonged. When the neurons belonged to a pool with one of the targets in the RF, the responses largely recapitulated observations from earlier reports (e.g., Roitman and Shadlen, 2002; Churchland et al., 2008). Figure 3 shows the average population response of all neurons in the Target-in-RF configuration, aligned to either the onset of RDM (Fig. 3A) or to the saccade (Fig. 3B). The response was elevated before the onset of the RDM reflecting the presence of a choice target in the RF of the neurons. Following motion onset, there was a stereotyped dip in activity before the responses began to separate by motion strength. The evolution, beginning ∼180 ms after stimulus onset, is best appreciated in the detrended responses (Fig. 3A, inset). These features and those next described were evident in both of the monkeys, shown individually in Fig. 3-1 and Fig. 3-2.

Figure 3-1

Population responses of neurons in individual animals. Neural responses that were shown in Figure 3, panels A-D and F plotted from data pooled separately for each individual monkey. Download Figure 3-1, EPS file ^{(4.7MB, eps)}

Figure 3-2

Population responses of neurons in individual animals. Neural responses that were shown in Figure 3, panels A-D and F plotted from data pooled separately for each individual monkey. Download Figure 3-2, EPS file ^{(4.8MB, eps)}

The same neurons also exhibited differential responses to the two directions of motion being discriminated when they belonged to the pool representing the RDM. To combine responses across the population in this task configuration, we identified the preferred direction of motion for each neuron as the one that elicited the greater response. Figure 3C, D shows the responses of the population averaged after sorting by each neuron's preferred direction. After an initial rise in activity due to the appearance of the RDM in the RF, the responses exhibited a direction-dependent separation. Such modulation of LIP neuronal responses by motion direction has been previously reported in naive monkeys (Fanini and Assad, 2009). However, the direction-dependent modulation was slightly stronger in our neural population (median DI: 0.11 and 0.09, respectively for our neurons and those reported by Fanini and Assad, 2009; p = 0.06 rank-sum test; see Fig. 3E). We also measured the degree of overlap between the responses to the two directions of motion using an area under ROC metric (see Materials and Methods). The mean area under ROC of our population (0.71) is comparable with the degree of overlap reported for monkeys performing direction categorization tasks (0.72–0.74) (Swaminathan and Freedman, 2012, their Fig. 3A). Our neural population displays this degree of direction selectivity at a lower motion strength (51.2% coherence) than that used in the two studies being compared with (100% coherence). This result is consistent with previous reports of stronger directional selectivity in LIP neurons of monkeys trained on tasks that rely on direction discrimination (Sarma et al., 2016).

We quantified the time course of the evolution of direction selectivity at the highest motion strength (Fig. 3F) using an ROC metric (see Materials and Methods). The responses to the two motion directions were significantly different starting 190 ms after the onset of dot stimulus (p < 0.05 on Wilcoxon rank sum test). This is much later than the ∼50 ms latency of direction selectivity observed in naive monkeys (Fanini and Assad, 2009). This is also later than the ∼100 ms latency for direction category selectivity reported in monkeys trained to categorize sets of motion directions (Swaminathan and Freedman, 2012). As discussed below, the long latency in our neuronal pool may be an indication that the directional responses we observed in the RDM-in-RF configuration arise through a different mechanism than the direction- and category-selective responses previously reported in LIP.

The latency in the RDM-in-RF configuration lagged the direction selectivity seen in the same neurons in the Target-in-RF configuration (180 ms, p < 10⁻³, bootstrap analysis). However, the similarity of the latencies suggests that the RDM-in-RF population might also reflect the formation of the decision, as the Target-in-RF population has been shown to do (Roitman and Shadlen, 2002; Churchland et al., 2008). Consistent with this possibility, the rise and decline of neural activity depend on the strength of the RDM (Fig. 3C, inset), albeit with a smaller dynamic range compared with responses in the Target-in-RF configuration. In this configuration, directions are sorted based on the preferred direction of each neuron. The coherence-dependent ordering of responses could have been accentuated by this post hoc procedure. To quantify this coherence dependence, for each neuron and motion strength, we estimated the slope of the responses (buildup rate) in a 200 ms epoch beginning at the time of response separation as identified in the preceding analysis. We then characterized the relationship between motion strength and buildup rates separately for the preferred and nonpreferred directions of motion (Fig. 3G). The buildup rates of neurons in the Target-in-RF configuration showed a linear dependence on motion strength both when the motion direction was toward the RF (1.5 ± 0.2 spikes per s² per 1% coherence, p < 10⁻⁹) and when the motion was away from the RF (−1.2 ± 0.2, p < 10⁻⁵). A similar trend was observed in the RDM-in-RF configuration. However, this relationship was significant only for the nonpreferred direction of motion (−0.7 ± 0.2 spikes per s² per 1% coherence, p < 0.002). For the preferred direction, the buildup rates increased with coherence but not significantly so (0.6 ± 0.4 spikes per s² per 1% coherence, p = 0.13). In both configurations, these trends were preserved, even when the highest motion strength trials were excluded. Thus, neuronal pools in LIP representing the saccade targets and the RDM both differentiate the discriminanda during an epoch coinciding with decision formation. The buildup of neural activity depended on the strength of the stimulus in both populations, but this dependence was weaker when the RDM was in the RF.

We also compared the responses at the end of the decision process for the two task configurations (Fig. 3B,D). When the monkey chose the target in the neuron's RF, the responses appear to coalesce to a common firing rate just before the saccade, regardless of motion strength (Fig. 3B, solid curves), as shown previously (Roitman and Shadlen, 2002; Churchland et al., 2008). This pattern is thought to reflect a threshold level detected by another circuit to terminate the decision (Hanes and Schall, 1996; Mazurek et al., 2003; Hanks et al., 2014). When the same neurons contained the RDM in their RF, the responses to the different coherences remained separated until the saccade, and this held for either choice (Fig. 3D). This was also the case when the RF contained the unchosen target (Fig. 3B, dashed curves). Thus, only the responses of the pool representing the target chosen by the animal contains a possible neural signature of decision termination. In the ensuing sections, we support this qualitative observation with other lines of evidence that show that this pool alone signals decision termination and the time taken to reach it.

Correlation between neural responses and behavior

We examined whether the neural responses in the two stimulus configurations were predictive of the monkey's decisions. Specifically, we asked whether the trial to trial variation in the responses correlates with the trial to trial variation in the monkey's choice behavior. To test this for each neuron, we counted the spikes in a 200-ms-long epoch ending 100 ms before saccade initiation on each trial and incorporated this count in a logistic regression model of choice (GLM; see Materials and Methods). To facilitate comparison across the two stimulus configurations, we standardized the responses across trials of each configuration. We included the strength and direction of the presented stimulus as confounders, thus asking whether the variation in neural response tells us more about the upcoming choice than can be ascertained from the stimulus itself. This was indeed the case for 61.2% of cells in the Target-in-RF configuration and for 35.4% of cells in the RDM-in-RF configuration (30 of 49 and 17 of 48 cells, respectively; Eq. 5, H₀: β₂ = 0; p < 0.05; Fig. 4A). The leverage of the neural activity on choice was significantly stronger in the Target-in-RF configuration (p = 0.005, signed rank test).

In a complementary analysis, we assessed whether the neural responses on ambiguous trials (0% motion coherence) differed according to the eventual choice of the animal. We computed CP (Britten et al., 1996), a nonparametric statistic that quantifies the overlap between the distributions of responses of the neuron accompanying the two choices (see Materials and Methods). A CP of 0.5 indicates that the two distributions are completely overlapping and therefore uninformative about the ensuing choice. At the single neuron level, CP of 32.4% and 25.8% of the neurons was significantly different from 0.5 in the Target-in-RF and RDM-in-RF configurations, respectively (12 of 37 and 8 of 31 cells with at least 10 trials at 0% coherence, respectively, p < 0.05, permutation test). In both stimulus configurations, the mean CP of the neuronal population was significantly >0.5 (Fig. 4B, population mean ± SEM of 0.66 ± 0.03 and 0.59 ± 0.04 for Target-in-RF and RDM-in-RF, respectively; p < 10⁻⁵ and p < 0.02 on t test). For comparison between the two configurations, we calculated “grand” CP from standardized responses of all neurons on the 0% coherence trials (see Materials and Methods) (Britten et al., 1996). This CP was significantly stronger in the Target-in-RF configuration (0.65 vs 0.56, p < 10⁻³, permutation test). From the analyses of CP and firing rate leverage on choice (Fig. 4A,B), we adduce that LIP neurons responsive to both the RDM and the choice targets are informative about the choice, but it is the latter set of neurons (Target-in-RF) that covary more strongly with choice.

Finally, because the neurons exhibit time-dependent changes in their activity in both stimulus configurations, we asked whether the variation of the buildup rates were predictive of the variation in the RTs on a trial-by-trial basis. We used the trials in which the monkey chose the target in the RF or the target consistent with the direction of motion preferred by the neuron (RDM-in-RF). For a majority of neurons recorded in the Target-in-RF configuration (36 of 49), the RTs were inversely correlated with the slope of the neural responses (population mean: −0.08, p < 0.01). In the RDM-in-RF configuration, the correlation was not significantly different from 0 (mean: 0.03, p > 0.33) (Fig. 4C) and significantly weaker than the correlations seen in the Target-in-RF configuration (p < 0.01, Kolmogorov–Smirnov test). This comparison suggests that only the pool of neurons that contain the chosen target in their RF carries information about the time the animal will take to report its decision.

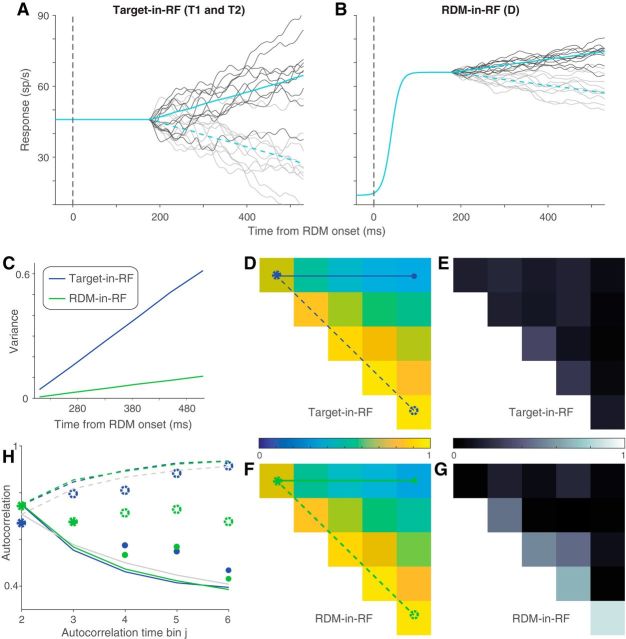
Signatures of noisy evidence accumulation in the response variance

We also wished to ascertain whether the responses on single trials conform to the expectations of noisy evidence accumulation. If so, the variance of the firing rates across trials should increase linearly as a function of time (i.e., the number of samples accumulated). Also, the autocorrelation between firing rates at different times within a trial should conform to the pattern associated with the cumulative sum of random numbers. Such correlation should decay as a function of separation in time from the first sample and increase for equidistant samples as a function of time from the onset of accumulation (see Materials and Methods). We used the method developed by de Lafuente et al. (2015), based on Churchland et al. (2011), to estimate these quantities.

The variance and autocorrelation patterns varied markedly based on whether the neurons contained the target or the RDM in their RF. In the Target-in-RF configuration, the variance increased linearly with time during the same epoch that the mean firing rates seemed to reflect the integration of evidence (Fig. 5A, shaded region). In the RDM-in-RF configuration, the rise in variance was significantly weaker (p < 10⁻¹⁰, bootstrap analysis). Also, the observed autocorrelation matrix for the responses in the Target-in-RF configuration (Fig. 6B,D,F) resembled the theoretical prediction (R² = 0.88). In contrast, the pattern of autocorrelations (Fig. 6C,E,G) for the responses in the RDM-in-RF configuration diverged markedly from the predicted pattern (R² = 0.2). A bootstrap analysis confirmed that the difference in R² values between the two configurations was statistically reliable (p < 10⁻¹⁰; see Materials and Methods). Later, we show that the deviation of the autocorrelation pattern from theoretical prediction cannot be attributed to a muted drift diffusion process unfolding on the background of a strong nondirectional sensory response (see Fig. 9).

The variance of the neural response also affords a more refined examination of the mechanism of decision termination. The firing rate averages in Figure 3B suggest the possibility that decisions terminate when the firing rate of the neurons with the chosen target in their RF reach a threshold. A more stringent test of a threshold is that, even for the same motion strength, the variance of the neural response should approach a minimum just before the saccade. Indeed, we observed a precipitous decline in the variance in the ∼100 ms preceding the saccade for the neuronal pool with the chosen target in the RF (Fig. 5B, solid blue line). The variance in the time bin preceding the saccade was significantly lower than the variance in its prior time bin (p < 0.01, t test). This decline in variance was more precipitous than that seen for the other three conditions shown in Figure 5B (ANOVA, p < 0.03; see Materials and Methods).

Together, the analyses of time-dependent variance and autocorrelation reveal that neurons in the Target-in-RF configuration exhibit firing rate patterns consistent with a process that represents the running sum of noisy samples of evidence to a criterion level. The analyses complement the observations made earlier on the mean firing rates by demonstrating conformance with the second-order statistics of diffusion to a bound. These features were less apparent when the same neurons were studied in the RDM-in-RF configuration. This neural population does not appear to represent the accumulation of the noisy evidence that supports the monkey's decisions. They reflect the direction of motion during the time course of decision formation but not the state of the accumulated evidence that can be used to terminate the decision process. We next consider a possible account of their pattern of activity.

A model of interaction between populations

How could the responses of neurons with the RDM in their RF correlate with the decision outcome without representing the process of evidence accumulation? One possibility is that the weaker decision-related signals observed in the population with the RDM in their RF are inherited from the populations that have the choice targets in their RF and are involved in the accumulation process. It has been shown that responses of LIP neurons to visual stimuli are suppressed by concurrently presented visual stimuli when they are well outside the RF (Balan et al., 2008; Churchland et al., 2008), even by as much as 50° visual angle (Falkner et al., 2010; Louie et al., 2011). An asymmetrical influence of the two Target-in-RF populations could lead to the appearance of direction selectivity and a correlation with the animal's choices in the RDM-in-RF population. Moreover, the noise added through this additional step could explain the divergence of the variance and autocorrelation of the RDM-in-RF population from the theoretical predictions of a diffusion process. Additionally, such an extra step could account for the timing of direction selectivity in the RDM-in-RF population, which lags slightly behind that of the Target-in-RF population.

To evaluate the plausibility of this idea, we simulated the responses of three neural populations (one representing the motion stimulus and two representing the choice targets) during the motion viewing epoch (Fig. 7A). In the model, the RDM-in-RF population receives direct excitation from the visual representation of the dynamic random dots. This direct excitation furnishes a constant firing rate that varies from trial to trial, but importantly, is not direction-selective (Fig. 7C). The two Target-in-RF populations start off at a steady firing rate, simulating the steady-state sensory response to the target already present in the RF. The responses then follow drift diffusion dynamics starting at 180 ms, simulating evidence accumulation. The drift rate was set to be directly or inversely proportional to motion coherence for the populations representing the correct and incorrect targets, respectively (Fig. 7B).

The three populations interact through divisive suppression (Sceniak et al., 2001; Carandini and Heeger, 2011; Louie et al., 2011) at each time point, parameterized by the ω terms in Equation 9 (see Materials and Methods). We set these parameters to approximate the observed neural responses to the 25.6% motion strength RDM (illustrated in Fig. 7F,G). We assumed that the early dip in the response of the Target-in-RF neurons (Fig. 7F, arrow) was caused by suppression from the neurons activated by the appearance of the RDM (ω_DT1 = ω_DT2) (Bollimunta and Ditterich, 2012). The suppression between the two Target-in-RF pools (ω_T1T2 = ω_T2T1) was estimated from the onset and steady-state responses after the appearance of the target in the RF. Suppression of the RDM-in-RF pool from the Target-in-RF pools (ω_T1D and ω_T2D) was adjusted around ω_DT to approximate the separation in firing rate traces shown in Figure 7G (see Materials and Methods). Such asymmetric influence of the two Target-in-RF populations might arise from differences in their spatial relationship (neuronal connectivity) with the RDM-in-RF population. These adjustments were sufficient to mimic the observed mean responses of the neural population in our simulations (Fig. 7D,E). In addition, we assumed that the suppressive interaction signals were corrupted by a small amount of noise (see Materials and Methods). Importantly, according to the model, the direction selectivity of the RDM-in-RF population is derived solely from the suppressive inputs from the Target-in-RF populations.

This simple model reproduced the main features of our results (Fig. 8). After the implementation of suppression, the Target-in-RF population retained the time course of the variance and the pattern of autocorrelation expected of a diffusion process. Notably, the variance and autocorrelation in the RDM-in-RF population also conformed to the patterns in the neural data: (1) the attenuated increase in variance as a function of time; and (2) the divergence in the pattern of autocorrelation from the theoretical prediction of diffusion. We also considered an alternative model in which the RDM-in-RF population itself represents an attenuated evidence accumulation signal in parallel with the Target-in-RF populations (Fig. 9). To do this, we removed the lateral interactions and implemented the accumulation identically to the Target-in-RF population, but matching the observed firing rate dynamics and variance in the RDM-in-RF data (displayed in Figs. 7G and 5A, respectively). This model was significantly worse in accounting for the pattern of autocorrelation observed in the data (ΔBIC > 5 × 10³). We thus favor the model with divisive suppression, which accounts for the presence of choice related activity in the RDM-in-RF population and the absence of clear signs of noisy evidence accumulation.

Discussion

We compared decision-related activity in the sensory and motor-planning responses of LIP neurons. We conclude that the process of evidence accumulation leading to choice is revealed primarily in motor preparatory responses. The sensory responses exhibit a weak relationship with the animal's behavior, but our results and simulations suggest that this relationship is likely inherited from the motor preparatory responses. We first discuss our results in the context of previous studies of area LIP and then consider their implication on the broader question of routing of information in the cortex.

Properties of neural responses in area LIP

There has been a long debate about the relative importance of sensory salience-related signals and saccade preparatory signals in area LIP (Bushnell et al., 1981; Barash et al., 1991a; Colby and Goldberg, 1999; Andersen and Buneo, 2002). Many neurons show inherent selectivity for visual features, such as direction and shape, even in monkeys that have never been trained to use such information (Sereno and Maunsell, 1998; Fanini and Assad, 2009). In addition, training induces stimulus selectivity that can be distinct from intrinsic selectivity (Toth and Assad, 2002; Sarma et al., 2016). LIP neurons also carry a rich representation of saccade plans. They display spatially selective persistent activity when the animal plans a saccade to a previously instructed, but no longer visible target (Gnadt and Andersen, 1988; Barash et al., 1991a). This persistent activity is dissociable from the sensory response evoked by the target (Mazzoni et al., 1996) and can encode other factors that bear on the saccade plan, such as the probability that a saccade will be instructed (Janssen and Shadlen, 2005) and the expected reward (Platt and Glimcher, 1999; Sugrue et al., 2004). The richness of saccadic planning is particularly evident in perceptual decision-making tasks, where the neuronal activity continually tracks the current state of the evidence for choosing the target in the neuron's RF (Mazurek et al., 2003; Bollimunta et al., 2012).

By recording from the same LIP neurons when they belonged to the population representing either the RDM or a choice target, we could directly compare the sensory- and saccade-related responses. While both populations modulated their activity in accordance with the strength and direction of the RDM, there were important differences. This modulation was more intense when a choice target was in the RF. While the RDM elicited a strong response when it was in the RF, the dependence on direction and stimulus strength was weaker. This is unlikely to be explained by saturation of the response because the same neurons attained higher firing rates before saccade onset when the target was in the RF (compare Fig. 3B and Fig. 3C). Further, the variance and autocorrelation patterns of the neuronal responses were consistent with the predictions of noisy evidence accumulation only when the neurons contained a target in their RF. Finally, a neural correlate of decision termination was only apparent when a target was in the RF.

Although we have used the term “sensory” to describe the direction-selective responses of neurons with the RDM in their RF, the gradual buildup of the firing rates of these neurons (Fig. 3C) differed from the constant firing rates reported in naive monkeys (Fanini and Assad, 2009). Moreover, it is known that the selectivity of LIP neurons to features of visual stimuli is mutable and is influenced by the training history of the animal and/or task demands (Toth and Assad, 2002; Sarma et al., 2016). We suspect that the responses are not sensory in the way one would characterize the responses of neurons in visual areas MT/MST or even the visual responses of LIP neurons to transient stimuli (e.g., targets) as they were remarkably slow, emerging 190 ms after stimulus onset (at the highest coherence). This is far later than the ∼50 ms latency of direction selectivity (Fanini and Assad, 2009) and the ∼100 ms latency for direction-category selectivity (Swaminathan and Freedman, 2012), and it is longer than the 180 ms latency of decision-related signals observed in the neuronal pool representing the targets.

Together, these considerations suggest that the neuronal pool representing the RDM inherits its direction and choice-related signals from the neuronal pools representing the targets. We demonstrated that a model of lateral interactions serving the general purpose of gain control (Carandini and Heeger, 2011) is sufficient to produce these effects. Such lateral interactions are well established in upstream visual areas (Schein and Desimone, 1990; Shushruth et al., 2009; Hunter and Born, 2011). In LIP, lateral interactions are thought to mediate the suppressive effect of visual stimuli presented outside a neuron's RF (Balan et al., 2008; Churchland et al., 2008; Zhang et al., 2017), even from distances >50° away from the RF (Falkner et al., 2010; Louie et al., 2011). A limitation of the present study is that we do not have access to two classes of neurons on the same trials. Recording simultaneously from neurons that represent the RDM and at least one choice target would allow for a direct test of the lateral interactions that we modeled. For example, we would predict that the weaker leverage of the RDM-in-RF neurons would be explained away (i.e., mediated) by inclusion of Target-in-RF responses in the same GLM.

Routing of information in cortex

We do not know how the momentary evidence represented by populations of direction-selective neurons in the visual cortex makes its way specifically to the target-representing neurons in LIP. There are projections from areas MT and MST to area LIP, but it is difficult to reconcile this direct pathway with the long latency of the decision-related activity in LIP. The delay of the decision-related responses relative to the latency of the visual responses in LIP (∼50 ms) suggests a role for some form of memory buffer and/or a multisynaptic chain through which decision-relevant information must pass before reaching the saccade planning neurons in LIP. This is one reason to suspect that apparently simple perceptual decisions may share similarities with more complex decisions that derive evidence from memory and other evaluations (Shadlen and Shohamy, 2016).

We must emphasize that area LIP is not the only region that receives decision-pertinent signals in this task. Other areas involved in the planning of eye movements, such as FEF/area 46, caudate nucleus, and superior colliculus, also have access to such input (Horwitz and Newsome, 1999; Kim and Shadlen, 1999; Ding and Gold, 2010, 2012; Mante et al., 2013). However, the decision-related activity in these areas arises with comparable latencies, so they do not furnish an explanation for the long latency in LIP. We favor the idea that the latency is necessitated by limitations in connectivity between the many possible sources of evidence bearing on the salience of an item and the neurons that represent such items as potential affordances to the motor system. This connectivity constraint might necessitate active routing (Olshausen et al., 1993; Kastner and Pinsk, 2004), although this process is poorly understood.

In monkeys trained to assign motion directions to arbitrary categories, LIP neurons have been shown to reflect the learnt categorical identities (Freedman and Assad, 2006; Swaminathan and Freedman, 2012). Before our experiment, it seemed possible that the neurons with the RDM in RF could have manifested such a categorical response to inform the Target-in-RF neurons of the decision. Our findings render this unlikely. The RDM-in-RF neurons do not exhibit signs of evidence accumulation, and their directional responses likely arise as a consequence of the inheritance of a decision variable represented by the Target-in-RF neurons. Thus, we suspect the directional responses of the RDM-in-RF neurons differ from category identity signals, but we are not proposing an account of their features. There are many differences in task, training, and the signals themselves (e.g., latency), which could explain the differences between category identity responses and the directional responses of our RDM-in-RF configuration.

If the neurons with the RDM in the RF in our task do not represent the evolving evidence, a natural question is what do these neurons signify? One obvious possibility is that they simply represent an object that might attract the gaze, as transient lights are wont to do. Another possibility is that they represent the focus of spatial attention (Colby and Goldberg, 1999). However, this focus should be initially on the RDM and then either remain stationary through the decision or gradually give way to the chosen target. This is inconsistent with the dynamics observed in our data, which look like a muted version of the decision-related signals exhibited by neurons with a choice target in the RF. The same objection applies to the proposal that these neurons represent the salience of the RDM (Bisley and Goldberg, 2010). A more speculative idea is that the neurons that contain the RDM in their RF confer information bearing on the spatial origins of the evidence: that is, they help to bind the location of the thing we are deciding about to the decision itself, which is about what to do.